Abstract
When converters are connected in parallel, a system with some benefits, including modularity and redundancy, is obtained. However, in these circumstances, circulating currents can appear that produce some adverse effects. In this work, a study of the low-frequency circulating currents that appear in three-phase inverters connected in parallel is performed. The study is focused on the effects produced by the parameter mismatch, namely inductance mismatches, power imbalance, and the use of different pulse with modulation (PWM) techniques. The nature of the circulating current produced by each of these factors were analyzed separately. Both simulation and experimental results are shown, which were obtained using a three-phase 10-kW prototype composed of two 5-kW inverters connected in parallel.
1. Introduction
The connection in parallel of converters has many advantages, such as modularity, better thermal management, higher power capacity, redundancy, and easy maintenance [1]. When inverters have a modular implementation, a redundant system is obtained, in which a module is easy to replace in case of failure [2], and the active modules can provide a fraction of the nominal power of the overall system. Moreover, the power of a system can be increased by adding new modules [3]. Another benefit of paralleling converters is that they allow for sharing of the current among the modules, so low-power devices that have a higher switching frequency and reduced inductor sizes can be used [4]. Finally, in some applications, such as high-power central inverters for photovoltaic farms, the connection in parallel of inverters that manage a fraction of the full power allows for the connection/disconnection of parallel modules, increasing the efficiency in low power conditions [5,6].
1.1. Potential Applications of Parallel Inverters
Due to the large number of advantages resulting from the parallel connection of inverters, this configuration has been extended to many applications, such as those described below.
1.1.1. Active Front-End
In recent years, power electronics have had a significant impact on renewable energy and the motor drive industry. However, the penetration of non-linear elements pollutes the grid, increasing the distortion of current and voltage waveforms (total harmonic distortion; THD) [7]. Therefore, it is a goal to reduce the distortion of the currents (THDi) injected into the grid. The Active Front End is currently a standard solution to reduce the THDi of the grid current in motor drives, grid energy storage systems, electrical vehicle chargers, etc. The Active Front End (AFE) is a controllable rectifier that has advantages such as a unity power factor and very low THDi, and it provides bidirectional power flow between AC and DC power [8]. The use of parallel AFE converters has become more popular due to their low cost and expandability [9].
1.1.2. Photovoltaic Inverters
In the context of photovoltaic fields, many studies have considered the use of decentralized inverters connected to a single string [10]. The greatest benefit of using decentralized inverters is the large number of maximum power point (MPP) inputs in this type of system. However, decentralized topologies are less interesting for high-power applications due to their high cost. As an alternative, centralized inverters are often used for high-power applications since they offer a good compromise between cost and efficiency [11]. Moreover, the use of central inverters composed of parallel inverter modules that can be connected and disconnected depending on the power generation is usually considered, so the performance of the central inverter increases at low power levels. Transformerless inverters connected in parallel can be employed to obtain a less bulky and expensive system.
1.1.3. Interlinking Converters in Microgrids
Microgrids make it possible to integrate loads and renewable energy sources at the local level. This integration has some advantages, such as reduced greenhouse emissions, reliable operation, reduced transmission and distribution pressure on existing power systems, etc. [12]. Moreover, in this context, in which renewable energy generation systems, such as photovoltaic generation systems, are becoming increasingly common at the local level, having a hybrid microgrid allows for great energy savings by managing both DC and AC loads/sources in independent buses, avoiding double conversions from DC to AC and from AC to DC. The power deficits or surpluses on the DC and/or AC side can be managed through interlinking converters. These interlinking converters can be formed by several inverters connected in parallel, resulting in a modular system in which inverter modules can be added in the case of increasing the maximum required power to be transmitted [13]. The parallelization of inverters also increases the resilience of the system since, in the event of failure of one of the inverters, the power flow between the AC and DC buses can continue, albeit with reduced power.
1.2. The Problem of Circulating Currents and the Main Contribution of This Work
However, when the converters are connected in parallel, circulating currents appear that can produce undesirable effects in the system [14]. They are produced due to hardware mismatches (filter inductors, power delivered by each inverter), or differences in the control parameters, such as the modulators of the inverters connected in parallel [15]. These currents can produce adverse effects, such as current distortion, unbalanced load sharing between modules, conduction losses in the commutation devices, and low efficiency in the system [15,16]. Moreover, circulating currents can produce additional thermal stress in the case of unsymmetrical load conditions, leading to the overloading of one of the inverters [17].
Circulating currents can be divided into low-frequency and high-frequency components [18,19]. The high-frequency component exhibits harmonics near the switching frequency and its multiples, while the low-frequency component has harmonics near the fundamental frequency [20].
Some studies have proposed control techniques to reduce the circulating currents [21,22,23,24,25,26], but the origin and the nature of the problem have not been analyzed in detail in these works. Reference [27] studied the circulating currents produced by phase shifting between the pulse with modulation (PWM) carrier signals of two inverters connected in parallel. Reference [28] studied the effects that appear when the fundamental voltages produced by several inverters working in island mode have different phases and frequencies.
The main contribution of this paper is that it deepens the study of the circulation currents that appear among several inverters connected in parallel. To achieve this goal, the following factors are analyzed that have not been considered in previous papers: mismatching among the phase inductances of the same inverter due to the inductance tolerances, mismatching among the nominal inductance of all the inverters connected in parallel, the influence of the load factor, and the use of different modulation techniques among inverters. In addition, it is shown that only a third harmonic and its odd multiples appear in the circulating currents when the three-phase inverters connected in parallel are balanced, whereas components at the fundamental frequency and its odd multiples also appear in case of power unbalances among inverters. Both simulation and experimental results are reported to validate the study.
2. Low-Frequency Circulating Currents’ Nature
For the study of the circulating currents’ nature, a 10-kW three-phase system composed of two 5-kW inverters connected in parallel is considered. The inverters are connected to the grid through the point of common coupling (PCC), following Figure 1. The parameters of the inverters are summarized in Table 1. The grid filter is composed of an LCL configuration with capacitors Cf, damping resistances Rd, and single-phase inductors in the converter side La. A three-phase inductor Lb is shared by both inverters connected in parallel. The parameters ra and rb are the equivalent series resistance of inductors La and Lb, respectively. Mb defines the mutual inductance of the three-phase inductor. Note that La1 and La2 are pictured in Figure 1 since imbalances in La inductor are considered, but the value of ra is maintained in all cases. The dc-link capacitors are defined as Co. In this work, the AC voltage is set by the grid to 230 V phase-phase and 50 Hz, and the voltage in the DC bus is fixed to 500 V.
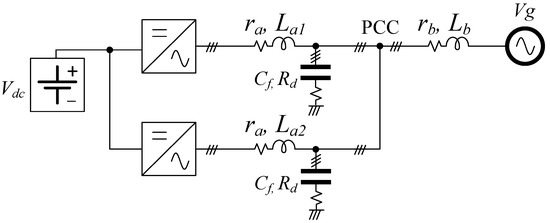
Figure 1.
One-line diagram of two three-phase inverters connected in parallel with LCL filters.

Table 1.
System parameters.
Figure 2 represents the simplified scheme of the two three-phase inverters connected in parallel. Note that the filter capacitors, the inductance Lb of the LCL filter, and the grid voltage do not affect the circulating currents. In Figure 2, express the phase voltages given by inverter #1, while are the voltages given by inverter #2. All the harmonic content is considered in these vectors. Similarly, the currents in both inverters are represented by Impedances and describe the impedance seen by the circulating currents.
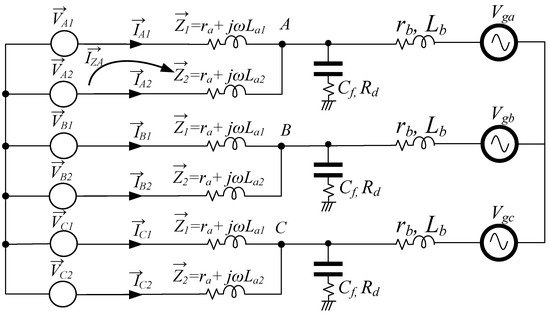
Figure 2.
Simplified scheme of two three-phase inverters connected in parallel.
From this scheme, it can be noted that a circulation current appears if an imbalance between the voltages given by voltage source inverters is produced [20]. As an example, the circulating current that appears when and are different is expressed by (1). The series resistance ra of the inductor La has been omitted.
From Figure 2, (2), and (3), the vector diagrams of Figure 3 are obtained. Figure 3a shows a vector diagram of the circuit when there are current variations between and . Similarly, Figure 3b shows and when the inductance value in both inverters is different. Then, if there is a mismatch between the current or the inductance of the grid filters, there will be an imbalance between the voltage inverters and , and circulating currents will appear, as (1) expresses.
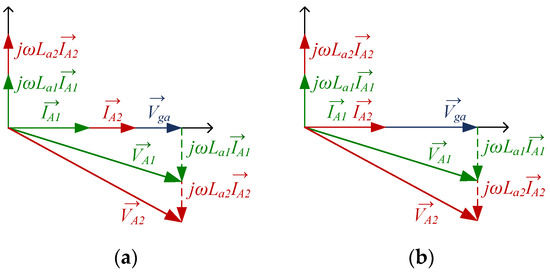
Figure 3.
VA1 and VA2 voltage variation according to: (a) current variation being > ; (b) inductance variation being La2 > La1.
Usually, the sum of the phase currents in a three-phase inverter is zero (4), but when several inverters are connected in parallel, the sum of the phase currents is expressed by (5) and (6), where and define the zero-sequence or homopolar component of the currents, respectively.
The circulating current in each inverter agrees with the zero-sequence component. When two inverters are connected in parallel, the circulating current in both inverters has the same value but opposite signs, following (7). For n inverters connected in parallel, the sum of the circulating currents of the inverters is zero (8).
In a three-phase system such as that represented in Figure 2, the circulating currents follow (9), where k represents the harmonic order; ω1 represents the grid frequency (first harmonic); and φAk, φBk, and φCk are the phase angle of each one of the k order harmonics [29].
It may be deduced from (9) that, when the three-phase inverter components are balanced, assuming that IAk = IBk = ICk = Ik and φAk = φBk = φCk = φk, (10) results.
Solving (10) for k = 1, 2…n, it can be noted that the components different from k = 3 and its multiples are canceled, while components k = 3 and its multiples produce a circulating current. Moreover, the value of even order harmonics is negligible due to medium wave symmetry in the grid voltages and currents. Thus, the circulating currents in balanced inverters are composed of k = 3 and its odd multiple harmonics. In other words, if each of the inverters connected in parallel supplies the same power, the circulating currents will only contain odd harmonic components and multiples of 3 of the fundamental (k = 3, 9, 15, etc.). The same conclusion is reached if non-zero phase angles of the harmonic components are considered. In practice, the most notable component is the third harmonic, and the others have very low values.
These harmonics produce an imbalance in the current-sharing between inverters. If the imbalance is produced among the phases of the same inverter, the currents in the phases of the same inverter will be unbalanced. From a practical point of view, one or more inverters will be overloaded, so their life cycles could be reduced.
3. Simulation and Experimental Results
In this section, both simulation and experimental results are obtained, showing the influence of the mismatches between inverters in the appearance of circulating currents. The simulation results were obtained by means of the simulation tool PSIMTM, and the experimental results were obtained using the laboratory setup that Figure 4 shows. The two parallel inverters were connected to an AC bus and a DC bus. The AC bus was powered by a Cinergia GL and EL-50 bidirectional power supply, which emulates a 230-V RMS (phase-phase) 50-Hz AC grid. In addition, a GSS Regatron power supply was connected to the DC bus to maintain a constant 500-V DC voltage. The digital control of the inverters was developed using a Texas Instruments TMS320F28379D dual-core microcontroller.

Figure 4.
Experimental setup.
In grid-connected inverters, the control variables are usually the DC voltage and AC currents. The AC voltage is not controlled since the inverters are working as grid-feeding. The control structure is shown in Figure 5. This control structure is implemented in the synchronous reference frame. The current control loops on the d-axis and q-axis regulate the active and reactive power of the inverters, respectively. To achieve a unity power factor, the reference for the reactive control loops was chosen to be zero. Since this work is focused on the analysis of circulating currents, a constant DC voltage was assumed, so the DC voltage control loop has been omitted. In this scheme, the currents on the d- and q-axes are defined as id1, id2, iq1, iq2. The current references in both channels are i*d and i*q., and the duty cycles are dd1, dd2, dq1, dq2. Gi(s) is a current control regulator, kdec1 and kdec2 are the decoupling terms implemented between the d- and q-axes, Ɵgrid is the grid angle obtained with a phase-locked loop, and Sap1, San1, Sbp1, Sbn1, Scp1, Scn1, Sap2, San2, Sbp2, Sbn2, Scp2, and Scn2 are the switching signals of the transistors.
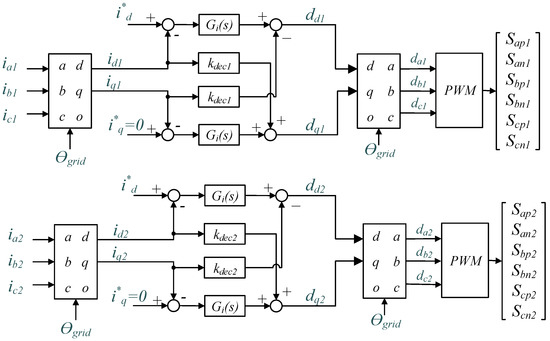
Figure 5.
Control structure.
Equations (11) and (12) define the decoupling terms kdec1 and kdec2, following [30]. In these equations, ω is the angular frequency of the grid, while c1 and c2 define the load factor of each of the inverters.
The nature of the circulating currents produced by inductance mismatching, the power imbalance, and the use of different modulators was evaluated. To analyze separately the influence of each factor in the circulating currents, two inverters with the same characteristics were employed. In each test, only one of the analyzed parameters mentioned above was changed to evaluate its influence on the resulting circulating currents. It is worth pointing out that, when the two inverters have identical parameters and are working at the same operational point, there are no circulating currents.
3.1. Circulating Currents in a Balanced System
First, the circulating currents in two identical inverters connected in parallel and with the nominal characteristics described in Table 1 were studied. Figure 6a,b shows the circulating currents obtained in the simulation and experiment, respectively.
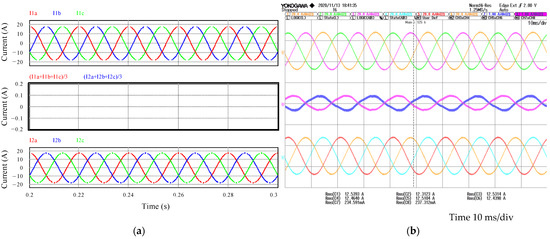
Figure 6.
Circulating current in a balanced system composed of two identical parallel inverters. Phase currents of inverter #1 at the top, circulating currents in the middle and phase currents of inverter #2 at the bottom. (a) 100% load factor simulation results; (b) 100% load factor experimental results.
Figure 6a depicts the currents in phase A (red), phase B (blue), and phase C (green) of inverter #1 (top) at full load. In the middle, the circulating currents expressed as (ia + ib + ic)/3, which are the zero-sequence currents of each inverter, are observed. At the bottom of this figure, the phase currents of inverter #2 are shown. It can be noted that, if both inverters have the same parameters, the circulating currents are zero in the whole range of power. Note that all the inductors in this test have a 5-mH inductance. This operation mode is purely theoretical, as component tolerances and differences between inverters will always exist, even if they are the same model from the same manufacturer.
Since in real conditions, the inductors have some tolerances, the six inductors that were available in the laboratory were measured. The real values of these inductors are presented in Table 2. To approach ideal conditions, the inductors were distributed among the different phases, seeking to reduce the differences among phases, so they affected as little as possible the circulating currents. Note that the inductor connected to the C phase of inverter #1 La_c1 is 5.4% higher than the nominal value, and La_b2 is 3% lower.

Table 2.
Measured values of inductances La.
Figure 6b shows the experimental results in which the inductors in Table 2, with a nominal value of 5 mH and a 10% tolerance, were used. At the top of the figure are represented the currents in phases A (orange, CH1), B (green, CH2) and C (pink, CH3) of inverter #1. In the middle are represented the circulating currents of inverter #1 (purple, CH7) and inverter #2 (pink, CH8) as (ia + ib + ic). At the bottom are represented the currents in phases A (blue, CH4), B (red, CH5), and C (orange, CH6) of inverter #2. Because the inductors are real components, the inductance connected at each phase of the inverters is influenced by the tolerance, so it is not possible to experimentally reproduce a case in which all the inductances are identical. In this case, it can be noted that a circulating current appears, which has a principal component of 50 Hz.
The same tests were performed in the whole power range of the inverters. Figure 7 shows the 50-Hz component of the circulating currents obtained from both the simulation and experimental results. Note that the 50-Hz homopolar component I1h is expressed in normalized values with regard to the positive sequence fundamental component of the inverter currents I1+. Note that the harmonic at 50 Hz obtained by the simulation is zero in the whole range of power of the inverter.
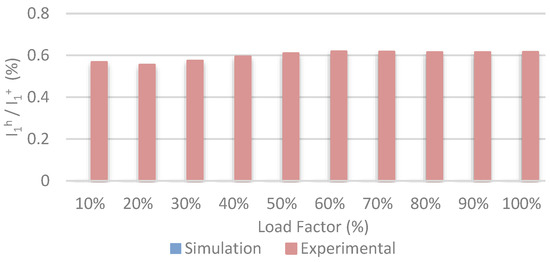
Figure 7.
Simulation and experimental harmonic of 50 Hz I1h/I1+ of the circulating current in the whole power range for a balanced system.
3.2. Circulating Currents with a Mismatch between the Inductances of the Inverters
The same inverters with the characteristics of Table 1 were used in these experiments, but the inductance La2 of phases A, B, and C of inverter #2 was modified. To achieve significant differences among the inductances of the inverters, additional inductors with a nominal value of 2 mH were added to the filters, with 7 mH being the value of the total inductance, so it is a 40% increase. In this case, La1 is 5 mH, and La2 is 7 mH. The simulation results are depicted in Figure 8a. The phase currents of inverter #1 are depicted on the top; at the bottom, the phase currents of inverter #2 are depicted, and in the middle, the circulating currents are depicted.
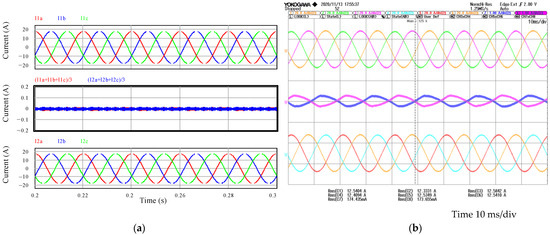
Figure 8.
Circulating current with unbalanced inductors between inverter #1 and #2 (La1 = 5 mH, and La2 = 7 mH). Phase currents of inverter #1 at the top, circulating currents in the middle, and phase currents of inverter #2 at the bottom (a) 100% load factor simulation results; (b) 100% load factor experimental results.
In Section 2, it was indicated that harmonics k = 3 and their multiples appear in a balanced system. In this section, it is emphasized that, although they are not of high values, the circulating currents under the evaluated conditions (different nominal inductances between inverters) have as main components the harmonics of 150 Hz, 450 Hz, etc. (that is, the components of the order of 3, 9, etc.).
The experimental results are reported in Figure 8b. As in the previous case, real inductances were employed, with the values summarized in Table 3. The 7-mH inductances were composed of the 5-mH inductances employed in the previous section and the 2-mH inductances connected in series. The 50-Hz component for the experimental results, which is represented in Figure 9a, had similar values as in the previous case since the differences in inductance between the phases were similar. However, for the simulation results, this harmonic was zero in the whole range of power since the inductances in the same inverter are balanced. Figure 9b shows the 150-Hz harmonic k = 3 varying the power throughout the range of 10–100% for both the experimental and simulation results. The percentage value of the harmonic with respect to the fundamental harmonic of the direct sequence of the current is represented in this figure.

Table 3.
Real inductance values.
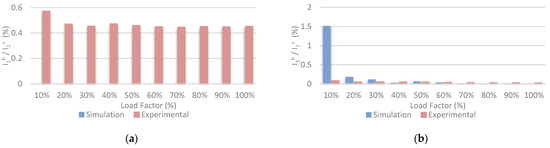
Figure 9.
Simulation and experimental harmonics of: (a) 50 Hz I1h/I1+; and (b) 150 Hz I3h/I1+ in the whole range of power of the circulating current with unbalanced inductors between inverter #1 and #2 (La1 = 5 mH and, La2 = 7 mH).
From the obtained results, it can be concluded that the use of inductors of different nominal values for each of the inverters connected in parallel does not have a significant effect on the appearance of circulating currents.
3.3. Circulating Currents with an Unbalanced Load Factor between Inverters
In this section, load factor imbalances are considered, with inverter #1 operating at half the power of inverter #2 in the whole range of the supplied power.
Figure 10a,b shows, respectively, the simulated and experimental phase currents and the circulating currents. The load factor of inverter #1 is 25%, and that of inverter #2 is 50% for both the simulation and experimental results. For the same reason previously outlined, the 50-Hz component does not appear in the circulating current obtained by the simulation because no differences among the phase inductors of each inverter were considered. In the experimental results, in which the real inductors of Table 2 were used, the 50-Hz harmonic of the circulating currents exists, as Figure 11 shows. This figure shows the 50-Hz and 150-Hz harmonics of the homopolar component, which are expressed as a percentage of the fundamental positive sequence component of the phase current. The load factor represented on the x-axis is that of inverter #2.
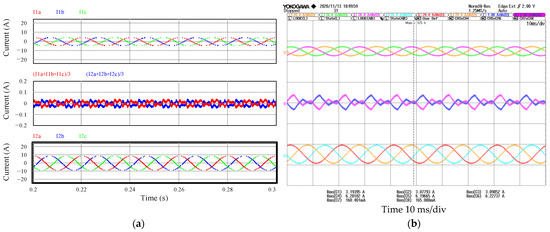
Figure 10.
(a) Simulation results with 25% load factor in inverter #1 and 50% in inverter #2; (b) experimental results with 25% load factor in inverter #1 and 50% in inverter #2. Phase currents of inverter #1 at the top, circulating currents in the middle, and phase currents of inverter #2 at the bottom.
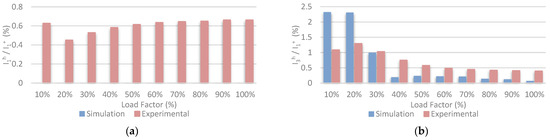
Figure 11.
Simulation and experimental harmonics of: (a) 50 Hz I1h/I1+; and (b) 150 Hz I3h/I1+ in the whole range of power of the circulating current with unbalanced load factor between inverter #1 and #2.
From the obtained results, it can be concluded that the power imbalance between the inverters connected in parallel does not have a significant effect on the appearance of circulation currents either. Actually, the effect of considering different inductances in the inverters is similar to the effect obtained by unbalancing the currents supplied by each inverter. Both factors produce a different voltage decease in the grid connection impedances of each inverter, which is the cause of circulating currents.
3.4. Circulating Currents with a Mismatch between the Inductances of the Same Inverter
To evaluate the influence of a serious mismatch among the phase inductances of each inverter, the configuration that Table 4 shows was implemented. The nominal value was used in the simulations, while real values were employed in the experiments.

Table 4.
Value of inductances la with a 40% imbalance in phase A of inverter #2.
Figure 12 shows the simulated (a) and experimental (b) circulating currents between inverters. It may be noted that the phase A current amplitude of the second inverter is approximately 8% lower than those of phases B and C. In contrast, phase A of inverter #1 presents an 8% increase.
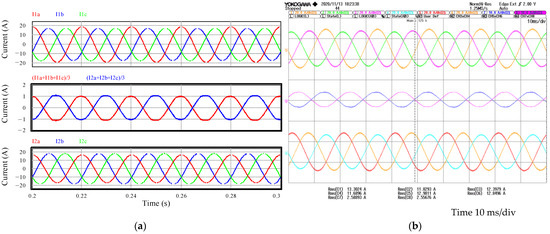
Figure 12.
Circulating current with a 40% increase in the inductance of phase A of inverter #2. Phase currents of inverter #1 at the top, circulating currents in the middle, and phase currents of inverter #2 at the bottom: (a) 100% load factor simulation results; (b) 100% load factor experimental results.
Figure 13 details the 50-Hz harmonic value of the circulating currents in the whole power range. As explained before, the 50-Hz harmonic appears due to the phase inductance mismatch. Harmonics of 150 Hz, 250 Hz, 350 Hz, etc., also appear, but their value is negligible compared to the 50-Hz component.
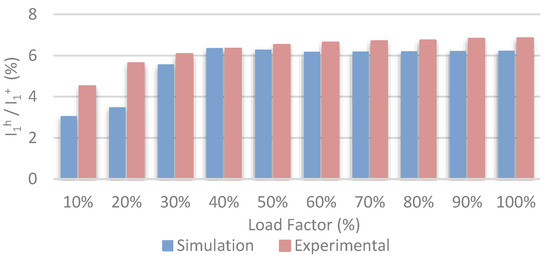
Figure 13.
Simulation and experimental harmonic of 50 Hz I1h/I1+ in the whole range of power of the circulating current with a 40% increase in the inductance of phase A of inverter #2.
It can be concluded that the tolerance of the inductors of the same inverter has an appreciable effect on the appearance of circulating currents, which mainly present large fundamental harmonics (50 Hz in the case under study) that increase as the power of the inverter increases. In practically the entire power range, this harmonic represents 6% of the inverter current, which has a clear, negative effect on the parallelized system by notably increasing the current flow through each module, without this current reaching the grid. It should be noted that, in this case, a nominal inductance of 5 mH was defined, and a 7-mH inductance was considered in phase A of inverter #2, representing a variation of +40% with respect to the nominal value. These values were those available in the laboratory to perform the experimental tests. However, the results obtained allow for predicting the perverse effects that would appear when considering a tolerance of the inductors of approximately ±16%, considering that the nominal value is 6 mH, and 5 mH–7 mH are the extreme values in the range of expected variation. Considering that the tolerance of power inductors has typical values of ±20% and even higher, it follows that this factor can produce the appearance of a significant 50-Hz harmonic in the circulating currents.
3.5. Circulating Currents with Different Modulation Techniques between Inverters
In this section, the effects of using inverters that implement a different type of PWM modulator are studied. This use could occur in practice, for example, if one of the inverters is installed some time after the other to extend the power supply. In this case, if the inverters are of different models and manufacturers, the type of PWM modulation used by each could be different. To evaluate this scenario, it is considered in this section that inverter #1 uses a symmetric space vector modulator (SVM), while inverter #2 works with a sinusoidal PWM (SPWM). This case is considered to be particularly disadvantageous for the reasons detailed below [31]. Symmetric SVM is usually used in three-wire three-phase inverters, and it produces a third harmonic of zero-sequence in phase voltages, which disappears in phase-to-phase voltages. Sinusoidal PWM does not introduce any homopolar component in the phase voltages. Consequently, when inverters that operate in parallel implement these different types of modulators, a large zero-sequence voltage component appears in the phase voltages of the inverter controlled by SVM that is not compensated for by the phase voltages of the sinusoidal PWM inverter. As a result, a very large zero-sequence circulating current appears, which is only limited by the impedances of the loop. It should be noted that this phenomenon does not appear if both inverters implement sinusoidal PWM and neither if both are controlled by symmetric SVM. If both inverters implement SVM, the homopolar components generated by the modulator in the phase voltages of each inverter are compensated for by the voltages generated by the other one. The study could also be extended by considering different types of SVM modulators (asymmetric, discontinuous sequence, etc.), but it is considered sufficient to evaluate the worst case described since the rest of the cases will present a certain influence on the currents of circulation but always a much smaller influence than the extreme case evaluated.
Figure 14 shows the simulated (a) and experimental (b) circulating currents between the two inverters. In this case, the 150-Hz component of the circulating current is very high, about 4 A in amplitude, in the whole range of power. This component has a value of approximately 25% of the fundamental positive sequence at nominal power, and it considerably increases at light power. Specifically, with a 10% load factor, the circulating current has a value of 225% with regard to the fundamental component of the phase currents. Figure 15a,b expresses the value of the 50-Hz and 150-Hz harmonics of the circulating currents in percentages with regard to the fundamental component of the phase currents. It is worth noting that a 450-Hz harmonic also appears, which is represented in Figure 15c, because the third harmonic introduced by symmetric SVM is not perfectly sinusoidal, but it is a triangular component, adding higher-frequency harmonic components, of which only the order 9 harmonic is considered to be relevant.
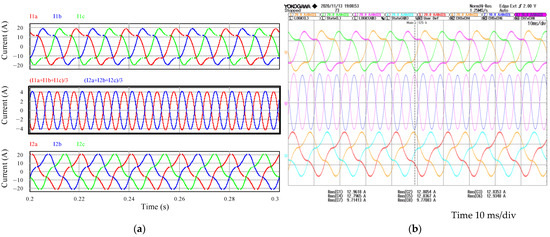
Figure 14.
Circulating current with SVM in inverter #1 and SPWM in inverter #2. Phase currents of inverter #1 at the top, circulating currents in the middle, and phase currents of inverter #2 at the bottom: (a) 100% load factor simulation results; (b) 100% load factor experimental results.
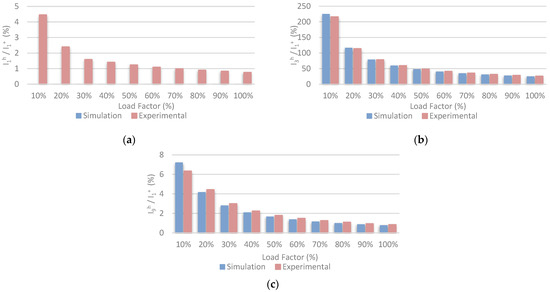
Figure 15.
Simulation and experimental harmonics of: (a) 50 Hz I1h/I1+; (b) 150 Hz I3h/I1+; and (c) 450 Hz I9h/I1+ in the whole range of power of the circulating current with SVM in inverter #1 and SPWM in inverter #2.
As can be seen in Figure 14a,b, due to the harmonics contained in the circulating currents, there is great distortion in the phase currents of both inverters. These currents could stress both the filter components and the power stage semiconductors.
From the obtained results, it can be concluded that the use of very different PWM modulators has a great effect on the appearance of circulating currents, which only depends on the mismatch between the phase voltages generated by the inverters. Therefore, they practically do not vary with the load factor.
3.6. Current Sharing in Dynamic Conditions
Experimental results were obtained in dynamic conditions performing load steps of the load factor. The following figures show the phase currents in inverters #1 and #2 (upper and lower waveforms, respectively) and the resulting circulating currents (in the middle). Figure 16 shows the circulating currents when inverter #1 is working at 25% of the load factor and inverter #2 is working at 50%. A load step is performed in which inverter #1 is working at 50% of the load factor and inverter #2 is working at 100%. Figure 17 shows the circulating currents in dynamic conditions with a load step from 50% to 100% in the case in which an imbalance in the inductance value of phase A of the second inverter exists. Finally, Figure 18 shows the phase currents and the circulating currents in dynamic conditions when inverter #1 is controlled by SVM and inverter #2 by SPWM.
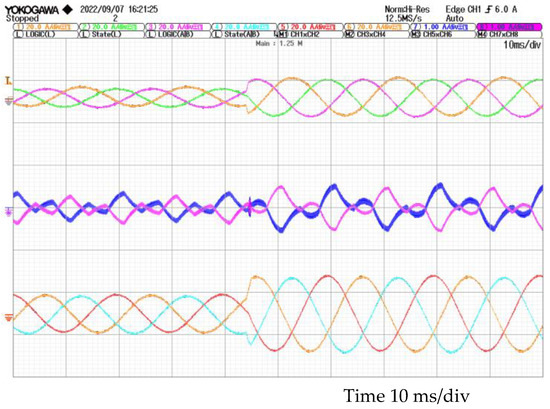
Figure 16.
Experimental circulating current with a load step from 25% to 50% in inverter #1 and from 50% to 100% in inverter #2. Phase currents of inverter #1 at the top, circulating currents in the middle, and phase currents of inverter #2 at the bottom.
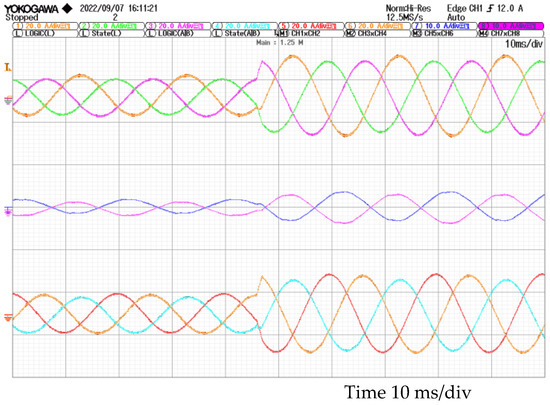
Figure 17.
Experimental circulating current with a load step from 50% to 100% when the inductance of phase A of inverter #2 is increased by 40%. Phase currents of inverter #1 at the top, circulating currents in the middle, and phase currents of inverter #2 at the bottom.
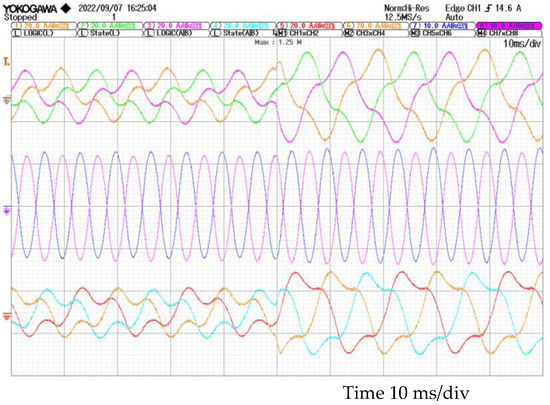
Figure 18.
Experimental circulating current with a load step from 50% to 100%when inverter #1 is controlled by SVM and inverter #2 by SPWM. Phase currents of inverter #1 at the top, circulating currents in the middle, and phase currents of inverter #2 at the bottom.
As indicated in previous sections, in most cases, circulating currents are directly proportional to the load factor, as in the cases of Figure 16 and Figure 17. However, the circulating currents are constant and especially large when inverter #1 is controlled by SVM and inverter #2 by SPWM (Figure 18).
4. Circulating Currents in Photovoltaic High-Power Applications
In the introduction, the advantages were described of implementing centralized inverters in megawatt photovoltaic fields by connecting photovoltaic inverter modules that handle a fraction of the generated power in parallel. These advantages include scalability, redundancy, and a certain degree of fault tolerance.
For the study of circulating currents in large power photovoltaic inverters, a 2-MW system composed of four modules, each of 500 kW, is considered. Figure 19 shows the scheme of the photovoltaic inverters connected in parallel, and Table 5 shows the parameters of the high-power system.
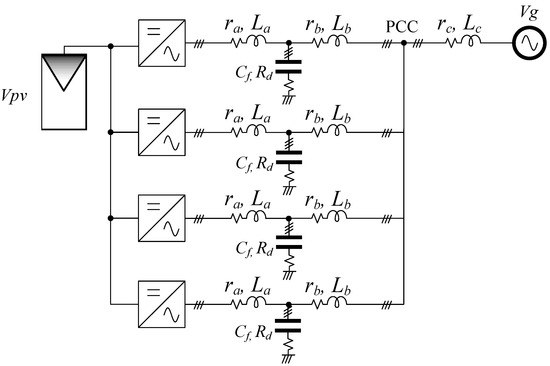
Figure 19.
High-power photovoltaic inverters connected in parallel.

Table 5.
Parameters of the high-power photovoltaic inverters.
Figure 20 shows the circulating currents that appear in a 2-MW photovoltaic system. A 10% tolerance in the inductances of the filters is considered since it is the most realistic imbalance that can appear in these systems, in which generally all the modules are desired to be equal. In Figure 20, the phase currents of all the inverters are represented from #inverter 1 at the top to inverter #4, and at the bottom, the circulating currents are represented.
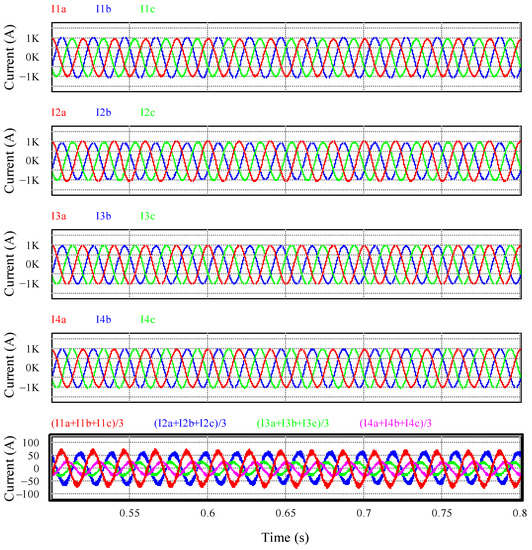
Figure 20.
Circulating currents in high-power photovoltaic farms. From top to bottom, phase currents in inverters #1, #2, #3, and #4 and circulating currents.
Since a 10% tolerance in the inductances of the filter has been considered, the circulating currents have a large first harmonic. The circulating current in inverter #1, which is the largest, has a value of 6.5% with regard to the fundamental components of the phase currents. Note that, in this case, in which more than two inverters are connected in parallel, the circulating currents do not have the same value. However, the sum of the circulating currents is zero.
5. Discussion and Comparison with Previous Works
Table 6 compares the results obtained in this work with those presented in previous works.

Table 6.
Comparison with previous works.
As previously highlighted in Section 3, the use of inductances with a different nominal value in the LCL filter among inverters produces a low third harmonic component in the circulating currents. A higher value of the circulating current is obtained by imposing a different load factor on the inverters. By unbalancing the inductances between the phases of an inverter, a high first harmonic appears in the circulating current. Finally, the use of different modulation techniques (SPWM and SVM) between inverters produces a large value of both the RMS circulating current and distortion of the phase currents. The THDi reaches a value of 31%, so the power factor of the inverters is significantly degraded.
For the sake of enriching the overall conclusions, the results obtained in this work were compared with those of previous works, as Table 6 shows. In particular, the following were represented: the 50 Hz I1h and 150 Hz I3h homopolar components of the circulating currents, expressed in normalized values with regard to the positive sequence fundamental component of the inverter currents I1+; the RMS value of the circulating currents; and THDi of the inverter phase currents.
Note that the relative influence of each parameter has been considered when composing the table. Thus, the table represents, starting on the left, the parameter that produces the least important effects and, ending on the right, that with the greatest effects. Regarding the results of previous works, Table 6 shows the worst case produced by a phase shift between the carrier signals of PWM modulators, following [27]. The effects produced by a difference between the phase and the frequency of the voltages of islanded inverters can also be seen in Table 6, as presented in [27]. Percentage values were used in all cases to ensure a fair comparison. Where results were not available, this fact has been indicated by a dash.
Summing up, this work is an extension of the previous literature regarding the study of circulating currents among several inverters connected in parallel. Other factors have been considered that were not previously studied.
6. Conclusions
The main original contribution of this work is a detailed study of the low-frequency circulation currents that can appear between inverters connected in parallel in both AC and DC buses, showing that, for the cases in which the currents in the phases of each of the inverters are balanced, the circulating current presents harmonics of order k = 3 and their multiples, while in systems in which an inverter has unbalanced phases, a significant component appears in the circulating currents at the fundamental frequency. The study evaluated the influence of several factors on low-frequency circulating currents: inductance mismatching between the phases of an inverter and between different inverters (different nominal inductance from one inverter to another), power imbalances, and the use of different PWM modulations. The results confirm that the use of inductors of different nominal values and different load factors between inverters produces insignificant circulation currents that are practically negligible. However, variations in the inductance of the grid filter between phases of the same inverter due to the tolerances of the components produce an imbalance in the inverter currents, in turn causing the appearance of circulating currents with a notable component at the fundamental frequency. The first harmonic component of these circulating currents is proportional to the load factor of the inverters since the current imbalance is greater as the power increases, and in the case under study, this circulating current has a value of 6% with regard to the phase inverter current. Finally, it has been shown that a factor that causes the appearance of high-circulation currents between inverters is the use of different PWM modulators. Specifically, it has been verified that the use of a sinusoidal PWM modulator in one of the inverters and SVM in the other one causes a large circulating current due to the homopolar third harmonic component that is generated by the SVM modulator in phase voltages. In the case under study, the third harmonic component of the circulating current represents 25% with regard to the positive sequence fundamental phase current at nominal power, and it increases considerably at low power, i.e., 225% at 10% of the load factor. This circulating current produces a great distortion in the phase currents, reaching a value of THDi = 30.91%.
Author Contributions
Conceptualization, M.L., E.F. and G.G.; methodology, M.L., R.G.-M. and E.F.; software, M.L. and E.T.; validation, M.L., R.G.-M., I.P. and E.T., formal analysis, M.L. and E.F.; investigation, M.L., R.G.-M. and I.P.; writing—original draft preparation, M.L. and E.F.; writing—review and editing, M.L., R.G.-M., G.G. and E.F.; supervision, G.G. and E.F.; project administration, G.G. and E.F.; funding acquisition G.G. and E.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Spanish “Ministerio de Asuntos Económicos y Transformación Digital” and the European Regional Development Fund (ERDF) under Grants RTI2018-100732-B-C21 and PID2021-122835OB-C22.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aleem, Z.; Shin, D.; Cha, H.; Lee, J.-P.; Yoo, D.-W.; Peng, F.Z. Parallel Operation of Inverter Using Trans-Z-Source Network. IET Power Electron. 2015, 8, 2176–2183. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Aeloiza, E.; Enjeti, P.N.; Blaabjerg, F. Shunt Active-Power-Filter Topology Based on Parallel Interleaved Inverters. IEEE Trans. Ind. Electron. 2008, 55, 1175–1189. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, X.; Wang, F.; Cao, R. Modeling and Elimination of Zero-Sequence Circulating Currents in Parallel Three-Level T-Type Grid-Connected Inverters. IEEE Trans. Power Electron. 2015, 30, 1050–1063. [Google Scholar] [CrossRef]
- Abusara, M.A.; Sharkh, S.M. Design and Control of a Grid-Connected Interleaved Inverter. IEEE Trans. Power Electron. 2013, 28, 748–764. [Google Scholar] [CrossRef]
- Kim, K.-T.; Kwon, J.-M.; Kwon, B.-H. Parallel Operation of Photovoltaic Power Conditioning System Modules for Large-Scale Photovoltaic Power Generation. IET Power Electron. 2013, 7, 406–417. [Google Scholar] [CrossRef]
- Liberos, M.; González-Medina, R.; Garcerá, G.; Figueres, E. A Method to Enhance the Global Efficiency of High-Power Photovoltaic Inverters Connected in Parallel. Energies 2019, 12, 2219. [Google Scholar] [CrossRef]
- Matijević, E.; Sharma, R.; Zare, F. A Higher-Order Filter Approach to Implement Grid Current Based Active Damping in Active Front End Converters. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–6. [Google Scholar]
- Zare, F.; Yaghoobi, J.; Gharani, K.; Kumar, D. Harmonic Cancellations in Parallel Active Front End Inverters in Distribution Networks: IEC 61000-3-16 and Phase-Angles. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6–7 July 2020; pp. 1–6. [Google Scholar]
- Hou, C.-C. A Multicarrier PWM for Parallel Three-Phase Active Front-End Converters. IEEE Trans. Power Electron. 2013, 28, 2753–2759. [Google Scholar] [CrossRef]
- Duman, T.; Marti, S.; Moonem, M.A.; Abdul Kader, A.A.R.; Krishnaswami, H. A Modular Multilevel Converter with Power Mismatch Control for Grid-Connected Photovoltaic Systems. Energies 2017, 10, 698. [Google Scholar] [CrossRef]
- Araujo, S.V.; Zacharias, P.; Mallwitz, R. Highly Efficient Single-Phase Transformerless Inverters for Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Electron. 2010, 57, 3118–3128. [Google Scholar] [CrossRef]
- Dagar, A.; Gupta, P.; Niranjan, V. Microgrid Protection: A Comprehensive Review. Renew. Sustain. Energy Rev. 2021, 149, 111401. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Abedi, M.; Gharehpetian, G.B. Robust Nonlinear State Feedback Control of Bidirectional Interlink Power Converters in Grid-Connected Hybrid Microgrids. IEEE Syst. J. 2020, 14, 1117–1124. [Google Scholar] [CrossRef]
- Lyu, J.; Zhang, J.; Cai, X.; Wang, H.; Dai, J. Circulating Current Control Strategy for Parallel Full-Scale Wind Power Converters. IET Power Electron. 2016, 9, 639–647. [Google Scholar] [CrossRef]
- Jiang, W.; Ma, W.; Wang, J.; Wang, W.; Zhang, X.; Wang, L. Suppression of Zero Sequence Circulating Current for Parallel Three-Phase Grid-Connected Converters Using Hybrid Modulation Strategy. IEEE Trans. Ind. Electron. 2018, 65, 3017–3026. [Google Scholar] [CrossRef]
- Narimani, M.; Moschopoulos, G. Improved Method for Paralleling Reduced Switch VSI Modules: Harmonic Content and Circulating Current. IEEE Trans. Power Electron. 2014, 29, 3308–3317. [Google Scholar] [CrossRef]
- Fu, X.; Wang, H.; Guo, X.; Shi, C.; Jia, D.; Chen, C.; Guerrero, J.M. A Novel Circulating Current Suppression for Paralleled Current Source Converter Based on Virtual Impedance Concept. Energies 2022, 15, 1952. [Google Scholar] [CrossRef]
- Prasad, J.S.S.; Ghosh, R.; Narayanan, G. Common-Mode Injection PWM for Parallel Converters. IEEE Trans. Ind. Electron. 2015, 62, 789–794. [Google Scholar] [CrossRef]
- Abbes, M.; Mehouachi, I.; Chebbi, S. Circulating Current Reduction of a Grid-Connected Parallel Interleaved Converter Using Energy Shaping Control. Electr. Power Syst. Res. 2019, 170, 184–193. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, G.; Du, H. Circulating Current Suppression of Parallel Photovoltaic Grid-Connected Converters. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1214–1218. [Google Scholar] [CrossRef]
- Ye, Z.; Boroyevich, D.; Lee, F.C. Modeling and Control of Zero-Sequence Current in Parallel Multi-Phase Converters. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference. Conference Proceedings (Cat. No.00CH37018), Galway, Ireland, 23 June 2000; Volume 2, pp. 680–685. [Google Scholar]
- Mazumder, S.K. A Novel Discrete Control Strategy for Independent Stabilization of Parallel Three-Phase Boost Converters by Combining Space-Vector Modulation with Variable-Structure Control. IEEE Trans. Power Electron. 2003, 18, 1070–1083. [Google Scholar] [CrossRef]
- Pan, C.-T.; Liao, Y.-H. Modeling and Control of Circulating Currents for Parallel Three-Phase Boost Rectifiers with Different Load Sharing. IEEE Trans. Ind. Electron. 2008, 55, 2776–2785. [Google Scholar] [CrossRef]
- Ogasawara, S.; Takagaki, J.; Akagi, H.; Nabae, A. A Novel Control Scheme of a Parallel Current-Controlled PWM Inverter. IEEE Trans. Ind. Appl. 1992, 28, 1023–1030. [Google Scholar] [CrossRef]
- Chen, T. Dual-Modulator Compensation Technique for Parallel Inverters Using Space-Vector Modulation. IEEE Trans. Ind. Electron. 2009, 56, 3004–3012. [Google Scholar] [CrossRef]
- Liberos, M.; González-Medina, R.; Patrao, I.; Garcerá, G.; Figueres, E. A Control Scheme to Suppress Circulating Currents in Parallel-Connected Three-Phase Inverters. Electronics 2022, 11, 3720. [Google Scholar] [CrossRef]
- Maheshwari, R.; Gohil, G.; Bede, L.; Munk-Nielsen, S. Analysis and Modelling of Circulating Current in Two Parallel-Connected Inverters. IET Power Electron. 2015, 8, 1273–1283. [Google Scholar] [CrossRef]
- Roslan, M.A.; Ahmad, M.S.; Isa, M.A.M.; Rahman, N.H.A. Circulating Current in Parallel Connected Inverter System. In Proceedings of the 2016 IEEE International Conference on Power and Energy (PECon), Melaka, Malaysia, 28–29 November 2016; pp. 172–177. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; ISBN 978-0-7923-7270-7. [Google Scholar]
- Figueres, E.; Garcera, G.; Sandia, J.; Gonzalez-Espin, F.; Calvo Rubio, J. Sensitivity Study of the Dynamics of Three-Phase Photovoltaic Inverters with an LCL Grid Filter. IEEE Trans. Ind. Electron. 2009, 56, 706–717. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 978-0-471-20814-3. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).