Evaluating Water Infiltration and Runoff: Stretcher Bond vs. 45° Herringbone Patterns in Permeable Interlocking Concrete Pavements
Abstract
1. Introduction
1.1. Research Background
- Needs to be swept with a vacuum regularly
- Effective soil stabilization and erosion control measures are necessary to avoid clogging.
1.2. Literature Review
1.3. Research Novelty
1.4. Research Objectives
1.5. Research Motivation
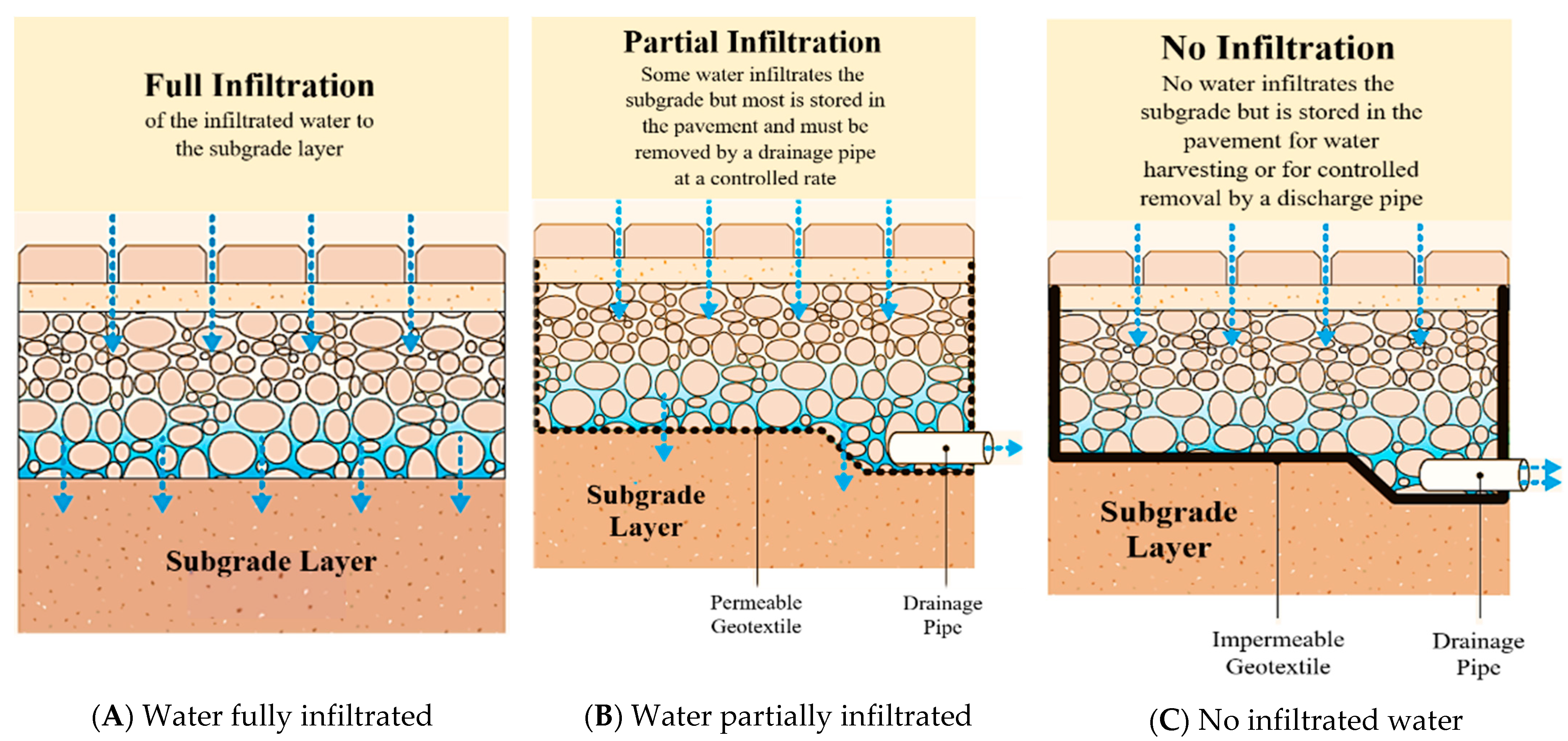
2. Experimental Work
2.1. Designing the Principal PICP Cross-Sections
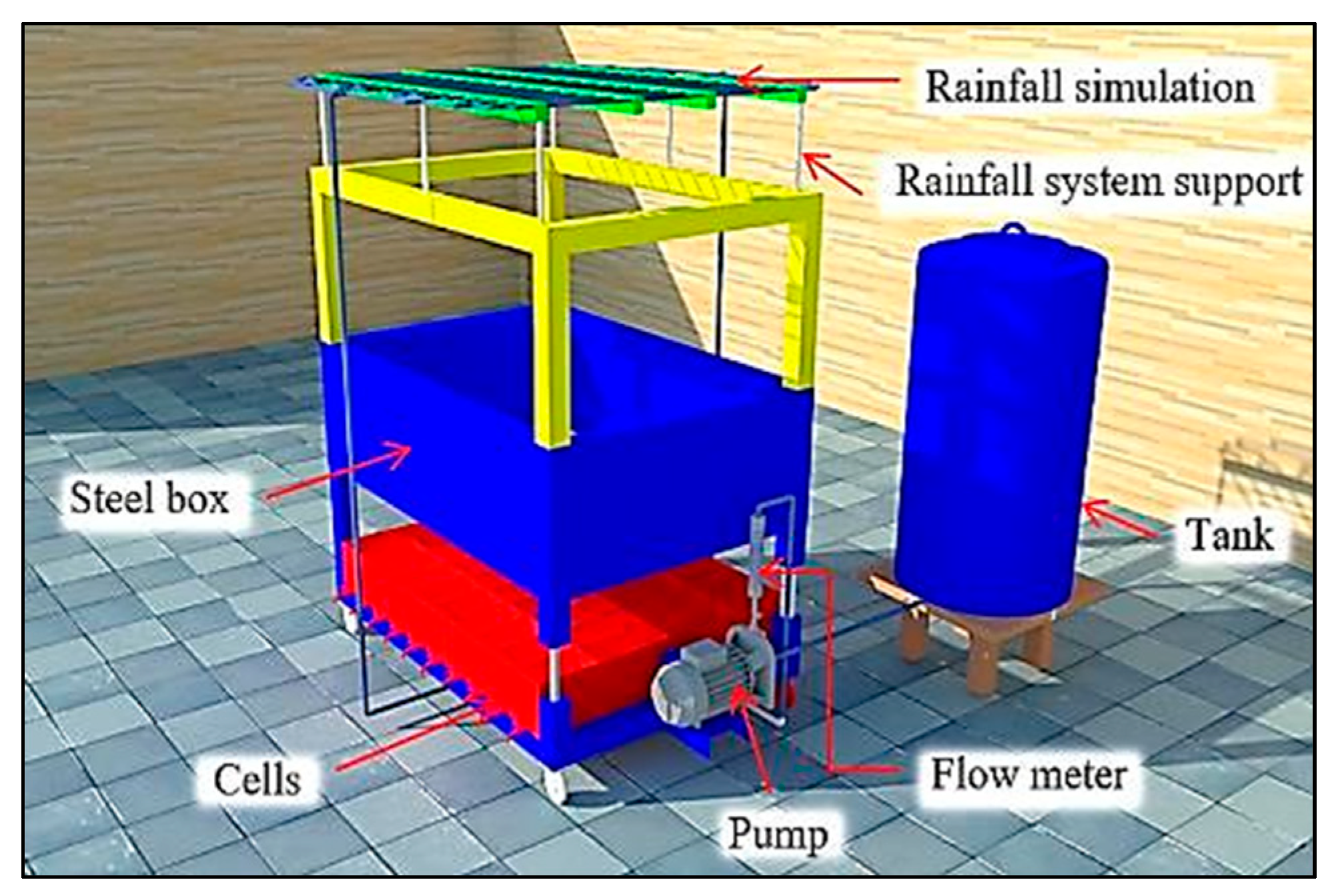
2.2. Constructing the Rainfall Simulator
2.3. Constructing the PICP Layers
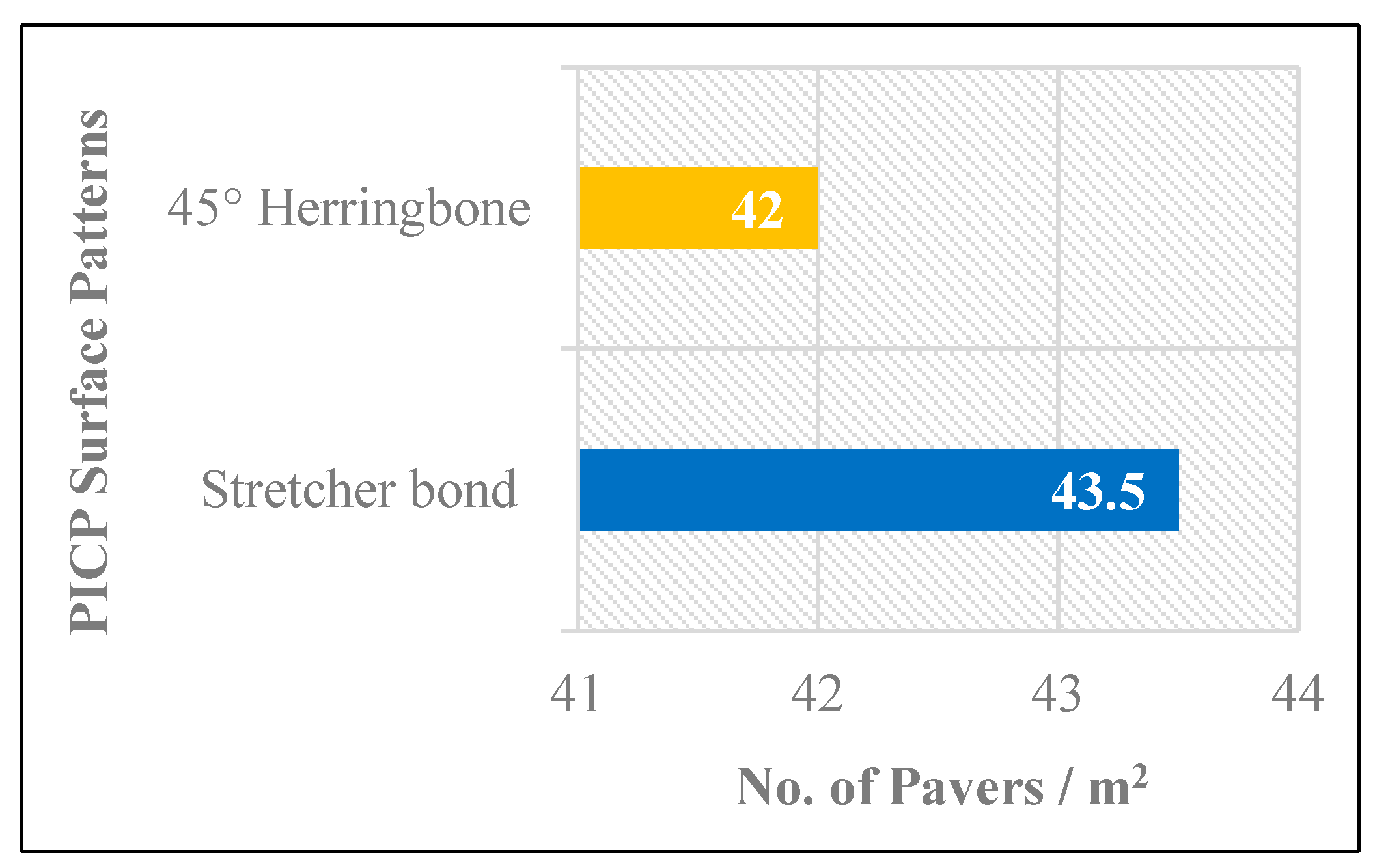
2.3.1. Paver Surface Layer
2.3.2. Surface Joint Filing
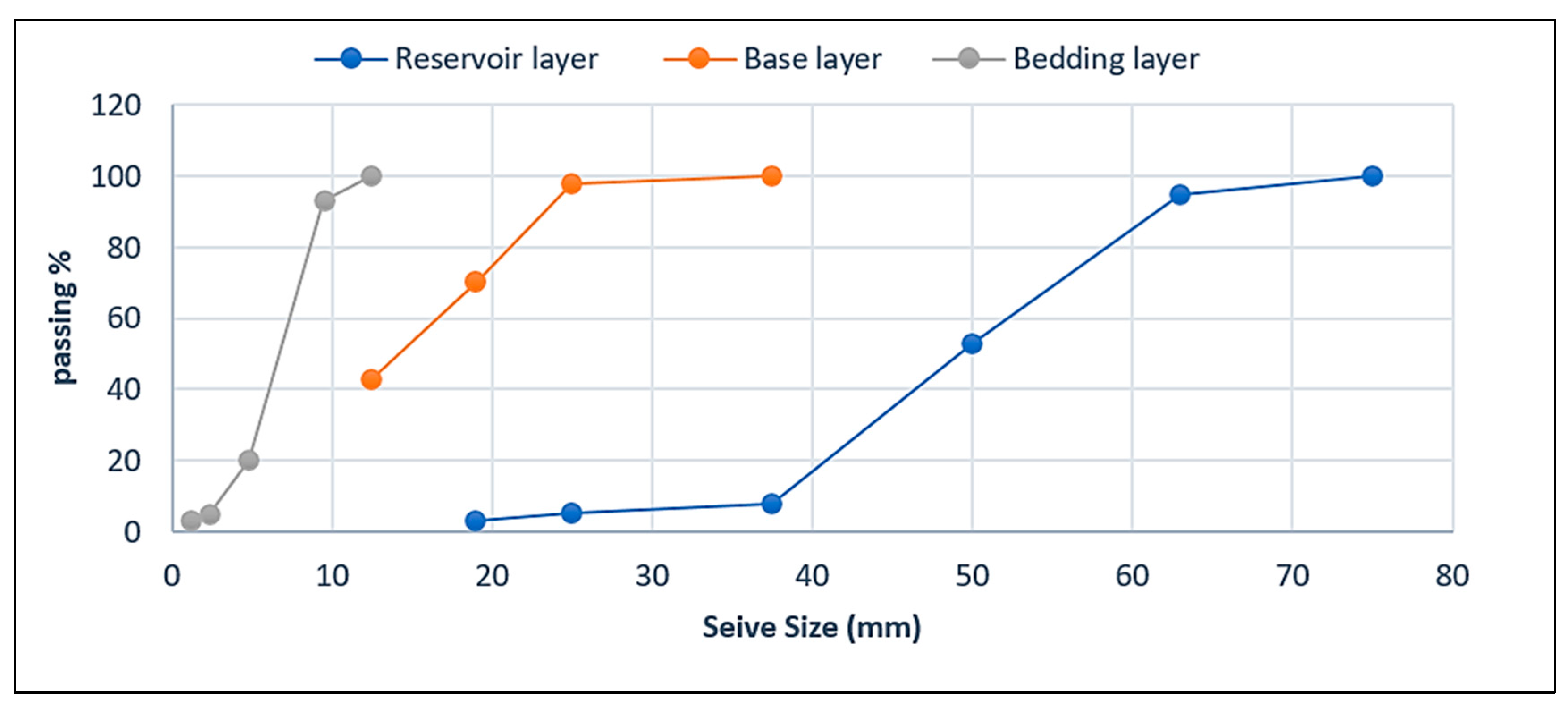
2.3.3. Bedding Layer
2.3.4. Base Layer
2.3.5. Subbase or Reservoir Layer
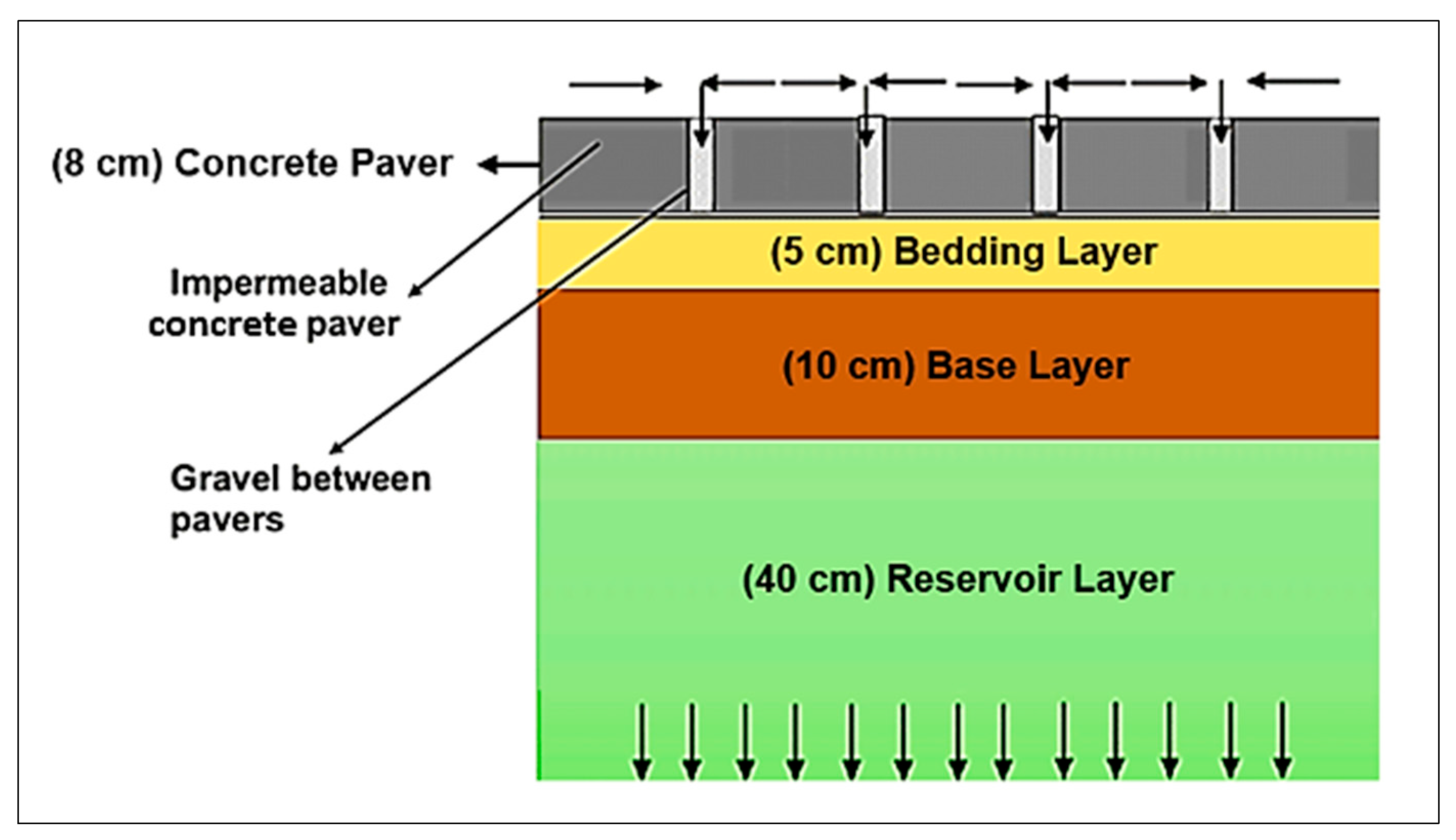
2.4. Estimating the Depth of the Reservoir
2.4.1. Using a Structural Approach to Design
2.4.2. Using a Hydraulic Approach to Design
- Rvi = The impermeability factor for runoff is 0.95
- P = The depth of rain that falls during a storm and is retained in the Stormwater Retention Volume (SWRv) in (ft).
- DA = The area in (ft2) of the permeable pavement surface or drainage system that contributes to the retention of water
- Ap = The surface area of the permeable pavement, measured in (ft2)
- tf = The time it takes to fill the container, approximately 2 h per day
- i = The rate at which water infiltrates the subgrade soils in the field, measured in (ft) per day
- ηr = The porosity of the reservoir, with a value of 0.4
- The calculated depths used in both structural and hydraulic engineering designs are presented in Table 3 below.
- According to the structural design method, the chosen depth of the reservoir layer is 40 cm, which is the highest value for safety considerations, as shown in Figure 18, below
2.5. Placing the Layers of PICP Within the Steel Container
3. Results and Discussions
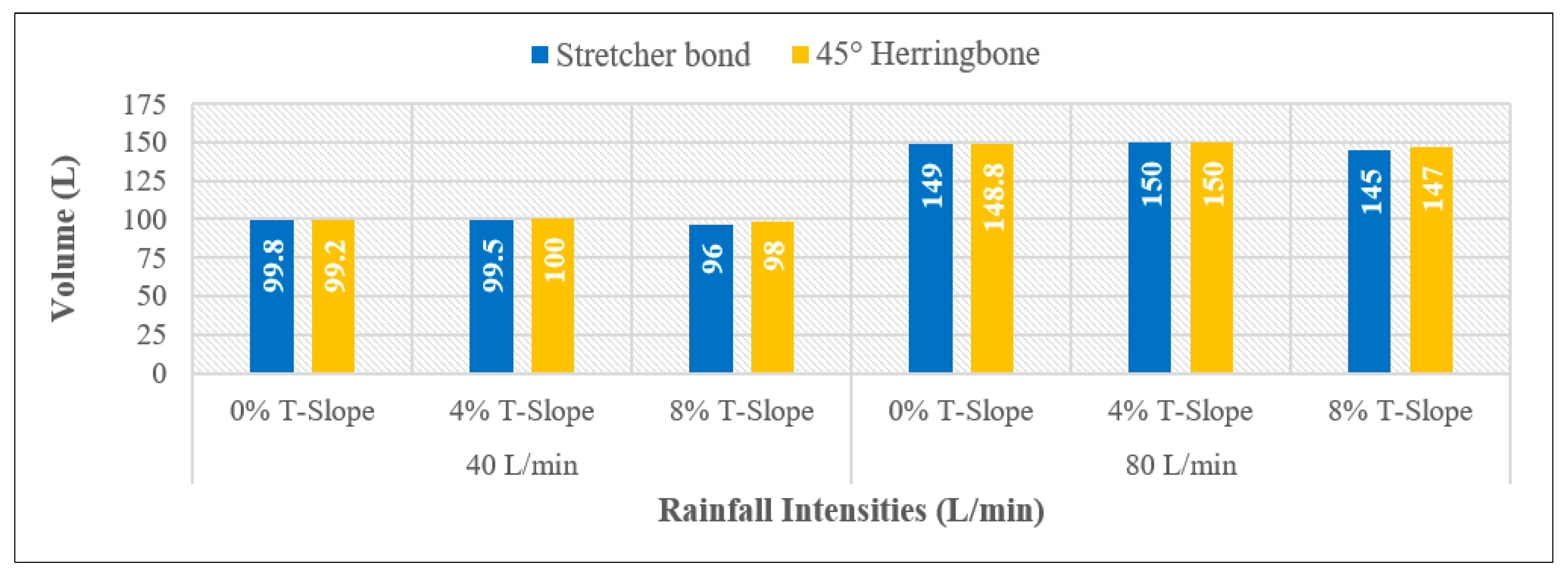
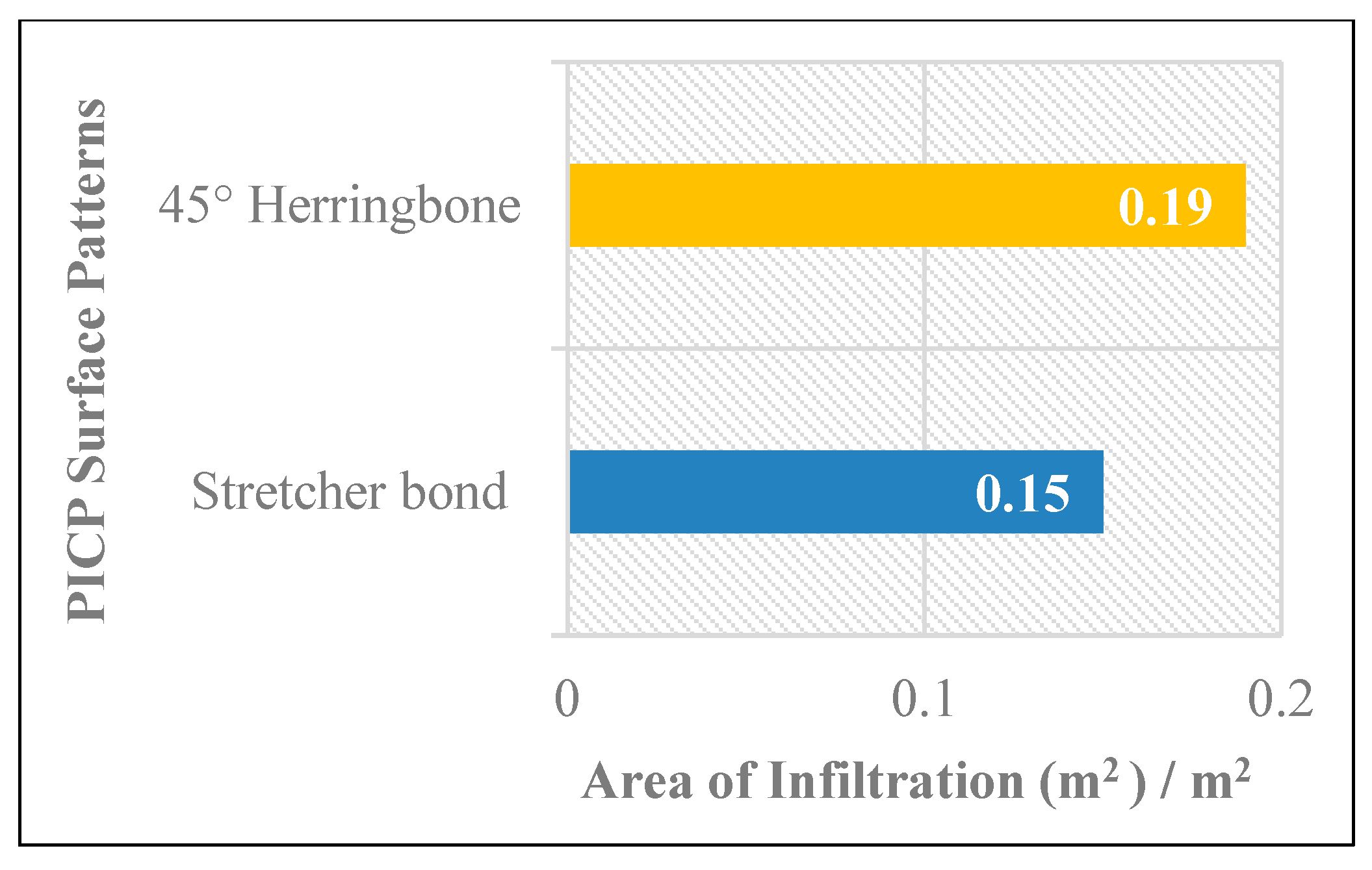
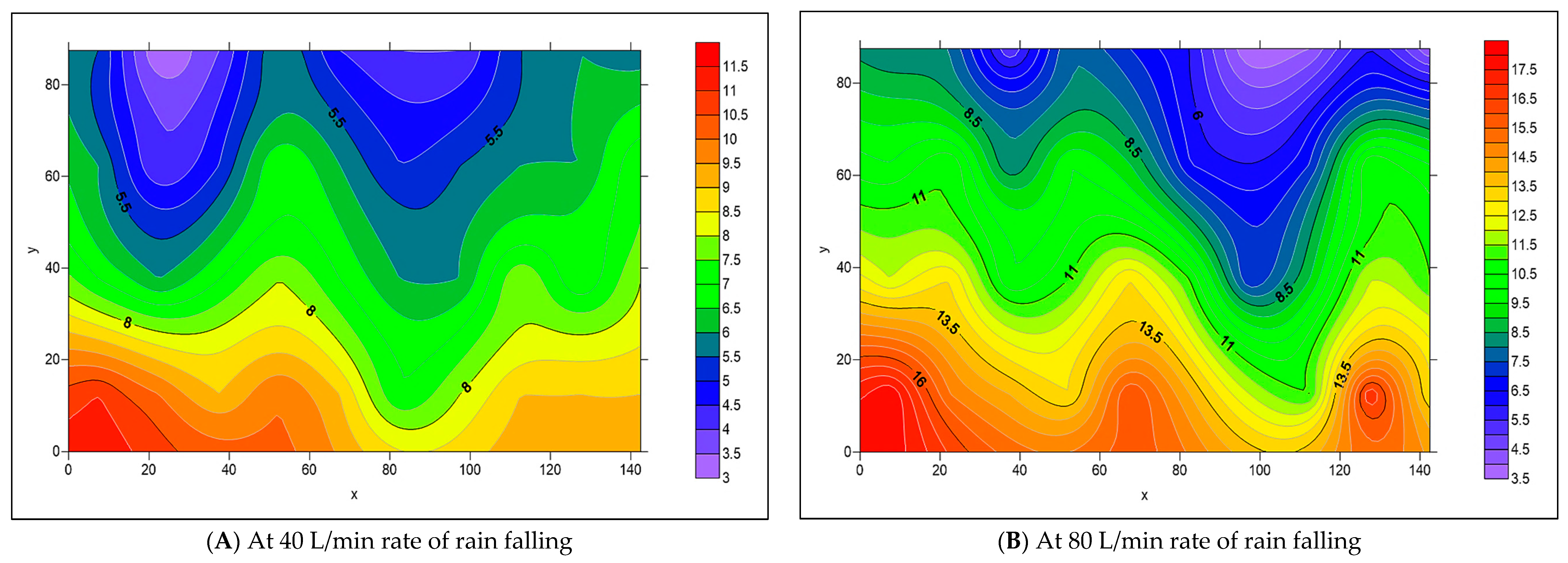
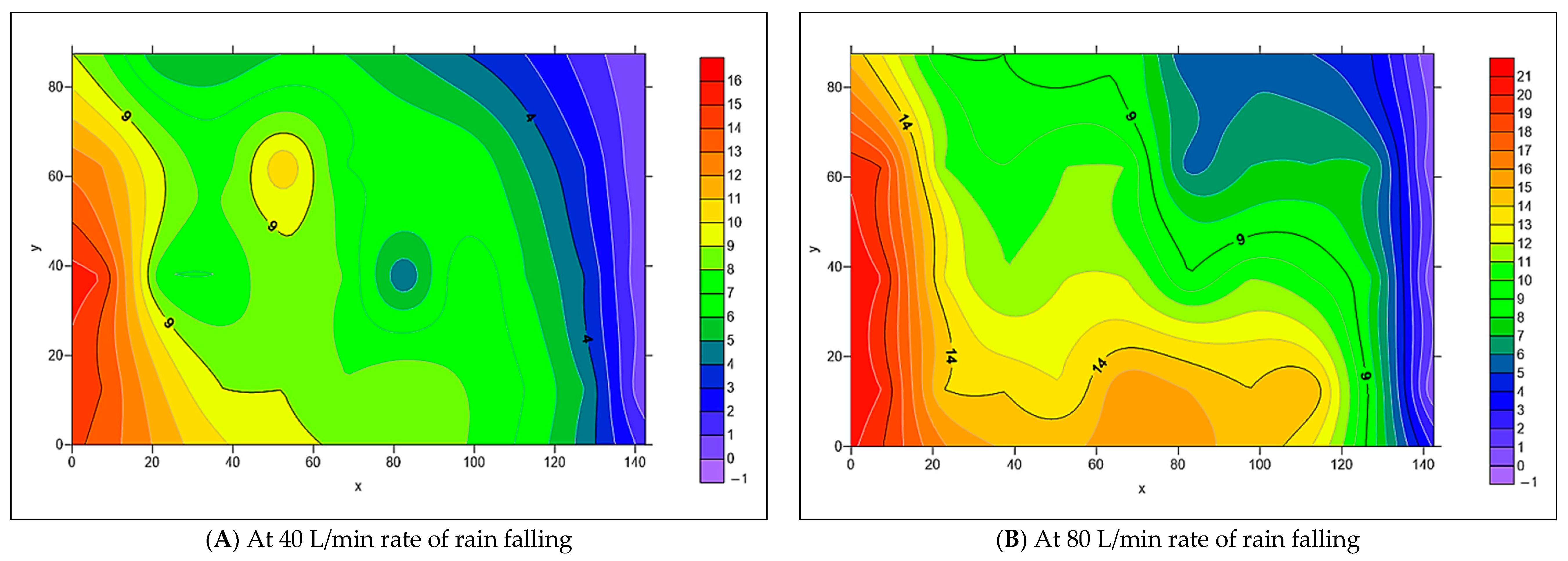
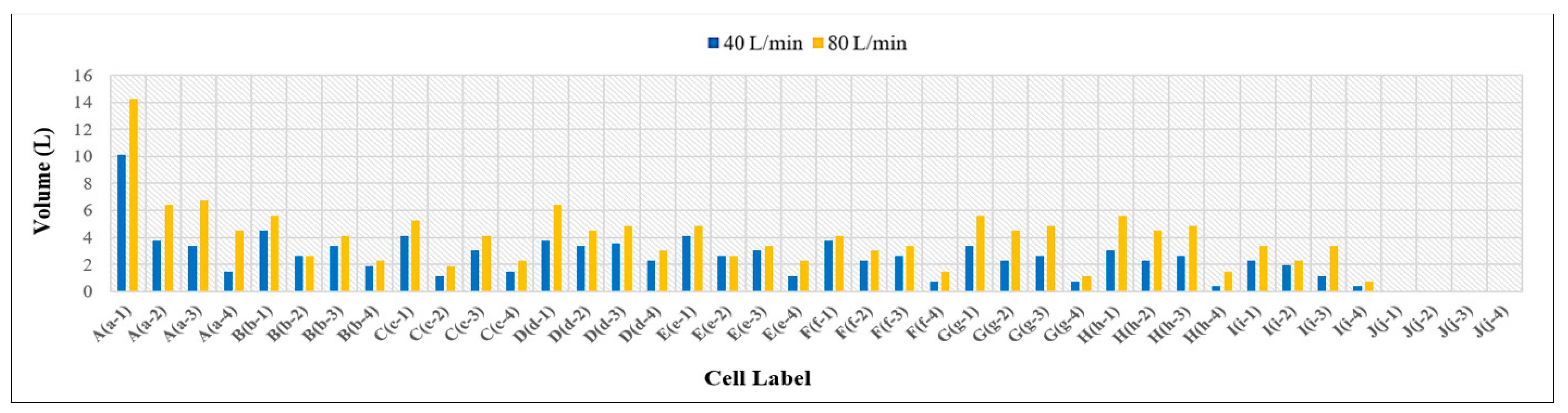
3.1. Examining the Infiltration of Water Through Surface Patterns with Stretcher Bond and 45° Herringbone Arrangements
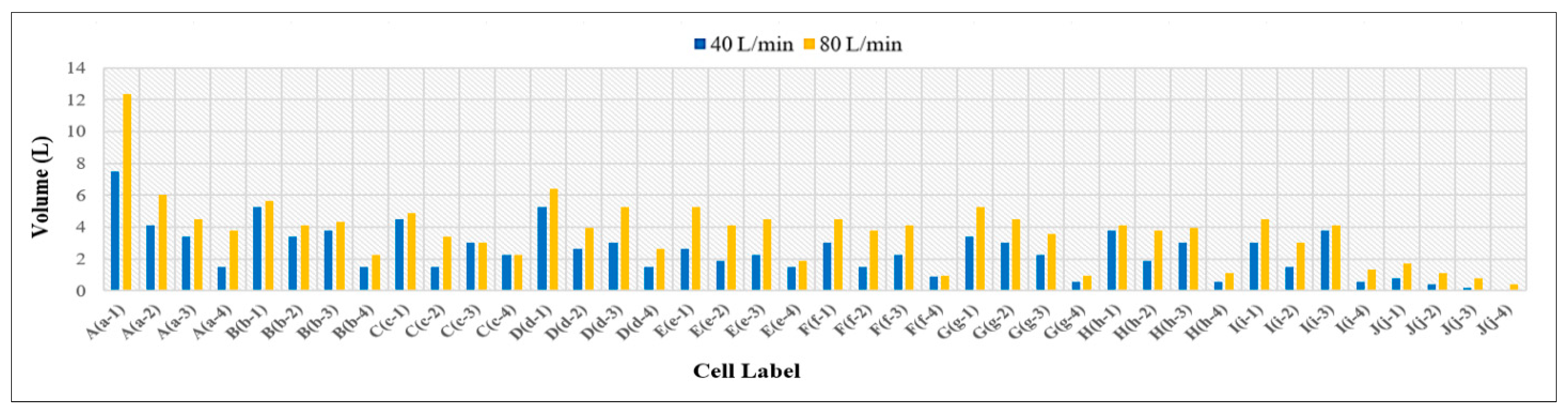
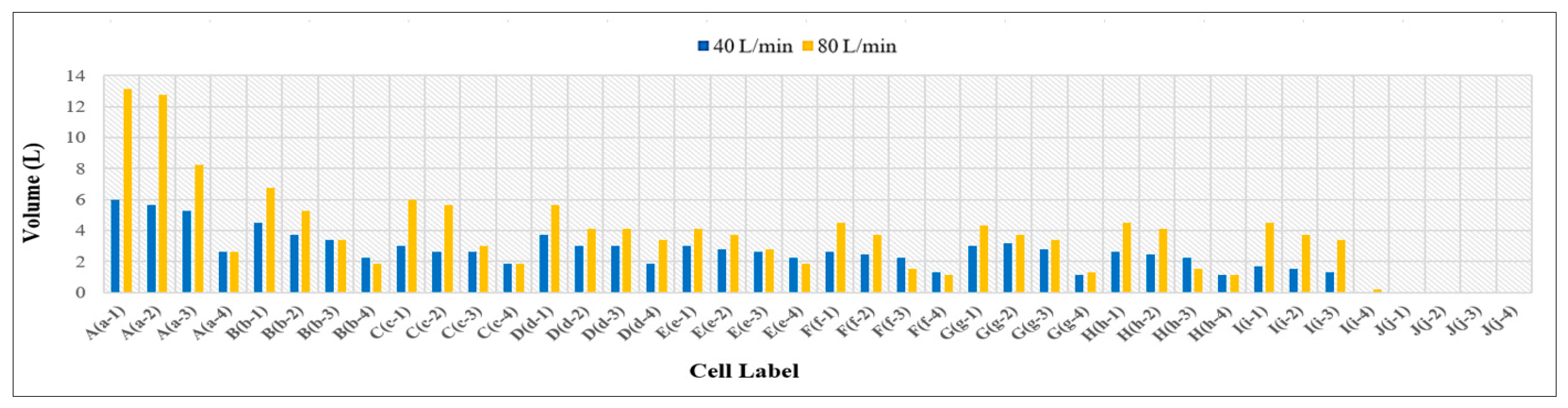
- At 40 L/min rainfall intensity under all the adopted longitudinal slopes, approximately an equal level of water has infiltrated through both patterns at (0 and 4%) T-Slope, whereas the cause of such behavior is that the surface joints of both types effectively absorb all the surface water, regardless of the slope, due to their equal efficiency. At 8% T-Slope, the infiltration of 45° herringbone PICP is higher than the stretcher bond, owing to the laying pattern of the 45° herringbone, which tends to infiltrate water rather than runoff, especially at high slopes. In addition, a higher surface area of joints is occupied by the 45° herringbone PICP in comparison to the stretcher bond.
- At 80% L/min rainfall intensity under 0% L-Slope, the level of water infiltration for both patterns is approximately equal for (0% and 4%) T-Slope, while at 8% T-Slope, the infiltration level for 45° herringbone PICP has become higher than the stretcher bond. By adjusting the longitudinal slope to (4% and 8%), the water infiltration for 45° herringbone PICP became higher than the stretcher bond for all the adopted transverse slopes. In addition, that behavior can be interpreted due to the higher surface area of the joints in the 45° herringbone pattern in comparison to the joints in the stretcher bond pattern, as depicted in Figure 26 and Figure 27. Consequently, the 45° herringbone pattern demonstrates a clear advantage, especially under high rainfall intensities (≥80 L/min). Put differently, the stretcher bond pattern exhibits greater runoff compared to the 45° herringbone pattern.
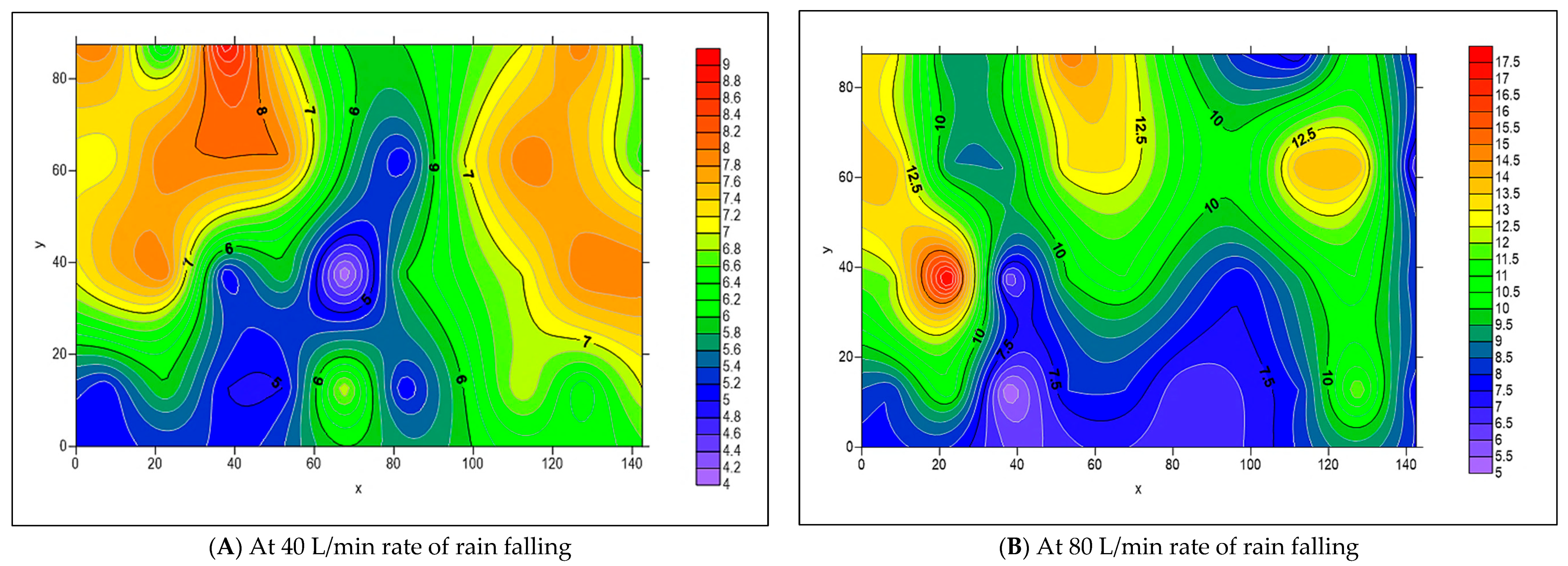
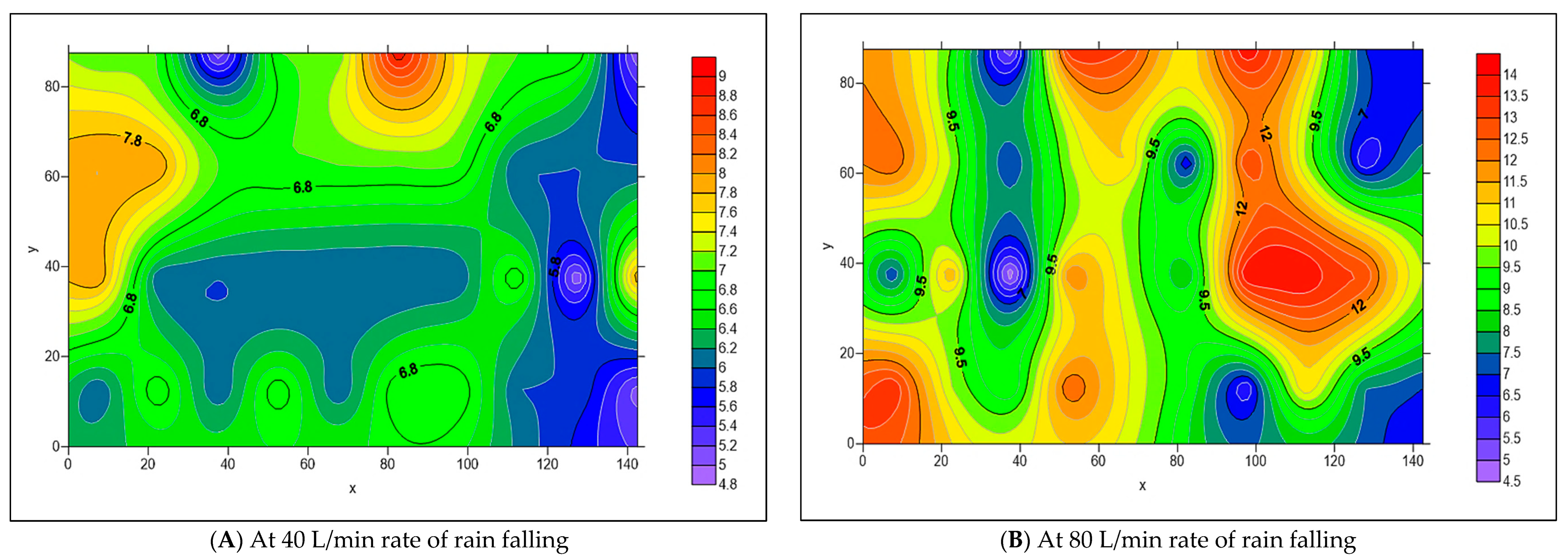
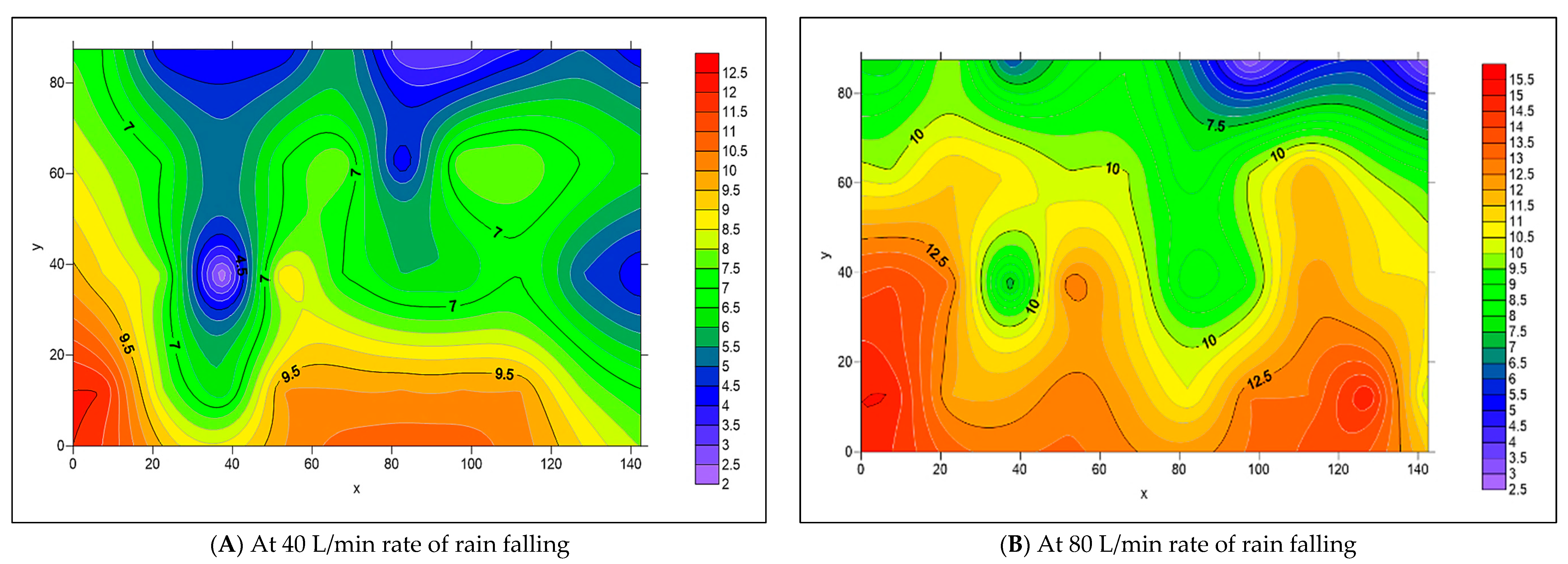
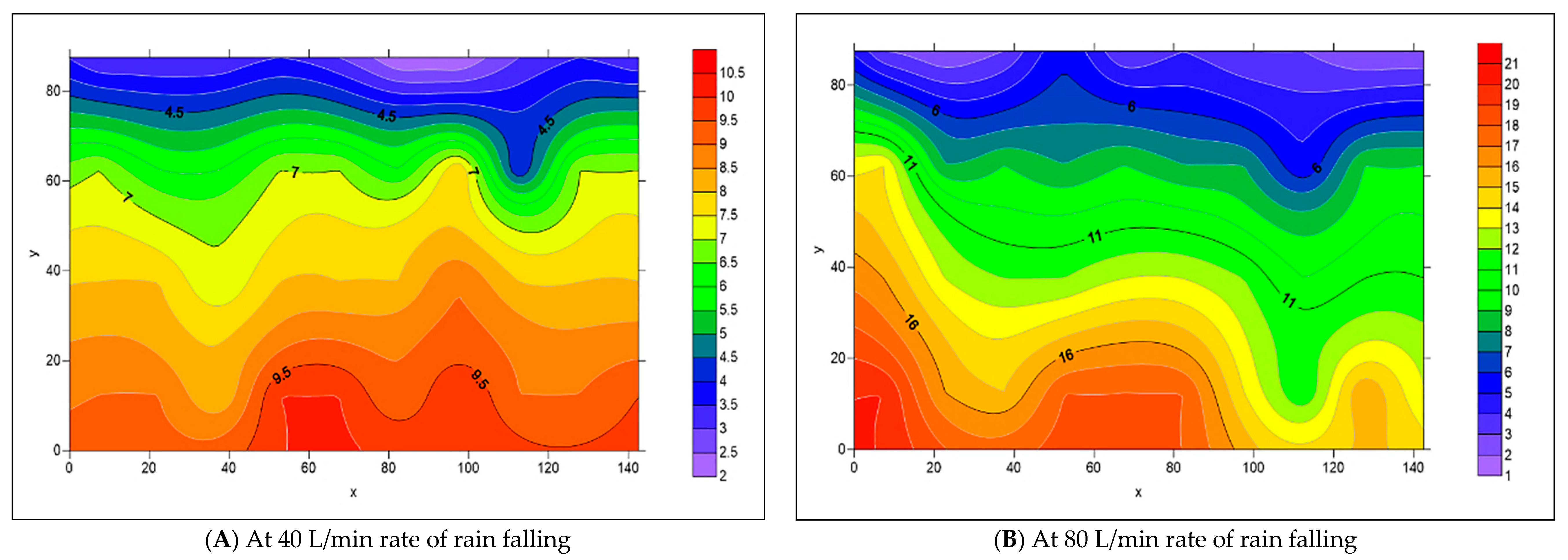
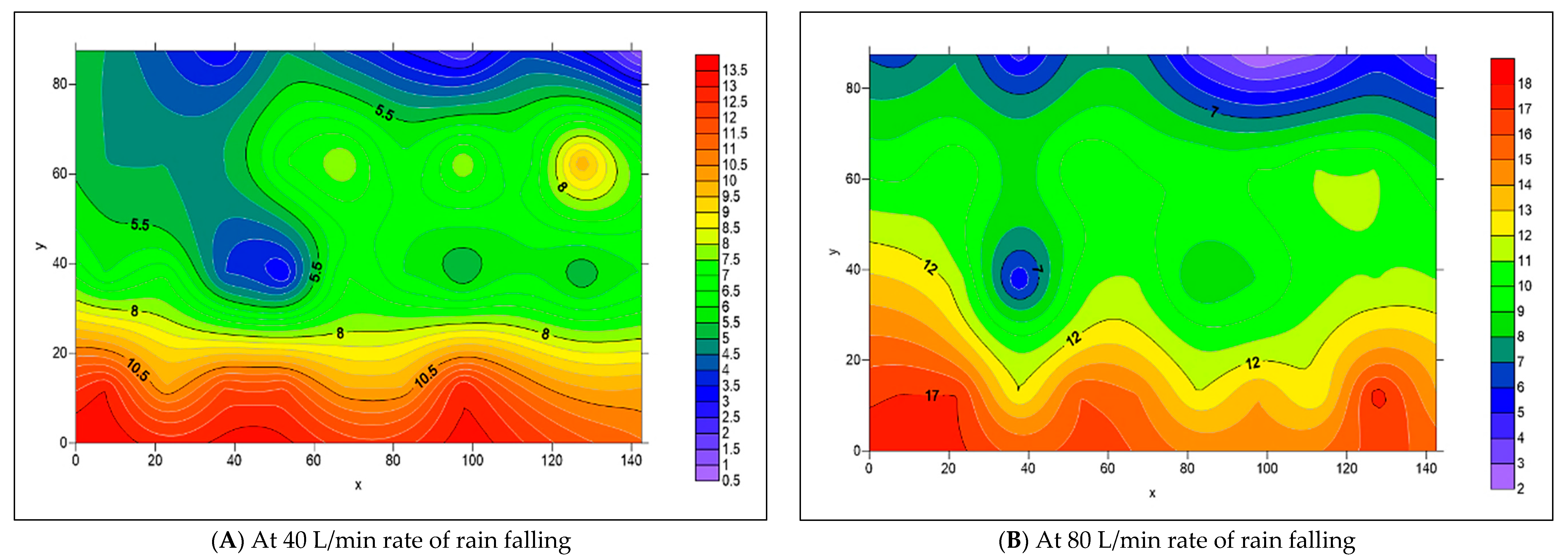
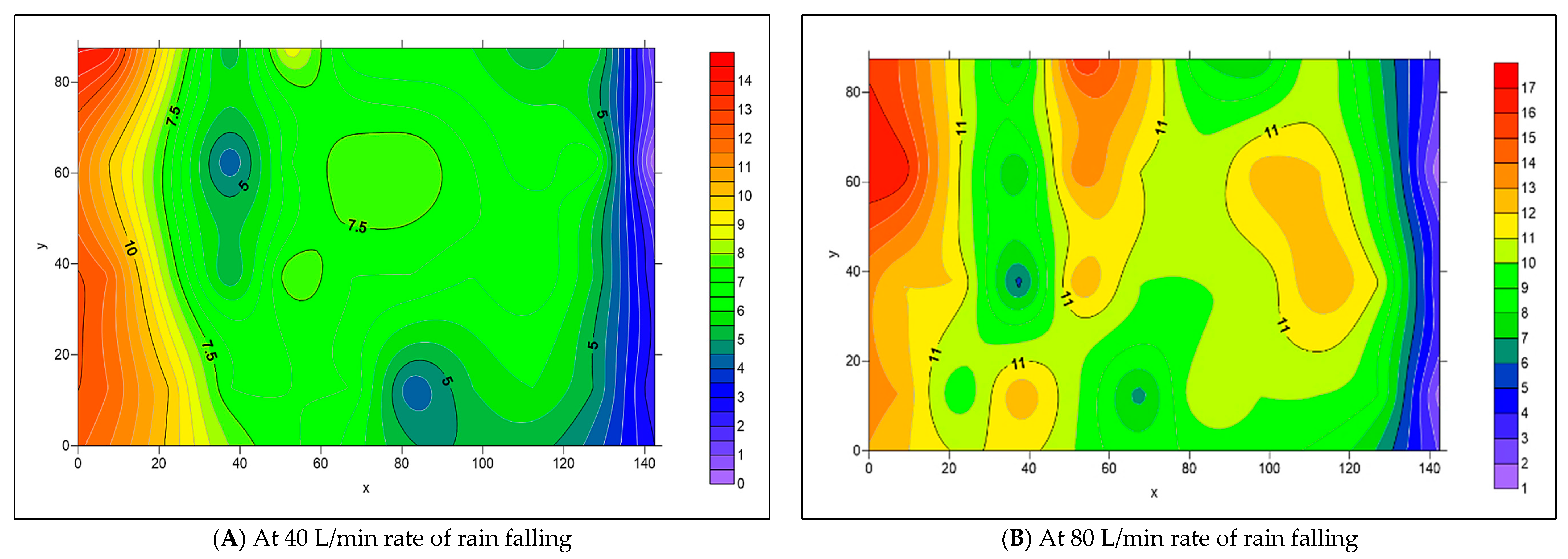
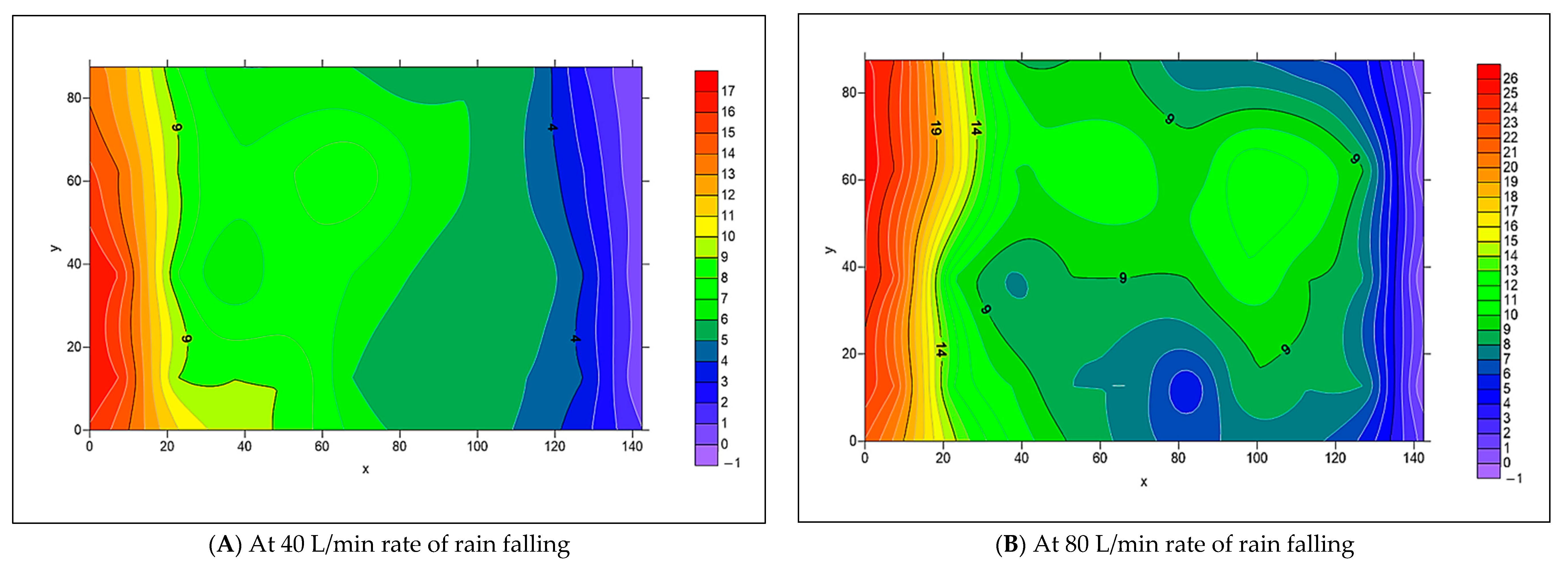
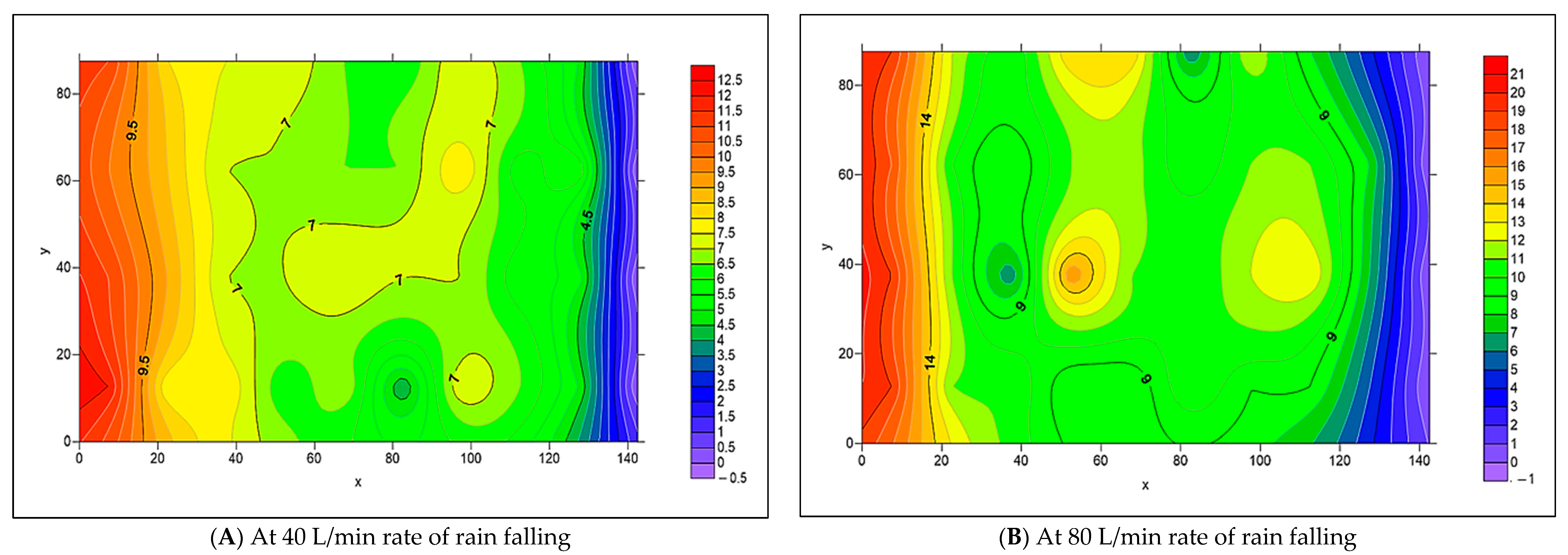
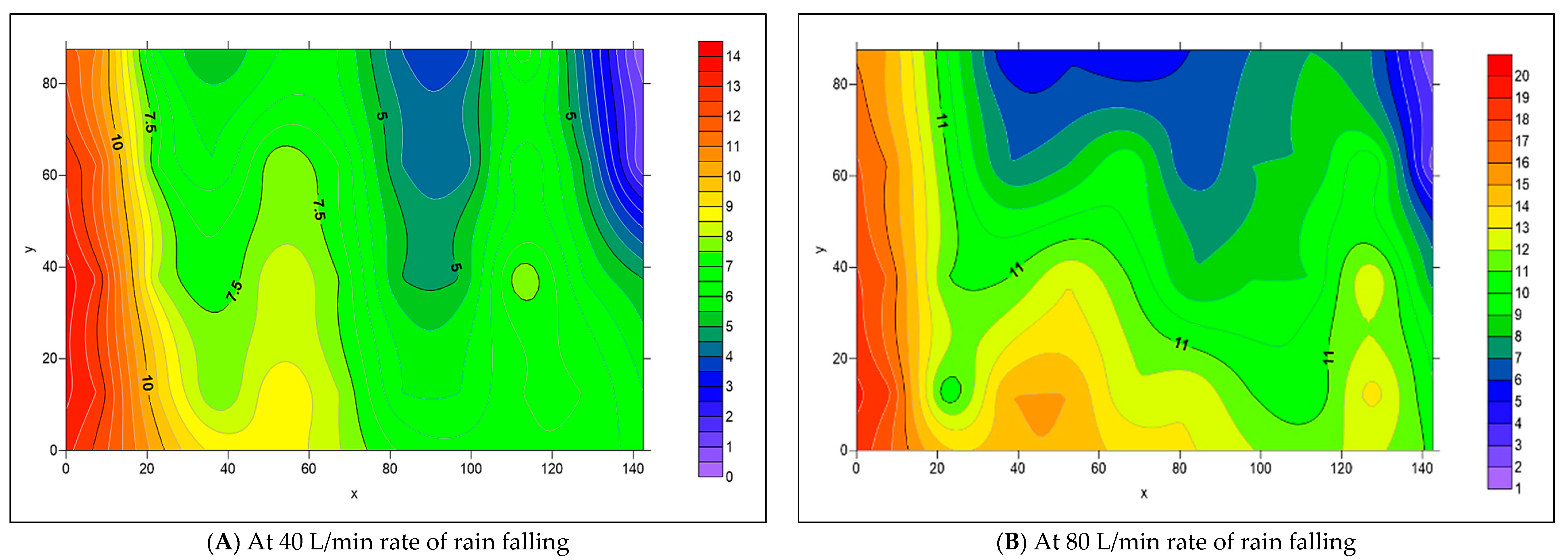
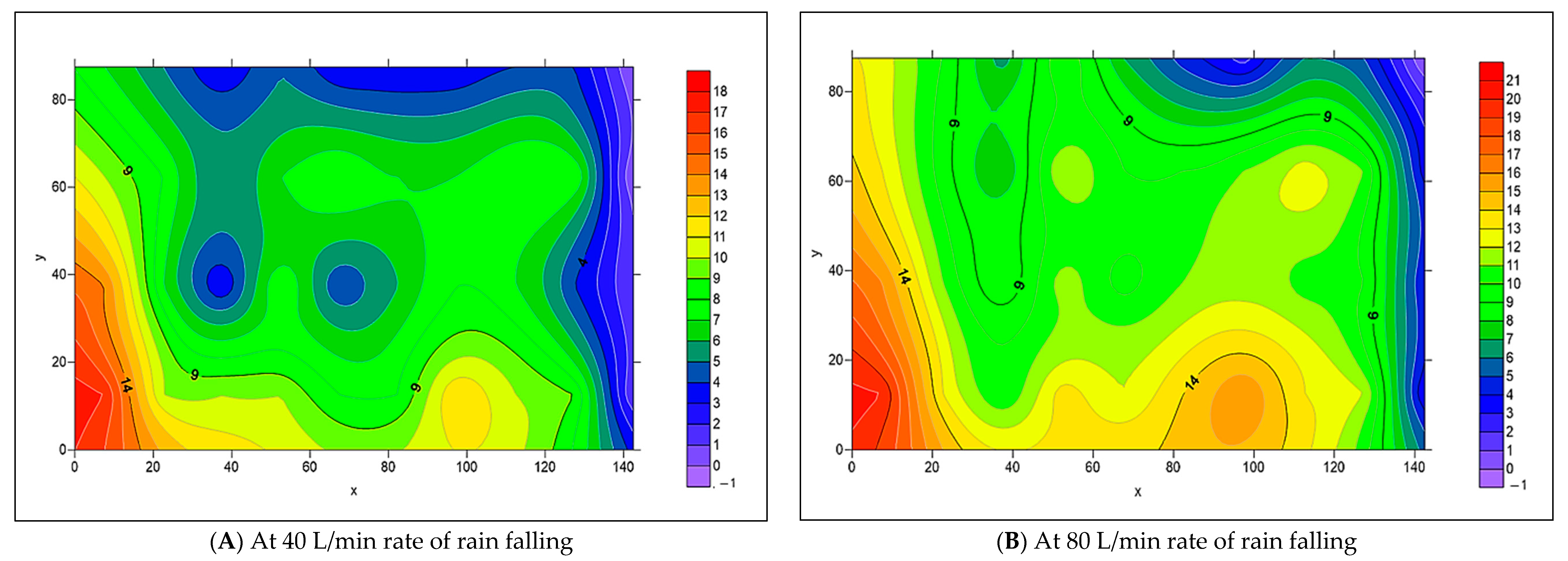
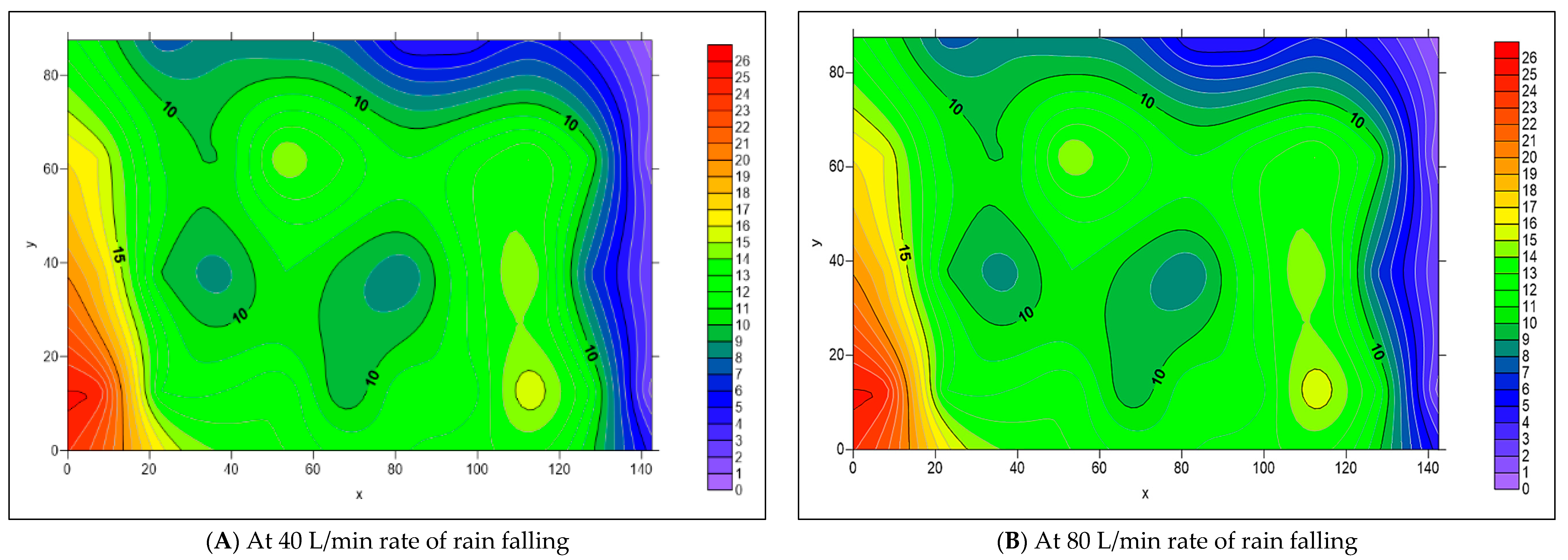
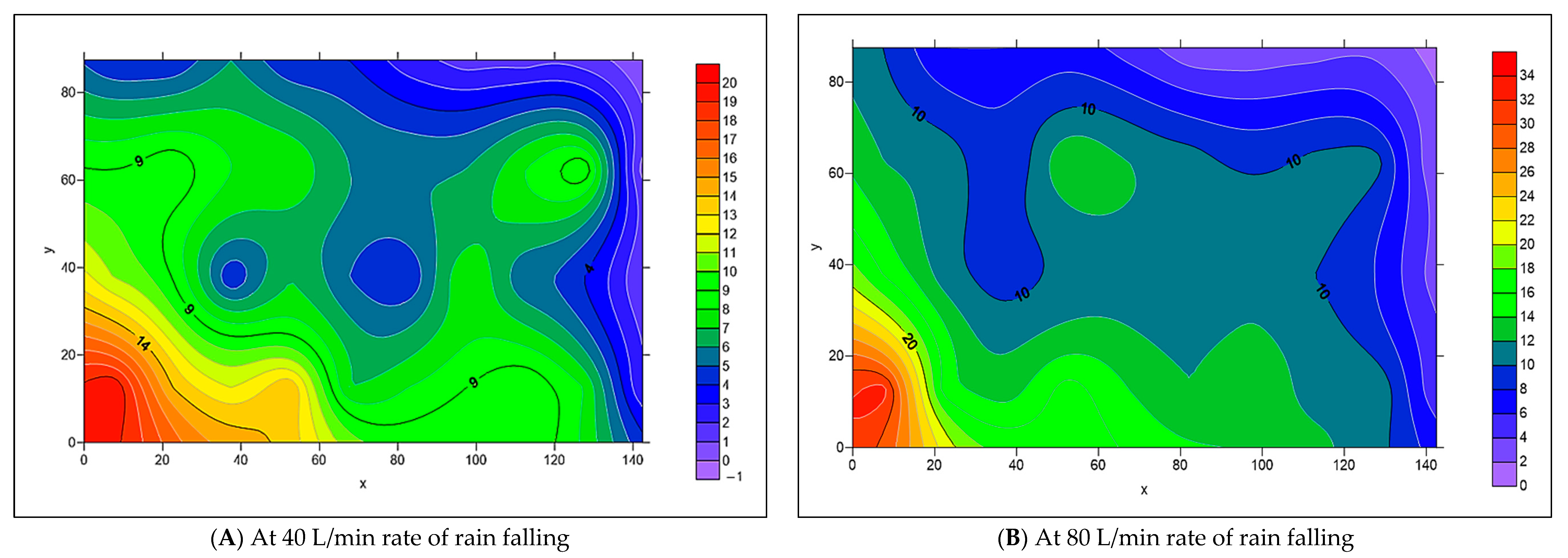
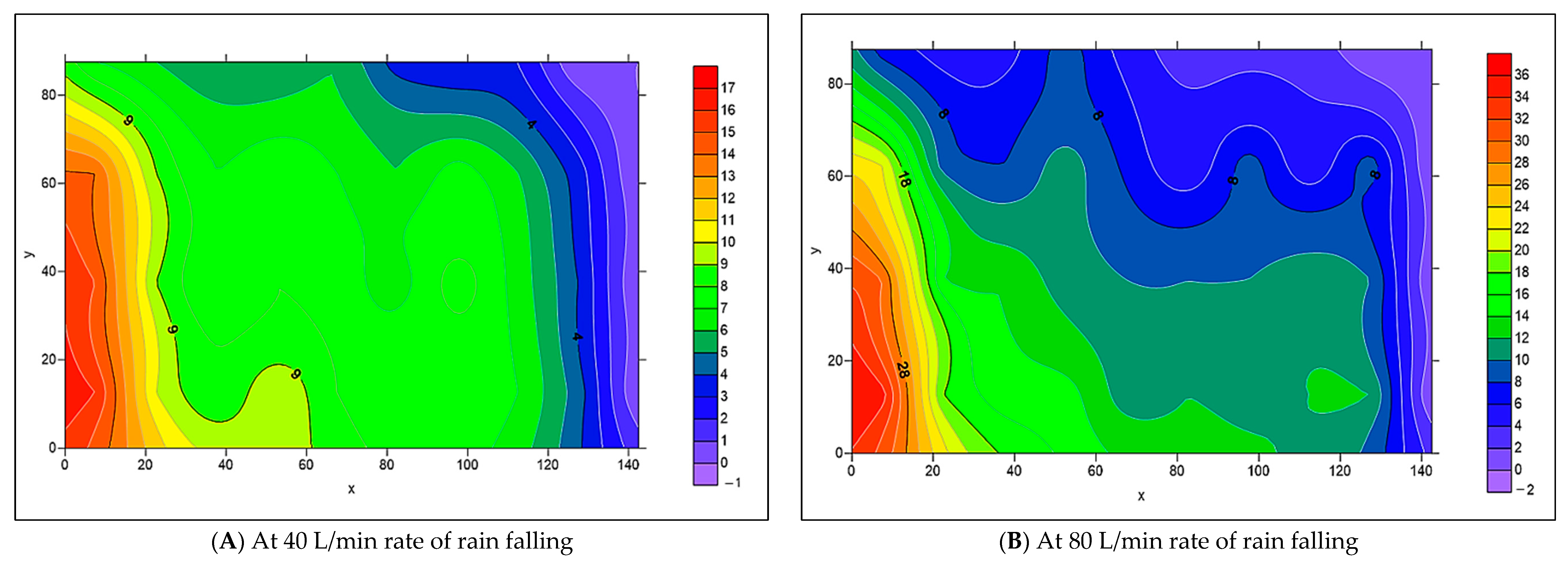
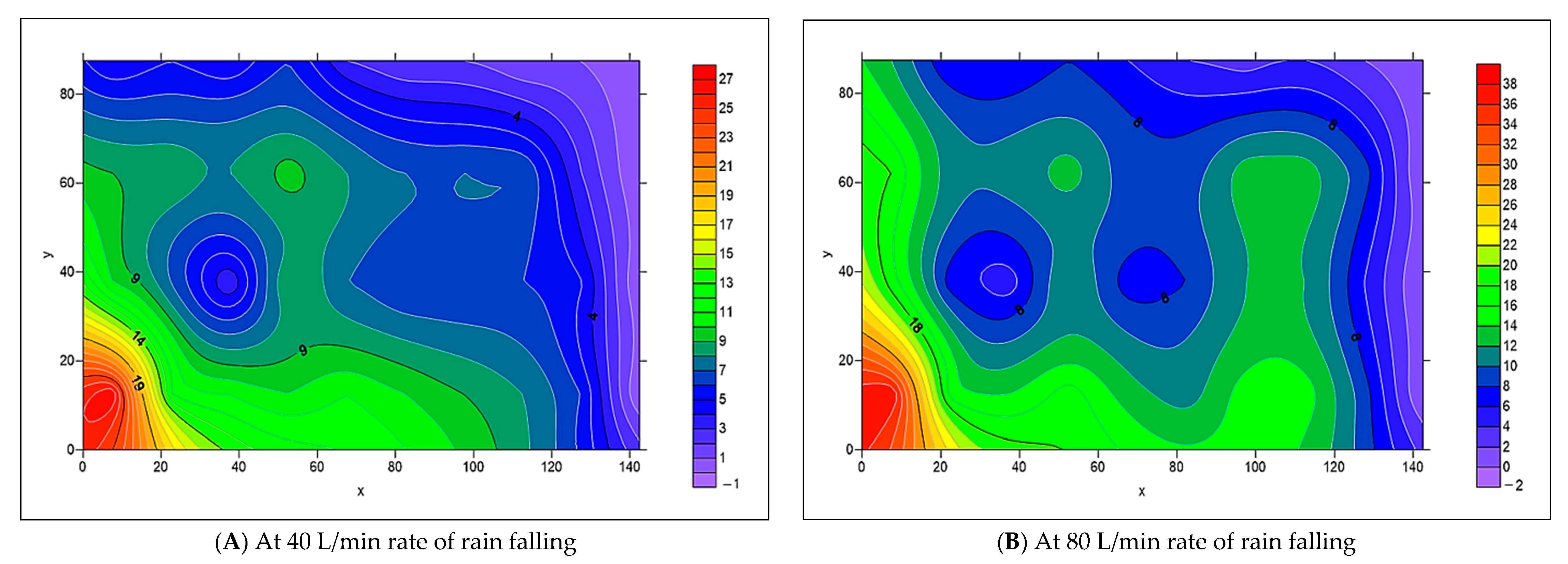
3.2. The Spread of Infiltrated Water Throughout the PICP Layers
- When both L-Slope and T-Slope are applied to the paver’s surface, the seeped water will collect at the corners of the iron frame of the apparatus, as shown in Figure 48, Figure 49, Figure 50, Figure 51, Figure 52, Figure 53, Figure 54, Figure 55, Figure 56, Figure 57, Figure 58, Figure 59, Figure 60, Figure 61, Figure 62 and Figure 63. The way the water behaves under these slopes is due to the force of gravity causing it to flow in the direction of runoff rather than infiltration.
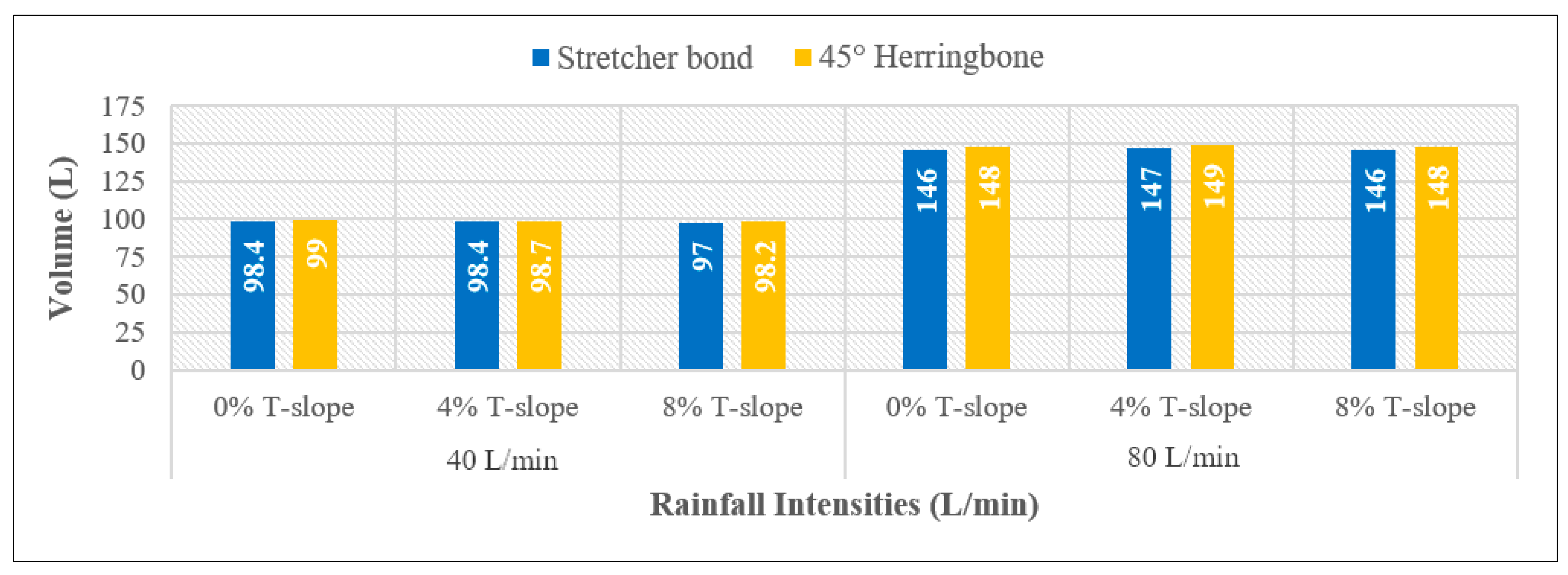
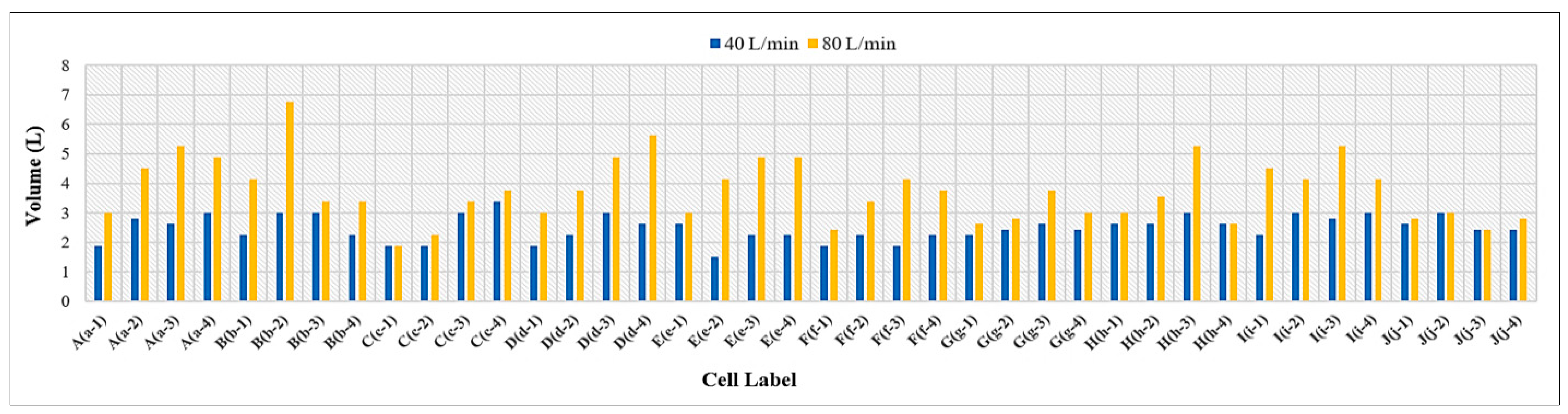
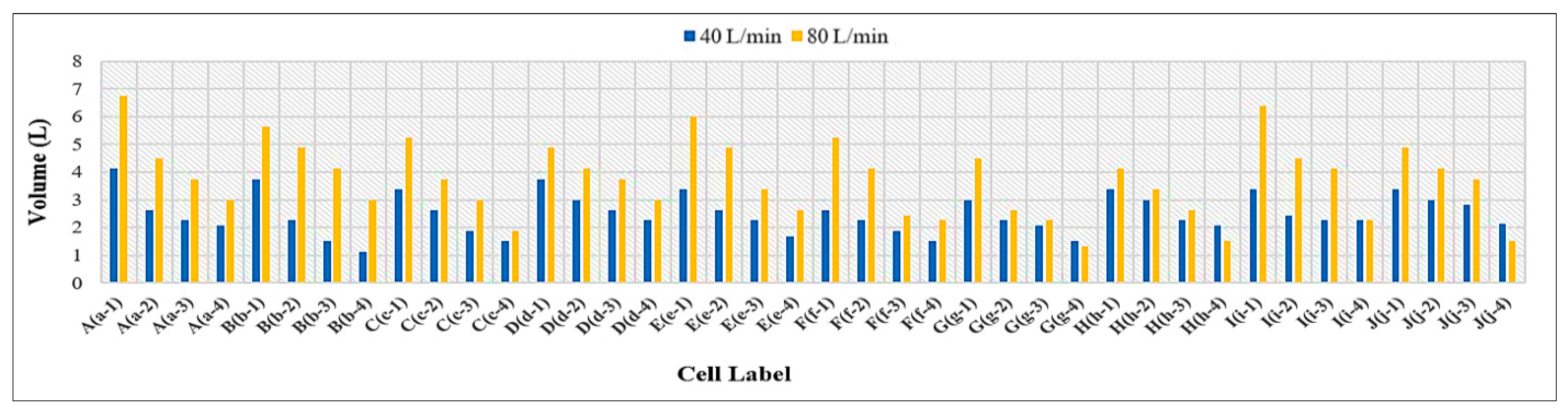
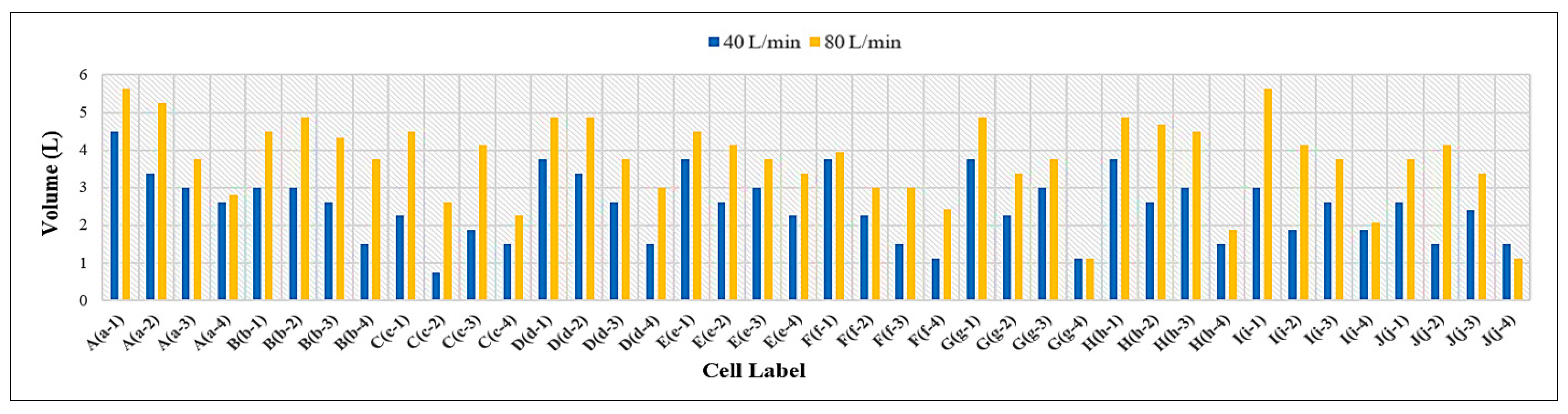
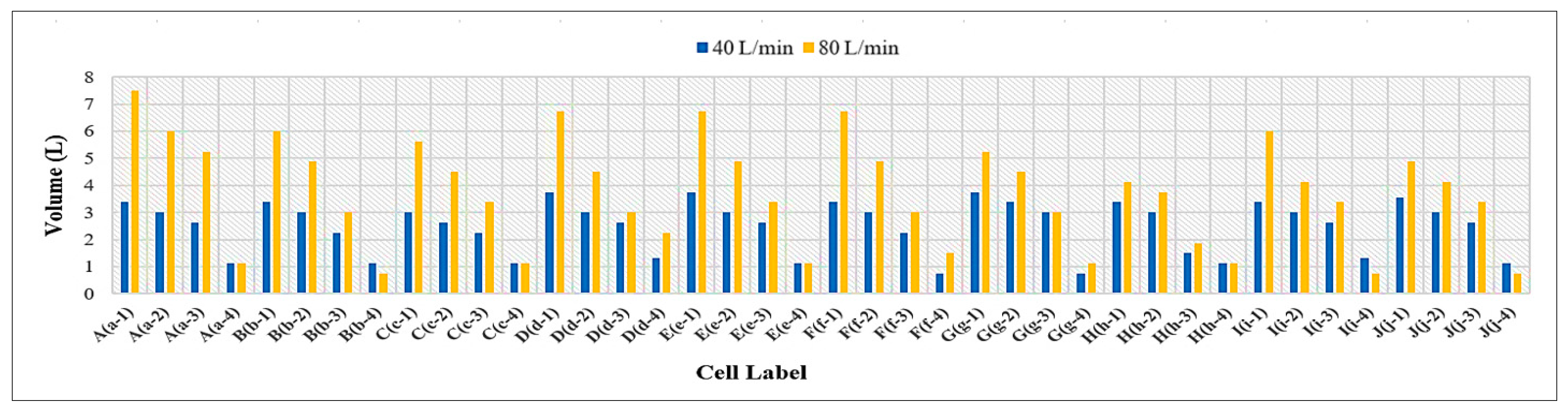
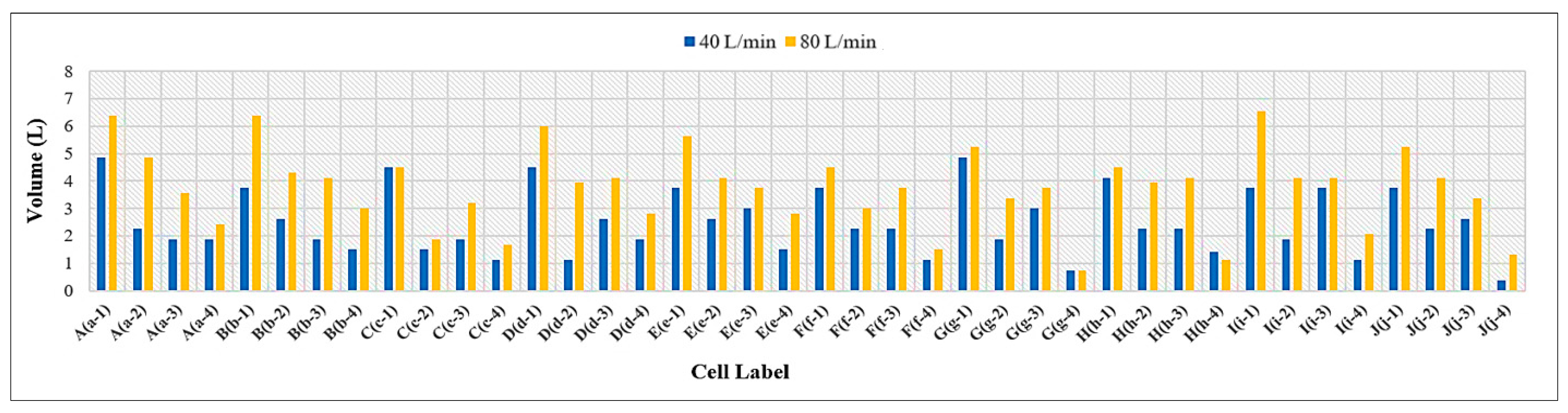
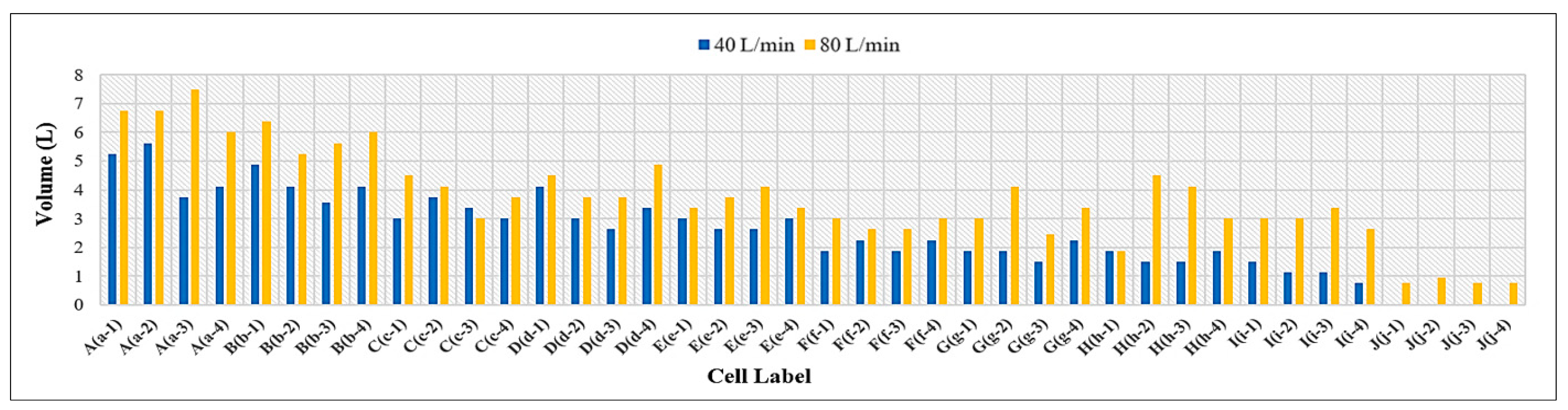
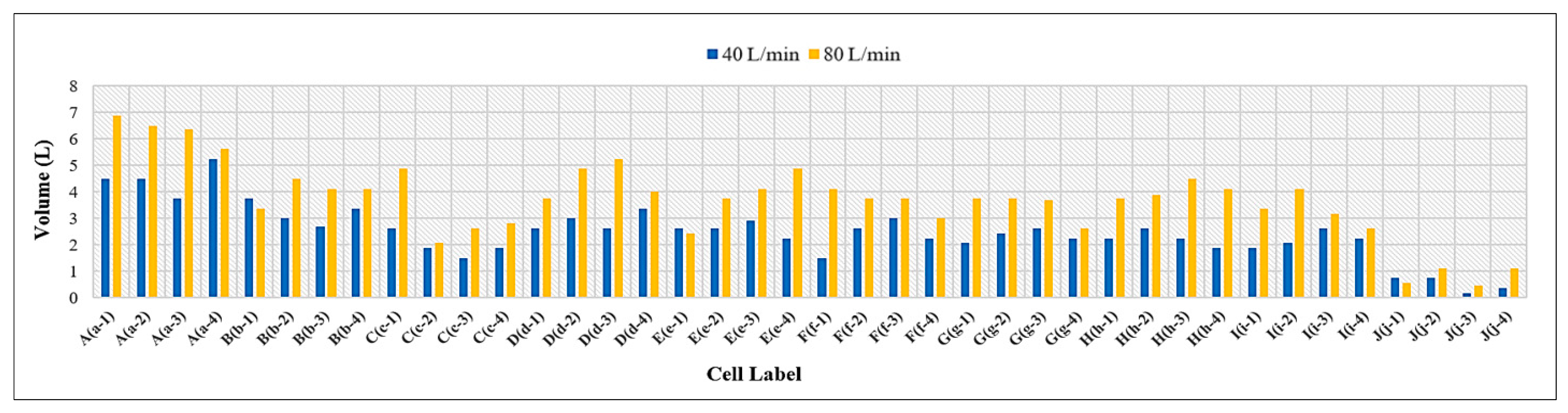
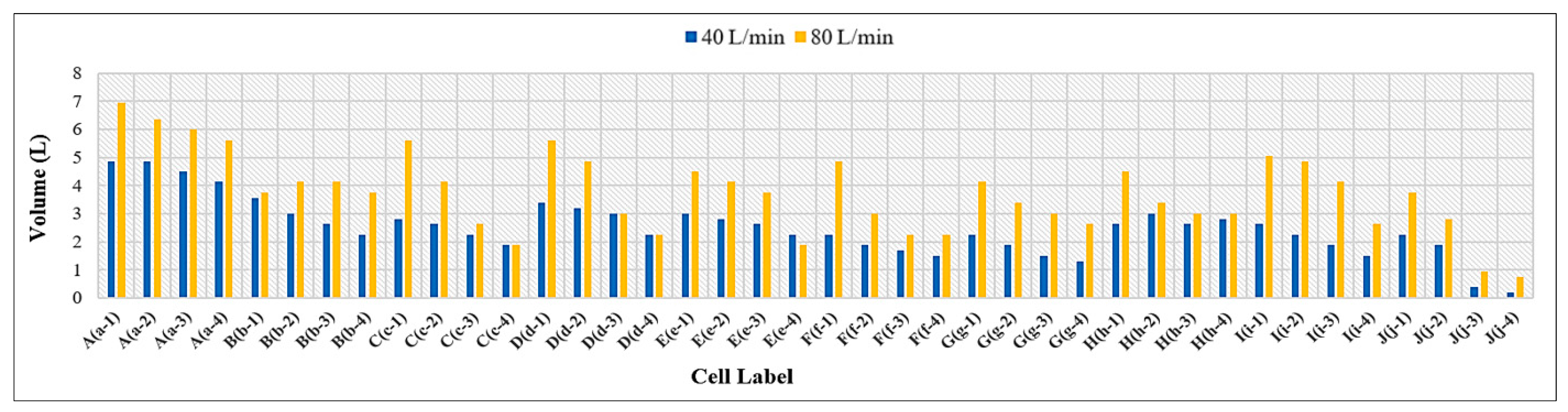
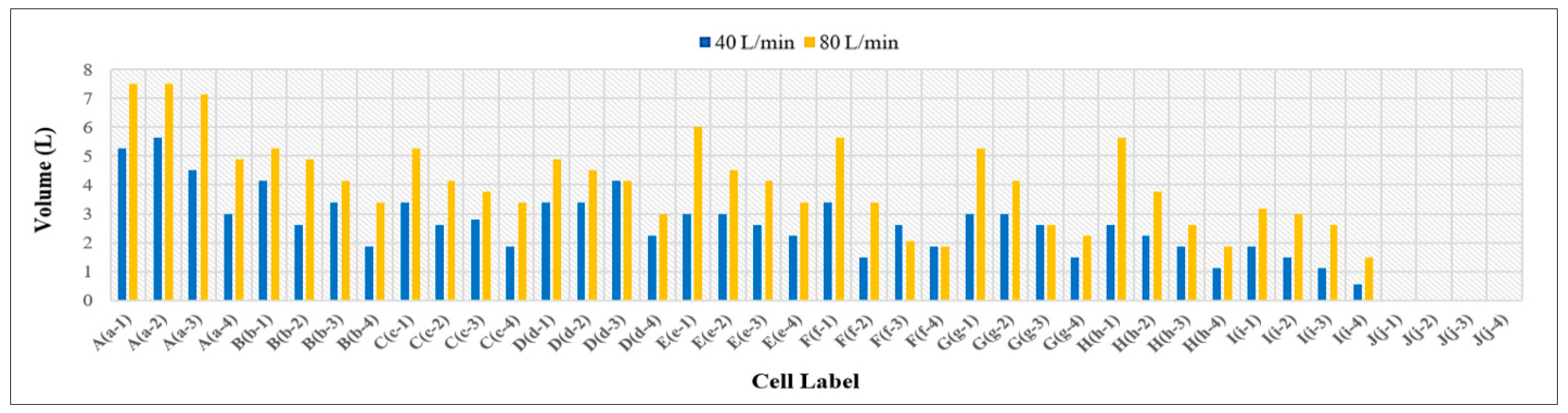
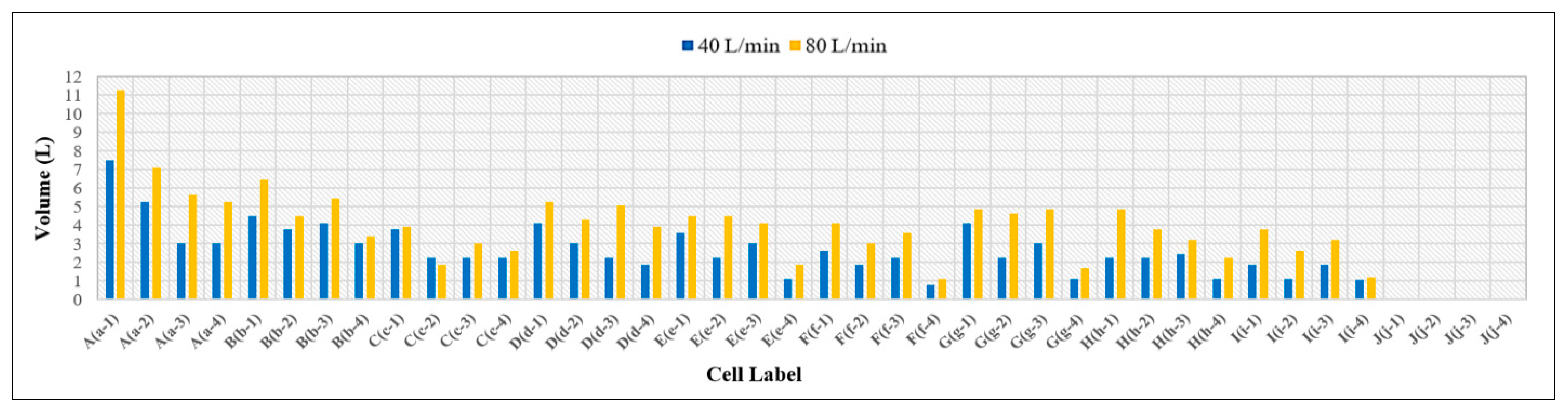
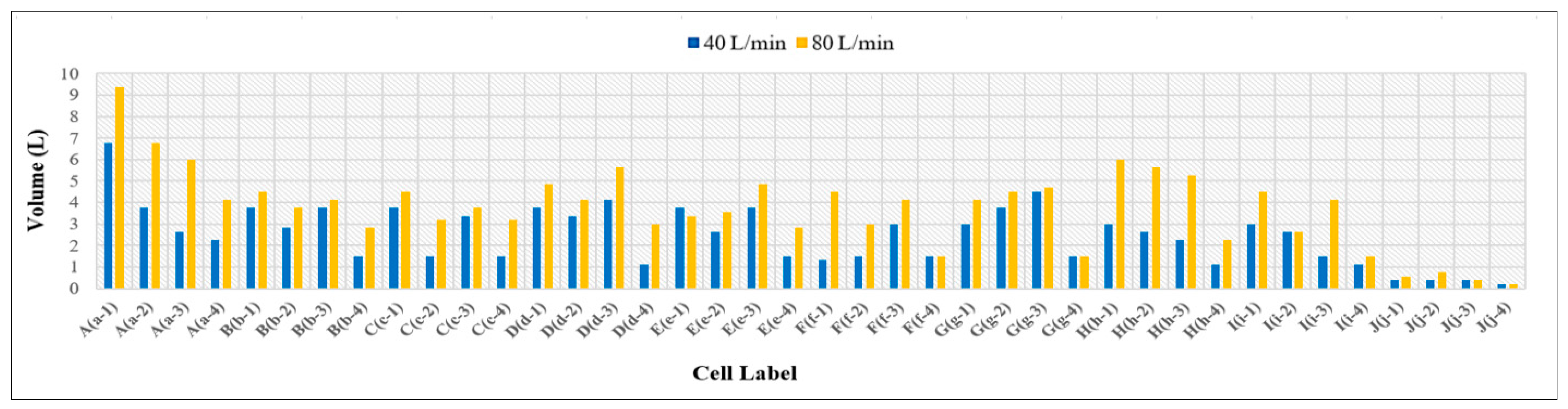
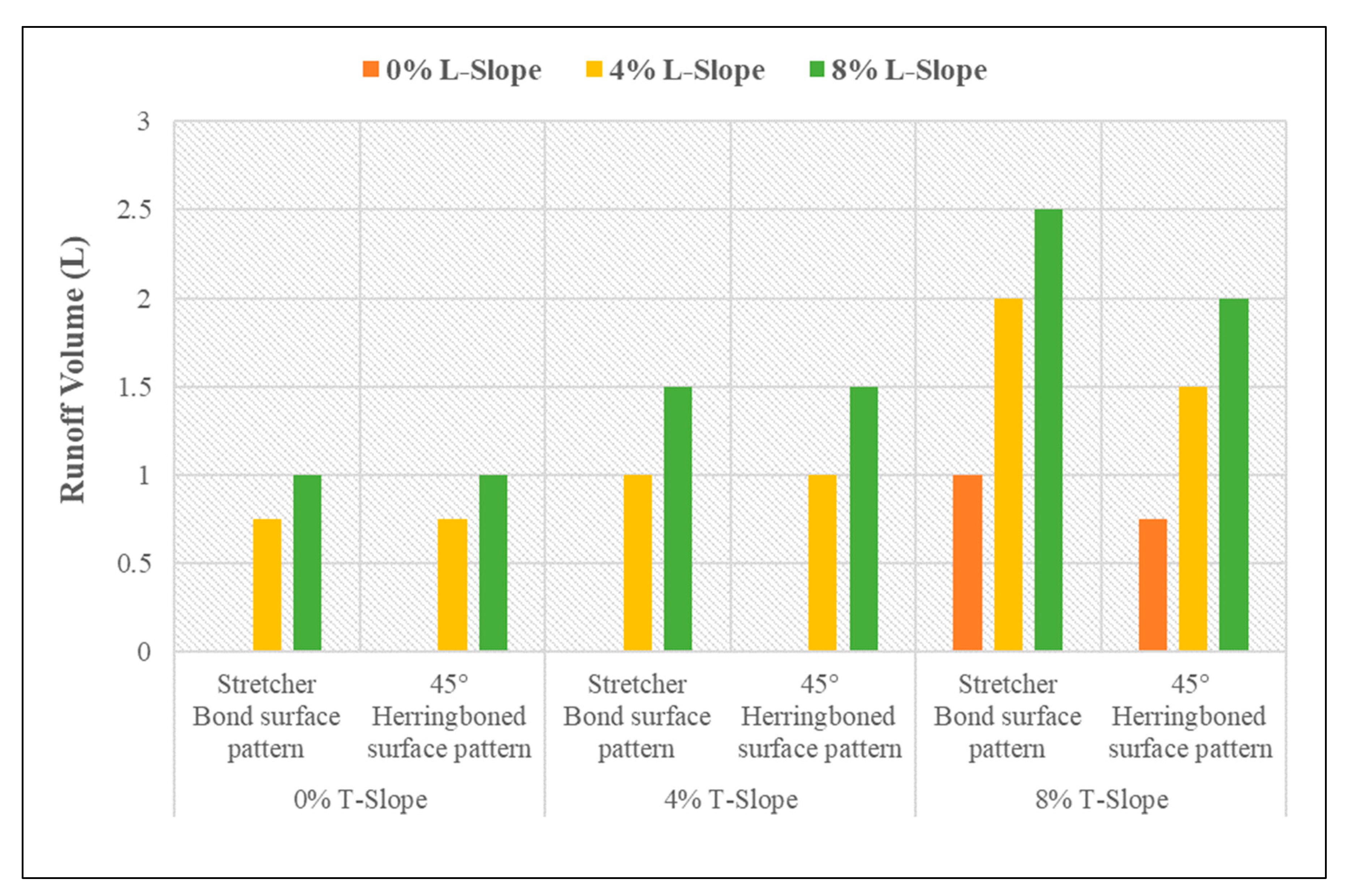
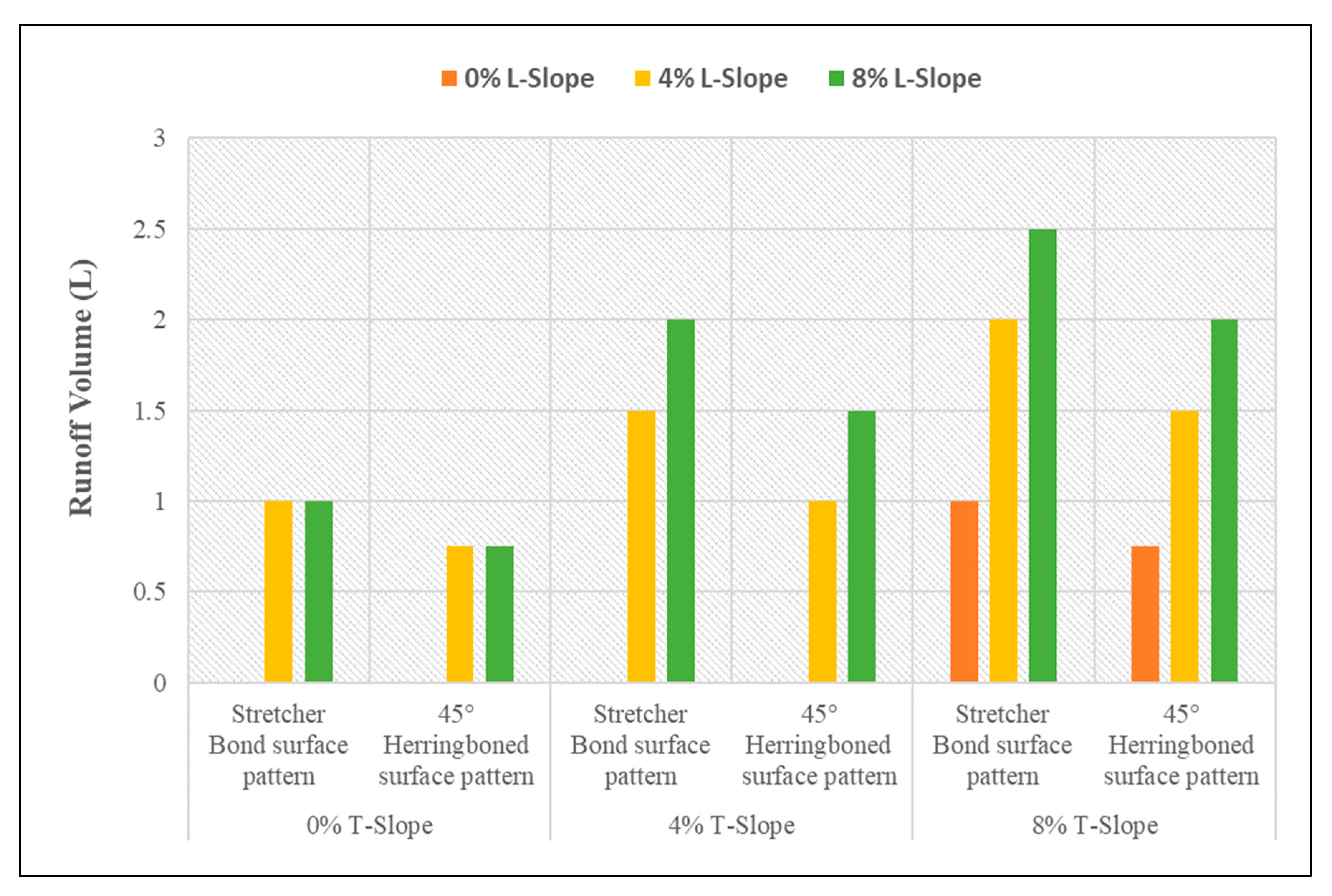
3.3. Volume of Runoff Water for PICPs’ Both Surface Types
3.4. Modeling Analysis
3.4.1. Introduction
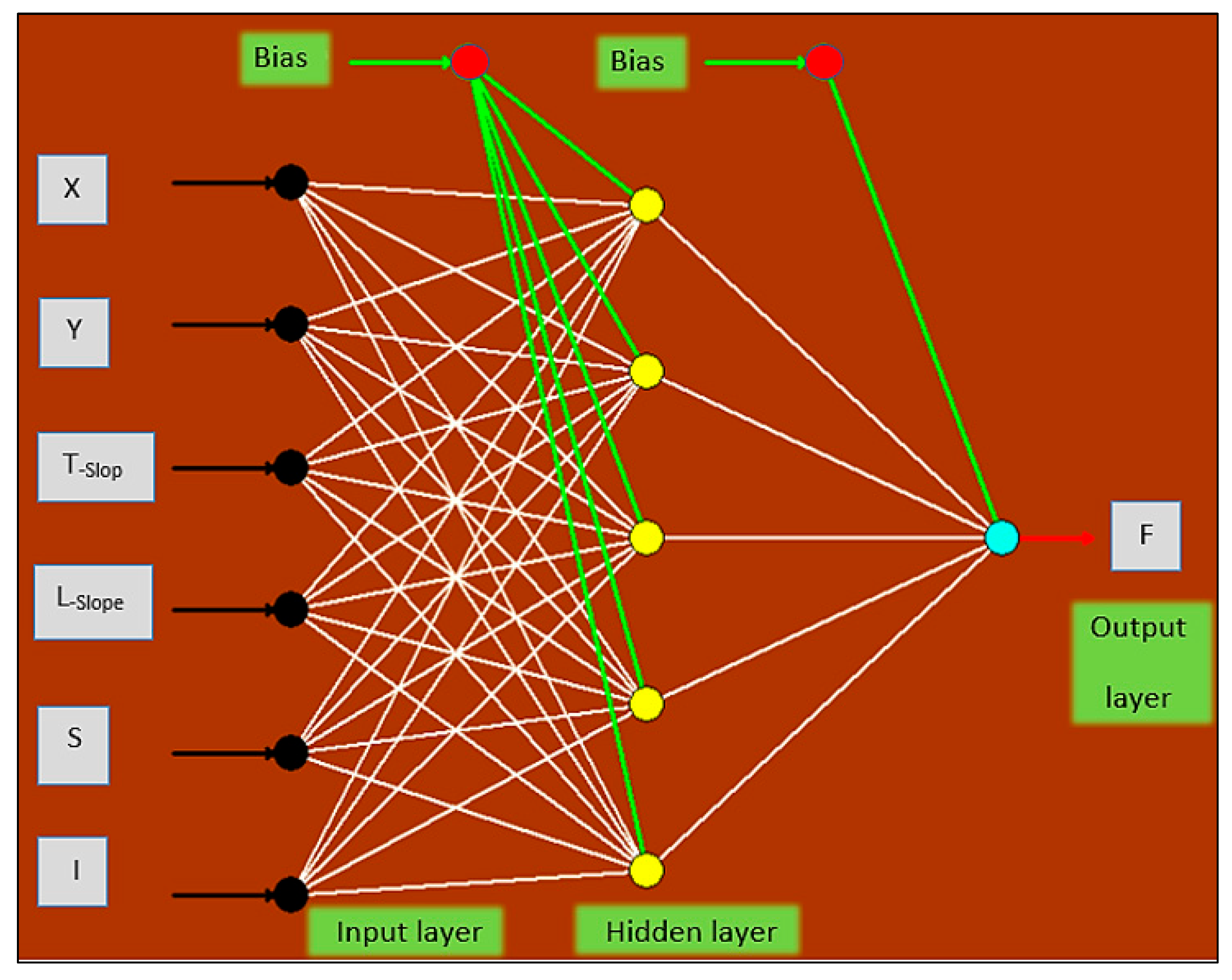
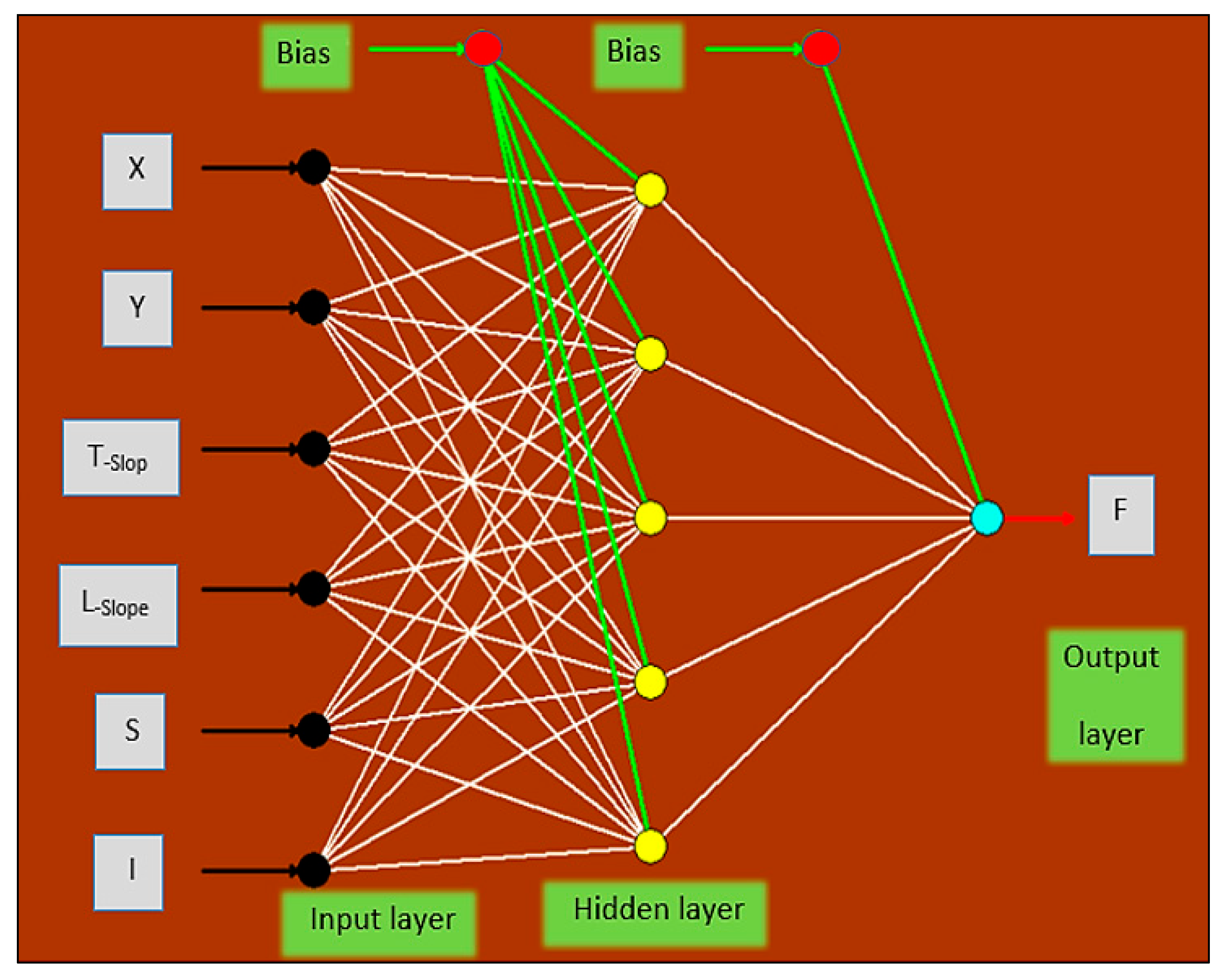
3.4.2. Artificial Neural Networks (ANNs)
3.4.3. Adequacy of the Model
- Input Layer
- A.
- Output ParametersF: The infiltration (cm/hr).
- B.
- Input ParametersX: Distance from the upper side of the road length (cm).Y: Distance from the upper side of the road width (cm).L-Slope: Surface slope in the long direction (%).T-Slop: Surface slope in the transverse direction (%).S: The gap between paving blocks (cm).I: Rainfall intensity by (L/min).
- 2.
- Hidden Layer
- 3.
- Output Layer
- Yi: Denotes the input variables.
- Xj and Xk: Power value of the sigmoid function for input and output, respectively.
- and : Bias values for neurons in the hidden and output layers, respectively.
- Wi, j and Wj, k: weights of the connections between neurons in the input and hidden layers, respectively.
- σxj and σxk: output values of the hidden and output layers, respectively.
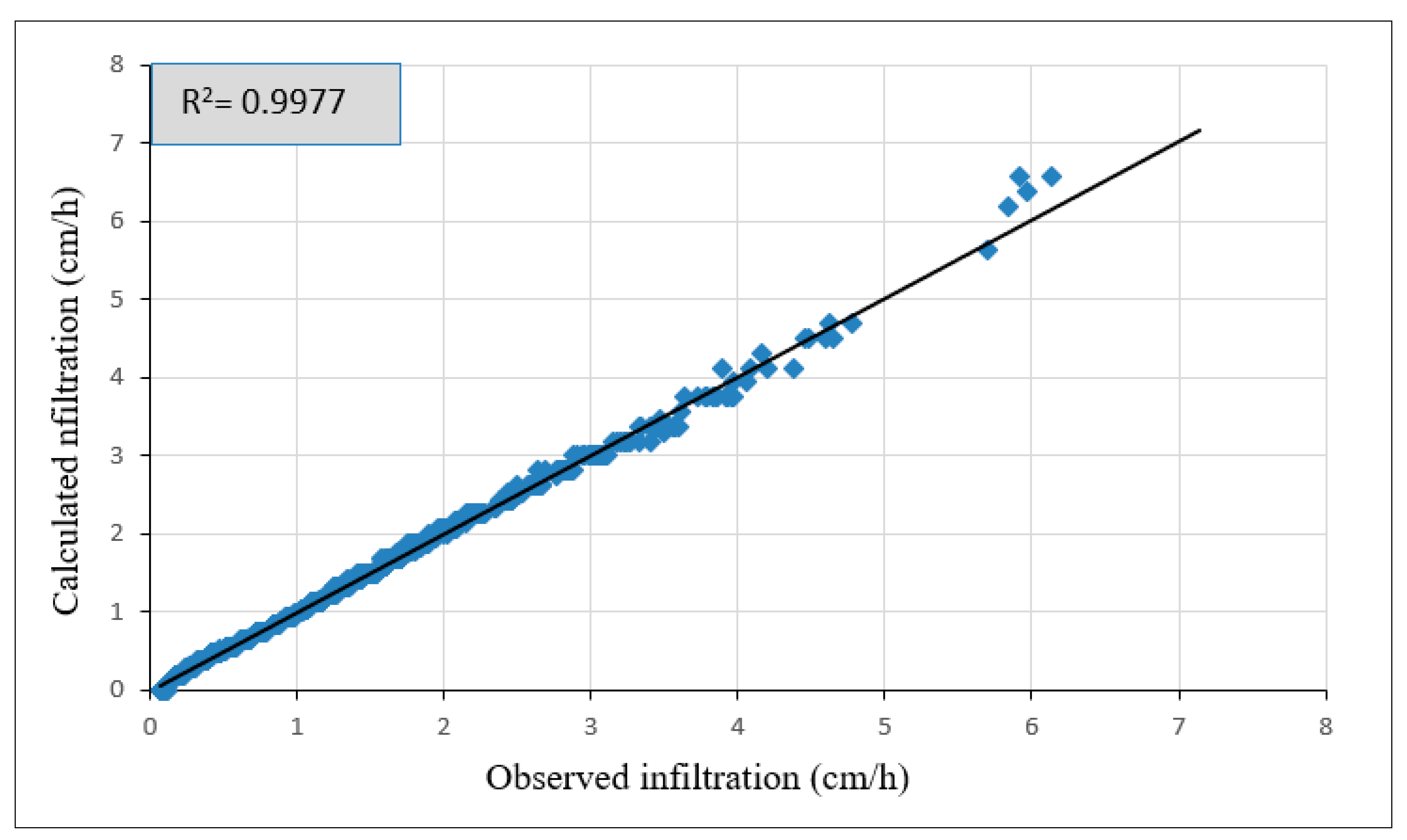
3.4.4. Validation of Modeling
4. Conclusions
- Under a rainfall intensity of 40 L/min, both stretcher bond and 45° herringbone PICP patterns exhibit comparable water infiltration rates at longitudinal slopes of 0% and 4% T-Slope. However, at an 8% T-Slope, the 45° herringbone pattern outperforms the stretcher bond by demonstrating higher infiltration rates, attributable to its design facilitating greater water penetration over runoff on steeper slopes. This suggests that the 45° herringbone configuration is more effective for enhancing stormwater management in areas with increased gradients.
- At a rainfall intensity of 80 L/min and a 0% longitudinal slope (L-Slope), both stretcher bond and 45° herringbone PICP patterns exhibited similar water infiltration rates at transverse slopes (T-Slope) of 0% and 4%. However, at an (8% T-Slope), the 45° herringbone pattern surpassed the stretcher bond with greater infiltration. This trend persisted as the longitudinal slope increased to 4% and 8%, where the 45° herringbone PICP consistently outperformed the stretcher bond across all tested transverse slopes. These findings indicate that the 45° herringbone pattern is more effective at enhancing water infiltration under higher slopes and intense rainfall, making it a superior choice for managing stormwater in such conditions.
- Under the same geometrical and weathering conditions, the PICP’s performance in reducing runoff with a 45° herringbone surface pattern is superior compared to the stretcher bond pattern.
- The operating tests revealed that both PICP surface patterns, the stretcher bond and 45° herringbone, performed highly and are on par with traditional pavement.
- The results of the simulation process for the distribution of infiltrated water, as modeled by Surfer 2.0 software, matched the actual distribution in the collection cells.
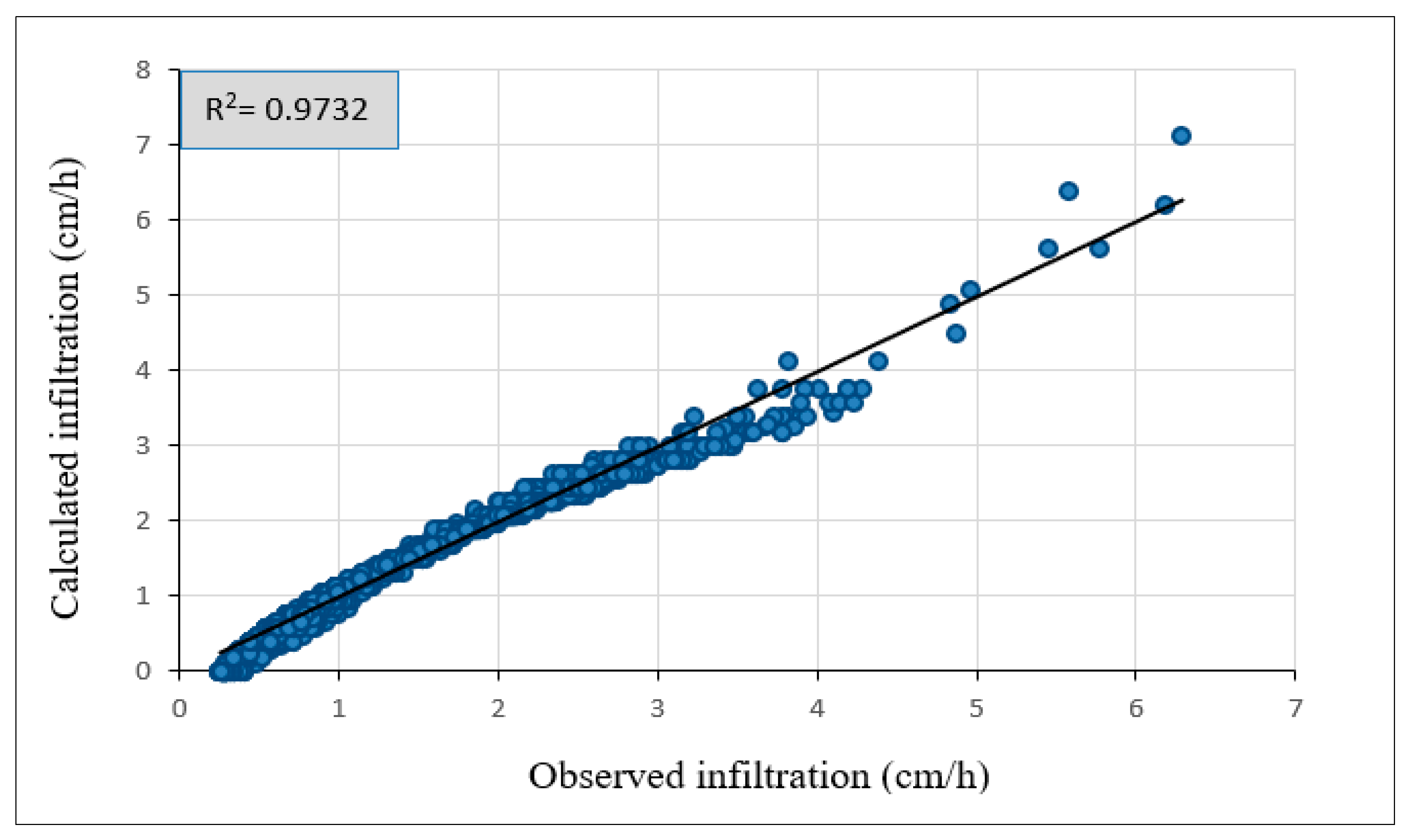
- The statistical models for the stretcher bond and 45° herringbone patterns exhibit high accuracy, with R2 values of 99.97% and 97.32%, respectively, indicating their validity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hein, D.K.; Eng, P. Development of an ASCE standard for permeable interlocking concrete pavement. In Proceedings of the of the 2014 Conference of the Transportation Association of Canada Montréal, Québec, QC, Canada, 28 September–1 October 2014; Volume 416, pp. 1–15. [Google Scholar]
- Leipard, A.R.; Kevern, J.T.; Richardson, J.R. Hydraulic characterization and design of permeable interlocking concrete pavement. In Proceedings of the World Environmental and Water Resources Congress 2015, Austin, TX, USA, 17–21 May 2015. [Google Scholar]
- Smith, D.R. Permeable Interlocking Concrete Pavement [Techbrief]; Federal Highway Administration: Washington, DC, USA, 2019. [Google Scholar]
- Kayhanian, M.; Li, H.; Harvey, J.T.; Liang, X. Application of permeable pavements in highways for stormwater runoff management and pollution prevention: California research experiences. Int. J. Transp. Sci. Technol. 2019, 8, 358–372. [Google Scholar] [CrossRef]
- Al Qurishee, M. Application of geosynthetics in pavement design. Int. Res. J. Eng. Technol. 2017, 4, 1–7. [Google Scholar]
- Zhang, K.; Kevern, J. Review of porous asphalt pavements in cold regions: The state of practice and case study repository in design, construction, and maintenance. J. Infrastruct. Preserv. Resil. 2021, 2, 1–17. [Google Scholar] [CrossRef]
- Fanijo, E.O.; Kolawole, J.T.; Babafemi, A.J.; Liu, J. A comprehensive review on the use of recycled concrete aggregate for pavement construction: Properties, performance, and sustainability. Clean. Mater. 2023, 9, 100199. [Google Scholar] [CrossRef]
- Khan, Z.A.; Balunaini, U.; Costa, S.; Nguyen, N. A review on sustainable use of recycled construction and demolition waste aggregates in pavement base and subbase layers. Clean. Mater. 2024, 13, 100266. [Google Scholar] [CrossRef]
- Putman, B.J.; Neptune, A.I. Comparison of test specimen preparation techniques for pervious concrete pavements. Constr. Build. Mater. 2011, 25, 3480–3485. [Google Scholar] [CrossRef]
- Mo, L.T.; Huurman, M.; Wu, S.P.; Molenaar, A.A.A. Investigation into stress states in porous asphalt concrete on the basis of FE-modelling. Finite Elem. Anal. Des. 2007, 43, 333–343. [Google Scholar] [CrossRef]
- Park, D.-G.; Sandoval, N.; Lin, W.; Kim, H.; Cho, Y.-H. A case study: Evaluation of water storage capacity in permeable block pavement. KSCE J. Civ. Eng. 2014, 18, 514–520. [Google Scholar] [CrossRef]
- W. B.Nichols, P.; Lucke, T.; Dierkes, C. Comparing two methods of determining infiltration rates of permeable interlocking concrete pavers. Water 2014, 6, 2353–2366. [Google Scholar] [CrossRef]
- Smith, D.R.; Earley, K.; Lia, J. Potential application of ASTM C 1701 for evaluating Surface infiltration of permeable interlocking concrete pavements; ASTM Special Technical Publication: West Conshohocken, PA, USA, 2012; pp. 97–105. [Google Scholar] [CrossRef]
- Smith, D.R.; Hein, D.K. Development of a National ASCE standard for permeable interlocking concrete pavement. In Green Streets, Highways, and Development 2013: Advancing the Practice; ASCE: Reston, VA, USA, 2013; pp. 89–105. [Google Scholar]
- Hashim, T.M.; Al-mulali, M.Z.; Al-Khafaji, F.F.; Alwash, A.A.A.; Ali, Y.A. An experimental comparison between different types of surface patterns of permeable interlocking concrete pavement for roadway subsurface drainage. Case Stud. Constr. Mater. 2022, 17, e01227. [Google Scholar] [CrossRef]
- Hein, D.K.; Strecker, E.; Poresky, A.; Roseen, R.; Venner, M. Permeable Shoulders with Stone Reservoirs; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2013. [Google Scholar]
- Yusuf, K.O.; Olaoke, S.O.; Iwayemi, A.K.; Adewoye, W.A.; Oyebode, O.O.; Omokore, S. Design and construction of a simple rainfall simulator from locally available materials. LAUTECH J. Eng. Technol. 2015, 9, 13–19. [Google Scholar]
- Mendes, T.A.; Pereira, S.A. dos S.; Rebolledo, J.F.R.; Gitirana Jr, G. de F.N.; Melo, M.T. da S.; Luz, M.P. da Development of a rainfall and runoff simulator for performing hydrological and geotechnical tests. Sustainability 2021, 13, 3060. [Google Scholar] [CrossRef]
- Alzamly, S.A.; Aldefae, A.H.; Humaish, W.H.; Sinichenko, E.K.; Zubaidi, S.L. Design and manufacturing of rainfall simulator machine for the soil erosion investigation. In Geotechnical Engineering and Sustainable Construction: Sustainable Geotechnical Engineering; Springer: Berlin/Heidelberg, Germany, 2022; pp. 177–190. [Google Scholar]
- Mhaske, S.N.; Pathak, K.; Basak, A. A comprehensive design of rainfall simulator for the assessment of soil erosion in the laboratory. Catena 2019, 172, 408–420. [Google Scholar] [CrossRef]
- ASTM C418; Standard Test Method for Abrasion Resistance of Concrete by Sandblasting. ASTM International: West Conshohocken, PA, USA, 2012.
- ASTM C563; Standard Test Method for Approximation of Optimum SO3 in Hydraulic Cement Using Compressive Strength. ASTM International: West Conshohocken, PA, USA, 1996.
- ASTM C140; Standard Test Methods for Sampling and Testing Concrete Masonry Units and Related Units. ASTM International: West Conshohocken, PA, USA, 2008.
- ASTM D448; Standard Classification for Sizes of Aggregate for Road and Bridge Construction. ASTM International: West Conshohocken, PA, USA, 2008.
- Abdollahi, S.F.; Lanotte, M.; Kutay, M.E.; Bahia, H. AASHTO 1993 Plus: An alternative procedure for the calculation of structural asphalt layer coefficients. Int. J. Pavement Eng. 2022, 24, 2118273. [Google Scholar] [CrossRef]
- Knothe, G.J. The Influence of Urbanization on Streams: The Use of GIS Spatial Analysis to Study Land Use Influence on Fish Communities, Water Quality and Physical Habitats in Southeast Texas; University of Houston-Clear Lake: Houston, TX, USA, 2012. [Google Scholar]
- Hashim, T.M.; Al-Fatlawi, T.J.; Al-Abody, A.A.; Musa, D.A.; Nasr, M.S. The behavior of permeable interlocking concrete pavement under different rainfall intensities and design conditions. Int. J. Pavement Eng. 2023, 24, 2152026. [Google Scholar] [CrossRef]
- Smith, D.R.; Sinagra, E.; Duvall, J. Surface Characteristics of Segmental Concrete Pavements Acceptable to Wheelchair Users. In Proceedings of the 12th International Conference on Concrete Block Pavement, Seoul, Republic of Korea, 16–19 October 2018; Volume 16. [Google Scholar]
- Chatfield, C. Prediction intervals for time-series forecasting. In Principles of Forecasting: A Handbook for Researchers and Practitioners; Springer: Boston, MA, USA, 2001; pp. 475–494. [Google Scholar]
- Gershenson, C. Artificial neural networks for beginners. arXiv 2003, arXiv:cs/0308031. [Google Scholar]
- Karsoliya, S. Approximating number of hidden layer neurons in multiple hidden layer BPNN architecture. Int. J. Eng. Trends Technol. 2012, 3, 714–717. [Google Scholar]
- Ghanizadeh, A.R.; Heidarabadizadeh, N.; Jalali, F. Artificial neural network back-calculation of flexible pavements with sensitivity analysis using Garson’s and connection weights algorithms. Innov. Infrastruct. Solut. 2020, 5, 1–19. [Google Scholar] [CrossRef]
- Shubbar, A.; Nasr, M.S.; Kadhim, A.; Hashim, T.M.; Sadique, M. Performance Comparison of 45° and 90° Herringboned Permeable Interlocking Concrete Pavement. Infrastructures 2023, 8, 97. [Google Scholar] [CrossRef]

























| Characteristic | Result | Criteria | Specification |
|---|---|---|---|
| Loss in thickness as a result of abrasion | 1.79 mm | ASTM C418 [21] | Max. level (3.0 mm) |
| SO3 | 2.69% | ASTM C563-96 [22] | Max. level (6%) by weight of cement |
| Absorption | 2.70% | ASTM C140 [23] | Max. level (7%) |
| Compressive strength | 37.83 MPa | ASTM C140 [23] | Min. level (20 MPa) |
| Layers of Pavement | The Values of (a), Layers Coefficient |
|---|---|
| Surface and bedding | a1 = 0.3 |
| Base | a2 = 0.09 |
| Subbase (reservoir) | a3 = 0.06 |
| Design Approach | Reservoir Depth | Minimum Limit |
|---|---|---|
| Structural design | 40 cm | 20 cm |
| Hydraulic design | 35 cm |
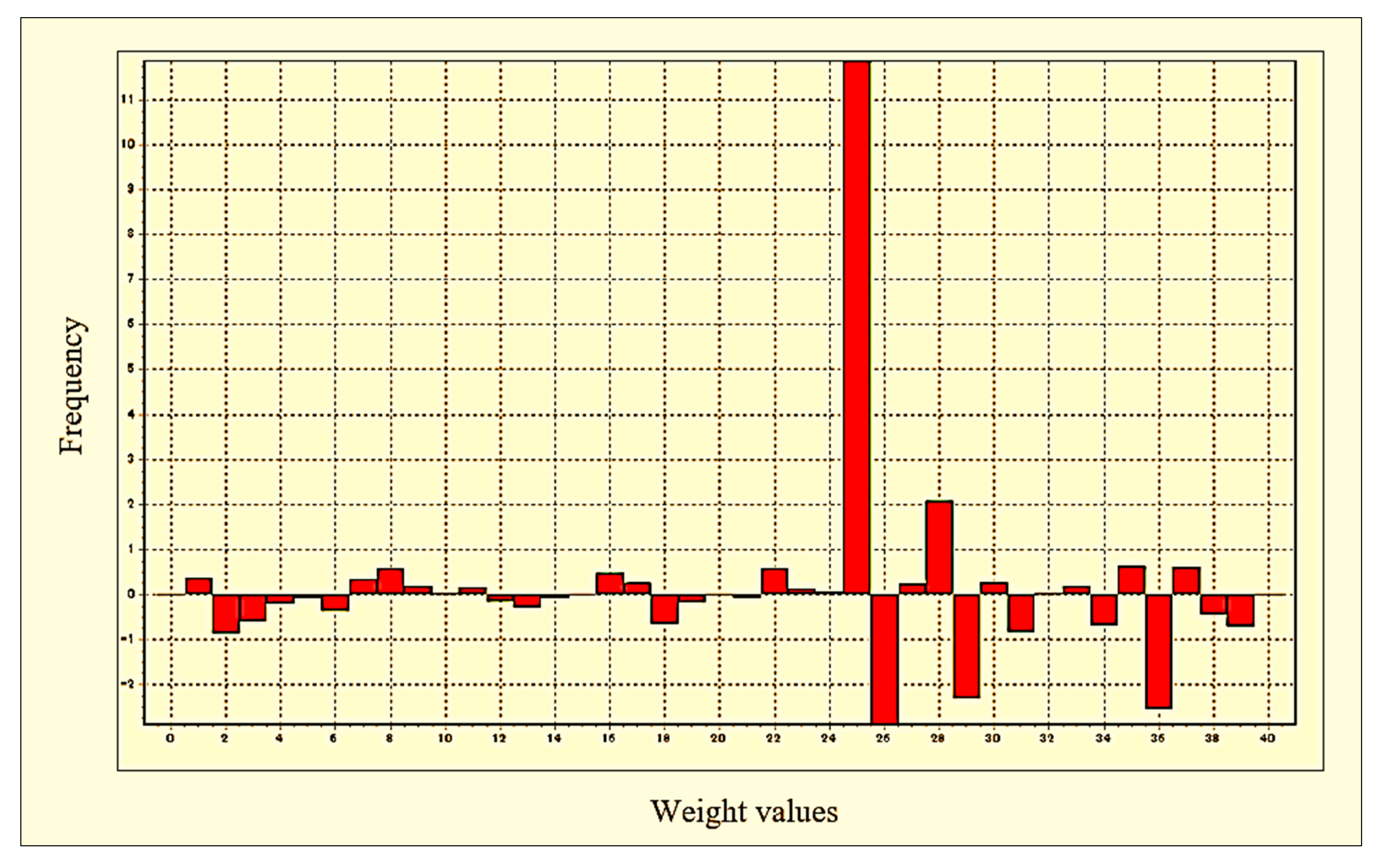
| Series | Node-Line Connection | Weights | Series | Node-Line Connection | Weights |
|---|---|---|---|---|---|
| W1 | N1L1-N1L2 | −0.0277 | W22 | N5L1-N2L2 | −0.0719 |
| W2 | N1L1-N2L2 | 0.3773 | W23 | N5L1-N3L2 | 0.5719 |
| W3 | N1L1-N3L2 | −0.877 | W24 | N5L1-N4L2 | 0.1279 |
| W4 | N1L1-N4L2 | −0.6111 | W25 | N5L1-N5L2 | 0.0582 |
| W5 | N1L1-N5L2 | −0.2072 | W26 | N6L1-N1L2 | 11.856 |
| W6 | N2L1-N1L2 | −0.0659 | W27 | N6L1-N2L2 | −2.8843 |
| W7 | N2L1-N2L2 | −0.3729 | W28 | N6L1-N3L2 | 0.2384 |
| W8 | N2L1-N3L2 | 0.3528 | W29 | N6L1-N4L2 | 2.061 |
| W9 | N2L1-N4L2 | 0.5816 | W30 | N6L1-N5L2 | −2.3189 |
| W10 | N2L1-N5L2 | 0.1727 | Q31 | B1-N1L2 | 0.6431 |
| W11 | N3L1-N1L2 | 0.0196 | Q32 | B1-N2L2 | −2.551 |
| W12 | N3L1-N2L2 | 0.1665 | Q33 | B1-N3L2 | 0.6061 |
| W13 | N3L1-N3L2 | −0.1611 | Q34 | B1-N4L2 | −0.4507 |
| W14 | N3L1-N4L2 | −0.2924 | Q35 | B1-N5L2 | −0.7204 |
| W15 | N3L1-N5L2 | −0.0848 | W36 | N1L2-N1L3 | 0.2504 |
| W16 | N4L1-N1L2 | −0.0102 | W37 | N2L2-N1L3 | −0.8357 |
| W17 | N4L1-N2L2 | 0.4785 | W38 | N3L2-N1L3 | 0.0369 |
| W18 | N4L1-N3L2 | 0.2593 | W39 | N4L2-N1L3 | 0.1956 |
| W19 | N4L1-N4L2 | −0.647 | W40 | N5L2-N1L3 | −0.6857 |
| W20 | N4L1-N5L2 | −0.1726 | Q41 | B2-N1L3 | −0.017 |
| W21 | N5L1-N1L2 | −0.0366 |
| Series | Node-Line Connection | Weights | Series | Node-Line Connection | Weights |
|---|---|---|---|---|---|
| W1 | N1L1-N1L2 | −0.0088 | W22 | N5L1-N2L2 | −0.6679 |
| W2 | N1L1-N2L2 | −0.1813 | W23 | N5L1-N3L2 | 0.7279 |
| W3 | N1L1-N3L2 | 0.2189 | W24 | N5L1-N4L2 | 0.1254 |
| W4 | N1L1-N4L2 | −0.2727 | W25 | N5L1-N5L2 | 0.7597 |
| W5 | N1L1-N5L2 | −0.0145 | W26 | N6L1-N1L2 | 1.646 |
| W6 | N2L1-N1L2 | 0.0864 | W27 | N6L1-N2L2 | −0.2469 |
| W7 | N2L1-N2L2 | 0.1435 | W28 | N6L1-N3L2 | 1.6375 |
| W8 | N2L1-N3L2 | −0.1535 | W29 | N6L1-N4L2 | 3.3364 |
| W9 | N2L1-N4L2 | −0.0625 | W30 | N6L1-N5L2 | 1.0578 |
| W10 | N2L1-N5L2 | −0.228 | Q31 | B1-N1L2 | 0.2936 |
| W11 | N3L1-N1L2 | 0.0737 | Q32 | B1-N2L2 | 0.4334 |
| W12 | N3L1-N2L2 | −0.6341 | Q33 | B1-N3L2 | 0.5343 |
| W13 | N3L1-N3L2 | −0.3155 | Q34 | B1-N4L2 | −0.2177 |
| W14 | N3L1-N4L2 | 0.0865 | Q35 | B1-N5L2 | −0.943 |
| W15 | N3L1-N5L2 | 0.8044 | W36 | N1L2-N1L3 | 0.7718 |
| W16 | N4L1-N1L2 | 0.0625 | W37 | N2L2-N1L3 | −0.478 |
| W17 | N4L1-N2L2 | −0.731 | W38 | N3L2-N1L3 | 0.3384 |
| W18 | N4L1-N3L2 | −0.2891 | W39 | N4L2-N1L3 | 0.6166 |
| W19 | N4L1-N4L2 | 0.035 | W40 | N5L2-N1L3 | −0.9633 |
| W20 | N4L1-N5L2 | 0.7239 | Q41 | B2-N1L3 | 0.4636 |
| W21 | N5L1-N1L2 | −0.3792 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Fatlawi, M.; Hadi, F.M.; Al-khafaji, B.M.H.; Hussein, S.S.; Al-Asedi, T.M.; Al-Aarajy, M.M.; Al-Khazraji, A.A.; Hashim, T.M.; Shubbar, A.; Nasr, M.S.; et al. Evaluating Water Infiltration and Runoff: Stretcher Bond vs. 45° Herringbone Patterns in Permeable Interlocking Concrete Pavements. CivilEng 2025, 6, 24. https://doi.org/10.3390/civileng6020024
Al-Fatlawi M, Hadi FM, Al-khafaji BMH, Hussein SS, Al-Asedi TM, Al-Aarajy MM, Al-Khazraji AA, Hashim TM, Shubbar A, Nasr MS, et al. Evaluating Water Infiltration and Runoff: Stretcher Bond vs. 45° Herringbone Patterns in Permeable Interlocking Concrete Pavements. CivilEng. 2025; 6(2):24. https://doi.org/10.3390/civileng6020024
Chicago/Turabian StyleAl-Fatlawi, Mohammed, Fatima Muslim Hadi, Baneen M. H. Al-khafaji, Sally Selan Hussein, Tamar Maitham Al-Asedi, Maryam M. Al-Aarajy, Ashraf Anwar Al-Khazraji, Tameem Mohammed Hashim, Ali Shubbar, Mohammed Salah Nasr, and et al. 2025. "Evaluating Water Infiltration and Runoff: Stretcher Bond vs. 45° Herringbone Patterns in Permeable Interlocking Concrete Pavements" CivilEng 6, no. 2: 24. https://doi.org/10.3390/civileng6020024
APA StyleAl-Fatlawi, M., Hadi, F. M., Al-khafaji, B. M. H., Hussein, S. S., Al-Asedi, T. M., Al-Aarajy, M. M., Al-Khazraji, A. A., Hashim, T. M., Shubbar, A., Nasr, M. S., & Alfatlawi, T. J. (2025). Evaluating Water Infiltration and Runoff: Stretcher Bond vs. 45° Herringbone Patterns in Permeable Interlocking Concrete Pavements. CivilEng, 6(2), 24. https://doi.org/10.3390/civileng6020024









