1. Introduction
Highways and bridges can be identified as critical components of civil infrastructure systems that deliver essential services whilst also underpinning the growth and resilience of communities, industries, and economies. They facilitate daily transportation whilst also driving the long-term development and prosperity of a country. However, due to the aging and increased usage of bridges to fulfil the recent demands, bridges tend to be degraded over time. Accordingly, if proper monitoring and maintenance procedures are not followed, bridge failures may occur, potentially leading to devastating consequences [
1]. For instance, Adam, Makoond [
2] reported that, over the past 20 years, the highest number of fatalities in bridge failures resulted from improper monitoring and maintenance whilst ranking the collapses of the Morbi suspension bridge, India, which happened in 2022, Polcevera viaduct, Italy, which happened in 2018 and a bridge in Southeastern Guinea that happened in 2007 as the incidents that reported the highest fatalities. Hence, performing frequent inspections and maintenance of bridges systematically is vital to ensure the safety of a country from both economic and social perspectives. However, traditional inspection and maintenance methods often lead to high costs and time consumption whilst resulting in potential safety hazards, as direct human involvement is required to physically inspect a bridge. The annual maintenance cost of a bridge usually lies between 0.4% to 2% of its construction cost, whereas that is even higher than twice its construction cost if the bridge continues for a 100-year life span [
1,
3]. Consequently, modern investigations are focused on more intelligent approaches to inspect bridges remotely to diagnose any differences happening in the structure and to suggest proper maintenance methods immediately prior to the occurrence of any failure. As one example of advanced frameworks in the structural health monitoring (SHM) of bridges, Martucci Civera [
4] attempted to utilise extreme function theory (EFT) and Gaussian process regression (GPR) to identify damage based on the mode shapes obtained from the dynamic response of a bridge. This method effectively detects and localises structural damage under various scenarios, providing a new intelligent approach for enhancing the SHM of bridges. DBSCAN-based automated operational modal analysis (AOMA) is another novel technology of the SHM of bridges, which integrates the density-based spatial clustering of applications with noise (DBSCAN) algorithm to enhance the identification and classification of vibrational modes. This method automatically detects and removes spurious modes and outliers, leveraging a data-driven approach for setting clustering parameters and thereby, it can be effectively used for the structural health monitoring of bridges [
5]. However, these methods lack the ability to continuously update and adapt based on real-time operational conditions or changing configurations, and they are primarily data-driven and rely on static or pre-recorded data for analysis. Hence, there is a clear demand for more advanced methodologies, such as digital twins, which integrate real-time monitoring, adaptive modelling, and comprehensive physics-based simulations to address these limitations and enhance accuracy and applicability of structural health monitoring.
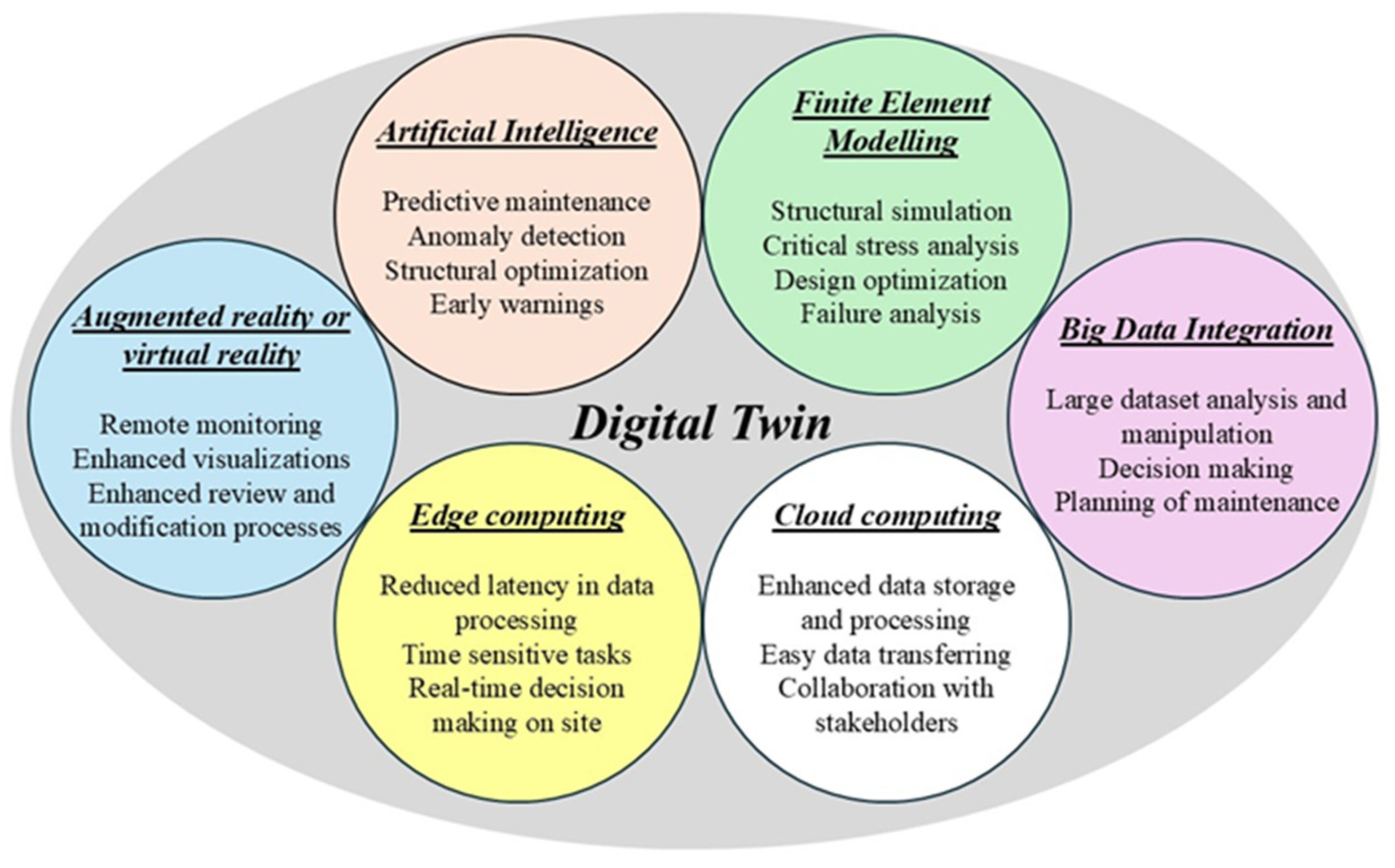
Digital twins (DTs), which are often recognised as virtual replicas of actual structures, play a vital role in this regard due to the harmonic coexistence that they offer between actual and virtual models [
6,
7]. Such a system could potentially result in assisting in monitoring the structural health of a bridge remotely and for its entire life cycle management. However, the application of DTs is mostly restricted to the design stage of a structure whilst mostly interpreting the geometry, and hence, most of the existing DTs are geometric DTs (such as CAD files) [
8]. DTs can be seamlessly integrated with various advanced technologies, such as finite element modelling (FEM), artificial intelligence (AI), or the Internet of Things (IoT). Accordingly, this integration significantly enhances the predictive maintenance of bridges by enabling real-time monitoring, advanced data analysis, and more accurate simulations, ultimately leading to improved structural health management and optimised maintenance strategies [
1]. The potential benefits of a DT system can be presented in
Figure 1 with different integrated technologies.
The implementation of a DT of a bridge initiates from installing sensors for data acquisition and continues until the DT model receives the data, conducts an inverse structural analysis and visualises stresses to identify critical areas; see
Figure 2. The implementation of the digital model with the help of FE modelling, specifically the integration of finite element modelling (FEM) and artificial intelligence (AI) techniques with the DT concept for that purpose, has been primarily focused on in this paper. DTs with FEM could also result in significant benefits, as the critical stresses can be analysed and visualised in bridge DTs at the same time [
9]. Further, to ensure continuous alignment with the actual structure, it is essential to perform the FEM in real time. However, conducting FEM in real time is inherently challenging due to its computational complexity, and it offers the opportunity to explore surrogate models that can replace the time-consuming computational process of FEM whilst reducing its computational burden by simplifying the high-fidelity models without affecting its accuracy. It has been identified that a combination of data-driven methods with a physics-based modelling technique, like FEM, could substantially benefit in simplifying the complexities of the computational process and achieving real-time conditions [
10]. Another merit of incorporating a data-driven method arises during the inverse analysis of a structural response upon the received measurements of data acquisition sensors, as such methods enable the inverse analysis in leveraging sensor measurements to enhance the accuracy and reliability of the structural health assessment [
11]. However, inverse analysis processes often lead to be presented with challenges of being ill-conditioned [
12,
13], where the results may be largely deviated even for a small change in inputs. Hence, AI techniques, specifically machine learning (ML) algorithms, have recently been identified as a powerful tool to address these issues and produce a real-time FE model whilst also conducting an inverse analysis process [
14,
15]. Also, recent advancements in artificial intelligence (AI) have shown significant potential in enhancing structural health management (SHM) processes for existing bridges, including automated visual inspections, sensor-based structural monitoring, and predictive risk assessments. AI techniques, such as machine learning and deep learning, have been applied to improve defect detection, performance analysis, and deterioration prediction, offering promising pathways to optimise bridge assessment and maintenance strategies [
16]. The FEM excels at producing highly precise results of analyses, whilst AI or ML algorithms offer the opportunity of reducing the time factor once trained with FEM data and enabling real-time predictions, optimisation, and decision-making for structural health management. Hence, it would be an ideal option to incorporate ML algorithms in surrogating the inverse FEM for the development of DTs for real-time structural health assessment.
Studies have demonstrated the effectiveness of ML algorithms in serving as surrogates for the finite element (FE) analysis process. However, their application in successfully surrogating inverse analysis processes remains far less explored, raising questions about their true effectiveness in this domain. Inverse surrogate modelling has been observed to require a larger number of input parameters while producing a relatively smaller set of output parameters [
14]. However, in the context of DT development, the inverse modelling approach must be adopted to generate comprehensive structural behaviour from a limited set of inputs. This has been successfully demonstrated with artificial neural networks (ANN) [
9,
17,
18]; however, the impact of different types of ML models on this process remains largely unexplored and unclear. Hence, a novel approach is presented in the current study to demonstrate the potential of DTs and AI techniques for real-time static structural analyses of bridges. While this study focuses on static monitoring using strain gauges to capture the structural response under controlled loading conditions, dynamic monitoring is equally critical for real-world applications. Dynamic monitoring involves capturing the structural response to time-varying loads, such as vehicular movement, wind, or seismic activities, using sensors such as accelerometers or displacement transducers. Such a time-sensitive analysis is achievable via recurrent neural networks (RNNs) due to their ability to handle time-dependent patterns [
19,
20]. However, the dynamic aspect of the structural behaviour has not been considered in the current study. The proposed methodology emphasises the use of the random forest (RF) algorithm, extreme gradient-boosting (XGBoost) and multi-layer perceptron (MLP) algorithms as surrogate models for performing real-time inverse static structural analysis using the FEM whilst comparing the effectiveness of each algorithm. Therefore, the main target of this study is to conduct a comprehensive analysis of different ML algorithm types to assess their capability of conducting real-time inverse structural analysis whilst investigating optimum model parameters to enhance the accuracy of the model training process to develop an accurate real-time DT model of bridges.
2. ML Algorithms and FE Modelling
FE analysis is a widely used and powerful computational technique that enables efficient structural analysis through sophisticated modelling and simulation [
21]. FE modelling can also be identified as the most preferred physics-based modelling technique for DTs [
21]. In FE modelling, the structure is divided into smaller, discrete elements (FE mesh), and each element is analysed independently rather than evaluating the entire structure as a single entity [
22]. The mathematical model of the actual structure is required to be implemented first, incorporating boundary conditions and material assignment under the FE modelling process, whilst the FE mesh is generated afterwards and solved at the end. This approach yields highly accurate results but comes at the cost of substantial computational resources. Specifically, when the structure includes a higher number of degrees of freedom, it requires substantial time to solve the problem even when a minor change happens with the input parameters, necessitating a full re-analysis, potentially doubling the computational demand [
22]. These challenges make real-time simulations of structural behaviour particularly difficult to achieve with traditional methods. However, due to the massive importance of achieving such a real-time analysis, it is required to reduce the computational complexity of FE modelling via a surrogate model. Surrogate models follow an alternative to overpass the direct calculations of results and obtain the end results in an indirect way [
23]. Hence, the computational time will be significantly reduced. Several popular surrogate models are model order reduction techniques, adaptive mesh refinements, and the application of ML. Amongst, the ML concepts gained huge popularity due to their high efficiency [
9,
24]. However, powerful hardware components are also required to be used together with surrogate models to achieve real-time FE modelling.
AI is a vast domain that is dedicated to creating smart systems that can handle tasks without human involvement. ML is the heart of AI, a specialised branch that equips computers with algorithms and statistical tools, allowing them to learn, adapt, and make choices on their own rather than relying on explicit programming instructions [
25]. The main branches of ML are supervised learning, unsupervised learning, and reinforcement learning. Supervised learning uses labelled data for the training process where both the input and output are known, whilst unsupervised learning uses unlabelled data where only the input is known. Reinforcement learning is a different paradigm in ML where an agent learns through a trial-and-error process by interacting with an environment [
26]. Amongst these, supervised learning is the primary type of algorithm that is being used as surrogates for FE modelling, as typically, the surrogate models are being trained on datasets generated through FE simulations [
27,
28]. The surrogation process can also be done in three distinct ways: (i) Replacing part of the FE analysis with ML models [
29,
30], (ii) formulating empirical equations based on ML models [
31], and (iii) training a ML model specifically to target the required parameters [
9,
32,
33]. The most suitable approach should be chosen based on the scenario and the specific objectives of the problem. For instance, Calò, Ruggieri [
33] used an ML-based surrogate model for non-linear FE modelling to predict the reduction in prestressing girders of concrete box girder bridges. The inputs were obtained as the elastic modulus of concrete, initial prestressing force, and strain increment of fibres, while the output was selected as a residual prestressing force. In this study, the third approach was specifically targeted, as it involves implementing ML models in between the desired inputs and outputs, making it the most suitable choice for the inverse structural analysis required in developing the DT model. In this study, three main ML models, random forest (RF), extreme gradient boosting (XGBoost) and multi-layer perceptron (MLP) neural network, were selected to test their suitability as surrogates for a laboratory-scale bridge, and these algorithms were selected due to their complementary strengths in handling non-linear relationships, efficiency, and adaptability for the surrogation process. Each algorithm was extensively researched for its existing applications in surrogate modelling before being implemented in the DT framework.
Even though this study focuses on traditional ML models as an initial step, other advanced artificial neural network (ANN) architectures have also shown significant potential for surrogating FEMs. For instance, convolutional neural networks (CNNs) have been successfully applied for predicting stress variations in composite materials [
34]. Their ability to extract spatial hierarchies and features from multidimensional data makes them particularly suitable for problems involving spatial dependencies, such as material behaviour analysis and structural image data. Graph neural networks (GNNs), on the other hand, are particularly effective for problems involving graph-based relationships such as nodal connectivity and structural topology [
35]. By leveraging the inherent graph structure of FEMs, GNNs can model complex interactions between nodes and elements, making them an excellent choice for tasks like topology optimisation and structural connectivity analysis. Furthermore, recurrent neural networks (RNNs) have been employed for time-dependent or sequential predictions in dynamic structural analyses [
27,
36]. Their ability to handle temporal sequences allows them to excel in scenarios where the structural response evolves over time, such as vibration analysis or impact simulations. These advanced ANN models not only enhance prediction accuracy but also offer improved scalability and computational efficiency, especially for high-dimensional or complex structural problems. Incorporating such models could open new possibilities for real-time structural analysis by providing faster and more precise predictions under varying conditions. However, these advanced architectures are beyond the scope of the current study, which focuses on traditional ML models as a foundational exploration. Future work is recommended to investigate and compare the efficiencies of these advanced models in surrogating FEM. Such studies could provide a comprehensive understanding of their strengths and limitations, enabling the development of optimised frameworks tailored to specific engineering problems.
2.1. Random Forest Algorithm
The random forest (RF) algorithm is a robust ensemble method that constructs multiple independent decision trees, incorporating randomness to enhance predictive accuracy [
37]. Its effectiveness has been demonstrated across various prediction tasks within the civil engineering field [
38,
39], including the surrogation of FE modelling [
15]. If a model is represented as a set of
independent and uncorrelated trees
, with randomness introduced through a combination of bootstrapping and aggregation [
40], it can be defined as a RF model. This model can be expressed as
. RF models are typically used for classification tasks and during training, the data are randomly distributed among multiple decision trees, where each tree classifies the data based on specific criteria. The outcome is determined by aggregating the predictions from all trees, typically through the majority decision. However, for the surrogation process of FE modelling that is required for the implementation of DTs, it is required that the RF model generate some output based on the given inputs by the sensors. Hence, such a task is typically framed as a regression problem, requiring the RF model to be trained accordingly for regression tasks. Hence, if the target variable is
for the RF model
which is surrogating the FE model, these trees are constructed by randomly sampling
via bootstrap resampling and selecting subsets of the
sensor measurements to form the decision nodes. The nodes are split for the regression case using mean squared error (
MSE), and it can be obtained as in Equation (1) where m is the number of samples,
is the actual value of sample i, and
is the mean value of the samples at the node.
Accordingly, the ultimate outcome of the regression task is obtained by averaging the predictions across all trees [
39]. In such a manner, the RF model is trained to conduct the surrogation process. The average predictions can be obtained as in Equation (2), where
is the number of trees, and
is the prediction of each tree.
The RF models are effective in surrogating FE modelling, and they provide highly accurate results [
41]. Also, as RF models are based on decision trees, they simply identify the most important features that have a high influence on the results and focus on them more [
42]. Additionally, for the regression tasks, since the average of multiple decision trees is obtained, it reduces the risk of overfitting [
43]. However, training RF models for extensive datasets may be computationally intensive [
44]. The FE modelling process will be more statistical when surrogating using RF models, and the physical insight of the problem will be avoided during the training process [
45]. Also, RF models have been predominantly trained based on specific criteria within decision trees, where their extrapolation capability may be limited.
2.2. XGBoost Algorithm
The XGBoost algorithm is also a highly effective prediction algorithm based on the gradient-boosting framework, renowned for its speed and superior performance. It has also demonstrated success in various predictive tasks within the civil engineering domain [
46,
47]. Similar to the RF model, this is also a tree-based algorithm. The XGBoost algorithm was initially introduced by, Chen and Guestrin [
48] and the XGBoost algorithm has been designed to iteratively apply gradient boosting, enhancing the performance of both classification and regression models by improving the accuracy and predictive capabilities [
49]. Additionally, it mitigates overfitting whilst reducing the complexity of the model. The prediction for a data point
is obtained as the prediction from all decision trees where
is the predicted value,
is the number of trees, and
is the prediction from the
th tree, which can be presented as Equation (3):
Also, Chen and Guestrin [
48] mentioned that XGBoost optimises an objective function that combines a loss function and a regularisation term where
is the loss function and
is the regularisation term to control model complexity. The objective function can be presented as Equation (4):
The integration of XGBoost with FEM happens in a similar manner to the RF model. This model can be trained by using the desired inputs and outputs to predict the output with respect to the unseen input. Typically, XGBoost models have faster training times and inference times [
50]. Hence, this could be a viable option for surrogating FE simulations and generating results in real time. Also, due to its ability to handle large datasets, complex FE meshes could also be effectively analysed [
51]. However, similar to the RF models, the extrapolation ability of XGBoost is also limited due to the tree-based nature of these models [
52].
2.3. Multi-Layer Perceptron (MLP) Neural Networks
Multi-layer Perceptron (MLP) neural networks are among the most used types of neural networks, renowned for their versatility in handling tasks like regression, classification, and pattern recognition. As a straightforward form of feedforward artificial neural network (ANN), MLPs consist of fully connected layers, typically organised into three main layers: an input layer, one or more hidden layers, and an output layer. The number of nodes in the input layer and output layers can be decided upon the number of available features and the number of target variables of the model, whilst the number of nodes in the hidden layers can be customised depending on the complexity of the model [
53]. All nodes in one layer connect to the nodes in the next layer, and hence, it follows a feedforward nature, which does not allow it to assess time history analyses [
54]. Multi-layer Perceptrons (MLPs) utilise a compositional optimisation function of the form (where
represents the weights of interconnections)
where
denotes the regularisation term to prevent overfitting [
55]. The optimisation process minimises the difference between the network’s predicted output and the target output by reducing a scalar loss function, such as the mean squared error. This process, commonly referred to as training the neural network, relies on gradient-based optimisation algorithms to adjust the weights and biases iteratively [
56]. Two key algorithms in this optimisation process are backpropagation [
57], which computes the gradients using the chain rule, and stochastic gradient descent (SGD) [
55], which updates the weights based on these gradients. Together, these methods enable MLPs to effectively learn from data and approximate complex non-linear relationships.
In the integration of MLPs with FE modelling, the input and output parameters are determined based on the specific problem that needs to be analysed. Once these parameters are defined, an appropriate MLP model can be developed to serve as a surrogate for the FE analysis process. Due to this versatility, MLPs have been widely employed as surrogates for FE modelling across various applications, including forward analysis, inverse analysis, and parametric simulations. Several studies have compared the effectiveness of MLP regressors with other ML algorithms when used as surrogates in FE analysis. Findings from these studies [
15,
58] indicate that MLPs often outperform these alternative models in terms of predictive accuracy and reliability. Liu [
59] attempted to apply the MLP models for both forward and inverse analysis problems, and it has been identified that inverse analysis needs more training samples for better generalisation when compared to forward analysis. A review of the existing literature reveals that MLPs have primarily been employed as surrogates for 1D, 2D, or simple 3D models with basic geometries [
14]. Additionally, they have mostly been applied to problems requiring the prediction of a limited number of outputs [
17,
60]. Consequently, studies that focus on predicting the entire FE mesh are rare, highlighting a significant gap in current research. Also, determining the optimal architecture of an MLP for surrogating FEM remains an open challenge, with most studies relying on a trial-and-error approach to configure the model’s architecture [
58]. However, MLPs have demonstrated a significantly higher time efficiency compared to traditional FE analysis [
9,
53], making them an ideal choice for developing surrogate models capable of real-time FE analysis. Despite their advantages, MLPs come with certain limitations. One notable drawback is their reliance on statistical modelling, which often overlooks the underlying physical relationships within the system. To address this, physics-informed neural networks (PINNs) have been developed, incorporating physical laws directly into the loss function. Additionally, MLPs tend to struggle with models involving complex FE meshes, particularly when a large number of trainable parameters are required, leading to diminished performance and scalability issues [
24].
3. Methodology: Development of the Digital Twin (DT)
The step-by-step approach of developing the DT of a laboratory-scaled bridge, using ML to enable the real-time health assessment of a bridge, is explained in detail in this section. The methodology has been divided into three main sections; see
Figure 3.
(1) Instrumentation of the bridge: This phase includes the identification of the critical locations of the bridge to install sensors (i.e., strain gauges) to measure the structural response.
(2) Training the ML algorithm: This phase establishes a robust ML model to accurately estimate the structural behaviour of the bridge. The model learns from various simulated structural conditions.
(3) Real-time visualisation of structural response: Once trained, the model is deployed to monitor the real-time response of the bridge. The resulting visualisation from this phase allows for an instant observation of the structural integrity, capturing changes under different loading conditions and consequently enabling proactive maintenance.
In essence, these phases combine predictive accuracy with real-time monitoring, forming an innovative, dynamic DT capable of providing ongoing insights into the performance of the bridge.
3.1. Experimental Setup
A 2D truss bridge was used in this study to represent the primary load-bearing component of a 3D truss bridge. In a 3D truss bridge, each truss on either side of the bridge supports loads acting solely within its own plane. These loads are transferred to each truss through horizontal beams in the deck, which connect the two trusses and form the complete 3D bridge structure. Hence, a 2D truss acts as a fair representation of a 3D truss bridge. In this study, the STR8 pin-jointed symmetrical truss bridge model, located at RMIT University in Melbourne, Australia, serves as the experimental structure. This truss comprises 13 steel members with circular cross-sections, each having a diameter of 6 mm and a Young’s modulus of approximately 193 GPa; see
Figure 4. The truss is supported by a pin at one end and a roller at the other, allowing it to handle applied loads within a range of −500 N (compression) to +500 N (tension). Loads can be applied at any pin joint, with angles reaching up to 45°, and are precisely measured and displayed by integrated load cells within the loading mechanism, ensuring accurate monitoring of applied forces. This setup provides a reliable model for studying load responses in truss structures under varied conditions.
As illustrated in
Figure 4, the experimental setup highlights the specific sections used for testing. For this study, a new set of sensors—ten strain gauges manufactured by Tokyo Measuring Instruments Laboratory Co., Ltd. (Tokyo, Japan)—were employed. These strain gauges, used in a 120 Ohm quarter bridge configuration with 2-wire sensors, were affixed to the experimental truss structure using adhesive. Notably, a wire loom is visible along the truss structure, a result of the pre-installed sensors on several members. However, for this research, strain gauges were strategically placed on nearly every member of the truss to enable effective inverse load identification. The strain data collected from the sensors were initially routed to a MAS21 bridge completion module by MeasureX (Melbourne, Victoria, Australia), which completes the quarter bridge circuit configuration. Subsequently, these data were transmitted to a data logger from Almemo (Bestech Australia Pty Ltd., Melbourne, Victoria, Australia) measuring devices. The data logger processes the electrical resistance readings from the strain gauges, converting them into digital values. These values are then fed into a custom-developed Python code for conducting structural analysis in real time. To ensure a stable connection, the data logger was linked to the computer via a USB cable, though it is also capable of connecting remotely if required.
Figure 5 illustrates the schematic arrangement of the strain gauges (SG) and loading cells (P1 and P2). In SG_n, n refers to the strain gauge number, and the nodes have been numbered from 1 to 8 in
Figure 5. The P1 loading cell applies load on the structure vertically upwards while the P2 load cell applies load towards the structure at a 30° angle to the horizontal.
The loading cell positions were chosen to ensure that the uninstrumented members experienced no stress, and these locations were fixed for the duration of the experiment. To optimise sensor placement, the zero-force members within the truss were identified, allowing for a targeted deployment of 10 strain gauges across the selected members (out of a total of 13). These gauges were directly connected to the data acquisition module and for the remaining three members, which include two vertical and one inclined member, strain responses were assumed to be negligible, registering as zero due to their minimal load-bearing roles. Furthermore, the stress–strain behaviour of the material was modelled using the known elastic modulus (193 GPa) of the material and yield and ultimate stress values for structural steel (250 MPa and 400 MPa, respectively) as mentioned in the manufacturer’s guidelines; see
Figure 6. Up to 250 MPa, the structure behaves linearly elastic and shows a yield strain of 0.0013. Beyond the yield point, the material undergoes plastic deformation, characterised by a yield plateau and strain hardening, until reaching the ultimate stress of 400 MPa. At this point, the material begins to neck and eventually fractures at a strain of approximately 0.25, indicating a ductile failure.
3.2. FE Model Validation
The FE modelling of the truss was conducted using Python code. Initially the geometry was defined, materials properties were assigned, and constraints were defined. Before proceeding with the dataset preparation stage, it is required to conduct the validation of the FE model to ensure accuracy. Hence, with that purpose and to establish a reliable basis for validating the DT model, a thorough calibration process was conducted. First, the loading cells within the experimental setup were adjusted to zero, resulting in zero stress in all members as measured by the strain gauges. Next, compression and tension forces were gradually applied in negative and positive directions, respectively, while closely monitoring the structural responses. Both the horizontal and vertical loads, which have the potential to provide a clockwise moment, were taken as positive loads. After each loading cycle returned to zero, the stress and deformation measurements were verified to confirm that they reverted to the original reference points. As shown in
Figure 7, the structure actively responded to the applied loads, with the measured responses returning accurately to their calibrated baselines. This consistency in response verified the calibration and validation of the model with a high degree of accuracy.
Then, to further verify the validation of the model, the loads were then gradually applied to the structure, increasing from 0 N to 500 N in 100 N. Then, the experimental strain values and the strain values that were obtained from the FE model were compared.
Table 1 represents the similarity between the results. The testing was done under three different scenarios. As shown in
Figure 5, the loading cells in the experimental model were fixed, and three loading cases were considered as follows: (1) vertical load only, (2) inclined load only, and (3) a combination of vertical and inclined loads. The vertical load was added to the positive y-direction whilst the inclined load was added in such a way that it provides the x and y components in the negative directions.
It is highly noticeable that for most members, the FE-predicted strain shows strong agreement with the experimental results, as indicated by the ratios close to 1.0 across all loading cases. The consistency of results across these three loading conditions demonstrated the reliability of the FE model in predicting the strain behaviour of the structure. Under vertical loading, the ratios range between 0.87 and 1.0, with most values lying between 0.92 and 0.98. For inclined loading, the strain ratios exhibit slightly more variability compared to vertical loading, particularly for members SG_2 and SG_10, where the values deviate slightly above 1.0. This deviation may be attributed to the complex nature of inclined loading, introducing additional components of strain not perfectly captured by the model. For combined loading, the values also show a similar variation as seen in the other two loading conditions. Minor discrepancies can be observed for specific members, such as SG_6, SG_8, and SG_10, under vertical and inclined loading, where the ratios slightly deviated from unity. These variations could arise from factors such as localised stress concentrations and experimental errors. However, this comparison of FE and experimental strain values shows strong overall agreement, and the minimum and maximum offsets of the comparison are less than 15%. Hence, the results validate the accuracy and robustness of the FE model in predicting strain behaviour across multiple members and loading scenarios. Also, it was concluded that the developed model achieves a high level of precision, supporting continued progress towards the preparation of the dataset and the development of the DT.
3.3. Overview of the Dataset
As shown in
Figure 5, this structure consists of eight nodes and 13 members, resulting in a total of 16 degrees of freedom. Three of these degrees of freedom are constrained by the roller support and the pin support located at each end of the structure, and hence, only 11 degrees of freedom will show deflections in the horizontal direction (x displacement) and in the vertical direction (y displacement). Also, only 10 strain gauges were installed in the structure. Hence, the dataset should include the strain values as the input for the machine learning model and it has 10 parameters in such a way that each value represents each strain gauge reading. The number of outputs depends on the number of degrees of freedom that are not restrained and that was 13 degrees of freedom altogether. The FE model of the truss that was validated earlier was used to develop the dataset representing all possible behaviours of the structure under various loading conditions. Loads can be applied to any of the nodes, which are labelled 1 through 8, and can include both horizontal and vertical components. This variability is essential to capture in the dataset. To introduce randomness and ensure diverse loading patterns, variations were applied to the location, magnitude, and direction of loads. The load magnitudes were kept within the structure’s capacity, ranging from −500 N to 500 N, to reflect realistic operational limits. This dataset, therefore, represents a comprehensive array of scenarios, ensuring the model accurately reflects the full range of structural responses.
Table 2 explains the dataset.
The dataset included 6000 loading patterns with random magnitudes of loads between −500 N and 500 N and random locations of load applications. Hence, it included 60,000 (6000 × 10) input data points and 78,000 (6000 × 13) output data points. Machine learning models were primarily supposed to be trained on this dataset. Prior to the training of a machine learning model, it is required to have a better understanding of the dataset. Hence, the dataset was analysed to check the distribution and variation in the data; see
Figure 7. As mentioned above, the FE-generated data represent the strain values on each member containing strain gauges, as well as the nodal displacement values, excluding the restrained degrees of freedom. Here, SG_n denotes the strain gauge number, and Xm or Ym refers to the X or Y displacement of the m node, corresponding to
Figure 5. The displacement values were taken with respect to the positive X- and Y-directions, where the positive deflection values indicate displacements in the positive directions, and the negative values represent displacements in the opposite directions. Both positive and negative values were considered when analysing the distribution and variability of the data, as shown in
Figure 8.
It can be seen that the strain distribution across 10 strain gauge positions and the nodal displacements of all nodes exhibit consistent behaviour, and this is due to the linear elasticity of the structural behaviour. Also, the median values for most positions are also centred around zero. It is further noticeable that outliers are present in both panels, but their number and spread are more significant in certain positions like SG_5 to SG_8 and X5 to X8. These outliers suggest that while the overall behaviour remains consistent, localised peaks or anomalies in strain values exist, which are associated with the geometry, load distribution, or boundary conditions. Further, it can be identified that nodal displacement values are relatively smoother and more consistent when compared to the distribution of strain values. Certain strain gauge locations, i.e., SG_5 to SG_7, exhibit a wider range of strain values, indicating areas of increased deformation or stress, which are likely influenced by the geometry and boundary conditions of the structure. However, that might not depend on the load application point since the location of the load application was randomised for preparing the dataset. Overall, it can be seen that the data behaviour reflects a combination of global structural stability and localised effects, and such an understanding of the dataset is useful for identifying critical regions and ensuring the behaviour of the structure under the modelled conditions.
3.4. Machine Learning Models
In this study, three machine learning algorithms—RF, XGBoost, and MLP—were tested to evaluate their predictive capabilities for inverse structural modelling. A dataset containing 6000 records of strain values as input and the corresponding displacements at each node as output was used to train the models. The data were divided into 80% for training, with the remaining 20% set aside for testing and an additional 20% of the data designated for validation purposes. Model performance was assessed using the root mean square error (RMSE) metric.
The RF algorithm is recognised as a robust ensemble method that employs numerous independent decision trees, each constructed with added randomness, to improve predictive accuracy and reduce overfitting [
38]. This algorithm has shown high effectiveness in various predictive tasks within the civil engineering domain, particularly for handling complex and non-linear relationships [
39,
40]. In this study, the RF model was configured with 100 estimators, ensuring an ensemble with sufficient depth to capture the data patterns accurately. To promote consistency and reproducibility, a random state was set, which controls the randomness in data sampling and feature selection. Additionally, a 5-fold cross-validation was applied to provide a reliable evaluation of the model’s performance across different data splits, with root mean square error (RMSE) selected as the metric to assess prediction accuracy. This approach helps to mitigate overfitting, enabling the model to generalise well on unseen data. Moreover, the RF’s inherent feature importance ranking offers valuable insights into the influence of each input variable, contributing to improved interpretability of the model’s decisions. These parameters collectively enhance the reliability and robustness of the RF model for inverse structural modelling tasks. The first two levels of one decision tree of the developed RF model are presented in
Figure 9. SG refers to the strain gauges that are mentioned in
Figure 5. The values were decided by the RF algorithm automatically for the decisions. As can be seen in
Figure 5, the topmost node or the root node of the decision tree splits the data based on the condition SG_1 ≤ 0.068, the squared error before the split is 0.001, and the total number of samples, which, considered at this node, is 3947. The ‘value’ term represents the predicted values of the model, which are, in this case, the displacement values of each node. Then, the two child nodes are presented, and they check certain conditions for SG_7. Likewise, this continues to predict output for a certain set of sensor readings, and the grey boxes indicate that in third level.
The XGBoost algorithm is a widely used gradient-boosting technique known for its speed and predictive power, making it popular in a variety of machine learning applications. In civil engineering, it has successfully addressed several predictive tasks [
47,
48]. For this study, XGBoost was developed with a focus on optimising the hyperparameters to maximise accuracy. The hyperparameters were optimised using Bayesian optimisation with a tree-structured Parzen estimator (TPE) algorithm [
61]. The objective function was defined to minimise the mean squared error (MSE) over a maximum of 100 evaluations. The selected settings included a maximum tree depth of 7, a min_child_weight of 4, a learning rate of 0.1, and 100 estimators. Additionally, colsample_bytree was set to 0.52, and L1 and L2 regularisation were applied to control model complexity. A 5-fold cross-validation scheme assessed the model’s robustness using root mean squared error (RMSE) as the evaluation metric. Hyperparameter tuning was performed via Bayesian optimisation, which iteratively searched for optimal settings to minimise the validation error. The final model was trained on the complete training data, while early stopping helped prevent overfitting by halting training once performance ceased to improve. The first few stages of one decision tree of the developed XGBoost algorithm are shown in
Figure 10. SG refers to the strain gauges that are presented in
Figure 5, and the values have been decided by the XGBoost algorithm automatically. It shows the prediction of the target variable based on the input feature SG_1. The tree splits the data sequentially at various threshold values of SG_1, creating decision boundaries to minimise the prediction error at each level. It further demonstrates how the model identifies optimal thresholds for the feature SG_1 to segment the input space and predict the target variable. It also highlights the tree’s capability to handle missing values, as indicated by the “No, missing” branches.
MLP neural networks are among the most widely used neural network architectures, particularly due to their straightforward, fully connected structure as feedforward ANNs. An MLP typically includes three or more layers: an input layer, one or more hidden layers, and an output layer. The interconnected nodes across these layers enable effective predictive capabilities, and MLPs have shown notable success as surrogates for finite element (FE) models [
15,
59]. In this study, min–max scaling was applied to normalise the data, promoting faster convergence during the training of the MLP. The tested MLP architecture was implemented using Keras and consisted of four layers, including three hidden layers. The input layer received ten features, while the hidden layers contained 64, 32, and 16 units, respectively. The output layer was defined with 13 units, accounting for the constraints applied to three nodes in the modelled structure. ReLU was used as the activation function to handle non-linearity, and the model’s parameters were optimised using the Adam optimiser. RMSE was employed as the loss metric to gauge performance. Training was conducted over 200 epochs with a batch size of 32, and early stopping was implemented to prevent overfitting. The architecture of the used MLP model is presented in
Figure 11.
Table 3 also provides an overview of the hyperparameters of each model.
4. Results and Discussion
The models were trained upon the generation of the dataset and defining the neural network models. This section includes the results and a discussion based on the obtained results.
4.1. Variations in the Model Accuracy with the Model Type
Models were trained one by one to assess the accuracy of each of the models. The loss function was based on the mean squared error (MSE), and the root mean squared error (RMSE) value was used to assess the accuracies.
- (i)
RF model
The RF model was developed for the laboratory-scale bridge model, as explained in
Section 3.4, and was subsequently trained using a cross-validation approach. The variations in the RMSE values over the five folds are presented in
Figure 12.
It is noticeable from
Figure 12 that the RMSE values across the five folds are relatively close to each other (changing between 0.000342 and 0.00036), confirming the consistency of the performance of the model across different subsets of the data. Also, it confirms that the model has a high generalisation capacity. However, a noticeable drop can be observed from fold 1 to fold 3, where the RMSE values reach the lowest point (0.000342) and again slightly increased in fold 4 and again reduced in fold 5 to a relatively similar value that was observed in fold 3. The reason for these changes would be due to the different distribution of data among different folds. Then, the trained model was tested using a randomly selected dataset.
Figure 13 shows the comparison between the predicted data and the actual data for node number 2’s x displacement for 100 testing samples. It can be clearly seen that both the predicted and actual data are highly similar, and overall, the model demonstrated excellent performance.
To further present the overall agreement between the predicted data by the trained model and the actual data in the dataset, a violin plot was drawn.
- (ii)
XGBoost algorithm
Similarly, the XGBoost algorithm was also tested on the bridge. It ended up with an error of 0.00051. The variations in the error with each iteration are presented in
Figure 14. It can be observed that the RMSE for both training and validation datasets decreased rapidly in the initial iterations and flattened out around the 40th iteration. Further training beyond the 40th iteration resulted in minimal improvements and the model has been further converged. Hence, it is noticeable that the model has learned primary patterns in the data early in the training process. Also, the RMSE values of training and validation have been reduced, showing a minimal gap between them, confirming that the model is not overfitting and generalised well for unseen data. When comparing it with the RF model, the XGBoost algorithm for this bridge showed a higher error. However, since this model also showed a significantly lower error when compared with the actual output data, it can be concluded that the performance of the model is acceptable.
Figure 15 further illustrates the comparison between the predicted data and the actual data for node number 2’s x displacement for 100 testing samples. It is evident that the predicted values closely align with the actual values, indicating that the model performed exceptionally well overall.
- (iii)
MLP algorithm
The MLP algorithm was also tested on the bridge model. The model error was 0.000524 and the MLP algorithm also provided a significantly lower error rate. The variations in the RMSE value with the epoch are illustrated in
Figure 16a. The plot showed that the model rapidly reached its optimal performance, with the convergence and stabilisation of both training and validation losses. Whilst training, the model experienced early stopping at the 98th epoch; however, it can be clearly seen that the RMSE was not significantly improved after the 10th epoch. To demonstrate a clearer view of the variations in the RMSE value until the early stopping epoch,
Figure 16b shows the variations in a logarithmic scale. Even though some fluctuations are observed in the validation dataset, they remain within a relatively low range and, hence, the model is not overfitting significantly. Further,
Figure 17 presents the comparison between the predicted data and the actual data for node number 2’s x displacement for 100 testing samples. It demonstrates that both the actual and predicted data are closely similar, indicating a highly effective model performance.
Table 4 compares the differences in errors and training times of each model. The models were trained in a computer with an AMD Ryzen 7 5800H with a Radeon graphics processor and 16 GB RAM. It is noticeable that all three models showed an excellent performance, whilst the RF model showed the lowest RMSE for both testing and validation sets. This indicates that the RF model is very effective in surrogating the FE model for this small-scale bridge. RF models are usually robust to overfitting due to their ensemble nature and can capture non-linear relationships well, especially with structured data. The training time of the RF model is relatively low, as well, but is larger than XGBoost. This may be due to the ensemble nature of RF models that allows for the training of the multiple decision trees independently. The RMSE value of the XGBoost is higher than the RF. However, it reported the lowest training time, and this can be expected from these models as they are optimised for fast training and support efficient gradient-boosting techniques [
50]. The MLP model has the highest RMSE and highest training time in this case. The highest training time can be expected due to the iterative training process in neural networks. However, MLPs can be optimised more to enhance the quality of the results and it needs more data than the other two algorithms to generalise well. However, MLPs can be customised upon the purpose of the surrogate model, and it has many advantages when the model parameters are optimised.
4.2. Variations in Model Accuracy with the Dataset Size
Upon testing the efficiency of each model, it was observed how the testing error of each model changed whilst reducing the size of the dataset. Accordingly, different portions (25%, 50%, 75% and 100%) of this dataset were tested, and the error for each subset was analysed.
Figure 18 shows how the testing error changed for each model architecture and each portion of the dataset.
Immediately, the RMSE values for testing were reduced when the dataset size increased. Such a trend is expected, as when the datasets become larger, they will provide more information for the model to train on and be generalised well whilst reducing the overall error of the trained model. The same trend was observed within each model architecture, and as soon as the size of the dataset reached 100%, the RMSE value of all models achieved relatively lower values compared to other sizes of the dataset. Also, it can be further investigated that the RF model has performed better in handling smaller datasets than the other models, and hence, it can be concluded that the RF model is less sensitive to the size of the dataset, whilst the MLP was found to be the most sensitive model for smaller datasets among the smaller datasets.
4.3. Variations in Model Accuracy with Deficiencies in Sensor Readings
To evaluate the robustness of the proposed model, a sensitivity analysis was conducted while considering variations in the sensor accuracy and missing sensor data. Initially, to assess the accuracy of the model under missing sensor data, measurements of one sensor were avoided at a time and a new dataset was prepared. For instance, the new dataset consisted of data records 10 times more than the original dataset, including the possible combinations of missing strain gauge readings, and the model was trained based on that. Then, the model was tested on a randomly selected test dataset for three ML models, and the test RMSE values were compared.
Table 5 summarises the performance and computational efficiency of those three machine learning models when applied to the dataset containing missing sensor readings. The comparison was done based on two key metrics: the test RMSE and training time.
As shown in
Table 5, the test RMSE values and training times provide valuable insights into the performance of the three models. The XGBoost algorithm achieved the lowest test RMSE value (0.00080 mm), significantly outperforming the RF model (0.00759 mm) and MLP algorithm (0.00117 mm). This superior accuracy can be attributed to XGBoost’s advanced regularisation techniques and its ability to capture complex, non-linear relationships in the data. The robust handling of missing sensor readings highlights XGBoost’s adaptability to datasets with incomplete information, which is critical in real-world scenarios. Moreover, the training time for XGBoost (15.56 s) was substantially lower compared to the RF model (100.93 s) and MLP algorithm (115.71 s). The highly optimised tree-based architecture of XGBoost, which includes parallelised processing and efficient memory usage, contributes to this faster training time. This makes XGBoost a practical choice for applications where both accuracy and computational efficiency are essential. However, it is important to note that all three models experienced longer training times when compared to their performance on the original clean dataset. This increase in computational effort can be attributed to the additional complexity introduced by missing data, requiring models to process sparse information more effectively. While XGBoost’s design inherently addresses sparsity and missing values, the RF model and MLP algorithm may require additional preprocessing steps or more complex imputation strategies, potentially increasing the training duration. The RF model, while less accurate in this case, remains a strong contender due to its interpretability and resilience against overfitting, particularly when working with smaller datasets. The MLP algorithm, on the other hand, demonstrated competitive accuracy but required the longest training time, likely due to its dependence on iterative optimisation processes and sensitivity to hyperparameter tuning.
Also, the originally tested models were fed with the same test dataset with missing strain values, and the RMSE values were calculated to assess the capacity of the models to deal with the missing strain values.
Figure 19 illustrates the variations in RMSE values for those models under two scenarios: the original model trained on complete data and the modified model trained with missing sensor data.
It can be seen that the results have noticeably improved in the RMSE values for the modified models compared to the original ones, particularly for the XGBoost and MLP algorithms. For the XGBoost algorithm, the RMSE value showed a significant decline, demonstrating its robustness and adaptability when dealing with noisy or incomplete datasets. Similarly, the MLP algorithm also exhibited a considerable improvement in accuracy, which can be attributed to its capability to learn and model complex non-linear relationships within the data. In contrast, the RF model experienced a marginal decrease in the RMSE value, improving from approximately 0.009 to 0.007. While this indicates a slight improvement, it highlights the limitations of RF in handling noisy or incomplete datasets compared to XGBoost and MLP. The ensemble-based nature of RF is generally effective for reducing variance and improving predictions, but its reliance on simpler decision trees may make it less adept at capturing intricate patterns in the data. The stark differences in RMSE improvements among the models suggest that both XGBoost and MLP leverage advanced optimisation techniques to mitigate the impact of data imperfections. XGBoost’s gradient-boosting framework, combined with regularisation, enables it to prioritise key features and manage missing values effectively. Similarly, the MLP algorithm, with its multi-layer architecture, benefits from backpropagation and non-linear activation functions, allowing it to refine its weights and enhance predictive accuracy, even with incomplete data.
To assess the robustness of the model to inaccuracies in sensors, the same dataset was augmented, introducing ±5%, ±10%, and ±15% errors for each sensor at a time, and the models were tested for both clean data and deficient data to assess the generalisation capacity of each model. The maximum error percentage was selected as 15% with respect to the obtained results under the validation process.
Table 6 presents the test RMSE values of those three ML models for each error level.
As shown in
Table 6, the XGBoost algorithm consistently outperformed the other models, achieving the lowest RMSE values across all error levels, with a minimal increase in the RMSE as the error level rose. This highlights its superior ability to generalise and handle noisy or inaccurate sensor data, which is critical in real-world scenarios where imperfect measurements are common. XGBoost’s gradient-boosting framework and regularisation techniques allow it to prioritise relevant patterns and mitigate the impact of noise effectively, resulting in more stable performance. In contrast, the RF model exhibited a more pronounced increase in the RMSE as the error level increased, indicating a higher sensitivity to inaccuracies in the input data. This could be attributed to RF’s reliance on discrete splits in decision trees, which can amplify the effects of noise. Although RF models are robust to overfitting due to their ensemble nature, they may require additional preprocessing, such as advanced imputation techniques or noise reduction methods, to better handle such scenarios. The MLP algorithm demonstrated moderate robustness, achieving RMSE values slightly higher than XGBoost but exhibiting less sensitivity to increasing error levels compared to RF. The multi-layer architecture and use of non-linear activation functions enable MLP models to learn complex relationships, but they may still be influenced by the quality of input data, necessitating careful tuning and regularisation for optimal performance.
In conclusion, these findings highlight the importance of selecting machine learning models based on the specific requirements of the task, including accuracy, training time, and dataset characteristics. XGBoost demonstrated superior robustness and adaptability, particularly in handling incomplete or noisy data, while the RF and MLP models showed potential for improvement. Future work should focus on optimising these models through techniques such as hyperparameter tuning, feature engineering, and hybrid approaches, as well as incorporating comprehensive sensitivity analyses to enhance their resilience and performance in real-world scenarios.
4.4. Implementation of Real-Time DTs
The trained models were then applied to implement the DT model of the laboratory-scaled bridge. The locations of the sensors and the installation are explained in
Section 3.1. Sensors were installed in 10 different locations on the bridge, and they came up with the inbuilt software that allows the transfer of the measured strain values to the computer. They were updated as per the sampling rate, and it was set to one second to achieve near real-time conditions. The measured sensor values were then transferred to a Python code, which was applied to the trained model and generated the displacement values as the output of the model. It was assumed that the bridge was acting linearly elastic, and the displacement values were then used to obtain the stress values of each member. Ultimately, the stress variation and the deformed shape of the bridge were displayed on the screen. A snapshot of one instance has been presented in
Figure 20. For every instance where the applied load is changing, the stress variation also changes under near real-time conditions.
All the tested models were used for this process one by one and the inference time of each model to generate one set of outputs was noted to select the optimum model architecture that can be used to achieve near real-time conditions.
Table 7 presents the inference time of each model. The inference times of all models are less than one second, and as that is higher than the sampling rate of the tested sensors, it is possible to achieve near real-time conditions using all three models. However, the XGBoost algorithm showed the lowest inference time, which is one millisecond, whereas the MLP showed the highest inference time, which is 44 milliseconds. The RF model also showed a closer inference time to the XGBoost algorithm, which is around 5 milliseconds. Overall, it can be observed that the tree-based models are relatively faster than the neural network models here. XGBoost is typically optimised for both training and inference speed, as it tends to use fewer trees than the RF model and, hence, it is justifiable to have the lowest times for that in this case. Even though the MLPs are generally efficient, they may be slower than the tree-based models, as they need to perform matrix multiplications and apply activation function computations for each layer.
5. Limitations and Future Work
While the current study makes significant contributions in developing surrogate models for real-time FE modelling for the purpose of advancing the capacities of DT implementations, certain limitations have also been identified. It is important to delve deeper into these limitations and suggest potential avenues for future research in this field. Several identified limitations can be presented as follows.
(1) The implemented DT models based on FE modelling have focused on presenting only the deformed shape and stress variations in the structure in real time and identifying the critical locations of the bridge if there is any anomaly in the structural behaviour. However, further extensions can be made to estimate the future state and to suggest suitable maintenance measures for the structure in order to achieve a remote structural health monitoring and maintenance process via DTs.
(2) The linear elasticity of the structure has been assumed when developing the dataset for the training of the machine learning models. However, it is understandable that due to the statistical nature of machine learning models, it is possible to implement the same scenario for a non-linear model, as well, and further experimental investigations are suggested for that.
(3) As suggested by the current study, it was identified that the tree-based models showed a better performance than the neural network models in surrogating real-time FE modelling. However, many more neural network architectures exist, and their efficiency has not been checked in the current study and the performance of the model may also be able to be significantly improved with other neural network models.
(4) While the current study demonstrates the feasibility of predicting deformed shapes and stress variations using traditional ML models as surrogates of high-fidelity FE models, future work will focus on exploring the efficiency of other artificial neural network (ANN) models, such as graph neural networks (GNNs), which have the potential to leverage the nodal connectivity and the geometric relationships of structures, further improving prediction accuracy and generalisability.
(5) Though the results obtained in this study were based on a laboratory-scale truss bridge, it provides an insight into the structural behaviour of real-world structures, particularly for capturing strain and deformation trends under loading. While the simplified setup ensures controlled validation, it is recognised that full-scale structures exhibit additional complexities, such as scale effects, non-linear material responses, and intricate boundary conditions. Future work is suggested on addressing these aspects to further validate the applicability of the model to enhance its scalability to practical scenarios.
(6) This study focuses on a single laboratory-scale bridge to validate the proposed models, showcasing their accuracy and feasibility under controlled conditions. However, this limited scope raises questions about their transferability to other structural configurations, such as large-scale bridges or complex geometries. Structural behaviour varies with material properties, boundary conditions, and loading scenarios, necessitating further validation across diverse structures and conditions. Future research should explore the generalisation capability of these models by applying them to real-world structures, incorporating complexities like multi-span systems and environmental effects. This would enhance their robustness and scalability for broader structural engineering applications.
6. Conclusions
The digital twin concept advances the traditional structural health monitoring systems whilst providing a more intelligent facet for predictive maintenance and decision-making strategies by integrating the real-time monitoring data of infrastructure systems with their own digital models. The capability of digital twins is further possible when expanded to predict critical stresses in real time and to immediately trigger possible failures whilst in synergy with finite element modelling (FEM). However, due to the computational intensity of the FEM, achieving real-time computations is challenging, and hence, a surrogate model is required to approximate this high-fidelity model with a lower-order representation. Also, since the measured structural response is used to predict the overall structural behaviour, an inverse structural analysis process should be conducted. In this light, the current study presents a combination of machine learning (ML) algorithms and FEM to develop digital twins that run in real time to advance the current structural health monitoring processes.
A laboratory-scaled bridge was tested in this study, which was instrumented with strain gauges in ten distinct locations on the bridge. When the strain gauges measure the strain variations in each member, the readings will then be directly transferred to a trained ML model that surrogates an inverse structural analysis process of FEM. Three machine learning models were tested in this study, and they were trained based on a dataset that was implemented by a validated FE model of the bridge. Although the dataset preparation and the model training require more computational resources and time, the trained model resulted in significant benefits, as it allows the generation of the outputs immediately once trained. It was challenging to identify the optimum parameters of the ML models to achieve the optimum performance and also, the efficiency of the model depends on the selected model architecture. Hence, three ML models, random forest (RF), XGBoost, and multi-layer perceptron (MLP), were selected to assess their capacities in implementing real-time FE-based digital twins.
It was identified that the tree-based models outperformed the neural network model in the surrogation process for this tested bridge. Also, the accuracy of the models strongly depends on the size of the dataset, and when more data are available, more information can be provided to the ML models for better generalisation. Also, it was identified that the model should be trained in such a way that it includes missing or deficient sensor data, and the model will be able to accurately capture any deviations of sensor readings, which are very common in real-world cases. Based on the inference times of the tested ML models, it can be concluded that a real-time analysis process is possible to achieve. Also, the achieved precision of the models is extremely high, and it is understandable that a combination of FE modelling with data-driven techniques like machine learning is an ideal option for implementing real-time digital twins. The suggested methodology can possibly be expanded for a much larger structure, as well, since the model accuracy strongly depends on the quality of the dataset and the optimisation of the model architecture. Such a digital twin system is extremely beneficial for asset owners, as it offers a powerful tool for real-time visualisation, enabling them to monitor the condition of the actual structure without the need for physical inspection.
Author Contributions
Conceptualisation, S.J. and A.A.; Methodology, S.J.; Validation, S.J.; Investigation, F.S.; Writing—review and editing, S.J., M.M., A.A., A.S., Z.S. and F.S.; Visualisation, Z.S. and F.S.; Supervision, M.M., A.A., A.S., S.S. and J.T.; Project administration, M.M.; Funding acquisition, M.M. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research work has been conducted with the support of the SmartCrete CRC project program (21.PP.0112—digital twin of reinforced concrete infrastructure for intelligent asset management). The project is led by RMIT University and supported by local governments, several universities and industry partners, including the Victoria State Government (Department of Transport and Planning), New South Wales (Transport of New South Wales), Melbourne Water, Australia Curtin University, Western Sydney University and University of Technology Sydney, Beta International Associates, Upward Technology, Ash Development Association of, Lastek, Macdonald Lucas and Bentley.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mahmoodian, M.; Shahrivar, F.; Setunge, S.; Mazaheri, S. Development of Digital Twin for Intelligent Maintenance of Civil Infrastructure. Sustainability 2022, 14, 8664. [Google Scholar] [CrossRef]
- Adam, J.M.; Makoond, N.; Riveiro, B.; Buitrago, M. Risks of bridge collapses are real and set to rise—Here’s why. Nature 2024, 629, 1001–1003. [Google Scholar] [CrossRef] [PubMed]
- Artus, M.; Koch, C. State of the art in damage information modeling for RC bridges—A literature review. Adv. Eng. Inform. 2020, 46, 101171. [Google Scholar] [CrossRef]
- Martucci, D.; Civera, M.; Surace, C. Bridge monitoring: Application of the extreme function theory for damage detection on the I-40 case study. Eng. Struct. 2023, 279, 115573. [Google Scholar] [CrossRef]
- Civera, M.; Sibille, L.; Zanotti Fragonara, L.; Ceravolo, R. A DBSCAN-based automated operational modal analysis algorithm for bridge monitoring. Meas. J. Int. Meas. Confed. 2023, 208, 112451. [Google Scholar] [CrossRef]
- Callcut, M.; Cerceau Agliozzo, J.-P.; Varga, L.; McMillan, L. Digital twins in civil infrastructure systems. Sustainability 2021, 13, 11549. [Google Scholar] [CrossRef]
- van Dinter, R.; Tekinerdogan, B.; Catal, C. Predictive maintenance using digital twins: A systematic literature review. Inf. Softw. Technol. 2022, 151, 107008. [Google Scholar] [CrossRef]
- Lu, R.; Brilakis, I. Digital twinning of existing reinforced concrete bridges from labelled point clusters. Autom. Constr. 2019, 105, 102837. [Google Scholar] [CrossRef]
- Jayasinghe, S.C.; Mahmoodian, M.; Sidiq, A.; Nanayakkara, T.M.; Alavi, A.; Mazaheri, S.; Shahrivar, F.; Sun, Z.; Setunge, S. Innovative digital twin with artificial neural networks for real-time monitoring of structural response: A port structure case study. Ocean Eng. 2024, 312, 119187. [Google Scholar] [CrossRef]
- Ye, C.; Butler, L.; Calka, B.; Iangurazov, M.; Lu, Q.; Gregory, A.; Girolami, M.; Middleton, C. A digital twin of bridges for structural health monitoring. In Proceedings of the 12th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 10–12 September 2019. [Google Scholar] [CrossRef]
- Moi, T.; Cibicik, A.; Rølvåg, T. Digital twin based condition monitoring of a knuckle boom crane: An experimental study. Eng. Fail. Anal. 2020, 112, 104517. [Google Scholar] [CrossRef]
- Gupta, D.K. Inverse Methods for Load Identification Augmented by Optimal Sensor Placement and Model Order Reduction; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Wang, Y.; Zhou, Z.; Xu, H.; Li, S.; Wu, Z. Inverse load identification in stiffened plate structure based on in situ strain measurement. Struct. Durab. Health Monit. 2021, 15, 85–101. [Google Scholar] [CrossRef]
- Kononenko, O.; Kononenko, I. Machine Learning and Finite Element Method for Physical Systems Modeling. arXiv 2018, arXiv:1801.07337. [Google Scholar] [CrossRef]
- Badarinath, P.V.; Chierichetti, M.; Kakhki, F.D. A machine learning approach as a surrogate for a finite element analysis: Status of research and application to one dimensional systems. Sensors 2021, 21, 1654. [Google Scholar] [CrossRef] [PubMed]
- Di Mucci, V.M.; Cardellicchio, A.; Ruggieri, S.; Nettis, A.; Renò, V.; Uva, G. Artificial intelligence in structural health management of existing bridges. Autom. Constr. 2024, 167, 105719. [Google Scholar] [CrossRef]
- Conceição António, C.; Rasheed, S. A displacement field approach based on FEM-ANN and experiments for identification of elastic properties of composites. Int. J. Adv. Manuf. Technol. 2018, 95, 4279–4291. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Kim, H.S. Development of seismic response simulation model for building structures with semi-active control devices using recurrent neural network. Appl. Sci. 2020, 10, 3915. [Google Scholar] [CrossRef]
- Cao, B.T.; Obel, M.; Freitag, S.; Mark, P.; Meschke, G. Artificial neural network surrogate modelling for real-time predictions and control of building damage during mechanised tunnelling. Adv. Eng. Softw. 2020, 149, 102869. [Google Scholar] [CrossRef]
- Marinkovic, D.; Zehn, M. Survey of finite element method-based real-time simulations. Appl. Sci. 2019, 9, 2775. [Google Scholar] [CrossRef]
- Logan, D.L. A First Course in the Finite Element Method, 5th ed.; Cencage Learning: Stamford, CT, USA, 2012. [Google Scholar]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Kevin Tucker, P. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef]
- Ibragimova, O.; Brahme, A.; Muhammad, W.; Connolly, D.; Lévesque, J.; Inal, K. A convolutional neural network based crystal plasticity finite element framework to predict localised deformation in metals. Int. J. Plast. 2022, 157, 103374. [Google Scholar] [CrossRef]
- Vita, V.; Fotis, G.; Chobanov, V.; Pavlatos, C.; Mladenov, V. Predictive Maintenance for Distribution System Operators in Increasing Transformers’ Reliability. Electronics 2023, 12, 1356. [Google Scholar] [CrossRef]
- Flah, M.; Nunez, I.; Ben Chaabene, W.; Nehdi, M.L. Machine Learning Algorithms in Civil Structural Health Monitoring: A Systematic Review. Arch. Comput. Methods Eng. 2021, 28, 2621–2643. [Google Scholar] [CrossRef]
- Guan, Q.Z.; Yang, Z.X.; Guo, N.; Hu, Z. Finite element geotechnical analysis incorporating deep learning-based soil model. Comput. Geotech. 2023, 154, 105120. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Nabian, M.A.; Alemazkoor, N. Multifidelity graph neural networks for efficient and accurate mesh-based partial differential equations surrogate modeling. Comput. Aided Civ. Infrastruct. Eng. 2024, 1–18. [Google Scholar] [CrossRef]
- Javadi, A.A.; Tan, T.P.; Zhang, M. Application of artificial neural network for constitutive modeling in finite element analysis. Comput. Assist. Mech. Eng. Sci. 2003, 10, 523–530. [Google Scholar]
- Tao, F.; Liu, X.; Du, H.; Yu, W. Finite element coupled positive definite deep neural networks mechanics system for constitutive modeling of composites. Comput. Methods Appl. Mech. Eng. 2022, 391, 114548. [Google Scholar] [CrossRef]
- Tohidi, S.; Sharifi, Y. Load-carrying capacity of locally corroded steel plate girder ends using artificial neural network. Thin-Walled Struct. 2016, 100, 48–61. [Google Scholar] [CrossRef]
- Shahani, A.R.; Setayeshi, S.; Nodamaie, S.A.; Asadi, M.A.; Rezaie, S. Prediction of influence parameters on the hot rolling process using finite element method and neural network. J. Mater. Process. Technol. 2009, 209, 1920–1935. [Google Scholar] [CrossRef]
- Calò, M.; Ruggieri, S.; Buitrago, M.; Nettis, A.; Adam, J.M.; Uva, G. An ML-based framework for predicting prestressing force reduction in reinforced concrete box-girder bridges with unbonded tendons. Eng. Struct. 2025, 325, 119400. [Google Scholar] [CrossRef]
- Shokrollahi, Y.; Nikahd, M.M.; Gholami, K.; Azamirad, G. Deep Learning Techniques for Predicting Stress Fields in Composite Materials: A Superior Alternative to Finite Element Analysis. J. Compos. Sci. 2023, 7, 311. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, N.-Z. Graph Neural Networks (GNNs) based accelerated numerical simulation. Eng. Appl. Artif. Intell. 2023, 123, 106370. [Google Scholar] [CrossRef]
- Greve, L.; van de Weg, B.P. Surrogate modeling of parametrized finite element simulations with varying mesh topology using recurrent neural networks. Array 2022, 14, 100137. [Google Scholar] [CrossRef]
- El Mrabet, Z.; Sugunaraj, N.; Ranganathan, P.; Abhyankar, S. Random Forest Regressor-Based Approach for Detecting Fault Location and Duration in Power Systems. Sensors 2022, 22, 458. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Duan, T.; Zhang, Y.; Liu, J.; Zhang, J.; Lei, Y. Predicting the Permeability of Pervious Concrete Based on the Beetle Antennae Search Algorithm and Random Forest Model. Adv. Civ. Eng. 2020, 2020, 8863181. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Zhang, L.; Wang, X. Risk prediction and diagnosis of water seepage in operational shield tunnels based on random forest. J. Civ. Eng. Manag. 2021, 27, 539–552. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jayasinghe, S.C.; Nanayakkara, T.M.; Alavi, A.; Mahmoodian, M.; Sidiq, A.; Sun, Z.; Shahrivar, F.; Setunge, S. Real-time Structural Integrity Assessment of Bridge Infrastructure. In Proceedings of the IABMAS 2024, Copenhagen, Denmark, 24–28 June 2024. [Google Scholar]
- Wu, B.; Sun, W.; Meng, G. Sensitivity Analysis of Influencing Factors of Karst Tunnel Construction Based on Orthogonal Tests and a Random Forest Algorithm. Appl. Sci. 2024, 14, 2079. [Google Scholar] [CrossRef]
- Ramagiri, K.K.; Boindala, S.P.; Zaid, M.; Kar, A.; Marano, G.C.; Prasad, R.; Ray Chaudhuri, S.; Kavitha, P.E.; Unni Kartha, G.; Achison, R.J.; et al. Random Forest-Based Algorithms for Prediction of Compressive Strength of Ambient-Cured AAB Concrete—A Comparison Study; Springer International Publishing AG: Cham, Switzerland, 2021; Volume 171, pp. 717–725. [Google Scholar]
- Aminpour, M.; Alaie, R.; Kardani, N.; Moridpour, S.; Nazem, M. Slope stability predictions on spatially variable random fields using machine learning surrogate models. arXiv 2022, arXiv:2204.06097. [Google Scholar] [CrossRef]
- Wu, Y.; He, X. Using the automated random forest approach for obtaining the compressive strength prediction of RCA. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 855–867. [Google Scholar] [CrossRef]
- de-Prado-Gil, J.; Palencia, C.; Jagadesh, P.; Martínez-García, R. A Comparison of Machine Learning Tools That Model the Splitting Tensile Strength of Self-Compacting Recycled Aggregate Concrete. Materials 2022, 15, 4164. [Google Scholar] [CrossRef] [PubMed]
- Tuken, A.; Abbas, Y.M.; Siddiqui, N.A. Efficient prediction of the load-carrying capacity of ECC-strengthened RC beams—An extra-gradient boosting machine learning method. Structures 2023, 56, 105053. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Rathakrishnan, V.; Bt. Beddu, S.; Ahmed, A.N. Predicting compressive strength of high-performance concrete with high volume ground granulated blast-furnace slag replacement using boosting machine learning algorithms. Sci. Rep. 2022, 12, 9539. [Google Scholar] [CrossRef] [PubMed]
- Le Nguyen, K. Application of XGBoost Model for Predicting the Dynamic Response of High-Speed Railway Bridges. In Proceedings of the CIGOS 2021, Emerging Technologies and Applications for Green Infrastructure, Singapore, 28–29 October 2021; pp. 1765–1773. [Google Scholar]
- Jodeiri Shokri, B.; Mirzaghorbanali, A.; McDougall, K.; Karunasena, W.; Nourizadeh, H.; Entezam, S.; Hosseini, S.; Aziz, N. Data-Driven Optimised XGBoost for Predicting the Performance of Axial Load Bearing Capacity of Fully Cementitious Grouted Rock Bolting Systems. Appl. Sci. 2024, 14, 9925. [Google Scholar] [CrossRef]
- Wu, L.-j.; Li, X.; Yuan, J.-d.; Wang, S.-j. Real-time prediction of tunnel face conditions using XGBoost Random Forest algorithm. Front. Struct. Civ. Eng. 2023, 17, 1777–1795. [Google Scholar] [CrossRef]
- Ferrario, E.; Pedroni, N.; Zio, E.; Lopez-Caballero, F. Bootstrapped Artificial Neural Networks for the seismic analysis of structural systems. Struct. Saf. 2017, 67, 70–84. [Google Scholar] [CrossRef]
- Lara-Benítez, P.; Carranza-García, M.; Riquelme, J.C. An Experimental Review on Deep Learning Architectures for Time Series Forecasting. arXiv 2021, arXiv:2103.12057. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control, 2nd ed.; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Dadras Eslamlou, A.; Huang, S. Artificial-Neural-Network-Based Surrogate Models for Structural Health Monitoring of Civil Structures: A Literature Review. Buildings 2022, 12, 2067. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hoffer, J.G.; Geiger, B.C.; Ofner, P.; Kern, R. Mesh-free surrogate models for structural mechanic FEM simulation: A comparative study of approaches. Appl. Sci. 2021, 11, 9411. [Google Scholar] [CrossRef]
- Liu, G.R. FEA-AI and AI-AI: Two-Way Deepnets for Real-Time Computations for Both Forward and Inverse Mechanics Problems. Int. J. Comput. Methods 2019, 16, 1950045. [Google Scholar] [CrossRef]
- Zeroual, A.; Fourar, A.; Djeddou, M. Predictive modeling of static and seismic stability of small homogeneous earth dams using artificial neural network. Arab. J. Geosci. 2019, 12, 16. [Google Scholar] [CrossRef]
- Ma, Z.; Chang, H.; Sun, Z.; Liu, F.; Li, W.; Zhao, D.; Chen, C. Very Short-Term Renewable Energy Power Prediction Using XGBoost Optimized by TPE Algorithm. In Proceedings of the 2020 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 1236–1241. [Google Scholar]
Figure 1.
Benefits of DTs when integrated with different technologies.
Figure 1.
Benefits of DTs when integrated with different technologies.
Figure 2.
The DT of a bridge based on FE modelling.
Figure 2.
The DT of a bridge based on FE modelling.
Figure 3.
The schematic of the methodology.
Figure 3.
The schematic of the methodology.
Figure 4.
Experimental laboratory-scale bridge.
Figure 4.
Experimental laboratory-scale bridge.
Figure 5.
Configuration of sensors and loading cells.
Figure 5.
Configuration of sensors and loading cells.
Figure 6.
Stress–strain relationship of the material.
Figure 6.
Stress–strain relationship of the material.
Figure 7.
Validated FE model of the bridge for zero loads.
Figure 7.
Validated FE model of the bridge for zero loads.
Figure 8.
Distribution of input and output data.
Figure 8.
Distribution of input and output data.
Figure 9.
The first two levels of one decision tree of the developed model.
Figure 9.
The first two levels of one decision tree of the developed model.
Figure 10.
The first few stages of one decision tree of the developed XGBoost model.
Figure 10.
The first few stages of one decision tree of the developed XGBoost model.
Figure 11.
The schematic of the developed MLP model.
Figure 11.
The schematic of the developed MLP model.
Figure 12.
RMSE values of 5 folds.
Figure 12.
RMSE values of 5 folds.
Figure 13.
Comparison of the predicted and actual data of the RF model.
Figure 13.
Comparison of the predicted and actual data of the RF model.
Figure 14.
Variations in the error with iterations.
Figure 14.
Variations in the error with iterations.
Figure 15.
Comparison of the predicted and actual data for XGBoost algorithm.
Figure 15.
Comparison of the predicted and actual data for XGBoost algorithm.
Figure 16.
Variations in the error with iterations (a) in normal scale (b) in original scale.
Figure 16.
Variations in the error with iterations (a) in normal scale (b) in original scale.
Figure 17.
Comparison of the predicted and actual data for MLP model.
Figure 17.
Comparison of the predicted and actual data for MLP model.
Figure 18.
Variations in the RMSE value with the size of the dataset.
Figure 18.
Variations in the RMSE value with the size of the dataset.
Figure 19.
Variations in the RMSE value with original and modified models.
Figure 19.
Variations in the RMSE value with original and modified models.
Figure 20.
Variation of the stress in each member that is changing in real-time.
Figure 20.
Variation of the stress in each member that is changing in real-time.
Table 1.
Comparison between FE strain and experimental strain values.
Table 1.
Comparison between FE strain and experimental strain values.
| Member | FE Strain/Exp Strain |
|---|
| Vertical Loading | Inclined Loading | Combined Loading |
|---|
| 100 N | 300 N | 500 N | 100 N | 300 N | 500 N | 100 N | 300 N | 500 N |
|---|
| SG_1 | 0.9335 | 0.9718 | 0.9798 | 0.8811 | 0.8819 | 0.9448 | 0.8819 | 0.9524 | 0.9600 |
| SG_2 | 0.9335 | 0.9524 | 0.9561 | 1.1329 | 0.9524 | 0.9228 | 0.9158 | 0.9785 | 0.9373 |
| SG_3 | 0.8817 | 0.9718 | 0.9798 | 0.8811 | 0.9158 | 0.9018 | 1.1343 | 0.8819 | 0.9228 |
| SG_4 | 0.9335 | 0.9718 | 0.9678 | 0.9913 | 0.9524 | 0.9228 | 0.9925 | 0.9524 | 0.9448 |
| SG_5 | 0.9165 | 0.9818 | 0.9854 | 0.9160 | 0.9479 | 0.9546 | 0.8336 | 0.8868 | 0.9749 |
| SG_6 | 0.8729 | 0.9646 | 0.9646 | 0.8327 | 0.9163 | 0.9351 | 0.8336 | 0.8591 | 0.9546 |
| SG_7 | 0.9165 | 0.9818 | 0.9854 | 0.9160 | 0.9479 | 0.9749 | 1.0189 | 0.9479 | 0.9749 |
| SG_8 | 0.8729 | 0.9996 | 0.9749 | 0.8327 | 0.9163 | 1.0182 | 1.0189 | 0.8868 | 0.9546 |
| SG_9 | 1.0000 | 1.0000 | 1.0000 | 0.9165 | 0.9479 | 0.9854 | 0.9165 | 0.9818 | 0.9646 |
| SG_10 | 0.9165 | 0.9646 | 0.9854 | 1.1450 | 1.0181 | 0.9749 | 0.9640 | 0.8868 | 0.9546 |
Table 2.
Overview of the dataset.
Table 2.
Overview of the dataset.
| For FE Model |
|---|
| Input | Output |
|---|
Loading patterns randomising both the magnitude (−500 N to 500 N) and location of application Geometrical properties, material properties, and boundary conditions
| |
| Extracted parameters from validated FE model to ML models |
| Input | Output |
| Strain values of the members that are instrumented with strain gauges | Displacements of each node along x- and y-directions |
Table 3.
Hyperparameters of each ML model.
Table 3.
Hyperparameters of each ML model.
| Model | Hyperparameter | Value |
|---|
| RF Model | Number of estimators | 100 |
| Maximum depth of each decision tree | 10 |
| XGBoost | Optimiser | Bayesian |
| Number of estimators | 100 |
| Maximum depth of each decision tree | 7 |
| colsample_bytree | 0.5165 |
| gamma | 8.5629 |
| min_child_weight | 4 |
| reg_alpha | 73 |
| reg_lambda | 0.6518 |
| ANN Model | Optimiser | Adam |
| Number of hidden layers | 3 |
| Neurons in first hidden layer | 64 |
| Neurons in second hidden layer | 32 |
| Neurons in third hidden layer | 16 |
| Activation function | ReLU |
| Batch size | 32 |
| Epochs | 200 |
| Early stopping patience | 20 |
Table 4.
Comparison of RMSE values and training times.
Table 4.
Comparison of RMSE values and training times.
| Model Type | Test RMSE (mm) | Validation RMSE (mm) | Training Time (s) |
|---|
| RF model | 0.000350 | 0.000341 | 13.60 |
| XGBoosting algorithm | 0.000494 | 0.000507 | 1.10 |
| MLP algorithm | 0.000524 | 0.000535 | 20.99 |
Table 5.
Comparison of RMSE values and training times for the dataset with missing sensor readings.
Table 5.
Comparison of RMSE values and training times for the dataset with missing sensor readings.
| Model Type | Test RMSE (mm) | Training Time (s) |
|---|
| RF model | 0.00759 | 100.93 |
| XGBoosting algorithm | 0.00080 | 15.56 |
| MLP algorithm | 0.00117 | 115.71 |
Table 6.
Robustness assessment of models to sensor inaccuracies.
Table 6.
Robustness assessment of models to sensor inaccuracies.
| Model Type | Testing RMSE for Different Error Levels of Sensor Readings (mm) |
|---|
| ±5% | ±10% | ±15% |
|---|
| RF model | 0.000352 | 0.000644 | 0.000936 |
| XGBoosting algorithm | 0.000344 | 0.000380 | 0.000425 |
| MLP algorithm | 0.000455 | 0.000462 | 0.000551 |
Table 7.
Inference times of each model.
Table 7.
Inference times of each model.
| Model Architecture | Inference Time (s) |
|---|
| RF model | 0.005 |
| XGBoost | 0.001 |
| MLP | 0.044 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).