Structural Performance of a Hollow-Core Square Concrete Column Longitudinally Reinforced with GFRP Bars under Concentric Load
Abstract
1. Introduction
2. Experimental Procedure and Methodology
2.1. Column Specimens
2.2. Material Characteristics
2.2.1. Concrete
2.2.2. GFRP and Steel
2.3. Test Specimen Preparation
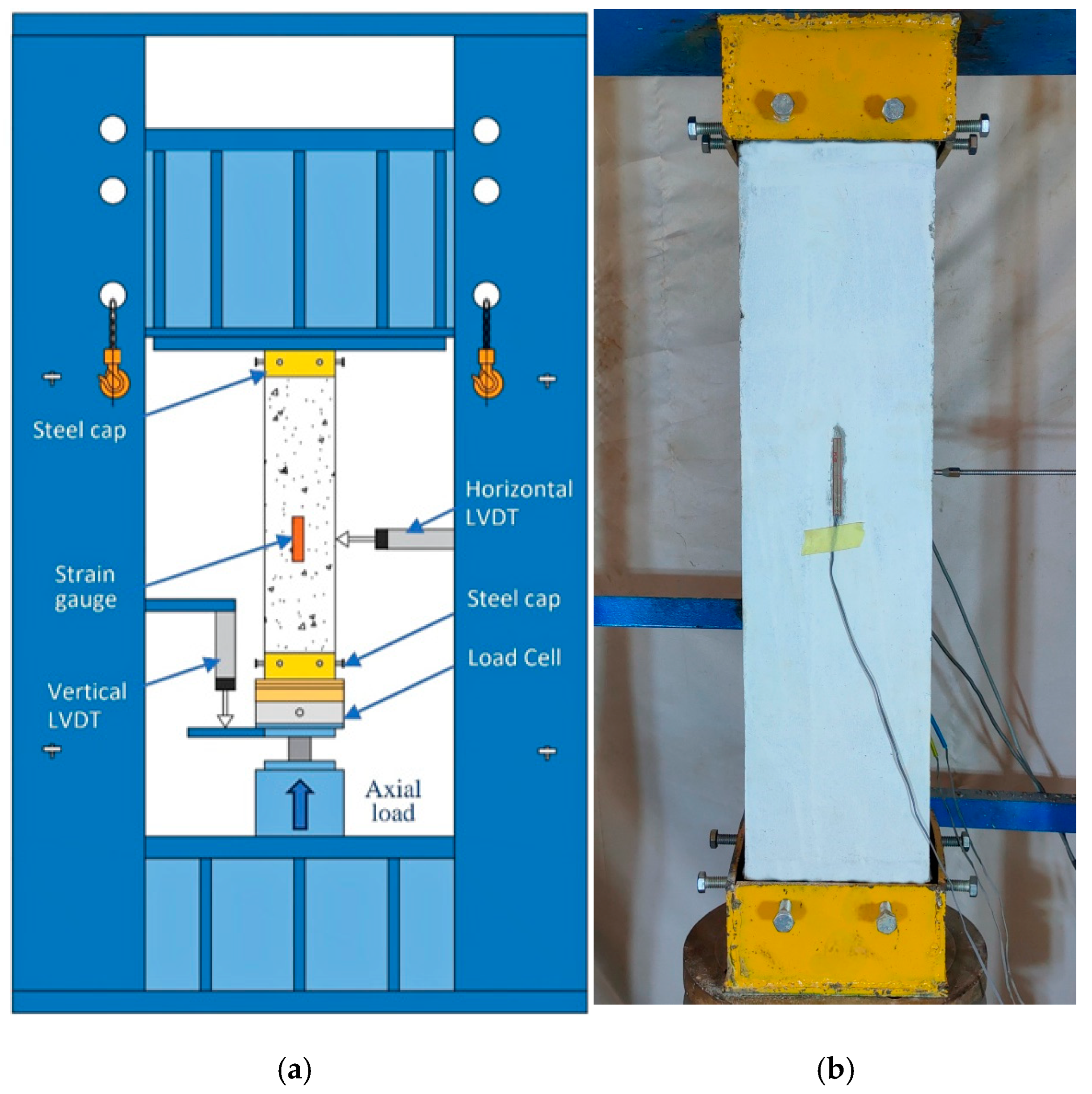
2.4. Test Configuration and Equipment
3. Experimental Outcomes
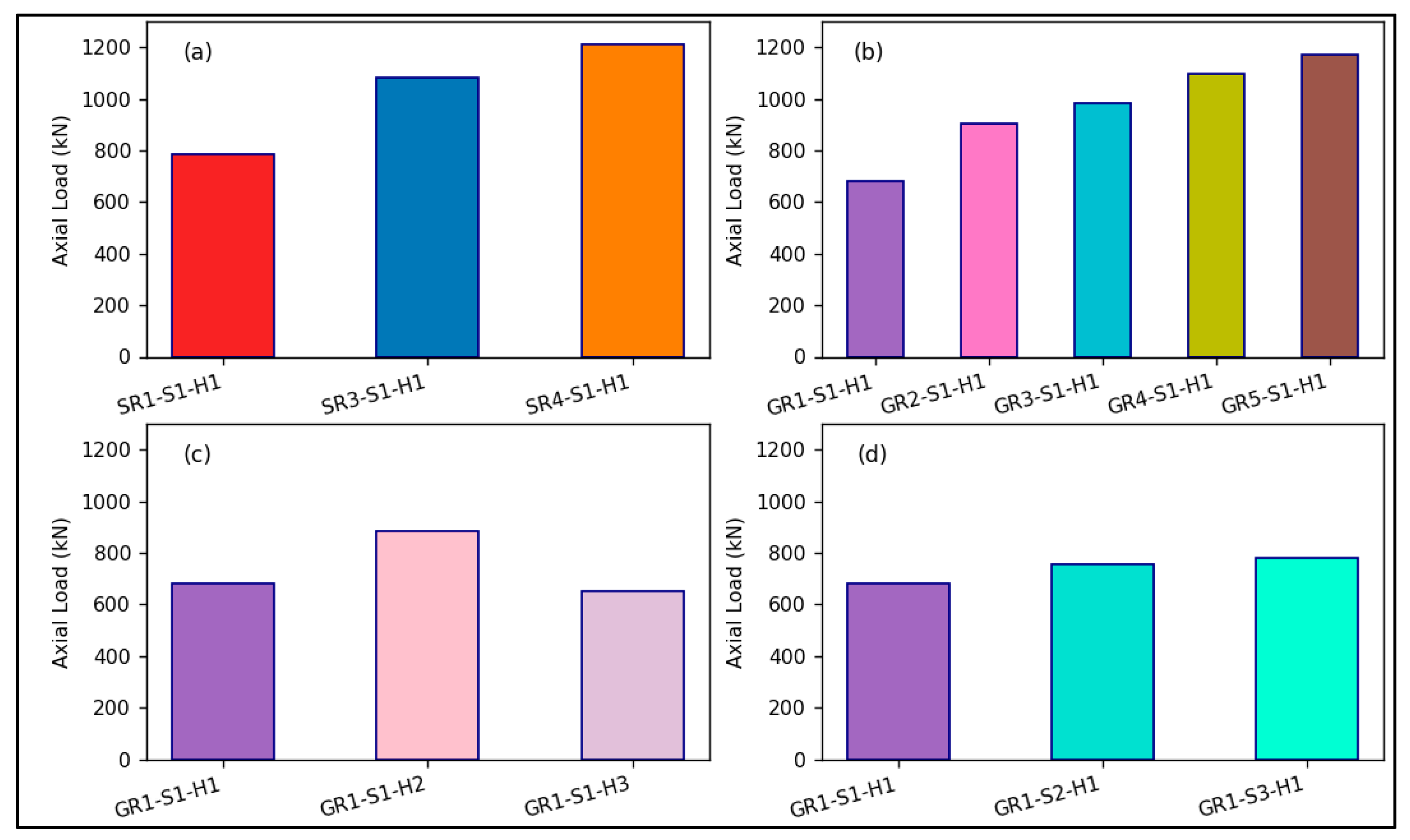
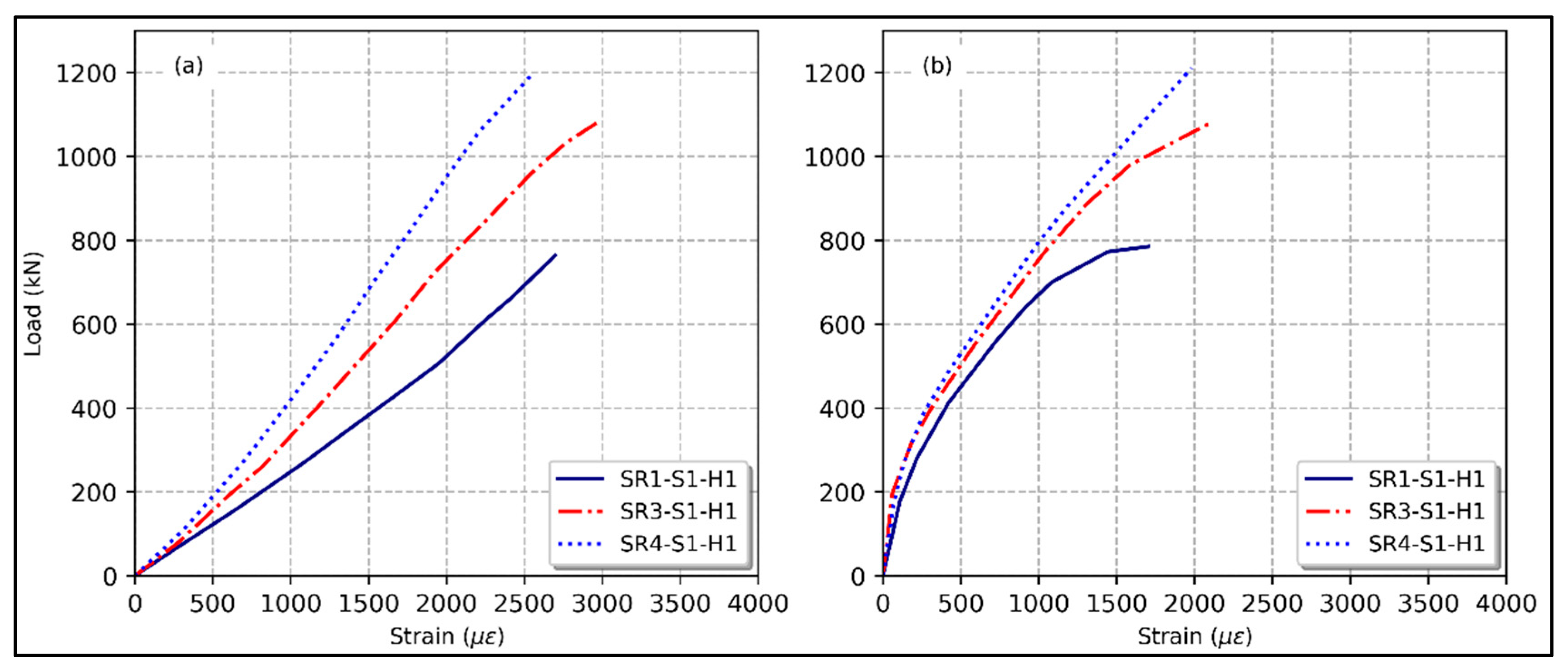
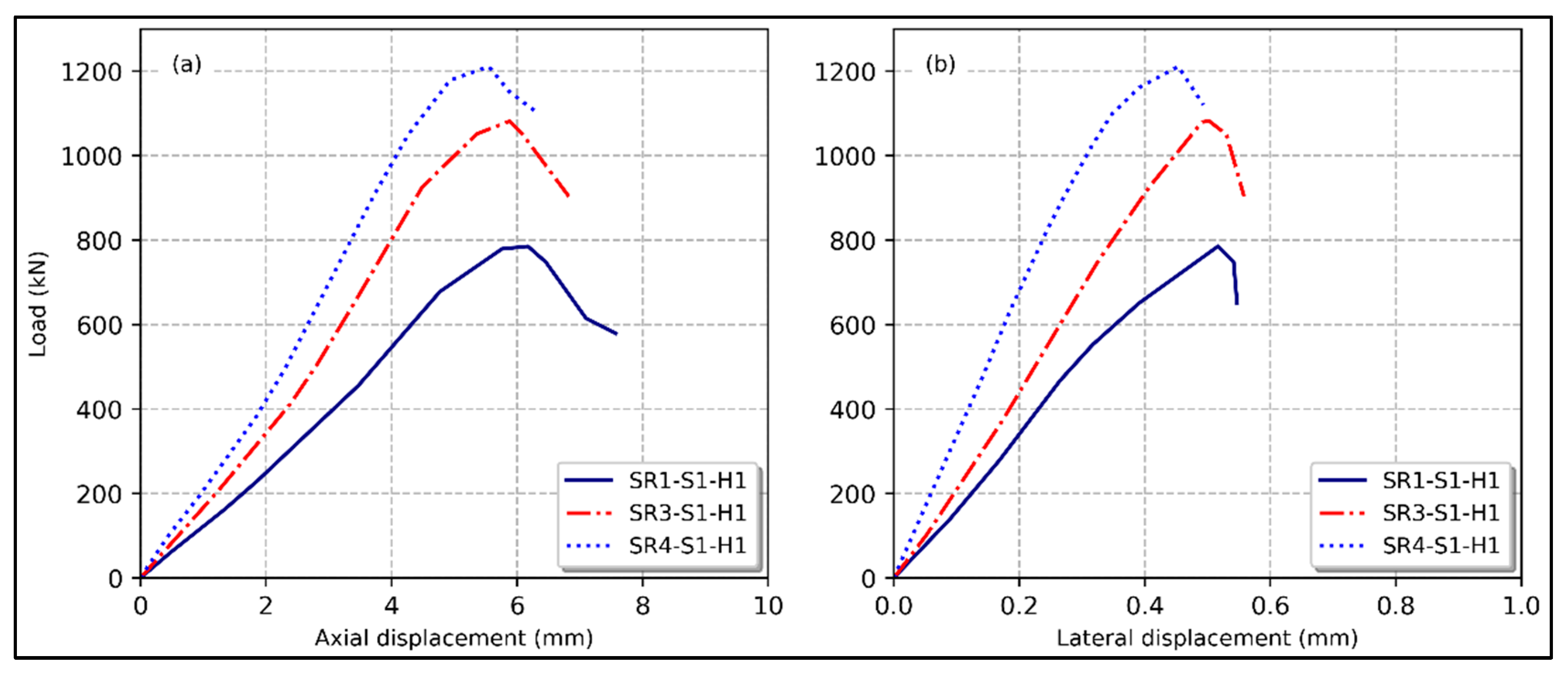
3.1. Steel Reinforcement Ratio
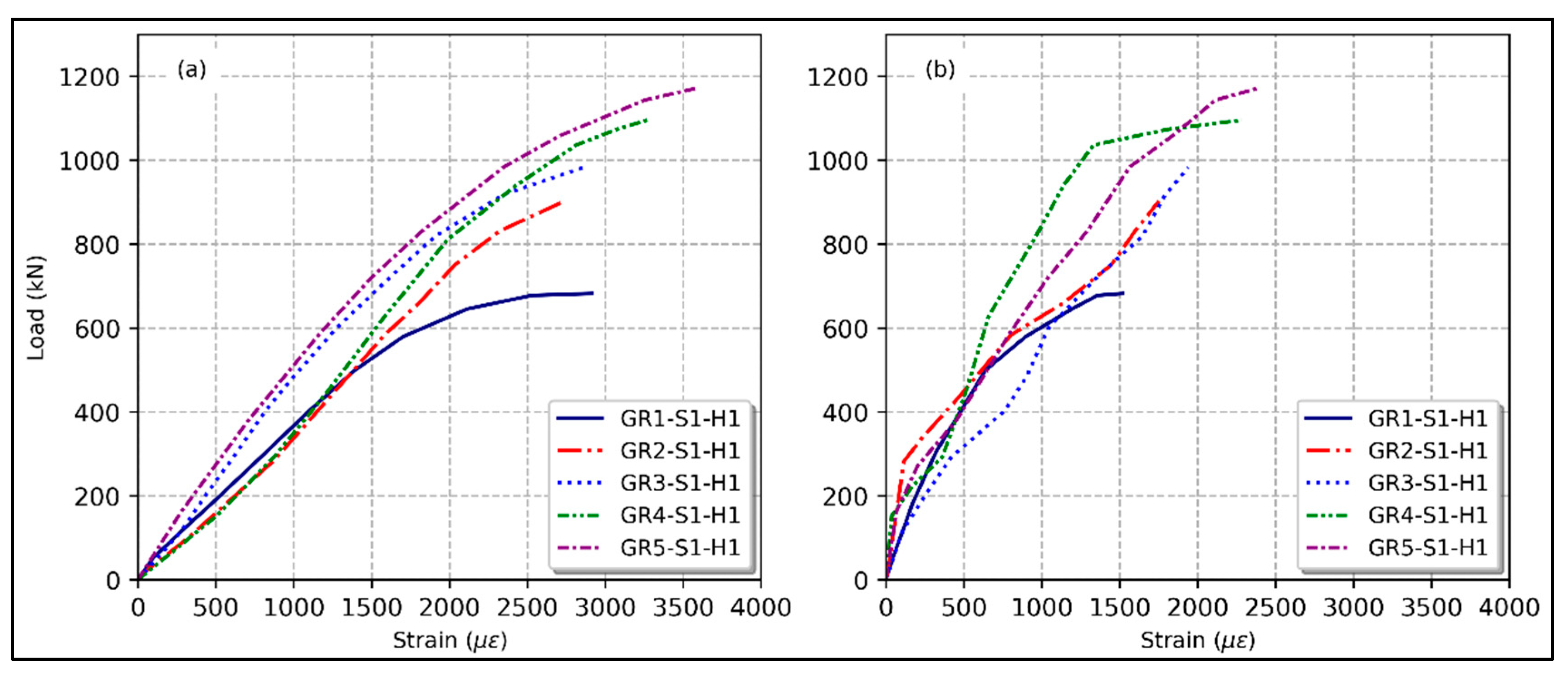
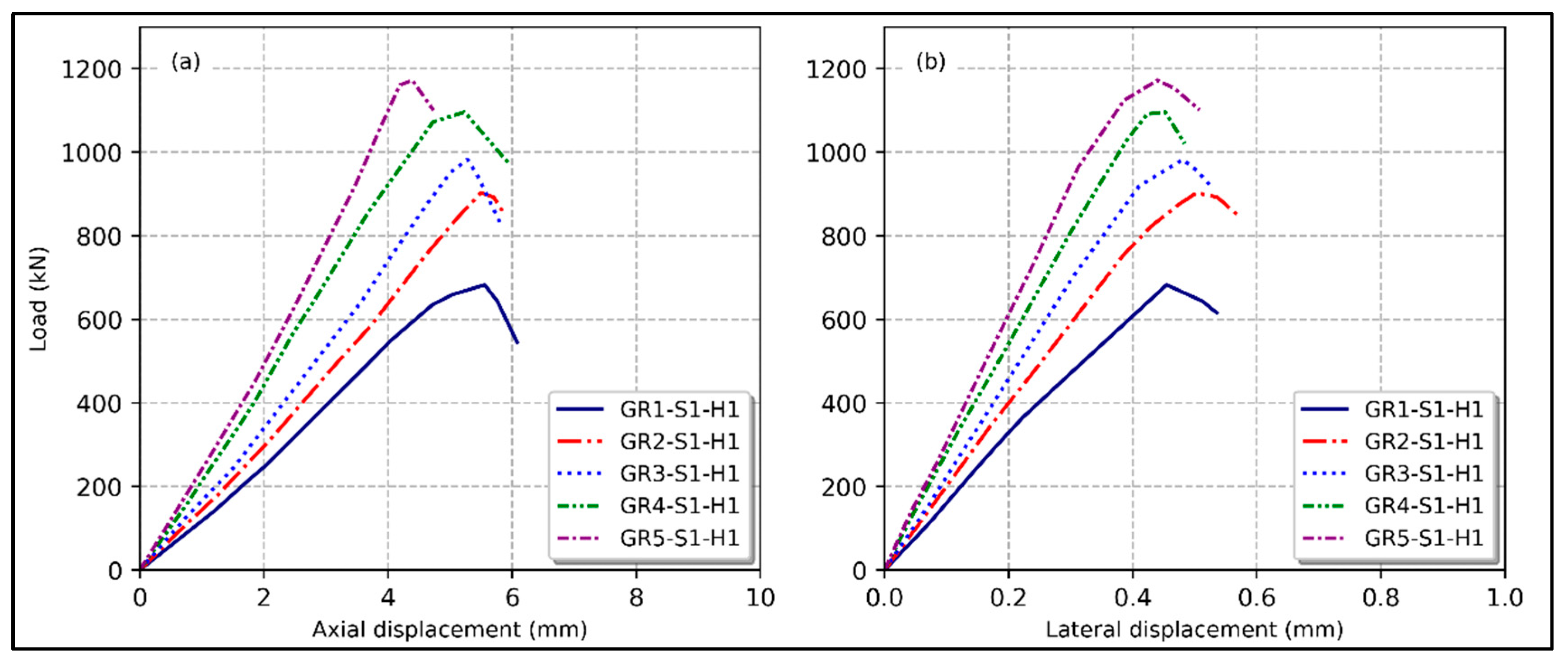
3.2. GFRP Reinforcement Ratio
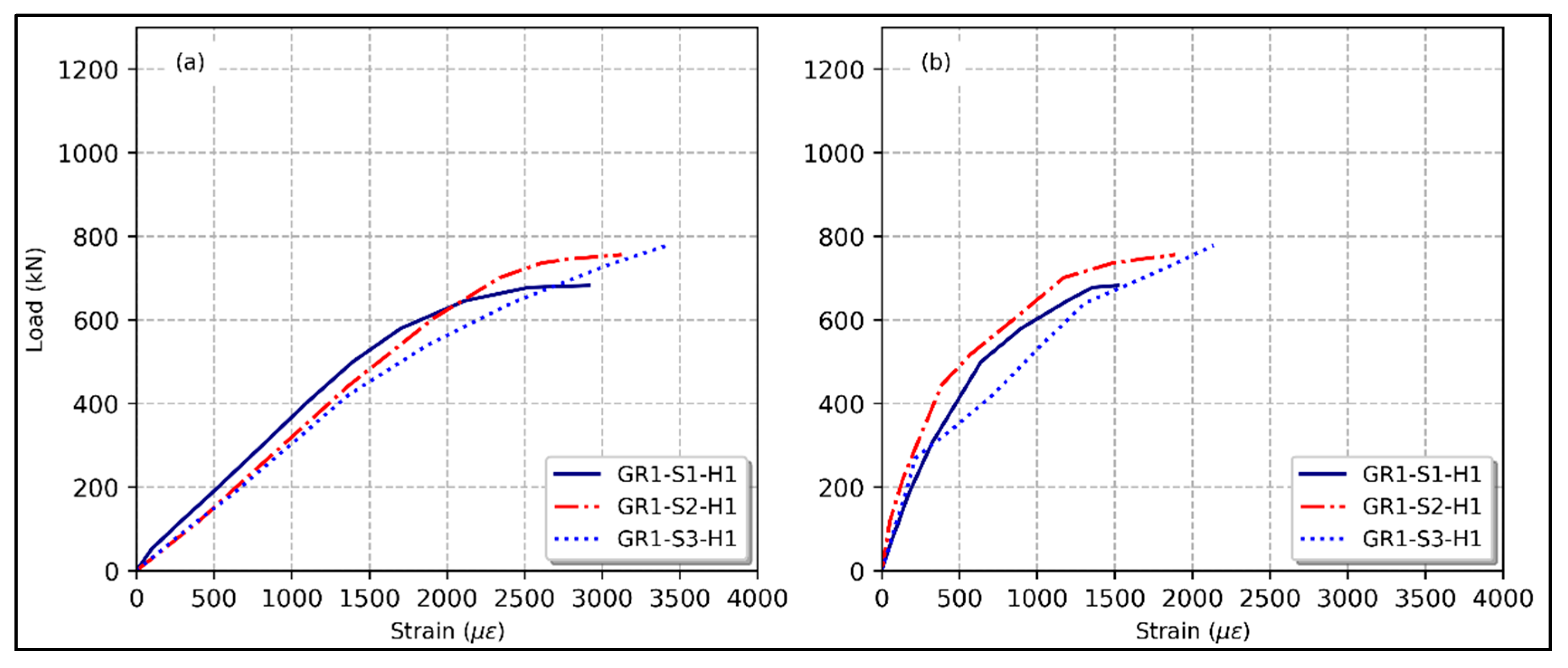
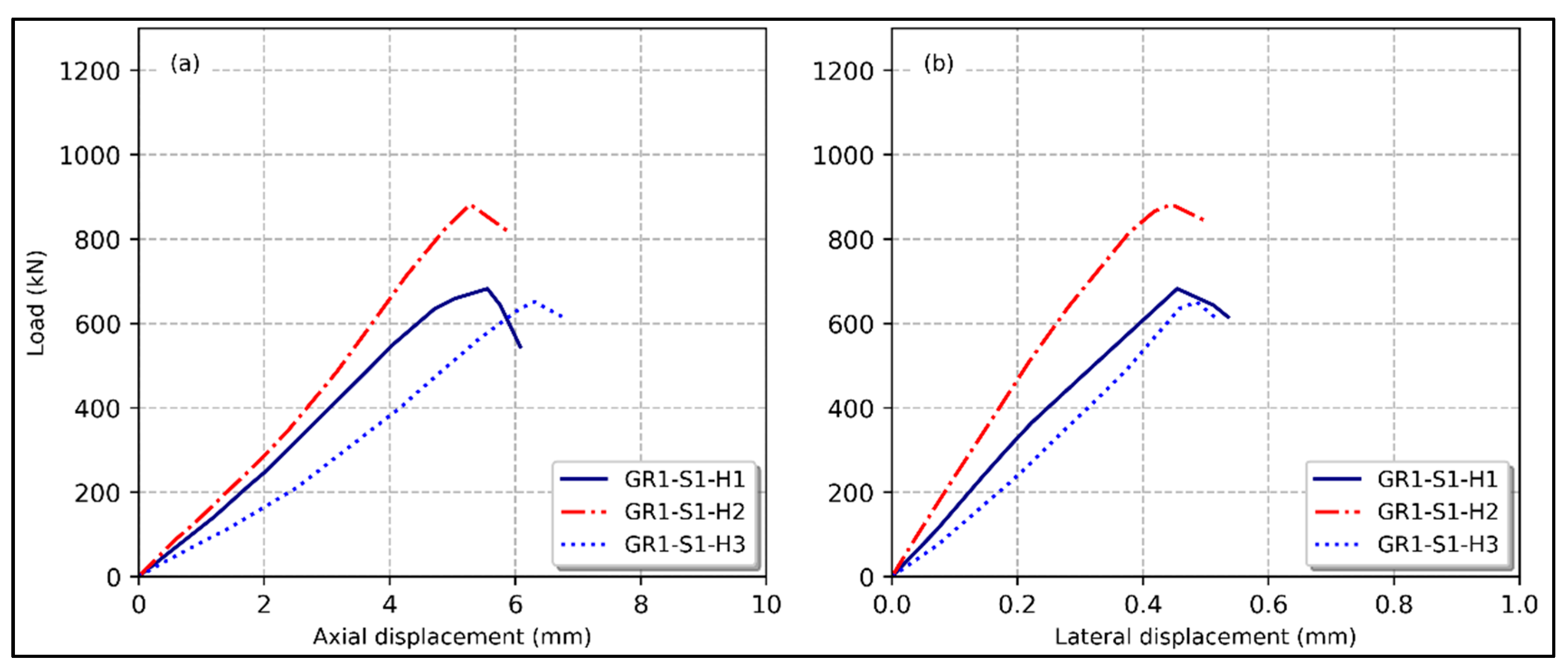
3.3. Hollow Ratio
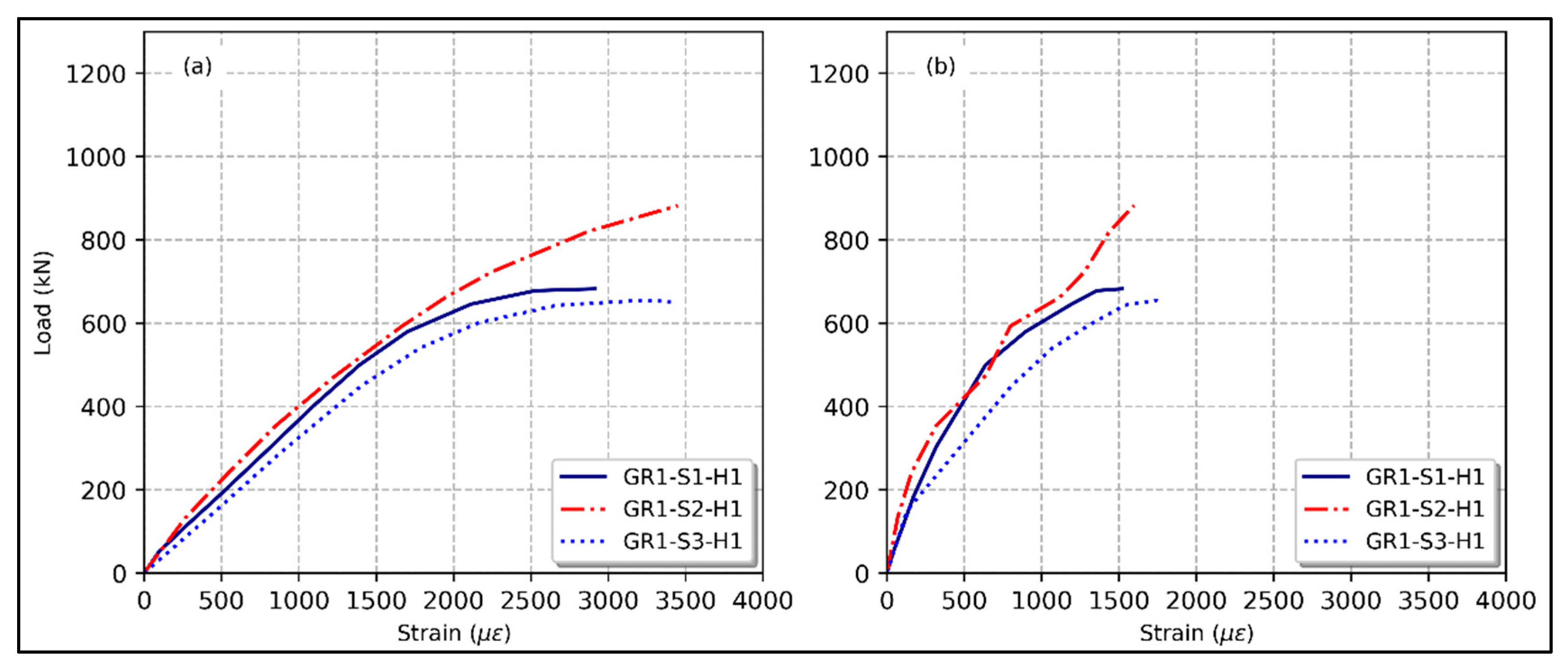
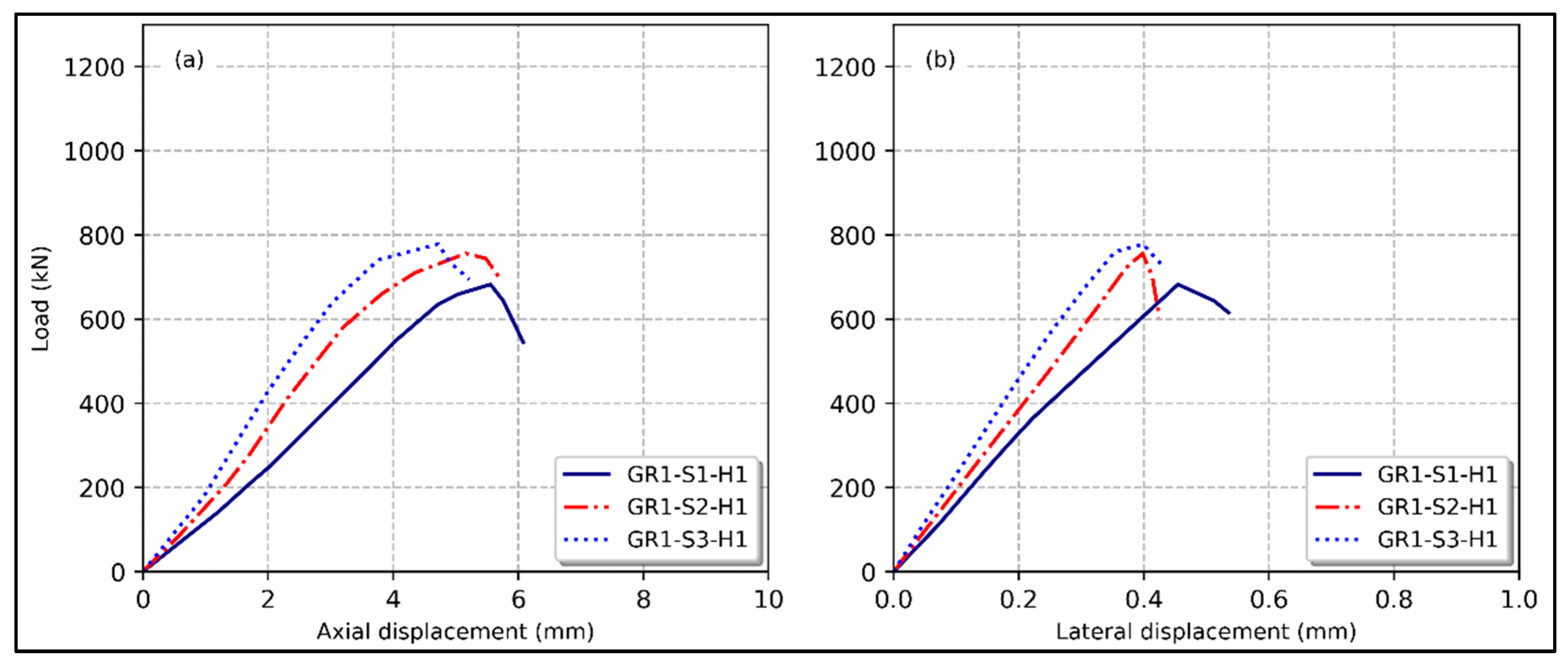
3.4. Spacing between Ties
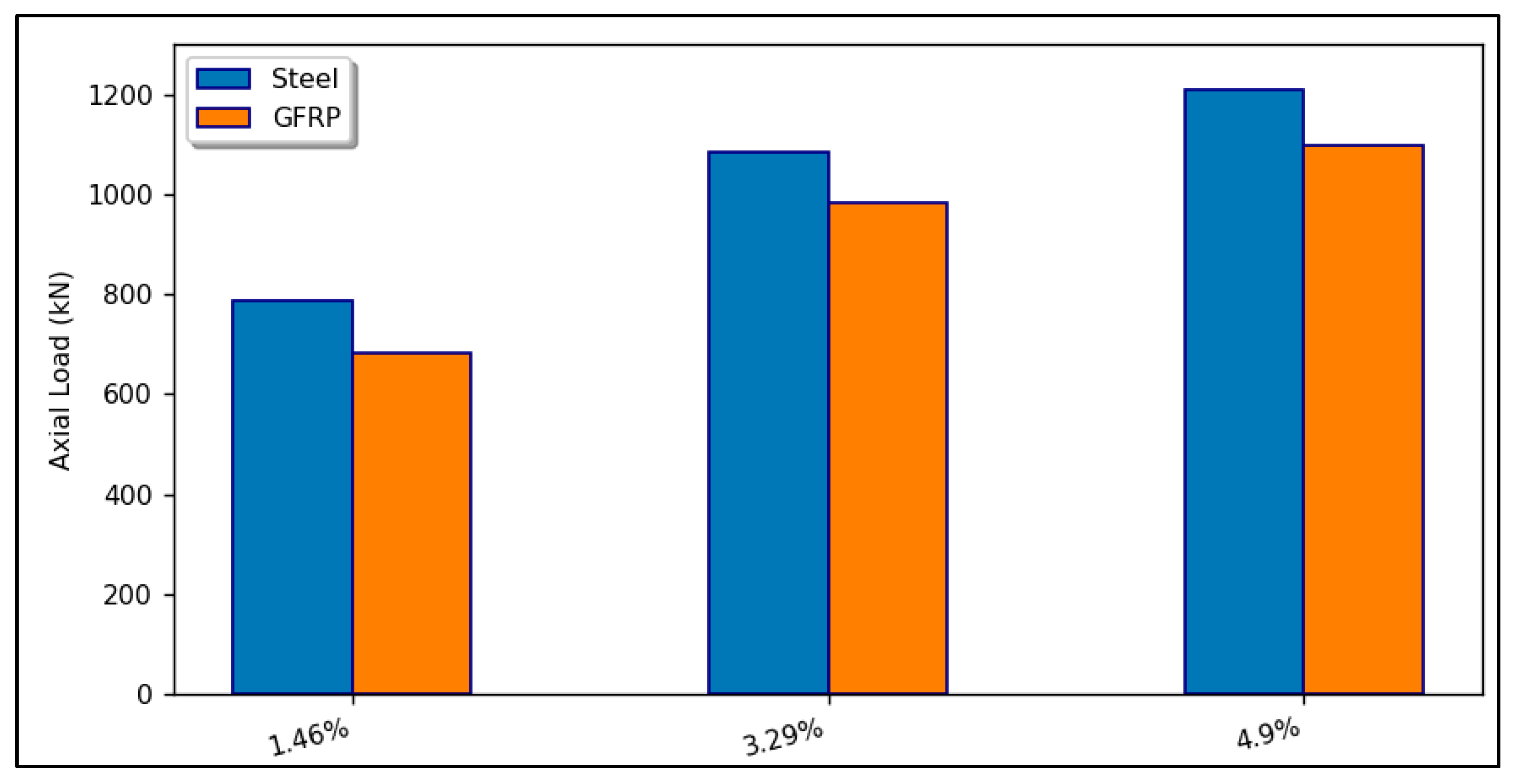
3.5. Longitudinal Reinforcement Type
3.6. Failure Modes
3.7. Load–Strain Relationship
3.8. Load–Displacement Relation
3.9. Longitudinal Bars’ Contribution to the Maximum Load Capacity
3.10. Analytical Prediction of Ultimate Load Capacity
- fc: compressive strength of concrete.
- Ag: total area of the column’s cross-section.
- Ast: steel reinforcement’s cross-sectional area.
- fy: steel bar’s yield strength.
- AGFRP: GFRP reinforcement’s cross-sectional area.
- fu,GFRP: GFRP bar’s tensile strength.
4. Result of Numerical Study
5. Conclusions
- The cross-section area of GFRP-reinforced concrete columns determines their load-bearing capability. As a result of insufficient experimental data, existing design standards such as CAN/CSA-S806-12 and ACI 440.1R-22 do not expressly take GFRP bars into account. However, our findings indicate that the involvement of longitudinal GFRP bars may be adequately approximated by assuming that their compressive strength is around 35% of the GFRP bars’ tensile strength.
- Increased internal longitudinal reinforcement provided by steel bars improved the structural efficacy of hollow square concrete columns regarding strength and deformation capacity. Specifically, raising the reinforcement ratio from 1.46% to 3.29% and 4.9% for the control column resulted in axial strength gains of 37.8% and 54.1%, respectively.
- Compared to the GFRP control column, increasing the reinforcement ratio from 1.46% to 2.9%, 3.29%, 4.9%, and 5.85% achieved enhancements in axial strength of 32.3%, 43.9%, 60.5%, and 71.7%, respectively.
- GFRP specimens had an axial load capacity of 13.1%, 9.2%, and 9.4% lower than steel-reinforced hollow columns with identical reinforcement ratios (1.46%, 3.29%, and 4.9%), respectively.
- Reduced lateral tie reinforcement spacing positively impacted the maximum load-bearing capability. For instance, the axial bearing load increased by 10.8% and 14%, respectively, when the lateral tie spacing was decreased from 170 mm to 120 mm and 85 mm.
- The load capacity of the hollow column decreased with an increase in the hollow ratio due to the reduced cross-sectional area. Additionally, faster crack propagation occurred in hollow columns with smaller concrete wall thicknesses. For instance, decreasing the hollow ratio from 0.15 to 0.07 increased the axial load capacity by 29.2%, while increasing it from 0.15 to 0.25 resulted in only a 4.5% increase.
- The failure mechanisms of longitudinally reinforced columns exhibited significant differences when steel bars were replaced with GFRP bars. In hollow columns reinforced with GFRP longitudinally, failure typically manifested after the rupture of the longitudinal bars, which can occur due to buckling or crushing, leading to an abrupt loss of load-bearing capacity. Conversely, columns reinforced with longitudinal steel bars predominantly failed due to excessive bar buckling without the rupture of ties. Remarkably, hairline cracks in the outer concrete cover of hollow steel-reinforced columns appeared at around 65% of the maximum applied load; in contrast, crack initiation in GFRP-reinforced columns happened at almost 90% of the maximum applied load.
- The compressive strain experienced by longitudinal GFRP bars was approximately 3000 με, corresponding to approximately 17.6% of the maximum strain capacity of GFRP bars. When comparing steel reinforcement to GFRP reinforcement with similar sectional areas, the load participation of steel reinforcement was from three to four times greater than the GFRP reinforcement’s axial peak load. This difference could be due to the significantly higher elastic modulus of steel reinforcement.
- In summary, the numerical analysis exhibited favorable agreement with experimental results, validating the efficacy of the proposed modeling approach for simulating compression behavior in the studied columns.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mander, J.B.; Priestley, M.J.; Park, R. Behavior of ductile hollow reinforced concrete column. Bull. N. Z. Soc. Earthq. Eng. 1983, 16, 273–290. [Google Scholar] [CrossRef]
- Zahn, F. Design of Reinforced Concrete Bridges Column for Strength and Ductility. Ph.D. Thesis, University of Canterbury, Canterbury, UK, 1986. [Google Scholar]
- Whittaker, D. Seismic Performance of Off-Shore Concrete Gravity Platform. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1987. [Google Scholar]
- Said, A.I.; Abbas, O.M. Serviceability behavior of high-strength concrete I-beam reinforced with carbon fiber reinforced polymer bar. J. Eng. 2013, 19, 1515–1530. [Google Scholar] [CrossRef]
- Ibrahim, T.H.; Allawi, A.A.; El-Zohairy, A. Impact Behavior of Composite Reinforced Concrete Beams with Pultruded I-GFRP Beam. Materials 2022, 15441, 441. [Google Scholar] [CrossRef] [PubMed]
- Kashani, M.M.; Madocks, J.; Dizaj, E.A. Residual Capacity of Corroded Reinforced Concrete Bridges Component: State-Of-The-Art Review. J. Bridges Eng. 2019, 24, 03119001. [Google Scholar] [CrossRef]
- Salh, L. Analysis and Behaviour of Structural Concrete Reinforced with Sustainable Material. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2014. [Google Scholar]
- Mohammed, S.A.; Said, A.I. Analysis of concrete beam reinforced by GFRP bar with varying parameters. J. Mech. Behav. Mater. 2022, 31, 767–774. [Google Scholar] [CrossRef]
- Ali, H.H.; Said, A.I. Flexural behavior of concrete beam with horizontal and vertical openings reinforced by glass-fiber-reinforced polymers (GFRP) bars. J. Mech. Behav. Mater. 2022, 31, 407–415. [Google Scholar] [CrossRef]
- AbdulMuttalib Issa, M.; Allawi, A.A.; Oukaili, N. Performance of doubly reinforced concrete beam with GFRP bar. J. Mech. Behav. Mater. 2024, 33, 20220308. [Google Scholar] [CrossRef]
- Issa, M.A.; Allawi, A.A.; Oukaili, N. Effects of GFRP Stirrup Spacings on the Behaviour of Doubly GFRP-Reinforced Concrete Beam. Civ. Eng. J. 2024, 10, 502–520. [Google Scholar] [CrossRef]
- Said, A.I. Evaluation of deflection in high strength concrete (HSC) I-beam reinforced with carbon fiber reinforced polymers (CFRP) bars. In Proceedings of the 7th Asia Pacific Young Researcher and Graduates Symposium, Innovations in Materials and Structural Engineering Practices, Kuala Lumpur, Malaysia, 20–21 August, 2015; pp. 519–533. [Google Scholar]
- ACI Committee 440; Guide for the Design and Constructions of Concrete Reinforced with FRP Bars (ACI 440.1R-15). American Concrete Institute: Philadelphia, PA, USA, 2015.
- CAN/CSA-S806-12; Design and Constructions of Buildings Structure with Fiber-Reinforced Polymer. Canadian Standards Association: Toronto, ON, Canada, 2012.
- ACI Code-440.11-22; Building Code Requirement for Structural Concrete Reinforced with GFRP Bar and Commentary. American Concrete Institute: Philadelphia, PA, USA, 2022.
- Castro, P.F.; Howie, I.; Karbhari, V. Concrete column reinforced with FRP rod. Int. J. Mater. Prod. Technol. 1995, 10, 338–343. [Google Scholar]
- Mirmiran, A.; Yuan, W.; Chen, X. Design for slenderness in concrete column internally reinforced with fiber-reinforced polymers bar. ACI Struct. J. 2001, 98, 116–125. [Google Scholar]
- Choo, C.C. Investigations of Rectangular Concrete Column Reinforced or Prestressed with Fiber Reinforced Polymers (FRP) Bar or Tendon. Ph.D. Thesis, University of Kentucky, Lexington, KY, USA, 2005. [Google Scholar]
- De Luca, A.; Matta, F.; Nanni, A. Behaviour of Full-Scale Glass Fiber-Reinforced Polymers Reinforced Concrete Column under Axial Loads. ACI Struct. J. 2010, 107, 589–596. [Google Scholar]
- Tavassoli, A. Behaviour of GFRP-Reinforced Concrete Column under Combined Axial Loads and Flexure. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Al-Ajarmeh, O.S.; Manalo, A.C.; Benmokrune, B.; Karonasena, W.; Mendis, P.; Nguyen, K.T. Compressive behaviour of axially loaded circular hollow concrete column reinforced with GFRP bar and spiral. Constr. Build. Mater. 2019, 194, 12–23. [Google Scholar] [CrossRef]
- Abed, F.; El Refai, A.; El-Mesalami, N. Compressive Behaviour of Glass Fiber-Reinforced Polymers (GFRP) Reinforced Concrete Column. In Proceedings of the 10th International Conferences on FRP Composite in Civil Engineering: Proceeding of CICE 2020/2021, Istanbul, Turkey, 8–10 December 2021; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 858–861. [Google Scholar]
- Lotfy, E.M. Behavior of reinforced concrete short column with fiber reinforced polymer bars. Int. J. Civ. Struct. Eng. 2010, 1, 545–557. [Google Scholar]
- ACI Committee 318; Building Code Requirement for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19). American Concrete Institute: Philadelphia, PA, USA, 2019.
- Tobbi, H.; Farghaly, A.S.; Benmokrune, B. Behaviour of Concentrically Loaded Fiber-Reinforced Polymers Reinforced Concrete Column with Varying Reinforcement Type and Ratio. ACI Struct. J. 2014, 111, 375–386. [Google Scholar] [CrossRef]
- Said, A.I.; Tu’ma, N.H. Numerical modeling for flexural behaviour of UHPC beam reinforced with steel and sand-coated CFRP bars. In Proceedings of the IOP Conferences Series: Earth and Environmental Sciences, Baghdad, Iraq, 22–23 June 2021; IOP Publishing: Bristol, UK, 2021; Volume 866. [Google Scholar]
- Hussein, H.A.; Said, A.I. Finite Element Analysis of Axially Loaded GFRP-Reinforced Concrete Hollow Square Column. In Proceedings of the E3S Web International Conference on Geotechnical Engineering and Energetic-Iraq (ICGEE 2023); EDP Sciences: Hulis, France, 2023; Volume 427. [Google Scholar]
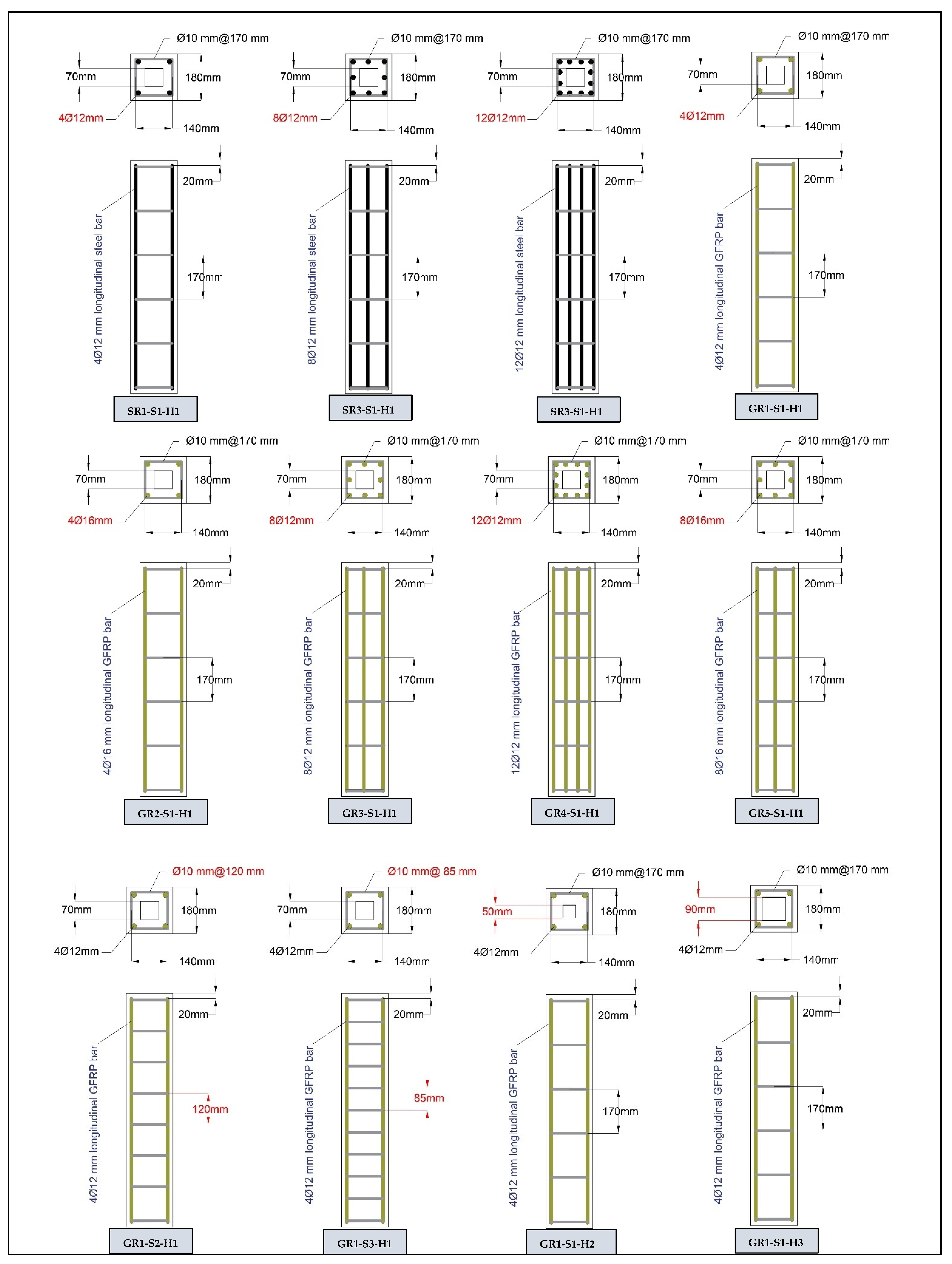




| Group No. | Specimens Identification | Reinforcement Type | Reinforcement Ratio of Longitudinal Bar % | Ties Spacing (mm) | Hollow Ratio |
|---|---|---|---|---|---|
| Group 1 | SR1-S1-H1 | STEEL | 1.46 | 170 | 0.15 |
| SR3-S1-H1 | STEEL | 3.29 | 170 | 0.15 | |
| SR4-S1-H1 | STEEL | 4.91 | 170 | 0.15 | |
| Group 2 | GR1-S1-H1 | GFRP | 1.46 | 170 | 0.15 |
| GR2-S1-H1 | GFRP | 2.9 | 170 | 0.15 | |
| GR3-S1-H1 | GFRP | 3.29 | 170 | 0.15 | |
| GR4-S1-H1 | GFRP | 4.9 | 170 | 0.15 | |
| GR5-S1-H1 | GFRP | 5.85 | 170 | 0.15 | |
| Group 3 | GR1-S1-H2 | GFRP | 1.46 | 170 | 0.07 |
| GR1-S1-H3 | GFRP | 1.46 | 170 | 0.25 | |
| Group 4 | GR1-S2-H1 | GFRP | 1.46 | 120 | 0.15 |
| GR1-S3-H1 | GFRP | 1.46 | 85 | 0.15 |
| Ingredients | Quantities |
|---|---|
| cement | 370 (kg/m3) |
| sand | 645 (kg/m3) |
| gravel | 935 (kg/m3) |
| water | 167 (kg/m3) |
| (cement:sand:gravel) | 1:1.7:2.5 |
| (w/c) | 0.45 |
| Average compressive strength | 24.01 (MPa) |
| Bar Type | Diameter (mm) | Modulus of Elasticity (GPa) | Tensile Strength (MPa) |
|---|---|---|---|
| GFRP | 12 | 50 | 1205 |
| GFRP | 16 | 50 | 1214 |
| Steel | 12 | 200 | 532 |
| Steel | 10 | 200 | 528 |
| Group No. | Column ID | Ultimate Load (kN) | Δaxial (mm) | Δlateral (mm) | εconcrete (με) | εbar (με) |
|---|---|---|---|---|---|---|
| Group 1 | SR1-S1-H1 | 785.2 | 6.17 | 0.51 | 1701.1 | 2696.5 |
| SR3-S1-H1 | 1082.5 | 5.88 | 0.49 | 2107.6 | 2970.1 | |
| SR4-S1-H1 | 1210.3 | 5.47 | 0.45 | 1980.7 | 2553.2 | |
| Group 2 | GR1-S1-H1 | 682.6 | 5.54 | 0.47 | 1519.2 | 2913.9 |
| GR2-S1-H1 | 903.1 | 5.39 | 0.51 | 1751.6 | 2739.1 | |
| GR3-S1-H1 | 982.6 | 5.28 | 0.48 | 1938.6 | 2854.6 | |
| GR4-S1-H1 | 1096.2 | 5.23 | 0.45 | 2280.9 | 3269.3 | |
| GR5-S1-H1 | 1172.3 | 4.39 | 0.41 | 2388.7 | 3586.2 | |
| Group 3 | GR1-S1-H2 | 882.6 | 5.28 | 0.44 | 1579.2 | 3450.1 |
| GR1-S1-H3 | 651.4 | 6.3 | 0.49 | 1763.6 | 3424.6 | |
| Group 4 | GR1-S2-H1 | 756.3 | 5.16 | 0.41 | 1886.3 | 3126.3 |
| GR1-S3-H1 | 778.4 | 4.72 | 0.38 | 2134.8 | 3417.2 |
| Group No. | Column ID | Pult (kN) | Pbar (kN) | Pbar/Pult |
|---|---|---|---|---|
| Group 1 | SR1-S1-H1 | 785.2 | 243.7 | 0.28 |
| SR3-S1-H1 | 1082.5 | 536.9 | 0.49 | |
| SR4-S1-H1 | 1210.3 | 692.3 | 0.57 | |
| Group 2 | GR1-S1-H1 | 682.6 | 65.8 | 0.09 |
| GR2-S1-H1 | 903.1 | 110.1 | 0.12 | |
| GR3-S1-H1 | 982.6 | 129 | 0.13 | |
| GR4-S1-H1 | 1096.2 | 221.6 | 0.2 | |
| GR5-S1-H1 | 1172.3 | 288.3 | 0.24 | |
| Group 3 | GR1-S1-H2 | 882.6 | 77.9 | 0.08 |
| GR1-S1-H3 | 651.4 | 77.3 | 0.11 | |
| Group 4 | GR1-S2-H1 | 756.3 | 70.6 | 0.09 |
| GR1-S3-H1 | 778.4 | 77.2 | 0.1 |
| Group No. | Column ID | Experimental PExp (kN) | Calculated PCal (kN) | (PExp/PCal) |
|---|---|---|---|---|
| Group 1 | SR1-S1-H1 | 785.2 | 731.3 | 1.07 |
| SR3-S1-H1 | 1082.5 | 1021.7 | 1.05 | |
| SR4-S1-H1 | 1210.3 | 1252.1 | 0.96 | |
| Group 2 | GR1-S1-H1 | 682.6 | 741.6 | 0.92 |
| GR2-S1-H1 | 903.1 | 882.3 | 1.02 | |
| GR3-S1-H1 | 982.6 | 922.2 | 1.06 | |
| GR4-S1-H1 | 1096.2 | 1102.9 | 0.99 | |
| GR5-S1-H1 | 1172.3 | 1203.6 | 0.97 | |
| Group 3 | GR1-S1-H2 | 882.6 | 799.8 | 1.1 |
| GR1-S1-H3 | 651.4 | 685.6 | 0.95 | |
| Group 4 | GR1-S2-H1 | 756.3 | 741.6 | 1.02 |
| GR1-S3-H1 | 778.4 | 741.6 | 1.05 |
| Column ID | Numerical PNum (kN) | Experimental PExp (kN) | (PNum/PExp) |
|---|---|---|---|
| SR1-S1-H1 | 803.1 | 785.2 | 1.02 |
| SR3-S1-H1 | 1074.5 | 1082.5 | 0.99 |
| SR4-S1-H1 | 1168.4 | 1210.3 | 0.97 |
| GR1-S1-H1 | 685.3 | 682.6 | 1.01 |
| GR2-S1-H1 | 889.7 | 903.1 | 1.02 |
| GR3-S1-H1 | 945.6 | 982.6 | 0.99 |
| GR4-S1-H1 | 1080.2 | 1096.2 | 0.98 |
| GR5-S1-H1 | 1142.3 | 1172.3 | 0.99 |
| GR1-S1-H2 | 857.7 | 882.6 | 0.97 |
| GR1-S1-H3 | 637.6 | 651.4 | 0.98 |
| GR1-S2-H1 | 748.7 | 756.3 | 0.99 |
| GR1-S3-H1 | 739.1 | 778.4 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Said, A.I.; Hilfi, H.A.; Allawi, A.A.; Wardeh, G. Structural Performance of a Hollow-Core Square Concrete Column Longitudinally Reinforced with GFRP Bars under Concentric Load. CivilEng 2024, 5, 928-948. https://doi.org/10.3390/civileng5040047
Said AI, Hilfi HA, Allawi AA, Wardeh G. Structural Performance of a Hollow-Core Square Concrete Column Longitudinally Reinforced with GFRP Bars under Concentric Load. CivilEng. 2024; 5(4):928-948. https://doi.org/10.3390/civileng5040047
Chicago/Turabian StyleSaid, AbdulMuttalib I., Hussein A. Hilfi, Abbas A. Allawi, and George Wardeh. 2024. "Structural Performance of a Hollow-Core Square Concrete Column Longitudinally Reinforced with GFRP Bars under Concentric Load" CivilEng 5, no. 4: 928-948. https://doi.org/10.3390/civileng5040047
APA StyleSaid, A. I., Hilfi, H. A., Allawi, A. A., & Wardeh, G. (2024). Structural Performance of a Hollow-Core Square Concrete Column Longitudinally Reinforced with GFRP Bars under Concentric Load. CivilEng, 5(4), 928-948. https://doi.org/10.3390/civileng5040047









