Weighting Variables for Transportation Assets Condition Indices Using Subjective Data Framework
Abstract
1. Introduction
2. Literature Review
2.1. Condition Indicators
2.2. Machine Learning Models
2.3. Feature Importance
3. Materials and Methods
3.1. Framework
3.1.1. Database
3.1.2. Data Preprocessing
- Data Cleaning: This step involves addressing missing values, outliers, and inconsistencies within the datasets. Missing data can be handled either by removing incomplete records, provided this does not result in significant data loss, or through imputation techniques. Common methods include mean or mode imputation, while more advanced approaches, such as Fractional Hot Deck Imputation (FHDI) and Fully Efficient Fractional Imputation (FEFI), can also be employed [63].
- Normalization: This involves standardizing the scales of objective measures to ensure comparability. This is particularly important when dealing with parameters that may have different units (e.g., roughness in inch per mile vs. cracking in foot).
- Data Splitting: This involves dividing the data into training and testing subsets, where the training set will be used to build the machine learning model and the testing set will validate its performance.
- Random Sampling: Suitable for small-scale analysis like city road networks, where random subsets of data can be drawn to create multiple samples for analysis.
- Geographical Sampling: For large-scale analysis (e.g., state or national networks), data can be segmented based on jurisdictional boundaries (e.g., county or district) to ensure that different geographic or administrative regions are represented.
3.1.3. Initial Weight Estimation
- Weightij is the weight of the ith variable in the jth sample.
- Feature Importance Scoreij is the feature importance score of the ith variable in the jth sample obtained from the random forest model.
- Measures of Central Tendency: Such as mean, median, and mode.
- Dispersion Metrics: Including standard deviation and interquartile range, which provide insight into the variability and spread of the variables.
- Other Statistical Measures: Such as skewness, kurtosis, etc., that describe the shape of the data distribution.
3.1.4. Final Weight Estimation
3.2. Case Study
3.2.1. Data Preparation
- Pavement surface distress data that were collected using automated pavement distress data collection equipment.
- OCI data were acquired using the Pavement Surface Evaluation and Rating (PASER) method [12].
3.2.2. Weight Estimation
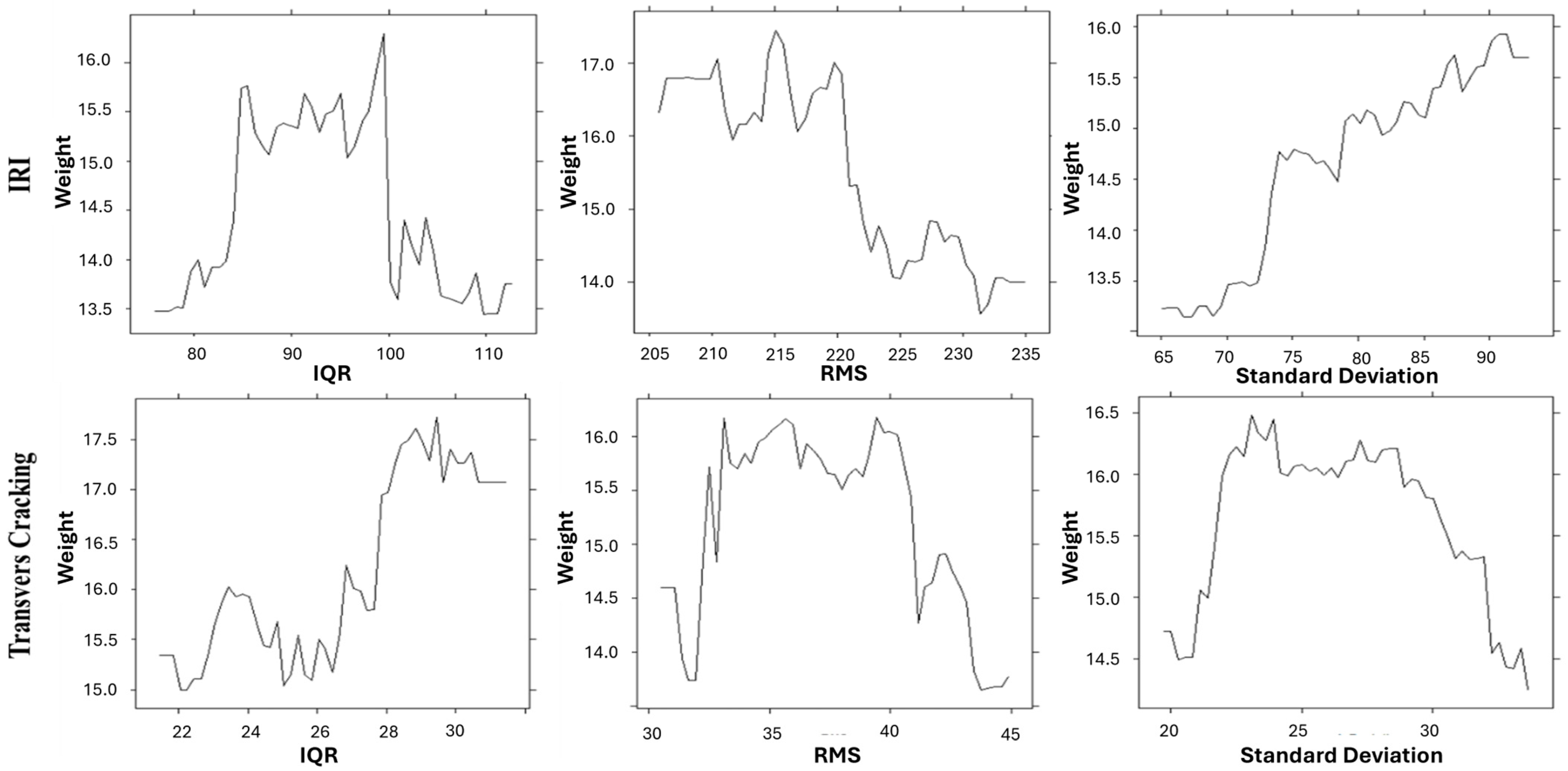
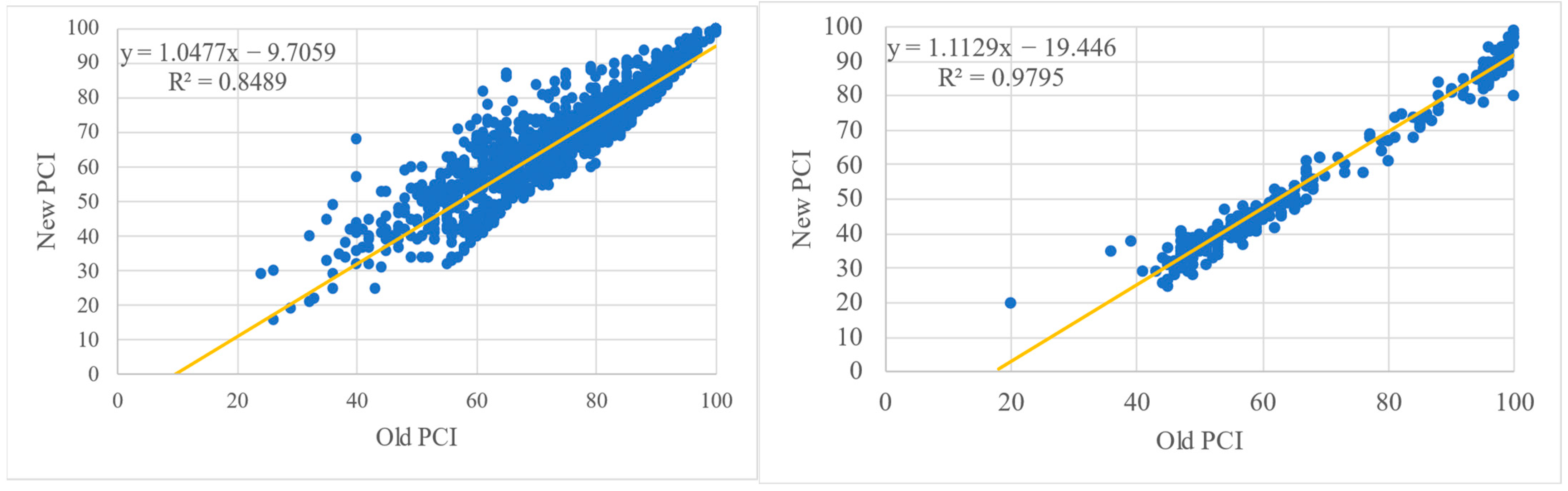
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mneina, A.; Smith, J. Harmonization of Pavement Condition Evaluation for Enhanced Pavement Management: An Ontario Case Study. In Proceedings of the Transportation Association of Canada 2022 Conference and Exhibition-Changing Ways for Our Changing Climate//Association des Transports du Canada 2022 Congrès et Exposition-Approches Adaptées pour un Climat Changeant, Edmonton, AB, Canada, 2–5 October 2022. [Google Scholar]
- Chen, Z.; Liang, Y.; Wu, Y.; Sun, L. Research on Comprehensive Multi-Infrastructure Optimization in Transportation Asset Management: The Case of Roads and Bridges. Sustainability 2019, 11, 4430. [Google Scholar] [CrossRef]
- Urrea-Mallebrera, M.; Altarejos-García, L.; García-Bermejo, J.; Collado-López, B. Condition Assessment of Water Infrastructures: Application to Segura River Basin (Spain). Water 2019, 11, 1169. [Google Scholar] [CrossRef]
- Famurewa, S.M.; Stenström, C.; Asplund, M.; Galar, D.; Kumar, U. Composite Indicator for Railway Infrastructure Management. J. Mod. Transp. 2014, 22, 214–224. [Google Scholar] [CrossRef]
- Shahin, M.Y. Pavement Management for Airports, Roads, and Parking Lots; Springer: Cham, Switzerland, 2005; Volume 501. [Google Scholar]
- ASTM D6433-07; Standard Practice for Roads and Parking Lots Pavement Condition Index Surveys. ASTM International: West Conshohocken, PA, USA, 2015.
- Li, Q.; Peng, Q.; Liu, R.; Liu, L.; Bai, L. Track Grid Health Index for Grid-Based, Data-Driven Railway Track Health Evaluation. Adv. Mech. Eng. 2019, 11, 168781401988976. [Google Scholar] [CrossRef]
- Lubis, R.R.A.; Widyastuti, H. Penentuan Rekomendasi Standar Track Quality Index (TQI) Untuk Kereta Semicepat Di Indonesia (Studi Kasus: Surabaya—Cepu). J. Apl. Tek. Sipil 2020, 18, 39. [Google Scholar] [CrossRef]
- Fereshtehnejad, E.; Hur, J.; Shafieezadeh, A.; Brokaw, M. Ohio Bridge Condition Index: Multilevel Cost-Based Performance Index for Bridge Systems. Transp. Res. Rec. J. Transp. Res. Board 2017, 2612, 152–160. [Google Scholar] [CrossRef]
- Abiola, O.; Kupolati, W.K. Modelling Present Serviceability Rating of Highway Using Artificial Neural Network. OIDA Int. J. Sustain. Dev. 2014, 7, 91–98. [Google Scholar]
- Bou-Saab, G.; Nlenanya, I.; Alhasan, A. Correlating Visual–Windshield Inspection Pavement Condition to Distresses from Automated Surveys Using Classification Trees. In Proceedings of the 12th International Conference on Low-Volume Roads, Kalispell, MT, USA, 15–18 September 2019; p. 589. [Google Scholar]
- Walker, D.; Entine, L.; Kummer, S. Pavement Surface Evaluation and Rating: PASER Manual. 1987. Available online: https://trid.trb.org/View/260614 (accessed on 10 October 2024).
- Taghaddos, M.; Mohamed, Y. Predicting Bridge Conditions in Ontario: A Case Study. In Proceedings of the 36th International Symposium on Automation and Robotics in Construction (ISARC), Banff, AB, Canada, 21–24 May 2019. [Google Scholar]
- Rogulj, K.; Kilić Pamuković, J.; Jajac, N. Knowledge-Based Fuzzy Expert System to the Condition Assessment of Historic Road Bridges. Appl. Sci. 2021, 11, 1021. [Google Scholar] [CrossRef]
- Darban, S.; Ghasemzadeh Tehrani, H.; Karballaeezadeh, N.; Mosavi, A. Application of Analytical Hierarchy Process for Structural Health Monitoring and Prioritizing Concrete Bridges in Iran. Appl. Sci. 2021, 11, 8060. [Google Scholar] [CrossRef]
- Darban, S.; Tehrani, H.G.; Karballaeezadeh, N. Presentation a New Method for Determining of Bridge Condition Index by Using Analytical Hierarchy Process. Preprints 2020. [Google Scholar] [CrossRef]
- Ren, Y.; Xu, X.; Liu, B.; Huang, Q. An Age- and Condition-Dependent Variable Weight Model for Performance Evaluation of Bridge Systems. KSCE J. Civ. Eng. 2021, 25, 1816–1825. [Google Scholar] [CrossRef]
- Pederson, N.J. Pavement Lessons Learned from the AASHO Road Test and Performance of the Interstate Highway System. Transp. Res. Board 2007. Available online: https://onlinepubs.trb.org/onlinepubs/circulars/ec118.pdf (accessed on 10 October 2024).
- Alatoom, Y.I.; Obaidat, T.I. Measurement of Street Pavement Roughness in Urban Areas Using Smartphone. Int. J. Pavement Res. Technol. 2022, 15, 1003–1020. [Google Scholar] [CrossRef]
- Cary, W.N. The Pavement Serviceability-Performance Concept. HRB Bull. 1960, 250. Available online: https://cir.nii.ac.jp/crid/1570854174154516096 (accessed on 10 October 2024).
- McNeil, S.; Markow, M.; Neumann, L.; Ordway, J.; Uzarski, D. Emerging Issues in Transportation Facilities Management. J. Transp. Eng. 1992, 118, 477–495. [Google Scholar] [CrossRef]
- Smith, K.; Harrington, D.; Pierce, L.; Ram, P.; Smith, K. Concrete Pavement Preservation Guide, 2nd ed.; FHWA Publication No. FHWA-HIF-14-014; Institute for Transportation, Iowa State University: Ames, IA, USA, 2014. [Google Scholar]
- Gross, J.; King, D.; Harrington, D.; Ceylan, H.; Chen, Y.; Kim, S.; Taylor, P.; Kaya, O. Concrete Overlay Performance on Iowa’s Roadways; IHRB Project TR-698; Iowa Highway Research Board: Ames, IA, USA, 2017. [Google Scholar]
- Chen, Y.-A.; Ceylan, H.; Nlenanya, I.; Kaya, O.; Smadi, O.G.; Taylor, P.C.; Kim, S.; Gopalakrishnan, K.; King, D.E. Long-Term Performance Evaluation of Iowa Concrete Overlays. Int. J. Pavement Eng. 2022, 23, 719–730. [Google Scholar] [CrossRef]
- Bektas, F.; Smadi, O.; Nlenanya, I. Pavement Condition: New Approach for Iowa Department of Transportation. Transp. Res. Rec. J. Transp. Res. Board 2015, 2523, 40–46. [Google Scholar] [CrossRef]
- Patil, M.; Majumdar, B.B.; Sahu, P.K. Evaluating Pedestrian Crash-Prone Locations to Formulate Policy Interventions for Improved Safety and Walkability at Sidewalks and Crosswalks. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 675–689. [Google Scholar] [CrossRef]
- Kim, J.; Park, D.; Suh, Y.; Jung, D. Development of Sidewalk Block Pavement Condition Index (SBPCI) Using Analytical Hierarchy Process. Sustainability 2019, 11, 7086. [Google Scholar] [CrossRef]
- Alatoom, Y.I.; Al-Suleiman (Obaidat), T.I. Development of Pavement Roughness Models Using Artificial Neural Network (ANN). Int. J. Pavement Eng. 2022, 23, 4622–4637. [Google Scholar] [CrossRef]
- Zhou, Q.; Okte, E.; Al-Qadi, I.L. Predicting Pavement Roughness Using Deep Learning Algorithms. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 1062–1072. [Google Scholar] [CrossRef]
- Kumar, R.; Suman, S.K.; Prakash, G. Evaluation of Pavement Condition Index Using Artificial Neural Network Approach. Transp. Dev. Econ. 2021, 7, 20. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Alhasan, A.; Smadi, O. Use of Deep Learning to Study Modeling Deterioration of Pavements a Case Study in Iowa. Infrastructures 2020, 5, 95. [Google Scholar] [CrossRef]
- Sadeghi, J.; Askarinejad, H. Application of Neural Networks in Evaluation of Railway Track Quality Condition. J. Mech. Sci. Technol. 2012, 26, 113–122. [Google Scholar] [CrossRef]
- Fabianowski, D.; Jakiel, P.; Stemplewski, S. Development of Artificial Neural Network for Condition Assessment of Bridges Based on Hybrid Decision Making Method—Feasibility Study. Expert. Syst. Appl. 2021, 168, 114271. [Google Scholar] [CrossRef]
- Damirchilo, F.; Hosseini, A.; Mellat Parast, M.; Fini, E.H. Machine Learning Approach to Predict International Roughness Index Using Long-Term Pavement Performance Data. J. Transp. Eng. Part B Pavements 2021, 147, 04021058. [Google Scholar] [CrossRef]
- Marcelino, P.; de Lurdes Antunes, M.; Fortunato, E.; Gomes, M.C. Machine Learning Approach for Pavement Performance Prediction. Int. J. Pavement Eng. 2021, 22, 341–354. [Google Scholar] [CrossRef]
- Madeh Piryonesi, S.; El-Diraby, T.E. Using Machine Learning to Examine Impact of Type of Performance Indicator on Flexible Pavement Deterioration Modeling. J. Infrastruct. Syst. 2021, 27, 04021005. [Google Scholar] [CrossRef]
- Bashar, M.Z.; Torres-Machi, C. Performance of Machine Learning Algorithms in Predicting the Pavement International Roughness Index. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 226–237. [Google Scholar] [CrossRef]
- Rashidi Nasab, A.; Elzarka, H. Optimizing Machine Learning Algorithms for Improving Prediction of Bridge Deck Deterioration: A Case Study of Ohio Bridges. Buildings 2023, 13, 1517. [Google Scholar] [CrossRef]
- Guo, G.; Cui, X.; Du, B. Random-Forest Machine Learning Approach for High-Speed Railway Track Slab Deformation Identification Using Track-Side Vibration Monitoring. Appl. Sci. 2021, 11, 4756. [Google Scholar] [CrossRef]
- Alatoom, Y.I.; Zihan, Z.U.; Nlenanya, I.; Al-Hamdan, A.B.; Smadi, O. A Sequence-Based Hybrid Ensemble Approach for Estimating Trail Pavement Roughness Using Smartphone and Bicycle Data. Infrastructures 2024, 9, 179. [Google Scholar] [CrossRef]
- Al-Hamdan, A.B.; Nlenanya, I.; Smadi, O. Data-Driven Approach to Identify Maintained Pavement Segments and Estimate Maintenance Type for Local Roads. In Proceedings of the 13th International Conference on Low-Volume Roads, Cedar Rapids, IA, USA, 23–26 July 2023; Transportation Research Board: Cedar Rapids, IA, USA, 2023; pp. 188–205. [Google Scholar]
- Arezoumand, S.; Sassani, A.; Smadi, O. Data-Driven Approach to Decision-Making for Pavement Preservation. In Proceedings of the Second International Conference on Maintenance and Rehabilitation of Constructed Infrastructure Facilities (MAIREINFRA2), Honolulu, HI, USA, 16–19 August 2023; MDPI: Basel, Switzerland, 2023; p. 61. [Google Scholar]
- Arezoumand, S.; Sassani, A.; Smadi, O.; Buss, A. From Data to Decision: Integrated Approach to Pavement Preservation in Iowa through Treatment Effectiveness Analysis. Int. J. Pavement Eng. 2024, 25, 2361085. [Google Scholar] [CrossRef]
- Mansour, M.; Martens, J.; Blankenbach, J. Hierarchical SVM for Semantic Segmentation of 3D Point Clouds for Infrastructure Scenes. Infrastructures 2024, 9, 83. [Google Scholar] [CrossRef]
- Bloetscher, F.; Farmer, Z.; Barton, J.; Chapman, T.; Fonseca, P.; Shaner, M. Water System Condition and Asset Replacement Prioritization. J. Water Resour. Prot. 2023, 15, 165–178. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Shoghli, O. Predictive Analytics for Roadway Maintenance: A Review of Current Models, Challenges, and Opportunities. Civ. Eng. J. 2020, 6, 602–625. [Google Scholar] [CrossRef]
- Jung, H.; Kim, B. Identifying Research Topics and Trends in Asset Management for Sustainable Use: A Topic Modeling Approach. Sustainability 2021, 13, 4792. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble Learning: A Survey. WIREs Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Alatoom, Y.I.; Al-Hamdan, A.B. A Comparative Study Between Different Machine Learning Algorithms for Estimating the Vehicular Delay at Signalized Intersections. J. Soft Comput. Civ. Eng. 2024, 9, 123–158. [Google Scholar] [CrossRef]
- Yu, T.; Pei, L.-I.; Li, W.; Sun, Z.; Huyan, J. Pavement Surface Condition Index Prediction Based on Random Forest Algorithm. J. Highw. Transp. Res. Dev. (Engl. Ed.) 2021, 15, 1–11. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T. Climate Change Impact on Infrastructure: A Machine Learning Solution for Predicting Pavement Condition Index. Constr. Build. Mater. 2021, 306, 124905. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, J.; Cao, D.; Yao, H. Cost-Effective Assessment of in-Service Asphalt Pavement Condition Based on Random Forests and Regression Analysis. Constr. Build. Mater. 2022, 330, 127219. [Google Scholar] [CrossRef]
- Guo, X.; Hao, P. Using a Random Forest Model to Predict the Location of Potential Damage on Asphalt Pavement. Appl. Sci. 2021, 11, 10396. [Google Scholar] [CrossRef]
- Jia, X.; Woods, M.; Gong, H.; Zhu, D.; Hu, W.; Huang, B. Evaluation of Network-Level Data Collection Variability and Its Influence on Pavement Evaluation Utilizing Random Forest Method. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 331–345. [Google Scholar] [CrossRef]
- Assaad, R.; El-adaway, I.H. Bridge Infrastructure Asset Management System: Comparative Computational Machine Learning Approach for Evaluating and Predicting Deck Deterioration Conditions. J. Infrastruct. Systems. 2020, 26. [Google Scholar] [CrossRef]
- Kong, X.; Li, Z.; Zhang, Y.; Das, S. Bridge Deck Deterioration: Reasons and Patterns. Transp. Res. Rec. J. Transp. Res. Board 2022, 2676, 570–584. [Google Scholar] [CrossRef]
- Cheng, C.; Ye, C.; Yang, H.; Wang, L. Predicting Rutting Development of Pavement with Flexible Overlay Using Artificial Neural Network. Appl. Sci. 2023, 13, 7064. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T. Using Data Analytics for Cost-Effective Prediction of Road Conditions: Case of The Pavement Condition Index: [Summary Report] (FHWA-HRT-18-065); Federal Highway Administration, Office of Research, Development, and Technology: Washington, DC, USA, 2018. [Google Scholar]
- Adesunkanmi, R.; Al-Hamdan, A.; Nlenanya, I. Prediction of Pavement Overall Condition Index Based on Wrapper Feature-Selection Techniques Using Municipal Pavement Data. Transp. Res. Rec. J. Transp. Res. Board 2024, 2678, 208–221. [Google Scholar] [CrossRef]
- Zeiada, W.; Dabous, S.A.; Hamad, K.; Al-Ruzouq, R.; Khalil, M.A. Machine Learning for Pavement Performance Modelling in Warm Climate Regions. Arab. J. Sci. Eng. 2020, 45, 4091–4109. [Google Scholar] [CrossRef]
- Guo, R.; Fu, D.; Sollazzo, G. An Ensemble Learning Model for Asphalt Pavement Performance Prediction Based on Gradient Boosting Decision Tree. Int. J. Pavement Eng. 2022, 23, 3633–3646. [Google Scholar] [CrossRef]
- Im, J.; Cho, I.-H.; Kim, J.K. FHDI: An R Package for Fractional Hot Deck Imputation. 2018. Available online: https://www.researchgate.net/profile/In-Ho-Cho-2/publication/328074285_FHDI_An_R_package_for_fractional_hot_deck_imputation/links/605ce5d7299bf173676ba434/FHDI-An-R-package-for-fractional-hot-deck-imputation.pdf (accessed on 10 October 2024).
- Al-Suleiman (Obaidat), T.I.; Alatoom, Y.I. Development of Pavement Roughness Regression Models Based on Smartphone Measurements. J. Eng. Des. Technol. 2024, 22, 1136–1157. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification Using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Greenwell, B.M. Pdp: An R Package for Constructing Partial Dependence Plots. R J. 2017, 9, 421. [Google Scholar] [CrossRef]
- Kheirati, A.; Golroo, A. Machine Learning for Developing a Pavement Condition Index. Autom. Constr. 2022, 139, 104296. [Google Scholar] [CrossRef]




| Asset Type | Key Indicators | Method of Assessment | Scale of Assessment |
|---|---|---|---|
| Roads | Pavement Condition Index (PCI) | Visual inspection of cracks, rutting, etc. | 0–100 scale |
| Overall Condition Index (OCI) | Visual inspection (subjective ratings) | 1–10 scale (PASER system) | |
| International Roughness Index (IRI) | Objective roughness measurement | Continuous scale (m/km) | |
| Bridges | Bridge Condition Index (BCI) | Inspection of structural elements | 0–9 component rating scale |
| Railways | Track Quality Index (TQI) | Measurements of track geometry | Varies by parameter (e.g., gauge, cant) |
| Sidewalks | Sidewalk Condition Index (SCI) | Visual inspection of sidewalk conditions | 0–100 scale |
| Variable | Abbreviation | STD | Skewness | Kurtosis | Mean | Median | Min | Max | IQR |
|---|---|---|---|---|---|---|---|---|---|
| Transverse Cracking | TRANS | 6.78 | 14.93 | 413.80 | 2.86 | 1.08 | 0.00 | 219.37 | 3.28 |
| Joint Spalling | JSPAL | 4.48 | 6.14 | 67.76 | 2.25 | 1.00 | 0.00 | 82.00 | 3.00 |
| Longitudinal Wheel path Cracking | LONG_WP | 12.96 | 22.33 | 588.60 | 0.96 | 0.00 | 0.00 | 413.55 | 0.00 |
| Longitudinal Cracking | LONG_NP | 88.68 | 4.02 | 27.31 | 49.05 | 13.62 | 0.00 | 1387.31 | 58.14 |
| D-Cracking | DCRK | 9.44 | 6.57 | 68.10 | 3.86 | 0.00 | 0.00 | 160.00 | 3.50 |
| Patching | PATCH | 4.04 | 7.41 | 94.78 | 1.36 | 0.00 | 0.00 | 83.00 | 1.00 |
| International Roughness Index | IRI | 90.02 | 0.79 | 0.90 | 233.16 | 223.87 | 64.53 | 684.86 | 126.16 |
| Overall Condition Index | OCI | 0.756 | −1.94 | 7.35 | 8.60 | 8.5 | 2.0 | 10.00 | 1.5 |
| Variable | Abbreviation | STD | Skewness | Kurtosis | Mean | Median | Min | Max | IQR |
|---|---|---|---|---|---|---|---|---|---|
| Transverse Cracking | TRANS | 25.49 | 2.76 | 18.38 | 26.67 | 20.77 | 0.00 | 354.02 | 27.00 |
| Rutting | RUT | 0.09 | 0.88 | 0.76 | 0.20 | 0.19 | 0.04 | 0.60 | 0.13 |
| Longitudinal Wheel path Cracking | LONG_WP | 127.68 | 2.78 | 10.42 | 92.35 | 50.01 | 0.00 | 1115.01 | 114.38 |
| Longitudinal Cracking | LONG_NP | 261.50 | 3.02 | 19.33 | 236.12 | 167.76 | 0.00 | 3179.33 | 261.93 |
| Alligator Cracking | ALLIG | 9.42 | 9.05 | 100.84 | 1.72 | 0.00 | 0.00 | 136.28 | 0.00 |
| Patching | PATCH | 1.28 | 5.49 | 39.65 | 0.42 | 0.00 | 0.00 | 13.00 | 0.00 |
| International Roughness Index | IRI | 79.19 | 1.49 | 4.35 | 205.76 | 191.79 | 70.10 | 712.59 | 96.36 |
| Overall Condition Index | OCI | 1.392 | −0.55 | −0.34 | 7.25 | 7.5 | 2.00 | 10.00 | 2.5 |
| Rank | Variable | |
|---|---|---|
| PCC | COM | |
| 1 | Distress Type | Distress Type |
| 2 | Standard Deviation | Standard Deviation |
| 3 | RMS | RMS |
| 4 | IQR | IQR |
| 5 | Maximum Value | Skewness |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Hamdan, A.B.; Alatoom, Y.I.; Nlenanya, I.; Smadi, O. Weighting Variables for Transportation Assets Condition Indices Using Subjective Data Framework. CivilEng 2024, 5, 949-970. https://doi.org/10.3390/civileng5040048
Al-Hamdan AB, Alatoom YI, Nlenanya I, Smadi O. Weighting Variables for Transportation Assets Condition Indices Using Subjective Data Framework. CivilEng. 2024; 5(4):949-970. https://doi.org/10.3390/civileng5040048
Chicago/Turabian StyleAl-Hamdan, Abdallah B., Yazan Ibrahim Alatoom, Inya Nlenanya, and Omar Smadi. 2024. "Weighting Variables for Transportation Assets Condition Indices Using Subjective Data Framework" CivilEng 5, no. 4: 949-970. https://doi.org/10.3390/civileng5040048
APA StyleAl-Hamdan, A. B., Alatoom, Y. I., Nlenanya, I., & Smadi, O. (2024). Weighting Variables for Transportation Assets Condition Indices Using Subjective Data Framework. CivilEng, 5(4), 949-970. https://doi.org/10.3390/civileng5040048








