Abstract
Artificial neural networks (ANN) have a great promise in predicting the load-bearing capacity of building structures. The purpose of this work was to develop ANN models to determine the ultimate load of eccentrically compressed concrete-filled steel tubular (CFST) columns of circular cross-sections, which operated on the widest possible range of input parameters. Short columns were considered for which the amount of deflection does not affect the bending moment. A feedforward network was selected as the neural network type. The input parameters of the neural networks were the outer diameter of the columns, the thickness of the pipe wall, the yield strength of steel, the compressive strength of concrete and the relative eccentricity. Artificial neural networks were trained on synthetic data generated based on a theoretical model of the limit equilibrium of CFST columns. Two ANN models were created. When training the first model, the ultimate loads were determined at a given eccentricity of the axial force without taking into account additional random eccentricity. When training the second model, additional random eccentricity was taken into account. The total volume of the training dataset was 179,025 samples. Such a large training dataset size has never been used before. The training dataset covers a wide range of changes in the characteristics of the pipe metal and concrete of the core, pipe diameters and wall thicknesses, as well as eccentricities of the axial force. The trained models are characterized by high mean square error (MSE) scores. The correlation coefficients between the predicted and target values are very close to 1. The ANN models were tested on experimental data for 81 eccentrically compressed samples presented in five different works and 265 centrally compressed samples presented in twenty-six papers.
1. Introduction
Concrete-filled steel tubular columns are a promising type of building structure. They are widely used in the construction of high-rise buildings, transport structures, overpasses, etc. [1,2,3,4]. Compared to traditional reinforced concrete elements, CFST structures have a number of advantages, which primarily include an increase in load-bearing capacity due to the work of concrete under conditions of triaxial compression [5], savings on formwork and reinforcement work, etc.
Improving methods for calculating the load-bearing capacity of CFST columns is an urgent task, which is confirmed by the large number of theoretical and experimental works published recently on this topic [6,7,8].
When determining the load-bearing capacity of CFST columns, two approaches are most common. The first approach is to use empirical dependencies obtained from experimental data [9]. These dependencies are quite simple and suitable for engineering calculations, but the range of parameter changes in which the experiments were carried out limits their scope.
The second approach is finite element modeling in a three-dimensional setting, taking into account the real deformation diagrams of concrete and steel, as well as the contact interaction between the shell and the concrete core. A significant number of publications are devoted to the issues of finite element modeling of the stress–strain state of CFST columns [10,11,12,13,14,15,16,17]. This approach provides good agreement with experimental data but requires great computational resources and time.
Recently, machine learning methods have been widely used in the task of predicting the load-bearing capacity of CFST columns. In the work by Tran et al. [18], an empirical formula was proposed to determine the load-bearing capacity of centrally compressed square-section concrete tubular columns using an artificial neural network (ANN). ANN training was performed on experimental data for 300 columns presented in the literature. A comparative analysis showed greater stability and accuracy of the ANN compared to other existing formulas.
In another work, Tran et al. [19] built an artificial neural network model to predict the load-bearing capacity of centrally compressed CFST columns with a circular cross-section. Unlike the previous work, training was carried out on the results of numerical experiments rather than full-scale ones. To generate the dataset, three-dimensional finite element analysis was used in a nonlinear formulation in the ABAQUS environment. The ANN training database included data for 768 columns with different lengths, outer cross-sectional diameters, pipe wall thickness, steel yield strength and concrete compressive strength. For practical engineering calculations, the authors prepared a tool with a graphical interface.
In ref [20], Du et al. proposed two ANN models to determine the ultimate load under central compression of square-section CFST columns. Both models were trained on experimental data for 275 samples, and 30 samples were used for testing. The output data of the neural networks was compared with the results of calculations according to the design codes of various countries, and it was found that the resulting functional dependence of the load-bearing capacity on the main parameters differs somewhat from those presented in the design codes.
In ref [21], Al-Khaleefi et al. discussed the issues of predicting the fire resistance of CFST columns using artificial neural networks. Based on neural network modeling, a functional dependence of the CFST columns’ fire resistance index on the parameters that determine the dimensions of the samples, material characteristics and loading conditions was constructed. The total dataset included 35 experimental samples, of which 27 samples were used for training and 8 for testing. Another study on predicting the fire resistance of CFST columns using an ANN is presented in the work of Moradi et al. [22]. This paper is based on a larger database, including testing of 300 samples.
In ref [23], Zarringol et al. built artificial neural network models to predict the ultimate load for CFST columns of rectangular and circular cross-sections under central and eccentric compression. Compared to the previous works, larger datasets were used to train the ANN: 895 experiments for centrally compressed rectangular columns, 392 experiments for eccentrically compressed rectangular columns, 1305 experiments for centrally compressed circular columns, and 499 experiments for circular columns subjected to eccentric compression. The accuracy of ultimate load prediction was also compared with design codes of various countries.
CFST columns are also the object of study of ref [24], in which the ultimate load under central compression of columns was predicted using Multiphysics Artificial Intelligence. This article compared models based on an artificial neural network, Adaptive Neuro-Fuzzy Inference System (ANFIS), and Gene Expression Programming (GEP). The research dataset contained data from 1667 experiments, of which 702 corresponded to short columns and 965 corresponded to long columns. Gene Expression Programming, in combination with the finite element method, was also used in [25] to predict the strength of CFST columns made of high-strength concrete.
Ref [26] proposes a hybrid model that includes an ANN with a particle swarm optimization (PSO) algorithm. This model was used to predict flexural bending capacity and flexural stiffness at the initial and serviceability limits of CFST beams.
Among recent artificial intelligence techniques, the gradient boosting algorithm is currently gaining great popularity. Ref [27] demonstrates the application of this algorithm to predicting the strength of centrally compressed CFST columns of circular cross-sections. A comparison was made with other machine learning algorithms, such as random forest (RF), support vector machines (SVM), decision tree (DT) and deep learning.
In ref [28], the following machine learning models were applied to solve the same problem: back-propagation neural network (BPNN), genetic algorithm (GA)-BPNN, radial basis function neural network (RBFNN), Gaussian process regression (GPR) and multiple linear regression (MLR). The training dataset included 2045 centrally compressed columns selected through an extensive literature review. This paper shows that forecasting efficiency can be improved by dividing columns into subgroups depending on slenderness.
There are also publications in which machine learning methods are used not only to predict the ultimate load but also to predict the load–strain curve. In ref [29], Zarringol et al. showed the successful use of an artificial neural network in engineering calculations, which predicts the complete deformation diagram of centrally compressed CFST columns of round and square sections. For training, a database was used that included the results of 1152 finite element calculations in the ABAQUS environment, as well as the results of 392 full-scale experiments.
The review shows that machine learning methods are a promising tool in predicting the load-bearing capacity of CFST columns. At the same time, most existing publications refer to centrally compressed elements. For eccentrically compressed columns, compared to centrally compressed structures, an additional parameter affecting the load-bearing capacity is the eccentricity of the axial force. Therefore, to build ANN models that predict the load-bearing capacity of eccentrically compressed CFST columns, a significantly larger dataset size is required. The purpose of this work is to develop artificial neural network models that could predict with high accuracy the ultimate load for the entire possible range of parameters affecting the load-bearing capacity of eccentrically compressed columns. In our case, neural networks will be trained on synthetic data obtained on the basis of a theoretical model, followed by comparison with experimental data.
2. Materials and Methods
The process of building a model of any artificial neural network includes choosing its architecture and training. As an environment for implementing the ANN model, the MATLAB package (Neural Network Toolbox) was selected.
The CFST columns of circular cross-sections were selected as the object of study since this cross-sectional shape is the most common in the designs of buildings and structures for various purposes. The prediction of the ultimate load (kN) in the developed ANN models was carried out according to 5 input parameters: outer diameter of the column (mm), pipe wall thickness (mm), yield strength of steel (MPa), compressive strength of concrete (MPa) and relative eccentricity . We were considering short columns for which deflection did not lead to a significant increase in the bending moment, so the length of the elements was not included in the input parameters. Columns, according to [30], are considered short if their slenderness (the ratio of the calculated length to the radius of gyration of the section) does not exceed 14.
A feedforward network architecture was selected as it is one of the most common neural network types. The developed ANN model contains 2 hidden layers. The number of neurons in each hidden layer is 16. The TANSIG (hyperbolic tangent) function was used as the activation function for neurons in both layers. The architecture of the developed neural networks is shown schematically in Figure 1.
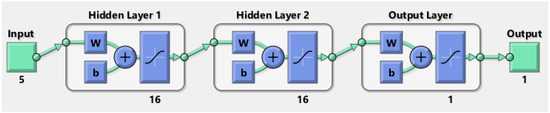
Figure 1.
Artificial neural network architecture.
Unlike most previous works, where training is carried out on experimental data, in our work the neural networks were trained on synthetic data. Experimental data were not used for training, since they are not so numerous and could not cover the full variety of column sizes and concrete and steel characteristics. However, after training the neural networks, their performance was tested using experimental data.
When generating a dataset for training, the provisions presented in the Russian design codes for composite steel and concrete structures SR 266.1325800.2016 [30] were used. Columns without bar reinforcement were considered, in which only a steel pipe acts as a reinforcement. When determining the breaking load, the stress diagrams in concrete and steel in the limit state were assumed to be rectangular; the work of tensile concrete was not taken into account. The diagram for determining the ultimate load under eccentric compression of a CFST column is shown in Figure 2.
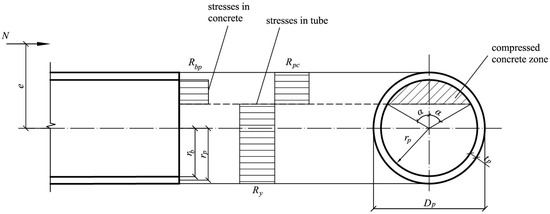
Figure 2.
Diagram for determining the ultimate load.
The strength calculation of normal sections of eccentrically compressed CFST elements without bar reinforcement according to SR 266.1325800.2016 is performed by the limit equilibrium method from the condition:
where is the axial force, is the eccentricity of the axial force, is the radius of the concrete core, is the compressive design strength of concrete taking into account the effect of lateral compression, is the angle that determines the size of the compressed zone of concrete, is the cross-sectional area of the steel pipe, is the average radius of the steel pipe, is the design strength of a steel pipe under compression.
The compressive design strength of concrete taking into account the effect of lateral compression in [30] is determined by the formula:
The coefficient in Formula (2) is taken equal to 25 MN.
The design strength of a pipe under compression is determined by the formula:
Angle α in Formula (1) is determined from the equation:
Expression (1) allows one to check the fulfillment of the column strength condition but does not find the ultimate load at a given eccentricity. For a given eccentricity of the axial force e, determining the magnitude of the ultimate load based on the SR 266.1325800.2016 method is a very non-trivial task. Equation (4) is transcendental and requires the use of numerical methods to solve. The task of determining the ultimate compressive force at a known value of e was solved by us by stepwise increasing the load from 0 to , where is the ultimate load for a given sample under central compression. At each step, the root of Equation (4) was numerically determined, and then the fulfillment of Condition (1) was checked. When generating the training sample, the range of changes in the compressive strength of concrete was taken from 10 to 65 MPa; the yield strength of the steel varied from 240 to 440 MPa. The relative eccentricity varied from 0 to 0.65. The values of outer diameters of pipes and wall thicknesses used during training corresponded to the Russian assortment of electric-welded straight-seam pipes GOST 10704-91 (Table 1).

Table 1.
The values of the outer diameters of pipes, as well as the minimum and maximum wall thicknesses used in training.
For quantities and , 5 different values were used from () to () with uniform steps. For wall thickness , 11 different values from to were used in uniform increments. For the relative eccentricity, 21 different values were taken from 0 to 0.65 with equal steps. Thus, the size of the training sample was 5 × 5 × 11 × 21 × 31 = 179,025.
During training, the sample was randomly divided into 3 parts: “Train”, “Validation” and “Test” in the proportion of 70%, 15% and 15%. To train the ANN, we used the Levenberg–Marquardt algorithm. The value of the mean square error (MSE) was taken as a criterion for the quality of training:
where is the sample size, are the target values and are the predicted values.
In addition to the ANN model trained to determine the maximum load at a given eccentricity value , another ANN model was also built to determine the value , taking into account additional random eccentricity. In accordance with Russian standards for the design of composite steel and concrete structures [30], the largest of the values [0.01 m; Dp/30; l/600] was taken as a random eccentricity, where l was the design length of the column. Since short columns were considered, the value of random eccentricity was taken as the largest of the two values [0.01 m; Dp/30].
3. Results and Discussion
Figure 3 shows the training performance graph for the model trained on ultimate loads without taking into account additional random eccentricities. Figure 4 is the same for the model trained taking into account additional random eccentricities. In the first case, the learning process took 474 epochs, and in the second case, it took 682 epochs. The model trained without taking into account additional random eccentricities is characterized by a four-times-smaller MSE value: 4693 vs. 18,940. The MSE values for the “Train”, “Validation” and “Test” parts of the sample are almost the same: the blue, green and red lines overlap each other. A small difference in MSE for the “Train”, “Validation” and “Test” parts of the sample indicates its sufficient volume.
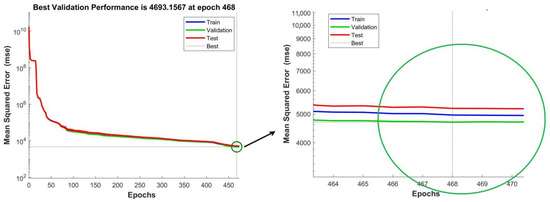
Figure 3.
Training performance graph for the model trained without taking into account random eccentricities.
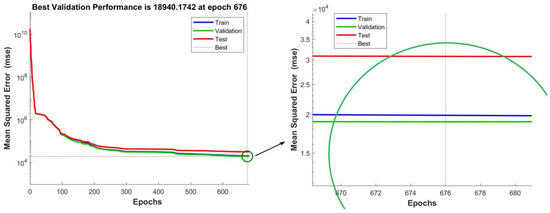
Figure 4.
Training performance plot for the model trained with additional random eccentricities.
Figure 5 and Figure 6 show regression plots for the two models. The x-axis shows the target values T of the ultimate load. The y-axis shows the predicted Y values of the ultimate load. Most of the points on the graphs fit on the straight line Y = T. The correlation coefficients R of both models are close to 1. High correlation coefficients between the target and predicted values are achieved thanks to the two-layer neural network architecture, large number of neurons in hidden layers and large dataset size.
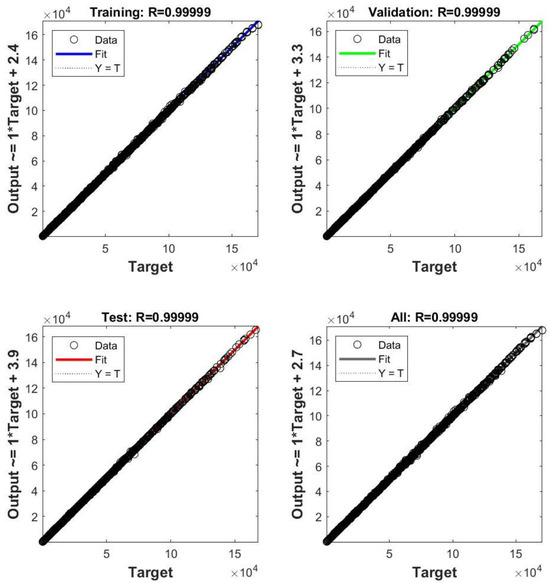
Figure 5.
Regression plot for the model trained without taking into account additional random eccentricities.
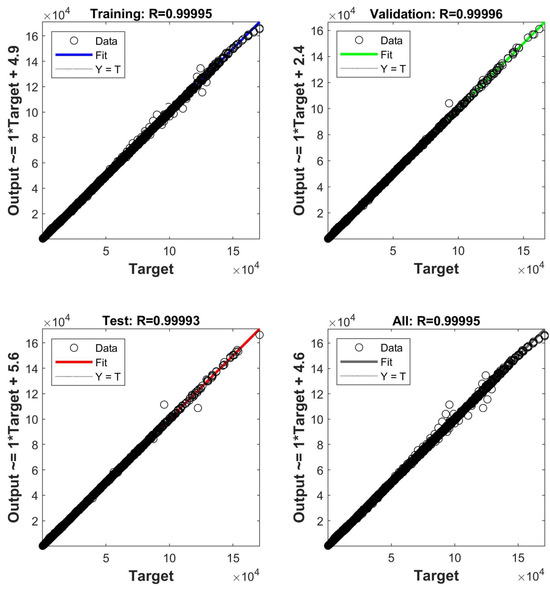
Figure 6.
Regression plot for a model trained taking into account additional random eccentricities.
The constructed models were tested on experimental data for 81 eccentrically compressed CFST columns of circular cross-sections, presented in five different works [31,32,33,34,35]. The diameter of the columns varied from 103 to 720 mm. The wall thickness changed from 1.81 to 11.95 mm. The yield strength of steel varied from 248.9 to 440 MPa. The compressive strength of concrete changed from 21.5 to 63.8 Mpa. The ratio of the axial force eccentricity to the outer diameter of the column e/Dp varied from 0.05 to 0.64. The results are summarized in Table 2. In this table, N1 are the values of the ultimate loads determined by the first ANN model (without taking into account additional random eccentricities), and N2 are the values of the ultimate loads determined by the second ANN model (taking into account additional random eccentricities).

Table 2.
Results of testing the developed models of artificial neural networks on experimental data for eccentrically compressed CFST columns.
From Table 2, it can be seen that for most samples the results predicted by the first model are in good agreement with the experimental data. The average value of the ratio N1/Nexp is 0.97, maximum value is 1.38 and minimum value is 0.79. The standard deviation σ = 0.11 and the coefficient of variation CV = 10.9%.
Deviations of the predicted values from the experimental results can be explained, on the one hand, by the scatter of experimental data and, on the other hand, by simplifications adopted in the theoretical model, which is used to train the artificial neural network. It should also be noted that, at present, there is no generally accepted criterion for CFST columns to reach the limit state. Some researchers take the magnitude of deformation as a criterion for destruction and others take the achievement of the pipe material’s yield point, etc.
The second model predicts the maximum load with a safety margin for most samples. The average value of the N2/Nexp ratio is 0.82, the maximum value is 1.11 and the minimum is 0.61. The standard deviation σ = 0.124 and the coefficient of variation CV = 15.1%. In the design practice, the second model should be used, which takes into account random eccentricities.
Also, the first model, which predicts the values of the ultimate load without taking into account additional random eccentricities, was tested on experimental data for 265 centrally compressed columns, presented in 26 different works [31,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. A comparison of the predicted values with the experimental data is given in Table 3. The diameter of the columns in papers [31,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60] varied from 100 to 1020 mm, the wall thickness varied from 0.86 to 13.25 mm, the yield strength of steel varied from 165.8 to 853 MPa and the compressive strength of concrete varied from 16.7 to 114.3 MPa.

Table 3.
Comparison of ANN predicted values with experimental data for centrally compressed CFST columns.
Despite the fact that some values of the input parameters in Table 3 are outside the range in which the neural network was trained, it showed good ability to extrapolate data. The average value of the ratio is 0.96. The maximum value of the ratio is 1.14, the minimum is 0.77. The standard deviation = 0.06 and the coefficient of variation CV = 5.9%.
4. Conclusions
During the conducted study, the following main results were obtained:
1. Two models of artificial neural networks have been developed to predict the ultimate load of eccentrically compressed short concrete-filled steel tubular columns of circular cross-sections either without taking into account or taking into account additional random eccentricities. The developed ANNs are based on the theoretical model of the limiting equilibrium of CFST columns. Machine learning models are trained on the entire possible range of the diameters and wall thicknesses of metal tubes, as well as on the wide range of changes in the design strength of concrete and steel. The volume of the training dataset was 179,025 samples, which is hundreds and thousands of times larger than the sample sizes previously used by other researchers.
2. Training of the ANN models on synthetic data was successful; the trained models are characterized by good performance in terms of mean squared error, and the correlation coefficients between the predicted and target values are close to 1.
3. The results of predicting ultimate loads using artificial neural networks were compared with the results of experiments for 81 eccentrically compressed samples presented in five different works and 265 centrally compressed samples presented in twenty-six papers. The first ANN model, which was trained on ultimate loads determined without taking into account random eccentricities, showed good agreement with experimental data for most samples. The second model, which takes into account random eccentricities in accordance with the requirements of design standards, predicts the maximum load with a safety margin for most prototypes. This model can be used in the design process to quickly determine the bearing capacity of columns at a given eccentricity.
In this work, when training artificial neural networks, the basis was a simplified model for determining the ultimate load, in which the stress diagrams in concrete and steel in the limit state were assumed to be rectangular, and the work of tensile concrete was not taken into account. The goal of our further research will be the development of artificial neural networks based on more complex models [61,62,63]. In this case, the nonlinearity of the diagrams of concrete and steel, as well as the dilatation effect, will be taken into account. Also, this article considers only short columns, for which the additional eccentricity of the axial force caused by the deflection of the element can be neglected. In the future, it is planned to build ANN models to predict the load-bearing capacity of slender CFST columns.
It should also be noted that artificial neural networks are not the only machine learning algorithm. In some cases, other algorithms turn out to be more effective when applied to concrete and reinforced concrete structures, for example, support vector regression (SVR) [64], multi-objective grasshopper optimization algorithm (MOGOA) [65] and others. In the future, it is also planned by us to use alternative algorithms to analyze the datasets generated in this work.
Author Contributions
Conceptualization, A.C. and V.A.; methodology, A.C.; software, V.T.; validation, A.C. and V.A.; formal analysis, A.C.; investigation, A.C.; resources, V.A.; data curation, V.T.; writing—original draft preparation, A.C.; writing—review and editing, V.T.; visualization, A.C.; supervision, A.C.; project administration, A.C.; funding acquisition, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The study did not report any data.
Acknowledgments
The authors would like to acknowledge the administration of Don State Technical University for their resources and financial support.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Tran, H.; Thai, H.T.; Ngo, T.; Uy, B.; Li, D.; Mo, J. Nonlinear inelastic simulation of high-rise buildings with innovative composite coupling shear walls and CFST columns. Struct. Des. Tall Spec. Build. 2021, 30, e1883. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, J.; Liu, Y.; Lin, X. Thin-walled CFST columns for enhancing seismic collapse performance of high-rise steel frames. Appl. Sci. 2017, 7, 53. [Google Scholar] [CrossRef]
- Kumari, B. Concrete filled steel tubular (CFST) columns in composite structures. IOSR J. Electr. Electron. Eng. 2018, 13, 11–18. [Google Scholar]
- Longarini, N.; Cabras, L.; Zucca, M.; Chapain, S.; Aly, A.M. Structural improvements for tall buildings under wind loads: Comparative study. Shock Vib. 2017, 2017, 2031248. [Google Scholar] [CrossRef]
- Xu, L.; Pan, J.; Yang, X. Mechanical performance of self-stressing CFST columns under uniaxial compression. J. Build. Eng. 2021, 44, 103366. [Google Scholar] [CrossRef]
- Wang, X.; Fan, F.; Lai, J. Strength behavior of circular concrete-filled steel tube stub columns under axial compression: A review. Constr. Build. Mater. 2022, 322, 126144. [Google Scholar] [CrossRef]
- Ilanthalir, A.; Regin, J.J.; Maheswaran, J. Concrete-filled steel tube columns of different cross-sectional shapes under axial compression: A review. IOP Conf. Ser. Mater. Sci. Eng. 2020, 983, 012007. [Google Scholar] [CrossRef]
- Bhatia, S.; Tiwary, A.K. Axial Compression Behavior of Single-Skin and Double-Skin Concrete-Filled Steel Tube Columns: A Review. In Advances in Construction Materials and Sustainable Environment: Select Proceedings of ICCME 2020; Springer: Singapore, 2022; pp. 849–861. [Google Scholar] [CrossRef]
- Yang, C.; Gao, P.; Wu, X.; Chen, Y.F.; Li, Q.; Li, Z. Practical formula for predicting axial strength of circular-CFST columns considering size effect. J. Constr. Steel Res. 2020, 168, 105979. [Google Scholar] [CrossRef]
- Erdoğan, A.; Güneyisi, E.M.; Süleyman, I.P.E.K. Finite Element Modelling of Ultimate Strength of CFST Column and Its Comparison with Design Codes. Bilecik Şeyh Edebali Univ. Fen Bilim. Derg. 2022, 9, 324–339. [Google Scholar] [CrossRef]
- Ding, F.; Cao, Z.; Lyu, F.; Huang, S.; Hu, M.; Lin, Q. Practical design equations of the axial compressive capacity of circular CFST stub columns based on finite element model analysis incorporating constitutive models for high-strength materials. Case Stud. Constr. Mater. 2022, 16, e01115. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Hong, W.K.; Ko, H.J.; Kim, S.K. Finite element model for the interface between steel and concrete of CFST (concrete-filled steel tube). Eng. Struct. 2019, 185, 141–158. [Google Scholar] [CrossRef]
- İpek, S.; Güneyisi, E.M. Nonlinear finite element analysis of double skin composite columns subjected to axial loading. Arch. Civ. Mech. Eng. 2020, 20, 9. [Google Scholar] [CrossRef]
- Li, B.; Ding, F.; Lu, D.; Lyu, F.; Huang, S.; Cao, Z.; Wang, H. Finite Element Analysis of the Mechanical Properties of Axially Compressed Square High-Strength Concrete-Filled Steel Tube Stub Columns Based on a Constitutive Model for High-Strength Materials. Materials 2022, 15, 4313. [Google Scholar] [CrossRef]
- Hilo, S.J.; Sabih, S.M.; Abdulrazzaq, M.M. Numerical Analysis on the Behavior of Polygonal CFST Composite Columns under Axial Loading Using Finite Element. J. Eng. Sci. Technol. 2021, 16, 4975–4999. [Google Scholar]
- Gupta, A.; Mohan, R.; Bisht, H.; Sharma, A. Experimental testing and numerical modelling of CFST columns under axial compressive load. Asian J. Civ. Eng. 2022, 23, 415–424. [Google Scholar] [CrossRef]
- Isleem, H.F.; Chukka, N.D.K.R.; Bahrami, A.; Oyebisi, S.; Kumar, R.; Qiong, T. Nonlinear finite element and analytical modelling of reinforced concrete filled steel tube columns under axial compression loading. Results Eng. 2023, 19, 101341. [Google Scholar] [CrossRef]
- Tran, V.L.; Thai, D.K.; Kim, S.E. Application of ANN in predicting ACC of SCFST column. Compos. Struct. 2019, 228, 111332. [Google Scholar] [CrossRef]
- Tran, V.L.; Thai, D.K.; Nguyen, D.D. Practical artificial neural network tool for predicting the axial compression capacity of circular concrete-filled steel tube columns with ultra-high-strength concrete. Thin-Walled Struct. 2020, 151, 106720. [Google Scholar] [CrossRef]
- Du, Y.; Chen, Z.; Zhang, C.; Cao, X. Research on axial bearing capacity of rectangular concrete-filled steel tubular columns based on artificial neural networks. Front. Comput. Sci. 2017, 11, 863–873. [Google Scholar] [CrossRef]
- Al-Khaleefi, A.M.; Terro, M.J.; Alex, A.P.; Wang, Y. Prediction of fire resistance of concrete filled tubular steel columns using neural networks. Fire Saf. J. 2002, 37, 339–352. [Google Scholar] [CrossRef]
- Moradi, M.J.; Daneshvar, K.; Ghazi-Nader, D.; Hajiloo, H. The prediction of fire performance of concrete-filled steel tubes (CFST) using artificial neural network. Thin-Walled Struct. 2021, 161, 107499. [Google Scholar] [CrossRef]
- Zarringol, M.; Thai, H.T.; Thai, S.; Patel, V. Application of ANN to the design of CFST columns. Structures 2020, 28, 2203–2220. [Google Scholar] [CrossRef]
- Khan, S.; Ali Khan, M.; Zafar, A.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predicting the Ultimate Axial Capacity of Uniaxially Loaded CFST Columns Using Multiphysics Artificial Intelligence. Materials 2022, 15, 39. [Google Scholar] [CrossRef] [PubMed]
- Hanoon, A.N.; Al Zand, A.W.; Yaseen, Z.M. Designing new hybrid artificial intelligence model for CFST beam flexural performance prediction. Eng. Comput. 2022, 38, 3109–3135. [Google Scholar] [CrossRef]
- Jiang, H.; Mohammed, A.S.; Kazeroon, R.A.; Sarir, P. Use of the Gene-Expression Programming Equation and FEM for the High-Strength CFST Columns. Appl. Sci. 2021, 11, 10468. [Google Scholar] [CrossRef]
- Vu, Q.V.; Truong, V.H.; Thai, H.T. Machine learning-based prediction of CFST columns using gradient tree boosting algorithm. Compos. Struct. 2021, 259, 113505. [Google Scholar] [CrossRef]
- Hou, C.; Zhou, X.G. Strength prediction of circular CFST columns through advanced machine learning methods. J. Build. Eng. 2022, 51, 104289. [Google Scholar] [CrossRef]
- Zarringol, M.; Thai, H.T. Prediction of the load-shortening curve of CFST columns using ANN-based models. J. Build. Eng. 2022, 51, 104279. [Google Scholar] [CrossRef]
- SR 266.1325800.2016; Composite Steel and Concrete Structures. Design Rules. Ministry of Construction of Russia: Moscow, Russia, 2017. Available online: https://meganorm.ru/Data2/1/4293747/4293747659.htm (accessed on 18 December 2023).
- Luksha, L.K.; Nesterovich, A.P. Strength testing of large-diameter concrete filled steel tubular members. In Proceedings of the Third International Conference on Steel-Concrete Composite Structures, Fukuoka, Japan, 26–29 September 1991; Wakabayashi, M., Ed.; Association for International Cooperation and Research in Steel-Concrete Composite Structures: Bradford, UK, 1991; pp. 67–72. [Google Scholar]
- Matsui, C. Slender Concrete Filled Steel Tubular Columns Combined Compressionsnd Bending, Strutural Steel. Steel-Concert. Compos. Struct. 1995, 3, 29–36. [Google Scholar]
- Huixian, T.G.; Ximin, S. Study on the fundamental structural behavior of concrete filled steel tubular columns. J. Build. Struct. 1982, 3, 13. [Google Scholar]
- Zhong, S. Research of confining load of CFST under eccentric loading. J. Harbin Univ. Civ. Eng. Archit. 1983, 3, 1–18. [Google Scholar]
- Cai, Z. Behavior and ultimate strength of short concrete-filled steel tubular columns. J. Build. Struct. 1984, 6, 13–29. [Google Scholar]
- Lai, M.H.A.; Ho, J.C.M. Theoretical axial stress-strain model for circular concrete-filled-steel-tube columns. Eng. Struct. 2016, 25, 124–143. [Google Scholar] [CrossRef]
- Gardner, N.J.; Jacobson, E.R. Structural behavior of concrete-filled steel tubes. ACI J. 1967, 64, 404–412. [Google Scholar]
- Sakino, K.; Hayashi, H. Behavior of concrete filled steel tubular stub columns under concentric loading. In Proceedings of the Third International Conference on Steel-Concrete Composite Structures, Fukuoka, Japan, 26–29 September 1991; pp. 25–30. [Google Scholar]
- Kato, B. Compressive strength and deformation capacity of concrete-filled tubular stub columns. J. Struct. Constr. Eng. AIJ 1995, 468, 183–191. [Google Scholar] [CrossRef]
- Saisho, M.; Abe, T.; Nakaya, K. Ultimate bending strength of high-strength concrete filled steel tube column. J. Struct. Constr. Eng. AIJ 1999, 523, 133–140. [Google Scholar]
- Yamamoto, K.; Kawaguchi, J.; Morino, S. Experimental study of the size effect on the behaviour of concrete filled circular steel tube columns under axial compression. J. Struct. Constr. Eng. AIJ 2002, 561, 237–244. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.P. Axially loaded concrete-filled steel tubes. J. Struct. Eng. 1998, 124, 1125–1138. [Google Scholar] [CrossRef]
- O’Shea, M.D.; Bridge, R.Q. Design of circular thin-walled concrete filled steel tubes. J. Struct. Eng. 2000, 126, 1295–1303. [Google Scholar] [CrossRef]
- Elremaily, A.; Azizinamini, A. Behavior and strength of circular concrete-filled tube columns. J. Constr. Steel Res. 2002, 58, 1567–1591. [Google Scholar] [CrossRef]
- Johansson, M. The efficiency of passive confinement in CFT columns. Steel Compos. Struct. 2002, 2, 379–396. [Google Scholar] [CrossRef]
- Yu, Z.W.; Ding, F.X.; Lin, S. Researches on behavior of high-performance concrete filled tubular steel short columns. J. Build. Struct. 2002, 23, 41–47. [Google Scholar]
- Giakoumelis, G. Axial capacity of circular concrete-filled tube columns. J. Constr. Steel Res. 2004, 60, 1049–1068. [Google Scholar] [CrossRef]
- Gu, W.; Guan, S.W.; Zhao, Y.H.; Cao, H. Experimental study on concentrically-compressed circular concrete filled CFRP-steel composite tubular short columns. J. Shenyang Arch. Civ. Eng. Inst. 2004, 20, 118–120. [Google Scholar]
- Han, L.H.; Yao, G.H. Experimental behaviour of thin-walled hollow structural steel (HSS) columns filled with self-consolidating concrete (SCC). Thin-Wall Struct. 2004, 42, 1357–1377. [Google Scholar] [CrossRef]
- Sakino, K.; Nakahara, H.; Morino, S.; Nishiyama, I. Behavior of centrally loaded concrete-filled steel-tube short columns. J. Struct. Eng. ASCE 2004, 130, 180–188. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.Y. Failure modes of short columns of high-strength concrete filled steel tubes. China Civ. Eng. J. 2004, 37, 1–10. [Google Scholar]
- Han, L.H.; Yao, G.H.; Zhao, X.L. Tests and calculations for hollow structural steel (HSS) stub columns filled with self-consolidating concrete (SCC). J. Constr. Steel Res. 2005, 61, 1241–1269. [Google Scholar] [CrossRef]
- Tan, K.F. Analysis of formulae for calculating loading bearing capacity of steel tubular high strength concrete. J. Southwest. Univ. Sci. Technol. 2006, 21, 7–10. [Google Scholar]
- Gupta, P.K.; Sarda, S.M.; Kumar, M.S. Experimental and computational study of concrete filled steel tubular columns under axial loads. J. Constr. Steel Res. 2007, 63, 182–193. [Google Scholar] [CrossRef]
- Yu, Z.W.; Ding, F.X.; Cai, C.S. Experimental behavior of circular concrete-filled steel tube stub. J. Constr. Steel Res. 2007, 63, 165–174. [Google Scholar] [CrossRef]
- Lai, M.H.; Ho, J.C.M. Confinement effect of ring-confined concrete-filled-steel-tube columns under uniaxial load. Eng. Struct. 2014, 67, 123–141. [Google Scholar] [CrossRef]
- Liao, F.Y.; Han, L.H.; He, S.H. Behavior of CFST short column and beam with initial concrete imperfection: Experiments. J. Constr. Steel Res. 2011, 67, 1922–1935. [Google Scholar] [CrossRef]
- Uy, B.; Tao, Z.; Han, L.H. Behaviour of short and slender concrete-filled stainless steel tubular columns. J. Constr. Steel Res. 2011, 67, 360–378. [Google Scholar] [CrossRef]
- Xue, J.Q.; Briseghella, B.; Chen, B.C. Effects of debonding on circular CFST stub columns. J. Constr. Steel Res. 2012, 69, 64–76. [Google Scholar] [CrossRef]
- Abed, F.; AlHamaydeh, M.; Abdalla, S. Experimental and numerical investigations of the compressive behavior of concrete filled steel tubes (CFSTs). J. Constr. Steel Res. 2013, 80, 429–439. [Google Scholar] [CrossRef]
- Chepurnenko, A.; Yazyev, B.; Meskhi, B.; Beskopylny, A.; Khashkhozhev, K.; Chepurnenko, V. Simplified 2D Finite Element Model for Calculation of the Bearing Capacity of Eccentrically Compressed Concrete-Filled Steel Tubular Columns. Appl. Sci. 2021, 11, 11645. [Google Scholar] [CrossRef]
- Chepurnenko, V.S.; Khashkhozhev, K.N.; Yazyev, S.B.; Avakov, A.A. Improving the calculation of flexible CFST-columns taking into account stresses in the section planes. Constr. Mater. Prod. 2021, 4, 41–53. [Google Scholar] [CrossRef]
- Chepurnenko, A.; Turina, V.; Akopyan, V. Simplified Method for Calculating the Bearing Capacity of Slender Concrete-Filled Steel Tubular Columns. CivilEng 2023, 4, 1000–1015. [Google Scholar] [CrossRef]
- Kandiri, A.; Shakor, P.; Kurda, R.; Deifalla, A.F. Modified Artificial neural networks and support vector regression to predict lateral pressure exerted by fresh concrete on formwork. Int. J. Concr. Struct. Mater. 2022, 16, 64. [Google Scholar] [CrossRef]
- Izadgoshasb, H.; Kandiri, A.; Shakor, P.; Laghi, V.; Gasparini, G. Predicting compressive strength of 3D printed mortar in structural members using machine learning. Appl. Sci. 2021, 11, 10826. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).