Priority Criteria (PC) Based Particle Swarm Optimization of Reinforced Concrete Frames (PCPSO)
Abstract
1. Introduction and State of the Art
2. Study Approach
- Discussing the need for priority criteria (PC) and PC formulation;
- Integrating PC to basic PSO formulation;
- Defining objective functions, constraints, and penalty function;
- Formulation of procedure and approach for the SAP 2000, v24 structural analysis, and Matlab 2021a computation, and writing several Matlab functions and scripts;
- Conducting case study for comparison and verification.
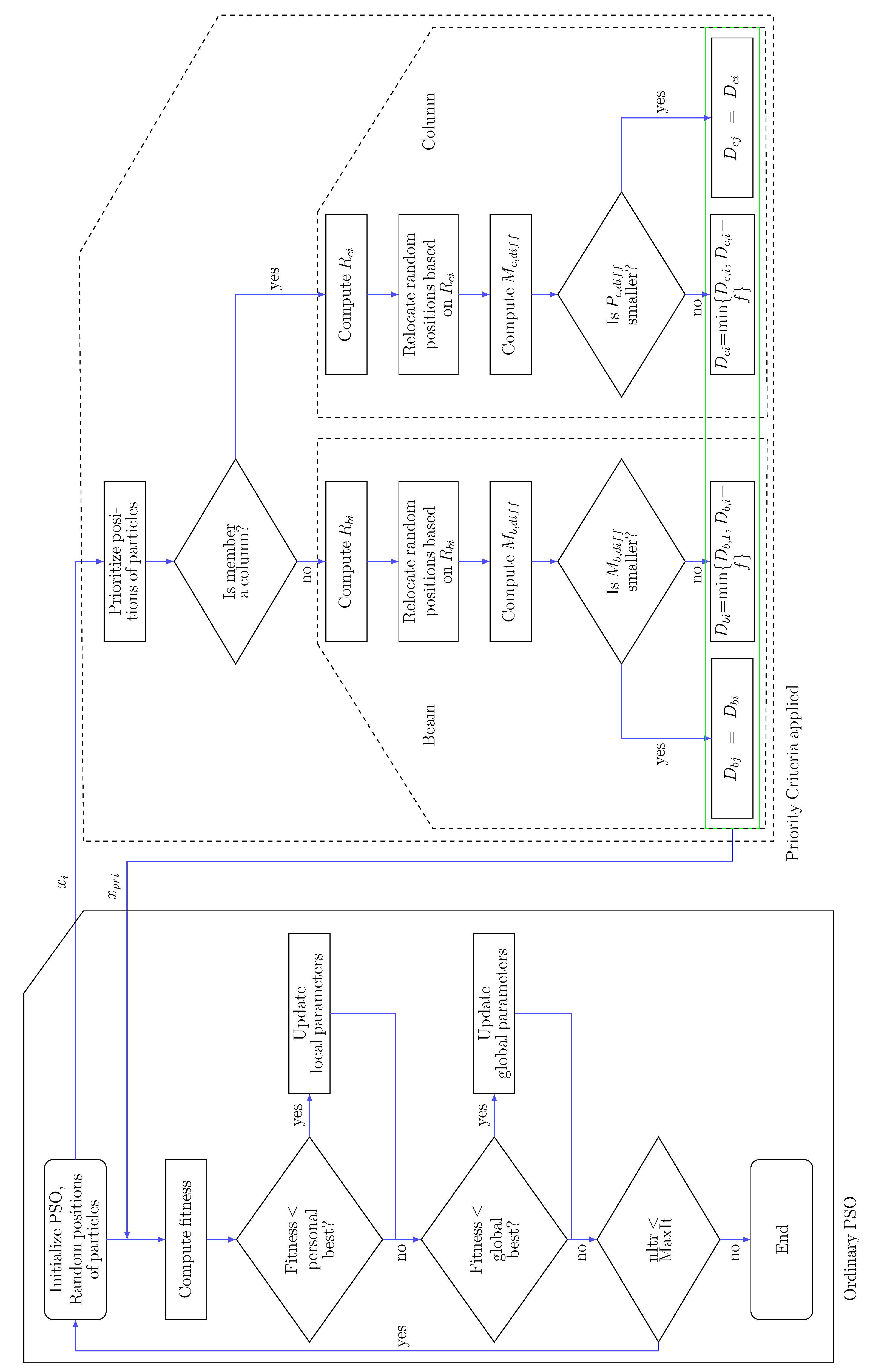
3. Priority Criteria (PC) and Priority Criteria PSO (PCPSO)
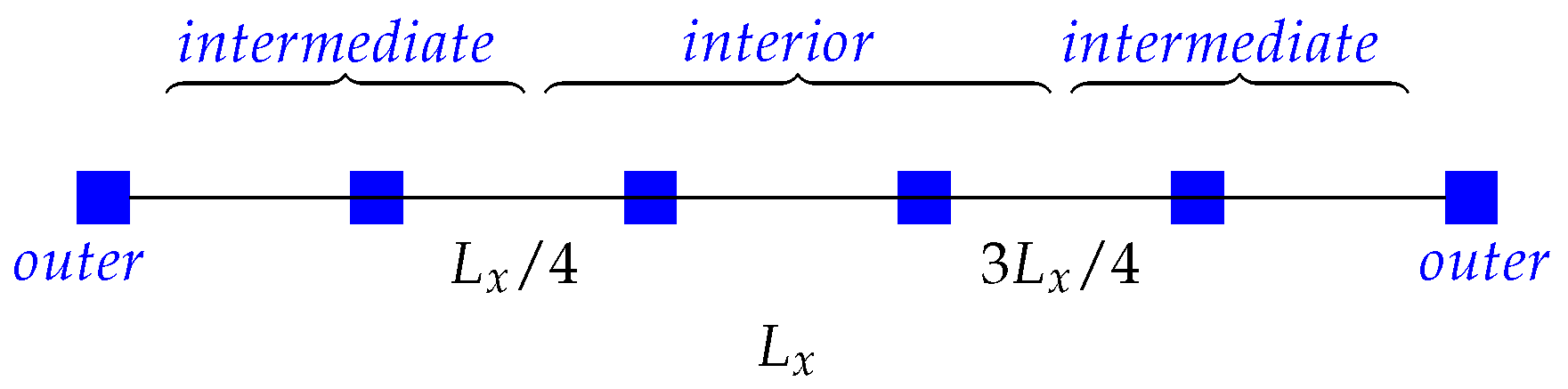
3.1. The Need for Priority
3.2. Priority Criteria (PC) Formulation
3.3. Objective Function Formulation
3.4. Setting Constraints
3.4.1. Beam Constraints
3.4.2. Column Constraints
3.5. Constraint Handling
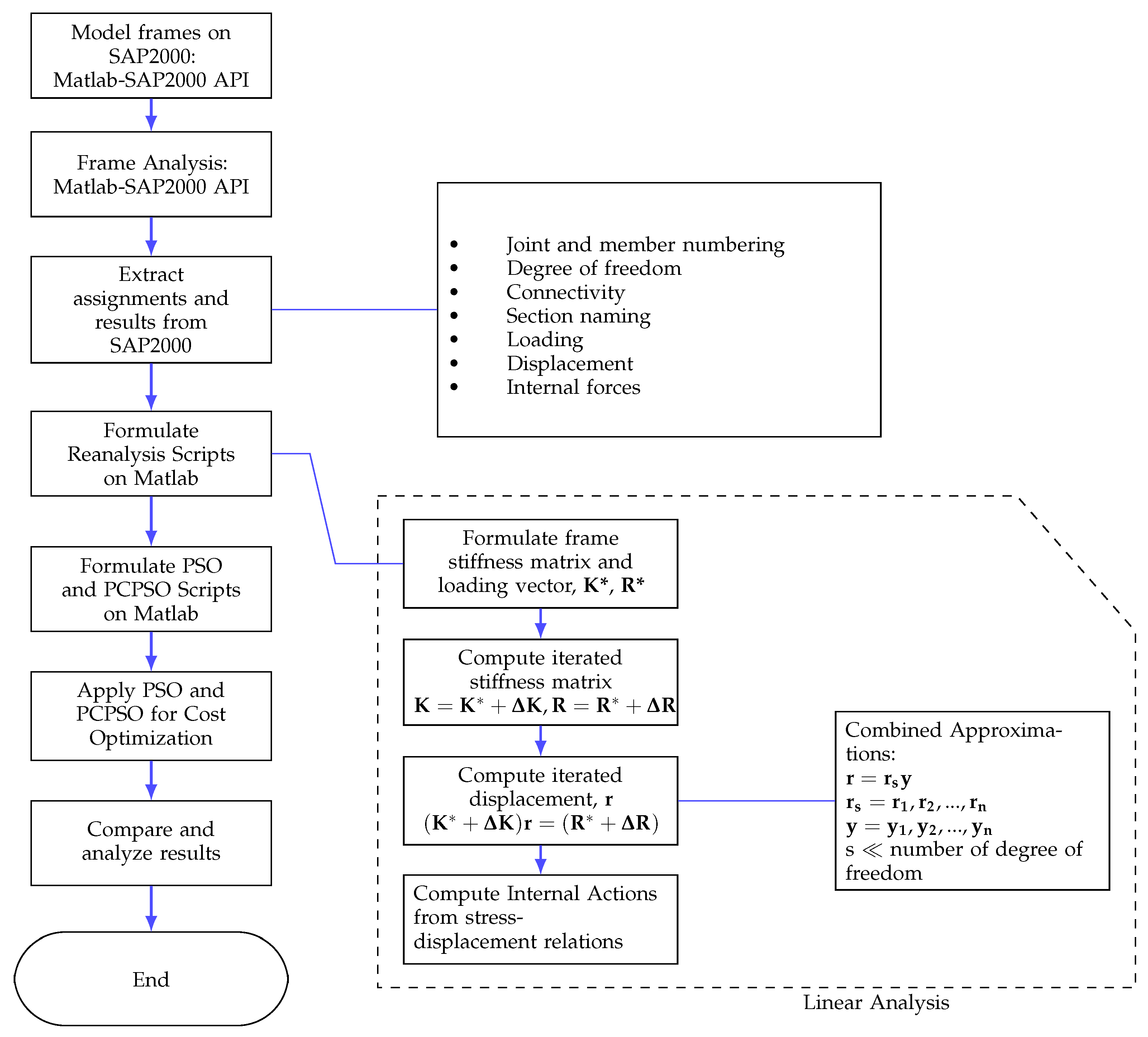
4. Analysis Approach
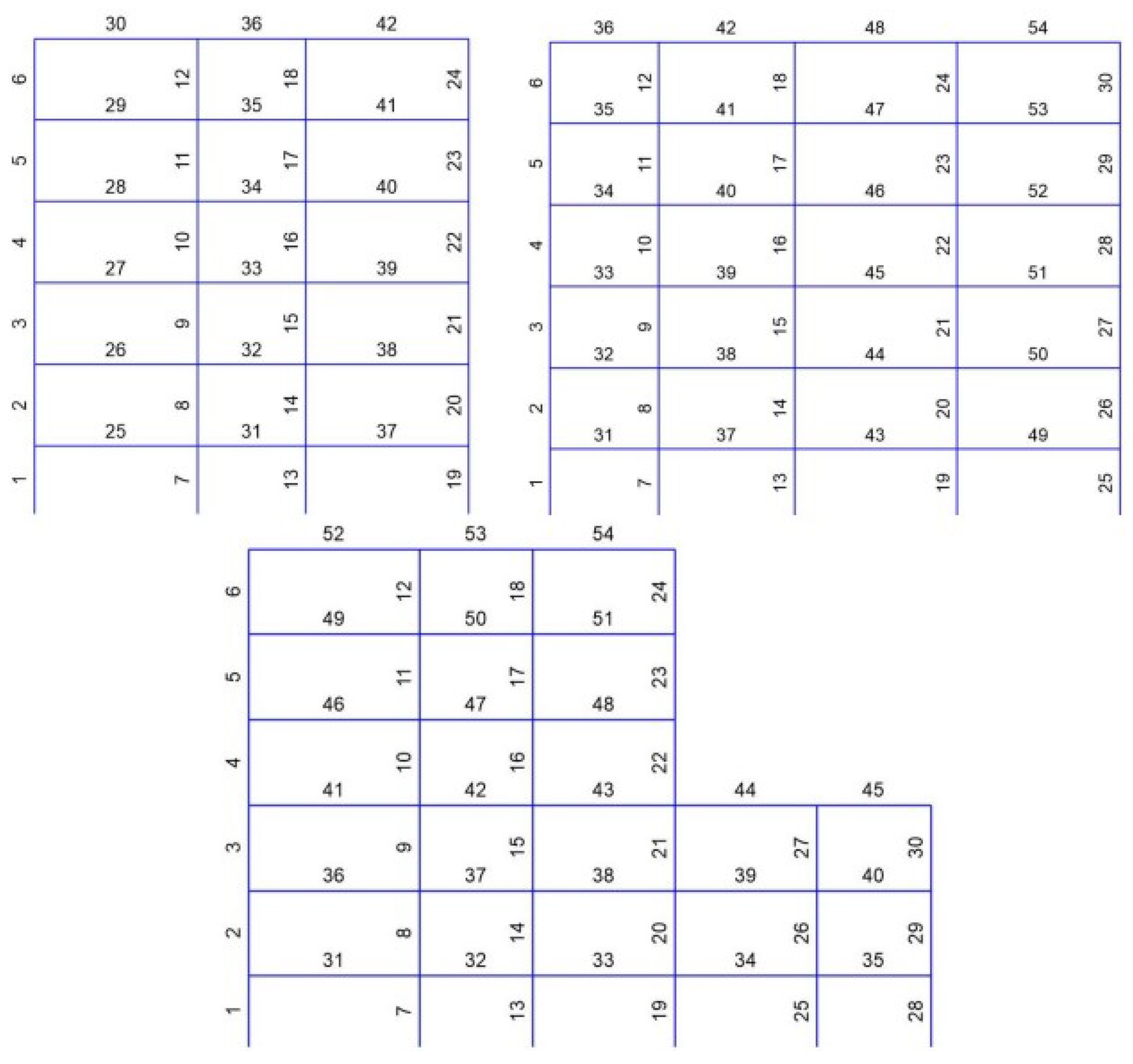
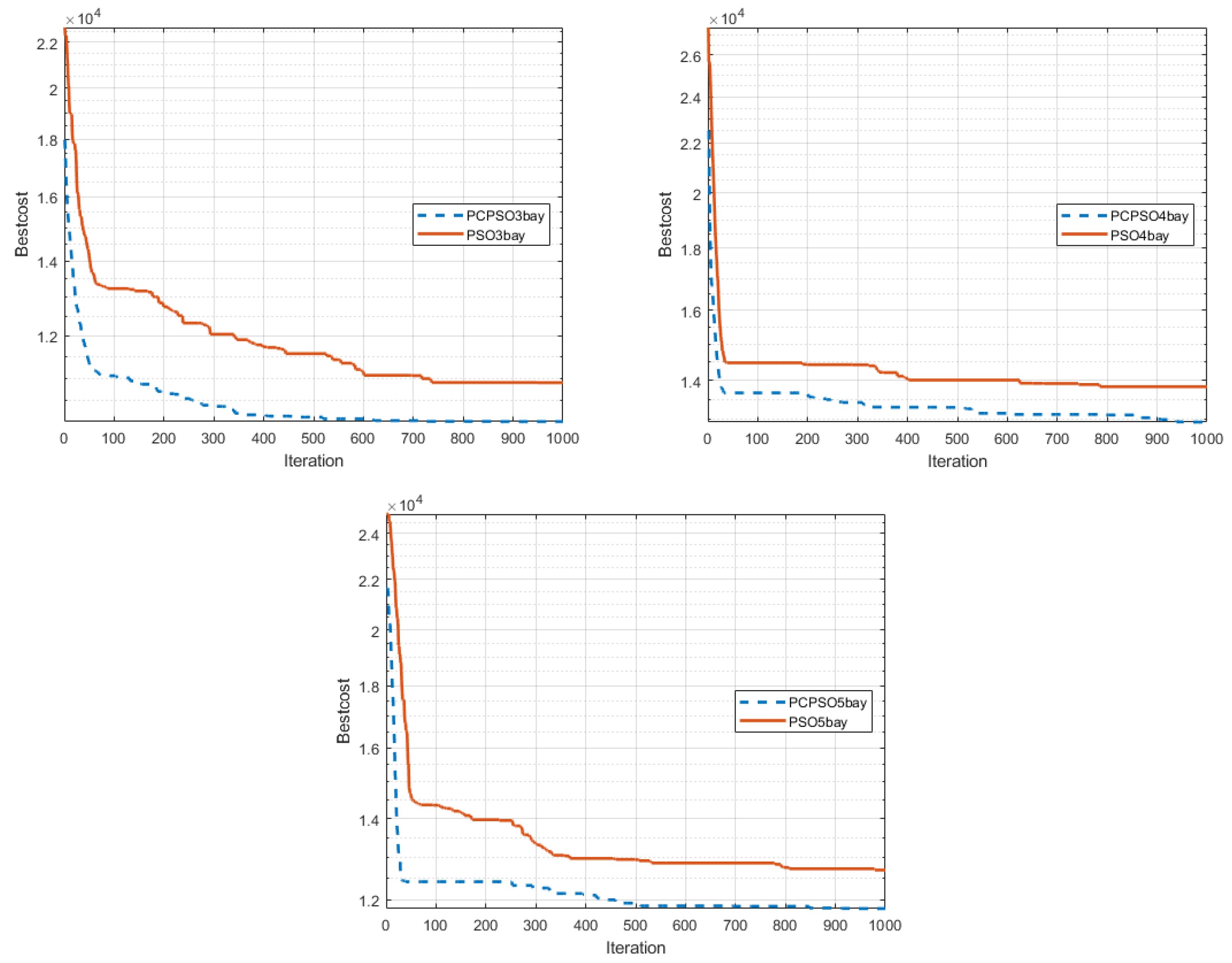
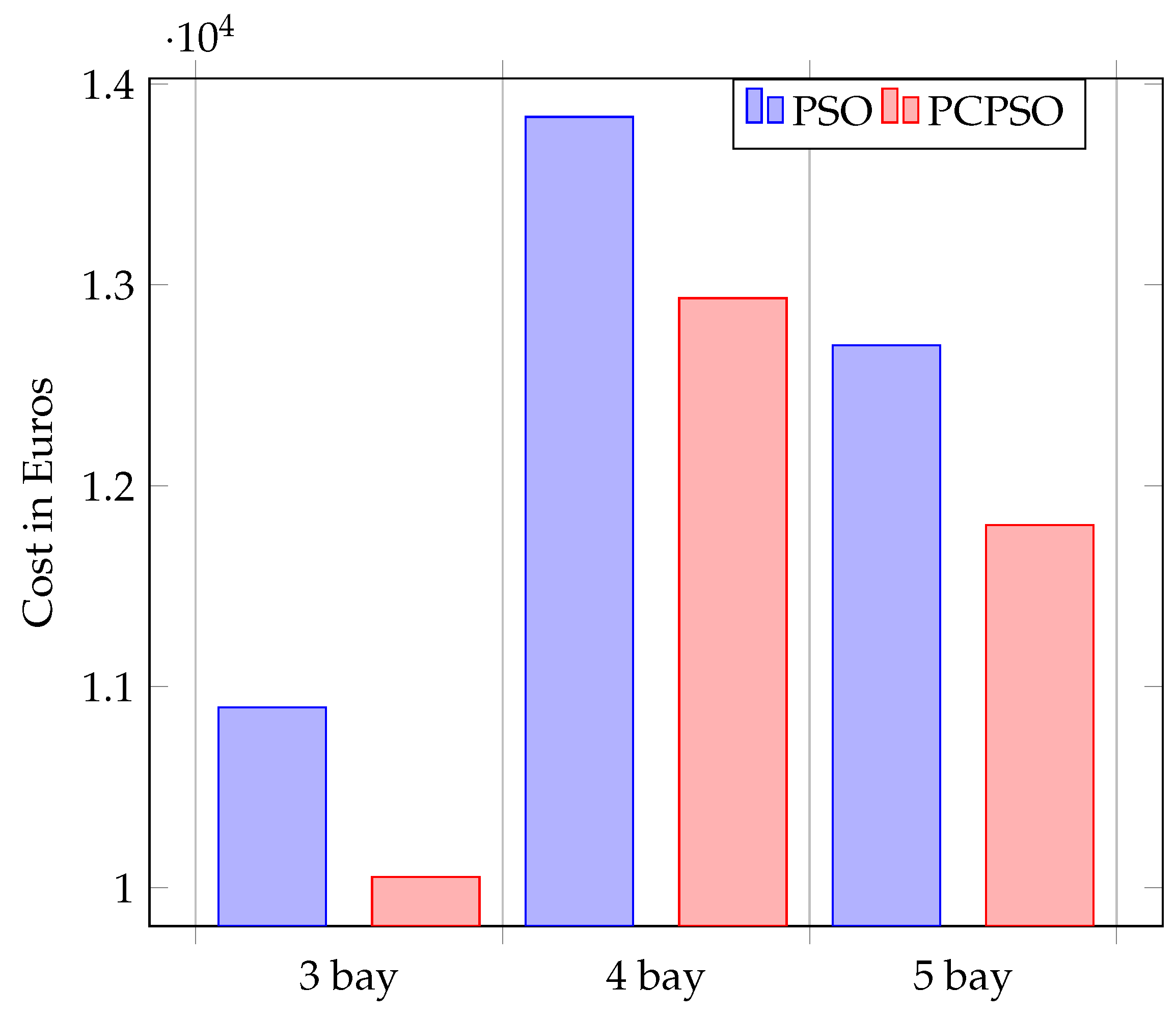
5. Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CA | Combined Approximations |
| PCPSO | Priority Criteria Particle Swarm Optimization |
| PSO | Particle Swarm Optimization |
| RC | Reinforced Concrete |
| area of formwork for beam, column | |
| Area of reinforcement | |
| width of beam, column | |
| cost of beam, column | |
| unit rate of concrete, formwork, reinforcement | |
| interior, intermediate, outer column | |
| penalty factor | |
| depth of beam, column | |
| effective depth of beam, column | |
| design load | |
| workable size difference of sections | |
| objective function unconstrained, constrained | |
| design strength of concrete, reinforcement | |
| constraint of beam, column | |
| inequality constraint | |
| permanent actions | |
| constraint function | |
| length of a beam, column | |
| m | design strength ratio of reinforcement to concrete divided by |
| design moment of beam, column | |
| beam moment difference | |
| moment capacity of beam, column | |
| number of beams | |
| design axial of a column | |
| column moment difference | |
| axial capacity of a column | |
| variable actions | |
| priority rank of beam, column | |
| design shear of a beam | |
| shear capacity of a beam | |
| volume of concrete for beam, column | |
| externally applied load on a beam | |
| weight of reinforcement for beam, column | |
| allowed constraint limit | |
| slenderness ratio for sway, non sway frames | |
| beam deflection | |
| column reinforcement diameter longitudinal shear | |
| reinforcement to section ratio | |
| balanced reinforcement to section ratio | |
| actions factors for permanent, variable actions | |
| moment, shear, axial reduction factor |
References
- McCarthy, T.J.; McCluskey, S. A particle swarm optimisation approach to reinforced concrete beam design according to AS3600. In Proceedings of the 1st International Conference on Soft Computing Technology in Civil, Structural and Environmental Engineering, Orlando, FL, USA, 12–14 September 2021; University of Wollongong: Wollongong, Australia, 2009. [Google Scholar]
- Qin, H.; Guo, Y.; Liu, Z.; Liu, Y.; Zhong, H. Shape optimization of automotive body frame using an improved genetic algorithm optimizer. Adv. Eng. Softw. 2018, 121, 235–249. [Google Scholar] [CrossRef]
- Greco, A.; Pluchino, A.; Cannizzaro, F. An improved ant colony optimization algorithm and its applications to limit analysis of frame structures. Eng. Optim. 2019, 51, 1867–1883. [Google Scholar] [CrossRef]
- Doğan, E.; Saka, M.P. Optimum design of unbraced steel frames to LRFD–AISC using particle swarm optimization. Adv. Eng. Softw. 2012, 46, 27–34. [Google Scholar] [CrossRef]
- Yildiz, A.R. Comparison of evolutionary-based optimization algorithms for structural design optimization. Eng. Appl. Artif. Intell. 2013, 26, 327–333. [Google Scholar] [CrossRef]
- Paya, I.; Yepes, V.; González-Vidosa, F.; Hospitaler, A. Multiobjective optimization of concrete frames by simulated annealing. Comput.-Aided Civ. Infrastruct. Eng. 2008, 23, 596–610. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Huynh, N.T.; Nguyen, T.V.; Nguyen, Q.M. Optimum Design for the Magnification Mechanisms Employing Fuzzy Logic-ANFIS. Comput. Mater. Contin. 2022, 73, 5961–5983. [Google Scholar]
- Huynh, N.T.; Nguyen, T.V.; Tam, N.T.; Nguyen, Q.M. Optimizing Magnification Ratio for the Flexible Hinge Displacement Amplifier Mechanism Design. In Proceedings of the 2nd Annual International Conference on Material, Machines and Methods for Sustainable Development (MMMS2020), Nha Trang, Vietnam, 12–15 November 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 769–778. [Google Scholar]
- Tsiptsis, I.N.; Liimatainen, L.; Kotnik, T.; Niiranen, J. Structural optimization employing isogeometric tools in Particle Swarm Optimizer. J. Build. Eng. 2019, 24, 100761. [Google Scholar] [CrossRef]
- Perez, R.E.; Behdinan, K. Particle swarm optimization in structural design. Swarm Intell. Focus Ant Part. Swarm Optim. 2007, 532, 1579–1588. [Google Scholar] [CrossRef]
- Elbes, M.; Alzubi, S.; Kanan, T.; Al-Fuqaha, A.; Hawashin, B. A survey on particle swarm optimization with emphasis on engineering and network applications. Evol. Intell. 2019, 12, 113–129. [Google Scholar] [CrossRef]
- Jain, N.; Nangia, U.; Jain, J. A review of particle swarm optimization. J. Inst. Eng. Ser. B 2018, 99, 407–411. [Google Scholar] [CrossRef]
- Barman, S.K.; Maiti, D.K.; Maity, D. Damage detection of truss employing swarm-based optimization techniques: A comparison. In Advanced Engineering Optimization through Intelligent Techniques; Springer: Berlin/Heidelberg, Germany, 2020; pp. 21–37. [Google Scholar]
- Omidinasab, F.; Goodarzimehr, V. A hybrid particle swarm optimization and genetic algorithm for truss structures with discrete variables. J. Appl. Comput. Mech. 2020, 6, 593–604. [Google Scholar]
- Sun, Y.; Li, H.; Shabaz, M.; Sharma, A. Research on building truss design based on particle swarm intelligence optimization algorithm. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 38–48. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Prayogo, D.; Wu, Y.W.; Lukito, M.M. A Hybrid Harmony Search algorithm for discrete sizing optimization of truss structure. Autom. Constr. 2016, 69, 21–33. [Google Scholar] [CrossRef]
- Khaledy, N.; Habibi, A.; Memarzadeh, P. A Comparison between different techniques for optimum design of steel frames subjected to blast. Lat. Am. J. Solids Struct. 2018, 15, 9. [Google Scholar] [CrossRef]
- Aloysius, J.; Sumito, J.; Prayogo, D.; Santoso, H. Optimization of concentrically braced steel frame structures based on SNI 1726: 2019, SNI 1727: 2020, SNI 1729: 2020, and AISC 341-16. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 907, p. 012010. [Google Scholar]
- Van, T.H.; Tangaramvong, S.; Limkatanyu, S.; Xuan, H.N. Two-phase ESO and comprehensive learning PSO method for structural optimization with discrete steel sections. Adv. Eng. Softw. 2022, 167, 103102. [Google Scholar] [CrossRef]
- Barg, S.; Flager, F.; Fischer, M. A design-focused, cost-ranked, structural-frame sizing optimization. J. Build. Eng. 2020, 30, 101269. [Google Scholar] [CrossRef]
- Boscardin, J.T.; Yepes, V.; Kripka, M. Optimization of reinforced concrete building frames with automated grouping of columns. Autom. Constr. 2019, 104, 331–340. [Google Scholar] [CrossRef]
- Varaee, H.; Ahmadi-Nedushan, B. Minimum cost design of concrete slabs using particle swarm optimization with time varying acceleration coefficients. World Appl. Sci. J. 2011, 13, 2484–2494. [Google Scholar]
- Chutani, S.; Singh, J. Design optimization of reinforced concrete beams. J. Inst. Eng. Ser. A 2017, 98, 429–435. [Google Scholar] [CrossRef]
- Chutani, S.; Singh, J. Evaluation of enhanced particle swarm optimization techniques for design of RC structural elements. J. Mater. Eng. Struct. JMES 2017, 4, 65–78. [Google Scholar]
- Esfandiari, M.J.; Urgessa, G.S.; Sheikholarefin, S.; Manshadi, S.D. Optimum design of 3D reinforced concrete frames using DMPSO algorithm. Adv. Eng. Softw. 2018, 115, 149–160. [Google Scholar] [CrossRef]
- Chegini, S.N.; Bagheri, A.; Najafi, F. PSOSCALF: A new hybrid PSO based on Sine Cosine Algorithm and Levy flight for solving optimization problems. Appl. Soft Comput. 2018, 73, 697–726. [Google Scholar] [CrossRef]
- Aote, S.S.; Raghuwanshi, M.; Malik, L. A brief review on particle swarm optimization: Limitations & future directions. Int. J. Comput. Sci. Eng. 2013, 14, 196–200. [Google Scholar]
- Peng, J.; Li, Y.; Kang, H.; Shen, Y.; Sun, X.; Chen, Q. Impact of population topology on particle swarm optimization and its variants: An information propagation perspective. Swarm Evol. Comput. 2022, 69, 100990. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Population size in particle swarm optimization. Swarm Evol. Comput. 2020, 58, 100718. [Google Scholar] [CrossRef]
- Ghasemi, M.; Akbari, E.; Rahimnejad, A.; Razavi, S.E.; Ghavidel, S.; Li, L. Phasor particle swarm optimization: A simple and efficient variant of PSO. Soft Comput. 2019, 23, 9701–9718. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures. Comput. Struct. 2009, 87, 267–283. [Google Scholar] [CrossRef]
- Devi, S.; Garg, D. Hybrid genetic and particle swarm algorithm: Redundancy allocation problem. Int. J. Syst. Assur. Eng. Manag. 2020, 11, 313–319. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Cheng, C.T.; Zhou, J.Z. Forecasting daily runoff by extreme learning machine based on quantum-behaved particle swarm optimization. J. Hydrol. Eng. 2018, 23, 04018002. [Google Scholar] [CrossRef]
- Wang, R.; Hao, K.; Chen, L.; Wang, T.; Jiang, C. A novel hybrid particle swarm optimization using adaptive strategy. Inf. Sci. 2021, 579, 231–250. [Google Scholar] [CrossRef]
- Wang, Y.; Li, B.; Weise, T.; Wang, J.; Yuan, B.; Tian, Q. Self-adaptive learning based particle swarm optimization. Inf. Sci. 2011, 181, 4515–4538. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Umar, T.; Tahir, A.; Umeokafor, N.; Nawarathna, A.; Zia, A.; Vali, M. An experimental investigation on strength characteristics of concrete using Wastepaper Sludge Ash (WPSA). In Proceedings of the 12th International Conference on Construction in the 21st Century (CITC-12), CITC Global, Amman, Jordan, 16–19 May 2022; pp. 130–137. [Google Scholar]
- Zia, A.; Pu, Z.; Holly, I.; Umar, T.; Tariq, M.A.U.R.; Sufian, M. A comprehensive review of incorporating steel fibers of waste tires in cement composites and its applications. Materials 2022, 15, 7420. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Ochoa, D.D.; Pérez-Domínguez, L.A.; Martínez-Gómez, E.A.; Luviano-Cruz, D. PSO, a swarm intelligence-based evolutionary algorithm as a decision-making strategy: A review. Symmetry 2022, 14, 455. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Jaouadi, Z.; Abbas, T.; Morgenthal, G.; Lahmer, T. Single and multi-objective shape optimization of streamlined bridge decks. Struct. Multidiscip. Optim. 2020, 61, 1495–1514. [Google Scholar] [CrossRef]
- Standard, B. Eurocode 2: Design of Concrete Structures. Part 1; European Commission: Singapore, 2004; Volume 1, p. 230. [Google Scholar]
- Datta, R.; Deb, K. An adaptive normalization based constrained handling methodology with hybrid bi-objective and penalty function approach. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Coello, C.A.C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Kirsch, U. Reanalysis and sensitivity reanalysis by combined approximations. Struct. Multidiscip. Optim. 2010, 40, 1–15. [Google Scholar] [CrossRef]
- Kirsch, U. Combined approximations—A general reanalysis approach for structural optimization. Struct. Multidiscip. Optim. 2000, 20, 97–106. [Google Scholar] [CrossRef]
- The European Union. 1-1: 2002 Eurocode 1. Actions on Structures. General Actions. Densities, Self-Weight, Imposed Loads for Buildings BSI. 1991. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1991.1.1.2002.pdf (accessed on 2 June 2023).
- Standard, B. Eurocode—Basis of Structural Design. Eurocode 0. 2002. Available online: https://www.diies.unirc.it/documentazione/materiale_didattico/599_2010_260_7481.pdf (accessed on 2 June 2023).


| Type of Action | Description | Amount in kNm | Amount in kNm |
|---|---|---|---|
| Transferred from a 6 m square slab | 3.75 | 5.625 | |
| Transferred from a floor finish | 1.15 | 1.725 | |
| Permanent | Partition wall on the beam | - | 7.5 |
| Beam and Column self-weights | - | Program Computed | |
| Variable | Action on the slab | 2 | 3 |
| Section (m) | Reinft (D in mm, Stirrup D8) | Section (m) | Reinft (D in mm) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beam ID | PSO | PCPSO | PSO | PCPSO | Col. ID | PSO | PCPSO | PSO | PCPSO | ||||||||||
| D | W | D | W | Neg | Pos | C/C | Neg | Pos | C/C | D | W | D | W | Axial | C/C | Axial | C/C | ||
| 25 | 0.5 | 0.35 | 0.4 | 0.3 | 3D16 | 2D16 | 100 | 3D16 | 2D16 | 100 | 1 | 0.45 | 0.3 | 0.35 | 0.3 | 6D8 | 250 | 6D10 | 200 |
| 26 | 0.5 | 0.3 | 0.4 | 0.3 | 3D16 | 2D16 | 100 | 3D16 | 2D16 | 100 | 2 | 0.4 | 0.3 | 0.35 | 0.3 | 4D8 | 160 | 4D8 | 230 |
| 27 | 0.45 | 0.3 | 0.4 | 0.25 | 3D16 | 2D16 | 100 | 3D16 | 2D16 | 100 | 3 | 0.4 | 0.3 | 0.35 | 0.25 | 4D8 | 100 | 4D8 | 220 |
| 28 | 0.45 | 0.3 | 0.35 | 0.25 | 3D16 | 2D16 | 120 | 3D16 | 2D14 | 130 | 4 | 0.4 | 0.3 | 0.35 | 0.25 | 4D8 | 100 | 4D8 | 200 |
| 29 | 0.45 | 0.3 | 0.3 | 0.25 | 3D16 | 2D16 | 100 | 3D16 | 2D14 | 120 | 5 | 0.4 | 0.3 | 0.35 | 0.25 | 4D8 | 160 | 4D8 | 210 |
| 30 | 0.4 | 0.3 | 0.35 | 0.25 | 4D16 | 2D16 | 100 | 3D16 | 2D14 | 130 | 6 | 0.4 | 0.3 | 0.3 | 0.25 | 4D8 | 160 | 4D8 | 210 |
| 31 | 0.4 | 0.3 | 0.3 | 0.25 | 2D12 | 2D12 | 200 | 2D16 | 2D12 | 100 | 7 | 0.35 | 0.25 | 0.4 | 0.3 | 6D8 | 160 | 6D8 | 160 |
| 32 | 0.4 | 0.3 | 0.3 | 0.25 | 2D14 | 2D12 | 130 | 2D16 | 2D12 | 100 | 8 | 0.35 | 0.25 | 0.35 | 0.3 | 6D8 | 160 | 4D8 | 160 |
| 33 | 0.4 | 0.25 | 0.3 | 0.25 | 2D12 | 2D12 | 190 | 2D12 | 2D12 | 160 | 9 | 0.35 | 0.25 | 0.35 | 0.3 | 6D8 | 230 | 4D8 | 240 |
| 34 | 0.35 | 0.25 | 0.3 | 0.25 | 2D12 | 2D12 | 120 | 2D16 | 2D12 | 100 | 10 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 220 | 4D8 | 210 |
| 35 | 0.35 | 0.25 | 0.3 | 0.25 | 3D12 | 2D12 | 190 | 2D16 | 2D12 | 100 | 11 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 250 | 4D8 | 220 |
| 36 | 0.35 | 0.25 | 0.3 | 0.25 | 2D12 | 2D12 | 190 | 2D16 | 2D12 | 100 | 12 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 160 | 4D8 | 210 |
| 37 | 0.35 | 0.25 | 0.3 | 0.25 | 3D20 | 3D16 | 100 | 2D20 | 3D16 | 100 | 13 | 0.35 | 0.25 | 0.35 | 0.3 | 6D8 | 190 | 4D8 | 250 |
| 38 | 0.35 | 0.25 | 0.3 | 0.25 | 3D20 | 3D16 | 100 | 4D16 | 2D16 | 100 | 14 | 0.35 | 0.25 | 0.35 | 0.3 | 6D8 | 220 | 4D8 | 250 |
| 39 | 0.35 | 0.25 | 0.3 | 0.25 | 3D16 | 4D20 | 100 | 4D20 | 4D20 | 240 | 15 | 0.35 | 0.25 | 0.35 | 0.3 | 4D8 | 220 | 4D8 | 230 |
| 40 | 0.35 | 0.25 | 0.3 | 0.25 | 4D20 | 3D16 | 100 | 4D16 | 2D16 | 100 | 16 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 210 | 4D8 | 220 |
| 41 | 0.35 | 0.25 | 0.35 | 0.25 | 4D20 | 3D16 | 100 | 4D16 | 2D16 | 100 | 17 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 210 | 4D8 | 210 |
| 42 | 0.35 | 0.25 | 0.3 | 0.25 | 3D16 | 2D16 | 100 | 3D16 | 2D16 | 100 | 18 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 210 | 4D8 | 210 |
| 19 | 0.35 | 0.25 | 0.35 | 0.3 | 6D8 | 200 | 6D8 | 230 | |||||||||||
| 20 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 200 | 4D8 | 230 | |||||||||||
| 21 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 140 | 4D8 | 190 | |||||||||||
| 22 | 0.3 | 0.25 | 0.35 | 0.25 | 4D8 | 140 | 4D8 | 120 | |||||||||||
| 23 | 0.3 | 0.25 | 0.35 | 0.25 | 4D8 | 210 | 4D8 | 210 | |||||||||||
| 24 | 0.3 | 0.25 | 0.3 | 0.25 | 4D8 | 210 | 4D8 | 200 | |||||||||||
| Section (m) | Reinft (D in mm, Stirrup D8) | Section (m) | Reinft (D in mm) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beam ID | PSO | PCPSO | PSO | PCPSO | Col. ID | PSO | PCPSO | PSO | PCPSO | ||||||||||
| D | W | D | W | Neg | Pos | C/C | Neg | Pos | C/C | D | W | D | W | Axial | C/C | Axial | C/C | ||
| 31 | 0.5 | 0.3 | 0.3 | 0.25 | 2D12 | 2D12 | 170 | 2D14 | 2D16 | 120 | 1 | 0.45 | 0.35 | 0.35 | 0.25 | 6D10 | 270 | 4D8 | 220 |
| 32 | 0.45 | 0.3 | 0.3 | 0.25 | 2D14 | 2D12 | 160 | 2D16 | 2D14 | 100 | 2 | 0.45 | 0.3 | 0.35 | 0.25 | 6D10 | 180 | 4D8 | 210 |
| 33 | 0.4 | 0.3 | 0.3 | 0.25 | 2D14 | 2D12 | 170 | 2D16 | 2D14 | 100 | 3 | 0.45 | 0.3 | 0.35 | 0.25 | 6D10 | 160 | 4D8 | 200 |
| 34 | 0.4 | 0.3 | 0.3 | 0.25 | 2D12 | 2D12 | 210 | 2D16 | 2D14 | 100 | 4 | 0.45 | 0.3 | 0.35 | 0.25 | 4D8 | 100 | 4D8 | 180 |
| 35 | 0.4 | 0.3 | 0.3 | 0.25 | 2D14 | 2D12 | 160 | 2D16 | 2D14 | 100 | 5 | 0.4 | 0.3 | 0.3 | 0.25 | 4D8 | 180 | 4D8 | 210 |
| 36 | 0.4 | 0.3 | 0.3 | 0.25 | 2D14 | 3D12 | 160 | 2D16 | 2D14 | 100 | 6 | 0.4 | 0.3 | 0.3 | 0.25 | 4D8 | 270 | 4D8 | 210 |
| 37 | 0.4 | 0.3 | 0.35 | 0.25 | 3D14 | 2D14 | 110 | 4D14 | 3D14 | 100 | 7 | 0.4 | 0.3 | 0.35 | 0.25 | 6D10 | 170 | 6D8 | 230 |
| 38 | 0.4 | 0.3 | 0.35 | 0.25 | 2D16 | 2D14 | 130 | 4D14 | 3D14 | 100 | 8 | 0.4 | 0.3 | 0.35 | 0.25 | 6D10 | 160 | 4D8 | 230 |
| 39 | 0.4 | 0.25 | 0.35 | 0.25 | 3D14 | 2D14 | 110 | 4D14 | 2D14 | 100 | 9 | 0.4 | 0.3 | 0.35 | 0.25 | 6D10 | 160 | 4D8 | 220 |
| 40 | 0.4 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 140 | 3D16 | 2D16 | 100 | 10 | 0.4 | 0.3 | 0.35 | 0.25 | 4D8 | 210 | 4D8 | 220 |
| 41 | 0.4 | 0.25 | 0.3 | 0.25 | 3D16 | 2D16 | 100 | 3D16 | 2D16 | 100 | 11 | 0.4 | 0.3 | 0.35 | 0.25 | 4D8 | 250 | 4D8 | 210 |
| 42 | 0.4 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 140 | 3D16 | 2D16 | 100 | 12 | 0.35 | 0.3 | 0.3 | 0.25 | 4D8 | 250 | 4D8 | 210 |
| 43 | 0.35 | 0.25 | 0.4 | 0.25 | 3D20 | 3D16 | 100 | 2D20 | 2D16 | 100 | 13 | 0.35 | 0.3 | 0.4 | 0.3 | 6D8 | 160 | 6D8 | 240 |
| 44 | 0.35 | 0.25 | 0.35 | 0.25 | 3D14 | 2D16 | 110 | 3D16 | 2D16 | 100 | 14 | 0.35 | 0.3 | 0.35 | 0.3 | 6D8 | 250 | 4D8 | 160 |
| 45 | 0.35 | 0.25 | 0.35 | 0.25 | 3D20 | 3D16 | 100 | 3D20 | 3D16 | 100 | 15 | 0.35 | 0.3 | 0.35 | 0.3 | 6D8 | 240 | 4D8 | 230 |
| 46 | 0.35 | 0.25 | 0.4 | 0.25 | 3D20 | 3D16 | 100 | 3D16 | 2D16 | 100 | 16 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 190 | 4D8 | 220 |
| 47 | 0.35 | 0.25 | 0.35 | 0.25 | 3D20 | 3D16 | 100 | 3D16 | 2D16 | 100 | 17 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 230 | 4D8 | 220 |
| 48 | 0.35 | 0.25 | 0.4 | 0.25 | 3D20 | 3D16 | 100 | 2D20 | 2D16 | 100 | 18 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 230 | 4D8 | 210 |
| 49 | 0.35 | 0.25 | 0.35 | 0.25 | 4D20 | 3D16 | 100 | 3D20 | 3D16 | 100 | 19 | 0.35 | 0.25 | 0.4 | 0.25 | 6D8 | 230 | 6D8 | 250 |
| 50 | 0.35 | 0.25 | 0.35 | 0.25 | 4D20 | 3D16 | 100 | 3D20 | 3D16 | 100 | 20 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 230 | 4D8 | 160 |
| 51 | 0.35 | 0.25 | 0.35 | 0.25 | 3D16 | 2D16 | 100 | 3D20 | 3D16 | 100 | 21 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 200 | 4D8 | 230 |
| 52 | 0.3 | 0.25 | 0.35 | 0.25 | 3D20 | 3D20 | 100 | 3D16 | 4D20 | 100 | 22 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 210 | 4D8 | 220 |
| 53 | 0.3 | 0.25 | 0.35 | 0.25 | 4D20 | 3D16 | 100 | 3D16 | 2D16 | 100 | 23 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 200 | 4D8 | 220 |
| 54 | 0.3 | 0.25 | 0.35 | 0.25 | 4D20 | 3D16 | 100 | 3D16 | 2D16 | 100 | 24 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 210 | 4D8 | 190 |
| 25 | 0.35 | 0.25 | 0.35 | 0.3 | 6D8 | 210 | 6D8 | 210 | |||||||||||
| 26 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 210 | 6D8 | 210 | |||||||||||
| 27 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 210 | 6D8 | 170 | |||||||||||
| 28 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 140 | 4D8 | 210 | |||||||||||
| 29 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 210 | 4D8 | 200 | |||||||||||
| 30 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 210 | 4D8 | 190 | |||||||||||
| Section (m) | Reinft (D in mm, Stirrup D8) | Section (m) | Reinft (D in mm) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beam ID | PSO | PCPSO | PSO | PCPSO | Col. ID | PSO | PCPSO | PSO | PCPSO | ||||||||||
| D | W | D | W | Neg | Pos | C/C | Neg | Pos | C/C | D | W | D | W | Axial | C/C | Axial | C/C | ||
| 31 | 0.45 | 0.3 | 0.4 | 0.3 | 3D16 | 2D16 | 100 | 3D16 | 2D16 | 100 | 1 | 0.45 | 0.35 | 0.35 | 0.25 | 6D8 | 160 | 4D8 | 230 |
| 32 | 0.4 | 0.3 | 0.35 | 0.25 | 2D14 | 2D14 | 140 | 2D16 | 2D14 | 100 | 2 | 0.4 | 0.35 | 0.35 | 0.25 | 6D8 | 160 | 4D8 | 220 |
| 33 | 0.4 | 0.3 | 0.35 | 0.25 | 3D14 | 2D14 | 100 | 2D14 | 2D14 | 130 | 3 | 0.4 | 0.35 | 0.35 | 0.25 | 4D8 | 160 | 4D8 | 220 |
| 34 | 0.4 | 0.3 | 0.35 | 0.25 | 3D16 | 2D14 | 100 | 3D16 | 2D14 | 100 | 4 | 0.4 | 0.35 | 0.35 | 0.25 | 4D8 | 260 | 4D8 | 220 |
| 35 | 0.4 | 0.25 | 0.35 | 0.25 | 2D14 | 2D14 | 180 | 2D16 | 2D14 | 100 | 5 | 0.4 | 0.35 | 0.3 | 0.25 | 4D8 | 260 | 4D8 | 200 |
| 36 | 0.35 | 0.25 | 0.4 | 0.3 | 4D16 | 3D14 | 100 | 4D16 | 2D14 | 100 | 6 | 0.4 | 0.35 | 0.3 | 0.25 | 4D8 | 160 | 4D8 | 210 |
| 37 | 0.35 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 110 | 2D14 | 2D14 | 160 | 7 | 0.4 | 0.3 | 0.35 | 0.25 | 6D8 | 160 | 4D8 | 230 |
| 38 | 0.35 | 0.25 | 0.35 | 0.25 | 3D16 | 2D14 | 100 | 2D16 | 2D14 | 140 | 8 | 0.35 | 0.3 | 0.35 | 0.25 | 6D8 | 250 | 4D8 | 230 |
| 39 | 0.35 | 0.25 | 0.35 | 0.25 | 3D14 | 2D14 | 140 | 4D14 | 2D14 | 100 | 9 | 0.35 | 0.3 | 0.35 | 0.25 | 6D8 | 160 | 4D8 | 230 |
| 40 | 0.35 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 110 | 2D16 | 2D14 | 110 | 10 | 0.35 | 0.3 | 0.35 | 0.25 | 6D8 | 250 | 4D8 | 220 |
| 41 | 0.35 | 0.25 | 0.4 | 0.3 | 3D20 | 3D14 | 100 | 3D20 | 2D14 | 100 | 11 | 0.35 | 0.3 | 0.35 | 0.25 | 4D8 | 160 | 4D8 | 200 |
| 42 | 0.35 | 0.25 | 0.35 | 0.25 | 3D16 | 3D16 | 100 | 2D16 | 3D16 | 100 | 12 | 0.35 | 0.3 | 0.3 | 0.25 | 4D8 | 170 | 4D8 | 210 |
| 43 | 0.35 | 0.25 | 0.4 | 0.25 | 2D16 | 2D14 | 120 | 2D16 | 2D14 | 200 | 13 | 0.35 | 0.3 | 0.35 | 0.25 | 6D8 | 160 | 4D8 | 230 |
| 44 | 0.35 | 0.25 | 0.35 | 0.25 | 3D16 | 2D14 | 100 | 3D16 | 2D14 | 100 | 14 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 240 | 4D8 | 230 |
| 45 | 0.35 | 0.25 | 0.3 | 0.25 | 2D16 | 2D14 | 100 | 2D16 | 2D14 | 100 | 15 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 100 | 4D8 | 110 |
| 46 | 0.35 | 0.25 | 0.4 | 0.3 | 3D20 | 3D16 | 100 | 2D20 | 2D14 | 100 | 16 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 120 | 4D8 | 110 |
| 47 | 0.35 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 100 | 2D14 | 2D14 | 110 | 17 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 190 | 4D8 | 210 |
| 48 | 0.35 | 0.25 | 0.35 | 0.25 | 4D16 | 2D14 | 100 | 4D16 | 2D14 | 100 | 18 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 230 | 4D8 | 210 |
| 49 | 0.3 | 0.25 | 0.4 | 0.25 | 4D20 | 3D16 | 100 | 4D16 | 2D14 | 100 | 19 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 160 | 4D8 | 230 |
| 50 | 0.3 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 100 | 2D12 | 2D14 | 160 | 20 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 220 | 4D8 | 190 |
| 51 | 0.3 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 120 | 3D16 | 2D14 | 100 | 21 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 220 | 4D8 | 220 |
| 52 | 0.3 | 0.25 | 0.4 | 0.3 | 3D16 | 2D14 | 100 | 3D16 | 2D14 | 100 | 22 | 0.35 | 0.25 | 0.35 | 0.25 | 4D8 | 100 | 4D8 | 170 |
| 53 | 0.3 | 0.25 | 0.35 | 0.25 | 2D16 | 2D14 | 100 | 2D12 | 2D14 | 160 | 23 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 200 | 4D8 | 210 |
| 54 | 0.3 | 0.25 | 0.35 | 0.25 | 3D16 | 2D14 | 100 | 3D16 | 2D14 | 100 | 24 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 200 | 4D8 | 210 |
| 25 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 200 | 4D8 | 220 | |||||||||||
| 26 | 0.35 | 0.25 | 0.35 | 0.25 | 6D8 | 200 | 4D8 | 220 | |||||||||||
| 27 | 0.35 | 0.25 | 0.3 | 0.25 | 4D8 | 200 | 4D8 | 210 | |||||||||||
| 28 | 0.35 | 0.25 | 0.3 | 0.25 | 6D8 | 220 | 4D8 | 190 | |||||||||||
| 29 | 0.35 | 0.25 | 0.3 | 0.25 | 6D8 | 190 | 4D8 | 210 | |||||||||||
| 30 | 0.35 | 0.25 | 0.3 | 0.25 | 6D8 | 210 | 4D8 | 210 | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alemu, Y.L.; Habte, B.; Lahmer, T.; Urgessa, G. Priority Criteria (PC) Based Particle Swarm Optimization of Reinforced Concrete Frames (PCPSO). CivilEng 2023, 4, 679-701. https://doi.org/10.3390/civileng4020039
Alemu YL, Habte B, Lahmer T, Urgessa G. Priority Criteria (PC) Based Particle Swarm Optimization of Reinforced Concrete Frames (PCPSO). CivilEng. 2023; 4(2):679-701. https://doi.org/10.3390/civileng4020039
Chicago/Turabian StyleAlemu, Yohannes L., Bedilu Habte, Tom Lahmer, and Girum Urgessa. 2023. "Priority Criteria (PC) Based Particle Swarm Optimization of Reinforced Concrete Frames (PCPSO)" CivilEng 4, no. 2: 679-701. https://doi.org/10.3390/civileng4020039
APA StyleAlemu, Y. L., Habte, B., Lahmer, T., & Urgessa, G. (2023). Priority Criteria (PC) Based Particle Swarm Optimization of Reinforced Concrete Frames (PCPSO). CivilEng, 4(2), 679-701. https://doi.org/10.3390/civileng4020039








