Experimental Seismic Evaluation of Novel Buckling-Restrained Braced Frames Containing Tire-Derived Aggregate Concrete
Abstract
1. Introduction
2. Experimental Procedure
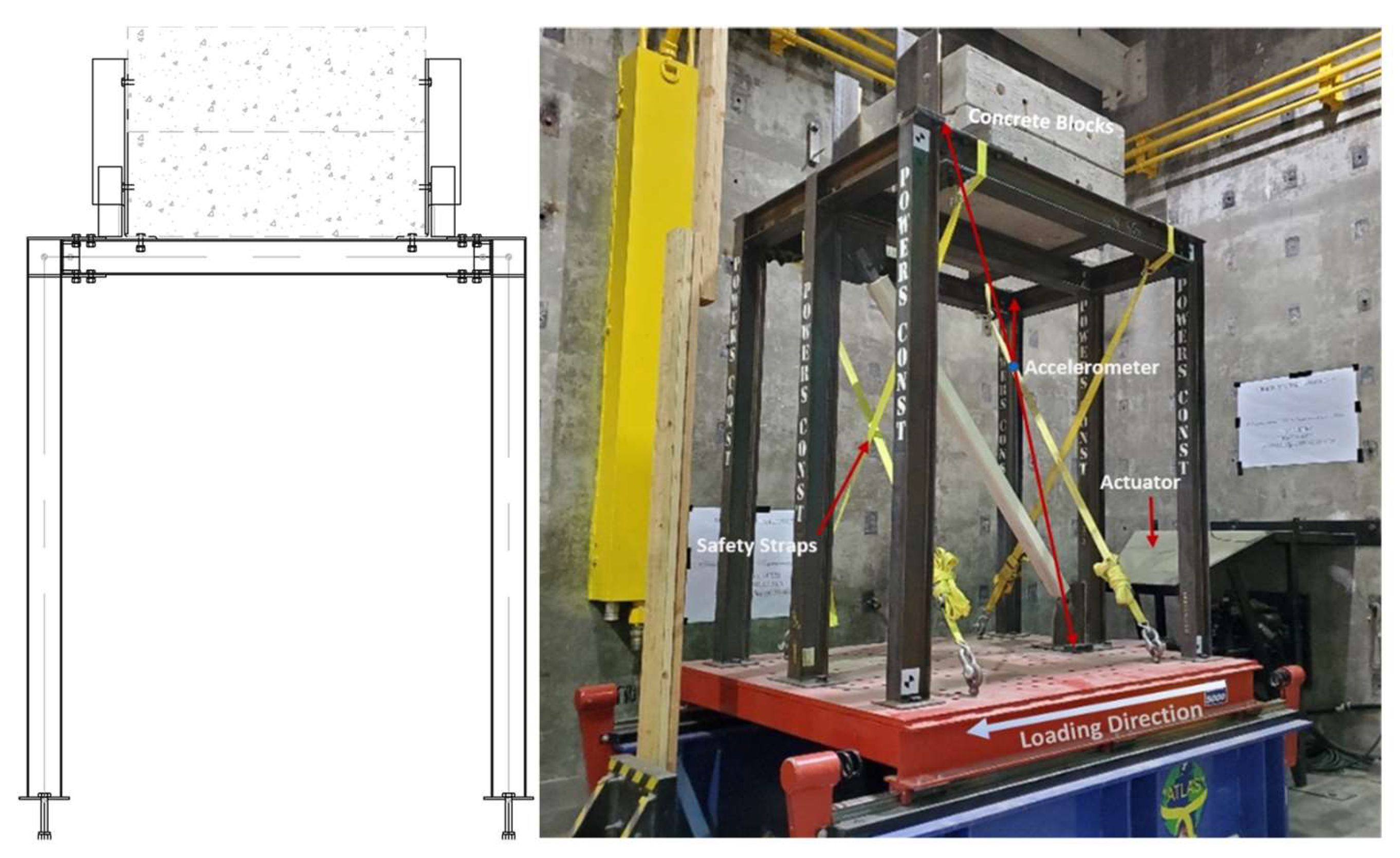
2.1. Shake Table
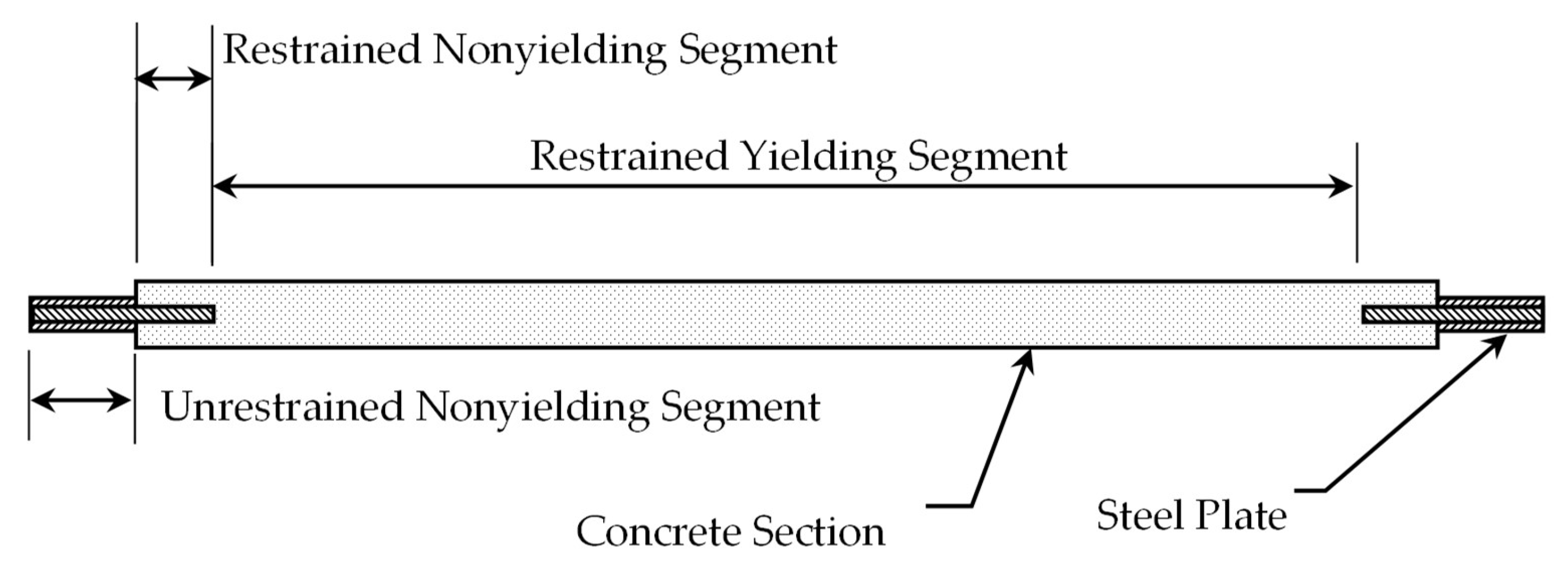
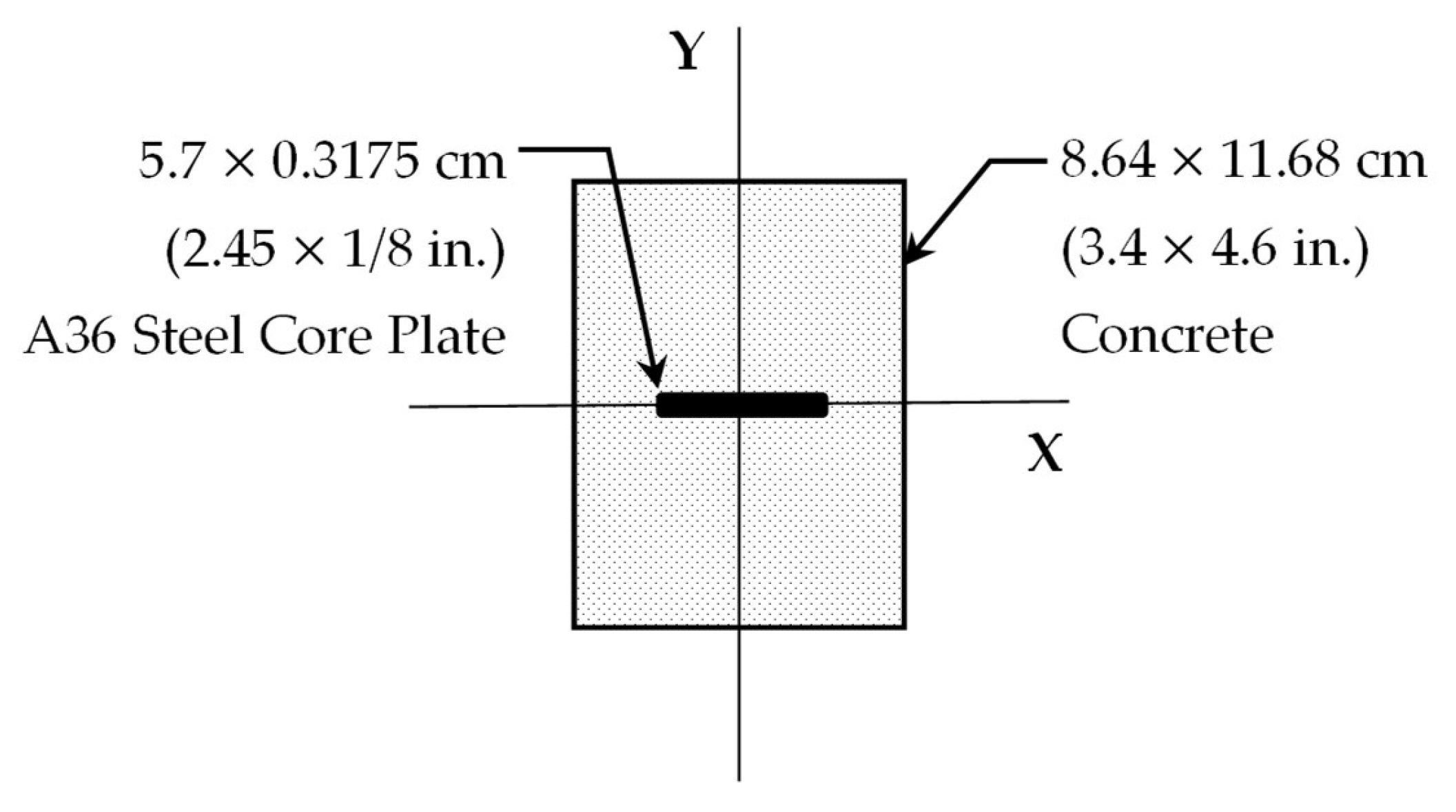
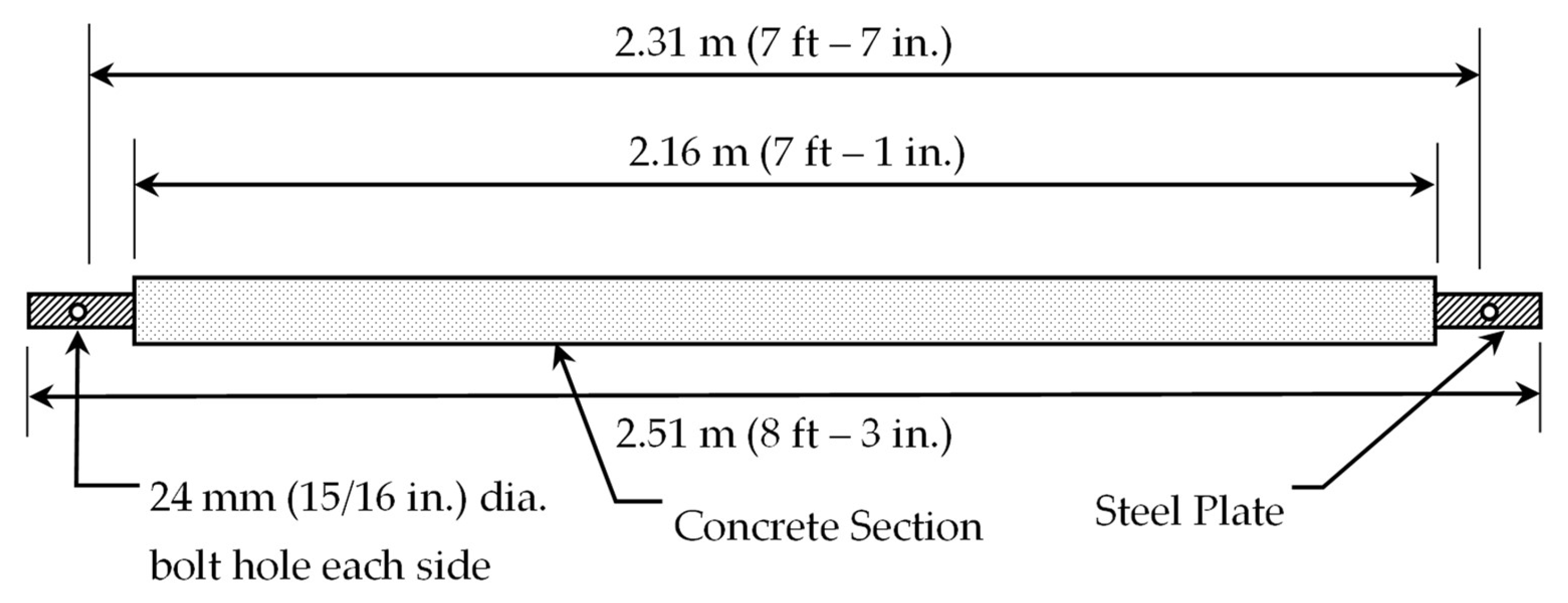
2.2. Specimens
2.3. Material Testing
2.4. Testing Steel Frame
2.5. Instrumentation
2.6. Base Excitations
3. Results and Discussions
3.1. Concrete Material Properties
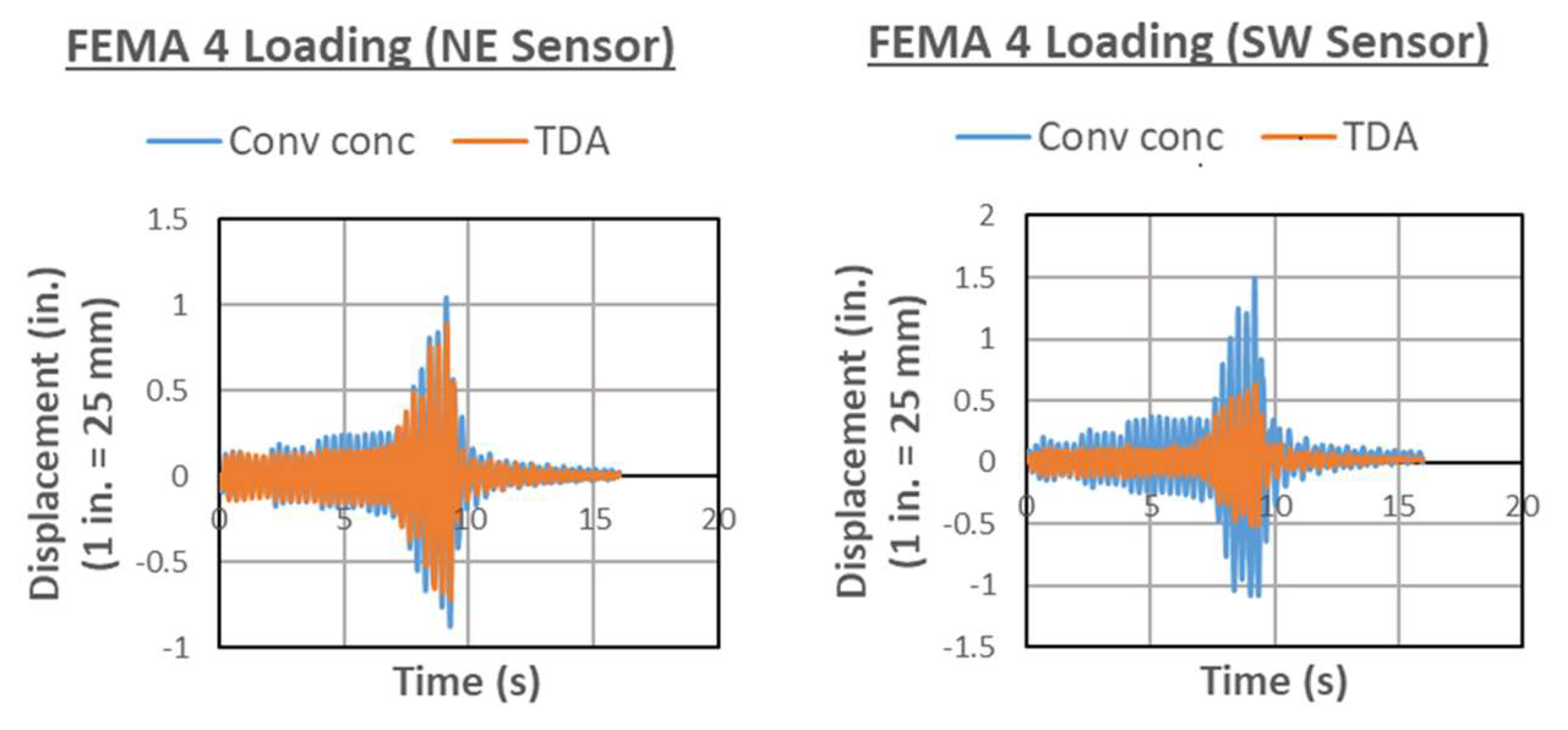
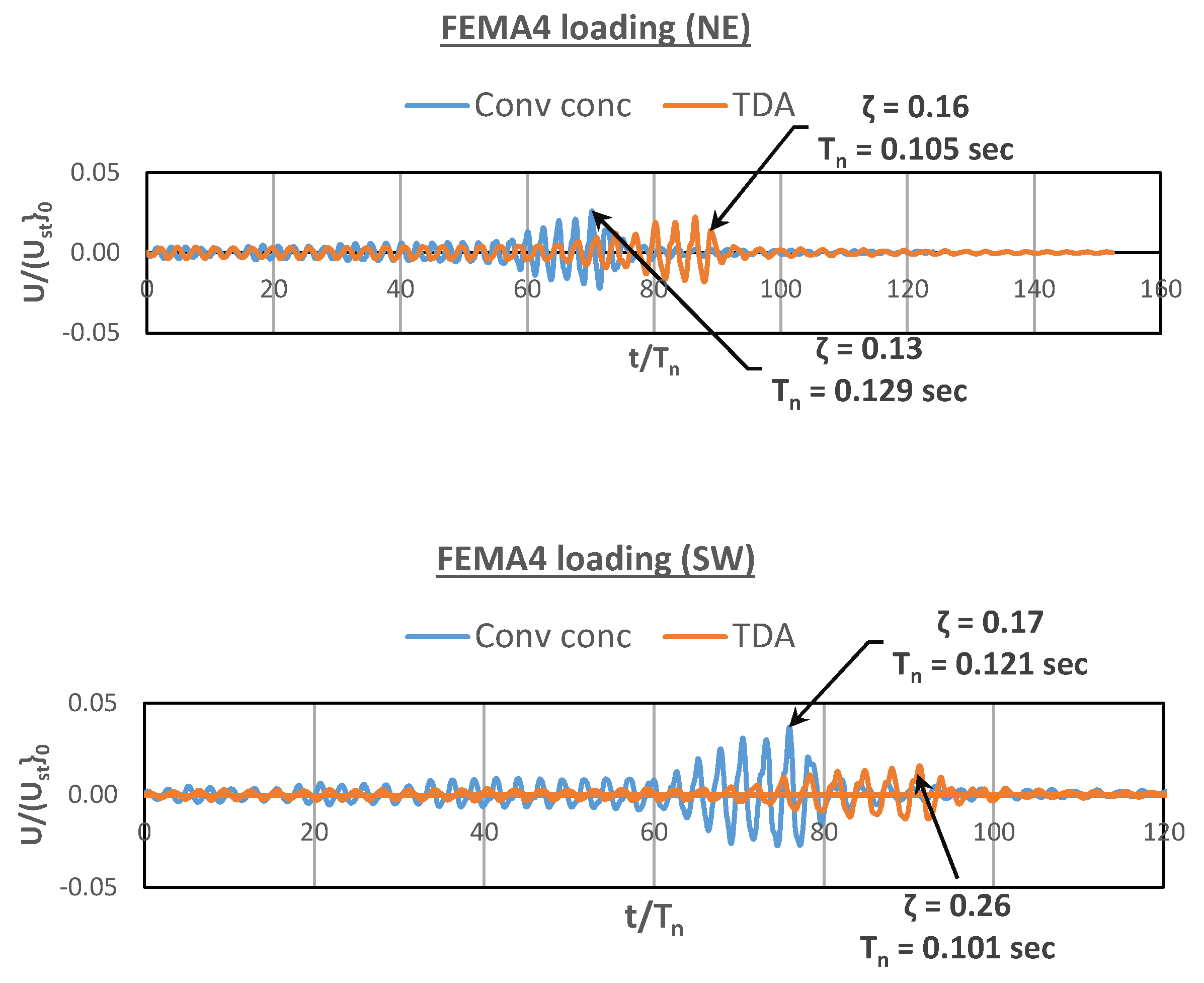
3.2. Time History Responses
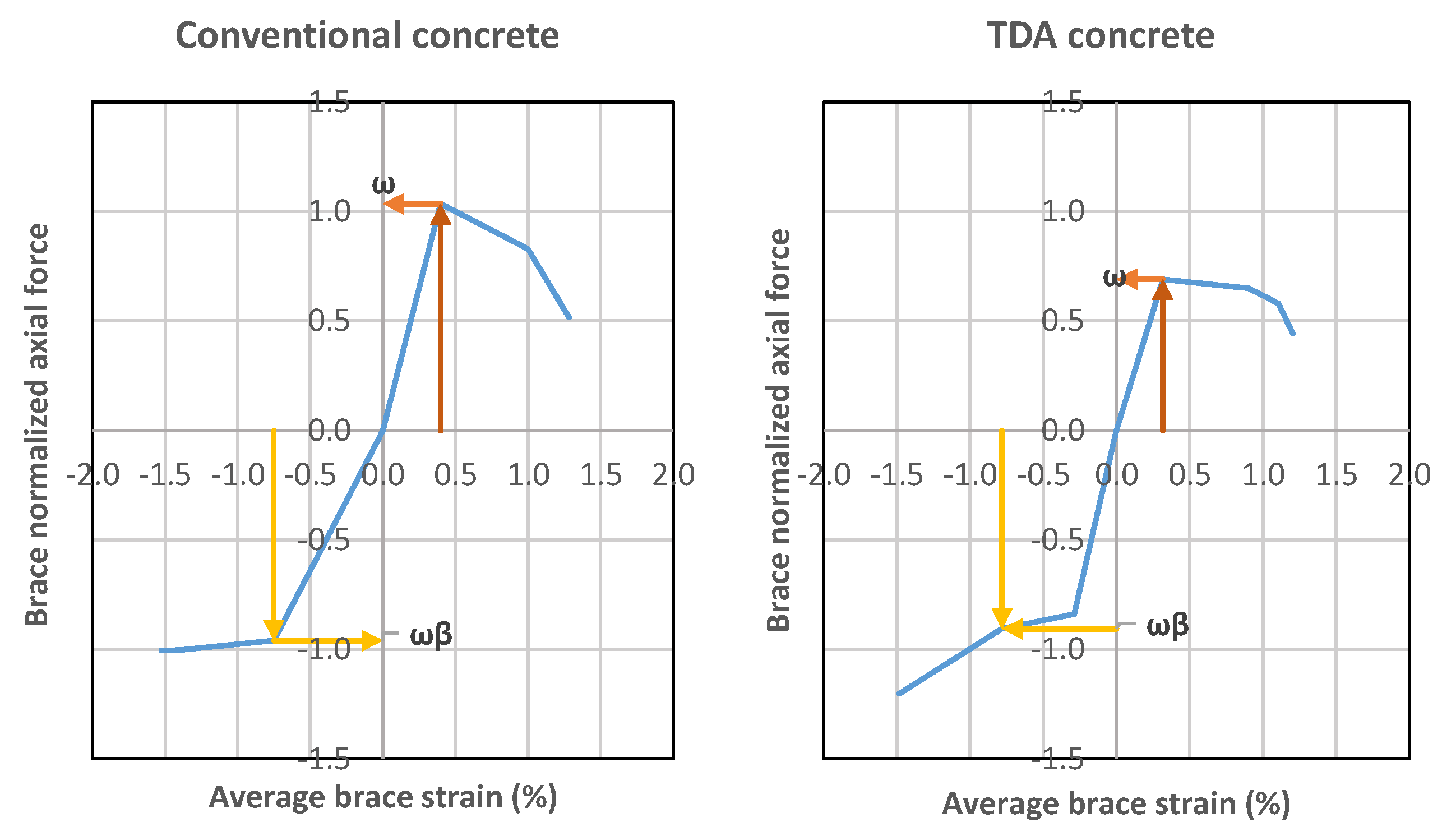
3.3. Design Parameters
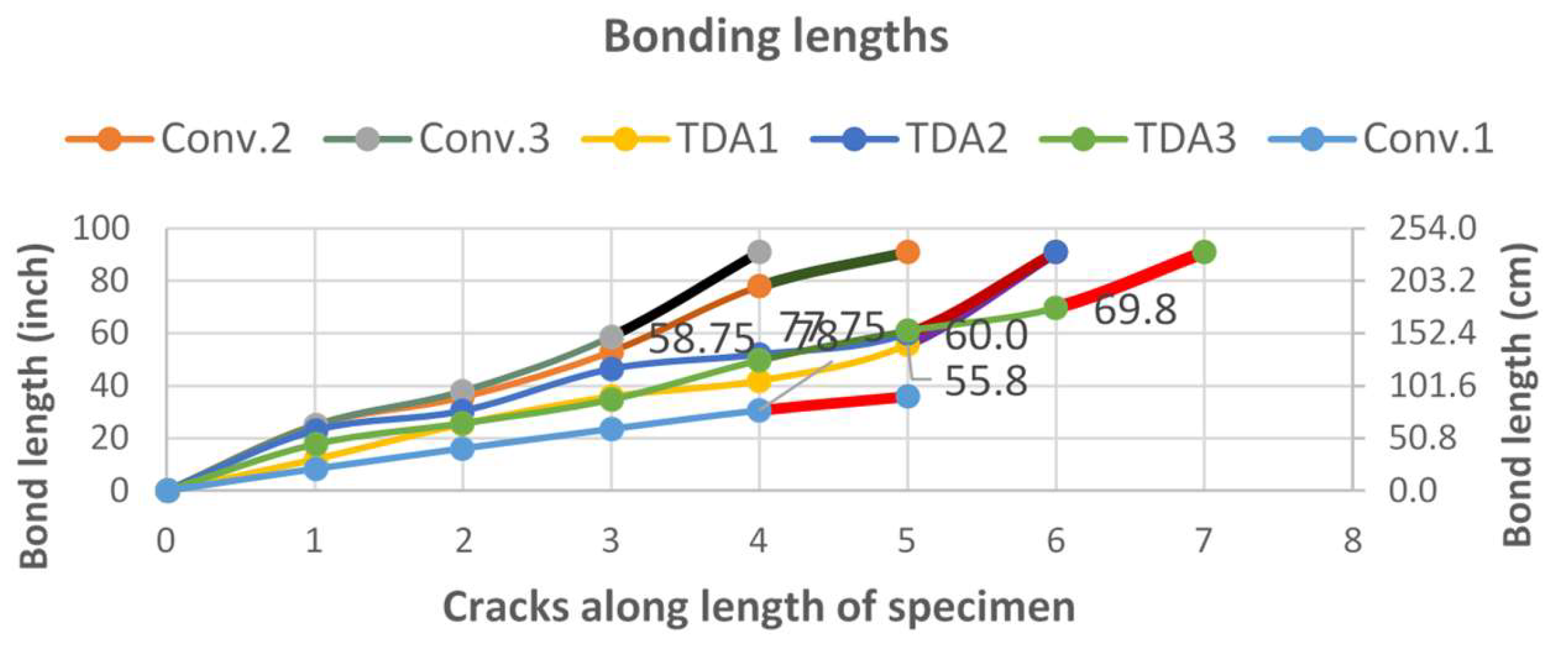
3.4. Debonding and Failure
4. Conclusions
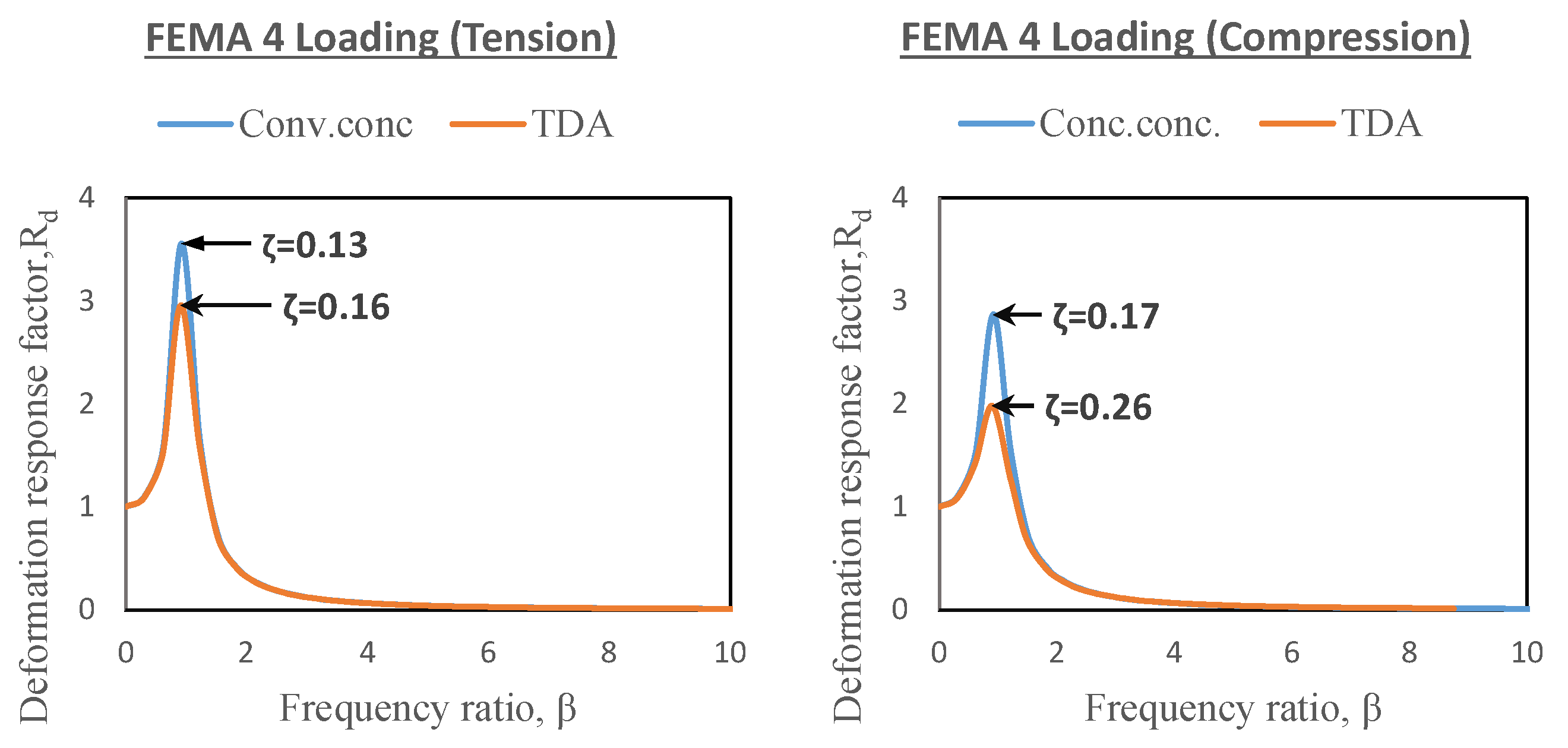
- Compared to a conventional concrete brace, a TDA concrete brace provides the additional benefit of increasing damping on the frames (ζ > 17% in tension and ζ > 34% in compression).
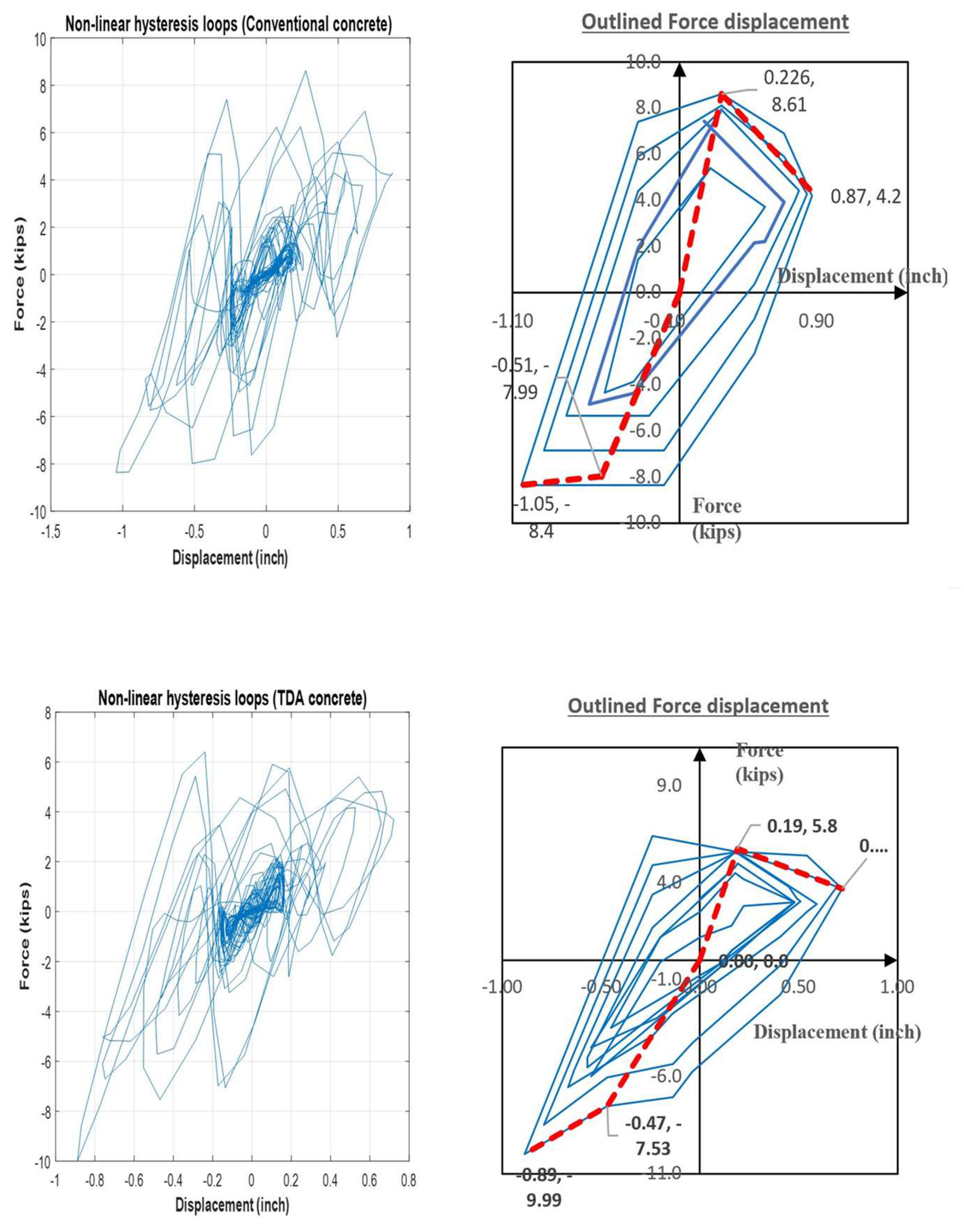
- Although TDA braces increased both the frame’s damping levels and fundamental period, they dissipated less energy than conventional braces due to a lack of ductility. Therefore, it can be concluded that TDA concrete braces may be a superior alternatives in a system where damping is of primary concern.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruneau, M.; Uang, C.M.; Sabelli, R. Ductile Design of Steel Structures; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Dehghani, A.; Fischer, G.; Nateghi Alahi, F. Strengthening masonry infill panels using engineered cementitious composites. Mat. Struct. 2015, 48, 185–204. [Google Scholar] [CrossRef]
- Chen, C.C.; Chen, S.Y.; Liaw, J.J. Application of low yield strength steel on controlled plastification ductile concentrically braced frames. Can. J. Civ. Eng. 2001, 28, 823–836. [Google Scholar] [CrossRef]
- Sabelli, R.; Mahin, S.; Chang, C. Seismic demands on steel braced frame buildings with buckling-restrained braces. Eng. Struct. 2003, 25, 655–666. [Google Scholar] [CrossRef]
- Scholl, R.E. Observations of the performance of buildings during the 1985 Mexico earthquake, and structural design implications. Int. J. Min. Geol. Eng. 1989, 7, 69–99. [Google Scholar] [CrossRef]
- Kim, H.I.; Goel, S.C. Upgrading of braced frames for potential local failures. J. Struct. Eng. 1996, 122, 470–475. [Google Scholar] [CrossRef]
- Goltz, J.D. The Northridge, California Earthquake of January 17, 1994: General Reconnaissance Report; Report No. NCEER-94-0005; National Centre for Earthquake Engineering Research: Buffalo, NY, USA, 1994. [Google Scholar]
- Nakashima, M.; Inoue, K.; Tada, M. Classification of damage to steel buildings observed in the 1995 Hyogoken-Nanbu earthquake. Eng. Struct. 1998, 20, 271–281. [Google Scholar] [CrossRef]
- López-Almansa, F.; Castro-Medina, J.C.; Oller, S. A numerical model of the structural behavior of buckling-restrained braces. Eng. Struct. 2012, 41, 108–117. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Mohebi, B. Seismic evaluation of all-steel buckling restrained braces using finite element analysis. J. Const. Steel Res. 2016, 119, 76–84. [Google Scholar] [CrossRef]
- Pham, T.M.; Zhang, X.; Elchalakani, M.; Karrech, A.; Hao, H.; Ryan, A. Dynamic response of rubberized concrete columns with and without FRP confinement subjected to lateral impact. Const. Buil. Mat. 2018, 186, 207–218. [Google Scholar] [CrossRef]
- Black, C.; Aiken, I.D.; Makris, N. Component Testing, Stability Analysis, and Characterization of Buckling-Restrained Unbonded Braces (TM); PEER 2002/08; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Sun, H.; Jia, M.; Zhang, S.; Wang, Y. Study of buckling-restrained braces with concrete infilled GFRP tubes. Thin-Walled Struct. 2019, 136, 16–33. [Google Scholar] [CrossRef]
- Flogeras, A.K.; Papagiannopoulos, G.A. On the Seismic Response of Steel Buckling-Restrained Braced Structures Including Soil-Structure Interaction. Earthq. Struct. 2017, 12, 469–478. [Google Scholar] [CrossRef]
- Sabelli, R.; López, W. Design of buckling-restrained braced frames. Mod. Steel Constr. 2004, 44, 67–74. [Google Scholar]
- Yu, Y.J.; Tsai, K.C.; Li, C.H.; Weng, Y.T.; Tsai, C.Y. Analytical simulations for shaking table tests of a full scale buckling restrained braced frame. Procedia Eng. 2011, 14, 2941–2948. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H. Behavior and design of structures with buckling-restrained braces. Eng. Struct. 2004, 26, 693–706. [Google Scholar] [CrossRef]
- Guerrero, H.; Escobar, J.A.; Teran-Gilmore, A. Experimental damping on frame structures equipped with buckling-restrained braces (BRBs) working within their linear-elastic response. Soil Dyn. Earthq. Eng. 2018, 106, 196–203. [Google Scholar] [CrossRef]
- Sabelli, R. Recommended provisions for buckling-restrained braced frames. Eng. J. Am. Inst. Steel Const. 2004, 41, 155–176. [Google Scholar]
- Fahnestock, L.A.; Sause, R.; Ricles, J.M.; Lu, L.W. Ductility demands on buckling-restrained braced frames under earthquake loading. Earthq. Eng. Eng. Vib. 2003, 2, 255–268. [Google Scholar] [CrossRef]
- Tremblay, R.; Bolduc, P.; Neville, R.; DeVall, R. Seismic testing and performance of buckling-restrained bracing systems. Can. J. Civ. Eng. 2006, 33, 183–198. [Google Scholar] [CrossRef]
- Asgarian, B.; Shokrgozar, H.R. BRBF response modification factor. J. Constr. Steel Res. 2009, 65, 290–298. [Google Scholar] [CrossRef]
- Sadrinezhad, A.; Tehrani, F.M.; Jeevanlal, B. Shake Table Test of Railway Embankment Consisting of TDA and LECA. In Proceedings of the Geo-Congress 2019: Earthquake Engineering and Soil Dynamics, Philadelphia, PA, USA, 24–27 March 2019; pp. 31–39. [Google Scholar] [CrossRef]
- Tehrani, F.M.; Sadrinezhad, A.; Bajestani, M.S. Numerical simulation of the dynamic response of rail ballast with tire-derived aggregates. In Proceedings of the 11th US National Conference on Earthquake Engineering, Los Angeles, CA, USA, 25–29 June 2018; p. 1337. [Google Scholar]
- Tehrani, F.M. Noise abatement of rubberized hot mix asphalt: A brief review. Int. J. Pavement Res. Tech. 2015, 8, 58–61. [Google Scholar] [CrossRef]
- Tehrani, F.M.; Miller, N.M. Tire-derived aggregate cementitious materials: A Review of Mechanical Properties. In Cement-Based Materials; Saleh, H., Ed.; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Nazari, M.; Tehrani, F.M.; Ansari, M.; Jeevanlal, B.; Rahman, F.; Farshidpour, R. Green Strategies for Design and Construction of Non-Auto Transportation Infrastructure; Project 1872; Mineta Transportation Institute: San Jose, CA, USA, 2019. [Google Scholar]
- Nazari, M.; Tehrani, F.M.; Ansari, M. Lightweight Rubberized Concrete Slabs for Sustainable Road Pavements Serving Non-Auto Traffic. Period. Polytech. Civ. Eng. 2022, 66, 460–470. [Google Scholar] [CrossRef]
- Miller, N.M.; Tehrani, F.M. Mechanical properties of rubberized lightweight aggregate concrete. Constr. Build. Mat. 2017, 147, 264–271. [Google Scholar] [CrossRef]
- Tehrani, F.M.; Carreon, J.; Miller, N. An investigation of tire-derived lightweight aggregate concrete. ACI Spec. Publ. 2019, 334–335, 68–98. [Google Scholar]
- Tehrani, F.M.; Masswadi, N.A.; Miller, N.M.; Sadrinezhad, A. An Experimental Investigation of Dynamic Properties of Fiber-Reinforced Tire-Derived Lightweight-Aggregate Concrete. Eur. J. Eng. Tech. Res. 2020, 5, 702–707. [Google Scholar] [CrossRef]
- Tehrani, F.M.; Nazari, M.; Truong, D.; Farshidpour, R. Sustainability of tire-derived aggregate concrete: A case study on energy, emissions, economy, and ENVISION. In Proceedings of the International Conference on Sustainable Infrastructure 2019: Leading Resilient Communities through the 21st Century, Los Angeles, CA, USA, 6–9 November 2019; pp. 399–408. [Google Scholar] [CrossRef]
- Jia, M.M.; Yu, X.H.; Lu, D.G.; Lu, B.B. Experimental research of assembled buckling-restrained braces wrapped with carbon or basalt fiber. J. Constr. Steel Res. 2017, 131, 144–161. [Google Scholar] [CrossRef]
- Dusicka, P.; Tinker, J. Global restraint in ultra-lightweight buckling-restrained braces. J. Compos. Constr. 2013, 17, 139–150. [Google Scholar] [CrossRef]
- Deng, K.L.; Pan, P. Study of GFRP steel buckling restraint braces. J. Compos. Constr. 2015, 19, 04015009-1-8. [Google Scholar] [CrossRef]
- Naghshineh, A.; Tehrani, F.M.; Fischer, O. Application of sustainable concrete in an Innovative type of Buckling Restrained Brace. Sustainability 2022, 14, 16344. [Google Scholar] [CrossRef]
- Couch, L.; Tehrani, F.M.; Naghshineh, A.; Frazao, R. Shake Table Response of a Dual System with Inline Friction Damper. Eng. Struct. 2023, 281, 115776. [Google Scholar] [CrossRef]
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P.; Seyhan, E.; Silva, W.J.; Chiou, B.S.; Wooddell, K.E.; Graves, R.W.; Kottke, A.R.; Boore, D.M.; et al. PEER NGA-West2 Database; PEER 2013/03; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2013. [Google Scholar]
- Pan, C.; Zhang, R.; Luo, H.; Shen, H. Baseline correction of vibration acceleration signals with inconsistent initial velocity and displacement. Adv. Mech. Eng. 2016, 8, 1687814016675534. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Pearson: Upper Saddle River, NJ, USA, 2017. [Google Scholar]
- López, W.A.; Sabelli, R. Seismic design of buckling-restrained braced frames. Steel Tips 2004, 78. [Google Scholar]
- Merritt, S.; Uang, C.M.; Benzoni, G. Subassemblage Testing of Core Brace Buckling Restrained Braces; Report No. TR 2003/01; Department of Structural Engineering, University of California: San Diego, La Jolla, CA, USA, 2003. [Google Scholar]








| Specimen | Tensile Load, kN (kips) | Buckling Load, kN (kips) |
|---|---|---|
| Conventional concrete | 44.5 (10) | 246.32 (55.6) |
| TDA concrete | 44.5 (10) | 228.4 (50.9) |
| Material Properties | Conventional | TDA |
|---|---|---|
| Riverside Type III Low Alkali Cement | 11.2 kg (25 lb) | 6.5 kg (19.6 lb) |
| Natural Sand | 12.8 kg (29 lb) | 14.8 kg (33.1 lb) |
| Pea Gravel (Caltrans)—1829, 9.5 mm (3/8 in.) | 33.7 kg (75.7 lb) | None |
| Tire-Derived Aggregate, 9.5 mm (3/8 in.) | None | 22.4 kg (50.3 lb) |
| Water | 5.6 L (1.5 gals) | 7.1 L (1.9 gals) |
| MasterPozzolith 322N Water Reducing Admixture | 334 mL (11.3 fl. oz) | 334 mL (11.3 fl. oz) |
| Darex II ARA Air Entraining Admixture | 14.8 mL (0.5 fl. oz) | 14.8 mL (0.5 fl. oz) |
| Test | Prototype | Loadings |
|---|---|---|
| NC1 | Normal-weight Concrete | El Centro, FEMA Sweep, Gazli, Loma Prieta |
| NC2 | Normal-weight Concrete | Impulse |
| NC3 | Normal-weight Concrete | FEMA |
| TDA1 | Tire-Derived Aggregate Concrete | FEMA |
| TDA2 | Tire-Derived Aggregate Concrete | Sweep |
| TDA3 | Tire-Derived Aggregate Concrete | Impulse, FEMA, Dutzce, Northridge, Tabas |
| Brace | Load | Time Step, s | Peak Ground Acceleration, g | Displacement, cm (in.) | |
|---|---|---|---|---|---|
| Tensile, cm (in.) | Compressive, cm (in.) | ||||
| NC1 | El Centro | 0.005 | 0.407 | 5 (1.99) | 2.3 (0.9) |
| FEMA | 0.0125 | 1.0 (0.4) | 1.0 (0.4) | ||
| Sweep | 0.0125 | 0.5 (0.2) | 0.5 (0.2) | ||
| Gazli (25% scale) | 0.0066 | 0.15 | 6.8 (2.7) | 6.1 (2.4) | |
| Loma Prieta (33% scale) | 0.005 | 0.2 | 3.1 (1.2) | 2.2 (0.89) | |
| FEMA 2 1 | 0.00625 | 1.02 (0.4) | 1.0 (0.4) | ||
| FEMA 4 1 | 0.003125 | 1.0 (0.4) | 1.0 (0.4) | ||
| NC2 | Compressive Impulse 1 | 0.01 | 2.54 (1.0) | 2.54 (1.0) | |
| Tensile Impulse 1 | 0.01 | 2.54 (1.0) | 2.54 (1.0) | ||
| Compressive Impulse 2 | 0.01 | 5.08 (2.0) | 5.08 (2.0) | ||
| Compressive Impulse 3 | 0.01 | 8.9 (3.5) | 8.9 (3.5) | ||
| NC3 | FEMA 2 1 | 0.00625 | 1.02 (0.4) | 1.02 (−0.4) | |
| FEMA 4 1 | 0.003125 | 1.02 (0.4) | 1.02 (0.4) | ||
| TDA1 | FEMA 2 1 | 0.00625 | 1.02 (0.4) | 1.02 (0.4) | |
| FEMA 4 1 | 0.003125 | 1.02 (0.4) | 1.02 (0.4) | ||
| TDA2 | Sweep Normal Loading | 0.0125 | 0.5 (0.2) | 0.5 (0.2) | |
| Sweep 1 Hz 1 inch | 0.0125 | 2.54 (1.0) | 2.54 (1.0) | ||
| Sweep 2 Hz 1 inch | 0.0125 | 2.54 (1.0) | 2.54 (1.0) | ||
| Sweep 3 Hz 1 inch | 0.0125 | 2.54 (1.0) | 2.54 (1.0) | ||
| TDA3 | Compressive Impulse 1 | 0.01 | 2.54 (1.0) | 2.54 (1.0) | |
| FEMA 2 1 | 0.00625 | 1.02 (0.4) | 1.02 (0.4) | ||
| Dutzce (15% Scaled) | 0.005 | 0.06 | 7.4 (2.93) | 4.8 (1.9) | |
| Northridge 4 (7% Scaled) | 0.005 | 0.04 | 2.9 (1.15) | 1.5 (0.57) | |
| Tabas 2 1 | 0.00845 | 0.776 | 6.7 (2.63) | 5.2 (2.03) | |
| Tabas 4 1 | 0.004225 | 2.1 | 6.7 (2.63) | 5.2 (2.03) | |
| Prototype | Tensile Load, kN (kips) | Buckling Load, kN (kips) |
|---|---|---|
| Conventional Concrete | 44.5 (10) | 319.8 (71.9) |
| TDA Concrete | 44.5 (10) | 176.9 (39.77) |
| Record | LED 1, cm (in.) | NED 2, cm (in.) | ||
|---|---|---|---|---|
| NE | SW | NE | SE | |
| El Centro | 5.26 (2.07) | 2.44 (0.96) | 3.99 (1.57) | 5.05 (1.99) |
| Gazli | 6.91 (2.72) | 6.19 (2.44) | 6.33 (2.49) | 7.70 (3.03) |
| Loma Prieta | 3.17 (1.25) | 2.31 (0.91) | 3.84 (1.51) | 4.19 (1.65) |
| Northridge | 2.94 (1.16) | 1.25 (0.57) | 2.85 (1.12) | 2.49 (0.98) |
| Dutzce | 7.45 (2.94) | 4.85 (1.91) | 3.15 (1.24) | 3.81 (1.50) |
| Tabas 2 | 6.73 (2.65) | 5.18 (2.04) | 5.77 (2.27) | 4.34 (1.71) |
| Tabas 4 | 6.73 (2.65) | 5.18 (2.04) | 5.28 (2.08) | 5.84 (2.30) |
| FEMA 4 | 6.73 (2.65) | 5.18 (2.04) | 3.78 (1.49) | 2.67 (1.05) |
| SWEEP | 6.73 (2.65) | 5.18 (2.04) | 3.78 (1.49) | 2.67 (1.05) |
| Record | Rotation (deg) | |
|---|---|---|
| NE | SW | |
| El Centro | 0.03 | 0.03 |
| Gazli | 0.12 | 0.07 |
| Loma Prieta | 0.08 | 0.08 |
| Northridge | 0.01 | 0.08 |
| Dutzce | 0.76 | 0.18 |
| Tabas 2 | 0.04 | 0.13 |
| Tabas 4 | 0.16 | 0.47 |
| FEMA 4 | 0.35 | 0.60 |
| Description | Conventional | TDA | ||
|---|---|---|---|---|
| Tension | Compression | Tension | Compression | |
| Frequency, rad/s | 48.9 | 51.9 | 59.6 | 43.3 |
| Natural period, s | 0.129 | 0.121 | 0.105 | 0.145 |
| Modulus of elasticity, MPa (ksi) | 62,253 (9.02 3) | 64,466 (9.35 3) | 84,957 (12.3 3) | 48,815 (7.08 3) |
| Stiffness, kN/m (kips/in.) | 4606 (26.3) | 4658 (29.6) | 6830 (39.0) | 3608 (20.6) |
| Specimen | Logarithmic Decrement, 25 mm (1 in.) Impulse | Logarithmic Decrement, FEMA 4 | Deformation Response Factor, FEMA 4 | |||
|---|---|---|---|---|---|---|
| Tension | Compression | Tension | Compression | Tension | Compression | |
| TDA Concrete | 15.3% | 20.7% | 13.7% | 16.4% | 19% | 30% |
| Conventional Concrete | 10.5% | 18.6% | 12.2% | 18.8% | 17% | 14% |
| Specimen | Ductility Demand | Toughness, J (kips in.) | |
|---|---|---|---|
| Tension | Compression | ||
| Conventional Concrete | 3.9 | 2.7 | 15,410 (136.4) |
| TDA Concrete | 3.2 | 2.2 | 11,468 (101.5) |
| Specimen | Strength Adjustment Factors | |
|---|---|---|
| Conventional Concrete | 1.01 | 1.04 |
| TDA Concrete | 0.69 | 1.20 |
| Specimen | Damping Ratio | |
|---|---|---|
| Tension | Compression | |
| Conventional Concrete | 13% | 17% |
| TDA Concrete | 16% | 26% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pathan, N.B.; Couch, L.; Tehrani, F.M.; Naghshineh, A.; Fischer, O. Experimental Seismic Evaluation of Novel Buckling-Restrained Braced Frames Containing Tire-Derived Aggregate Concrete. CivilEng 2023, 4, 551-566. https://doi.org/10.3390/civileng4020032
Pathan NB, Couch L, Tehrani FM, Naghshineh A, Fischer O. Experimental Seismic Evaluation of Novel Buckling-Restrained Braced Frames Containing Tire-Derived Aggregate Concrete. CivilEng. 2023; 4(2):551-566. https://doi.org/10.3390/civileng4020032
Chicago/Turabian StylePathan, Nasreen B., Logan Couch, Fariborz M. Tehrani, Ali Naghshineh, and Oliver Fischer. 2023. "Experimental Seismic Evaluation of Novel Buckling-Restrained Braced Frames Containing Tire-Derived Aggregate Concrete" CivilEng 4, no. 2: 551-566. https://doi.org/10.3390/civileng4020032
APA StylePathan, N. B., Couch, L., Tehrani, F. M., Naghshineh, A., & Fischer, O. (2023). Experimental Seismic Evaluation of Novel Buckling-Restrained Braced Frames Containing Tire-Derived Aggregate Concrete. CivilEng, 4(2), 551-566. https://doi.org/10.3390/civileng4020032








