Next Article in Journal / Special Issue
Site-Specific Response Spectra and Accelerograms on Bedrock and Soil Surface
Previous Article in Journal / Special Issue
Site-Specific Seismic Analysis of Buildings Supported by Lightly Reinforced Precast Concrete Walls
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
CivilEng
Volume 4
Issue 1
10.3390/civileng4010017
civileng-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Beam-Truss Models to Simulate the Axial-Flexural-Torsional Performance of RC U-Shaped Wall Buildings

by
Ryan Hoult
1,*,
António A. Correia
2 and
João Pacheco de Almeida
1
1
Institute of Mechanics, Materials and Civil Engineering, Université Catholique de Louvain, 1348 Louvain-la-Neuve, Belgium
2
National Laboratory for Civil Engineering (LNEC), 1700 Lisbon, Portugal
*
Author to whom correspondence should be addressed.
CivilEng 2023, 4(1), 292-310; https://doi.org/10.3390/civileng4010017
Submission received: 2 January 2023 / Revised: 4 March 2023 / Accepted: 9 March 2023 / Published: 13 March 2023
(This article belongs to the Special Issue Site-Specific Seismic Design of Buildings)
Browse Figures
Review Reports Versions Notes

Abstract

:
Reinforced concrete (RC) core walls are commonly used to provide buildings with lateral and torsional resistance against the actions of wind and earthquakes. In low-to-moderate seismic regions, it is not unusual to find a single peripheral core wall that alone should resist these actions, where the torsional (rotational) twist cannot be neglected. It has previously been difficult to have confidence in simulating the axial-flexure-torsion behavior of these RC core walls, primarily due to: (i) some types of modelling approaches being unable to appropriately account for the shear-flexural action, as well as torsional response; and (ii) the scarcity of experimental data, particularly for walls under torsional loads, which would be required to validate such models. In this research, beam-truss models (BTMs), which correspond to an interesting compromise between detailed modelling and practical applications, were used to simulate the in-plane and diagonal flexural response of RC U-shaped walls. Furthermore, the global torque-rotation results from a recent experimental wall test provided the evidence to further validate this powerful modelling technique. A case study building, comprising an RC U-shaped core wall structure with varying eccentricity values, was evaluated for an earthquake event with a 2475-year return period in the city of Melbourne, Australia, using the capacity spectrum method. Nonlinear static pushover analyses showed that, depending on the magnitude of torsion, the in-plane flexural strength and displacement capacity can be significantly reduced. The results from this research emphasize the importance of including torsional actions in the design and assessment of reinforced concrete buildings.

1. Introduction

Reinforced concrete (RC) core wall buildings are one of the most popular and efficient lateral load-resisting structures in the world, used in both low-to-moderate [1,2,3,4] and high seismic regions [5], such as Australia and the west coast of North America, respectively. In contrast to planar (i.e., rectangular) walls, non-planar core wall(s) can efficiently provide lateral strength in all orthogonal (horizontal) directions. Furthermore, architects are favorable to non-planar RC walls, as the openings between the flange(s) and web(s) of the cross-section have the potential to accommodate elevator cabs, stairs, or service ducts [6] while also providing some fireproofing requirements according to many building standards. The U-shaped section is a popular construction choice for the aforementioned reasons.
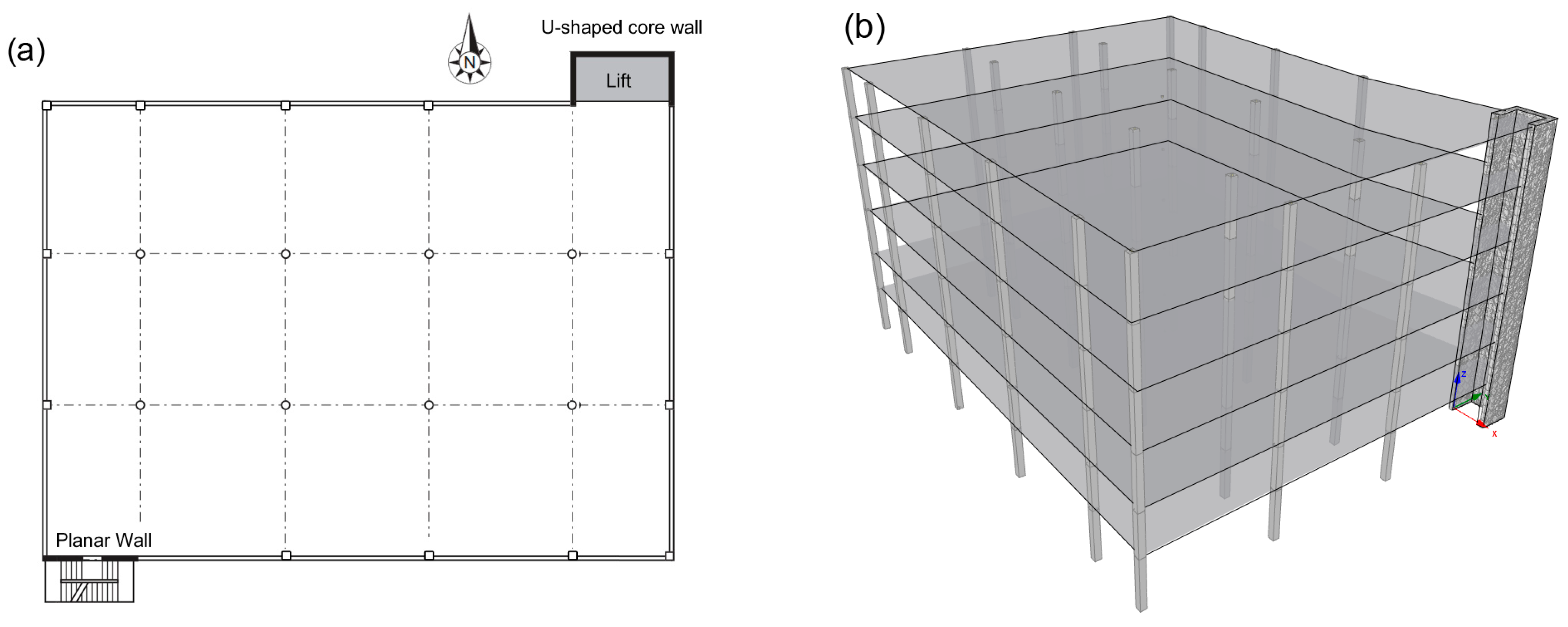
Due to the increasing demand for more efficient use of the building area, the core wall is sometimes placed on the perimeter of the building (Figure 1). As the lateral stiffness of the RC wall is typically much higher than that of any other vertical structural elements in the building, plan asymmetry is created due to the offset of stiffness center from the center of mass. In fact, even for symmetric structures, accidental loading, mass eccentricities, and even material strength variabilities [7] are inevitable and can trigger critical, unforeseen torsional responses. This was most recently observed in a 51-storey RC core wall building in downtown Los Angeles, which exhibited torsional behavior for a moment magnitude Mw 7.1 earthquake event at a distance of ~200 km [5]. Çelebi et al. [5] believe that this behavior was likely due to the ”abrupt symmetrical changes in the thickness and size in-plane of the core-shear walls”. In low-to-moderate seismic regions, such as Australia, it is common to find just a single, peripheral U-shaped wall. For this building type (Figure 1), the torsional twist can be relevant; hence, the influence of torsion on the response and design of walls should be considered. It has even been suggested that the longitudinal stresses at the base of the core wall caused by warping could be of the same order of magnitude as longitudinal stresses caused by the bending [8]. Moreover, the torsional response of these structures increases the displacement demand on other structural elements, such as the RC frame. For example, it is likely that the asymmetry of the CTV building in Christchurch, New Zealand, caused by the peripheral RC core wall, increased the deformations during the Mw 6.2 earthquake event in 2011 [9,10], which ultimately caused the RC frame’s “pancake” collapse, taking the lives of 115 people [11].
Whilst RC U-shaped core walls are predominantly used as the cross-section of choice for many engineers and architects, there appears to be a limited amount of experimental research focusing on its seismic performance. The limited experimental studies on RC U-shaped walls include in-plane quasi-static loading [13,14,15], shaking table tests [16], and a combination of in-plane and diagonal loading [17,18,19]. In two of these experimental programs [17,19], a small twist was applied at some key load stages to indicate the decrease in torsional stiffness as a function of the in-plane ductility, which was subsequently studied in a separate investigation [20]. Thus, while the international engineering community now widely accepts that the rotational behavior of structural elements can significantly contribute to its overall seismic response [21], there appears to be a lack of evidence and experimental research in this area. Therefore, researchers and design engineers cannot fully validate micro- and macro-models of RC buildings with non-planar walls that are subjected to some torsional response.
A recent experimental program conducted at the Université catholique de Louvain (UCLouvain), in Belgium, tested two RC U-shaped wall units subjected to axial-flexure and axial-torsion [22]. The latter of these wall units is deemed to be important for the purpose of validating numerical analyses and simulations of non-planar walls subjected to torsion. This paper investigates the use of beam-truss models (BTMs) to simulate the axial-flexure-torsional performance of RC U-shaped walls. Beam-truss models have proven to be a simple yet effective method for simulating non-planar RC walls [23], consisting of a rather refined mesh of vertical, horizontal, and diagonal elements to emulate the axial-flexure-shear-torsional interaction, as explained in Section 3. The recent experimental tests from UCLouvain, as well as other experimental results in the literature, were used to validate the beam-truss models developed in this research, with recommendations on the modelling procedure adopted by others. A six-story case study building with a periphery RC U-shaped core wall was then analyzed for an earthquake with a 2475-year return period in the city of Melbourne, Australia. The case-study structure is here used as an example of how this modelling procedure can be applied by practicing engineers, intending to improve the accuracy of the results while maintaining its simplicity of use.

2. Experimental Tests on U-Shaped Walls

The models employed for this research investigation will first be validated using some experimental results. Three different RC U-shaped wall specimens will be used for validation purposes. While all three units have the same cross-section and similar reinforcement detailing (Figure 2a), the shear spans differ across all three, as does the type of loading. For example, unit TUB from Beyer et al. [19] was subjected to a “sweeping” loading protocol, which included pushing the wall in the two orthogonal and diagonal directions. More recently, Hoult et al. [22] subjected the wall unit UW1 to in-plane bending about its minor axis, while another wall unit, UW2, was subjected to a reverse-cyclic rotation about its vertical axis. More details on these three units are given in the sub-sections below, while some of the differing design parameters are summarized in Table 1.

2.1. Unit TUB from Beyer et al. (2008)

An experimental campaign was conducted by Beyer et al. [19] to investigate the in-plane and diagonal seismic performance of half-scale RC U-shaped walls. Depending on the applied loading directions, the shear span of wall unit TUB was 3.35 m and 2.95 m for the wall bending about the strong axis (i.e., east–west direction, positions A–B in Figure 2b) and weak axis (i.e., north–south direction, positions C-D in Figure 2b), respectively. A “sweeping” loading protocol, initially developed by Hines et al. (2002), was used to assess the cyclic behavior of the RC wall specimens. The complete loading history for one cycle of TUB, corresponding to the positions indicated in Figure 2b, was the following:
  • ▪ EW cycle: full cycle about the major axis (O→A→B→O);
  • ▪ NS cycle: full cycle about the minor axes (O→C→D→O);
  • ▪ Diagonal cycle: full cycle in the diagonal direction (O→E→F→O);
  • ▪ “Sweep” (O→A→G→D→C→H→B→O)
As explained in Beyer et al. [19], the amplitudes of the first four cycles of the loading protocol were force-controlled with limits of 25%, 50%, 75%, and 100% applied of the lateral forces predicted at first yield. The loading pattern was then repeated for displacement ductility levels of 1, 2, 3, 4, 6, and 8 until failure was apparent. During these cycles, the twisting of the collar (or head) of TUB was restrained. It should be noted that a small twist was applied at some key loading stages to determine the torsional stiffness of the walls. These small twists will not be used in the validation process herein, but were investigated by one of the authors in a previous publication [20]. An axial load ratio of 4% was applied to unit TUB and held constant throughout testing. The material properties of the concrete and reinforcing steel are given in Table 1. Further information on test unit TUB can be found in research by Beyer et al. [19].

2.2. Units UW1 and UW2 from Hoult et al. (2022)

An experimental campaign was conducted by Hoult et al. [22] to investigate the in-plane and torsional seismic performance of two half-scale RC U-shaped walls, denoted UW1 and UW2. The first test unit, UW1, was subjected to reverse-cyclic loading with bending about its minor axis (i.e., north–south directions, positions C-D in Figure 2b). An overturning moment was applied to unit UW1 to increase the shear span of the unit to approximately 6.72 m, with the application of the axial load slightly affecting this shear span depending on the loading direction. At the peak of the horizontal loading, the shear span of UW1 was found to be approximately 5.7 m and 7.9 m pushing towards positions D and C, respectively [22]. The second test unit, UW2, was subjected to a reverse-cyclic rotation about its vertical axis to positions O± (in Figure 2b). No additional overturning moment was applied to increase the shear span of UW2, where the application height from the foundation to the collar of the wall units was 2.25 m. An axial load ratio of 5% was applied to both UW1 and UW2 and held constant throughout the testing. The material properties of the reinforcing steel and concrete for both units are given in Table 1. Further information on the testing of units UW1 and UW2 can be found in research by Hoult et al. [22]. It is worth noting that the experimental response of these two walls was the object of an international blind prediction competition, wherein several well-known international modelling experts participated [24,25].

3. Beam-Truss Models (BTMs)

The widely used stick model, using one-dimensional classical beam elements assigned with the entire cross-section of the wall, cannot be used to simulate the global behavior of non-planar RC core walls because there is no degree of freedom associated with warping displacements [2]. Instead, two simulation approaches, which build on the assembly of stick models, have been commonly used to simulate non-planar walls: wide-column models (WCMs) and beam-truss models (BTMs). Each of these modelling approaches is discussed in more depth below, with more scope provided for the latter as this is the approach undertaken herein. The authors acknowledge that there are other modelling approaches that could be used to simulate the behavior of non-planar walls, such as the Multiple-Vertical-Line-Element-Model, or MVLEM [26,27,28,29]. Alternatively, refined finite element models have also been extensively employed [30]. However, a parametric study of some sort simulating these experimental wall units using different modelling techniques, as well as providing an in-depth literature review of these methods with potential advantages and disadvantages, is outside of the scope of this study. Instead, interested readers should consult the literature (e.g., [31,32,33,34,35]).
Inelastic WCMs are thought to be used heavily in engineering practice to simulate these types of structures [36]. The WCM, also referred to as the “wide-column analogy” or the “equivalent frame method”, was originally developed for planar wall structures [37,38] and later extended to non-planar structures [39,40]. Applying WCMs to non-planar walls consists of modelling the web and flanges separately using vertical elements located at their respective centroid and treating them as planar segments. Horizontal rigid links are then used to connect the vertical elements along the weak axis of the sections. There have been different recommendations about the spacing of the rigid links, which can significantly influence the behavior of the WCMs [36,41,42]. The vertical elements are typically made to be rigid in shear and flexible in torsion, which are decoupled from the axial and flexural flexibilities [36]. To allow warping, which is remarkably important for simulating the torsional performance of these structures, the links, rigid in bending, shear, and axial extension [43,44], have a pre-assigned finite Saint-Venant torsional stiffness value. However, there is some contention in the literature as to what finite value should be used to represent the torsional stiffness [36,43,44,45], which has been shown to decrease as a function of the ductility [20] (i.e., as the wall degrades and softens). Thus, it is likely that using a constant finite torsional stiffness value, typically chosen to be equivalent to a fraction of the elastic Saint-Venant torsional stiffness, would result in a poor simulation of the torsional performance of RC U-shaped walls, particularly for large rotations (e.g., rotations greater than yield). Numerous numerical investigations have shown that WCMs can simulate U-shaped walls reasonably well, particularly with regard to their in-plane flexural behavior [2,36,46,47,48]. However, WCMs have only been assessed for torsion using the experimental results regarding RC beams rather than walls, because experimental data for the latter did not exist at the time. As reported by Pelletier and Léger [2], “…the accuracy of WCM for torsional loads could not be assessed, especially in terms of the nonlinear warping behavior”.
Another difficulty in implementing WCMs is the simulation of the truss action mechanism corresponding to the shear forces, which cannot be properly considered with WCMs since only one beam element per wall segment is typically used [2]. To overcome this limitation, a number of numerical investigations have used zero-length spring elements at the nodes between the placement of the rigid links to account for the shear flexibility of the wall segments, using a stiffness value corresponding to their uncracked sections (i.e., elastic) [2,36,46,47]. However, this requires yet another finite, constant value to be chosen by the designer or evaluator. Modelling the shear performance of non-planar walls is important, since these types of structures have been shown to exhibit more shear deformation in comparison to planar walls [18,49]. Furthermore, non-planar walls subjected to torsion also exhibit significant shear deformation due to the combination of circulatory and warping torsion behavior [50].
While WCMs remain popular in engineering practice, the authors expect that simulating RC U-shaped walls to torsional loads may be difficult due to the expected large shear contributions, but also the number of required pre-determined values for parameter inputs, the recommendations of which widely vary and could impact the resulting simulations. It is recommended that a future study focus on the applicability of WCMs for RC walls subjected to torsional loads. Instead, for the work herein, the authors have used a different modelling approach to overcome some of the aforementioned problems.

3.1. Beam-Truss Model Overview

The beam-truss model was developed to overcome the challenges of simulating the nonlinear flexure-shear interaction and seismic response of both planar and non-planar RC walls [51]. Later extended by Lu et al. [23], the BTM uses Euler–Bernoulli fiber-section beam elements in the horizontal and vertical directions and nonlinear truss elements in the diagonal directions. In comparison to the WCM, the BTM can account for the inelastic response of steel in the horizontal direction and the biaxial behavior of the concrete diagonals in compression [51]. 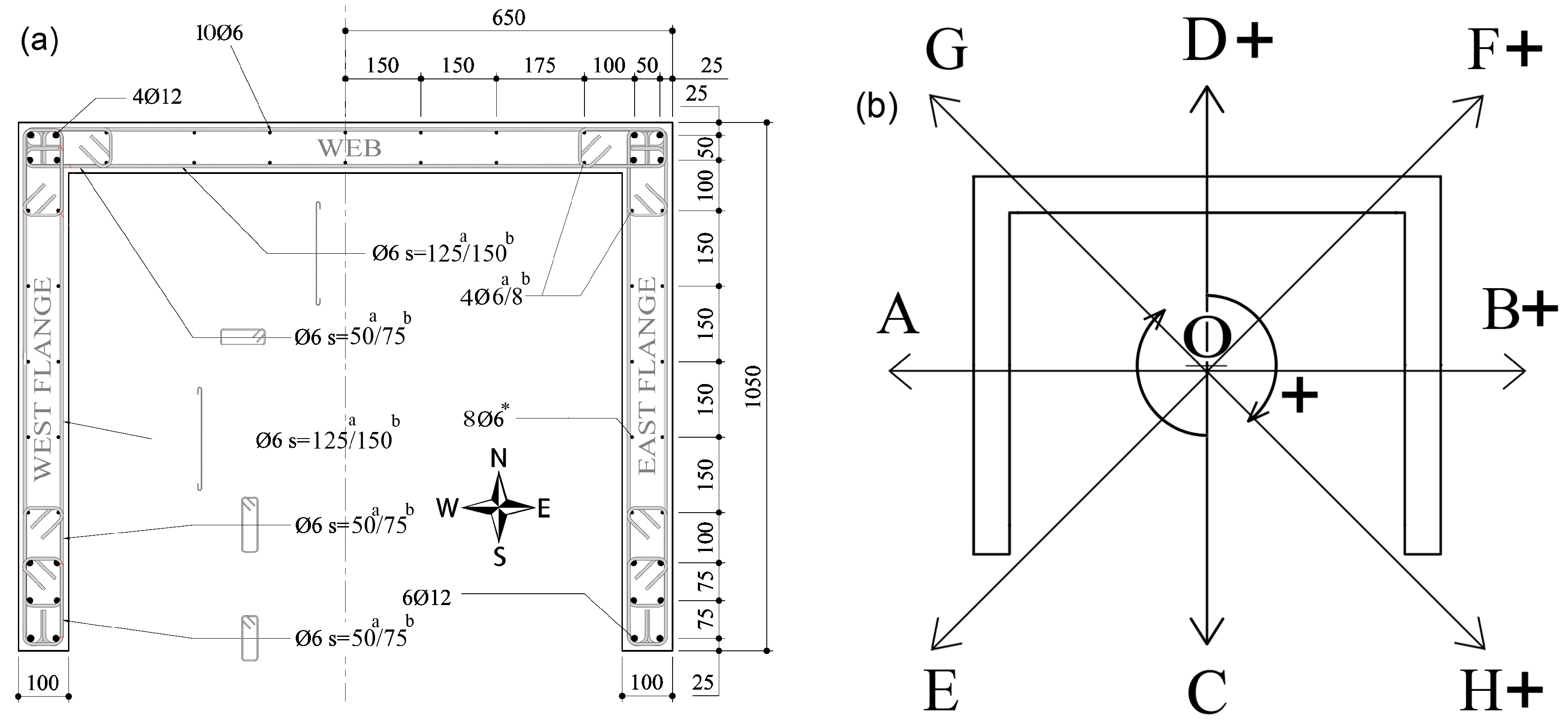An idealized RC U-shaped wall unit is illustrated in Figure 3a, where the wall lengths in the x- and y-directions are Lf and Lw, respectively, corresponding to the wall segment definitions in Figure 2a (i.e., the flange and web lengths). The thicknesses of the planar wall segments parallel to the x- and y-directions correspond to tw and tf, respectively, whereas the height of the wall unit is H (not to be confused with point H, also in the same figure). The BTM of this wall is illustrated in Figure 3b, which consists of two types of elements: (i) nonlinear fiber-section Euler–Bernoulli beam elements in the vertical and horizontal directions, and (ii) nonlinear truss elements in the diagonal directions. These illustrations are similar to those used by Lu and Panagiotou [51], but adapted here for a U-shaped section. For ease of illustration, the reinforcement detailing of a sub-segment of the west flange is shown in Figure 3c. The vertical and horizontal beam elements model the concrete and steel included within the section area that each element represents. Figure 3d,e illustrate the area of concrete and steel, as well as the reinforcement layout, for the vertical and horizontal elements. To model the compressive field of concrete, truss elements were employed in the diagonal directions. The effective width (beff) of the diagonal elements can be calculated as a function of the angle of the diagonal elements with the horizontal (θd), as indicated in Figure 3g (i.e., beff = asin(θd)). In the initial study by Lu and Panagiotou [51], an angle θd between 45° and 50° was employed. It has been argued that a fixed inclination angle—and the same for every member—may be inappropriate for simulating RC beams, piers, or walls. Consequently, the angle θd was revised by Lu et al. [23] to be based on a function of the shear force capacity and the amount of transverse reinforcement. Equation (1) was proposed for θd [23], with an upper limit of 65°, and a lower limit of 45° was later suggested by Arteta et al. [52] for walls with aspect ratios (i.e., H/L) greater than 1.0.
45° ≤ θd = tan−1(Vmax/fytρttwd) ≤ 65°,
where Vmax is the maximum shear force capacity (taken from experimental testing or, in the absence of experimental data, determined from moment-curvature analysis), fyt is the yield strength of the transverse reinforcement, ρt is the transverse reinforcement ratio, tw is the thickness of the wall, and d is the distance between the outer vertical lines of the model in the direction of loading. As practiced by others, the tensile strength of the concrete for these diagonal elements was ignored [51] and no reinforcement is considered in its cross-section.
It should be mentioned that the winners of the abovementioned blind prediction competition, for walls UW1 and UW2, also resorted to the BTM simulation technique. This provides further reason for the authors to have also employed it for the present investigation. A dedicated journal special issue will be soon launched in the Bulletin of Earthquake Engineering, where the contest participants—and other contributors, will have the opportunity to expand on the most recent advances on modelling and design of RC structural wall systems.

3.2. SeismoStruct

For this research investigation, the BTMs were simulated in SeismoStruct [12], a commercial software package for static and dynamic analysis of framed structures. The two-node inelastic displacement-based frame element (infrmDB) with two Gauss–Legendre integration points along their length were used for the vertical and horizontal beam elements. Although force-based elements have some advantages, displacement-based elements were chosen for this study, as this reflects what is commonly used in most engineering software packages [36]. The infrmDB elements in SeismoStruct utilize the fiber-section approach to represent the cross-section behavior, with each of the selected 150 discretized fibers associated with a uniaxial stress–strain relationship. The elastic section properties (i.e., axial, flexural, and torsional rigidity) were automatically calculated and assigned for the vertical and horizontal elements employed in the software used for this research. 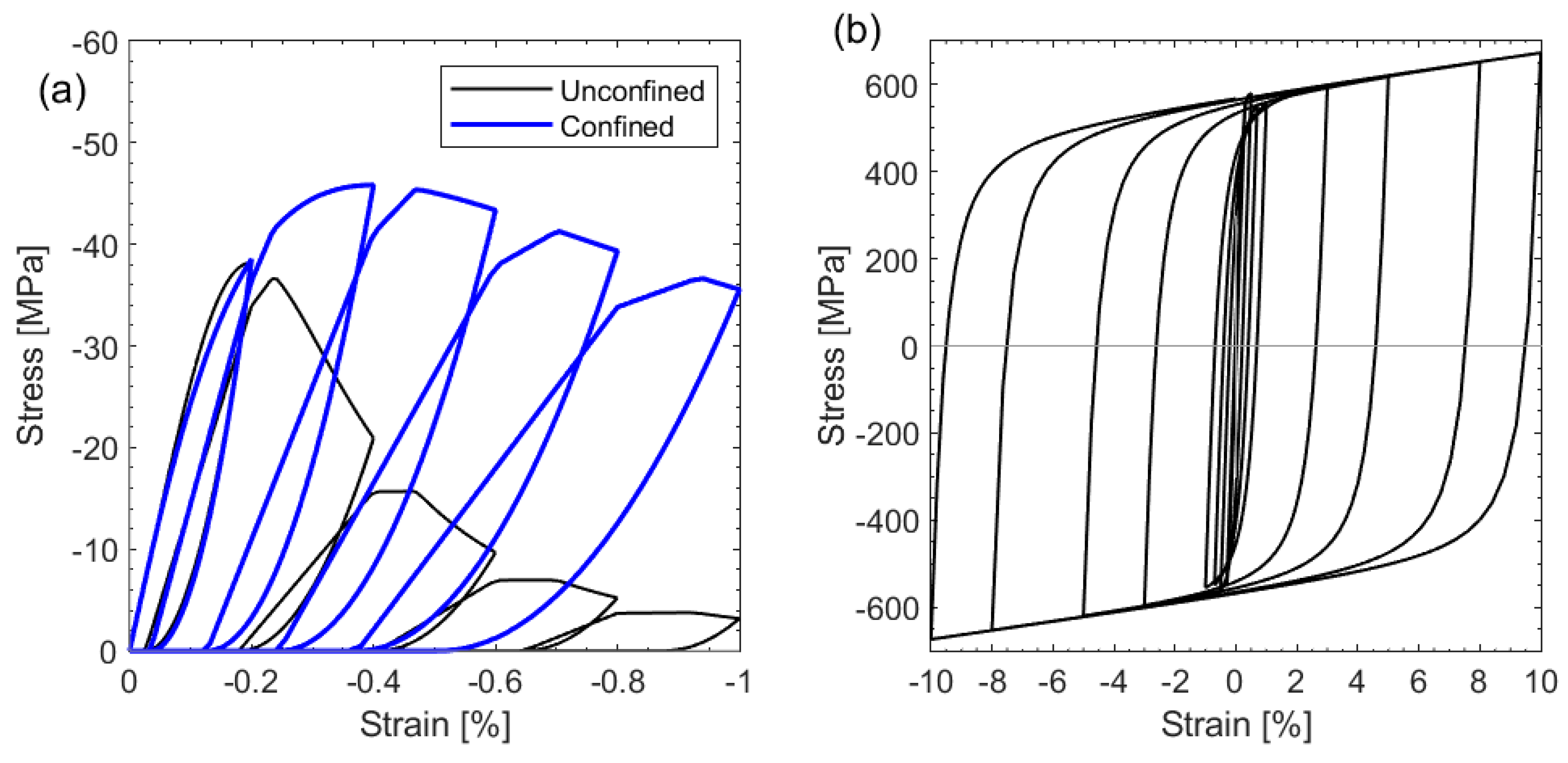As illustrated in Figure 4, the constitutive models used for the concrete and reinforcing steel correspond to those proposed by Mander et al. [53] and Menegotto-Pinto [54], respectively. Although the compression-softening behavior of the concrete in the diagonal elements has been accounted for in other numerical research using BTMs [23,51,52,55], this was not possible in the current study due to the impossibility to implement, within the commercial software, a dependence of the concrete compressive strength on the normal strain. Furthermore, reinforcement bar buckling is not modelled. However, strain limits (εlim) have been used with these simulations to help indicate some performance and failure criteria, including confined concrete crushing (εlim = −0.015), rebar buckling in compression (εlim = 0.03), and rebar fracture in tension (εlim = 0.06). These limiting strain values are based on similar values used in the literature [56,57,58,59]; when attained, the software notifies the user that they have been reached, but does not prevent loading past these points. For this study, other failure modes were not considered.
To validate the use of the proposed BTM approach for RC U-shaped wall structures, three experimental wall units, which were presented previously in Section 2, will be simulated in the next section.

3.3. BTM Results for Unit TUB

The BTM results for wall unit TUB when subjected to different reverse-cyclic loading directions are presented in Figure 5. Overall, the results from the BTM provide good comparisons to the global response of wall unit TUB for the different loading directions, comparable or superior to that obtained by other researchers using other modelling approaches [2,20,23,36]. The BTM appears to capture the force-displacement of wall unit TUB for the two in-plane directions (Figure 5a,b), including a good representation of the initial stiffness, ultimate lateral force, and unloading stiffness. The strength of one of the diagonal directions, to position F (denoted in Figure 2b), appears to have been overestimated by the BTM, shown in Figure 5c, whereas a reasonable match was obtained for the cycles toward position E. For the diagonal direction, the force and displacement were calculated as the square-root-of-the-sum-of-squares (SRSS) using the two directions of loading, consistent with the approach undertaken by Beyer et al. [19]. It is interesting to note that BTMs [23] and WCMs [2,36], as well as other modelling approaches [60], attempting to simulate the same wall unit, TUB, and in the diagonal loading direction have encountered similar strength discrepancies. In Figure 5d, the BTM numerical results compare acceptably well to the experimental restraining rotational (torsional) moment of the wall collar (i.e., head) while pushing towards position A and B. Without any restraints applied, the head of the wall would normally twist with the applied east–west loading, as the shear center of the wall is located at some distance offset from the cross-section [19]. This restraint was applied experimentally with two north–south actuators, whereas, numerically, restraints were applied (in the x-direction, according to the convention in Figure 3) to two single nodes close to the locations of the placement of the actuators. The torsional moment in Figure 5d was calculated as the average of the two restraining forces, i.e., (F1 − F2)/2, multiplied by the lever arm distance of approximately 1.2 m. Numerically, the restraining forces were extracted from SeismoStruct at the locations of the two nodes with restraints applied. It was found that the BTM developed underestimates the elastic shear center distance in comparison to that found experimentally [20], which results in a poor estimate of the early stages of torsional stiffness in Figure 5d, after an initially correct stiffness but with strength underprediction. The defined strain limits, discussed in the previous section, also reasonably predict the displacement capacity of wall unit TUB, with crushing of the confined flange boundary ends pushing towards position C (Figure 5b).

3.4. BTM Results for Units UW1 and UW2

The BTM results for wall units UW1 and UW2 are presented in Figure 6. The overall simulations from the BTM in comparison to the experimental results are very reasonable. In particular, the simulated in-plane reverse-cyclic loading to positions C–D for wall unit UW1 (Figure 6a) compare very well to the experimental global wall response. It is worth noting that the application of the axial load was found to be an important factor in simulating the correct wall response for UW1, predominantly with regards to the simulated strength in both in-plane directions. As explained by Hoult et al. [22], the axial load application experimentally caused a small overturning moment to the wall, which influenced the resulting shear span in either direction. For wall unit UW2, which was subjected to a reverse-cyclic rotation about its vertical axis, Figure 6b shows a reasonable simulated response attained from the BTM model in comparison to the experimental results. The last cycle of the simulated model wall incorrectly predicted the torque attained, which was primarily a result of the modelling method not considering buckling of the rebars. However, it is worth emphasizing that the strain limits corresponding to the performance criteria of rebar buckling (circle marker) and crushing of the confined core (cross marker) were attained during this last cycle, as depicted in Figure 6b, which not only reasonably predicts the ultimate rotation capacity of the wall unit but also correctly indicates the type of failure mode observed [22]. The strain limits also correctly indicate the ultimate displacement capacity and failure mode of wall unit UW1 in Figure 6a.

4. Case Study Structure

To further illustrate how BTMs can be used to model RC U-shaped walls, the RC core of an idealized six-storey prototype building, similar to that presented in Figure 1, was modelled using SeismoStruct [12]. For this exercise, simple pushover (or, twist-over) analyses were used to determine the capacity curves (i.e., global force-displacement or torque-rotation) for RC U-shaped core walls, i.e., applying progressively increasing levels of torque or bending moment. While it could be argued that nonlinear dynamic response-history analyses are more accurate [61,62], this method is also very time consuming and computationally expensive. Instead, the capacity spectrum method [63,64,65] was used; this method compares the capacity curve obtained from a simple pushover analysis to the seismic demand in the format of an acceleration-displacement response spectrum (ADRS). Furthermore, for this case study, it is assumed that this building is located in Melbourne, Australia, a region considered to be of low-to-moderate seismicity [66]. It should be noted that the reinforcement detailing corresponding to this modelled wall conforms more with building standards for high seismic regions, and, according to the Concrete Structures building standard of Australia AS 3600:2018 [67], this level of reinforcement detailing would likely be considered a ‘moderately ductile structural wall’ with an assigned ductility (μ) factor of 3. As civil and structural engineers in Australia have only been considering earthquake actions in their designs since 1995, it is expected that most RC walls in the building stock of low-, mid-, and even high-rise buildings are likely to have a light amount of reinforcement, which likely results in a non-ductile performance [68,69,70,71]. As such, the authors would like to emphasize that this case study building, and the resulting performance, should not be indicative of typical RC structural wall buildings in Australia. Instead, this case study is simply used to illustrate how BTMs can be used to analyze non-planar RC walls using commercial software with typical beam and truss elements.
The building plan in Figure 1a was used as a basis to design and simulate the behavior of the half-scale unit UW1 (see Section 2) prior to experimental testing. Thus, for this exercise, the original, full-scale dimensions of UW1 were used to model the RC U-shaped core wall for this building, resulting in a web length (Lw), flange length (Lf), and thickness (tw) of 2600 mm, 2100 mm, and 200 mm, respectively. Some justifications for these dimensions were given in the original Data Paper [22]. For the purpose of this exercise, the planar peripheral wall illustrated in Figure 1a on the southwest corner of the building plan is not included in these analyses. For consistency, the same longitudinal and transversal reinforcement ratios for the experimental unit UW1 were used for this model wall, and this was achieved by doubling the diameter of the rebars (see Figure 2a), with the mechanical properties of these rebars remaining unchanged (Table 1). An interstory height of 3.2 m was assumed [69], whereas the columns have a 8.4 m grid spacing, which is commonly used in office buildings in Australia [72]. The columns on the east and west building perimeters have a reduced spacing of 4.2 m. Note that it is assumed that no columns are placed close to the RC U-shaped core, where the gravity loads from the slab in this area feed directly into the flange ends of the core wall. For simplicity, distributed dead (G) and live (Q) loads of 6 kPa and 2 kPa [69] were used to calculate the axial load and, ultimately, the seismic mass of the building. This resulted in an axial load ratio (ALR) of the core wall, including self-weight, of 3.1%, whereas the total building mass (mt) was 3481.44 t. The axial load was distributed to three nodes of the BTM, corresponding to the distribution of mass from the floor plan shown in Figure 1a: the west flange boundary end (17.82 t per floor), east flange boundary end (5.94 t per floor), and middle of the web (10 t, self-weight of wall per floor). This axial load distribution is similar to what was conducted experimentally (see Section 2.2).
For this case study, the RC U-shaped core wall was modelled and subjected to different torque-to-bending-moment (T-M) ratios, considered at the base of the wall and around its weak axis, corresponding to seismic loading in the N–S direction. Such ratios represent possible different offset distances between the building center of stiffness (or rigidity) and the center of mass where the inertial loads are applied. The bending moment around the weak axis (M) was assumed to be equivalent to the applied force (F) at the effective height (i.e., M = F.he), where he was taken as 70% of the full height of the structure (i.e., he = 0.70H ≈ 13.4 m). The applied torque (T) was calculated as the applied force (F) multiplied by the offset east–west distance e of the center of stiffness (or rigidity, of the U-shaped core wall) to the building center of mass. For example, the location of the RC U-shaped core wall at the periphery of the building in Figure 1 represents the greatest offset distance (e) of approximately 16.8 m (assuming that the center of mass coincides with the center of the floor plan). The different T-M ratios and corresponding T, M, and e values are given in Table 2. A pushover analysis (i.e., pure axial–bending, T-M = 0–1) and twist-over analysis (i.e., pure axial–torque, T-M = 1–0) were also conducted to explore these limit cases.
Using these different T-M ratios (Table 2), the BTM in SeismoStruct was analyzed using a force-controlled static nonlinear pushover analysis until failure, which was determined either by the strain limits (previously discussed in Section 3.2), or when convergence could no longer be attained. Importantly, the force imposed on the wall was such that bending occurred towards position C (Figure 2b), or to the south (Figure 2a), such that the flange boundary ends were in compression, as this was previously found to be the governing direction of in-plane loading capacity (see Section 3.3 and Section 3.4).
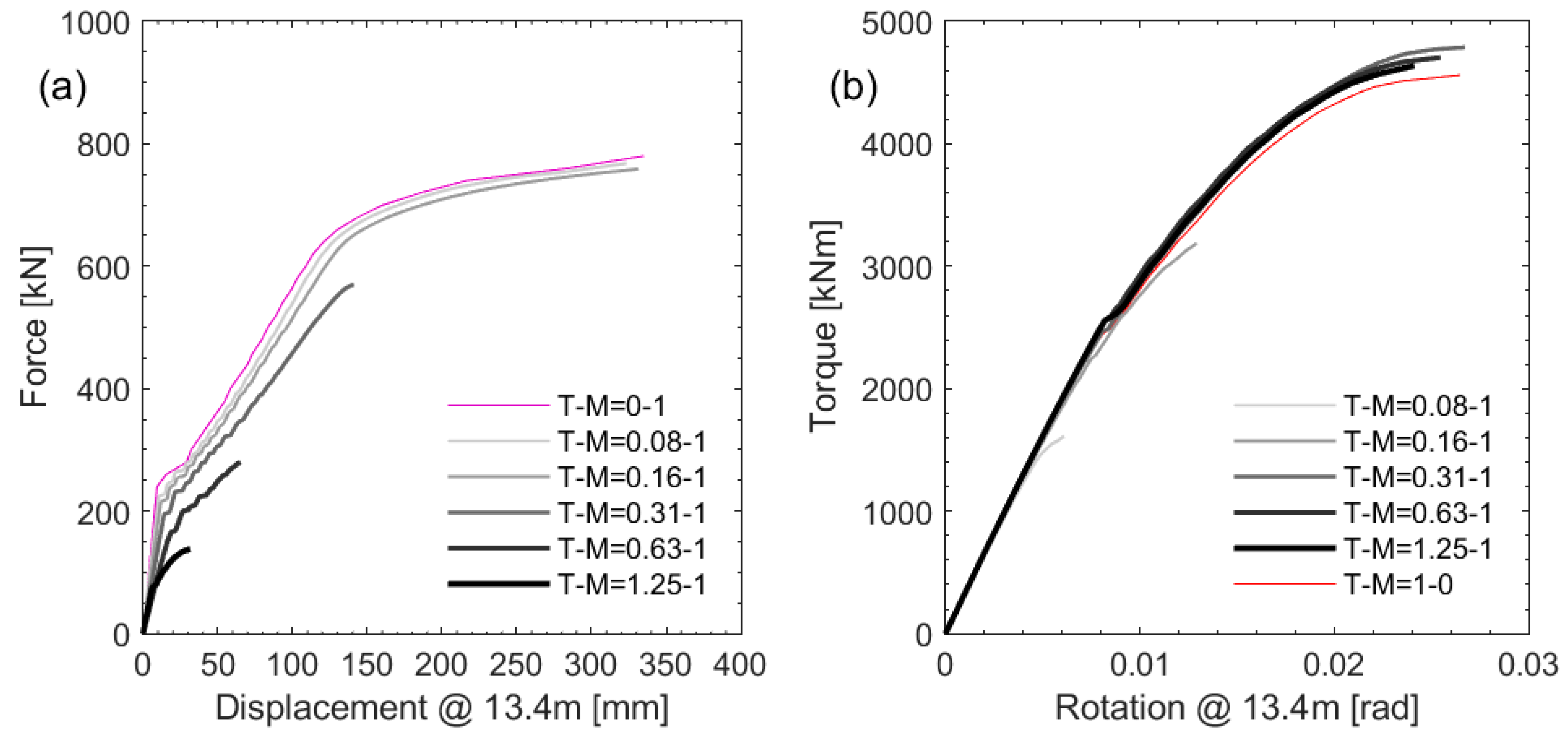
Figure 7a,b present the force-displacement and torque-rotation curves, respectively, resulting from the analyses for the different referred T-M combinations. The displacement and rotation were determined from the nodes at the effective height (he) of the wall, at 13.4 m above the base. The increasing torque contribution resulted in a decrease in both the ultimate force and translation displacement capacity attained (Figure 7a). For the case-study shown in Figure 1a, where the offset distance (e) of the RC U-shaped wall from the building center of mass was approximately 16.8 m (e.g., T-M = 1.25–1), a very large reduction in bending strength was observed, with the results in Figure 7a indicating an 82% decrease in comparison to the case with pure bending (e.g., T-M = 0–1). The results in Figure 7a also suggest that, for some T-M ratios, when a reasonably small amount of torque is applied but flexure ultimately governs the behavior of the wall (e.g., for e values in Table 2 less than 4 m), no obvious reduction in lateral strength or displacement capacity is observed.
Similar observations can be made for the torque-rotation curves, where a decrease in the contributions of the torque to the core wall (or, an increase in the contributions of the bending moment) generally results in a reduction in the ultimate torque and rotation attained at failure. Interestingly, for some T-M ratios, when the torque is still governing the behavior of the wall (e.g., for e values in Table 2 greater than 4), a small increase in the torque capacity is attained from the BTM with increasing flexure response, with no apparent decrease (or increase) in the rotation capacity. It is possible that the axial-flexure contribution to a torsion-governing core wall can increase the stiffness due to the compression zone that forms as a consequence of the translation (and pre-compression axial) loading, as postulated by Hoult and Beyer [20]. A more complete and general understanding would also require analyzing the bending towards position D (north).
The results of the static nonlinear pushover analyses presented in Figure 7 emphasize the importance of including torsional effects in the design and analysis of RC buildings, where a reduction in the bending strength of the core wall was observed for relatively low offset distances (e.g., e = 4.2 m) of the wall center of stiffness from the building’s center of mass. The pushover results with different T-M ratios were further analyzed, as shown in in Figure 8a, which presents the normalized maximum bending moment and normalized maximum torque attained for each pushover (i.e., for each T-M ratio). These values have been normalized to the maximum bending moment attained with pure axial bending (i.e., a T-M of 0–1) and maximum torque attained with pure axial torsion (i.e., a T-M of 1–0). The relationship between T and M in Figure 8a is not too dissimilar from the biaxial bending interaction curves that are typically used for the design of RC columns. It has also been noted by Maruta et al. [73] that the experimental results of different T-M combinations applied to scaled RC H-shaped walls had a similar relationship to moment-axial-force (M-N) interaction curves. The reduction in either bending strength or torque, depending on the applied combination, is clearly visible in Figure 8a.
It is likely that the RC U-shaped core wall building that has been analyzed here using a BTM would perform reasonably well in pure axial bending caused by translational ground motion accelerations along the building’s shortest direction (i.e., north–south), during a moderate earthquake (i.e., the curve corresponding to T-M = 0–1 in Figure 7a). However, the combination of torsion and bending, which can be caused by, among many factors, the natural or accidental eccentricity of the center of stiffness from the center of mass, may increase the risk of damage or even collapse due to the potentially large reduction in the bending strength. To illustrate this further, the different force-displacement capacity curves attained in Figure 7a are used in the capacity spectrum method to determine the vulnerability of the structure to an earthquake event. A force-displacement curve is presented in Figure 8b in the form of an acceleration-displacement capacity curve, which was calculated using the effective mass of the building (taken as 70% of the total seismic mass [58], i.e., 0.7 × 3481.44 t). For this example, the RC U-shaped core wall with a T-M ratio of 0.31–1 was used, corresponding to an eccentricity of the core walls of e = 4.2 m. For the seismic demand, the ground motions chosen represent an earthquake event with a 2475-year return period in the city of Melbourne using a kpZ (i.e., probability × hazard) factor of 0.144 g according to the Earthquake Actions in Australia building standard AS 1170.4:2007 [74]. The study conducted by Hoult et al. [69] found that the large majority of the RC building stock for the city of Melbourne is sited on soil class C according to AS 1170.4:2007 [74]. Furthermore, a numerical study focusing on seismicity in Australia [75] found that the influence of site resonance and low earthquake intensity resulted in spectral shape factors for soil class C that were higher than those stipulated by AS 1170.4:2007. For these reasons, the building is assumed to be on site class C. The spectral acceleration response from six scaled ground motions have been adopted from Hu et al. [76], where site-specific (i.e., class C) response spectra were derived for an event with a 2475-year return period (as classified above). The corresponding spectra for the six ground motions are superimposed in Figure 8b in the form of an acceleration-displacement response spectra (ADRS), with the mean of these six ground motions also shown. Furthermore, the ‘Target Spectrum’, which is specified in AS 1170.4:2007 [74], is also presented in Figure 8b. All elastic spectra have been scaled to an inelastic equivalent in Figure 8b by using the methods proposed by Fajfar [77], corresponding to the N2-method adopted by European standards.
The peak acceleration and displacement capacities, as determined by the capacity curve corresponding to the RC U-shaped core wall building with a T-M ratio of 0.31–1, presented in Figure 8b is found to be greater than the acceleration and displacement demand from the ground motions and target spectrum. The resulting displacement performance points for this structure, corresponding to the intersection of the capacity curve and the demand curve, are 41.5 mm and 33 mm when compared to the ground motion mean (i.e., GM Mean) and Target Spectrum, respectively. These displacements represent the order of magnitude of seismic demand that could be expected for this structure from an earthquake of this size (e.g., magnitude-distance of approximately M 6 R 23 km according to Lam et al. [78]). While the ultimate displacement capacity for this structure is 113.6 mm, reduced from 341.2 mm for pure in-plane bending, the capacity spectrum method has estimated that this structure would not reach a ‘life safe’ (or ‘no collapse’) state under the earthquake scenario considered. These values are reflected in Table 3, which reports all the performance points for the capacity curves of the RC U-shaped core wall structure with different T-M ratios, expressed in terms of the displacement and (acceleration) capacity of the structure.
While the RC U-shaped core wall with a T-M of 0.31–1 was found likely to have the capacity required to withstand an event with a 2500-year return period (on site class C) in Melbourne, there are a few points that need to be considered.
Firstly, for this structure, the capacity curve, in comparison to the demand curves in Figure 8b, indicate that it is likely that the structure would yield and perform inelastically, and thus accumulate some damage. The yielding and inelasticity of the reinforcing steel bars of the core walls are typically a source of residual displacements of RC buildings (i.e., the permanent relative deformation of a structure with respect to its initial geometry) [30]. Thus, while the primary performance level of ‘life safe’ could be achieved, the damage and permanent deformation of this structure could prevent the building from being serviceable and, in some cases, require demolition. For an example, see the number of demolitions that were required for modern-designed RC buildings in the Christchurch Central Business District (CBD) [79,80]. The authors are conducting ongoing research in this area using smarter reinforcing materials to reduce the residual displacements of RC walls.
Secondly, not all of the RC U-shaped core wall structures investigated here, with different T-M ratios, were determined to have sufficient in-plane bending capacity for the earthquake ground motions considered. For example, for the core wall with a T-M of 0.63–1, Table 3 indicates that the displacement capacity satisfies the ‘life safety’ performance if compared to the demand from the inelastic Target Spectrum (adopted from AS 1170.4:2007 [74])—however, the displacement demand of some ground motions exceeded the capacity of the core wall with a T-M of 0.63–1. Furthermore, the structure with T-M of 1.25–1, which represents the building plan in Figure 1a, was determined to reach collapse under these ground motions due to the dominance of torsional actions severely reducing the in-plane flexural strength and displacement capacity.
Finally, the authors want to re-emphasize that the reinforcement detailing of this RC U-shaped core wall does not reflect current construction practices in Australia, where most walls are only now (i.e., post-2018) being designed for ‘limited ductility’ [67], corresponding to very little, if any, confinement, but providing a sufficient amount of longitudinal reinforcement to allow secondary cracking [81]. However, prior to the revised concrete structures Australian Standards building code AS 3600:2018 [67], the minimum longitudinal reinforcement ratio requirements for RC walls were derived for the control of shrinkage and thermal effects [68,82] and not for ductility. Thus, it is likely that typical RC core walls in the Australian building stock would be more vulnerable to the earthquake demands used for this case study, and as such the results herein should not be indicative of their performance.

5. Conclusions

Beam-truss models (BTMs) were used in this numerical investigation to simulate the axial, flexure, and torsional performance of non-planar RC walls, with a primary focus on the popular U-shaped cross-section. The BTMs developed in this research, using the recommendations from other researchers, were shown to simulate the experimental behavior of previously tested RC walls to a high degree of accuracy, including their torsional performance. To the knowledge of the authors, previous macro and micro models in the literature used to simulate RC walls have not been fully validated for torsional actions given the scarcity of experimental data. The experimental results for at least one wall unit tested at UCLouvain, Belgium, has helped overcome some of these limitations by subjecting the wall to pure reverse-cyclic axial torsion (rotation) until failure. The global torque-rotation performance experimentally measured in this test was used in this research to further validate the BTM developed using the commercial software SeismoStruct. However, it is worth noting that the ability of BTMs developed here in simulating torsional behavior implies that circulatory torsion, or Saint-Venant torsion, is negligible, which is typical of open, non-planar sections. The dataset from this recent experimental program at UCLouvain is now readily available (DOI: 10.14428/DVN/FDJ4EU) and can be used to help validate future macro and micro models of non-planar walls on the global level (e.g., force displacement) and also on the local level (e.g., strain profiles of the longitudinal reinforcement).
BTMs were further utilized in a case study of an idealized RC building with varying eccentricity between the center of stiffness, provided mainly by a single RC U-shaped periphery core wall, to the assumed center of mass. As such, different torque-to-bending-moment (T-M) ratios were subjected to the BTM in SeismoStruct to develop a set of force-displacement and torque-rotation curves using simple static nonlinear pushover analyses. The pushover analyses showed that the increasing contribution of torque reduced, sometimes significantly, the in-plane bending strength and displacement capacity of the RC U-shaped core wall structure. The capacity spectrum method was then used to estimate the seismic performance of these RC-wall buildings, with different T-M ratios, using demand curves representative of an event with a 2475-year return period in Melbourne, Australia, sited on soil class C. It was shown that this ‘moderately ductile’ RC core wall was likely to have a sufficient strength and displacement capacity for the earthquake event considered if no torsion is assumed (i.e., T-M = 0–1). However, eccentricity distances of the core wall from the center of mass greater than approximately 2.1 m (i.e., T-M = 0.16–1) resulted in a substantial decrease in the in-plane flexural strength and displacement capacity of the building due to the contribution of torsion, resulting in potential collapse of the structure under this earthquake scenario. These results emphasize the importance of including torsional actions in simulating the seismic performance of RC buildings.
The authors, as part of a larger user group, expect to conduct further experimental testing on RC U-shaped core walls in 2023, including the testing of two large-scale units subjected to earthquake ground motions using a shaking table at the National Laboratory for Civil Engineering (LNEC), Portugal. The experimental results from these tests will help to further validate macro and micro models of non-planar walls, particularly with regard to the use of nonlinear response-history analyses, rather than simpler methods of assessment, such as the capacity spectrum method that was used in the work undertaken here. A dedicated journal special issue will also be soon launched to present and discuss the most recent advances in the modelling and design of RC structural wall systems.

Author Contributions

Conceptualization, R.H., A.A.C. and J.P.d.A.; methodology, R.H., A.A.C. and J.P.d.A.; software, R.H., A.A.C. and J.P.d.A.; data curation, R.H.; writing—original draft preparation, R.H.; writing—review and editing, R.H., A.A.C. and J.P.d.A.; funding acquisition, J.P.d.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Fonds de la Recherche Scientifique (FNRS) grant number F.4501.21.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original experimental dataset for units UW1 and UW2, which was used to help validate some of the beam-truss models used in this paper, can be downloaded from the publicly accessible platform Dataverse, https://doi.org/10.14428/DVN/FDJ4EU. Furthermore, the original experimental dataset for unit TUB, also used in this paper for validation purposes, can be downloaded from the publicly accessible platform Zenodo, https://doi.org/10.5281/zenodo.21846.

Acknowledgments

The authors’ gratitude goes to the efforts and invaluable assistance of Mathis Keirle, who numerically simulated non-planar RC walls using beam-truss models as part of his Master of Civil Engineering studies http://hdl.handle.net/2078.1/thesis:37860 (accessed on 10 March 2023).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hoult, R.D.; Lumantarna, E.; Goldsworthy, H.M. Torsional displacement for asymmetric low-rise buildings with RC C-shaped cores. In Proceedings of the Tenth Pacific Conference on Earthquake Engineering, Sydney, Australia, 6–8 November 2015. [Google Scholar]
  2. Pelletier, K.; Léger, P. Nonlinear seismic modeling of reinforced concrete cores including torsion. Eng. Struct. 2017, 136, 380–392. [Google Scholar] [CrossRef] [Green Version]
  3. Peng, X.N.; Wong, Y.L. Seismic behavior of asymmetric RC frame building systems with one major wall. In Proceedings of the 14th World Conference on Earthquake Engineering (14WCEE), Beijing, China, 12–17 October 2008. [Google Scholar]
  4. Menegon, S.J.; Wilson, J.L.; Lam, N.T.K.; Gad, E.F. RC walls in Australia: Reconnaissance survey of industry and literature review of experimental testing. Aust. J. Struct. Eng. 2017, 18, 24–40. [Google Scholar] [CrossRef]
  5. Çelebi, M.; Ghahari, S.F.; Haddadi, H.; Taciroglu, E. Response study of the tallest California building inferred from the Mw7.1 Ridgecrest, California earthquake of 5 July 2019 and ambient motions. Earthq. Spectra 2020, 36, 1096–1118. [Google Scholar] [CrossRef]
  6. Coull, A.; Tawfik, S.Y. Analysis of core structures subjected to torsion. Build. Environ. 1981, 16, 221–228. [Google Scholar] [CrossRef]
  7. Stefano, M.D.; Tanganelli, M.; Viti, S. Concrete strength variability as a source of irregularity for existing RC structures. In Computational Methods, Seismic Protection, Hybrid Testing and Resilience in Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2015; pp. 287–306. [Google Scholar]
  8. Stafford Smith, B.; Coull, A. Tall Building Structures: Analysis and Design; Wiley: New York, NY, USA, 1991. [Google Scholar]
  9. Cooper, M.; Carter, R.; Fenwick, R. Canterbury Earthquakes Royal Commission (CERC) Final Report; Royal Commission of Inquiry: Christchurch, New Zealand, 2012. [Google Scholar]
  10. Marcilla, T.; Leil, A. Torsional irregularity as a collapse indicator for older concrete buildings. In Proceedings of the 11th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Los Angeles, CA, USA, 25–29 June 2018. [Google Scholar]
  11. Seibel, W. Erosion of professional integrity: The collapse of the canterbury TV building in christchurch on 22 February 2011. In Collapsing Structures and Public Mismanagement; Springer International Publishing: Cham, Switzerland, 2022; pp. 87–128. [Google Scholar]
  12. SeismoSoft SeismoStruct. Release-1 Build-5. 2023. Available online: www.seismosoft.com (accessed on 30 December 2022).
  13. Ile, N.; Reynouard, J.M. Behaviour of U-shaped Walls Subjected to Uniaxial and Biaxial Cyclic Lateral Loading. J. Earthq. Eng. 2005, 9, 67–94. [Google Scholar] [CrossRef]
  14. Behrouzi, A.A.; Mock, A.W.; Lehman, D.E.; Lowes, L.N.; Kuchma, D.A. Impact of bi-directional loading on the seismic performance of C-shaped piers of core walls. Eng. Struct. 2020, 225, 111289. [Google Scholar] [CrossRef]
  15. Li, J.; Chen, L.; Wang, X.; Li, F. Study and Numerical Analysis on Seismic Performance of Concrete U-Shaped Shear Wall. Adv. Mater. Sci. Eng. 2022, 2022, 2838691. [Google Scholar] [CrossRef]
  16. Ile, N.; Plumier, C.; Reynouard, J.M. Test program on U-shaped walls leading to model validation and implications to design. In Proceedings of the The 12th European Conference on Earthquake Engineering, Barbicon Centre, London, UK, 9–13 September 2002. [Google Scholar]
  17. Hoult, R.; Appelle, A.; Almeida, J.; Beyer, K. Seismic performance of slender RC U-shaped walls with a single-layer of reinforcement. Eng. Struct. 2020, 225, 111257. [Google Scholar] [CrossRef]
  18. Constantin, R.; Beyer, K. Behaviour of U-shaped RC walls under quasi-static cyclic diagonal loading. Eng. Struct. 2016, 106, 36–52. [Google Scholar] [CrossRef] [Green Version]
  19. Beyer, K.; Dazio, A.; Priestley, M.J.N. Quasi-Static Cyclic Tests of Two U-Shaped Reinforced Concrete Walls. J. Earthq. Eng. 2008, 12, 1023–1053. [Google Scholar] [CrossRef]
  20. Hoult, R.; Beyer, K. Decay of Torsional Stiffness in RC U-Shaped Walls. J. Struct. Eng. 2020, 146, 04020176. [Google Scholar] [CrossRef]
  21. Guéguen, P.; Astorga, A. The torsional response of civil engineering structures during earthquake from an observational point of view. Sensors 2021, 21, 342. [Google Scholar] [CrossRef]
  22. Hoult, R.; Doneux, C.; Almeida, J.P.d. Tests on Reinforced Concrete U-shaped Walls Subjected to Torsion and Flexure. Earthq. Spectra 2022, Submitted. [Google Scholar]
  23. Lu, Y.; Panagiotou, M.; Koutromanos, I. Three-dimensional beam-truss model for reinforced concrete walls and slabs—Part 1: Modeling approach, validation, and parametric study for individual reinforced concrete walls. Earthq. Eng. Struc. 2016, 45, 1495–1513. [Google Scholar] [CrossRef]
  24. Hoult, R.; Doneux, C.; Almeida, J.P.d. A blind prediction of the seismic and torsional performance of RC U-shaped core walls. In Proceedings of the 3rd European Conference on Earthquake Engineering and Seismology, Bucharest, Romania, 4–9 September 2022. [Google Scholar]
  25. Hoult, R.; Doneux, C.; Almeida, J.P.d. Blind prediction results of two RC U-shaped walls subjected to flexure and torsion. In Proceedings of the Australian Earthquake Engineering (AEES) Conference, Mt Macedon, Victoria, Australia, 24–25 November 2022. [Google Scholar]
  26. Vulcano, A.; Bertero, V.V.; Colotti, V. Analytical modeling of RC structural walls. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1988; pp. 41–46. [Google Scholar]
  27. Orakcal, K.; Wallace, J.W.; Conte, J.P. Flexural modeling of reinforced concrete walls-model attributes. ACI Struct. J. 2004, 101, 688–698. [Google Scholar]
  28. Kolozvari, K.; Kalbasi, K.; Orakcal, K.; Wallace, J. Three-dimensional shear-flexure interaction model for analysis of non-planar reinforced concrete walls. J. Build. Eng. 2021, 44, 102946. [Google Scholar] [CrossRef]
  29. Isaković, T.; Fischinger, M. Assessment of a force–displacement based multiple-vertical-line element to simulate the non-linear axial–shear–flexure interaction behaviour of reinforced concrete walls. Bull. Earthq. Eng. 2019, 17, 6369–6389. [Google Scholar] [CrossRef]
  30. Hoult, R.D.; Almeida, J.P.d. Residual displacements of reinforced concrete walls detailed with conventional steel and shape memory alloy rebars. Eng. Struct. 2022, 256, 114002. [Google Scholar] [CrossRef]
  31. Clark, B.J.; Farrokhi, R.; Abdelbadie, A.; Epackachi, S.; Sadeghian, V. Macro modelling of RC shear walls. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 13–18 September 2020. [Google Scholar]
  32. Almeida, J.P.; Tarquini, D.; Beyer, K. Modelling Approaches for Inelastic Behaviour of RC Walls: Multi-level Assessment and Dependability of Results. Arch. Comput. Methods Eng. 2016, 23, 69–100. [Google Scholar] [CrossRef] [Green Version]
  33. Pozo, J.D.; Hube, M.A.; Kurama, Y.C. Quantitative assessment of nonlinear macro-models for global behavior and design of planar RC walls. Eng. Struct. 2020, 224, 111190. [Google Scholar] [CrossRef]
  34. Wu, Y.-T.; Lan, T.-Q.; Xiao, Y.; Yang, Y.-B. Macro-Modeling of Reinforced Concrete Structural Walls: State-of-the-Art. J. Earthq. Eng. 2017, 21, 652–678. [Google Scholar] [CrossRef]
  35. Kolozvari, K.; Arteta, C.; Fischinger, M.; Gavridou, S.; Hube, M.; Isakovic´, T.; Lowes, L.; Orakcal, K.; Vásquez, J.; Wallace, J. Comparative Study of State-of-the-Art Macroscopic Models for Planar Reinforced Concrete Walls. ACI Struct. J. 2018, 115, 1637–1657. [Google Scholar] [CrossRef]
  36. Beyer, K.; Dazio, A.; Priestley, M.J.N. Inelastic Wide-Column Models for U-Shaped Reinforced Concrete Walls. J. Earthq. Eng. 2008, 12, 1–33. [Google Scholar] [CrossRef]
  37. Clough, R.W.; King, I.P.; Wilson, E.L. Structural analysis of multistory buildings. J. Struct. Div. 1964, 90, 19–34. [Google Scholar] [CrossRef]
  38. MacLeod, I. Analysis of shear wall buildings by the frame method. Proc. Inst. Civ. Eng. 1973, 55, 593–603. [Google Scholar] [CrossRef]
  39. MacLeod, I.A.; Hosny, H.M. Frame analysis of shear wall cores. J. Struct. Div. 1977, 103, 2037–2047. [Google Scholar] [CrossRef]
  40. Stafford Smith, B.; Abate, A. Analysis of non-planar shear wall assemblies by analogous frame. Proc. Inst. Civ. Eng. 1981, 71, 395–406. [Google Scholar] [CrossRef]
  41. Xenidis, H.; Avramidis, I. Comparative performance of code prescribed analysis methods for R/C buildings with shear wall cores. In Structural Dynamics: EURODYN’99; Balkema Publishers: Leiden, The Netherlands, 1999; Volume 2, pp. 869–875. [Google Scholar]
  42. Stafford-Smith, B.; Girgis, A. Deficiencies in the Wide Column Analogy for Shearwall Core Analysis. Concr. Int. 1986, 8, 58–61. [Google Scholar]
  43. Reynouard, J.; Fardis, M. Shear wall structures. In CAFEEL-ECOEST/ICONS Thematic Report No. 5; LNEC (Laboratório Nacional de Engenharia Civil): Lisboa, Portgual, 2001. [Google Scholar]
  44. Avramidis, I. Zur Kritik des äquivalenten Rahmenmodells für Wandscheiben und Hochhauskerne (Criticism of the equivalent frame model for structural walls and cores in high-rise buldings). Bautechnik 1991, 68, 275–285. [Google Scholar]
  45. Xenidis, H.; Athanatopoulou, A.; Avramidis, I. Modelling of shear wall cores under earthquake loading using equivalent frames. In Proceedings of the 2nd European Conference on Structural Dynamics: EURODYN ’93, Trondheim, Norway, 21–23 June 1993; pp. 901–910. [Google Scholar]
  46. Arabzadeh, H.; Galal, K. Seismic-Response Analysis of RC C-Shaped Core Walls Subjected to Combined Flexure, Shear, and Torsion. J. Struct. Eng. 2018, 144, 04018165. [Google Scholar] [CrossRef]
  47. Arabzadeh, H.; Galal, K. Seismic Collapse Risk Assessment and FRP Retrofitting of RC Coupled C-Shaped Core Walls Using the FEMA P695 Methodology. J. Struct. Eng. 2017, 143, 04017096. [Google Scholar] [CrossRef]
  48. Encina, J.; de la Llera, J.C. A simplified model for the analysis of free plan buildings using a wide-column model. Eng. Struct. 2013, 56, 738–748. [Google Scholar] [CrossRef]
  49. Beyer, K.; Dazio, A.; Priestley, M.J.N. Shear Deformations of Slender Reinforced Concrete Walls under Seismic Loading. ACI Struct. J. 2011, 108, 167–177. [Google Scholar]
  50. Krpan, P.; Collins, M.P. Predicting Torsional Response of Thin-Walled Open RC Members. J. Struct. Div. 1981, 107, 1107–1127. [Google Scholar] [CrossRef]
  51. Lu, Y.; Panagiotou, M. Three-Dimensional Cyclic Beam-Truss Model for Nonplanar Reinforced Concrete Walls. J. Struct. Eng. 2014, 140, 04013071. [Google Scholar] [CrossRef]
  52. Arteta, C.A.; Araújo, G.A.; Torregroza, A.M.; Martínez, A.F.; Lu, Y. Hybrid approach for simulating shear–flexure interaction in RC walls with nonlinear truss and fiber models. Bull. Earthq. Eng. 2019, 17, 6437–6462. [Google Scholar] [CrossRef]
  53. Mander, J.; Priestley, N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
  54. Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending. In Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1973; pp. 15–22. [Google Scholar]
  55. Carrillo, J.; Cubillos, E.; Parra, P.F. Modeling the seismic response of thin concrete walls using the non-linear Beam-Truss Model. J. Build. Eng. 2022, 52, 104424. [Google Scholar] [CrossRef]
  56. Deng, X.; Koutromanos, I.; Murcia-Delso, J.; Panagiotou, M. Nonlinear truss models for strain-based seismic evaluation of planar RC walls. Earthq. Eng. Struc. 2021, 50, 2939–2960. [Google Scholar] [CrossRef]
  57. Hoult, R.D.; Goldsworthy, H.M.; Lumantarna, E. Plastic hinge analysis for lightly reinforced and unconfined concrete structural walls. Bull. Earthq. Eng. 2018, 16, 4825–4860. [Google Scholar] [CrossRef]
  58. Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M.J. Displacement-Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007. [Google Scholar]
  59. Menegon, S.J.; Wilson, J.L.; Lam, N.T.K.; Gad, E.F. Experimental Testing of Nonductile Reinforced Concrete Wall Boundary Elements. ACI Struct. J. 2019, 116, 213–225. [Google Scholar] [CrossRef] [Green Version]
  60. Kolozvari, K.; Piatos, G.; Beyer, K. Practical nonlinear modeling of U-shaped reinforced concrete walls under bi-directional loading. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
  61. Causevic, M.; Mitrovic, S. Comparison between non-linear dynamic and static seismic analysis of structures according to European and US provisions. Bull. Earthq. Eng. 2011, 9, 467–489. [Google Scholar] [CrossRef]
  62. Antoniou, S.; Pinho, R. Advantages and limitations of adaptive and non-adaptive force-based pushover procedures. J. Earthq. Eng. 2004, 08, 497–522. [Google Scholar] [CrossRef]
  63. Freeman, S.; Nicoletti, J.; Tyrell, J. Evaluations of existing buildings for seismic risk–A case study of puget sound naval shipyard, Bremerton, Washington. In Proceedings of the 1st US National Conference on Earthquake Engineering, Ann Arbor, Michigan, 18–20 June 1975. [Google Scholar]
  64. Freeman, S.A. Prediction of response of concrete buildings to severe earthquake motion. Spec. Publ. 1978, 55, 589–606. [Google Scholar]
  65. Freeman, S.A. The capacity spectrum method as a tool for seismic design. In Proceedings of the 11th European conference on earthquake engineering, Paris, France, 6–11 September 1998; pp. 6–11. [Google Scholar]
  66. Hoult, R.D.; Pascal, A.; Jones, A.; Allen, T. The mw 5.9 woods point earthquake: A preliminary investigation of the ground motion observations. In Proceedings of the Australian Earthquake Engineering Society 2021 Conference, Virtual, 25–26 November 2021. [Google Scholar]
  67. AS 3600-2018; Concrete Structures. Standards Australi: Sydney, Australia, 2018.
  68. Hoult, R.; Goldsworthy, H.; Lumantarna, E. Plastic Hinge Length for Lightly Reinforced Rectangular Concrete Walls. J. Earthq. Eng. 2018, 22, 1447–1478. [Google Scholar] [CrossRef]
  69. Hoult, R.; Goldsworthy, H.; Lumantarna, E. Fragility Functions for RC Shear Wall Buildings in Australia. Earthq. Spectra 2019, 35, 333–360. [Google Scholar] [CrossRef]
  70. Lu, Y.; Henry, R.S. Comparison of Minimum Vertical Reinforcement Requirements for Reinforced Concrete Walls. ACI Struct. J. 2018, 115, 673–687. [Google Scholar] [CrossRef]
  71. Lu, Y.; Henry, R.S.; Gultom, R.; Ma, Q.T. Cyclic Testing of Reinforced Concrete Walls with Distributed Minimum Vertical Reinforcement. J. Struct. Eng. 2016, 143, 04016225. [Google Scholar] [CrossRef]
  72. Hoult, R.D.; Goldsworthy, H.M.; Lumantarna, E. Seismic assessment of non-ductile reinforced concrete C-shaped walls. In Proceedings of the SEC 2015-8th International Structural Engineering and Construction Conference: Implementing Innovative Ideas in Structural Engineering and Project Management, Sydney, Australia, 23–28 November 2015; pp. 331–336. [Google Scholar]
  73. Maruta, M.; Suzuki, N.; Miyashita, T.; Nishioka, T. Structural capacities of H-shaped RC core wall subjected to lateral load and torsion. In 12th WCEE; The New Zealand Society for Earthquake Engineering: Wellington, New Zealand, 2000. [Google Scholar]
  74. AS 1170.4-2007; Structural Design Actions, Part 4: Earthquake Actions in Australia (Incorporating Amendments Nos 1 and 2). Standards Australia: Sydney, Australia, 2007.
  75. Hoult, R.D.; Lumantarna, E.; Goldsworthy, H.M. Soil amplification in low-to-moderate seismic regions. Bull. Earthq. Eng. 2017, 15, 1945–1963. [Google Scholar] [CrossRef]
  76. Hu, Y.; Lam, N.; Khatiwada, P.; Lumantarna, E.; Tsang, H.H.; Menegon, S. Site specific response spectra and accelerograms on bedrock and soil structure. CivilEng 2023, 4, 134–150. [Google Scholar] [CrossRef]
  77. Fajfar, P. A Nonlinear Analysis Method for Performance-Based Seismic Design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
  78. Lam, N.; Sinadinovski, C.; Koo, R.; Wilson, J.L.; Doherty, K. Peak ground velocity modelling for Australian intraplate earthquakes. J. Seismol. Earthq. Eng. 2003, 5, 11–22. [Google Scholar]
  79. Muir-Wood, R. The Christchurch earthquakes of 2010 and 2011. In The Geneva Risk Reports. Risk and Insurance Research. Extreme Events and Insurance: 2011 Annus Horribilis; The Geneva Association: Zurich, Switzerland, 2015. [Google Scholar]
  80. Gonzalez, R.E.; Stephens, M.T.; Toma, C.; Elwood, K.J.; Dowdell, D. Post-earthquake demolition in Christchurch, New Zealand: A case-study towards incorporating environmental impacts in demolition decisions. In Advances in Assessment and Modeling of Earthquake Loss; Akkar, S., Ilki, A., Goksu, C., Erdik, M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 47–64. [Google Scholar]
  81. Hoult, R. Minimum Longitudinal Reinforcement Requirements for Boundary Elements of Limited Ductile Walls for AS 3600. Electron. J. Struct. Eng. 2017, 17, 43–52. [Google Scholar] [CrossRef]
  82. AS 3600-2009 Supp 1:2014; Concrete Structures-Commentary (Supplement to AS 3600-2009). Standards Australia: Sydney, Australia, 2014.
Civileng 04 00017 g001 550
Figure 1. (a) Building plan with an RC U-shaped peripheral core wall (b) three-dimensional (3D) elevation view of an idealized six-story building with a single peripheral RC U-shaped core wall (adapted from SeismoStruct [12]; other structural members, such as beams, are not illustrated).
Figure 1. (a) Building plan with an RC U-shaped peripheral core wall (b) three-dimensional (3D) elevation view of an idealized six-story building with a single peripheral RC U-shaped core wall (adapted from SeismoStruct [12]; other structural members, such as beams, are not illustrated).
Civileng 04 00017 g001
Civileng 04 00017 g002 550
Figure 2. (a) Cross-section and reinforcement detailing of TUB [19], UW1, and UW2 [22], with dimensions in mm (b) loading positions for the test units. The superscripts “a” and “b” denote the different spacing or diameter of the rebar for units TUB and UW1/UW2, respectively. The positive (or plus “+”) signs indicate the experimental convention for positive direction of loading.
Figure 2. (a) Cross-section and reinforcement detailing of TUB [19], UW1, and UW2 [22], with dimensions in mm (b) loading positions for the test units. The superscripts “a” and “b” denote the different spacing or diameter of the rebar for units TUB and UW1/UW2, respectively. The positive (or plus “+”) signs indicate the experimental convention for positive direction of loading.
Civileng 04 00017 g002
Civileng 04 00017 g003 550
Figure 3. Schematic illustration of the beam-truss model approach for a U-shaped wall (adapted from Lu et al. [23] and modified for the wall section of interest for this work).
Figure 3. Schematic illustration of the beam-truss model approach for a U-shaped wall (adapted from Lu et al. [23] and modified for the wall section of interest for this work).
Civileng 04 00017 g003
Civileng 04 00017 g004 550
Figure 4. Constitutive stress–strain models for the material models’ (a) concrete proposed by Mander et al. [53] (a confinement factor of 1.2 was used) and (b) reinforcing steel proposed by Menegotto-Pinto [54]. For these illustrated cyclic (or reverse-cyclic) stress–strain examples, the material properties correspond to those for wall unit UW1.
Figure 4. Constitutive stress–strain models for the material models’ (a) concrete proposed by Mander et al. [53] (a confinement factor of 1.2 was used) and (b) reinforcing steel proposed by Menegotto-Pinto [54]. For these illustrated cyclic (or reverse-cyclic) stress–strain examples, the material properties correspond to those for wall unit UW1.
Civileng 04 00017 g004
Civileng 04 00017 g005 550
Figure 5. Beam-truss model results using SeismoStruct compared to the experimental results for wall unit TUB [19] for (a) east–west cycles, position A–B (b) north–south cycles, position C–D, (c) diagonal cycles, position E–F, and (d) restraining torsional moment. The cross, circle, and square markers indicate the numerically estimated concrete crushing, rebar buckling, and rebar fracture, respectively, corresponding to the defined strain limits.
Figure 5. Beam-truss model results using SeismoStruct compared to the experimental results for wall unit TUB [19] for (a) east–west cycles, position A–B (b) north–south cycles, position C–D, (c) diagonal cycles, position E–F, and (d) restraining torsional moment. The cross, circle, and square markers indicate the numerically estimated concrete crushing, rebar buckling, and rebar fracture, respectively, corresponding to the defined strain limits.
Civileng 04 00017 g005
Civileng 04 00017 g006 550
Figure 6. Beam-truss model results using SeismoStruct compared to the experimental results for (a) wall unit UW1 [22], north–south cycles, positions C–D and (b) wall unit UW2 [22], rotation cycles, positions O±. The cross and circle markers indicate the numerically estimated concrete crushing and rebar buckling, respectively, corresponding to the defined strain limits.
Figure 6. Beam-truss model results using SeismoStruct compared to the experimental results for (a) wall unit UW1 [22], north–south cycles, positions C–D and (b) wall unit UW2 [22], rotation cycles, positions O±. The cross and circle markers indicate the numerically estimated concrete crushing and rebar buckling, respectively, corresponding to the defined strain limits.
Civileng 04 00017 g006
Civileng 04 00017 g007 550
Figure 7. Results from the static pushover analysis performed on the RC U-shaped core wall modelled in SeismoStruct using the beam-truss modelling approach regarding (a) force-displacement and (b) torque-rotation. Different torque-to-bending-moment (T-M) ratios were used in these analyses.
Figure 7. Results from the static pushover analysis performed on the RC U-shaped core wall modelled in SeismoStruct using the beam-truss modelling approach regarding (a) force-displacement and (b) torque-rotation. Different torque-to-bending-moment (T-M) ratios were used in these analyses.
Civileng 04 00017 g007
Civileng 04 00017 g008 550
Figure 8. (a) Normalized maximum bending moment (M) and torque (T) relationship using the last converged point (corresponding to peak strength) of the different nonlinear pushover analyses performed; (b) the capacity spectrum method using inelastic spectra is applied to the pushover result for the wall with T-M = 0.31–1, comparing it to the acceleration-displacement inelastic response spectra corresponding to an event with a 2500-year return period in Melbourne on site class C.
Figure 8. (a) Normalized maximum bending moment (M) and torque (T) relationship using the last converged point (corresponding to peak strength) of the different nonlinear pushover analyses performed; (b) the capacity spectrum method using inelastic spectra is applied to the pushover result for the wall with T-M = 0.31–1, comparing it to the acceleration-displacement inelastic response spectra corresponding to an event with a 2500-year return period in Melbourne on site class C.
Civileng 04 00017 g008
Table
Table 1. Comparison of wall parameters and material property values of wall units.
Table 1. Comparison of wall parameters and material property values of wall units.
TUBUW1UW2
Shear span M/V, m2.95 a/3.35 b6.72 c2.25
Axial Load, kN780.0611.2593.6
Axial load ratio, %455
Concrete strength (fc), MPa54.738.237.1
Young’s modulus of concrete, MPa-27,49425,891
Yield strength of 12 mm steel (fy), MPa471580580
Ultimate strength of 12 mm steel (fu), MPa574690690
Ultimate strain of 12 mm steel (εsu), %12.710.110.1
Yield strength of 6 mm steel (fy), MPa518550550
Ultimate strength of 6 mm steel (fu), MPa681676676
Ultimate strain of 6 mm steel (εsu), %8.49.59.5
a NS direction, parallel to the flanges (positions C–D), b EW direction, parallel to the web (positions A–B), c excluding the pre-compression overturning moment.
Table
Table 2. Torque-to-bending-moment (T-M) ratios used to load the RC U-shaped core wall structure (where N/A means “not applicable”).
Table 2. Torque-to-bending-moment (T-M) ratios used to load the RC U-shaped core wall structure (where N/A means “not applicable”).
T-M RatioT [kNm]M [kNm]e (m)
0–1N/A13.4 F0
0.08–11.05 F13.4 F1.05
0.16–12.1 F13.4 F2.1
0.31–14.2 F13.4 F4.2
0.63–18.4 F13.4 F8.4
1.25–116.8 F13.4 F16.8
1–0N/AN/A∞
Table
Table 3. The displacement demand (in mm) and acceleration demand (in parenthesis, given in ‘g’ units) are presented for the equivalent single-degree-of-freedom system, representing the RC U-shaped wall building structure, subjected to different combinations of torque and bending moment (T-M). The peak capacity for the building is presented (final column), which can be compared to the ground motion demands, their mean, or the demand calculated from the code spectrum (AS 1170.4:2007).
Table 3. The displacement demand (in mm) and acceleration demand (in parenthesis, given in ‘g’ units) are presented for the equivalent single-degree-of-freedom system, representing the RC U-shaped wall building structure, subjected to different combinations of torque and bending moment (T-M). The peak capacity for the building is presented (final column), which can be compared to the ground motion demands, their mean, or the demand calculated from the code spectrum (AS 1170.4:2007).
T-MGM1GM 2GM 3GM 4GM 5GM 6MeanTarget SpectrumUltimate Capacity
0–121.821.957.823.034.758.136.231.3341.2
(0.11)(0.11)(0.16)(0.11)(0.13)(0.16)(0.13)(0.12)(0.32)
0.08–121.721.759.923.634.670.538.732.0321.2
(0.11)(0.11)(0.16)(0.11)(0.12)(0.17)(0.13)(0.12)(0.31)
0.16–121.421.259.924.234.570.938.732.1321.4
(0.10)(0.10)(0.16)(0.11)(0.12)(0.17)(0.13)(0.12)(0.31)
0.31–136.321.058.324.734.673.941.533.0113.6
(0.12)(0.10)(0.15)(0.10)(0.12)(0.17)(0.13)(0.11)(0.23)
0.63–1-20.8-27.036.7--34.936.8
-(0.09)-(0.10)(0.11)--(0.11)(0.11)
1.25–1--------31.5
--------(0.06)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Hoult, R.; Correia, A.A.; de Almeida, J.P. Beam-Truss Models to Simulate the Axial-Flexural-Torsional Performance of RC U-Shaped Wall Buildings. CivilEng 2023, 4, 292-310. https://doi.org/10.3390/civileng4010017

AMA Style

Hoult R, Correia AA, de Almeida JP. Beam-Truss Models to Simulate the Axial-Flexural-Torsional Performance of RC U-Shaped Wall Buildings. CivilEng. 2023; 4(1):292-310. https://doi.org/10.3390/civileng4010017

Chicago/Turabian Style

Hoult, Ryan, António A. Correia, and João Pacheco de Almeida. 2023. "Beam-Truss Models to Simulate the Axial-Flexural-Torsional Performance of RC U-Shaped Wall Buildings" CivilEng 4, no. 1: 292-310. https://doi.org/10.3390/civileng4010017

APA Style

Hoult, R., Correia, A. A., & de Almeida, J. P. (2023). Beam-Truss Models to Simulate the Axial-Flexural-Torsional Performance of RC U-Shaped Wall Buildings. CivilEng, 4(1), 292-310. https://doi.org/10.3390/civileng4010017

Article Metrics

Back to TopTop