Assessment of Torsional Amplification of Drift Demand in a Building Employing Site-Specific Response Spectra and Accelerograms
Abstract
1. Introduction
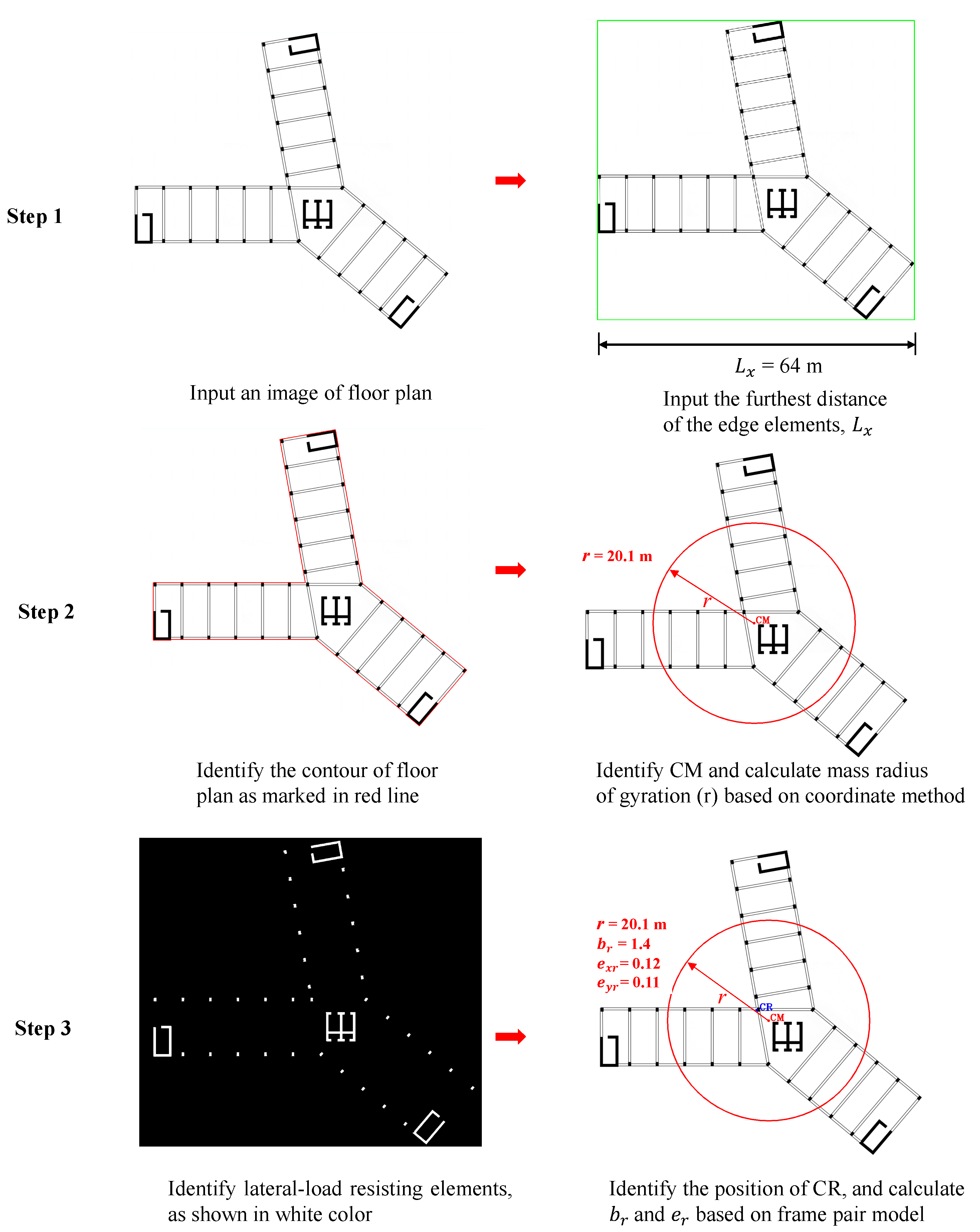
2. Image Scanning Method for Determining Torsional Parameters
3. Site-Specific 3D Linear Elastic Dynamic Analysis
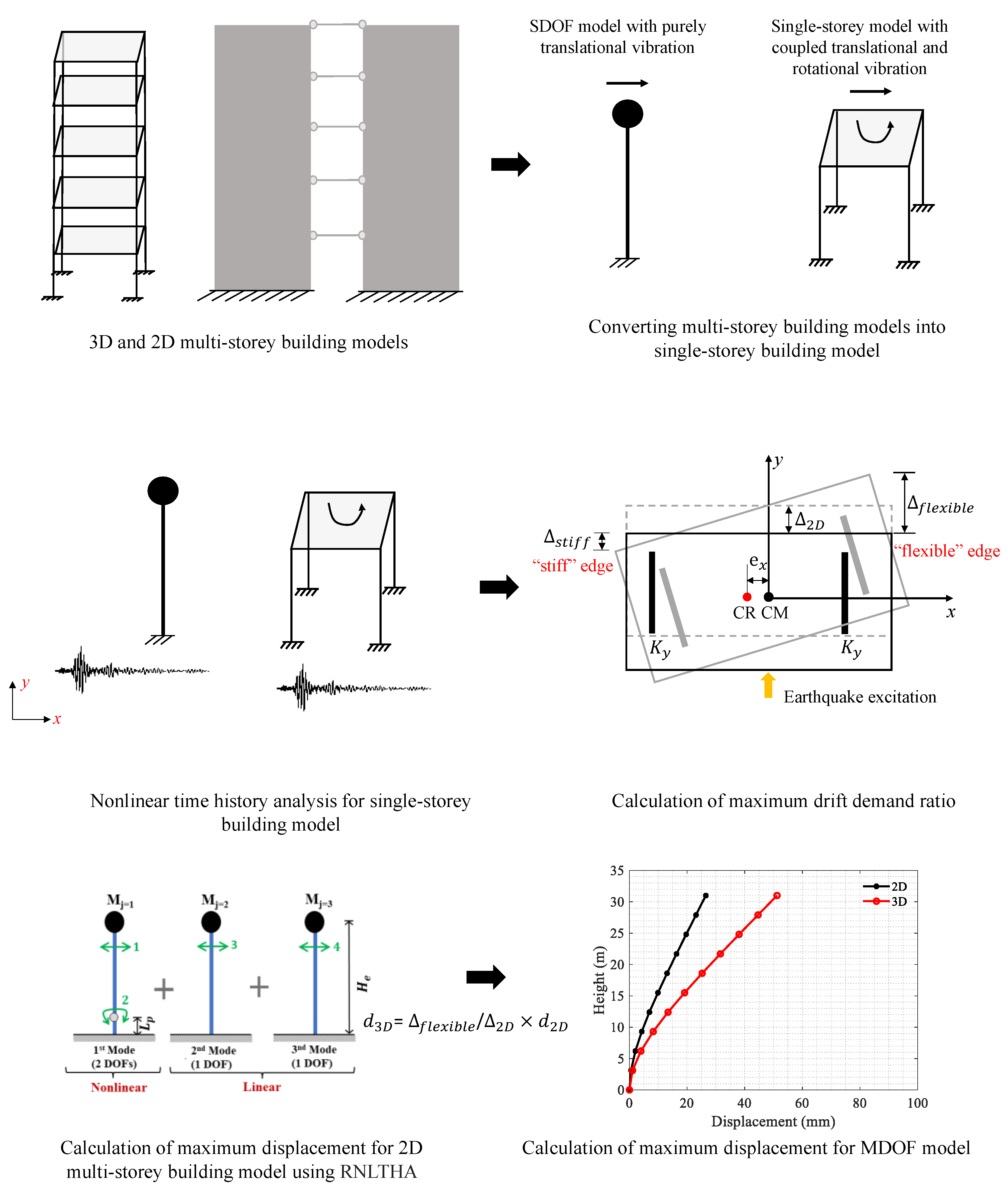
4. Site-Specific 3D Nonlinear Dynamic Analysis
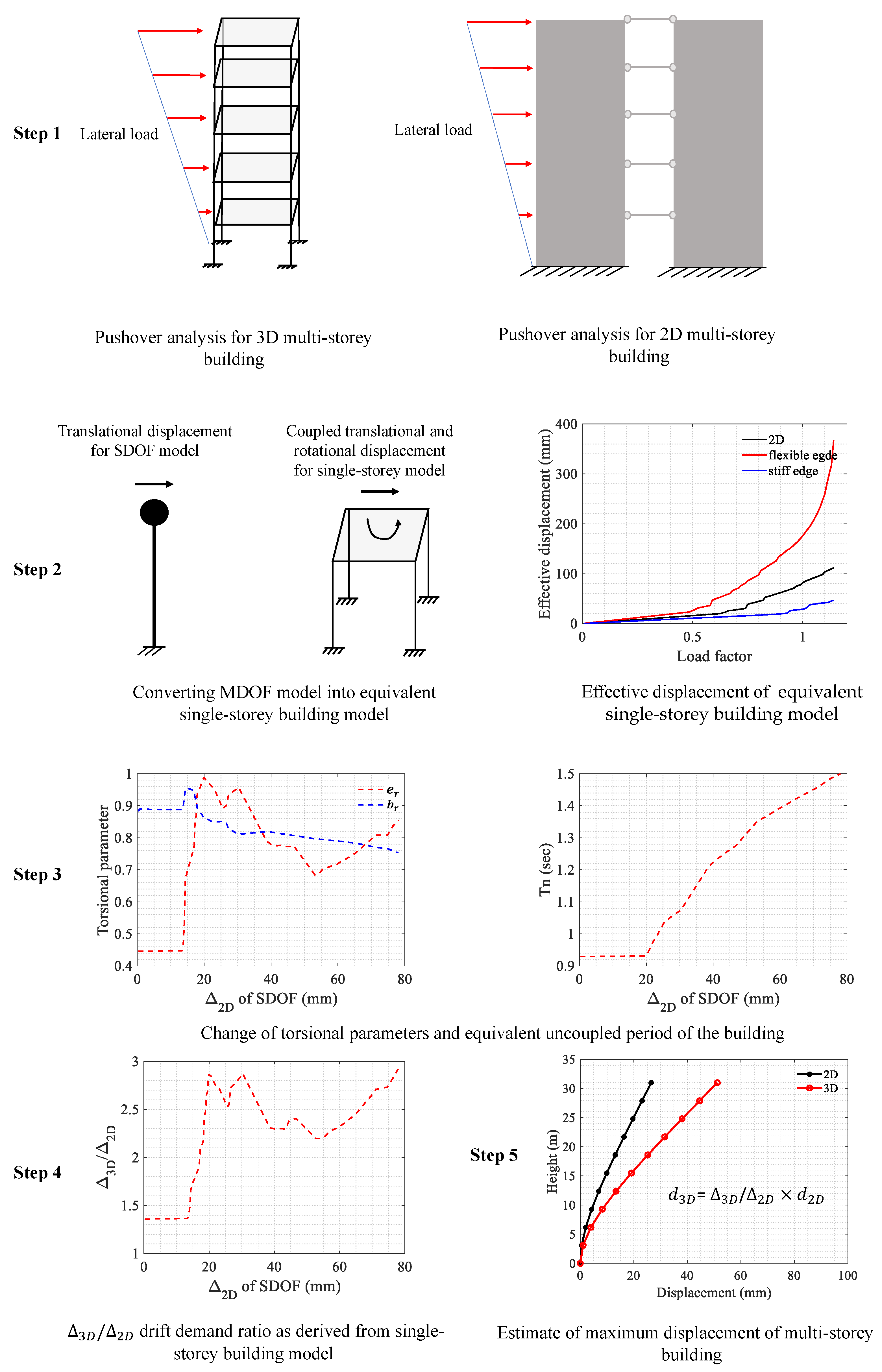
4.1. Determination of the Maximum Inelastic Drift Demand Ratio
4.2. Nonlinear Response Spectrum Analysis
4.3. Nonlinear Time History Analysis
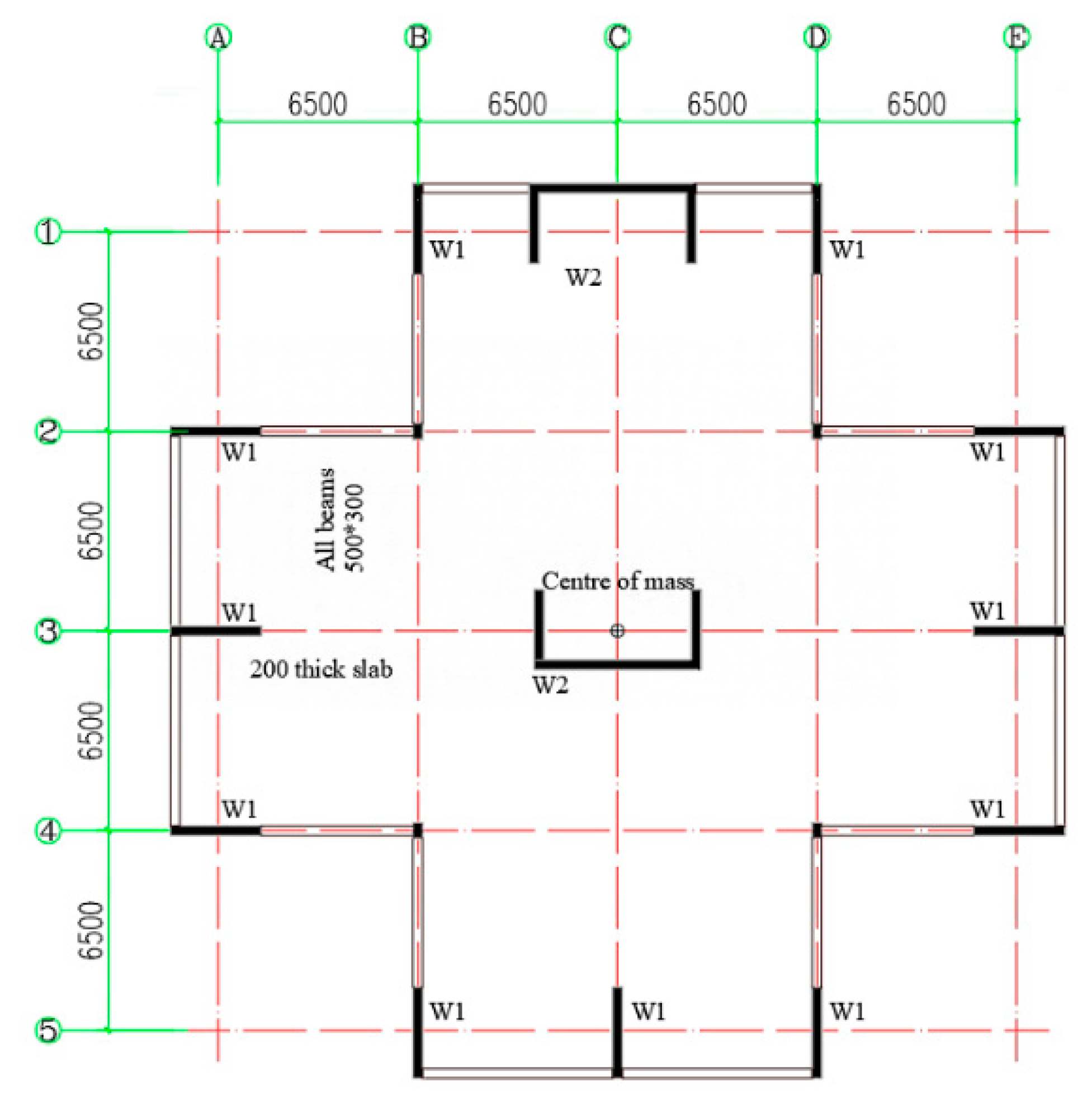
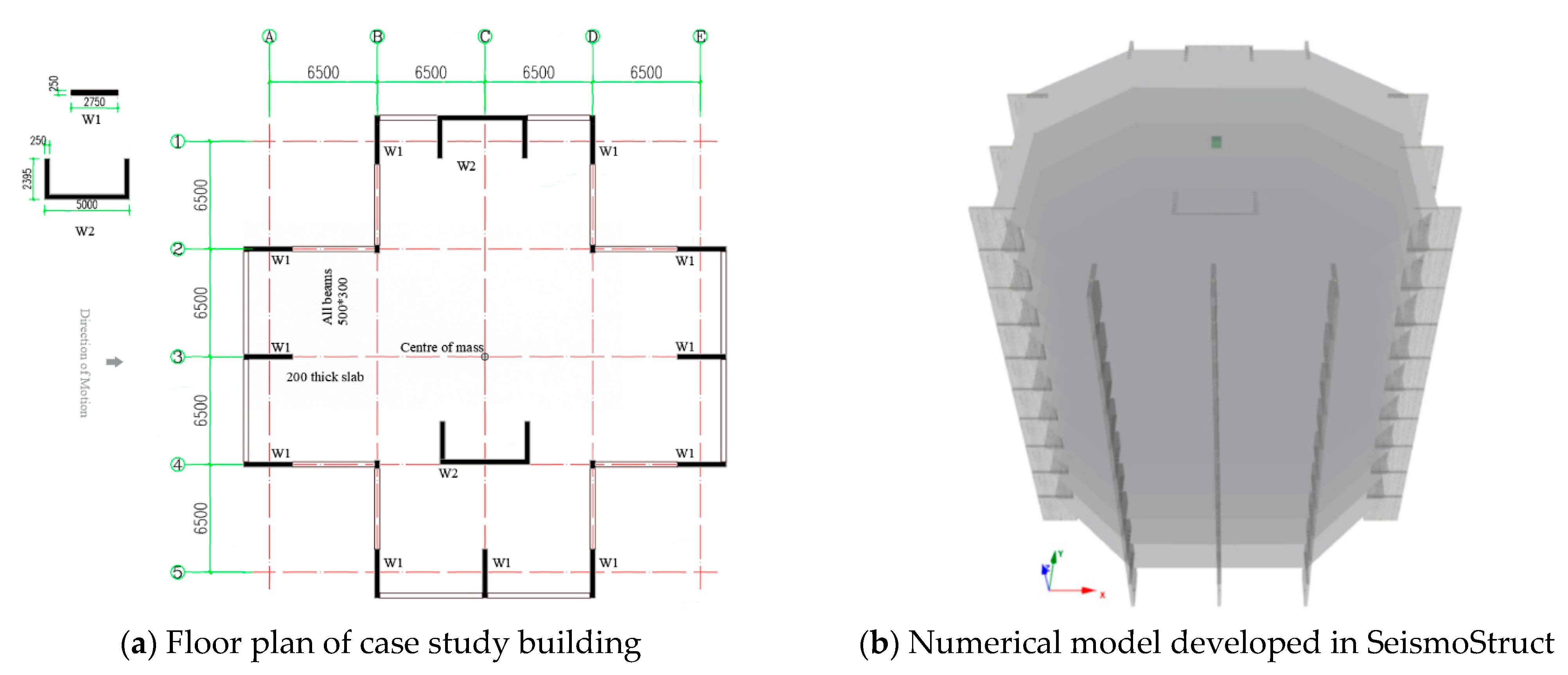
5. Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Comparison of Torsional Parameters Obtained by Using the Imaging Scanning Method and the 3D Numerical Model
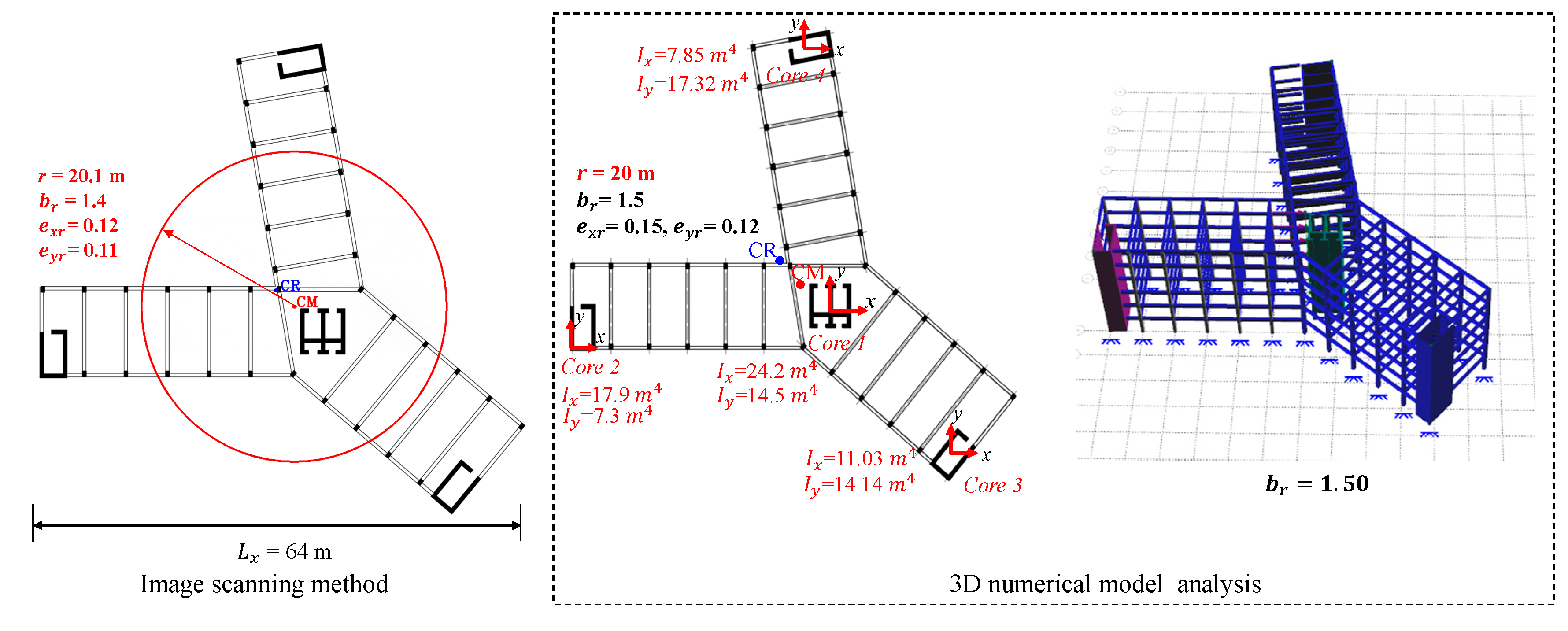
Appendix B. Calculation of the Torsional Parameters from the Static Analysis Procedure
Appendix C. Implementation of Newmark Constant Average Acceleration Time Step Integration in Rapid Nonlinear Time History Analysis in 2D (RNLTHA-2D)
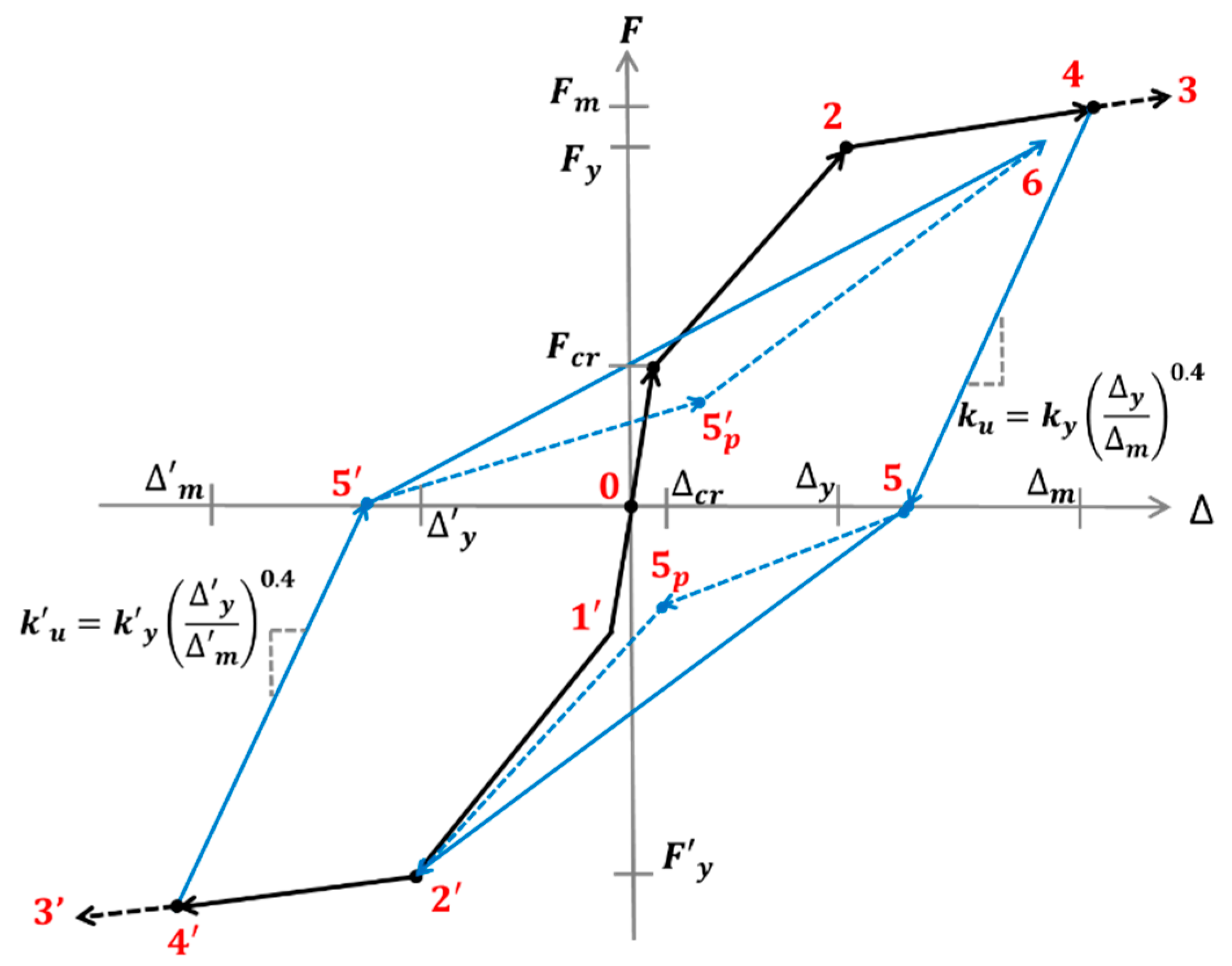
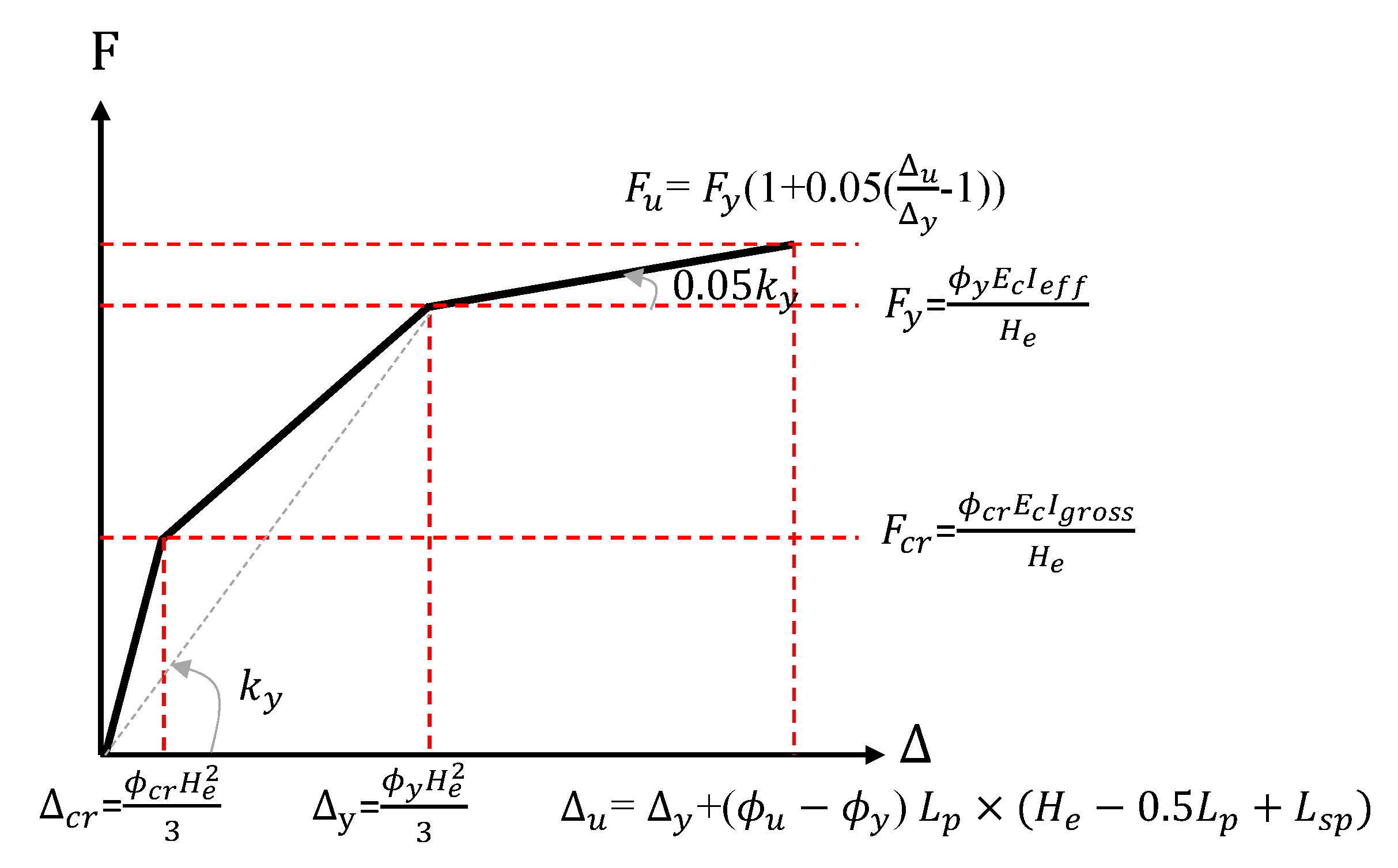
Appendix D. Trilinear Hysteresis Model
Appendix E. Material and Dynamic Properties of the Case Study Building
| Parameters | Walls 1 and 2 |
|---|---|
| Diameter of vertical reinforcement | 20 mm |
| Vertical reinforcement ratio | 0.015 (1.5%) |
| Yield strength of reinforcement | 500 MPa |
| Ultimate strength of reinforcement | 600 MPa |
| Characteristic strength of concrete | 40 MPa |
| Axial load ratio (n) | 0.11 |
| Parameters | Mode 1 | Mode 2 | Mode 3 |
|---|---|---|---|
| Effective mass (tonnes) | 2735 | 840 | 290 |
| Mass participation ratio (%) | 65 | 20 | 7 |
| Period (s) | 0.810 | 0.129 | 0.046 |
| Displacement coefficient at the roof level, | 1.56 | 0.70 | 0.33 |
Appendix F. Details of the Site−Specific Accelerograms Generated from QuakeAdvice
| Spectra No. | Acc No. | Earthquake Name | Reference Periods (s) | Year | Station Name | Magnitude | Rjb (km) | PGA (g) | Scaling Factor |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | Whittier Narrows-02 | 0.2 | 1987 | Mt Wilson—CIT Seis Sta | 5.27 | 16.45 | 0.175 | 1.21 |
| 2 | 2 | Northridge-06 | 0.2 | 1994 | Beverly Hills—12520 Mulhol | 5.28 | 10.57 | 0.130 | 0.85 |
| 3 | Christchurch—2011 | 0.2 | 2011 | PARS | 5.79 | 8.5 | 0.126 | 0.61 | |
| 4 | Sierra Madre | 0.2 | 1991 | Cogswell Dam—Right Abutment | 5.61 | 17.79 | 0.151 | 0.50 | |
| 5 | Friuli (aftershock 9)_ Italy | 0.2 | 1976 | San Rocco | 5.5 | 11.92 | 0.127 | 1.41 | |
| 6 | Lytle Creek | 0.2 | 1970 | Wrightwood—6074 Park Dr | 5.33 | 10.7 | 0.215 | 1.06 | |
| 7 | 3 | Christchurch—2011 | 0.5 | 2011 | GODS | 5.79 | 9.1 | 0.175 | 0.63 |
| 8 | 4 | Chi-Chi_ Taiwan-05 | 0.5 | 1999 | HWA031 | 6.2 | 39.29 | 0.128 | 1.91 |
| 9 | 5 | Chi-Chi_ Taiwan-05 | 0.5 | 1999 | HWA005 | 6.2 | 32.71 | 0.124 | 1.46 |
| 10 | 6 | Whittier Narrows-01 | 0.5 | 1987 | Pacoima Kagel Canyon | 5.99 | 31.59 | 0.169 | 1.04 |
| 11 | Chi-Chi_ Taiwan-03 | 0.5 | 1999 | CHY041 | 6.2 | 40.79 | 0.132 | 1.00 | |
| 12 | N. Palm Springs | 0.5 | 1986 | Anza—Red Mountain | 6.06 | 38.22 | 0.171 | 1.77 | |
| 13 | 7 | Chi-Chi_ Taiwan-06 | 1 | 1999 | CHY041 | 6.3 | 45.68 | 0.094 | 0.53 |
| 14 | 8 | San Fernando | 1 | 1971 | Lake Hughes #4 | 6.61 | 19.45 | 0.198 | 1.27 |
| 15 | 9 | Coalinga-01 | 1 | 1983 | Parkfield—Fault Zone 11 | 6.36 | 27.1 | 0.084 | 1.08 |
| 16 | 10 | Coalinga-01 | 1 | 1983 | Parkfield—Stone Corral 3E | 6.36 | 32.81 | 0.170 | 1.13 |
| 17 | 11 | Northridge-01 | 1 | 1994 | LA—Temple & Hope | 6.69 | 28.82 | 0.113 | 0.62 |
| 18 | 12 | Niigata_ Japan | 1 | 2004 | NGNH29 | 6.63 | 45.39 | 0.193 | 1.58 |
| 19 | 13 | Loma Prieta | 2 | 1989 | SF—Diamond Heights | 6.93 | 71.23 | 0.076 | 0.67 |
| 20 | 14 | Iwate_ Japan | 2 | 2008 | Maekawa Miyagi Kawasaki City | 6.9 | 74.82 | 0.159 | 0.95 |
| 21 | Chuetsu-oki_ Japan | 2 | 2007 | NGNH28 | 6.8 | 76.68 | 0.051 | 1.42 | |
| 22 | Iwate_ Japan | 2 | 2008 | AKT009 | 6.9 | 118.9 | 0.086 | 1.66 | |
| 23 | Loma Prieta | 2 | 1989 | Berkeley—Strawberry Canyon | 6.93 | 78.32 | 0.077 | 1.01 | |
| 24 | Chuetsu-oki_ Japan | 2 | 2007 | NGNH27 | 6.8 | 91.38 | 0.050 | 1.29 |
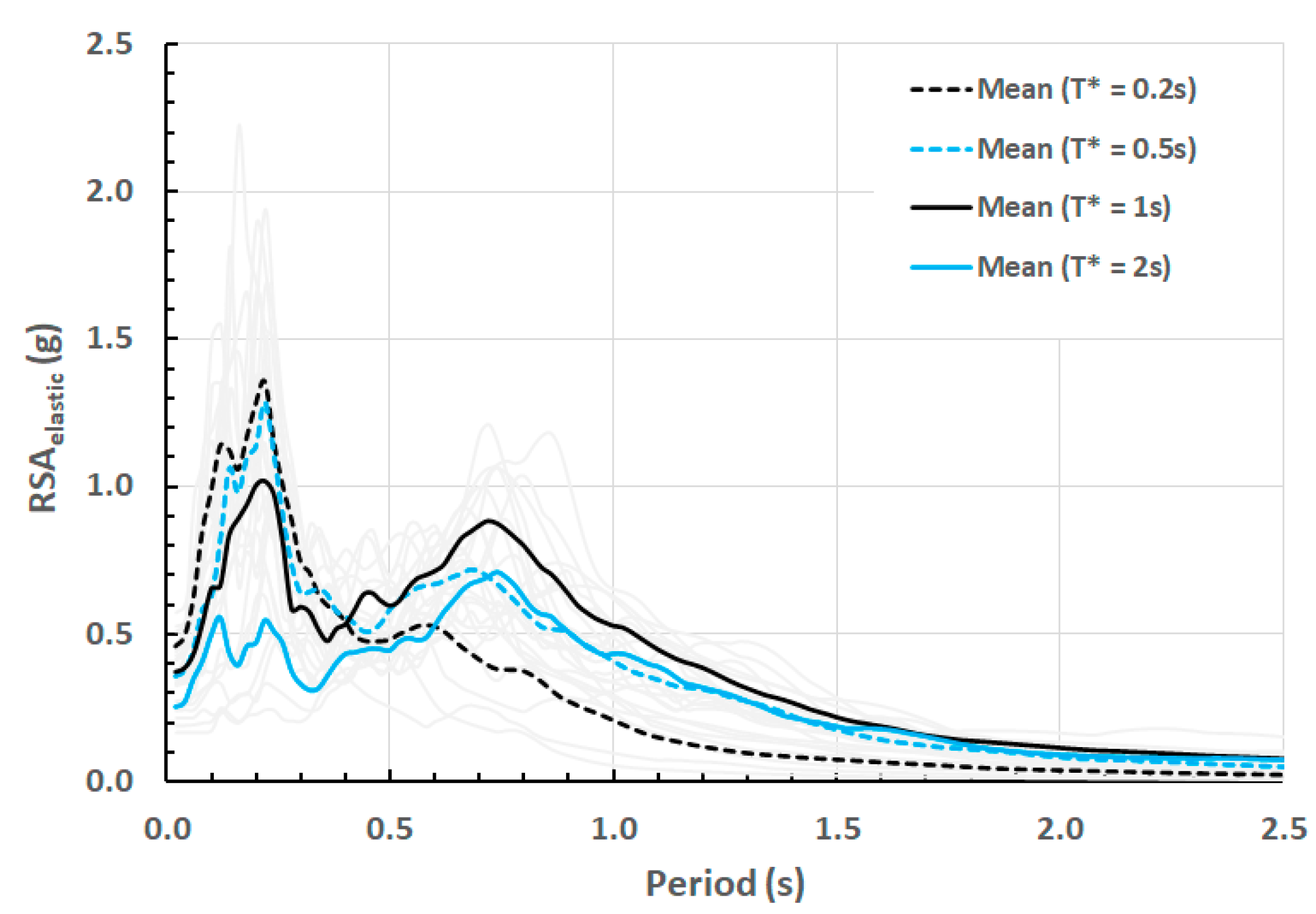
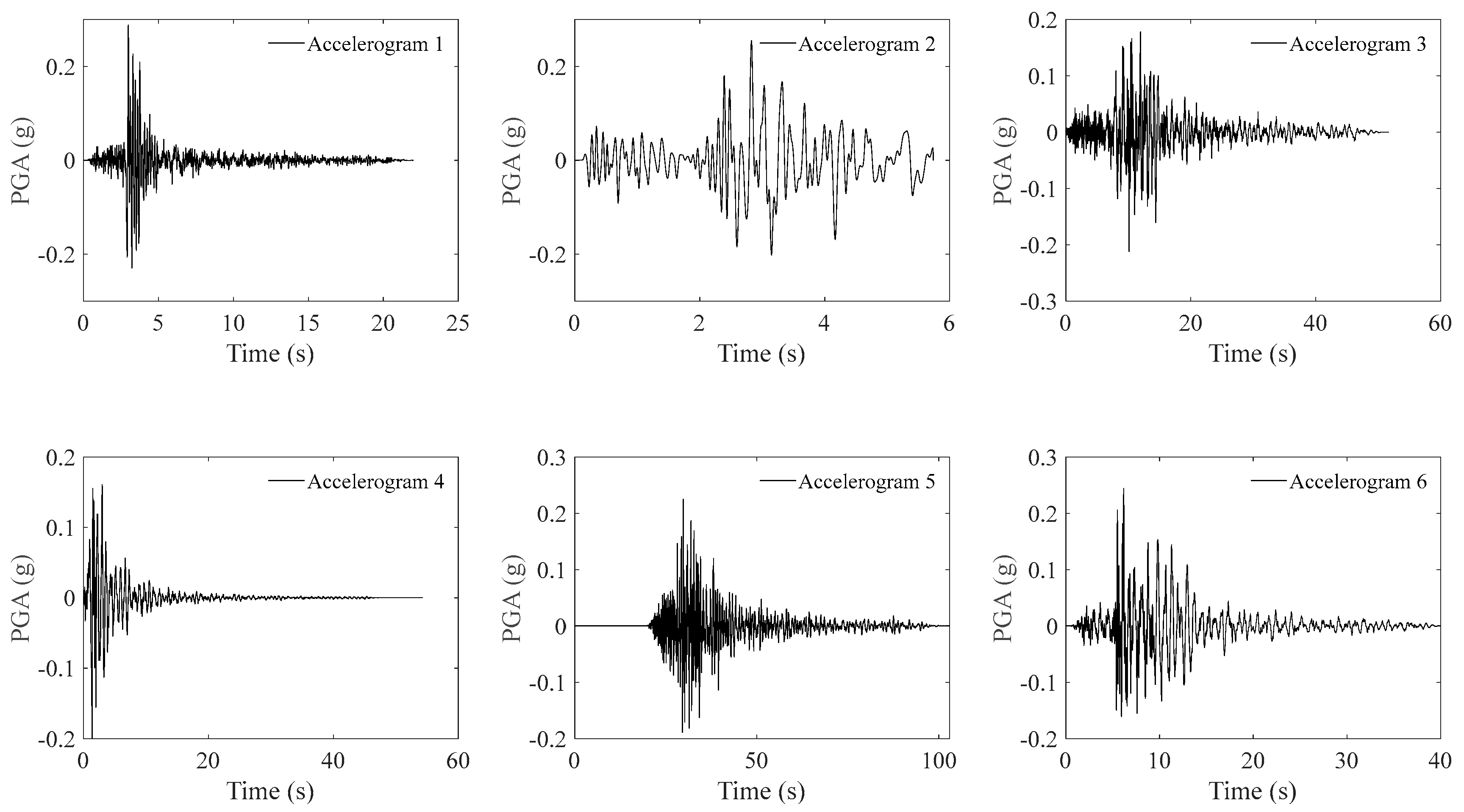
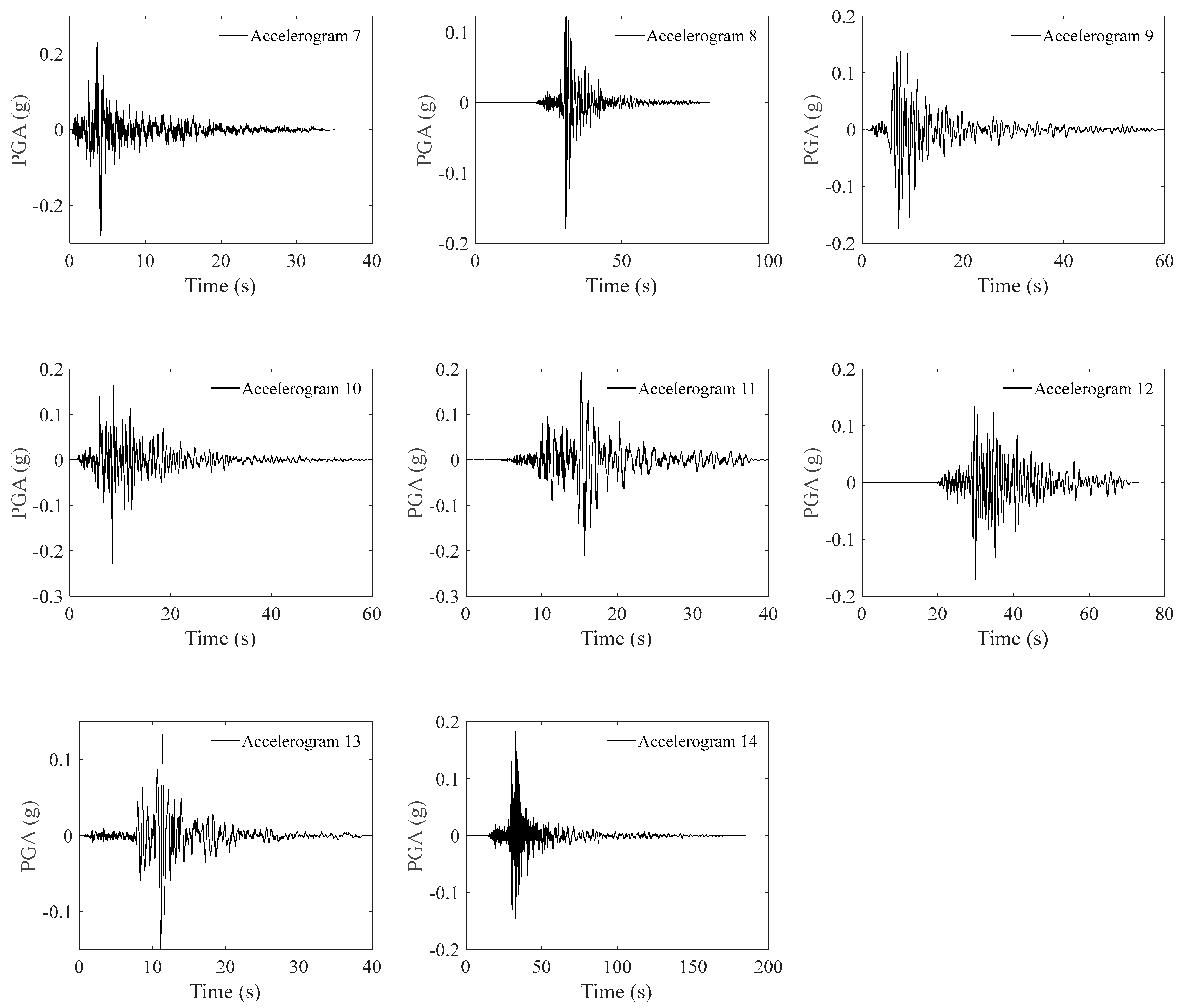
Appendix G. Comparison of the 3D Nonlinear Displacement Time History Response of the Case Study Building
| No. | RNLTHA-2D | RNLTHA-3D | SeismoStruct-3D | |
|---|---|---|---|---|
| 1 | 1.14 | 27 | 31 | 39 |
| 2 | 1.11 | 26 | 29 | 31 |
| 3 | 1.87 | 109 | 204 | 182 |
| 4 | 1.86 | 75 | 140 | 161 |
| 5 | 1.38 | 112 | 155 | 194 |
| 6 | 1.69 | 90 | 152 | 127 |
| 7 | 2.39 | 132 | 315 | 303 |
| 8 | 1.87 | 140 | 262 | 226 |
| 9 | 1.84 | 167 | 307 | 262 |
| 10 | 1.61 | 95 | 153 | 163 |
| 11 | 1.54 | 182 | 280 | 263 |
| 12 | 1.67 | 106 | 177 | 190 |
| 13 | 1.71 | 65 | 111 | 135 |
| 14 | 1.78 | 82 | 146 | 168 |
Appendix H. Comparison of the 3D Nonlinear Displacement Time History Response of the Case Study Building #2

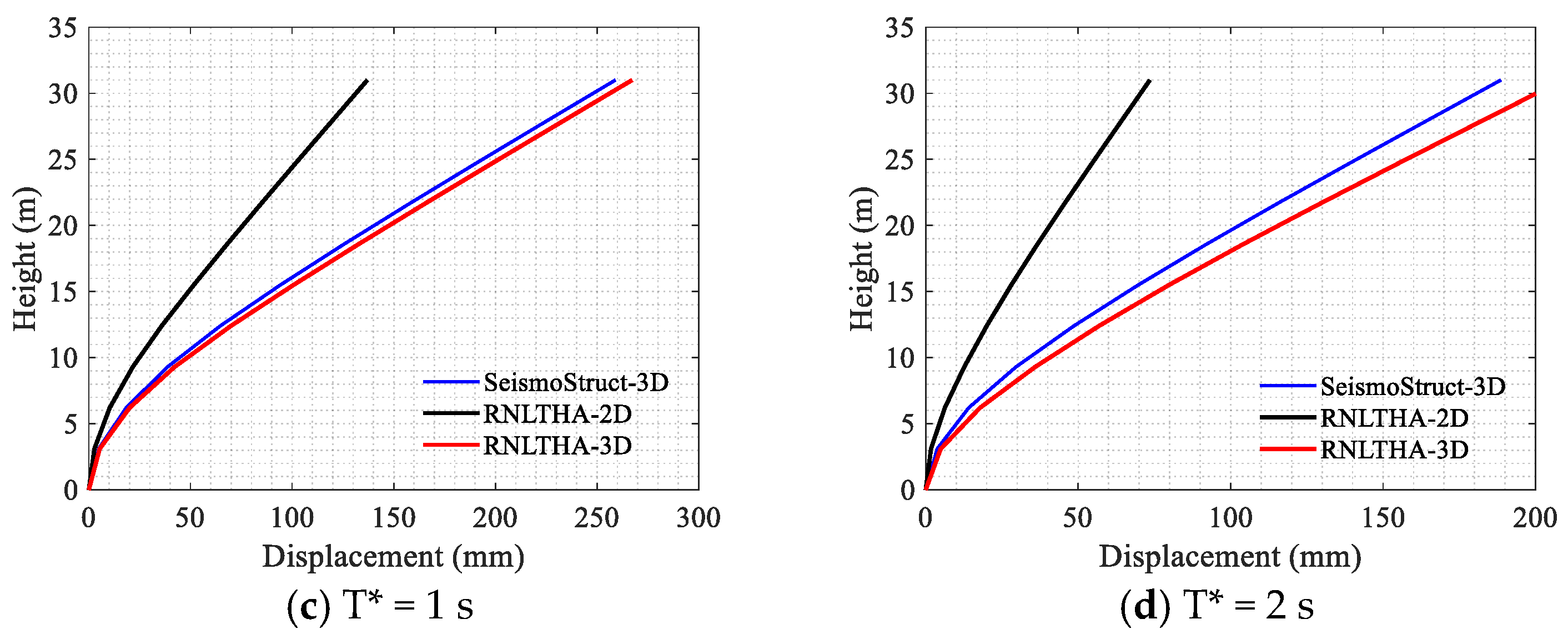
| Reference Period (T*) | |||
|---|---|---|---|
| 0.2 s | 34 | 42 | −19.0% |
| 0.5 s | 191 | 189 | 1.0% |
| 1 s | 257 | 259 | −0.6% |
| 2 s | 204 | 189 | 8.1% |
| Earthquake No. | RNLTHA-2D | RNLTHA-3D | SeismoStruct-3D | |
|---|---|---|---|---|
| 1 | 1.15 | 27 | 31 | 49 |
| 2 | 1.38 | 26 | 36 | 36 |
| 3 | 1.98 | 109 | 216 | 209 |
| 4 | 2.29 | 75 | 171 | 187 |
| 5 | 1.58 | 112 | 177 | 165 |
| 6 | 2.23 | 90 | 200 | 196 |
| 7 | 2.03 | 132 | 268 | 279 |
| 8 | 1.54 | 140 | 215 | 241 |
| 9 | 1.85 | 167 | 308 | 305 |
| 10 | 2.27 | 95 | 216 | 236 |
| 11 | 1.46 | 182 | 265 | 243 |
| 12 | 2.56 | 106 | 272 | 250 |
| 13 | 3.43 | 65 | 223 | 203 |
| 14 | 2.25 | 82 | 185 | 175 |
References
- Kewalramani, M.A.; Syed, Z.I. Seismic analysis of torsional irregularity in multi-storey symmetric and asymmetric buildings. Test Eng. Manag. 2020, 82, 3553–3558. [Google Scholar]
- Athanassiadou, C.J. Seismic performance of RC plane frames irregular in elevation. Eng. Struct. 2008, 30, 1250–1261. [Google Scholar] [CrossRef]
- Khatiwada, P.; Lumantarna, E.; Lam, N.; Looi, D. Fast Checking of Drift Demand in Multi-Storey Buildings with Asymmetry. Buildings 2020, 11, 13. [Google Scholar] [CrossRef]
- Suryawanshi, M.; Kadam, S.B.; Tande, S.N. Torsional Behaviour of Asymmetrical Buildings in Plan under Seismic Forces. Int. J. Eng. Res. Technol. 2014, 2, 170–176. [Google Scholar]
- Dutta, S.C. Effect of strength deterioration on inelastic seismic torsional behaviour of asymmetric RC buildings. Build. Environ. 2001, 36, 1109–1118. [Google Scholar] [CrossRef]
- CEN. Eurocode 8: Design Provisions for Earthquake Resistance of Structures; Part 1.1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- ASCE/SEI 41-06; Seismic Rehabilitation of Existing Buildings. ASCE: Reston, VA, USA, 2007.
- Student, A.; Goel, R.K. Seismic code analysis of multi-storey asymmetric buildings. Earthq. Eng. Struct. Dyn. 1998, 27, 173–185. [Google Scholar]
- Kyrkos, M.T.; Anagnostopoulos, S.A. An assessment of code designed, torsionally stiff, asymmetric steel buildings under strong earthquake excitations. Earthq. Struct. 2011, 2, 109–126. [Google Scholar] [CrossRef]
- Ayala, A.G.; Tavera, E.A. A new approach for the evaluation of the seismic performance of asymmetric buildings. In Proceedings of the 7th National Conference on Earthquake Engineering, Boston, MA, USA, 21–25 July 2002. [Google Scholar]
- Fajfar, P.; Marusic, D.; Perus, I. Torsional effects in the pushover-based seismic analysis of buildings. J. Earthq. Eng. 2005, 9, 831–854. [Google Scholar] [CrossRef]
- Sasaki, K.K.; Freeman, S.A.; Paret, T.F. Multimode pushover procedure (MMP): A method to identify the effects of higher modes in a pushover analysis. In Proceedings of the 6th U.S. National Conference on Earthquake Engineering, Seattle, WA, USA, 31 May–4 June 1998. [Google Scholar]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedures for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings. Earthq. Eng. Struct. Dyn. 2010, 33, 903–927. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K.; Chintanapakdec, C. Evaluation of a modified mpa procedure assuming higher modes as elastic to estimate seismic demands. Earthq. Spectra 2004, 20, 757–778. [Google Scholar] [CrossRef]
- Poursha, M.; Khoshnoudian, F.; Moghadam, A.S. A consecutive modal pushover procedure for estimating the seismic demands of tall buildings. Eng. Struct. 2009, 31, 591–599. [Google Scholar] [CrossRef]
- Kreslin, M.; Fajfar, P. The extended n2 method considering higher mode effects in both plan and elevation. Bull. Earthq. Eng. 2012, 10, 695–715. [Google Scholar] [CrossRef]
- Ansal, A. Perspectives on european earthquake engineering and seismology. In Geotechnical, Geological and Earthquake Engineering; Springer: Cham, Switzerland, 2015; Volume 34. [Google Scholar] [CrossRef]
- Bhatt, C.; Bento, R. Estimating Torsional Demands in Plan Irregular Buildings Using Pushover Procedures Coupled with Linear Dynamic Response Spectrum Analysis. In Seismic Behaviour and Design of Irregular and Complex Civil Structures; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Mahdi, T.; Soltangharaie, V. Static and Dynamic Analyses of Asymmetric Reinforced Concrete Frame. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisboa, Portugal, 24–28 September 2012. [Google Scholar]
- Lucchini, A.; Monti, G.; Kunnath, S. Seismic behavior of single-story asymmetric-plan buildings under uniaxial excitation. Earthq. Eng. Struct. Dyn. 2009, 38, 1053–1070. [Google Scholar] [CrossRef]
- Belejo, A.; Barbosa, A.R.; Bento, R. Influence of ground motion duration on damage index-based fragility assessment of a plan-asymmetric non-ductile reinforced concrete building. Eng. Struct. 2017, 151, 682–703. [Google Scholar] [CrossRef]
- Khatiwada, P.; Hu, Y.; Lumantarna, E.; Menegon, S.J. Dynamic Modal Analyses of Building Structures Employing Site-Specific Response Spectra Versus Code Response Spectrum Models. CivilEng 2023, 4, 134–150. [Google Scholar] [CrossRef]
- Khatiwada, P.; Hu, Y.; Lam, N.; Menegon, S.J. Nonlinear Dynamic Analyses Utilising Macro-Models of Reinforced Concrete Building Structures and Site-Specific Accelerograms. CivilEng 2023. (companion papers in the special issue of Site-Specific Seismic Design of Buildings). [Google Scholar]
- Khatiwada, P. Determination of center of mass and radius of gyration of irregular buildings and its application in torsional analysis. Int. Res. J. Eng. Technol. 2020, 7, 1–7. [Google Scholar]
- Wang, H.; Tian, Q.; Hu, Z.; Guo, J. Image Feature Detection Based on OpenCV. J. Res. Sci. Eng. 2020, 2, 16–18. [Google Scholar]
- Khatiwada, P.; Lumantarna, E. Simplified Method of Determining Torsional Stability of the Multi-Storey Reinforced Concrete Buildings. CivilEng 2021, 2, 290–308. [Google Scholar] [CrossRef]
- Lam, N.T.; Wilson, J.L.; Lumantarna, E. Simplified elastic design checks for torsionally balanced and unbalanced low-medium rise buildings in lower seismicity regions. Earthq. Struct. 2016, 11, 741–777. [Google Scholar] [CrossRef]
- Lumantarna, E.; Lam, N.; Wilson, J. Methods of analysis for buildings with uni-axial and bi-axial asymmetry in regions of lower seismicity. Earthq. Struct. 2018, 15, 81–95. [Google Scholar]
- Hu, Y.; Lam, N.; Khatiwada, P.; Lumantarna, E.; Tsang, H.H.; Menegon, S.J. Site-specific response spectra and accelerograms on bedrock and soil surface. CivilEng 2023. (companion papers in the special issue of Site-Specific Seismic Design of Buildings). [Google Scholar]
- Hu, Y.; Lam, N.; Khatiwada, P.; Lumantarna, E.; Tsang, H.H.; Menegon, S.J. Site specific response spectra and accelerograms as derived from processing and analysis of multiple borelog records taken from the same site. CivilEng 2023. (companion papers in the special issue of Site-Specific Seismic Design of Buildings). [Google Scholar]
- Chopra, A.K. Dynamics of Structures; Pearson Education India: Noida, India, 2007. [Google Scholar]
- Tso, W.K.; Moghadam, A.S. Seismic response of asymmetrical buildings using pushover analysis. In Seismic Design Methodologies for the Next Generation of Codes; Routledge: Abingdon, UK, 2019; pp. 311–321. [Google Scholar]
- Fujii, K. Prediction of the largest peak nonlinear seismic response of asymmetric buildings under bi-directional excitation using pushover analyses. Bull. Earthq. Eng. 2014, 12, 909–938. [Google Scholar] [CrossRef]
- Fujii, K. Nonlinear static procedure for multi-story asymmetric frame buildings considering bi-directional excitation. J. Earthq. Eng. 2011, 15, 245–273. [Google Scholar] [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance-based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. Capacity-demand-diagram methods based on inelastic design spectrum. Earthq. Spectra 1999, 15, 637–656. [Google Scholar] [CrossRef]
- Menegon, S.J. Displacement Behaviour of Reinforced Concrete Walls in Regions of Lower Seismicity. Ph.D. Thesis, Department of Civil and Construction Engineering, Swinburne University of Technology, Melbourne, VIC, Australia, 2018. [Google Scholar]
- Lam, N.; Wilson, J.; Lumantarna, E. Force-deformation behaviour modelling of cracked reinforced concrete by EXCEL spreadsheets. Comput. Concr. 2011, 8, 43–57. [Google Scholar] [CrossRef]
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members; University of Toronto: Toronto, ON, Canada, 2000; p. 310. [Google Scholar]
- SeismoStruct—A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures. Available online: www.seismosoft.com (accessed on 10 December 2022).
- Site Specific Response Spectrum. Available online: http://quakeadvice.org/index.php/advanced-seismic-design/australia-adv/site-specific-response-spectrum/ (accessed on 10 December 2022).
- Motion, P.G. Pacific Earthquake Engineering Research Center; University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- AS 1170.4-2007 (R2018)/Amdt 2-2018; Structural Design Actions; Part 4: Earthquake Actions in Australia. Standards Australia: Sydney, NSW, Australia, 2018.

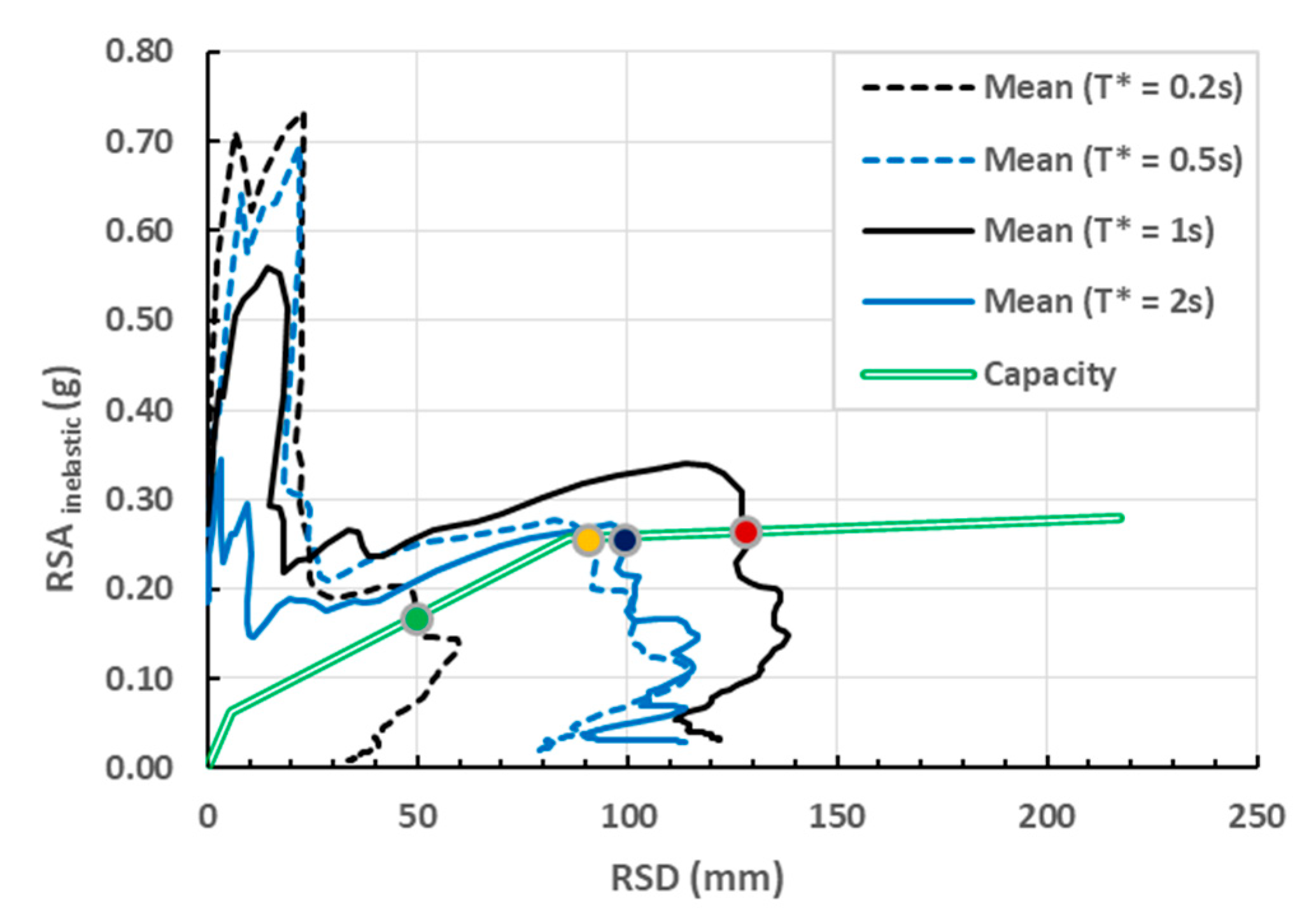
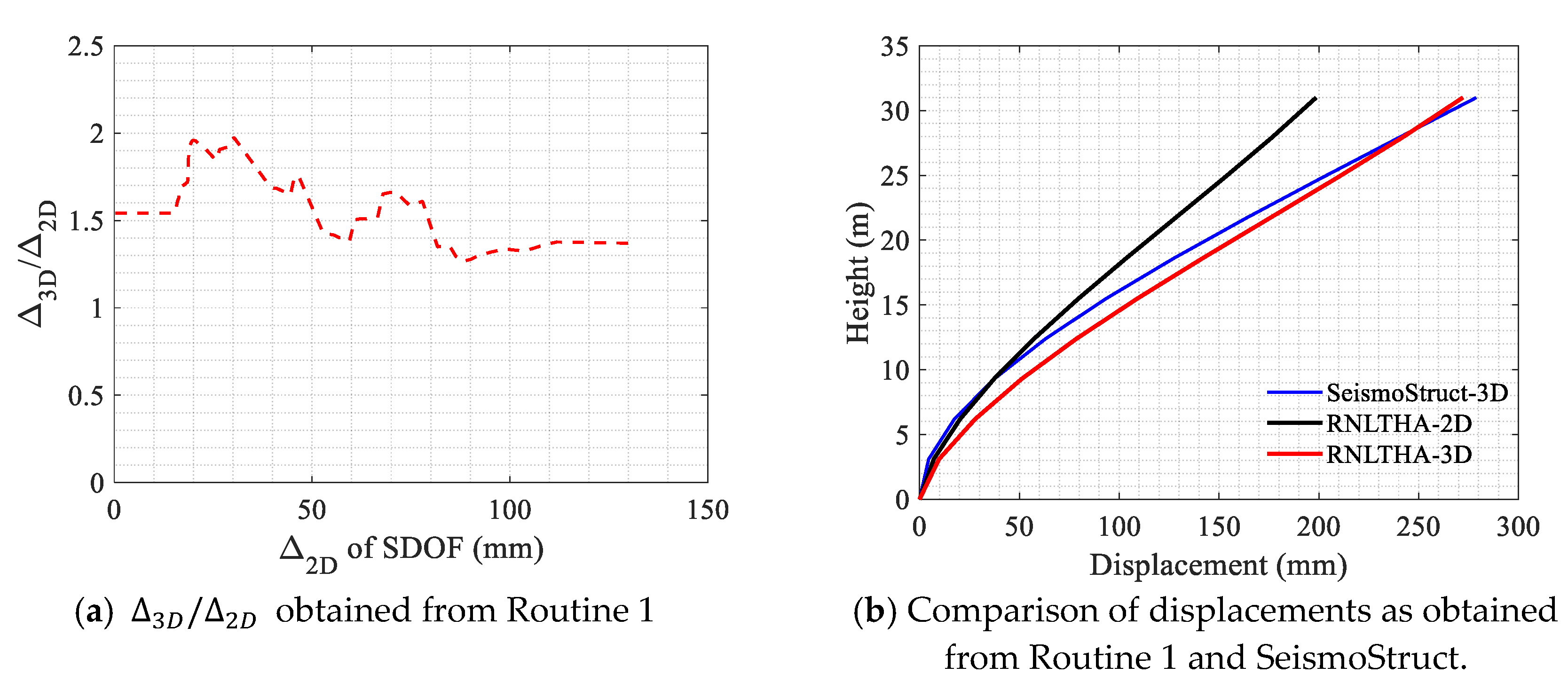
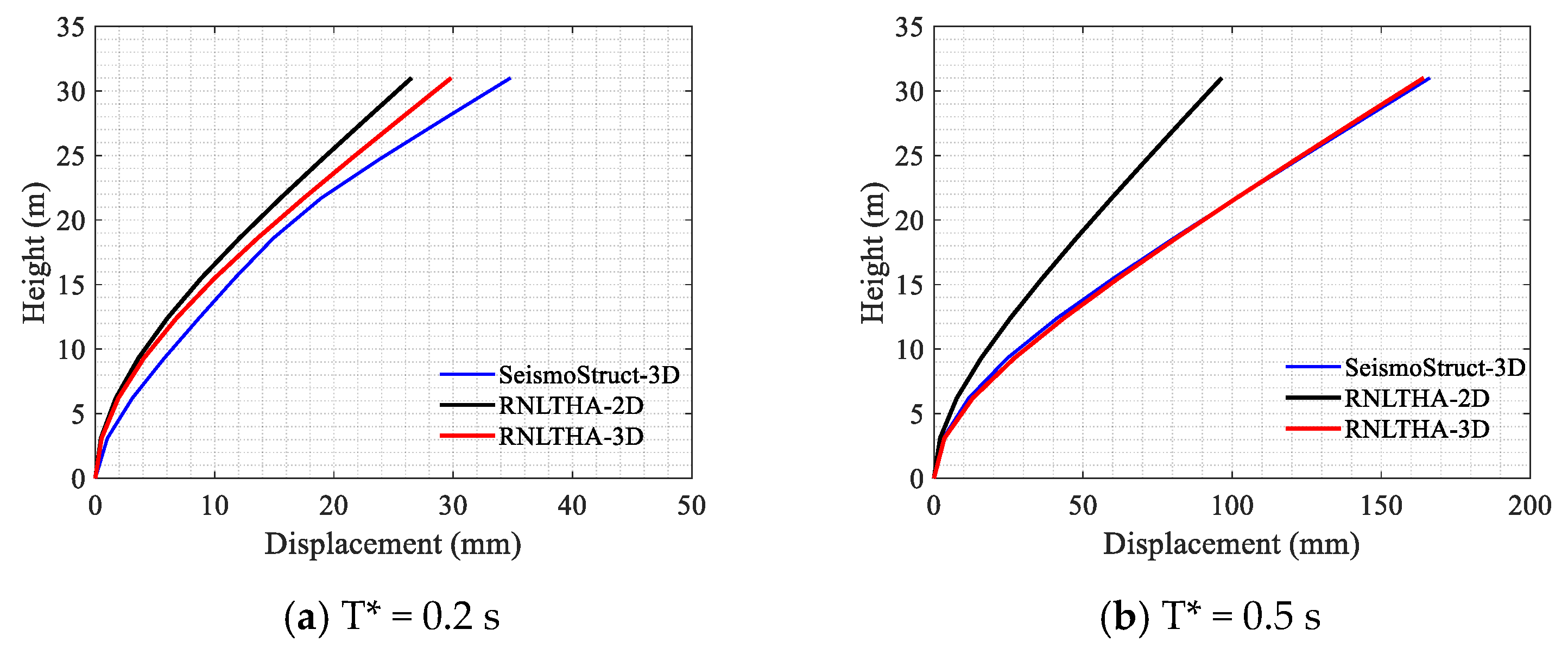

| Reference Period (T*) | |||
|---|---|---|---|
| 0.2 s | 30 | 35 | 14.3% |
| 0.5 s | 162 | 166 | 2.4% |
| 1 s | 249 | 235 | −6.0% |
| 2 s | 129 | 152 | 14.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Khatiwada, P.; Lumantarna, E.; Tsang, H.H. Assessment of Torsional Amplification of Drift Demand in a Building Employing Site-Specific Response Spectra and Accelerograms. CivilEng 2023, 4, 248-269. https://doi.org/10.3390/civileng4010015
Hu Y, Khatiwada P, Lumantarna E, Tsang HH. Assessment of Torsional Amplification of Drift Demand in a Building Employing Site-Specific Response Spectra and Accelerograms. CivilEng. 2023; 4(1):248-269. https://doi.org/10.3390/civileng4010015
Chicago/Turabian StyleHu, Yao, Prashidha Khatiwada, Elisa Lumantarna, and Hing Ho Tsang. 2023. "Assessment of Torsional Amplification of Drift Demand in a Building Employing Site-Specific Response Spectra and Accelerograms" CivilEng 4, no. 1: 248-269. https://doi.org/10.3390/civileng4010015
APA StyleHu, Y., Khatiwada, P., Lumantarna, E., & Tsang, H. H. (2023). Assessment of Torsional Amplification of Drift Demand in a Building Employing Site-Specific Response Spectra and Accelerograms. CivilEng, 4(1), 248-269. https://doi.org/10.3390/civileng4010015