Predictive BIM with Integrated Bayesian Inference of Deterioration Models as a Four-Dimensional Decision Support Tool
Abstract
1. Introduction
1.1. Digitalization in Construction
1.2. Modeling and Probabilistic Analysis of Durability
2. Data and Methods
2.1. Models, Assumptions, and Constraints
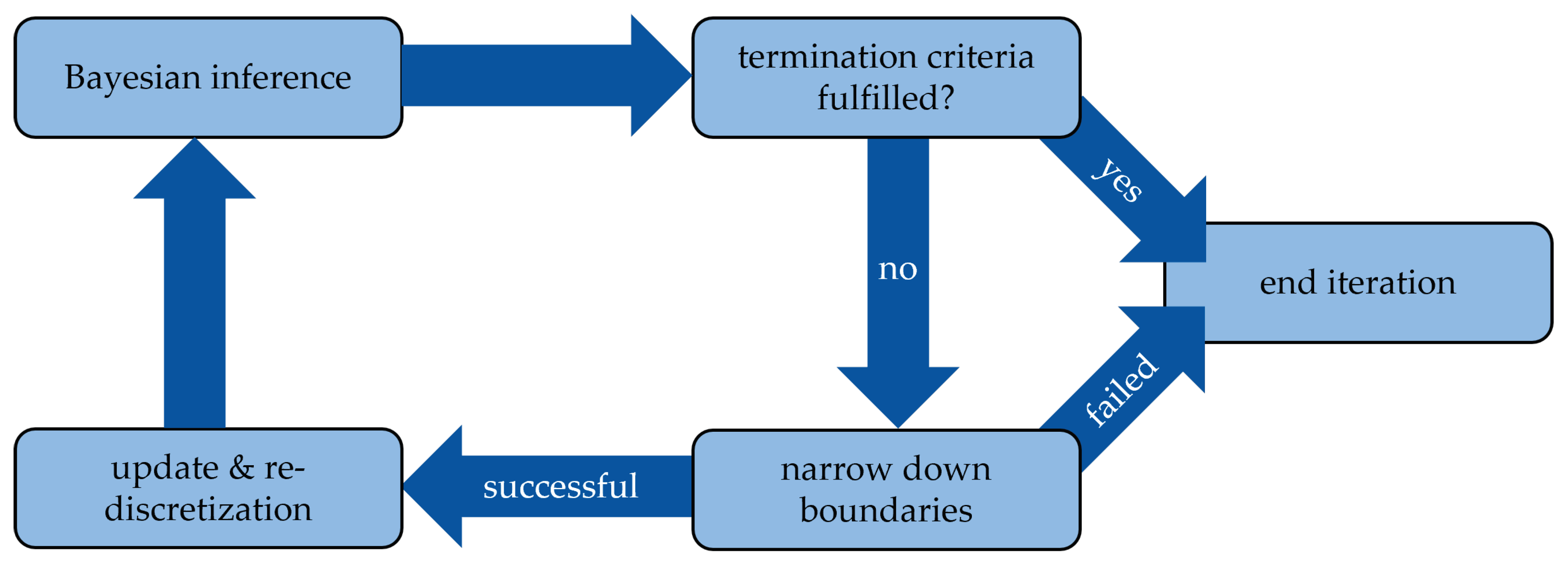
2.2. Automation of Bayesian Inference
2.3. Implementation in BIM
- A
- Input
- 1
- select components to be evaluated:
- these components can be any objects with flat surfaces and do not need to be a certain object type;
- there must be diagnosis data implemented in those objects for the script to run properly, as the calibration requires evidence;
- all available evidence (diagnosis data) in these components will be combined into one sample.
- 2
- select plane (can be any pickable object surface) as the reference for the z-axis;
- 3
- geometries (such as width, height, etc.) of selected components are extracted;
- 4
- previously implemented objects carrying the concrete cover (measured with linear scans during the building diagnosis) as properties available in the selected components are extracted;
- 5
- previously implemented objects carrying the carbonation depths and chloride profiles as properties available in the selected components are extracted;
- 6
- grouping of concrete cover in different rebar layers.
- B
- Analysis
- 1
- Python environment with SMILE, the configuration of Bayesian networks (sample size, number of bins), and further input such as critical chloride threshold:
- the user is required to define the values for certain configuration parameters via Dynamo as additional input if the default values are not used;
- the user is required to navigate to the folder in which the Python environment with SMILE was installed so that Revit can add this folder to its system path and assess the functionality of SMILE.
- 2
- monitoring data as a CSV data set, if available;
- 3
- analysis of concrete cover (mean, standard deviation, quantiles);
- 4
- Bayesian inference, using all available diagnosis data as evidence;
- 5
- analysis of rebar location (eccentricity, tilting);
- 6
- reliability assessment, including prognoses of carbonation and chloride ingress, as well as calculation of probabilities of failure (depassivation) and reliability indices;
- 7
- assessment of repair methods.
- C
- Output
- 1
- export of analysis results as CSV, TXT, XDSL;
- 2
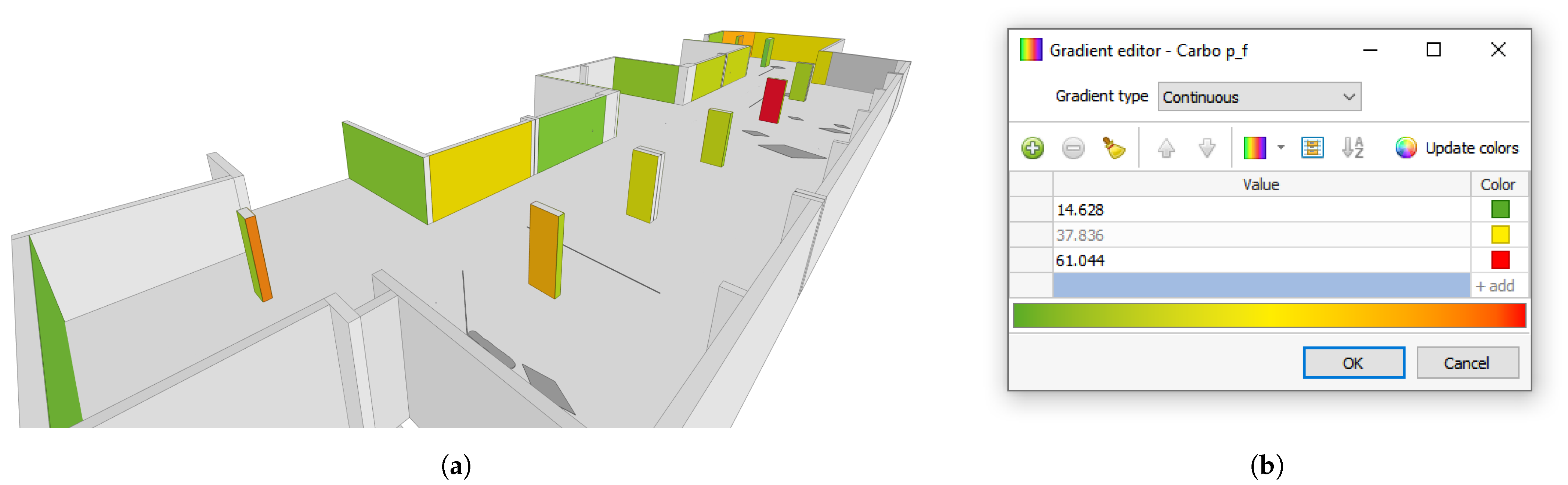
- creation of additional BIM objects (flat layers) hovering over the component surface containing the most relevant analysis data that are IFC compatible.
3. Results
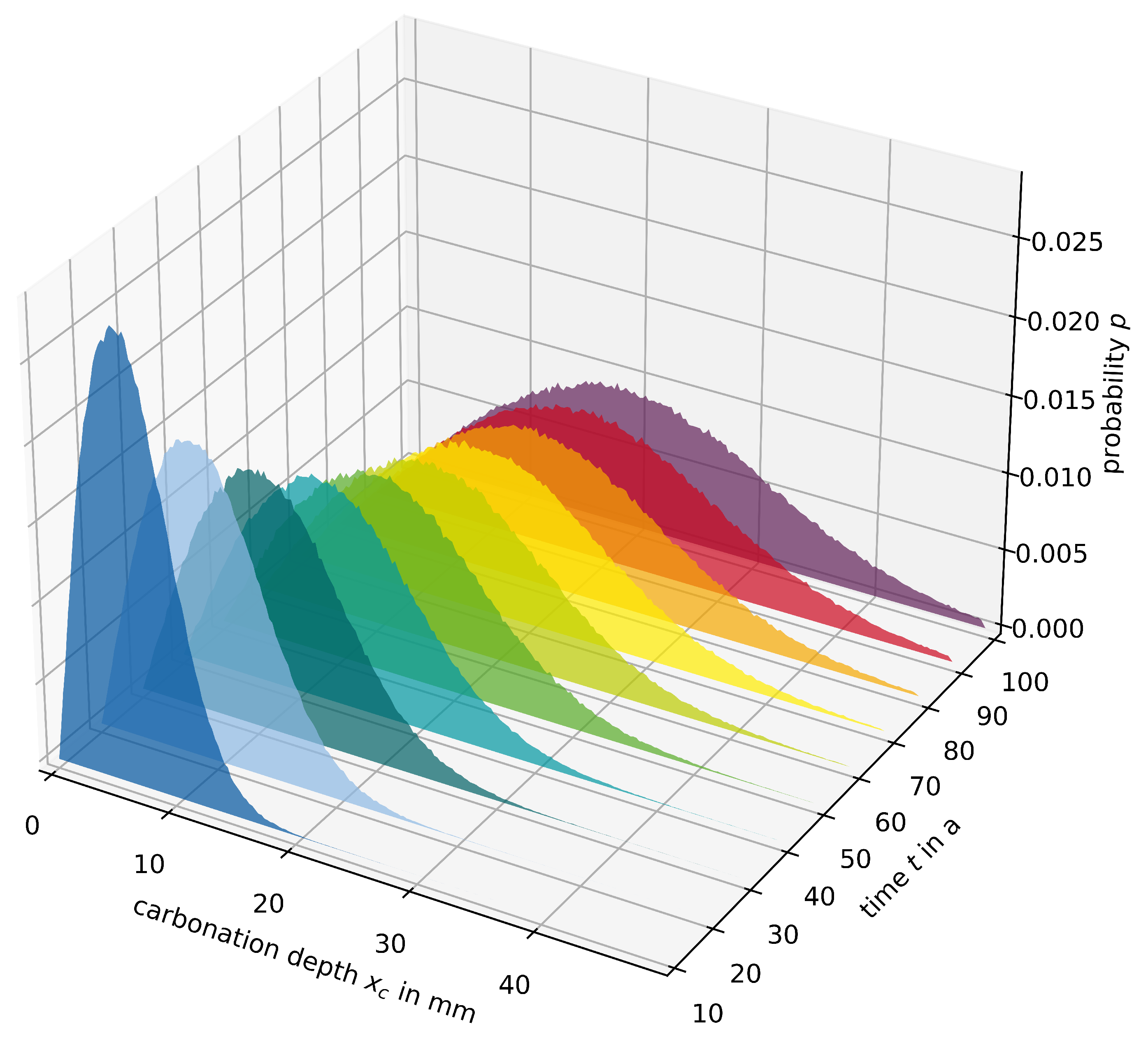
3.1. Calibration of Carbonation Model
3.2. Calibration of Chloride Model
3.3. Bayesian Inference in BIM
4. Discussion
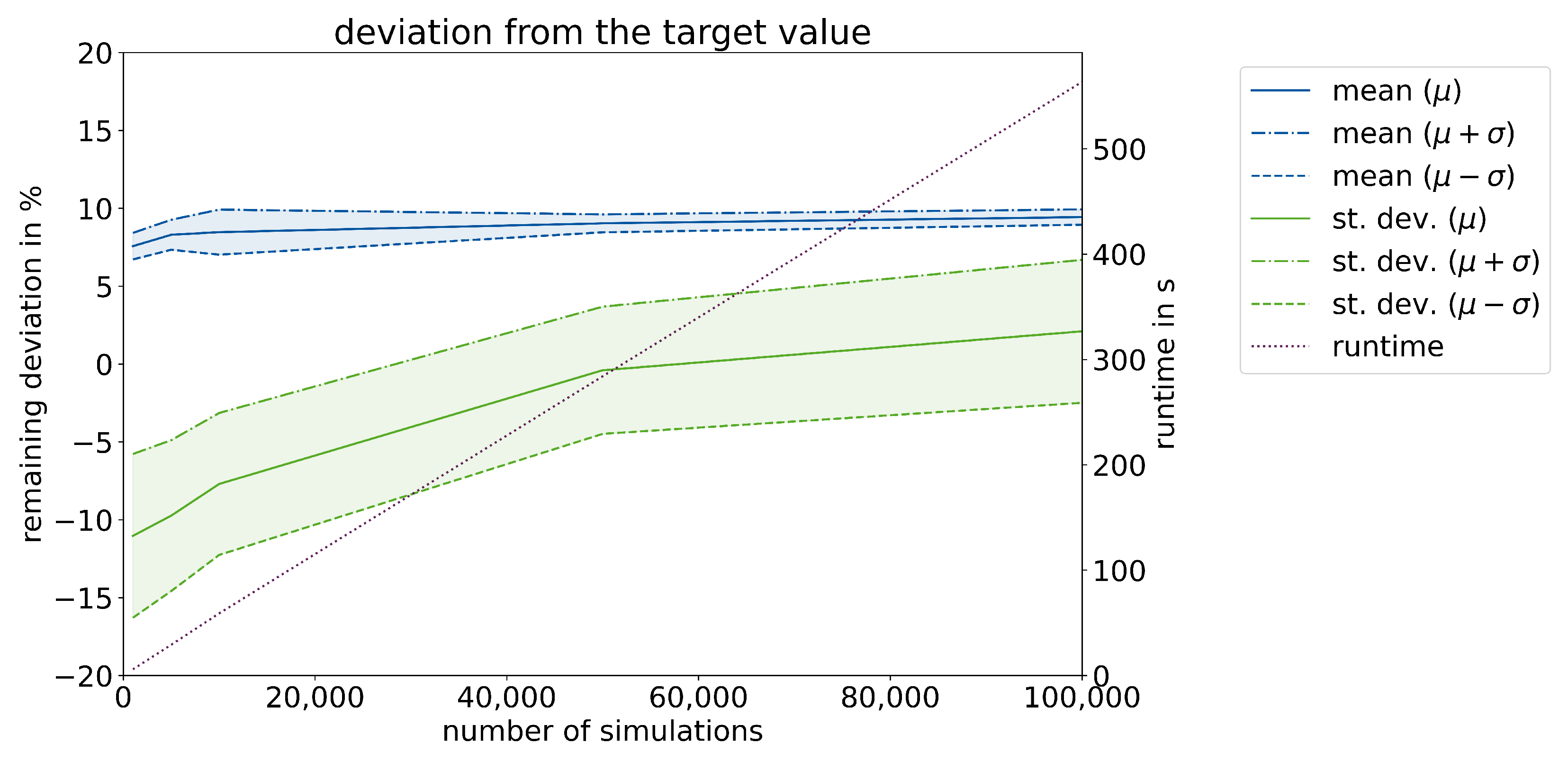
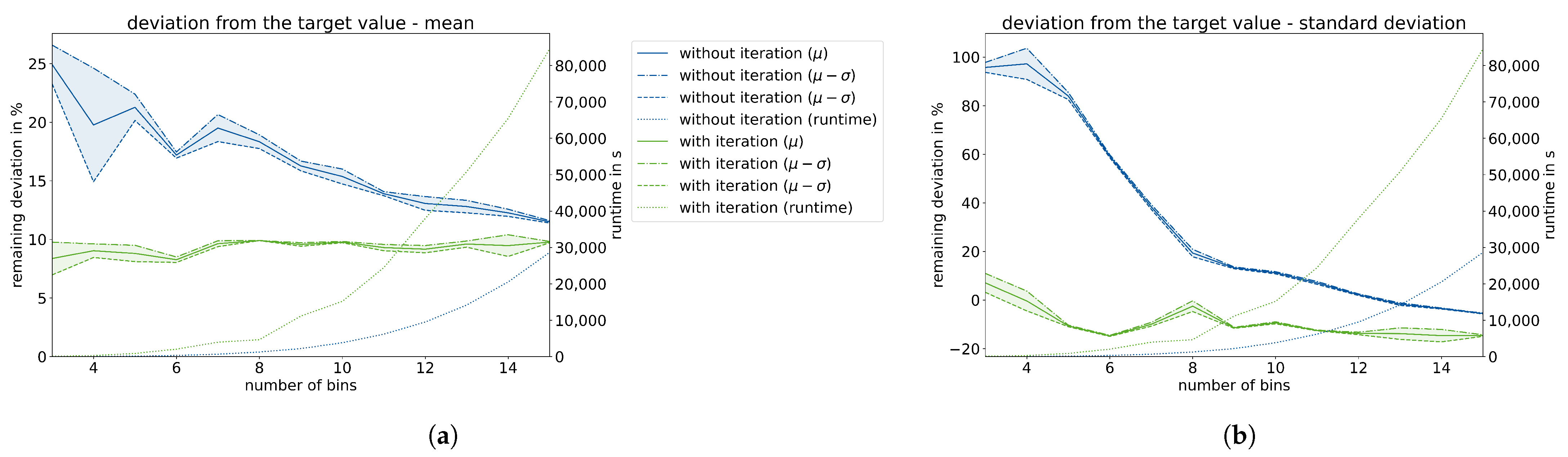
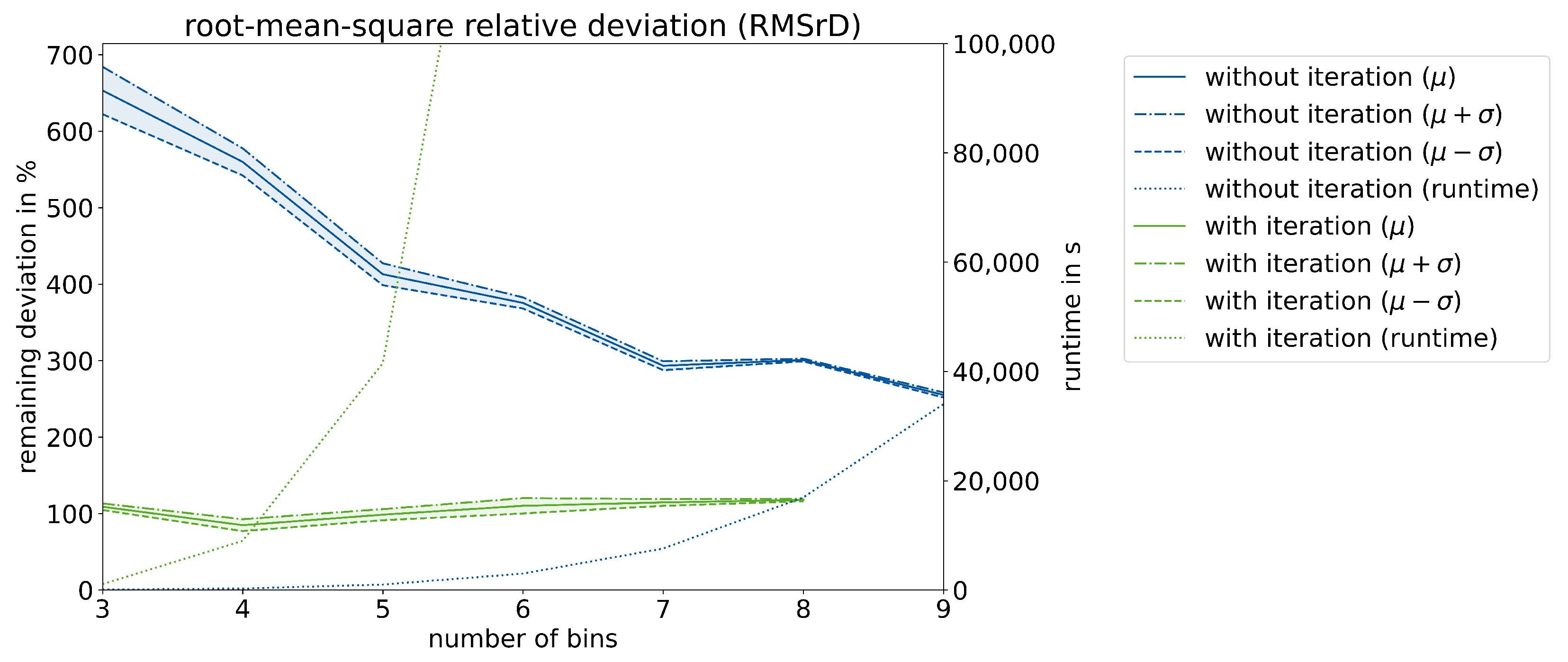
4.1. Automated Bayesian Inference with Iteration
4.2. Predictive BIM as Decision Support Tool
5. Conclusions and Outlook
- The automation of iterative Bayesian inference leads to significantly more efficient calibrations, as the processing times can be reduced by 99.7% for carbonation and 98.8% for chloride ingress compared to the conventional approach with similar precision.
- The precision of the calibration process can be influenced by adjustable termination criteria, allowing individual configurations to be adjusted to project requirements.
- As the deterioration models are calibrated according to the actual carbonation depths and chloride contents, the need for models for the combined effect of carbonation and chloride ingress, as well as alternative binders or concrete compositions, diminishes. The influence of these aspects is incorporated automatically, as well as the actual concrete cover per component.
- The functionality of BIM can be extended significantly by combining BIM with Python according to wrappers. This way, the interoperability of several programs can be achieved while the user only operates one piece of software containing the combined functionality of all the implemented software.
- By exporting the Bayesian networks and analysis results as CSV, TXT, and XDSL files, the workflow is transparent and traceable. The final results of the assessment are stored in automatically created BIM objects serving as data layers on the corresponding components. These objects are IFC compatible, allowing interoperability with other BIM software via enriched IFC files.
- The combination of timely and spatially resolved, reliable deterioration models can be used to establish predictive BIM for maintenance and repair as a resource-efficient way of working.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAM | Alkali-Activated Materials |
| AI | Artificial Intelligence |
| BIM | Building Information Modeling |
| BMS | Bridge Monitoring System |
| CSV | Comma-Separated Values |
| DT | Digital Twin |
| DTC | Digital Twin Construction |
| GUI | Graphical User Interface |
| IFC | Industry Foundation Classes |
| IoT | Internet of Things |
| shBIM | Structural Health BIM |
| SHM | Structural Health Monitoring |
| TR IH | Technical Standard “Maintenance of Concrete Structures” |
| TXT | text file format |
| XDSL | GeNIe’s native file format |
References
- ISO 16311-3; Maintenance and Repair of Concrete Structures—Part 3: Design of Repairs and Prevention. Beuth: Berlin, Germany, 2014.
- DIN EN 1504-9; Produkte und Systeme für den Schutz und die Instandsetzung von Betontragwerken—Definitionen, Anforderungen, Qualitätsüberwachung und Beurteilung der Konformität—Teil 9: Allgemeine Grundsätze für die Anwendung von Produkten und Systemen. European Standard. Beuth: Berlin, Germany, 2008.
- Deutsches Institut für Bautechnik (DIBt). Technische Regel—Instandhaltung von Betonbauwerken (TR Instandhaltung); German Institut for Building Technology: Berlin, Germany, 2020. [Google Scholar]
- Driessen-Ohlenforst, C. SMART-DECK: Multifunctional carbon-reinforced concrete interlayer for bridges. Mater. Corros. 2020, 71, 786–796. [Google Scholar] [CrossRef]
- Herbrand, M.; Wenner, M.; Ullerich, C.; Rauert, T.; Zehetmaier, G.; Marx, S. Beurteilung der Bauwerkszuverlässigkeit durch Bauwerksmonitoring. Bautechnik 2021, 98, 93–104. [Google Scholar] [CrossRef]
- Sacks, R.; Girolami, M.; Brilakis, I. Building Information Modelling, Artificial Intelligence and Construction Tech. Dev. Built Environ. 2020, 4, 100011. [Google Scholar] [CrossRef]
- Yang, A.; Han, M.; Zeng, Q.; Sun, Y.; Liu, H. Adopting Building Information Modeling (BIM) for the Development of Smart Buildings: A Review of Enabling Applications and Challenges. Adv. Civ. Eng. 2021, 2021, 1–26. [Google Scholar] [CrossRef]
- Hamooni, M.; Maghrebi, M.; Majrouhi Sardroud, J.; Kim, S. Extending BIM Interoperability for Real-Time Concrete Formwork Process Monitoring. Appl. Sci. 2020, 10, 1085. [Google Scholar] [CrossRef]
- Byun, N.; Han, W.S.; Kwon, Y.W.; Kang, Y.J. Development of BIM-Based Bridge Maintenance System Considering Maintenance Data Schema and Information System. Sustainability 2021, 13, 4858. [Google Scholar] [CrossRef]
- Hartung, R.; Schönbach, R.; Liepe, D.; Klemt-Albert, K. Automatized Parametric Modeling to Enhance a data-based Maintenance Process for Infrastructure Buildings, 2020. In Proceedings of the 37th ISARC, Kitakyushu, Japan, 27–28 October 2020. [Google Scholar] [CrossRef]
- Boje, C.; Guerriero, A.; Kubicki, S.; Rezgui, Y. Towards a semantic Construction Digital Twin: Directions for future research. Autom. Constr. 2020, 114, 103179. [Google Scholar] [CrossRef]
- Sacks, R.; Brilakis, I.; Pikas, E.; Xie, H.S.; Girolami, M. Construction with digital twin information systems. Data-Centric Eng. 2020, 1, e14. [Google Scholar] [CrossRef]
- Camposano, J.C.; Smolander, K.; Ruippo, T. Seven Metaphors to Understand Digital Twins of Built Assets. IEEE Access 2021, 9, 27167–27181. [Google Scholar] [CrossRef]
- Kaewunruen, S.; AbdelHadi, M.; Kongpuang, M.; Pansuk, W.; Remennikov, A.M. Digital Twins for Managing Railway Bridge Maintenance, Resilience, and Climate Change Adaptation. Sensors 2022, 23, 252. [Google Scholar] [CrossRef]
- Nour El-Din, M.; Pereira, P.F.; Poças Martins, J.; Ramos, N.M.M. Digital Twins for Construction Assets Using BIM Standard Specifications. Buildings 2022, 12, 2155. [Google Scholar] [CrossRef]
- Uddin, M.N.; Wang, Q.; Wei, H.H.; Chi, H.L.; Ni, M. Building information modeling (BIM), System dynamics (SD), and Agent-based modeling (ABM): Towards an integrated approach. Ain Shams Eng. J. 2021, 12, 4261–4274. [Google Scholar] [CrossRef]
- Desogus, G.; Quaquero, E.; Rubiu, G.; Gatto, G.; Perra, C. BIM and IoT Sensors Integration: A Framework for Consumption and Indoor Conditions Data Monitoring of Existing Buildings. Sustainability 2021, 13, 4496. [Google Scholar] [CrossRef]
- Gerbino, S.; Cieri, L.; Rainieri, C.; Fabbrocino, G. On BIM Interoperability via the IFC Standard: An Assessment from the Structural Engineering and Design Viewpoint. Appl. Sci. 2021, 11, 11430. [Google Scholar] [CrossRef]
- Panah, R.S.; Kioumarsi, M. Application of Building Information Modelling (BIM) in the Health Monitoring and Maintenance Process: A Systematic Review. Sensors 2021, 21, 837. [Google Scholar] [CrossRef]
- Morgenstern, H.; Raupach, M. BIM-centred building diagnoses as a decision support tool for maintenance and repair. e-J. Nondestruct. Test. 2022, 27, 9. [Google Scholar] [CrossRef]
- Morgenstern, H.; Raupach, M. Quantified point clouds and enriched BIM-Models for digitalised maintenance planning. MATEC Web Conf. 2022, 364, 05001. [Google Scholar] [CrossRef]
- Morgenstern, H.; Raupach, M. A Novel Approach for Maintenance and Repair of Reinforced Concrete Using Building Information Modeling with Integrated Machine-Readable Diagnosis Data. Constr. Mater. 2022, 2, 314–327. [Google Scholar] [CrossRef]
- Collao, J.; Lozano-Galant, F.; Lozano-Galant, J.A.; Turmo, J. BIM Visual Programming Tools Applications in Infrastructure Projects: A State-of-the-Art Review. Appl. Sci. 2021, 11, 8343. [Google Scholar] [CrossRef]
- Possan, E.; Andrade, J.J.O.; Dal Molin, D.C.C.; Ribeiro, J.L.D. Model to Estimate Concrete Carbonation Depth and Service Life Prediction. In Hygrothermal Behaviour and Building Pathologies; Building Pathology and Rehabilitation; Book Section Chapter 4; Springer: Cham, Switzerland, 2021; pp. 67–97. [Google Scholar] [CrossRef]
- Xia, J.; Shen, J.; Li, T.; Jin, W.L. Corrosion prediction models for steel bars in chloride-contaminated concrete: A review. Mag. Concr. Res. 2022, 74, 123–142. [Google Scholar] [CrossRef]
- Al-Ameeri, A.S.; Rafiq, M.I.; Tsioulou, O. Combined impact of carbonation and crack width on the Chloride Penetration and Corrosion Resistance of Concrete Structures. Cem. Concr. Compos. 2021, 115, 103819. [Google Scholar] [CrossRef]
- Zhu, X.; Zi, G.; Sun, L.; You, I. A simplified probabilistic model for the combined action of carbonation and chloride ingress. Mag. Concr. Res. 2019, 71, 327–340. [Google Scholar] [CrossRef]
- Shen, X.H.; Jiang, W.Q.; Hou, D.; Hu, Z.; Yang, J.; Liu, Q.F. Numerical study of carbonation and its effect on chloride binding in concrete. Cem. Concr. Compos. 2019, 104, 103402. [Google Scholar] [CrossRef]
- Zhu, X.; Zi, G.; Lee, W.; Kim, S.; Kong, J. Probabilistic analysis of reinforcement corrosion due to the combined action of carbonation and chloride ingress in concrete. Constr. Build. Mater. 2016, 124, 667–680. [Google Scholar] [CrossRef]
- Li, K.; Zhao, F.; Zhang, Y. Influence of carbonation on the chloride ingress into concrete: Theoretical analysis and application to durability design. Cem. Concr. Res. 2019, 123, 105788. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, Y.; Xi, Y. Modeling the effect of temperature gradient on moisture and ionic transport in concrete. Cem. Concr. Compos. 2020, 106, 103454. [Google Scholar] [CrossRef]
- Pacheco, J. Incorporating Cracks in Chloride Ingress Modeling and Service Life Predictions. ACI Mater. J. 2019, 116, 113–118. [Google Scholar] [CrossRef]
- Mundra, S.; Prentice, D.P.; Bernal, S.A.; Provis, J.L. Modelling chloride transport in alkali-activated slags. Cem. Concr. Res. 2020, 130, 106011. [Google Scholar] [CrossRef]
- Mangat, P.S.; Ojedokun, O.O.; Lambert, P. Chloride-initiated corrosion in alkali activated reinforced concrete. Cem. Concr. Compos. 2021, 115, 103823. [Google Scholar] [CrossRef]
- Beushausen, H.; Torrent, R.; Alexander, M.G. Performance-based approaches for concrete durability: State of the art and future research needs. Cem. Concr. Res. 2019, 119, 11–20. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Fink, O.; Wang, Q.; Svensén, M.; Dersin, P.; Lee, W.J.; Ducoffe, M. Potential, challenges and future directions for deep learning in prognostics and health management applications. Eng. Appl. Artif. Intell. 2020, 92, 103678. [Google Scholar] [CrossRef]
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of Bridge Structural Health Monitoring Aided by Big Data and Artificial Intelligence: From Condition Assessment to Damage Detection. J. Struct. Eng. 2020, 146, 22. [Google Scholar] [CrossRef]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, A.; Dutta, N.C.; Le, H.Q.; Biondi, B.; Mukerji, T. Approximate Bayesian inference of seismic velocity and pore-pressure uncertainty with basin modeling, rock physics, and imaging constraints. Geophysics 2020, 85, ID19–ID34. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, Z.; Zhao, X.; Li, Z.; Qin, P. Bayesian Calibration for Office-Building Heating and Cooling Energy Prediction Model. Buildings 2022, 12, 1052. [Google Scholar] [CrossRef]
- Ashtari, M.A.; Ansari, R.; Hassannayebi, E.; Jeong, J. Cost Overrun Risk Assessment and Prediction in Construction Projects: A Bayesian Network Classifier Approach. Buildings 2022, 12, 1660. [Google Scholar] [CrossRef]
- Jung, H.; Im, S.B.; An, Y.K. Probability-Based Concrete Carbonation Prediction Using On-Site Data. Appl. Sci. 2020, 10, 4330. [Google Scholar] [CrossRef]
- Hackl, J.; Kohler, J. Reliability assessment of deteriorating reinforced concrete structures by representing the coupled effect of corrosion initiation and progression by Bayesian networks. Struct. Saf. 2016, 62, 12–23. [Google Scholar] [CrossRef]
- Straub, D.; Papaioannou, I. Bayesian Updating with Structural Reliability Methods. J. Eng. Mech. 2015, 141, 13. [Google Scholar] [CrossRef]
- Cai, B.; Kong, X.; Liu, Y.; Lin, J.; Yuan, X.; Xu, H.; Ji, R. Application of Bayesian Networks in Reliability Evaluation. IEEE Trans. Ind. Inform. 2019, 15, 2146–2157. [Google Scholar] [CrossRef]
- Straub, D.; Papaioannou, I.; Betz, W. Bayesian analysis of rare events. J. Comput. Phys. 2016, 314, 538–556. [Google Scholar] [CrossRef]
- Büchter, T.; Eichler, A.; Steib, N.; Binder, K.; Böcherer-Linder, K.; Krauss, S.; Vogel, M. How to Train Novices in Bayesian Reasoning. Mathematics 2022, 10, 1558. [Google Scholar] [CrossRef]
- Schneider, R.; Fischer, J.; Bügler, M.; Nowak, M.; Thöns, S.; Borrmann, A.; Straub, D. Assessing and updating the reliability of concrete bridges subjected to spatial deterioration - principles and software implementation. Struct. Concr. 2015, 16, 356–365. [Google Scholar] [CrossRef]
- Fédération Internationale du Béton (fib). Model Code for Service Life Design; fib Bulletins; International Federation for Structural Concrete: Lausanne, Switzerland, 2006; Volume 34. [Google Scholar] [CrossRef]
- Grantham, M.G.; Gulikers, J.; Mircea, C. Predicting residual service life of concrete infrastructure: A considerably controversial subject. MATEC Web Conf. 2019, 289, 08002. [Google Scholar] [CrossRef]
- Kosalla, M.; Raupach, M. Diagnosis of concrete structures: The influence of sampling parameters on the accuracy of chloride profiles. Mater. Struct. 2018, 51, 75. [Google Scholar] [CrossRef]
- Bichara, L.; Saad, G.; Slika, W. Probabilistic identification of the effects of corrosion propagation on reinforced concrete structures via deflection and crack width measurements. Mater. Struct. 2019, 52, 89. [Google Scholar] [CrossRef]
- Marx, S.; Grünberg, J.; Schacht, G. Methoden zur Bewertung experimenteller Ergebnisse bei kleinem Stichprobenumfang. Betonund Stahlbetonbau 2018, 114, 2–13. [Google Scholar] [CrossRef]
- Chalhoub, C.; François, R.; Garcia, D.; Laurens, S.; Carcasses, M. Macrocell corrosion of steel in concrete: Characterization of anodic behavior in relation to the chloride content. Mater. Corros. 2020, 71, 1424–1441. [Google Scholar] [CrossRef]
- Angst, U.M. Predicting the time to corrosion initiation in reinforced concrete structures exposed to chlorides. Cem. Concr. Res. 2019, 115, 559–567. [Google Scholar] [CrossRef]


| Parameter | Lower Bound | Upper Bound | Unit |
|---|---|---|---|
| 0 | 100 | % | |
| 0 | 5 | – | |
| 0 | 20,000 | (mm/a)/(kg/m) | |
| 1 | 1000 | (mm/a)/(kg/m) | |
| 0 | 0.01977 | kg/m |
| Parameter | Lower Bound | Upper Bound | Unit |
|---|---|---|---|
| 0 | 5 | wt% | |
| 0 | 50 | mm | |
| 0 | 10,000 | K | |
| 233.15 | 333.15 | K | |
| 0 | 200 | mm/a | |
| a | 0 | 1 | – |
| Software | Version | Developer | Location | Function |
|---|---|---|---|---|
| Revit | 22.0.2.392 | Autodesk | San Rafael, USA | BIM author software |
| BIMvision | 2.25.2 | Datacomp | Cracow, Poland | BIM viewer |
| Dynamo | 2.10.1.4002 | Autodesk | San Rafael, USA | (Visual) Programming in BIM |
| Python | 3.8.3 | Python Software Foundation | Wilmington, USA | Programming language |
| GeNIe | 4.0.2304.0 | BayesFusion | Pittsburgh, USA | Bayesian network software |
| PySMILE | 2.0.8 | BayesFusion | Pittsburgh, USA | Python wrapper for GeNIe |
| Depth | Evidence | Calculation | Relative Deviation |
|---|---|---|---|
| in mm | in wt% | in wt% | in % |
| 0–15 | 1.915 | 1.463 | −23.60 |
| 15–30 | 0.294 | 0.404 | 37.37 |
| 30–45 | 0.022 | 0.053 | 140.0 |
| Parameter | Lower Bound | Upper Bound | Mean | Standard Deviation | Unit |
|---|---|---|---|---|---|
| 43.75 | 92.97 | 70.00 | 9.81 | % | |
| 0.352 | 2.813 | 1.525 | 0.543 | – | |
| 1230 | 9844 | 5030 | 1851 | (mm/a)/(kg/m) | |
| 1 | 562.9 | 330.1 | 143.3 | (mm/a)/(kg/m) | |
| 0 | 0.00352 | 0.00045 | 0.00027 | kg/m | |
| 1.421 | 1.914 | 1.645 | 0.100 | wt% | |
| 3.434 | 8.759 | 5.760 | 1.156 | mm | |
| 2500 | 4463 | 3337 | 440 | K | |
| 265.8 | 278.7 | 272.8 | 2.8 | K | |
| 47.59 | 89.67 | 67.82 | 8.32 | mm/a | |
| a | 0.374 | 0.461 | 0.418 | 0.019 | – |
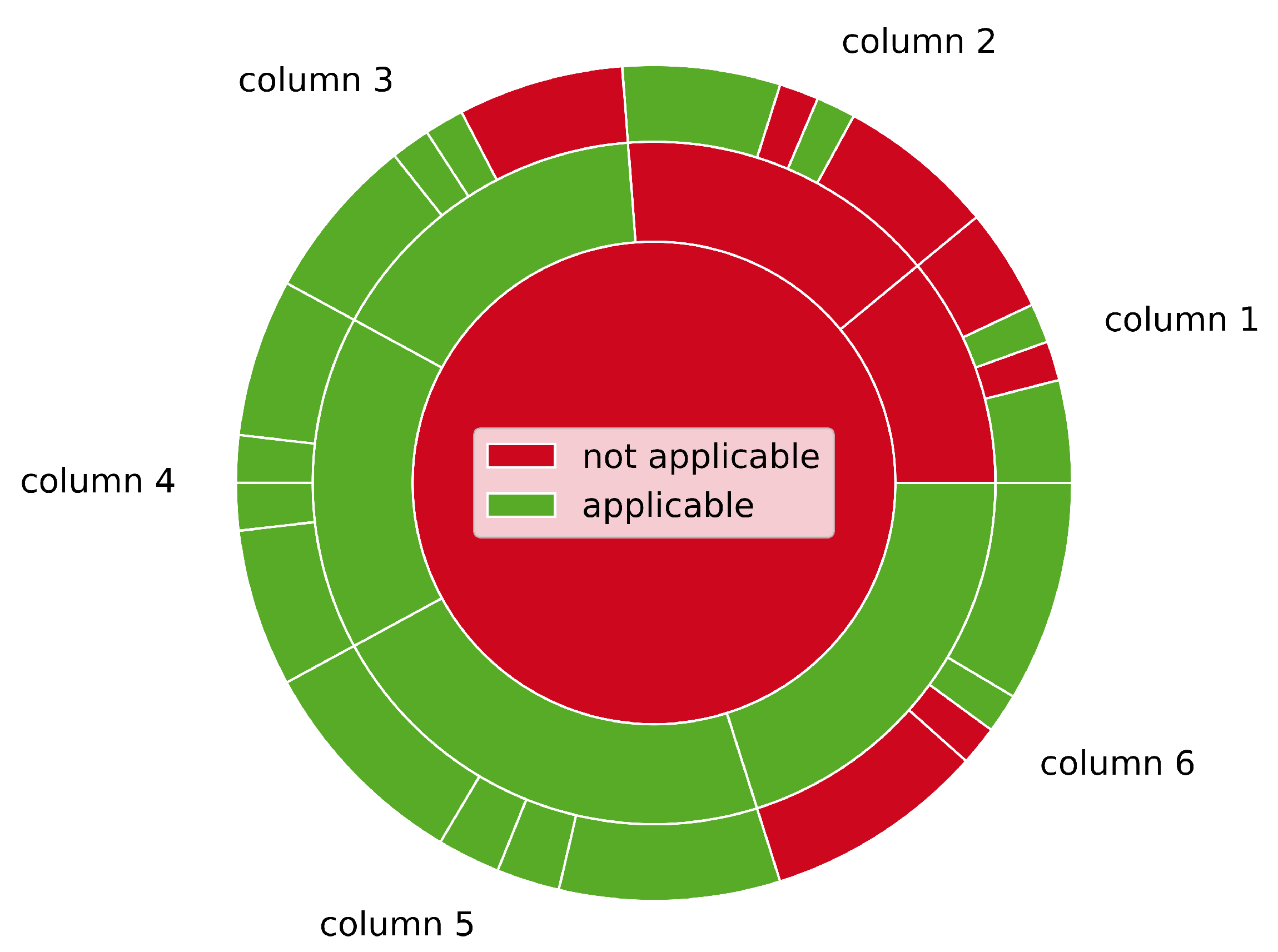
| Selection | Applicative Elements | Applicative Area | ||
|---|---|---|---|---|
| - | # | % | m | % |
| group | 0 of 1 | 0.0 | 0.0 of 44.9 | 0.0 |
| component | 4 of 6 | 66.7 | 33.1 of 44.9 | 73.8 |
| sides | 17 of 24 | 70.8 | 31.6 of 44.9 | 70.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morgenstern, H.; Raupach, M. Predictive BIM with Integrated Bayesian Inference of Deterioration Models as a Four-Dimensional Decision Support Tool. CivilEng 2023, 4, 185-203. https://doi.org/10.3390/civileng4010012
Morgenstern H, Raupach M. Predictive BIM with Integrated Bayesian Inference of Deterioration Models as a Four-Dimensional Decision Support Tool. CivilEng. 2023; 4(1):185-203. https://doi.org/10.3390/civileng4010012
Chicago/Turabian StyleMorgenstern, Hendrik, and Michael Raupach. 2023. "Predictive BIM with Integrated Bayesian Inference of Deterioration Models as a Four-Dimensional Decision Support Tool" CivilEng 4, no. 1: 185-203. https://doi.org/10.3390/civileng4010012
APA StyleMorgenstern, H., & Raupach, M. (2023). Predictive BIM with Integrated Bayesian Inference of Deterioration Models as a Four-Dimensional Decision Support Tool. CivilEng, 4(1), 185-203. https://doi.org/10.3390/civileng4010012










