Abstract
Dynamic façades play an important role in enhancing the overall performance of buildings: they respond to the environmental conditions and adjust the amount of transmitted solar radiation. This paper proposes a simulation-based framework to evaluate the energy and comfort performance of different control strategies for switchable electrochromic glazing (EC). The presented method shows the impact of a model predictive control (MPC) on energy savings and on visual and thermal comfort for different orientations compared to other strategies. Besides manual operation and conventional rule-based controls, the benchmark in this study was a simulation-based control (multi-objective penalty-based control) with optimal performance. The hourly results of various control cases were analyzed based on the established performance indicators and criteria. The cumulative annual results show the capabilities and limitations of each control strategy for an EC glazing. For a temperate climate (Mannheim, Germany), results showed that an MPC for EC glazing provides visual and thermal comfort while saving energy of up to 14%, 37%, 37%, and 34% respectively for facing north, east, south, and west relative to the base-case.
1. Introduction
Buildings are responsible for over 36% of the total global energy consumption, and windows have the most significant impact on the energy balance of buildings [1]. Harvesting solar gains can cover a considerable part of the heating demand in cold climates. However, glare protection in winter limits the required solar gain and leads to poor daylighting and view obstruction. Moreover, using shading and blocking the sunlight can reduce cooling demand and the risk of overheating up to 57% for a house located in a continental climate with warm summer [2]. Providing daylight and outside view is the main priority of occupants [3] and finding an agreement between energy savings and comfort is often challenging.
Despite the potential of switchable electrochromic glazing (EC), automating EC glazing requires fast and reliable control strategies and optimization methods. Developing predictive algorithms to optimize a multi-objective problem and achieve a trade-off between saving energy and providing comfort was the main goal of this study.
1.1. Switchable Electrochromic Glazing (EC)
Switchable glazing systems are capable of changing optical properties. Liquid crystal (LC), suspended particle (SP), and electrochromic (EC) are controllable systems, and their state on demand can be changed in response to signal input from Building Automation Systems (BASs), networked sensors, or occupant feedback [4].
From early 2006, switchable EC technology was in the building market. The electrochromic coating is highly absorptive, and it should be positioned on the inner surface of the outer glass, where a low-E coating protects the inward longwave radiative heat flux to the occupants inside the room [4]. By changing voltage in EC coating, the oxidation state of tungsten oxide varies [5]. Consequently, the optical properties of the glazing can be regulated.
Different products with various tinting levels, from the clear state (with the highest transmissivity, also called bleached) to fully tinted (with the lowest transmissivity), are available. These transmittance states are discrete, and with the control signal, the tinting level switches. A wider range of transmissivity and several stable intermediate states make the EC systems more efficient for controlling. Automated EC glazing allows visible light to enter into space and blocks the solar radiation when overheating protection is required. EC glazing can reduce both heating and cooling loads and protect users from discomfort glare.
1.2. Simulation-Based Evaluation
During the last decade, extensive research has been conducted for investigating the potential energy savings of dynamic EC glazing by using verified simulation tools such as EnergyPlus (EnergyPlus™ is a whole building energy simulation program. https://energyplus.net/ (accessed on 3 December 2021)), ESP-r (ESP-r (Environmental Systems Performance-Research) is a modelling tool for building performance simulation. https://www.strath.ac.uk/research/energysystemsresearchunit/applications/esp-r/ (accessed on 3 December 2021)), and TRNSYS (TRNSYS (pronounced ‘tran-sis’) is an extremely flexible graphically based software environment used to simulate the behavior of transient systems. http://www.trnsys.com/ (accessed on 3 December 2021)). These studies applied many different control strategies with various parameters and thresholds.
Lee et al. published results from a full-scale test cell with EC glazing (Window-to-Wall Ratio of 40%), which showed that EC glazing provided greater energy efficiency. The above-mentioned study reported that the lighting energy was reduced by 91%, while the estimated annual energy savings and electricity peak demand were decreased by 48% and 35%, respectively [6].
Belzer also reported simulation results for small and medium office buildings in several US climate regions. The lighting, cooling, and heating savings range between 15 to 25%, 3 to 17%, and 7 to 15%, respectively, in his study. The total source-level savings range between 2 to 7%, depending on the window area, building location, and orientation [7].
Afterward, Lee et al. investigated more the impact of EC glazing with overhangs on visual comfort and energy. The findings clearly showed significant reductions in average annual daylight glare index (DGI) and relevant energy savings (10%). The study also noted that the electricity peak demand could be reduced by 14 to 16% for large-area windows in some US climate regions [8].
Furthermore, using EnergyPlus, DeForest et al. estimated the annual energy performance of a dual-band (visible and infrared) EC glazing for three building types in several US climate regions. They estimated the primary energy savings between 65 kWh/m2a and 323 kWh/m2a per window area [9]. For Mediterranean climates, Tavares et al. carried out an energy performance simulation, finding energy savings of about 20 and 37 kWh/m2a per windows surface for the east/west-facing facades [10].
Cannavale et al. studied the energy and visual comfort performance of a reference office building equipped with different glass technologies for Rome, London, and Aswan. The EC glazing improved the daylight performance and overall yearly energy savings as high as 40 kWh/m2a (referred to window surface) in the hottest climates, assuming clear glazing as a benchmark [11].
Despite the proven potential of EC glazing for saving energy, previous researchers suggested simulation studies to evaluate the impact of the EC system for each specific climate and window orientation. These simulations during the early stage of design help the building owners to make a more sustainable decision for selecting a proper sun-protection system.
1.3. The Role of Control Strategies
Precedent experiments proved that automated dynamic shading saves more energy compared to manual operations or static systems. The automated blinds saved 21% in cooling load and 21% in lighting energy use in comparison to a fixed shading in private offices in Oakland, California [12]. For switchable EC glazing, the maximum reduction in annual total electricity use was reported as 63% for an office building with large glazing in New York [13]. This reduction was a combined lighting and cooling energy use provided by EC glazing with day-lighting controls.
Dussault et al. [14] showed that automated EC glazing allows significant energy savings for south, west, and east-oriented facades (8 to 53% for Quebec, Canada). Through a simulation-based sensitivity analysis, Dussault et al. [15] concluded that the greatest total energy savings can be achieved for automated EC glazing in warmer climates with higher solar radiation exposure.
In addition to the window size, orientation, climatic conditions, and latitude, the overall performance of EC glazing highly depends on the control strategy applied for automation. Previous research [15] found that the choice of the specific control strategy had a limited impact on energy savings but a larger impact on visual comfort.
Over the past few decades, researchers have developed different rule-based strategies for shading systems based on conditions (e.g., “if… then…”). These algorithms switch the state of the shading in response to the difference between measured (or simulated) values and the set point (or desired) values. Many single variables such as indoor temperature, glare, the illuminance at the workplace, and radiation level have been used in precedent studies, while there are few numbers of studies considering multiple criteria (e.g., both energy-saving and comfort) for controlling dynamic shadings [16] or EC glazing [17].
In real buildings, rule-based algorithms are mainly applied. Mainly two-step control (clear/tinted) has been used on the entire area of glazing without zoning control. These conventional control strategies are mostly incapable of considering multiple variables and all the necessary aspects of energy and comfort. The so-called “cut-off” controller for blinds blocks the direct solar transmittance according to the actual position of the sun and avoids diminishing daylight and view [18], but this is not applicable for EC glazing systems.
Despite all the benefits of automated dynamic shading systems, many post-occupancy studies reported users’ dissatisfaction [3]. This can be explained by the fact that, so far, even advanced heuristic strategies for EC glazing were limited to a few numbers of physical variables (e.g., temperature and illuminance) and ignored local position and view direction of occupants for visual comfort consideration [19,20].
Jonsson et al. [21] studied the importance of control strategy through simulations and clarified that only a near-optimal control for smart window balance between energy saving and comfort provision. Concerning the installation and maintenance cost of EC windows [22], simulation results answer whether the amount of energy savings is paying back the initial investment or not.
For simulation studies, we can evaluate the impact of different control strategies by providing control profiles. These profiles are time series containing control signals (state of shading) from 1st hour to the 8760th hour in a complete year. A profile for manual operation or rule-based strategy can be generated by applying simple rules (or “if” conditions) while providing a control profile for predictive control [16] or “optimal” or “sub-optimal” control scenario [23] needs complicated steps and involves post-processing the results or reverse modeling
1.4. Simulation-Based Control/Optimization
The term “optimization” is often referred to as the procedure(s) of making something as effective or functional as possible [24]. Simulation-based “optimization” is a method for finding the optimal input values based on the desired outcomes.
The challenge of simulation-based optimization is twofold. On the one hand, simulating switchable glazing has some central difficulties due to (i) complexity in modeling dynamic shading systems, (ii) integrating climate-based daylight and building energy programs, and (iii) applying multi-variable control strategies during simulations. On the other hand, available building performance simulation (BPS) tools are not initially developed for optimizing and finding the optimal control solutions and need to be tailored [25].
An algorithm can search hourly results of all simulation runs to find the “optimal” or “near-optimal” state of the EC glazing. This optimal state can be the state with minimum penalty among all possible states at the time step. The minimum penalty (or minimum sum weighted penalty) ensures the provision of the desired conditions in the room. This searching method for optimal points among infinite design space (feasible states) can be impractical due to the huge number of possibilities. However, for a dynamic system such as EC glazing with discrete decision variables (4 states) and a relatively small feasible set (64 combinations), the simulation-based optimization method is applicable.
After finding the optimal states (or near-optimal) of the EC glazing for a whole year, these data can be used for generating the optimal control profile. A general technique is to pick the best hourly control inputs and put them one after the other. The main problem of this so-called “collage” technique is ignoring the impact of the previous state of shading on thermal inertia and forthcoming energy balance in the room [25]. This may lead to an error according to the amount of applied/active thermal mass in the building.
Favoino et al. introduced a novel simulation framework for evaluating the performance of switchable glazing. By integrating energy and daylight simulations, they provide a framework for control optimization considering building energy use, Useful Daylight Illuminance, glare risk, and load profile matching indicators [26].
Similar to this approach, the authors previously introduced another advanced technique using a sum weighted penalty-based ranking method and several sequential TRNSYS simulations to overcome the shortcoming of the “collage” method. By running simulation over a defined period, it is possible to predict the optimal state of EC for the time t (e.g., simulation runs from 0 to t). If the time slot moves forward, a new set of simulations start with perfectly adjusted initialization to evaluate possible states at time t + 1 (e.g., simulation runs from 0 to t + 1).
This way, the history and the impact of the previous time step on the next time step can be taken into account carefully [23]. The main difference between Favoino’s and Ganji’s framework is that the penalty-based method uses some weighted sum penalty functions for considering different performance indicators. This makes prioritizing energy versus visual or thermal comfort possible for designers/engineers.
1.5. Model Predictive Control (MPC)
Model Predictive Control (MPC) in the building has been reported as a promising solution for saving energy [27,28,29]. The MPC reacts to the current state of the building and future conditions accordingly. Other control strategies—even a proportional–integral–derivative (PID) controller—lack this prediction ability. MPC algorithm uses an explicit model of the building to predict its state over a defined horizon. At each time step, MPC minimizes a “cost function” assuming weather forecast and predefined constraints and occupation schedule.
Even though the MPC application in the building seems very effective, the development and calibration process for setting up a predictive controller requires extensive skills and knowledge [30]. For developing such a model, detailed knowledge about the building properties and active systems is required. Moreover, the same MPC model is not fully applicable to new conditions (new orientation, room geometry, and plan layout) and needs some major adjustments. The key question is whether the energy savings and comfort improvements compensate for the development, operation, and maintenance costs of an MPC or not.
Precedent studies are mainly focused on using MPC for regulating the temperature and HVAC systems for the energy-saving purpose and thermal comfort [29], while controlling dynamic shading and lighting systems for providing both energy and comfort remained less investigated [14,31,32]. Favoino et al. [26] studied optimal control and performance of switchable glazing in temperate climates and concluded that more advanced control strategies (such as reactive and predictive control) show a higher potential in energy saving while providing visual comfort.
In major sectors of the existing buildings, active HVAC systems are not controllable at all. In this case, MPC can only regulate the shading system and lighting while considering the state of other systems. This strategy can be used for retrofitting, and an MPC is still able to reduce overall energy and satisfy the occupants, even though the HVAC systems cannot be regulated directly. In this paper, the main goal of the MPC controller was defined not only to reduce the overall energy consumption but also to provide minimum thermal and visual comfort by controlling both shading and artificial lighting.
In building control engineering, a dynamic model refers to a set of functions that describes the time-dependent state of a system. A robust optimization algorithm in MPC relies on a reliable dynamic model of the system(s) described with differential equations. Developing this model for dynamic EC glazing is critical due to some known obstacles:
Firstly, a dynamic model should be as simple as possible, yet without influencing the prediction outcome. Here the model estimates the state of the building for both energy and non-energy (visual and thermal comfort) performance. For thermal model application with MPC, the resistance-capacitance (RC) modeling approach with different levels of complexity has been used in previous researches [27,33,34].
Secondly, most optimization methods work for continuous systems. This means the possibility of continuous change in the state of EC glazing over time (which is not feasible). The solution space for the EC glazing system is discrete due to the nature of electrochromic coating technology [28]. Here, for instance, between the “clear” state of the EC and the “low-tinted” state, no stable intermediate state can be considered. This “continuous versus discrete” problem leads to some challenges during the optimization and needs special treatment.
Recently, Isaia et al. [32] showed enhancing energy efficiency and comfort in buildings is possible by using a Hybrid-model predictive control for switchable EC glazing. In theoretical investigations, discrete and switched systems are controlled with Hybrid-MPC methods, combining continuous and discrete states. In a numerical manner, the convergence and real-time usability of solving the hybrid optimization problem cannot be guaranteed and is a drawback for running these methods on a prototype. Furthermore, the dimensions and size of the system model have a huge influence on the solving time, while with continuous methods, a fast solving is possible.
Thirdly, the prediction of daylighting and glare in a room with dynamic EC glazing is challenging. Glare is a view-dependent parameter, and the distribution of daylight in a room is complex and involves many elements. Differential equations for MPC cannot describe the complex steady-state behavior of light. Light distribution should be defined as a simple linear function including every variable, which influences daylighting (on the work-plane or at eye-level). This variable list includes sky condition, sun position, room geometry, opening dimensions, obstructions, surface reflectivity, and transmissivity of EC glazing and their interactions within the room. For instance, since the common indicator for glare (DGP) has a non-linear description, an alternative metric based on vertical illuminance was used in this study. Appendix A.4 describes the linear function and the way daylight prediction can be possible based on pre-simulated results from Radiance (Radiance is a validated lighting simulation tool, https://radiance−online.org/ (accessed on 3 December 2021)).
Simulation tools and virtual test beds can be used to evaluate a newly developed MPC before even applying it to a real building [35]. This process is usually performed by coupling between a building simulation program (here TRNSYS) and an optimization tool (here Matlab/Simulink). The optimization algorithm uses simulated values at every time step as dynamic inputs.
Investigating the potential of different control strategies for an automated EC glazing system is only possible through a multi-objective approach and considering the interaction of the fenestration system with daylighting, thermal inertia, and HVAC systems. In this study, the Building Controls Virtual Test Bed (BCVTB) (Building Controls Virtual Test Bed (BCVTB) is an open-source, freely available software that can link different simulation programs (EnergyPlus, Modelica, Radiance, MATLAB/Simulink) for co-simulation. https://simulationresearch.lbl.gov/projects/building−controls−virtual−test−bed (accessed on 3 December 2021)) was used for linking different simulation programs.
This paper is intended to evaluate the overall performance of an electrochromic glazing system in a temperate climate (Mannheim, Germany) under different control strategies. Therefore, a simulation-based framework is proposed to assess the impact of an MPC controller on both energy-saving and providing visual and thermal comfort.
Firstly, a model for integrated climate-based daylight and energy simulation is required. Section 2 mainly describes how the EC glazing and the prototypical office room should be defined for such simulations.
Secondly, as described in Section 3, different control strategies need to be generated and then applied in dynamic simulations over the course of a year. Control profiles representing a manual operation or a radiation-based controller can be generated easier. However, for generating a control profile that represents a predictive controller, the process is more complicated. Section 3.4 explains this process in detail. Section 3.5 also describes how we provide our penalty-based control profile.
Finally, this paper provides results in Section 4, where different evaluation criteria were described, and the impact of control strategies on the overall performance of an office room facing north, east, south, and west was compared.
2. Simulation Methods
In a building simulation, the goal is normally to investigate the effect of different parameters on the overall performance of the buildings. It is also possible to go reverse, search among the outcomes, and find the optimal inputs. For investigating the impact of different control strategies, advanced tools and techniques were applied for both (i) generating the simulation-based control profile (CtrlPen) and (ii) simulating the annual performance of a reference room with EC glazing and comparing the impact of different strategies and finding the best one.
Despite all the challenges, a well-defined simulation study is the most promising method for assessing the impact of automated EC glazing under different control strategies and various environmental conditions.
The following sections describe the techniques for modeling and simulating the prototypical room with switchable EC glazing. The simulation model was prepared to read different control profiles (state of the tinting) for each window zone (top, middle, and bottom) and calculate the respective energy demand at every time step.
Verified simulation toolchains were used for modeling dynamic EC glazing and implementing it in building simulations. Firstly, using WINDOW, we can generate the optical and thermal properties of a switchable glazing (here for each state of EC). Secondly, the angular-dependent properties and the BSDF data sets (for each state of EC) were applied in Radiance for a climate-based annual simulation. After providing the annual daylight results for all EC combinations (here 64), the TRNSYS model reads the daylight results for a daylight-based artificial lighting control.
In this study, the same simulation model—the same properties and boundary conditions—was used for three different purposes:
- Applying different control profiles in the simulation to calculate annual hourly results and the overall performance of EC glazing;
- Generating the MPC control profile by coupling Matlab/Simulink and TRNSYS via BCVTB (in Section 3.4);
- Generating the simulation-based control (CtrlPen) as the benchmark (in Section 3.5).
2.1. Switchable Electrochromic Glazing (EC)
To simulate a switchable EC glazing in Radiance and TRNSYS, the first step is to make the configuration of the glazing system (including glass panes, coatings, and gaps) in WINDOW and export the necessary data into the simulation tools. Figure 1 shows a double-glazing EC window with overall Ug of 1.3 W/m2K. The outer pane includes the electrochromic coating attached to the inside face (#1 thickness: 7 mm), the 15.5 mm gap filled with argon, and the inner pane is a laminated pane with a low-e coating (#2 thickness: 12.9 mm, emissivity: 0.07). The frame U-value was assumed to be 0.19 W/m2K, similar to the external wall.
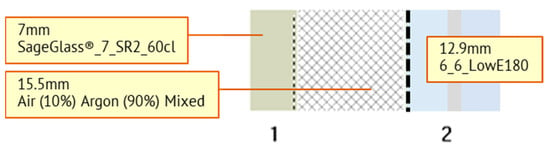
Figure 1.
EC glazing system configuration modeled in LBNL WINDOW (v. 7.6).
Table 1 shows the overall performance of the EC glazing calculated by WINDOW under CEN (European Committee for Standardization: For calculating Ug, 20 °C and 0 °C are assumed for Tin and Tout respectively. For calculation of the SHGC (aka g-value) Tin and Tout of 25 °C and 30 °C respectively are considered and the solar radiation is assumed to be 500 W/m2 with 0° incident angle (perpendicular to the window surface)) environmental conditions. The Solar Heat Gain Coefficient (SHGC), Tsol, and Tvis are based on the normal incidence on the center of the glass for every state of tinting (four states from clear to fully tinted). Table 1 also shows the base-case window, a conventional double-glazing insulating window (with low-e) without any sun protection. We used this base-case as a reference for comparing the annual results in Section 4.

Table 1.
Overall performance of EC glazing and base-case calculated by WINDOW (v. 7.6).
2.2. Prototypical Office Room
Figure 2 shows the 3D geometry of a prototypical office room and its workplace layout. The side-lit space dimensions are 6 m depth, 5 m width, and 3.3 m height. It has a large window-to-wall ratio (85% WWR), which is common for an office building. The window area is split into three independently controllable EC zones: top, middle, and bottom.

Figure 2.
(Left) Three-dimensional model of the reference room with different window zones (top, middle, bottom). (Right) Plan layout of four occupants’ positions in the open office and groups 1 (G1) and 2 (G2).
The room represents a typical office space shared between four occupants. We put the occupants into two groups: (G1) the occupants sitting closer to the window (1.26 m away from the window) and (G2) the occupants sitting deeper inside the room (2.74 m away). From a controlling perspective, grouping is helpful to understand the role of actuating EC tinting or artificial lighting in response to the individual needs in a shared office.
For glare evaluation, four individual users’ positions/view directions were considered. The eye-level was 120 cm above the floor, and the view directions were parallel to the window. For calculating available daylighting on the task area, horizontal illuminance was simulated on multiple sensor points located on the four desks, 80 cm above the floor. The individual position of the users was also considered in TRNSYS for evaluating mean radiant temperature (MRT) and thermal comfort.
The same 3D geometry was used in both Radiance and TRNSYS (as a single thermal zone). Table 2 shows the construction properties of the surfaces used in the simulations. The U-value of the external walls was 0.19 W/m2K, and other surfaces (including internal walls, ceiling, and floor) were adiabatic.

Table 2.
Properties of the surfaces for energy simulation in TRNSYS.
Table 2 also shows the reflectivity of the surfaces applied in Radiance (as diffuse reflectance with specularity = 0 and roughness = 0). After running an annual simulation for all the window combinations, the hourly results were post-processed to be used as dynamic input in TRNSYS for lighting controller (Type4).
Maximum supplemental artificial lighting equal to 5 W/m2 was added into the internal gain based on the available daylight in TRNSYS. According to the state of the EC system at every hour, TRNSYS reads corresponding horizontal illuminance values (pre-simulated in Radiance). The daylight-based lighting control in TRNSYS (controller Type 4) works with these hourly average daylight values for each lighting group (G1 and G2). This controller has a continuous dimming function and on/off with the first illuminance setpoint = 500 lx and the second illuminance setpoint = 300 lx.
Table 3 shows the simulation setup and conditions for the thermal zone. A typical meteorological year (TMY) for Mannheim, Germany (.epw file format) was used for both climate-based daylight and thermal simulations. During the working hours (Mon–Fri: 8:00–18:00), 75 W for each seated person (light office work) and 140 W for each computer device were assumed as internal gain.

Table 3.
Simulation setups in TRNSYS and model description.
The infiltration of the building was assumed n = 0.1 h−1, which increased during the working hours into n = 1.45 h−1. We assumed no increased night ventilation in this study. We used an ideal heating and cooling system with a cooling setpoint temperature of 27 °C and a heating setpoint temperature of 20 °C during the occupied hours. A reversible heat pump with the efficiency of η = 4.2 for heating and COP = 4 for cooling was assumed to calculate the total annual end-use energy values (electricity). For artificial lighting, efficiency = 1 was assumed.
The hourly local predicted mean vote (PMV) [36] was internally calculated by TRNSYS to evaluate thermal comfort. Local PMV involves the main environmental parameters (air temperature, relative humidity, etc.) and the calculation of view factor and MRT at the individual occupant’s location. In this study, personal parameters, including clothing factor of 1 clo, the metabolic rate of 1 met, and air velocity of 0.1 m/s, were considered constantly over the year.
2.3. Implementing Different Control Strategies in Simulation
Using a variable configuration ID for the detailed window and a “Data Reader” component in TRNSYS, we can make TRNSYS read the control inputs line by line from a generated control profile (.csv file format). During simulation, TRNSYS reads the EC state (S0: clear to S3: fully tinted) from the control profile and switches the configuration ID. This way the corresponding optical and thermal properties will be applied into thermal calculations at every time step. Since the simulation time step was set 15 min, the TRNSYS model receives one control signal every four time-steps (meaning that the window does not change during one hour). Knowing the current state of the EC, TRNSYS finds the corresponding pre-simulated daylight results for controlling electric lighting.
The technique of variable window ID facilitates our proposed simulation framework for evaluating the performance of different control strategies. Figure 3 shows how various control profiles are generated and applied in a prototypical office model. As explained in Section 3.4, the control profile representing MPC (MPCtrl) was generated by coupling Matlab (including the RC model (as a slave model) and optimization algorithm) and TRNSYS (as a master model representing a real building). Additionally, the process of generating the pre-determined penalty-based control profile (CtrlPen) was explained in Section 3.5. Finally, in our simulations, different control scenarios were applied for providing the results and comparing the overall performance of different cases.
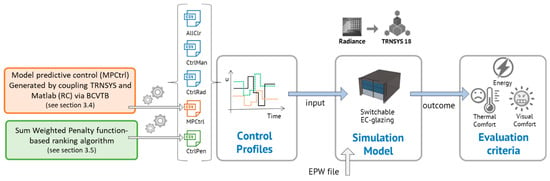
Figure 3.
Simulation framework for evaluating different control strategies.
3. The Operation and Control Strategies
The control strategies can be derived in an easy or complicated way based on the complexity of the algorithms. From simple rule-based strategies to predictive control or “near-optimal” control, generating control profiles needs post-processing of the hourly weather parameters or reverse modeling techniques.
The proposed simulation framework requires an annual control profile for each strategy. These time-series data include hourly control signals (states of EC glazing for each window zone) from the first to 8760th hour in a year. Therefore, in addition to two not-controlled cases (base-case + one static case), four various control algorithms were defined (dynamic: one manual operation and three automatic controls) for simulations.
The following sections describe how these control profiles were generated for various cases. For manual operation, simple rule-based control (radiation-based), the profiles were generated after post-processing a single parameter in the weather data or simulated results.
Finally, Section 3.5 describes the provision of the “near-optimal” control scenario and the way it was derived from the simulated results by considering a sum-weighted penalty function.
3.1. No Control
3.1.1. No Shading (Base-Case)
To show the impact of having a switchable glazing system, a double-glazing insulating window without a shading device was assumed as the base-case (see Table 1). The base-case represents the performance of the reference room without any solar protection, which is expected to lead to major issues such as discomfort glare and overheating even during wintertime. During the simulations, the base-case window was kept always not-shaded.
3.1.2. Static, Always Clear State (AllClr)
Using EC glazing affects the overall performance of the building even without applying any control (due to the lower SHGC in comparison to the base-case window). Therefore, we studied also the impact of a static EC façade (not controlled) and left the EC always in a clear state for a complete year. By comparing the results of static EC glazing with other dynamic strategies, this paper aimed to picture the significance of an automated system. When EC glazing is always in the clear state (AllClr), the reference room requires minimum heating demand and artificial lighting use (since it has the maximum solar gain), which can be assumed as an energy base-line.
3.2. Manual Operation (CtrlMan)
Previous researchers have observed the occupants’ control of window blinds and other shading systems in offices. In general, users tend to avoid direct sunlight in the workplace by using shading; but the shading remains pulled down (or tinted in case of EC) until the lunch-time break or the next morning upon arrival. In addition, it was reported that the occupants might accept intensive irradiance if that gives them a good view outside [37].
To generate the control profile for manual operation, in this study, a similar algorithm introduced by Reinhart for blinds [37] was adapted for EC glazing. According to Herkel et al. [38], we assumed that a user activates the EC tinting for low solar altitude angles (α ≤ 60°) if the specific radiation set point is exceeded (here Idir ≥ 50 W/m2 for direct radiation). When the solar altitude angles are high (α > 60°) and the sun is not visible to the eyes, it was assumed that the users would prefer to keep the view outside unobstructed (less tinted).
The manual control profile (CtrlMan) was applied in the simulation to compare the annual results of automatic controllers with possible manual operation. However, the authors are aware that due to the complexity of modeling user behavior, the current manual operation algorithm is still far from a real representation.
3.3. Radiation-Based Control (CtrlRad)
Radiation-based control is one of the most frequently used strategies, which activates the shading when the single variable of global radiation exceeds the reference irradiance upper limit or when direct radiation falling on the occupants or workplace goes beyond tolerable level.
In previous studies, various radiation thresholds have been reported for control. These values vary according to climate conditions, window orientation, and window-to-wall ratios. Wymelenberg [39] and Tavares et al. [40] found a wide range of various global (from 150 to 850 W/m2) and direct (from 20 to 100 W/m2) irradiance thresholds for controlling an EC glazing in the literature. Finally, Tavares et al. found 150 W/m2 solar radiation received on the window surface as the most effective control set-point for taking advantage of EC glazing for energy saving [40].
In this paper, we used 200 W/m2 as the set point for radiation-based control according to DIN 4108-2. Thus, the radiation-based control profile (CtrlRad) was generated by checking the amount of global radiation (Iglob) on the vertical facade and selecting the EC glazing state accordingly. This reference irradiance limit was considered 150 W/m2 for the north-facing façade. To avoid unfeasible cases (all three zones fully tinted) for both “CtrlIll” and “CtrlRad” control profiles, the bottom zone of the window was kept always clear to provide minimum daylighting in the space.
In the Conclusion, we only compare the results of the simulation based on the “CtrlRad” profile with the results of the other control profiles for the sake of simplicity.
3.4. Model Predictive Control (MPCtrl)
In this paper, a novel MPC algorithm is developed to regulate the tinting state of the EC glazing and save energy while providing comfort. To evaluate the overall performance, the control profile for MPC needs to be generated for comparison with other control strategies. A simulation-based framework was used to generate the MPC control profile by coupling the MPC algorithm (in MATLAB) and TRNSYS via BCVTB.
Comparing the performance of a reference room under the MPC controller with other controllers shows the efficiency of the algorithm in achieving the objectives. This helps developers to tune the thresholds and criteria in MPC before applying them in an actual building.
In this section, firstly, the necessary steps for developing a model-based predictive algorithm are described. Secondly, after providing the MPC algorithm, the technique used in this study to generate the MPC profile by coupling the MATLAB algorithm and TRNSYS via BCVTB was explained. In addition, some of the MPC model details are described in Appendix A, including the definition of the simplified RC model, the radiative heat exchange model, and the linear illuminance model. Appendix A also discusses the error and shortcomings of these simplifications and their possible impact on the MPC controller.
It is worth mentioning that the focus of this study was only controlling the EC glazing. Therefore, neither active heating/cooling nor ventilation system was regulated by the MPC. The impact of other systems in the room was taken into account as an additional disturbance to the MPC model. With this approach, the potential of an automated EC system is emphasized more. This gives us also the flexibility to add any additional HVAC system to the building and deal with their impacts by the algorithm without any major adjustment.
In addition, since the model-based predictive control applied in this paper was developed to control both shading systems and lighting in a real office building, artificial lighting control was part of the MPC algorithm. However, for the sake of comparison, control of supplemental lighting was conducted by a daylight-based control in TRNSYS for all different control strategies in this paper.
3.4.1. MPC Controller
The MPC controller consists of different parts, including the optimization of the model predictive controller and an observer. From the controller, the signal for the shading system is generated and additionally the dimming fraction for the electrical lights. This structure results from the missing active control over the HVAC system. The reduction in energy consumption is achieved by keeping the operative temperature in the predefined range. With the additional power consumption in the cost function, a reduction in electrical power is achieved.
The MPC and all components are developed with Matlab and Simulink. The general structure of the system for simulation is given in Figure 4. Before observation and control, the available external data are processed. From forecast data, the predictions of solar radiation and outside temperature are set up. Solar radiation is considered in the thermal model as a time-varying component, and the outside temperature is considered the known disturbance input d. Both data are available for the following components.
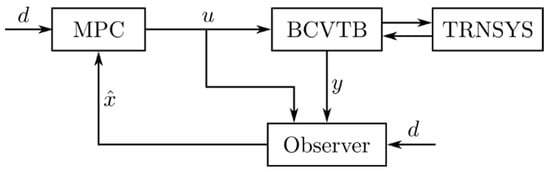
Figure 4.
The general structure of the control loop for the simulation.
Due to the nonlinearities from the longwave radiation heat exchange, an Extended Kalman filter is used (aka linear quadratic estimation (LQE) in statistics and control theory). From the input data and measurements, the missing states (temperatures) are estimated. Not all temperatures on the surfaces and inside the walls are measurable, so we need this additional estimation.
A quadratic programming approach is used. The goal is to find the best control signal for the shading system and the electric lighting. The linearized model of the thermal state equation describes the system dynamics. In every time step, the linearization is updated for the new temperatures. The illumination and glare data are used for inequality constraints. The controller can find the best control signal and still guarantee the constraints. Due to the lack of active cooling and heating, thermal comfort is considered a soft constraint. With the optimization, every variance of the operative temperature beside the allowed comfort zone is penalized.
The optimization problem is set up in a quadratic manner. The cost function in Equation (1), also known as a quality criterion, includes the derivation of the shading system and the energy consumption of electrical lighting. On an important note, this cost function does not contain any money-related parts, and it is more like a penalty function. During the optimization, the cost function is minimized.
The quadratic part is used for the input derivative with the weighting . With the penalty for shading derivations, the user experience and the life span of the shading system will be extended with less switching. The penalty for electric lighting considers power consumption as defined in the second part of Equation (1). With the linear penalty, the weighting R map the light input to the regarding power consumption. Only the absolute value is penalized for the artificial lights. This linear part is working because for the control input, holds. With the weightings and , a tuning between the power consumption of the artificial lights and the shading derivation can be achieved. A wrong selection of the weightings has a negative influence on the control performance. As mentioned before, the resulting control signal for the light is not sent to TRNSYS for comparison reasons.
For solving the optimization problem, qpOASES [41] is used. Based on the online active set strategy, a solver is a fast approach for solving quadratic programming problems. Additionally, equality and inequality constraints are included. It is possible to use qpOASES in online applications. The system must be linear to be solved. Special treatment of the thermal model and visual comfort is necessary.
The MPC algorithm is executed at every time step. In this study, only the control time frame was one hour (one control action per hour) for the MPC equivalent to the control time frame required in the TRNSYS model (hourly values as control profile). Then the optimization solves the ideal control signals over the horizon with steps, and this results in a prediction horizon of 30 h with the sampling rate of the controller. This horizon length was selected to cover all the relevant actions of a day and the slow response of the thermal room behavior. Only the solution for the next control time frame is sent to the TRNSYS model. In the next time frame, the procedure is repeated.
3.4.2. Constraints and Restrictions
The control approach is conducted without active heating and cooling manipulation possibilities. This restriction implies some problems for the shading systems controlled by MPC. It is not possible to keep the thermal comfort in a predefined set with only controlling the incoming radiation. With adding soft constraints, every derivation from the chosen set is penalized. The drawback of this approach is a high effort for reducing the incoming radiation if the thermal comfort bounds are violated.
Another drawback is the discrete transmittance states of the EC shading systems. Typical solving methods for quadratic optimization are based on a convex set of inputs. Nonlinear solving methods do not apply to real-time settings. This issue is solved by considering continuous transmittance for the EC glass shading during the optimization. The optimal solution for the EC glass is discretized to the nearest transmittance, so the control signal becomes sub-optimal. This is a trade-off between online solving the MPC and considering discrete EC states.
The constraints for the different comfort metrics are considered inside the optimization problem. The visual comfort part considers glare and illuminance at the workplace separately. On the one hand, the illuminance-based glare metric (Ev) should be kept below 2750 lx. This threshold is based on investigations from [42] and was tuned to the named value by comparing the DGP and vertical illumination in our setting. With the adjustment, the building properties are reflected into the bound. On the other hand, a minimum illuminance (Eh) of 300 lx should be provided at the workplace. These constraints are only held during occupied hours.
The limits for the operative temperature are more restricted because soft constraints are used. Soft constraints are not necessarily guaranteed due to the missing controllability of heating and cooling. The MPC tries to stay inside the soft constraints set to . The controller tries to keep the operative temperature in a range and does not track a fixed set point. These boundaries are active during occupied hours. The active shading control can improve the energy consumption of a building if the incoming radiation is blocked during the summer or vice versa during the winter.
Moreover, the number of EC glazing changes was limited to ensure sustained performance over the life of the window, which was reported 30,000–50,000 cycles [6], and to avoid fast changes in lighting conditions that are disruptive. Additionally, the limitation of switching enhances the user’s comfort with fewer visual changes. This is more important for applications with a faster sampling time of the controller, as introduced in Section 1.5.
3.4.3. Coupling the TRNSYS Model and the MPC Algorithm via BCVTB
The MPC optimization algorithm requires current environmental conditions (real or simulated values) at every time step as input to minimize the cost function and satisfy the constraints for the selected time. This process can be performed by coupling an optimization algorithm and a building simulation model. In this study, the Building Controls Virtual Test Bed (BCVTB) was used for linking Matlab/Simulink to TRNSYS simulation.
The same simulation model and typical weather data (for Mannheim) were used in TRNSYS as described earlier in Section 2. By coupling TRNSYS and Matlab, the simulation provides the current environmental conditions to be used in the MPC optimization process for solving the future problem of a time-step. In other words, the simulation model assists the controller in obtaining real-time building status, minimizing the cost function, finding the best state of EC, and sending it as a signal to the simulation model for the next time step. In addition, the same typical weather file used in TRNSYS (for Mannheim) was assumed to be the source of weather “forecast” for MPC.
Finally, the coupling continued for a complete year (8760 h) to generate the full control profile representing the behavior of the developed MPC. Using this method, the overall performance of the newly developed controller can be evaluated even before being applied to the actual building and automation systems.
3.5. Simulation-Based Control (CtrlPen)
This section describes the process of generating the “optimal” control profile also called penalty-based control (CtrlPen). As mentioned earlier (see Section 1.4), simulation-based “optimization” is a method for finding the ideal input values based on the desired outcomes. It is worth mentioning that in this study, the so-called “optimal” control is not the absolute optimum solution but something near to the optimal point (aka “sub-optimal”). Thus, after tackling the shortcomings of a simulation model and optimization process, there may be some better solutions.
The authors previously introduced an algorithm that involved several sequential simulations, ranking, and re-ranking processes to generate the most optimal control profile [23,43]. This algorithm searches all possible EC states (64 combinations) and finds the optimal states (top-ranked with minimum sum weighted penalty) at every time step. Repeating this searching process for every hour in a year, the algorithm generates a control profile. Previously, the authors introduced additional steps to overcome the ignorance of thermal inertia [23,43].
In this study, the error of the “collage” technique was found negligible. The main reasons that this error did not occur significantly in this specific room can be explained as: (a) the reference room does not contain a noticeable amount of thermal mass (constructed from drywalls, elevated floor, and suspended ceiling), and (b) the room does not have an exterior wall and thus does not receive radiation on the backside.
Moreover, the authors conducted a sensitivity study for the south-facing room. The near-optimal control profile both with the ranking method (with collage error) and the re-ranking method (without collage error) was generated and applied in a continuous TRNSYS simulation. The results showed that the improvements of the total annual end-use energy (electricity) were limited to 6% for both heating and cooling and limited to 7% for electrical lighting.
In the simulation-based method, each performance indicator (e.g., energy or comfort) has a pre-defined weighting fraction (ωi). These fractions influence the ranking procedure and the outcome. Figure 5 shows how the near-optimal control profile (CtrlPen) was derived through the following steps: (i) parametric simulations for all possible EC combinations and then (ii) ranking and selection procedure considering a weighted sum penalty function including energy, visual comfort, and thermal comfort.
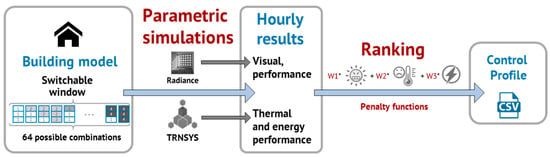
Figure 5.
The simulation-based framework was used to derive the penalty-based profile (CtrlPen) (adapted from [23]).
3.5.1. Parametric Simulations
In the first step, the reference room was simulated for all possible EC combinations (see the properties in Table 2 and Table 3). The hourly values of vertical (Ev) and horizontal illuminance (Eh) were simulated in Radiance using the 3-Phase method. The energy demand values (for heating, cooling, and electricity for lighting) and thermal comfort index (local PMV) were calculated in TRNSYS while the air temperature was kept within the range between 20 °C to 27 °C (see Section 2 for more details about simulation boundaries).
3.5.2. Ranking and Selection Procedure
In the second step, a weighted sum penalty function with multiple criteria was applied to evaluate the results (design space). Based on the pre-defined weighting fractions (priorities), all hourly results were ranked to select the top-ranked states (with minimum total penalty). At every hour, when the overall performance in the room is not satisfying, the algorithm rejects the unacceptable cases by applying a greater penalty and pushes those cases more to the end of the ranked list.
Running the ranking procedure over a year generates the annual near-optimal control profile (CtrlPen). Certainly, this profile is limited to the boundaries and parameters assumed for the simulation and cannot be generally used for other geometry, climate, or altered set of pre-defined priorities (ωi). Nevertheless, it also gives us the ideal performance of predictive control for such conditions, which is a baseline for the comparison study.
Equation (2) shows the total weighted penalty function. The index “i” shows different components of the penalty function; and “n” expresses the number of EC possible combinations (from 1 to 64), and “t” shows the time step. Therefore, Equation (2) can be extended to Equation (3) by specifying individual penalty functions and respective weighting fractions for calculating penalty for every EC combination and every time step.
Penaltytotal n,t = ∑ωi,n,t × Pi,n,t
Penaltytotal n,t = (ω1 × Pdgp n,t + ω2 × Pdaylight n,t
+ ω3 × Part.light n,t + ω4 × Ppmv n,t
+ ω5 × Penergy n,t)
+ ω3 × Part.light n,t + ω4 × Ppmv n,t
+ ω5 × Penergy n,t)
Each penalty function takes one (or more) hourly inputs and gives a number between zero and one. For visual discomfort assessment, daylight discomfort glare, useful daylight availability, and the usage of electric lighting were taken into account with individual penalty functions as Pdgp, Pdaylight, and Part.light, respectively. The thermal discomfort penalty function was also defined as Ppmv based on the worst hourly local PMV index inside the room. Figure 6 shows these individual penalty functions.
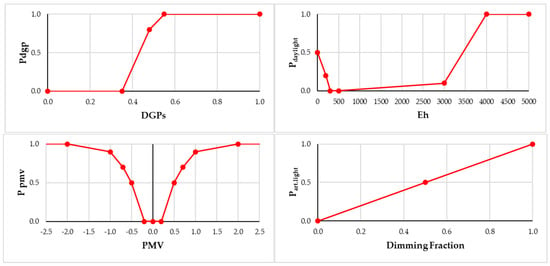
Figure 6.
Penalty functions for discomfort glare (up,left), daylight (up,right), thermal discomfort (bottom,left), and electrical lighting (bottom,right).
Hourly simplified daylight glare probability values (DGPs) are the inputs for the glare evaluation and the maximum penalty among the four view directions is the output of the Pdgp function. The hourly averaged horizontal illuminance value (Eh) at each workplace (G1 and G2) are the inputs for the Pdaylight function, and the maximum penalty between the two groups is the output. Similarly, based on the dimming fraction of luminaires for G1 and G2, the biggest penalty is Part.light. These considerations ensure using daylighting as often as possible and avoiding discomfort glare.
The Penalty function for energy consumption (Equations (4) and (5)) was defined as Penergy considering the hourly sensible energy (Q) and assumed constant efficiency for heating (η), and coefficient of performance for cooling (COP). These values should be defined before the ranking process to determine end-use energy.
To make a penalty value (between 0 and 1), we normalized this end-use energy by dividing by the maximum of the end-use energy at that specific hour among all 64 cases (). The index “n” shows the number of cases (from 1 to 64), and “t” is the time step (here hourly from 1 to 8760).
The weighting fractions (ωi) in the total penalty function (Equations (2) and (3)) can be altered based on the users’/designers’ priorities for different aspects of visual comfort, thermal comfort, or energy. For instance, if the users want to find the ideal control input by only considering glare, it can be possible by giving zero weighting fraction to the rest of the penalty functions. Previously, the authors have investigated different weighting fractions (ωi) and their impacts on the outcome [23,43,44]. In this paper, the weighting fractions were equally prioritized in the total penalty function (see Table 4). Meaning, the results are expected to show a good trade-off between energy savings and comfort provision.

Table 4.
Weighting fractions used in penalty function for near-optimal control (CtrlPen).
We should mention that the generated near-optimal control profile is not necessarily the absolute optimal solution, and a slightly better solution may be found by tuning the penalty functions and weighting fractions. Nevertheless, previous studies by the authors [23,43] showed that applying this near-optimal (aka sub-optimal) control profile represents the best energy and non-energy performance of the building. Thus, the penalty-based control profile (CtrlPen) can be used as a benchmark of the best predictive control under the assumed circumstances (location, orientation, geometry, shading type, and weather data).
Moreover, the possible errors during the process of ranking, re-ranking, and generating the simulation-based near-optimal control profile do not influence the overall results in Section 4. Because in the end, all the control profiles were applied in a continuous TRNSYS simulation with the same boundaries (and there is no error due to the generation process of control profiles).
3.6. Summary of the Operation and Control Scenarios
To summarize, the TRNSYS simulation model can read a control profile (a time series of state of the EC) and calculate the respective solar transmittance through the whole window surface and its impact on the overall room performance. Therefore, after generating different control profiles, it is possible to compare the overall performance and find the ideal control strategy for EC glazing. Generating control profiles for manual operation, illuminance-based, and radiation-based is straightforward while providing the MPC control profile, and the near-optimal control scenario is only possible through many steps and considerations. Table 5 summarizes different control strategies and their criteria for controlling EC glazing used in this paper.

Table 5.
Various control strategies were used in this study.
Finally, different control profiles (.csv files) were used in continuous annual simulations in TRNSYS to provide the annual performance of EC glazing under different control strategies. These results are discussed in Section 4 to depict the overall potential of an automated EC glazing applied in a temperate climate (Mannheim, Germany).
4. Evaluation Criteria, Results, and Discussions
The overall performance of a shading system can be assessed by comparing the annual simulated results for each performance indicator (e.g., glare, daylight, thermal comfort, and energy) and predefined acceptance criteria. The performance indicators and criteria were defined for both energy and non-energy aspects. In terms of energy saving, the total annual end-use energy consumption was compared. Section 4.1 describes how the hourly results of sensible heating and cooling converted to end-use energy.
In terms of visual and thermal comfort, we categorized the state of the space into satisfactory and dissatisfactory and expressed the overall performance as an annual percentage during occupied hours. In other words, this percentage is the number of occupied hours with discomfort (or other categories) divided by the total number of occupied hours (here 2610 h).
Visual comfort is normally referred to as a situation with sufficient and uniform daylight and no glare issue. Section 4.2 explains glare assessment, and Section 4.3 defines useful daylight. The authors are aware of the influence of using EC glazing on the Color Rendering Index (CRI) [45]. However, ensuring a good color rendering was not defined as the main performance indicator and can only be assessed by minimizing the total number of occupied hours when all EC glazing zones are fully tinted (when the CRI falls below 80 and becomes unacceptable) [23].
Similarly, in terms of thermal comfort, Section 4.4 explains the process of evaluating hourly results of local PMV for every occupant in the room and the overall values.
Some of these indicators and criteria were directly considered in the MPC optimization procedure (MPCtrl) and the penalty-based ranking and selection algorithms (CtrlPen).
To make the comparison easier, a Relative Improvement (RI%) was used to indicate the impact of different control strategies (Equation (6)). For each performance indicator, the actual improvement was calculated by , when is the overall performance of the reference control strategy. Here we used base-case (not-shaded window), manual operation (CtrlMan), and radiation-based control (CtrlRad) as references. Each time, the performance of other control strategies () were compared to the reference performance () as below:
4.1. Energy Consumption
TRNSYS simulates hourly sensible heating and cooling based on the set point temperature assigned in the model (here 20 °C and 27 °C, respectively, for heating and cooling). The dead band was defined quite loosely intentionally to focus on the impact of EC glazing.
Electricity demand for supplemental artificial lighting was calculated based on the integrated daylight-based control in TRNSYS. The hourly average of available daylight in the workplaces (G1 and G2) was used, and the controller (Type4) regulates the dimming fraction of each luminaire to keep the average illuminance on the desks in the range of 300 lx to 500 lx.
Recently, the use of heat-pump-based systems is growing significantly in buildings for both cooling and heating. Therefore, we assume a heat pump and a chiller system in this study to convert energy demand into end-use energy (aka. site energy). The annual average seasonal performance factor was considered 4.2 for heating (aka. η: efficiency for heating) and 4 for cooling (aka. COP for cooling) [46]. Figure 7 shows the breakdown of annual end-use energy kWh/m2a (blue: cooling, red: heating, and yellow: electrical lighting) for different cases.
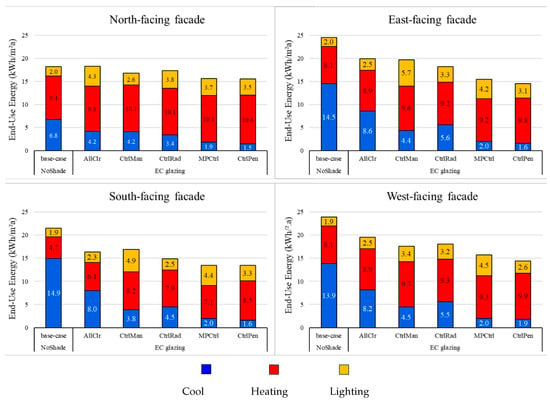
Figure 7.
The annual end-use energy of the office room with EC glazing system for different orientations (set point temp. 20–27 °C).
Looking at the results (Figure 7 and Table 6), one can compare the overall potentials of a switchable EC glazing under different control conditions by looking at the relative percentage difference (percentage of improvement) to the selected reference control in three scenarios:

Table 6.
The Relative Improvement (RI%) in terms of saving total end-use energy for different cases.
- a.
- In relation to a conventional double-glazing window without any sun protection (base-case: SHGC = 0.61, and Tsol = 0.42, see Table 1);
- b.
- To a manual operation (CtrlMan): this scenario shows the importance of using an automatic controller for a switchable EC system;
- c.
- To a radiation-based control (CtrlRad): this scenario shows the full potential of a predictive control (MPCtrl) in relation to a commercially available classic control. We can assume that the performance of penalty-based control (CtrlPen) will be achieved by a well-engineered MPC.
The results clearly show the impact of EC glazing on the reduction in overall end-use energy, particularly by using automatic control. Considering a conventional double-glazing window without any sun protection (see Table 1 base-case, SHGC = 0.61, and Tsol = 0.42), applying an EC glazing under penalty-based control (CtrlPen) may save up to 14%, 41%, 38%, and 40% for the north-, east-, south-, and west-facing windows, respectively. The same reduction ratio can be expected in terms of total primary energy and CO2 emission, which leads to significant potential in reducing global warming issues.
The results show that a manual operation (CtrlMan) of EC glazing cannot make the most of potential energy saving. It is mainly limited to 50% of the reduction achieved by the penalty-based control. The sensor-based control (CtrlRad) reduced 8% and 12% more end-use energy compared to the manual control (CtrlMan) for the east- and south-facing windows, respectively, while for north- and west-facing windows, end-use energy did not improve by using the “CtrlRad”.
In relation to the radiation-based control (CtrlRad), the near-optimal control reduced more end-use energy. The minimum improvement is only 2% for the north-facing window, and the maximum improvement is 10% for the south-facing window.
In summary, applying switchable EC glazing and developing a predictive control strategy led to a significant energy saving (up to 41% reduction for East-facing).
4.2. Glare
Glare is a view-dependent measure of visual discomfort caused by physical (e.g., excessive light or contrast or both), psychological and physiological factors [47]. To date, the most reliable metric to assess glare is Daylight Glare Probability (DGP), which involves generating High Dynamic Range (HDR) images [48]. Simulating HDR images through raytracing is computationally expensive and inapplicable for using for predictive controlling dynamic façade.
While the shortcomings of an illuminance-based glare metric against a more detailed luminance-based metric are well-known by the lighting community [48], many studies used simplified Daylight Glare Probability (DGPs) based on vertical illuminance for annual glare evaluation and controlling dynamic shadings [27,42,49]. Vertical illuminance (Ev) at eye-level correlates to the DGP when the sun is not directly exposed to the eye [50], and DGPs can be calculated as below (Equation (7)) [50]:
As mentioned earlier, the use of vertical illuminances to control dynamic glazing to were thoroughly studied by Giovannini et al. [42,51]. In this study, vertical illuminance values for all four occupants (height = 120 cm, side view directions, perpendicular to the window) were simulated in Radiance using the three-phase method. In reality, if anybody in a group confronts discomfort glare, EC needs to be tinted to protect the users. Therefore, hourly DGPs values were post-processed by taking the maximum hourly DGPs of the two values in every group (for G1 and G2; see Figure 2).
The resultant DGPs are divided into four categories of visual discomfort used by Wienold: imperceptible (0.30), noticeable (0.35), disturbing (0.40), and intolerable (0.45) [50]. Figure 8 shows the overall performance of the EC glazing system in terms of discomfort glare protection for G1 (closer to the window) for different cases (green: imperceptible, yellow: perceptible, orange: disturbing, and red: intolerable). The total percentage of occupied hours in two dissatisfying categories (disturbing and intolerable) indicates the probability of discomfort glare issue for each case.
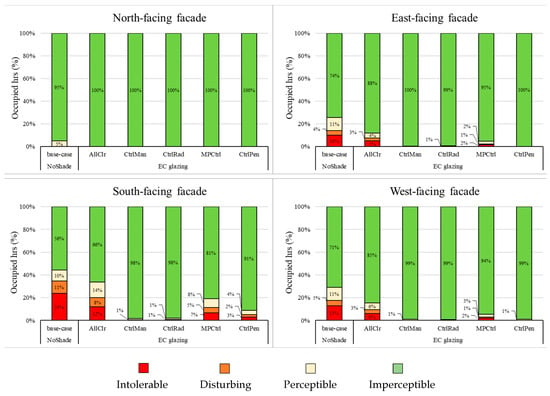
Figure 8.
The overall performance of the EC glazing system in terms of discomfort glare protection for different orientations, results for occupants closer to the façade (G1).
Alternatively, the percentage of occupied hours when DGPs values exceeded the threshold (here is 0.4) can be expressed as “exceeded DGP” values (here as DGPexceeded aka DGPe). Again, since the office was shared between four users with different view directions when one DGPs exceeded 0.4, that hour was considered with discomfort glare. Following DIN EN 17037 (2019), the annual DGPexceeded above 5% must be prevented for a “good-class” glare protection.
The final DGPexceeded results for the base-case window were calculated as 0%, 21%, 46%, and 24% for the north-, east-, south-, and west-facing windows, respectively. Applying EC glazing and the optimal controller reduced the DGPexceeded values to zero percent for east- and west-facing windows. However, for the south-facing window, the DGPexceeded was only reduced to 9%.
The results in Figure 8 clearly show that glare is not an issue for the north-facing façade in this latitude (49.48°). The impact of EC glazing on reducing the number of annually exceeded glare is significant for other orientations (south-, west-, and east-facing).
In relation to the base-case window (see Table 1 for base-case, Tvis = 0.58), the manual operation of EC glazing can avoid discomfort glare effectively. One may notice that applying the radiation-based control strategy (CtrlRad) and the MPC does not show any improvement for glare protection in relation to manual operation (CtrlMan). Nevertheless, one should consider that an MPC control always tries to find a trade-off between multiple performance indicators, and it may work effectively for some (particularly energy-saving and thermal comfort) but not for all indices.
To summarize, by improving the control strategy from manual operation to near-optimal control, the full potential of the automated system for glare protection can be depicted. The annual discomfort glare can be completely avoided (DGPexceeded = 0% for the east- and west-facing window) or limited effectively (DGPexceeded = 9% for the south-facing window).
4.3. Useful Daylight
Several climate-based lighting measures have been proposed to ensure the quality of daylight. Commonly used illuminance-based annual metrics such as Daylight Autonomy (DA) and Spatial Daylight Autonomy (sDA) only ensure daylight sufficiency by providing the required illuminance level on the task area (e.g., 500 lx for office space) [52]. Another metric called Annual Sun Exposure (ASE) is required in LEED (Leadership in Energy and Environmental Design accreditation system (LEED v4)) v4 to prevent over-lighting by direct sunlight above 1000 lx. Besides the concerns regarding the threshold [53], ASE describes how much of the space receives bright direct sunlight, but it ignores diffuse and reflected light that may also cause glare. Alternatively, Mardaljevic’s Useful Daylight Illuminance (UDI) [54,55] takes into account both daylight sufficiency and over-lighting. UDI is the percentage of occupied hours over a year, which falls into these three categories (or four in some publications): supplemental (UDI-s, Eh < 300 lx), autonomous (UDI-a, 300–3000 lx), and exceeded (UDI-e, Eh ≥ 3000 lx).
In this paper, by using the Radiance three-phase method, illuminance values (Eh) were simulated for all four workplaces (h = 80 cm). Later, the average of hourly values was considered for each group (for G1 and G2; see Figure 2). Figure 9 shows the annual results of the UDI percentage for the first group (G1: closer to the window) (yellow: UDI-a, gray: UDI-s, and red: UDI-e).
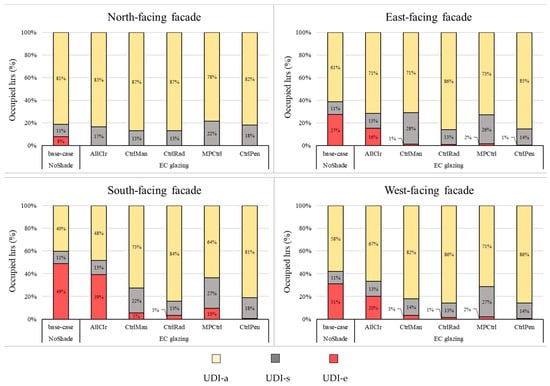
Figure 9.
The overall performance of the EC glazing system in terms of daylight availability for different orientations results for occupants closer to the façade (G1).
The UDI-a corresponds to the percentage of the occupied hours when the preferred daylight is provided. Therefore, the case with maximum UDI-a shows the best performance of a control strategy for providing daylight sufficiency and avoiding the risk of glare.
In relation to the base-case window (see Table 1 base-case, Tvis = 0.58), the results show applying an EC glazing protects the occupants in group G1 from “too bright” daylighting, while it causes “too dark” cases for the occupants in group G2 deeper inside the room.
For group G1 (closer to the window), the UDI-a for the base-case window was 81%, 61%, 40%, and 58% for the north-, east-, south-, and west-facing windows, respectively. By applying the EC glazing with the optimal control, the UDI-a was improved to 85%, 81%, and 86% for the east-, south-, and west-facing windows, respectively. For the north-facing window, the UDI-a was about 81% for both cases.
By using more advanced control strategies (from manual operation to optimal control), the full potential of an automated system for providing useful daylight can be achieved. It is worth mentioning that this performance could be different for a different shading system, particularly for a non-coplanar device (e.g., Venetian blind), which can redirect daylight into deeper space.
4.4. Thermal Comfort
Even though the air temperature stays in the acceptable range (here 20 °C to 27 °C), thermal comfort especially for the occupants close to the façade needs to be evaluated. Fanger’s Predicted Mean Vote (PMV) method has been widely used for the estimation of thermal sensation and comfort in the built environment [56]. Local PMV was internally calculated in TRNSYS for each occupant position. The calculation involves room temperature, relative humidity, and local mean radiant temperature (MRT). Other personal parameters such as clothing and metabolic rate were assumed constant for year-round.
A satisfying thermal condition (neutral state) can be achieved when the PMV stays between −0.7 and +0.7 (ASHRAE 55: Class IV) [57]. Therefore, simulated hourly local PMV values were post-processed for all occupied hours over a year. Figure 10 shows the total percentage of occupied hours with thermal discomfort when PMV value lies below −0.7 (blue: cold) or above +0.7 (red: warm) for group G1.
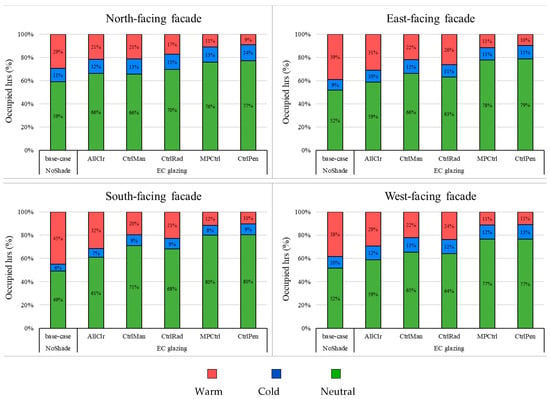
Figure 10.
The overall performance of the EC glazing system in terms of thermal comfort for different orientations results for occupants closer to the façade (G1). The results for thermal comfort clearly show that using EC glazing improves providing thermal comfort for all orientations, particularly by using an automatic control.
In relation to the base-case (see Table 1 base-case, SHGC = 0.61, and Tsol = 0.42), the near-optimal control improved thermal comfort for users closer to the window (G1) up to 44%, 56%, 61% and 52% for the north-, east-, south-, and west-facing windows, respectively.
The results show that both manual operations of EC glazing and radiation-based control strategy can improve thermal comfort. By improving the control strategy from radiation-based to optimal control, the total dissatisfying number of occupied hours can be even reduced more by 37%, 39%, 39%, and 33% more for the north-, east-, south-, and west-facing windows, respectively.
5. Conclusions
This paper proposes a simulation-based framework to evaluate the performance of a MPC controlled electrochromic glazing system (EC) with respect to end use energy, visual comfort (glare and daylight availability), and thermal comfort in comparison to different control strategies.
Advanced verified simulation tools and techniques were applied in this paper for modeling the switchable EC glazing system for an annual climate-based integrated daylight simulation (using Radiance) and energy simulation (using TRNSYS). The simulation model was enabled to read various control profiles which represent different control strategies and adjust the state of EC glazing during the simulation. Therefore, based on different algorithms, different control profiles (CtrlMan, CtrlRad, MPCtrl, and CtrlPen) were provided and applied in dynamic simulations. This study proved that, despite the complexity of a dynamic system, a well-engineered predictive control is able to regard all aspects of visual and thermal comfort successfully as well as save energy.
The results clearly showed that, firstly, applying a rule-based controller (CtrlRad) reduces cooling demand. Secondly, developing advanced strategies such as predictive control has a significant impact not only on energy savings but also on visual and thermal comfort provided. During the early stage of design, the information about the full potential of shading systems will help consultants/designers to convince clients of an investment in applying switchable systems and developing an automatic control strategy.
Moreover, the results showed that:
- a.
- In comparison to the base-case window, the use of an automated EC controlled by MPC can reduce the total annual end-use energy by 14%, 37%, 37%, and 34%, respectively, for north, east, south, and west orientations;
- b.
- With a penalty-based control (CtrlPen), the energy-saving can be improved up to 14%, 41%, 38%, and 40%, respectively, for facing north, east, south, and west;
- c.
- The differences between manual operation and rule-based algorithms regarding energy saving and thermal comfort are noticeable, which shows the impact of automation on EC glazing.
In this study, the penalty-based control (CtrlPen) outperformed MPC in many aspects, especially in providing useful daylight, avoiding discomfort glare, and saving electricity for lighting. Therefore, there is room for improving the MPC to predict the illuminance more accurately.
In terms of energy savings, both control strategies (CtrlPen and MPC) performed similarly. For heating, the MPC saved more (up to 1.4 kWh/m2a for south orientation) compared to CtrlPen. For cooling, the CtrlPen performed only slightly better (maximum 0.4 kWh/m2a). Regarding electric lighting the MPC performance suffers due to the misprediction of direct light. One can see for the north-facing window (where mainly diffused light is received), that the electricity demand for lighting is similar for both controllers. Conversely, for other orientations (south, east, and west), electricity for lighting is the main drawback of MPC. This disability to save more electrical lighting occurred due to misprediction of indoor illuminance that influences the other overall performance indicators such as glare and UDI as well.
The authors want to discuss some of the reasons that made the overall performance of the penalty-based control (CtrlPen) different from MPC:
- i.
- Even though the RC model used in MPC was verified earlier by the authors versus other simulation tools [58], the prediction of glazing surface temperatures was imperfect on some occasions (RC vs. TRNSYS).
- ii.
- Due to the complexity of daylight penetrating through a switchable window, prediction of available lighting inside a room (both vertical and horizontal illuminance) was a challenge, especially when multi-reflection of the direct beam one high reflective surface plays an important role.
- iii.
- The optimization method in MPC was fundamentally different from the one used in penalty-based control (CtrlPen). In the weighted sum penalty function, the authors had the chance to tune the weighting coefficients based on their earlier studies [44] and found the best set of coefficients that led to a good trade-off between energy saving and comfort provision. This consideration was not applied in the MPC and can be further investigated.
The performance of the penalty-based control (CtrlPen) was expected to be slightly better than MPC, especially according to some indicators that were not addressed directly in the cost function of the MPC algorithm. Metrics such as useful daylight illuminance (UDI) or operative temperature (Top) were defined just as constraints in MPC.
The control strategies for shading automation have a strong influence on users’ connectivity to outside (view/privacy), lighting quality, and color rendering (particularly in the case of EC glazing). In this paper, we did not assess these parameters directly, but through the optimal predictive controller we minimized the number of occupied hours when all EC glazing zones were fully tinted (which would lead to an unacceptable color rendering index (CRI) below 80).
Despite all the benefits of a predictive controlled façade with switchable electrochromic glazing, the use of dynamic façades in real buildings has been limited to affordable sensor-based solutions so far. Due to the high level of complexity of (day)lighting and thermal models as well as the level of uncertainty of weather forecasts and user behavior, the development of new controls remains a challenging task for the future.
Author Contributions
Conceptualization, A.G.K. and S.H.; methodology, A.G.K.; software, A.G.K. and T.S.; validation, A.G.K. and T.S.; formal analysis, A.G.K.; investigation, A.G.K.; resources, A.G.K. and S.H.; data curation, A.G.K.; writing—original draft preparation, A.G.K.; writing—review and editing, A.G.K. and T.S.; visualization, A.G.K. and T.S.; supervision, S.H. and S.L.; project administration, S.H.; funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was part of the LiSA project (“Licht- und Solarmanagement mit aktiven und modellprädiktiv geregelten Komponenten”; grant agreement number: 03ET1416A) at Techniche Universität Kaiserslautern in Germany. The Federal Ministry for Economic Affairs and Energy funded the project.
Data Availability Statement
Ganji, Abolfazl (2021), “Controlling Switchable Electrochromic Glazing for Energy Savings, Visual Comfort and Thermal Comfort: A Model Predictive Control”, Mendeley Data, V1, DOI: 10.17632/9pj3dk63bm.1.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this appendix, some parts of the MPC model are described in detail, including the definition of the simplified RC model, the radiative heat exchange model, and the linear illuminance model. This section also discusses the error and shortcomings of these simplifications and their possible impact on the MPC controller.
Appendix A.1. Defining a Simplified Resistance-Capacitance (RC) Thermal Model
The main objective of the prediction of indoor air temperature and heating/cooling power is to estimate the dynamic thermal behavior of the room under different boundary conditions. Despite the models applied in previous studies [29], the proposed model in this study requires the surrounding surface temperatures in the room around the occupants to consider the radiative longwave exchange in thermal comfort precisely.
Existing ideas for thermal models were extended to reflect the additional heat transfer. As presented in previous studies [29,34], an RC equivalent network model is used. Despite the previous models, the inner and outer RC block represents the real inner and outer layer so that the longwave radiation can be included. Figure A1 shows the RC model for a multi-layer opaque wall. This model was defined with four resistors and three capacitors (4R3C model). It is important to find the best representative model for each multi-layer opaque or transparent construction surface in a room with a similar overall thermal property. Here, RC parameters of the building envelope and thermal mass are calculated using theoretical physical properties of the building construction layers, material, and layer’s order similar to what were defined for the simulation model in TRNSYS (see Table 3). Additional total radiative gain ( in Figure A1) on the surface was added to the heat balance to the inner/outer thin layer of surfaces.
Figure A1.
RC model for a multi-layer internal surface.
For the external surfaces, the outdoor temperature was considered as well as total radiative gain ( in Figure A1) including direct and diffuse radiation (shortwave) received on the external surface and longwave radiative heat exchange to the ground and sky.
For modeling the EC window (transparent surface), a 3R2C reduced-order network was considered. Here, R stands for the resistance of the double-glazing EC window, including the gap in between the panes, and C reflects the thermal capacitance of the glass panes. Similar to what was defined for the EC glazing model in TRNSYS simulation, the required R and C values were calculated from the angular-dependent physical properties of the glazing system.
To enhance the performance of the simplified RC thermal model, a wide variety of calibration methods were recommended in publications [27,59]. In this paper, the calibration step was not considered due to the application of MPC for simulation study only. With the thermal model, the parameter is equal to the simulation base. Both systems use the same initialization data for the states. The authors published earlier a comparison between the RC model and other simulation tools that showed a good agreement [58]. Further comparison between TRNSYS and the RC model is in the appendix.
The air temperature in the room center (air-node) was assumed uniformly distributed and similar in every position in the room. The convective heat coefficient towards the air node was also assumed constant (3.05 and 17.78 W/m2K for the inner and outer face of the surfaces, respectively).
Appendix A.2. The Radiative Heat Exchange Model
Due to the large glazing façade, the temperatures at the surfaces may differ significantly. Therefore, besides the convective and conductive heat flux, the radiative heat exchange between surfaces needs to be considered carefully. As it was explained earlier, additional total radiative gain ( in Figure A1) on the surface was added to the heat balance in a simplified RC thermal model. For the external surfaces, the outdoor temperature was considered as well as total radiative gain including direct and diffuse radiation received on the external surface and longwave radiative heat exchange to the surrounding buildings and sky. For internal surfaces, the connection to the adjacent rooms was assumed to be adiabatic (no heat exchange to/from adjacent rooms) plus total radiative gain added to the heat balance.
The definition of longwave radiative heat exchange (Qij) between two gray bodies is known as Equation (A2) (the net heat flux from surface to surface ), where is the material-specific absorption, is the emissivity considered for the inner face of surfaces, and is the Stefan–Boltzmann constant. represents the surfaces area, and is the view factor between surface and surface , which defines how much these two surfaces are exposed to each other. The view factors can be pre-calculated and can be effortlessly used as long as the geometry and the material ( and ) are not changed.
The operative temperature () is defined as the average of the air temperature and the mean radiant temperature (MRT). In this study, was used for evaluating thermal comfort inside the room at the occupant’s position. The combination of air temperature and local MRT values can enhance the thermal comfort assessment, especially for a high glazed façade, and by using the improved method for calculating local MRT values and considering view factors for longwave radiative heat exchange.
The method for estimating local MRT values at each occupant’s position is considered from [60]. The nonlinear description is defined as Equation (A3), where is the total number of surfaces, is the surface temperature, stands for the diffuse solar radiation, and represents the direct solar radiation transmitted through the EC glazing. It is worth mentioning that the view factor () used to calculate MRT was different from the view factor used in Equation (A2) between the occupant and the surrounding surfaces in the room. For indirect solar radiation distribution, all the surfaces (including window surfaces) and their corresponding view factors towards the individual occupant’s position are taken into account. Regarding direct radiation falling on the occupants, the pre-calculated “projected area” fractions () was used from ASHRAE Standard 55 [57,61]. In the calculation method, the projected area fraction shows how much of the occupant’s body may be exposed to direct solar radiation.
Through the EC window, solar radiation transmits and heats the surfaces. Based on the sun’s position, the area of each surface that receives direct sunlight varies over a day. Here, the area that is heated by the direct sun is calculated at every time step to consider it more precisely into the overall radiative heat exchange. The incoming radiation is split onto the radiated surfaces based on the heated areas. This can be seen as a fractional split up onto the different inner surfaces. Accordingly, an additional heat source regarding solar radiation was considered at the inner facing thin layer.
Appendix A.3. The Overall Dynamic Model
The final dynamic thermal model applied in the MPC algorithm is defined in Equations (A4) and (A5). From the previously introduced models, including the convective, conductive, and radiative thermal and daylight model, the final state-space representation is formulated to be used in the MPC controller. In control engineering, a state-space representation is a mathematical model of the reference room (a physical system) as a set of input, output, and state variables.
In this study, input variables are the tinting states of the EC glazing that are regulated over time. Equation (A4) includes the linear part of the state-space as , which contains the considerations for conductive and convective heat transfer, the nonlinear part as , which contains the longwave heat exchange between surfaces. These main components are also combined with the time-dependent inputs matrix for the shading system and the disturbance matrix for the uncontrolled but known inputs, such as the outdoor temperature.
The output-equation considers the two different measurements used for the MPC and the later introduced observer. Equation (A5) describes the connection between the states and input to the available and measurable system output . First, the nonlinear MRT, and second, the room temperature. Both are used for estimating the operative temperature. All model parts for the measurements are summarized in the matrices , and .
The introduced state-space system is the model representation for the model-based control design. The thermal and visual part is combined into one mathematical model.
Appendix A.4. Lighting Model and Predicting Local Illuminance and Glare Values
Predicting local illuminance and glare values is a crucial part of considering visual comfort in a predictive controller. The static behavior of lighting phenomena enables the usage of offline data-based models by using simulated results. Both levels of lighting at the workplace and glare perception on the eye position need to be estimated carefully for visual comfort provision.
The transmitted radiation through the window should be modeled linearly based on the distribution of light inside the room. In Radiance, the Perez sky model [20] and bidirectional scattered distribution functions (BSDF) methods are implemented. Thus, climate-based simulation results can be used for providing an approximation model called the “surrogate model” for lighting prediction. The light at a certain point inside the room is expressed in Equation (A6), with the solar radiation onto the window, when the direct and diffuse are the controlled inputs to the model.
The geometrical distribution factor depends on the selected location in the room, the position of the sun, and the surrounding surface contribution. A Polynomial Regression model depending on solar angles azimuth and zenith can be generated as and is assumed to be a polynomial function of 5th order in and . The coefficients in this function were found offline based on the simulated climate-based annual results (hourly) in Radiance for each sensor point in the room under different sky conditions, including sunny sky and overcast sky. First, the function for the fully cloudy sky is fitted and then the data for the sunny sky is calculated. With this method, the influence of diffuse radiation in the sunny data is neglected and only the relationship towards the direct radiation is established. For the usage in the controller, the current situation is considered by the direct and diffuse radiation because the geometrical distribution factor was calculated individually for both.
This method was used not only for estimating the horizontal illuminance in workplaces but also for estimating vertical illuminance at eye positions. Therefore, two different sets of parameters for were generated for horizontal illuminance and vertical illuminance separately. Estimating the vertical eye illuminance is necessary for estimating the risk of glare for different view directions.
Figure A2 is the distribution of the root mean square error of the and the for a year, and the weather file is given. Further, all four orientations are considered. Certainly, the model is not perfect, but the overall error is in an acceptable range for a nonlinear system and is usable in a control setup. The use of vertical illuminances to control dynamic glazing to minimize glare and the relevant thresholds that could be used were also studied by Giovannini et al. [42,51].

Figure A2.
Root mean square error distribution of horizontal illumination (Eh, left) and vertical illumination (Ev, right). Both are generated based on the weather file with different conditions.
Appendix A.5. Weather Forecast
In general, for a predictive model, a forecast service needs to be provided for weather data such as air temperature, direct and diffuse radiation, wind velocity, and wind direction. The radiation data are mainly available for the horizontal surface at the selected location. From the horizontal, a transformation onto the window surface’s orientation needs to be conducted and is well described by [62]. The same weather condition was applied to all different control cases. Thus, the very same weather file (epw file format) was used as the source of the weather forecast (perfect forecast) while coupling MPC with TRNSYS.
Appendix A.6. The Comparison between the TRNSYS and RC Model
The comparison between the TRNSYS and RC model is provided in the following. Both models obtained the same input data and considered the model parameter introduced in the paper. Because the direct comparison of both models was not carried out, a comparison between TRNSYS and the state estimator with the RC model is discussed in the following. The results are still meaningful because the MRT at workplaces is used as measurements, so the wall temperatures are strongly connected to the model performance of the RC model.
In Figure A3, the inner face temperatures of the TRNSYS simulation and the RC model are provided. After the first initialization phase, both models have a good overall performance. For window surface temperature, the overall trend is also in agreement. However, the window temperature fluctuates more in the TRNSYS model compared to the RC model. This is mainly due to the complex thermal window model in TRNSYS, which does not include the capacitance of the glazing panes. With the simple 3R2C approach, the performance is limited and the nonlinear effect of solar radiation and its inter-reflections cannot be covered.
Furthermore, the previously discussed results are supported by Figure A4, which shows the differences between both models. As expected, the window model has the worst agreement, but the other parts of the model are in a reasonable correlation.
The previous results are similar to the analysis in [58]. Both comparisons result in a good reproduction of the surface temperatures and some shortcomings for the windows. Additionally, the deviation between the TRNSYS and RC model is during the daytime, and the rapid thermal changes are influenced by solar radiation. On the other hand, the RC model provides the same overall trend but with a delay due to the linear solar radiation model and the impact of thermal capacitance.
Figure A3.
Temperatures at the inner faces and inside the room for verification.
Figure A4.
The deviation between the TRNSYS results and the RC model results.
Finally, it is worth mentioning that the overall zone air temperature (and energy demand estimations based on that) are not influenced by this shortcoming, and this error may only appear in the evaluation of the thermal comfort by the MPC for an occupant close to the window and under significant direct solar radiation. Since the impact of this error on the overall MRT was acceptable, the authors agreed on using the RC model for further application in MPC.
References
- IEA; UNEP. 2019 Global Status Report for Buildings and Construction: Towards a Zero-Emissions, Efficient and Resilient Buildings and Constructi on Sector; IEA: Paris, France, 2019; Volume 224. [Google Scholar]
- Nikoofard, S.; Ugursala, V.I.; Beausoleil-Morrison, I. Technoeconomic Assessment of the Impact of Window Shading Retrofits on the Heating and Cooling Energy Consumption and GHG Emissions of the Canadian Housing Stock. Energy Build. 2014, 69, 354–366. [Google Scholar] [CrossRef]
- Inkarojrit, V. Developing Predictive Venetian Blinds Control Models Using Visual Comfort Predictors. In Proceedings of the PLEA 2006 23rd International Conference on Passive and Low Energy Architecture, Geneva, Switzerland, 6–8 September 2006; pp. 6–8. [Google Scholar]
- Konis, K.; Selkowitz, S. Effective Daylighting with High-Performance Facades; Cambridge University Press: Cambridge, UK, 2017; Volume 53, pp. 1–30. [Google Scholar]
- Lim, S.H.N.; Isidorsson, J.; Sun, L.; Kwak, B.L.; Anders, A. Modeling of optical and energy performance of tungsten-oxide-based electrochromic windows including their intermediate states. Sol. Energy Mater. Sol. Cells 2013, 108, 129–135. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.S.; Dibartolomeo, D.L. Application issues for large-area electrochromic windows in commercial buildings. Fuel Energy 2003, 44, 103. [Google Scholar] [CrossRef] [Green Version]
- Belzer, D.B. An Exploratory Energy Analysis of Electrochromic Windows in Small and Medium Office Buildings—Simulated Results Using EnergyPlus; Pacific Northwest National Laboratory PNNL: Richland, WA, USA, 2010; pp. 20–37. [Google Scholar]
- Lee, E.S.; Tavil, A. Energy and visual comfort performance of electrochromic windows with overhangs. Build. Environ. 2007, 42, 2439–2449. [Google Scholar] [CrossRef]
- DeForest, N.; Shehabi, A.; Garcia, G.; Greenblatt, J.; Masanet, E.; Lee, E.S.; Selkowitz, S.; Milliron, D.J. Regional performance targets for transparent near-infrared switching electrochromic window glazings. Build. Environ. 2013, 61, 160–168. [Google Scholar] [CrossRef]
- Tavares, P.F.; Gaspar, A.R.; Martins, A.G.; Frontini, F. The impact of electrochromic windows on the energy performance of buildings in Mediterranean climates: A case study. In Eco-Efficient Materials for Mitigating Building Cooling Needs; Woodhead Publishing: Cambridge, UK, 2015; Volume 67, pp. 499–524. [Google Scholar]
- Cannavale, A.; Ayr, U.; Martellotta, F. Innovative electrochromic devices: Energy savings and visual comfort effects. Energy Procedia 2018, 148, 900–907. [Google Scholar] [CrossRef]
- Lee, E.S.; DiBartolomeo, D.; Selkowitz, S. Thermal and daylighting performance of an automated venetian blind and lighting system in a full-scale private office. Energy Build. 1998, 29, 47–63. [Google Scholar] [CrossRef]
- Lee, E.S.; Zhou, L.; Yazdanian, M.; Inkarojrit, V.; Slack, J.; Rubin, M.; Selkowitz, S.E. Energy Performance Analysis of Electrochromic Windows in New York Commercial Office Buildings; FINAL (No. LBNL--50096); Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2002. [Google Scholar]
- Dussault, J.-M.; Sourbron, M.; Gosselin, L. Reduced energy consumption and enhanced comfort with smart windows: Comparison between quasi-optimal, predictive and rule-based control strategies. Energy Build. 2016, 127, 680–691. [Google Scholar] [CrossRef]
- Dussault, J.-M.; Gosselin, L. Office buildings with electrochromic windows: A sensitivity analysis of design parameters on energy performance, and thermal and visual comfort. Energy Build. 2017, 153, 50–62. [Google Scholar] [CrossRef]
- Firląg, S.; Yazdanian, M.; Curcija, C.; Kohler, C.; Vidanovic, S.; Hart, R.; Czarnecki, S. Control algorithms for dynamic windows for residential buildings. Energy Build. 2015, 109, 157–173. [Google Scholar] [CrossRef] [Green Version]
- Dutta, R. Modeling an Electrochromic Window Using a Multi-Criteria Control Strategy. In Proceedings of the Building Performance Analysis Conference and Simbuild Co-Organized by ASHRAE and IBPSA-USA, Chicago, IL, USA, 26–28 September 2018; pp. 149–156. [Google Scholar]
- Bueno, B.; Wienold, J.; Katsifaraki, A.; Kuhn, T. Fener: A Radiance-based modelling approach to assess the thermal and daylighting performance of complex fenestration systems in office spaces. Energy Build. 2015, 94, 10–20. [Google Scholar] [CrossRef]
- Cannavale, A.; Ayr, U.; Fiorito, F.; Martellotta, F. Smart Electrochromic Windows to Enhance Building Energy Efficiency and Visual Comfort. Energies 2020, 13, 1449. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, L.; Lee, E.S.; Ward, G. Lighting energy savings potential of split-pane electrochromic windows controlled for daylighting with visual comfort. Energy Build. 2013, 61, 8–20. [Google Scholar] [CrossRef] [Green Version]
- Jonsson, A.; Roos, A. Evaluation of control strategies for different smart window combinations using computer simulations. Sol. Energy 2010, 84, 1–9. [Google Scholar] [CrossRef]
- Fernandes, L.L.; Lee, E.S.; Dickerhoff, D.; Thanachareonkit, A.; Wang, T.; Gehbauer, C. Electrochromic Window Demonstration at the John E. Moss Federal Building, 650 Capitol Mall, Sacramento, California; (No. LBNL-2001183); Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2018. [Google Scholar]
- Kheybari, A.G.; Hoffmann, S. A Simulation-based Framework Exploring the Controls for a Dynamic Facade with Electrochromic Glazing (EC) A Simulation-Based Framework Exploring the Controls for a Dynamic Facade with Electrochromic Glazing. In Proceedings of the PowerSkin Conference, Munich, Germany, 17 January 2019. [Google Scholar]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Loonen, R.C.G.M.; Favoino, F.; Hensen, J.L.M.; Overend, M. Review of current status, requirements and opportunities for building performance simulation of adaptive facades. J. Build. Perform. Simul. 2017, 10, 205–223. [Google Scholar] [CrossRef] [Green Version]
- Favoino, F.; Fiorito, F.; Cannavale, A.; Ranzi, G.; Overend, M. Optimal control and performance of photovoltachromic switchable glazing for building integration in temperate climates. Appl. Energy 2016, 178, 943–961. [Google Scholar] [CrossRef] [Green Version]
- Gehbauer, C.; Blum, D.H.; Wang, T.; Lee, E.S. An assessment of the load modifying potential of model predictive controlled dynamic facades within the California context. Energy Build. 2020, 210, 109762. [Google Scholar] [CrossRef]
- Gehbauer, C.; Blum, D.H.; Wang, T.; Lee, E.S. Integrated Dynamic Facade Control with an Agent-Based Architecture for Commercial Buildings; Berkley Lab: Berkeley, CA, USA, 2020. [Google Scholar]
- Mirakhorli, A.; Dong, B. Occupancy behavior based model predictive control for building indoor climate—A critical review. Energy Build. 2016, 129, 499–513. [Google Scholar] [CrossRef]
- Cigler, J.; Gyalistras, D.; Siroky, J.; Tiet, V.-N.; Ferkl, L. Beyond Theory: The Challenge of Implementing Model Predictive Control in Buildings. In Proceedings of the11th REHVA World Congress and 8th International Conference Energy Efficient, Smart and Healthy Buildings, Prague, Czech Republic, 16–19 June 2013; pp. 1008–1018. [Google Scholar]
- Salakij, S.; Yu, N.; Paolucci, S.; Antsaklis, P. Model-Based Predictive Control for building energy management. I: Energy modeling and optimal control. Energy Build. 2016, 133, 345–358. [Google Scholar] [CrossRef]
- Isaia, F.; Fiorentini, M.; Serra, V.; Capozzoli, A. Enhancing energy efficiency and comfort in buildings through model predictive control for dynamic façades with electrochromic glazing. J. Build. Eng. 2021, 43, 102535. [Google Scholar] [CrossRef]
- Lehmann, B.; Gyalistras, D.; Gwerder, M.; Wirth, K.; Carl, S. Intermediate complexity model for Model Predictive Control of Integrated Room Automation. Energy Build. 2013, 58, 250–262. [Google Scholar] [CrossRef]
- Ogunsola, O.T.; Song, L.; Wang, G. Development and validation of a time-series model for real-time thermal load estimation. Energy Build. 2014, 76, 440–449. [Google Scholar] [CrossRef]
- Wetter, M. Co-simulation of building energy and control systems with the Building Controls Virtual Test Bed. J. Build. Perform. Simul. 2011, 4, 185–203. [Google Scholar] [CrossRef] [Green Version]
- ANSI/ASHRAE 55-2013: Thermal Environmental Conditions for Human Occupancy; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2013.
- Reinhart, C.F. Lightswitch-2002: A model for manual and automated control of electric lighting and blinds. Sol. Energy 2004, 77, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Herkel, S.; Kuhn, T.; Wienold, J. Comparison of Control Strategies for Shading Devices (White Paper); Fraunhofer: Munich, Germany, 2018. [Google Scholar]
- Van Den Wymelenberg, K. Patterns of occupant interaction with window blinds: A literature review. Energy Build. 2012, 51, 165–176. [Google Scholar] [CrossRef]
- Tavares, P.; Bernardo, H.; Gaspar, A.; Martins, A. Control Criteria of Electrochromic Glasses for Energy Savings in Mediterranean Buildings Refurbishment. Sol. Energy 2016, 134, 236–250. [Google Scholar] [CrossRef] [Green Version]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Giovannini, L.; Favoino, F.; Verso, V.R.M.L.; Pellegrino, A.; Serra, V. A Simplified Approach for the Annual and Spatial Evaluation of the Comfort Classes of Daylight Glare Using Vertical Illuminances. Buildings 2018, 8, 171. [Google Scholar] [CrossRef] [Green Version]
- Kheybari, A.G.; Hoffmann, S. Exploring the Potential of The Dynamic Facade: Simulating Daylight and Energy Performance of Complex Fenestration Systems (Venetian Blinds). In Proceedings of the BauSIM Conference, Karlsruhe, Germany, 26–28 September 2018. [Google Scholar]
- Kheybari, A.G.; Hoffmann, S. Exploring the potential of dynamic façade systems: An exterior shading system versus a switchable window. Bauphysik 2020, 42, 277–288. [Google Scholar] [CrossRef]
- Kheybari, A.G.; Hoffmann, S. A Data-driven Model for Controlling Smart Electrochromic Glazing: Living Lab smart office space. In Proceedings of the 2nd National Conference on knowledge-based Civil, Architecture and Urbanism, Tehran, Iran, 11 November 2019; pp. 1–17. [Google Scholar]
- International Organization for Standardization (ISO). ISO 52000:1. Energy Performance of Buildings—Overarching EPB Assessment—Part 1: General Framework and Procedures; International Organization for Standardization: Geneva, Switzerland, 2018. [Google Scholar]
- Wasilewski, S.; Grobe, L.O.; Wienold, J.; Andersen, M. A critical literature review of spatio-temporal simulation methods for daylight glare assessment. Sustain. Des. Eng. Built. Environ. 2019, 7, 32–42. [Google Scholar]
- Jakubiec, J.A.; Reinhart, C.F.; van den Wymelenberg, K. Towards an integrated framework for predicting visual comfort conditions from luminance-based metrics in perimeter daylit spaces. In Proceedings of the 14th IBPSA Conference, Hyderabad, India, 7–10 December 2015; pp. 1189–1196. [Google Scholar]
- Jakubiec, J.A. Validation of Simplified Visual Discomfort Calculations; Singapore University of Technology and Design: Singapore, 2018; pp. 11–12. [Google Scholar]
- Wienold, J. Dynamic daylight glare evaluation. In Proceedings of the IBPSA 2009 Conference 2009, Glasgow, Scotland, 27–30 July 2009; pp. 944–951. [Google Scholar]
- Giovannini, L.; Favoino, F.; Verso, V.R.M.L.; Serra, V.; Pellegrino, A. GLANCE (GLare ANnual Classes Evaluation): An approach for a simplified spatial glare evaluation. Build. Environ. 2020, 186, 107375. [Google Scholar] [CrossRef]
- DIN. DIN EN 12464. Light and Lighting—Lighting of Work Places—Part 1: Indoor Work Places; Beuth Publishing Company: Berlin, Germany, 2011. [Google Scholar]
- Reinhart, C. Opinion: Climate-based daylighting metrics in LEEDv4—A fragile progress. Light. Res. Technol. 2015, 47, 388. [Google Scholar] [CrossRef]
- Nabil, A.; Mardaljevic, J. Useful daylight illuminance: A new paradigm for assessing daylight in buildings. Light. Res. Technol. 2005, 37, 41–57. [Google Scholar] [CrossRef]
- Mardaljevic, J.; Andersen, M.; Roy, N.; Christoffersen, J. Daylighting metrics: Is there a relation between useful daylight illuminance and daylight glare probabilty? In Proceedings of the Building Simulation and Optimization Conference BSO12, Loughborough, UK, 10–11 September 2012. [Google Scholar]
- Olesen, B.; Parsons, K. Introduction to thermal comfort standards and to the proposed new version of EN ISO 7730. Energy Build. 2002, 34, 537–548. [Google Scholar] [CrossRef]
- ASHRAE. ANSI/ASHRAE 55-2004: Thermal Environmental Conditions for Human Occupancy. In ANSI/ASHRAE Standard; ASHRAE: Peachtree Corners, GA, USA, 2004; pp. 1–24. [Google Scholar]
- Steiner, T.; Liu, S. Interconnected model with distributed thermal comfort for model based shading control. Energy Build. 2021, 253, 111530. [Google Scholar] [CrossRef]
- Yu, N.; Salakij, S.; Chavez, R.; Paolucci, S.; Sen, M.; Antsaklis, P. Model-based predictive control for building energy management: Part II—Experimental validations. Energy Build. 2017, 146, 19–26. [Google Scholar] [CrossRef]
- La Gennusa, M.; Nucara, A.; Rizzo, G.; Scaccianoce, G. The calculation of the mean radiant temperature of a subject exposed to the solar radiation—A generalised algorithm. Build. Environ. 2005, 40, 367–375. [Google Scholar] [CrossRef]
- ASHRAE. Standard 55-2013 User’s Manual: ANSI/ASHRAE Standard 55-2013, Thermal Environmental Conditions for Human Occupancy; ASHRAE Research: Atlanta, GA, USA, 2016; pp. 21–33. ISBN 1939200385. [Google Scholar]
- Wesselak, V.; Schabbach, T.; Link, T.; Fischer, J. Regen. Energietechnik, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 123–130. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).