Seismic Design of Offshore Structures under Simplified Pulse-Like Earthquakes
Abstract
:1. Introduction
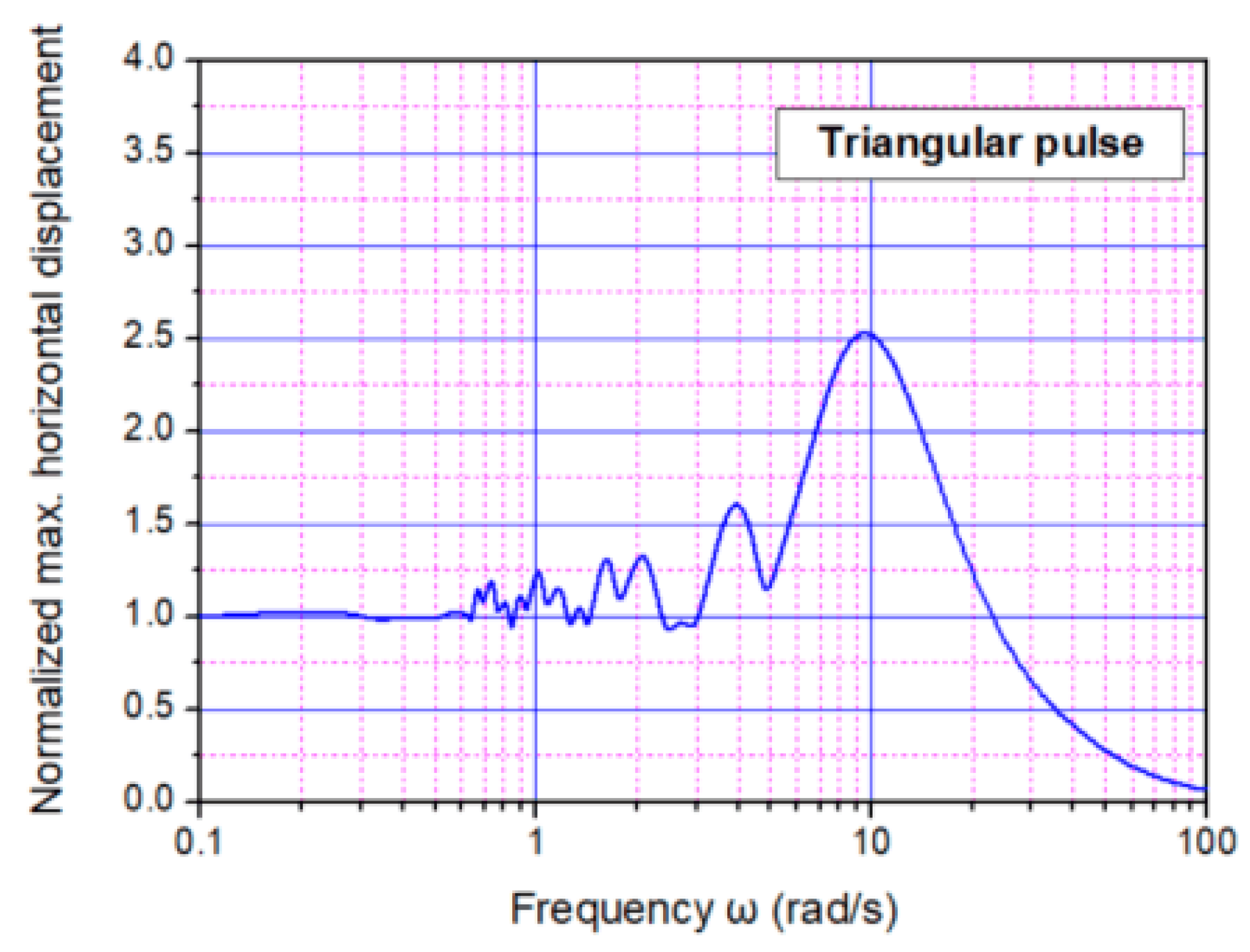
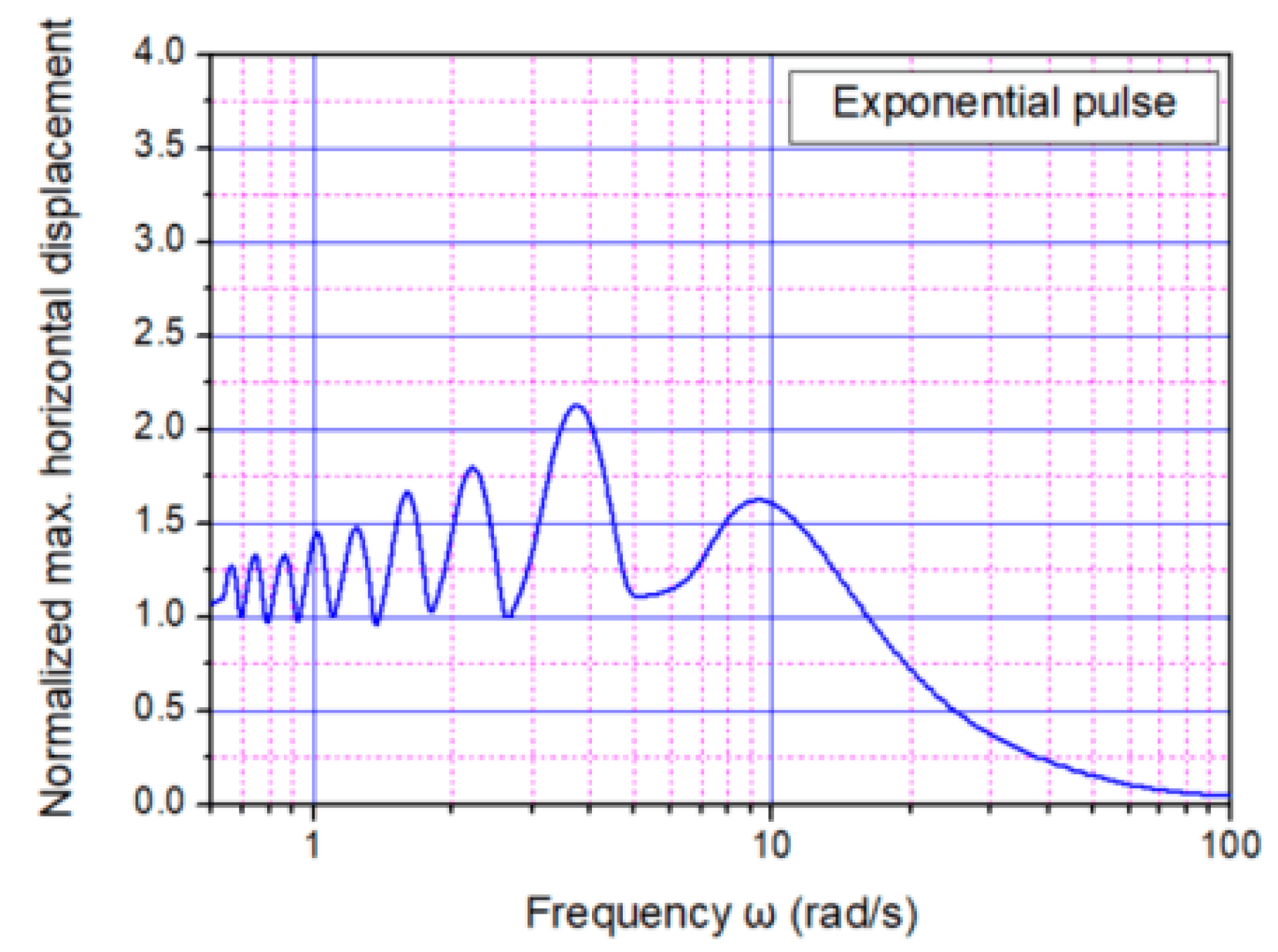
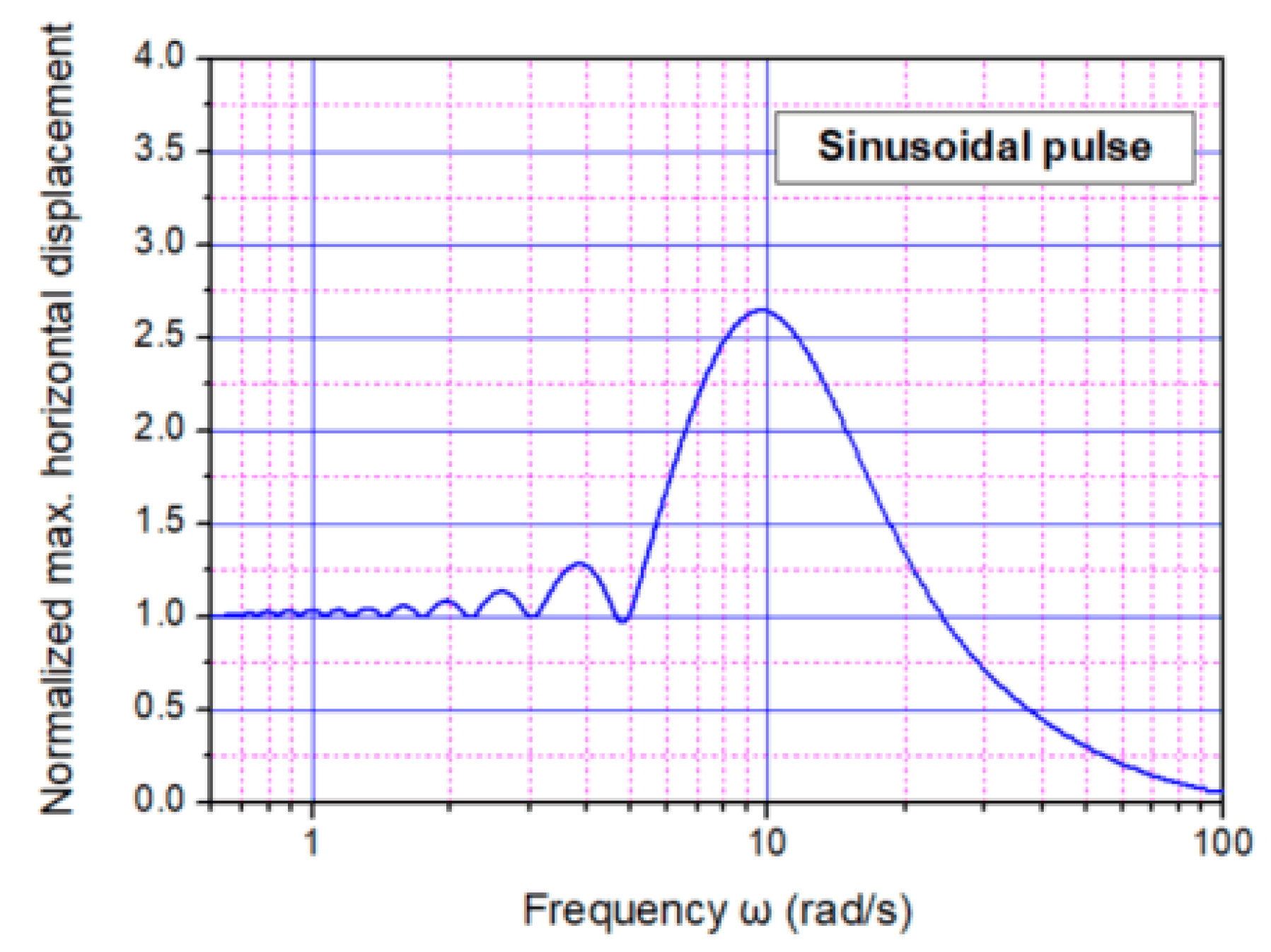
2. Simplified Pulse-Type Ground Motions
3. Offshore Jacket Platforms
4. Selected Results
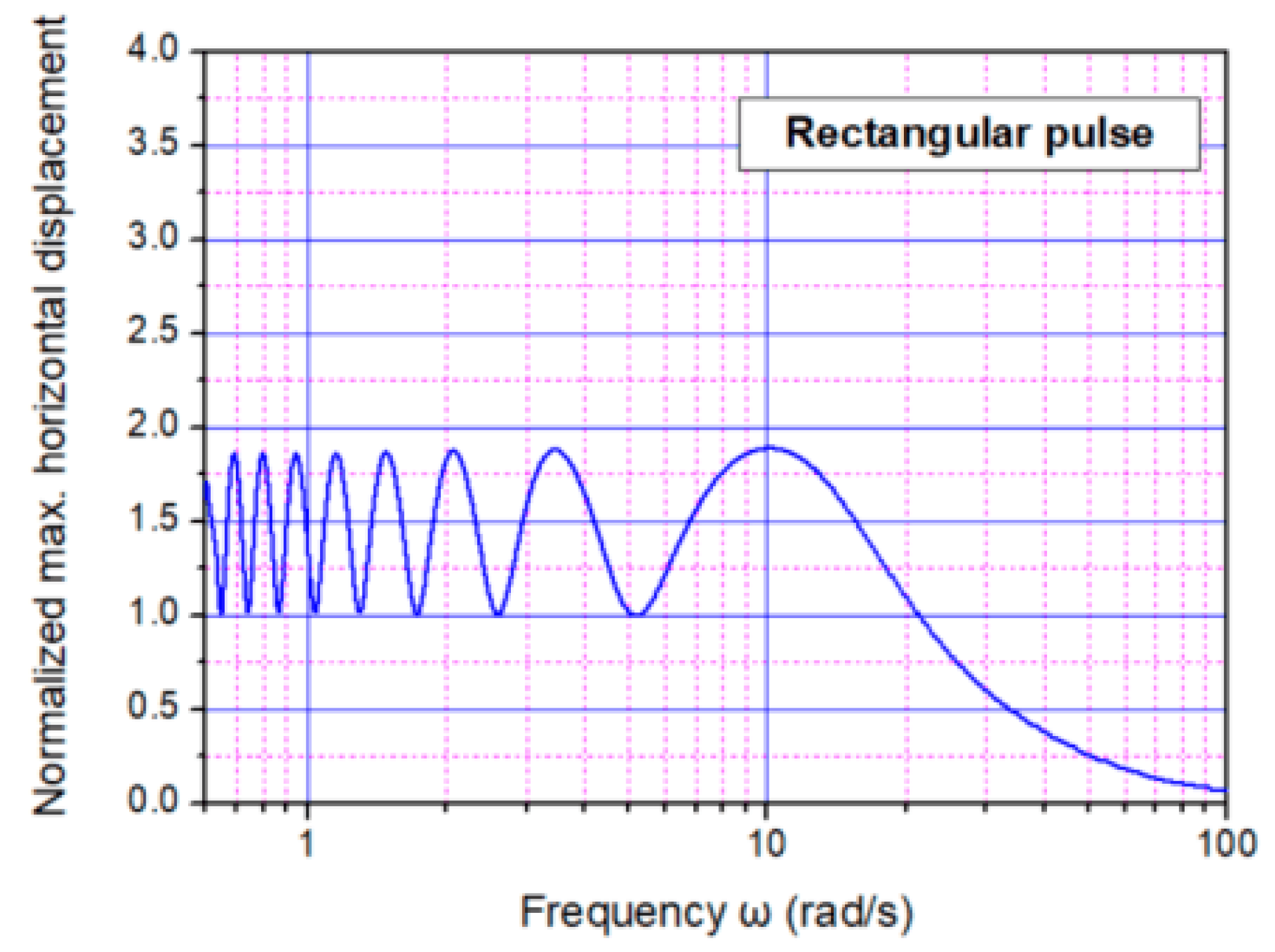
4.1. Linear Analysis
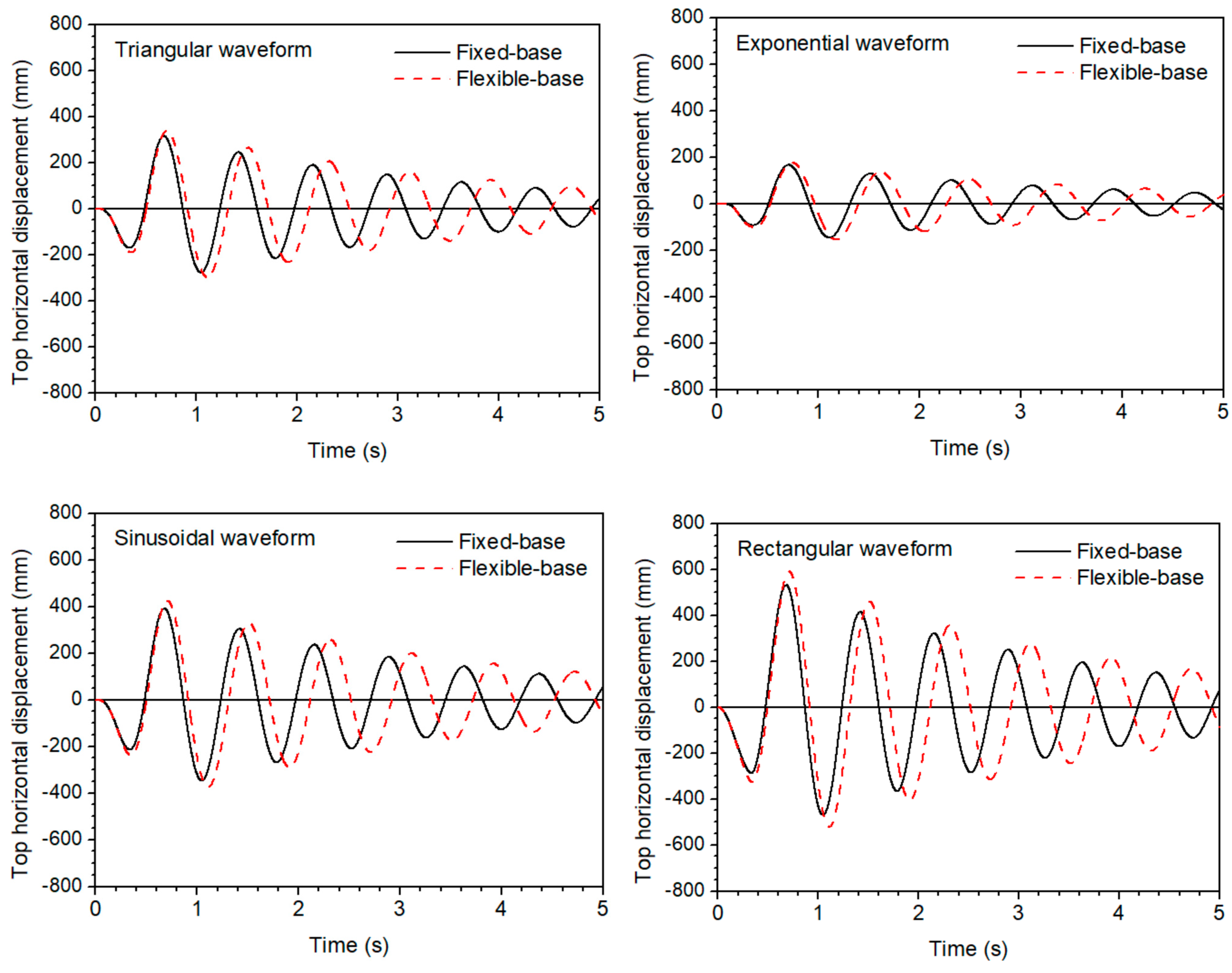
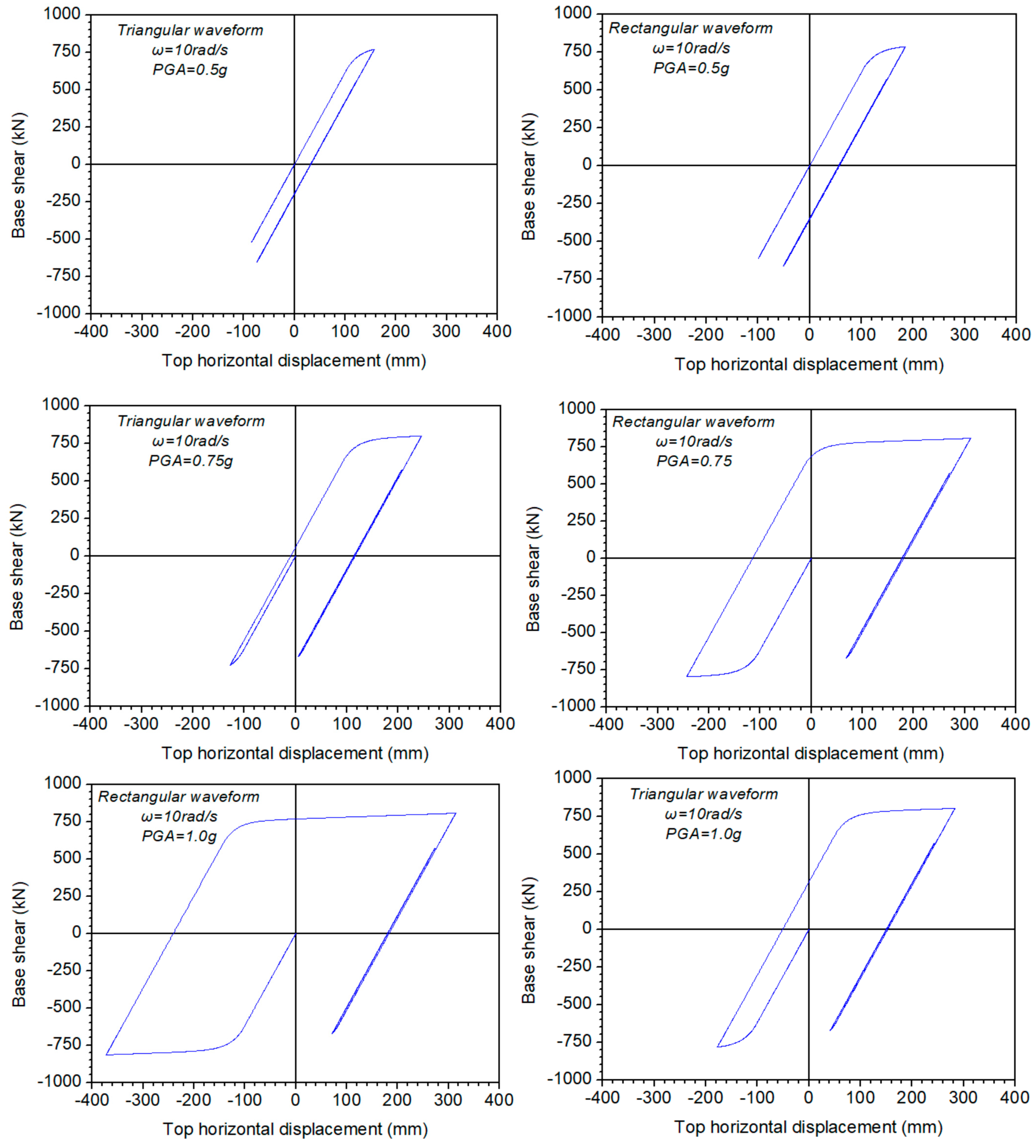
4.2. Nonlinear Analysis
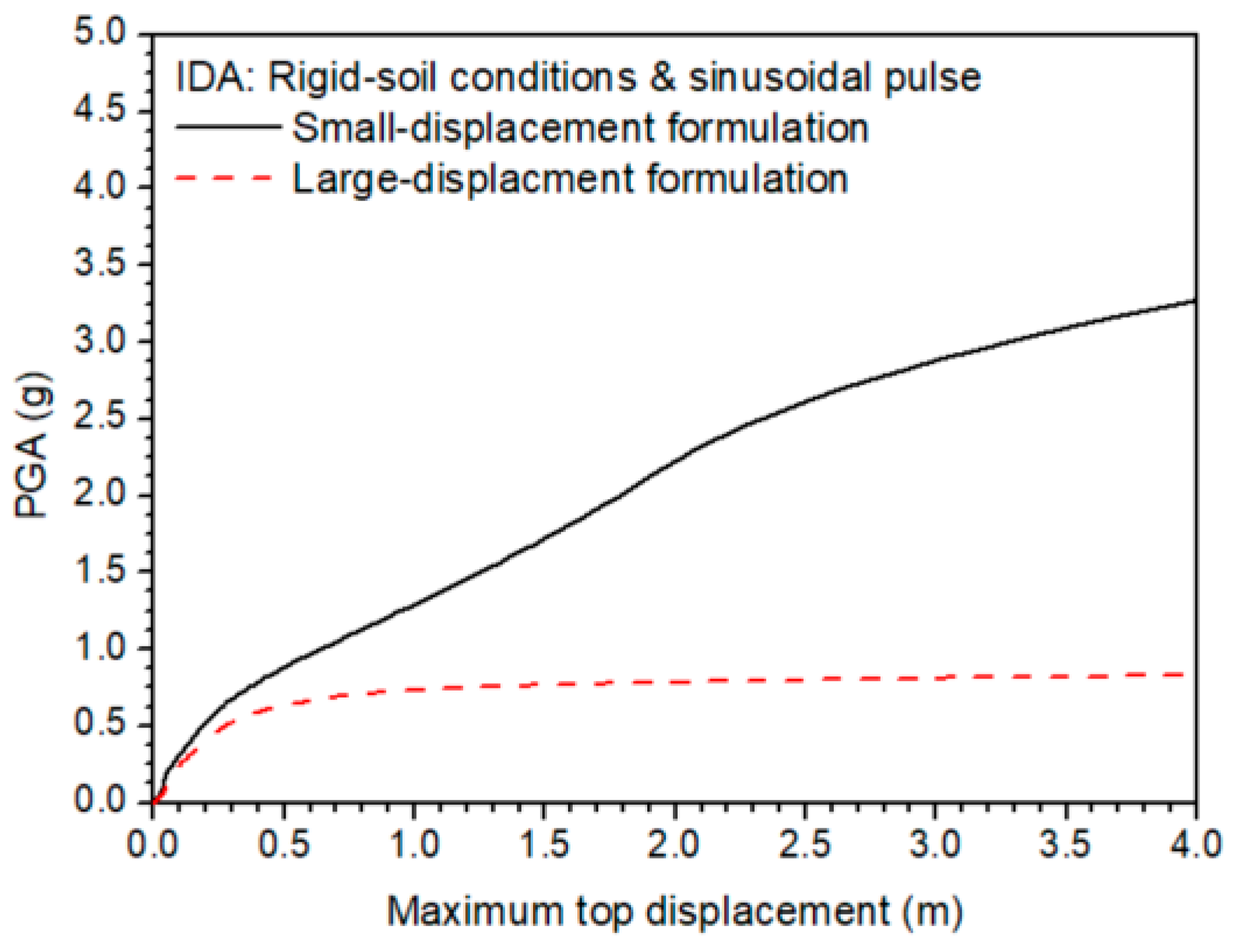
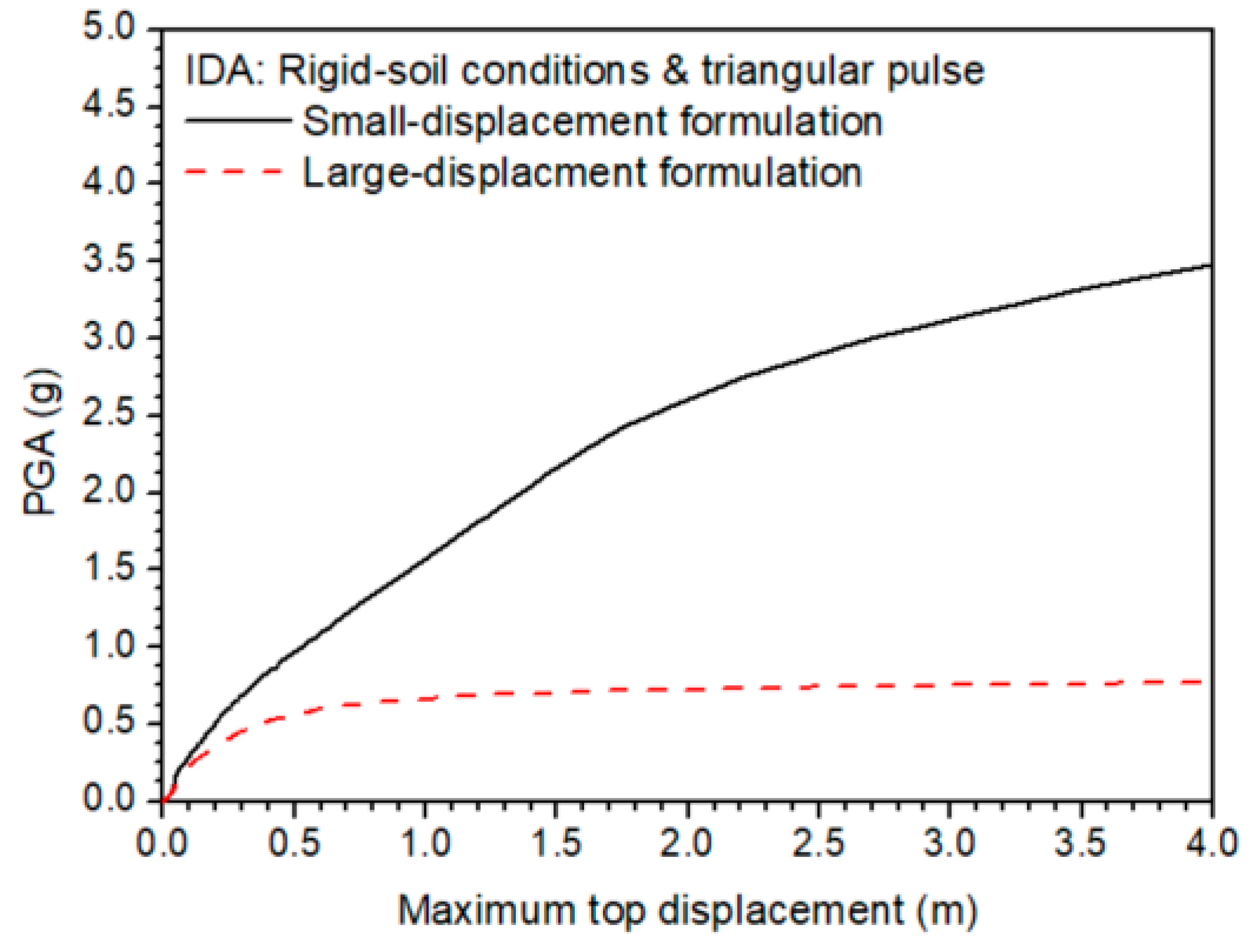
4.3. Small- and Large-Displacement Formulation
4.4. The Effects of the Angle of Incident of Seismic Pulses on the Platforms’ Dynamic Response
5. Conclusions
- (1)
- Although this investigation considers only simplified pulses, its importance seems to be noteworthy taking into account that near-fault ground motions are frequently characterized by simple waveforms.
- (2)
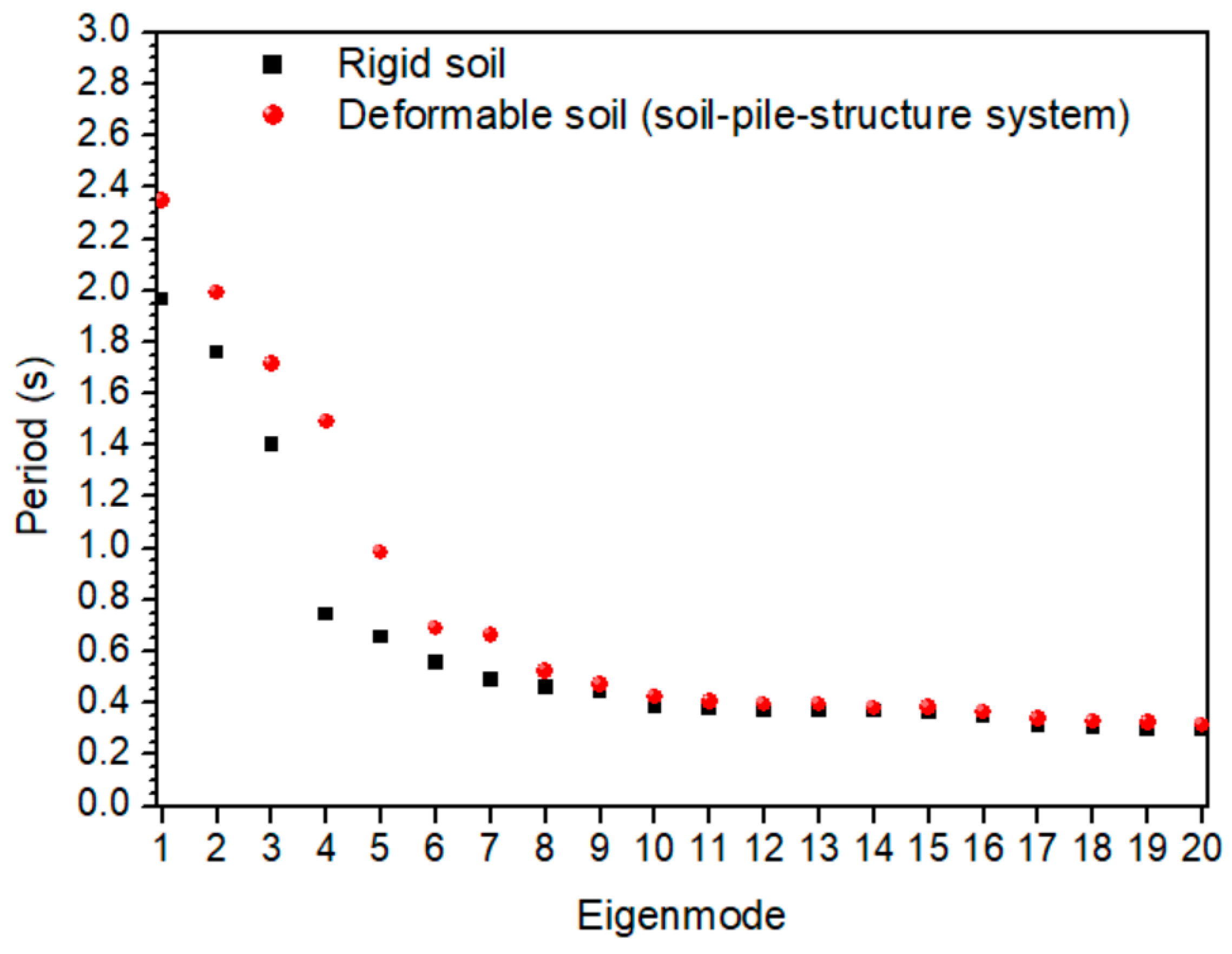
- The consideration of rigid soil strongly affects the response in comparison to the case of deformable soil, and the dynamic inelastic pile-soil-platform interaction should be taken into account. More specifically, the flexibility of the soil elongates the whole set of eigenperiods of platforms and, in most of the cases, it leads to higher values of maximum deformations in comparison with the case of fixed-based platforms.
- (3)
- Each type of pulse under consideration led to different results, even in the case where the circular frequency and the maximum peak ground acceleration was identical in any case.
- (4)
- When executing incremental dynamic analysis, it was found that geometric nonlinearity should be taken into account since their ignorance leads to a fictitious higher seismic performance and strength of platforms. More specifically, both the geometric nonlinearity of the soil and the diagonal braces, which lost their out-of-plane stability, leads to buckling-prone structures.
- (5)
- The incidence angle of seismic waves appears to be a crucial parameter where, for some critical angles, the maximum deformation can be increased significantly in comparison to the ones corresponding to other, less crucial angles.
- (6)
- The aforementioned findings and conclusions can be generalized to other types of platforms and pulses than those examined, but more analyses and investigations will be required.
Author Contributions
Funding
Conflicts of Interest
References
- Ji, C.Y.; Xue, H.Z.; Shi, X.H.; Gaidai, O. Experimental and numerical study on collapse of aged jacket platforms caused by corrosion or fatigue cracking. Eng. Struct. 2016, 112, 14–22. [Google Scholar] [CrossRef]
- Nabavian, M.; Morshed, A. Extending life of fixed offshore installations by integrity management: A structural overview. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 1–4 November 2010; Society of Petroleum Engineers: Abu Dhabi, UAE, 2010. [Google Scholar]
- Chen, J.Y.; Litton, R.; Ku, A.; Fraser, R.; Jeanjean, P. Seismic soil-structure interaction design considerations for offshore platforms. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Korea, 19–24 June 2016; American Society of Mechanical Engineers: Busan, Korea, 2016; Volume 49927, p. V001T10A003. [Google Scholar]
- El-Din, M.N.; Kim, J. Simplified seismic life cycle cost estimation of a steel jacket offshore platform structure. Struct. Infrastruct. Eng. 2017, 13, 1027–1044. [Google Scholar] [CrossRef]
- Jahanitabar, A.A.; Bargi, K. Time-dependent seismic fragility curves for aging jacket-type offshore platforms subjected to earthquake ground motions. Struct. Infrastruct. Eng. 2018, 14, 192–202. [Google Scholar] [CrossRef]
- Konstandakopoulou, F.D.; Papagiannopoulos, G.A.; Pnevmatikos, N.G.; Hatzigeorgiou, G.D. Seismic hazard assessment of offshore platforms. Int. J. Civ. Environ. Eng. 2019, 13, 272–276. [Google Scholar]
- Konstandakopoulou, F.D.; Evangelinos, K.I.; Nikolaou, I.E.; Papagiannopoulos, G.A.; Pnevmatikos, N.G. Seismic analysis of offshore platforms subjected to pulse-type ground motions compatible with European Standards. Soil Dyn. Earthq. Eng. 2020, 129, 105713. [Google Scholar] [CrossRef]
- Elsayed, T.; El-Shaib, M.; Gbr, K. Reliability of fixed offshore jacket platform against earthquake collapse. Ships Offshore Struct. 2016, 11, 167–181. [Google Scholar] [CrossRef]
- Som, A.; Das, D. Seismic vibration control of offshore jacket platforms using decentralized sliding mode algorithm. Ocean Eng. 2018, 152, 377–390. [Google Scholar] [CrossRef]
- Park, M.S.; Koo, W.; Kawano, K. Dynamic response analysis of an offshore platform due to seismic motions. Eng. Struct. 2011, 33, 1607–1616. [Google Scholar] [CrossRef]
- Ajamy, A.; Asgarian, B.; Ventura, C.E.; Zolfaghari, M.R. Seismic fragility analysis of jacket type offshore platforms considering soil-pile-structure interaction. Eng. Struct. 2018, 174, 198–211. [Google Scholar] [CrossRef]
- Zarrin, M.; Asgarian, B.; Abyani, M. Probabilistic seismic collapse analysis of jacket offshore platforms. J. Offshore Mech. Arct. Eng. 2018, 140, 031601. [Google Scholar] [CrossRef]
- Abyani, M.; Bahaari, M.R.; Zarrin, M.; Nasseri, M. Effects of sample size of ground motions on seismic fragility analysis of offshore jacket platforms using Genetic Algorithm. Ocean Eng. 2019, 189, 106326. [Google Scholar] [CrossRef]
- Lotfollahi-Yaghin, M.A.; Ahmadi, H.; Tafakhor, H. Seismic responses of an offshore jacket-type platform incorporated with tuned liquid dampers. Adv. Struct. Eng. 2016, 19, 227–238. [Google Scholar] [CrossRef]
- Minasidis, G.; Hatzigeorgiou, G.D.; Beskos, D.E. SSI in steel frames subjected to near-fault earthquakes. Soil Dyn. Earthq. Eng. 2014, 66, 56–68. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D.; Pnevmatikos, N.G. Maximum damping forces for structures with viscous dampers under near-source earthquakes. Eng. Struct. 2014, 68, 1–13. [Google Scholar] [CrossRef]
- Konstandakopoulou, F.; Hatzigeorgiou, G. Constant-ductility inelastic displacement, velocity and acceleration ratios for systems subjected to simple pulses. Soil Dyn. Earthq. Eng. 2020, 131, 106027. [Google Scholar] [CrossRef]
- Zhao, C.; Valliappan, S. Incident P and SV wave scattering effects under different canyon topographic and geological conditions. Int. J. Numer. Anal. Methods Geomech. 1993, 17, 73–94. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D. Damping modification factors for SDOF systems subjected to near-fault, far-fault and artificial earthquakes. Earthq. Eng. Struct. Dyn. 2020, 39, 1239–1258. [Google Scholar] [CrossRef]
- Konstandakopoulou, F.D.; Hatzigeorgiou, G.D. Water and wastewater steel tanks under multiple earthquakes. Soil Dyn. Earthq. Eng. 2017, 100, 445–453. [Google Scholar] [CrossRef]
- Baker, J.W. Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- Champion, C.; Liel, A. The effect of near-fault directivity on building seismic collapse risk. Earthq. Eng. Struct. Dyn. 2012, 41, 1391–1409. [Google Scholar] [CrossRef]
- He, W.L.; Agrawal, A.K. Analytical model of ground motion pulses for the design and assessment of seismic protective systems. J. Struct. Eng. 2008, 134, 1177–1188. [Google Scholar] [CrossRef]
- Christidis, A.A.; Dimitroudi, E.G.; Hatzigeorgiou, G.D.; Beskos, D.E. Maximum seismic displacements evaluation of steel frames from their post-earthquake residual deformation. Bull. Earthq. Eng. 2013, 11, 2233–2248. [Google Scholar] [CrossRef]
- Pnevmatikos, N.G.; Hatzigeorgiou, G.D. Damage detection of framed structures subjected to earthquake excitation using discrete wavelet analysis. Bull. Earthq. Eng. 2017, 15, 227–248. [Google Scholar] [CrossRef]
- Carr, A.J. RUAUMOKO-Inelastic Dynamic Analysis Program; Department of Civil Engineering, University of Canterbury: Christchurch, New Zealand, 2008. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; Technical Note No. 902, National Advisory Committee for Aeronautics; NASA: Washington, DC, USA, 1943; p. 4.
- American Petroleum Institute (API). RP2A-WSD AP: Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms; API: Washington, DC, USA, 2007. [Google Scholar]
- Boulanger, R.W.; Curras, C.J.; Kutter, B.L.; Wilson, D.W.; Abghari, A. Seismic soil-pile-structure interaction experiments and analyses. J. Geotech. Geoenviron. Eng. 1999, 125, 750–759. [Google Scholar] [CrossRef]
- Remennikov, A.; Walpole, W.R. Analytical prediction of seismic behaviour for concentrically-braced steel systems. Earthq. Eng. Struct. Dyn. 1997, 26, 859–874. [Google Scholar] [CrossRef]
- Al-Bermani, F.G.A.; Li, B.; Zhu, K.; Kitipornchai, S. Cyclic and seismic response of flexibly jointed frames. Eng. Struct. 1994, 16, 249–255. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, TBS, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Li, Z.; Hatzigeorgiou, G.D. Seismic damage analysis of RC structures using fiber beam-column elements. Soil Dyn. Earthq. Eng. 2012, 32, 103–110. [Google Scholar] [CrossRef]

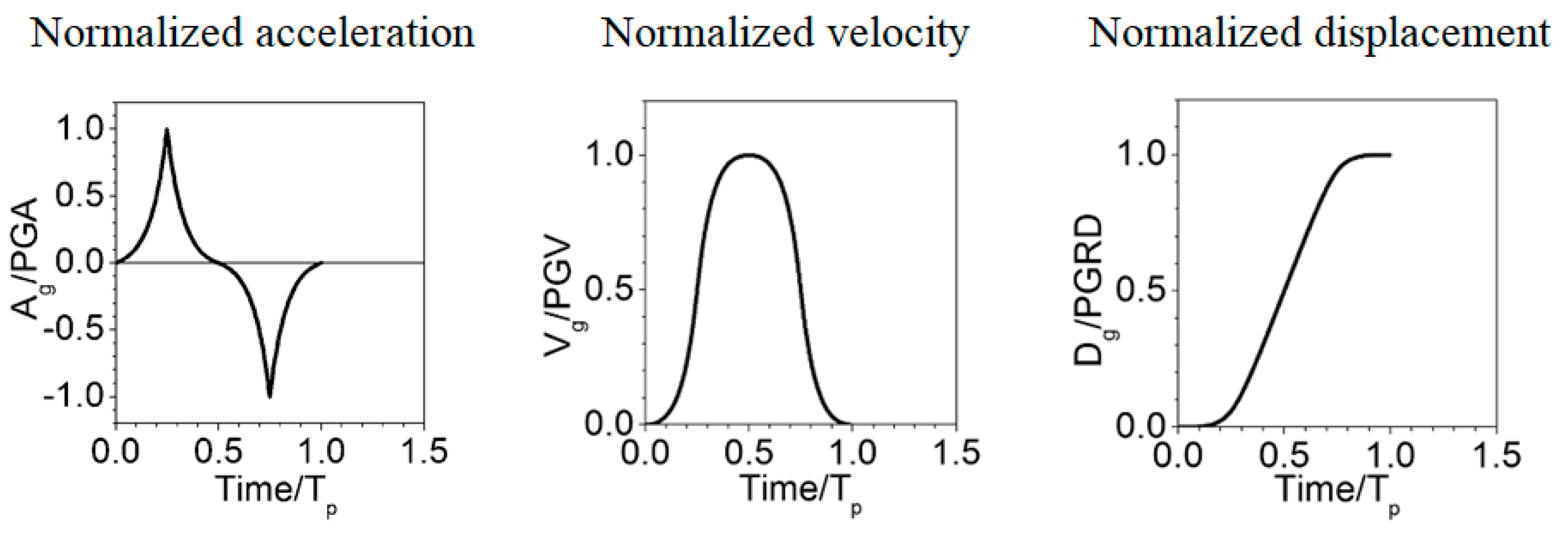
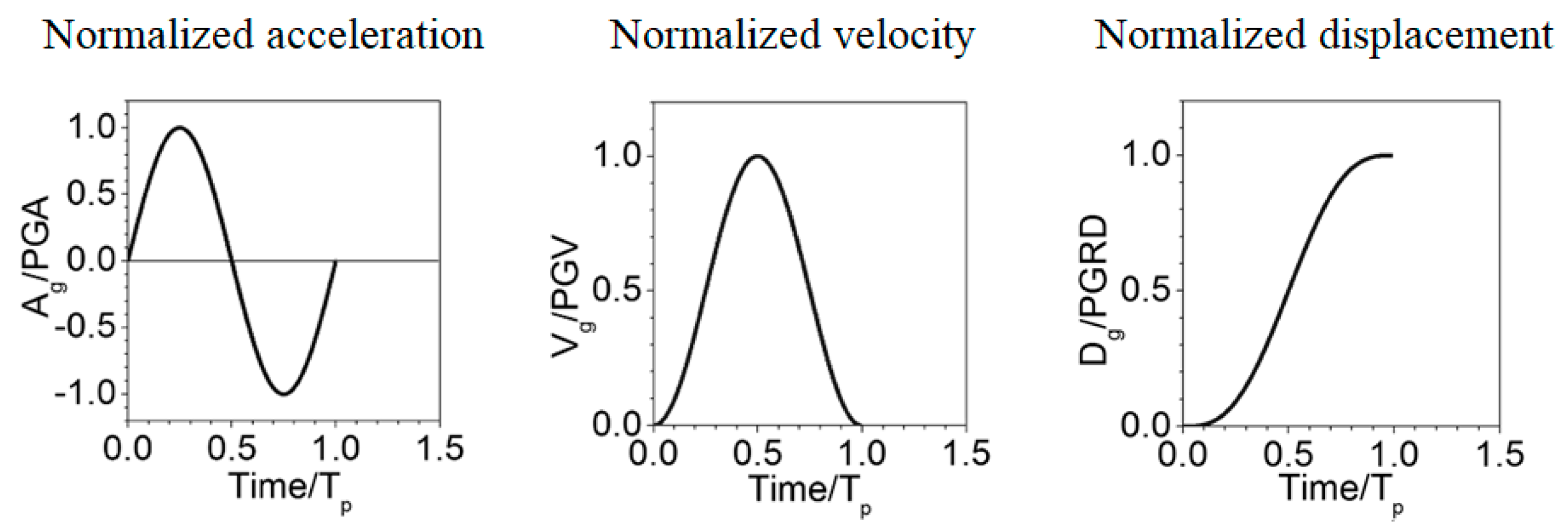
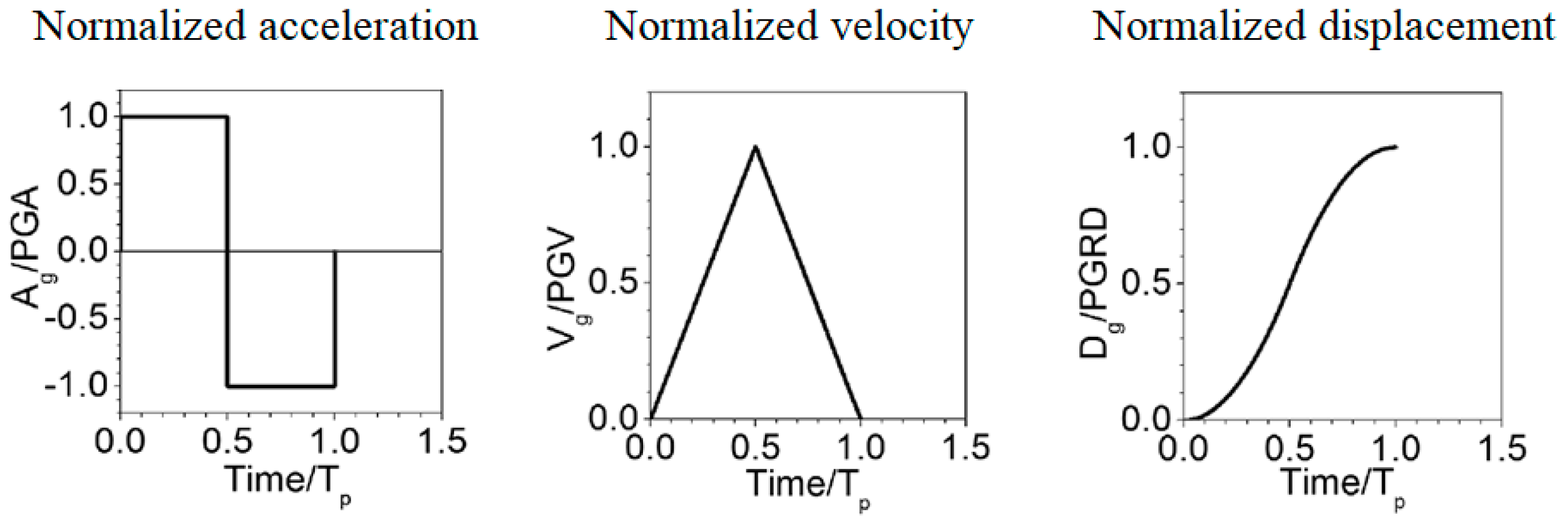
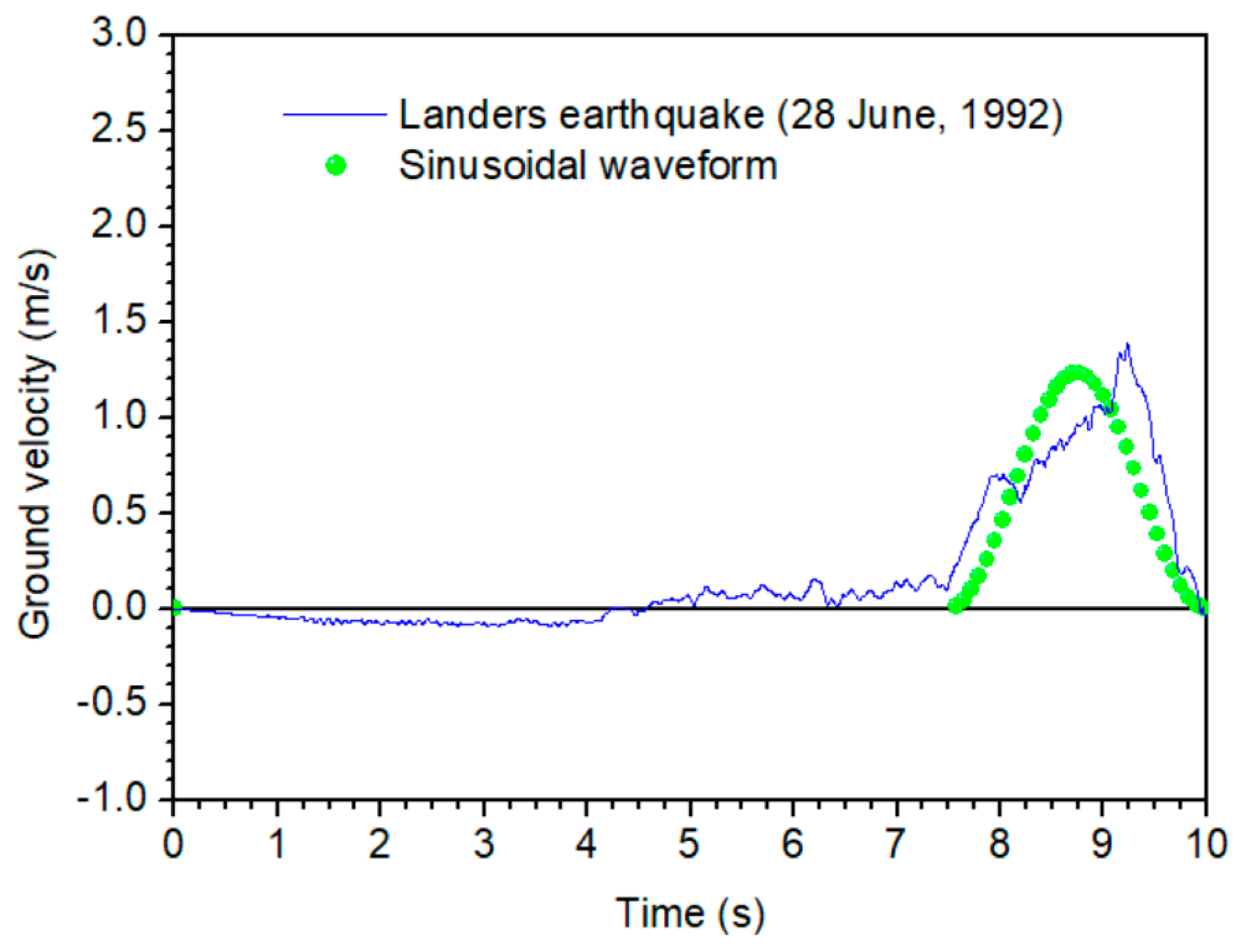

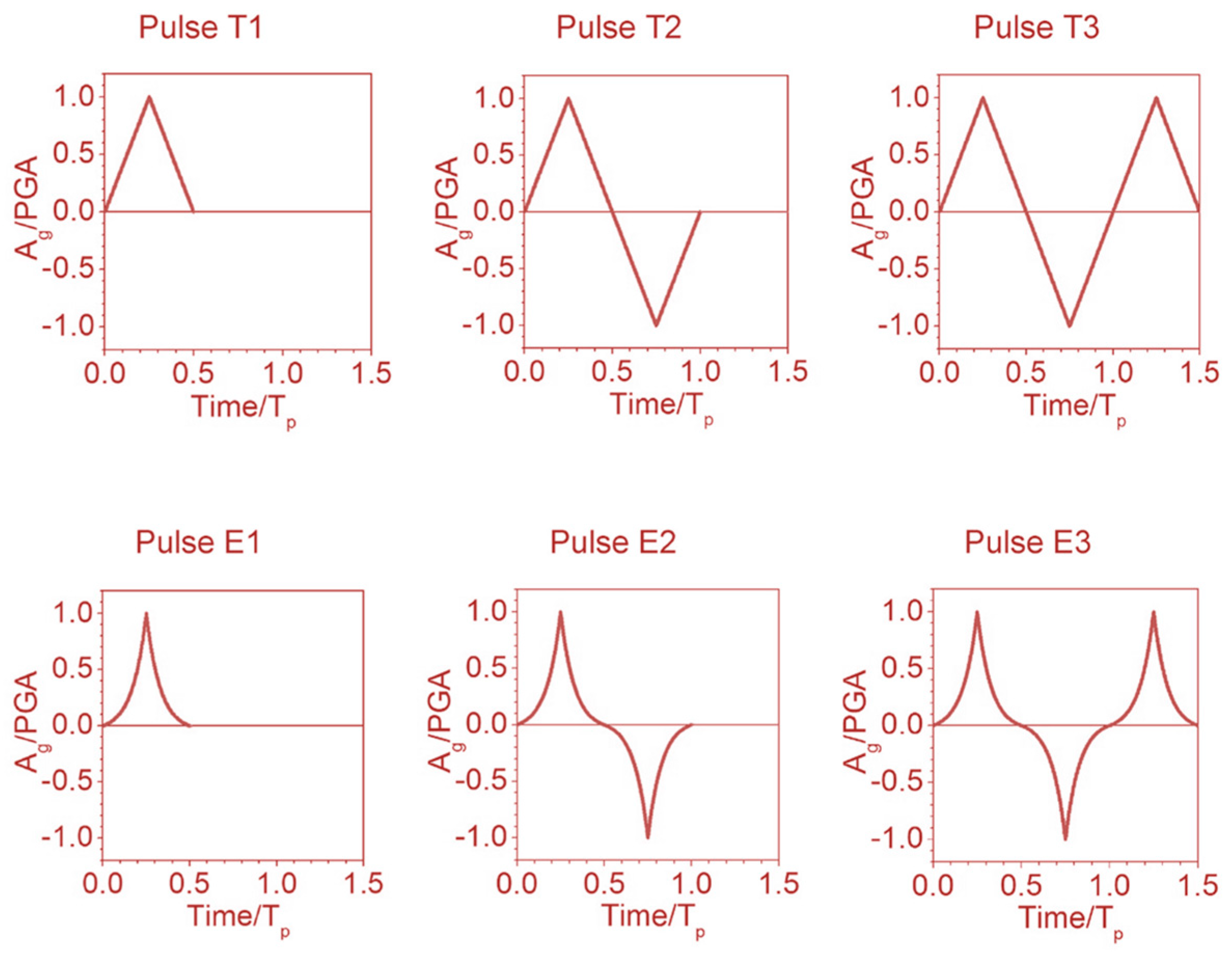
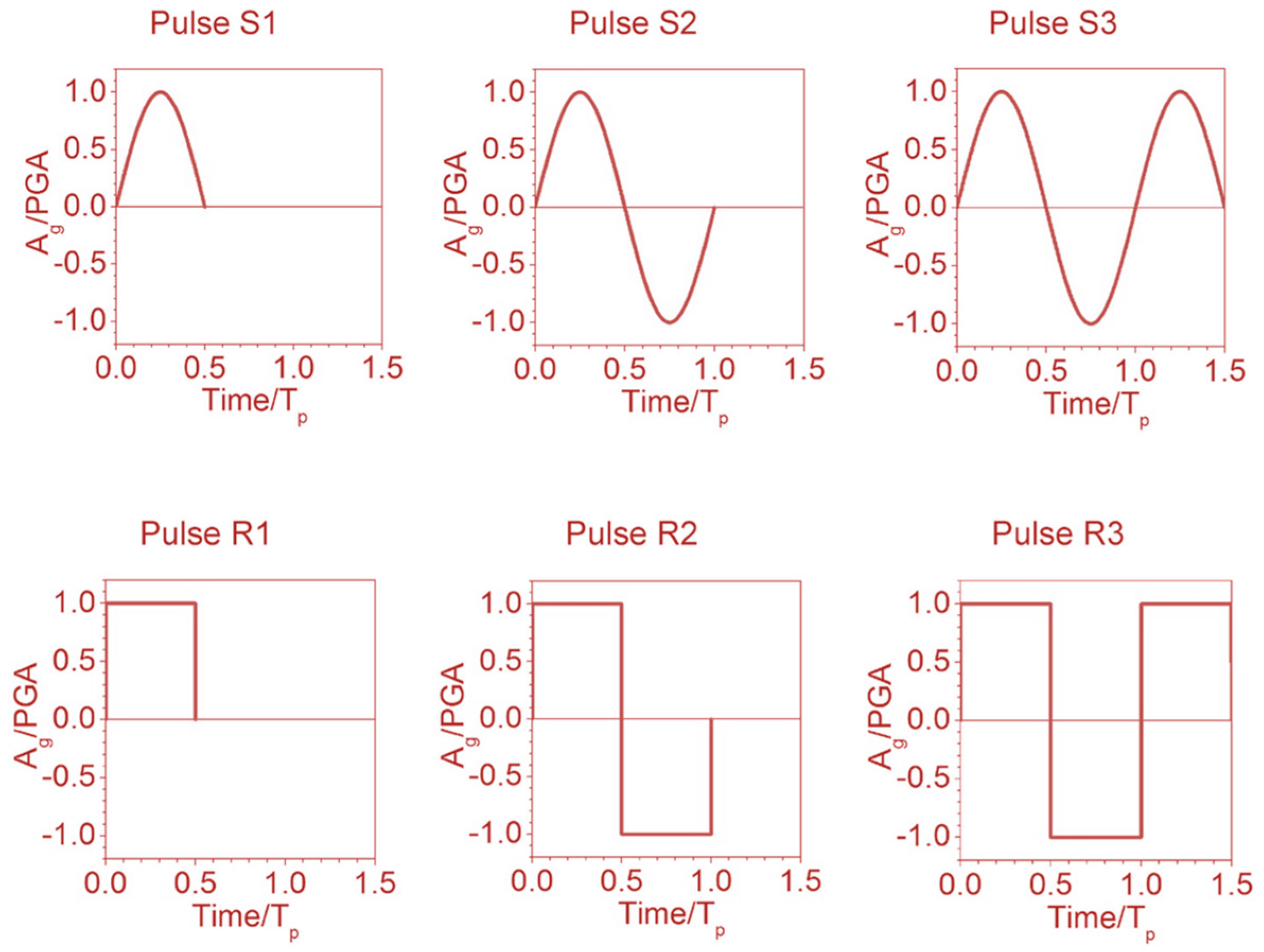
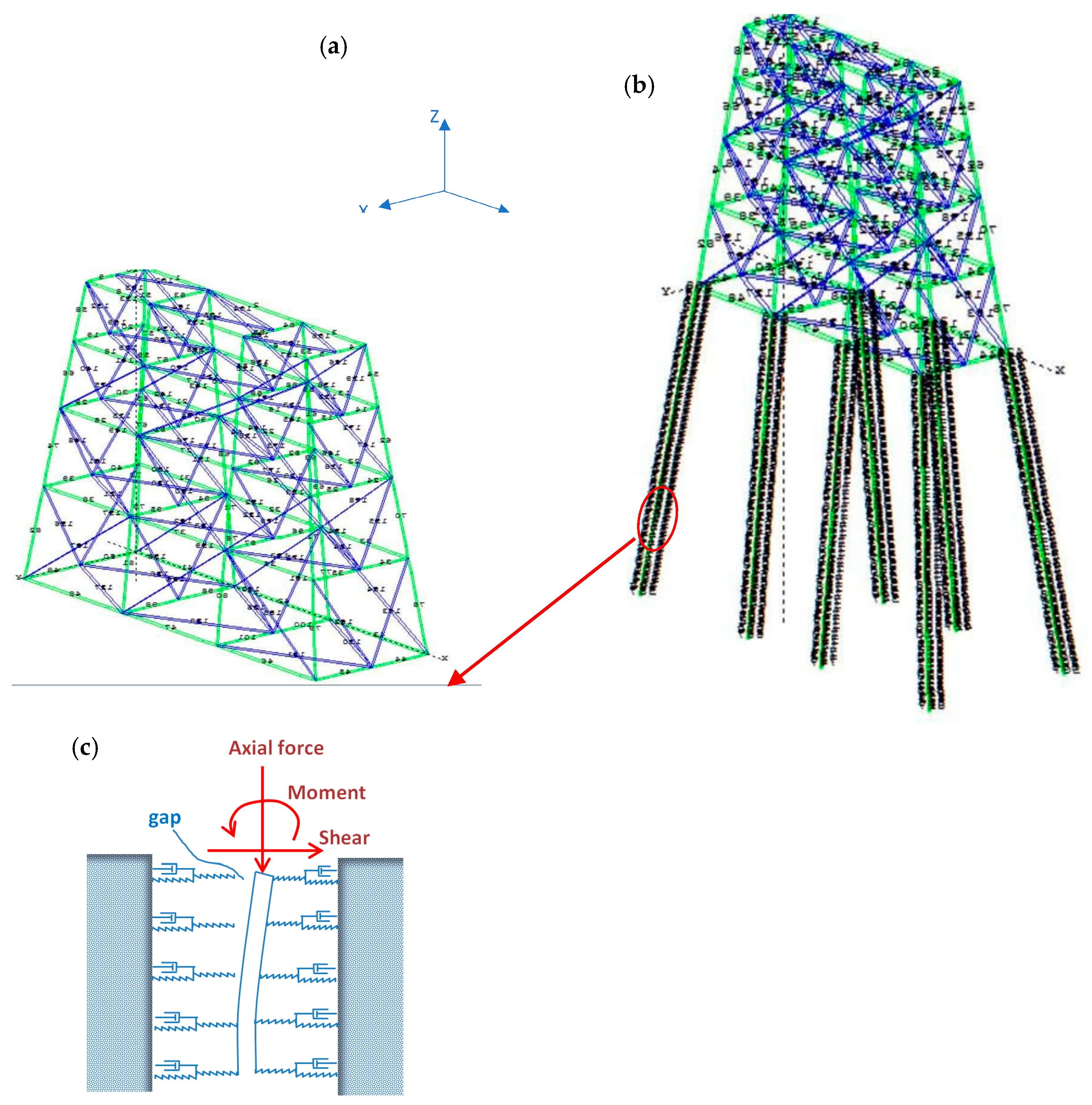
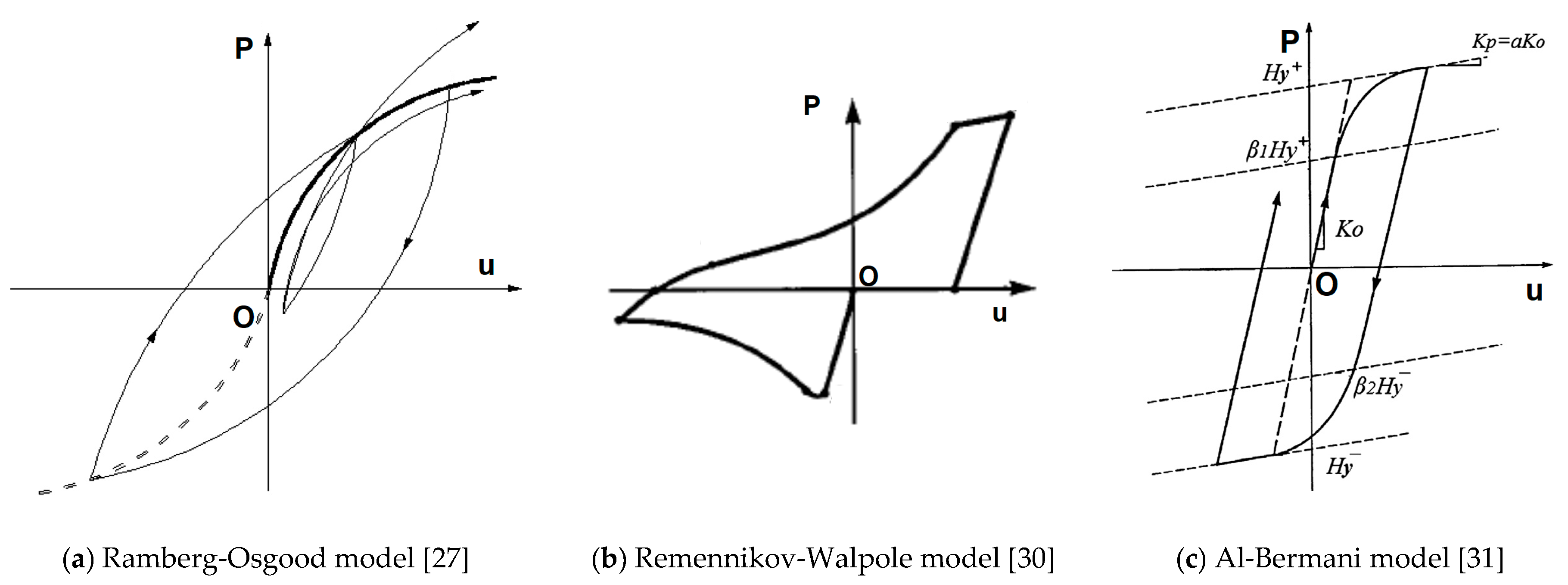

| Members | Storey | Circular Cross-Sections-ext. Diameter × Thickness [mm] |
|---|---|---|
| Columns | 0 | 110.0 × 5.0 |
| 1 | 110.0 × 5.0 | |
| 2 | 100.0 × 4.5 | |
| 3 | 90.0 × 4.0 | |
| 4 | 90.0 × 4.0 | |
| Beams | 0 | 75.0 × 4.5 |
| 1 | 75.0 × 4.5 | |
| 2 | 80.0 × 4.2 | |
| 3 | 75.0 × 4.0 | |
| 4 | 50.0 × 2.5 | |
| Braces | 0 | 55.0 × 2.5 |
| 1 | 55.0 × 2.5 | |
| 2 | 60.0 × 2.2 | |
| 3 | 50.0 × 2.6 | |
| 4 | 50.0 × 2.2 |
| Rigid-Soil Assumption | Soil-Pile-Structure System | |||
|---|---|---|---|---|
| Eigenvalue | Natural Frequency ωn (rad/s) | Period Tn (s) | Natural Frequency ωn (rad/s) | Period Tn (s) |
| 1 | 3.199 | 1.964 | 2.675 | 2.349 |
| 2 | 3.572 | 1.759 | 3.154 | 1.992 |
| 3 | 4.488 | 1.400 | 3.666 | 1.714 |
| 4 | 8.470 | 0.742 | 4.217 | 1.490 |
| 5 | 9.587 | 0.655 | 6.397 | 0.982 |
| 6 | 11.278 | 0.557 | 9.111 | 0.690 |
| 7 | 12.837 | 0.489 | 9.475 | 0.663 |
| 8 | 13.729 | 0.458 | 12.020 | 0.523 |
| 9 | 14.118 | 0.445 | 13.407 | 0.469 |
| 10 | 16.148 | 0.389 | 14.771 | 0.425 |
| 11 | 16.776 | 0.375 | 15.431 | 0.407 |
| 12 | 16.845 | 0.373 | 15.943 | 0.394 |
| 13 | 16.936 | 0.371 | 16.002 | 0.393 |
| 14 | 17.059 | 0.368 | 16.530 | 0.380 |
| 15 | 17.097 | 0.367 | 16.474 | 0.381 |
| 16 | 18.121 | 0.347 | 17.238 | 0.364 |
| 17 | 20.207 | 0.311 | 18.617 | 0.337 |
| 18 | 20.603 | 0.305 | 19.252 | 0.326 |
| 19 | 21.068 | 0.298 | 19.340 | 0.325 |
| 20 | 21.124 | 0.297 | 20.050 | 0.313 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstandakopoulou, F.; Papagiannopoulos, G.; Pnevmatikos, N.; Evangelinos, K.; Nikolaou, I.; Hatzigeorgiou, G. Seismic Design of Offshore Structures under Simplified Pulse-Like Earthquakes. CivilEng 2020, 1, 310-325. https://doi.org/10.3390/civileng1030020
Konstandakopoulou F, Papagiannopoulos G, Pnevmatikos N, Evangelinos K, Nikolaou I, Hatzigeorgiou G. Seismic Design of Offshore Structures under Simplified Pulse-Like Earthquakes. CivilEng. 2020; 1(3):310-325. https://doi.org/10.3390/civileng1030020
Chicago/Turabian StyleKonstandakopoulou, Foteini, George Papagiannopoulos, Nikos Pnevmatikos, Konstantinos Evangelinos, Ioannis Nikolaou, and George Hatzigeorgiou. 2020. "Seismic Design of Offshore Structures under Simplified Pulse-Like Earthquakes" CivilEng 1, no. 3: 310-325. https://doi.org/10.3390/civileng1030020
APA StyleKonstandakopoulou, F., Papagiannopoulos, G., Pnevmatikos, N., Evangelinos, K., Nikolaou, I., & Hatzigeorgiou, G. (2020). Seismic Design of Offshore Structures under Simplified Pulse-Like Earthquakes. CivilEng, 1(3), 310-325. https://doi.org/10.3390/civileng1030020









