Depolarization Block in the Endocannabinoid System of the Hippocampus
Abstract
1. Introduction
- Phyto-CBs, they occur in flowering plants, liverworths and fungi. They were first isolated from Cannabis sativa L., more thant 113 different cannabinoids were classified into distinct types: cannabigerols (CBGs), cannabichromenes (CBCs), cannabidiols (CBDs), (-)--trans- tetrahydrocannabinols (-THCs), (-)--trans-tetrahydrocannabinols (-THCs), cannabicyclols (CBLs), cannabielsoins (CBEs), cannabinols (CBNs), cannabinodiols (CBNDs), cannabitriols (CBTs), and miscellaneus cannabinoids;
- Synthetic-CBs (produced in the laboratory);
- Endocannabidoids (eCBs), naturally produced by the human body.
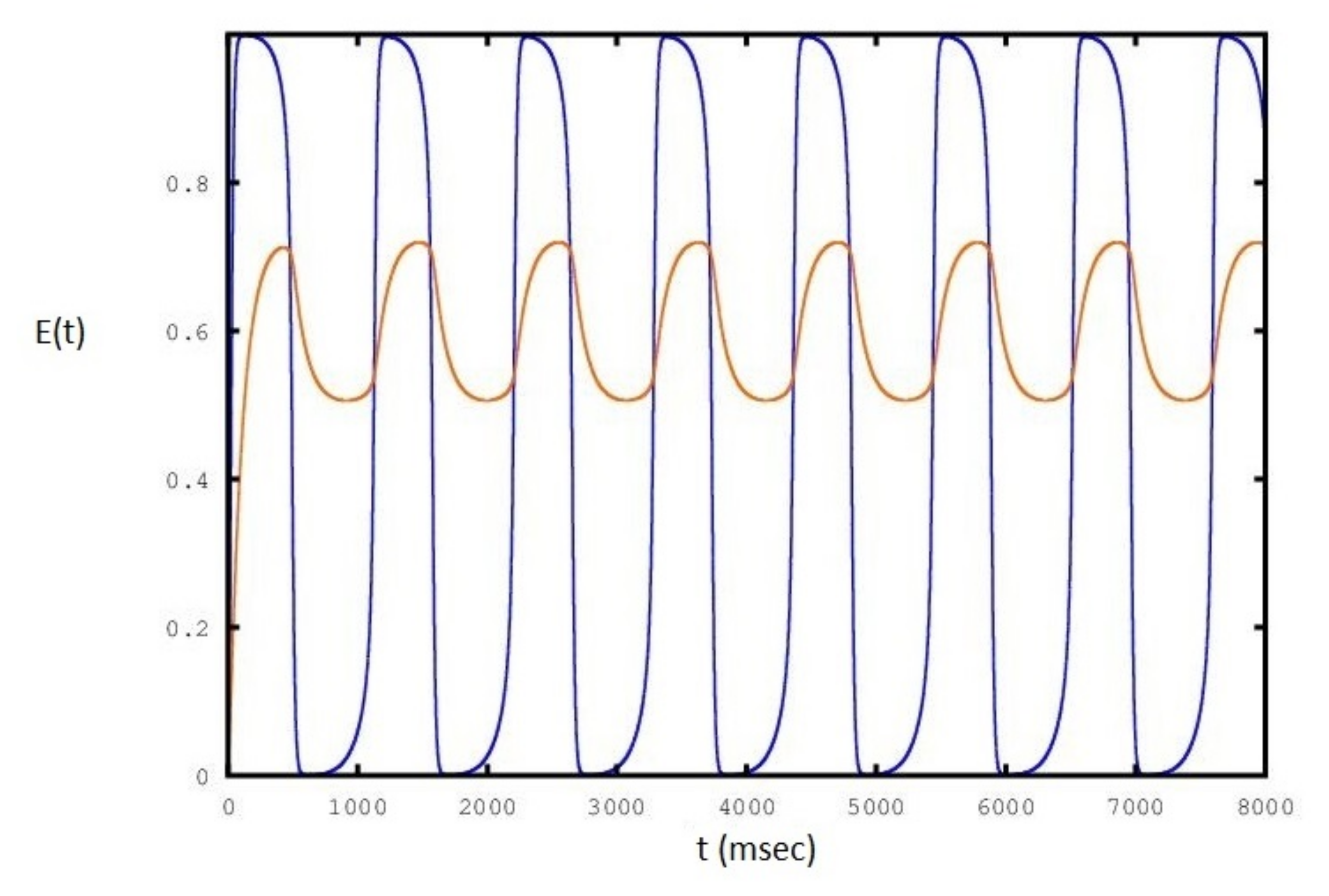
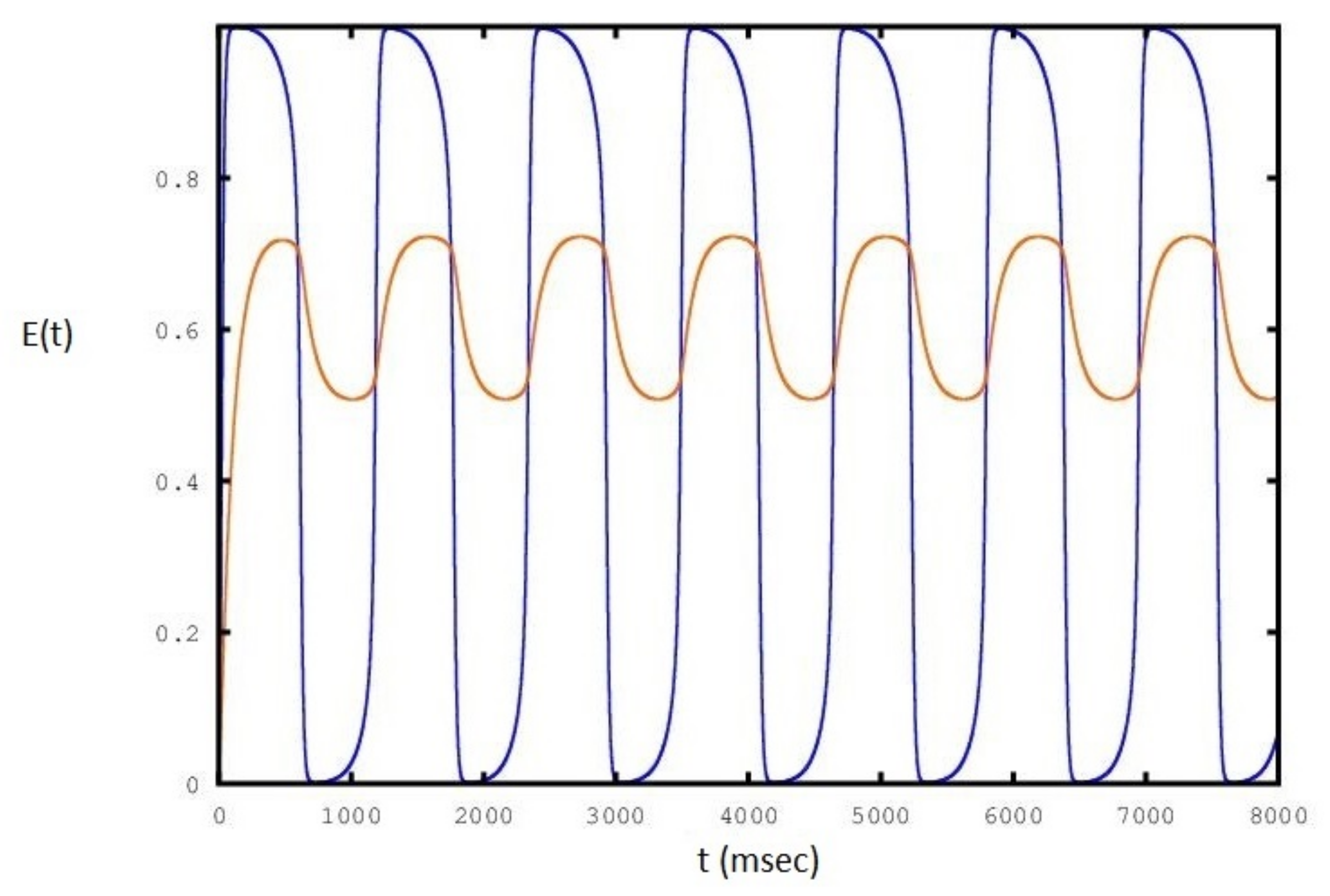
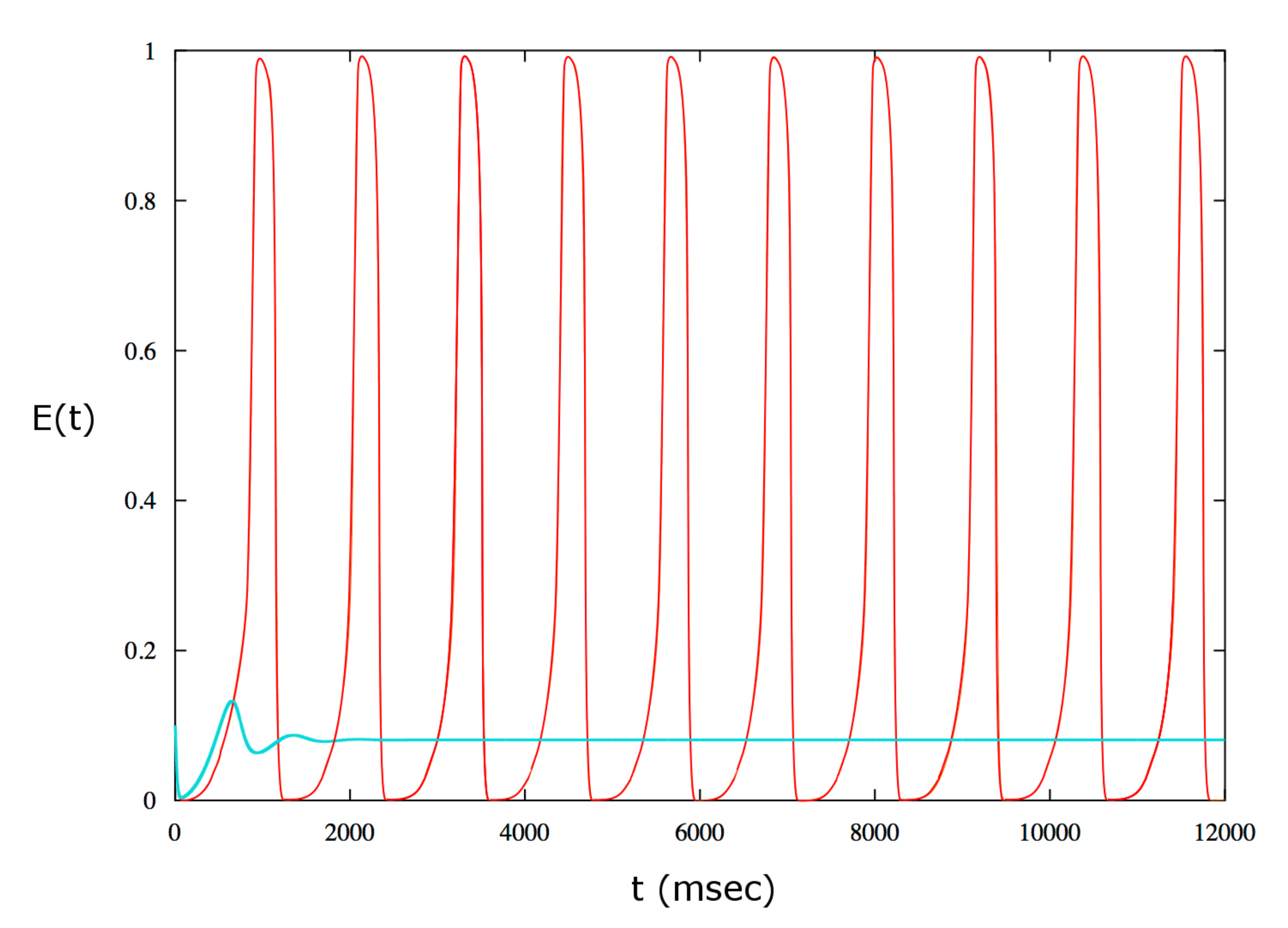
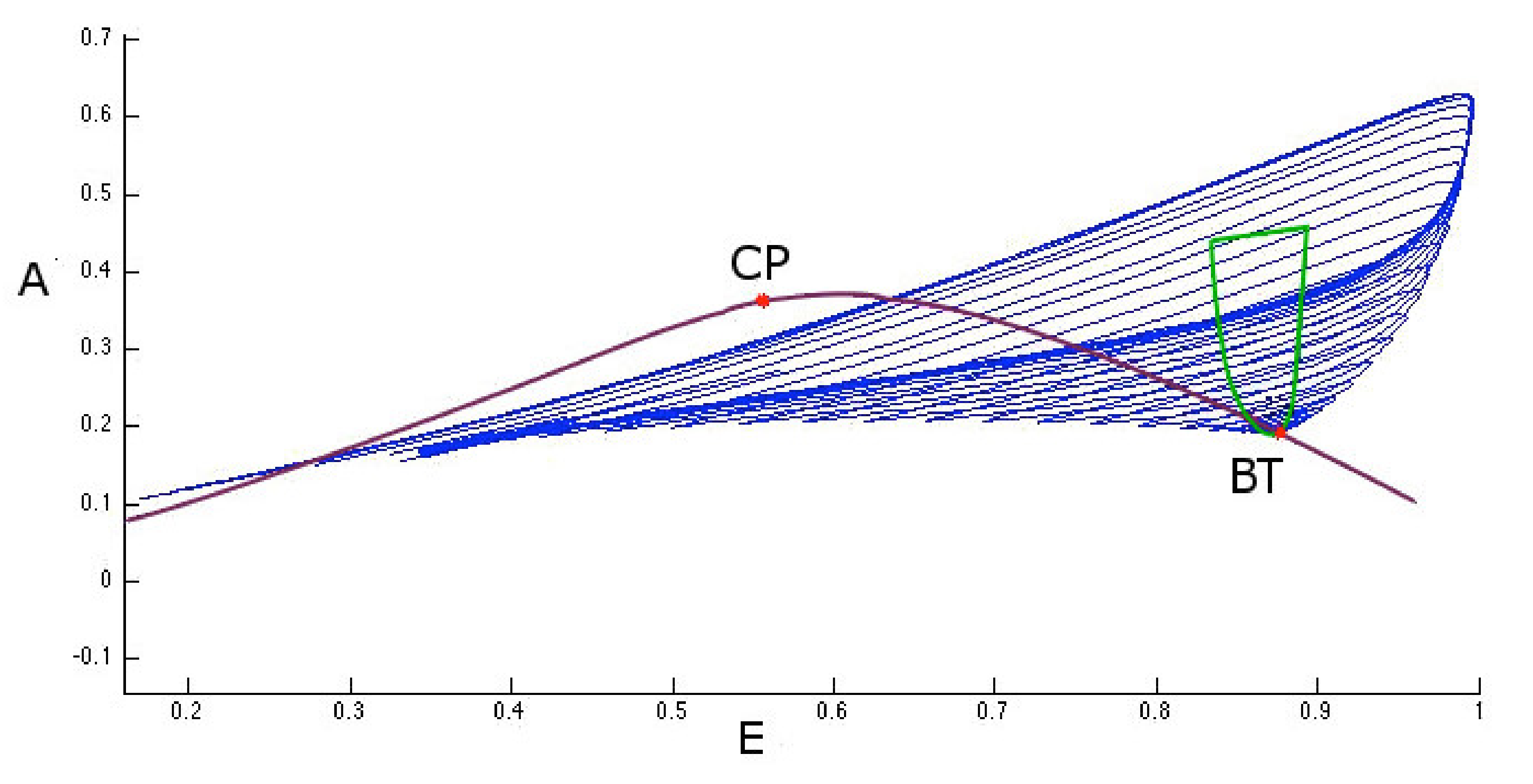
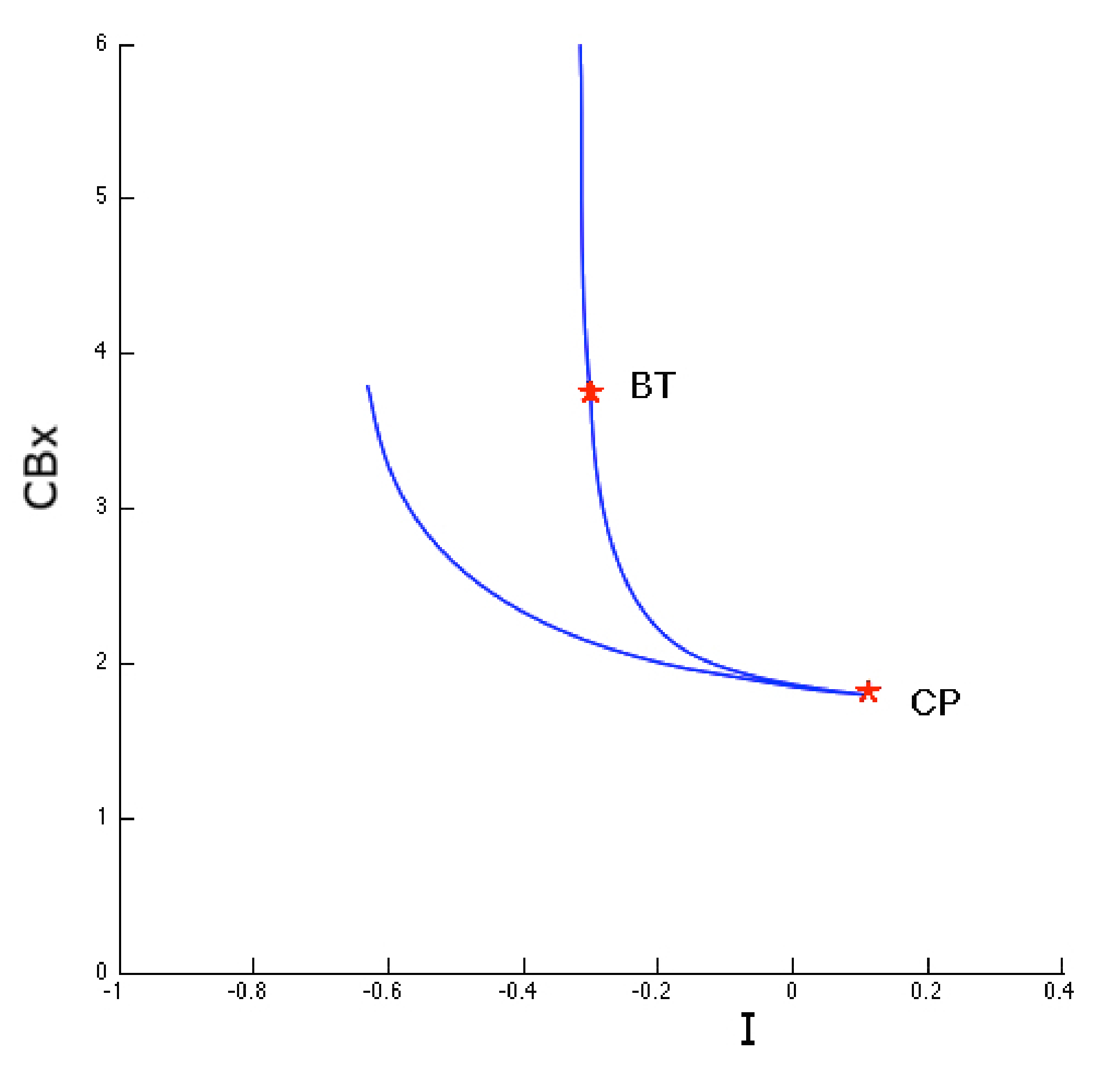
2. Results
3. Discussion
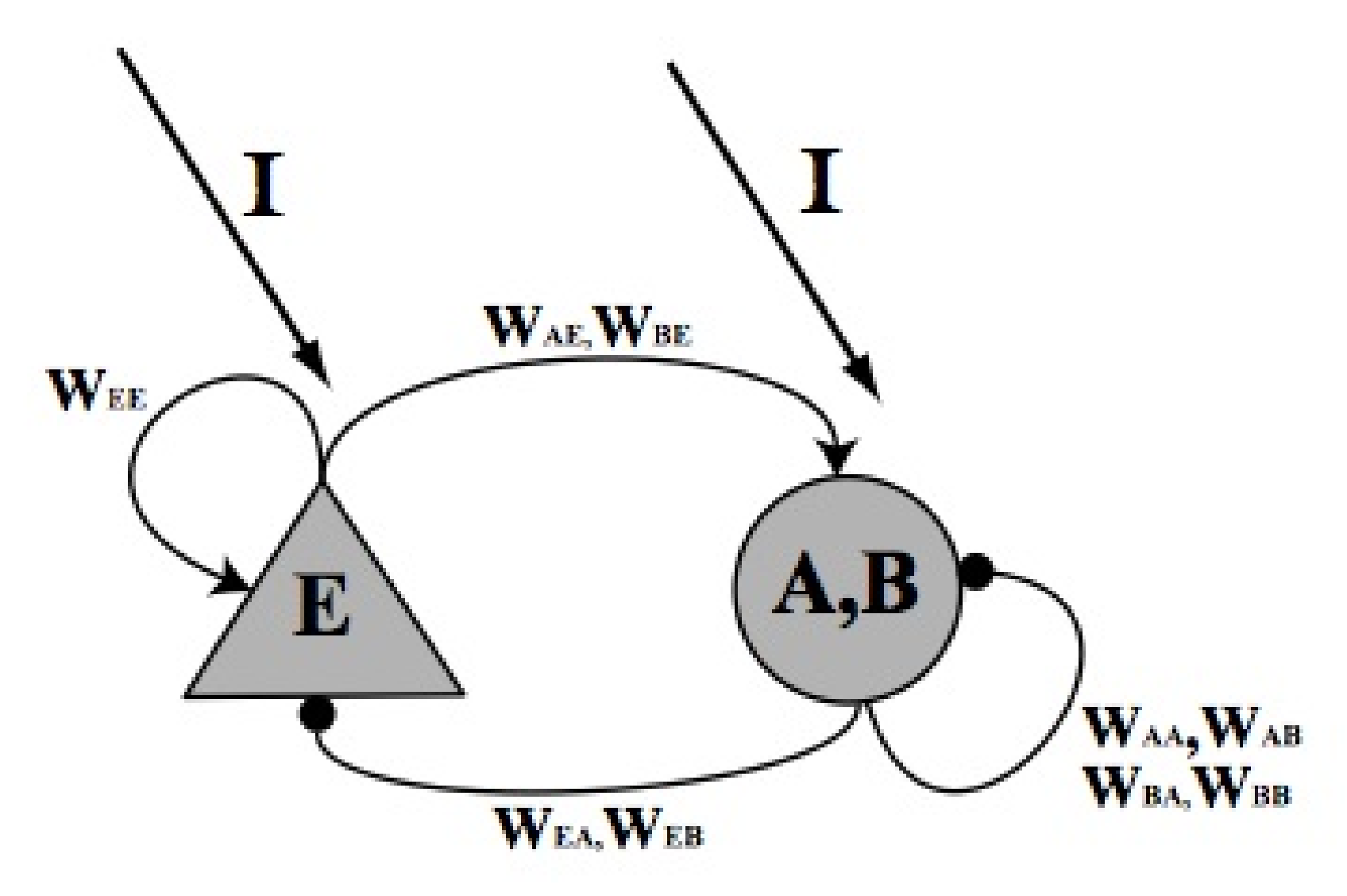
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heifets, B.D.; Castillo, P.E. Endocannabinoid signaling and long-term synaptic plasticity. Annu. Rev. Physiol. 2009, 71, 283–306. [Google Scholar] [CrossRef]
- Ohno-Shosaku, T.; Maejima, T.; Kano, M. Endogenous Cannabinoids Mediate Retrograde Signals from Depolarized Postsynaptic Neurons to Presynaptic Terminals. Neuron 2001, 29, 729–738. [Google Scholar] [CrossRef]
- Wilson, R.I.; Nicoll, R.A. Endogenous cannabinoids mediate retrograde signaling at hippocampal synapses. Nature 2001, 410. [Google Scholar] [CrossRef]
- Zachariou, M.; Alexander, S.P.H.; Coombes, S.; Christodoulou, C. A Biophysical Model of Endocannabinoid-Mediated Short Term Depression in Hippocampal Inhibition. PLoS ONE 2013, 8, e58926. [Google Scholar] [CrossRef]
- Dissanayake, D.W.N.; Zachariou, M.; Marsden, C.A.; Mason, R. Abolition of sensory gating by the cannabinoid WIN55, 212-2 in the rat hippocampus. Psychpharmacol. J. 2006, 20, A45. [Google Scholar]
- Zachariou, M.; Dissanayake, D.W.N.; Owen, M.R.; Mason, R.; Coombes, S. The role of cannabinoids in the neurobiology of sensory gating: A firing rate model study. Neurocomputing 2007, 70, 1902–1906. [Google Scholar] [CrossRef]
- Wilson, H.R.; Cowan, J.D. Excitatory and Inhibitory interactions in localized populations of model neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef]
- Bianchi, D.; Marasco, A.; Limongiello, A.; Marchetti, C.; Marie, H.; Tirozzi, B.; Migliore, M. On the mechanisms underlying the depolarization block in the spiking dynamics of CA1 pyramidal neurons. J. Comput. Neurosci. 2012, 33, 207–225. [Google Scholar] [CrossRef]
- Dovzhenok, A.; Kutznetzov, A.S. Exploring neuronal bistability at the depolarization block. PLoS ONE 2012, 7, e42811. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hebb, D.O. The Organization of Behavior; Wiley Interscience: New York, NY, USA, 1949. [Google Scholar]
- Marr, D. Simple memory: A theory of archicortex. Philos. Trans. R. Soc. London B 1971, 262, 23–81. [Google Scholar]
- Bliss, T.; Lomø, T. Long-lasting potentiation of synaptic transmission in the dentate gyrus of the anesthetized rabbit following stimulation of the perforant path. J. Phys. 1973, 232, 331–356. [Google Scholar]
- Larimer, P.; Strowbridge, B.W. Representing information in cell assemblies: Persistent activity mediated by semilunar granule cells. Nat. Neurosci. 2009, 13, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Aimone, J.B.; Gage, F.H. New neurons and new memories: How does adult hippocampal neurogenesis affect learning and memory? Nat. Rev. Neurosci. 2010, 11, 339–350. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.B.; Todorova, M. Asynchronous release of GABA via tonic cannabinoid receptor activation at identified interneuron synapses in rat CA1. Eur. J. Neurosci. 2010, 31, 1196–1207. [Google Scholar] [CrossRef] [PubMed]
- Wikipedia Endocannabinoid System. Available online: https://en.wikipedia.org/wiki/Endocannabinoid_system (accessed on 4 October 2020).
- Gederman, G.L.; Ronesi, J.; Lovinger, D.M. Postsynaptic endocannabinoid release is critical to long- term depression in striatum. Nat. Neurosci. 2002, 5, 446–451. [Google Scholar]
- Pertwee, R.G. Cannabinoid receptors and pain. Prog. Neurobiol. 2001, 63, 569–611. [Google Scholar] [CrossRef]
- Hampson, R.E.; Deadwyler, S.A. Cannabinoids, hippocampal function and memory. Life Sci. 1999, 65, 715–723. [Google Scholar] [CrossRef]
- Hines, M.L.; Carnevale, N.T. The NEURON Simulation Environment in the Handbook of Brain Theory and Neural Networks, 2nd ed.; MIT Press: Cambridge, UK, 2003; pp. 769–773. [Google Scholar]

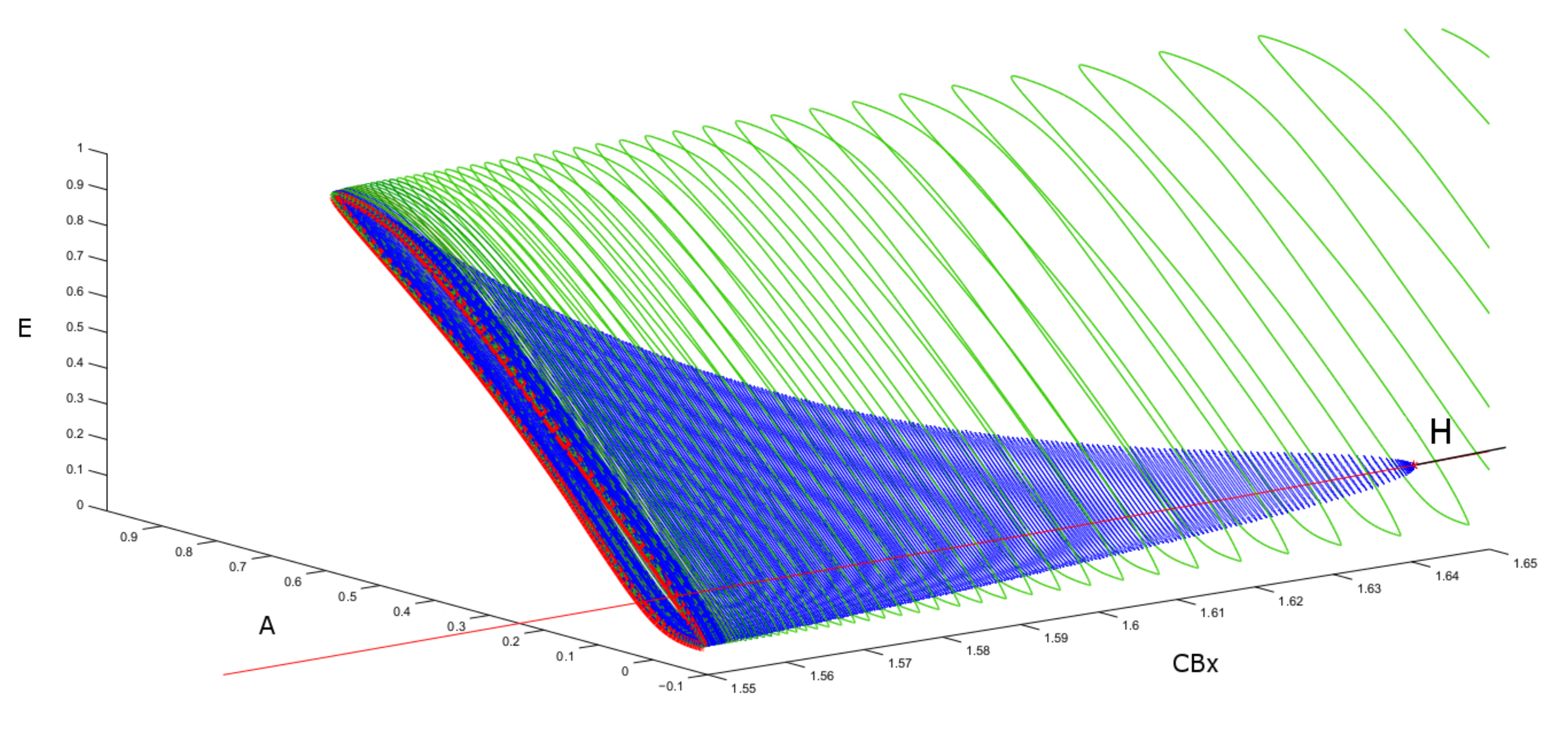
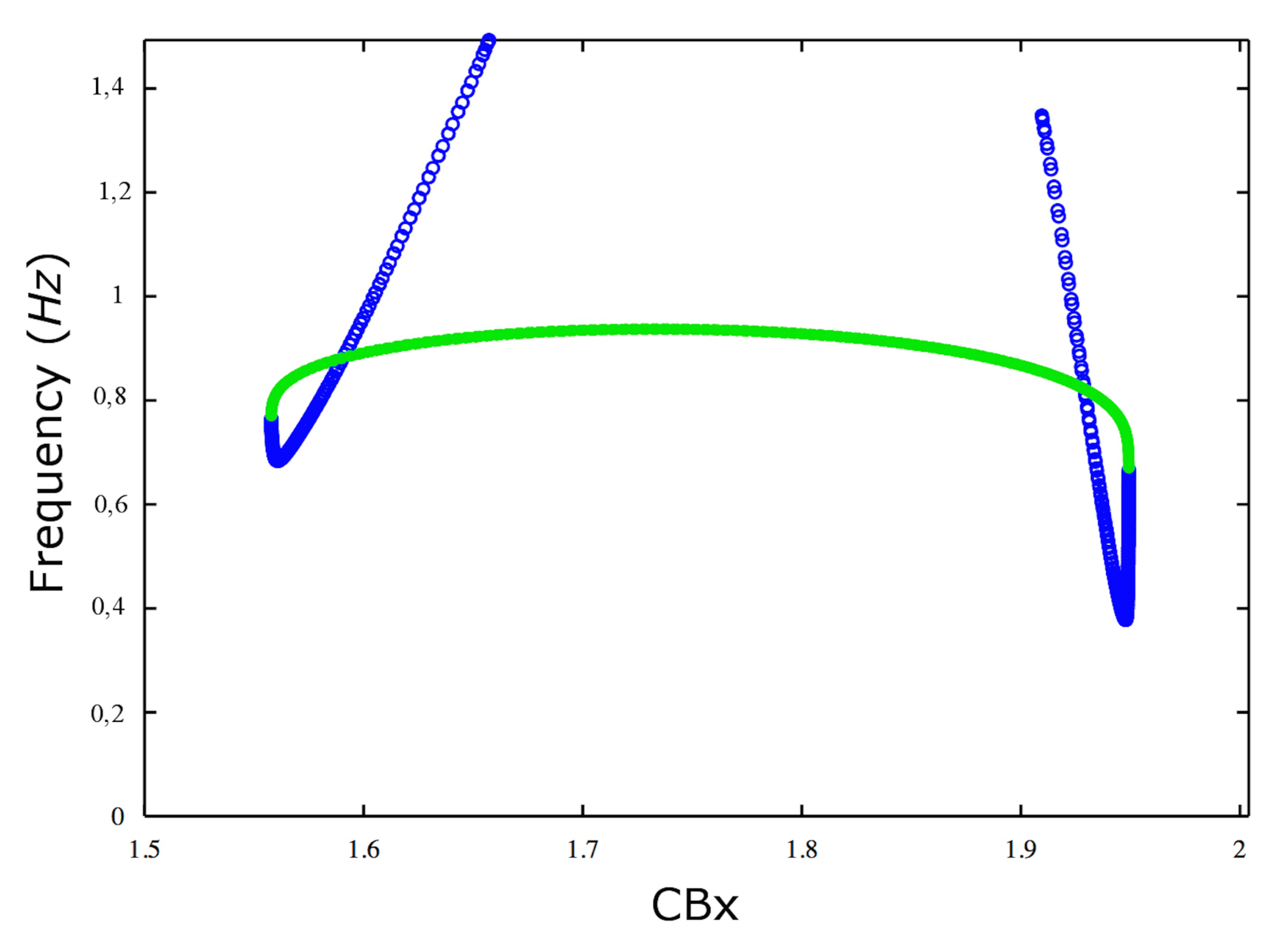
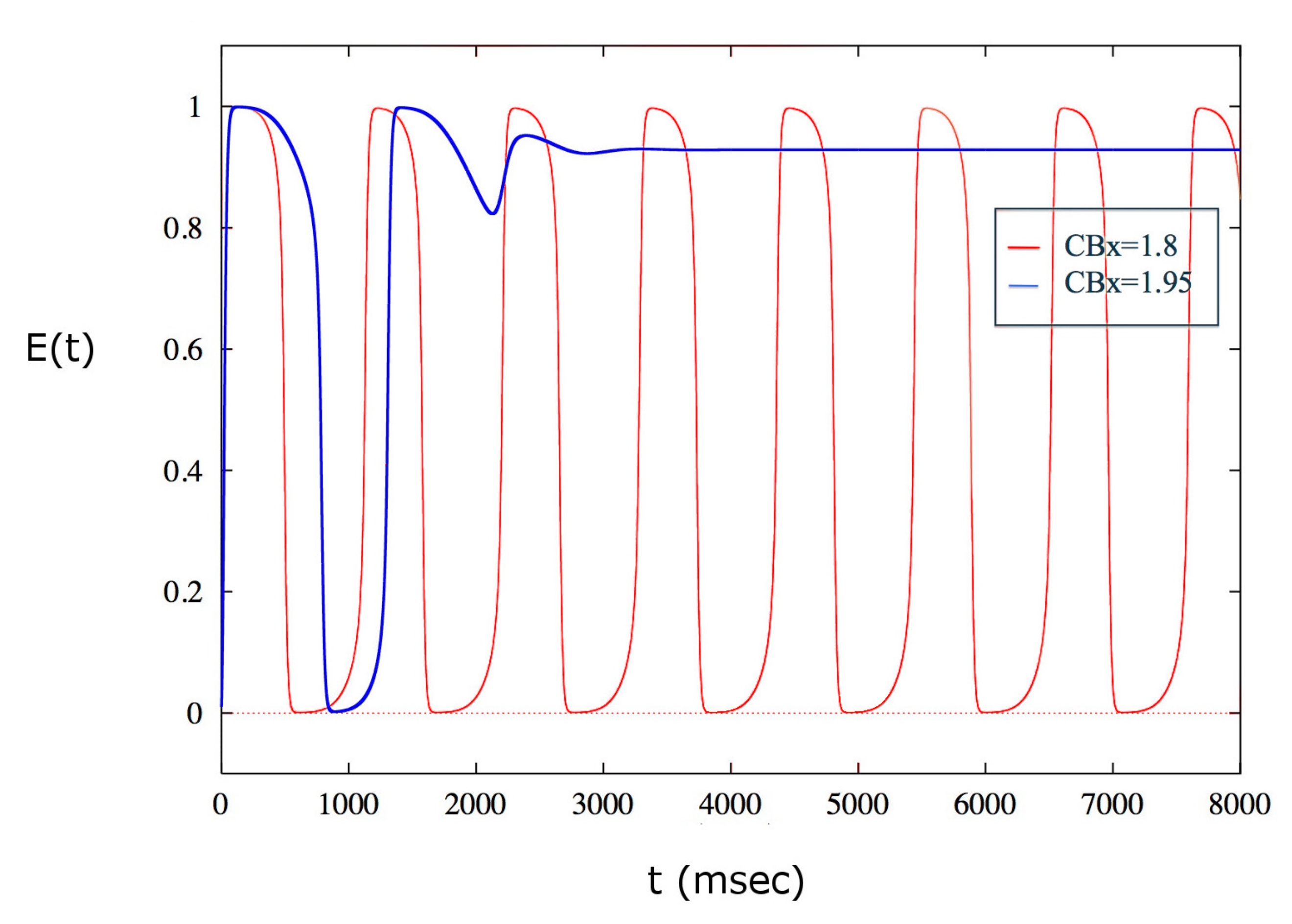
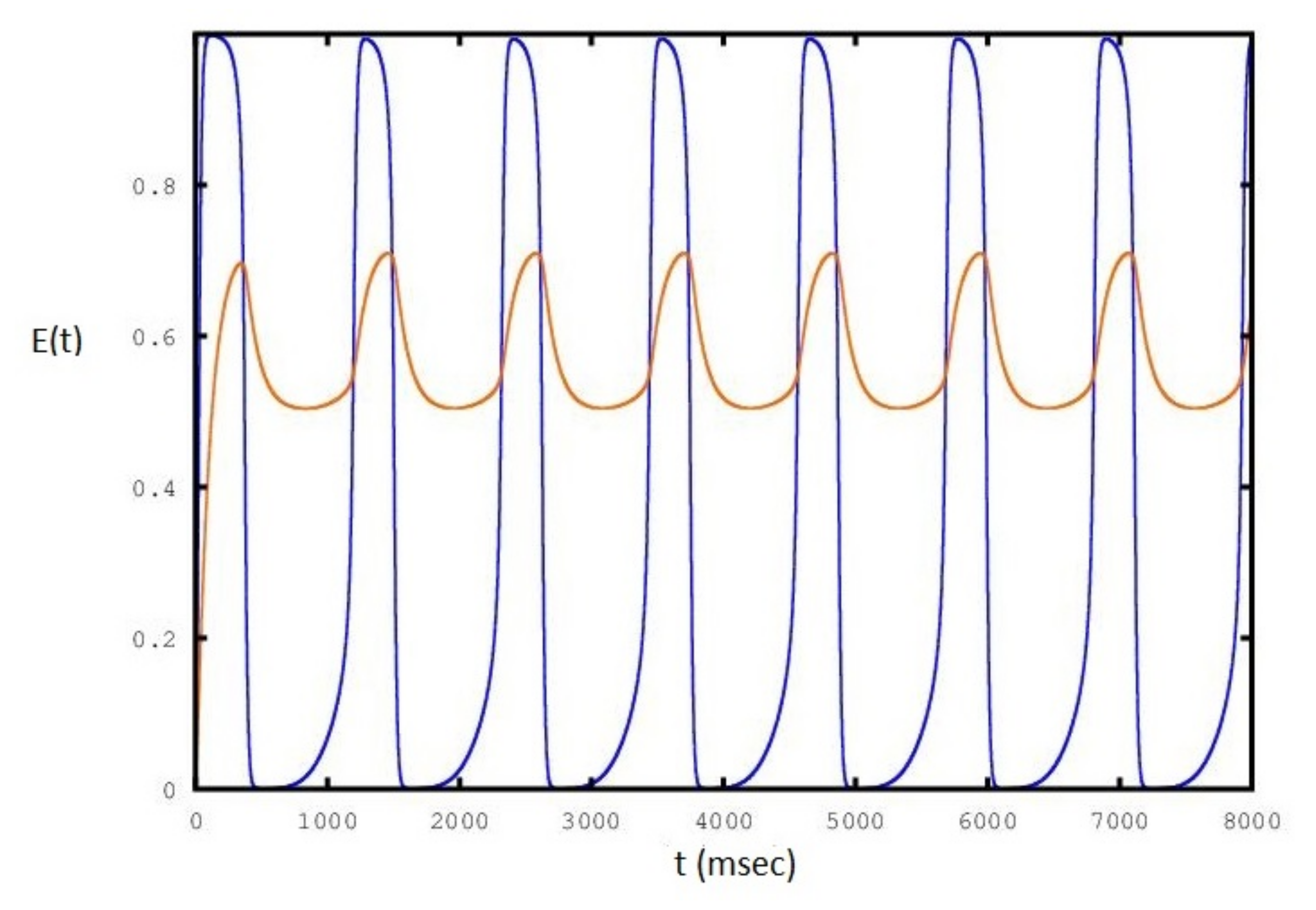
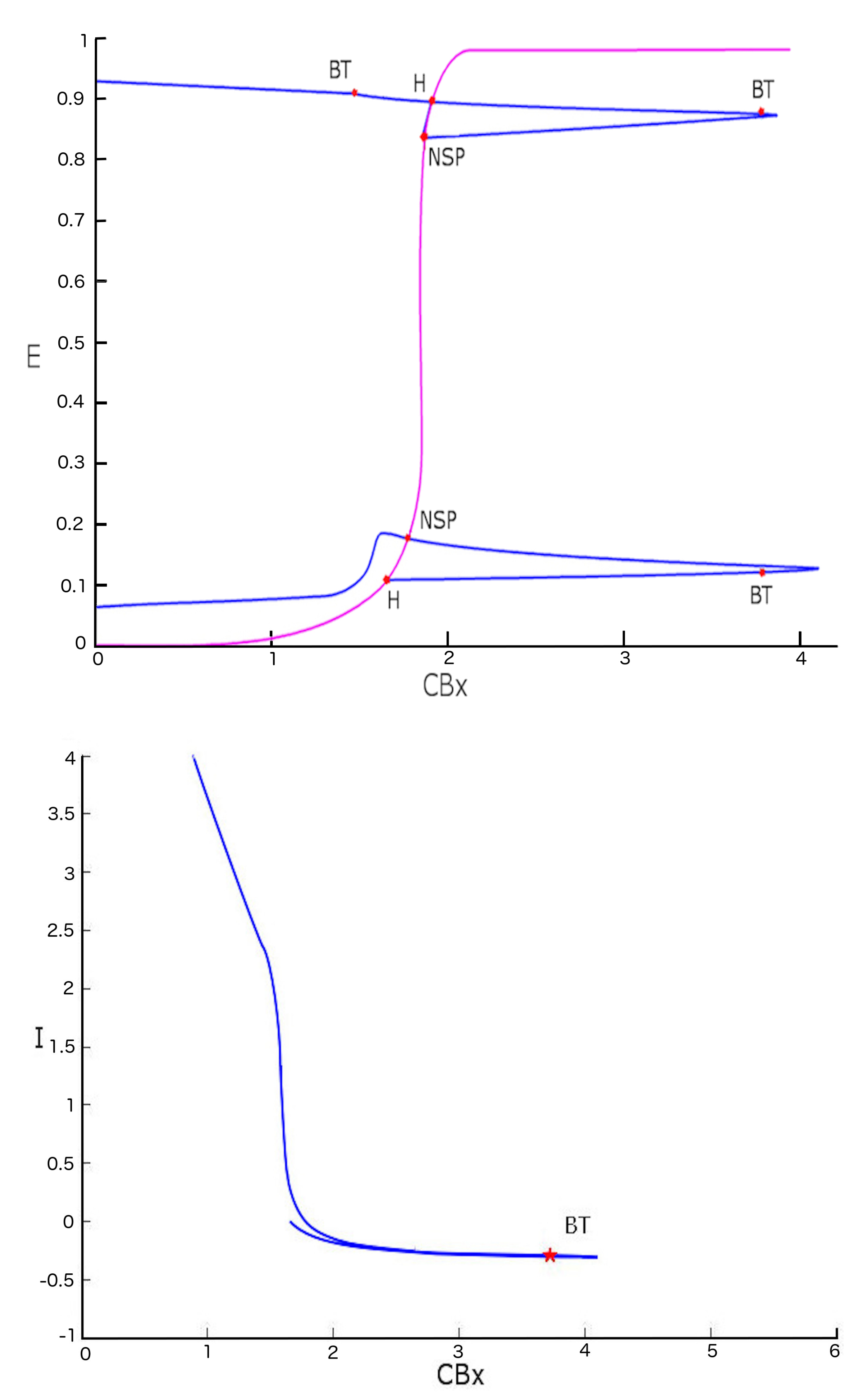
| Label | E | A | B | CBx | I | First Lyapunov Coefficient |
|---|---|---|---|---|---|---|
| LPC | 0.9860651 | 0.6967288 | 0.7902171 | 1.557807 | 0 | |
| H | 0.108009 | 0.143380 | 0.143380 | 1.657289 | 0 | 6.530075 × 10 |
| NSP | 0.176740 | 0.16826 | 0.168268 | 1.778074 | ||
| NSP | 0.893573 | 0.455675 | 0.455675 | 1.909606 | ||
| H | 0.893573 | 0.455675 | 0.455675 | 1.909606 | 0 | 8.212023 × 10 |
| LPC | 0.9980815 | 0.7236474 | 0.4869734 | 1.950302 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tirozzi, B.; Londei, F.; Gianani, S. Depolarization Block in the Endocannabinoid System of the Hippocampus. NeuroSci 2020, 1, 85-97. https://doi.org/10.3390/neurosci1020008
Tirozzi B, Londei F, Gianani S. Depolarization Block in the Endocannabinoid System of the Hippocampus. NeuroSci. 2020; 1(2):85-97. https://doi.org/10.3390/neurosci1020008
Chicago/Turabian StyleTirozzi, Brunello, Fabrizio Londei, and Simona Gianani. 2020. "Depolarization Block in the Endocannabinoid System of the Hippocampus" NeuroSci 1, no. 2: 85-97. https://doi.org/10.3390/neurosci1020008
APA StyleTirozzi, B., Londei, F., & Gianani, S. (2020). Depolarization Block in the Endocannabinoid System of the Hippocampus. NeuroSci, 1(2), 85-97. https://doi.org/10.3390/neurosci1020008






