Statistical Properties in Jazz Improvisation Underline Individuality of Musical Representation
Abstract
1. Introduction
1.1. Statistical Learning: A Mathematical Model of a Learning System in the Brain
1.2. Corpus Study in Music: Classical and Jazz Music
1.3. Computational Modeling of Musical Improvisation
1.4. Study Purpose
2. Study 1
2.1. Methods
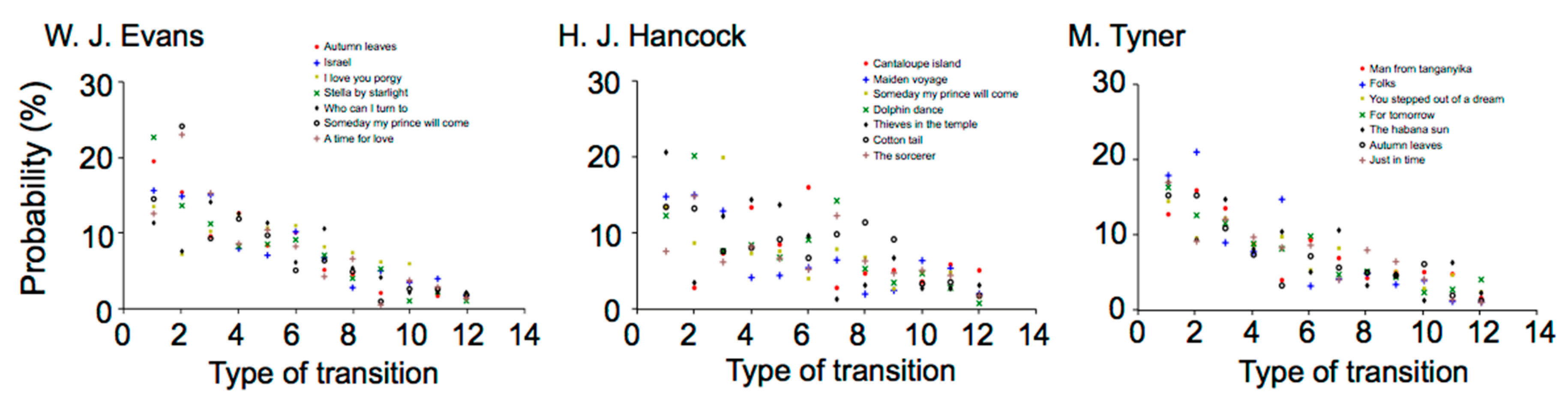
2.2. Results
2.2.1. Time-Course Variation in Musical Improvisation
W. J. Evans
H. J. Hancock
M. Tyner
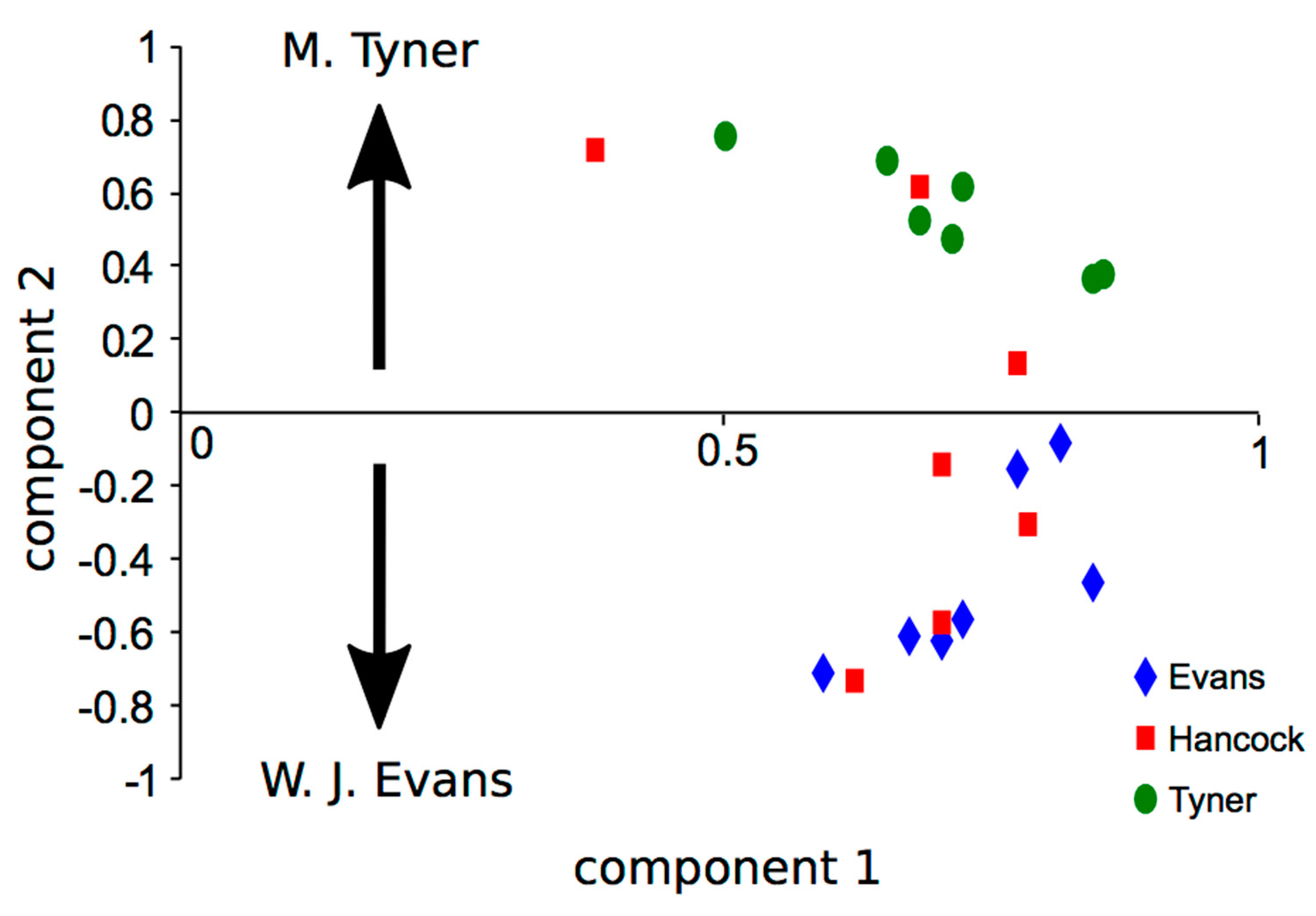
2.2.2. Difference in Statistical Characteristics between Pieces of Music and between Musicians
2.3. Discussion
2.3.1. Time-Course Variation of Statistics in Musical Representation
2.3.2. Statistical Characteristics that Depend on Music and Musician
2.3.3. Improvisation
3. Study 2
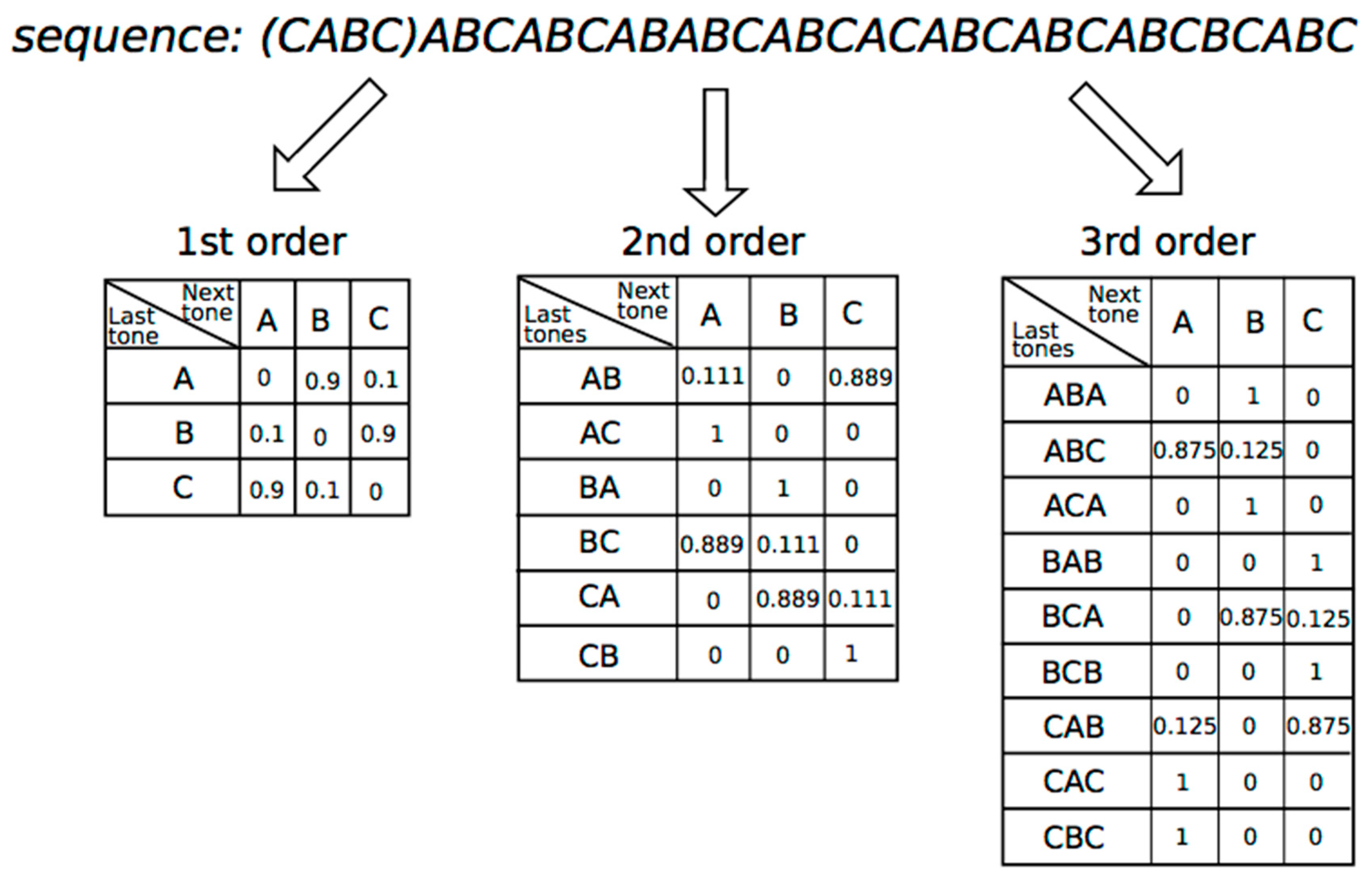
3.1. Methods
3.2. Results
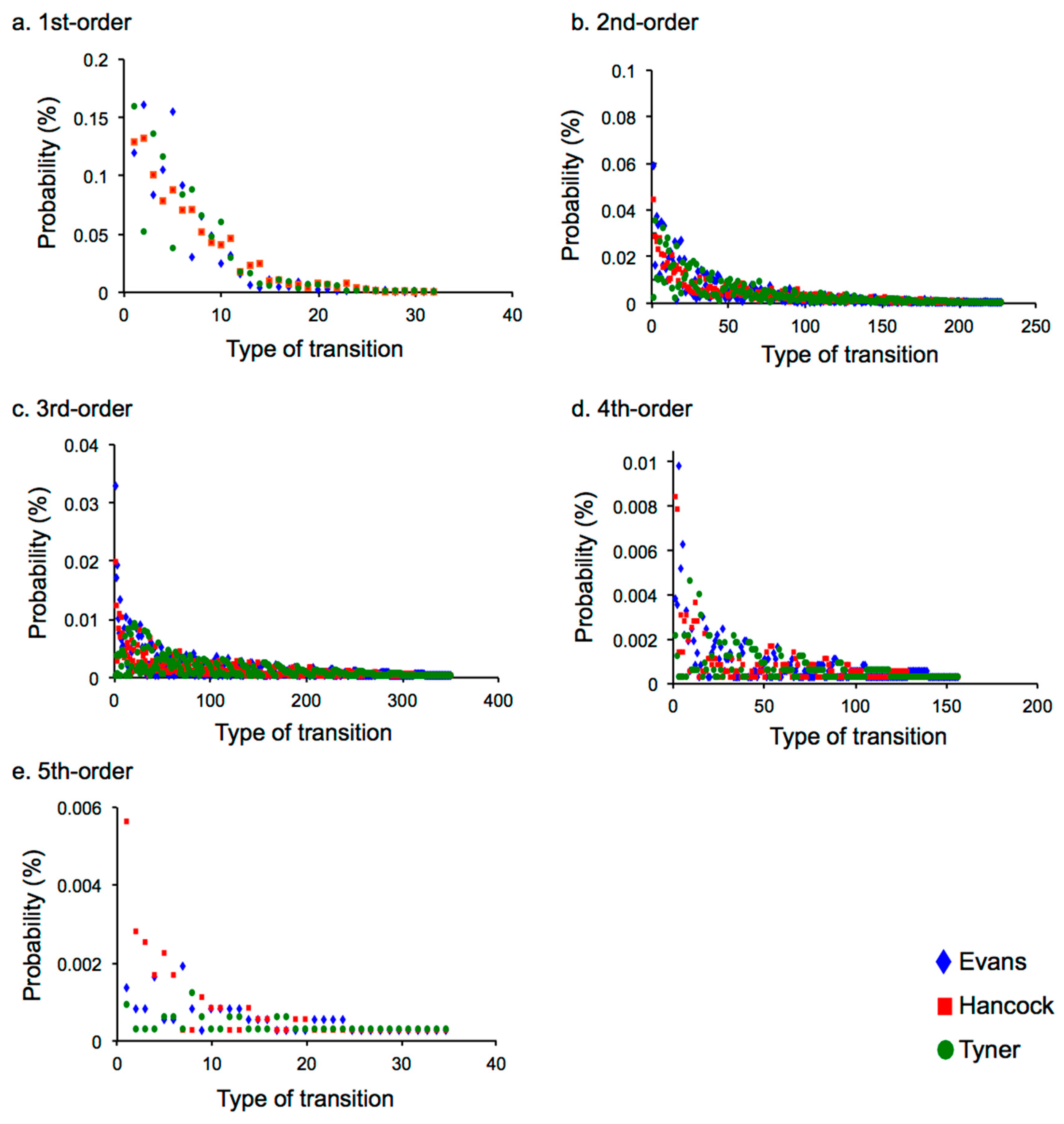
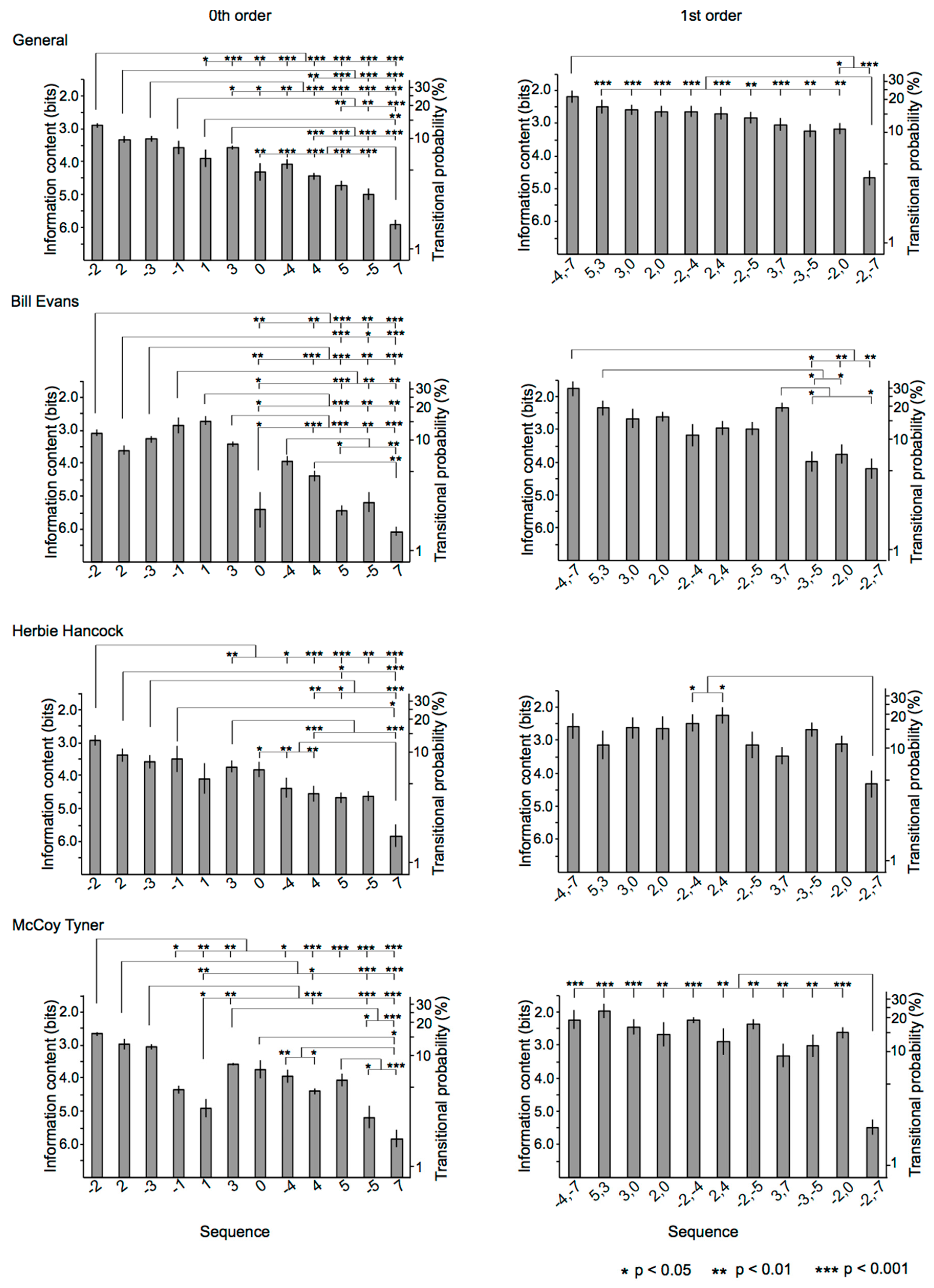
3.2.1. 0th-Order Markov Model
3.2.2. First-Order Markov Model
3.3. Discussion
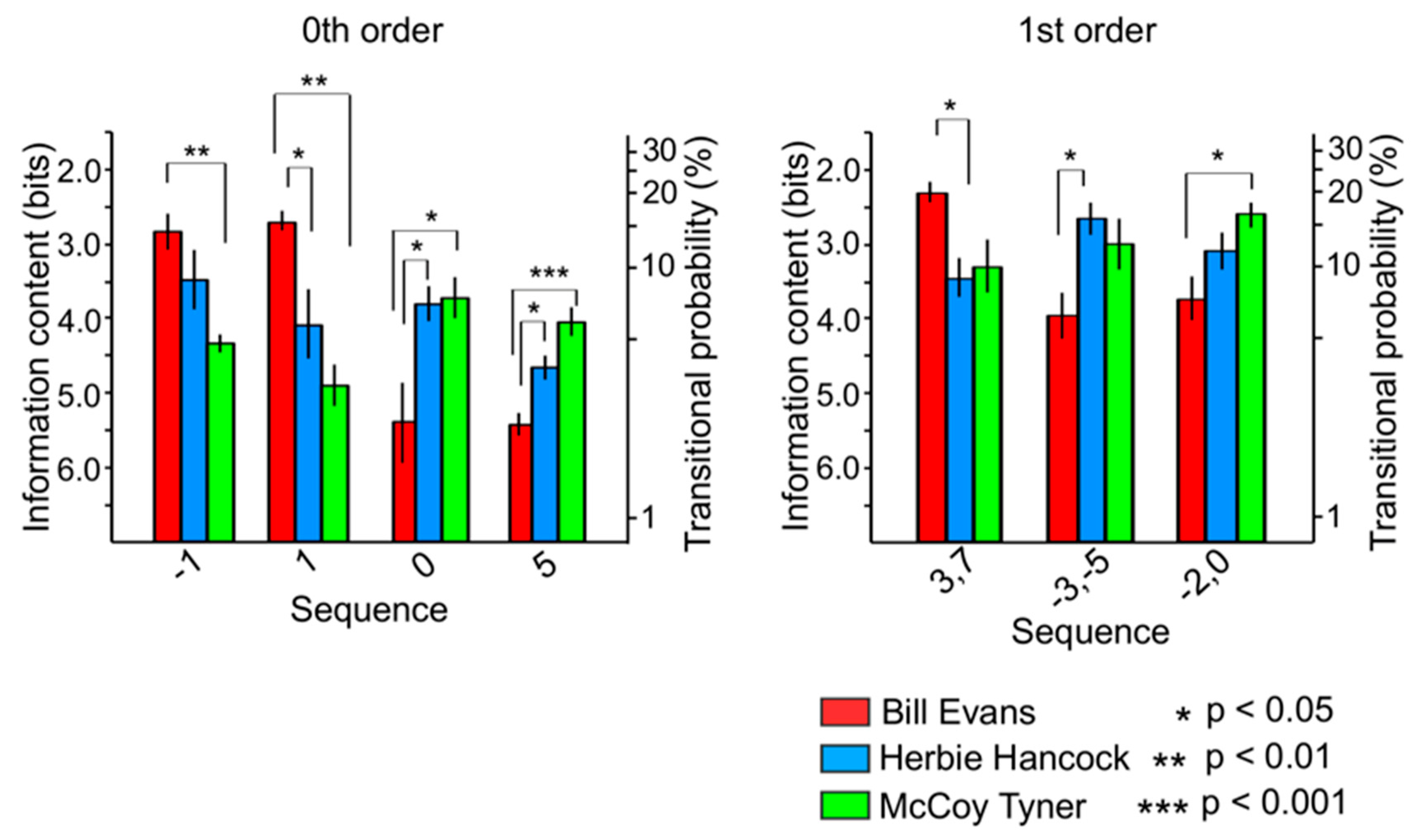
3.3.1. Relationships among Sequences
3.3.2. Relationships among Improvisers
3.3.3. Statistical Learning in Psychological and Computational Studies
4. Conclusions
Supplementary Materials
Funding
Acknowledgments
Additional Information
Conflicts of Interest
References
- Perruchet, P.; Pacton, S. Implicit learning and statistical learning: one phenomenon, two approaches. Trends Cogn. Sci. 2006, 10, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Saffran, J.R.; Aslin, R.N.; Newport, E.L. Statistical learning by 8-month-old infants. Science 1996, 274, 1926–1928. [Google Scholar] [CrossRef] [PubMed]
- Cleeremans, A.; Destrebecqz, A.; Boyer, M. Implicit learning: News from the front. Trends Cogn. Sci. 1998, 2, 406–416. [Google Scholar] [CrossRef]
- Teinonen, T.; Fellman, V.; Näätänen, R.; Alku, P.; Huotilainen, M. Statistical language learning in neonates revealed by event-related brain potentials. BMC Neurosci. 2009, 10. [Google Scholar] [CrossRef] [PubMed]
- Kudo, N.; Nonaka, Y.; Mizuno, N.; Mizuno, K.; Okanoya, K. On-line statistical segmentation of a non-speech auditory stream in neonates as demonstrated by event-related brain potentials. Dev. Sci. 2011, 5, 1100–1106. [Google Scholar] [CrossRef] [PubMed]
- Furl, N.; Kumar, S.; Alter, K.; Durrant, S.; Shawe-Taylor, J.; Griffiths, T.D. Neural prediction of higher-order auditory sequence statistics. NeuroImage 2011, 54, 2267–2277. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T.; Yatomi, Y.; Yumoto, M. Statistical learning of music- and language-like sequences and tolerance for spectral shifts. Neurobiol. Learn. Mem. 2015, 118, 8–19. [Google Scholar] [CrossRef]
- Daikoku, T.; Yatomi, Y.; Yumoto, M. Implicit and explicit statistical learning of tone sequences across spectral shifts. Neuropsychologia 2014, 63. [Google Scholar] [CrossRef]
- Daikoku, T.; Yatomi, Y.; Yumoto, M. Pitch-class distribution modulates the statistical learning of atonal chord sequences. Brain Cogn. 2016, 108. [Google Scholar] [CrossRef]
- Daikoku, T.; Yumoto, M. Single, but not dual, attention facilitates statistical learning of two concurrent auditory sequences. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Daikoku, T.; Yumoto, M. Concurrent statistical learning of ignored and attended sound sequences: An MEG study. Front. Hum. Neurosci. 2019. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T.; Yatomi, Y.; Yumoto, M. Statistical learning of an auditory sequence and reorganization of acquired knowledge: A time course of word segmentation and ordering. Neuropsychologia 2017, 95, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Koelsch, S.; Busch, T.; Jentschke, S.; Rohrmeier, M. Under the hood of statistical learning: A statistical MMN reflects the magnitude of transitional probabilities in auditory sequences. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T. Tonality Tunes the Statistical Characteristics in Music: Computational Approaches on Statistical Learning. Front. Comput. Neurosci. 2019, 13, 70. [Google Scholar] [CrossRef]
- Daikoku, T. Statistical learning and the uncertainty of melody and bass line in music. PLoS ONE 2019, 14, e0226734. [Google Scholar] [CrossRef]
- Daikoku, T. Time-course variation of statistics embedded in music: Corpus study on implicit learning and knowledge. PLoS ONE 2018, 13, e0196493. [Google Scholar] [CrossRef]
- Boenn, G.; Brain, M.; De Vos, M.; Ffitch, J. Automatic Composition of Melodic and Harmonic Music by Answer Set Programming BT. In Logic Programming; Garcia de la Banda, M., Pontelli, E., Eds.; Springer: Heidelberg, German, 2008; pp. 160–174. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Pearce, M.T.; Wiggins, G.A. Auditory Expectation: The Information Dynamics of Music Perception and Cognition. Top. Cogn. Sci. 2012, 4, 625–652. [Google Scholar] [CrossRef]
- Pearce, M.; Wiggins, G. Expectation in melody: The Influence of Context and Learning. Music Percept. 2006, 23, 377–405. [Google Scholar] [CrossRef]
- Pearce, M.T.; Ruiz, M.H.; Kapasi, S.; Wiggins, G.A.; Bhattacharya, J. Unsupervised statistical learning underpins computational, behavioural, and neural manifestations of musical expectation. NeuroImage 2010, 50, 302–313. [Google Scholar] [CrossRef]
- Omigie, D.; Pearce, M.T.; Stewart, L. Tracking of pitch probabilities in congenital amusia. Neuropsychologia 2012, 50, 1483–1493. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.C.; Pearce, M.T. Predictive uncertainty in auditory sequence processing. Front. Psychol. 2014, 5, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T. Depth and the Uncertainty of Statistical Knowledge on Musical Creativity Fluctuate Over a Composer’s Lifetime. Front. Comput. Neurosci. 2019, 13, 27. [Google Scholar] [PubMed]
- Daikoku, T. Method and Apparatus for Analyzing Characteristics of Music Information. U.S. Patent US20190189100, 1 October 2019. [Google Scholar]
- Daikoku, T. Implicit learning in the developing brain: An exploration of ERP indices for developmental disorders. Clin. Neurophysiol. 2019, 130, 2166–2168. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T. Computational models and neural bases of statistical learning in music and language: Comment on “Creativity, information, and consciousness: The information dynamics of thinking” by Wiggins. Phys. Life. Rev. 2019. [Google Scholar] [CrossRef]
- Jackendoff, R.; Lerdahl, F. The capacity for music: What is it, and what’s special about it? Cognition 2006, 100, 33–72. [Google Scholar] [CrossRef]
- Hauser, M.D.; Chomsky, N.; Fitch, W.T. The Faculty of Language: What Is It, Who Has It, and How Did It Evolve? Science 2002, 298, 1569 LP-1579. [Google Scholar] [CrossRef]
- Clark, R.E.; Squire, L.R. Classical Conditioning and Brain Systems: The Role of Awareness. Science 1998, 280, 77–81. [Google Scholar] [CrossRef]
- De Jong, N. Learning Second Language Grammar by Listening. Ph.D. Thesis, Netherlands Graduate School of Linguistics, Amsterdam, The Netherlands, 2005. [Google Scholar] [CrossRef]
- Ellis, R. Implicitand Explicit Learning, Knowledge and Instruction. In Implicit and Explicit Knowledge in Second Language Learning, Testing and Teaching; Ellis, R., Loewen, S., Elder, C., Erlam, R., Philip, J., Reinders, H., Eds.; Multilingual Matters: Bristol, UK, 2009; pp. 3–25. [Google Scholar] [CrossRef]
- Paradis, M. A Neurolinguistic Theory of Bilingualism; John Benjamins: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Berry, D.; Dienes, Z. Implicit Learning: Theoretical and Empirical Issues; Lawrence Erlbaum: Hove, UK, 1993. [Google Scholar]
- Reber, A.S. Implicit Learning and Tacit Knowledge: An Essay on the Cognitive Unconscious; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Perkovic, S.; Orquin, J.L. Implicit Statistical Learning in Real-World Environments Leads to Ecologically Rational Decision Making. Psychol. Sci. 2017, 29, 34–44. [Google Scholar] [CrossRef]
- Egermann, H.; Pearce, M.T.; Wiggins, G.A.; McAdams, S. Probabilistic models of expectation violation predict psychophysiological emotional responses to live concert music. Cogn. Affect. Behav. Neurosci. 2013, 13, 533–553. [Google Scholar] [CrossRef]
- Pearce, M.T.; Müllensiefen, D.; Wiggins, G.A. The Role of Expectation and Probabilistic Learning in Auditory Boundary Perception: A Model Comparison. Perception 2010, 39, 1367–1391. [Google Scholar] [CrossRef] [PubMed]
- Zioga, I.; Harrison, P.M.C.; Pearce, M.T.; Bhattacharya, J.; Di Bernardi Luft, C. From learning to creativity: Identifying the behavioural and neural correlates of learning to predict human judgements of musical creativity. NeuroImage 2019, 206, 116311. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T. Entropy, Uncertainty, and the Depth of Implicit Knowledge on Musical Creativity: Computational Study of Improvisation in Melody and Rhythm. Front. Comput. Neurosci. 2018, 12, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T. Musical Creativity and Depth of Implicit Knowledge: Spectral and Temporal Individualities in Improvisation. Front Comput. Neurosci. 2018, 12, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Raphael, C.; Stoddard, J. Functional Harmonic Analysis Using Probabilistic Models. Comput. Music J. 2004, 28, 45–52. [Google Scholar] [CrossRef]
- Eigenfield, A.; Pasquier, P. Realtime Generation of Harmonic Progressions Using Controlled Markov Selection. Available online: http://metacreation.net/wp-content/uploads/2014/09/Controlled_Markov_Selection_2010.pdf (accessed on 20 September 2020).
- Olshausen, B.A.; Field, D.J. Sparse coding of sensory inputs. Curr. Opin. Neurobiol. 2004, 14, 481–487. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T. Neurophysiological markers of statistical learning in music and language: Hierarchy, entropy, and uncertainty. Brain Sci. 2018, 8, 114. [Google Scholar] [CrossRef]
- Yumoto, M.; Daikoku, T. Neurophysiological Studies on Auditory Statistical Learning (in Japanese). Jpn. J. Cogn. Neurosci. 2018, 20, 38–43. [Google Scholar]
- Daikoku, T.; Yumoto, M. Musical Expertise Facilitates Statistical Learning of Rhythm and the Perceptive Uncertainty: A cross-cultural Study. Neuropsychologia 2020, 146, 107553. [Google Scholar] [CrossRef]
- Daikoku, T.; Ogura, H.; Watanabe, M. The variation of hemodynamics relative to listening to consonance or dissonance during chord progression. Neurological Res. 2012, 34, 557–563. [Google Scholar] [CrossRef]
- Conklin, D.; Witten, I.H. Multiple viewpoint systems for music prediction. J. New Music. Res. 1995, 24, 51–73. [Google Scholar] [CrossRef]
- Daikoku, T.; Takahashi, Y.; Futagami, H.; Tarumoto, M.; Yasuda, H. Physical fitness modulates incidental but not intentional statistical learning of simultaneous auditory sequences during concurrent physical exercise. Neurol. Res. 2017, 30, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Daikoku, T.; Takahashi, Y.; Tarumoto, M.; Yasuda, H. Auditory Statistical Learning During Concurrent Physical Exercise and the Tolerance for Pitch, Tempo, and Rhythm Changes. Motor Control 2018, 22, 233–244. [Google Scholar] [CrossRef] [PubMed]

| Improvisors | Titles |
|---|---|
| W. J. Evans | Autumn Leaves from Portrait in Jazz, 1959 |
| Israel from Explorations, February 1961 | |
| I Love You Porgy from Waltz for Debby, June 1961 | |
| Stella by Starlight from Conversations with Myself, 1963 | |
| Who Can I Turn To from Bill Evans at Town Hall, 1966 | |
| Some Day My Prince Will Come from the Montreux Jazz Festival, 1968 | |
| A Time for Love from Alone, 1969 | |
| H. J. Hancock | Cantaloupe Island from Empyrean Isles, 1964 |
| Maiden Voyage from Flood, 1975 | |
| Some Day My Prince Will Come from The Piano, 1978 | |
| Dolphin Dance from Herbie Hancock Trio ’81, 1981 | |
| Thieves in the Temple from The New Standard, 1996 | |
| Cotton Tail from Gershwin’s World, 1998 | |
| The Sorcerer from Directions in Music, 2001 | |
| M. Tyner | Man from Tanganyika from Tender Moments, 1967 |
| Folks from Echoes of a Friend, 1972 | |
| You Stepped Out of a Dream from Fly with the Wind, 1976 | |
| For Tomorrow from Inner Voice; 1977 | |
| The Habana Sun from The Legend of the Hour, 1981 | |
| Autumn Leaves from Revelations, 1988 | |
| Just in Time from Dimensions from Dimensions, 1984 |
| a. W. J. Evans | |||||||||||
| Model 1 | Model 2 | ||||||||||
| Hierarchy | Variable | B | SE B | β | VIF | CI | B | SE B | β | VIF | CI |
| Third | 0,2,3,5 | −171.28 | 66.20 | −0.76 * | 1.00 | 4.08 | −144.06 | 42.75 | −0.64 * | 1.05 | 3.33 |
| 0,−3,−4,−6 | 627.99 | 214.37 | 0.55 * | 1.05 | 6.85 | ||||||
| R2 | 0.49 | 0.80 | |||||||||
| F | 6.69 * | 12.71 * | |||||||||
| Forth | 0,1,3,4,6 | −317.34 | 97.30 | −0.83 * | 1.00 | 3.92 | |||||
| R2 | 0.62 | ||||||||||
| F | 10.64 * | ||||||||||
| b. M. Tyner | |||||||||||
| Model 1 | Model 2 | ||||||||||
| Hierarchy | Variable | B | SE B | β | VIF | CI | B | SE B | β | VIF | CI |
| Second | 0,−2,−5 | 172.15 | 38.79 | 0.89 ** | 1.00 | 6.37 | 191.08 | 20.78 | 0.99 ** | 1.06 | 5.51 |
| 0,5.7 | −485.35 | 127.57 | −0.41 * | 1.06 | 7.89 | ||||||
| R2 | 0.76 | 0.93 | |||||||||
| F | 19.70 ** | 43.63 ** | |||||||||
| a Eigenvalue, percentages of variance and cumulative variance. | ||||||||
| Total | Variance * | Cumulative * | ||||||
| Component 1 | 10.79 | 51.40 | 51.40 | Component 1 | ||||
| Component 2 | 5.91 | 28.15 | 79.55 | Component 2 | ||||
| Component 3 | 1.37 | 6.52 | 86.07 | Component 3 | ||||
| Component 4 | 1.21 | 5.76 | 91.84 | Component 4 | ||||
| b. Eigenvectors for the principal components | ||||||||
| Component 1 | Component 2 | Component 3 | Component 4 | |||||
| W. J. Evans | Autumn leaves | 0.71 | −0.62 | 0.09 | −0.18 | |||
| Israel | 0.85 | −0.46 | −0.12 | 0.02 | ||||
| I Love You Porgy | 0.78 | −0.15 | 0.34 | −0.39 | ||||
| Stella by Starlight | 0.68 | −0.61 | 0.12 | −0.16 | ||||
| Who Can I Turn To | 0.82 | −0.08 | 0.52 | −0.12 | ||||
| Some Day My Prince Will Come | 0.60 | −0.71 | 0.07 | 0.19 | ||||
| A Time for Love | 0.73 | −0.56 | −0.12 | 0.20 | ||||
| H. J. Hancock | Cantaloupe Island | 0.39 | 0.72 | 0.24 | 0.38 | |||
| Maiden Voyage | 0.71 | −0.14 | −0.64 | 0.23 | ||||
| Some Day My Prince Will Come | 0.78 | 0.14 | −0.47 | −0.38 | ||||
| Dolphin Dance | 0.71 | −0.57 | −0.11 | 0.34 | ||||
| Thieves in the Temple | 0.69 | 0.62 | 0.12 | 0.12 | ||||
| Cotton Tail | 0.79 | −0.30 | 0.21 | 0.13 | ||||
| The Sorcerer | 0.63 | −0.73 | 0.01 | 0.15 | ||||
| M. Tyner | Man fromTanganyika | 0.72 | 0.48 | −0.06 | −0.42 | |||
| Folks | 0.69 | 0.53 | −0.32 | −0.01 | ||||
| You Stepped Out of a Dream | 0.66 | 0.69 | 0.03 | 0.23 | ||||
| For Tomorrow | 0.73 | 0.62 | 0.03 | −0.03 | ||||
| The Habana Sun | 0.51 | 0.76 | 0.03 | 0.23 | ||||
| Autumn Leaves | 0.85 | 0.37 | −0.13 | −0.31 | ||||
| Just in Time | 0.86 | 0.38 | 0.20 | 0.18 | ||||
| 0th-Order | 1st-Order |
|---|---|
| 0 | 2,0 |
| 1 | −2,0 |
| −1 | 2,4 |
| 2 | −2,−4 |
| −2 | −2,−5 |
| 3 | −2,−7 |
| −3 | 3,0 |
| 4 | −3,−5 |
| −4 | 3,7 |
| 5 | −4,−7 |
| −5 | 5,3 |
| 7 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daikoku, T. Statistical Properties in Jazz Improvisation Underline Individuality of Musical Representation. NeuroSci 2020, 1, 24-43. https://doi.org/10.3390/neurosci1010004
Daikoku T. Statistical Properties in Jazz Improvisation Underline Individuality of Musical Representation. NeuroSci. 2020; 1(1):24-43. https://doi.org/10.3390/neurosci1010004
Chicago/Turabian StyleDaikoku, Tatsuya. 2020. "Statistical Properties in Jazz Improvisation Underline Individuality of Musical Representation" NeuroSci 1, no. 1: 24-43. https://doi.org/10.3390/neurosci1010004
APA StyleDaikoku, T. (2020). Statistical Properties in Jazz Improvisation Underline Individuality of Musical Representation. NeuroSci, 1(1), 24-43. https://doi.org/10.3390/neurosci1010004




