Revisiting the Spectral Displacement Method for Estimation of the Binding Constants in Systems Involving Multiple Equilibria

Abstract

The old spectral displacement method can be suitably revitalized for a didactic experimental approach to fundamental concepts of supramolecular chemistry and to the study of complex equilibria in general. In particular, the case of the β-cyclodextrin/phenolphthalein/adamantane ternary system has been taken into account as a viable and impressive example due to the remarkable color changes that can be observed when performing the experiments. A new method for data regression analysis is proposed, with a smart trick able to overcome the mathematical difficulties arising whenever multiple equilibria must be considered. Hence, some aspects of the reliability of fitting procedures are discussed.

1. Introduction

After the Nobel Prizes awarded to Cram, Lehn and Pedersen (1987) and to Sauvage, Stoddart and Feringa (2016), interest in supramolecular chemistry has undergone a burst among researchers in different fields of molecular sciences, and among teachers as well. Supramolecular chemistry can be defined as “the Chemistry of non-covalent interactions”, or even “the chemistry beyond molecules”, focusing on molecular aggregates held together by weak interactions (Coulomb and van der Waals interactions, hydrogen bonding, π-stacking, etc.), on their characterization, properties, and thermodynamic stability. It is important to stress that supramolecular systems play a key role in the development of advanced and sustainable technologies [1,2,3], as accounted for by a massive literature. The development of new industrial separation techniques [4], advanced catalysts [5,6,7], eco-friendly deep-eutectic solvents [8], smart materials [9,10,11], energy materials [12,13], water remediation techniques [14,15], and so on, largely benefits from the concepts and methodologies developed in supramolecular chemistry. Of course, supramolecular systems are complex ones, perfectly aligning with the new paradigms of scientific research, which focus on the concept that complexity generates functionalities that go beyond those of the single counterparts [16]. Approaching the study of a complex system requires a smart mathematical and analytical approach. Therefore, the study of supramolecular systems may offer interesting teaching opportunities, and their implementation in didactics programs, particularly directed to undergraduate students approaching the problem of multiple equilibria treatment, might be highly desirable.

Host–guest complexes, i.e., systems constituted by a large hollow molecule (Host) including a suitably shaped smaller one (Guest), are the simplest and most studied examples of supramolecular systems. Cyclodextrins (CDs) are probably the most representative macromolecules able to act as hosts [17]. They are water-soluble cyclic oligosaccharides (obtained by enzymatic digestion of starch) that constitute of α-glucopyranose units linked by 1,4-glycosidic bridges. The heptameric βCD is the most common commercially available term (Figure 1).

CDs possess a fairly flexible torus-like structure characterized by hydrophilic rims and a hydrophobic cavity; therefore, they can form inclusion complexes with diverse organic molecules and vehicle them into aqueous solution [18,19]. This fact, together with their non-toxic biocompatible nature, has made them molecules of choice for applications in various fields, spanning from pharmaceuticals and drug carrier systems to catalysis, chiral separations, etc. The versatile inclusion abilities, safety, and easy availability of CDs make these macromolecules ideal candidates for a didactic presentation of basic supramolecular chemistry concepts [20], for approaching the experimental study of host–guest systems [21], and even for the presentation of competitive equilibria, which may occur when different guests compete for the same host/receptor.

In order to detect host–guest binding (and evaluate the relevant equilibrium constant K as well), the detection of a significant change in any physical/chemical property of either component is required. Various techniques can be exploited [22], spanning from calorimetry to spectroscopy (UV-Vis, NMR) and chiroptical methods (polarimetry, circular dichroism). From an educational viewpoint, the possibility to observe a visual color change for a UV-Vis absorptive (chromophoric) guest represents a viable opportunity. For instance, a purple-colored solution of phenolphthalein (Php) at pH 11.0 turns outstandingly colorless upon progressive addition of βCD [23]. Suitable regression analysis of the optical absorptivity of the solution (easily determined by UV-Vis spectrophotometry) as a function of the βCD concentration enables estimating the relevant binding constant. Spectrophotometry, of course, cannot be used whenever the interaction with a non-chromophoric guest has to be studied. In this case, techniques able to detect the properties of the host can be useful, such as polarimetry [24,25]. Alternatively, the problem can be approached by exploiting the competition for the host between the non-chromophoric guest and a chromophoric one. For instance, a nearly colorless solution of the Php-βCD complex turns back to purple after the addition of potassium adamantane (Ada), which is able to progressively displace Php and form a very stable complex with βCD (Figure 2) [23]. Again, the binding constant of the new complex can be determined by a suitable regression analysis of the absorbance data as a function of the competitor guest concentration. This procedure is referred to as the “spectral displacement” method, the use of which has been occasionally reported in some old research works [26,27]. However, owing to the occurrence of multiple equilibria, the mathematical issues relevant to data regression analysis are quite complicated. Different authors have proposed various simplified solutions, but their approaches have appeared somewhat unsatisfactory; so, this method has been progressively abandoned. In the present paper, however, we will show that spectral displacement can be suitably revitalized for an educational approach to supramolecular chemistry and to the study of simultaneous equilibria as well, provided that the relevant mathematical problems are re-addressed. In particular, we present here a study of the βCD-Php-Ada ternary system by means of a new method for data regression analysis that overcomes, with a smart trick, the intrinsic difficulties of the exact solution for the multiple-equilibria problem.

2. Materials and Methods

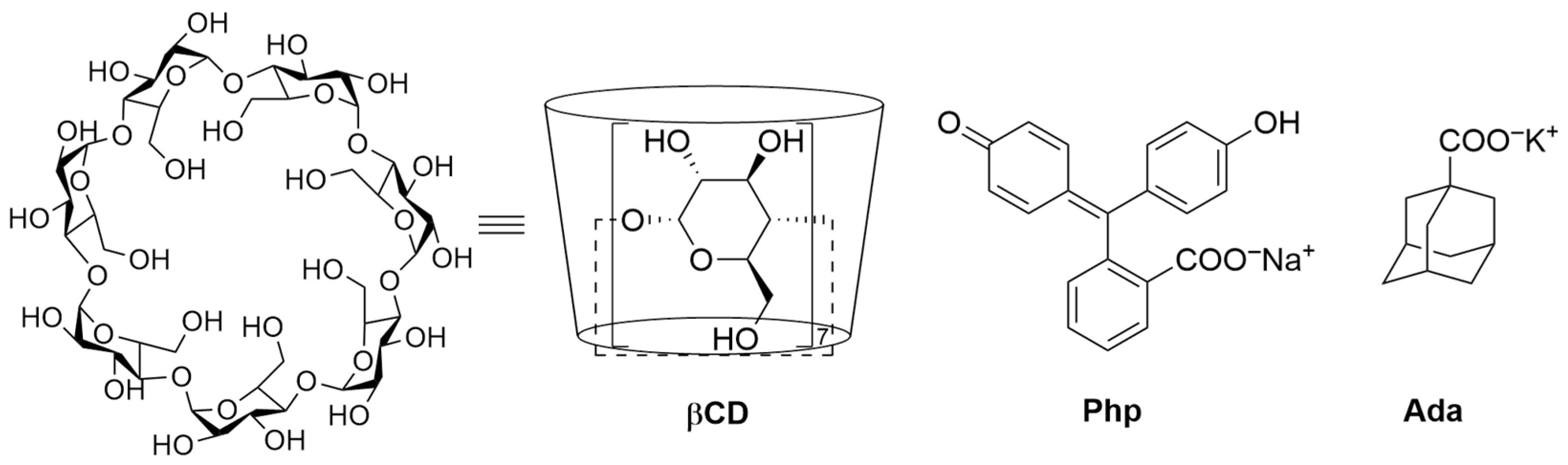
2.1. Materials and Hazard Statements

All the reagent used for the experiments were used as purchased from suppliers (Aldrich, St. Louis, MO, USA; Fluka, Morris Plains, NJ, USA; Carlo Erba, Cornaredo, Italy). K₂CO₃ and βCD were dried overnight on P₂O₅ at 60 °C under vacuum. Ada was prepared by precipitating it from a methanol solution of 1-adamantanecarboxylic acid treated with a methanol solution of KOH; the resulting white powder was filtered off under vacuum and dried. Different stock solutions of Php were freshly prepared and used within a few hours due to the slow degradation of Php in alkaline solution. Stock βCD and Ada solutions were prepared by dissolving the proper weighed amount of the compounds in carbonate buffer. The proper aliquots of the stock solutions were diluted with the buffer to obtain the required measurement samples.

All chemicals used in the experiments should never be consumed outside the laboratory. Proper laboratory clothing, gloves, and glasses must be used, and the chemicals must be handled according to ordinary safety procedures. Sodium hydroxide is a highly corrosive chemical, and contact with skin or eyes can seriously irritate and burn the skin and eyes, with permanent damage possible. Other chemicals, including potassium carbonate, 1-adamantane carboxylic acid, Ada, and Php may cause eye and skin irritation as well. In case of eye or skin contact, wash with plenty of water for at least 15 min.

2.2. Spectrophotometric Measurements

All the spectrophotometric measurements were performed on a Beckman Coulter DU800 instrument equipped with a Peltier thermostatic apparatus (25 °C), using polystyrene cuvettes of 1 cm optic path.

The experiment begins recording the UV-Vis absorption spectra of Php at pH 11.0 (using a carbonate buffer solution as the solvent) and different concentrations ranging up to 60 μM, in order to identify the maximum absorption wavelength (550 nm), verify the validity of Beer–Lambert’s law, and determine the molar extinction coefficient ε_Php. The linearity of the absorbance vs. concentration relationship must be verified, and the data subjected to linear regression analysis. In a second step, the Php-βCD binding constant is determined by measuring the absorbance change in sample solutions containing a fixed concentration of Php and different amounts of βCD. Finally, the Ada-βCD binding constant is determined by measuring the absorbance change in sample solutions with fixed Php and βCD concentrations upon addition of increasing amounts of Ada.

2.3. Concepts and Mathematical Background

2.3.1. Formation of a Single 1:1 Host–Guest Inclusion Complex

Let us consider first the simple system, in which a generic host H interacts with a chromophoric guest G, and forms a 1:1 complex HG only, according to the following equilibrium:

$$\mathrm{H} \mathrm{+} \mathrm{G} \rightleftharpoons \mathrm{H}\mathrm{G}$$

In order to estimate the relevant binding constant (K_G), the preparation of a series of samples, at a fixed analytical concentration G₀ of the guest and increasing analytical concentrations H_i of the host, is required. Then, the equilibrium concentrations are subjected to the conditions given by mass balances and mass action, i.e., G₀ = [G] + [HG], H_i = [H] + [HG] and K_G = [HG]/([H]·[G]). Furthermore, according to Beer–Lambert’s law and under the hypothesis that only the guest is chromophoric, the absorbance of the generic i-th sample (for a unit light path) will be given by the following expression: A_i = ε_G[G] + ε_HG[HG] = ε_GG₀ + (ε_HG − ε_G)[HG], where ε_G and ε_HG are the molar absorptivity of the free and the complexed guest, respectively. Hence, one can algebraically derive (see Supporting Information for details) the following exact relationship:

$${\mathit{A}}_{\mathit{i}}={\mathit{A}}_{\mathbf{0}}\mathbf{+}{\displaystyle \frac{\mathsf{\Delta }\mathit{\epsilon }}{\mathbf{2}}}\left[{\mathit{H}}_{\mathit{i}}\mathbf{+}{\mathit{G}}_{\mathbf{0}}\mathbf{+}{\displaystyle \frac{\mathbf{1}}{{\mathit{K}}_{\mathbf{G}}}}\mathbf{-}\sqrt{{\left({\mathit{H}}_{\mathit{i}}\mathbf{+}{\mathit{G}}_{\mathbf{0}}\mathbf{+}{\displaystyle \frac{\mathbf{1}}{{\mathit{K}}_{\mathbf{G}}}}\right)}^{\mathbf{2}}\mathbf{-}\mathbf{4}{\mathit{H}}_{\mathit{i}}{\mathit{G}}_{\mathbf{0}}}\right]$$

(1)

where A₀ is the absorbance of the pure guest solution, and Δε = ε_HG − ε_G. However, under the hypothesis that the concentration of the guest is negligible with respect to the host, i.e., G₀ << H_i, Equation (1) can be replaced by a simpler expression:

$${\mathit{A}}_{\mathit{i}}\mathbf{=}{\mathit{A}}_{\mathbf{0}}\mathbf{+}{\displaystyle \frac{\mathsf{\Delta }\mathit{\epsilon }{\mathit{K}}_{\mathbf{G}}{\mathit{G}}_{\mathbf{0}}{\mathit{H}}_{\mathit{i}}}{\mathbf{1}\mathbf{+}{\mathit{K}}_{\mathbf{G}}{\mathit{H}}_{\mathit{i}}}}$$

(2)

From the latter, the well-known Benesi–Hildebrand’s linearized equation [28] can be easily derived:

$${\displaystyle \frac{\mathbf{1}}{{\mathit{A}}_{\mathit{i}}\mathbf{-}{\mathit{A}}_{\mathbf{0}}}}\mathbf{=}{\displaystyle \frac{\mathbf{1}}{\mathsf{\Delta }\mathit{\epsilon }{\mathit{G}}_{\mathbf{0}}}}\mathbf{+}{\displaystyle \frac{\mathbf{1}}{\mathsf{\Delta }\mathit{\epsilon }{\mathit{G}}_{\mathbf{0}}{\mathit{K}}_{\mathbf{G}}}}\left({\displaystyle \frac{\mathbf{1}}{{\mathit{H}}_{\mathit{i}}}}\right)$$

(3)

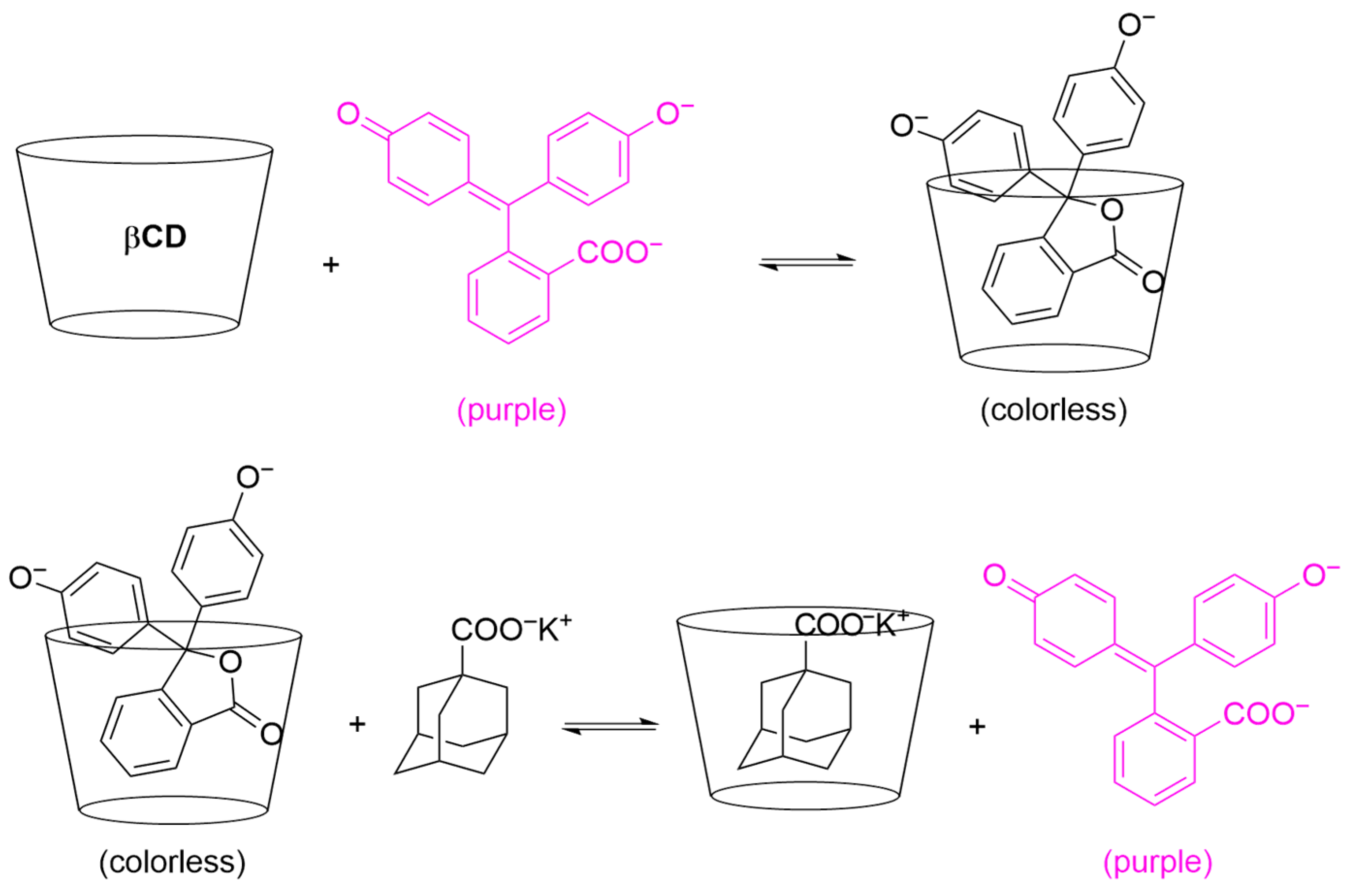
2.3.2. Multiple Equilibria: The Spectral Displacement Method

As we mentioned previously, the spectral displacement method requires that a non-chromophoric guest X is added in increasing amounts (X_i) to a set of samples containing fixed amounts of a non-chromophoric host H and a chromophoric guest G (H₀ and G₀, respectively). Under the hypothesis that only 1:1 complexes are formed according to the simultaneous equilibria,

$$\begin{gathered} \mathrm{H} \mathrm{+} \mathrm{G} \rightleftharpoons \mathrm{H}\mathrm{G} \\ \mathrm{H} \mathrm{+} \mathrm{X} \rightleftharpoons \mathrm{H}\mathrm{X} \end{gathered}$$

the concentrations at equilibrium are subjected to the relevant stoichiometric and mass action conditions, i.e.,: H₀ = [H] + [HG] + [HX], G₀ = [G] + [HG], X_i = [X] + [HX], K_G = [HG]/([H]·[G]), and K_X = [HX]/([H]·[X]), where K_X is the required binding constant of the competitor guest X. The addition of X subtracts the free host from equilibrium; therefore, according to Le Chatelier’s principle, the HG complex must partly dissociate, i.e., the formation equilibrium for HG must move backwards, and X progressively displaces G from the host H. If free G is the only chromophoric species, its displacement can be immediately evidenced. The expression for absorbances can be rearranged as follows: A_i = ε_G[G] + ε_HG[HG] = ε_GG₀ + (ε_G − ε_HG)[G]; consequently [G] = (A_i − ε_HGG₀)/(ε_G − ε_HG). However, if one can also assume ε_HG ≈ 0, the latter expression simplifies to [G] = A_i/ε_G. Hence, the following equilibrium concentration expressions can be obtained (see Supporting Information):

$$\begin{gathered} [\mathbf{H}\mathbf{G}]={\mathit{G}}_{\mathbf{0}}-[\mathbf{G}]={\displaystyle \frac{{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-\mathit{A}}_{\mathit{i}}}{{\mathit{\epsilon }}_{\mathbf{G}}}} \\ [\mathbf{H}]={\displaystyle \frac{\mathbf{1}}{{\mathit{K}}_{\mathbf{G}}}}·{\displaystyle \frac{\left[\mathbf{H}\mathbf{G}\right]}{\left[\mathbf{G}\right]}}={\displaystyle \frac{\mathbf{1}}{{\mathit{K}}_{\mathbf{G}}}}·{\displaystyle \frac{{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-\mathit{A}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{i}}}} \end{gathered}$$

Consequently, a simple spectrophotometric determination immediately enables a quantitative estimation of the equilibrium concentrations of both the free H and the complex HG. In order to deduce the relationship between the absorbance and the analytical concentration of X, i.e., the required fitting equation correlating A vs. X_i, the mass balance for H must be considered. After having substituted [H] and [HG] with the relevant expressions as a function of A_i, the following equation is obtained:

$${\mathit{H}}_{\mathbf{0}}={\displaystyle \frac{\mathbf{1}}{{\mathit{K}}_{\mathbf{G}}}}\left({\displaystyle \frac{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-{\mathit{A}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{i}}}}\right)+\left({\displaystyle \frac{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-{\mathit{A}}_{\mathit{i}}}{{\mathit{\epsilon }}_{\mathbf{G}}}}\right)+{\mathit{X}}_{\mathit{i}}{\displaystyle \frac{\frac{{\mathit{K}}_{\mathit{X}}}{{\mathit{K}}_{\mathbf{G}}}\left(\frac{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-{\mathit{A}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{i}}}\right)}{\mathbf{1}+\frac{{\mathit{K}}_{\mathit{X}}}{{\mathit{K}}_{\mathbf{G}}}\left(\frac{{{\mathit{\epsilon }}_{\mathit{G}}\mathit{G}}_{\mathbf{0}}-{\mathit{A}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{i}}}\right)}}$$

(4)

Unfortunately, from Equation (4), it is not possible to derive a viable expression for A_i as a function of X_i, because it would resolve into a cubic form. The latter could be worked out, for instance, with smart use of the MS Excel software package [29]. Notably, an alternative treatment proposed by Mohamed et al. retrieves a cubic expression in [H] that is worked out by the Newton–Raphson method [27]. This challenging problem has been occasionally approached by different authors, who have proposed different alternative simplifications. In particular, Connors [30] proposed a linearized method by introducing the following variables Q and R [31]:

$$\begin{gathered} \mathit{Q}={\displaystyle \frac{{\mathit{A}}_{\mathit{i}}}{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-{\mathit{A}}_{\mathit{i}}}} \\ \mathit{R}={\mathit{H}}_{\mathbf{o}}-{\displaystyle \frac{\mathbf{1}}{\mathit{Q}·{\mathit{K}}_{\mathbf{G}}}}-{\displaystyle \frac{{\mathit{G}}_{\mathbf{0}}}{\mathbf{1}+\mathit{Q}}} \end{gathered}$$

and then reporting X_i/R vs. Q according to the formally linear relationship:

$${\displaystyle \frac{{\mathit{X}}_{\mathit{i}}}{\mathit{R}}}={\displaystyle \frac{{\mathit{K}}_{\mathbf{G}}}{{\mathit{K}}_{\mathit{X}}}}·\mathit{Q}+\mathbf{1}$$

(5)

A little trick, however, allows for circumventing the intrinsic difficulties inherent to the use of the cubic equation, introducing no approximation or simplification. In fact, Equation (4) can be easily transformed, solving it for X_i by a few trivial algebraic passages, i.e.,

$${\mathit{X}}_{\mathit{i}}=\left[{\mathit{H}}_{\mathbf{0}}-\left({\displaystyle \frac{\mathbf{1}}{{\mathit{K}}_{\mathbf{G}}}}+{\displaystyle \frac{{\mathit{A}}_{\mathit{i}}}{{\mathit{\epsilon }}_{\mathbf{G}}}}\right)\left({\displaystyle \frac{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-{\mathit{A}}_{\mathit{i}}}{{\mathit{A}}_{\mathit{i}}}}\right)\right]·\left[\mathbf{1}+{\displaystyle \frac{{\mathit{K}}_{\mathbf{G}}}{{\mathit{K}}_{\mathit{X}}}}\left({\displaystyle \frac{{\mathit{A}}_{\mathit{i}}}{{{\mathit{\epsilon }}_{\mathbf{G}}\mathit{G}}_{\mathbf{0}}-{\mathit{A}}_{\mathit{i}}}}\right)\right]$$

(6)

Therefore, by plotting X_i vs. A_i, Equation (6) can be suitably exploited for a nonlinear regression data analysis.

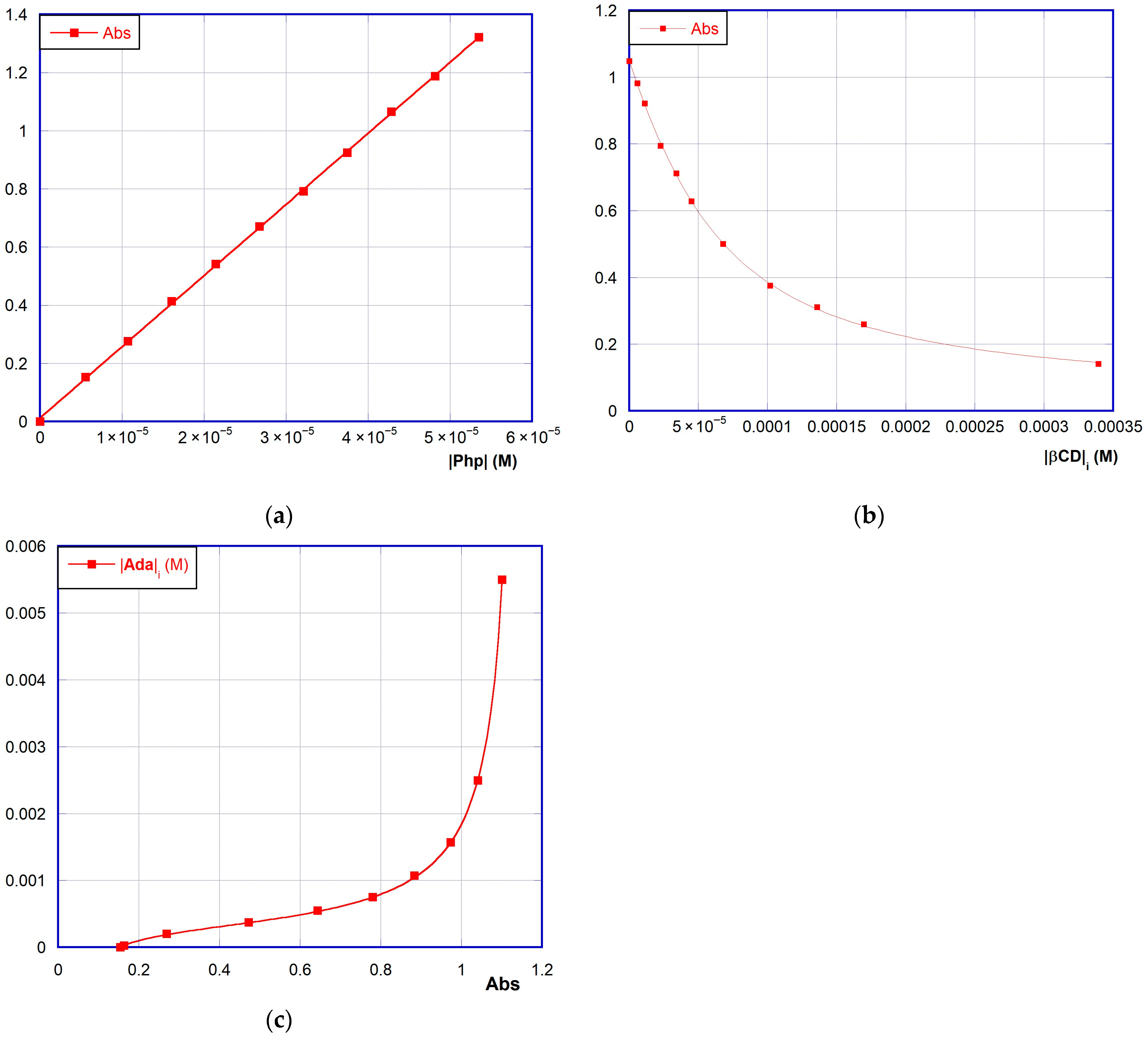
3. Results and Discussion

As we mentioned in the Introduction, the ternary system βCD-Php-Ada undoubtedly constitutes an excellent model for didactic purposes. The Php is a well-known acid–base indicator, which turns from colorless to a characteristic purple shade at pH values above 9 and forms a stable 1:1 inclusion complex with βCD, characterized by a binding constant in the 10⁴ M⁻¹ order of magnitude. Surprisingly, the resulting inclusion complex is colorless, owing to the blocked structure assumed by the lactone ring, which interrupts the electron delocalization of the deprotonated phenolic ring (Figure 2). Therefore, the addition of βCD to an alkaline solution of Php causes a decrease in the color intensity. On the other hand, the non-chromophoric competitor guest Ada shows a very strong affinity for the βCD cavity due to the almost perfect size fit of the adamantyl moiety and the resulting optimization of van der Waals interactions. The βCD-Ada 1:1 complex possesses a binding constant of the same order of magnitude as the βCD-Php complex. Consequently, if Ada is added to an alkaline solution of Php and βCD, Php is displaced from the βCD cavity, and an increase in the intensity of the purple coloration is observed.

Students are introduced to the different problems step by step. Hereafter, we will present some of the data obtained in a typical student-performed experiment. First, the molar extinction coefficient of Php ε_Php is determined under the pH conditions used for the subsequent study of complex formation equilibria (Figure 3a), in order to verify the observance of Beer–Lambert’s law (in our case, it was found that ε_Php = 24,500 ± 400 at pH 11.0, as the weighted average from three independent determinations).

In the second step, the βCD-Php binding constant is estimated. A typical dataset is plotted in Figure 3b; data have been fitted by means of Equation (1) (further discussion about the possible use of Equations (2) and (3) is reported in the Supporting Materials). Under the hypothesis that the βCD-Php complex has a negligible absorptivity, one could assume that Δε = − ε_Php. However, in order to overcome possible systematic errors in the determination of A_i values, it is necessary to leave Δε as a fitting parameter (in our case, Δε = 23,800 ± 200 and K_Php = (2.56 ± 0.08)·10⁴ M⁻¹ was found, which is consistent with the value of 2.3·10⁴ M⁻¹ found by Buvári et al. [32]). The third and final step is the evaluation of K_Ada, using Equation (6) for data fitting analysis (Figure 3c). Even in this case, one can either assume the values of ε_Php and K_Php from the previous determinations, or leave them as fitting parameters (with a typical dataset as the one depicted in Figure 3c, K_Ada = (5.4 ± 0.2)·10⁴ M⁻¹ was found in the former case, whereas in the second case ε_Php = 24,874 ± 12, K_Php = (2.22 ± 0.07) × 10⁴ M⁻¹ and K_Ada = (3.16 ± 0.11)·10⁴ M⁻¹ was obtained).

From a methodological and educational standpoint, the execution of this sequence of experiments provides evidence of several conceptual and practical issues, which can stimulate students’ critical judgment and awareness. As a first observation, it is important to stress that obedience to Beer–Lambert’s law, i.e., the linearity of the spectrophotometric response to the concentration of the chromophoric species in the system, is a prerequisite to perform the entire activity. This drives students’ attention to the problem of the reliability and reproducibility of the analytical methods (and of the measurement tools in general) used for the determination of thermodynamic parameters such as equilibrium constants. Second, it is interesting to compare the results of the fitting procedures performed by means of Equations (1) and (6), respectively, with the ones obtained from different equations (Benesi–Hildebrand, Connors, etc., see Supporting Materials for exhaustive discussion). It can be verified that the estimation of K_Php by means of Equations (2) or (3) gives poor results. This is the obvious consequence of the fact that the latter simplified equations can be applied only under relatively strict stoichiometric conditions, namely whenever the analytical concentration of the guest is negligible as compared to the host. The latter condition implies that one can reasonably assume that the analytical and equilibrium concentrations of the host are equivalent. Clearly, in the present case, this is not verified. The double use of Equation (6), i.e., either optimizing or not the values of ε_Php and K_Php, is quite intriguing. At first sight, verifying that the optimized values of these parameters are in agreement with those independently obtained in the first two steps of the experimental protocol may seem a good way to “validate” the entire procedure, or to verify the accuracy of the experimental work. In the case presented here, it can be immediately noticed that the two values obtained for ε_Php are consistent within the experimental uncertainties, whereas the values for K_Php are not. This can stimulate the students towards a deeper critical examination of the reliability of both the experimental work and the mathematical methods for data treatment. Students might be a little upset upon discovering that for the same host–guest systems, different values of the relevant binding constant can be found in the literature, depending on the author and the experimental method used. In the case of the βCD–benzoic acid inclusion complex, for instance, the values reported in the literature span over an entire order of magnitude [24]. To the best of our knowledge, only two examples concerning the spectral displacement technique exist for the determination of K_Ada, which can be suitably compared with our results. Selvidge and Eftink reported [33] the determination of K_Ada using both methyl orange and phenolphthalein as colored guests, obtaining values of (4.2 ± 0.1) × 10⁴ and (1.6 ± 0.1) × 10⁴ M⁻¹, respectively. Moreover, in order to have an independent estimation, they have also determined by calorimetry a further value of K_Ada of 3.6 × 10⁴ M⁻¹. On the other hand, Alper et al. reported the determination of K_Ada using phenolphthalein as a colored guest, obtaining a value as large as (3.60 ± 0.06) × 10⁴ M⁻¹. Furthermore, a wide range of K_Ada values are reported in the literature, determined by calorimetric measurement, spanning from 2.0 × 10⁴ to 4.0 × 10⁴ M⁻¹. Hence, our results are indeed consistent with values obtained with different techniques. At this point, students must ask themselves the reason why such large discrepancies are possible. Experimental results may be critically affected not only by the peculiarities of the experimental tool chosen (calorimetry, spectrophotometry, etc.) but also by physical and chemical parameters (pH, ionic strength, nature of the buffering electrolyte, presence of impurities in the reactants or the solvent) which are not trivial to control. As a consequence, one can compare different results on homologous systems (i.e., for instance, binding constants for a set of different, structurally related guests) if and only if the methodologies and the experimental conditions under which these data have been obtained are strictly comparable.

Further issues pertain to the fitting procedure. Close examination of Equation (6) easily reveals that the estimation of the value of K_Ada is strictly affected by the concomitant estimation of K_Php. In fact, K_Ada is present only once in Equation (6), namely in the ratio (K_Php/K_Ada). As an immediate consequence, any error in the estimation of K_Php will be mirrored in a parallel error on the value of K_Ada. Students are seldom aware of these mathematical cheats. A particular discussion is owed to the use of Connor’s equation to obtain K_Ada. As well as for Benesi–Hildebrand’s data treatment, particular caution is needed in considering the linearization of the dataset as a viable option. In fact, the calculation of the variables Q and R, requiring the introduction of the values for ε_Php and K_Php, sneakily introduces a source of systematic error, which may heavily affect the final results. In general, this kind of data treatment can modify the statistical weight of the various experimental points subjected to the regression procedure in an unpredictable way. Therefore, it can be reasoned out that, in principle, it is always preferable to use a regression procedure (i.e., a fitting equation) able to work directly on the source experimental dataset.

As a concluding remark, the experiments presented in this work can be adapted to classes of both high school and undergraduate students. Of course, in the first case, quantitative aspects could be skipped or only hinted at, whereas in the second case, they may constitute a main point of interest.

The spectral displacement method could also be adapted for the detection of biologically relevant non-chromophore guests whose binding to βCD does not lead to detectable color change. An example of such a colorless interaction is given by the βCD–cholesterol host–guest complex [34,35]. The βCD–cholesterol interaction has been extensively studied due to the strong affinity of cholesterol to the hydrophobic cavity of βCD, which has been used as a scavenger of cholesterol in cell membranes, serum, and food [36]. Few examples of systems for examining βCD–cholesterol interaction detectable by optical switching have been reported in the literature. Systems based on the competitive host–host interaction between AuNPs-βCD [37] or graphene–βCD [38] with fluorescent molecules (fluorescein and rhodamine, respectively) and cholesterol have been reported as fluorescent probes for cholesterol detection. Indeed, when fluorescent molecules are located within the βCD cavity, the proximity to the fluorescent quencher (graphene or AuNPs) quenches their fluorescence. The displacement of fluorescent molecules from the βCD cavity by cholesterol switches on fluorescence that can be detected as an optical signal. Conceptually, this analytical method is based on the same principles as the spectral displacement method that uses phenolphthalein as a colored probe but requires the preparation of customized molecular systems and the use of equipment to detect fluorescence, which makes this method inaccessible for educational purposes. The spectral displacement method, on the other hand, can be easily adapted for the qualitative as well as quantitative detection of cholesterol in blood serum or in foods such as egg white (colorless matrices), making students aware of the potential of combining supramolecular chemistry and the study of multiple equilibria.

4. Conclusions

The spectral displacement method can be a useful tool for introducing the study of multiple equilibria and supramolecular chemistry in different educational contexts. Experiments can be presented qualitatively to high school students to show a system for detecting colorless molecules. The use of a revised mathematical approach to describe the multiple equilibria involved allows for the implementation of an articulated experimental set-up for the quantitative determination of the binding constants of both the phenolphthalein colored probe and the competitive colorless host. The latter set-up of the experiment can be introduced as an experiment in a laboratory of physical methods in organic chemistry.

Finally, as a further implementation, the experiment could also be introduced into a multidisciplinary biotechnology laboratory pathway for the detection of colorless molecules of biological or nutritional relevance, provided that these molecules are characterized by a βCD binding constant of the same order of magnitude as that of phenolphthalein.