Similarity and Homogeneity of Climate Change in Local Destinations: A Globally Reproducible Approach from Slovakia
Abstract
1. Introduction
2. Literature Review
2.1. DMOs and Climate Change
2.2. Open Data and Climate Analysis in Tourism
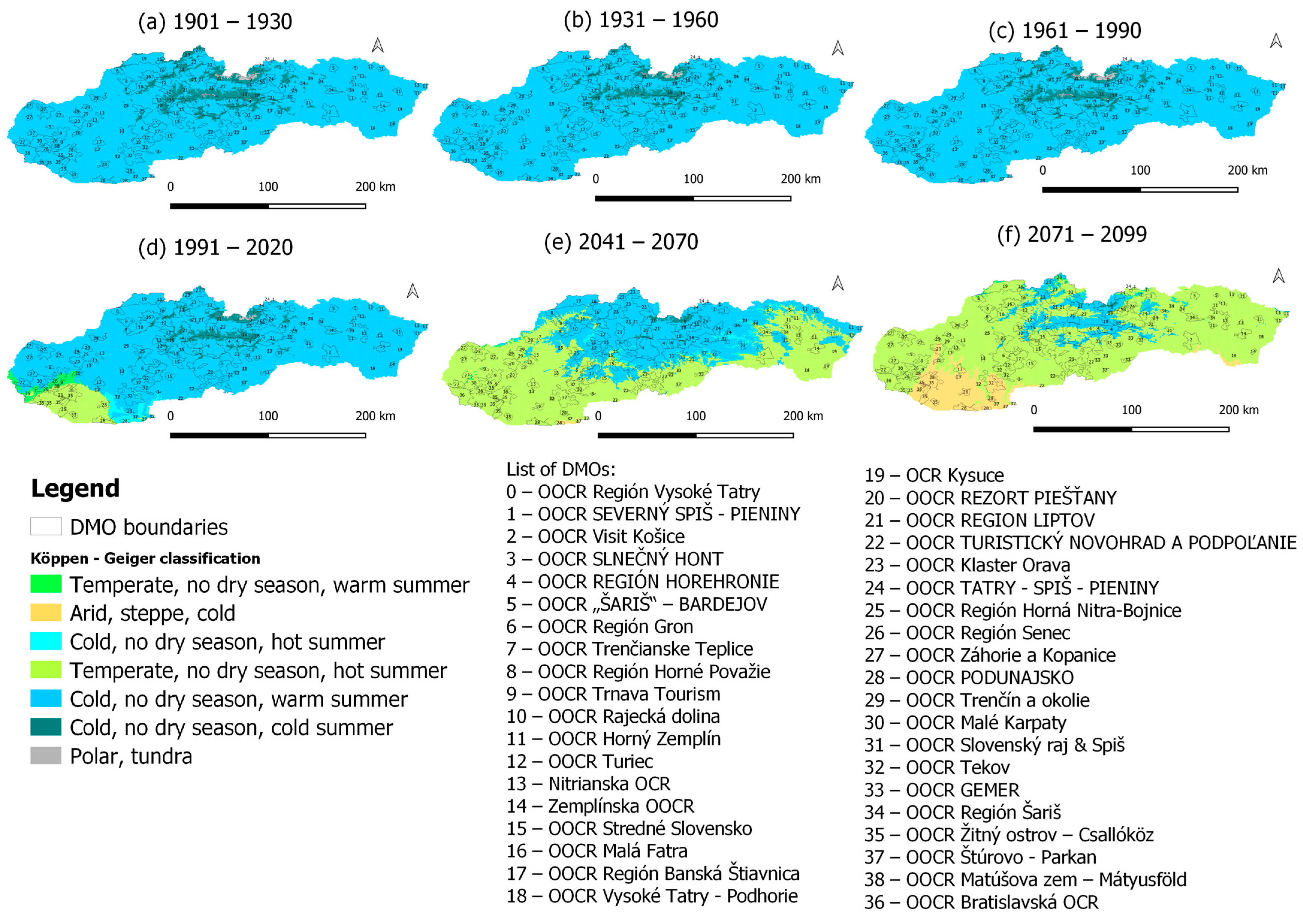
2.3. Köppen–Geiger Climate Classification
3. Materials and Methods
3.1. Input Data and Preprocessing
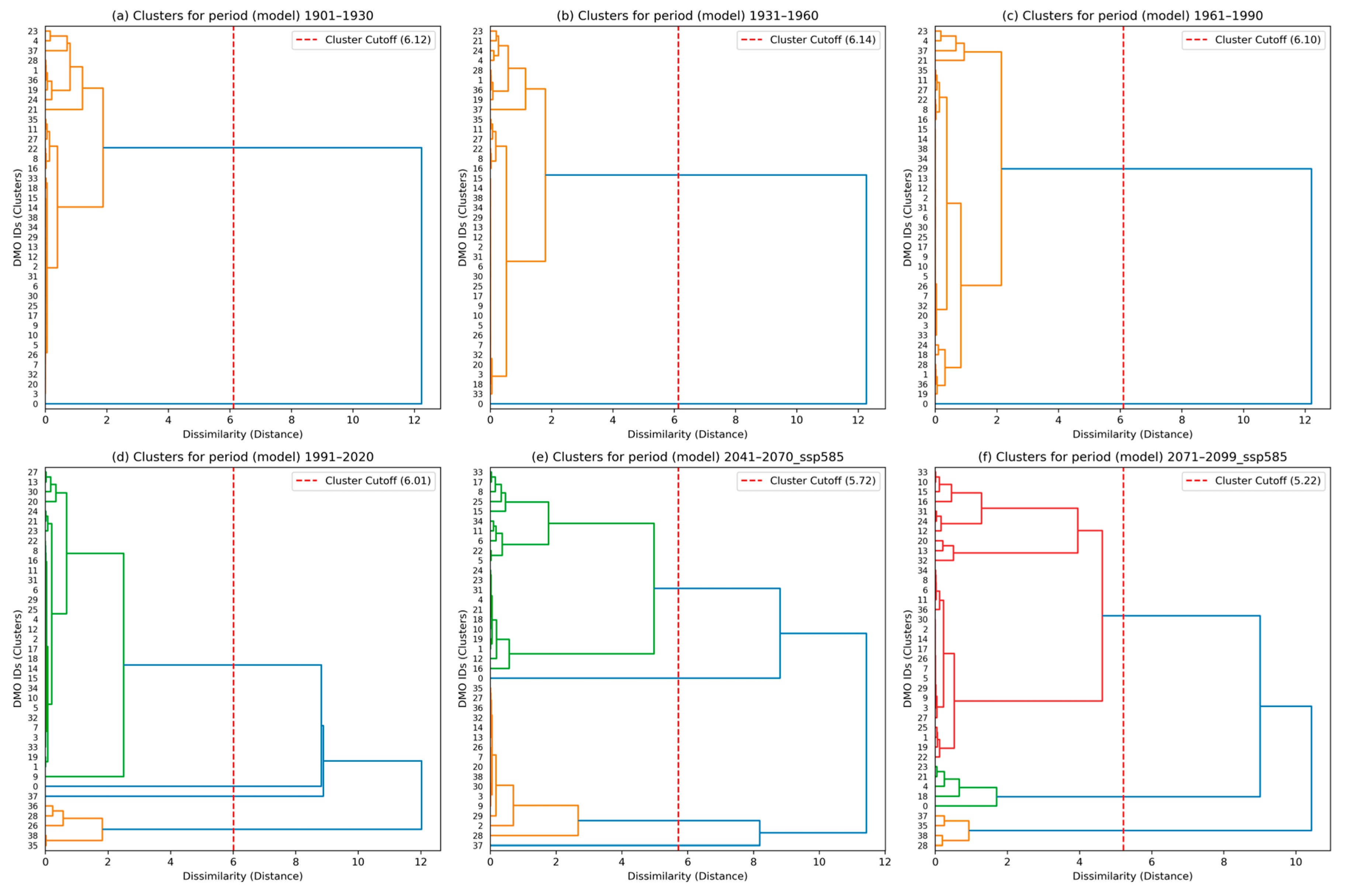
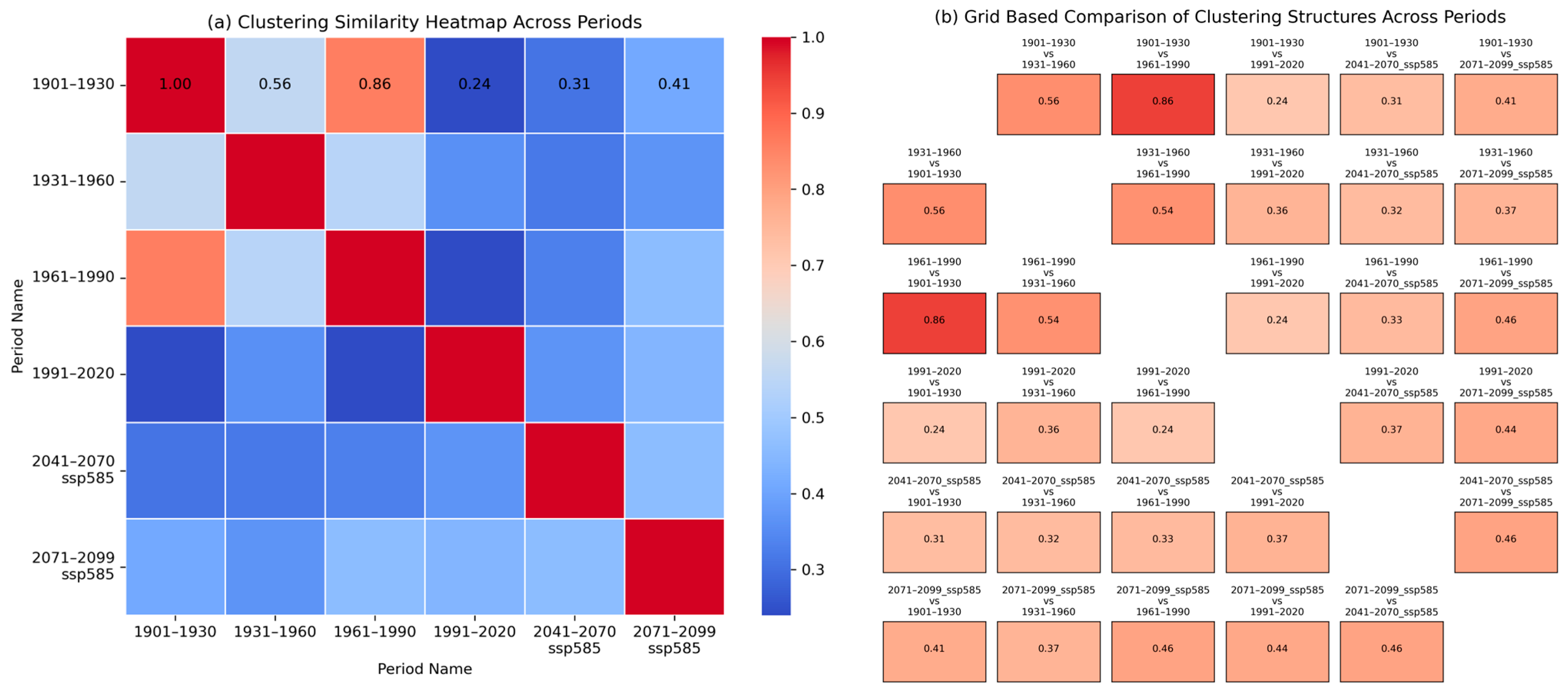
3.2. Statistical Methods
- is the main climate weight (feature j) in a DMO (sample i);
- is the mean of the main climate weight (feature j);
- is the standard deviation of the main climate weight (feature j).
- are the number of elements in clusters being merged;
- are the mean vectors of clusters being merged (centroids of A, B);
- is the square of the Euclidean distance between the centroids of the A, B clusters.
- are the linkage matrices of input periods (vectors);
- are individual points within the input linkage matrices.
- are the pairwise distances of cluster from two input periods;
- are the means of distance for each matrix.
- is the proportion (probability) of weight for the main climate in a group (DMO and period);
- is the total number of unique weights in a group;
- is the base 2 logarithm for the proportion of a weight.
- is a data point (the weight for the main climate category) in a group (DMO and period);
- is the weighted mean of the data points;
- is the weight of the data point.
- is the residual;
- is the threshold for quadratic loss (small residuals) and linear loss (large residuals).
4. Results
4.1. Clusters of DMOs by Köppen–Geiger Classification Main Groups
4.1.1. Clusters’ Structural Similarity
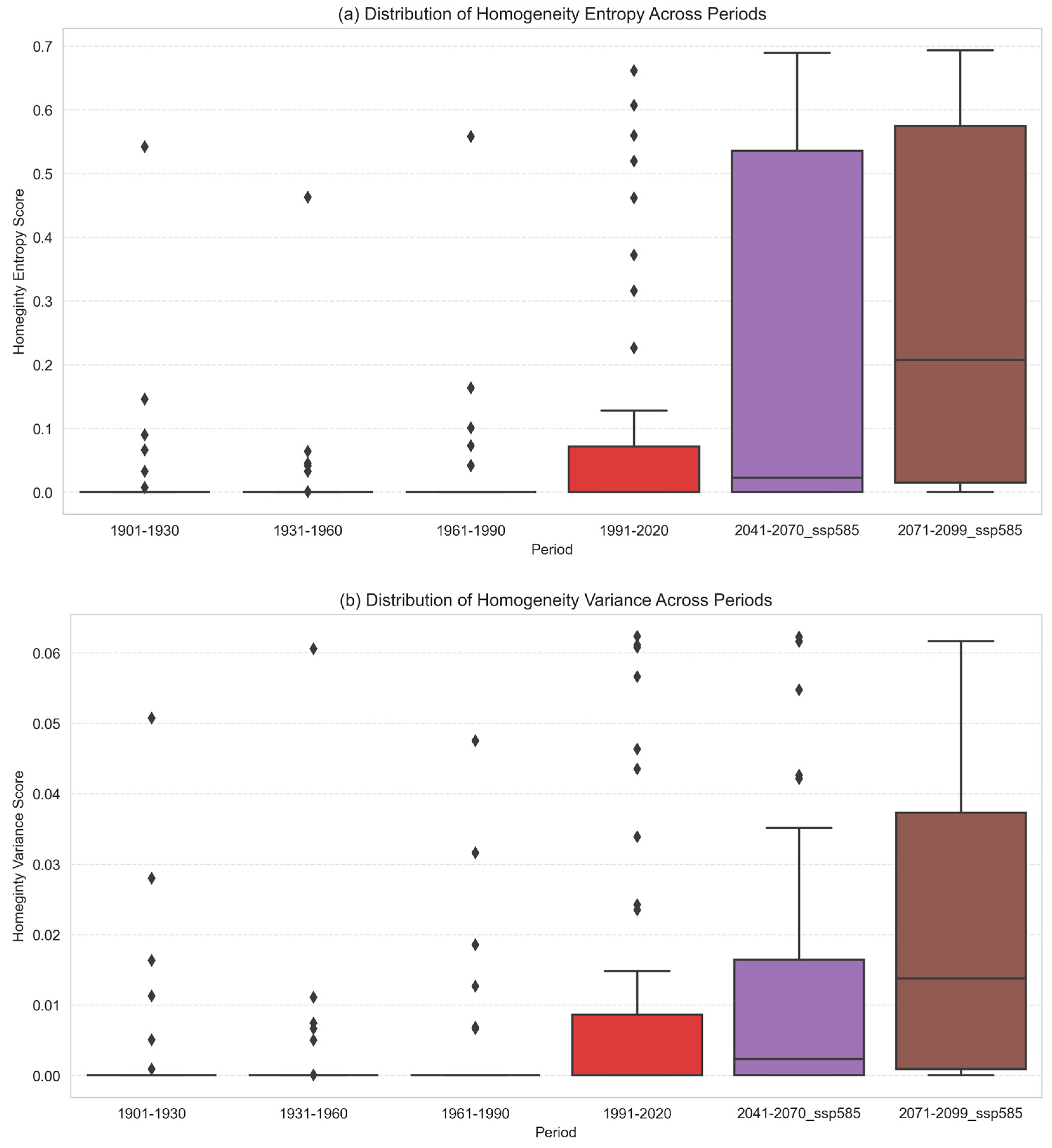
4.1.2. Change in Homogeneity Within the Köppen–Geiger Classification’s Main Climate
4.1.3. DMOs’ Main Climate Classification Changes
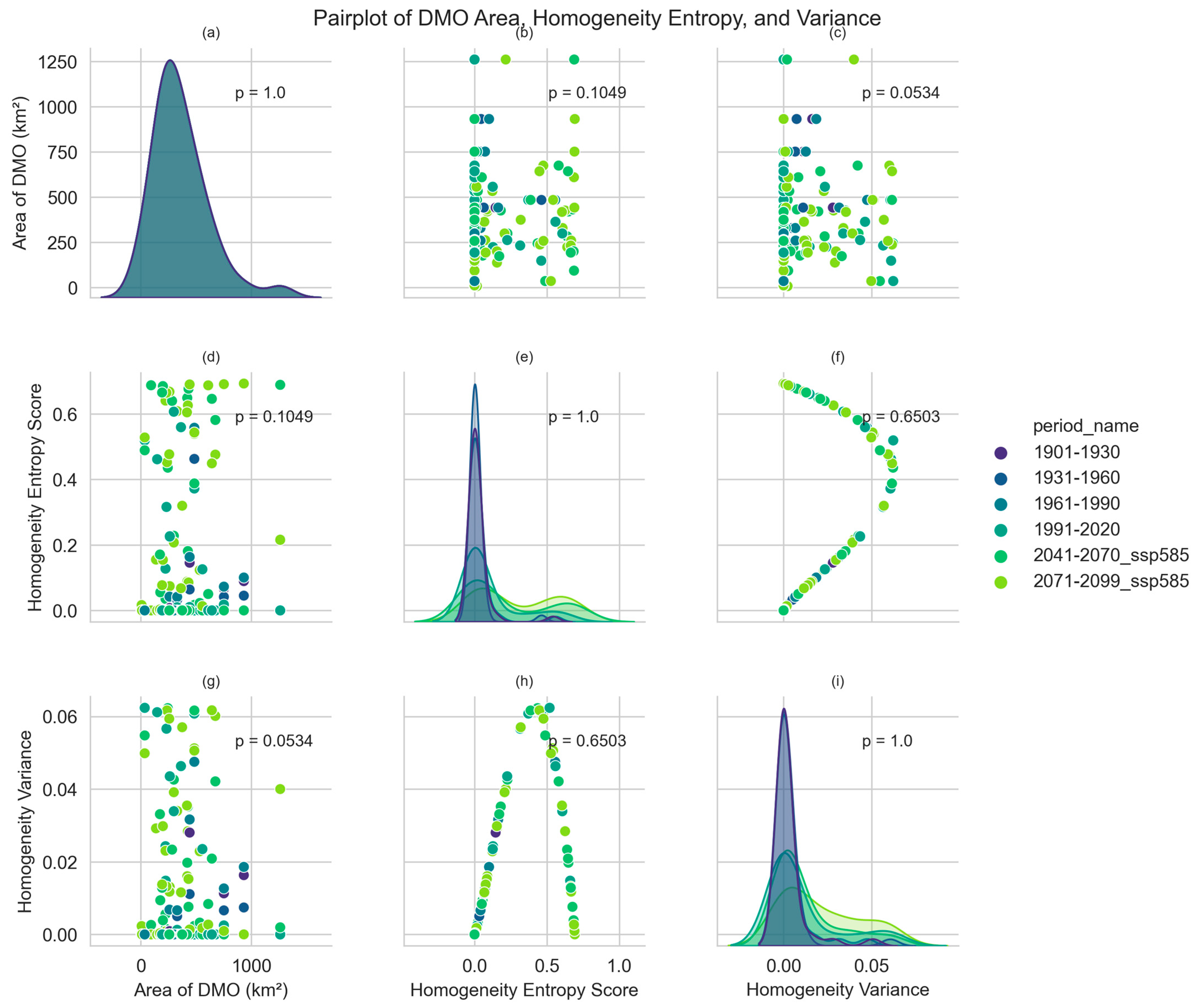
4.1.4. DMOs’ Area Size Relationship to Climate Homogeneity and Fluctuation
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMIP | Coupled Model Intercomparison Project |
| DMO | Destination Management Organizations |
| DMO ID | Destination Management Organizations’ identification via a unique integer |
| GHG | Greenhouse Gas |
| NDVI | Normalized Difference Vegetation Index |
| OOCR | Oblastná organizácia cestovného ruchu, the Slovak equivalent of a DMO |
| UNWTO | United Nations World Tourism Organization |
Appendix A. Results of Robust Regression Analysis
Appendix A.1. Robust Regression Analysis
| Dependent Variable | Model | Method | Norm | Scale Estimator | Cov Type | Number of Observations | Degrees of Freedom (Residuals) | Degrees of Freedom (Model) | Scale Estimate |
|---|---|---|---|---|---|---|---|---|---|
| homogeneity_entropy | RLM | IRLS | HuberT | mad | H1 | 234 | 232 | 1 | 0.030221 |
| Coefficient | Standard Error | z-Value | p-Value | 95% CI Lower | 95% CI Upper | |
|---|---|---|---|---|---|---|
| const | 0.008951 | 0.004347 | 2.059416 | 0.039454 | 0.000432 | 0.017471 |
| sqkm | 0.000028 | 0.00001 | 2.811246 | 0.004935 | 0.000008 | 0.000047 |
| Dependent Variable | Model | Method | Norm | Scale Estimator | Cov Type | Number of Observations | Degrees of Freedom (Residuals) | Degrees of Freedom (Model) | Scale Estimate |
|---|---|---|---|---|---|---|---|---|---|
| homogeneity_entropy | RLM | IRLS | HuberT | mad | H1 | 234 | 232 | 1 | 0.001887 |
| Coefficient | Standard Error | z-Value | p-Value | 95% CI Lower | 95% CI Upper | |
|---|---|---|---|---|---|---|
| const | 0.000772 | 2.74 × 10−4 | 2.821674 | 0.004777 | 2.36 × 10−4 | 0.001309 |
| Sqkm | 0.000001 | 6.24 × 10−7 | 1.922035 | 0.054601 | −2.37 × 10−8 | 0.000002 |
References
- United Nations. Paris Agreement. United Nations Framework Convention on Climate Change, 2015. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 1 January 2025).
- One Planet Sustainable Tourism Programme. Glasgow Declaration: A Commitment to a Decade of Climate Action. 2021. Available online: https://www.oneplanetnetwork.org/sites/default/files/2022-02/GlasgowDeclaration_EN_0.pdf (accessed on 1 January 2025).
- World Tourism Organization. Policy Guidance to Support Climate Action by National Tourism Administrations; UN Tourism: Madrid, Spain, 2024. [Google Scholar] [CrossRef]
- Council of the European Union. European Agenda for Tourism 2030—Council Conclusions (Adopted on 01/12/2022); General Secretariat of the Council: Brussel, Belgique, 2022; Available online: https://data.consilium.europa.eu/doc/document/ST-15441-2022-INIT/en/pdf (accessed on 1 January 2025).
- Scott, D.; Amelung, B.; Becken, S.; Ceron, J.P.; Dubois, G.; Gössling, S.; Peeters, P.; Simpson, M.C. Climate Change and Tourism: Responding to Global Challenges; World Tourism Organization (UNWTO): Madrid, Spain; United Nations Environment Programme (UNEP): Nairobi, Kenya, 2008. [Google Scholar]
- Dodds, R. Destination marketing organizations and climate change: The need for leadership and education. Sustainability 2010, 2, 3449–3464. [Google Scholar] [CrossRef]
- Bhandari, K.; Cooper, C.P.; Ruhanen, L. The Role of the Destination Management Organisation in Responding to Climate Change: Organisational Knowledge and Learning. Acta Tur. 2014, 26, 91–102. [Google Scholar]
- Bhandari, K.; Cooper, C.; Ruhanen, L. Climate change knowledge and organizational adaptation: A destination management organization case study. Tour. Recreat. Res. 2015, 41, 60–68. [Google Scholar] [CrossRef]
- Gössling, S.; Higham, J. The low-carbon imperative: Destination management under urgent climate change. J. Travel Res. 2020, 59, 581–598. [Google Scholar] [CrossRef]
- MacEachern, J.; MacInnis, B.; MacLeod, D.; Munkres, R.; Jaspal, S.K.; Kinay, P.; Wang, X. Destination Management Organizations’ Roles in Sustainable Tourism in the Face of Climate Change: An Overview of Prince Edward Island. Sustainability 2024, 16, 3049. [Google Scholar] [CrossRef]
- Kaaya, N.D. The Role of Networks Among Destination Management Organizations in Promoting Destinations’ Sustainability and Resilience: A Mixed-Methods Study. Doctoral Dissertation, University of South-Eastern Norway, Notodden, Norway, 2025. [Google Scholar]
- Rahman, T.U.; Saud, D.; Nawaz, T. Sustainable tourism in a changing climate: Strategies for management, adaptation, and resilience. Int. J. Sustain. Tour. 2024, 1, e-24001. Available online: https://journals.penrosehub.org/index.php/home/article/view/13 (accessed on 1 January 2025). [CrossRef]
- d’Angella, F.; Maccioni, F.; De Carlo, M. Exploring destination sustainable development strategies: Triggers and levels of maturity. Sustain. Futures 2025, 9, 100515. [Google Scholar] [CrossRef]
- Scott, D.; Lemieux, C.J.; Malone, L. Climate services to support sustainable tourism development and adaptation to climate change. Clim. Res. 2011, 47, 111–122. [Google Scholar] [CrossRef]
- Hamilton, J.M.; Maddison, D.J.; Tol, R.S.J. The effects of climate change on international tourism. Clim. Res. 2005, 29, 245–254. [Google Scholar] [CrossRef]
- Ciscar, J.-C.; Iglesias, A.; Feyen, L.; Szabó, L.; Van Regemorter, D.; Amelung, B.; Nicholls, R.; Watkiss, P.; Christensen, O.B.; Dankers, R.; et al. Physical and economic consequences of climate change in Europe. Proc. Natl. Acad. Sci. USA 2011, 108, 2678–2683. [Google Scholar] [CrossRef]
- Carrillo, J.; González, A.; Pérez, J.C.; Expósito, F.J.; Díaz, J.P. Projected impacts of climate change on tourism in the Canary Islands. Reg. Environ. Change 2022, 22, 61. [Google Scholar] [CrossRef]
- Farooq, M.A.; Ghufran, M.A.; Ahmed, N.; Attia, K.A.; Mohammed, A.A.; Hafeez, Y.M.; Amanat, A.; Farooq, M.S.; Uzair, M.; Naz, S. Remote sensing analysis of spatiotemporal impacts of anthropogenic influence on mountain landscape ecology in Pir Chinasi National Park. Sci. Rep. 2024, 14, 20695. [Google Scholar] [CrossRef]
- Boori, M.S.; Choudhary, P.; Kučera, F. Land use/cover disturbance due to tourism in Jeseníky Mountain, Czech Republic: A remote sensing and GIS-based approach. Environ. Earth Sci. 2015, 74, 997–1006. [Google Scholar] [CrossRef]
- Helali, J.; Asaadi, S.; Jafarie, T.; Habibi, M.; Salimi, S.; Momenpour, S.E.; Shahmoradi, S.; Hosseini, S.A.; Hessari, B.; Saeidi, V. Drought monitoring and its effects on vegetation and water extent changes using remote sensing data in Urmia Lake watershed, Iran. J. Water Clim. Change 2022, 13, 2107–2128. [Google Scholar] [CrossRef]
- Xue, Z.; Chen, L.; Gong, J.; Shen, S. Assessing the impact of climate change on tourism climate resources using high-resolution remote sensing data. Remote Sens. 2022, 14, 2857. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Zhou, L. Future risk of tourism pressures under climate change: A remote sensing approach. Remote Sens. 2022, 14, 3758. [Google Scholar] [CrossRef]
- García, D.H.; Rezapouraghdam, H.; Hall, C.M.; Karatepe, O.M.; Koupaei, S.N. Spatio-temporal variability of the earth’s surface temperature and the changes in land use/land cover: Implications for sustainable tourism development. J. Sustain. Tour. 2023, 17, 557–584. [Google Scholar] [CrossRef]
- Köppen, W. Klassification der Klimate nach Temperatur, Niederschlag and Jahreslauf. In Petermanns Geographische Mitteilungen; Gotha: Hamburg, Germany, 1918; Volume 64, pp. 193–203, 243–248. Available online: https://koeppen-geiger.vu-wien.ac.at/pdf/Koppen_1918.pdf (accessed on 1 January 2025).
- Geiger, R. Klassifikation der Klimate nach W. Köppen. In Landolt-Börnstein—Zahlenwerte und Funktionen aus Physik, Chemie, Astronomie, Geophysik und Technik, Alte Serie; Springer: Berlin/Heidelberg, Germany, 1954; Volume 3, pp. 603–607. [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Beck, H.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Lutsko, N.J.; Dufour, A.; Zeng, Z.; Jiang, X.; van Dijk, A.I.J.M.; Miralles, D. High-resolution (1 km) Köppen-Geiger maps for 1901–2099 based on constrained CMIP6 projections. Sci. Data 2023, 10, 724. [Google Scholar] [CrossRef]
- Sidor, C. SK DMOs Territory Köppen-Geiger Climate Classification. Github. 2025. Available online: https://github.com/csabasidor/SK-DMOs-territory---Koppen-Geiger-climate-classification-/tree/main (accessed on 1 January 2025).
- Sidor, C. get_dmo_base_data.py. SK-Geoheritage-at-TripAdvisor. Github. 2024. Available online: https://github.com/csabasidor/SK-Geoheritage-at-TripAdvisor/blob/main/source_codes/modules/get_dmo_base_data.py (accessed on 1 January 2025).
- Sidor, C. SK DMOs Change of Köppen-Geiger Climate Classification (1901–2099). 2025. Available online: https://cases.idoaba.eu/sk_dmos_kgc/ (accessed on 1 January 2025).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: https://jmlr.org/papers/v12/pedregosa11a.html (accessed on 1 January 2025).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Pearson, K. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28–30 June 2010; pp. 92–96. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidor, C.; Kršák, B.; Štrba, Ľ. Similarity and Homogeneity of Climate Change in Local Destinations: A Globally Reproducible Approach from Slovakia. World 2025, 6, 68. https://doi.org/10.3390/world6020068
Sidor C, Kršák B, Štrba Ľ. Similarity and Homogeneity of Climate Change in Local Destinations: A Globally Reproducible Approach from Slovakia. World. 2025; 6(2):68. https://doi.org/10.3390/world6020068
Chicago/Turabian StyleSidor, Csaba, Branislav Kršák, and Ľubomír Štrba. 2025. "Similarity and Homogeneity of Climate Change in Local Destinations: A Globally Reproducible Approach from Slovakia" World 6, no. 2: 68. https://doi.org/10.3390/world6020068
APA StyleSidor, C., Kršák, B., & Štrba, Ľ. (2025). Similarity and Homogeneity of Climate Change in Local Destinations: A Globally Reproducible Approach from Slovakia. World, 6(2), 68. https://doi.org/10.3390/world6020068






