Approach for the Assessment of Stability and Performance in the s- and z-Complex Domains
Abstract
1. Introduction
1.1. Brief Overview
1.2. Brief Comparison and Explanation
1.3. Research Aim and Motivation
1.4. Problem Statement
- The absence of a unified framework that integrates classical and robust methods while ensuring comparability between the s- and z-planes.
- Limited consideration of discretization, where typically only the method or only the sampling period is analyzed, without treating them as sources of parametric uncertainty.
- Insufficient visualization tools for engineers and designers to support intuitive selection of control strategies.
- Incomplete coverage of extended scenarios, including systems with time delays, mild nonlinearities, or variable sampling periods.
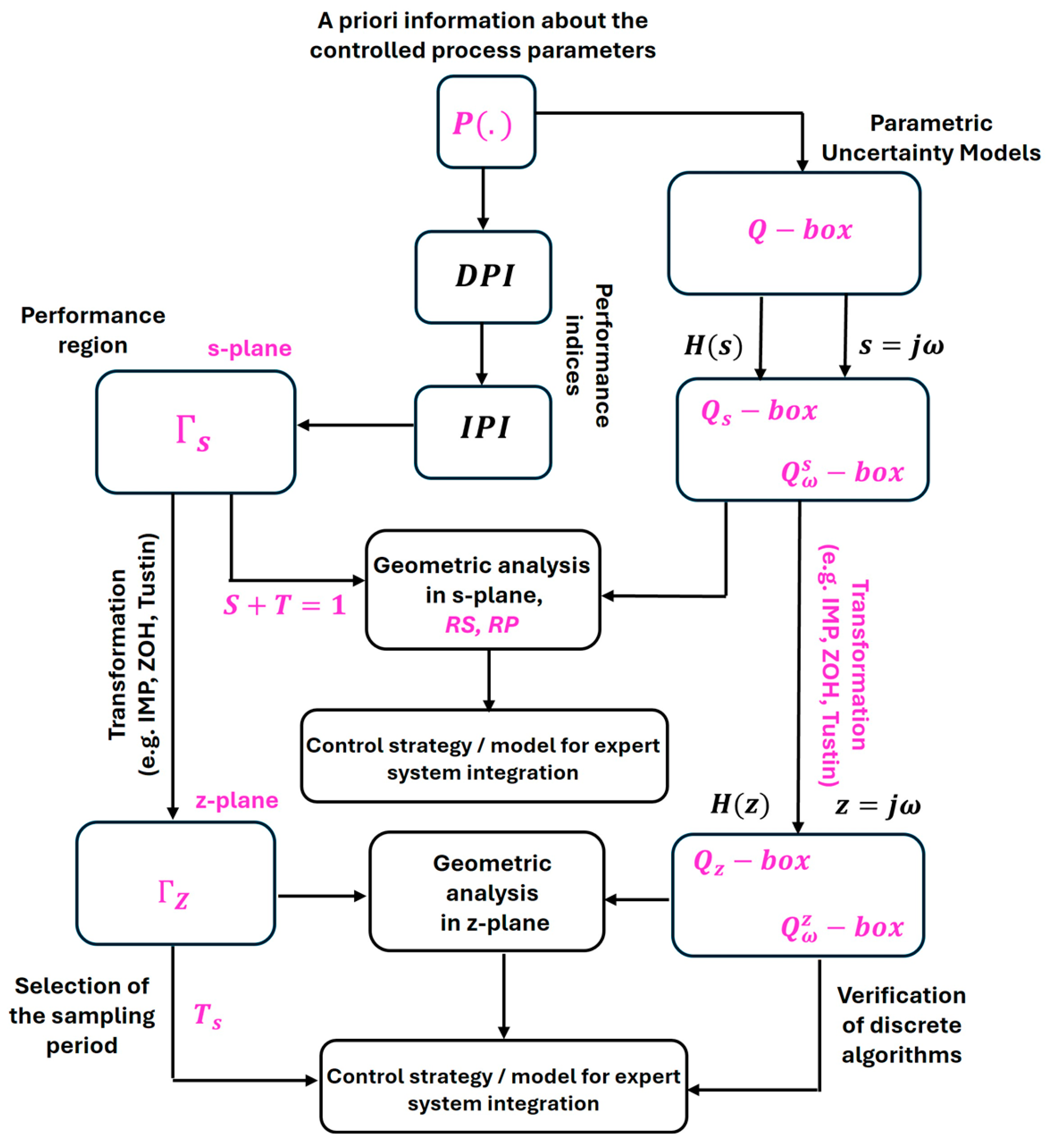
2. Gamma Regions
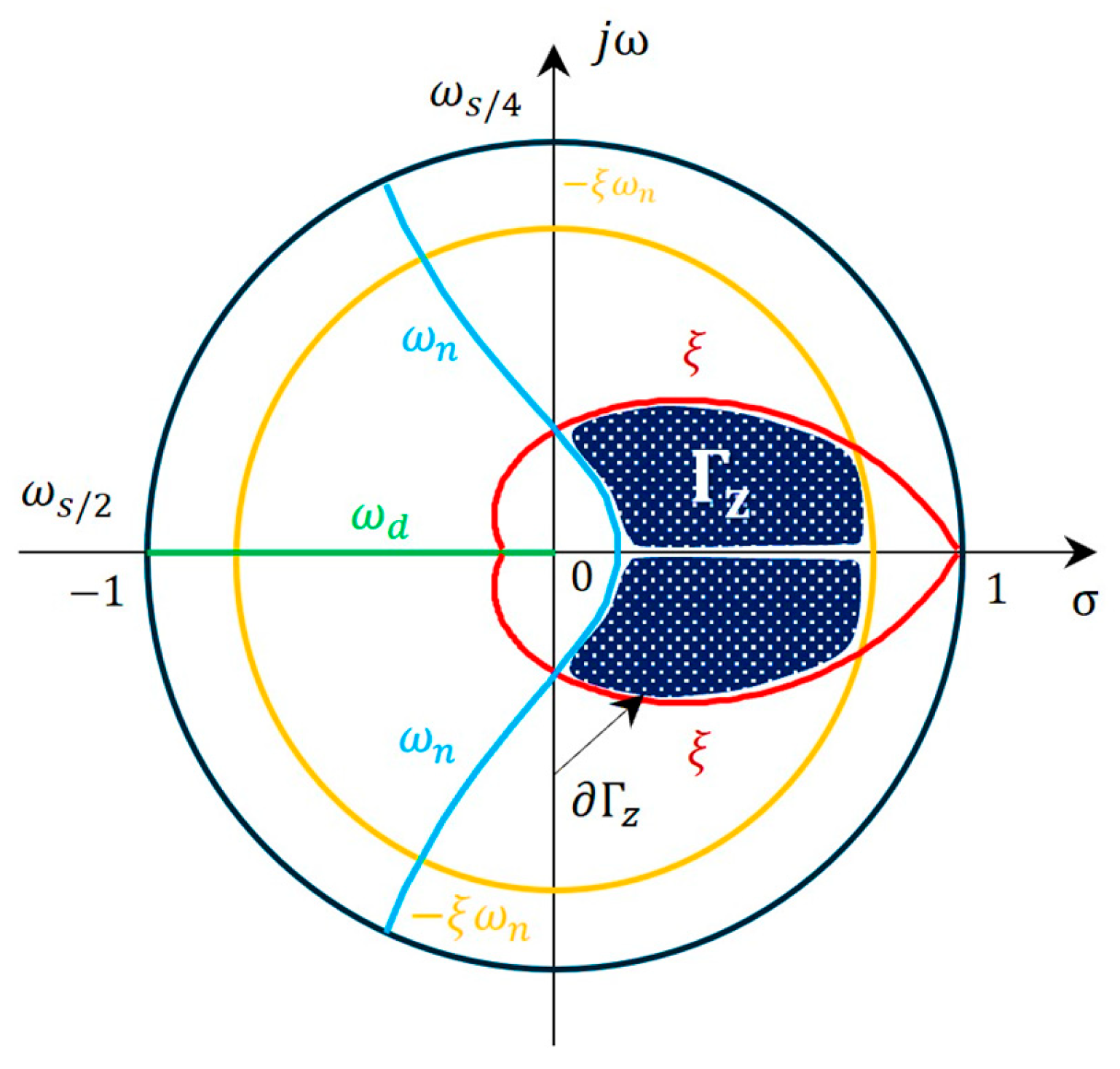
2.1. Definition of the Performance -Region in the -Plane
2.2. Defining of the Performance -Region in the -Plane
- , —for .
- , —for .
- , —for
- —for .
- , —for
3. Robustness in the s-Plane
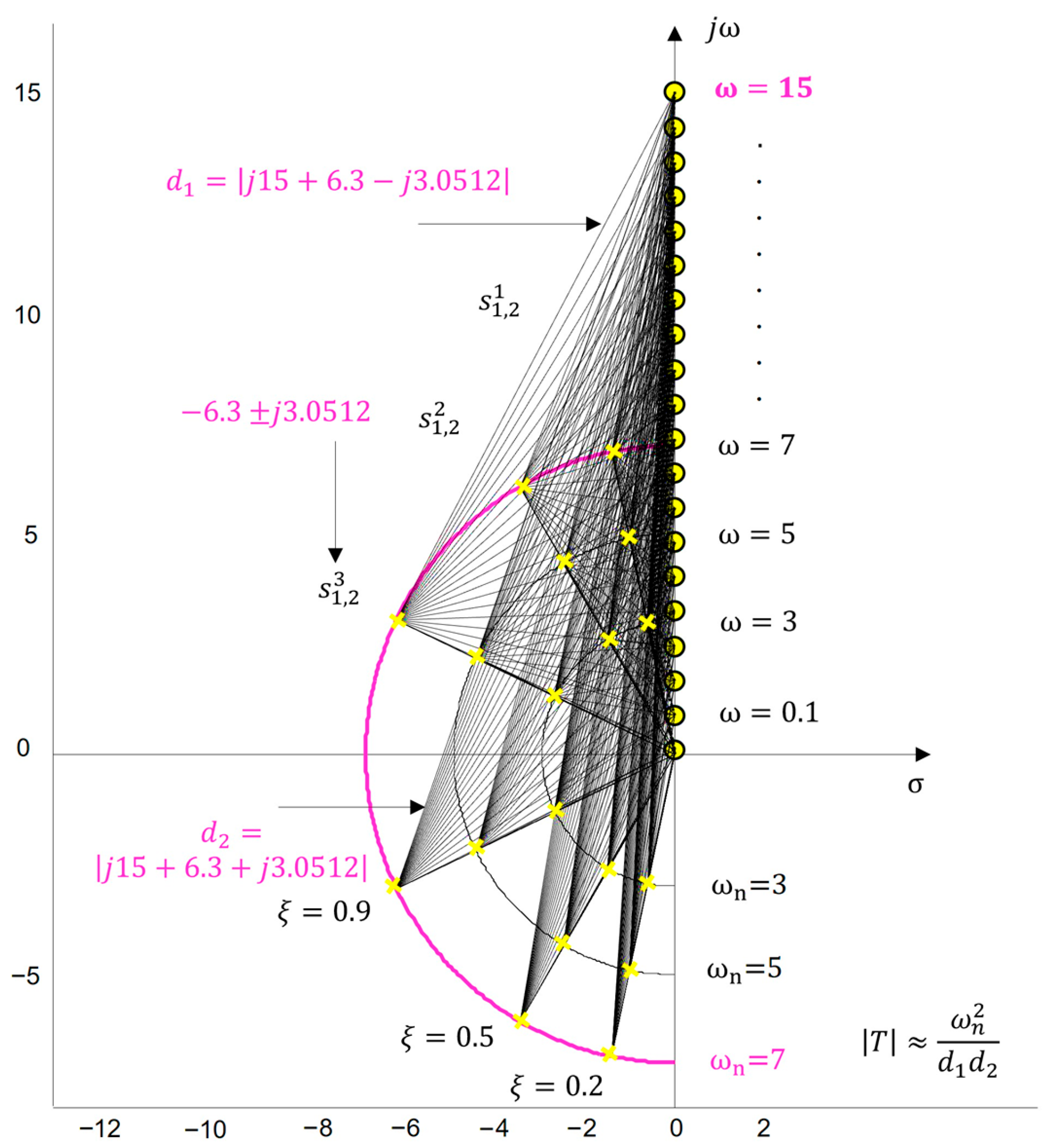
3.1. Calculation of Sensitivity Functions and
- If the control point frequency is close to the dominant poles and the distance to the imaginary axis is small, the magnitude becomes large, and the control system will exhibit oscillatory-damped transient responses.
- If the control point is far from the poles , is smaller, and the control system will show faster time response at that frequency .
- When , the magnitude of the closed-loop system tends to approach 1 more rapidly, and the system sensitivity remains low for a fixed damping ratio . However, if the value of , where changes, the real part of the dominant poles decreases, leading to an increase in the magnitude of the sensitivity function , as shown in Table A1.
- When , the magnitude , regardless of the value of the damping ratio , which results in , also shown in Table A1.
Discussion
- The dominant roots of the closed-loop system , which characterize the control of the real process , must be located sufficiently far from every point on the imaginary axis so that the magnitude remains acceptably small to compensate for the uncertainty .
- If the magnitude is larger, this leads to oscillations in the transient responses, a general reduction in system stability, and the robustness condition (31) will be violated.
- If are located close to the points on the imaginary axis , the distances and become small, i.e., is large, and stability decreases. On the other hand, this implies that will be small, (30), which is an indication of insensitivity.
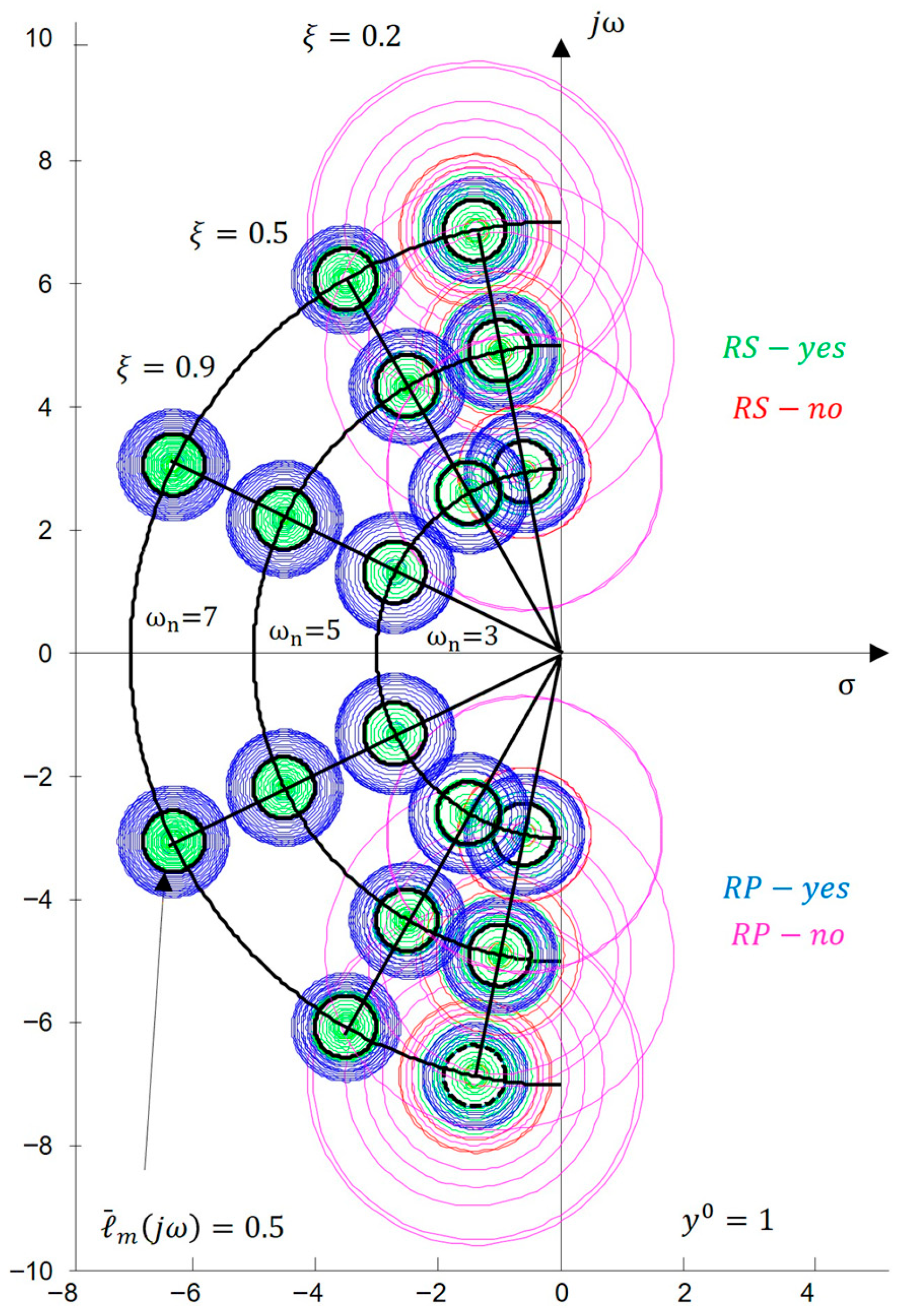
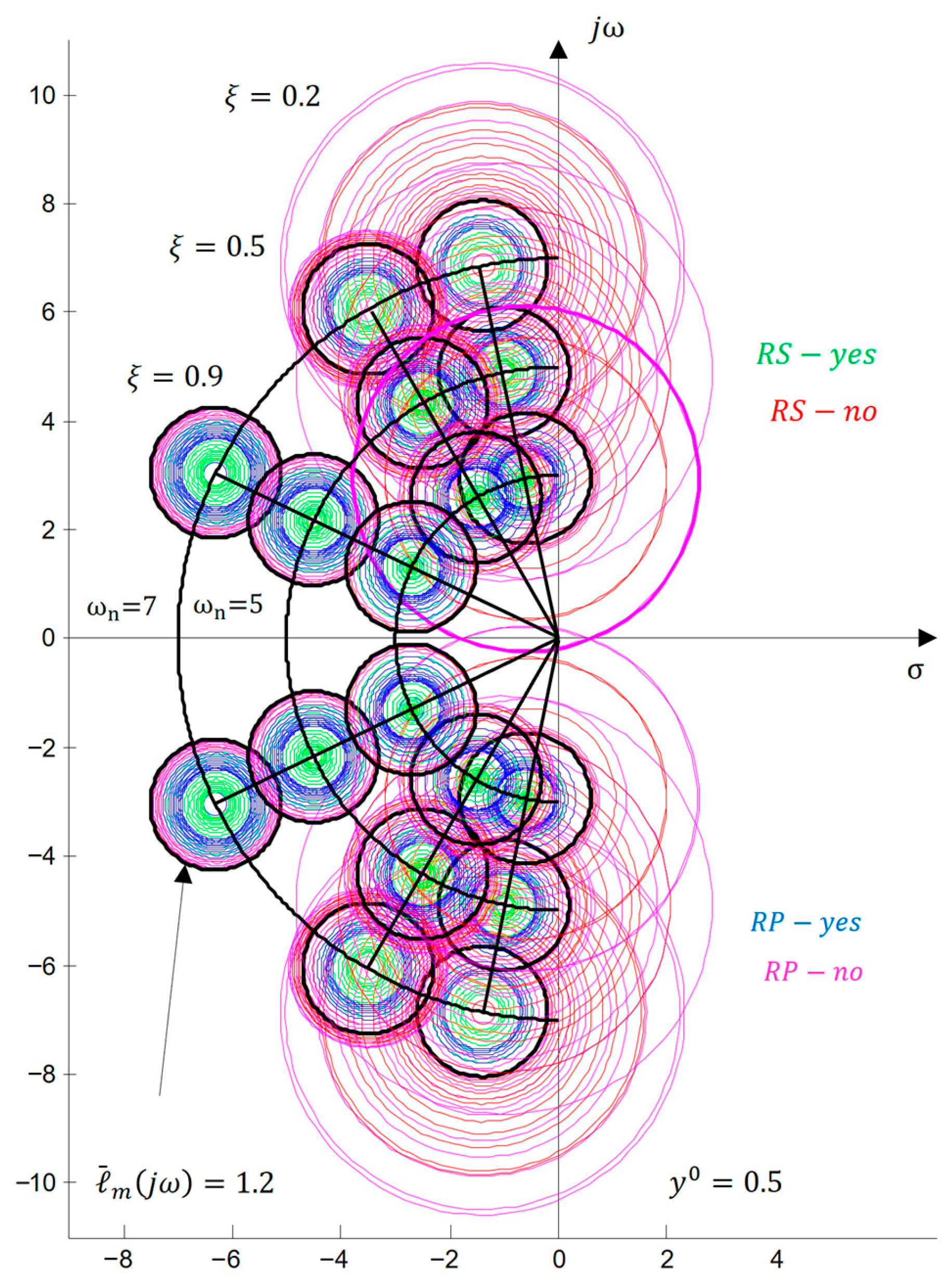
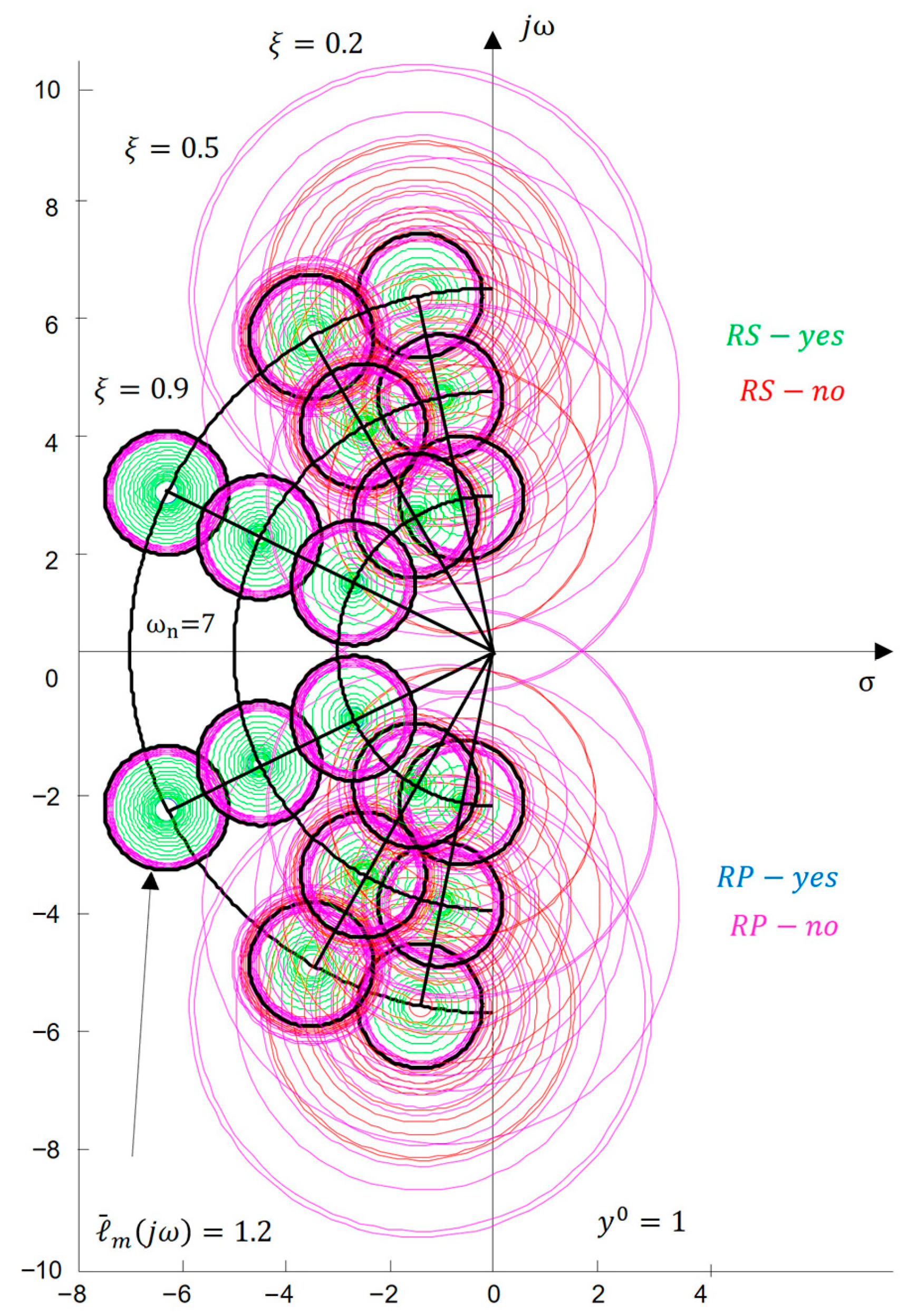
3.2. Robust Stability and Robust Performance (
Discussion
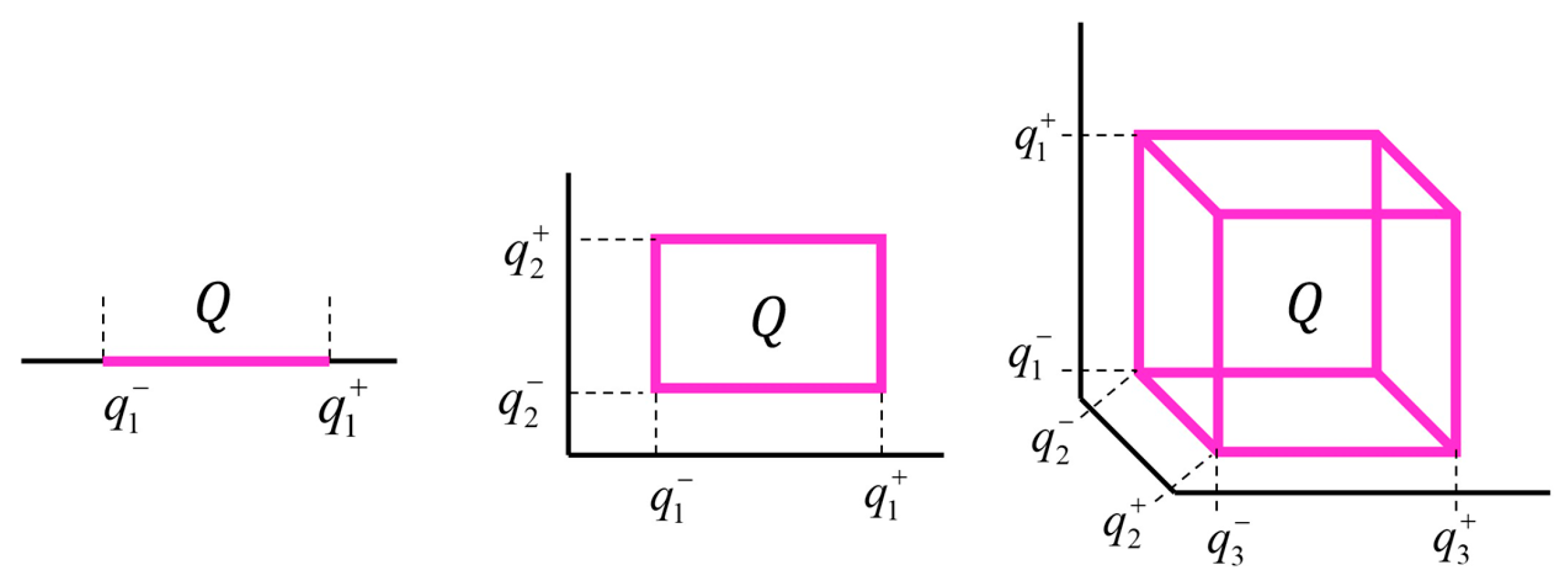
4. Parametric Uncertainty Models
4.1. Parameter Uncertainty
4.2. Generation in s-Complex Roots Plane
- For values of , the root locus enters the class of negative root locus ()).
- When modifying Equation (52), it is possible that Equation (53) violates the physical realizability condition, resulting in —that is, the order of the numerator polynomial exceeds the order of the denominator polynomial in the open-loop transfer function. Therefore, instead of using , as the varying parameter, the Evans coefficient function is represented by .
- In case of a nonlinear dependence of , the usual rules for constructing the root locus are not applicable.
4.2.1. Numerical Example
- Discussion
- Case 1—.
- 2.
- Case 2—.
- 3.
- Case 3— for , , , .
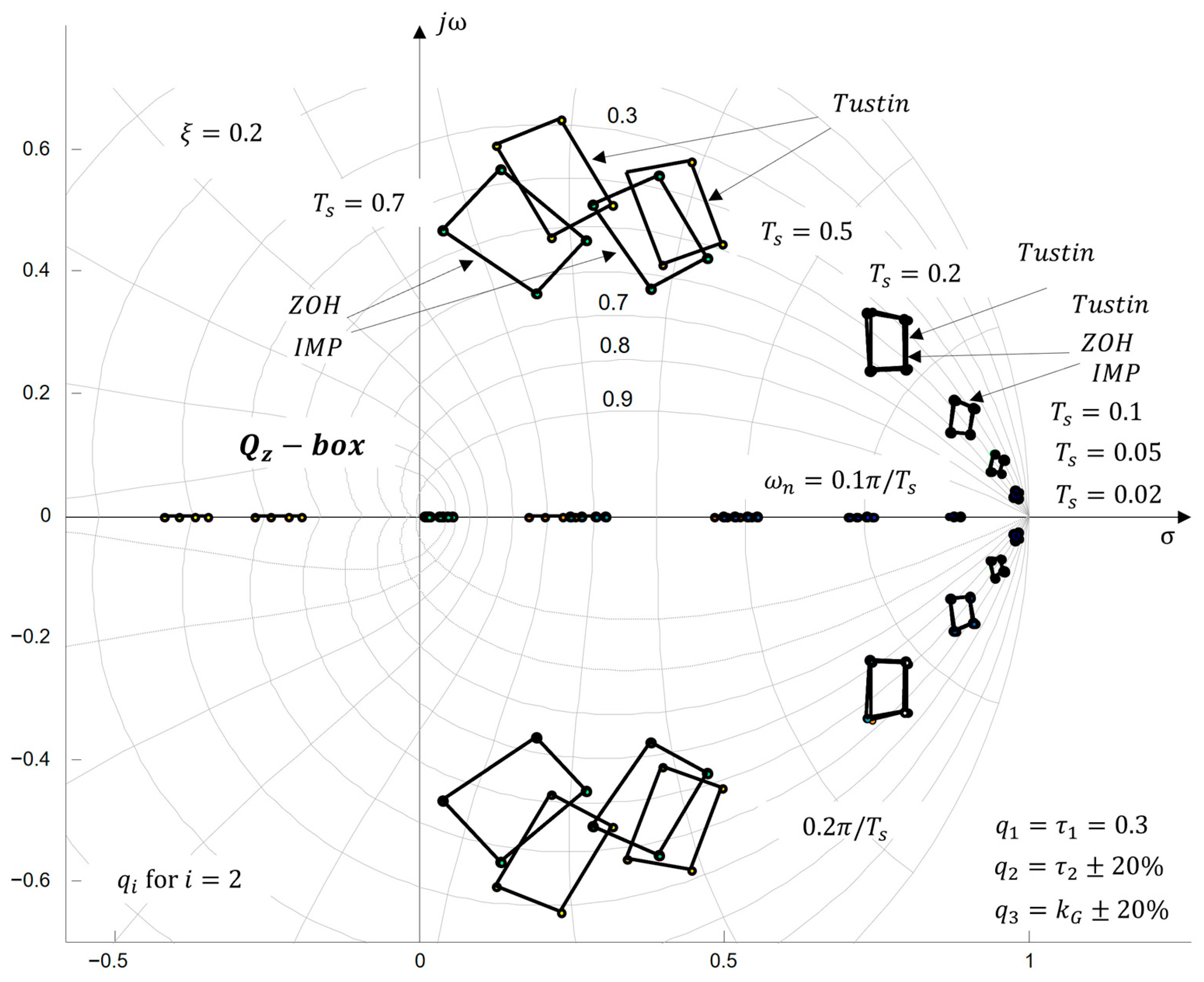
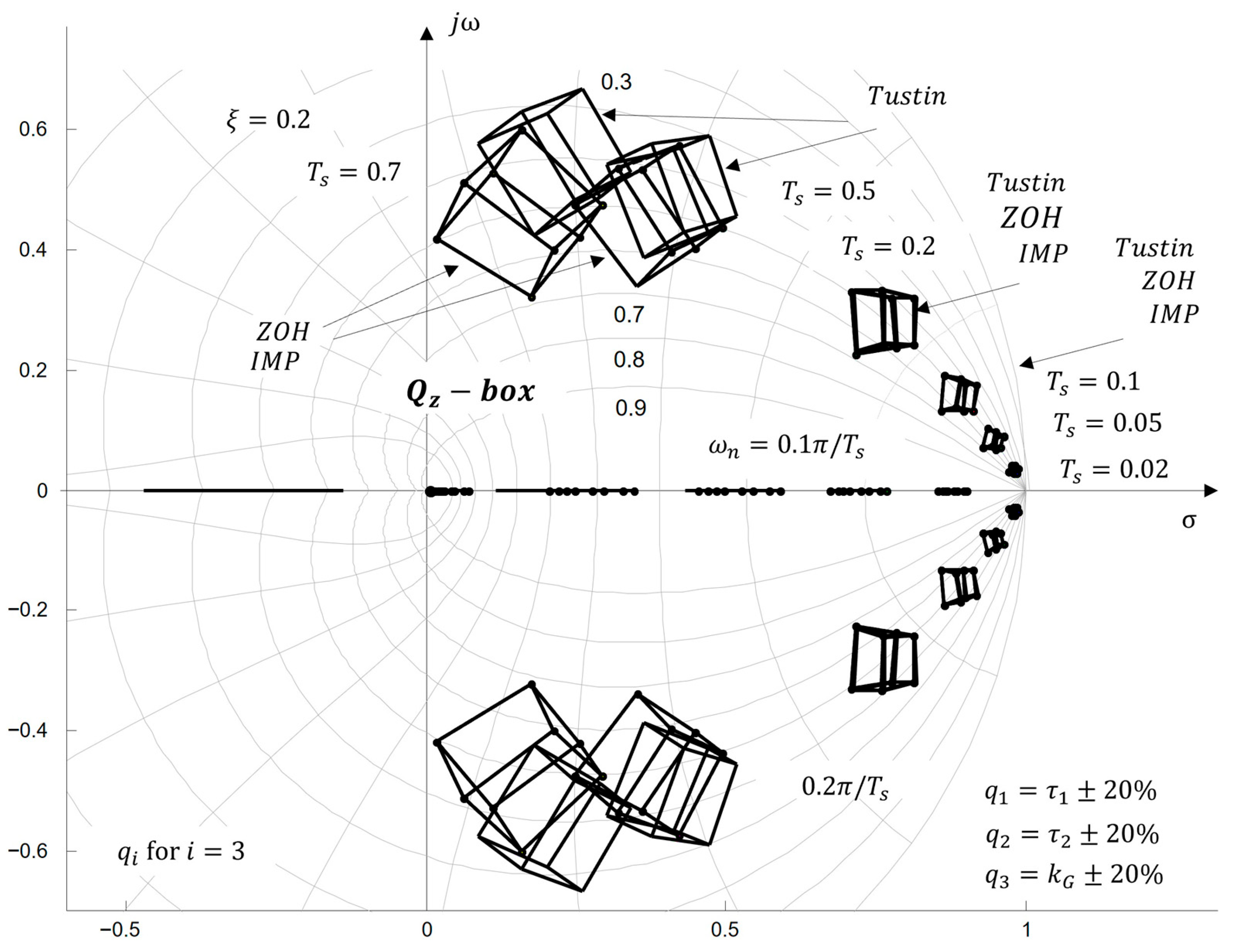
4.3. Generation in z-Complex Roots Plane
4.3.1. Numerical Example
- Discussion
- Discussion
4.3.2. Study of the Influence of Sampling Time
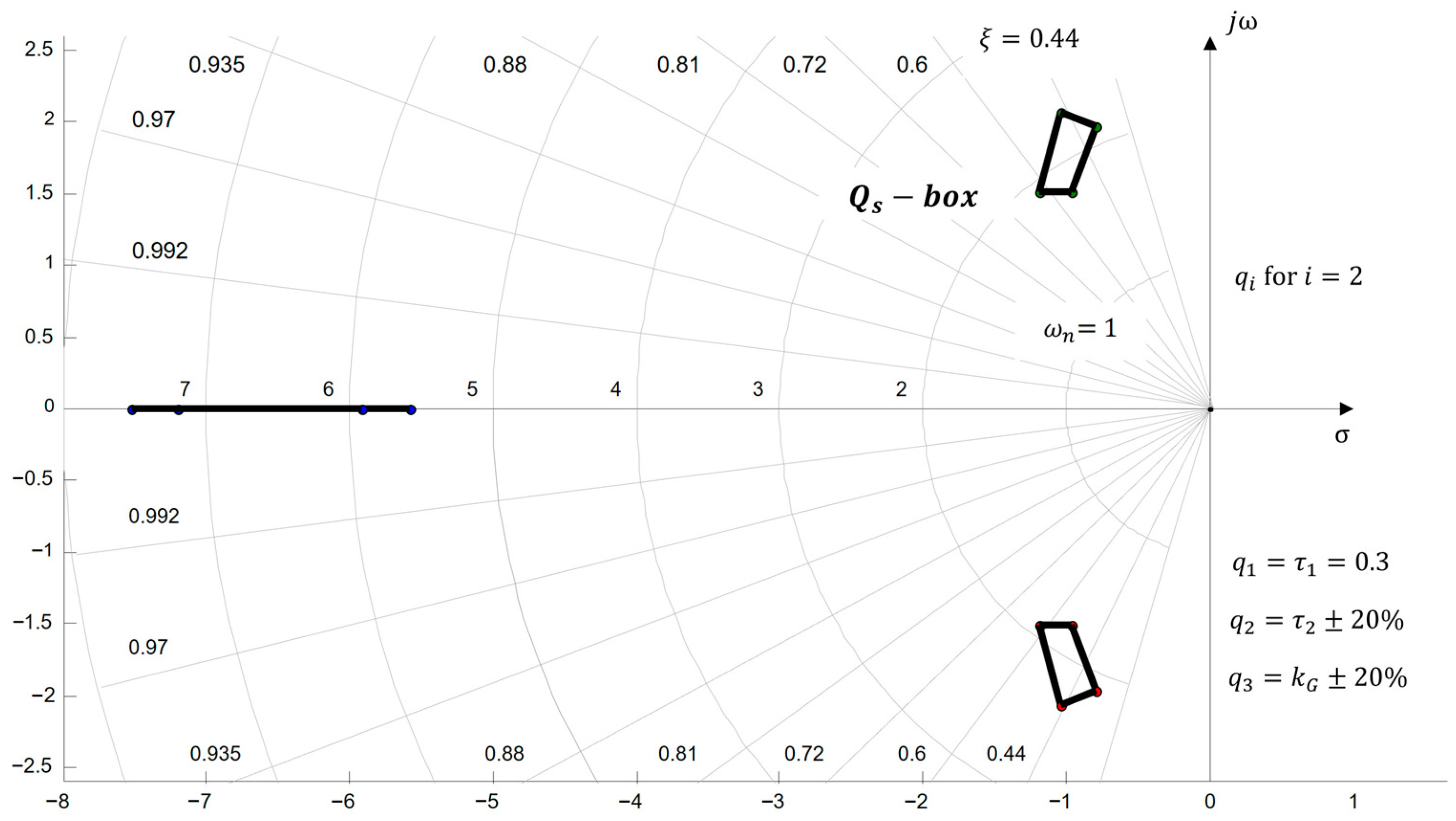
4.4. Generation in a Frequency Domain Design Template
4.4.1. Numerical Example
- Discussion
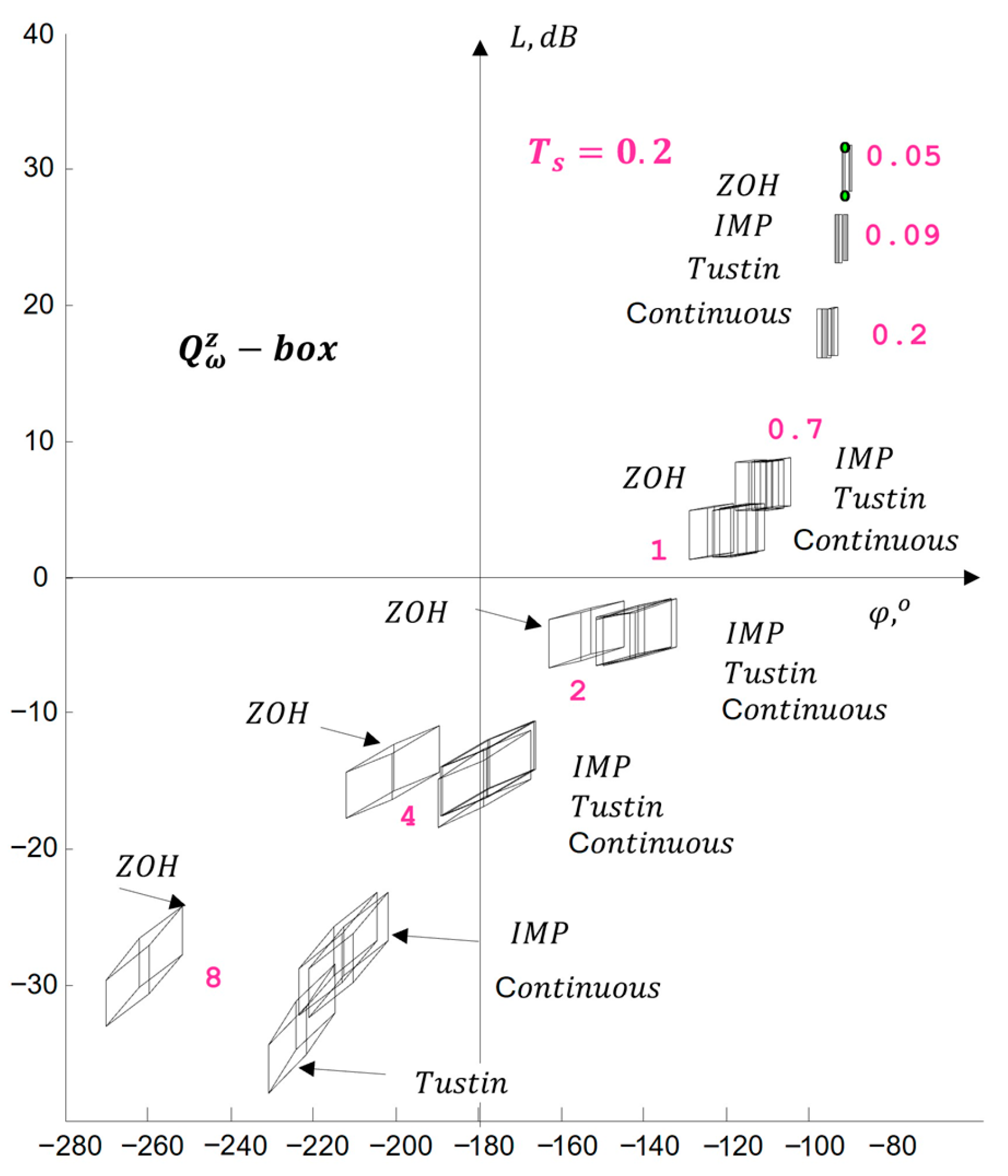
4.4.2. Robustness in the Frequency Domain
- —represented in the -complex plane, where each parameter set defines roots of the characteristic equation. The union of all roots forms a geometric field that illustrates the influence of uncertainty on the stability and performance of the continuous system.
- —a projection of the into the continuous frequency domain. It shows the range of frequency responses covered by parametric uncertainty and serves for graphical verification of robustness using the Nyquist and Nichols planes.
- —the discrete version of the in the -complex plane, obtained through discretization (I, , and ). It enables the analysis of the digital system and evaluation of stability and performance in its discrete implementation.
- —a projection of the into the discrete frequency domain, allowing analysis of the frequency responses of the digital system and assessment of robustness with respect to specific frequencies.
5. Discussion
- Graphical representation of performance regions and in the complex s- and z-planes through the integration of indirect performance indices (), presented in both continuous and discrete forms. Their relationship to direct performance indices () provides a practical basis for synthesizing control algorithms that ensure dominant closed-loop poles remain within the desired quality regions or under digital control implementations.
- Development of a graphical model of parametric uncertainty () in the space defined by process parameters. Models with one, two, and three varying parameters are discussed, with parallels drawn between the number of parameters and the resulting graphical form. Through analytical transformations based on characteristic equations, this model is mapped into the complex and -planes as and , enabling graphical assessment of stability and performance from the root locations of real controlled processes.
- Combining analysis of and with performance regions and , offering a visual tool to determine whether process uncertainty compromises or satisfies desired performance. This graphical integration supports the selection of appropriate control algorithms. Such visualization is particularly useful in engineering practice, as it simplifies the interpretation of complex dependencies and reduces the risk of errors in decision-making.
- Validation of control performance for existing algorithms or alternative strategies in the discrete domain, achieved by visualizing the impact of different discretization methods () and sampling periods . This evaluation is performed through the joint visualization of , and , analytically derived for various discretization methods and sampling times.
- Design of visual tools in the complex -plane based on established conditions for robust stability and robust performance formulated in the frequency domain. This enables the interpretation of robust stability () and robust performance () in the -plane of the roots through circles of radii , and , allowing for the calculation of a robust performance margin under different scenarios .
- Treatment of the sampling period as a priori uncertainty, by analyzing the effects of different discretization methods () on the shape and position of regions. An adapted root locus approach is used, modifying the characteristic equation to treat the Evans coefficient as a surrogate for sampling period .
- Derivation of the model in the discrete frequency domain from the parametric model with three varying parameters. This allows evaluation of the effects of discretization methods and sampling periods on uncertainty, guiding the choice or adjustment of discretization strategies. For completeness, the analysis also includes parametric uncertainty in in the continuous frequency domain, where graphical equivalents of robust stability and performance conditions are examined, alongside differences from multiplicative uncertainty .
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 0.10 | 3.00 | 0.20 | 2.9021 | 3.0980 | 1.0010 | 0.0010 | 1.202 | 1.201 | |
| 0.10 | 3.00 | 0.50 | 2.9138 | 3.0870 | 1.0006 | 0.0006 | 1.201 | 1.201 | |
| 0.10 | 3.00 | 0.90 | 2.9578 | 3.0449 | 0.9993 | 0.0007 | 1.200 | 1.199 | |
| 0.10 | 5.00 | 0.20 | 4.9021 | 5.0980 | 1.0004 | 0.0004 | 1.201 | 1.200 | |
| 0.10 | 5.00 | 0.50 | 4.9137 | 5.0868 | 1.0002 | 0.0002 | 1.200 | 1.200 | |
| 0.10 | 5.00 | 0.90 | 4.9572 | 5.0444 | 0.9998 | 0.0002 | 1.200 | 1.200 | |
| 0.10 | 7.00 | 0.20 | 6.9020 | 7.0980 | 1.0002 | 0.0002 | 1.200 | 1.200 | |
| 0.10 | 7.00 | 0.50 | 6.9136 | 7.0868 | 1.0001 | 0.0001 | 1.200 | 1.200 | |
| 0.10 | 7.00 | 0.90 | 6.9570 | 7.0442 | 0.9999 | 0.0001 | 1.200 | 1.200 | |
| 3.83 | 3.00 | 0.20 | 1.0697 | 6.7909 | 1.2389 | 0.2389 | 1.606 | 1.487 | |
| 3.83 | 3.00 | 0.50 | 1.9379 | 6.5959 | 0.7041 | 0.2959 | 0.993 | 0.845 | |
| 3.83 | 3.00 | 0.90 | 3.6915 | 5.7995 | 0.4204 | 0.5796 | 0.794 | 0.504 | |
| 3.83 | 5.00 | 0.20 | 1.4675 | 8.7811 | 1.9401 | 0.9401 | 2.798 | 2.328 | |
| 3.83 | 5.00 | 0.50 | 2.5505 | 8.5297 | 1.1491 | 0.1491 | 1.454 | 1.379 | |
| 3.83 | 5.00 | 0.90 | 4.7914 | 7.5036 | 0.6954 | 0.3046 | 0.987 | 0.834 | |
| 3.83 | 7.00 | 0.20 | 3.3410 | 10.7749 | 1.3611 | 0.3611 | 1.814 | 1.633 | |
| 3.83 | 7.00 | 0.50 | 4.1539 | 10.4884 | 1.1247 | 0.1247 | 1.412 | 1.350 | |
| 3.83 | 7.00 | 0.90 | 6.3473 | 9.3259 | 0.8278 | 0.1722 | 1.079 | 0.993 | |
| 7.55 | 3.00 | 0.20 | 4.6495 | 10.5065 | 0.1842 | 0.8158 | 0.629 | 0.221 | |
| 7.55 | 3.00 | 0.50 | 5.1741 | 10.2583 | 0.1696 | 0.8304 | 0.619 | 0.203 | |
| 7.55 | 3.00 | 0.90 | 6.8012 | 9.2600 | 0.1429 | 0.8571 | 0.600 | 0.171 | |
| 7.55 | 5.00 | 0.20 | 2.8334 | 12.4891 | 0.7065 | 0.2935 | 0.995 | 0.848 | |
| 7.55 | 5.00 | 0.50 | 4.0765 | 12.1403 | 0.5052 | 0.4948 | 0.854 | 0.606 | |
| 7.55 | 5.00 | 0.90 | 7.0066 | 10.7197 | 0.3328 | 0.6672 | 0.733 | 0.399 | |
| 7.55 | 7.00 | 0.20 | 1.5614 | 14.4764 | 2.1678 | 1.1678 | 3.185 | 2.601 | |
| 7.55 | 7.00 | 0.50 | 3.8031 | 14.0549 | 0.9167 | 0.0833 | 1.142 | 1.100 | |
| 7.55 | 7.00 | 0.90 | 7.7414 | 12.3319 | 0.5133 | 0.4867 | 0.859 | 0.616 | |
| 11.28 | 3.00 | 0.20 | 8.3572 | 14.2270 | 0.0757 | 0.9243 | 0.553 | 0.091 | |
| 11.28 | 3.00 | 0.50 | 8.8056 | 13.9539 | 0.0732 | 0.9268 | 0.551 | 0.088 | |
| 11.28 | 3.00 | 0.90 | 10.326 | 12.8691 | 0.0677 | 0.9323 | 0.547 | 0.081 | |
| 11.28 | 5.00 | 0.20 | 6.4540 | 16.2049 | 0.2390 | 0.7610 | 0.667 | 0.287 | |
| 11.28 | 5.00 | 0.50 | 7.3811 | 15.8041 | 0.2143 | 0.7857 | 0.650 | 0.257 | |
| 11.28 | 5.00 | 0.90 | 10.147 | 14.1870 | 0.1736 | 0.8264 | 0.622 | 0.208 | |
| 11.28 | 7.00 | 0.20 | 4.6330 | 18.1875 | 0.5815 | 0.4185 | 0.907 | 0.698 | |
| 11.28 | 7.00 | 0.50 | 6.2788 | 17.6869 | 0.4412 | 0.5588 | 0.809 | 0.529 | |
| 11.28 | 7.00 | 0.90 | 10.359 | 15.6503 | 0.3022 | 0.6978 | 0.712 | 0.363 | |
| 15.00 | 3.00 | 0.20 | 12.075 | 17.9494 | 0.0415 | 0.9585 | 0.529 | 0.050 | |
| 15.00 | 3.00 | 0.50 | 12.492 | 17.6619 | 0.0408 | 0.9592 | 0.529 | 0.049 | |
| 15.00 | 3.00 | 0.90 | 13.956 | 16.5297 | 0.0390 | 0.9610 | 0.527 | 0.047 | |
| 15.00 | 5.00 | 0.20 | 10.148 | 20.0351 | 0.1211 | 0.8789 | 0.690 | 0.325 | |
| 15.00 | 5.00 | 0.50 | 10.991 | 19.6020 | 0.1059 | 0.8941 | 0.667 | 0.287 | |
| 15.00 | 5.00 | 0.90 | 13.610 | 17.7170 | 0.0847 | 0.9153 | 0.573 | 0.124 | |
| 15.00 | 7.00 | 0.20 | 8.2194 | 22.0674 | 0.2840 | 0.7160 | 0.690 | 0.325 | |
| 15.00 | 7.00 | 0.50 | 9.7930 | 21.5540 | 0.2106 | 0.7894 | 0.582 | 0.140 | |
| 15.00 | 7.00 | 0.90 | 13.932 | 19.3397 | 0.1433 | 0.8567 | 0.633 | 0.228 |
| Method | |||||
|---|---|---|---|---|---|
| 0.02 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.02 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.02 | 0.341 | 0.681 | 1.674 | 2.511 | |
| 0.05 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.05 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.05 | 0.4 | 0.681 | 1.674 | 2.510 | |
| 0.1 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.1 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.1 | 0.339 | 0.679 | 1.672 | 2.505 | |
| 0.2 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.2 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.2 | 0.333 | 0.671 | 1.666 | 2.484 | |
| 0.5 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.5 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.5 | 0.298 | 0.614 | 1.623 | 2.334 | |
| 0.7 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.7 | 0.341 | 0.682 | 1.674 | 2.511 | |
| 0.7 | 0.267 | 0.554 | 1.571 | 2.173 |
References
- Horowitz, I.M. Quantitative Feedback Design Theory: Fundamentals and Applications; IEEE Press: Piscataway, NJ, USA, 1992. [Google Scholar]
- Goodwin, G.C.; Graebe, S.F.; Salgado, M.E. Control System Design; Prentice Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- Panahi, M.; Porta, G.M.; Riva, M.; Guadagnini, A. Modelling parametric uncertainty in PDEs models via Physics-Informed Neural Networks. Adv. Water Resour. 2025, 195, 104870. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C.; Glover, K. Robust and Optimal Control; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Tredinnick, M.; da Silveira, M.; de Oliveira e Souza, M. Sampling-Period Influence in Performance and Stability in Sampled-Data Control Systems. SAE Tech. Paper. 2003, 01, 3507. [Google Scholar] [CrossRef]
- Ádám, D.; Dadvandipour, M.; Futás, J. Influence of discretization method on the digital control system performance. Int. J. Control. 2009, 82, 853–865. [Google Scholar]
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson: London, UK, 2021. [Google Scholar]
- Golnaraghi, F.; Kuo, B.C. Automatic Control Systems, 10th ed.; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Richard, C.D.; Robert, H.B. Modern Control Systems, 14th ed.; Pearson: London, UK, 2021. [Google Scholar]
- Ackermann, J.; Kaesbauer, D.; Sienel, W.; Steinhauser, R.; Bartlett, A. Robust Control—Systems with Uncertain Parameters; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Sanchez-Pena, R.S.; Sznaier, M. Robust Systems—Theory and Applications; Jonh Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Barmish, B.R.; Tempo, R. The Robust Root Locus. International Federation of Automatic Control. Automatica 1990, 26, 283–292. [Google Scholar] [CrossRef]
- Henrion, D.; Šebek, M.; Kučera, V. Robust pole placement for second-order systems: An LMI approach. Kybernetika 2005, 41, 1–14. [Google Scholar] [CrossRef]
- Garcia-Sanz, M.; Houpis, C.H. Wind Energy Systems, Control Engineering Design; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Zhang, Y.; Wang, Z.; Zhang, L. Control Strategy and Corresponding Parameter Analysis of a Virtual Synchronous Generator. Electronics 2022, 11, 2806. [Google Scholar] [CrossRef]
- Wang, J.; Liu, T.; Li, J. Stable PIR Controller Design Using Stability Boundary Locus. Processes 2023, 13, 1535. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, Q.; Liu, J.; Wang, H. Small-Signal Stability Analysis of DC Microgrids Based on Root Locus Method. Energies 2023, 18, 2467. [Google Scholar] [CrossRef]
- Mondal, A.; Dolai, S.K.; Sarkar, P. A unified direct approach for digital realization of fractional order operator in delta domain. Facta Univ. Ser. Electron. Energetics 2023, 35, 313–331. [Google Scholar] [CrossRef]
- Baños, A.; Salt, J.; Casanova, V. A QFT approach to robust dual-rate control systems. arXiv 2020, arXiv:2002.03718. [Google Scholar] [CrossRef]
- Khozhaev, I.V.; Gayvoronskiy, S.A.; Ezangina, T.A. Adaptive-Robust Stabilization of Interval Control System Quality on a Base of Dominant Poles Method. Autom. Remote Control. 2021, 82, 132–144. [Google Scholar] [CrossRef]
- Nesenchuk, A.A. The root-locus method of synthesis of stable polynomials by adjustment of all coefficients. Autom. Remote Control. 2010, 71, 1515–1525. [Google Scholar] [CrossRef]
- Tanaka, S.; Ohnishi, K. Robust stability for uncertain sampled-data systems with discrete disturbance observers. arXiv 2019, arXiv:1901.08722. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Ohnishi, K. A guide to design disturbance observer-based motion control systems in discrete-time domain. IEEE Access 2021, 9, 32842–32860. [Google Scholar] [CrossRef]
- Biannic, J.-M.; Roos, C.; Cumer, C. LFT modelling and μ-based robust performance analysis of hybrid multi-rate control systems. arXiv 2024, arXiv:2407.04463. [Google Scholar]
- Zhang, X.; Kamgarpour, M.; Georghiou, A.; Goulart, P.; Lygeros, J. Robust optimal control with adjustable uncertainty sets. arXiv 2015, arXiv:1511.04700. [Google Scholar] [CrossRef]
- Arceo, V.M.; Arceo, R.P.; Cervantes, E.F. Robust Control for Uncertain Systems: A Unified Approach. Mathematics 2022, 10, 583. [Google Scholar] [CrossRef]
- Bartlett, A.C.; Hollot, C.V.; Huang, L. Root locations of polynomials with parametric uncertainty. IEEE Trans. Autom. Control. 1992, 37, 127–131. [Google Scholar]
- Noury, K.; Yang, B. A Pseudo S-Plane Mapping of Z-Plane Root Locus. In Proceedings of the ASME 2020 International Mechanical Engineering Congress and Exposition (IMECE2020), Portland, OR, USA, 15–19 November 2020; p. IMECE2020-23096. [Google Scholar]
- Alla, N. Investigation and Synthesis of Robust Polynomials in Uncertainty on the Basis of the Root Locus Theory. In Polynomials—Theory and Application; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Nesenchuk, A.A. Synthesis of Hurwitz Polynomial Families Using Root Locus Portraits. Autom. Control. Intell. Syst. 2019, 7, 84–91. [Google Scholar] [CrossRef]
- Arceo, M.I.; Lee, T.H.; Kim, J.H. On robust stability for Hurwitz polynomials via recurrence relations and linear combinations of orthogonal polynomials. Appl. Math. Comput. 2022, 427, 127004. [Google Scholar] [CrossRef]
- Bartlett, A.C.; Hollot, C.V.; Huang, L. A structural approach to robust stability of polynomials. Syst. Control. Lett. 1992, 19, 207–212. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y. Robust stability of fractional order polynomials with complicated uncertainty structure. Fract. Calc. Appl. Anal. 2017, 20, 649–672. [Google Scholar] [CrossRef]
- Gayvoronskiy, S.A.; Ezangina, T.A.; Khozhaev, I.V. Parametrical Synthesis of Linear Controllers in Aperiodical Systems on Basis of Decomposition Approach. Int. Rev. Autom. Control. (IREACO) 2019, 12, 192–199. [Google Scholar] [CrossRef]
- Karimi, A. Frequency-domain robust control toolbox. In Proceedings of the 2013 IEEE 52nd Annual Conference on Decision and Control (CDC), Florence, Italy, 10–13 December 2013. [Google Scholar] [CrossRef]
- Morari, M.; Zafiriou, E. Robust Process Control; Prentice Hall: Hoboken, NJ, USA, 1989. [Google Scholar]
- Karlova-Sergieva, V.A. Robust Performance Assessment of Control Systems with Root Contours Analysis. Cybern. Inf. Technol. 2025, 25, 83–99. [Google Scholar] [CrossRef]















| References | Approach/ Method | What It Evaluates | Limitations | Difference with the Present Research |
|---|---|---|---|---|
| [1,2,3] | Classical control | Stability and control performance | Lack of discretization and visualization | Integration of s-/z-planes with visual robustness assessment |
| [4,5,6] | H∞, μ-analysis, and discretization | Robustness under parameter variations | Focus on continuous-time systems | Integration of s-/z-planes and discretization as a priori uncertainty |
| [7,8,9,10,11,12,13,14] | Root locus and robust control | Tracking root trajectories | No discrete domain or visual assessment | Graph–analytic evaluation and visualization for MISO systems |
| [15,16,17,18,19,20] | Root locus and stability margins | Influence of parameters on behavior | Limited to s- or z-plane | Integrated s/z analysis with visual robustness assessment |
| [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] | Polynomials, convex combinations, and toolbox | Robustness under parametric uncertainty | Lack of integrated analysis and visualization | Combination of s-/z-planes, discretization, and visual robustness |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karlova-Sergieva, V. Approach for the Assessment of Stability and Performance in the s- and z-Complex Domains. Automation 2025, 6, 61. https://doi.org/10.3390/automation6040061
Karlova-Sergieva V. Approach for the Assessment of Stability and Performance in the s- and z-Complex Domains. Automation. 2025; 6(4):61. https://doi.org/10.3390/automation6040061
Chicago/Turabian StyleKarlova-Sergieva, Vesela. 2025. "Approach for the Assessment of Stability and Performance in the s- and z-Complex Domains" Automation 6, no. 4: 61. https://doi.org/10.3390/automation6040061
APA StyleKarlova-Sergieva, V. (2025). Approach for the Assessment of Stability and Performance in the s- and z-Complex Domains. Automation, 6(4), 61. https://doi.org/10.3390/automation6040061





