Intelligent Fault Diagnosis of Gas Pressure Regulator Based on AE-GWO-SVM Algorithm

Abstract

A pressure regulator is essential for pressure control in a gas transmission system. The traditional maintenance approaches for pressure regulators involve equipment disassembly that disrupts normal production. In response, this paper proposes a support vector machine (SVM) model improved by the grey wolf optimization algorithm (GWO) and autoencoder (AE), i.e., the AE-GWO-SVM model. It achieves intelligent fault diagnosis on pressure regulators based on operation data collected by the SCADA system. Firstly, a number of actual pressure regulator faults are counted, and it is found that internal and external leakages are key problems faced by pressure regulators. To address the limited fault data available in field practice, a dataset of pressure regulator faults is constructed using numerical simulation. Additionally, 18 new features are obtained through feature combination, and an improved distance evaluation method (IDE) is utilized to select highly correlated features as input for the machine learning model. Furthermore, an autoencoder (AE) is employed to overcome the interference from abnormal data, which significantly enhances the fault identification process of GWO-SVM. To verify the performance of the AE-GWO-SVM model, an experimental platform for pressure regulators is designed and constructed. Compared with conventional SVM, the accuracy of the AE-GWO-SVM model increases from 60.4% to 86.7%, indicating its strong diagnosis capability for pressure regulator faults.

1. Introduction

The gas transmission station is the heart of natural gas pipeline systems, serving as critical infrastructure for energy security. The safe and stable operation of the station is essential for normal the functioning of society and the economy. The flow process in these stations is complex with a wide variety of equipment, and various faults and abnormal conditions inevitably occur over time. A pressure regulator, which is key in controlling the pressure of gas transmission systems, is crucial for ensuring stable network operation [1]. High-frequency mechanical movement, high pressure, and corrosive environments easily lead to frequent malfunction and failure of pressure regulators. At present, most gas transmission stations carry out routine maintenance of pressure regulators that requires the disassembly of equipment and thus affects normal production. To a certain extent, it causes unreasonable allocation of maintenance resources and easily leads to “insufficient maintenance” or “excessive maintenance”. In practical applications, only the equipment diagnosed with a fault needs further repair, which helps to reduce the impact on normal production and save a lot of costs. In response, maintenance that judges the fault status of pressure regulators based on operational data has drawn much attention recently [2,3,4].

The mechanism of pressure regulator failure is complex with varieties of influencing factors. It is rather difficult to establish theoretical models between operating parameters and fault states at a mechanistic level, but the strong mathematical relationship between them makes data-driven machine learning feasible to assess the malfunction of pressure regulators. By inputting the operating parameters of the pressure regulator, its fault state can be determined, bypassing the complex failure mechanism. This maintenance strategy relies on two aspects, namely the collection of effective operational data of pressure regulators and reliability of the machine learning model [2]. As the stability of outlet pressure is one of the most important parameters that reflects the performance of gas regulators, varieties of fault diagnosis algorithms have been proposed by analyzing the outlet pressure of gas pressure regulators, such as fast Fourier transform (FFT) [5,6], short-time Fourier transform (STFT) [7], wavelet transform (WT) and wavelet packet decomposition (WPD) [8], empirical mode decomposition (EMD) [9,10], and Hilbert–Huang transform (HHT) [11,12]. For example, Hao et al. [13,14] conducted empirical mode decomposition and Hilbert–Huang transform to decompose the outlet pressure data of the regulator and proposed a safety warning method for gas pressure regulators based on support vector machines. Tian et al. [15] proposed a fault diagnosis approach combining complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and fuzzy c-means (FCM) clustering to classify three typical faults of gas regulators. Although outlet pressure is closely correlated to the malfunction of pressure regulators, it is by no means the only indicator, where other parameters such as flow rate and temperature also play important roles in the fault diagnosis of pressure regulators.

To achieve the intelligent fault diagnosis of pressure regulators based on their operating status, this work uses numerical simulation to obtain basic data for fault diagnosis. Methods for data preprocessing and feature parameter selection are proposed. A support vector machine (SVM) model is used to calculate the characteristic parameters of the flow field within the gas pressure regulator. A grey wolf optimizer (GWO) is employed to optimize penalty factors and kernel function parameters of the SVM. Then autoencoders (AE) are used to determine the deviation between the predicted and actual flow field parameters for fault diagnosis. By inputting parameters such as temperature, pressure, flow rate, and opening degree collected from the SCADA system, it achieves the identification of internal leakage and external leakage of the gas pressure regulator. It enhances the precision of equipment maintenance and helps to ensure the production safety of gas transmission stations.

2. Theoretical Basis

2.1. Support Vector Machine (SVM)

Support vector machine (SVM) is a machine learning method based on statistical learning theory and the structural risk minimization principle. It has many unique advantages in solving small sample, nonlinear and high-dimensional pattern recognition problems [16], especially in overcoming the problems of “dimension disaster” and “overlearning”. It has been widely used in pattern recognition, regression analysis, function estimation, time series prediction, and so on. The basic principle of SVM is to find an optimal classification hyperplane and maximize the distance between different sample datasets and the hyperplane, so as to achieve good classification effects.

Penalty factor C and kernel function parameter $\gamma$ are key parameters that impact the classification performance of SVM. The penalty factor C is used to balance the complexity and stability of the SVM, while the kernel function parameter $\gamma$ is responsible for regulating the classification accuracy. In application, it is necessary to select the appropriate penalty factor C and kernel function parameter $\gamma$ according to the specific circumstance to improve prediction accuracy. In this work, the grey wolf optimization algorithm (GWO) is used to obtain the optimal parameters of the SVM model.

2.2. Grey Wolf Optimizer (GWO)

The swarm intelligence optimization algorithm is inspired by the interaction behaviours between social animals. It simulates the social structure and survival behaviour characteristics of the animals in nature. The grey wolf optimizer (GWO) is a bionic heuristic algorithm that mimics the communication and sharing mechanisms as well as the hierarchical division principles of grey wolf packs [17]. Grey wolf packs have a social class structure, dividing the grey wolf population into four levels, namely α, β, δ, and ω, based on the roles and advantages the wolves play in hunting, following a pyramid principle. In grey wolf population, the α wolf holds the highest authority and manages the pack, though it is not necessarily the strongest wolf. The β wolves assist the α wolf in decision-making and relay orders from the α wolf to lower-ranking wolves, allowing them to control wolves of lower ranks. The δ wolves are responsible for reconnaissance and pursuit, obeying orders from the α and β wolves. The ω wolves have the lowest rank in the pack. They coordinate internal relations of the pack and hunt prey under the leadership of higher-ranking wolves [18].

For optimization problems, finding the final position of the prey is a prerequisite for obtaining the global optimal solution. After clear division of labour, the positions of each level of grey wolves are firstly judged, then the ω wolves surround and attack the prey under the leadership of the α, β, and δ wolves.

$$\begin{array}{l}D=|C\cdot X_p(t)-X(t)|\\ X(t+1)=X_p(t)+A\cdot D\end{array}$$

(1)

where X_p(t) is the position of the prey; X(t) is the position of the grey wolf individual at the t-th iteration; and A and C are coefficient vectors.

The hunting process of grey wolves is guided by α, β, and δ wolves. Position updating of grey wolf individuals can be described as

$$\left\{\begin{array}{l}{D}_{\alpha }=|C_1{X}_{\alpha }(t)-X(t)|\\ D_{\beta }=|C_2{X}_{\beta }(t)-X(t)|\\ D_{\delta }=|C_3{X}_{\delta }(t)-X(t)|\end{array}\right.$$

(2)

where D_α, D_β, and D_δ are the distance between the candidate and optimal grey wolves after t iterations; C₁, C₂, and C₃ are random coordinate coefficients; and X_α(t), X_β(t), and X_δ(t) are the position vectors of the current α, β, and δ wolves.

The movement direction of each grey wolf is

$$\left\{\begin{array}{l}{X}_1=X_{\alpha }(t)-A_1{D}_{\alpha }\\ X_2=X_{\beta }(t)-A_2{D}_{\beta }\\ X_3=X_{\delta }(t)-A_3{D}_{\delta }\end{array}\right.$$

(3)

After the t + 1 iteration, the position of grey wolf is

$$X(t+1)=(X_1+X_2+X_3)/3$$

(4)

3. Fault Statistics of Pressure Regulator in Field

In actual production, pressure regulators seldom break down and are generally repaired immediately to resume production. Moreover, destructive fault testing is not allowed at the production site. Therefore, it is difficult to obtain enough fault data of the pressure regulator to support the training and testing of machine learning models. Hence, numerical simulation is used to acquire field characteristic parameters of pressure regulators and to establish the basic fault dataset.

3.1. Fault Data of Pressure Regulator in Field

A total of 68 actual pressure regulator faults were counted, including 15 cases of gasket damage, 10 cases of foreign object blocking, 12 cases of external leakage caused by aging and failure of sealing parts, 7 cases of sleeve jamming by impurities, 3 cases of connection column damage, and the others are mainly electrical faults (Figure 1).

Foreign object blocking and sleeve jamming by impurities make the sleeve irremovable, which can be directly observed from the travel indicator. Damage of connection column leads to a complete loss of both the valve core and seat, making the pressure regulator a straight-through structure that losses the capability of pressure regulation. Therefore, numerical modelling in this work mainly focuses on two faults, i.e., internal leakage caused by gasket damage and external leakage caused by aging and failure of sealing parts.

3.2. Physical Model and Meshing

According to the geometry of actual pressure regulators, the gas flow space of the regulator is filled using the SolidWorks 2022 software, obtaining the fluid domain and fluid boundaries (Figure 2). Internal leakage is achieved by setting a square notch on the gasket, and external leakage is simulated by setting a leakage hole near the seal.

The obtained geometric model of the internal flow field of the pressure regulator is imported into the Workbench meshing module (Figure 3). The overall grid size is set to be 0.006 m. As the flow condition at the sleeve and core of the valve drastically changes, the mesh are densified at these locations, with a grid size of 0.002 m. Additionally, an expansion layer is set at the boundaries to better simulate the flow boundary layer. The final number of mesh nodes obtained is 237,259.

3.3. Simulation Settings

Due to the throttling effect of natural gas, the energy equation needs to be solved. In turbulent flow model selection, the Realizable k-epsilon model achieves consistent Reynolds stress with actual turbulent flow; thus, we chose the Realizable k-epsilon model as the turbulent flow model, with the standard wall function employed. Gas composition is set based on the actual composition of natural gas. The inlet is a mass flow boundary and the outlet is a pressure exit boundary. The SIMPLEC algorithm is taken to solve the model. The turbulent kinetic energy and turbulent dissipation rate are calculated using the second-order upwind scheme to achieve second-order accuracy.

By numerical simulation, characteristic parameters of the pressure regulator flow field under normal, internal leakage, and external leakage conditions are obtained. Monitoring points are set at 0.5 m upstream and downstream of the valve port. Then, 72 sets of temperature, pressure, velocity, and density data at each monitoring point under different fault modes, opening degrees, inlet flow rates, and outlet pressures are obtained, forming a foundational dataset for fault diagnosis of pressure regulators.

4. Fault Diagnosis of Pressure Regulators

4.1. The GWO-SVM Model

When the SVM model is optimized by GWO, the penalty factor C and kernel function parameter $\gamma$ are mapped into position parameters of grey wolf individuals to generate α, β, and δ wolves, further updating the position of omega wolves. Next, continuous iterative optimization is performed until convergence conditions are met. Then the position of the α wolf is the output as the optimal solution for penalty factor and kernel function parameters. The SVM classification model is rebuilt using this optimal solution to obtain prediction results. As shown in Figure 4, implementation of the GWO-SVM model proceeds as follows:

(1) Preprocess the data of the regulator and divide the data into the training set and test set at a particular ratio.

(2) Initialize the number and position of the wolf packs, as well as the maximum iteration number, then set the optimization range of C and $\gamma$ in the SVM. In optimization, the position of the α wolf represents a feasible solution of the parameter combination.

(3) Before the maximum iteration number is reached, the α, β, and δ wolves estimate the position of the prey. The position vectors of α, β, and δ wolves are calculated. Based on fitness, three optimal individuals and their historical optimal position X₁ + X₂ + X₃ are determined and the location of the prey is updated.

(4) Repeat the above step and update the positions of the grey wolves until the termination condition is met or the fitness threshold is reached. Then output the position of the alpha wolf as penalty factor C and kernel function parameters $\gamma$ to build the SVM model.

4.2. Data Preprocessing

Insufficient feature data dimension may be unable to cover potential hidden patterns or information, leading to neglect of important details and thus limiting the performance of fault identification models. Moreover, information loss in data makes the model highly sensitive to minor changes in input data, causing instability in recognition of pressure regulator faults.

Feature engineering is a common data preprocessing method that improves model performance by extracting, transforming, and combining features from raw data. Feature combination integrates multiple related features to enable the model to capture nonlinear relationships and interaction effects in data, which reflects the physical properties of the system better, thereby enhancing prediction accuracy. As shown in

Table 1. Combined features obtained from original features and feature engineering.

Raw Feature	Combination Features
F1 = Opening	$F_6=F_2/F_4$	$F_{12}=F_2-F_1$	$F_{18}=F_2\times F_3^2$
F2 = Temperature	$F_7=F_1\times F_3$	$F_{13}=F_2/F_4$	$F_{19}=F_2\times F_3$
F3 = Flow rate	$F_8=F_4-F_3$	$F_{14}=F_1-F_5$	$F_{20}=F_2\times F_4$
F4 = Pressure	$F_9=F_1\times F_2$	$F_{15}=F_5/F_6$	$F_{21}=F_4\times F_5$
F5 = Density	$F_{10}=F_4/F_3$	$F_{16}=F_2\times F_1^2$	$F_{22}=\ln (F_4)$
	$F_{11}=F_1-F_4$	$F_{17}=F_1\times \ln (F_2)$	$F_{23}=F_4\times F_2^2$

, this work supplements the original data using feature combination methods. A total of 18 combined features are obtained.

4.3. Selection of Characteristic Parameter

Characteristic parameter selection is the process of identifying relevant features and removing irrelevant or redundant characteristic parameters to identify a subset of features that can effectively describe the problem. In this work, the improved distance evaluation (IDE) method is used to rank the features in Table 1 and to select the appropriate feature subset as input for the machine learning classifier. The distance evaluation method assesses the classification contribution of features based on the distance or similarity between different samples, then returns a score for each feature. The feature score ranges from 0 to 1, where a higher score indicates greater contribution for classification and more information that helps to distinguish the categories. A lower score indicates less contribution and irrelevant features may interfere in the learning process, further deteriorating the predictive performance of the machine learning model. More detailed information regarding the IDE method is given elsewhere [19,20]. Features with scores exceeding 0.5 are selected as input for the subsequent classification model.

To avoid misjudgment of model performance caused by information leakage, nested cross-validation with ensemble feature selection is adopted. Initially, the training set is divided into k folds. IDE feature selection and model training are performed on k − 1 fold and model performance is evaluated on the i-th fold. Then all folds are cycled to obtain the average performance of cross-validation. The average standard deviations of five-fold cross-validation of GWO-SVM include RMSE = 0.1410 ± 0.0042, R² = 0.9968 ± 0.0006, MAPE = 10.87 ± 0.35, indicating that the fitting process of the model in the training set is stable. Next, feature selection is carried out on the complete training set. In this work, F7, F8, F4, F15, F22, F2, and F1 are selected as the input features of the model.

4.4. Performance Verification

To demonstrate the performance of the GWO-SVM model, three evaluation indicators are introduced to evaluate its prediction performance, namely root mean square deviation (RMSE), coefficient of determination (R²), and mean absolute percentage error (MAPE).

$$\left\{\begin{array}{l}\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n(Y_{i\exp }-Y_{i\mathrm{pred}}})}\\ {\mathrm{R}}^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{(Y_{i\exp }-Y_{i\mathrm{pred}})}^2}}{{\displaystyle \sum _{i=1}^n{(Y_{i\mathrm{pred}}-\overline{Y})}^2}}}\\ \mathrm{MAPE}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|\frac{Y_{i\exp }-Y_{i\mathrm{pred}}}{Y_{i\exp }}\right|}\times 100\%\end{array}\right.$$

(5)

Five other parallel models are established to verify the fitting ability of the GWO-SVM model for fault mode recognition of pressure regulators, including traditional SVM, GA-SVM, SSA-SVM, WOA-SVM, and BES-SVM. The characteristics of each optimization algorithm are as follows.

Genetic algorithm (GA) [21]: A genetic algorithm is a random global search optimization method that adjusts the position of individuals by simulating natural selection and genetic behaviours such as replication, crossover, and variation, and passes it on from generation to generation. Finally, it converges to a group of individuals that is most suitable for the environment, so as to find the optimal solution of the problem.

Sparrow search algorithm (SSA) [22]: It is primarily inspired by the foraging and anti-predation behaviours of sparrows. In foraging, the population is divided into discoverers and followers. The discoverers are responsible for finding food, while the followers use the discoverers to obtain food and simultaneously monitor the discoverers. Additionally, when the sparrow population senses danger, they engage in anti-predation.

Whale optimization algorithm (WOA) [23]: It mimics the group behaviour of whales and the bubble netting technique. The position of each whale represents a viable solution. In prey hunting, each whale exhibits two behaviours: one is to encircle the prey, where all whales move towards the prey, and the other is bubble netting where the whales swim in a circular pattern and release bubbles to drive away the prey.

Bald eagle search algorithm (BES) [24,25]: By simulating the fish hunting behaviour of bald eagles, this algorithm has advantages of strong convergence, few parameters, and easy implementation. According to the hunting strategy and social behaviour of bald eagles, the algorithm is mainly divided into three stages: selection, searching, and diving.

The relationship between pressure regulator failure mode and parameters such as temperature, pressure, and flow velocity is not a simple one-to-one correspondence. It is insufficient to describe the complex failures modes including internal and external leakage from the perspective of these parameters. Therefore, the direct judgement of pressure regulator failure mode using machine learning may not be accurate. In this work, machine learning is employed to calculate parameters such as temperature, pressure, flow rate, and velocity before and after the valve under normal, internal leakage, and external leakage conditions. The actual operating parameters are then compared with predicted values under different fault states (the normal condition can be considered a special type of fault condition) to determine the type of pressure regulator failure mode. The population size for each model is set to be 50, and the number of iterations is set to be 500. SVM is optimized using the above algorithms to predict the outlet velocity of the pressure regulator. A performance comparison is shown in

Table 2. Comparison of SVM models optimized by different algorithms.

Evaluation Indicator	RMSE	R2	MAPE (%)
Not optimized	0.3740	0.9784	30.93
GA-SVM	0.2913	0.9836	20.15
SSA-SVM	0.1591	0.9914	14.87
WOA-SVM	0.1579	0.9963	12.45
BES-SVM	0.5538	0.9483	27.12
GWO-SVM	0.1243	0.9977	10.15

.

It can be seen that RMSE of the GWO-SVM model is only 0.1243, which is the lowest among all models, indicating that the dispersion degree of GWO-SVM prediction is the smallest. R² of the GWO-SVM model is 0.9977, which proves that it has the best fitting performance and the strongest correlation between predicted and simulated outlet velocities. In addition, MAPE of the GWO-SVM model is also the lowest, indicating that deviation between the predicted and simulated values of this model is the smallest. In short, the GWO-SVM model has the highest prediction accuracy.

Wilcoxon rank sum test is employed to compare the difference in distribution between two independent samples. By merging two sets of data and performing rank sorting, the difference in rank sum is calculated to verify whether there is a significant difference between the two sets of data.

Table 3. Summary of Wilcoxon rank sum test for RMSE of GWO-SVM and other algorithms.

Evaluation Indicator	Not Optimized	GA-SVM	SSA-SVM	WOA-SVM	BES-SVM	GWO-SVM
Not optimized	-
GA-SVM	•	-
SSA-SVM	•	◦	-
WOA-SVM	•	◦	•	-
BES-SVM					-
GWO-SVM	•	•	◦	◦	•	-

gives the statistical results of RMSE on the Wilcoxon rank sum test. In this table, the symbol • indicates that the algorithm in the row is significantly superior to that in the corresponding column, while the symbol ◦ indicates that the algorithm in the row is superior to the algorithm in the corresponding column, with the significance level set to be p = 0.1. The significance level of the diagonal is p = 0.05. As shown in Table 3, in terms of RMSE, GWO-SVM is superior to SSA-SVM and WOA-SVM, and it is significantly superior to unoptimized SVM, GA-SVM, and BES-SVM.

5. Improvement of GWO-SVM by Autoencoder (AE)

Residual statistical analysis is a common fault detection method. By comparing the difference between machine learning prediction and actual values under different fault modes, it takes the fault state with the smallest residual as the final judgement. This method has advantages of simple calculation and good interpretability. However, as residual statistical analysis directly focuses on data deviation, it is highly sensitive to abnormal values and may produce false positives or false negatives in the presence of noise and data changes. In this work, an autoencoder (AE) is used to mine the discriminative key features from the samples and determine the fault mode of the test samples. A machine learning model for the fault identification of pressure regulators based on the AE-GWO-SVM algorithm is constructed.

In the AE-GWO-SVM algorithm, GWO-SVM is used to predict the key parameters of the pressure regulator flow field under different fault modes with varying openings and boundary conditions. The AE technology is then employed to handle the difference between predicted and actual values and achieves the detection of abnormal features.

A single-layer sparse autoencoder is adopted for feature compression and reconstruction. The encoder–decoder employs a symmetrical structure, with the bottleneck dimension set to be 4 to achieve effective compression while maintaining key information. The activation function of the hidden layer is logsig, and the output layer uses linear activation for continuous value reconstruction. The mean squared error (MSE) is used as reconstruction loss in training. L2 weight regularization and sparse constraints are applied to prevent overfitting and encourage sparse activation of the hidden units. The maximum number of training iterations is set to be 400.

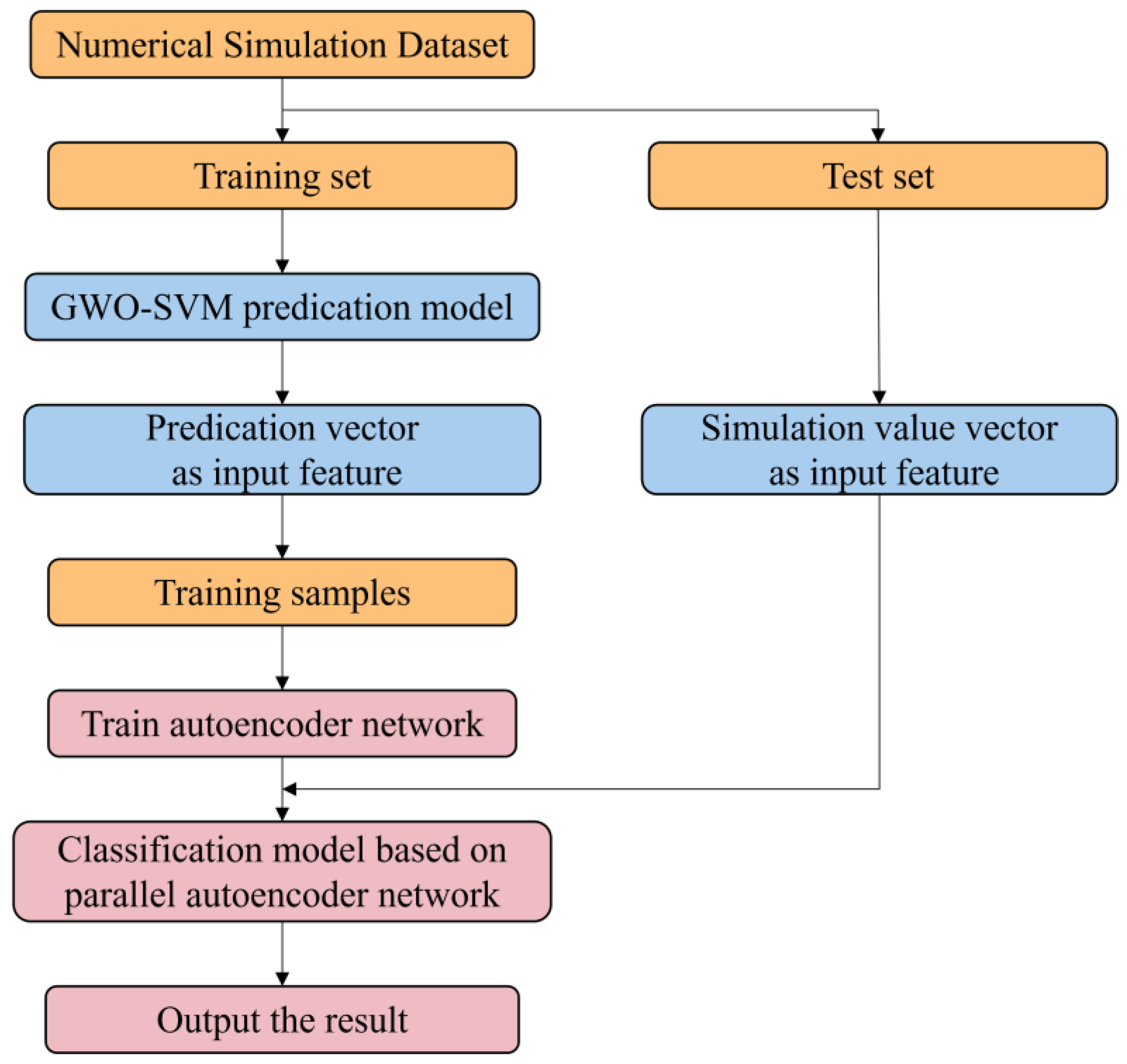
Two parallel AE networks are trained, where AE1 is responsible for distinguishing the normal and fault states of the pressure regulator, and AE2 is used for identifying internal leakage and external leakage. The combination of AE1 and AE2 realizes the classification of three operating conditions, normal, internal leakage, and external leakage, as shown in Figure 5.

(1) Based on the numerical simulation of pressure regulator fault modes, temperature, pressure, fluid velocity, density, and other parameters at monitoring points upstream and downstream of the pressure regulator are measured and recorded under different fault modes and different boundary conditions.

(2) The data are divided into training set and test set at an 8:2 ratio, and the downstream gas velocity is obtained by the GWO-SVM model in the training set.

(3) Construction of the AE network is conducted through unsupervised pre-training and supervised fine-tuning. Pre-training learns the complex nonlinear transformations of input signals, while the fine-tuning process enhances the network recognition accuracy. These two processes ensure that the AE network can extract effective information from feature vectors composed of predicted values and establish a nonlinear mapping relationship between feature vectors and actual categories.

(4) Test the performance of the trained AE network and output fault classification results of the pressure regulator.

6. Experimental Validation

An experimental platform was designed and constructed to carry out the pressure regulator fault diagnosis experiments (Figure 6a). The experimental medium is compressed air at 1 MPa, which is stored in 8 series of 10-m³ air tanks. The gas is introduced into the experimental setup through a high-pressure flexible hose. At the inlet, there are temperature and pressure transmitters, as well as a gas turbine flow metre. The axial pressure regulator (Figure 6b) is located downstream of the filter separator, with a flow diameter of 50 mm, and equipped with a silencer. The temperature transmitter, pressure transmitter, and gas turbine flow metre are also installed downstream of the pressure regulator. Compressed air passes through a spring-loaded safety valve and a ball valve, then gets released into the atmosphere. Internal and external leakage experiments of compressed gas were conducted at different pressures and flow rates. Internal leakage was achieved by cutting the valve gasket (as shown in Figure 6c), and external leakage was realized by loosening the valve bolts.

To assess the performance of the AE-GWO-SVM model in the classification of pressure regulator fault, a direct SVM model is established as a parallel reference. The accuracy index is introduced to estimate the classification capacity of the models.

$$ACC={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}\times 100\%$$

(6)

Fault tests of pressure regulators under different operating conditions were conducted, and the fault modes are identified using conventional SVM and AE-GWO-SVM models. The accuracy rate of direct classification by SVM is only 60.4%, while that of the AE-GWO-SVM model reaches up to 86.7%, achieving an improvement of 26.3%. This demonstrates the effectiveness of the AE-GWO-SVM model in diagnosing pressure regulator faults. Expanding the basic dataset size and improving data quality will further enhance the fault diagnosis accuracy of the AE-GWO-SVM model.

7. Conclusions

For traditional periodic maintenance of pressure regulators in gas transmission and distribution stations, the disassembly of equipment is required. It affects production and easily leads to “under-maintenance” and “over-maintenance”. In response, this work proposes an optimized support vector machine model using the grey wolf algorithm. By directly utilizing parameters collected from the SCADA system, including opening degree, temperature, pressure, and flow rate downstream and upstream of the regulator, this model achieves the automatic diagnosis of internal leakage and external leakage of pressure regulators. This model optimizes the penalty factor C and kernel function parameter $\gamma$ of the SVM using the grey wolf optimizer, obtaining 18 composite features beyond the original data through feature engineering. An improved distance evaluation (IDE) is employed to select the high-priority features. Given the difficulty in obtaining on-site pressure regulator faults to establish a basic dataset for machine learning, numerical simulations on normal, internal leakage, and external leakage of pressure regulators are performed. Compared with SVM models optimized by other swarm intelligence optimization algorithms such as genetic algorithm (GA), sparrow search algorithm (SSA), whale optimization algorithm (WOA), and bald eagle search (BES), the GWO-SVM model shows the best performance. Moreover, an autoencoder (AE) is used to avoid interference by abnormal data, which significantly improves the fault identification process of the GWO-SVM model. An experimental platform was constructed to conduct fault diagnosis experiments for pressure regulators. The results show that compared with direct classification by SVM, the AE-GWO-SVM model improves the accuracy of fault diagnosis from 60.4% to 86.7%, demonstrating the effectiveness of the proposed model in pressure regulator fault diagnosis.