Analysis of Security–Reliability Tradeoff of Two-Way Hybrid Satellite–Terrestrial Relay Schemes Using Fountain Codes, Successive Interference Cancelation, Digital Network Coding, Partial Relay Selection, and Cooperative Jamming

Abstract

In this paper, we propose a two-way hybrid satellite–terrestrial relay scheme employing Fountain codes (FCs). In the proposed model, a satellite and a ground user exchange data through a group of terrestrial relay stations, in the presence of an eavesdropper. In the first phase, the satellite and the ground user simultaneously transmit their encoded packets to the relay stations. The relay stations then apply a successive interference cancelation (SIC) technique to decode the received packets. To reduce the quality of the eavesdropping links, a cooperative jammer is employed to transmit jamming signals toward the eavesdropper during the first phase. Next, one of the relay stations which can successfully decode the encoded packets from both the satellite and the ground user is selected for data forwarding, by using a partial relay selection method. Then, this selected relay performs an XOR operation on the two encoded packets, and then broadcasts the XOR-ed packet to both the satellite and the user in the second phase. We derive exact closed-form expressions of outage probability (OP), system outage probability (SOP), intercept probability (IP), and system intercept probability (SIP), and realize simulations to validate these expressions. This paper also studies the trade-off between OP (SOP) and IP (SIP), as well as the impact of various system parameters on the performance of the proposed scheme.

1. Introduction

Hybrid satellite–terrestrial relay $\left(\mathrm{HSTR}\right)$ schemes have emerged as a promising solution to overcome the inherent limitations of conventional satellite and terrestrial systems [1,2,3], where terrestrial relay stations are used to support the communication link between the satellite and ground users. The $\mathrm{HSTR}$ models can enhance the system throughput and reliability, and they are considered as a key enabler for beyond-5G and 6G networks. In recent years, research on the $\mathrm{HSTR}$ systems have advanced in several closely related directions, including system reliability improvement, physical-layer security, spectrum sharing, and advanced multiple-access schemes. For example, the authors in ref. [4] presented a space–air–ground free-space optical network that employs a high-altitude relay to improve the robustness of satellite communication links. Beyond reliability enhancement, security has become a critical concern in the $\mathrm{HSTR}$ systems due to the broadcast nature of satellite transmissions. In refs. [5,6], the authors investigated the secrecy performance of the $\mathrm{HSTR}$ schemes in the presence of eavesdroppers. Specifically, ref. [5] focused on the secure $\mathrm{HSTR}$ scenarios with multiple eavesdroppers, whereas reference [6] introduced relay station selection methods to enhance secrecy outage probability. The authors in ref. [7] analyzed the relationship between intercept probability $\left(\mathrm{IP}\right)$ at the eavesdropper and outage probability $\left(\mathrm{OP}\right)$ at the legitimate receiver for the secure $\mathrm{HSTR}$ models. In addition, reference [7] introduced both full relay selection $\left(\mathrm{FRS}\right)$ and partial relay selection $\left(\mathrm{PRS}\right)$ to improve the security–reliability trade-off, under the impact of co-channel interference. These works collectively indicate that relay selection plays a pivotal role in balancing reliability and security in the $\mathrm{HSTR}$ networks.

Another important research direction considers spectrum efficiency through cognitive radio techniques. Published work [8] proposed the $\mathrm{HSTR}$ schemes operating in a cognitive radio environment, where the satellite and the relay station are secondary transmitters, and they are allowed to use the licensed spectrum if their transmissions do not degrade performance of the primary users. Meanwhile, full-duplex relaying has been explored as an effective means to further enhance spectral efficiency in the $\mathrm{HSTR}$ systems. In ref. [9], full-duplex relaying techniques were applied into the $\mathrm{HSTR}$ scheme, allowing the terrestrial stations to transmit and receive data at the same time. Moreover, the $\mathrm{PRS}$ technique was applied to select the best terrestrial station to improve the throughput and the $\mathrm{OP}$ performance, under the impact of co-channel interference. More recently, intelligent reconfigurable environments have been incorporated into the $\mathrm{HSTR}$ models. Reference [10] presented the $\mathrm{HSTR}$ scenario assisted by reconfigurable intelligent surfaces $\left(\mathrm{RIS}\right)$. In contrast to the traditional relaying schemes, where the relay nodes actively process the received signals, $\mathrm{RIS}$-aided relaying models rely on passive reflective elements that reflect the incoming signals toward the desired ground users in an optimized way. Compared with conventional active relays, RIS-assisted relaying offers a low-power and hardware-efficient alternative, making it attractive for satellite–terrestrial integration.

In parallel, non-orthogonal multiple access $\left(\mathrm{NOMA}\right)$ has been introduced into the $\mathrm{HSTR}$ systems to improve connectivity and spectral efficiency. In refs. [11,12,13], $\mathrm{NOMA}$ is applied into the $\mathrm{HSTR}$ systems, enabling the satellite to transmit different data to multiple ground users at the same time. In addition, the ground users have to use successive interference cancelation $\left(\mathrm{SIC}\right)$ to extract their desired data from the received signals. In ref. [11], the authors derived expressions of $\mathrm{OP}$ for the $\mathrm{NOMA}-\mathrm{HSTR}$ scheme, where the direct links between the satellite and the ground users are assumed to exist. The authors of ref. [12] studied the $\mathrm{IP}$ and $\mathrm{OP}$ performance for the secondary users in the secure cognitive $\mathrm{NOMA}-\mathrm{HSTR}$ scenarios. Reference [13] evaluated the $\mathrm{OP}$ performance of multi-relay $\mathrm{NOMA}-\mathrm{HSTR}$ models. These studies demonstrate that $\mathrm{NOMA}$ is an effective multiple-access technique for $\mathrm{HSTR}$, but they mainly focus on fixed-rate transmissions.

Unlike the aforementioned published works, this paper considers the $\mathrm{HSTR}$ scheme using Fountain codes $\left(\mathrm{FCs}\right)$. $\mathrm{FCs}$ [14,15,16] have proven to be effective in wireless networks due to the simple implementation and adaptability to varying environmental conditions. $\mathrm{FCs}$ are particularly well-suited for multi-user broadcast networks since the transmitter can generate encoded packets from its original data, and continuously send them to the intended receivers. In addition, $\mathrm{FCs}$ allow the receivers to recover the original data once a sufficient number of encoded packets $\left(\mathrm{EnPs}\right)$ have been collected, even in the presence of packet losses. In refs. [17,18], the authors considered the $\mathrm{HSTR}$ schemes employing $\mathrm{FCs}$. The authors of ref. [17] evaluated the $\mathrm{IP}$ and $\mathrm{OP}$ performance for the secure $\mathrm{HSTR}$ scheme, with the presence of a passive eavesdropper. Moreover, reference [17] employs a cooperative jammer that not only disrupts the eavesdropper with jamming signals but also works with the ground user to eliminate the noises from the received signals. Published work [18] studied the $\mathrm{OP}-\mathrm{IP}$ trade-off for the $\mathrm{NOMA}-\mathrm{HSTR}$ multicast schemes using $\mathrm{FCs}$ and PRS. Unlike refs. [17,18], this paper studies two-way $\mathrm{HSTR}$ models, while refs. [17,18] only consider the one-way $\mathrm{HSTR}$ ones. However, these works do not address two-way information exchange, which is essential for bidirectional satellite–ground communications.

Two-way relaying $\left(\mathrm{TWR}\right)$ (refs. [19,20]) has attracted significant attention due to its capability to improve spectral efficiency and throughput by allowing two sources to communicate simultaneously in both directions through one or multiple intermediate relays. In a conventional $\mathrm{TWR}$ model [21], during the first two phases, the first source transmits its data to the intermediate relay, which then forwards the data to the second source. Similarly, the next two phases are used to relay data from the second source to the first source via the relay node. As a result, the conventional $\mathrm{TWR}$ model uses 04 phases, and it achieves a throughput of only 2 data over the four phases. To enhance throughput for the $\mathrm{TWR}$ models, the relays in ref. [22] perform an $\mathrm{XOR}$ operation on the data received from two sources at two first phases, and then transmit the $\mathrm{XOR}-\mathrm{ed}$ packet to both the sources in the third phase. As a result, the $\mathrm{TWR}$ models in ref. [22] only use three phases, and they are called a Digital Network Coding $\left(\mathrm{DNC}\right)$-based $\mathrm{TWR}$. Published work [23] introduced two-phase $\mathrm{TWR}$ scenarios using Analog Network Coding $\left(\mathrm{ANC}\right)$, where the relays amplify the signals received from two sources in the first phase, and then transmit the amplified signals to both the sources in the second phase. In refs. [24,25], the $\mathrm{SIC}$ and $\mathrm{DNC}$ techniques are jointly employed at the relays in the $\mathrm{TWR}$ models so that only two phases are used. Indeed, in refs. [24,25,26], two sources at the same time send their packets to the relays which will perform the $\mathrm{SIC}$ technique to extract the received packets. Next, the relays perform the $\mathrm{XOR}$ operation over two packets before broadcasting the $\mathrm{XOR}-\mathrm{ed}$ packet to two sources in the second phase. Hence, both the $\mathrm{TWR}$ schemes using $\mathrm{ANC}$ and the $\mathrm{TWR}$ schemes using $\mathrm{SIC}$ and DNC only use two phases for the data exchange.

Until now, there have been several reports related to $\mathrm{TW}-\mathrm{HSTR}$ models [27,28,29,30]. The authors of ref. [27] examined the $\mathrm{TW}-\mathrm{HSTR}$ system integrating simultaneous wireless information and power transfer. Reference [28] analyzed the $\mathrm{OP}$ performance and the throughput for the $\mathrm{TW}-\mathrm{HSTR}$ system using $\mathrm{ANC}$ and considering the effects of hardware impairments. Also, the impact of hardware imperfection on performance of the $\mathrm{TW}-\mathrm{HSTR}$ networks was investigated in ref. [29], emphasizing the practical constraints introduced by non-ideal transceivers. Reference [30] proposed adaptive relay selection for TWR-HSTRNs, confirming that dynamic selection significantly improves throughput and spectral reuse efficiency. These studies confirm that the $\mathrm{TW}-\mathrm{HSTR}$ networks can significantly improve spectral efficiency and throughput, yet their integration with Fountain coding and cooperative jamming remains largely unexplored.

Despite these extensive studies, the joint consideration of $\mathrm{TW}-\mathrm{HSTR}$, Fountain-coded transmissions, and cooperative jamming for physical-layer security has not yet been adequately addressed. Different from the related works [27,28,29,30], this paper proposes the $\mathrm{TW}-\mathrm{HSTR}$ scheme using $\mathrm{FCs},$ $\mathrm{SIC},$ $\mathrm{DNC},$ $\mathrm{PRS}$ and the cooperative jamming technique. In the proposed scheme, a satellite and a ground user exchange data via the help of terrestrial relay stations, with the presence of an eavesdropper. Using $\mathrm{FCs}$, the satellite and the ground user generate $\mathrm{EnPs}$, and exchange them with each other. In the first phase, the satellite and the ground user at the same time transmit their $\mathrm{EnPs}$ to all relay stations. The relay stations then apply $\mathrm{SIC}$ to extract the received packets. In addition, to degrade the quality of the eavesdropping links, a cooperative jammer is employed to transmit interference toward the eavesdropper during the first phase. In the second phase, one of the relay stations which can successfully decode the packets from both the satellite and the ground user is selected for data forwarding, using the $\mathrm{PRS}$ approach. The chosen relay performs the $\mathrm{XOR}$ operation on two received $\mathrm{EnPs}$, and subsequently broadcasts the $\mathrm{XOR}-\mathrm{ed}$ packet to both the satellite and the user in the second phase. Before the data transmission ends, the satellite, the ground user, and the eavesdropper attempt to collect enough $\mathrm{EnPs}$ so that they can recover the desired data.

Now, the main contributions of this paper are summarized as follows:

-

First, we propose the novel $\mathrm{TW}-\mathrm{HSTR}$ scheme that integrates $\mathrm{FCs}$, $\mathrm{SIC},$ $\mathrm{DNC}$, relay station selection, and cooperative jamming. The proposed scheme enhances system throughput through the use of $\mathrm{SIC}$ and $\mathrm{DNC},$ enables simple implementation and reduced delay by employing $\mathrm{FCs}$, improves communication reliability via $\mathrm{PRS},$ and ensures secure communication through cooperative jamming.

-

Second, under practical fading conditions, we derive exact closed-form expressions of $\mathrm{OP}$, system outage probability $\left(\mathrm{SOP}\right)$, $\mathrm{IP}$, and system intercept probability $\left(\mathrm{SIP}\right)$, and validate these formulas through simulations. In addition, all derived formulas are expressed in closed form, which makes them highly useful for system design and performance optimization.

-

Finally, based on the analytical framework, we provide comprehensive performance insights that reveal the fundamental security–reliability tradeoff in the proposed scheme and demonstrate how critical system parameters influence both reliability and security performance.

The remaining structure of this paper is presented as follows. Section 2 presents the system model of the proposed model. Section 3 analyzes the exact and asymptotic $\mathrm{OP}\left(\mathrm{SOP}\right)$ and $\mathrm{IP}\left(\mathrm{SIP}\right)$ performance for the proposed scheme by deriving closed-form expressions. Section 4 performs computer simulations to validate the derived expressions. Finally, Section 5 provides conclusions.

2. System Model

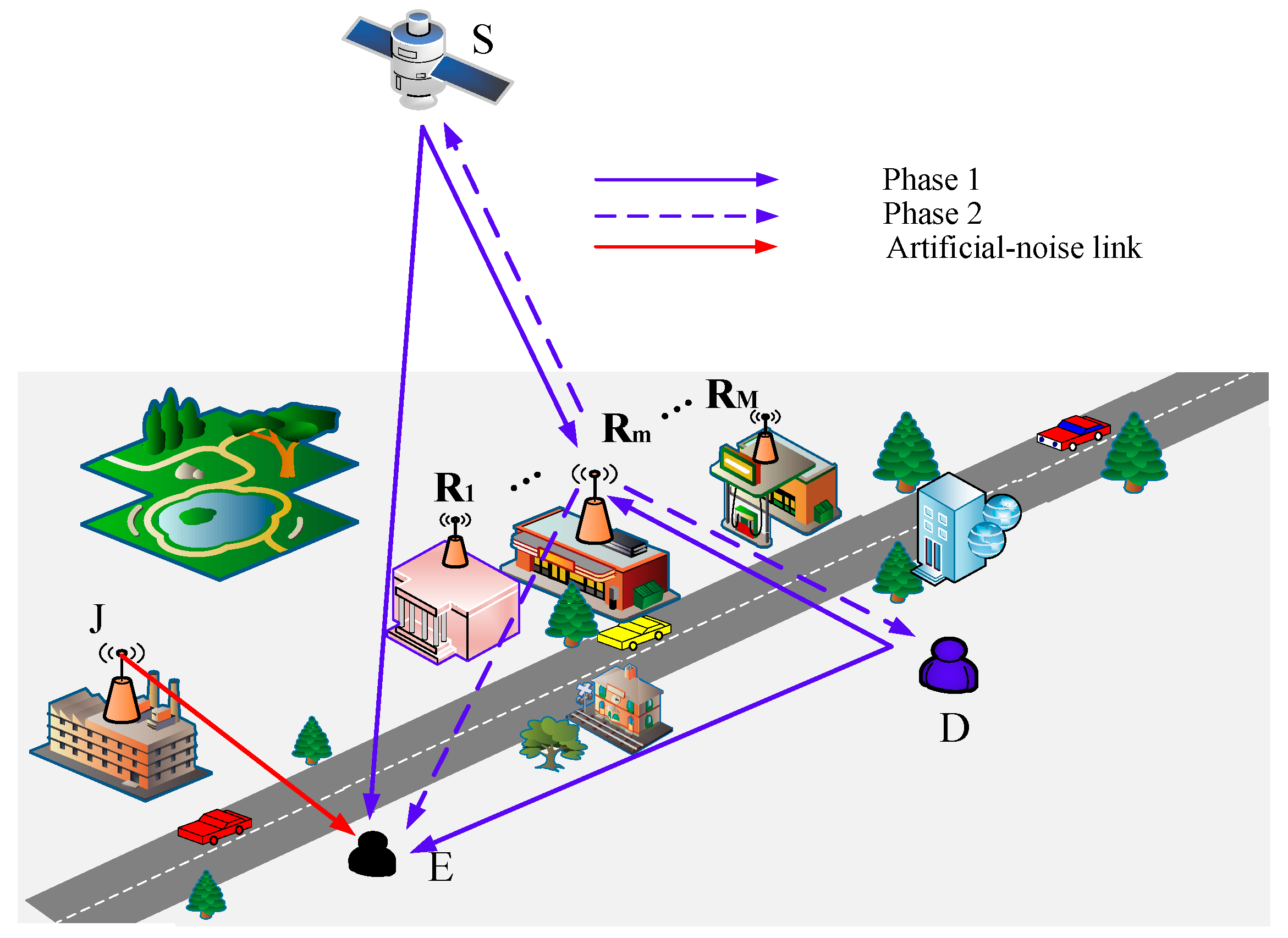
In Figure 1, we present a system model of the proposed $\mathrm{TW}-\mathrm{HSTR}$ scheme, where the satellite $\left(\mathrm{S}\right)$ and the ground user $\left(\mathrm{D}\right)$ attempt to exchange their data via the help of $M$ terrestrial relay stations denoted by ${\mathrm{R}}_1,{\mathrm{R}}_2,...,{\mathrm{R}}_M$. We assume that there is no direct link between $\mathrm{S}$ and $\mathrm{D}$ due to being obscured. Let $x_{\mathrm{S}}$ and $x_{\mathrm{D}}$ denote the data of $\mathrm{S}$ and $\mathrm{D}$, respectively. Using $\mathrm{FCs},$ the $\mathrm{S}\left(\mathrm{D}\right)$ node creates the $\mathrm{EnPs}$ $p_{\mathrm{S}}\left(p_{\mathrm{D}}\right)$ from the original data $x_{\mathrm{S}}\left(x_{\mathrm{D}}\right)$. Then, $\mathrm{S}$ and $\mathrm{D}$ exchange their $\mathrm{EnPs}$ via the help of the terrestrial relay stations. In order to successfully reconstruct the desired data $x_{\mathrm{S}}\left(x_{\mathrm{D}}\right)$, $\mathrm{D}\left(\mathrm{S}\right)$ must gather at least $G_{\min }$ $\mathrm{EnPs}$ $p_{\mathrm{D}}\left(p_{\mathrm{S}}\right)$. In addition, due to delay constraints, the maximum number of $\mathrm{EnP}$ exchange rounds is limited by $H_{\max }$ [18], where $H_{\max }\ge G_{\min }.$ It is worth noting that, in this paper, a generic $\mathrm{FC}$ framework is considered without restricting to a specific implementation (e.g., LT or Raptor codes), since the analysis is performed at the packet level and depends only on the number of successfully received $\mathrm{EnPs}$.

Due to the presence of the eavesdropper $\left(\mathrm{E}\right)$, the transmitters $\mathrm{S}$, $\mathrm{D}$, and ${\mathrm{R}}_m\left(m=1,2,...,M\right)$ employ the randomize-and-forward strategy [31] by randomly using code-books. Moreover, the cooperative jammer $\left(\mathrm{J}\right)$ is employed to generate the jamming noises over $\mathrm{E}$, as well as to cooperate with the relays ${\mathrm{R}}_m\left(m=1,2,...,M\right)$ for removing these noises from their received signals. We assume that the $\mathrm{J}$ and ${\mathrm{R}}_m$ nodes can securely exchange information about the jamming signals, enabling ${\mathrm{R}}_m$ to cancel them before decoding the desired data, while the $\mathrm{E}$ node is unable to do this [17]. Similarly, $\mathrm{E}$ attempts to collect at least $G_{\min }$ packets $p_{\mathrm{S}}\left(p_{\mathrm{D}}\right)$ to reconstruct the original data $x_{\mathrm{S}}\left(x_{\mathrm{D}}\right)$. Finally, all the nodes including $\mathrm{S}$, $\mathrm{D}$, ${\mathrm{R}}_m$, and $\mathrm{E}$ are assumed to be single-antenna wireless devices.

We denote $h_{\mathrm{AB}}$ as channel coefficient of the $\mathrm{A}\to \mathrm{B}$ link, where $\mathrm{A}$ is a transmitter and $\mathrm{B}$ is a receiver, i.e., $\left(\mathrm{A},\mathrm{B}\right)\in \left\{{\mathrm{S},\mathrm{R}}_m,\mathrm{D},\mathrm{E},\mathrm{J}\right\}.$ Then, the corresponding channel gain is denoted by $g_{\mathrm{AB}}$, i.e., $g_{\mathrm{AB}}=|h_{\mathrm{AB}}{|}^2.$ Assume that all channels are block and flat, i.e., $g_{\mathrm{AB}}$ remains unchanged during one phase, and varies independently after each phase.

As given in ref. [18], the satellite links (i.e., $\mathrm{S}\to {\mathrm{R}}_m$, ${\mathrm{R}}_m\to \mathrm{S}$ and $\mathrm{S}\to \mathrm{E}$) are Shadowed-Rician channels, and $g_{\mathrm{AB}}$ has the following probability density function $\left(\mathrm{PDF}\right)$:

$$f_{{\gamma }_{\mathrm{AB}}}\left(x\right)={\displaystyle \frac{1}{2b_{\mathrm{AB}}}}{\left({\displaystyle \frac{2a_{\mathrm{AB}}{b}_{\mathrm{AB}}}{2a_{\mathrm{AB}}{b}_{\mathrm{AB}}+{\Omega }_{\mathrm{AB}}}}\right)}^{a_{\mathrm{SR}}}\exp \left(-{\displaystyle \frac{x}{2b_{\mathrm{AB}}}}\right){}_{1}F_1\left(a_{\mathrm{AB}};1;{\displaystyle \frac{{\Omega }_{\mathrm{AB}}x}{2b_{\mathrm{AB}}\left(2a_{\mathrm{AB}}{b}_{\mathrm{AB}}+{\Omega }_{\mathrm{AB}}\right)}}\right),$$

(1)

where $\mathrm{A}\in \left\{{\mathrm{S},\mathrm{R}}_m\right\},$ $\mathrm{B}\in \left\{{\mathrm{R}}_m,\mathrm{E}\right\},$ $2b_{\mathrm{AB}}$ and ${\Omega }_{\mathrm{AB}}$ are the expected power of the multi-path and Line of Sight $\left(\mathrm{LOS}\right)$ components, respectively, $a_{\mathrm{AB}}$ is a fading parameter, and ${}_{1}F_1\left(.;.;.\right)$ is a confluent hypergeometric function of the first kind [18].

For ease of presentation and analysis, we can assume that the channel gains $g_{{\mathrm{SR}}_m}$ and $g_{{\mathrm{R}}_m\mathrm{S}}$ are identical and independent, i.e., $a_{{\mathrm{SR}}_m}\triangleq a_{\mathrm{SR}},$ $b_{{\mathrm{SR}}_m}\triangleq b_{\mathrm{SR}}$ and ${\Omega }_{{\mathrm{SR}}_m}\triangleq {\Omega }_{\mathrm{SR}},$ for all $m=1,2,...,M.$ Using [18], cumulative distribution function $\left(\mathrm{CDF}\right)$ of $g_{\mathrm{AB}}$ in (1) can be expressed under the following form:

$$\begin{array}{l}{F}_{g_{\mathrm{AB}}}\left(x\right)=1-{\alpha }_{\mathrm{AB}}^{a_{\mathrm{AB}}}{\psi }_{\mathrm{AB}}\left[{\displaystyle \sum _{n=0}^{a_{\mathrm{AB}}-1}{\displaystyle \sum _{q=0}^n\frac{n!}{q!}\frac{{\xi }_{\mathrm{AB}}\left(n\right)}{{\left({\psi }_{\mathrm{AB}}-{\beta }_{\mathrm{AB}}\right)}^{n-q+1}}}}{x}^q\exp \left(-\left(\psi -\beta \right)x\right)\right]\\ =1-{\displaystyle \sum _{n=0}^{a_{\mathrm{AB}}-1}{\displaystyle \sum _{q=0}^n{\Psi }_{\mathrm{AB}}}}{x}^q\exp \left(-\left({\psi }_{\mathrm{AB}}-{\beta }_{\mathrm{AB}}\right)x\right),\end{array}$$

(2)

where

$$\begin{array}{l}{\psi }_{\mathrm{AB}}={\displaystyle \frac{1}{2b_{\mathrm{AB}}}},{\alpha }_{\mathrm{AB}}={\left({\displaystyle \frac{2a_{\mathrm{AB}}{b}_{\mathrm{AB}}}{2a_{\mathrm{AB}}{b}_{\mathrm{AB}}+{\Omega }_{\mathrm{AB}}}}\right)}^{a_{\mathrm{AB}}},{\beta }_{\mathrm{AB}}=\left({\displaystyle \frac{{\Omega }_{\mathrm{AB}}}{2b_{\mathrm{AB}}\left(2a_{\mathrm{AB}}{b}_{\mathrm{AB}}+{\Omega }_{\mathrm{AB}}\right)}}\right),\\ {\xi }_{\mathrm{AB}}\left(n\right)={\displaystyle \frac{{\left(-1\right)}^n\left(1-a_{\mathrm{AB}}\right){\beta }_{\mathrm{AB}}^{n_{\mathrm{AB}}}}{\left(n_{\mathrm{SR}}\right)!}},{\Psi }_{\mathrm{AB}}={\displaystyle \frac{n!}{q!}}{\displaystyle \frac{{\alpha }_{\mathrm{AB}}^{a_{\mathrm{AB}}}{\psi }_{\mathrm{AB}}{\xi }_{\mathrm{AB}}\left(n\right)}{{\left({\psi }_{\mathrm{AB}}-{\beta }_{\mathrm{AB}}\right)}^{n-q+1}}}.\end{array}$$

(3)

For the terrestrial links, we assume that all the channels are Rayleigh fading. Hence, the channel gain $g_{\mathrm{AB}}$ is an exponential random variable whose $\mathrm{CDF}$ and $\mathrm{PDF}$ can be expressed, respectively, as

$$F_{g_{\mathrm{AB}}}\left(x\right)=1-\exp \left(-{\lambda }_{\mathrm{AB}}x\right),f_{g_{\mathrm{AB}}}\left(x\right)={\lambda }_{\mathrm{AB}}\exp \left(-{\lambda }_{\mathrm{AB}}x\right),$$

(4)

where $\mathrm{A}\in \left\{{\mathrm{R}}_m,\mathrm{D},\mathrm{J}\right\}$, $\mathrm{B}\in \left\{{\mathrm{R}}_m,\mathrm{D},\mathrm{E}\right\}$, and ${\lambda }_{\mathrm{AB}}$ is a fading parameter of the $\mathrm{A}\to \mathrm{B}$ link. We also assume that the channel gains $g_{{\mathrm{AR}}_m}$ and $g_{{\mathrm{R}}_m\mathrm{B}}$ are identical and independent, i.e., ${\lambda }_{{\mathrm{AR}}_m}\triangleq {\lambda }_{\mathrm{AR}}$ and ${\lambda }_{{\mathrm{R}}_m\mathrm{B}}\triangleq {\lambda }_{\mathrm{RB}},$ for all $m$ and for all the $\mathrm{A}$ and $\mathrm{B}$ nodes.

We now describe the exchange of $\mathrm{EnPs}$ in Figure 1, which is carried out over two time slots. At the first time slot, $\mathrm{S}$ and $\mathrm{D}$ at the same time transmits $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ to all the relay stations, while $\mathrm{J}$ generates the jamming noises. Therefore, the received signals at ${\mathrm{R}}_m$ and $\mathrm{E}$ can be expressed, respectively, as

$$y_{{\mathrm{R}}_m}=\sqrt{P_{\mathrm{S}}}{h}_{{\mathrm{SR}}_m}{p}_{\mathrm{S}}^{*}+\sqrt{P_{\mathrm{D}}}{h}_{{\mathrm{DR}}_m}{p}_{\mathrm{D}}^{*}+\sqrt{P_{\mathrm{J}}}{h}_{{\mathrm{JR}}_m}{x}_{\mathrm{J}}+n_{{\mathrm{R}}_m},$$

(5)

$$y_{\mathrm{E}}=\sqrt{P_{\mathrm{S}}}{h}_{\mathrm{SE}}{p}_{\mathrm{S}}^{*}+\sqrt{P_{\mathrm{D}}}{h}_{\mathrm{DE}}{p}_{\mathrm{D}}^{*}+\sqrt{P_{\mathrm{J}}}{h}_{\mathrm{JE}}{x}_{\mathrm{J}}+n_{\mathrm{E}},$$

(6)

where $P_{\mathrm{S}}$, $P_{\mathrm{D}}$ and $P_{\mathrm{J}}$ are transmit power of the $\mathrm{S}$, $\mathrm{D}$, and $\mathrm{J}$, respectively, $p_{\mathrm{S}}^{*}$ and $p_{\mathrm{D}}^{*}$ are modulated signals of the packets $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$, respectively, $x_{\mathrm{J}}$ is transmitted signal of $\mathrm{J}$, $n_{{\mathrm{R}}_m}$ and $n_{\mathrm{E}}$ are Gaussian noises at ${\mathrm{R}}_m$ and $\mathrm{E}$, respectively.

Since the node ${\mathrm{R}}_m$ can cooperate with the jammer $\mathrm{J}$ to remove the jamming noise (the component $\sqrt{P_{\mathrm{J}}}{h}_{{\mathrm{JR}}_m}{x}_{\mathrm{J}}$), Equation (5) can be rewritten as

$${\hat{y}}_{{\mathrm{R}}_m}=\sqrt{P_{\mathrm{S}}}{h}_{{\mathrm{SR}}_m}{p}_{\mathrm{S}}^{*}+\sqrt{P_{\mathrm{D}}}{h}_{{\mathrm{DR}}_m}{p}_{\mathrm{D}}^{*}+n_{{\mathrm{R}}_m}.$$

(7)

Remark 1.

Since the satellite $\left(\mathrm{S}\right)$ is the well-equipped device, it is reasonable to assume that the transmit power of $\mathrm{S}$ is higher than that of the ground user $\left(\mathrm{D}\right)$, i.e., $P_{\mathrm{S}}>P_{\mathrm{D}}$. In addition, the channels between $\mathrm{S}$ and the relay station $\left({\mathrm{R}}_m\right)$ exhibit the $\mathrm{LOS}$ component. Moreover, the terrestrial link between $\mathrm{D}$ and ${\mathrm{R}}_m$ experience Rayleigh fading which does not contain $\mathrm{LOS}$. Therefore, it is reasonable to assume that the $\mathrm{S}\to {\mathrm{R}}_m$ link is better than the $\mathrm{D}\to {\mathrm{R}}_m$ link. Similarly, we can assume that the $\mathrm{S}\to \mathrm{E}$ link is better than the $\mathrm{D}\to \mathrm{E}$ link. Therefore, the ${\mathrm{R}}_m$ and $\mathrm{E}$ nodes will decode the packet $p_{\mathrm{S}}$ first. If the decoding of $p_{\mathrm{S}}$ is successful, ${\mathrm{R}}_m$ and $\mathrm{E}$ will remove $p_{\mathrm{S}}$ out from their received signals and will then decode $p_{\mathrm{D}}$ [18]. It is noted that, if ${\mathrm{R}}_m$ and $\mathrm{E}$ cannot decode $p_{\mathrm{S}}$ correctly, then they cannot also decode $p_{\mathrm{D}}$ correctly because they cannot perform the $\mathrm{SIC}$ operation. Finally, it is assumed that the Gaussian noises at all the receivers $\mathrm{B}$ have zero mean and variance of ${\sigma }_0^2$.

From (7), we can express the signal-to-noise ratio $\left(\mathrm{SNR}\right)$ obtained at ${\mathrm{R}}_m$ for decoding $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$, respectively, as

$$\begin{array}{l}{\gamma }_{\mathrm{S},{\mathrm{R}}_m}^{p_{\mathrm{S}}}={\displaystyle \frac{P_{\mathrm{S}}|h_{{\mathrm{SR}}_m}{|}^2}{P_{\mathrm{D}}|h_{{\mathrm{DR}}_m}{|}^2+{\sigma }_0^2}}={\displaystyle \frac{P_{\mathrm{S}}{g}_{{\mathrm{SR}}_m}}{P_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}+{\sigma }_0^2}}={\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{{\mathrm{SR}}_m}}{{\Delta }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}+1}},\\ {\gamma }_{\mathrm{S},{\mathrm{R}}_m}^{p_{\mathrm{D}}}={\displaystyle \frac{P_{\mathrm{D}}|h_{{\mathrm{DR}}_m}{|}^2}{{\sigma }_0^2}}={\displaystyle \frac{P_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}}{{\sigma }_0^2}}={\Delta }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m},\end{array}$$

(8)

where ${\Delta }_{\mathrm{S}}=P_{\mathrm{S}}/{\sigma }_0^2$ and ${\Delta }_{\mathrm{D}}=P_{\mathrm{D}}/{\sigma }_0^2.$

Since the eavesdropper $\mathrm{E}$ cannot remove the jamming noises $x_{\mathrm{J}}$ out from the received signals, from (6), the $\mathrm{SNR}$ obtained at $\mathrm{E}$ for decoding $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ can be formulated, respectively, as

$$\begin{array}{l}{\gamma }_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{S}}}={\displaystyle \frac{P_{\mathrm{S}}|h_{\mathrm{SE}}{|}^2}{P_{\mathrm{D}}|h_{\mathrm{DE}}{|}^2+P_{\mathrm{J}}|h_{\mathrm{JE}}{|}^2+{\sigma }_0^2}}={\displaystyle \frac{P_{\mathrm{S}}{g}_{\mathrm{SE}}}{P_{\mathrm{D}}{g}_{\mathrm{DE}}+P_{\mathrm{J}}{g}_{\mathrm{JE}}+{\sigma }_0^2}}={\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{\mathrm{SE}}}{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}+{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}+1}},\\ {\gamma }_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{D}}}={\displaystyle \frac{{\Delta }_{\mathrm{D}}|h_{\mathrm{DE}}{|}^2}{{\Delta }_{\mathrm{J}}|h_{\mathrm{JE}}{|}^2+1}}={\displaystyle \frac{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}}{{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}+1}}.\end{array}$$

(9)

Considering the terrestrial relay stations which can decode both $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ successfully. Without loss of generality, we can denote the set of successful relay stations as $W=\left\{{\mathrm{R}}_1,{\mathrm{R}}_2,...,{\mathrm{R}}_N\right\}$, where $0\le N\le M,$ and $N$ is the number of successful relay stations.

If $N=0$, then $W=\left\{\varnothing \right\}$, and, in this case, no operation takes place during the second phase. Let us consider the case where $N>0$; one of the relay stations belonging to the set $W$ is selected by using the $\mathrm{PRS}$ method as

$${\mathrm{R}}_b:g_{{\mathrm{R}}_b\mathrm{D}}=\underset{n=1,2,...,N}{\max }\left(g_{{\mathrm{R}}_n\mathrm{D}}\right).$$

(10)

In (10), the selected relay station is denoted by ${\mathrm{R}}_b$, which is the relay providing the highest channel gain to the ground user $\left(\mathrm{D}\right)$.

Remark 2.

In (10), the relay selection is based on the channel state information $\left(\mathrm{CSI}\right)$ of the ${\mathrm{R}}_n\to \mathrm{D}$ links, which can be easily performed through the exchange of local $\mathrm{CSI}$ among the nodes. It is worth noting that this relay selection is difficult to implement between the relay stations ${\mathrm{R}}_n$ and the satellite $\mathrm{S}$, because they are located far apart and hence the selection process would introduce a significant delay.

Next, ${\mathrm{R}}_b$ performs the $\mathrm{XOR}$ operation as follows: $p_{\mathrm{S}}\oplus p_{\mathrm{D}}=p_{\mathrm{R}},$ and it will transmit the $\mathrm{XOR}-\mathrm{ed}$ packet $p_{\mathrm{R}}$ to $\mathrm{S}$ and $\mathrm{D}$ in the second phase, which is also overheard by $\mathrm{E}$. Then, the $\mathrm{SNR}$ obtained at the node $\mathrm{B}\left(\mathrm{B}\in \left\{\mathrm{S},\mathrm{D},\mathrm{E}\right\}\right)$ can be expressed as

$${\gamma }_{{\mathrm{R}}_b,\mathrm{B}}^{p_{\mathrm{R}}}={\displaystyle \frac{P_{\mathrm{R}}{g}_{{\mathrm{R}}_b\mathrm{B}}}{{\sigma }_0^2}}={\Delta }_{\mathrm{R}}{g}_{{\mathrm{R}}_b\mathrm{B}},$$

(11)

where $P_{\mathrm{R}}$ is transmitted power of all the relay stations, and ${\Delta }_{\mathrm{R}}=P_{\mathrm{R}}/{\sigma }_0^2$.

Remark 3.

Firstly, we note that no cooperative jamming technique is performed in the second phase. Secondly, if the node $\mathrm{S}\left(\mathrm{D}\right)$ can decode $p_{\mathrm{R}}$ correctly, $\mathrm{S}\left(\mathrm{D}\right)$ will obtain the desired packet $p_{\mathrm{D}}\left(p_{\mathrm{S}}\right)$ by performing the $\mathrm{XOR}$ operation as $p_{\mathrm{D}}=p_{\mathrm{S}}\oplus p_{\mathrm{R}}\left(p_{\mathrm{S}}=p_{\mathrm{D}}\oplus p_{\mathrm{R}}\right).$ For the eavesdropper $\mathrm{E}$, it can only obtain $p_{\mathrm{S}}$ successfully in the first time slot. Finally, $\mathrm{E}$ can successfully obtain $p_{\mathrm{D}}$ in two possible ways: (i) $\mathrm{E}$ correctly decodes both $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ in the first phase; (ii) $\mathrm{E}$ correctly decodes $p_{\mathrm{S}}$ (but $p_{\mathrm{D}}$) in the first phase, and $p_{\mathrm{R}}$ from $\mathrm{R}$ in the second phase, and then performs the $\mathrm{XOR}$ operation between $p_{\mathrm{S}}$ and $p_{\mathrm{R}}$ to obtain $p_{\mathrm{D}}$.

Because the $\mathrm{EnP}$ exchange is realized into two phases, the channel capacity of the $\mathrm{A}\to \mathrm{B}$ link is calculated as

$$C_{\mathrm{A},\mathrm{B}}^{p_{\mathrm{X}}}={\displaystyle \frac{1}{2}}{\log }_2\left(1+{\gamma }_{\mathrm{A},\mathrm{B}}^{p_{\mathrm{X}}}\right),$$

(12)

where $\left(\mathrm{A},\mathrm{B}\right)\in \left\{{\mathrm{S},\mathrm{R}}_m,\mathrm{D},\mathrm{E},\mathrm{J}\right\},$ and $p_{\mathrm{X}}\in \left\{p_{\mathrm{S}},p_{\mathrm{D}},p_{\mathrm{R}}\right\}$.

3. Performance Analysis

3.1. Mathematical Preparation

Considering the transmission of the packet $p_{\mathrm{X}}\left(\mathrm{X}\in \left\{\mathrm{S},\mathrm{D},\mathrm{R}\right\}\right)$ between the transmitter $\mathrm{A}$ and the receiver $\mathrm{B}$, we assume that the decoding of $p_{\mathrm{X}}$ is successful if the obtained channel capacity $C_{\mathrm{A},\mathrm{B}}^{p_{\mathrm{X}}}$ is higher than a threshold $C_{\mathrm{th}}$, i.e., $C_{\mathrm{A},\mathrm{B}}^{p_{\mathrm{X}}}\ge C_{\mathrm{th}}$. If $C_{\mathrm{A},\mathrm{B}}^{p_{\mathrm{X}}}<C_{\mathrm{th}},$ it is assumed that the receiver $\mathrm{B}$ cannot decode $p_{\mathrm{X}}$ correctly.

3.1.1. Decoding Probability over the Data Links

We first formulate the probability that the relay station ${\mathrm{R}}_m$ can decode both $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ successfully in the first phase as

$${\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}=\mathrm{Pr}\left(C_{\mathrm{S},{\mathrm{R}}_m}^{p_{\mathrm{S}}}\ge C_{\mathrm{th}},C_{\mathrm{D},{\mathrm{R}}_m}^{p_{\mathrm{D}}}\ge C_{\mathrm{th}}\right).$$

(13)

Substituting (8) and (12) into (13), we have

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}=\mathrm{Pr}\left({\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{{\mathrm{SR}}_m}}{{\Delta }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}+1}}\ge {\rho }_{\mathrm{th}},{\Delta }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}\ge {\rho }_{\mathrm{th}}\right)\\ =\mathrm{Pr}\left(g_{{\mathrm{SR}}_m}\ge {\omega }_1{g}_{{\mathrm{DR}}_m}+{\omega }_0,g_{{\mathrm{DR}}_m}\ge {\omega }_2\right)\\ ={\displaystyle {\int }_{{\omega }_2}^{+\infty }\left[1-F_{g_{{\mathrm{SR}}_m}}\left({\omega }_{1}x+{\omega }_0\right)\right]f_{g_{{\mathrm{DR}}_m}}\left(x\right)}dx,\end{array}$$

(14)

where ${\rho }_{\mathrm{th}}=2^{2C_{\mathrm{th}}}-1,{\omega }_0={\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{S}}}},{\omega }_1={\displaystyle \frac{{\rho }_{\mathrm{th}}{\Delta }_{\mathrm{D}}}{{\Delta }_{\mathrm{S}}}},{\omega }_2={\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{D}}}}$. It is noted that ${\omega }_0$ and ${\omega }_1$ are intermediate parameters introduced for notational simplicity.

Using (2), we can write $1-F_{g_{{\mathrm{SR}}_m}}\left({\omega }_{1}x+{\omega }_0\right)$ in (14) under the following form:

$$\begin{array}{l}1-F_{g_{{\mathrm{SR}}_m}}\left({\omega }_{1}x+{\omega }_0\right)={\displaystyle \sum _{n=0}^{a_{\mathrm{SR}}-1}{\displaystyle \sum _{q=0}^n{\Psi }_{\mathrm{SR}}}}{\left({\omega }_{1}x+{\omega }_0\right)}^q\exp \left(-\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right)\left({\omega }_{1}x+{\omega }_0\right)\right)\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SR}}-1}{\displaystyle \sum _{q=0}^n{\Psi }_{\mathrm{SR}}}}{\left({\omega }_1\right)}^q\exp \left(-\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right){\omega }_0\right){\left(x+{\omega }_3\right)}^q\exp \left(-{\omega }_{4}x\right)\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SR}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{C}_q^t{\Psi }_{\mathrm{SR}}}}}{\left({\omega }_1\right)}^q{\left({\omega }_3\right)}^{q-t}\exp \left(-\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right){\omega }_0\right)x^t\exp \left(-{\omega }_{4}x\right),\end{array}$$

(15)

where $C_q^t$ is a binomial coefficient, i.e., $C_q^t={\displaystyle \frac{q!}{t!\left(t-q\right)!}},$ ${\omega }_3={\displaystyle \frac{{\omega }_0}{{\omega }_1}},$ and ${\omega }_4=\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right){\omega }_1$.

Combining (4), (13), (14), and (15), after some manipulation, we obtain

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}={\displaystyle \sum _{n=0}^{a_{\mathrm{SR}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{C}_q^t{\Psi }_{\mathrm{SR}}}}}{\left({\omega }_1\right)}^q{\left({\omega }_3\right)}^{q-t}\exp \left(-\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right){\omega }_0\right)\\ \times {\displaystyle {\int }_{{\omega }_2}^{+\infty }{\lambda }_{\mathrm{DR}}{x}^t\exp \left(-\left({\omega }_4+{\lambda }_{\mathrm{DR}}\right)x\right)}dx.\end{array}$$

(16)

Our objective is to evaluate the integral in (16). To this end, we first consider the following general integral (see [32], Equation (2.321.2)):

$${\displaystyle \int x^t\exp \left(-\Phi x\right)}dx=-{\displaystyle \sum _{v=0}^t\frac{t!}{v!}\frac{x^v}{{\left(\Phi \right)}^{t+1-v}}}\exp \left(-\Phi x\right),$$

(17)

where $\Phi >0$. From (17), we can obtain the results as in (18), (19), and (20) as:

$${\displaystyle {\int }_0^{+\infty }{x}^t\exp \left(-\Phi x\right)}dx={\displaystyle \frac{t!}{{\left(\Phi \right)}^{t+1}}},$$

(18)

$${\displaystyle {\int }_{\vartheta }^{+\infty }{x}^t\exp \left(-\Phi x\right)}dx={\displaystyle \sum _{v=0}^t\frac{t!}{v!}\frac{{\vartheta }^v}{{\left(\Phi \right)}^{t+1-v}}}\exp \left(-\Phi \vartheta \right),$$

(19)

and

$${\displaystyle {\int }_0^{\vartheta }{x}^t\exp \left(-\Phi x\right)}dx={\displaystyle \frac{t!}{{\left(\Phi \right)}^{t+1}}}-{\displaystyle \sum _{v=0}^t\frac{t!}{v!}\frac{{\vartheta }^v}{{\left(\Phi \right)}^{t+1-v}}}\exp \left(-\Phi \vartheta \right).$$

(20)

Then, applying (19) to calculate the integral in (16), we then have

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}={\displaystyle \sum _{n=0}^{a_{\mathrm{SR}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{C}_q^t{\Psi }_{\mathrm{SR}}}}}{\left({\omega }_1\right)}^q{\left({\omega }_3\right)}^{q-t}\exp \left(-\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right){\omega }_0\right)\\ \times \left[{\displaystyle \sum _{v=0}^t\frac{t!}{v!}\frac{{\lambda }_{\mathrm{DR}}{\left({\omega }_2\right)}^v}{{\left({\omega }_4+{\lambda }_{\mathrm{DR}}\right)}^{t+1-v}}\exp \left(-\left({\omega }_4+{\lambda }_{\mathrm{DR}}\right){\omega }_2\right)}\right].\end{array}$$

(21)

It is worth noting that the probability that ${\mathrm{R}}_m$ cannot decode both $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ successfully is given as $1-{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}$.

Considering the successful decoding at the satellite at the second phase, using (2), (11), and (12), we can calculate this probability exactly as

$$\begin{array}{l}{\theta }_{{\mathrm{R}}_b,\mathrm{S}}^{p_{\mathrm{R}}}=\mathrm{Pr}\left(C_{{\mathrm{R}}_b,\mathrm{S}}^{p_{\mathrm{R}}}\ge C_{\mathrm{th}}\right)=\mathrm{Pr}\left(g_{{\mathrm{R}}_b\mathrm{S}}\ge {\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right)=1-F_{g_{{\mathrm{R}}_b\mathrm{S}}}\left({\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right)\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SR}}-1}{\displaystyle \sum _{q=0}^n{\Psi }_{\mathrm{SR}}}}{\left({\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right)}^q\exp \left(-\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right){\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right).\end{array}$$

(22)

It is noted that the probability that $\mathrm{S}$ cannot decode $p_{\mathrm{R}}$ successfully in the second phase is expressed as $1-{\theta }_{{\mathrm{R}}_b,\mathrm{S}}^{p_{\mathrm{R}}}$.

Next, we formulate the probability that $\mathrm{D}$ can decode $p_{\mathrm{R}}$ successfully at the second phase as

$$\begin{array}{l}{\theta }_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}=\mathrm{Pr}\left(C_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}\ge C_{\mathrm{th}}\right)=\mathrm{Pr}\left(g_{{\mathrm{R}}_b\mathrm{D}}\ge {\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right)\\ =1-\mathrm{Pr}\left(g_{{\mathrm{R}}_b\mathrm{D}}<{\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right).\end{array}$$

(23)

Combining (4), (10), and (23), we obtain an exact closed-form expression ${\theta }_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}$ as

$$\begin{array}{l}{\theta }_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}=1-\mathrm{Pr}\left(\underset{n=1,2,...,N}{\max }\left(g_{{\mathrm{R}}_n\mathrm{D}}\right)<{\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right)=1-{\displaystyle \prod _{n=1}^N{F}_{g_{{\mathrm{R}}_n\mathrm{D}}}\left(\frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}\right)}\\ =1-{\left(1-\exp \left(-{\displaystyle \frac{{\lambda }_{\mathrm{RD}}{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right)\right)}^N.\end{array}$$

(24)

It is also noted that the probability that $\mathrm{D}$ cannot decode $p_{\mathrm{R}}$ correctly in the second phase is exactly computed as $1-{\theta }_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}$.

3.1.2. Decoding Probability over the Eavesdropping Links

This sub-section derives the decoding probability of $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ at the eavesdropper $\mathrm{E}$. At first, using (9) and (12), we can formulate the probability that $\mathrm{E}$ can successfully decode both $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ in the first phase as

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}}}=\mathrm{Pr}\left(C_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{S}}}\ge C_{\mathrm{th}},C_{\mathrm{D},\mathrm{E}}^{p_{\mathrm{D}}}\ge C_{\mathrm{th}}\right)\\ =\mathrm{Pr}\left({\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{\mathrm{SE}}}{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}+{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}+1}}\ge {\rho }_{\mathrm{th}},{\displaystyle \frac{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}}{{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}+1}}\ge {\rho }_{\mathrm{th}}\right)\\ =\mathrm{Pr}\left(g_{\mathrm{SE}}\ge {\omega }_1{g}_{\mathrm{DE}}+{\omega }_5{g}_{\mathrm{JE}}+{\omega }_0,g_{\mathrm{DE}}\ge {\omega }_6{g}_{\mathrm{JE}}+{\omega }_2\right)\\ ={\displaystyle {\int }_0^{+\infty }{f}_{g_{\mathrm{JE}}}\left(x\right)\left[\underset{I_1\left(x\right)}{\underbrace{{\displaystyle {\int }_{{\omega }_{6}x+{\omega }_2}^{+\infty }\left(1-F_{g_{\mathrm{SE}}}\left({\omega }_{1}y+{\omega }_{5}x+{\omega }_0\right)\right)f_{g_{\mathrm{DE}}}\left(y\right)dy}}}\right]}dx,\end{array}$$

(25)

where ${\omega }_5={\displaystyle \frac{{\rho }_{\mathrm{th}}{\Delta }_{\mathrm{J}}}{{\Delta }_{\mathrm{S}}}},{\omega }_6={\displaystyle \frac{{\Delta }_{\mathrm{J}}{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{D}}}}.$ To calculate the integral $I_1\left(x\right)$ in (25), we have to write $1-F_{g_{\mathrm{SE}}}\left({\omega }_{1}y+{\omega }_{3}x+{\omega }_0\right)$ in (25) under the following form:

$$\begin{array}{l}1-F_{g_{\mathrm{SE}}}\left({\omega }_{1}y+{\omega }_{5}x+{\omega }_0\right)={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\Psi }_{\mathrm{SE}}}}{\left({\omega }_{1}y+{\omega }_{5}x+{\omega }_0\right)}^q\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right)\left({\omega }_{1}y+{\omega }_{5}x+{\omega }_0\right)\right)\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\Psi }_{\mathrm{SE}}}}\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right){\left({\omega }_1\right)}^q{\left(y+{\omega }_{7}x+{\omega }_8\right)}^q\exp \left(-{\omega }_{9}y-{\omega }_{10}x\right)\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{C}_q^t}{\Psi }_{\mathrm{SE}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right){\left(x+{\omega }_{11}\right)}^{q-t}\exp \left(-{\omega }_{10}x\right)y^t\exp \left(-{\omega }_{9}y\right)\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{C}_q^t{C}_{q-t}^r}}{\Psi }_{\mathrm{SE}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)\\ \times x^r\exp \left(-{\omega }_{10}x\right)y^t\exp \left(-{\omega }_{9}y\right),\end{array}$$

(26)

where ${\omega }_7={\displaystyle \frac{{\omega }_5}{{\omega }_1}},{\omega }_8={\displaystyle \frac{{\omega }_0}{{\omega }_1}},{\omega }_9=\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_1,{\omega }_{10}=\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_5,{\omega }_{11}={\displaystyle \frac{{\omega }_8}{{\omega }_7}}$.

Combining (4), (19), (25), and (26), $I_1\left(x\right)$ can be obtained as

$$\begin{array}{l}{I}_1\left(x\right)={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{C}_q^t{C}_{q-t}^r}}{\Psi }_{\mathrm{SE}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)x^r\exp \left(-{\omega }_{10}x\right)\\ \times {\displaystyle {\int }_{{\omega }_{6}x+{\omega }_2}^{+\infty }{\lambda }_{\mathrm{DE}}{y}^t\exp \left(-\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)y\right)dy}\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{C}_q^t{C}_{q-t}^r}}{\Psi }_{\mathrm{SE}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)x^r\exp \left(-{\omega }_{10}x\right)\\ \times \left[{\displaystyle \sum _{v=0}^t\frac{t!}{v!}\frac{{\lambda }_{\mathrm{DE}}{\left({\omega }_{6}x+{\omega }_2\right)}^v}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}}\exp \left(-\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)\left({\omega }_{6}x+{\omega }_2\right)\right)}\right]\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{\displaystyle \sum _{v=0}^t{\displaystyle \sum _{u=0}^v\frac{t!}{v!}}}}}\frac{C_q^t{C}_{q-t}^r{C}_v^u{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}{\left({\omega }_6\right)}^v{\left({\omega }_{12}\right)}^{v-u}}}\\ \times \exp \left(-\left({\psi }_{\mathrm{AB}}-{\beta }_{\mathrm{AB}}\right){\omega }_0\right)\exp \left(-\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right){\omega }_2\right)x^{u+r}\exp \left(-{\omega }_{13}x\right),\end{array}$$

(27)

where ${\omega }_{12}={\omega }_2/{\omega }_6,{\omega }_{13}=\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right){\omega }_6$.

Substituting (27) into (25), and using (18) to calculate the corresponding integral, we finally obtain the following result:

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}}}={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{\displaystyle \sum _{v=0}^t{\displaystyle \sum _{u=0}^v\frac{t!}{v!}}}}}\frac{C_q^t{C}_{q-t}^r{C}_v^u{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}{\left({\omega }_6\right)}^v{\left({\omega }_{12}\right)}^{v-u}}}\\ \times \exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)\exp \left(-\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right){\omega }_2\right){\displaystyle {\int }_0^{+\infty }{\lambda }_{\mathrm{DE}}{x}^{u+r}\exp \left(-\left({\omega }_{13}+{\lambda }_{\mathrm{DE}}\right)x\right)dx}\\ ={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{\displaystyle \sum _{v=0}^t{\displaystyle \sum _{u=0}^v\frac{t!}{v!}}}}}\frac{C_q^t{C}_{q-t}^r{C}_v^u{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}{\left({\omega }_6\right)}^v{\left({\omega }_{12}\right)}^{v-u}}}\\ \times \exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)\exp \left(-\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right){\omega }_2\right){\displaystyle \frac{\left(u+r\right)!{\lambda }_{\mathrm{JE}}}{{\left({\omega }_{13}+{\lambda }_{\mathrm{JE}}\right)}^{u+r+1}}}.\end{array}$$

(28)

Next, we consider the probability that $\mathrm{E}$ correctly decodes $p_{\mathrm{S}}$ and incorrectly decodes $p_{\mathrm{D}}$ in the first phase. Indeed, this probability can be formulated as

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\mathrm{not}{p}_{\mathrm{D}}}=\mathrm{Pr}\left(C_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{S}}}\ge C_{\mathrm{th}},C_{\mathrm{D},\mathrm{E}}^{p_{\mathrm{D}}}<C_{\mathrm{th}}\right)=\mathrm{Pr}\left(g_{\mathrm{SE}}\ge {\omega }_1{g}_{\mathrm{DE}}+{\omega }_5{g}_{\mathrm{JE}}+{\omega }_0,g_{\mathrm{DE}}<{\omega }_6{g}_{\mathrm{JE}}+{\omega }_2\right)\\ ={\displaystyle {\int }_0^{+\infty }{f}_{g_{\mathrm{JE}}}\left(x\right)\left[\underset{I_2\left(x\right)}{\underbrace{{\displaystyle {\int }_0^{{\omega }_{6}x+{\omega }_2}\left[1-F_{g_{\mathrm{SE}}}\left({\omega }_{1}y+{\omega }_{5}x+{\omega }_0\right)\right]f_{g_{\mathrm{DE}}}\left(y\right)dy}}}\right]}dx.\end{array}$$

(29)

With the same method as deriving $I_1\left(x\right)$ in (25), we can obtain $I_2\left(x\right)$ in (29) as

$$\begin{array}{l}{I}_2\left(x\right)={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}\frac{t!C_q^t{C}_{q-t}^r{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}}}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}\\ \times \exp \left(-\left({\psi }_{\mathrm{AB}}-{\beta }_{\mathrm{AB}}\right){\omega }_0\right)x^r\exp \left(-{\omega }_{10}x\right)\\ -{\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{\displaystyle \sum _{v=0}^t{\displaystyle \sum _{u=0}^v\frac{t!}{v!}}}}}\frac{C_q^t{C}_{q-t}^r{C}_v^u{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}{\left({\omega }_6\right)}^v{\left({\omega }_{12}\right)}^{v-u}}}\\ \times \exp \left(-\left({\psi }_{\mathrm{AB}}-{\beta }_{\mathrm{AB}}\right){\omega }_0\right)\exp \left(-\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right){\omega }_2\right)x^{u+r}\exp \left(-{\omega }_{13}x\right)\end{array}$$

(30)

Then, substituting (30) into (29), and using (18) to calculate the corresponding integral, we finally obtain

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\mathrm{not}{p}_{\mathrm{D}}}={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}\frac{r!t!C_q^t{C}_{q-t}^r{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}{\lambda }_{\mathrm{JE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}{\left({\omega }_{10}+{\lambda }_{\mathrm{JE}}\right)}^{r+1}}}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)\\ -{\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}{\displaystyle \sum _{v=0}^t{\displaystyle \sum _{u=0}^v\frac{t!}{v!}}}}}\frac{C_q^t{C}_{q-t}^r{C}_v^u{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1-v}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}{\left({\omega }_6\right)}^v{\left({\omega }_{12}\right)}^{v-u}}}\\ \times \exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)\exp \left(-\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right){\omega }_2\right){\displaystyle \frac{\left(u+r\right)!{\lambda }_{\mathrm{JE}}}{{\left({\omega }_{13}+{\lambda }_{\mathrm{JE}}\right)}^{u+r+1}}}.\end{array}$$

(31)

Now, we calculate the probability that $\mathrm{E}$ can correctly decode $p_{\mathrm{S}}$, regardless of the decoding of $p_{\mathrm{D}}$. Indeed, this probability can be formulated as

$$\begin{array}{l}{\chi }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}}}=\mathrm{Pr}\left(C_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{S}}}\ge C_{\mathrm{th}}\right)=\mathrm{Pr}\left(g_{\mathrm{SE}}\ge {\omega }_1{g}_{\mathrm{DE}}+{\omega }_5{g}_{\mathrm{JE}}+{\omega }_0\right)\\ ={\displaystyle {\int }_0^{+\infty }{f}_{g_{\mathrm{JE}}}\left(x\right)\left[\underset{I_3\left(x\right)}{\underbrace{{\displaystyle {\int }_0^{+\infty }\left[1-F_{g_{\mathrm{SE}}}\left({\omega }_{1}y+{\omega }_{5}x+{\omega }_0\right)\right]f_{g_{\mathrm{DE}}}\left(y\right)dy}}}\right]}dx.\end{array}$$

(32)

With the same method as deriving $I_1\left(x\right)$ in (25), we can obtain $I_3\left(x\right)$ in (32) as

$$\begin{array}{l}{I}_3\left(x\right)={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}\frac{t!C_q^t{C}_{q-t}^r{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1}}}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}\exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right)\\ \times x^r\exp \left(-{\omega }_{10}x\right).\end{array}$$

(33)

Then, substituting (33) into (32), and using (18) to calculate the corresponding integral, we finally obtain

$$\begin{array}{l}{\chi }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}}}={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{r=0}^{q-t}\frac{t!r!C_q^t{C}_{q-t}^r{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}{\lambda }_{\mathrm{JE}}}{{\left({\omega }_9+{\lambda }_{\mathrm{DE}}\right)}^{t+1}{\left({\omega }_{10}+{\lambda }_{\mathrm{JE}}\right)}^{r+1}}}}}}{\left({\omega }_1\right)}^q{\left({\omega }_7\right)}^{q-t}{\left({\omega }_{11}\right)}^{q-t-r}\\ \times \exp \left(-\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\omega }_0\right).\end{array}$$

(34)

Now, we consider the successful decoding of the packet $p_{\mathrm{R}}$ at $\mathrm{E}$ in the second phase, which can be expressed by an exact expression as

$${\theta }_{{\mathrm{R}}_b,\mathrm{E}}^{p_{\mathrm{R}}}=\mathrm{Pr}\left(C_{{\mathrm{R}}_b,\mathrm{E}}^{p_{\mathrm{R}}}\ge C_{\mathrm{th}}\right)=\mathrm{Pr}\left(g_{{\mathrm{R}}_b\mathrm{E}}\ge {\displaystyle \frac{{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right)=\exp \left(-{\displaystyle \frac{{\lambda }_{\mathrm{RE}}{\rho }_{\mathrm{th}}}{{\Delta }_{\mathrm{R}}}}\right).$$

(35)

3.1.3. Decoding Probability at High Transmit $\mathrm{SNR}$

We now consider the decoding probability of the data and eavesdropping links at high $\mathrm{SNR}$, i.e., $P_{\mathrm{S}},P_{\mathrm{R}},P_{\mathrm{D}},P_{\mathrm{J}}\to +\infty$. Indeed, we can set $P_{\mathrm{R}}={\mu }_{\mathrm{R}}{P}_{\mathrm{S}},$ $P_{\mathrm{D}}={\mu }_{\mathrm{D}}{P}_{\mathrm{S}},$ and $P_{\mathrm{J}}={\mu }_{\mathrm{J}}{P}_{\mathrm{S}},$ where ${\mu }_{\mathrm{R}},$ ${\mu }_{\mathrm{D}}$ and ${\mu }_{\mathrm{J}}$ are constants. At high $\mathrm{SNR}$ values, we can approximate ${\gamma }_{\mathrm{S},{\mathrm{R}}_m}^{p_{\mathrm{S}}}$ in (8), ${\gamma }_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{S}}}$ and ${\gamma }_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{D}}}$ in (9), respectively, as

$$\begin{array}{l}{\gamma }_{\mathrm{S},{\mathrm{R}}_m}^{p_{\mathrm{S}}}={\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{{\mathrm{SR}}_m}}{{\Delta }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}+1}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{{\mathrm{SR}}_m}}{{\Delta }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}}}={\displaystyle \frac{g_{{\mathrm{SR}}_m}}{{\mu }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}}},\\ {\gamma }_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{S}}}={\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{\mathrm{SE}}}{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}+{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}+1}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \frac{{\Delta }_{\mathrm{S}}{g}_{\mathrm{SE}}}{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}+{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}}}={\displaystyle \frac{g_{\mathrm{SE}}}{{\mu }_{\mathrm{D}}{g}_{\mathrm{DE}}+{\mu }_{\mathrm{J}}{g}_{\mathrm{JE}}}},\\ {\gamma }_{\mathrm{S},\mathrm{E}}^{p_{\mathrm{D}}}={\displaystyle \frac{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}}{{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}+1}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \frac{{\Delta }_{\mathrm{D}}{g}_{\mathrm{DE}}}{{\Delta }_{\mathrm{J}}{g}_{\mathrm{JE}}}}={\displaystyle \frac{{\mu }_{\mathrm{D}}{g}_{\mathrm{DE}}}{{\mu }_{\mathrm{J}}{g}_{\mathrm{JE}}}}.\end{array}$$

(36)

Using (36), we can approximate ${\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}$ in (14) at high $\mathrm{SNR}$ region as

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }=\mathrm{Pr}\left(g_{{\mathrm{SR}}_m}\ge {\rho }_{1,\mathrm{th}}{\mu }_{\mathrm{D}}{g}_{{\mathrm{DR}}_m}\right)\\ ={\displaystyle {\int }_0^{+\infty }{f}_{g_{{\mathrm{DR}}_m}}\left(x\right)\left(1-F_{g_{{\mathrm{SR}}_m}}\left(x\right)\right)dx}.\end{array}$$

(37)

Substituting (2) and (4) into (37), and using (18) to calculate the corresponding integral, we then obtain

$${\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }={\displaystyle \sum _{n=0}^{a_{\mathrm{SR}}-1}{\displaystyle \sum _{q=0}^n\frac{q!{\Psi }_{\mathrm{SR}}{\lambda }_{\mathrm{DR}}{\left({\rho }_{\mathrm{th}}{\mu }_{\mathrm{D}}\right)}^q}{{\left({\lambda }_{\mathrm{DR}}+\left({\psi }_{\mathrm{SR}}-{\beta }_{\mathrm{SR}}\right){\rho }_{\mathrm{th}}{\mu }_{\mathrm{D}}\right)}^{q+1}}.}}$$

(38)

For ${\theta }_{{\mathrm{R}}_b,\mathrm{S}}^{p_{\mathrm{R}}}$ in (22) and ${\theta }_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}$ in (24), it is straightforward that

$${\theta }_{{\mathrm{R}}_b,\mathrm{S}}^{p_{\mathrm{R}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }1,{\theta }_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }1.$$

(39)

.

Again, using (36), we can approximate ${\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}}}$ in (25) at high $\mathrm{SNR}$ regime as

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }=\mathrm{Pr}\left({\displaystyle \frac{g_{\mathrm{SE}}}{{\mu }_{\mathrm{D}}{g}_{\mathrm{DE}}+{\mu }_{\mathrm{J}}{g}_{\mathrm{JE}}}}\ge {\rho }_{\mathrm{th}},{\displaystyle \frac{{\mu }_{\mathrm{D}}{g}_{\mathrm{DE}}}{{\mu }_{\mathrm{J}}{g}_{\mathrm{JE}}}}\ge {\rho }_{\mathrm{th}}\right)\\ =\mathrm{Pr}\left(g_{\mathrm{SE}}\ge {\xi }_1{g}_{\mathrm{DE}}+{\xi }_2{g}_{\mathrm{JE}},g_{\mathrm{DE}}\ge {\xi }_3{g}_{\mathrm{JE}}\right)\\ ={\displaystyle {\int }_0^{+\infty }{f}_{g_{\mathrm{JE}}}\left(x\right)\left[{\displaystyle {\int }_{{\xi }_{3}x}^{+\infty }\left(1-F_{g_{\mathrm{SE}}}\left({\xi }_{1}y+{\xi }_{2}x\right)\right)f_{g_{\mathrm{DE}}}\left(y\right)dy}\right]}dx,\end{array}$$

(40)

where ${\xi }_1={\rho }_{\mathrm{th}}{\mu }_{\mathrm{D}},{\xi }_2={\rho }_{\mathrm{th}}{\mu }_{\mathrm{J}},{\xi }_3={\displaystyle \frac{{\mu }_{\mathrm{J}}{\rho }_{\mathrm{th}}}{{\mu }_{\mathrm{D}}}}.$ With the same manner as deriving ${\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}}}$, we also obtain the following result:

$${\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{v=0}^t{C}_q^t}}\frac{t!\left(v+q-t\right)!}{v!}\frac{{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}{\lambda }_{\mathrm{JE}}{\left({\xi }_1\right)}^q{\left({\xi }_3\right)}^v{\left({\xi }_4\right)}^{q-t}}{{\left({\lambda }_{\mathrm{DE}}+{\xi }_5\right)}^{t+1}{\left({\xi }_6+{\xi }_7\right)}^{v+q-t+1}}}}.$$

(41)

where ${\xi }_4={\displaystyle \frac{{\xi }_2}{{\xi }_1}},{\xi }_5=\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\xi }_1,{\xi }_6=\left({\psi }_{\mathrm{SE}}-{\beta }_{\mathrm{SE}}\right){\xi }_2,{\xi }_7=\left({\lambda }_{\mathrm{DE}}+{\xi }_5\right){\xi }_3$.

Similarly, ${\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\mathrm{not}{p}_{\mathrm{D}}}$ in (29) at high $\mathrm{SNR}$ values can be approximately computed as

$$\begin{array}{l}{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\mathrm{not}{p}_{\mathrm{D}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\mathrm{not}{p}_{\mathrm{D}},\infty }=\mathrm{Pr}\left(g_{\mathrm{SE}}\ge {\xi }_1{g}_{\mathrm{DE}}+{\xi }_2{g}_{\mathrm{JE}},g_{\mathrm{DE}}<{\xi }_3{g}_{\mathrm{JE}}\right)\\ \stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle {\int }_0^{+\infty }{f}_{g_{\mathrm{JE}}}\left(x\right)\left[{\displaystyle {\int }_0^{{\xi }_{3}x}\left(1-F_{g_{\mathrm{SE}}}\left({\xi }_{1}y+{\xi }_{2}x\right)\right)f_{g_{\mathrm{DE}}}\left(y\right)dy}\right]}dx\\ \stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\Psi }_{\mathrm{SE}}}\frac{C_q^{t}t!\left(q-t\right)!{\left({\xi }_1\right)}^q{\left({\xi }_4\right)}^{q-t}{\lambda }_{\mathrm{DE}}{\lambda }_{\mathrm{JE}}}{{\left({\lambda }_{\mathrm{DE}}+{\xi }_5\right)}^{t+1}{\left({\xi }_6+{\lambda }_{\mathrm{JE}}\right)}^{q-t+1}}}}\\ -{\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{\displaystyle \sum _{v=0}^t{C}_q^t}}\frac{t!\left(v+q-t\right)!}{v!}\frac{{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}{\lambda }_{\mathrm{JE}}{\left({\xi }_1\right)}^q{\left({\xi }_3\right)}^v{\left({\xi }_4\right)}^{q-t}}{{\left({\lambda }_{\mathrm{DE}}+{\xi }_5\right)}^{t+1-v}{\left({\xi }_6+{\xi }_7\right)}^{v+q-t+1}}}}.\end{array}$$

(42)

For ${\chi }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}}}$ in (32), we can approximately calculate it as

$$\begin{array}{ll}{\chi }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\chi }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\infty }\hfill & =\mathrm{Pr}\left(g_{\mathrm{SE}}\ge {\xi }_1{g}_{\mathrm{DE}}+{\xi }_2{g}_{\mathrm{JE}}\right)\\ & ={\displaystyle \sum _{n=0}^{a_{\mathrm{SE}}-1}{\displaystyle \sum _{q=0}^n{\displaystyle \sum _{t=0}^q{C}_q^t}t!\left(q-t\right)!\frac{{\Psi }_{\mathrm{SE}}{\lambda }_{\mathrm{DE}}{\lambda }_{\mathrm{JE}}{\left({\xi }_1\right)}^q{\left({\xi }_4\right)}^{q-t}}{{\left({\lambda }_{\mathrm{DE}}+{\xi }_5\right)}^{t+1}{\left({\lambda }_{\mathrm{JE}}+{\xi }_6\right)}^{q-t+1}}.}}\end{array}$$

(43)

Finally, the successful decoding of the packet $p_{\mathrm{R}}$ at $\mathrm{E}$ in the second phase can be approximated by

$${\theta }_{{\mathrm{R}}_b,\mathrm{E}}^{p_{\mathrm{R}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }1.$$

(44)

3.2. Decoding of One Encoded Packet

We now calculate the probability that one encoded packet can be correctly received by the satellite, the ground user and the eavesdropper.

Let us consider the satellite; the probability that $\mathrm{S}$ can obtain one packet $p_{\mathrm{D}}$ successfully can be formulated as

$${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}={\displaystyle \sum _{N=1}^M{C}_M^N}{\left({\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\right)}^N{\left(1-{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\right)}^{M-N}{\theta }_{{\mathrm{R}}_b,\mathrm{S}}^{p_{\mathrm{R}}}.$$

(45)

Equation (45) implies that, for $\mathrm{S}$ to successfully obtain $p_{\mathrm{D}}$, at least one relay station must decode both $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ correctly in the first phase (i.e., $1\le N\le M$). In addition, the transmission of $p_{\mathrm{R}}$ between ${\mathrm{R}}_b$ and $\mathrm{S}$ in the second phase must also be successful. Substituting (21) and (22) into (45), we obtain an exact closed-form expression of ${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}$.

Similarly, we can compute the probability that $\mathrm{D}$ can obtain one packet $p_{\mathrm{S}}$ successfully as

$${\Omega }_{\mathrm{D}}^{p_{\mathrm{S}}}={\displaystyle \sum _{N=1}^M{C}_M^N}{\left({\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\right)}^N{\left(1-{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\right)}^{M-N}{\theta }_{{\mathrm{R}}_b,\mathrm{D}}^{p_{\mathrm{R}}}.$$

(46)

At high transmit $\mathrm{SNR}$ values, using (38) and (39), we can approximate ${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}$ and ${\Omega }_{\mathrm{D}}^{p_{\mathrm{S}}}$, respectively, as

$$\begin{array}{l}{\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty }={\displaystyle \sum _{N=1}^M{C}_M^N}{\left({\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }\right)}^N{\left(1-{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }\right)}^{M-N}.\\ {\Omega }_{\mathrm{D}}^{p_{\mathrm{S}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\Omega }_{\mathrm{D}}^{p_{\mathrm{S}},\infty }={\displaystyle \sum _{N=1}^M{C}_M^N}{\left({\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }\right)}^N{\left(1-{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }\right)}^{M-N}.\end{array}$$

(47)

For the eavesdropper E; from Remark 3, the probability that $\mathrm{E}$ can obtain one packet $p_{\mathrm{S}}$ and one packet $p_{\mathrm{D}}$ successfully can be given, respectively, as

$${\Omega }_{\mathrm{E}}^{p_{\mathrm{S}}}={\chi }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}}},$$

(48)

$${\Omega }_{\mathrm{E}}^{p_{\mathrm{D}}}={\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}}}+{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\mathrm{not}{p}_{\mathrm{D}}}{\displaystyle \sum _{N=1}^M{C}_M^N}{\left({\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\right)}^N{\left(1-{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}}}\right)}^{M-N}{\theta }_{{\mathrm{R}}_b,\mathrm{E}}^{p_{\mathrm{R}}}.$$

(49)

Then, substituting (34) into (38), we obtain an exact closed-form expression of ${\Omega }_{\mathrm{E}}^{p_{\mathrm{S}}}$. Substituting (21), (28), (31), and (35) into (49), we obtain an exact closed-form expression of ${\Omega }_{\mathrm{E}}^{p_{\mathrm{D}}}$. At high $\mathrm{SNR}$ values, using (38), (41)–(44), we can approximate ${\Omega }_{\mathrm{E}}^{p_{\mathrm{S}}}$ and ${\Omega }_{\mathrm{E}}^{p_{\mathrm{D}}}$, respectively, as

$$\begin{array}{l}{\Omega }_{\mathrm{E}}^{p_{\mathrm{S}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\Omega }_{\mathrm{E}}^{p_{\mathrm{S}},\infty }={\chi }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\infty },\\ {\Omega }_{\mathrm{E}}^{p_{\mathrm{D}}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\Omega }_{\mathrm{E}}^{p_{\mathrm{D}},\infty }={\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }+{\theta }_{\mathrm{SD},\mathrm{E}}^{p_{\mathrm{S}},\mathrm{not}{p}_{\mathrm{D}},\infty }{\displaystyle \sum _{N=1}^M{C}_M^N}{\left({\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }\right)}^N{\left(1-{\theta }_{\mathrm{SD},\mathrm{R}}^{p_{\mathrm{S}},p_{\mathrm{D}},\infty }\right)}^{M-N}.\end{array}$$

(50)

Remark 4.

We first observe from (47) and (50) that the approximate expressions of  ${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty },{\Omega }_{\mathrm{D}}^{p_{\mathrm{S}},\infty },$${\Omega }_{\mathrm{E}}^{p_{\mathrm{S}},\infty }$, and ${\Omega }_{\mathrm{E}}^{p_{\mathrm{D}},\infty }$ do not depend on ${\Delta }_{\mathrm{S}}.$ In addition, at high SNR values, ${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}$ and ${\Omega }_{\mathrm{D}}^{p_{\mathrm{S}}}$ have the same value, i.e., ${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty }={\Omega }_{\mathrm{D}}^{p_{\mathrm{S}},\infty }$.

3.3. Outage Probability (OP) and Intercept Probability (IP)

Let $L_{\mathrm{S}}^{p_{\mathrm{D}}}\left(L_{\mathrm{D}}^{p_{\mathrm{S}}}\right)$ denote the number of the packets $p_{\mathrm{D}}\left(p_{\mathrm{S}}\right)$ that $\mathrm{S}\left(\mathrm{D}\right)$ can correctly obtain after the data exchange ends. Then, if $L_{\mathrm{S}}^{p_{\mathrm{D}}}<G_{\min }\left(L_{\mathrm{D}}^{p_{\mathrm{S}}}<G_{\min }\right),$ the node $\mathrm{S}\left(\mathrm{D}\right)$ is outage. Therefore, we can express $\mathrm{OP}$ at $\mathrm{S}$ and $\mathrm{D},$ respectively, as

$$\begin{array}{l}{\mathrm{OP}}_{\mathrm{S}}={\displaystyle \sum _{L_{\mathrm{S}}^{p_{\mathrm{D}}}=0}^{G_{\min }-1}{C}_{H_{\max }}^{L_{\mathrm{S}}^{p_{\mathrm{D}}}}{\left({\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}\right)}^{L_{\mathrm{S}}^{p_{\mathrm{D}}}}{\left(1-{\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}\right)}^{H_{\max }-L_{\mathrm{S}}^{p_{\mathrm{D}}}},}\\ {\mathrm{OP}}_{\mathrm{D}}={\displaystyle \sum _{L_{\mathrm{D}}^{p_{\mathrm{S}}}=0}^{G_{\min }-1}{C}_{H_{\max }}^{L_{\mathrm{D}}^{p_{\mathrm{S}}}}{\left({\Omega }_{\mathrm{D}}^{p_{\mathrm{S}}}\right)}^{L_{\mathrm{D}}^{p_{\mathrm{S}}}}{\left(1-{\Omega }_{\mathrm{D}}^{p_{\mathrm{S}}}\right)}^{H_{\max }-L_{\mathrm{D}}^{p_{\mathrm{S}}}},}\end{array}$$

(51)

where $\left(1-{\Omega }_{\mathrm{S}}^{p_{\mathrm{D}}}\right)$ and $\left(1-{\Omega }_{\mathrm{D}}^{p_{\mathrm{S}}}\right)$ are the probabilities that $\mathrm{S}$ and $\mathrm{D}$ cannot successfully obtain one packet $p_{\mathrm{D}}$ and one packet $p_{\mathrm{S}}$, respectively.

Let $L_{\mathrm{E}}^{p_{\mathrm{S}}}\left(L_{\mathrm{E}}^{p_{\mathrm{D}}}\right)$ denote the number of the packet $p_{\mathrm{S}}\left(p_{\mathrm{D}}\right)$ that $\mathrm{E}$ can correctly gather after the data exchange ends. If $L_{\mathrm{E}}^{p_{\mathrm{S}}}\ge G_{\min }\left(L_{\mathrm{E}}^{p_{\mathrm{D}}}\ge G_{\min }\right),$ the data $x_{\mathrm{S}}\left(x_{\mathrm{D}}\right)$ is intercepted. Hence, the probability that $\mathrm{E}$ can intercept $x_{\mathrm{S}}$ and $x_{\mathrm{D}}$ can be given, respectively, as

$$\begin{array}{l}{\mathrm{IP}}_{\mathrm{xS}}={\displaystyle \sum _{L_{\mathrm{E}}^{p_{\mathrm{S}}}=G_{\min }}^{H_{\max }}{C}_{H_{\max }}^{L_{\mathrm{E}}^{p_{\mathrm{S}}}}{\left({\Omega }_{\mathrm{E}}^{p_{\mathrm{S}}}\right)}^{L_{\mathrm{E}}^{p_{\mathrm{S}}}}{\left(1-{\Omega }_{\mathrm{E}}^{p_{\mathrm{S}}}\right)}^{H_{\max }-L_{\mathrm{E}}^{p_{\mathrm{S}}}},}\\ {\mathrm{IP}}_{\mathrm{xD}}={\displaystyle \sum _{L_{\mathrm{E}}^{p_{\mathrm{D}}}=G_{\min }}^{H_{\max }}{C}_{H_{\max }}^{L_{\mathrm{E}}^{p_{\mathrm{D}}}}{\left({\Omega }_{\mathrm{E}}^{p_{\mathrm{D}}}\right)}^{L_{\mathrm{E}}^{p_{\mathrm{D}}}}{\left(1-{\Omega }_{\mathrm{E}}^{p_{\mathrm{D}}}\right)}^{H_{\max }-L_{\mathrm{E}}^{p_{\mathrm{D}}}},}\end{array}$$

(52)

where $\left(1-{\Omega }_{\mathrm{E}}^{p_{\mathrm{S}}}\right)$ and $\left(1-{\Omega }_{\mathrm{E}}^{p_{\mathrm{D}}}\right)$ are the probabilities that $\mathrm{E}$ cannot successfully obtain one packet $p_{\mathrm{S}}$ and one packet $p_{\mathrm{D}}$, respectively.

Moreover, substituting (47) and (50) into (51) and (52), respectively, we obtain the asymptotic expressions of OP and IP as

$$\begin{array}{l}{\mathrm{OP}}_{\mathrm{S}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \sum _{L_{\mathrm{S}}^{p_{\mathrm{D}}}=0}^{G_{\min }-1}{C}_{H_{\max }}^{L_{\mathrm{S}}^{p_{\mathrm{D}}}}{\left({\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty }\right)}^{L_{\mathrm{S}}^{p_{\mathrm{D}}}}{\left(1-{\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty }\right)}^{H_{\max }-L_{\mathrm{S}}^{p_{\mathrm{D}}}},}\\ {\mathrm{OP}}_{\mathrm{D}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \sum _{L_{\mathrm{D}}^{p_{\mathrm{S}}}=0}^{G_{\min }-1}{C}_{H_{\max }}^{L_{\mathrm{D}}^{p_{\mathrm{S}}}}{\left({\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty }\right)}^{L_{\mathrm{D}}^{p_{\mathrm{S}}}}{\left(1-{\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty }\right)}^{H_{\max }-L_{\mathrm{D}}^{p_{\mathrm{S}}}},}\\ {\mathrm{IP}}_{\mathrm{xS}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \sum _{L_{\mathrm{E}}^{p_{\mathrm{S}}}=G_{\min }}^{H_{\max }}{C}_{H_{\max }}^{L_{\mathrm{E}}^{p_{\mathrm{S}}}}{\left({\Omega }_{\mathrm{E}}^{p_{\mathrm{S}},\infty }\right)}^{L_{\mathrm{E}}^{p_{\mathrm{S}}}}{\left(1-{\Omega }_{\mathrm{E}}^{p_{\mathrm{S}},\infty }\right)}^{H_{\max }-L_{\mathrm{E}}^{p_{\mathrm{S}}}},}\\ {\mathrm{IP}}_{\mathrm{xD}}\stackrel{{\Delta }_{\mathrm{S}}\to +\infty }{\approx }{\displaystyle \sum _{L_{\mathrm{E}}^{p_{\mathrm{D}}}=G_{\min }}^{H_{\max }}{C}_{H_{\max }}^{L_{\mathrm{E}}^{p_{\mathrm{D}}}}{\left({\Omega }_{\mathrm{E}}^{p_{\mathrm{D}},\infty }\right)}^{L_{\mathrm{E}}^{p_{\mathrm{D}}}}{\left(1-{\Omega }_{\mathrm{E}}^{p_{\mathrm{D}},\infty }\right)}^{H_{\max }-L_{\mathrm{E}}^{p_{\mathrm{D}}}}.}\end{array}$$

(53)

Remark 5.

As mentioned in Remark 4, ${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty },{\Omega }_{\mathrm{D}}^{p_{\mathrm{S}},\infty },$${\Omega }_{\mathrm{E}}^{p_{\mathrm{S}},\infty }$, and ${\Omega }_{\mathrm{E}}^{p_{\mathrm{D}},\infty }$ do not depend on ${\Delta }_{\mathrm{S}}$, and hence ${\mathrm{OP}}_{\mathrm{S}},{\mathrm{OP}}_{\mathrm{D}},{\mathrm{IP}}_{\mathrm{xS}},{\mathrm{IP}}_{\mathrm{xD}}$ do not depend on ${\Delta }_{\mathrm{S}}$ at high $\mathrm{SNR}$ values. Also, since ${\Omega }_{\mathrm{S}}^{p_{\mathrm{D}},\infty }={\Omega }_{\mathrm{D}}^{p_{\mathrm{S}},\infty },$ ${\mathrm{OP}}_{\mathrm{S}}$ and ${\mathrm{OP}}_{\mathrm{D}}$ have the same value at high ${\Delta }_{\mathrm{S}}$ region.

3.4. System Outage Probability (SOP) and System Intercept Probability (SIP)

$\mathrm{SOP}$ is defined as the probability that either the satellite or the ground user experiences an outage. Hence, $\mathrm{SOP}$ of the proposed scheme can be formulated as

$$\mathrm{SOP}=1-\left(1-{\mathrm{OP}}_{\mathrm{S}}\right)\left(1-{\mathrm{OP}}_{\mathrm{D}}\right).$$

(54)

In (42), $\left(1-{\mathrm{OP}}_{\mathrm{S}}\right)\left(1-{\mathrm{OP}}_{\mathrm{D}}\right)$ is the probability that both $\mathrm{S}$ and $\mathrm{D}$ are not in outage.

Next, $\mathrm{SIP}$ is defined as the probability that $\mathrm{E}$ can intercept either the data $x_{\mathrm{S}}$ or the data $x_{\mathrm{D}}$, and $\mathrm{SIP}$ of the proposed scheme can be given as

$$\mathrm{SIP}=1-\left(1-{\mathrm{IP}}_{{\mathrm{x}}_{\mathrm{S}}}\right)\left(1-{\mathrm{IP}}_{{\mathrm{x}}_{\mathrm{D}}}\right).$$

(55)

In (55), $\left(1-{\mathrm{IP}}_{{\mathrm{x}}_{\mathrm{S}}}\right)\left(1-{\mathrm{IP}}_{{\mathrm{x}}_{\mathrm{D}}}\right)$ is the probability that both $x_{\mathrm{S}}$ and $x_{\mathrm{D}}$ is not intercepted.

4. Simulation Results

In this section, we realize Monte Carlo simulations $\left(\mathrm{Sim}\right)$ to validate the formulas of $\mathrm{OP}$, $\mathrm{SOP}$, $\mathrm{IP}$, and $\mathrm{SIP}$ given in Section 3. We denote the exact theoretical results by $\mathrm{Exact},$ and the asymptotic theoretical results by $\mathrm{Asym}$. To ensure that the $\mathrm{Sim}$ results converge to the $\mathrm{Exact}$ results (with the deviation between them ranging from 0.001 to 0.01), we perform from ${10}^4$ trials to ${10}^5$ trials for each Monte Carlo simulation. For analyzing the performance trends and evaluating the influence of the key parameters on the system performance, several parameters are fixed as follows: $b_{\mathrm{SR}}=0.251,$ $a_{\mathrm{SR}}=5,$ ${\Omega }_{\mathrm{SR}}=0.279,$ $C_{\mathrm{th}}=0.5,$ ${\lambda }_{\mathrm{RD}}={\lambda }_{\mathrm{RE}}={\lambda }_{\mathrm{DE}}={\lambda }_{\mathrm{JE}}=1,$ $G_{\min }=5$, and ${\sigma }_0^2=1$. The transmit power of the transmitters is set up as follows: $P_{\mathrm{D}}=0.25P_{\mathrm{S}}\left({\mu }_{\mathrm{D}}=0.25\right),P_{\mathrm{R}}=0.5P_{\mathrm{S}}\left({\mu }_{\mathrm{R}}=0.5\right),$ and $P_{\mathrm{J}}=0.1P_{\mathrm{S}}\left({\mu }_{\mathrm{J}}=0.1\right)$.

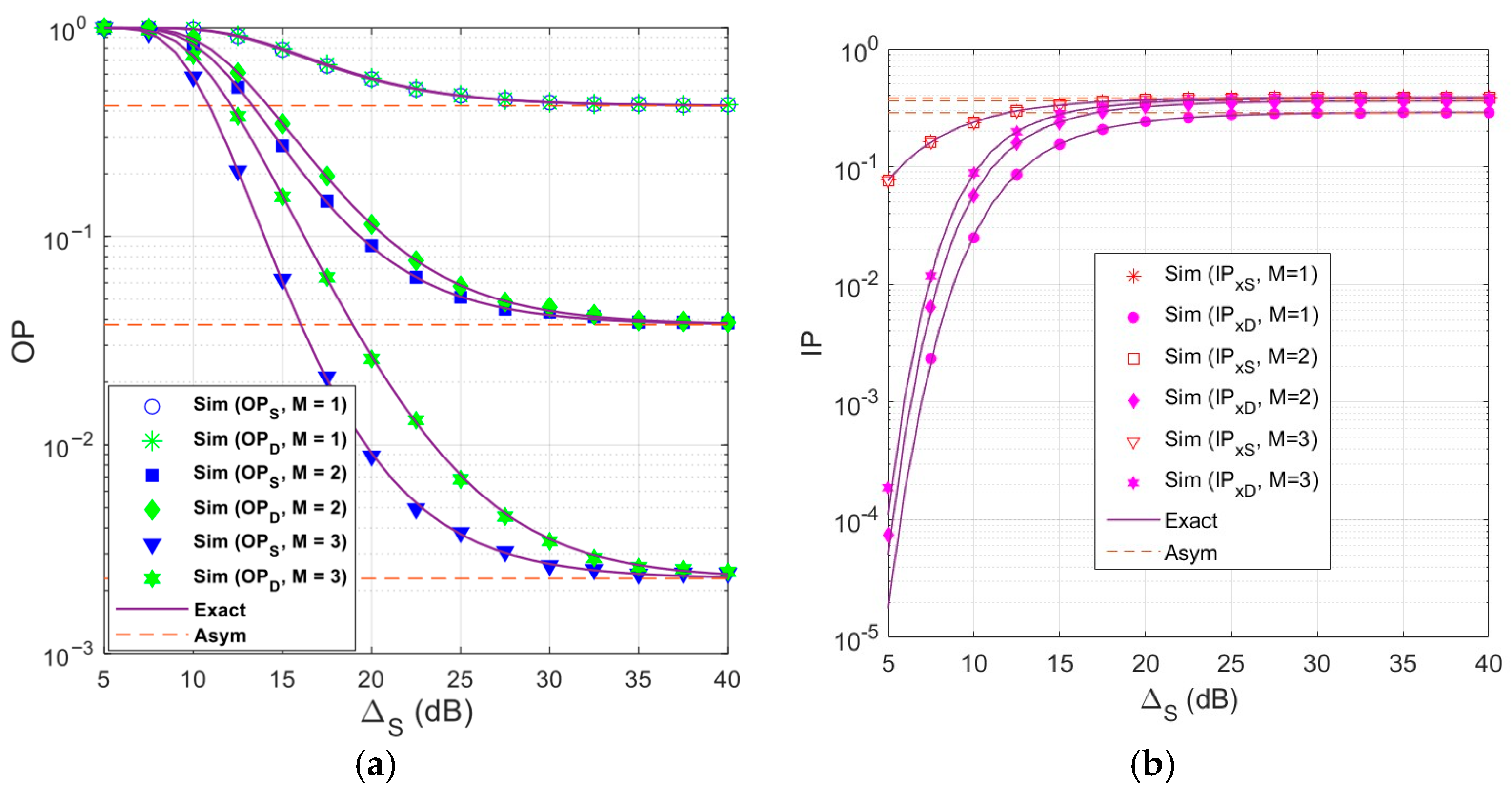
Figure 2 illustrates $\mathrm{OP}$ (Figure 2a) and $\mathrm{IP}$ (Figure 2b) as a function of ${\Delta }_{\mathrm{S}}\left({\Delta }_{\mathrm{S}}=P_{\mathrm{S}}/{\sigma }_0^2\right)$ in dB with different number of relay stations $\left(M\right)$ and with $H_{\max }=6$. As observed in Figure 2a, $\mathrm{OP}$ at $\mathrm{S}$ and $\mathrm{D}$ decreases as ${\Delta }_{\mathrm{S}}$ increases (or the transmit power of all the transmitters increases). However, at high ${\Delta }_{\mathrm{S}}$ values, the values of ${\mathrm{OP}}_{\mathrm{S}}$ and ${\mathrm{OP}}_{\mathrm{D}}$ converge to the same outage floors, as proved in Section 3. It is also seen that $\mathrm{OP}$ at $\mathrm{S}$ is lower than that at $\mathrm{D}$, and the $\mathrm{OP}$ performance at both $\mathrm{S}$ and $\mathrm{D}$ improves substantially with increasing $M$. It is due to the fact that increasing $M$ improves the probability that at least one relay station can successfully decode both $p_{\mathrm{S}}$ and $p_{\mathrm{D}}$ in the first phase, and it also enhances the channel quality of the ${\mathrm{R}}_b\to \mathrm{D}$ links. However, when $M=1$, the OP performance of S and D is quite identical because there is no relay selection at the second phase, and the system is hence symmetric for $\mathrm{S}$ and $\mathrm{D}$. It is worth noting that the scheme with $M=1$ corresponds to the random relay selection scheme. Hence, Figure 2a shows that the proposed scheme achieves significantly better $\mathrm{OP}$ performance than the random relay selection scheme.

In Figure 2b, we can observe that ${\mathrm{IP}}_{\mathrm{xS}}$ and ${\mathrm{IP}}_{\mathrm{xD}}$ increase as ${\Delta }_{\mathrm{S}}$ increases. As proved in Section 3, we can see that ${\mathrm{IP}}_{\mathrm{xS}}$ and ${\mathrm{IP}}_{\mathrm{xD}}$ converge to statured values at high ${\Delta }_{\mathrm{S}}$ regime. It is also seen from Figure 2b that ${\mathrm{IP}}_{\mathrm{xS}}$ is higher ${\mathrm{IP}}_{\mathrm{xD}}$, and ${\mathrm{IP}}_{\mathrm{xD}}$ increases with the increasing of $M$. It is worth noting that ${\mathrm{IP}}_{\mathrm{xS}}$ does not depend on the number of relays because $\mathrm{E}$ only decodes $p_{\mathrm{S}}$ directly from the satellite (See Remark 3). On the other hand, $\mathrm{E}$ can decode $p_{\mathrm{D}}$ indirectly via the relay stations, so ${\mathrm{IP}}_{\mathrm{xD}}$ depends on the number of relays. In particular, the more relays there are, the greater the opportunity that E will successfully decode $p_{\mathrm{D}}$.

From Figure 2a,b, we can see that the $‘\mathrm{Sim}’$ results confirm the correction of the theoretical results. In addition, we can observe that there exists the trade-off between reliability and security. Indeed, as ${\Delta }_{\mathrm{S}}$ increases, the ${\mathrm{OP}}_{\mathrm{S}}$ and ${\mathrm{OP}}_{\mathrm{D}}$ values decrease, but while the ${\mathrm{IP}}_{\mathrm{xS}}$ and ${\mathrm{IP}}_{\mathrm{xD}}$ values increase. Furthermore, the proposed scheme obtains better outage performance as increasing $M$; however, the ${\mathrm{IP}}_{\mathrm{xD}}$ performance is worse with high value of $M$. Finally, we can see that ${\mathrm{OP}}_{\mathrm{S}}>{\mathrm{OP}}_{\mathrm{D}}$ and ${\mathrm{IP}}_{\mathrm{xS}}>{\mathrm{IP}}_{\mathrm{xD}},$ which means that the reliability of transmitting the data $x_{\mathrm{S}}$ is better than that of $x_{\mathrm{D}}$, but the security of $x_{\mathrm{S}}$ is lower.

Figure 3 presents $\mathrm{OP}$ (Figure 3a) and $\mathrm{IP}$ (Figure 3b) as a function of ${\Delta }_{\mathrm{S}}$ in dB with different values of $H_{\max }$ and with $M=3$. As presented in Figure 3a, $\mathrm{OP}$ at $\mathrm{S}$ and $\mathrm{D}$ significantly decreases as $H_{\max }$ increases. This is because increasing $H_{\max }$ raises the probability that $\mathrm{S}$ and $\mathrm{D}$ can receive enough $G_{\min }$ encoded packets $p_{\mathrm{D}}$ and $p_{\mathrm{S}}$, respectively, thereby reducing outage probability at both $\mathrm{S}$ and $\mathrm{D}$.

In contrast to $\mathrm{OP}$, Figure 3b shows that the $\mathrm{IP}$ values increase with increasing $H_{\max }$, because a larger $H_{\max }$ also enhances the probability that the $\mathrm{E}$ node receives sufficiently the encoded packets.

From Figure 3a,b, we can see that the $‘\mathrm{Sim}’$ results again validate the theoretical results. We also observe that there exists the trade-off between $\mathrm{OP}$ and $\mathrm{IP}$, as $H_{\max }$ changes from 5 to 7.

In Figure 4, we present both $\mathrm{SOP}$ and $\mathrm{SIP}$ as a function of ${\Delta }_{\mathrm{S}}$ in dB with various values of $M$ and $H_{\max }$. Since the IP and OP values converge to their saturated levels at high ${\Delta }_{\mathrm{S}}$ values, the SIP and SOP values also converge to their saturated levels. Similarly to the $\mathrm{OP}$ performance, the $\mathrm{SOP}$ performance also improves as $M$ and $H_{\max }$ increase. Conversely, the SIP performance is worse as $M$ and $H_{\max }$ increase. However, it is seen that the SIP values in the cases of $\left(M=3,H_{\max }=6\right)$ and $\left(M=4,H_{\max }=6\right)$ are quite similar. This means that, as $M$ increases from 3 to 4, the SOP performance improves significantly, while the SIP performance changes only slightly.

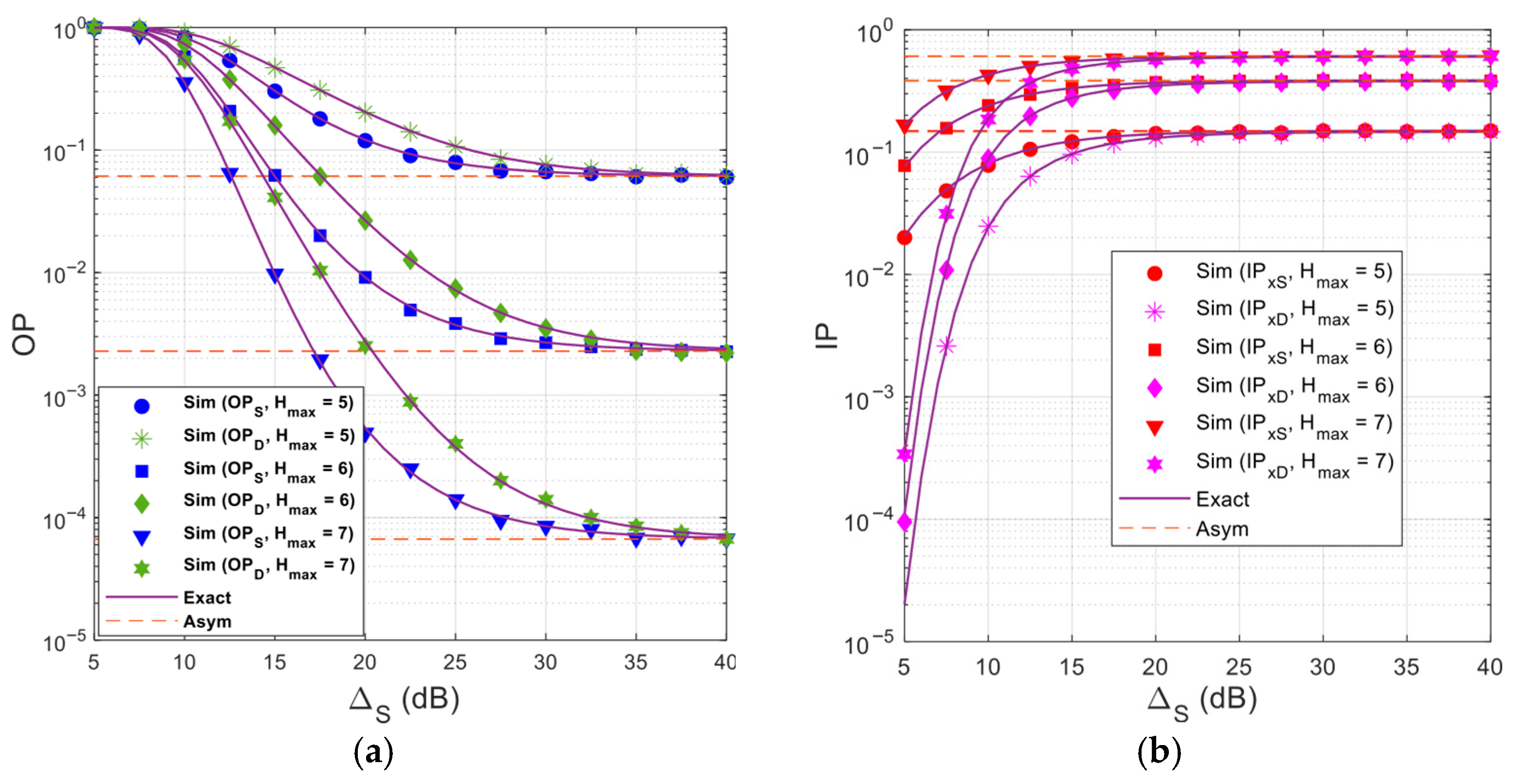
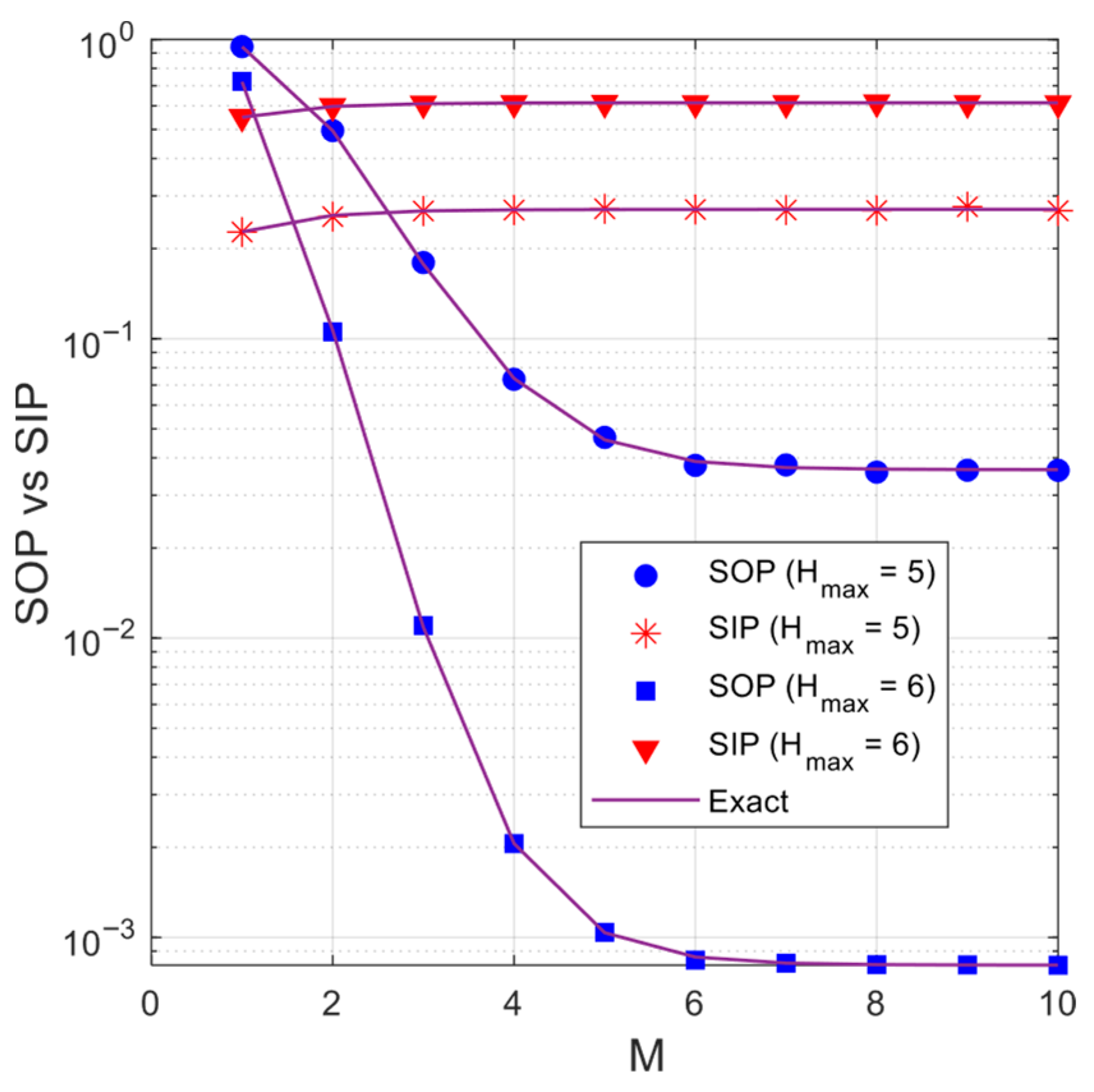
Figure 5 investigates the impact of the number of relay stations on the $\mathrm{SOP}$ and $\mathrm{SIP}$ performance with $\Delta =25$ (dB). As observed, the $\mathrm{SOP}$ values decrease rapidly as $M$ increases. However, when $M$ becomes sufficiently large, the $\mathrm{SOP}$ values no longer decrease. This behavior is due to the $\mathrm{PRS}$ method, i.e., at high $M$ values, the quality of the ${\mathrm{R}}_b\to \mathrm{D}$ link is good, and hence, the quality of the ${\mathrm{R}}_b\to \mathrm{S}$ link dominates the $\mathrm{SOP}$ performance. For the $\mathrm{SIP}$ performance, we can see that the $\mathrm{SIP}$ values rapidly increase as $M$ changes from 1 to 3. As $M\ge 3$, the SIP performance varies only slightly, as also seen in Figure 4 above. Similarly to Figure 2a,b, Figure 5 shows that the proposed scheme achieves significantly better $\mathrm{SOP}$ performance than the random relay selection scheme ($M=1$). In return, the proposed scheme incurs a slightly higher $\mathrm{SIP}$.

To more clearly analyze the impact of $H_{\max }$ and $M$ on the security–reliability tradeoff, Figure 6 and Figure 7 present $\mathrm{SIP}$ as a function of $\mathrm{SOP}$. To realize this, we first determine the target $\mathrm{SOP}$ values, e.g., $\mathrm{SOP}={\epsilon }_{\mathrm{SOP}},$ where ${\epsilon }_{\mathrm{SOP}}$ changes from ${10}^{-0.25}$ to ${10}^{-3}$, as presented in Figure 6 and Figure 7. Then, we use the $\mathrm{SOP}$ formula derived in Section 3 to find the corresponding transmit power $P_{\mathrm{S}}$. Next, we use the obtained values of $P_{\mathrm{S}}$ to calculate the corresponding values of $\mathrm{SIP}$. Finally, we plot SIP as a function of SOP.

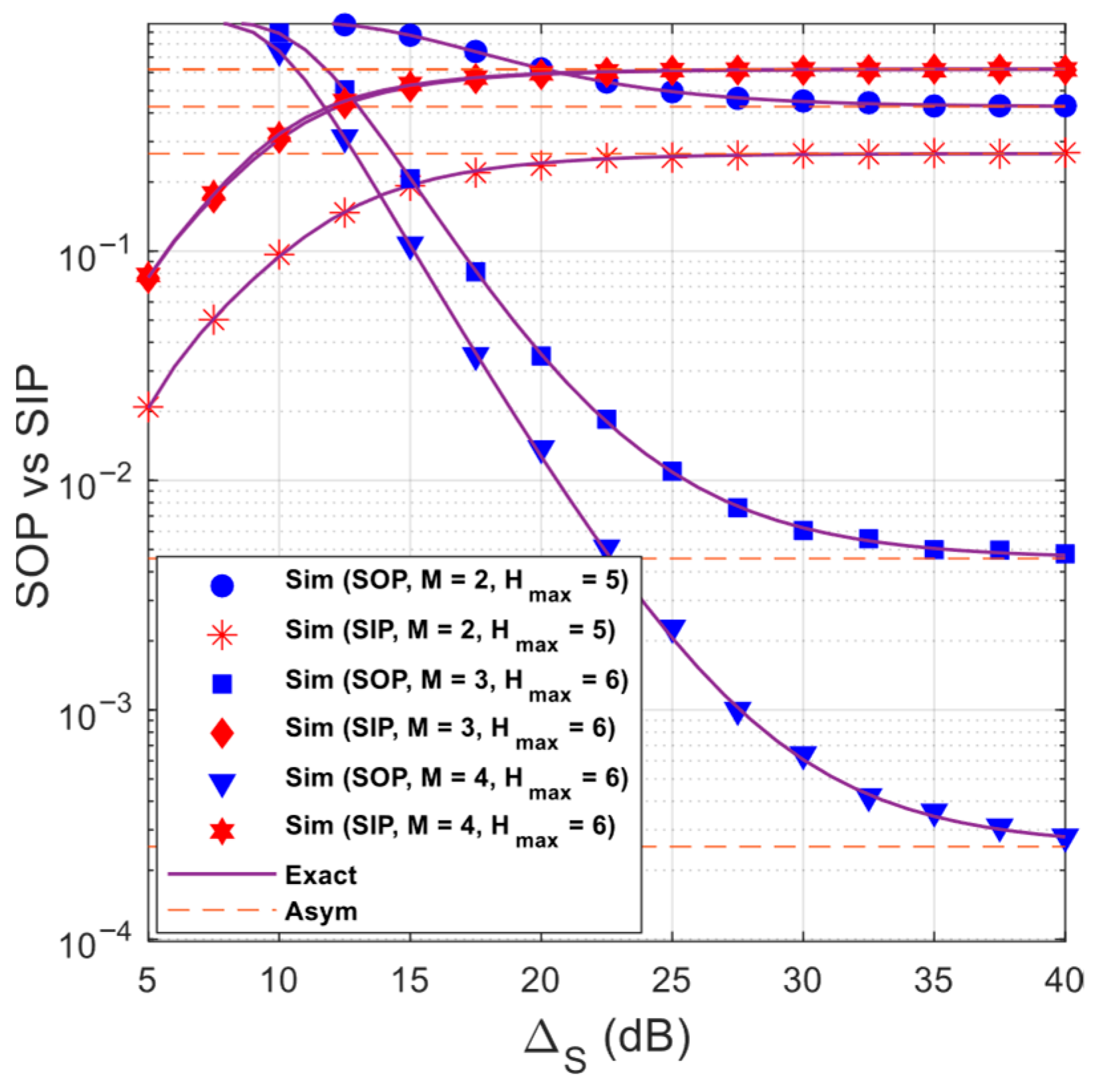
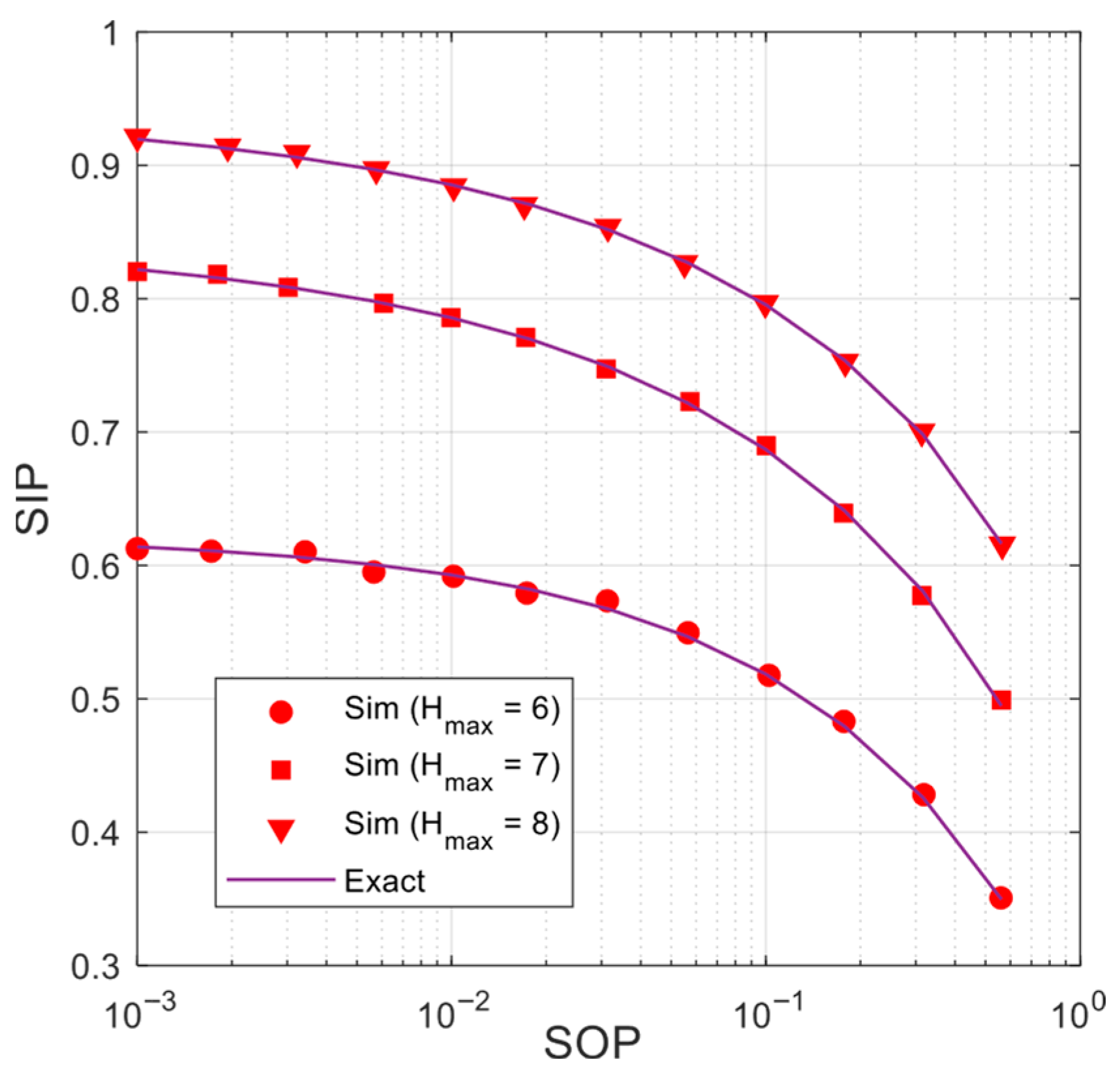
Figure 6 presents the trade-off between $\mathrm{SOP}$ and $\mathrm{SIP}$ with various values of $H_{\max }$ and with $M=5$. In particular, achieving better $\mathrm{SOP}$ performance in the proposed scheme comes at the cost of worse $\mathrm{SIP}$ performance. For example, with $H_{\max }=7$, if the target $\mathrm{SOP}$ value is 0.1, then the $\mathrm{SIP}$ value is 0.6869. However, if the required SOP performance is 0.01 then the corresponding $\mathrm{SIP}$ performance is 0.7857. Figure 6 also shows that increasing $H_{\max }$ decreases the trade-off between $\mathrm{SOP}$ and $\mathrm{SIP}$. For example, with $\mathrm{SOP}=0.1$, the value of $\mathrm{SIP}$ with $H_{\max }=6,7,8$ are 0.5185; 0.6869 and 0.7955, respectively.

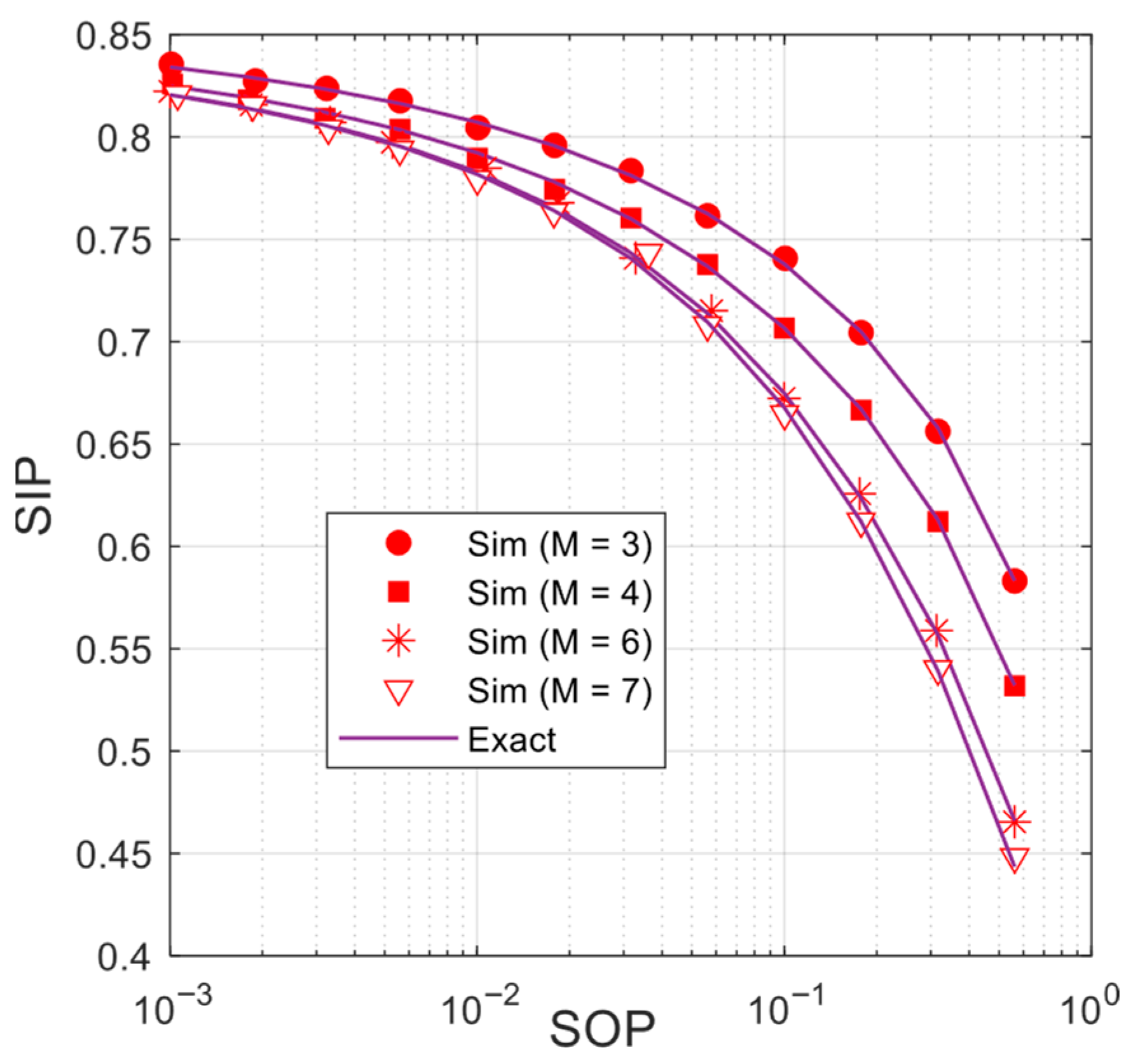
Figure 7 presents the trade-off between $\mathrm{SOP}$ and $\mathrm{SIP}$ with various values of $M$ and with $H_{\max }=7$. As we can observe, the trade-off between SOP and SIP is better as increasing $M$. However, as mentioned in Figure 5, as $M$ is high enough, both the $\mathrm{SOP}$ and $\mathrm{SIP}$ performance do not change any more. Indeed, as seen from Figure 7, the SIP performance only changes slightly as $M=6$ and $M=7$.

5. Conclusions

This paper proposes a two-phase $\mathrm{TW}-\mathrm{HSTR}$ scheme that incorporates $\mathrm{FCs}$, $\mathrm{SIC}$, $\mathrm{DNC}$, $\mathrm{PRS}$, and cooperative jamming. We derive exact closed-form expressions for $\mathrm{OP}/\mathrm{SOP}$ and $\mathrm{IP}/\mathrm{SIP}$, and perform Monte Carlo simulations to validate the analytical results. The obtained results reveal several key characteristics of the proposed scheme. First, the $\mathrm{OP}/\mathrm{SOP}$ performance saturates at high transmit $\mathrm{SNR}$, implying that the diversity order is zero. Second, the $\mathrm{OP}$ performance at both the satellite and the ground user converges as the transmit $\mathrm{SNR}$ becomes sufficiently large, which indicates that their $\mathrm{OP}$ performance becomes balanced at high $\mathrm{SNR}$ regime. Third, the $\mathrm{OP}$ performance improves significantly when increasing the number of terrestrial relay stations ($M$) and the number of encoded-packet transmissions ($H_{\max }$). However, both the $\mathrm{OP}$ and $\mathrm{IP}$ performances eventually saturate when the number of relays becomes sufficiently large. In contrast to the outage behavior, the $\mathrm{IP}$ performance is worse as $M$ and $H_{\max }$ increase. Similarly to the outage performance, the interception performance also converges when the transmit $\mathrm{SNR}$ and the number of relays are sufficiently large. The results further show that the three main factors affecting the security–reliability tradeoff are the transmit power, the number of transmission rounds, and the number of relays. In particular, the SOP–SIP tradeoff becomes better (worse) when increasing the number of relays (increasing the number of transmission rounds). In future work, we will extend our scheme to scenarios involving multiple eavesdroppers, multiple cooperative jammers, and multiple ground users.