A Quantum MIMO-OFDM Framework with Transmit and Receive Diversity for High-Fidelity Image Transmission

Abstract

This paper proposes a quantum multiple-input multiple-output orthogonal frequency division multiplexing (MIMO-OFDM) framework for image transmission, which combines quantum multi-qubit encoding with spatial and frequency diversity to enhance noise resilience and image quality. The system utilizes joint photographic experts group (JPEG), high efficiency image file format (HEIF), and uncompressed images, which are first source-encoded (if applicable) and then processed using classical channel encoding. The channel-encoded bitstream is mapped into quantum states via multi-qubit encoding and transmitted through a 2 × 2 MIMO system with varied diversity schemes. The spatially mapped qubits undergo the quantum Fourier transform (QFT) to form quantum OFDM subcarriers, with a cyclic prefix added before transmission over fading quantum channels. At the receiver, the cyclic prefix is removed, the inverse QFT is applied, and the quantum MIMO decoder reconstructs spatially diverged quantum states. Then, quantum decoding reconstructs the bitstreams, followed by channel decoding and source decoding to recover the final image. Experimental results show that the proposed quantum MIMO-OFDM system outperforms its classical counterpart across all evaluated diversity configurations. It achieves peak signal-to-noise ratio (PSNR) values up to 58.48 dB, structural similarity index measure (SSIM) up to 0.9993, and universal quality index (UQI) up to 0.9999 for JPEG; PSNR up to 70.04 dB, SSIM up to 0.9998, and UQI up to 0.9999 for HEIF; and near-perfect reconstruction with infinite PSNR, SSIM of 1, and UQI of 1 for uncompressed images under high channel noise. These findings establish quantum MIMO-OFDM as a promising architecture for high-fidelity, bandwidth-efficient quantum multimedia communication.

1. Introduction

The ever-increasing demand for high-resolution visual content in applications such as autonomous driving, real-time remote diagnostics, unmanned aerial surveillance, and immersive virtual [1] and augmented reality [2] imposes stringent requirements on modern wireless communication systems, necessitating ultra-reliable, high-throughput image transmission where even minor latency, distortion, or packet loss can critically impact safety, diagnostic precision, or user experience. Traditional wireless systems, grounded in classical Shannon-based information theory [3], face growing challenges in meeting these demands due to inherent limitations, including susceptibility to noise, quantization and compression artifacts, and sensitivity to multipath fading, all of which degrade image quality, especially in high-frequency and texture-rich regions, while performance is ultimately bounded by the Shannon capacity limit. Compounding these issues, compressed image formats such as joint photographic experts group (JPEG) and high efficiency image file format (HEIF) exploit spatial and spectral redundancies to reduce file size, producing bitstreams with high entropy and localized error sensitivity; thus, errors caused by noise, interference, or packet loss can propagate nonlinearly, corrupting entire image blocks and severely impacting visual fidelity. These vulnerabilities are further amplified by channel fading [4], including time-varying Rayleigh fading, which introduces amplitude and phase fluctuations, often generating burst errors that affect clustered bit sequences. Consequently, even advanced error correction and equalization techniques struggle to maintain reliable high-fidelity image transmission, highlighting the limitations of classical systems for real-time, image-intensive applications.

To address these challenges, modern wireless communication frameworks have adopted multiple-input multiple-output (MIMO) architectures [5], which exploit spatial diversity [6] and multiplexing gains by employing multiple antennas at both the transmitter and the receiver. MIMO systems significantly improve spectral efficiency and link robustness, offering substantial throughput gains under favorable propagation conditions. These features are particularly advantageous for image and video transmission scenarios, where large volumes of data must be delivered with high fidelity and low latency. However, MIMO performance deteriorates in frequency-selective fading environments, where variations across frequency bands introduce inter-symbol interference (ISI), which becomes a major bottleneck that limits both reliability and throughput in broadband settings.

To combat ISI and ensure robust broadband performance, orthogonal frequency division multiplexing (OFDM) divides the available spectrum into multiple orthogonal subcarriers, each experiencing flat fading, which simplifies equalization and allows high-throughput, low-distortion image and video transmission [7]. However, OFDM is susceptible to synchronization errors, inter-carrier interference (ICI), high peak-to-average power ratio (PAPR), Doppler-induced distortions in high-mobility scenarios, and imperfect channel estimation [8], which collectively limit reliable, high-quality image transmission under adverse or time-varying channel conditions.

In response, OFDM is often combined with MIMO technology, resulting in the widely adopted MIMO-OFDM architecture [9]. This integration takes advantage of both spatial and frequency diversity, offering improved spectral efficiency and better adaptability to multipath effects. MIMO-OFDM forms the foundation of many current wireless standards and provides a scalable and flexible framework for image transmission in dynamic channel environments. However, despite its benefits, MIMO-OFDM still faces core physical-layer limitations such as channel capacity saturation, synchronization complexity, and persistent PAPR issues. These challenges are particularly significant when operating under constrained bandwidth, severe fading, or high-noise conditions, where consistent image quality and transmission reliability are difficult to maintain.

These constraints highlight the need to explore alternative physical-layer paradigms capable of going beyond classical communication boundaries. In this context, quantum communication [10] has emerged as a promising candidate. Using quantum mechanical principles such as superposition [11] and entanglement [12], quantum communication systems have the potential to redefine the limits of channel capacity and noise resistance. When appropriately designed, quantum-enabled frameworks offer fundamentally new degrees of freedom for encoding, transmitting, and processing image data, potentially achieving higher fidelity and robustness under conditions where classical systems fail.

Building on these principles, quantum MIMO extends classical MIMO into the quantum domain, enabling simultaneous transmission of quantum information streams with enhanced capacity, noise tolerance, and robustness against spatial fading through quantum correlations. In addition, quantum OFDM (QOFDM) [13] can utilize quantum Fourier transform (QFT) [14] to encode data into orthogonal quantum frequency subcarriers, providing enhanced resilience against frequency-selective fading. By combining this with spatial diversity, the quantum MIMO-OFDM framework effectively merges both spatial and frequency diversity, resulting in a scalable, adaptive, and noise-resilient system that surpasses classical performance limits. This makes it an ideal solution for next-generation, high-fidelity image transmission applications.

Although basic encoding and decoding techniques in quantum communication have been extensively studied for media transmission [15,16], the application of quantum MIMO is still considered a relatively new and emerging area, with its full potential to enhance efficiency and robustness currently being explored. Similarly, QOFDM has received comparatively less attention, particularly with respect to practical applications for multimedia data. In particular, the application of QOFDM techniques for high-fidelity image transmission remains largely unexplored. Moreover, most existing communication frameworks focus on single-qubit or simple encoding schemes, limiting their abilities to fully exploit the advantages of multi-qubit encoding and advanced frequency-domain processing. Furthermore, there is a lack of integrated approaches that combine quantum MIMO and OFDM to take advantage of spatial and frequency diversity to improve data throughput and noise resistance in quantum channels. These gaps indicate a clear need for a quantum communication framework that leverages quantum encoding and quantum communication architectures to overcome the limitations of current classical communication systems and enable reliable high-quality image transmission in challenging wireless environments.

Therefore, the integration of quantum MIMO and QOFDM into a quantum MIMO-OFDM framework with multi-qubit encoding represents an extremely novel and pioneering approach. This system uniquely leverages the combined strengths of spatial and frequency domain quantum diversity, as enabled by MIMO and OFDM techniques, to enable efficient, scalable, and robust transmission of complex image data. It addresses critical gaps in existing quantum communication research and opens new pathways for next-generation image communication technologies.

The proposed system begins by compressing images using JPEG and HEIF formats, while uncompressed images are also included for performance analysis. All image bitstreams are then channel encoded using polar codes for error correction. The resulting bitstream is then mapped into quantum states using multi-qubit encoding. These encoded quantum states are processed through a 2 × 2 quantum MIMO encoder, which spatially distributes the quantum information across different transmit and receive antennas under various antenna configurations, namely single-input single-output (SISO, 1 × 1), multiple-input single-output (MISO, 2 × 1), and single-input multiple-output (SIMO, 1 × 2). The spatially mapped qubits are then transformed into orthogonal subcarriers using the QFT, forming the QOFDM encoding. A cyclic prefix is added before transmission over fading quantum channels, incorporating decoherence and environmental noise. At the receiver, the cyclic prefix is removed and the inverse QFT (IQFT) is applied to recover the frequency-domain quantum components. The signal then passes through the quantum MIMO decoder, which reconstructs the received quantum states by combining information across the receive antennas. This is followed by quantum-to-classical decoding, polar decoding, and source decoding to retrieve the original image. The results show that the proposed quantum MIMO-OFDM system consistently outperforms the classical MIMO-OFDM system across all diversity configurations, including SISO, MISO, and SIMO, particularly in preserving image quality under challenging channel conditions. By demonstrating superior image quality, this study validates the potential of quantum MIMO-OFDM as a foundational architecture for advanced quantum communication systems, paving the way for next-generation high-fidelity and bandwidth-efficient multimedia transmission.

The main novelties of this study are as follows:

1.

Development of a quantum MIMO-OFDM system that combines spatial and frequency diversity in the quantum domain for high-fidelity image transmission.

2.

Design of a multi-qubit quantum encoding scheme integrated with quantum MIMO-OFDM modulation to enhance spectral efficiency and robustness.

3.

Introduction of a robust QOFDM system using QFT and IQFT to effectively mitigate channel noise and fading in image transmission.

4.

Empirical validation demonstrating significant improvements in image quality and transmission reliability over classical MIMO-OFDM systems under realistic fading channel conditions.

The remainder of the paper is organized as follows: Section 2 reviews related work on classical and quantum communication systems. Section 3 describes the proposed quantum MIMO-OFDM methodology in detail. Section 4 presents and analyzes the simulation results, and Section 5 concludes the paper with a summary of the findings and potential future directions.

2. Related Work

Quantum communication has steadily evolved over the past few decades, originating from the foundational concept of using quantum states to transmit information [17]. Early research explored how the core principles of quantum mechanics, particularly superposition and entanglement [18], could overcome the limitations of classical communication systems. The foundation of this paradigm is the qubit, a quantum unit of information capable of existing in a superposition of both 0 and 1 simultaneously, unlike a classical bit. This unique property enables innovative approaches to information encoding and transmission, paving the way for the development of highly efficient and secure communication protocols. As the field advances, increasingly sophisticated quantum communication technologies are being built upon these fundamental principles, marking a shift from theoretical models toward practical implementation.

2.1. Advantages of Quantum Communication

Quantum communication exploits fundamental principles of quantum mechanics [19], including superposition, entanglement, and quantum measurement, to enable capabilities beyond classical communication systems [20,21,22,23]. A primary advantage lies in encoding and processing information using qubits. Unlike classical bits, which represent either 0 or 1, qubits can exist in a superposition of both states simultaneously [24], allowing more compact and efficient data representation. Entanglement is another critical feature, creating strong correlations between quantum particles regardless of their physical separation [25]. This enables unique protocols for synchronization, coordination, and secure communication that classical systems cannot achieve without additional latency or external mechanisms. From a security perspective, entanglement underpins protocols such as quantum key distribution (QKD) [26], allowing two parties to generate and share encryption keys with unconditional security. In addition to security and efficiency, quantum systems are inherently suitable for parallel processing and techniques in the frequency domain [27]. For example, quantum analogs of the Fourier transform allow operations on all components of a quantum state simultaneously, leading to faster and more efficient processing in certain tasks, such as signal transformation, compression, or spectral analysis.

2.2. Efficient and Reliable Quantum Communication Systems

Although secure communication protocols such as QKD and quantum teleportation are well-established [28,29,30,31], quantum communication systems that primarily exploit quantum superposition to achieve efficient, high-throughput data transmission remain relatively underexplored. Unlike entanglement-based secure communication methods, these approaches offer a potentially lower complexity and more scalable alternative for certain communication scenarios. Several studies have explored the superposition property in the context of analysis of the complexity of communication systems [32,33,34] and have implemented quantum communication schemes in the time domain using single-qubit encoding and decoding methods [15,35,36]. These methods typically rely on the representation of classical information using superposition states, enabling parallelism and more compact data representations.

However, multi-qubit encoding schemes [16,37] based on quantum superposition, especially tailored for image transmission, are still in their infancy. Although single-qubit systems offer simplicity, they often fall short in terms of capacity and robustness, particularly under noisy conditions. Multi-qubit superposition encoding allows for the simultaneous processing of larger data segments, enabling higher throughput and improved error tolerance. Despite its potential, this area remains underdeveloped due to the challenges of quantum state preparation, decoherence, and decoding complexity. These emerging approaches hold significant promise for enhancing the efficiency and noise resilience of quantum communication systems, particularly in the presence of channel-induced distortions and quantum noise. As research progresses, such techniques could play a pivotal role in realizing practical and scalable quantum communication frameworks for high-fidelity image and video transmission.

2.3. The Importance of MIMO Technology

Multipath propagation and fading in wireless environments degrade signal quality and reliability, which classical MIMO systems address using multiple antennas to provide spatial diversity, multiplexing, and improved spectral efficiency, forming the basis of modern standards like LTE, Wi-Fi, and 5G [38,39,40], while classical MIMO enhances robustness and throughput, it faces hardware complexity, power consumption, antenna spacing constraints, and spatial interference challenges. In contrast to the extensive progress made in classical communication, quantum MIMO systems are still in their early stages of development [41,42,43]. Furthermore, there have been initial investigations into quantum superposition-based MIMO systems, aimed at analyzing the performance of transmit and receive diversity under simplified and idealized conditions [44,45], particularly targeting high-quality media transmission. These studies demonstrate the theoretical feasibility of applying MIMO principles in the quantum domain with single-qubit encoding and suggest potential performance benefits.

2.4. The Importance of OFDM Technology

OFDM is a well-established technique that divides bandwidth into orthogonal subcarriers, enabling high-rate data transmission with robustness against frequency-selective fading and ISI, making it ideal for broadband communications. In classical systems, OFDM underpins standards such as LTE, Wi-Fi, DVB-T, and 5G [46,47,48,49], with extensive research optimizing adaptive modulation, channel estimation, synchronization, and PAPR reduction, as well as enhancing media transmission under fading and noise [50,51,52,53,54,55,56,57]. Inspired by these successes, QOFDM has emerged as a promising approach to extend frequency-domain multiplexing to quantum channels, potentially improving quantum data throughput, spectral efficiency, and noise resilience, which is critical for future quantum networks and the quantum internet [58,59,60]. However, QOFDM is still in early theoretical or low-dimensional stages, facing challenges such as generating and controlling quantum subcarrier states, maintaining orthogonality under decoherence, and implementing quantum-compatible operations. Moreover, no QOFDM frameworks currently target image or multimedia transmission, highlighting a significant gap and a promising research direction for practical, high-fidelity quantum media communication.

2.5. The Importance of MIMO-OFDM Technology

The combination of MIMO and OFDM, commonly referred to as MIMO-OFDM, represents a cornerstone of modern wireless communication systems. A large body of research has investigated various aspects of MIMO-OFDM systems, including channel estimation, adaptive modulation and coding, beamforming algorithms, synchronization techniques, and interference suppression mechanisms in the classical domain [9,61,62,63,64]. These advancements have led to robust implementations that can dynamically adapt to varying channel conditions, optimize resource allocation, and deliver high-quality communication over diverse and challenging environments. Despite the proven success of MIMO-OFDM in classical wireless networks, its potential within the quantum domain remains vastly underexplored. Although preliminary research has addressed the theoretical aspects of quantum MIMO and QOFDM independently, a significant research gap remains in combining these technologies into a unified framework. In particular, the development of quantum MIMO-OFDM systems for the transmission of high-dimensional data, such as images and videos, has not yet been realized.

2.6. Research Gaps

In summary, the research gaps of this study are as follows.

Classical MIMO-OFDM systems are widely employed for wireless multimedia transmission but are affected by fundamental limitations such as channel capacity saturation, synchronization complexity, reduced noise resilience, and high PAPR. These limitations become more pronounced with bandwidth limitations, severe fading, and noisy channel conditions, resulting in poor image quality and unreliable transmission.

In response, quantum communication offers promising advantages to address these issues. However, the practical application of quantum communication techniques to multimedia transmission remains underexplored. In particular:

• The development of quantum MIMO systems for spatial diversity in quantum domains is still in its infancy, with limited research exploring their potential to enhance multimedia transmission using only single-qubit encoding.
• QOFDM leveraging QFT has been theoretically proposed using only single-qubit encoding and without accounting for real-world quantum noise, but lacks practical investigation for high-fidelity image transmission.
• Existing studies primarily address bit-level quantum communication performance or security aspects, with minimal focus on the impact of quantum techniques on perceptual image quality metrics under realistic wireless channel conditions.
• No integrated framework currently combines quantum MIMO and QOFDM techniques to harness both spatial and frequency quantum diversity for robust and efficient image transmission.
• No existing approach has developed or demonstrated a scalable multi-qubit encoding scheme specifically tailored for media transmission, which is essential to fully exploit the advantages of quantum parallelism and fidelity in practical applications.

These gaps indicate a clear need for a quantum communication framework that leverages quantum encoding and quantum communication architectures to overcome the limitations of current classical communication systems and enable reliable high-quality image transmission in challenging wireless environments.

3. Proposed Framework

The complete end-to-end workflow is illustrated in Figure 1 and operates through the following core stages:

• Input Images: For evaluation, we use 100 images (256 × 192 pixels) from the Microsoft COCO dataset [65] and 20 high-resolution 4K images from the Kaggle dataset [66], ensuring diverse spatial information and detail levels. The framework supports a variety of image types, including grayscale and color, ensuring flexibility in various visual content regardless of the color format, resolution, or compression method.
• Source Encoder: This step compresses the image data using standard formats (e.g., JPEG, HEIF) or passes it through uncompressed, producing a classical bitstream. This stage evaluates the system’s adaptability to different compression standards and uncompressed data.
• Channel Encoder: Next, this bitstream is channel encoded using polar codes [67] with a code rate of 1/2 to improve robustness against channel impairments. Polar codes are selected because they are the first class of error-correcting codes that provably achieve the capacity of symmetric binary-input discrete memoryless channels with low encoding and decoding complexity. Their excellent performance at moderate code lengths and suitability for efficient hardware implementation make them highly advantageous compared to other classical error correction codes, such as the low-density parity check (LDPC) or Turbo codes. The code rate of 1/2 is chosen as a balanced trade-off between error correction capability and transmission efficiency, providing strong error resilience while maintaining reasonable data throughput.
• Quantum Encoder: The channel encoded bitstream is then segmented into bit blocks based on qubit encoding sizes ranging from 1 to 8. These bit blocks are subsequently quantum encoded into quantum superposition states using a multi-qubit encoding scheme, where each block of classical bits is mapped to a corresponding quantum state. Although the upper bound is not theoretically restricted and larger encodings are possible, the system limits the encoding to 8 qubits, as this is sufficient to represent the full range of pixel values (e.g., $2^8=256$) required for image transmission.
• MIMO Encoder: To exploit spatial diversity, the quantum encoded data are processed through a MIMO encoder in various antenna configurations, including SISO (1 × 1), MISO (2 × 1), and SIMO (1 × 2). The MIMO encoder distributes the quantum encoded symbols across multiple transmit antennas according to the chosen diversity scheme.
• QOFDM Encoder: Following the MIMO encoding stage, each transmit antenna applies an independent quantum-assisted OFDM modulation process. In this system, conventional inverse fast Fourier transform (IFFT) is replaced by the QFT, which operates on the quantum-encoded bitstream to generate orthogonal subcarriers in the quantum domain. Prior to this, the quantum encoded states were rearranged from serial to parallel form and input to the QFT. This transformation allows the data to be distributed across orthogonal quantum subcarriers, enabling efficient transmission in frequency-selective fading environments.
• Transmission: The resulting quantum subcarriers are then converted back to serial form, and a cyclic prefix is appended to each, which helps to mitigate ISI caused by multipath delay spread. Each processed stream is transmitted through the noisy quantum channel. In MIMO-OFDM systems, the channel is generally modeled to incorporate quantum noise effects along with frequency-selective fading, which reflects the multipath propagation characteristics across different subcarriers. Depending on the scenario, a flat fading model may be used for simplified simulations or narrowband cases, whereas frequency-selective fading models are applied in wideband and more realistic channel conditions.
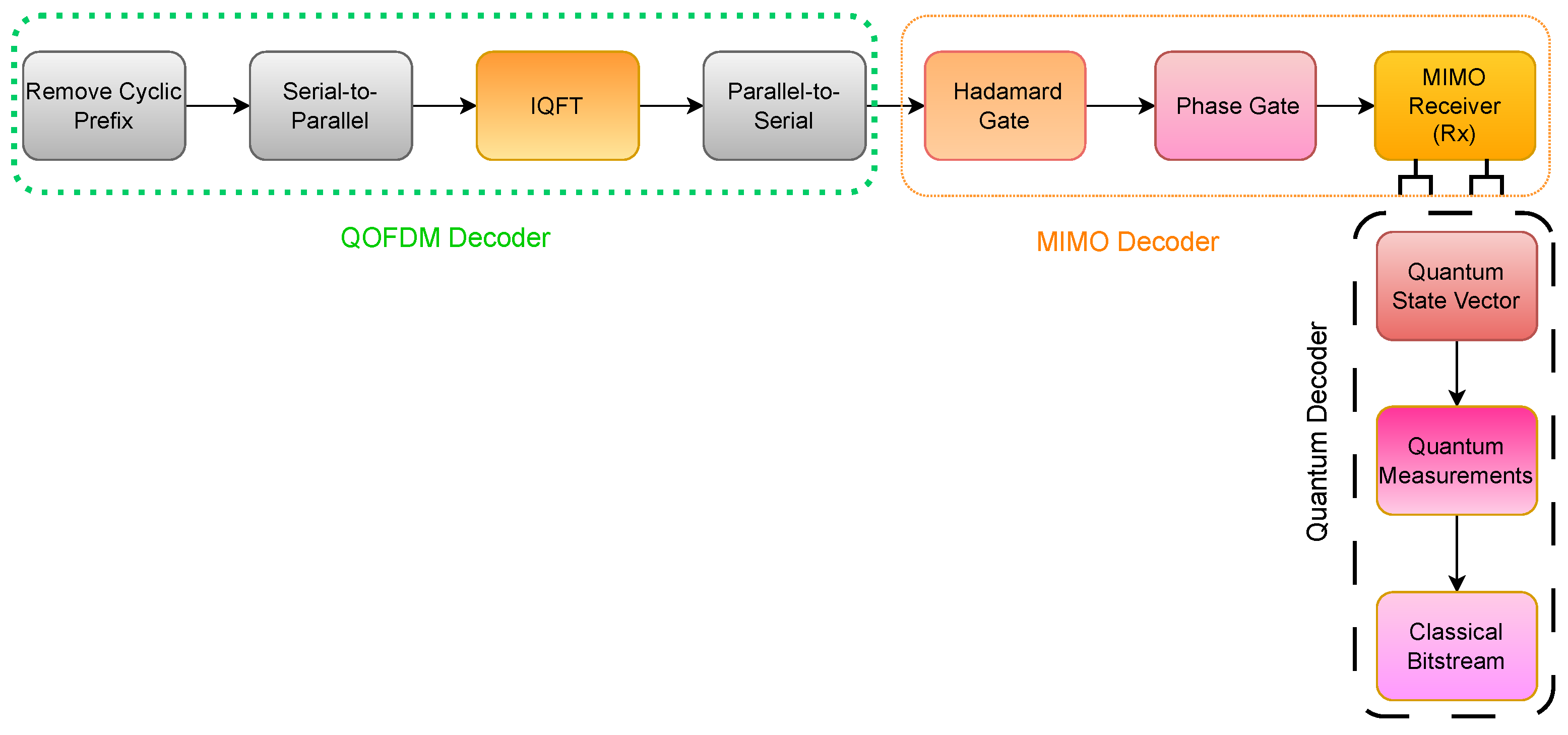
• QOFDM Decoder: First, the cyclic prefix is removed and the received signal is converted from serial to parallel. The IQFT is then applied to recover the time-domain quantum data from the frequency-domain quantum subcarriers.
• MIMO Decoder: MIMO decoding to extract the individual streams transmitted from the received signals.
• Quantum Decoder: After spatial separation, quantum decoding is performed to recover the classical bitstream from the quantum states.
• Channel Decoder: The bitstream is then passed through polar decoding (with a code rate of 1/2) to correct any errors introduced by the channel.
• Source Decoder: Finally, source decoding is performed according to the original format used during source encoding (e.g., JPEG or HEIF), or directly applied to uncompressed data if no compression was used, to reconstruct the transmitted images.

To better explain the quantum system, each quantum block of the proposed framework is described in detail below with proper indentation for clarity.

3.1. Proposed Quantum MIMO-OFDM Transmitter

As shown in Figure 2, the diagram illustrates the overall architecture of the quantum MIMO-OFDM transmitter. The system comprises multiple encoding stages, including quantum encoding, MIMO encoding, and QOFDM encoding. Each stage plays a vital role in preparing the image data for robust and high-fidelity transmission over quantum channels. The quantum encoder converts classical bits, obtained after channel encoding, into quantum states using multi-qubit superposition encoding. The resulting quantum states are then passed through the MIMO encoder, which applies spatial mapping strategies to exploit spatial diversity. Finally, the QOFDM encoder performs a QFT on the quantum-encoded symbols, enabling the use of orthogonal subchannels for efficient frequency-domain multiplexing. These encoding techniques collectively aim to enhance reliability, spectral efficiency, and resistance to noise and multipath effects in quantum communication scenarios.

The following section explains these encoding techniques in detail.

3.1.1. Quantum Encoder

The quantum encoder converts the channel-encoded classical bitstream into quantum states suitable for transmission over quantum channels. The classical bits are first segmented into fixed-length blocks according to the selected qubit encoding size (n).

For single-qubit encoding ($n=1$), each classical bit $c_i\in \{0,1\}$ is mapped to a computational basis state, as shown in Equation (1).

$$0\to |0\rangle =\left(\begin{array}{c}1\\ 0\end{array}\right),1\to |1\rangle =\left(\begin{array}{c}0\\ 1\end{array}\right)$$

(1)

To enable quantum superposition, the Hadamard gate (H) is applied, as shown in Equation (2).

$$H={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right),H|0\rangle ={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle +|1\rangle ),H|1\rangle ={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle -|1\rangle )$$

(2)

For complex-valued modulation suitable for MIMO transmission, a phase gate (S) is applied after the Hadamard gate, as shown in Equation (3).

$$S=\left(\begin{array}{cc}1& 0\\ 0& i\end{array}\right),{\psi }_0=SH|0\rangle ={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle +i|1\rangle ),{\psi }_1=SH|1\rangle ={\displaystyle \frac{1}{\sqrt{2}}}(|0\rangle -i|1\rangle )$$

(3)

For multi-qubit encoding ($n>1$), the n-qubit basis states are generated using tensor products of single-qubit states. For example, for $n=2$, the state $|01\rangle$ is constructed as shown in Equation (4).

$$|01\rangle =|0\rangle \otimes |1\rangle =\left(\begin{array}{c}1\\ 0\end{array}\right)\otimes \left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)$$

(4)

All other two-qubit states $|00\rangle ,|10\rangle ,|11\rangle$ can be constructed similarly. In addition, required multi-qubit quantum gates ($H^{\otimes n}$ and $S^{\otimes n}$) can be built from tensor products of single-qubit gates [16]. A multi-qubit superposition state is then generated by applying these gates, as shown in Equation (5).

$$|{\psi }^{\prime }\rangle =H^{\otimes n}|\psi \rangle ,|{\psi }^{\prime \prime }\rangle =S^{\otimes n}|{\psi }^{\prime }\rangle$$

(5)

In general, for an n-qubit system, the quantum state vector has dimension $2^n\times 1$, and the corresponding quantum gates are $2^n\times 2^n$ matrices constructed via tensor products of the single-qubit gates. This approach ensures efficient encoding and modulation of classical information for transmission over quantum channels.

3.1.2. MIMO Encoder

In the proposed quantum communication system, quantum symbols are transmitted according to different configurations of spatial diversity to enhance signal reliability and robustness against channel impairments. For this study, a 2 × 2 MIMO configuration is employed, which corresponds directly to classical MIMO systems in terms of spatial diversity. These approaches are adapted from classical MIMO diversity techniques to suit quantum symbol transmission while maintaining similar principles of exploiting multiple antennas for improved performance [44].The three primary diversity scenarios implemented are SISO, MISO, and SIMO.

• SISO (1 × 1, no diversity): A single quantum transmitter antenna sends the encoded quantum symbol to a single receiver antenna. This represents the baseline transmission scenario without spatial diversity.
• MISO (2 × 1, transmit diversity): Multiple transmitter antennas send the quantum symbol to a single receiver antenna. Transmit diversity schemes such as Alamouti coding [68] can be employed to exploit spatial diversity. For a 2-transmitter antenna system using the Alamouti code, the transmitted symbol matrix over two time slots can be represented as Equation (6).

  $$\mathbf{R}=\left[\begin{array}{cc}{r}_1& -r_2^{*}\\ r_2& r_1^{*}\end{array}\right]$$

  (6)

  where $r_1$ and $r_2$ are quantum symbols transmitted from the two antennas. The received signals are combined at the receiver to recover $r_1$ and $r_2$ with improved robustness.
• SIMO (1 × 2, receive diversity): A single transmitter antenna sends the quantum symbol to multiple receiver antennas. The received signals are combined using maximal-ratio combining (MRC) to improve detection reliability.
  The received signal vector $\mathbf{y}\in {\mathbb{C}}^{N_r\times 1}$ can be modeled as in Equation (7).

  $$\mathbf{y}=\mathbf{h}r+\mathbf{n}$$

  (7)

  where
  • $\mathbf{y}$ is the received signal vector with $N_r$ receiver antennas,
  • $\mathbf{h}\in {\mathbb{C}}^{N_r\times 1}$ is the channel vector representing the complex channel gains between the transmitter and each of the $N_r$ receiver antennas,
  • r is the transmitted quantum symbol (scalar),
  • $\mathbf{n}\in {\mathbb{C}}^{N_r\times 1}$ is the noise vector.
  The combined signal after MRC is given by Equation (8).

  $$\widehat{r}={\mathbf{h}}^{†}\mathbf{y}$$

  (8)

  where ${\mathbf{h}}^{†}$ denotes the conjugate transpose (Hermitian transpose) of $\mathbf{h}$.

This spatial allocation of quantum symbols according to SISO, MISO, and SIMO configurations enhances the effective quality of the quantum channel and increases the fidelity of the transmitted quantum information.

3.1.3. QOFDM Encoder

The quantum symbol streams from each diversity scenario are processed by applying the corresponding inverse quantum gates to eliminate the complex-valued superposition and phase shifts introduced during the MIMO encoding stage, as shown in Figure 2. This inverse transformation is necessary because, in the QOFDM system, the input to the OFDM encoding stage must be valid quantum states on the computational basis, rather than superposed states. Therefore, inverse Hadamard and inverse phase gates are applied to remove the complex-valued superposition. The single-qubit Hadamard gate H is represented by Equation (2) and since it is Hermitian and unitary, its inverse is equal to itself, $H^{†}=H$. In addition, the phase gate S is represented as in Equation (3) with its inverse (conjugate transpose) given by Equation (9).

$$S^{†}=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]$$

(9)

For an n-qubit system, the inverse gates are applied as tensor products of the single-qubit inverses, i.e., ${\left(H^{†}\right)}^{\otimes n}$ and ${\left(S^{†}\right)}^{\otimes n}$. The application of these inverse gates transforms the complex-valued superposition states back to quantum states without complex superposition, simplifying them before the QFT is applied in the OFDM transmission process. This step is necessary because the QOFDM system is designed to incorporate quantum superposition states and complex baseband modulation using the QFT; if superposition states existed before the QFT, they would collapse prematurely.

Once the inverse gates have simplified the quantum states, they are arranged in parallel form, preparing them for application of the QFT. This transformation organizes quantum information across orthogonal subcarriers, establishing the core mechanism of the QOFDM system. In classical OFDM systems, orthogonality is achieved by applying the IFFT to modulated complex symbols, effectively mapping frequency-domain data onto time-domain orthogonal sinusoids. In contrast, QOFDM operates on computational-basis quantum states rather than numerical symbols, meaning that conventional techniques such as the IFFT or the IQFT cannot be directly applied. Instead, the forward QFT is applied at the transmitter to encode the frequency components within the quantum framework. This operation transforms each computational-basis state into a superposition of all basis states, with carefully assigned phase factors, creating a set of mutually orthogonal quantum subcarriers. By leveraging quantum parallelism and superposition, the QFT distributes the encoded information across multiple qubits and subcarriers simultaneously, preserving the total energy of the quantum state and maintaining orthogonality. This design ensures interference-free transmission, enables multi-qubit diversity, and allows the inverse QFT at the receiver to perfectly reconstruct the original computational-basis states, providing a natural and necessary analog to classical OFDM orthogonality within the quantum domain.

In summary, IQFT also generates an orthogonal set of states similar to the QFT but is primarily intended to reverse the QFT operation at the receiver. If applied at the transmitter, the receiver would instead need to perform the QFT, reversing the intended communication flow. Moreover, the IQFT is incompatible with transmitter input states, as it transforms frequency-like superpositions into computational-basis states. At the transmitter, distributed superposition states are required to form quantum subcarriers, preserve orthogonality, and enable multi-qubit diversity. Applying the IQFT would collapse these amplitudes, disrupting subcarrier formation and removing advantages such as constant-envelope transmission and interference-free MIMO operation. Hence, the QFT is applied at the transmitter to generate suitable superposition states for transmission, while the IQFT is reserved for the receiver to reconstruct the original computational-basis information [13].

For the transformation to function correctly, the QFT matrix must be dimensionally compatible with the input quantum state vector. In particular, when operating on an n-qubit state, represented by a vector of size $2^n\times 1$, the QFT matrix must have dimension $2^n\times 2^n$ to facilitate proper unitary evolution.

The QFT matrix $F_N$ is defined as in Equation (10).

$$F_N={\displaystyle \frac{1}{\sqrt{N}}}\left(\begin{array}{ccccc}1& 1& 1& \dots & 1\\ 1& \omega & {\omega }^2& \dots & {\omega }^{N-1}\\ 1& {\omega }^2& {\omega }^4& \dots & {\omega }^{2(N-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }^{N-1}& {\omega }^{2(N-1)}& \dots & {\omega }^{(N-1)(N-1)}\end{array}\right)$$

(10)

where $\omega$ denotes the primitive root of unity $N^{\mathrm{th}}$, calculated as in Equation (11).

$$\omega =e^{2\pi i/N}$$

(11)

Here, $N=2^n$, ensuring that the transformation spans the complete quantum basis space for n qubits. This matrix form is rooted in the standard formulation of QFT as described in the quantum computing literature [69], and is mathematically expressed as in Equation (12).

$$F_N|x\rangle ={\displaystyle \frac{1}{\sqrt{N}}}\sum _{k=0}^{N-1}{e}^{{\displaystyle \frac{2\pi ixk}{N}}}|k\rangle$$

(12)

This representation shows how each input basis state $|x\rangle$ is transformed into a weighted superposition over all computational basis states $|k\rangle$, the weights being determined by the exponential phase terms. To illustrate QFT for a simple two-qubit system where $N=4$, the transformation matrix $F_4$ is defined in Equation (13).

$$F_4={\displaystyle \frac{1}{2}}\left(\begin{array}{cccc}1& 1& 1& 1\\ 1& i& -1& -i\\ 1& -1& 1& -1\\ 1& -i& -1& i\end{array}\right)$$

(13)

As an example, when the QFT matrix $F_4$ is applied to the standard computational basis states of the two-qubit system, the output quantum states are transformed as follows from Equations (14)–(17).

$$v_1=F_4|00\rangle ={\displaystyle \frac{1}{2}}{\left(\begin{array}{cccc}1& 1& 1& 1\end{array}\right)}^T$$

(14)

$$v_2=F_4|01\rangle ={\displaystyle \frac{1}{2}}{\left(\begin{array}{cccc}1& i& -1& -i\end{array}\right)}^T$$

(15)

$$v_3=F_4|10\rangle ={\displaystyle \frac{1}{2}}{\left(\begin{array}{cccc}1& -1& 1& -1\end{array}\right)}^T$$

(16)

$$v_4=F_4|11\rangle ={\displaystyle \frac{1}{2}}{\left(\begin{array}{cccc}1& -i& -1& i\end{array}\right)}^T$$

(17)

Each vector $v_1$ through $v_4$ represents the QFT output corresponding to one of the basis states and can be interpreted as orthogonal quantum subcarriers. In addition, these vectors represent the columns of the QFT matrix. The column vectors of $F_4$ form an orthonormal basis, which is essential for QOFDM to ensure non-interfering subchannels.

To verify orthogonality, the Hermitian inner product is evaluated between the transformed vectors. For example, the inner product between $v_1$ and $v_2$ is calculated in Equation (18). Due to the inner product being zero, the vectors are mutually orthogonal.

$$\begin{array}{cc}\hfill \langle T_1|T_2\rangle & =\left({\displaystyle \frac{1}{2}}\left(\begin{array}{cccc}1& 1& 1& 1\end{array}\right)\right)\left({\displaystyle \frac{1}{2}}\left(\begin{array}{c}1\\ i\\ -1\\ -i\end{array}\right)\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{4}}(1+i-1-i)\hfill \\ \hfill & =0\hfill \end{array}$$

(18)

Other pairs also yield zero inner products, confirming the mutual orthogonality of the transformed vectors. This orthogonality is fundamental to the QOFDM design, as it guarantees that subcarriers do not interfere with each other, mirroring the principle used in classical OFDM. Therefore, the quantum states resulting from the MIMO diversity schemes, after the application of inverse phase shifts and Hadamard transformations, exhibit a similar structural pattern characterized by mutual orthogonality.

Moreover, QFT output can be interpreted as linear combinations of encoded quantum information symbols, showing how data are spread across orthogonal subcarriers as in Equations (19)–(22).

$$v_1=|00\rangle +|01\rangle +|10\rangle +|11\rangle$$

(19)

$$v_2=|00\rangle +i|01\rangle -|10\rangle -i|11\rangle$$

(20)

$$v_3=|00\rangle -|01\rangle +|10\rangle -|11\rangle$$

(21)

$$v_4=|00\rangle -i|01\rangle -|10\rangle +i|11\rangle$$

(22)

These relationships demonstrate how each transformed quantum state $v_j$ contains contributions from all four input symbols, modulated by complex phase factors in a structured and interference-free manner, fulfilling the role of OFDM in the quantum domain.

In the proposed QOFDM system, the number of quantum subcarriers N directly influences how the total available bandwidth B is divided among them. Each subcarrier is spaced by a frequency interval $\mathrm{\Delta }f$, calculated as in Equation (23).

$$\mathrm{\Delta }f={\displaystyle \frac{B}{N}}$$

(23)

To ensure orthogonality and computational efficiency, N is typically selected as a power of two. Specifically, in this framework, $N=2^n$, where n corresponds to the number of qubits encoded in each transmission unit. This choice strikes a balance between spectral granularity and algorithmic simplicity, while minimizing ISI.

The OFDM-modulated quantum states are then converted from parallel to serial format to prepare them for transmission. To minimize ISI caused by channel dispersion, a cyclic prefix (CP) is then appended. This involves copying the last samples ($L_{\mathrm{CP}}$) of the QFT output and inserting them at the beginning of the serialized symbol. The process extends the total duration of the transmitted symbol, as described by Equation (24).

$$T_{\mathrm{symbol}}=N+L_{\mathrm{CP}}$$

(24)

In addition, the cyclic prefix serves a critical role in preserving the orthogonality of quantum subcarriers, effectively absorbing delays introduced by the channel and preventing overlap between successive symbols. In this system, the CP length is chosen as 25% of the subcarrier count for each qubit encoding size, which is determined using Equation (25).

$$L_{\mathrm{CP}}=\mathrm{round}(N\times 0.25)$$

(25)

3.2. Quantum Channel

In this study, we employ an extended Rayleigh fading model [70] to represent the realistic transmission of quantum symbols through optical or wireless channels. Rayleigh fading naturally emerges from the linear superposition of multiple independent propagation paths, resulting in stochastic amplitude and phase variations that affect both classical and quantum signals [13,71]. This approach captures extrinsic environmental effects such as multipath interference, diffraction, scattering, and atmospheric turbulence, which are inherent in practical quantum communication systems. Intrinsic quantum noise, including decoherence and energy loss, is modeled independently using Kraus operators, allowing a clear separation between propagation-induced variations and fundamental quantum effects.

3.2.1. Intrinsic Quantum Noise

Within the simulation framework, quantum states transmitted in the frequency domain are subjected to multiple types of quantum noise to replicate realistic communication scenarios [69]. The considered noise channels include bit-flip, phase-flip, depolarizing, amplitude damping, and phase damping errors, which are generally represented by the operator $\mathcal{N}$.

The bit-flip noise randomly flips the state of a qubit from $|0\rangle$ to $|1\rangle$ or vice versa, with an associated probability $\alpha$. The action of this channel on a density matrix $\rho$ is given by Equation (26).

$${\mathcal{N}}_{\mathrm{bf}}\left(\rho \right)=(1-\alpha )\rho +\alpha X\rho X^{†}$$

(26)

where X denotes the Pauli-X operator.

Similarly, phase-flip noise, occurring with probability $\beta$, introduces a relative phase change between the basis states, as shown in Equation (27), where Z denotes the Pauli-Z operator.

$${\mathcal{N}}_{\mathrm{pf}}\left(\rho \right)=(1-\beta )\rho +\beta Z\rho Z^{†}$$

(27)

Depolarizing noise models complete randomization of the qubit, replacing the state partially with the maximally mixed state with probability $\gamma$, as shown in Equation (28).

$${\mathcal{N}}_{\mathrm{dp}}\left(\rho \right)=(1-\gamma )\rho +{\displaystyle \frac{\gamma }{3}}\left(X\rho X^{†}+Y\rho Y^{†}+Z\rho Z^{†}\right)$$

(28)

where Y is the Pauli-Y operator.

Amplitude damping, characterized by a damping probability $\delta$, models energy loss mechanisms such as spontaneous emission, as shown in Equation (29), while the corresponding Kraus operators $E_0$ and $E_1$ are defined in Equation (30).

$${\mathcal{N}}_{\mathrm{ad}}\left(\rho \right)=E_0\rho E_0^{†}+E_1\rho E_1^{†}$$

(29)

$$E_0=\left(\begin{array}{cc}1& 0\\ 0& \sqrt{1-\delta }\end{array}\right),E_1=\left(\begin{array}{cc}0& \sqrt{\delta }\\ 0& 0\end{array}\right)$$

(30)

Phase damping, characterized by probability $\theta$, introduces decoherence in the relative phase without affecting the population of basis states, as shown in Equation (31), and corresponding Kraus operators are defined in Equation (32).

$${\mathcal{N}}_{\mathrm{pd}}\left(\rho \right)=F_0\rho F_0^{†}+F_1\rho F_1^{†}$$

(31)

$$F_0=\left(\begin{array}{cc}1& 0\\ 0& \sqrt{1-\theta }\end{array}\right),F_1=\left(\begin{array}{cc}0& 0\\ 0& \sqrt{\theta }\end{array}\right)$$

(32)

To evaluate the combined effect of all noise sources, the total channel acting on a qubit is defined as in Equation (33).

$${\mathcal{N}}_{\mathrm{total}}\left(\rho \right)=\alpha {\mathcal{N}}_{\mathrm{bf}}\left(\rho \right)+\beta {\mathcal{N}}_{\mathrm{pf}}\left(\rho \right)+\gamma {\mathcal{N}}_{\mathrm{dp}}\left(\rho \right)+\delta {\mathcal{N}}_{\mathrm{ad}}\left(\rho \right)+\theta {\mathcal{N}}_{\mathrm{pd}}\left(\rho \right)$$

(33)

where $\rho$ is the MIMO-OFDM encoded quantum state. The symbol ^† represents the Hermitian conjugate.

The overall error probability is linked to the signal-to-noise ratio (SNR), as shown in Equation (34), with the total noise probability decreasing as SNR increases, as shown in Equation (35).

$$\mathrm{SNR}\left(\mathrm{dB}\right)=10{log}_{10}\left({\displaystyle \frac{P_{\mathrm{signal}}}{P_{\mathrm{noise}}}}\right)$$

(34)

$$p_{\mathrm{total}}=min\left(1,{\displaystyle \frac{1}{1+{10}^{\mathrm{SNR}/10}}}\right)$$

(35)

where $P_{\mathrm{signal}}$ is fixed and $P_{\mathrm{noise}}$ is varied during simulations.

The total noise probability is then distributed dynamically among the five noise types using independent random weighting factors, as shown in Equation (36).

$$r_1,r_2,r_3,r_4,r_5\sim \mathcal{U}(0,1)$$

(36)

These random factors are adjusted and rescaled so that each individual noise channel contributes a fraction of the overall noise probability, as expressed in Equation (37).

$$[\alpha ,\beta ,\gamma ,\delta ,\theta ]={\displaystyle \frac{[r_1,r_2,r_3,r_4,r_5]}{{\sum }_{j=1}^5{r}_j}}·p_{\mathrm{total}}$$

(37)

which ensures the total probability constraint, as shown in Equation (38).

$$\alpha +\beta +\gamma +\delta +\theta =p_{\mathrm{total}}$$

(38)

This method allows the simulation to reflect practical quantum communication channels, where noise is both dependent on the signal quality and heterogeneous across different error mechanisms [35,37]. By dynamically varying the contribution of each error type, the framework captures a realistic and versatile model for benchmarking system performance under diverse quantum noise conditions.

3.2.2. Layered Channel Representation

By combining Rayleigh fading for environmental propagation effects with quantum decoherence, the channel model allows realistic evaluation of quantum communication systems. The two layers are:

• Rayleigh fading: models amplitude and phase variations due to environmental propagation. This Rayleigh fading model effectively characterizes multipath propagation in urban environments. In our simulations, the urban Rayleigh channel is defined by four distinct path delays of $(0,0.2,0.5,1.0)\mathsf{\mu }\mathrm{s}$, with corresponding path gains of $(0,-3,-10,-15)\mathrm{dB}$. A Doppler shift of 100 Hz is included to account for the relative motion between the transmitter and receiver, capturing the time-varying nature of the wireless channel typical in urban scenarios.
• Quantum decoherence: models intrinsic quantum processes such as bit-flip, phase-flip, depolarizing, amplitude damping, and phase damping using Kraus operators.

This layered approach captures both environmental fading effects and intrinsic quantum noise, providing a comprehensive framework for simulating realistic quantum communication channels [13,44,45].

In the simulation, Rayleigh fading is modeled by generating complex Gaussian coefficients for each OFDM subcarrier and MIMO path, which scale the transmitted quantum amplitudes prior to forming their corresponding density matrices. Intrinsic quantum noise is then applied using standard Kraus operators for bit-flip, phase-flip, depolarizing, amplitude-damping, and phase-damping channels. The overall noise level is controlled by the SNR according to Equation (35) and this total probability is proportionally distributed among the five noise types.

In addition, this study assumes ideal quantum gates and noiseless state preparation to isolate the effects of compression, transmission, and channel noise. This idealized setup enables rigorous validation of the proposed quantum MIMO-OFDM framework and establishes baseline performance benchmarks. Such an approach aligns with standard practice in early-stage communication research, where hardware imperfections are introduced only after the theoretical foundations have been validated.

3.3. Proposed Quantum MIMO-OFDM Receiver

As shown in Figure 3, the quantum MIMO-OFDM receiver consists of several decoding stages similar to those of the transmitter. The following subsection briefly explains these stages.

3.3.1. QOFDM Decoder

The first step at the receiver involves removing the cyclic prefix that was appended to the transmitter. The resulting sequence is then converted from serial to parallel form to restore the original structure of the quantum subcarriers. Subsequently, these are passed through the IQFT gate, which reverses the effect of the QFT applied during QOFDM encoding. The IQFT maps the received quantum states from the frequency domain back into the time domain, enabling the reconstruction of the initial QOFDM-encoded quantum information. Functionally, this is similar to how the FFT operates in classical OFDM systems, serving as a key operation before quantum decoding takes place.

Mathematically, the IQFT is defined as the Hermitian adjoint (denoted by †) of the QFT operator, as shown in Equation (39).

$$\mathrm{IQFT}={\mathrm{QFT}}^{†}$$

(39)

For an N-dimensional quantum register, the action of the IQFT on a computational basis state $|k\rangle$ can be expressed by Equation (40).

$$F_N^{-1}|k\rangle ={\displaystyle \frac{1}{\sqrt{N}}}\sum _{x=0}^{N-1}{e}^{-2\pi ixk/N}|x\rangle$$

(40)

This transformation recovers the time-domain quantum state from its frequency-domain representation, enabling proper interpretation and decoding of the transmitted qubits. The IQFT is therefore an essential component in QOFDM systems, as it facilitates accurate demodulation of the quantum subcarrier superposition states into a time-domain quantum state. After transforming the frequency domain superposition states back into computational basis quantum states using the IQFT, the data are converted from parallel to serial form.

3.3.2. MIMO Decoder

Each quantum state is then processed through a series of Hadamard and phase gates to prepare it for MIMO reception, since the MIMO receiver expects complex-valued superposition states, similar to those used at the MIMO transmitter. Each diversity scheme corresponding to the MIMO configuration is then decoded, yielding the received quantum state after the complete MIMO decoding process.

3.3.3. Quantum Decoder

At the receiver, each quantum state composed of n qubits arrives in a noisy superposition due to channel imperfections. To decode this state, the system first applies the Hadamard transform $H^{\otimes n}$, which reverses the superposition and brings the quantum state back into the computational basis. A quantum measurement is then performed, causing the state to collapse into a specific basis state and outputting a classical bitstring. Since noise may alter the state during transmission, the measured bitstring might not exactly match the original. To address this, the decoder compares the measured output to a predefined set of valid bit patterns and selects the one with the smallest Euclidean distance. This process enables accurate recovery of the transmitted classical information from the noisy quantum state.

It is important to highlight that the system operates under the assumption of perfect channel state information (CSI) at the receiver, which allows for ideal equalization and accurate signal recovery.

3.3.4. Coherent Processing and Hardware Requirements

The proposed receiver architecture is explicitly designed to maintain quantum coherence through unitary transformations. Each stage, from cyclic prefix removal to quantum measurement, can be implemented using unitary gate operations within standard gate-based quantum computing frameworks, including superconducting qubits, trapped ions, or spin qubits.

• Overview of the quantum hardware model: The overall receiver can be expressed as a sequence of unitary operators acting on the received quantum state ${\rho }_{\mathrm{rx}}$, as shown in Equation (41).

  $${\rho }_{\mathrm{out}}=U_{\mathrm{enc}}{U}_{\mathrm{MIMO}}{U}_{\mathrm{QFT}}{\rho }_{\mathrm{rx}}{U}_{\mathrm{QFT}}^{†}{U}_{\mathrm{MIMO}}^{†}{U}_{\mathrm{enc}}^{†}$$

  (41)

  where $U_{\mathrm{QFT}}$ represents the QFT, $U_{\mathrm{MIMO}}$ is the quantum MIMO operator, and $U_{\mathrm{enc}}$ is the quantum encoding operator. All transformations before measurement are strictly unitary to preserve coherence.
• Implementation of receiver stages: The cyclic prefix removal and serial-to-parallel conversion can be implemented as reversible data reordering operations using SWAP gates. Equivalently, these steps can be represented as a partial trace operation, as illustrated in Equation (42).

  $${\rho }_{\mathrm{post}-\mathrm{CP}}={\mathrm{Tr}}_{\mathrm{prefix}}\left({\rho }_{\mathrm{input}}\right)$$

  (42)
  Here, ${\rho }_{\mathrm{post}-\mathrm{CP}}$ represents the remaining data qubits, and ${\mathrm{Tr}}_{\mathrm{prefix}}(·)$ traces out the prefix qubits.
  Next, the IQFT maps frequency-domain superpositions to the computational basis and is implemented via Hadamard and controlled-phase gates, as shown in Equation (43).

  $$F_N^{†}=\prod _{j=0}^{n-1}\left(H_j\prod _{k=j+1}^{n-1}{\mathrm{CP}}_{jk}\left(-{\displaystyle \frac{\pi }{2^{k-j}}}\right)\right)$$

  (43)

  where $H_j$ is the Hadamard gate applied to qubit j and ${\mathrm{CP}}_{jk}\left(\varphi \right)$ denotes a controlled-phase rotation between qubits j and k.
  The quantum MIMO decoder $U_{\mathrm{MIMO}}^{†}$ implements the inverse channel unitary $U_H^{†}$, as shown in Equation (44), and acts on the quantum state ${\rho }_{\mathrm{IQFT}}$ following the application of the IQFT.

  $${\rho }_{\mathrm{decoded}}=U_{\mathrm{MIMO}}{\rho }_{\mathrm{IQFT}}{U}_{\mathrm{MIMO}}^{†},\mathrm{with}{U}_{\mathrm{MIMO}}=U_H$$

  (44)
  This operation can be decomposed into standard gates (Hadamard, CNOT, and phase gates) to maintain full coherence.
  In the quantum OFDM-MIMO framework, all unitary operations, including cyclic prefix removal, IQFT, and MIMO decoding, are applied prior to any measurement. Measurement irreversibly collapses the quantum state; performing it earlier would destroy superposition and entanglement, making further processing impossible.
  The final projective measurement is performed on the fully processed state, as shown in Equation (45).

  $${\rho }_{\mathrm{measured}}=\mathcal{M}\left({\rho }_{\mathrm{decoded}}\right)$$

  (45)

  where $\mathcal{M}(·)$ denotes the measurement superoperator. This procedure ensures that quantum collapse occurs only at the final stage, preserving superposition and enabling full exploitation of quantum parallelism and interference effects [13,44].

All operations are compatible with future quantum hardware:

• CP removal/serial-to-parallel conversion: Reversible qubit reordering using SWAP gates or partial trace.
• IQFT: Implemented via cascaded Hadamard and controlled-phase rotations.
• MIMO decoding: Implemented as inverse unitary using standard quantum gates.
• Measurement: Standard projective measurement readout on qubits.

Therefore, this receiver is a fully quantum-consistent analog of classical MIMO-OFDM [13,44,45]. All intermediate steps are unitary, preserving coherence, and measurement occurs only at the end, while the system is forward-looking and conceptual, it provides a scalable blueprint for performance analysis, algorithmic optimization, and future experimental deployment.

3.3.5. Classical MIMO-OFDM System

To provide a comparison, a classical MIMO-OFDM system is designed to match the bandwidth and operational parameters of the quantum MIMO-OFDM setup. This classical system utilizes several common digital modulation techniques, such as binary phase-shift keying (BPSK), quadrature phase-shift keying (QPSK), and 16-quadrature amplitude modulation (16-QAM). The subcarrier count is fixed at N = 256, corresponding to the maximum number of subcarriers used in the quantum system, ensuring a consistent and balanced performance comparison. Furthermore, the equalization stage assumes ideal channel knowledge, with the perfect CSI available to the receiver. To ensure consistency in source encoding, the same image compression methods are applied to both systems. All evaluations are conducted under identical SNR conditions, enabling a fair and meaningful evaluation of transmission quality across both classical and quantum communication frameworks. Therefore, this configuration serves as the fair and equivalent classical MIMO-OFDM benchmark, designed to match the proposed quantum MIMO-OFDM system in all operational parameters and evaluation settings.

4. Results and Discussion

This section analyzes the performance of the proposed quantum MIMO-OFDM system and compares it against a classical MIMO-OFDM system under various source coding formats. Specifically, we evaluate three types of image input: JPEG and HEIF compressed images at a quantization parameter (QP) value of 100, as well as uncompressed images. Comparative analysis is conducted under identical transmission conditions to ensure fairness. A total of 100 images are used for testing, and the results are reported as average values across these dataset. Performance metrics used for evaluation include the peak signal-to-noise ratio (PSNR), the structural similarity index measure (SSIM) [72], and the universal quality index (UQI) [73], providing a comprehensive assessment of image quality and system robustness. Performance assessments are conducted using Python 3 on a machine equipped with a 13th Gen Intel^® Core™ i5-1345U processor with 1.60 GHz and 16 GB of RAM.

The following subsections present detailed results and a discussion on the effectiveness of the systems with respect to these metrics.

4.1. Performance Comparison of JPEG Image Transmission Using Quantum MIMO-OFDM and Classical MIMO-OFDM Systems

The performance of JPEG image transmission is evaluated across three diversity scenarios: SISO (1 × 1), as shown in Figure 4; MISO (2 × 1), as shown in Figure 5; and SIMO (1 × 2), as shown in Figure 6, for both quantum and classical MIMO-OFDM systems. The quantum system utilizes Hadamard-based superposition encoding combined with phase encoding for quantum MIMO, and employs QFT-based QOFDM encoding with qubit encoding sizes ranging from 1 to 8. In contrast, the classical system uses conventional modulation schemes such as BPSK, QPSK, and 16-QAM. Image quality is assessed using PSNR, SSIM, and UQI metrics over a range of channel conditions with SNR values ranging from $-20\mathrm{dB}$ to $32\mathrm{dB}$.

Across all diversity modes, the number of encoded qubits in the quantum system plays a crucial role in enhancing noise resilience. In the SISO configuration, quantum systems using 1 to 3 qubits experience a steep decline in image quality below $0\mathrm{dB}$ SNR. However, increasing the qubit encoding size to 6, 7, or 8 significantly improves the robustness against noise. For example, the eight-qubit SISO configuration maintains maximum PSNR, SSIM, and UQI values down to $-6\mathrm{dB}$ SNR without noticeable degradation. In contrast, quantum encodings with fewer qubits degrade much earlier, while classical systems show substantially reduced image quality below $12\mathrm{dB}$ channel SNR. A consistent observation across SISO configurations is the presence of a performance crossover point near $8\mathrm{dB}$ SNR, where all classical systems exhibit PSNR, SSIM, and UQI values approaching zero. At this threshold, the quantum system, even when using single-qubit encoding, achieves the highest values for all three metrics, clearly outperforming its classical counterparts. Additionally, increasing the qubit encoding size improves performance, with the eight-qubit configuration showing the best results. Among the classical modulation schemes, BPSK shows the best performance, outperforming both QPSK and 16-QAM in noisy conditions. This trend continues in SIMO and MISO configurations, where spatial diversity leads to overall better performance for both quantum and classical systems compared to that of SISO. However, quantum systems still maintain a distinct advantage in noise resilience and image quality due to their advanced encoding schemes and the use of larger qubit encoding sizes.

In the SIMO (1 × 2) configuration as shown in Figure 6a–c, quantum systems benefit from multiple receive antennas, which enhance state recovery after measurement compared to SISO. Consequently, even lower-qubit systems demonstrate relatively stable performance under noisy conditions. In contrast, MISO (2 × 1) configurations as shown in Figure 5a–c, consistently exhibit a performance drop of approximately 3 dB compared to SIMO. This is attributed to equal power allocation on the transmitter side in both setups. However, if the transmitted power is adjusted such that the received signal power is equalized across both cases, their performance would converge.

Finally, these results demonstrate the suitability of quantum MIMO-OFDM systems for low-SNR, high-interference environments, such as urban or long-distance wireless transmission, while classical systems remain preferable in short-range, high-SNR scenarios. Overall, the JPEG image transmission results confirm that quantum systems scale well with the qubit encoding size and benefit significantly from spatial diversity (especially SIMO and MISO), making them a promising alternative to classical methods in challenging channel conditions.

4.2. Performance Comparison of HEIF Image Transmission Using Quantum MIMO-OFDM and Classical MIMO-OFDM Systems

The experimental results shown in Figure 7, Figure 8 and Figure 9 demonstrate that quantum communication systems consistently outperform classical schemes in HEIF image transmission below a critical noise threshold across all diversity configurations, including SISO, MISO, and SIMO setups. Classical SISO configurations, as shown in Figure 7, exhibit the weakest performance due to the absence of spatial diversity and the lack of any quantum processing advantages. Consequently, the resulting image quality metrics, PSNR, SSIM, and UQI, are significantly lower compared to the diversity-enhanced and quantum-assisted scenarios.

Incorporating diversity schemes such as SIMO, as shown in Figure 9, and MISO, as shown in Figure 8, yields noticeable performance improvements in classical systems by exploiting spatial diversity to mitigate channel fading and interference. This leads to better robustness and enhanced image fidelity compared to SISO configurations. However, classical systems still show limitations in fully overcoming channel impairments, especially in low SNR scenarios.

In contrast, quantum systems not only benefit from similar diversity gains but also offer additional advantages through multi-qubit encoding combined with MIMO-OFDM quantum transmission. This quantum diversity enhances noise resilience and strengthens error-correction capabilities. As the size of the qubit increases, the ability of the system to preserve image integrity improves significantly. Among all tested configurations, the eight-qubit setup achieves the highest PSNR, SSIM, and UQI values, demonstrating superior performance.

Compared to JPEG transmission under equivalent channel conditions, HEIF images transmitted via quantum systems achieve higher peak image quality metrics. This is attributed to the advanced source coding efficiency of HEIF, coupled with the inherent robustness of quantum encoding and decoding processes. The synergy between the quantum diversity gains and the HEIF compression mechanisms enables reliable and high-fidelity image transmission, even in challenging noisy environments.

In general, the proposed quantum MIMO-OFDM system interacts with classical image formats in a manner that fundamentally depends on their compression structure. JPEG images employ block-based DCT compression, which localizes most of the image energy in low-frequency coefficients. When converting JPEG images into classical bitstreams for quantum encoding, the resulting qubit states naturally reflect this frequency distribution, allowing the QFT to concentrate information efficiently and preserve high-fidelity reconstruction. In contrast, HEIF images, which use more flexible intra-frame coding and advanced predictive schemes, distribute pixel correlations across larger blocks and more varied frequency components. Consequently, the quantum encoding captures a wider range of information per qubit block, and the QFT effectively transforms these correlations into the frequency domain, enabling resilient transmission of the most significant information. This difference explains the variations observed results: JPEG-based images retain low-frequency structures strongly with fewer qubits, while HEIF images benefit from multi-qubit QFT processing to maintain high fidelity across more complex intra-frame correlations. Overall, the protocol leverages the inherent frequency-domain representation provided by the QFT in the quantum MIMO-OFDM framework to efficiently map and transmit diverse image formats, achieving robustness and fidelity levels unattainable with classical MIMO-OFDM alone.

4.3. Performance Comparison of Uncompressed Image Transmission Using Quantum MIMO-OFDM and Classical MIMO-OFDM Systems

While the previous discussions focused on compressed images, it is also important to evaluate the performance of quantum communication systems for uncompressed image transmission, as shown in Figure 10, Figure 11 and Figure 12. Uncompressed images contain significantly larger amounts of data and lack the compression efficiency provided by advanced source coding, resulting in increased bandwidth demands and increased susceptibility to channel noise.

In all channel configurations, including SISO as shown in Figure 10, MISO as shown in Figure 11, and SIMO as shown in Figure 12, quantum systems maintain a notable advantage over classical schemes when transmitting uncompressed images, as is also observed with compressed images. The multi-qubit encoding combined with MIMO-OFDM quantum transmission enhances noise resilience and error correction capabilities across these diversity modes. A key enabler of this robustness is the QFT, which maps multi-qubit image blocks from the computational (time) domain to a frequency-domain representation aligned with OFDM subcarriers. By delocalizing information across all qubits within a block, the QFT improves resilience to localized quantum noise and decoherence, while simultaneously facilitating seamless integration with the OFDM framework. This combination allows for efficient MIMO transmission and reception of multiple quantum-encoded state blocks. Collectively, these features of the QFT enhance both transmission efficiency and image fidelity, underscoring its pivotal role in the proposed quantum MIMO-OFDM protocol.

Classical systems transmitting uncompressed images suffer pronounced performance degradation across SISO, MISO, and SIMO setups, especially in low-SNR conditions, due to their inability to exploit compression and their limited noise resilience, while spatial diversity schemes such as MISO and SIMO provide some robustness, the inherently sequential and low-dimensional nature of classical bits prevents efficient encoding of highly correlated image data, resulting in reduced image fidelity under noisy channels.

In contrast, quantum MIMO-OFDM leverages the principles of superposition and multi-qubit encoding, allowing an n-qubit block to simultaneously represent $2^n$ states and resist localized noise. The QFT further enhances robustness by redistributing information across all qubits within a block, enabling high-dimensional, parallel transmission. This combination allows quantum systems to achieve image fidelity levels fundamentally unattainable by classical approaches, even under challenging channel conditions. Overall, although uncompressed image transmission poses greater challenges for all systems, quantum communication frameworks continue to outperform their classical counterparts across SISO, MISO, and SIMO configurations. This demonstrates the flexibility and robustness of quantum methods in a variety of image formats and channel scenarios.

These results across JPEG, HEIF, and uncompressed image transmissions collectively validate the effectiveness of the proposed quantum MIMO-OFDM system in enhancing image transmission quality over wireless channels. The system consistently outperforms classical modulation schemes, including BPSK, QPSK, and 16-QAM, across SISO, MISO, and SIMO configurations, particularly under low SNR conditions. This performance gain is attributed to the combined benefits of multi-qubit encoding, quantum spatial diversity, the efficiency of the QOFDM scheme, and the robustness of classical polar channel coding, which together provide superior resilience against noise and fading, ensuring improved image fidelity during transmission. Furthermore, classical modulation techniques such as BPSK, QPSK, and 16-QAM typically exhibit high PAPR, often ranging between 10 and 12 dB, leading to increased signal distortion and reduced power efficiency. In contrast, the proposed framework achieves a consistent PAPR of 0 dB across varying qubit dimensions, owing to the use of normalized quantum states and the energy-conserving nature of the unitary QFT and its inverse (IQFT).

Mathematical Justification of 0 dB PAPR

In the proposed quantum MIMO-OFDM framework, the claim of a 0 dB PAPR arises naturally from the quantum signal representation rather than classical amplitude superposition. In the quantum system, information is encoded within multi-qubit superposition states that represent frequency-domain components through unitary transformations such as the QFT. Because all quantum operations are norm-preserving and the QFT is a unitary transformation, the total state energy remains constant across all subcarriers. This results in a uniform probability amplitude distribution, which eliminates the large instantaneous power peaks observed in classical OFDM waveforms. In effect, each subcarrier contributes an equal probability amplitude, ensuring that the ratio between the instantaneous and average transmitted power is unity, corresponding to a PAPR of 0 dB. Mathematically, this can be derived as follows.

For an input state $|{\psi }_{\mathrm{in}}\rangle$ over N subcarriers, the transmitted quantum OFDM state $|{\rho }_{\mathrm{QOFDM}}\rangle$ is obtained by applying the QFT unitary operator $U_{\mathrm{QFT}}$, as shown in Equation (46), where the unitarity of $U_{\mathrm{QFT}}$ is expressed in Equation (47).

$$|{\rho }_{\mathrm{QOFDM}}\rangle =U_{\mathrm{QFT}}|{\psi }_{\mathrm{in}}\rangle$$

(46)

$$U_{\mathrm{QFT}}^{†}{U}_{\mathrm{QFT}}=I$$

(47)

The normalization of the transmitted state, ensuring unit total probability, is given in Equation (48).

$$\langle {\rho }_{\mathrm{QOFDM}}|{\rho }_{\mathrm{QOFDM}}\rangle =1$$

(48)

The instantaneous quantum power operator $\widehat{P}$ is defined in Equation (49), which projects the state onto itself.

$$\widehat{P}=|{\rho }_{\mathrm{QOFDM}}\rangle \langle {\rho }_{\mathrm{QOFDM}}|$$

(49)

The corresponding instantaneous $P_{\mathrm{inst}}$ and average $P_{\mathrm{avg}}$ powers are given in Equations (50) and (51), respectively, generating the PAPR shown in Equation (52), regardless of the encoding size of the qubit. Here, $P_{\mathrm{inst}}\left(t\right)$ denotes the instantaneous power at time t, and $E_t[·]$ represents the time expectation (average).

$$P_{\mathrm{inst}}=\langle {\rho }_{\mathrm{QOFDM}}|\widehat{P}|{\rho }_{\mathrm{QOFDM}}\rangle =1$$

(50)

$$P_{\mathrm{avg}}=E_t\left[P_{\mathrm{inst}}\left(t\right)\right]=1$$

(51)

$$\mathrm{PAPR}={\displaystyle \frac{P_{\mathrm{peak}}}{P_{\mathrm{avg}}}}=1\Rightarrow 0\mathrm{dB}$$

(52)

Furthermore, 4K images are integrated into the evaluation to demonstrate that the proposed system’s performance remains robust regardless of image resolution or source coding format. As shown in

Table 1. Maximum channel SNR gains (dB) for different image formats across multi-qubit MIMO-OFDM quantum systems compared to the classical MIMO-OFDM BPSK system.

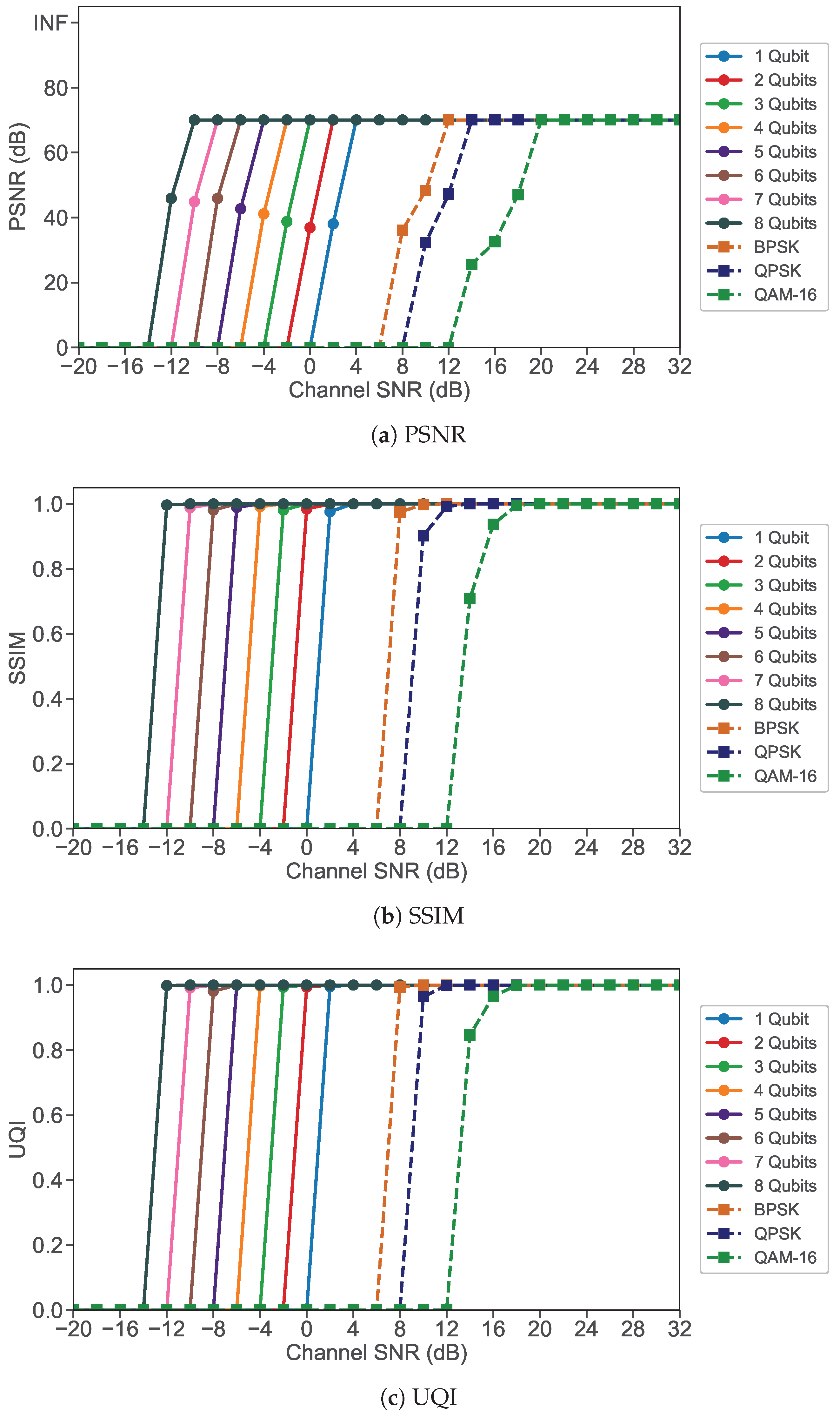
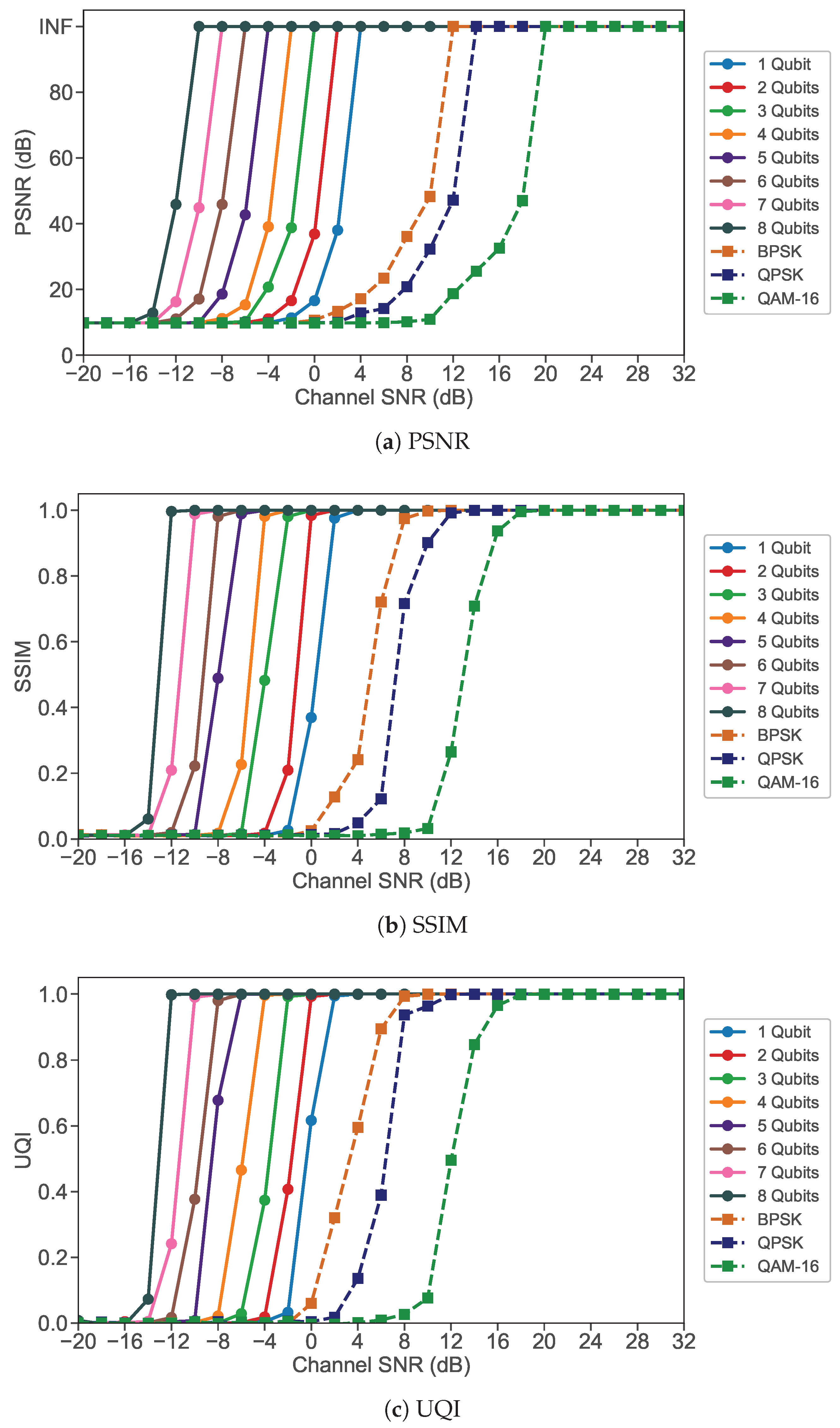
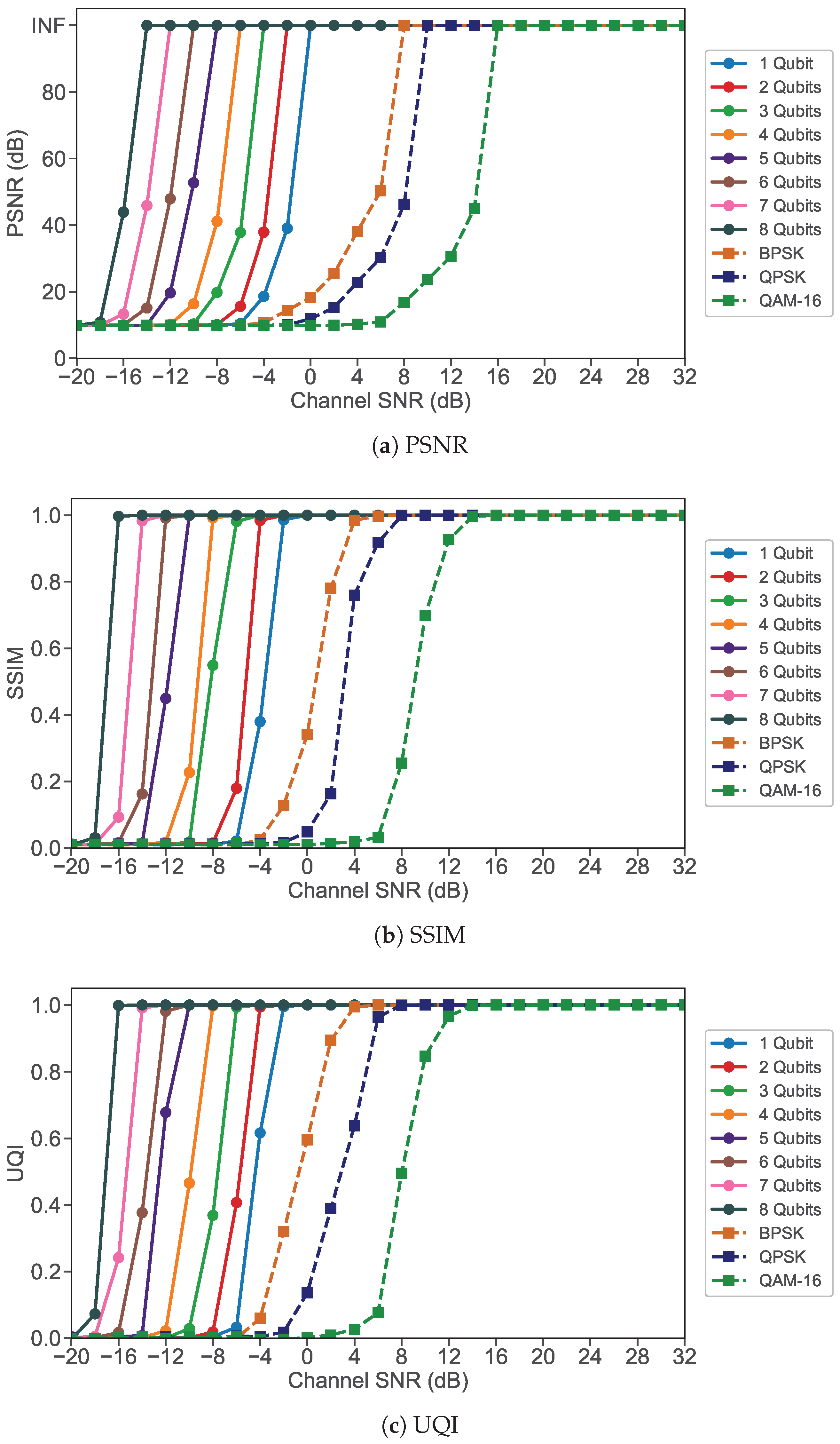
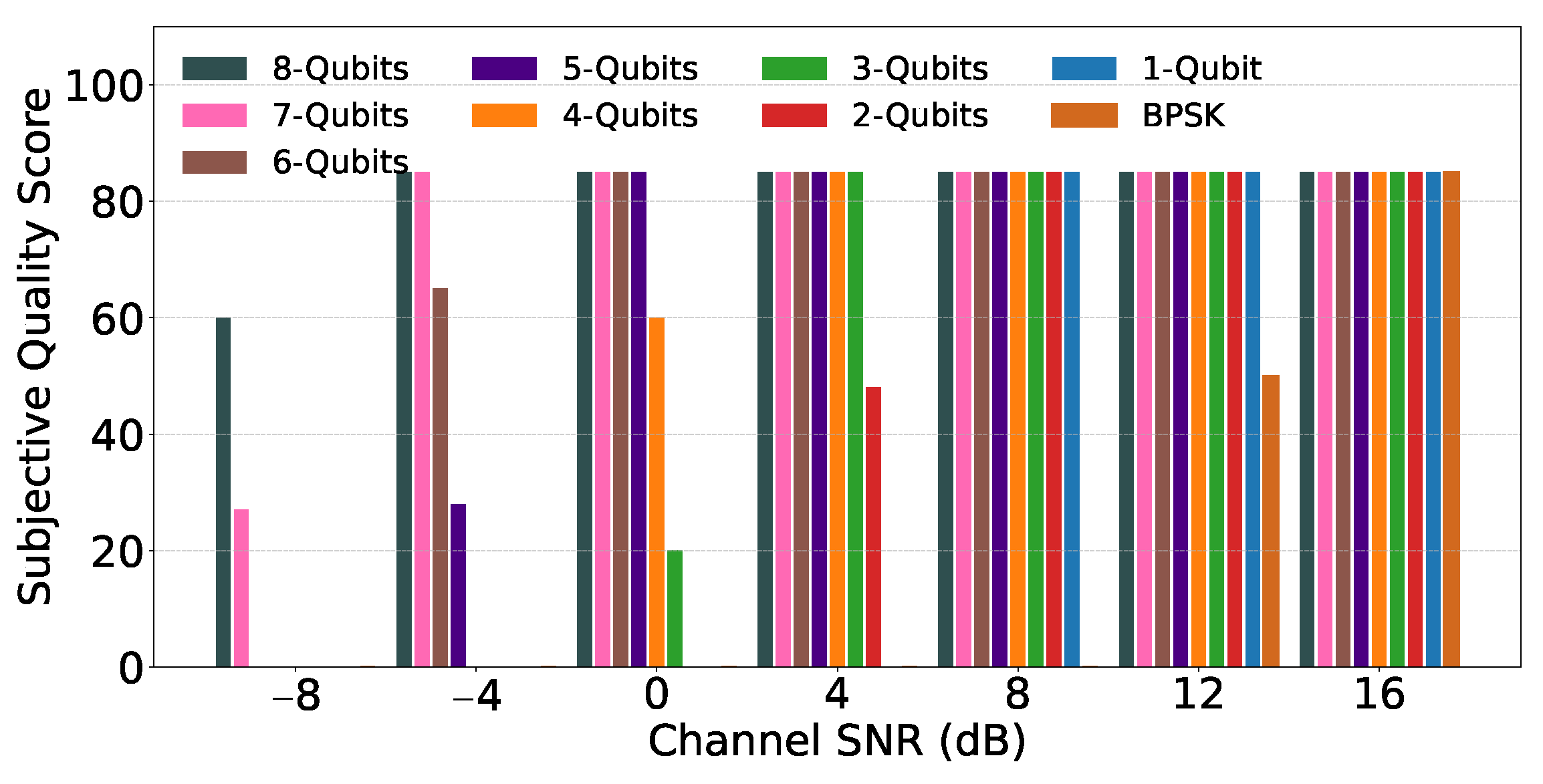
Image Format	Maximum Channel SNR Gains
	1 Qubit	2 Qubits	3 Qubits	4 Qubits	5 Qubits	6 Qubits	7 Qubits	8 Qubits
JPEG ($256\times 192$)	8	10	12	14	16	18	20	22
HEIF ($256\times 192$)	8	10	12	14	16	18	20	22
Uncompressed ($256\times 192$)	8	10	12	14	16	18	20	22
4K	8	10	12	14	16	18	20	22

, the quantum MIMO-OFDM system consistently achieves maximum channel SNR gains across all image formats and qubit configurations, with gains progressively increasing from 1 to 8 qubits compared to the classical BPSK scheme. These results highlight the scalability and resolution independence of the system, confirming its adaptability to both lightweight compressed images (e.g., JPEG, HEIF) and high-resolution content such as 4K. This makes the proposed approach suitable for a wide range of multimedia applications in next-generation wireless quantum networks.

In addition to the objective evaluation, a subjective quality assessment is performed to analyze the perceived visual quality of the transmitted images. Although the proposed MIMO-OFDM system is tested using JPEG, HEIF, and uncompressed image formats, subjective results are presented only for JPEG images as a representative case. The assessment is conducted following the ITU-R BT.500 double stimulus method [74], where visual quality ratings of images reconstructed via quantum and classical BPSK-based transmission systems are collected from 80 participants aged between 17 and 55, using uncompressed images as reference. Although this group cannot represent the full diversity of global perception, it exceeds the panel sizes recommended by ITU standards for statistically reliable mean opinion scores (MOS) and provides complementary validation to objective metrics such as PSNR, SSIM, and UQI. The evaluation is conducted across three diversity configurations: SISO (1 × 1), MISO (2 × 1), and SIMO (1 × 2). A standard MOS scale is used from 0 to 100, where scores of 0 to 20 indicate bad, 21 to 40 poor, 41 to 60 fair, 61 to 80 good and 81 to 100 excellent quality. The MOS values are averaged across all participants and are shown in Figure 13, Figure 14 and Figure 15 for the respective MIMO setups. A strong correlation is observed between these subjective scores and objective metrics such as PSNR, SSIM, and UQI, confirming the consistency between perceptual and quantitative evaluations.

Furthermore, this study assumes perfect CSI at the receiver to establish a theoretical upper bound on the performance of the proposed quantum MIMO-OFDM system. For fairness, the same perfect CSI assumption is applied to the classical MIMO-OFDM baseline. This assumption is standard in both early-stage classical and quantum communication research [13,44]. In classical systems, it allows the evaluation of intrinsic design advantages such as subcarrier orthogonality and spatial diversity, while in quantum systems, it facilitates the analysis of QFT-based subcarrier spreading and multi-qubit redundancy without the confounding influence of channel estimation errors. In practical quantum implementations, CSI would typically be estimated using quantum pilot states ( $|+\rangle$ and $|-\rangle$ ), which serve as quantum analogs of classical pilot tones. Moreover, the impact of imperfect CSI is naturally mitigated in the quantum domain: due to quantum encoding and QFT spreading, estimation errors are distributed across multiple subcarriers and qubits, leading to a more gradual performance degradation compared to classical OFDM. Therefore, adopting the perfect CSI assumption is a reasonable and widely accepted approach in the early stages of communication system design.

4.4. Complexity Analysis

The computational complexity of the proposed MIMO-OFDM framework is dominated by the QFT, which is employed in both the encoding and decoding stages. For an n-qubit register, the QFT requires $G_{\mathrm{QFT}}\left(n\right)=n(n+1)/2$, resulting in a quadratic growth in gate count. The corresponding circuit depth scales approximately linearly as $D_{\mathrm{QFT}}\left(n\right)\approx n$.

Table 2. QFT gate counts and circuit depth for varying qubit numbers.

n (Qubits)	QFT Gates ${\mathit{G}}_{\mathbf{QFT}}$	Circuit Depth
1	1	1
2	3	2
3	6	3
4	10	4
5	15	5
6	21	6
7	28	7
8	36	8

summarizes the gate counts and circuit depths for $n=1$–8 qubits. Even at the upper bound of eight qubits, the QFT consists of only 36 gates and a depth of eight layers, which is well within the capabilities of current classical simulators and near-term quantum devices. The modest growth in both gate count and depth confirms that the proposed 1–8 qubit encoding range introduces only minimal computational overhead while providing meaningful gains in representation and encoding flexibility.

Beyond gate-level complexity, classical simulation requirements further demonstrate practical feasibility. An n-qubit quantum state contains $2^n$ complex amplitudes, leading to memory usage that scales as $O\left(2^n\right)$. Because each QFT gate acts on the full state vector, the computational cost of simulating the QFT scales as $G_{\mathrm{QFT}}\left(n\right)·2^n$.

Table 3. State-vector size, memory usage, FLOPs, and estimated CPU runtime for QFT simulation.

n (Qubits)	State-Vector Size ($2^{\mathit{n}}$)	Memory (KB)	Estimated FLOPs	Runtime @ 50 GFLOPS
1	2	0.03	2	$4\times {10}^{-11}$ s
2	4	0.06	12	$2.4\times {10}^{-10}$ s
3	8	0.13	48	$9.6\times {10}^{-10}$ s
4	16	0.25	160	$3.2\times {10}^{-9}$ s
5	32	0.50	480	$9.6\times {10}^{-9}$ s
6	64	1.00	1344	$2.7\times {10}^{-8}$ s
7	128	2.00	3584	$7.2\times {10}^{-8}$ s
8	256	4.00	9216	$1.8\times {10}^{-7}$ s

provides a detailed breakdown of state-vector sizes, memory requirements, floating-point operation (FLOP) estimates, and representative execution times assuming a 50 GFLOPS CPU. Even for eight qubits, the state vector contains only 256 amplitudes (4 KB), and a full QFT requires fewer than ${10}^4$ FLOPs, corresponding to sub-microsecond runtime. These results quantitatively show that both quantum circuit execution and classical simulation remain lightweight for all qubit sizes considered. Therefore, the proposed system achieves an effective balance between computational practicality and performance up to eight qubits.

While traditional quantum error correction (QEC) techniques [75] offer theoretical improvements in error rates, they require substantial qubit overhead, deep circuit layering, and intricate feedback mechanisms [76], which render them unsuitable for near-term quantum MIMO-OFDM implementation. In this study, we instead employ a hybrid protection mechanism that combines multi-qubit superposition encoding with classical polar coding, providing a practical trade-off between robustness and complexity. The multi-qubit encoding process inherently distributes information across an expanded Hilbert space, thereby improving resilience to localized quantum noise and partial decoherence effects. Following quantum transmission and measurement, a rate-$\frac{1}{2}$ polar code is applied to the classical bitstream, ensuring efficient recovery from residual channel errors. This joint approach effectively mitigates noise while preserving scalability and computational feasibility, avoiding the excessive resource consumption associated with full QEC. Moreover, it aligns with the communication-oriented focus of this work, where the goal is reliable classical information transfer rather than universal fault-tolerant quantum computation. Consequently, the proposed hybrid strategy demonstrates a practical balance between theoretical rigor and hardware realizability in quantum MIMO-OFDM communication systems.

4.5. Scalability

The $2\times 2$ MIMO configuration is used for testing due to its relatively low complexity, allowing efficient evaluation of the benefits of spatial diversity and the flexibility of the proposed quantum MIMO-OFDM system. Designed for scalability, this framework can be readily extended to higher-order MIMO setups such as $4\times 4$ or $8\times 8$ as quantum hardware and processing capabilities continue to advance. Although increasing the number of antennas and qubits naturally leads to higher system complexity, the modular and hierarchical architecture of the proposed design allows efficient scaling without compromising performance or manageability. This ensures that the system can adapt to future technological improvements and meet the growing demands of high-throughput quantum communication applications.

4.6. Hardware Constraints and Practical Implementation

The practical realization of the proposed quantum MIMO-OFDM system is inherently constrained by the current limitations of quantum hardware. Quantum processors capable of executing large-scale multi-qubit operations with high fidelity are still under active development, restricting achievable qubit encoding sizes, gate operation speeds, and noise tolerance. These constraints directly influence overall system performance, particularly regarding coherence times and cumulative gate errors during complex transformations such as the QFT, IQFT, and multi-qubit MIMO decoding. Furthermore, implementing a quantum MIMO architecture requires precise control and synchronization of quantum channels across multiple transmit and receive nodes, which remains an engineering challenge. The exponential growth of the Hilbert space with increasing qubit and antenna dimensions further adds to computational and control complexity.

Despite these challenges, recent progress in superconducting, trapped-ion, and photonic quantum platforms indicates that scalable multi-qubit processing is becoming increasingly feasible. Emerging techniques such as fault-tolerant gate designs, approximate QFT circuits, and distributed quantum networking offer promising pathways for practical realization. In addition, hybrid quantum–classical strategies, such as integrating classical polar coding with quantum encoding, help reduce the demands for quantum resources while maintaining robust system performance.

Therefore, while large-scale deployment of the proposed framework is beyond current technological capabilities, its architectural scalability ensures readiness for future advancements. As quantum hardware matures, the system presented here provides a validated theoretical foundation for experimental prototyping and gradual upscaling. The findings thus serve as a bridge between theoretical innovation and real-world application, positioning this framework as a forward-compatible model for next-generation quantum communication systems.

In summary, the proposed quantum OFDM-MIMO system is a conceptual and forward-looking framework intended for theoretical analysis and system-level modeling rather than immediate deployment, while multi-qubit encoding, MIMO encoding, QFT, IQFT, MIMO decoding across multiple antennas, and cyclic prefix handling exceed the capabilities of current quantum hardware, the architecture provides a scalable blueprint for future implementation. It enables evaluation of performance limits under realistic channel conditions, exploration of algorithmic optimizations, and identification of hardware requirements such as qubit encoding size, coherence times, and gate fidelities. This approach mirrors classical OFDM and MIMO research, where architectures are first theoretically analyzed before the hardware becomes capable of supporting large-scale deployment. The framework thus defines the idealized operational behavior of quantum multi-qubit OFDM-MIMO receivers, guiding future experimental realization while preserving coherence and ensuring unitary processing throughout the end-to-end communication chain.

4.7. Potential Applications

This adaptable quantum MIMO-OFDM architecture supports varying qubit encoding sizes and diversity schemes, making it well-suited for a broad spectrum of applications. These include secure satellite communication links, long-range wireless sensor networks, and emerging 6G networks that demand ultra-reliable low-latency communication. Its inherent robustness and improved error resilience also make it ideal for quantum-enhanced imaging, remote sensing, and other high-fidelity data transmission scenarios. Moreover, the demonstrated performance SNR gains and system flexibility highlight its strong potential for practical deployment in challenging wireless environments. As quantum technology continues to mature, this system paves the way for integration into future quantum communication networks, enabling the reliable and efficient transmission of complex multimedia data.

In summary, the proposed quantum MIMO-OFDM system consistently outperforms classical MIMO-OFDM-based image transmission schemes across all tested configurations, including SISO, MISO, and SIMO, and for multiple image formats (JPEG, HEIF, and uncompressed). The combination of multi-qubit encoding, QFT-based frequency-domain processing, and classical polar coding provides superior noise resilience, scalability, and image fidelity, particularly in low-SNR environments where classical systems struggle. These findings highlight the advantages of quantum encoding and MIMO-OFDM integration, providing a clear depiction of how the proposed framework overcomes the inherent limitations of current classical methods, and set the stage for the concluding section that summarizes the broader impact and potential applications of this approach.

5. Conclusions and Future Work

The performance of the proposed quantum MIMO-OFDM system is evaluated for image transmission across SISO, MISO, and SIMO diversity configurations, using JPEG, HEIF, and uncompressed image formats. The results demonstrate that quantum communication systems consistently outperform classical schemes, especially in low SNR environments across all diversity schemes. This enhanced performance is achieved through a combination of multi-qubit encoding, spatial diversity, QOFDM efficiency, and advanced classical channel coding, which together improve noise resilience and image quality metrics such as PSNR, SSIM, and UQI. As the number of qubits increases, the robustness of the system improves significantly, but the complexity also increases. Although the eight-qubit configuration introduces higher computational complexity, it delivers the best performance across all metrics evaluated under both transmit and receive diversity, compared to the no diversity scenario. Notably, the eight-qubit configuration surpasses all other quantum and classical systems across all diversity schemes, achieving peak metrics such as PSNR values up to 58.48 dB, SSIM up to 0.9993, and UQI up to 0.9999 for JPEG images; PSNR up to 70.04 dB, SSIM up to 0.9998, and UQI up to 0.9999 for HEIF images; and nearly ideal performance with infinite PSNR, SSIM of 1, and UQI of 1 for uncompressed images at very low SNR levels. Compared to classical MIMO-OFDM-based image transmission technologies, the proposed quantum MIMO-OFDM system provides superior fidelity and robustness, demonstrating strong scalability and potential for practical applications. Its combination of quantum superposition, multi-qubit encoding, frequency-domain processing, and classical error correction makes the proposed system a promising solution, achieving levels of reliability and image fidelity that classical systems cannot reach. This approach is particularly relevant for future high-performance applications such as secure satellite communications, wireless sensor networks, and next-generation mobile networks.

Future research will focus on advancing the quantum MIMO-OFDM system along several critical directions to enhance its practical applicability and overall performance. In particular, the impact of imperfect CSI will be investigated to assess the robustness of quantum transmission under realistic estimation errors. Additionally, the effects of non-ideal quantum gates and state preparation errors on system fidelity will be analyzed, with the goal of developing mitigation strategies that preserve performance in non-ideal experimental conditions. The system will also be extended to support higher-order MIMO configurations and multi-user scenarios, improving reliability and scalability in practical wireless deployments. Furthermore, an adaptive quantum MIMO-OFDM framework will be explored, allowing dynamic adjustment of qubit encoding schemes based on real-time channel conditions to optimize communication performance under fluctuating environments. Collectively, these developments aim to establish a scalable, high-fidelity quantum communication platform that maintains robustness in realistic operational settings and meets the demands of next-generation wireless networks and quantum-enhanced applications.