Securing Elliptic Curve Cryptography with Random Permutation of Secret Key

Abstract

Scalar multiplication is the basis of the widespread elliptic curve public key cryptography. Standard scalar multiplication is vulnerable to side-channel attacks that are able to infer the secret bit values by observing the power or delay traces. This work utilizes the arithmetic properties of scalar multiplication to propose two scalar multiplication algorithms to insulate ECC implementations from side-channel attacks. The two proposed designs rely on randomly permuting the ordering and storage locations of the different scalar multiplication values $2^{i}G$ as well as the corresponding secret key bits $k_i$. Statistical analysis and Python 3.9.13implementations confirm the validity of the two algorithms. Numerical results confirm that both designs produce the same results as the standard right-to-left scalar multiplication algorithm. Welch’s t-test as well as numerical simulations confirm the immunity of our proposed protocols to side-channel attacks.

1. Introduction

Public key infrastructure (PKI) is the foundation for current security systems whether for encryption/decryption or digital signatures [1]. Elliptic curve cryptography (ECC) is the preferred means for data encryption, decryption and for digital signatures. This is due to its high level of security for a given key size compared to the more expensive Rivest–Shamir–Adleman (RSA) encryption [2,3,4]. This is the reason why it is very suited to internet of things (IoT) applications due to their limited compute and storage resources. Examples of infrastructure systems that rely heavily on IoT devices are smart transportation systems, telehealth, banking, and entertainment [5,6,7].

Due to the prevalence of ECC in everyday life, it is the subject of myriad types of attacks [8]. Side-channel attacks (SCAs) are particularly harmful since they utilize the algorithm implementation weaknesses to infer the secret key bits [9,10,11].

Over the years, few techniques have been developed to fix the vulnerability of ECC to side-channel attacks, as will be discussed in Section 3.

Elliptic curve point addition has two very useful properties: commutativity and associativity [12,13]. These two properties will prove useful to derive our proposed randomized and secure scalar multiplication algorithm in Section 4.

The contributions of this work are as follows:

• The basic loop of the standard right-to-left (RtL) algorithm, and most other similar implementations, is broken into two separate loops. One to calculate an array of scalar factors of the generator point $2^{i}G$ and one to calculate the final result $P=KP$.
• Random permutations are applied to both the array of generator point powers and the secret key bits.
• The random permutations are applied with a random seed for each implementation of scalar multiplication operation. This basically defeats simple SCA attacks as well as other more sophisticated attacks such as differential power analysis (DPA).
• Welch’s t-test analysis is performed to prove the security of the two proposed algorithms and also to assess the security of three other famous algorithms from the literature.
• Python implementations were performed to verify the algorithms.
• A complexity analysis comparison of our proposed algorithms and the other three algorithms was performed.

2. Background

Public key infrastructure uses elliptic curves for the discrete logarithm problem or uses RSA for the integer factorization problem. In the former, the two main operations are unconditional point doubling and conditional point addition. In the latter, the two main operations are unconditional modular squaring and conditional modular multiplication.

2.1. Elliptic Curves

An elliptic curve, denoted by $E_p(a,b)$, is given by the congruence:

$$y^{2}modp=x^3+ax+bmodp$$

(1)

where $x,y\in GF\left(p\right)$ define a point P on the plane elliptic curve and p is a large prime that defines the field. In addition to the points $P=(x,y)\in E_p(a,b)$, there is the identity element which is the point at infinity $\mathcal{O}$. A valid elliptic curve $E_p(a,b)$ must satisfy the Weierstrass equation

$$4a^3+27b^{2}modp\ne 0.a=0\mathrm{or}a=-3\left(\mathrm{typically}\right)$$

(2)

Figure 1 shows two examples of elliptic curves. Figure 1a shows an elliptic curve in the continuous domain where the point coordinates are are two real numbers $x,y\in \mathcal{R}$. The figure shows how adding two points $P_1$ and $P_2$ is performed. Figure 1b shows the practical discrete case where the points of the elliptic curve are in a finite field. The curve shown is for parameters $a=1$, $b=7$, and $p=19$.

The prime number defining the curve is p and is assumed to be composed of m bits and is typically described as a quasi-Mersenne prime [3]. We shall confine our discussion to the case of an elliptic curve over the prime field $GF\left(p\right)$, although extending the discussion to the binary extension field $Gf\left(2^m\right)$ is straightforward.

2.2. Scalar Multiplication

The defining equation for ECC is scalar multiplication:

$$P=KG\equiv \underset{k-terms}{\underbrace{G+G+\cdots +G}}$$

(3)

where $P,G\in E_p(a,b)$, K is an m-bit secret key, and G is the generator point. The points P and G are part of the public key, in addition to the curve parameters $a,b$, and $p$.

Figure 1. Two examples of elliptic curves. (a) Continuous case. (b) Discrete case for the curve $E{(1,7)}_{19}$.

Figure 1. Two examples of elliptic curves. (a) Continuous case. (b) Discrete case for the curve $E{(1,7)}_{19}$.

The addition operation in the above equation is the well-known point add operation which requires modular addition, multiplication, and finding the multiplicative inverse.

Assuming big endian notation, we can write the scalar factor K in Equation (3) in m-bit binary form:

$$K=k_{m-1}{2}^{m-1}+\cdots +k_1{2}^1+k_0$$

(4)

where $k_i\in \{0,1\}$. Scalar multiplication using this form requires the following:

• Unconditional generation of all the exponents of the generator points

  $$\begin{array}{ccc}\hfill \mathbf{G}& =& \left[\begin{array}{ccccc}{2}^{0}G& 2^{1}G& 2^{2}G& \cdots & 2^{m-1}G\end{array}\right]\hfill \end{array}$$

  (5)
• Conditional point addition to effect scalar multiplication:

  $$\begin{array}{ccc}\hfill P& =& \sum _{i=0}^{m-1}{2}^i{k}_{i}G,k_i\in \{0,1\}\hfill \end{array}$$

  (6)

2.3. Non-Adjacent Form Representation

We can use the redundant representation of K in Equation (4) using non-adjacent form (NAF) for scalar factor K representations. The corresponding NAF representation of K in Equation (4) is given by

$$K=k_m{2}^{m-1}+\cdots +k_1{2}^1+k_0$$

(7)

where $k_i\in \{-1,0,1\}$. NAF is obtained when we enforce the restriction that no two contiguous bits can be non-zero. For an m-bit key, NAF results in an $m+1$-bit key but has lower Hamming weight compared to the binary representation. This has the effect of reducing the number of conditional point additions/subtractions.

To effect scalar multiplication using NAF, we now require the following:

• Unconditional generation of G and $-G$ point doubling of the generator points

  $$\begin{array}{ccc}\hfill \mathbf{G}& =& \left[\begin{array}{ccccc}{2}^{0}G& 2^{1}G& 2^{2}G& \cdots & 2^{m-1}G\end{array}\right]\hfill \end{array}$$

  (8)
• Conditional point addition

  $$\begin{array}{ccc}\hfill P& =& \sum _{i=0}^{m-1}{2}^i{k}_{i}G,k_i\in \{-1,0,1\}\hfill \end{array}$$

  (9)

Table 1. Hierarchy of protocols and operations for elliptic curve cryptography.

Applications	E-commerce, communications, telehealth
Protocols	ECDH, ECDSA
Scalar multiplication	$kG$
Point operations	$P+Q$ and $2P$
Modular arithmetic	Addition ($x+y$), subtraction ($x-y$), multiplication ($x\times y$), squaring ($x^2$), multiplicative inverse ($x^{-1}$)

shows the protocols and hierarchical operations based on elliptic curve public key infrastructure.

NIST recommends the elliptic curves summarized in

Table 2. NIST-recommended elliptic curves.

Field	Field Size (Bits)	Prime Value
$p_{192}$	192	$2^{192}-2^{64}-1$
$p_{224}$	24	$2^{224}-2^{96}-1$
$p_{256}$	256	$2^{256}-2^{224}+2^{192}+2^{96}-1$
$p_{384}$	384	$2^{384}-2^{128}-2^{96}+2^{32}-1$
$p_{521}$	521	$2^{521}-1$

.

2.4. Right-to-Left Scalar Multiplication

What is known as the right-to-left algorithm performs the scalar multiplication operation in Equation (3). This is shown in Algorithm 1.

Algorithm 1: Right-to-left scalar multiplication algorithm.

Algorithm 1 requires performing $m-1$ point doubling operations. However, Algorithm 1 is vulnerable to SCA due to the conditional point add operation in Lines 3 to 7. At iteration i of the loop, if the secret key bit is $k_i=1$, then the conditional branch results in increased power consumption and delay even in the presence of other noise sources due to other running processes. An observer can filter out the noise and guess the value of the secret key bit.

For the case of NAF representation, Algorithm 1 is modified to Algorithm 2.

Algorithm 2: Right-to-left scalar multiplication algorithm using the NAF number representation.

The NAF algorithm is also vulnerable to SCA since the conditional point addition can be easily observed through delay or power traces. This leads to deducing the secret key bits. However, SCA observations of the NAF algorithm enables the attacker to detect point add or point subtract operations. Although it is unknown which operation is used, an exhaustive search is feasible since NAF results in 30% of the bits being non-zero on average.

3. Related Work

The basic vulnerability of scalar multiplication is the observation that when the secret key bit is 0, only point doubling is performed. On the other hand, a secret key bit value of 1 requires point addition plus point doubling. An obvious solution to this is to replace the double-and-add with double-and-add using dummy operations.

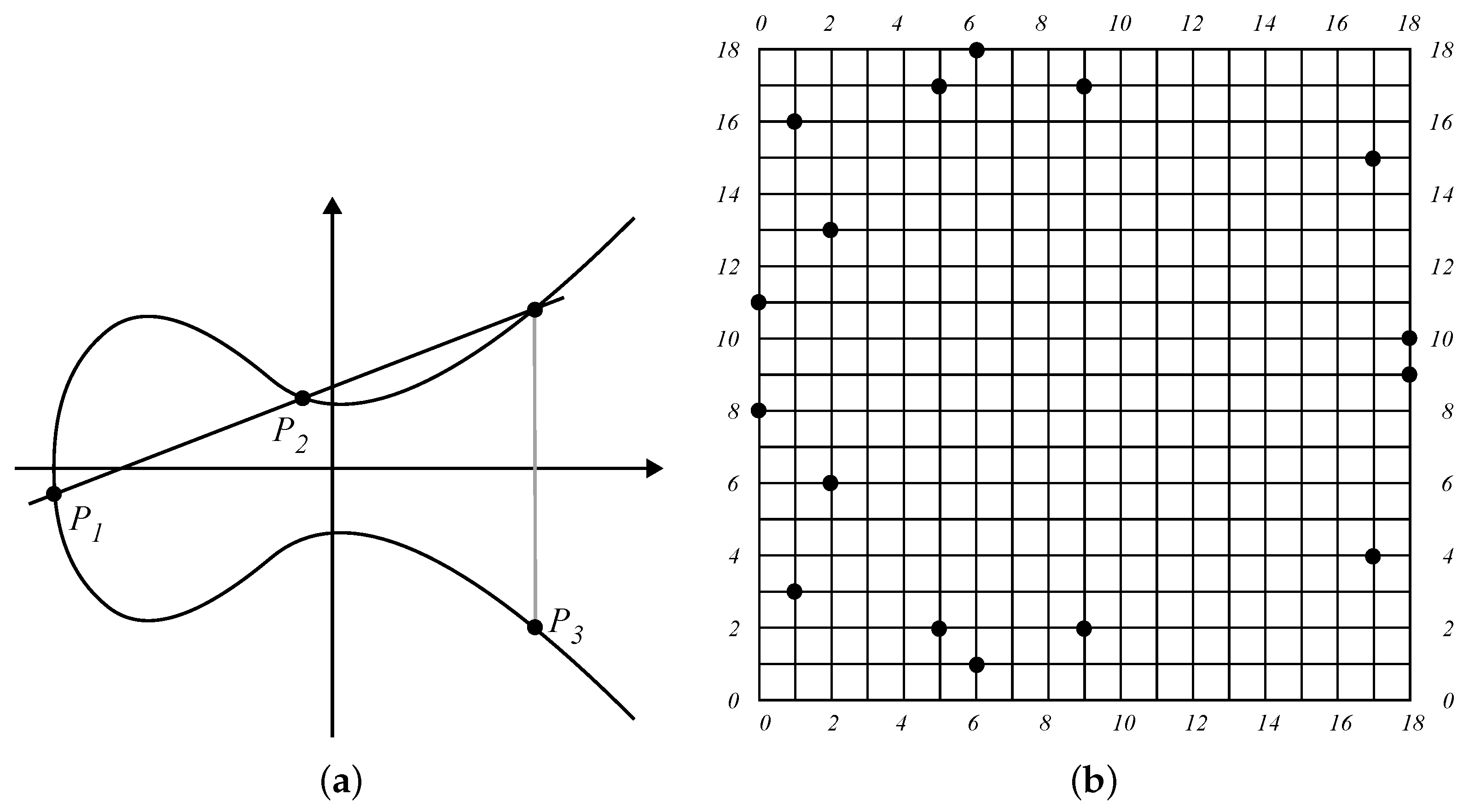
A slightly more sophisticated solution is the Montgomery ladder. The Montgomery ladder algorithm [14,15] is essentially similar to the LtR scalar multiplication algorithm as shown in Algorithm 3.

Algorithm 3: RtL algorithm using the Montgomery ladder technique.

From Algorithm 3 we see that the IF condition branch in Lines 4 or 6 results in the same amount of power consumption and delay. This effectively obfuscates any attempt to deduce the secret key bit values.

Longa [16] proposed composite or atomic operations based on point doubling and point addition to remove the SCA vulnerability and to speed up the operations. He used this approach for accelerating scalar multiplication and for accelerating precomputing in window-based approaches. The atomic operations performed point tripling ($3P$) and point quadrupling ($4P$). In addition, more atomic operations were proposed such as unified doubling-addition ($2P+Q$) and unified tripling-addition ($3P+Q$).

Sigourou et al. [8] implemented the scalar multiplication operation using Longa’s atomic pattern for point doubling and point addition discussed in the previous paragraph. The atomic blocks used in this work adopted the MNAMNAA, where M denotes field multiplication, N denotes negation, and A denotes addition. Using these techniques, point doubling and point add use the same registers and hence defeat SCA since the operations would be indistinguishable.

Wei et al. [17] considered cluster-based side-channel attacks that use clustering algorithms to analyze power traces together with principle component analysis to reduce the dimension of the data. They combined an intelligent framework that combines unsupervised clustering techniques and supervised deep learning. This approach is powerful for mining data for in-depth information. It can be used as a powerful tool to assess the vulnerability to proposed secure scalar multiplication algorithms.

Klavier and Joye [18] divided the scalar factor into two parts so that scalar multiplication is expressed as:

$$KG=K_{L}G+K_{H}G$$

(10)

where $K_L$ is the least significant bits and $K_H$ is the most significant bits. The number of bits representing $K_L$ or $K_H$ is randomly chosen. Next, the authors used left-to-right evaluation of the term $K_{L}G$ and right-to-left for evaluation of the term $K_{H}G$. Using LtR and RtL using parts of the secret key still relies on point doubling and conditional point add. In this fashion, an SCA attacker is able to detect the presence and the location of the ones in the secret key. The attacker, however, is not able to determine if this location is from the right of the MSB or from the left of the LSB. In addition, the SCA attacker is not able to determine when processing moves from $K_H$ to $K_L$ or vice versa.

Itoh et al. [19] proposed three windowing techniques to defeat differential power analysis (DPA) attacks:

• Overlapping window method (O-WM);
• Randomized table window method (RT-WM);
• Hybrid randomized window method (HR-WM).

Each technique has unique characteristics such as speed and security to suit the target environment. The basic idea is to randomly distribute the secret key bits among the overlapping windows.

Kolagatla and Desalphine [20] considered modular exponentiation for the RSA algorithm:

$$C=M^{K}modp$$

(11)

where $M,C,K\in p$ are the message, ciphertext, and secret or public key, respectively. p is the prime of the field and typically p is a quasi-Mersenne prime [3]. We should bear in mind that modular exponentiation in RSA and scalar multiplication in ECC are very much equivalent. Squaring and multiplication in RSA are replaced with doubling and addition in ECC. Modular exponentiation involves two modular operations: multiplication and squaring. The authors studied the vulnerability of the RSA implementation and proposed countermeasures against SCA to enhance the security. Their approach is to use the random radices Montgomery ladder algorithm to suppress SCA. The radices considered were $2^1$, $2^2$, $2^3$, $2^4$, $2^5$, $2^6$, $2^7$, and $2^8$. At each Montgomery ladder iteration, a radix is chosen at random and the processing of the radix representation of the secret key bits is done in parallel because of the digit representation in a high-radix format.

Ding et al. [21] investigated testing methods for mitigation against SCA. Specifically, the authors studied cluster-based SCA and introduced their adjacent distance coefficient to quantify the accuracy of recovering secret key bits. It is crucial for ECC systems to be resistant to the different forms of SCA techniques. The authors claim that their metric outperformed traditional metrics such as silhouette coefficient, membership degree, and information entropy.

Yang et al. [9] used a variable radix system to prevent SCA. Their method transforms the secret key into a variable-radix format. This approach is claimed to de-correlate the secret key bits and the power trace waveforms. The proposed implementation proved immune to simple power analysis, differential power analysis, and timing analysis.

Kido et al. [22] considered implementing the ECC curve GLS245 represented in $GF\left(q^2\right)$, where $q=2^{127}$. They targeted memory- and power-limited IoT devices. The authors used several coordinates like

• Modified $\sqrt{b}(x,s)$-Jacobian coordinates ${\mathcal{J}}^{mbxs}$ with X, Z multiplied by $\sqrt{b}$;
• $(x,s)$-affine coordinates;
• Proposed $(x,s)$-Jacobian coordinates ${\mathcal{J}}^{xs}$ consisting of three coordinates ($X,S,Z$).

It should be noted that the authors selected the best coordinates for each calculation.

4. Proposed Secure Randomized Elliptic Curve Scalar Multiplication

From Equation (3) we immediately notice two very useful properties that will prove crucial to our proposed technique. The point addition and doubling operations in Equation (3) and Algorithm 1 are both commutative and associative and the ordering of the different powers of the exponent terms can be performed in any order [12].

This gives us the opportunity to defeat SCA through randomization of executing Equation (3). In order to achieve that, we first perform the following modifications to Algorithm 1.

4.1. Proposed Design #1: Random Permutations (RP)

The first proposed design option in this section begins with decoupling unconditional point doubling and conditional point add in two separate loops. The modification also randomizes the order of the secret key bits and the corresponding point double vector. Lastly, it generates the desired point additions necessary to produce the desired result in a secure manner.

Algorithm 4 is a modification of the RtL Algorithm 1 by removing the conditional multiplication and breaks the loop in Algorithm 1 into three consecutive stages.

The stages of Algorithm 4 are shown in Figure 2. We see that the loop of Algorithm 4 has now been broken into three consecutive states and two independent loops.

Algorithm 4: Scalar multiplication algorithm for proposed random permutations (RP) design.

Stage 1 of Algorithm 4 performs the point doubling step and corresponds to Line 4 of Algorithm 1.

Stage 1 creates the vector array $\mathbf{G}$:

$$\begin{array}{}\mathrm{(12)}& \hfill \mathbf{G}& =& \left[\begin{array}{ccccc}{2}^{0}G& 2^{1}G& 2^{2}G& \cdots & 2^{m-1}G\end{array}\right]\hfill \mathrm{(13)}& & =& \left[\begin{array}{ccccc}{G}_0& G_1& G_2& \cdots & G_{m-1}\end{array}\right]\hfill \end{array}$$

Stage 1 does not reveal any harmful SCA since it is not related to the secret key bits of K.

Stage 2 of Algorithm 4 starts in Line 8 by selecting a random seed using any of the random libraries or methods available to the processor in hardware or software. Line 9 uses the randomly chosen seed to perform identical permutations on both the vector K and the array $\mathbf{G}$. It should be pointed out here that each run of the algorithm selects a new random seed to prevent any statistical SCA attacks such as Welch’s t-test.

The locations of the corresponding data in K and G now assume new positions. Once this step is performed, detecting a 1 bit in the shuffled secret key is unrelated to the actual location of that bit in the original secret key. Figure 3 shows the identical permutations on arrays K and $\mathbf{G}$. This has the crucial effect of obfuscating the correct location of the 0 and 1 bits of the original secret key K.

Table 3. Summarizing effect of applying random permutations at Stage 2 of Algorithm 4.

Before Permutation	$K=$	$k_0$	$k_1$	$k_2$	$k_3$	$k_4$	$k_5$	$k_6$	$k_7$
	G =	$G_0$	$G_1$	$G_2$	$G_3$	$G_4$	$G_5$	$G_6$	$G_7$
After Permutation	$K=$	$k_7$	$k_3$	$k_6$	$k_4$	$k_2$	$k_0$	$k_1$	$k_5$
	G =	$G_7$	$G_3$	$G_6$	$G_4$	$G_2$	$G_0$	$G_1$	$G_5$

shows in detail the process of applying random permutations to the secret key K and the doubling operation to generate vector G in Equation (13).

Stage 3 of Algorithm 4 performs conditional point addition but on the permuted vectors K and G. This conditional point addition does not reveal any useful information to SCA since the correlation between the conditional point add and the actual position of the secret key bits is completely lost.

Similar to the standard RtL design, the RP design needs to generate and store the two permuted arrays K and G, as shown in Figure 2 and Table 3. The memory required to store the data for K and G is estimated as:

$$\begin{array}{}\mathrm{(14)}& \hfill \mathrm{Memory}& =& 2m^2+3m\mathrm{bits}\hfill \mathrm{(15)}& & =& (2m^2+3m)/8\mathrm{bytes}\hfill \hfill \mathrm{(16)}& & =& (2m^2+3m)/W\mathrm{words}\hfill \end{array}$$

where the term $2m^2$ is the total number of bits required to store the vector G and the term $3m$ is the number of bits needed to store point P on the curve and the permuted secret key K, and W is the machine word size.

Let us consider a typical case of key size $m=256$ bits. The cache memory required to store G and K would be approximately 16.1 KB according to Equation (15). Assuming an ARM processor is used in an embedded IoT system, the L1 cache size is typically 16 KB to 64 KB. Therefore, the designed system could choose an L1 cache size that is over 16 KB.

4.2. Probability of Guessing the Secret Key Bits in the RP Design

The probability the attacker figures out the exact locations of those bits is given by:

$$\begin{array}{ccc}\hfill x& =& {\displaystyle \frac{1}{m}}·{\displaystyle \frac{1}{m-1}}·{\displaystyle \frac{1}{m-2}}\dots {\displaystyle \frac{1}{m-{\ell }_1}}\hfill \\ & =& {\displaystyle \frac{(m-\ell )!}{m!}}\hfill \end{array}$$

(17)

where m is the number of secret key bits and ℓ is the number of non-zero bits. For the ideal case of a well-balanced secret key, $\ell \approx m/2$. In that case, the above expression becomes

$$x\approx {\displaystyle \frac{(m/2)!}{\left(m\right)!}}$$

(18)

Using Stirling’s approximation of large factorials and after some manipulations, x could be approximated as:

$$x={\displaystyle \frac{1}{\sqrt{2}}}\times {\displaystyle \frac{1}{{(2m/e)}^{m/2}}}$$

(19)

The probability of guessing secret key K is diminutive, especially for typically large values of m.

4.3. Proposed Design #2: Truncated Random Permutations (TRP)

Similar to the proposed RP design, the second proposed design (TRP) eliminates the conditional point add altogether by creating a new list ${\mathbf{L}}_1$ that contains the locations of the non-zero bits of the permuted secret key.

Algorithm 5 shows the modifications to the standard RtL Algorithm 1 and the proposed RP Algorithm 4.

Algorithm 5: Proposed algorithm for Design #2 (TRP).

Figure 3 illustrates, using a block diagram, the iterative evaluation of the output P over I iterations.

The memory required to store the data for K, G, and ${\mathbf{L}}_1$ is given in Equations (14)–(16).

Stage #1 of Algorithm 5 constructs the vector G in Equation (13).

Stage #2 starts in Line 8 by selecting a random seed using any of the random libraries or methods available to the processor in hardware or software. Line 9 uses the randomly chosen seed to perform identical permutations on both the vector K and the array $\mathbf{G}$. It should be pointed out here that each run of the algorithm selects a new random seed to prevent any statistical SCA attacks such as Welch’s t-test.

This step randomizes the locations of the bits in K and the corresponding words $G_i$. This has the effect of de-correlating the point add operations from the actual location of the non-zero bits of K. An SCA attacker would have an almost vanishing probability of correctly figuring out the secret key, as in Equation (19).

Stage #3 builds the arrays ${\mathbf{L}}_1$. The conditional statement in Lines 13 to 15 will produce signals that might allow the SCA attacker to infer the number of ones in the secret key only. The actual location of these ones in the original vector K is lost due to the permutation performed in Stage #2.

Stage #4 computes the final result P.

Similar to the standard RtL design, the TRP design needs to generate and store the ${\mathbf{L}}_1$ and G. The memory required to store the data is estimated as:

$$\begin{array}{}\mathrm{(20)}& \hfill \mathrm{Memory}& =& 2m^2+0.5m{log}_{2}m+3m\mathrm{bits}\hfill \mathrm{(21)}& & =& (2m^2+0.5m{log}_{2}m+3m)/8\mathrm{bytes}\hfill \hfill \mathrm{(22)}& & =& (2m^2+0.5m{log}_{2}m+3m)/W\mathrm{words}\hfill \end{array}$$

where the term $2m^2$ inside the brackets is the number of bits of G and the term $m/2$ inside the brackets is length of list ${\mathbf{L}}_1$ for a well-chosen secret key.

Let us consider a typical case of key size $m=256$ bits; the length of list ${\mathbf{L}}_1$ is $m/2$ for a well-chosen key. The cache memory required to store G and ${\mathbf{L}}_1$ would be 16.2 KB, according to Equation (21). Assuming an ARM processor is used in an embedded IoT system, the L1 cache size is typically 16 KB to 64 KB. Therefore, the designed system could choose an L1 cache size that is over 16 KB.

5. Python Implementation Environment Configuration

Table 4. Simulation environment configuration.

Category	Specification
Operating System	Windows 10 Enterprise (64-bit)
CPU	Intel® Core™ i5-10210U (4 Cores, 8 Threads, 1.60 GHz)
Memory	16 GB DDR4 (8 GB @ 3200 MHz + 8 GB @ 2667 MHz)
GPU	Intel® UHD Graphics (1 GB), NVIDIA® GeForce® MX230 (2 GB)
Cache	L1: 256 KB, L2: 1 MB, L3: 6 MB
Programming Language	Python 3.9.13
IDE	PyCharm 2024.2.4 (Community Edition)

summarizes the hardware specifications for the Python implementation of the algorithms.

Computing Measurement Tool: The computer system performance monitoring was conducted using the Intel^® Performance Counter Monitor (PCM), compiled from the official GitHub 3.16 repository using Visual Studio 2022 Community Edition with the “Desktop Development with C++” workload and .NET Framework Developer Pack 4.7.2. PCM was integrated into Python scripts via the subprocess module to measure hardware metrics. Metrics collected were exported in CSV format and visualized with matplotlib.

6. Assessing the Security of ECC Protocols

This section develops the Welch’s t-test assessment of the five ECC algorithms discussed in this work: Standard RtL, Montgomery ladder [14], Klavier and Joye [18], and the two proposed algorithms, RP and TRP.

The evaluation procedure of side-channel resistance must be independent of the attack types, intermediate values, and hypothetical models [23]. A non-specific t-test reports whether the device under test (DUT) provides the aimed-for level of security without conducting an actual attack [24].

6.1. Standard RtL Algorithm Leakage Test Assessment

We assume that N traces are obtained for the RtL algorithm representing delay or power over time. This dataset is divided into two groups A and B such that the number of traces in the two groups are $N_A$ and $N_B$, respectively. Welch’s t-test formula is given by

$$t={\displaystyle \frac{X_A-X_B}{\sqrt{\frac{S_A^2}{N_A}+\frac{S_B^2}{N_B}}}}$$

(23)

where $X_A$ and $X_B$ are the point-wise (ensemble) means of the Group A and Group B traces, respectively:

$$X_A=E\left(T_A\right),X_B=E\left(T_B\right)$$

where $T_A$ and $T_B$ are composed of $N_A$ traces in Group A and $N_B$ traces in Group B, respectively. The means are in fact traces over time since the expectation operator is performed at each point in time.

$S_A$ and $S_B$ are the point-wise standard deviations of the traces of the two groups and are given, respectively, by

$$S_A=\sqrt{E{(T_A-X_A)}^2},S_B=\sqrt{E{(T_B-X_B)}^2}$$

In order to apply Equation (23) to assess the security of the RtL algorithm, we make several observations about Algorithm 1. Assuming the secret key bit $k_i$ is 0, all traces at time instance i will contain point doubling only. The mean is obtained as

$$X_0={\mu }_d+\epsilon$$

where ${\mu }_d$ is the mean of the point doubling operation and $ϵ$ is the unavoidable Gaussian noise that accounts for sampling alignment, operating system activity, and measurement noise.

When the secret key bit $k_i$ is 1, all traces at time instance i will contain point doubling plus point addition. The mean is obtained as

$$X_1={\mu }_d+{\mu }_a+\epsilon$$

where ${\mu }_a$ is the mean of point add operation.

The RtL maximum t-value is given by:

$$\begin{array}{ccc}\hfill t_{RtL}& =& {\displaystyle \frac{X_1-X_0}{\sqrt{\frac{S_A^2}{N_A}+\frac{S_B^2}{N_B}}}}\hfill \\ & =& {\displaystyle \frac{{\mu }_a+\epsilon }{\sqrt{\frac{S_A^2}{N_A}+\frac{S_B^2}{N_B}}}}\hfill \end{array}$$

(24)

The $t_{RtL}$ value in the above equation could exceed a given security threshold c and this proves that RtL is not secure in the Welch’s t-test context.

6.2. Montgomery Ladder Algorithm Leakage Test Assessment

For this algorithm, each iteration performs the same operations, point double and point add, regardless of the secret key bit value. In that sense, the mean of the traces has the same value:

$$X={\mu }_d+{\mu }_a+\epsilon$$

Maximum t-value for Montgomery ladder is given by:

$$\begin{array}{ccc}\hfill t_{Montgomery}& =& {\displaystyle \frac{X_1-X_0}{\sqrt{\frac{S_A^2}{N_A}+\frac{S_B^2}{N_B}}}}\hfill \\ & =& {\displaystyle \frac{\epsilon }{\sqrt{\frac{S_A^2}{N_A}+\frac{S_B^2}{N_B}}}}\hfill \end{array}$$

(25)

$t_{Montgomery}$ in the above equatoion is below a given security threshold c and this proves that the Montgomery ladder is secure in the Welch’s t-test context.

We should qualify this conclusion, however, when the attacker monitors the register addresses and the operation performed at each iteration since this could reveal the secret key bits.

6.3. Klavier and Joye Algorithm Leakage Test Assessment

In this algorithm, the main innovation is breaking the secret key into two parts, $K_L$ and $K_H$, where one part uses the LtR and the other part uses the RtL approach. However, the main point here is that the traces reveal the value of the secret key bit regardless of the secret key portion or whether RtL or LtR is used. We still have in this algorithm:

$$\begin{array}{c}\hfill X_0={\mu }_d+\epsilon \end{array}$$

(26)

$$\begin{array}{c}\hfill X_1={\mu }_d+{\mu }_a+\epsilon \end{array}$$

(27)

The performance of this algorithm is similar to the standard RtL algorithm and we see that the t-value for Klavier and Joye could exceed a given security threshold c, and this proves it is not secure in the Welch’s t-test context.

We should observe that the attacker is able to observe when the secret key bit is 1 or 0. However, the algorithm provides two sources of ambiguity:

• The bit obtained has an unknown location from either the start or end of the secret key bit since either RtL or LtR could be implemented.
• It is not obvious whether RtL or LtR is being observed at a given point in time.

From the above observations we conclude that the attacker can still figure out the secret key bit after performing $2m$ trials.

6.4. Design #1 (RP) Leakage Test Assessment

In order to apply Equation (23) to assess the security of our algorithm, we make several observations about Algorithm 4. Assuming the secret key bit is 0, all traces at time instance i will contain point doubling only. The mean is obtained as

$$X={\mu }_0+\epsilon$$

where $ϵ$ is Gaussian noise that accounts for unavoidable noise from sampling timing, operating system activity, and measurement noise.

On the other hand, assuming the secret key bit is 1, all traces at time instance i will contain point doubling only. The mean is obtained as

$$X={\mu }_1+\epsilon$$

The above X value illustrates the root cause of the vulnerability of RtL Algorithm 1.

For our case, the pervasive randomness of the permutations, as exemplified in Lines 8 and 9 of Algorithm 4, will result in the mean of the trace of value

$$X={\displaystyle \frac{{\mu }_0+{\mu }_1}{2}}+\epsilon$$

The values of $X_A$ and $X_B$ in Equation (23) are given by

$$X_A=X_B={\displaystyle \frac{{\mu }_0+{\mu }_1}{2}}+\epsilon$$

and this gives the t-value

$$t\approx \epsilon$$

The t-score in the above equation is mostly below the thresholds that the algorithm assessor might choose.

6.5. Design #2 (TRP) Leakage Test Assessment

Again we will use Welch’s t-test and break all traces into two groups, A and B, following the methodology of reference [23].

To assess the security of Algorithm 5, we note that there are two distinct segments in each trace. Samples in trace $T_d$ covering time instances 0 to $m-1$ all perform pure point doubling. Samples in trace $T_a$ from time instance m to $m+\ell -1$ all perform pure point add. Therefore, we can write the following statistical averages for $T_d$:

$$\begin{array}{ccc}\hfill N_d\left(i\right)& =& X_d;0\le i<m\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill N_a\left(i\right)& =& 0;0\le i<m\hfill \end{array}$$

(29)

The t-scores of trace $T_d$ is estimated as:

$$t_d\approx \epsilon$$

$t_d$ score is below any threshold that the algorithm assessor might choose.

For trace $T_a$ the number of point doubling and point add are given by

$$\begin{array}{ccc}\hfill N_d\left(i\right)& =& 0;m\le i<m+\ell \hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill N_a\left(i\right)& =& X_a;m\le i<m+\ell \hfill \end{array}$$

(31)

The t-score for the trace $T_a$ all have

$$t_a\approx \epsilon$$

$t_a$ score is below any threshold that the algorithm assessor might choose. This proves the security of the proposed Algorithm 5 (TRP).

7. Implementations and Performance Measurement

We start this section with a complexity comparison of the three algorithms discussed in this paper: Standard RtL and the two proposed algorithms, RP and TRP.

7.1. Complexity Analysis of RtL and Proposed RP and TRP Algorithms

Table 5. Comparing the $\mathcal{O}\left(m\right)$ complexity of the three algorithms, Standard RtL and the two proposed algorithms. RP and TRP.

Protocol	SCA	Scramble	Point	Point	Memory
	Immunity	$\mathit{K}$ and G	Double	Add	(Bytes)
RtL	No	No	m	ℓ	$5m/8$
Montgomery Ladder [14]	Yes	No	m	m	$5m/8$
Klavier and Joye [18]	No	No	m	ℓ	$9m/8$
Design #1 (RP)	Yes	Yes	m	ℓ	$(2m^2+3m)/8$
Design #2 (TRP)	Yes	Yes	m	ℓ	$(2m^2+3m+\mathit{\ell }{log}_{2}m)/8$

compares the $\mathcal{O}\left(m\right)$ complexities of the three algorithms, Standard RtL and the two proposed algorithms, RP and TRP.

We see that our two proposed designs manage to provide complete immunity to SCA and at the same do not incur any extra elliptic curve operations or variables.

7.2. Hardware SCA Monitoring Using Intel’s Tools

All implementations were developed in Python 3.9.13 and executed on the same hardware environment to ensure a fair comparison. The elliptic curve operations, including point addition, doubling, and scalar multiplication, were implemented in Python, providing a uniform baseline for evaluating both performance and side-channel resistance. The Intel^® Performance Counter Monitor (PCM) was used on Windows to collect precise hardware metrics [25]. The monitored metrics included Instructions Retired (INST), Active CPU Cycles (ACYC), L3 Cache Misses (L3MISS), Core and Package Energy (Joules), Core Temperature (°C), and Core Frequency (MHz). These metrics are not the only indicators of computational performance but also potential leakage sources as variations in instructions retired, cache behaviour, or energy draw can reveal patterns correlated with secret scalar bits. To evaluate both instantaneous leakage and statistical resistance, each design was executed once to capture single-run traces and repeated 100 times to analyze averaged and variance-based results. This dual perspective ensures that both single-execution leakage and long-term statistical leakage are addressed.

Python libraries such as PrimeFieldEllipticCurve [26] provide optimized and well-tested routines for point operations over prime fields; however, they are not used in our implementations. The main reason is that our study focuses on comparing the performance of several custom ECC operations, baseline, Design #1, and Design #2 algorithms, which involve custom transformations, randomized bit manipulations, and windowed doubling techniques for side-channel resistance. Using a library would abstract away these low-level operations, preventing us from accurately implementing, controlling, and analyzing the effects of these design strategies. Therefore, a manual implementation of elliptic curve operations is preferred, despite the additional complexity and potential performance overhead.

The elliptic curve implemented in all three algorithms is secp256k1, defined on a quasi-Mersenne prime $p=2^{256}-2^{32}-977$, which allows efficient modular arithmetic. Listing 1 shows the parameters defining the elliptic curve: a, b, prime p, generator point G, and scale factor k.

Listing 1. Curve secp256k1 parameters used in all experiments.

# Curve parameters p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F a = 0 b = 7 # Generator point Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798 Gy = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8 G = (Gx, Gy) # Secret scalar key k = 0x1234567890ABCDEF1234567890ABCDEF1234567890ABCDEF1234567890ABCDEF

These values allow direct and fair performance comparison of all algorithms and provide a consistent basis for side-channel analysis.

To select an appropriate sampling interval for PCM measurements, we considered both the execution time of the scalar multiplication algorithm and the number of key bits processed.

The effective interval observed in the CSV is about 0.25 ms, computed as $(t_{last}-t_{first})/(N_{rows}-1)$. Intel’s Running Average Power Limit (RAPL) interface PCM update cadence: energy and performance counters are exposed via Model-Specific Registers (MSRs) that the hardware driver updates at a fixed cadence, so user-space sampling cannot reliably exceed that refresh rate even if a finer period is requested. Second, operating-system scheduling overhead: PCM is a user-space process awakened by kernel timers; timer granularity, context switches, and competing threads that stretch the requested period. This does not affect our comparisons as all designs were recorded under identical PCM settings, and we analyze interval-normalized metrics—per-sample power and energy per operation. Consequently, the effective interval changes only the sample density, not the operation results.

The algorithm operates on a 256-bit key, requiring 256 point doublings and 128 point additions, with a total execution time of approximately 35.3 ms. To capture the effect of each individual key bit (0 or 1) in the performance metrics, we targeted at least one PCM sample per bit. Since the cost of processing a “0” bit doubling only differs from that of a “1” bit doubling plus addition, the execution time is not uniformly distributed across all 256 key bits. However, for analysis, we normalize by the key length and divide the total execution time by the number of key bits, yielding a minimum sampling interval of approximately 138 μs (0.138 ms):

$$\mathrm{Sampling}\mathrm{Interval}={\displaystyle \frac{\mathrm{Total}\mathrm{execution}\mathrm{time}}{\mathrm{Number}\mathrm{of}\mathrm{key}\mathrm{bits}}}.$$

(32)

In practice, we selected a sampling interval of 50 μs which balances resolution with manageable data size and provides sufficient detail to visualize operation patterns corresponding to the binary key.

7.3. Baseline: Standard Right-to-Left Scalar Multiplication (RtL)

The baseline implementation performs scalar multiplication using the well-known right-to-left double-and-add algorithm (RtL). Given a secret scalar K and a generator point G, the algorithm iteratively doubles and conditionally adds points based on the binary representation of K. Because the sequence of operations directly follows the scalar’s binary expansion, the resulting execution pattern leaks information about the positions of “1” bits, which can be observed in power or cache traces. This implementation serves as the reference against which our proposed improvements in randomization and side-channel resistance of subsequent designs are evaluated.

Listing 2 shows a Python code fragment for the conditional point add that depends on the value of the secret key bit being equal to “1”. The execution pattern directly follows the binary scalar, leaking key-dependent information.

Listing 2. Scalar multiplication using the right-to-left (LtR) add-and-double method.

# Standard double-and-add P = None for bit in bin(K)[2:]: P = point_double(P, a, p) if bit == "1": P = point_add(P, G, a, p)

7.4. Implementing Design #1: Permuted Scalar Multiplication

Design #1 modifies the baseline RtL algorithm by breaking the loop of Algorithm 1 or Algorithm 2 into four execution stages, as shown in Algorithm 4. The main innovation is randomly permuting the bits of K and applying the same operation on the point double array or vector $\mathbf{G}$.

Only the points corresponding to “1” bits in the permuted key are summed. The total number of additions is still determined by the scalar key; however, their positions are hidden. The decoupling of the execution order from the original bit sequence makes side-channel attacks more difficult.

Listing 3 shows the application of the same random permutations to the vectors K and G. This breaks the alignment between the actual secret key bit locations and the execution order of the point add operations. This completely prevents side-channel attack inferences.

Listing 3. Design #1 (RP) applies random permutation of K bits and G.

from random import SystemRandom # Securely permute points and bits indices = list (range (len (G_list))) SystemRandom (). shuffle (indices) G_perm = [G_ list[i] for i in indices] bits_perm = [bits [i] for i in indices]

The randomized order ensures that performance metrics such as energy consumption, cache misses, or execution cycles no longer directly reflect the original key bits. Although this randomization improves security by disrupting leakage patterns, it introduces additional computational overhead due to the cost of precomputation, storage, and shuffling.

7.5. Design #2: Windowed Double-and-Add with Permutation

Design #2 (TRP) modifies the random permutation scalar multiplication by the processing windowing strategy, in which consecutive B bits of the key are grouped. Each window precomputes a point doubling in advance, thereby reducing the number of point additions. After generating the windowed doubling vector, both the precomputed points and the associated key bits are randomly permuted, and only points corresponding to “1” bits in the permuted key are summed.

Listing 4 shows the application of the same random permutations to the vectors K and G.

Listing 4. Design #2 (TRP): truncated doubling with random permutation.

# Precompute windowed doubling vector G_list, total_len = generate_windowed_doubling_vector(G, K, n, a, p) # Permute both points and bits G_list, bits_perm, permutation = permute_lists(G_list, bits) # Sum points corresponding to “1” bits R = compute_from_L1(L1, G_list, a, p)

By combining precomputation, randomized permutation, and windowed computation, Design #2 reduces predictable patterns in performance metrics while maintaining efficient scalar multiplication. This design achieves a compromise between computational efficiency and resistance to side-channel leakage among the three implementations.

8. Results and Analysis

This section provides a more in-depth explanation of each performance and side-channel metric analyzed for the ECC designs.

8.1. Energy Consumption

Energy consumption, measured through Processor Energy and System Total Energy, represents the joules consumed by the CPU cores and the entire system. In the single-run results, the Normal baseline showed distinct spikes up to 0.030 J (processor) and 0.050 J (system), which repeated consistently across the scalar operations. These regular spikes create a strong leakage potential for power analysis. In contrast, Design 1 showed smaller and irregular spikes (0.010–0.020 J processor, 0.020–0.040 J system), while Design 2 maintained smoother values averaging 0.015–0.020 J (processor) and 0.030 J (system). Over 100 runs, the Normal implementation reinforced these repetitive patterns, with very low variance, confirming predictable leakage. Designs #1 and #2, however, produced highly variable traces from run to run, meaning that even after statistical averaging, the energy patterns could not be aligned with secret bits. This confirms that randomization effectively disrupts energy-based side-channel leakage.

8.2. Temperature and Thermal Stability

Temperature (TEMP) reflects the thermal dynamics of the CPU cores. For a single run, all three implementations showed similar cooling behaviour, decreasing from around 49 °C to 40 °C by the end of the execution. No significant differences were observed among Normal, Design #1, and Design #2. When extended to 100 runs, temperature traces became smoother but still overlapped closely across all designs. This indicates that thermal behaviour is not a useful leakage channel in this setup. The stability across runs suggests that temperature is dominated by background cooling trends rather than ECC computation differences. Side-channel attacks typically exploit differences in metrics such as cycles, energy, or cache misses that correlate with the secret key. In contrast, TEMP remains stable and uniform across all three designs, meaning attackers cannot rely on temperature traces to distinguish between key bits or implementations.

8.3. Resistance to Side-Channel Leakage

The Active CPU Cycles (ACYC) metric counts the cycles during which instructions are actively executed. In a single run, the Normal baseline showed large spikes up to 27 cycles, directly aligned with scalar operations, while Design #1 (18 cycles) and Design #2 (16 cycles) had reduced and irregular peaks. Across 100 runs, these distinctions became more apparent: the Normal case consistently reproduced its peaks, while the randomized designs varied from run to run, producing noisy averages that no longer correlated with scalar bits.

Instructions Retired (INST) and cache-related metrics (L3MISS, L3MPI) highlight how computation and memory activity expose leakage. In the single run, Normal retired bursts up to five instructions, with clear L3 cache miss spikes (0.030) and MPI values (0.006–0.007) aligned with scalar positions. Designs #1 and #2 reduced instruction bursts (3–4 and irregular 6, respectively) and distributed cache misses unpredictably. Over 100 runs, Normal preserved its repeating instruction and cache behaviour, while Designs 1 and 2 showed highly inconsistent traces that prevented alignment. This reinforces the claim that randomization mitigates cache and instruction-level leakage.

Execution efficiency metrics (IPC and EXEC), which measure how effectively instructions are executed per cycle, further highlight the trade-offs. In the single-run Normal baseline, IPC fluctuated between 0.2 and 1.2, with EXEC dropping as low as 0.15 during scalar-dependent phases. In Designs #1 and #2, IPC was stabilized between 0.8 and 1.2, with Design #2 maintaining near-constant values around 1.0–1.2 and EXEC rarely falling below 0.5. Over 100 runs, the Normal design retained its repetitive dips, while Designs #1 and #2 produced averages that smoothed out, showing consistently high IPC and EXEC. This confirms that randomization not only resists leakage but also sustains computational efficiency.

8.4. Overall Comparison

The single-run results demonstrated clear leakage in the Normal baseline, as multiple metrics (cycles, instructions, cache, and energy) showed repetitive patterns that aligned with scalar bit processing. Both Design #1 and Design #2 successfully disrupted these patterns, with Design #1 maximizing unpredictability at the cost of additional computation, and Design #2 offering a stronger balance of efficiency and security through windowed doubling. Over 100 runs, the Normal baseline became even more vulnerable, as its deterministic traces averaged into smooth, repeatable leakage patterns exploitable by attackers. On the contrary, the randomized designs preserved unpredictability, producing noisy averages that failed to reveal any scalar correlation. This demonstrates that randomization strategies remain effective even under statistical side-channel analysis, with Design #2 achieving the best trade-off between performance and resistance.

9. Experimental Evaluation

The scalar multiplication operation was expressed in terms of the two elliptic curve arithmetic operations: point addition and point doubling. These two elliptic curve arithmetic operations were in turn expressed in terms of basic field operations: modular multiplication, modular addition/subtraction, and finding the multiplicative inverse using the Extended Euclidean Algorithm (EEA).

There are three sources of delay/power randomness inherent in the scalar multiplication operation:

• The number of iterations in the EEA algorithm.
• The need to check if a reduction operation is needed after add/subtract operations.
• Random delays in wall clock, as opposed to CPU cycles, due to thread stalls and the operating system (OS) starting other processes or threads.

To eliminate the third source of random delays, a dedicated crypto accelerator is typically used, where specialized systolic arrays are used to implement modular multiplication and pipelining is used to implement EEA.

In order to reduce the effect of the first two sources of noise, multiple traces using the same key are used and the average trace is monitored. Typically any number of traces between 100 and 1000 is used. In this work we used 200 traces to find the average.

Typically ECC operations are performed on either general-purpose programmable processors or on specialized application-specific processors (ASPs). Most ASPs perform specialized applications and operations such as modular multipliers [27,28], cryptographic processors [29], and telecommunication processors [30]. Be that as it may, the area of the processor is independent of the algorithm being implemented. However, the delay is very much dependent on the algorithm implementation and the figure of merit would be the delay. The basic unit of delay in a processor is the adder speed since this determines the clock period, and hence, the clock speed. A processor with word size W bits determines the full-adder speed or delay. We take this as the unit of delay in our complexity analysis below.

The integer modular addition requires checking the sum result and there is a need to apply a reduction operation if the sum exceeds the modulo. The average delay complexity $T_{add}$ is estimated as

$$T_{add}=1.5L$$

(33)

where L is the number of words, assuming the processor word size is W and the factor 1.5 accounts for the random nature of the addition result. Here, we have L given by

$$L=⌈{\displaystyle \frac{m}{W}}⌉$$

The integer modular multiplier delay complexity $T_{mult}$ is estimated as

$$T_{mult}=1.5mL$$

(34)

where it was assumed that multiplying two m-bit integers is done using one of the systolic multipliers where multiplication and reduction operations are merged [28,31]. This design is much faster than the multiply-then-reduce approach.

The delay complexity of the extended Euclidean algorithm operation $T_{EEA}$ is estimated as

$$T_{EEA}=2(T_{add}+T_{mult})[1+0.5m]$$

(35)

where $0.5m$ is the average estimated number of iterations necessary to find the multiplicative inverse using the extended Euclidean algorithm.

Based on the above basic arithmetic complexity estimates, we can now estimate the complexities of elliptic curve point add and point double operations.

Elliptic curve point add complexity $T_{point\_add}$ is estimated as

$$T_{point\_add}=T_{EEA}+6T_{add}+3T_{mult}$$

(36)

Elliptic curve point double complexity $T_{point\_double}$ is estimated as

$$T_{point\_double}=T_{EEA}+6T_{add}+5T_{mult}$$

(37)

The typical elliptic curves in $GF\left(p\right)$ have p with number of bits varying between 192 and 521, which have similar security strengths in RSA with corresponding sizes between 1536 and 15,360 [32].

Figure 4 shows the performance of scalar multiplication for the case the key size is 512 bits for executing the RtL or RP scalar multiplication algorithms. Both curves show the same type of traces, except the RP algorithm, which shows traces that bear no relation to the actual location of the non-zero bits in the secret key K.

Figure 4a shows the average delay trace for a 512-bit key. Figure 4b shows the 512-bit key corresponding to the trace in (a). Figure 4c shows the expanded view of the average delay for the first 64 bits. Figure 4d shows the expanded view of the key for the first 64 bits.

The figure shows the delay per iteration for the RtL scalar multiplication algorithm listed in Algorithm 1. We see that the increased delay corresponds to the secret key bit of 1.

Using the same data but applying the proposed TRP Algorithm 5, we get the delay trace shown in Figure 5.

The first 512 samples correspond to the average delay trace due to performing the point double operations. The last 254 samples correspond to the average delay trace due to performing the point add operations. It is immediately apparent that distinguishing between the point double trace and the point add trace is very difficult. This is a unique feature of elliptic curves, and there are two reasons for this:

• The basic field operations in point add and point double are the same, but their number might differ slightly; c.f. Equations (36) and (37).
• There are sources of noise due to performing integer modular add/subtract operations and implementing the extended Euclidean algorithm.

Any SCA will only be able to detect that the number of non-zero secret key bits is 254. But their actual location is completely lost.

10. Discussion

We presented two ECC randomization algorithms to secure scalar multiplication against the different types of SCA. The two algorithms could be equally applied to standard secret key binary representation as well as NAF representation. An attractive feature of our two proposed designs is that they manage to provide complete immunity to SCA and at the same do not incur any extra elliptic curve operations or variables. This makes them very useful both in academia and the industry.

The two proposed algorithms completely mask the true locations of non-zero bits of the secret key such that they monitor the presence of point add operations.

Proposed design #1 (RP) still merges the point double and point add operations within the same loop. Unlike the standard RtL algorithm, however, detecting the location of the non-zero bits reveals no secret information since the secret key has been permuted and any correlation between the locations of the original secret key bits and the detected bits is completely lost. At most, the attacker can infer the number of non-zero bits. We proved that knowing this information and detecting the secret key has a vanishing probability, very much near zero.

Proposed design #2 (TRP) actually separates the point double in one loop and point add in another subsequent loop. The design eliminates the conditional point add by generating a truncated list of the non-zero bits.

Both proposed designs provide immunity to the SCA analysis and require simple control structures to effect the algorithms. The proposed algorithms also can be applied to other secret key representations such as NAF.

Delay analysis was performed to estimate the delays associated with the two operations in ECC scalar multiplication: point doubling and point adding. Simulations clearly showed that it is possible to separate point doubling from point addition and also to randomize the locations of the non-zero bits in the secret key. Therefore detecting when point addition takes place gives no information whatsoever about the true location of the secret key bit.