Spatio-Temporal Distribution of Visibility over Nigeria Using Kernel Density Estimation Techniques for Fog-Induced Attenuation
Abstract
1. Introduction
2. Methodology
2.1. Climatology of the Research Locations
2.2. Kernel Density Estimation (KDE) Techniques for Estimation of Seasonal Visibility
2.2.1. Gaussian Kernel
2.2.2. Epanechnikov Kernel
2.2.3. Triangular Kernel
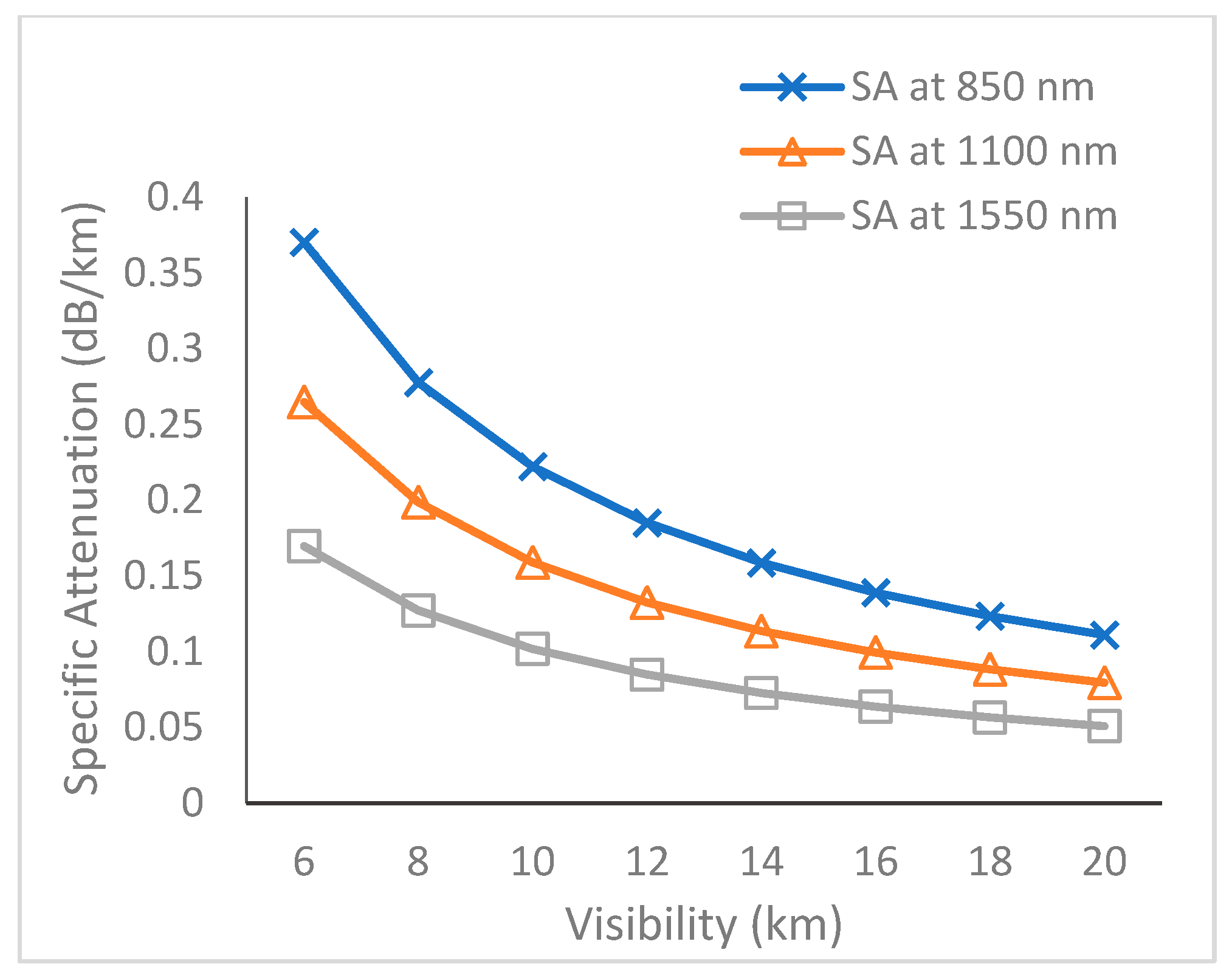
2.3. Estimation of Fog-Induced Attenuation
3. Results and Discussion
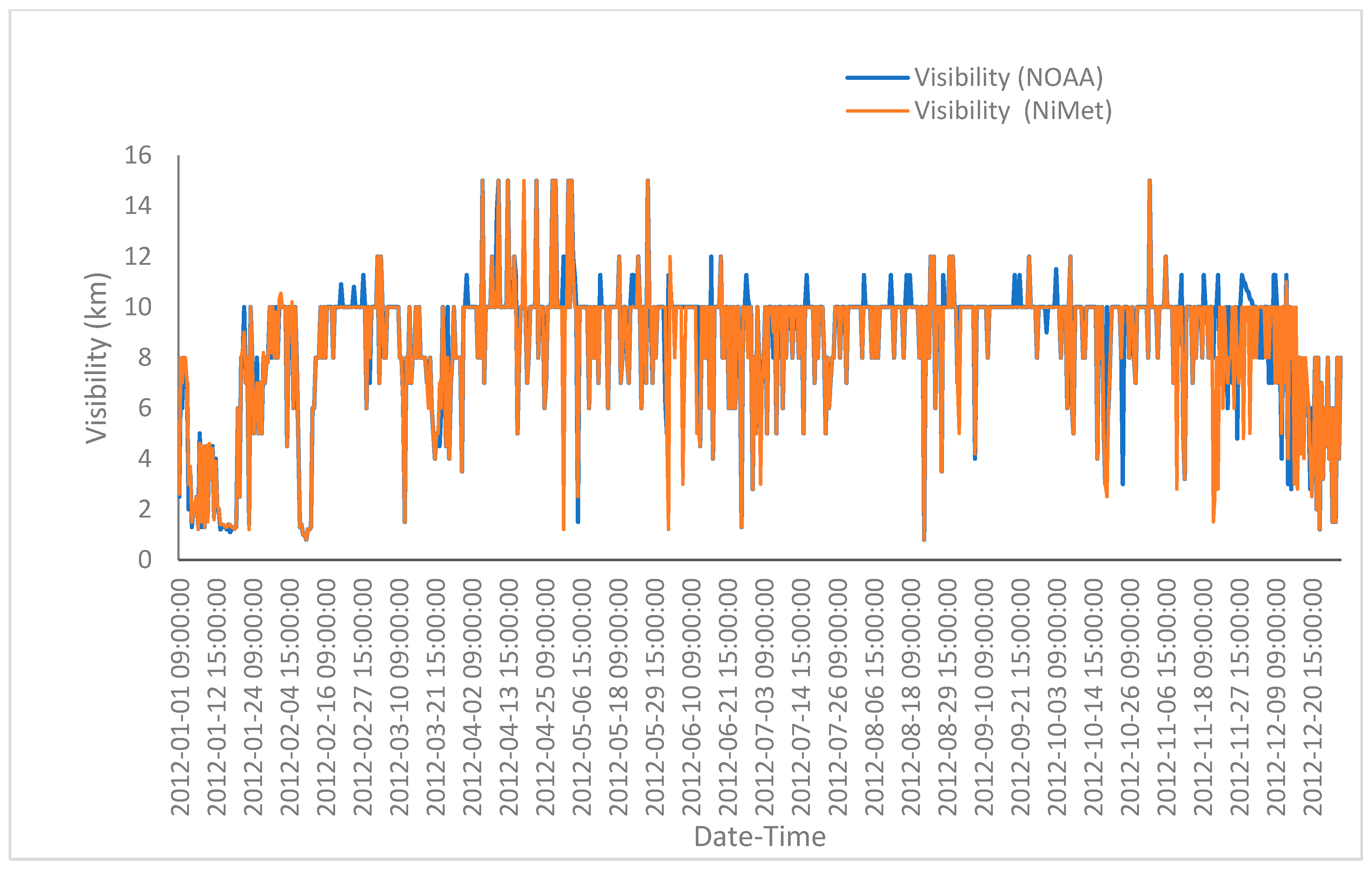
3.1. Validation of Visibility Data Retrieved from NOAA
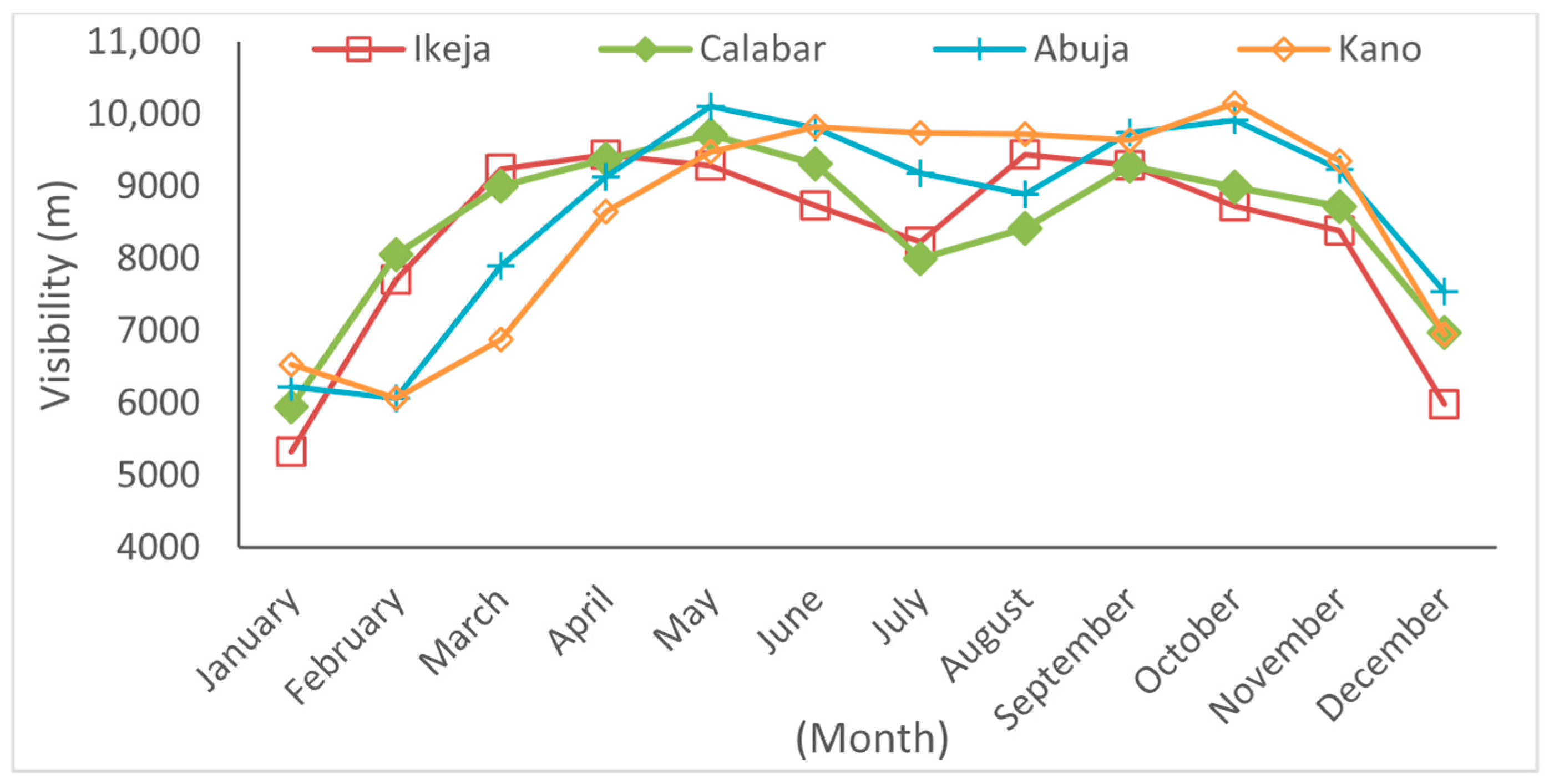
3.2. Monthly and Seasonal Variation in Visibility Across the Selected Stations
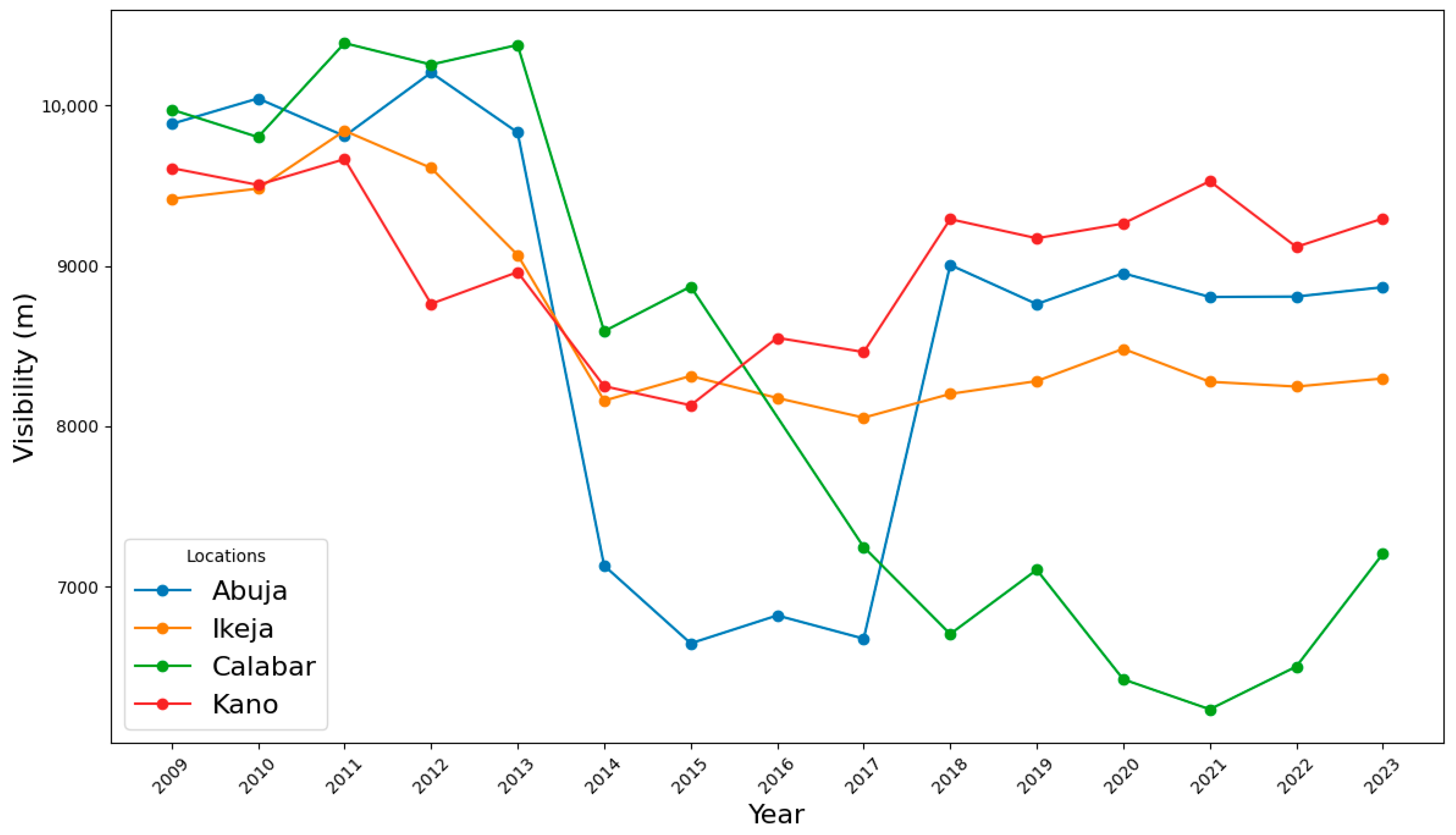
3.3. Annual Trend of Visibility Across the Study Locations
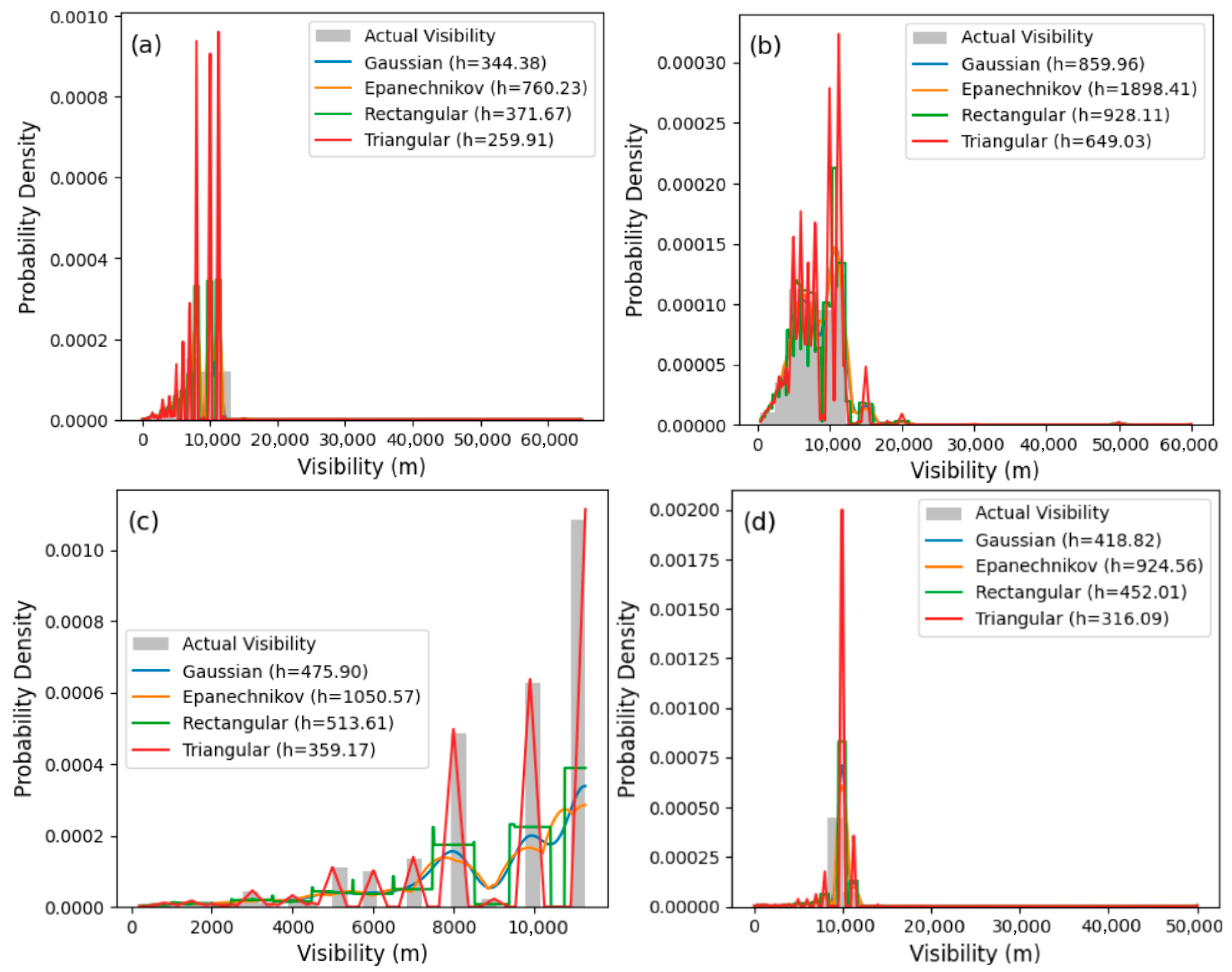
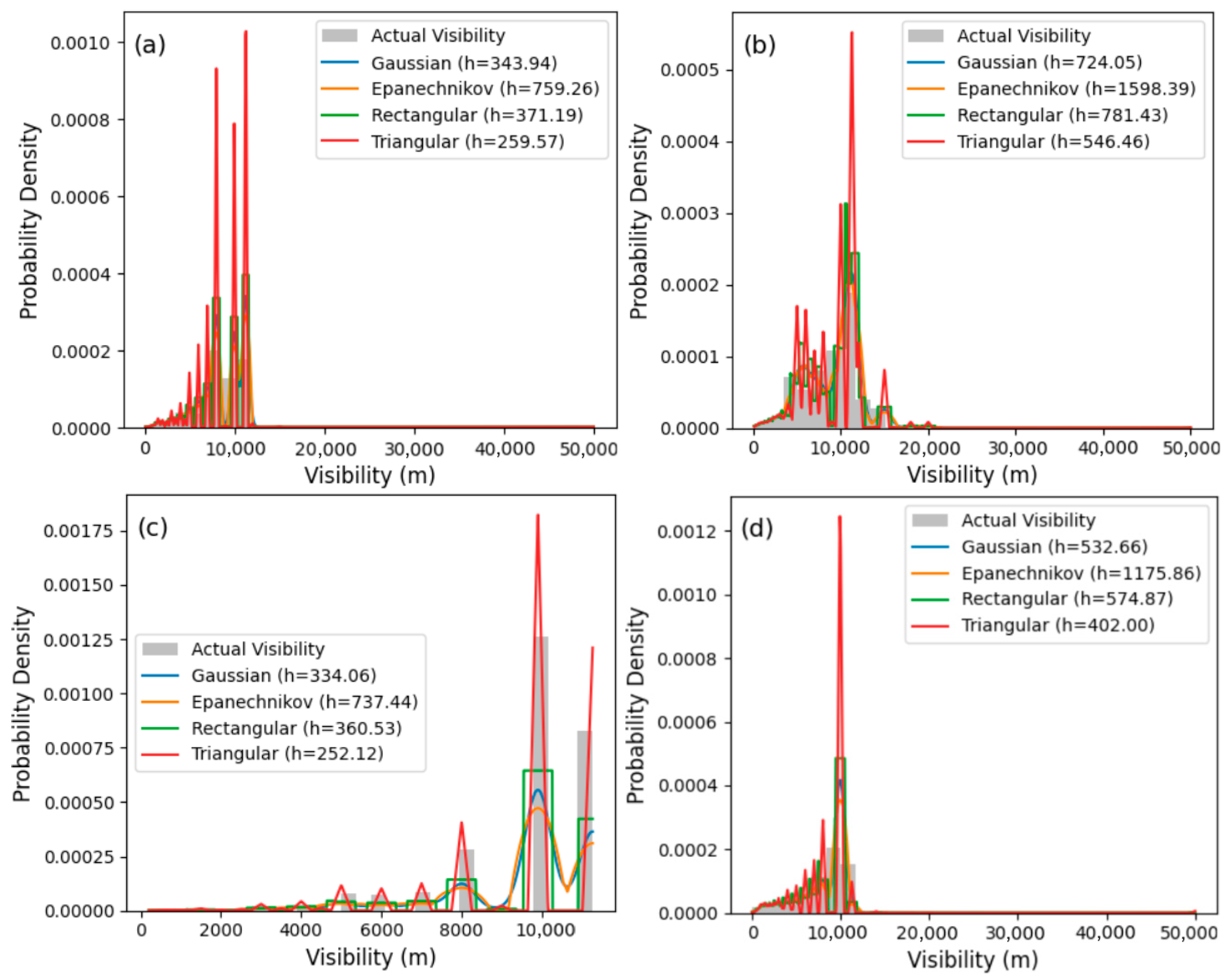
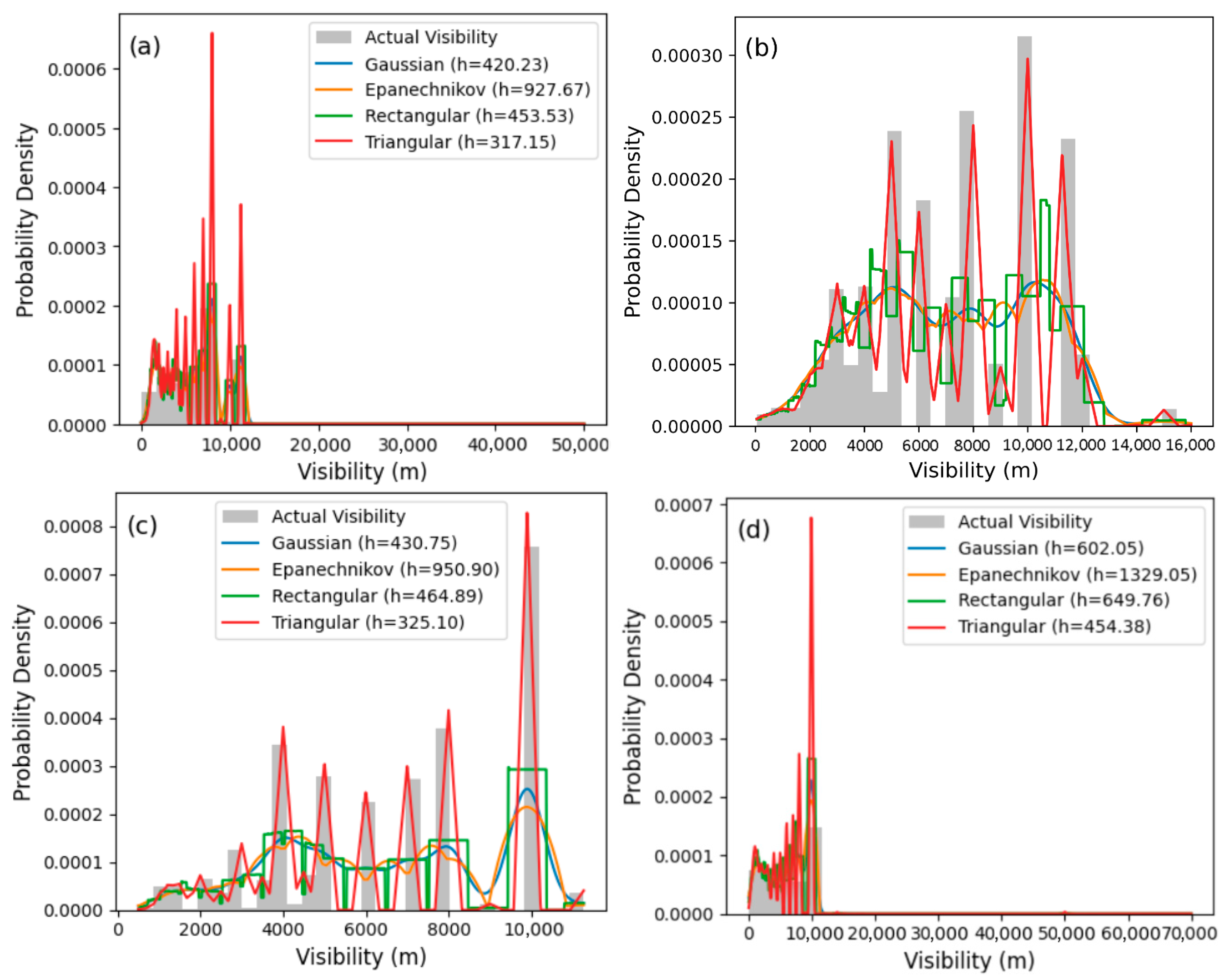
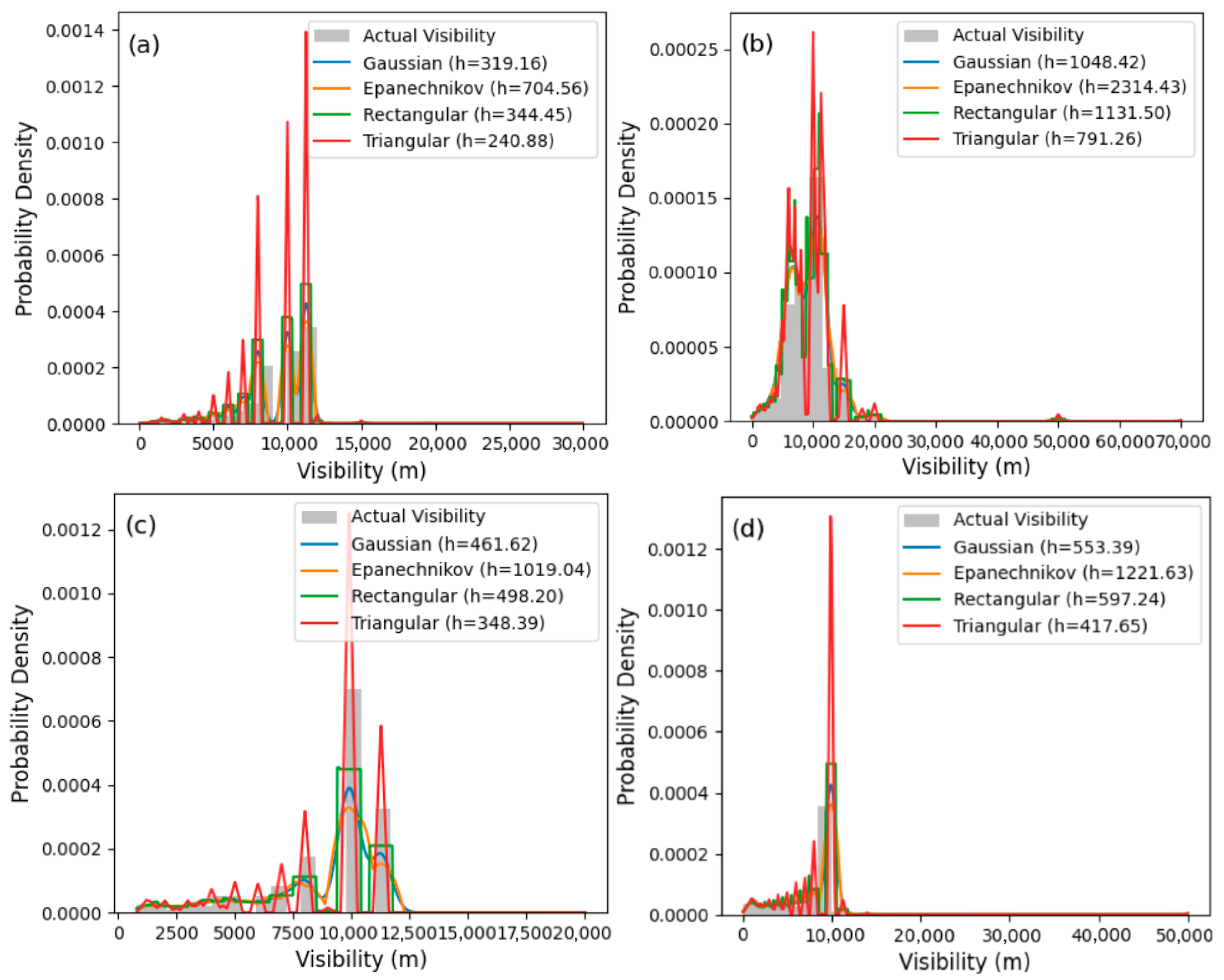
3.4. Application of KDE Techniques for the Estimation of Spatio-Temporal Distribution of Visibility
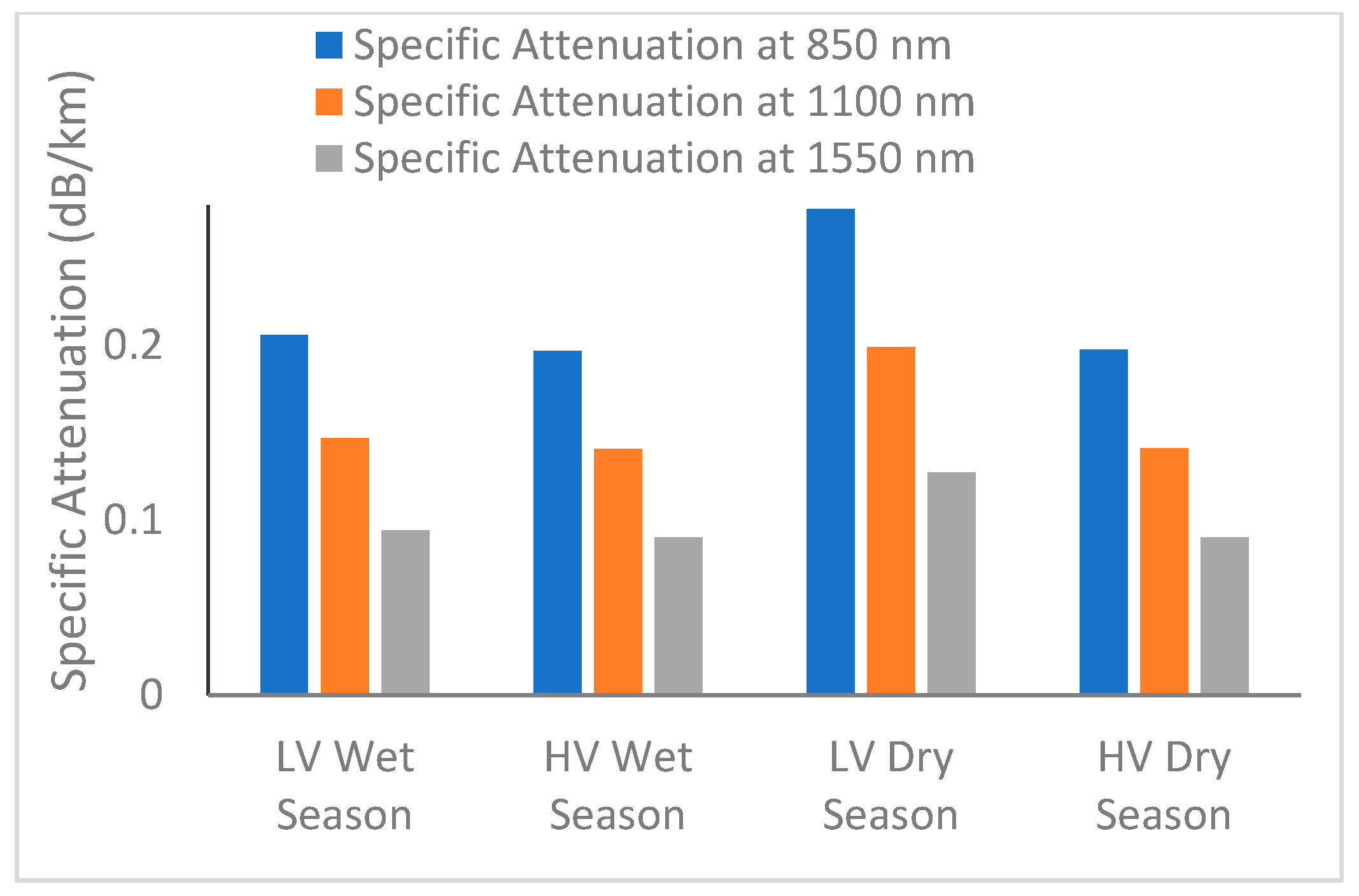
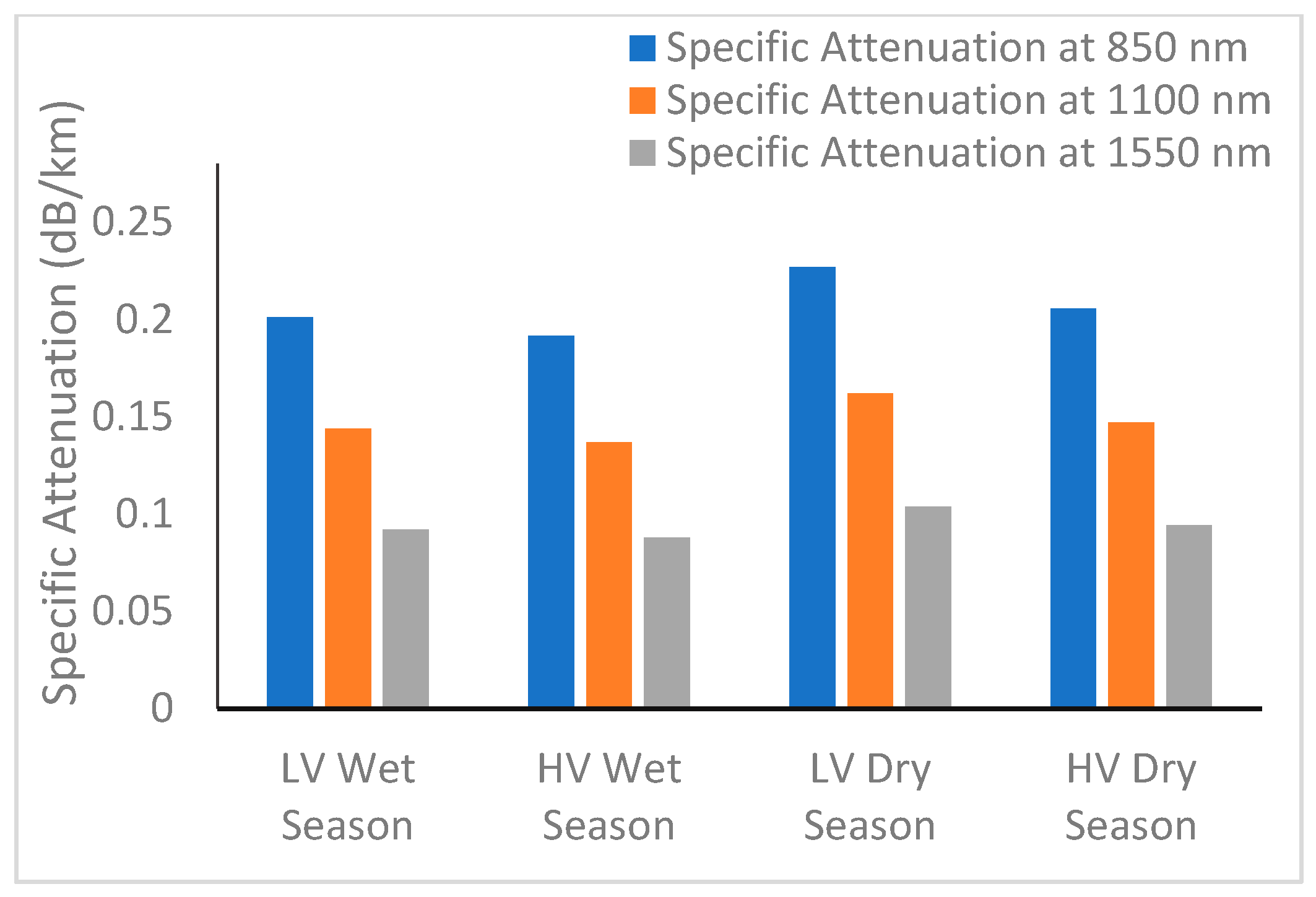
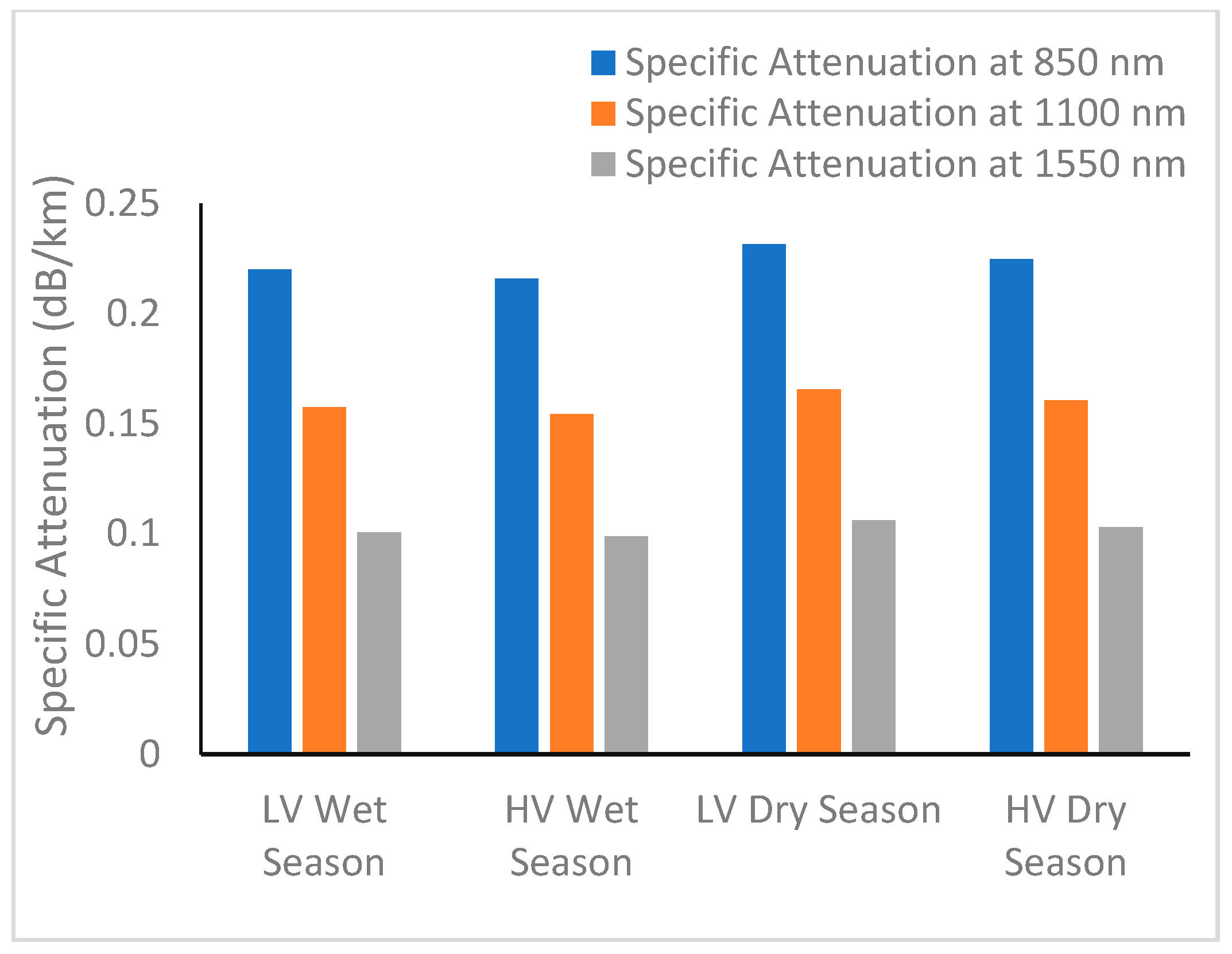
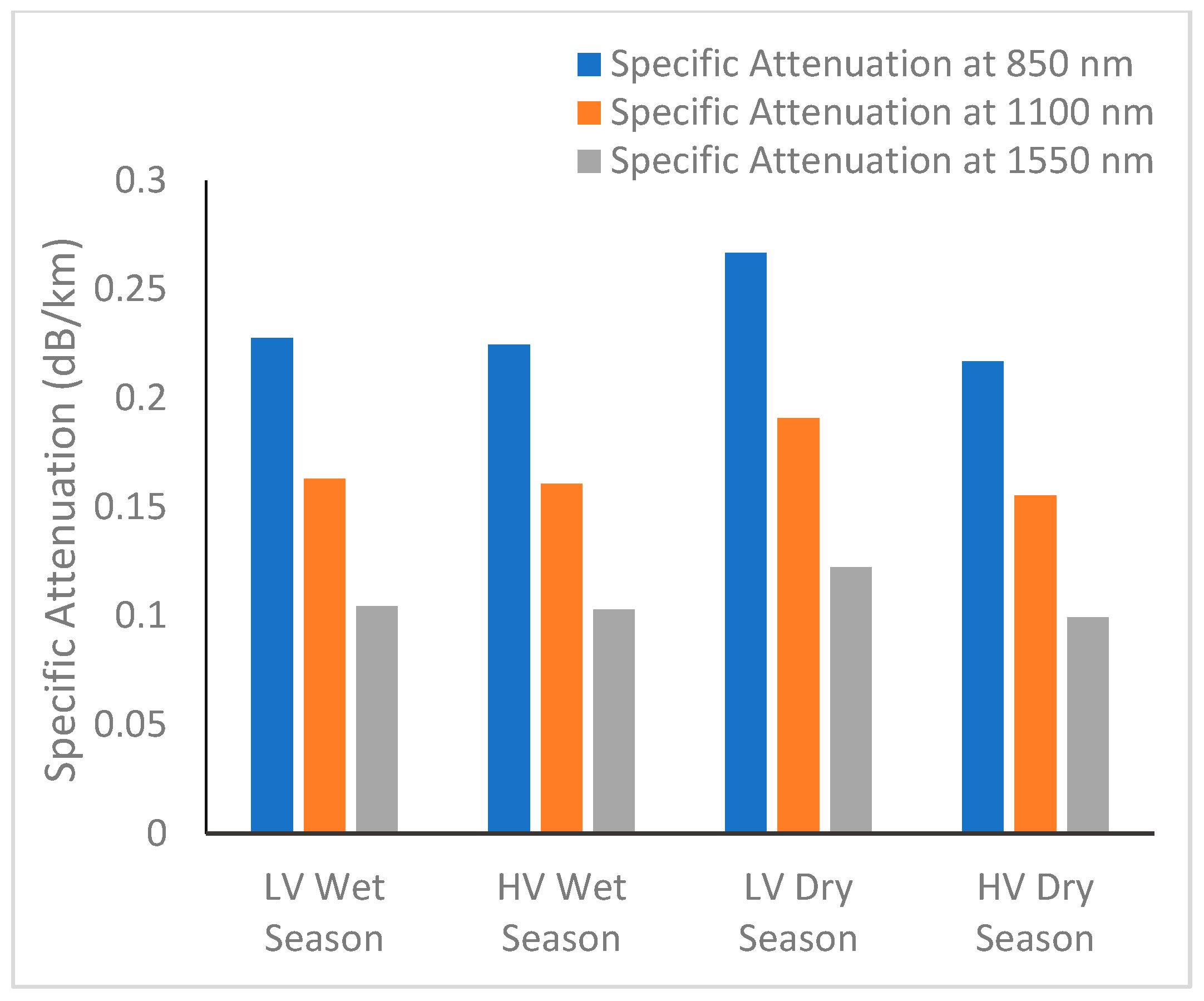
3.5. Variation in Fog-Induced Specific Attenuation with Visibility at Different Wavelengths
3.6. Estimation of Seasonal Fog-Induced Specific Attenuation for FSO Communication
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Viezee, W.; Lewis, R. Probing the Atmospheric Boundary Layer. Am. Meteorol. Soc. 1986, 44, 739. [Google Scholar] [CrossRef]
- González-Jorge, H.; Díaz-Vilariño, L.; Lorenzo, H.; Arias, P. Evaluation of driver visibility from mobile lidar data and weather conditions. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 577, 577–582. [Google Scholar] [CrossRef]
- Akanni, C.O.; Hassan, A.M.; Osuji, T. Empirical analysis of extreme weather conditions and aviation safety in Nigeria. Ethiop. J. Environ. Stud. Manag. 2016, 9, 680–690. [Google Scholar] [CrossRef]
- Balarabe, M.A.; Tan, F.; Abdullah, K.; Nawawi, M.N. Temporal-spatial variability of seasonal aerosol index and visibility—A case study of Nigeria. In Proceedings of the 2015 International Conference on Space Science and Communication (IconSpace), Langkawi, Malaysia, 10–12 August 2015; pp. 459–464. [Google Scholar] [CrossRef]
- Danlami, D.; Gwari, M.; Suleiman, S.A.; Bara, A. Temporal and spatial variations of ground surface visibility during Harmattan season in North-Eastern Nigeria. Ceylon J. Sci. 2018, 47, 337. [Google Scholar] [CrossRef]
- Koračin, D.; Dorman, C. (Eds.) Marine Fog: Challenges and Advancements in Observations, Modeling, and Forecasting; Early and Recent Observational Techniques for Fog; Springer: Berlin/Heidelberg, Germany, 2017; pp. 23–45. [Google Scholar] [CrossRef]
- David, N.; Alpert, P.; Messer, H. Novel method for fog monitoring using cellular networks infrastructures. Atmos. Meas. Tech. Discuss. 2012, 5, 5725–5752. [Google Scholar] [CrossRef]
- Nicholson, S.E. The West African Sahel: A review of recent studies on the rainfall regime and its interannual variability. ISRN Meteorol. 2013, 2013, 453521. [Google Scholar] [CrossRef]
- Kaur, S. Performance analysis of FSO link under the effect of fog in Delhi region, India. J. Opt. Commun. 2020, 44, s1385–s1393. [Google Scholar] [CrossRef]
- Nadeem, F.; Javornik, T.; Leitgeb, E.; Kvicera, V.; Kandus, G. Continental fog attenuation empirical relationship from measured visibility data. Radioengineering 2010, 19, 596–600. Available online: https://www.radioeng.cz/fulltexts/2010/10_04_596_600.pdf (accessed on 20 February 2025).
- Muhammad, S.K.; Muhammad, A.; Muhammad, S.A.; Abid, A.M.; Jawad, S.; Rahim, D. Statistical modeling of optical attenuation measurements in continental fog conditions. Opt. Eng. 2017, 56, 036113. [Google Scholar] [CrossRef]
- Verdugo, E.; Luini, L.; Riva, C.; Galzerano, G.; Resteghini, L.; da Silva Mello, L.; Nebuloni, R. Near-IR and Mid-IR wave propagation through patchy fog. In Free-Space Laser Communications XXXVI; SPIE: Bellingham, WA, USA, 2024; Volume 128771J. [Google Scholar] [CrossRef]
- Thurstain-Goodwin, M.; Unwin, D.J. Defining and delineating the central areas of towns for statistical monitoring using continuous surface representations. Trans. GIS 2000, 4, 305–317. [Google Scholar] [CrossRef]
- Lin, Y.; Chu, H.; Wu, C.; Chang, T.; Chen, C. Hotspot analysis of spatial environmental pollutants using kernel density estimation and geostatistical techniques. Int. J. Environ. Res. Public Health 2010, 8, 75–88. [Google Scholar] [CrossRef]
- Ojo, J.S.; Olaitan, J.A.; Ojo, O.L. Characterization and spatial distributions of atmospheric visibility, relative humidity, and temperature for application to optical propagation links over Nigeria. J. Opt. 2024, 53, 416–427. [Google Scholar] [CrossRef]
- Olaniran, O.J.; Sumner, G.N. A study of climatic variability in Nigeria based on the onset, retreat, and length of the rainy season. Int. J. Climatol. 1988, 9, 253–269. [Google Scholar] [CrossRef]
- Adeyemi, B.; Joerg, S. Analysis of water vapor over Nigeria using radiosonde and satellite data. J. Appl. Meteorol. Climatol. 2012, 51, 1855–1866. [Google Scholar] [CrossRef]
- Olaniran, O.J. The onset of the rainy season in Nigeria. Weather 1983, 38, 57–62. [Google Scholar]
- Adejuwon, J.O. Impact of climate variability and climate change on crop yield in Nigeria. Afr. J. Environ. Assess. Manag. 2004, 8, 1–13. [Google Scholar]
- Ogungbenro, S.B.; Morakinyo, T.E. Rainfall distribution and change detection across climatic zones in Nigeria. Weather Clim. Extrem. 2014, 5, 1–6. [Google Scholar] [CrossRef]
- Bergametti, G.; Rajot, J.; Marticorena, B.; Féron, A.; Gaimoz, C.; Chatenet, B.; Coulibaly, M.; Koné, I.; Maman, A.; Zakou, A. Rain, wind, and dust connections in the Sahel. J. Geophys. Res. Atmos. 2022, 127, e2021JD035802. [Google Scholar] [CrossRef]
- Weli, V.E.; Ohanuna, C.; Nwagbara, M.O. Atmospheric visibility and meteorological characteristics of the upper troposphere over selected cities in Nigeria. J. Climatol. Weather. Forecast. 2021, 9, 287. Available online: https://www.researchgate.net/publication/352541474_Journal_of_Climatology_Weather_Forecasting (accessed on 19 August 2025).
- Nigeria Climate Data, Nigeria Climate Information. Available online: https://en.climate-data.org/africa/nigeria-153/ (accessed on 19 August 2025).
- Altitude Maps, Find Your Altitude. Available online: https://www.altitude-maps.com/ (accessed on 24 January 2025).
- National Oceanic and Atmospheric Administration (NOAA). Atmospheric Visibility Dataset. Available online: https://www.ncei.noaa.gov/access/search/dataset-search?text=visibility (accessed on 19 December 2024).
- Cruz, M.G.; Hernández, E.A.; Uddameri, V. Climatic influences on agricultural drought risks using semiparametric kernel density estimation. Water 2020, 12, 2813. [Google Scholar] [CrossRef]
- Lawal, Y.B.; Owolawi, P.A.; Tu, C.; Van Wyk, E.; Ojo, J.S. The kernel density estimation technique for spatio-temporal distribution and mapping of rain heights over South Africa: The effects on rain-induced attenuation. Atmosphere 2024, 15, 1354. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: Boca Raton, FL, USA, 1986. [Google Scholar] [CrossRef]
- Epanechnikov, V.A. Non-parametric estimation of a multivariate probability density. Theory Probab. Its Appl. 1969, 14, 153–158. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar] [CrossRef]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; Chapman & Hall: Boca Raton, FL, USA, 1995. [Google Scholar] [CrossRef]
- Kim, I.I.; McArthur, B.; Korevaar, E. Comparison of laser beam propagation at 785 nm and 1550 nm in fog and haze for optical wireless communications. In Proceedings SPIE 4214, Optical Wireless Communications III; Spie: Bellingham, WA, USA, 2001; Volume 26. [Google Scholar] [CrossRef]
- Al Naboulsi, M.; Sizun, H.; Fornel, F. Fog attenuation prediction for optical and infrared waves. Opt. Eng. 2004, 43, 319–329. [Google Scholar] [CrossRef]
- Sharma, A.; Kaur, S. Performance evaluation and fog attenuation modelling of FSO link for hilly regions of India. Opt. Quantum Electron. 2021, 53, 697. [Google Scholar] [CrossRef]
- Fischer, K.W.; Witiw, M.R.; Baars, J.A.; Oke, T.R. Atmospheric laser communication: New challenges for applied meteorology. Bull. Am. Meteorol. Soc. 2004, 85, 725–732. [Google Scholar] [CrossRef]
- Elamassie, M.; Uysal, M. Unified atmospheric attenuation models for visible and infrared wavelengths. J. Opt. Soc. Am. A 2024, 41, 2099–2111. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Zeng, J.; Hao, S.; Fu, Y.; Ma, W.; Liu, Z. Transmission characteristics of free-space optical communication system with infrared working wavelength under complex channels. Opt. Eng. 2024, 63, 128103. [Google Scholar] [CrossRef]
- Cho, H.-J.; Kim, K.-S. Development of hazardous road fog index and its application. J. East. Asia Soc. Transp. Stud. 2005, 6, 3357–3371. [Google Scholar] [CrossRef]
- Singh, A.; Dey, S. Influence of aerosol composition on visibility in megacity Delhi. Atmos. Environ. 2012, 62, 367–373. [Google Scholar] [CrossRef]
- Shahzad, M.I.; Nichol, J.E.; Wang, J.; Campbell, J.R.; Chan, P.W. Estimating surface visibility at Hong Kong from ground-based LIDAR, sun photometer, and operational MODIS products. J. Air Waste Manag. Assoc. 2013, 63, 1098–1110. [Google Scholar] [CrossRef]
- Komeilian, H.; Bateni, S.M.; Xu, T.; Nielson, J. Estimating atmospheric visibility using synergy of MODIS data and ground-based observations. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 46–50. [Google Scholar] [CrossRef][Green Version]
- Werkmeister, A.; Lockhoff, M.; Schrempf, M.; Tohsing, K.; Liley, B.; Seckmeyer, G. Comparing satellite- to ground-based automated and manual cloud coverage observations—A case study. Atmos. Meas. Tech. 2015, 8, 2001–2013. [Google Scholar] [CrossRef]
- Distances From, Flight Distance Calculator. Available online: https://www.distancesfrom.com/Flight-Distance.aspx (accessed on 24 January 2025).
- Akpootu, D.O.; Iliyasu, M.I.; Mustapha, W.; Aruna, S.; Yusuf, S.O. The influence of meteorological parameters on atmospheric visibility over Ikeja, Nigeria. Arch. Curr. Res. Int. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Balogun, E.E. Seasonal and spatial variations in thunderstorm activity over Nigeria. J. Radio Meteorol. 1981, 36, 192–197. [Google Scholar] [CrossRef]
- Ibe, O.; Nymphas, E.F. Temperature variations and their effects on rainfall in Nigeria. In Global Warming: Engineering Solutions; Springer: Boston, MA, USA, 2009; pp. 565–578. [Google Scholar] [CrossRef]
- Falodun, S.E.; Lawal, Y.B. Investigation of non-standard refraction in a coastal area of Nigeria using radiosonde data. FUTA J. Res. Sci. 2015, 11, 358–368. Available online: https://journals.futa.edu.ng/home/paperd/1245/69/9 (accessed on 23 February 2025).
- Ihimekpen, N.I.; Ilaboya, I.R. Non-parametric Mann-Kendall test statistics for rainfall trend analysis in some selected states within the coastal region of Nigeria. J. Civ. Constr. Environ. Eng. 2018, 3, 17–28. [Google Scholar] [CrossRef]
- Balarabe, M.; Abdullah, K.; Nawawi, M. Long-term trend and seasonal variability of horizontal visibility in Nigerian troposphere. Atmosphere 2015, 6, 1462–1486. [Google Scholar] [CrossRef]
- Du, H.; Li, J.; Chen, X.; Yang, W.; Wang, Z.; Wang, Z. Quantifying the source contributions to poor atmospheric visibility in winter over the Central Plains Economic Region in China. Atmosphere 2022, 13, 2075. [Google Scholar] [CrossRef]
- Nwokocha, C.; Okujagu, C.; Enyinna, P. Meteorological variables that affect visibility degradation and their seasonal trends in the Niger Delta region of Nigeria. J. Geogr. Environ. Earth Sci. Int. 2019, 19, 1–10. [Google Scholar] [CrossRef]
- Diasso, U.H.; Abiodun, B.J. Drought modes in West Africa and how well CORDEX RCMs simulate them. Theor. Appl. Climatol. 2017, 128, 223–240. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Agutu, N.O.; Ferreira, V.G.; Getirana, A. Evolutionary drought patterns over the Sahel and their teleconnections with low frequency climate oscillations. Atmos. Res. 2020, 233, 104700. [Google Scholar] [CrossRef]
- Salami, A.A.; Olanrewaju, R.M.; Bakare, K.O.; Babatunde, O.R. Spatial distribution of rainfall in Nigeria. Arab. J. Geosci. 2025, 18, 29. [Google Scholar] [CrossRef]
- Ochei, M.C.; Adenola, E. Variability of Harmattan dust haze over northern Nigeria. J. Pollut. 2018, 1, 107. Available online: https://www.hilarispublisher.com/open-access/variability-of-harmattan-dust-haze-over-northern-nigeria.pdf (accessed on 3 March 2025).
- Ghoumid, M.; Ahmed, M.M.; Lbath, M. Optimization analysis of average message delivery time for healthcare monitoring using a developed NB-IoT technology in a smart city. Internet Things 2024, 27, 101290. [Google Scholar] [CrossRef]
| Station | Geoclimatic Zone | Lat (°E) | Lon (°N) | Elevation (m) | Annual Rainfall (mm) | Temperature Range (°C) |
|---|---|---|---|---|---|---|
| Ikeja | Tropical Coastal | 6.6018 | 3.351 | 35 | 1500–2000 | 22–33 |
| Calabar | Tropical Coastal | 4.975 | 8.341 | 32 | >3000 | 23–31 |
| Abuja | Midland Savannah | 9.056 | 7.498 | 840 | 1200–1500 | 19–37 |
| Kano | Sahel Savannah | 12.002 | 8.5919 | 469 | 600–1000 | 18–41 |
| Sub-Season | Months | Remarks | |
|---|---|---|---|
| 1 | Low-Visibility Wet Season | Jun–Aug | Caused by high humidity, water vapor content, and cloud cover |
| 2 | High-Visibility Wet Season | Sep–Nov | |
| 3 | Low-Visibility Dry Season | Dec–Feb | Caused by Harmattan, dust, and particulate matter |
| 4 | High-Visibility Dry Season | Mar–May |
| Weather Condition | Visibility (m) |
|---|---|
| Dense fog | <40 |
| Thick fog | 40–200 |
| Moderate fog | 200–770 |
| Light fog | 770–1000 |
| Mist | 1000–2000 |
| Haze | 2000–4000 |
| Poor Visibility | 4000–10,000 |
| Good Visibility | 10,000–40,000 |
| Excellent Visibility | >40,000 |
| Station | Season | Gaussian | Epanechnikov | Rectangular | Triangular | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h | Vis (m) | ISE (E-5) | h | Vis (m) | ISE (E-5) | h | Vis (m) | ISE (E-5) | h | Vis (m) | ISE (E-5) | ||
| Ikeja | LV Wet | 344.37 | 10,800 | 1.4 | 371.66 | 10,800 | 1.6 | 760.22 | 10,800 | 0.9 | 259.9 | 10,800 | 0.4 |
| HV Wet | 343.93 | 11,288 | 1.7 | 371.19 | 11,288 | 2.3 | 759.25 | 11,288 | 1.5 | 259.57 | 11,288 | 1 | |
| LV Dry | 420.22 | 8008 | 0.9 | 453.52 | 8008 | 1.1 | 927.67 | 8008 | 0.8 | 317.15 | 8008 | 0.3 | |
| HV Dry | 319.16 | 11,261 | 1.1 | 344.45 | 11,261 | 1.3 | 704.56 | 11,261 | 0.8 | 240.87 | 11,261 | 0.2 | |
| Calabar | LV Wet | 859.96 | 11,058 | 0.7 | 1898.41 | 11,058 | 0.9 | 928.11 | 11,058 | 0.4 | 649.03 | 11,058 | 0.6 |
| HV Wet | 724.06 | 11,600 | 0.8 | 1598.39 | 11,600 | 1.2 | 781.43 | 11,600 | 0.7 | 546.46 | 11,600 | 0.3 | |
| LV Dry | 738.61 | 9800 | 0.4 | 1630.53 | 9800 | 0.8 | 797.15 | 9800 | 0.9 | 557.45 | 9800 | 1.3 | |
| HV Dry | 1048.4 | 10,020 | 2.2 | 2314.42 | 10,020 | 0.7 | 1131.48 | 10,020 | 1.1 | 791.26 | 10,020 | 0.6 | |
| Abuja | LV Wet | 475.88 | 11,252 | 0.7 | 1050.57 | 11,252 | 0.9 | 513.61 | 11,252 | 0.5 | 359.17 | 11,252 | 0.4 |
| HV Wet | 334.06 | 9902 | 1.7 | 737.44 | 9902 | 2.4 | 360.53 | 9902 | 1.4 | 252.12 | 9902 | 0.8 | |
| LV Dry | 430.75 | 9850 | 1.2 | 950.9 | 9850 | 1.5 | 464.88 | 9850 | 0.9 | 325.22 | 9850 | 0.4 | |
| HV Dry | 461.62 | 9890 | 1.1 | 1019.04 | 9890 | 1.7 | 498.18 | 9890 | 1 | 348.4 | 9890 | 0.5 | |
| Kano | LV Wet | 418.82 | 9850 | 1.7 | 924.56 | 9850 | 2.1 | 452 | 9850 | 1.4 | 316.1 | 9850 | 0.7 |
| HV Wet | 532.65 | 9900 | 1.4 | 1175.86 | 9900 | 1.8 | 574.86 | 9900 | 1.1 | 402 | 9900 | 0.9 | |
| LV Dry | 602.05 | 9800 | 2.1 | 1329.05 | 9800 | 2.5 | 649.76 | 9800 | 1.8 | 454.38 | 9800 | 1.3 | |
| HV Dry | 553.38 | 9899 | 1.9 | 1221.63 | 9899 | 2.4 | 597.24 | 9899 | 1.5 | 417.67 | 9899 | 1.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawal, Y.B.; Owolawi, P.A.; Tu, C.; Ojo, J.S.; Ojo, O.L.; Sodunke, M.A. Spatio-Temporal Distribution of Visibility over Nigeria Using Kernel Density Estimation Techniques for Fog-Induced Attenuation. Telecom 2025, 6, 62. https://doi.org/10.3390/telecom6030062
Lawal YB, Owolawi PA, Tu C, Ojo JS, Ojo OL, Sodunke MA. Spatio-Temporal Distribution of Visibility over Nigeria Using Kernel Density Estimation Techniques for Fog-Induced Attenuation. Telecom. 2025; 6(3):62. https://doi.org/10.3390/telecom6030062
Chicago/Turabian StyleLawal, Yusuf Babatunde, Pius Adewale Owolawi, Chunling Tu, Joseph Sunday Ojo, Olakunle Lawrence Ojo, and Mobolaji Aduramo Sodunke. 2025. "Spatio-Temporal Distribution of Visibility over Nigeria Using Kernel Density Estimation Techniques for Fog-Induced Attenuation" Telecom 6, no. 3: 62. https://doi.org/10.3390/telecom6030062
APA StyleLawal, Y. B., Owolawi, P. A., Tu, C., Ojo, J. S., Ojo, O. L., & Sodunke, M. A. (2025). Spatio-Temporal Distribution of Visibility over Nigeria Using Kernel Density Estimation Techniques for Fog-Induced Attenuation. Telecom, 6(3), 62. https://doi.org/10.3390/telecom6030062





