Optimizing Weighted Fair Queuing with Deep Reinforcement Learning for Dynamic Bandwidth Allocation

Abstract

The rapid growth of high-quality telecommunications demands enhanced queueing system performance. Traditional bandwidth distribution often struggles to adapt to dynamic changes, network conditions, and erratic traffic patterns. Internet traffic fluctuates over time, causing resource underutilization. To address these challenges, this paper proposes a new adaptive algorithm called Weighted Fair Queues continual Deep Reinforcement Learning (WFQ continual-DRL), which integrates the advanced deep reinforcement learning Soft Actor-Critic (SAC) algorithm with the Elastic Weight Consolidation (EWC) approach. This technique is designed to overcome neural networks’ catastrophic forgetting, thereby enhancing network routers’ dynamic bandwidth allocation. The agent is trained to allocate bandwidth weights for multiple queues dynamically by interacting with the environment to observe queue lengths. The performance of the proposed adaptive algorithm was evaluated for eight queues until it expanded to twelve-queue systems. The model achieved higher cumulative rewards as compared to previous studies, indicating improved overall performance. The values of the Mean Squared Error (MSE) and Mean Absolute Error (MAE) decreased, suggesting effectively optimized bandwidth allocation. Reducing Root Mean Square Error (RMSE) indicated improved prediction accuracy and enhanced fairness computed by Jain’s index. The proposed algorithm was validated by employing real-world network traffic data, ensuring a robust model under dynamic queuing requirements.

1. Introduction

In recent years, the demand for high-speed data transmission, efficient resource management, and network communication has undergone a significant rise due to the rapid growth in the numbers of connected devices and data-intensive applications, leading to efforts to improve the performance of data transmission queueing systems and giving rise to congestion, latency, and dynamic bandwidth allocation challenges [1]. Due to the conflict between the growth in traffic and the constraints on bandwidth, it is crucial to utilize bandwidth resources efficiently to enhance the Quality of Service (QoS) [2]. Modern networks rely on advanced scheduling algorithms and optimized queueing mechanisms to address these issues, support performance, and ensure fair resource distribution. As networks evolve, achieving scalability, flexibility, and reliability remains an important goal for researchers and industry professionals [3]. Unfair resource allocation can lead to resource waste, starvation, or redundancy [4].

A system that allows devices to communicate and exchange data efficiently is known as a network. Networks vary in size and design, ranging from Local Area Networks (LANs) to Wide Area Networks (WANs). Routers serve as key components of network communication as they direct data packets between networks. Through network communication, routers manage traffic using queueing systems, which control how packets are processed and transmitted [5]. A queuing system is essential for handling varying traffic loads, reducing congestion, and ensuring smooth data flows. Different models, such as M/M/1, M/M/c, and G/G/1, determine how packets arrive, wait, and are then served in network queues. These models can optimize performance and reduce delays, thus supporting the design of efficient traffic management strategies [6].

Scheduling algorithms are implemented in routers to efficiently manage packets in queues [3]. These algorithms determine the packet processing order and aim to strike a balance between fairness and efficiency. Basic scheduling methods, such as First-In-First-Out (FIFO), process packets consecutively, whereas Priority Queuing (PQ) prioritizes essential traffic, such as real-time voice or video data. More advanced approaches, such as Weighted Fair Queuing (WFQ) [2,3] and Deficit Round Robin (DRR), ensure proportionate bandwidth allocation among traffic classes. These are crucial in achieving the desired QoS, optimizing bandwidth usage, and improving network reliability [3]. Reinforcement Learning (RL) is commonly used in resource allocation to optimize decision-making in dynamic and unsteady environments. Reinforcement learning-based resource allocation enables the efficient distribution of bandwidth, computing resources, scheduling priorities, and networking [1,4,7].

According to the aim of this paper, while effective in ensuring fair bandwidth distribution, traditional Weighted Fair Queuing (WFQ) systems struggle to adapt dynamically to varying network traffic patterns, such as bursty or periodic flows. Due to its adaptive learning capabilities, deep Reinforcement Learning (DRL) has become a profitable solution for dynamic bandwidth allocation. Regardless, typical DRL models suffer from catastrophic forgetting when exposed to new traffic scenarios, requiring frequent retraining. This limits scalability and robustness in real-time networking environments. Thus, there is a critical requirement to enhance DRL-based WFQ systems with continual learning mechanisms that can retain earlier obtained scheduling policies while adapting to new network conditions efficiently and without forgetting, therefore enabling a more intelligent and scalable bandwidth allocation strategy.

The remainder of this paper is organized as follows: Section 2 includes related work, Section 3 produces a contribution of this research, Section 4 describes a methodology for the proposed system model. Section 5 provides the results and analysis. Section 6 discusses the model parameters and the results. Section 7 includes the conclusions.

2. Related Work

Various scheduling disciplines are available for managing separate queues while maintaining fairness and balance in terms of Quality of Service (QoS). In communication networks, WFQ is a crucial scheduling discipline used to ensure fairness and QoS. Using a weight-based bandwidth allocation approach, WFQ assigns weights to various queues based on packet length, thereby ensuring equitable distribution of bandwidth [8]. A technique called PQ, which prioritizes the queue order, often causes resource starvation for lower-priority queues by serving the highest-priority option among non-empty queues. Simulation results show that PQ has a smaller memory queue size than WFQ and FIFO, and a more significant delay [9]. Scheduling disciplines such as WFQ cannot dynamically allocate bandwidth and must learn about the status of queues. The WFQ method has been extensively studied in the literature, with a focus on performance evaluation. Several metrics are typically used with the WFQ system, including the mean queue length, system throughput, and mean response time. It would be interesting to compare the performance of a WFQ system with a finite buffer to that of a WFQ system with an infinite buffer [10].

The authors of [3] presented mechanisms and approaches to implementing QoS services in packet networks and created and examined a network model that facilitated data transfer associated with various traffic classes. Traffic shaping techniques based on the WFQ method were utilized for QoS. In individual work, the study in [11] thoroughly investigated traffic scheduling in IPv4 and IPv6 networks for multimedia applications, examining the effectiveness of various scheduling methods for different types of traffic, including HTTP and FTP. Among the different approaches considered (WFQ, FIFO, PQ), WFQ was found to be the best option in terms of its improved performance over the other algorithms, as it offered suitable outcomes over both IPv4 and IPv6. In [12], a packet-scheduling technique was developed that combined WFQ with PQ to decrease latency, significantly improving network performance compared to scenarios where packet scheduling was not employed. By accounting for the extra waiting periods caused by variations in arrival rates, the proposed model was able to lower the estimation error. Even when traffic utilizes the exact network channel or session, it is necessary to consider a complex mix of network and application traffic. The authors also proposed an approximate analytical technique for this purpose. In these research works, specified weights were allocated based on traffic class or priority due to the absence of adaptability to real-time network requirements.

In [13], the QoS performance of the WFQ algorithm was investigated and evaluated, and various QoS results were examined. The average throughput, packet arrival ratio, packet loss ratio, and average latency were calculated. The study in [14] considered QoS factors such as jitter, delay, and packet loss probability and evaluated these for algorithms using PQ, FIFO, custom queuing, fair queueing, and WFQ. Given that PQ is usually regarded as the least efficient choice, it is recommended to employ it sparingly in situations where there is little chance of channel erasure [15]. The simulation referenced the approximation terms presented by Mahmood and Horvath for the mean response times in a two-class (ideal) WFQ system with a Poisson arrival process and exponentially distributed service times. The approximation is usually based on an arithmetical approach, and some decisions on how to approximate the behavior occasionally appear to be made ad hoc [16]. These approaches described above rely on predefined controls for resource allocation, which may limit their ability to adapt dynamically to unexpected changes in traffic patterns. Furthermore, these approaches may face challenges in regard to optimizing real-time performance compared to techniques that leverage predictive analysis and adaptive learning.

Studies have been conducted on the application of reinforcement learning (RL) to queueing systems. This research field can be categorized further based on the RL techniques used; for example, in model-based RL, a specific queueing network model is considered to optimize the network’s performance, and the focus is on the use of RL techniques and managing these limitations by exploring the effectiveness of this approach in other network architectures [17]. The authors propose a DRL-based AQM, Learning Fair Queue (LFQ), that dynamically adapts per-flow buffer sizes using a neural network. It addresses the challenge of managing real-time queues for diverse traffic conditions. Results display enhanced throughput fairness and lower latency compared to traditional AQMs [18]. The author presented a Deep Q-Network (DQN) algorithm employed for smart queue management. The procedure includes simulating traffic scenarios with two types of protocols, UDP and TCP, using a neural network. Specifically, the DQN agent can select to increase, decrease, or preserve weights for diverse classes of traffic: Gold, Silver, and Bronze. The outcomes show that the DQN agent can effectively manage the weights for the traffic flows. The average reward stabilizes positively, showing convergence after approximately 1500 training episodes [19]. The authors of [20] outlined the use of a Deep Deterministic Policy Gradient (DDPG) algorithm to reduce the service rate and provide a probabilistic latency guarantee, finding that the proposed method offered probabilistic upper bounds on the system’s end-to-end delay. This approach is more challenging than standard practice control methods, which only consider average performance metrics such as the mean delay. In the study in [21], a WFQ system achieved a reduction in the packet loss rate by utilizing a SAC technique, although this scheme did not account for latency. The solution in [22] employed deep RL (DRL) techniques for dynamic bandwidth allocation in WFQ routers. Specifically, it emphasized the application of algorithms such as DDPG and SAC to handle bandwidth allocation across multiple queues, with the goal of minimizing packet loss, reducing the average queue length, and decreasing the average delay.

3. Research Contributions

This paper contributes to the formulation of a G/G/1/K parallel queuing system by developing the WFQ continual DRL framework. The proposed approach integrates DRL with continual learning to enhance bandwidth utilization in the WFQ algorithm. The model ensures fairness by dynamically adapting allocations. Continual learning is represented by Elastic Weight Consolidation (EWC), a technique that protects the important parameters of a neural network when the model is trained on new tasks. The system continuously learns and adjusts according to network demands and objectives, thereby maximizing the cumulative reward. In addition, continual learning reduces the retraining overhead, making the model more efficient in dynamic environments compared to traditional DRL-based approaches, as demonstrated in this paper. It uses EWC to mitigate catastrophic forgetting, enabling real-time adaptation. In comparison to existing literature, this work proposes a reinforcement learning method to optimize QoS by adjusting actions based on the queue state, such as packet loss or transmission decisions. While effective, its approach is limited to static traffic environments, and the service rates chosen are such that the system stays stable, does not get congested, and lacks mechanisms for long-term adaption while network conditions grow [20]. Also, the paper [22] proposes using DRL to allocate bandwidth dynamically across WFQ queues, improving performance under varying traffic loads. Still, it does not consider the need for continual adaptation or knowledge retention when system configurations of queue length.

This paper presents an adaptive algorithm that integrates DRL with EWC to support continual learning across varying network conditions. This approach handles adaptive bandwidth allocation under WFQ. It maintains previously obtained knowledge, providing stability and reducing catastrophic forgetting as the number of queues increases, which leads to faster convergence and makes it more suitable for real-time and complex network scenarios where traffic dynamics evolve over time. The main contribution of the proposed approach can be illustrated as described below:

• The proposed model improves performance by integrating the SAC algorithm with EWC, enabling continual learning within the WFQ scheduling framework. Through integration, the system can handle dynamic traffic patterns, such as bursty or periodic flows, without forgetting previously learned scheduling policies, ensuring adaptability to new scenarios without frequent retraining.
• The approach dynamically learns optimal bandwidth allocation across multi-queue systems in WFQ in real-time, adapting to high traffic and queue length variations.
• EWC enables the agent to retain previously learned policies while learning new ones, eliminating the need to reprocess old data. This helps system stability and scalability in evolving network environments, particularly when facing unpredictable traffic patterns.
• By integrating SAC and EWC within the WFQ scheduling algorithm, the model achieves efficient resource allocation and robustness to changing network requirements. That helps fair queuing and constant performance across varying traffic scenarios.
• The new adaptive algorithm ensures high performance while increasing the queues, allowing the system to maximize performance.
• A real traffic network dataset provides a more realistic and complex testbed, capturing burstiness, and variability across multiple queues.

4. Proposed Model

4.1. Model Definition

Using the WFQ discipline as a scheduling algorithm, the information system can be described as a G/G/1/K parallel queueing system [22], where routers are modeled as such. Differential arrival flows arrive at each queue independently and are then sent at a rate determined by the appropriate bandwidth allocation. The arrival rates and patterns of incoming packets are erratic and change over time, whereas the router’s overall bandwidth resources are constant. To enhance the system’s performance, allocating limited bandwidth resources across queues with varying arrival attributes is crucial. The proposed system consists of n G/G/1/K queueing systems that share standard bandwidths in parallel, as shown in Figure 1.

In this study, it is assumed that the packets enter a matching buffer to wait for service after arriving at the system via a process with commonly dispersed interarrival periods, where $\lambda i$ represents the flow and $i$ is the arrival rate. The flow $i$ locates service times for packets from the associated buffer broadly and dispersedly. The service rate is ${\mathit{\mu }}_{\mathit{i}}=w_{\mathit{i}}\times b$, where b is the system’s total bandwidth and $w_{\mathit{i}}$ is the server’s allocated weight. $K_{\mathit{i}}$ is the buffer size for the queue_i. If the buffer is full, newly arriving packets will be discarded. The goal is to find a control policy that can effectively decrease the average latency and packet loss rate in a WFQ system.

4.2. Continual Learning

Continual learning, also known as incremental learning or lifelong learning, enables an agent, such as an artificial intelligence model, to continuously acquire new skills or knowledge while retaining previously learned information. A problem known as ‘catastrophic forgetting’ occurs when a model updates its parameters to learn a new task and, in doing so, loses its ability to perform the previously learned tasks effectively. It also refers to the process by which the human brain learns and retains information. In humans, the neocortex is believed to have mechanisms that enable the integration of new information without erasing old memories. This biological principle is a key aspect when learning languages or playing musical instruments, where new skills must coexist with existing knowledge [23].

4.3. Continual Learning in a Reinforcement Learning Field

RL is a type of machine learning that enables machines to make decisions. An agent learns to make decisions by interacting with an environment and receives rewards or penalties based on its actions, allowing it to learn optimal behaviors through trial and error. The goal is to learn a policy that maximizes cumulative rewards over time. An example of RL is the SAC algorithm, which utilizes a maximum entropy framework. This algorithm learns stochastic policies through an objective that maximizes both the expected reward and the policy’s entropy, thereby encouraging exploration [24]. To utilize the RL domain to address a more comprehensive set of conditions needed for successful continual learning systems, EWC can be used to retain previously acquired knowledge. In particular, higher-level mechanisms are needed to infer which task is currently being performed, to notice and incorporate new tasks as they are encountered, and to allow for rapid and elastic switching between tasks [23]. SAC is particularly effective for queueing and network scheduling tasks [22], as opposed to other algorithms such as Proximal Policy Optimization (PPO) and Twin Delayed Deep Deterministic Policy Gradient (TD3), because it balances sample efficiency, exploration, exploitation, and stability, which are essential in dynamic environments. Unlike PPO, which is an on-policy method requiring more data and computational resources, SAC’s off-policy procedure enables faster learning from fewer samples, which is essential for real-time queue management, where quick adaptation is crucial. Compared to TD3, SAC incorporates entropy maximization, enabling better exploration that can arise from early convergence, a common problem in non-stationary traffic scenarios. Regarding toTD3, it employs deterministic policies, which can result in insufficient exploration, particularly in dynamic or non-stationary environments, such as varying network traffic [25].

4.4. Continual Reinforcement Learning Framework for WFQ

The process allocates bandwidth weights in the WFQ system, which operates under a control policy that takes into consideration the system’s dynamic nature. The interaction between the algorithm and multi-queue systems is shown in Figure 2.

After observing the system’s status, represented in the form of queue lengths, the agent decides to allocate bandwidth weights as an action. Until the next decision is taken, the queueing system will use the allocated bandwidth and send rewards back to the agent, allowing it to adjust its policy accordingly. This study focuses on dynamic control and slot dependence, where the decision time is t seconds. Since the state may vary significantly within a specific time slot, it is more practical to implement it in the engineering field, but this also makes it more challenging to determine the optimal policy. By integrating continual learning with DRL, the agent learns optimal policies, retains knowledge from past experiences, and adapts to evolving network conditions without catastrophic forgetting. This approach enables the system to efficiently generalize across different traffic patterns, thus reducing the need for comprehensive retraining. A continual RL-based agent can enhance bandwidth allocation over time by leveraging past knowledge while adapting to previously unnoticed traffic behaviors, leading to optimal stability, scalability, and long-term performance in dynamic networks.

For a continuous state space and a continuous action space, the continual DRL situations are as follows:

State: $q_{\mathit{i}}$ is defined as the number of packets that are either serviced by the server i or are waiting in ${queue}_{\mathit{i}}$. $q_{\mathit{i}}=\left(q_1,q_2,...,q_{\mathit{n}}\right),i=1, 2,..., n$ also represents the state of the system. As it captures queue lengths, the continual DRL method is practical for use in telecommunications networks. If we assume $q_{\mathit{i}}\le K_{\mathit{i}}$, then each queue has a limited buffer. $s=\left\{q=\left(q_1,q_2,...,q_{\mathit{n}}\right)\in N_{\mathit{n}}:q_{\mathit{i}}\le K_{\mathit{i}}\right\}$ represents the state space. However, this is enhanced with historical states, thus allowing the model to be better generalized and to retain past traffic patterns. In the state of a multi-queue system, the input to the neural network is a vector representing the current queue lengths of the multi-queue queues as $s=\left\{q=\left(q_1,q_2,...,q_{\mathit{n}}\right)\in N_{\mathit{n}}:q_{\mathit{i}}\le K_{\mathit{i}}\right\}$. To confirm stable and efficient learning, each queue length was normalized before being input into the neural networks. The normalization approach involves logarithmic scaling $\sum _{i=1}^n⎾{\mathit{log}}_2(K_i+1)⏋$, which corresponds to the current queue length of $q_{\mathit{i}}$. This transformation reduces the impact of large values, ensuring the state input remains within a manageable range while preserving relative differences and stabilizing the training process. This normalized state vector is then provided into fully connected layers of the neural networks for policy and Critic network estimation, encouraging the agent to learn QoS-aware scheduling decisions effectively.

Action: At the decision-making step, the bandwidth weights for each queue are allocated, and this defines the action a. a represents the action space, where $\left\{a=\left(w_1,w_2,\dots \dots ,w_{\mathit{n}}\right)\in {\mathbb{R}}_{+}^{\mathit{n}}:\sum _{\mathit{i}=1}^{\mathit{n}}{w}_{\mathit{i}}=1\right\}.$ In continual DRL, the model leverages history-learned policies, adapting to new traffic patterns without relearning from scratch and improving the efficiency of decision-making.

Reward: In queueing systems, minimizing the average delay is equivalent to reducing the average queue length. It is assumed that for every packet in the queue, the cost per unit of time is equal to the cost of charging for the delay. The reward function is as follows:

$$\mathit{r}\left(\mathit{q},\mathit{a}\right)=-\sum _{\mathit{i}=1}^{\mathit{n}}({\mathit{h}}_{\mathit{i}}{\mathit{q}}_{\mathit{i}}+{\mathit{c}}_{\mathit{i}}{\mathit{l}}_{\mathit{i}})$$

(1)

where the symbol $l_{\mathit{i}}$ represents the number of lost packets in a given unit of time. In addition, the packet loss $l_{\mathit{i}}$, for $i,2,3,...,n$, $,q_{\mathit{i}}$, which includes the number of packets lost for queue length represented as a vector, where every packet loss results in a penalty $c_{\mathit{i}}$ represented as a scalar. We also assume that each packet in $q_{\mathit{i}}$ represents the current length of $q_{\mathit{i}}$ a vector number of packets generates a holding cost $h_{\mathit{i}}$ per unit of time, $h_{\mathit{i}}$ the holding cost per packet in $q_{\mathit{i}}$ representing a scalar equivalent to imposing a penalty for its delay. A counted continual DRL scheme includes a mechanism to evaluate how well past learning is transferred to the new requirements, thus confirming the adaptation of requirements and optimal dynamic bandwidth allocation. Each element in the vector of queue length $q_{\mathit{i}}$ is defined as the number of packets currently held in that queue. The packet loss is also described as a vector, where each element corresponds to the number of packets lost in the queue.

In this paper, we incorporate EWC into RL to prevent catastrophic forgetting when switching between diverse tasks, thereby ensuring that the agent retains knowledge of previous tasks while optimizing the current task. By assessing which parameters are critical for previously learned tasks and constraining their updates during training on new tasks, this approach helps maintain the performance on earlier tasks. This enables knowledge retention and adaptation to new traffic situations without catastrophic forgetting, thereby improving generalization to previously unnoticed workloads.

• EWC regulation: The loss function is modified by adding the EWC penalty to ensure stability when learning a new policy. The regularization term is added for each policy and critic losses, confirming that changes to parameters considered important for previous tasks are penalized. Thus, the final loss function employed in backpropagation is:

$${\mathcal{L}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}={\mathcal{L}}_{\mathit{R}\mathit{L}}+\sum _{\mathit{i}}{\displaystyle \frac{{\mathit{\lambda }}_{\mathit{E}\mathit{W}\mathit{C}}}{2}}{\mathit{F}}_{\mathit{i}}{\left({\mathit{\theta }}_{\mathit{i}}-{{\mathit{\theta }}_{\mathit{i}}}^{\ast }\right)}^2$$

(2)

where ${\mathcal{L}}_{RL}$ is the standard loss function, $\sum _i{\displaystyle \frac{{\lambda }_{EWC }}{2}} F_i{\left({\theta }_{\mathit{i}}-{{\theta }_{\mathit{i}}}^{\ast }\right)}^2$ is the term representing the EWC regulation function, ${\lambda }_{EWC}$ reflects the significance of the old task compared to the new task, ${\theta }_{\mathit{i}}^{\ast }$ is the optimal parameter from the previous task, and $i$ tags each parameter. $F_{\mathit{i}}$ is the Fisher Information Matrix (FIM), which measures the importance of each parameter. The aim of EWC is to maintain the network parameters relative to the learned parameters of both the first and second tasks. When the model is applied to a third task, this constraint can be enforced either with two separate penalties or by combining them into one, since the sum of two quadratic penalties is also a quadratic penalty [23].

• FIM: The FIM provides essential parameters for preserving primary tasks. It is an essential concept that reflects the amount of information an observable random variable carries about an unknown parameter upon which the probability of that random variable depends. It assesses the sensitivity of the network’s performance in terms of parameter variations ${\theta }_{\mathit{i}}^{\ast }$ and it quantifies the sensitivity of the model’s parameters to modifications in the loss function, capturing the importance of each parameter for previously learned tasks. In practice, the FIM is estimated by computing the squared gradients of the loss for the policy and critic networks with respect to their parameters, averaged over samples from the replay buffer. Where theta is the optimal parameter ${\theta }_{\mathit{i}}^{\ast }$ set after learning task A, these gradients function as a practical approximation of the FIM and are calculated as:

$$F_{\theta }=\mathbb{E}\left[{\left({\displaystyle \frac{\partial \mathit{log}{\pi }_{\varnothing } \left(aǀs\right)}{{\partial }_{\theta }}}\right)}^2\right]$$

(3)

Here, ${\pi }_{\mathit{\varnothing }}\left(a_{\mathit{t}}\mathit{ǀ}{s}_{\mathit{t}}\right)$ is a policy network, where s represents the state, and a represents the action [26]. This formula is also applicable to the critic network Q.

The FIM computing is as follows:

• Train networks (policy, two critic networks)
• From the replay buffer, sample a batch of experiences.
• Computing the loss function for the policy and critic.
• Obtain gradients by performing backpropagation with respect to their weights.
• Calculating the squared gradients and averaging them over the buffer size.
• Store ${\theta }_{\mathit{i}}^{\ast }$ and FIM for compute EWC loss (regulation term).

• In this study, the algorithm adapts bandwidth allocation decisions based on queue states. The theoretical fairness share for a given flow at any step-in episode is computed using the following formula [27]:

$$Fairness={\displaystyle \frac{{\mathrm{w}}_i}{{\sum }_{j=1}^i{\mathrm{w}}_j}}{\mathrm{w}}_i\ge 0$$

(4)

where ${\mathrm{w}}_{\mathit{i}}$ is the weight allocated for each $q_{\mathit{i}}$, and it is proportional to the total weights ${\sum }_{j=1}^i{\mathrm{w}}_{\mathit{j}}$. During training in each step, the theoretical fairness computes how each queue in the system should allocate bandwidth as a proportion of the total bandwidth based on its state (i.e., queue length), representing the actual value. According to the prediction, value came out of the policy network ${\pi }_{\mathit{\varphi }}$, which is a vector of action $a=\left(w_1,w_2,\dots \dots ,w_{\mathit{n}}\right)$ that will be implemented in the environment to allocate bandwidth for each queue and then the service rate will be computed.

• Root Mean Square Error (RMSE): A metric used to measure the root of average deviation of prediction value from target value, the measure is defined as indicated in equation [28]:

$$RMSE=\sqrt{{\displaystyle \frac{{\sum }_{N=1}^i{\left(\widehat{y}-y\right)}^2}{N}}}$$

(5)

where $\widehat{y}$ is the prediction value denoting weights allocated for each $q_{\mathit{i}}$, which came from policy network ${\pi }_{\mathit{\varphi }}$, $y$ is the actual value indicating the weights computed by fairness function. In this study, the RMSE metric can be used to assess the model during training, and it offers insight how the model accurately becomes close to the theoretical fairness, meaning that the deviation of prediction value (weight for each $q_{\mathit{i}}$ came from policy network) from the target value (weights of each queue computed by fairness function) into each step.

• Jain’s Fairness Index: It is a mathematical metric used to evaluate how fairly resources, such as bandwidth, are distributed among multiple flows or entities in a system. It is defined as [29]:

$$f\left(x\right)={\displaystyle \frac{{\left[\sum _{i=1}^n{x}_i\right]}^2}{N\sum _{i=1}^n{x_i}^2}} where x_i\ge 0$$

(6)

where $\sum _{\mathit{i}=1}^n{x}_i$ is represents the squared of stochastic action values predicated by the policy network ${\pi }_{\mathit{\varphi }}$, reflect the actual network in bandwidth allocation decision for each queue. $\sum _{\mathit{i}=1}^n{x_{\mathit{i}}}^2$ is optimal fitness of the bandwidth allocation (i.e., weight for each queue relative to the current queue state computed theoretically by fairness function). Specifically, in this study, a value of the Jain index near 1 indicates that the policy network’s predictions closely match the optimal fairness pattern. If the value of the Jain index is significantly less than 1, it indicates a deviation from fairness (optimal weights for each queue based on the current state computed by fairness function), indicating that some queues are over or under-served relative to their optimal share.

4.5. WFQ Continual-DRL Algorithm

This study integrated continual learning techniques with a DRL framework for weighted fair queues within the proposed WFQ continual-DRL algorithm to dynamically allocate bandwidths. In this approach, an agent explores the dynamics of the queueing system through periodical, recursive interactions within the architecture of WFQ continual DRL. The agent gains new insights about the environment’s surroundings and exploits them to obtain high rewards. The agent also retains and transfers history-learned policies to improve decision-making in dynamic traffic environments and accumulates knowledge over time. One challenge is that the huge buffer properties of the WFQ system and several queues contribute to the curse of dimensionality.

To address this issue, the WFQ continual-DRL algorithm is employed, providing the control policy estimates as input to the neural network parameters. As input for neural networks, the system’s state is transformed into a binary vector, thus eliminating the need for storage space. This enables us to receive normalized state information for various buffers, preventing a gradient explosion problem when computing policy gradients and accessing normalized queue lengths. This improvement enhances the numerical stability, interpretability, and learning efficiency of the system, where $K_{\mathit{i}}$ a vary widely. This ensures that the transformed values are more fluent for the WFQ continual DRL algorithm. $\sum _{\mathit{i}=1}^{\mathit{n}}\mathrm{⎾}{\mathit{log}}_2(K_{\mathit{i}}+1)\mathrm{⏋}$ is the dimension of s. The off-policy WFQ continual-DRL algorithm is also used to achieve high levels of data efficiency. In essence, the off-policy technique breaks the correlation between consecutive data using a replay buffer, and can, therefore, achieve more data usage efficiency by repeatedly utilizing historical data. After each investigation stage, transition data ${(s}_{\mathit{t}},a_{\mathit{t}},r_{\mathit{t}+1},s_{\mathit{t}+1})$ are gathered and saved in the replay buffer to be sampled later and used to modify the control strategy. In addition to the sampled updating policy strategy, the updated parameters of the neural network are used to compute the FIMs, to ensure that the most critical parameters from the past are preserved. Continual learning is used to overcome catastrophic forgetting.

The SAC procedure is a sophisticated technique that optimizes the expected reward and policy entropy simultaneously. The efficiency of the investigation is improved by enhancing the entropy and optimizing the expected reward by maximizing the entropy of the policy. SAC enhances the efficiency of self-exploration and has been shown to achieve stable performance in continuous action spaces. Stable performance in a continuous action space has also been demonstrated. SAC involves employing a policy network π, and a critic network Q to approximate a stochastic policy. The structure of the neural network integration of SAC with EWC for eight queues is illustrated in Figure 3.

Two critic networks are utilized in the SAC algorithm to mitigate the overestimation bias commonly found in DRL. To evaluate the Q-values corresponding to state-action pairs, the critics, represented as $Q_1$ and $Q_2$, are accountable, while their target networks, ${\overline{Q}}_1$ and ${\overline{Q}}_2$, facilitate stable learning through soft updates. The control calculates the target Q-value by selecting the minimum estimate from the two critics to reduce the likelihood of overestimation during training. The critics are updated using the MSE, which is the loss between the predicted Q-values and the computed target [24].

In the proposed algorithm of the WFQ continual-DRL algorithm, the integration of continual learning, represented by EWC, with the DRL algorithm, particularly in the WFQ system, enhances the agent’s ability to retain optimal scheduling knowledge across various traffic scenarios. EWC identifies important neural network weights from previous queue patterns and penalizes changes to these weights during training on new patterns, thereby decreasing catastrophic forgetting. This process helps preserve performance consistency across varying queue loads and quick convergence in the early training episodes. As a result, the continual-DRL agent adapts efficiently to changing traffic intensities while ensuring stable scheduling [23].

In this study, a simulation was conducted for twelve queues as an enhancement. The parameter tuning process of the neural network for integration of SAC-EWC into the WFQ continual-DRL algorithm involved expanding the number of queues to twelve, which increased the state as input to the neural network and the action space as output, making the scheduling problem more dynamic and complex. This adjustment demands a more capable model to allocate bandwidth effectively across a larger number of queues. However, increasing the number of neurons in the network to 128 enhances the model’s ability to approximate complex policies, resulting in improved decision-making. When extended to twelve queues, the input defined as state will be increased and output representing action will increase. Increasing the number of neurons from 64 to 128 to enhance the model’s learning allows the network to capture more complex patterns in the data training, which is mainly valuable in dynamic environments such as multi-queue systems. This adjustment aims to improve performance and reach higher prediction accuracy. This enables the model to capture more complex pattern in the data through training data and avoid underfitting. Underfitting occurs when the model is too simple to capture the underlying patterns in the training data, resulting in inadequate and poor learning. This results in increased errors and invariably low rewards, even during training. A larger replay buffer enables the agent to retain past experiences for a longer period, thereby enhancing training stability by providing a diverse range of samples during training. Additionally, increasing the batch size to 256 contributes to more stable updates by averaging gradients over a larger set of experiences, thereby reducing variance in training. These enhancements improve learning efficiency while providing excellent stability in dynamic bandwidth allocation scenarios. The structure of the neural network integrating SAC with EWC for twelve queues is shown in Figure 4.

In the SAC structure of the critic network, the use of target critics stabilizes the learning process for both critic networks $Q_1$ and $Q_2$. The π network produces the $\mu$ and $\sigma$ of the distribution. In this approach, the action is displayed as a probability distribution (Gaussian distribution). The Gaussian distribution is represented as follows:

$$f \left(a|\sigma , \mu \right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{exp}^{-{\displaystyle \frac{1}{2}} {\left({\displaystyle \frac{a-\mu }{\sigma }}\right)}^2}$$

(7)

where $\mu$, $\sigma$ represents the input to the Gaussian distribution formula predicted by the policy network. $a$ is the output from a Gaussian distribution. Whenever the action stays in the area around the mean, the action will be better [30].

The action was sampled randomly from a probability distribution defined by $\mu$, $\sigma$, which is known as a stochastic action or stochastic policy. A random noise $\epsilon$ is generated to confirm exploration, the value of the noise $\epsilon$ is drawn from a random distribution represented by $N\left(\mathrm{0,1}\right)$. The output action was sampled from $a=\mu +\sigma \epsilon$, which internally is computed in Gaussian distribution. This process, known as reparameterization sampling of the action value, allows for effective policy optimization as follows [24]:

$$a_t=f_{\varnothing }({\epsilon }_t;s_t) \mathrm{W}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \epsilon ~ N \left(\mathrm{0,1}\right)$$

(8)

where $a_{\mathit{t}}$ represents the action, $s_{\mathit{t}}$ represents the current state, and $\mathit{\epsilon }$ is the noise vector from the Gaussian distribution. This function $a_t=f_{\varnothing }\left({\epsilon }_t;s_t\right)$ means that internal noise addition allows the agent to produce stochastic actions necessary for exploration while trusting the training process is stable and efficient. The action reductions are set to be within the required range by applying the ReLU activation function, which is practical to eliminate negative values where only positive actions are valid, which is particularly useful in settings (bandwidth weights) for WFQ scheduling. The policy network effectively explores continuous action while a stochastic process balances between exploration and exploitation.

The approach presented in this study combines SAC with EWC. The goal is to integrate the EWC regulation mechanism into SAC to maintain stability across states while preserving knowledge learned from the first task through training. As usual, the end of the task includes calculating and storing the FIM and the parameters ${(\theta }_{\mathit{i}}^{\ast },{\mathit{\varnothing }}_{\mathit{i}}^{\ast })$. When reserving a new state, the training is initialized in that state. At the parameter update stage, the term representing the EWC loss function is added to the SAC losses. After completing the task, the Fisher matrix is updated, and the network parameters are saved. The combined losses that ensure the performance of the previous task are held constant while learning a new task, allowing the network to output the action [23].

In the WFQ continual-DRL algorithm, the significance of each model parameter is computed and evaluated. When the algorithm begins, the model is set to evaluation mode, and a dictionary is initialized to store Fisher information values for each parameter. Following this, a batch of experiences is sampled from the replay buffer, and the gradient is computed based on the loss function associated with either the actor or the critic network. In the actor network, the loss is defined as the mean of the predicted actions, whereas in the critic network, it is the mean squared error between the predicted Q-values and the target Q-values. After performing backpropagation, the Fisher information for each parameter is updated by averaging the squared gradients across the sampled batch. These values are then detached from the computation stored in a dictionary, to ensure that the learned values of the critical parameters are retained when the model is adapted to new tasks. The optimal parameter values are also stored to facilitate the EWC penalty calculations during training.

EWC characterizes itself from other continual learning methods, such as Gradient Episodic Memory (GEM) and Learning without Forgetting (LwF), by focusing on simplicity, memory efficiency, and biological probability. Unlike GEM, which requires high memory and computational costs, it stores data from previous tasks and performs confing on previous outputs or parameters, resulting in additional complexity and storage requirements. In contrast, EWC introduces a simple regularization based on the Fisher Information Matrix (FIM) to preserve important weights without requiring the preservation of old data or models, which makes EWC efficient, lightweight, and perfect for continual learning in dynamic resource settings, such as DRL-based queuing and scheduling systems [31].

The process of choosing the optimal value for ${\lambda }_{EWC }$ is conducted in two steps. In the first step, six distinct ranges are defined using the random function, and each one is explored independently. Each range is run over 1000 episodes of network training, and random values for the new ${\lambda }_{EWC}$ are sampled and evaluated. The performance of each sample is estimated based on the measure of the loss function and reward performance.

When the random function had been implemented, ${\lambda }_{EWC}$ was obtained based on six ranges, for each range created five values (random value), which were operated over 1000 episodes. The model then iteratively trains the SAC with EWC agent for each ${\lambda }_{EWC}$, which evaluates the agent’s performance. The loop stores tracking of the best-parameter ${\lambda }_{EWC}$, then updates the best ${\lambda }_{EWC}$ by comparing with performance whenever a higher-performing result is found. This procedure enables observed tuning of the ${\lambda }_{EWC}$ parameter to optimize learning stability and policy performance. Then, from each range, pick the best value of ${\lambda }_{EWC}$. In the second step, after all six ranges have been explored, obtain the optimal six ${\lambda }_{EWC}$ value by conducting a structural evaluation in which a grid search process is applied to systematically compare the performance of the six optimal ${\lambda }_{EWC}$ values that resulted from the random function used in training for 1000 episodes. The best-performing ${\lambda }_{EWC}$ is selected based on the impact of the MSE value and the reward performance, ensuring optimal performance in continual learning. The model reached the best performance with a rather high ${\lambda }_{EWC}$ value of 2271 for eight queues, 2275 for twelve queues, which led to significantly improved reward results and more stability in MSE and MAE. The high value of ${\lambda }_{EWC}$ demonstrates that the model strongly penalizes changes to significant parameters, thus preserving previously learned knowledge more effectively. It reflects the model’s dependance on stability over adaptivity, which is valuable in dynamic environments where continual learning is critical.

To cover the experimental characteristics of a random search, a combination of these two methods represented by the random function and grid search can control a wide range of possible values; this is followed by a refined grid-method evaluation to determine the best-performing ${\lambda }_{EWC}$.

The WFQ Continual-DRL Framework: Policy-Critic Update with EWC

The WFQ environment is designed to model multi-queue scheduling principles. It simulates multiple input traffic flows; each represented as a separate queue that shares a limited total bandwidth. Inter-arrival times and service times use gamma-distributed values that reflect the bursty nature of real network traffic. At every decision step (20 s), the state defined as queue length $s=\left\{q=\left(q_1,q_2,...,q_{\mathit{n}}\right)\in N_{\mathit{n}}:q_{\mathit{i}}\le K_{\mathit{i}}\right\}$ takes as input to actor network to stabilize learning, and queue states normalize as $\sum _{i=1}^n⎾{\mathit{log}}_2(K_i+1)⏋$, ensuring the agent perceives state change on a normalized scale and queues receive an action vector from an actor network $a_{\mathit{t}}~{\pi }_{\mathit{\varnothing }}\left(a_{\mathit{t}}\mathit{ǀ}{s}_{\mathit{t}}\right)$, describing the ratio of total bandwidth allocated to each queue. This allocation determines the service rate for each queue ${\mathit{\mu }}_{\mathit{i}}=w_{\mathit{i}}\times b$, and the number of packets served is calculated based on gamma-distributed service times noting action defined as $\left\{a=\left(w_1,w_2,\dots \dots ,w_{\mathit{n}}\right)\in {\mathbb{R}}_{+}^{\mathit{n}}:\sum _{\mathit{i}=1}^{\mathit{n}}{w}_{\mathit{i}}=1\right\}$, which account for variability in processing or transmission delays. The served packets are removed from the queue, while newly arrived packets arrive, ensuring a fluid and realistic evolution of the queue states. The reward function contains two forms of penalties: firstly, holding cost $h_{\mathit{i}}$ for unserved packets remaining in the queue, representing delay, and $l_{\mathit{i}}$ represents packet lost due to buffer overflow.

Two critics $Q_{{\mathit{\theta }}_1}\left(s_{\mathit{k}}\mathit{ǀ}{a}_{\mathit{k}}\right)$, $Q_{{\mathit{\theta }}_2}\left(s_{\mathit{k}}\mathit{ǀ}{a}_{\mathit{k}}\right)$ functions are maintained, which are trained to minimize the error between the predicted Q-values and the target Q-value. In this approach, the EWC method is added to preserve performance on previous tasks during continual learning. For a batch of sampled transitions ${(s}_{\mathit{t}},a_{\mathit{t}},r_{\mathit{t}+1},s_{\mathit{t}+1})$, the target value is computed as:

$$y_k=r_{k+1}+\gamma (1-d_k)\left[{min}_{\theta }{\overline{Q}}_{{\theta }_1}\right(s_{k+1},a_{k+1}),{\overline{Q}}_{ {\theta }_2}(s_{k+1},a_{k+1}\left)\right]-\alpha log {\pi }_{\varphi }(a_{k+1}\mid s_{k+1})$$

(9)

where $r_{\mathit{k}+1}$ is a reward function, $\gamma$ is discount factor, ${min}_{\mathit{\theta }}{\overline{Q}}_{{\mathit{\theta }}_1}(s_{\mathit{k}+1},a_{\mathit{k}+1}),{\overline{Q}}_{{\mathit{\theta }}_2}(s_{\mathit{k}+1},a_{\mathit{k}+1})]$ represent minimum of two target Q-networks, the algorithm reduces the risk of overestimation by selecting the smaller value from the two targets. The $\alpha log{\pi }_{\mathit{\varphi }}(a_{\mathit{k}+1}\mid s_{\mathit{k}+1})$ function, $\alpha$ is a temperature coefficient that controls the trade off between exploration and exploitation. $log{\pi }_{\mathit{\varphi }}(a_{\mathit{k}+1}\mid s_{\mathit{k}+1})$ is the probability of taking the next action from the next state observed. For two critic networks, the critic loss function along with computing an EWC regularization term is the given by:

$$J_Q={\displaystyle \frac{1}{m}} \sum _{k=1}^m{\displaystyle \frac{1}{2}} {\left[y_k-Q_{\theta }\left( s_kǀa_k\right)\right]}^2+\sum _i{\displaystyle \frac{{\lambda }_{EWC }}{2}} F_i{\left({\theta }_i-{{\theta }_i}^{\ast }\right)}^2$$

(10)

where $y_{\mathit{k}}$ is target value, $Q_{\mathit{\theta }}\left(s_{\mathit{k}}\mathit{ǀ}{a}_{\mathit{k}}\right)$ represents the predication value, which estimates future reward action from current state $s_{\mathit{t}}$. ${\lambda }_{EWC}$ is a hyperparameter that controls the strength of penalty. A higher value indicates that the actor is more constrained to preserve close to previous knowledge. $F_i{\left({\theta }_i-{{\theta }_i}^{\ast }\right)}^2$ function to compute how much the current critic network parameters deviate from previously learned parameters, using FIM to take important weight.

The updated actor network is represented as follows:

$$J_{\pi }={\displaystyle \frac{1}{m}} \sum _{k=1}^m \left[\alpha \mathit{log}{\pi }_{\varphi }\left(a_k∣s_k\right)-Q_{\theta }\left(\left( s_kǀa_k\right)\right)\right]+ \sum _i{\displaystyle \frac{{\lambda }_{EWC }}{2}} F_i{\left({\varphi }_i-{{\varphi }_i}^{\ast }\right)}^2$$

(11)

where $\alpha \log {\pi }_{\mathit{\varphi }}\left(a_{\mathit{k}}∣s_{\mathit{k}}\right)$ represents the entropy term and actor sampled actions from probability distribution leading to high Q values (expected reward), where $Q_{\mathit{\theta }}\left(s_{\mathit{k}}\mathit{ǀ}{a}_{\mathit{k}}\right)$ represents the predication value, which estimates future reward. $\sum _i{\displaystyle \frac{{\lambda }_{EWC }}{2}} F_i{\left({\varphi }_i-{{\varphi }_i}^{\ast }\right)}^2$ is a regulation term to compute how much the current critic network parameters deviate from previously learned parameters, and FIM means to take important weight.

To perform gradient updates for actor and critic networks:

$$\varphi \leftarrow \varphi -{\eta }_{\pi }{\nabla }_{\varphi } J_{\pi }$$

(12)

$${\theta }_1\leftarrow {\theta }_1-{\eta }_{Q_1}{\nabla }_{ {\theta }_1} J_Q$$

(13)

$${\theta }_2\leftarrow {\theta }_2-{\eta }_{Q_2}{\nabla }_{ {\theta }_2} J_Q$$

(14)

Slowly update the parameters of target Q networks to prevent instability caused by rapidly changing targets using a soft update:

$${\overline{\theta }}_1\leftarrow {\tau \theta }_1-\left(1-\tau \right){\overline{\theta }}_1$$

(15)

$${\overline{\theta }}_2\leftarrow {\tau \theta }_2-\left(1-\tau \right){\overline{\theta }}_2$$

(16)

The structure of the WFQ continual-DRL algorithm as illustrated in Figure 5.

The FIM is computed after finishing training on a task before starting on another task, including computing and storing the FIM. It is estimated by computing the squared gradients of the loss for the policy and critic networks with respect to their parameters, averaged over samples from the replay buffer size, where ${\theta }_{\mathit{i}}^{\ast }$ is the optimal parameter set after learning task A for future EWC loss computation. In our paper, the FIM was computed every 30 episodes, and then the parameters ${(\theta }_{\mathit{i}}^{\ast },{\mathit{\varnothing }}_{\mathit{i}}^{\ast })$ and FIM were stored until the next 30 episodes, in an algorithm of SAC with EWC. This interval was chosen based on empirical test observe improve stability and adaptability; updating too often restricts the agent from learn new information, while updating too rarely weakens the term of regularization. In the WFQ continual-DRL framework, the 30-episode interval provides an effective tradeoff between preserving previous knowledge and learning new tasks. Figure 6 illustrates the steps of the adaptive algorithm of WFQ continual-DRL.

The details of the WFQ continual-DRL algorithm are given in Algorithm 1.

Algorithm 1: The WFQ continual-DRL Algorithm (integration SAC with EWC)

1: Initialization: Initialize the parameters of network, policy π, critics networks ${\mathit{Q}}_{\mathit{\theta }1},{\mathit{Q}}_{\mathit{\theta }2}$, and target critics ${\overline{\mathit{Q}}}_{\mathit{\theta }1},{\overline{\mathit{Q}}}_{\mathit{\theta }2}$, i.e., ∅, θ1, θ2, respectively. Initialize Fisher Information Matrix ${\mathit{F}}_{\mathit{\theta }}$ and Optimal Parameters θ*, ∅*. 2: For each episode do:  Initialize environment and initialize state s0.  Initialize episode reward to 0.  3: For each environment step do:   Select action: ${\mathit{a}}_{\mathit{t}}~{\mathit{\pi }}_{\mathit{\varnothing }}\left({\mathit{a}}_{\mathit{t}}\mathit{ǀ}{\mathit{s}}_{\mathit{t}}\right)$.   Execute action in environment and observe next state $\left({\mathit{s}}_{\mathit{t}+1}\right)$, reward $\left({\mathit{r}}_{\mathit{t}+1}\right)$, and done signal.   Store transition: $\left({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}},{\mathit{r}}_{\mathit{t}+1},{\mathit{s}}_{\mathit{t}+1}\right)$ in replay buffer.   Store parameter θ*, and compute Fisher Information Matrix ${\mathit{F}}_{\mathit{\theta }}$ every X episode.   4: Update Parameters:   Randomly sample minibatch of m transitions $\left({\mathit{s}}_{\mathit{k}},{\mathit{a}}_{\mathit{k}},{\mathit{r}}_{\mathit{k}+1},{\mathit{s}}_{\mathit{k}+1}\right)$ from replay buffer.   Compute target Q-value using the minimum of two target Q-networks:   ${\mathit{y}}_{\mathit{k}}={\mathit{r}}_{\mathit{k}+1}+\mathit{\gamma }(1-{\mathit{d}}_{\mathit{k}})\left[{\mathit{m}\mathit{i}\mathit{n}}_{\mathit{\theta }}{\overline{\mathit{Q}}}_{{\mathit{\theta }}_1}\right({\mathit{s}}_{\mathit{k}+1},{\mathit{a}}_{\mathit{k}+1}),{\overline{\mathit{Q}}}_{{\mathit{\theta }}_2}({\mathit{s}}_{\mathit{k}+1},{\mathit{a}}_{\mathit{k}+1}\left)\right]-\mathit{\alpha }\mathit{l}\mathit{o}\mathit{g}{\mathit{\pi }}_{\mathit{\varphi }}({\mathit{a}}_{\mathit{k}+1}\mid {\mathit{s}}_{\mathit{k}+1})$   Update Critic networks ${\mathit{Q}}_{\mathit{\theta }1},{\mathit{Q}}_{\mathit{\theta }2}$ minimizing loss:   ${\mathit{J}}_{\mathit{Q}}={\displaystyle \frac{1}{\mathit{m}}}{\displaystyle \sum _{\mathit{k}=1}^{\mathit{m}}}{\displaystyle \frac{1}{2}}{\left[{\mathit{y}}_{\mathit{k}}-{\mathit{Q}}_{\mathit{\theta }}\left({\mathit{s}}_{\mathit{k}}\mathit{ǀ}{\mathit{a}}_{\mathit{k}}\right)\right]}^2+{\displaystyle \sum _{\mathit{i}}}{\displaystyle \frac{{\mathit{\lambda }}_{\mathit{E}\mathit{W}\mathit{C}}}{2}}{\mathit{F}}_{\mathit{i}}{\left({\mathit{\theta }}_{\mathit{i}}-{{\mathit{\theta }}_{\mathit{i}}}^{\mathit{*}}\right)}^2$   Where ${\mathit{\lambda }}_{\mathit{E}\mathit{W}\mathit{C}}$ is the EWC regularization strength.   Update Actor network ${\mathit{\pi }}_{\mathit{\varnothing }}$ by minimizing the loss:   ${\mathit{J}}_{\mathit{\pi }}={\displaystyle \frac{1}{\mathit{m}}}{\displaystyle \sum _{\mathit{k}=1}^{\mathit{m}}}\left[\mathit{\alpha }\mathit{log}{\mathit{\pi }}_{\mathit{\varphi }}\left({\mathit{a}}_{\mathit{k}}∣{\mathit{s}}_{\mathit{k}}\right)-{\mathit{Q}}_{\mathit{\theta }}\left(\left({\mathit{s}}_{\mathit{k}}\mathit{ǀ}{\mathit{a}}_{\mathit{k}}\right)\right)\right]+{\displaystyle \sum _{\mathit{i}}}{\displaystyle \frac{{\mathit{\lambda }}_{\mathit{E}\mathit{W}\mathit{C}}}{2}}{\mathit{F}}_{\mathit{i}}{\left({\mathit{\varphi }}_{\mathit{i}}-{{\mathit{\varphi }}_{\mathit{i}}}^{\mathit{*}}\right)}^2$   Perform gradient updates:   $\mathit{\varphi }\leftarrow \mathit{\varphi }-{\mathit{\eta }}_{\mathit{\pi }}{\nabla }_{\mathit{\varphi }}{\mathit{J}}_{\mathit{\pi }}$.   ${\mathit{\theta }}_1\leftarrow {\mathit{\theta }}_1-{\mathit{\eta }}_{{\mathit{Q}}_1}{\nabla }_{{\mathit{\theta }}_1}{\mathit{J}}_{\mathit{Q}}.$   ${\mathit{\theta }}_2\leftarrow {\mathit{\theta }}_2-{\mathit{\eta }}_{{\mathit{Q}}_2}{\nabla }_{{\mathit{\theta }}_2}{\mathit{J}}_{\mathit{Q}.}$   Soft update target networks:   ${\overline{\mathit{\theta }}}_1\leftarrow {\mathit{\tau }\mathit{\theta }}_1-\left(1-\mathit{\tau }\right){\overline{\mathit{\theta }}}_1.$   ${\overline{\mathit{\theta }}}_2\leftarrow {\mathit{\tau }\mathit{\theta }}_2-\left(1-\mathit{\tau }\right){\overline{\mathit{\theta }}}_2.$   5: Compute Fisher Information Matrix (FIM) Every X Episodes:   Compute gradient-based Fisher Information Matrix using log probabilities for the actor and critic losses:   ${\mathit{F}}_{\mathit{\theta }}=\mathbb{E}\left[{\left({\displaystyle \frac{\partial \mathit{log}{\mathit{\pi }}_{\mathit{\varnothing }}\left(\mathit{a}\mathit{ǀ}\mathit{s}\right)}{{\partial }_{\mathit{\theta }}}}\right)}^2\right]$   Store optimal parameters ${\mathit{\theta }}^{\mathit{*}}$ and Fisher Information Matrix ${\mathit{F}}_{\mathit{\theta }}$.

4.6. Real Traffic Implemented in Twelve Queues Experimental

This experiment was implemented with a real traffic dataset from a real telecommunication network to validate the efficiency of the proposed WFQ continual-DRL for real traffic applications. In this paper, the data set was collected from the Universidad Del Cauca, Popayán, Colombia network. Packet captures were performed at different morning and afternoon hours between April and June 2019. A total of 2,704,839 flow instances were gathered and stored [32].

Processing Real Traffic

In the first step of processing, a column of categories that consists of 24 categories and a column of their interarrival times are selected. Then, the category is split into multiple files. After that, twelve categories from the total categories selected represent twelve sources, as differential arrival flows arrive at each queue independently. The selection is based on the most common and rich categories (chat, media, web, VoIP, software update, email, music, collaboration, cloud, network, download file transfer sharing, system). The interarrival rate for each category meeting is selected. According to the filtered data, removing rows indicates that invalid or missing data is present. The total dataset after processing is 1,265,319. Then, the arrival rate λ_i for each category is computed as in equation [33]:

$$\lambda ={\displaystyle \frac{1}{\overline{T_A}}}$$

(17)

In addition to the initially selected twelve categories, the analysis was expanded to include the diversity of network traffic types. The 12 recent categories (Streaming, PRC, VPN, shopping, social media, data transfer, mining, game, remote access, database, video, unspecified) were also processed. The total dataset after processing is 128,458. Computing the arrival rate for each category, as in Equation (14), enables a more accurate characterization of traffic patterns, which is essential for simulating realistic queueing behavior. This measure enables us to compare performance metrics across a broader range of traffic resources, thereby improving the validation of the proposed adaptive algorithm, WFQ continual-DRL.

5. Results and Analysis

In this section, the proposed WFQ continual-DRL as the adaptive algorithm is evaluated in terms of optimizing bandwidth in the WFQ system. The experiments were implemented in Python 3.10 using PyTorch version: 2.6.0, a library for numerical computation in Python. TensorFlow is an open-source library facility for the computation and training of deep learning models. The network scheduling algorithm, represented as WFQ, manages the flow of packets across multi-queue systems. In this paper, the effectiveness of the proposed approach is evaluated through experiments conducted in an environment with the first eight and then twelve queues. A summary of the key parameters used in the implementation is given in

Table 1. Key parameters of experimentally implemented.

Parameters	Value
Learning rate $\mathit{\eta }$	${\eta }_{\pi }$ = 10−4, ${ \eta }_{Q_1}$ = 10−3, ${ \eta }_{Q_2}$= 10−3
Update rate $\mathit{\tau }$	10−2
Discount factor $\mathit{\gamma }$	0.99
Entropy coefficient $\mathit{\alpha }$	0.2
Regulation coefficient ${\mathit{\lambda }}_{\mathit{E}\mathit{W}\mathit{C}}$	${\lambda }_{EWC }$ for eight queues = 2271, ${\lambda }_{EWC }$ for twelve queues = 2275
Reply buffer	eight queues = 10,000, twelve queues = 30,000
Batch size	eight queues = 128, twelve queues = 512
Optimizer	Adam

.

The holding cost is $h_i={\displaystyle \frac{1}{n}}$, and the penalty for packet loss is $c_i=1, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} i=\mathrm{1,2},\dots .n$, and $n$ is the number of queues. The reward function is represented as:

$$r\left(q,a\right)=-\sum _{i=1}^8({\displaystyle \frac{1}{n}} q_i+l_i)$$

5.1. Experiment 1: Eight Queues

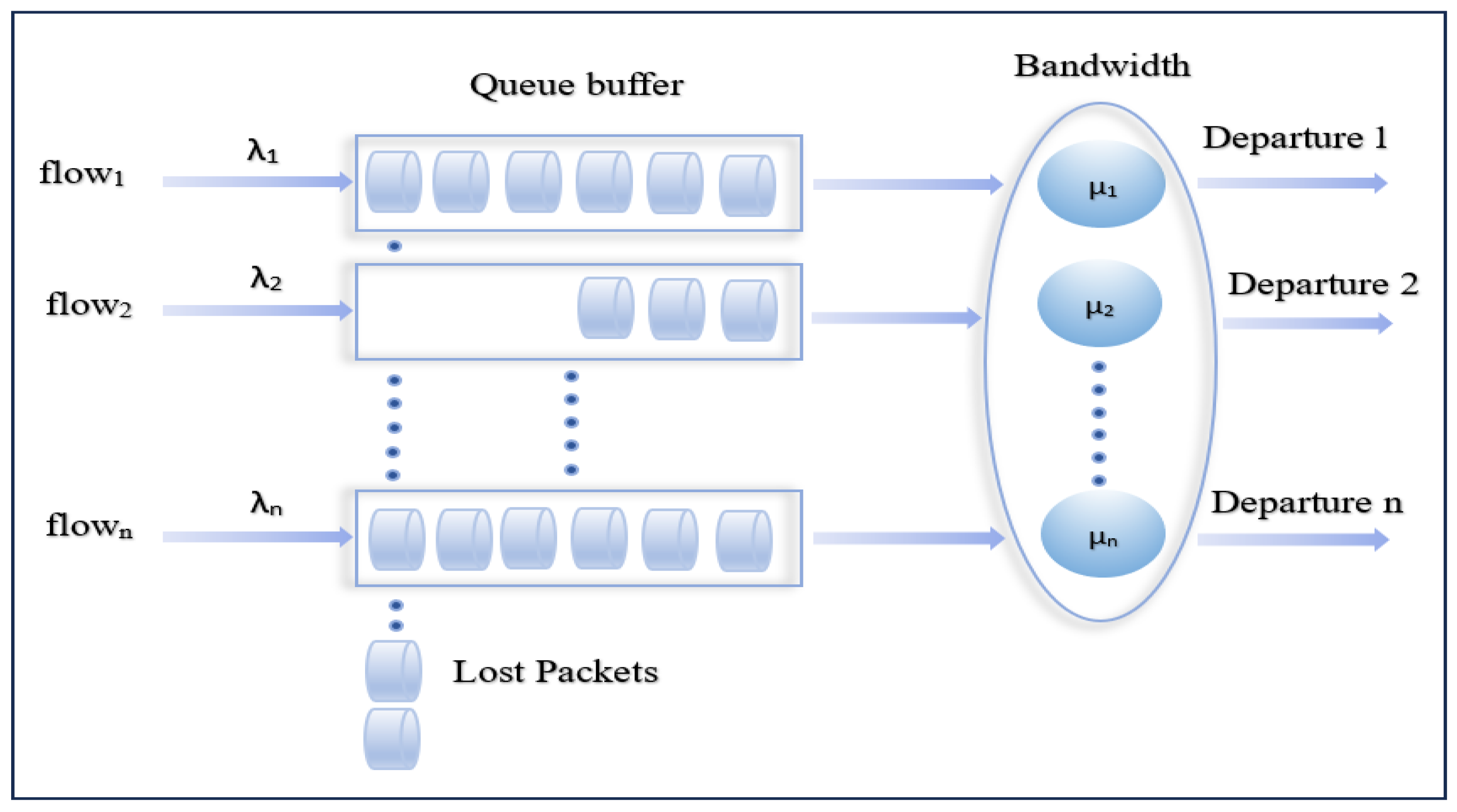
In this section, we describe an experiment involving eight queues in the form of an arrival flow with arrival rates λ_i = (0.03, 0.16, 0.2, 0.1, 0.08, 0.15, 0.06, 0.05) packets/s, where each arriving packet is classified and placed into its respective queue. The WFQ continual-DRL algorithm services queues in a manner that reflects their assigned weights. The interarrival times and service times were generated using a gamma distribution with a Squared Coefficient of Variation (SCV) of 0.8. The average packet size was 1 byte/packet, the buffers of queues were $K_1=K_2=\dots K_8=32$ packets, and the total finite bandwidth was 1 byte per second. The control policy allocated bandwidth weights satisfying $w_1+w_2+\dots \dots .+w_8=1$. The number of episodes was 1000, with a time length of 2000 s for each episode. The agent took action every 20 s.

When the random function had been implemented, ${\lambda }_{EWC }$ was obtained, as explained in Section 2, based on six ranges, each of which was operated over 1000 episodes. Next, we set the six values in the grid to search for optimal values from them. The optimal value of ${\lambda }_{EWC }$ was then obtained from the grid approach process, the FIM was computed every 30 episodes, and then the parameters ${\theta }_i^{\ast }$ and $F_i$ were stored.

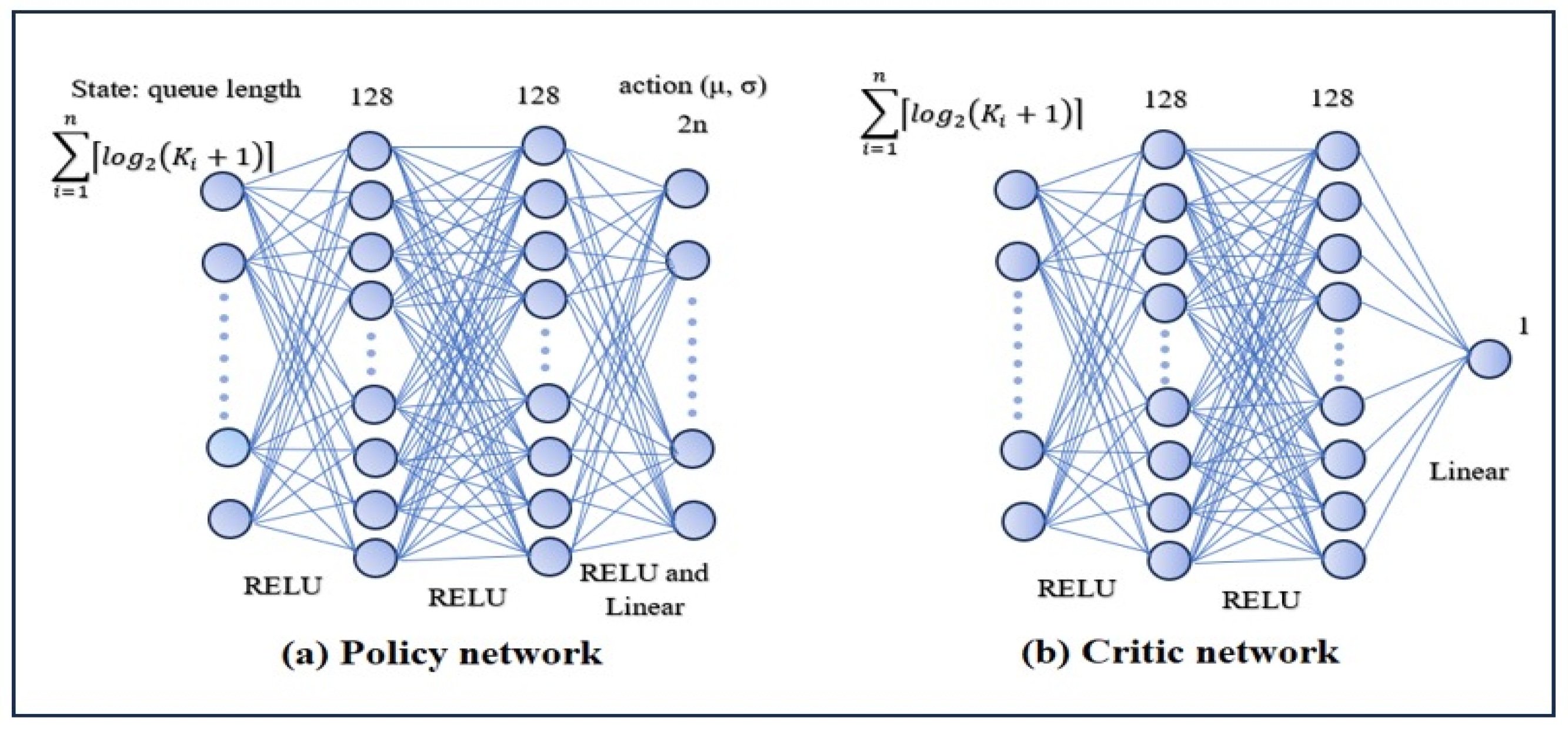
At the initial implementation step, a multi-queueing system consisting of eight queues was experimentally designed to evaluate the WFQ-DRL algorithm, as presented in [22]. This research aims to employ deep reinforcement learning for the allocation of dynamic bandwidth in router environments using a WFQ mechanism; each queue was modeled with identical arrival rates (λ) and buffer sizes, as detailed in the previous section. The implementation structure adopts a neural network containing policy and critic networks, as illustrated in Figure 3. The key hyperparameters of the network are summarized in Table 1.

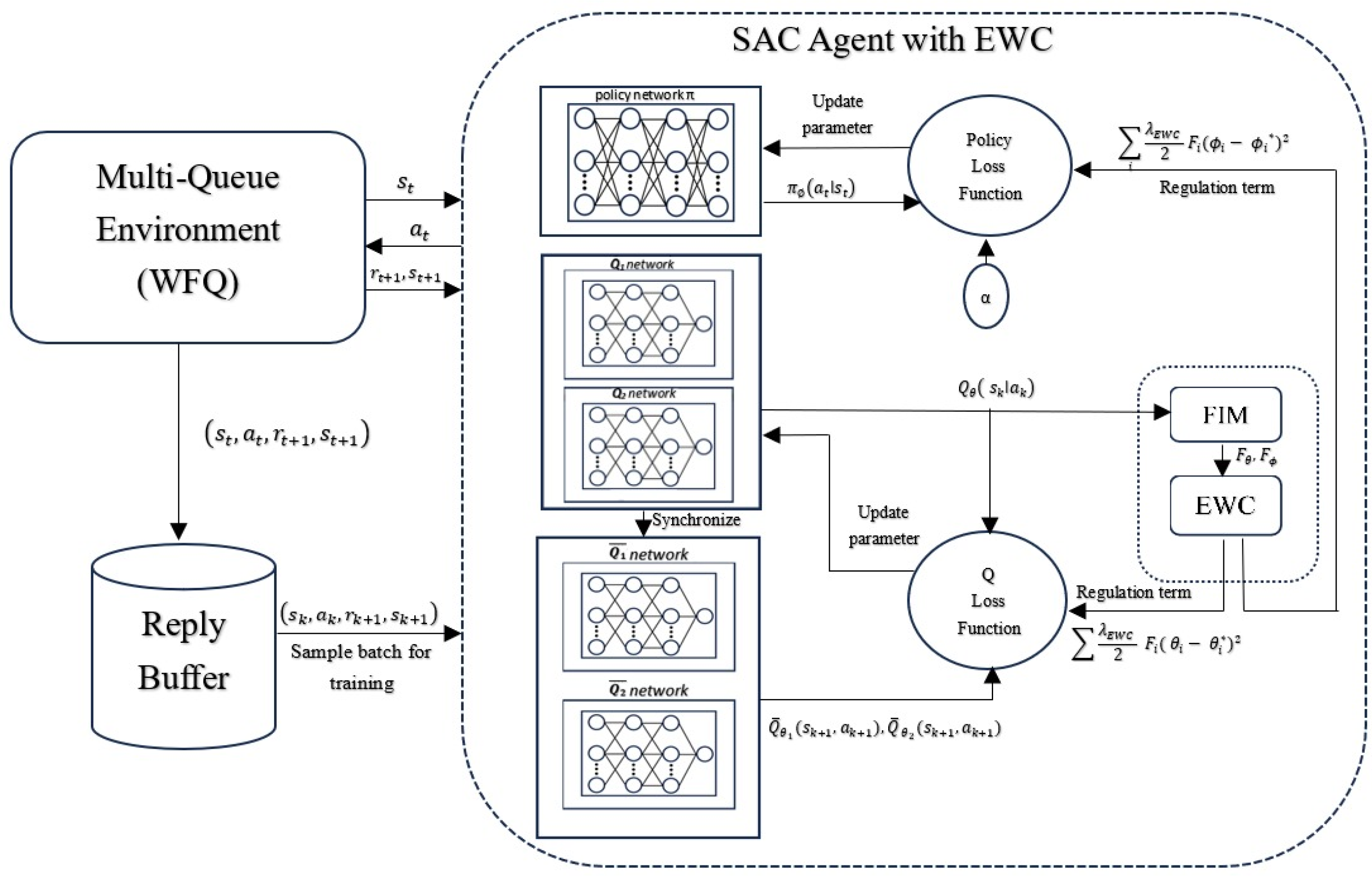
After this, improving the WFQ-DRL algorithm by integrating continual learning allows the model to adapt over time without forgetting previously acquired knowledge. It primarily utilizes the EWC mechanism to preserve important network parameters as the model learns new tasks. The adaptive algorithm of the WFQ continual-DRL enables ongoing learning and adaptation to varying network conditions and objectives while maintaining the same structural configuration and parameter settings across the eight queues. This technique effectively maximizes the cumulative reward over time, ensuring robust performance in dynamic networking environments.

The average reward is shown in Figure 7 for the curve of SAC, and it can be seen that the curve exponentially converges after a 200-episode run, and the fluctuation range for average reward is between −10 and −6.5, according to SAC with EWC curve of average reward for enhance algorithm resulting in consistent performance, and it can be seen that the curve exponentially converges after a 100-episode run. This indicates that the model was stable, with a steady range for the average rewards of between −2 and −1.5, resulting in consistent performance. At the beginning of training, the controller typically explores different assignments as action strategies (bandwidth weights) through queues, leading to increased fluctuation. In this step, the controller has the potential to explore all the probabilities of processes to achieve an action that yields benefits. During the learning process, the controller exploits actions, resulting in a rise in the reward curve, and the policy gradually converges toward the optimal allocation bandwidth, reducing the variability in the reward curve. The rise indicates that the policy used in the WFQ continual-DRL algorithm improves performance and provides a suitable understanding of the environment dynamics. Eventually, the reward stabilizes during training, indicating that the controller consistently produces optimal performance rewards, thereby balancing exploration with exploitation while preserving past knowledge.

A comparison of the SAC and SAC with EWC rewards in

Table 2. Comparison table of SAC and SAC with EWC rewards.

Episode Number	SAC Rewards	SAC with EWC Rewards
50	−8.891	−3.048
100	−10.579	−2.659
150	−10.699	−2.216
200	−10.029	−2.242
250	−9.929	−2.642
300	−10.286	−2.234
350	−8.322	−2.189
400	−7.872	−2.286
450	−9.479	−2.294
500	−8.709	−2.093
550	−10.896	−2.255
600	−9.008	−2.303
650	−7.381	−2.427
700	−7.226	−2.212
750	−7.311	−2.266
800	−6.999	−2.136
850	−8.165	−2.070
900	−8.011	−2.203
950	−7.897	−2.384
1000	−7.2	−2.048

, the standard SAC algorithm exhibits unsteady and fluctuating performance during training episodes from 50 to 1000. Initial rewards decline from −8.891 to −10.699 by episode 150, with only slight and inconsistent through episode 300. In middle training, rewards initially improve—reaching −7.381 at episode 650—but remain erratic. In the next steps, SAC achieves its best reward of −6.999 at episode 800; however, overall, SAC struggles to maintain stable and high rewards over time, reflecting challenges in long-term policy retention. The SAC with EWC consistently exceeds standard SAC across all training steps. At the same time, SAC shows unstable and suboptimal reward trends. The SAC with EWC maintains stable and significantly higher rewards, ranging nearly from −2.266 to −2. The EWC-enhanced model exhibits better learning and improved convergence, especially during the middle to late training steps, where SAC rewards remain inconsistent; in contrast, SAC with EWC approach near-optimal values. This highlights the effectiveness of EWC in supporting stable and high-quality policy learning in DRL for the WFQ system over time.

Table 3. The MSE and MAE results for eight queues.

Episode Number	MSE	MAE
50	0.612392	0.583208
100	0.639665	0.614071
150	0.597392	0.601428
200	0.547177	0.572127
250	0.505351	0.553376
300	0.467858	0.53599
350	0.466958	0.539003
400	0.418296	0.510907
450	0.455936	0.532404
500	0.464072	0.53763
550	0.491030	0.552584
600	0.445696	0.526634
650	0.426627	0.513851
700	0.407303	0.502012
750	0.405632	0.500403
800	0.413735	0.506038
850	0.393311	0.492884
900	0.382233	0.486044
950	0.39783	0.497124
1000	0.419463	0.510144

presents the MSE and MEA records for every 50 episodes during training for SAC with EWC in the WFQ system, using the WFQ continual-DRL algorithm, which enables an assessment of how well the environment supports adaptive training and learning. The MSE value is 0.612 at episode 50, which rises slightly to 0.639 and exhibits more fluctuations. At the start of training, the agent typically explores different assignment procedures as actions (bandwidth weights) for the queues, resulting in increased fluctuations in the system. That point to the agent explores all possible processes of the action it is learning to reach an action that yields benefits. Then, it decreases to 0.597 at episode 150, indicates that the model was successfully adjusted and improved its predictions. These fluctuations are common in reinforcement learning and reflect the balance between exploration and convergence.

It can be observed that the MSE values steadily decrease from 0.547 at episode 200 to 0.445 at episode 600, suggesting steady learning and improvement in the model’s predictions. The results demonstrate successful training with continuous improvement in MSE between episodes 650 and 1000, and the model achieves its best performance while maintaining stable operation within these values. The slight increase in the MSE values after episode 900 remains within an acceptable range. The models reflect more complex or bursty traffic patterns that appear in training. Yet, the values of MSE remain within an acceptable range (near 0.47), meaning that the model has reached stability and effectively minimizes prediction error, although it has increased variability. The training process is well optimized, resulting in high accuracy.

From the column of MAE values, we see that this parameter is 0.583208 at episode 50, fluctuates slightly, and then improves to 0.535 at episode 300. Between episodes 400 and 700, the error remains controlled and stable, with a decline, indicating strong generalization capabilities. This suggests that the model is learning effectively and reducing prediction errors over time. The lowest MAE values are achieved at episode 1000 (0.510144), indicating that the model performs optimally towards the end of training. The learning process of the WFQ continual-DRL algorithm was efficient, as the estimation of errors was reduced over time, resulting in a well-optimized algorithm for dynamic traffic management.

In Figure 8, during training, the model with eight queues of WFQ initially has an MSE curve that rises to 0.7, indicating the model’s adaptation to changing queue dynamics. Then, it decreases and fluctuates within the range of 0.35–0.45, indicating a change into a steady-state. These bounded fluctuations confirm robust error minimization and model stability under a dynamic environment.

According to Figure 9, the MAE rises above 0.6, indicating an early training prediction error, and then gradually declines and stabilizes, with fluctuations in the range of nearly 0.5–0.55, reflecting steady fluctuations and demonstrating the model’s consistent performance in its dynamic state.

Table 4. The comparison of RMSE and Jain’s Index for eight queues.

Episode Number	RMSE for SAC	RMSE of SAC with EWC	Jain’s Index of SAC	Jain’s Index of SAC with EWC
50	0.115270	0.583208	0.451633	0.511600
100	0.095618	0.614071	0.517129	0.618827
150	0.082627	0.601428	0.548154	0.661623
200	0.060702	0.572127	0.590348	0.765714
250	0.084624	0.553376	0.557582	0.660985
300	0.057694	0.53599	0.673834	0.775280
350	0.054768	0.539003	0.702753	0.803767
400	0.046266	0.510907	0.645746	0.828189
450	0.050000	0.532404	0.668195	0.762000
500	0.052254	0.53763	0.668355	0.790373
550	0.062156	0.552584	0.640962	0.784969
600	0.060979	0.526634	0.664703	0.757960
650	0.059234	0.513851	0.654715	0.767560
700	0.054519	0.502012	0.648057	0.777945
750	0.061864	0.500403	0.666093	0.769028
800	0.068272	0.506038	0.680141	0.737892
850	0.069809	0.492884	0.658749	0.743764
900	0.068197	0.486044	0.630024	0.732841
950	0.065631	0.497124	0.650287	0.797796
1000	0.058266	0.510144	0.66	0.803811

represents a comparison between the RMSE and Jain’s Index of the WFQ-DRL algorithm and the enhanced WFQ continual-DRL algorithm. SAC integration with EWC yields lower average and minimum RMSE and appears to have better prediction accuracy. The SAC with the EWC model achieved higher fairness in resource allocation compared to the baseline SAC, indicating that the enhanced model maintains a better allocation bandwidth among network flows. Jain’s Index confirms that incorporating EWC leads to more stable and fair decision-making during training in dynamic environment.

Figure 10 shows a comparison between the curve of RMSE computed for SAC and SAC with EWC. After 200 episodes, the curve of SAC decreased to a stable range between 0.07 and 0.09. According to the curve for SAC, the EWC declines after 200 episodes, stabilizing between 0.05 and 0.07. The enhanced SAC with EWC exhibits higher learning performance, achieving a lower and more stable RMSE compared to the SAC. This suggests that EWC helps mitigate catastrophic forgetting learning, especially in complex or dynamic environments of the WFQ system. The curve of enhancement appeared to decrease in RMSE, reflecting improved steadiness and adaptability in decision-making. Lower RMSE indicates better accuracy in predicting actions in dynamic queue management (resource allocation) with respect to optimal resource allocation computed in the Fairness function.

As shown in Figure 11, the comparison of the Jain’s index between SAC and SAC with EWC reveals that the results show the curve of SAC after a 200-episode rise and steady between 0.6 and 0.7, while the curve of SAC with EWC remains stable after a 200-episode rise and remains steady between 0.7 and 0.8. Whenever the Jain’s Index value is close to 1, it indicates excellent fairness, meaning better exploitation of resources.

Complexity Analysis

The computation and comparison of the time complexity of SAC were implemented in the WFQ-DRL algorithm [22], and SAC with EWC was implemented in the WFQ continual-DRL algorithm in this paper. Analysis of the execution time for both average step and overhead represented by periodic FIM in DRL as a continual process, providing insight into the tradeoff between learning stability of performance model and computational cost.

For policy (π) network structure:

• Input layer 8 → 64
• Hidden layer 64 → 64
• Two output layers (μ, σ) 64 → 8 for each layer

Calculating the parameter (P) for the policy (π) structure:

• For the first fully connected layer O (8 × 64) → O (512)
• Second fully connected layer O (64 × 64) → O (4096)
• Output fully connected layer 2 × (64 × 8) → O (1024)
• Total P for policy network (π): O (512 + 4096 + 1024) = O (5632)
• Complexity model:
• For policy network (π) is O (1) because the dimension is constant.
• For the critic network (Q) structure:
• Input layer (8 + 8) → 16
• Hidden layer 64 → 64
• The output layer is a 64 → 1 output layer in a neural network
• Calculating the parameter (P) for the policy (π) structure:
• For the first fully connected layer O (16 × 64) → O (1024)
• Second fully connected layer O (64 × 64) → O (4096)
• Output fully connected layer (64 × 1) → O (64)
• Total (P) for one critic network (π): O (1024 + 4096 + 64) = O (5184)
• Total P for both critic networks (Q1, Q2) and policy network (π)
• 5632 + 2 × 5148= P (16,000)

Since the network dimension remains constant, the per-step computational complexity remains O (1). Over the course of N training steps (100 steps per episode), the total complexity linearity is O(N); although, for WFQ continual-DRL using SAC with EWC step cost remains O (1), an additional overhead of O(P) arises for 30 episodes due to FIM, highlighting the computational trade-off between standard DRL algorithm and enhancement algorithm introduced by continual learning.

For the complexity model:

• For critic network (Q): O (1), because the dimension is constant.
• Overall complexity for N training network steps:
• Total time complexity O (N × 1) = O(N).
• One episode has 100 steps, which is O (100), where N = 100.
• For 1000 episodes (100,000) where N = 100,000, 100 steps for each episode.

Where FIM computes every 30 episodes, 100 steps per episode, P = 16,000 parameters.

Table 5. Complexity time comparison between SAC and SAC with EWC.

Operation	SAC	SAC with EWC	Notes
Time per step	O (1)	O (1)	Constant time for each step in each algorithm
Time per episode cost	O (100)	O (100) +O (16,000)/30	FIM cost is computed every 30 episodes
Time per 30 episodes	O (3000)	O (3000) + O (16,000)	One full FIM computation

illustrates the complexity time comparison between SAC and SAC with EWC algorithm.

For the SAC algorithm, 1 step requires 0.004 s, so for 100 steps, the total time is 0.4 s.

For (SAC with EWC), FIM step time = 0.00294 s every 30 episodes. Total 30 episodes (30 × 0.4) + 0.00294 s = 12.00294 s. Experimental time comparison between SAC and SAC with EWC algorithm is shown in

Table 6. Experimental time comparison between SAC and SAC with EWC.

Operation	SAC	SAC with EWC
Time per step	O (0.004)	O (0.004)
Time per episode cost (100 steps)	O (0.4)	O (0.4)
Time per 30 episodes	O (12)	O (12.00294)

.

FIM updates every 30 episodes (3000 steps), making the overhead negligible, which is only added at a rate of 0.00294 s every 30 episodes (3000 steps). Total time added when computing FIM through 1000 episodes about 33 times =33 × 0.000294 s = 0.009702 s. By observation, the overhead caused by using FIM in the WFQ continual-DRL algorithm is negligible compared to the performance enhancement, indicating that the new algorithm, WFQ continual-DRL, functions effectively.

5.2. Experiment 2: Twelve Queues

The experiment was extended by increasing the number of queues to twelve to evaluate the robustness and scalability of the proposed WFQ DRL-continual approach. This expansion enabled a more comprehensive evaluation of the algorithm’s capacity to allocate bandwidth dynamically in a complex network environment. The twelve arrival flows had arrival rates $\lambda i$ = (0.0713, 0.0563, 0.0840, 0.0395, 0.0879, 0.0873, 0.0631, 0.0453, 0.0257, 0.0869, 0.0407, 0.1420) packets/s, and the interarrival times and service times were generated using a gamma distribution with an SCV of 0.8. The average packet size was assumed to be 1 byte per packet, and the total bandwidth was 1 byte/s. An individual queue has a limited buffer $K_1=K_2=\dots K_{12}=32$ packet. The control policy allocated bandwidth weights to $w_1+w_2+\dots +w_{12}=1$. The number of episodes was 1000, with each episode having a time length of 2000 s. Every 20 s, the agent took action.

After the random function was performed, ${\lambda }_{EWC }$ was obtained as explained in Section 2, running over a range of 1000 episodes to find an optimal ${\lambda }_{EWC }$ the FIM was computed every 30 episodes, and $F_i$ were stored with the parameters ${\theta }_i^{\ast }$.

A plot of the run-average reward for SAC with the EWC algorithm in the WFQ continual DRL algorithm is shown in Figure 12. It can be seen that convergence occurs after 200 episodes, and the range of reward fluctuation stabilizes between −2.5 and −1.9, resulting in consistent performance. At the beginning of the reward curve, the agent typically explores different assignment strategies (bandwidth weights) for the queues, resulting in more fluctuation. This means that the controller explores all possible processes of the action it is learning in order to achieve an action that yields benefits. As learning progresses, the agent exploits the probabilities of action, resulting in an increase in the reward curve; the policy then gradually converges toward the optimal allocation bandwidth, reducing the variability in the reward curve.

5.3. Training Real Traffic

In the experiment, twelve arrival flows with various flows (categories) arrive at the WFQ system of twelve queues. Twelve category groups of traffic data were used to train the agent. The average arrival rates of twelve sources in these twelve categories are shown in

Table 7. The average arrival rate of the first twelve categories.

Queues	Categories	Average Arrival Rates (Packets/s)
1	Chat	0.047179
2	Media	0.038448
3	Web	0.031438
4	VoIP	0.030870
5	software update	0.023940
6	Email	0.023906
7	Music	0.022780
8	collaboration	0.021974
9	Cloud	0.015814
10	Network	0.011008
11	Download File Transfer, File Sharing	0.005254
12	System	0.002918

.

The remaining twelve arrival flows with different flows (categories) arrive at the WFQ system of twelve queues. Twelve category groups of traffic data were used to train the agent. The average arrival rates of twelve sources in these twelve categories are shown in

Table 8. The average arrival rate of the second twelve categories.

Queues	Categories	Average Arrival Rates (Packets/s)
1	streaming	0.051215
2	RPC	0.134050
3	VPN	0.017920
4	shopping	0.019674
5	social media	0.078182
6	data transfer	0.205775
7	Mining	0.016681
8	Game	0.030445
9	remote access	0.040550
10	database	0.016725
11	Video	0.026934
12	unspecified	0.036511

.

The reward function is calculated as an equation:

$$r\left(q,a\right)=-\sum _{i=1}^8({\displaystyle \frac{1}{n}} q_i+l_i)$$

The episode time length, buffer size, and the total bandwidth resources are T = 2000 s, $K_1=K_2=\dots K_{12}=32$, bandwidth = 1 byte/s, correspondingly. Running the 1000 episodes to train the agent by the SAC with EWC algorithms of twelve queues.

A plot of the run average reward comparison of the twelve queues simulation curves, along with two datasets according to SAC with the EWC algorithm in the WFQ continual-DRL algorithm, is shown in Figure 13. For the first simulation curve, it can be seen that convergence occurs after 200 episodes, and the range of reward fluctuation stabilizes between −2.5 and −2, resulting in consistent performance. At the beginning of the reward curve, the agent typically explores different assignment strategies (bandwidth weights) for the queues, resulting in more fluctuation. This means that the controller explores all possible processes of the action it is learning in order to achieve an action that yields benefits. As learning processing, the agent exploits the probabilities of action, resulting in an increase in the reward curve; the policy then gradually converges toward the optimal bandwidth allocation, reducing the variability in the reward curve.

Referring to the convergence of the curve average reward after around 200 episodes for the first 12 categories of the real traffic 2 dataset, the range of the fluctuation curve gradually increases and shows steady fluctuation between −2.5 and −1.5, indicating a stable performance. According to the recent 12 categories of the real traffic two of the dataset, the convergence of the average reward curve is before 200 episodes, and the range of the fluctuation curve is between −1.8 and −1, reducing the fluctuation in the curve.

Table 9. Comparison of MSE and MAE values for all twelve queue scenarios.

Episodes	Twelve Queues of Simulation		Twelve Queues of Real Traffic 1		Twelve Queues of Real Traffic 2
	MSE	MAE	MSE	MAE	MSE	MAE
50	0.868022	0.643713	0.533128	0.573652	0.788154	0.696236
100	1.048262	0.676523	0.508042	0.557808	0.724009	0.672481
150	0.868753	0.659184	0.441298	0.517397	0.634688	0.629618
200	0.670131	0.648144	0.412639	0.499913	0.614650	0.617652
250	0.797906	0.61379	0.392221	0.487977	0.551309	0.585325
300	0.88304	0.608288	0.344662	0.458005	0.475661	0.542329
350	0.727278	0.679143	0.317199	0.440590	0.511582	0.560313
400	0.530156	0.575429	0.356414	0.468477	0.423877	0.512770
450	0.52626	0.572744	0.346210	0.461428	0.409414	0.502853
500	0.570297	0.599337	0.321819	0.445289	0.525351	0.571535
550	0.769053	0.702485	0.351930	0.466554	0.496567	0.555185
600	0.498518	0.557347	0.350638	0.465073	0.423494	0.509751
650	0.583851	0.59942	0.310275	0.437058	0.429814	0.515980
700	0.589354	0.6057	0.322598	0.445472	0.400673	0.499607
750	0.51114	0.564016	0.353146	0.467203	0.510712	0.560117
800	0.535042	0.577101	0.310399	0.437901	0.390746	0.489732
850	0.496227	0.55432	0.349823	0.463259	0.381719	0.485158
900	0.544107	0.58117	0.308214	0.435233	0.660230	0.636922
950	0.515378	0.565431	0.328040	0.449288	0.423070	0.512251
1000	0.490912	0.552778	0.331264	0.453266	0.411846	0.505342

presents the results of computing the MSE and MEA values for the twelve-queue scenario, which are used to measure the effectiveness of the environment in supporting adaptive training. The column containing the MSE values shows that at the start of training, the MSE is initially 0.8680; it then undergoes fluctuations before increasing to 1.0482 as the environment is explored and gradually improves during training. The slight variation suggests that the model is still learning, adjusting parameters, and refining predictions. By episode 300, the error is relatively steady compared to the prior fluctuations, indicating better convergence. In the intervening episodes, from 300 to 700, the error is more stable than the previous fluctuations, indicating better convergence. A noteworthy development is observed in the value of the MSE, which drops to 0.5302 at episode 400 and remains low, at approximately 0.5263, until episode 450. In the steady state, from episodes 400 to 700, the MSE values exhibit strong consistency over time, indicating that the model makes predictions that are consistent and accurate. Small fluctuations are expected during training due to the dynamic nature of the environment. The lowest MSE value of 0.4909 is observed at episode 1000, confirming the optimal performance of the model. The results for the last 200 episodes suggest that the model has achieved high accuracy and stability, as the variation between episodes 750 and 950 remains controlled. From the column of MEA values at the start of training, showing that the MEA is 0.6437 at episode 50 and increases slightly to 0.6765 at episode 100. A slight increase is expected when the model adjusts at episode 300 during training, and the MEA value stabilizes, indicating that the model is starting to learn effectively. The MEA value decreases from episode 400 (0.5754) to episode 750 (0.5640), indicating that the model is learning to make more accurate predictions. The fluctuation between episodes 600 and 700 (between around 0.5994 and 0.6057) suggests that the model exhibits normal and healthy training behavior. At episode 1000, the lowest MAE value of 0.5528 is recorded, indicating optimal performance. From episode 850 (MAE values 0.5543 to 0.5528), the model maintains a constant learning rate with minimal fluctuations.

According to the evaluation of the twelve-queue real traffic for the first twelve categories using MSE and MAE metrics, there is an improvement in model stability over time. According to the MSE, a consistent decline across the training episodes indicates advanced improvement in the model’s predictive accuracy. Beginning at 0.533 in episode 50, the MSE declines to 0.317 in episode 350, reflecting effective start learning. Between episodes 400 and 700, the MSE values fluctuate between 0.322 and 0.356, suggesting a stabilization phase where the model fine-tunes its parameters. In the final episode, from 750 to 1000, the MSE continues its downward trend, reaching 0.331, which highlights the model’s capacity to minimize errors over time. The MAE shows below throughout the training process, suggesting improvements in the model’s average prediction accuracy, which starts at 0.574 in episode 50, then decreases to 0.441 in episode 350, indicating successful initial learning. Between episodes 400 and 700, the MAE values exhibit small fluctuations, ranging from 0.445 to 0.468, which reflects the model’s efforts to refine its predictions and handle more nuanced patterns in the data. From episode 750 to 1000, the MAE continues to decline, reaching 0.453, which underscores the model’s steady improvement in minimizing average absolute errors.

Referring to the twelve-queue real traffic for the second twelve categories using MSE and MAE metrics, the MSE indicates a decreasing trend through the training process, showing advanced improvement in the model’s predictive accuracy. Beginning at 0.788 in episode 50, the MSE declines to 0.511 by episode 350, which is effective in early-stage learning. Between episodes 400 and 700, the MSE values fluctuate within a range of around 0.400 to 0.525, suggesting a stabilization stage where the model fine-tunes its parameters. In the last phase, from 750 to 1000, the MSE continues its downward trend, reaching 0.412, which indicates the model’s capacity to minimize errors over time. The MAE for real traffic of the recent twelve categories also displays a decreasing trend throughout the training process, indicating improvements in the model’s average prediction accuracy. Initiating at 0.696 at episode 50, the MAE decreases to 0.560 at episode 350, indicating successful initial learning. Between episodes 400 and 700, the MAE values exhibit minor fluctuations, ranging from 0.499 to 0.571. From episode 750 to 1000, the MAE decreases, reaching 0.505, which highlights the model’s steady improvement in minimizing average absolute errors.

In conclusion of comparison Table, the simulation has higher MSE and MAE than real traffic 1 and traffic 2 for twelve queues of the dataset; it generalized well to real-world conditions. A G/G/1/K WFQ system parallel queuing model with a gamma distribution was formulated to simulate complicated network traffic. That indicates that the simulation accurately captured realistic traffic variability and system conditions. Thus, the WFQ scheduler, as implemented in continual and DRL framework, demonstrated robust performance, validating its effectiveness.

According to Figure 14, the MSE curve initially rises to 0.8, indicating prediction error during early adaptation. In the last episodes of training, it then decreases and enters a steady fluctuating range nearly between 0.5 and 0.7. This bounded variability indicates that the model has stabilized and maintains reliable performance under dynamic multi-queue conditions, although in extended queues.

As shown in Figure 15, during the early training, the MAE curve rises to 0.7 in the initial step, indicating a high error. In the last episodes, it then drops and stabilizes within a fluctuating range between nearly 0.55 and 0.65. This behavior suggests the model’s ability to generalize while maintaining consistent performance in a dynamic environment.

According to Figure 16, the MSE curve for the twelve-queue system trained on real traffic exhibits a high initial error due to the complexity of the traffic patterns. Still, it gradually decreases and stabilizes between 3.0 and 3.5, indicating that the model has effectively learned and adapted to real-world traffic.

For Figure 17, the MAE curve begins with a high error, reflecting meaningful early prediction deviations. As training advances, the error steadily declines. It stabilizes between nearly 4.0 and 4.5, demonstrating bounded fluctuations. That indicates the model has adapted well to real traffic dynamics and supports robust performance.

Regarding Figure 18, the MSE curve for the second real traffic dataset starts high, reflecting the initial instability of the prediction. It gradually decreases and stabilizes within the range of 4.5 to 5.5, showing enhanced model learning. This trend suggests that the model is evolving to accommodate more diverse traffic patterns over time. Despite the dynamic challenges, the error range suggests reliable convergence and robust performance.

Referring to Figure 19, the MAE curve for the second real traffic dataset initially increases sharply, exhibiting poor early prediction accuracy. As training progresses, the error decreases and stabilizes within a narrow range of 0.5 to 0.6. This steady fluctuation suggests the model has adapted better to the traffic dynamics. The bounded MAE range reflects consistent and robust performance under real-world dynamics.

The processing with statistical analysis addresses bursty real traffic for all categories, after which the dataset is equal to 1,393,777 [33].

Regarding the Square Coefficient of Variance ${CV}^2$ in the real traffic data, computed in equation [33]:

$${CV}^2={\displaystyle \frac{\sigma }{m}}$$

(18)

where $\sigma$ represent standard deviation, and $m$ represents the mean. As illustrated in Figure 20, a higher ${CV}^2$ indicated that the real traffic data arrival patterns were more unpredictable and random. High variance reflects the bursty and unpartable nature of real traffic conditions.

To compute correlation, the copy of interarrival time will be shifted to one position, and the correlation coefficient for real traffic will be computed in the equation of correlation coefficient [34]. The results shown in Figure 21 revealed that the real traffic data appear to have a more dynamic pattern in its correlation. The decline of correlation curves indicates more influence. The statistics clearly showed patterns of bursty traffic.

This paper presented knowledge that improved this algorithm by combining the continual learning technique with the DRL algorithm for the WFQ system. The development of the WFQ continual-DRL algorithm was achieved by contributing a continual learning method represented by the EWC technique, which helps to overcome catastrophic forgetting by remembering old tasks, selectively slowing down learning on the parameters important for those tasks, and improving the performance over time, which is combined with advanced deep reinforcement in the form of the SAC algorithm. In addition to developing this algorithm, the evaluation of the algorithm was expanded by increasing the number of queues to twelve. This expansion was considered to assess the scalability and robustness of the model in terms of managing higher traffic loads and more complex network conditions. The aim was to maximize the cumulative reward, and this approach achieved an improvement of approximately 76% in performance compared to the baseline reward curve in an experiment involving eight queues for WFQ-DRL. This finding demonstrates the effectiveness of our approach in regard to maintaining stable learning and adapting to new tasks while retaining previously learned knowledge. For the expansion in a second experiment involving twelve queues, the average reward curve shows an enhancement in performance by increasing reward with smother fluctuation, indicating that this new approach is more effective even with an expanded environment, is more robust, and is suitable for the nature of the queueing system, as it carries out dynamic bandwidth allocation control among WFQ parallel queues. The model shows higher reward than compared to simulation of twelve queues. This suggests that the model adapts well in real world traffic, and the result highlights the model’s effectiveness under realistic traffic environments.

6. Discussion

The proposed approach in the form of the WFQ continual-DRL algorithm and its implementation in the system model to achieve dynamic bandwidth allocation leads to the following observations:

• By dynamically adapting the weights assigned to each queue, the system can react to irregular traffic patterns, optimize bandwidth utilization, and maintain service quality.
• Training the agent encourages the development of adaptive policies for weight assignment in WFQ systems, enabling real-time optimization based on monitored network states through interaction with the network environment.
• Traffic patterns can change over time in dynamic network environments, meaning that the WFQ continual-DRL algorithm must continually adapt to these changes. Without an approach such as EWC, the agent may forget previously learned optimal policies, a phenomenon known as catastrophic forgetting. The EWC trains a regularization term added to the DRL loss function by penalizing significant deviations from parameters essential to previously learned tasks. This ensures that new learning does not overwrite valuable existing knowledge and maintains consistent performance across varying networks. In scenarios involving eight and twelve queues, a higher value of ${\lambda }_{EWC }$ strengthens regularization, meaning that important knowledge persists as complexity increases. This improves performance by balancing adaptability and memory retention, ensuring the effectiveness of the WFQ continual-DRL learning algorithm.
• Expanding the number of queues enables a more fine-grained allocation of bandwidth, representing a test of the adaptability of the WFQ continual-DRL approach in optimizing resource distribution under dynamic traffic scenarios. The results indicate that the model successfully generalizes to larger queue sets while maintaining stable performance, as reflected in the stabilization of the reward.
• When the number of queues is expanded, the parameters of the neural network structure in SAC-EWC need to be tuned by increasing the number of neurons, batch size, and buffer size, which enables the model to capture more complex patterns in the data. As a result, it enables the model to make more informed decisions, thereby improving performance and reward.
• The implementation of EWC as one mechanism of continual learning requires additional computational resources due to the regularization term in the loss function. It is, therefore, essential to balance the benefits of EWC with the available computational capacity. In this investigation, a random function was used to select an appropriate strength for the EWC regularization term. Appropriate tuning ensures that the model maintains stability without restricting its ability to learn new patterns in the network traffic.
• The steady decrease in MSE and MAE in both the eight- and twelve-queue systems suggests effective learning and enhanced prediction accuracy, ensuring reliable decision-making and consistent performance.
• The RMSE results clearly indicate that the SAC enhanced with EWC yields a lower prediction error compared to the baseline SAC model. After approximately 200 episodes, while the standard SAC stabilizes in the range of 0.07 to 0.09, the enhanced model further reduces the RMSE and stabilizes between 0.05and 0.07. This improvement demonstrates the effectiveness of EWC in preserving important learned parameters, resulting in more accurate and stable policy predictions over time.
• In addition to improving prediction accuracy, as shown by the RMSE results, SAC with EWC also achieves a higher Jain’s Fairness Index, indicating better resource allocation across various network flows. The fairness values are closer to 1, not only showing the enhanced model performance but also maintaining fairness in scheduling decisions. The importance of employing EWC in environments with a WFQ system lies in the fact that fairness is as critical as efficiency.
• The integration of EWC for continual learning within the DRL algorithm enhances accumulative rewards over time by preserving effective policies from prior network states, leading to enhanced performance as the agent encounters new traffic patterns. By mitigating the problem of catastrophic forgetting, the WFQ continual-DRL algorithm is an effective strategy.
• The real traffic in a network revealed a higher reward for two real traffic of various categories. On the other hand, they are more bursty with higher variance. Furthermore, they offer unpredictable patterns that the SAC with EWC for the proposed algorithm can exploit, resulting in better learning and higher cumulative rewards than simulation traffic.
• Continual learning through EWC helps retain practical knowledge across similar queue behaviors in real traffic, enhancing generalization and performance, meaning that the traffic generated in simulation is more aggressive, indicating that the model can handle various patterns and categories of real traffic.

Finally, integration of the EWC technique as a continual learning approach into DRL frameworks, realized here in the form of a new algorithm called WFQ continual-DRL for WFQ systems, facilitates adaptive dynamic bandwidth allocation, thereby enhancing the system’s ability to maintain optimal performance across varying network conditions. This new approach enables more robust and reliable network management, effectively reducing packet loss and queue lengths and enhancing the overall quality of service (QoS), although in real world conditions.

7. Conclusions

In this paper, a new integrated adaptive algorithm called WFQ continual-DRL was developed to enhance dynamic bandwidth allocation for each queue in a WFQ system. The proposed algorithm enables the system to obtain a policy agent that learns the optimal weights for different arrivals of network flows. Our contribution involves integrating the adopted reinforcement learning algorithm, known as the SAC algorithm, with the EWC approach, which supports continual learning in the more challenging field of DRL. To enable this implementation to be compared to the existing extensive telecommunication network, this investigation considered two scenarios: the first utilized eight queues, while the second employed twelve. The findings demonstrate that incorporating EWC effectively mitigates the issue of catastrophic forgetting in DRL models, thereby improving learning stability and the models’ adaptability to new tasks without compromising prior performance. This achieved high performance by enabling efficient learning, rapid adaptation, and scalability, even when the number of queues increases. This integration significantly improved the performance of the measurement system, as reflected in cumulative reward. The results achieved an improvement in the reward curve in an experiment involving eight queues, and expanding to twelve queues appears to result in increased and smoother fluctuation of average reward, indicating improved overall performance of the MSE, and MAE and resulting in more reliable decision making within WFQ environments, particularly through dynamic bandwidth allocation. The comparative evaluation between the enhanced WFQ continual-DRL algorithm demonstrates that integrating EWC significantly improves accuracy, as indicated by a lower RMSE, and fairness, as reflected in a higher Jain’s Index of the learning model. This enhancement of continual learning techniques in DRL and scheduling is important for resource allocation, mainly in complex network environments. Finally, training and evaluation of real traffic flows of the dataset indicate the agent to achieve better performance across diverse conditions, resulting in more adaptable and effective bandwidth allocation processes across twelve queues simulation, indicating that the model training is under aggressive traffic. An interesting direction for future study would involve integrating real network traffic data to effectively assess the algorithm’s performance under real-world conditions in dynamic and complex network environments.