Abstract
Vehicular Ad Hoc Networks (VANETs) serve as critical platforms for inter-vehicle communication within constrained ranges, facilitating information exchange. However, the inherent challenge of dynamic network topology poses persistent disruptions, hindering safety and emergency information exchange. An alternative generalised statistical model of the channel is proposed to capture the varying transmission range of the vehicle node. The generalised model framework uses simple wireless fading channel models (Weibull, Nakagami-m, Rayleigh, and lognormal) and the large vehicle obstructions to model the transmission range. This approach simplifies analysis of connection of vehicular nodes in environments were communication links are very unstable from obstructions from large vehicles and varying speeds. The connectivity probability is computed for two traffic models—free-flow and synchronized Gaussian unitary ensemble (GUE)—to simulate vehicle dynamics within a multi-lane road, enhancing the accuracy of VANET modeling. Results show that indeed the dynamic range distribution is impacted at shorter inter-vehicle distances and vehicle connectivity probability is lower with many obstructing vehicles. These findings offer valuable insights into the overall effects of parameters like path loss exponents and vehicle density on connectivity probability, thus providing knowledge on optimizing VANETs in diverse traffic scenarios.
1. Introduction
The advent of Vehicular Ad Hoc Networks (VANETs) has ushered in a new era of intelligent transportation systems, promising safer and more efficient roadways through real-time inter-vehicle communication. This technology is poised to revolutionize the automotive industry by enabling vehicles to share critical information, such as traffic updates, collision warnings, and emergency alerts, within the confines of limited communication ranges. Yet, as with any promising technology, VANETs confront formidable challenges that merit rigorous investigation.
Foremost among these challenges is the ever-shifting landscape of VANET network topology. The nature of vehicular networks, characterized by rapidly moving nodes and dynamic formations, engenders a highly variable communication environment. This dynamism, while inherent to VANETs, introduces a significant obstacle to sustaining reliable communication links. The intermittent disruptions in connectivity threaten to compromise the very safety and efficiency that VANETs are designed to enhance.
1.1. Contribution
This paper presents a simple analytical framework for connectivity that accounts for the statistical variations in network topology. Building upon existing research, probabilities of connectivity to encompass the impact of wireless fading channels and obstructions posed by large vehicles—a crucial consideration in real-world vehicular environments are derived. Our approach draws inspiration from well-established wireless fading models, including Weibull, Nakagami-m, Rayleigh and lognormal distributed channels capturing highway, urban and rural networks communication environments in order to improve vehicle connection as in [1]. These models have been instrumental in the field of wireless communication, providing valuable insights into the behavior of signal propagation in varying conditions. Our main contributions are:
- Firstly, the paper introduces a method for dynamically computing the probability of successful communication between vehicles in VANETs. Utilizing dynamic communication range statistics based on random channel models, the approach effectively accommodates the fluctuating nature of VANET environments, accounting for factors like vehicle density and signal propagation. This contribution enhances the accuracy of inter-vehicle communication assessment in dynamic VANET scenarios.
- Secondly, the paper contributes by introducing and utilizing two distinct traffic models—free-flow and synchronized Gaussian unitary ensemble (GUE)—to simulate nuanced vehicle dynamics on multi-lane roads. The free-flow model depicts independent vehicle movements, while the GUE model represents synchronized behaviors, enhancing the realism and applicability of traffic simulations. This dual-model approach enriches the understanding of multi-lane road scenarios, offering valuable insights for transportation and traffic engineering applications.
- Lastly, the paper also introduces a versatile mapping framework, enabling the calculation of vehicle-to-vehicle connectivity probability across diverse traffic models. The proposed framework offers a generalized approach, making it valuable for assessing connectivity probabilities in various traffic scenarios, particularly beneficial for applications in traffic simulation. This contribution enhances the adaptability and utility of connectivity assessments in dynamic traffic environments.
1.2. Related Works
1.2.1. Environmental Conditions
Several works investigate the connectivity of VANETs operating in dynamic environments such as urban, suburban, and city areas having highways with high mobility, fading channels, and shadowing effects, which typically affect communication links of vehicle nodes [1]. To understand these environmental conditions, ref. [2] authors present an obstacle-based radio propagation model that considers the effect caused by the presence of obstructing vehicles in the Line-of-Sight model. They conducted experiments to evaluate the model under different environmental conditions (city, highway, and rural) by varying vehicle density to study the effect of throughput operation and packet collision considering environmental factors for multi-channel dedicated short-range (DSRC) based vehicle-to-vehicle (V2V) communication. A mesoscopic vehicular mobility model in a multiple-lane highway with a steady-state traffic flow condition is adopted where different inter-vehicle distance distributions are utilized. Authors in [3] propose using the spatial point processes to model random vehicle locations in a two-dimension instead of the one-dimension in small and large cities. Works in [4,5] investigate vehicle connectivity probability in dynamic environments. Authors in [4] consider the different traffic conditions: high, medium, and low density based on the V2V measured data at 5.9 GHz, then simulate the connectivity of the VANETs. The work in [6] considers both cognitive and communication probability to derive cellular vehicular connectivity probability. However, most of these works do not consider the general channel effects that both fading and shadowing have on vehicle communications.
1.2.2. Propagation Channels
To understand the channel effects on VANETs communication works in [7,8,9] analyzed the performance of VANETs. An in-depth VANETs performance analysis under different channel models is discussed by combining Physical and MAC layers [7]. While authors in [8] derived closed-form expressions of packet loss, packet error, and outage probabilities under different fading channels. For vehicle mobility and signal propagation environment effects on the link duration, ref. [10] uses a modified Markov model to show transitions in the inter-vehicle distribution using a path loss transmission model. An alternative path loss and shadowing model is used to analyze at 5.9 GHz the auto-correlation of the large-scale fading process [8]. The overall connectivity of V2V with both vehicle travel directions is analyzed for spectrum-agile VANETs in fading channels in [9,11]. Lastly, authors in [11] analyzed how the effect of fading improves connectivity in VANETs.
1.2.3. Network Obstructions
Recent studies on large vehicle obstruction effects on VANET communication are considered in [12,13,14,15,16,17,18]. For single large vehicle obstruction effects, ref. [12] presents measurements of the impact of vehicle size on the Doppler spreads in the V2V radio channel at GHz. In contrast, authors in [16] present an analytical model for the power contributions from diffraction around a truck. They show that without a strong line-of-sight component, packet delivery depends on other propagation mechanisms that are statistically more likely to add destructively so that the signal falls below the noise threshold of the receiver vehicle. The work in [18] focuses on the directional analysis of large vehicle obstructions in V2V channels. They show that not only do large vehicles cause additional attenuation of signal energy but also significantly affect the angular distribution of multi-path components in three-dimensional space and bring larger angular dispersion.
In [17], channel measurements in an urban scenario for three test cases, non-obstruction, small-vehicle obstruction, and large-vehicle obstruction, are compared and analyzed for the performance of path loss characteristics. The joint effects of radio environment and traffic flow on link connectivity are investigated to represent the obstruction probability and inter-vehicle connectivity probability. Here, the authors considered highway moving obstacles following a light-of-sight blocked model [15]. The works in [12,14] use geometric and stochastic shadowing of multiple big vehicles on multiple lanes to understand their impact on V2V communications.
In [12], hardcore repulsive Poisson point process (HRPPP) was proposed to model the locations of vehicles, while [14], instead considers the big vehicle selective relaying strategy to enhance V2V communication. It can be observed that none of the works investigates the combined effect of obstruction and channel fading. The works that come close to giving a generalized connectivity analysis for VANETs is [19]. However, the closed-form generalized connectivity probability was not given for the Nakagami-m fading channel, which we provide in this work, and for other fading channels. Moreover, this paper further gives generalised connectivity expressions with big vehicle obstruction effect for all fading channels considered. While [20] analyzed the impact of the radio channel modeling on the connectivity performance of a VANET with incomplete random communication range statistics, it ignored generalized inter-vehicle distribution, a modal considered in [19].
1.3. Notations Used
Table 1, lists the notations used in this paper.

Table 1.
Notations used throughout the paper.
2. System Model
We consider an unidirectional and uninterrupted two-way vehicle traffic highway for simplicity. The network consists of N vehicles, which are randomly distributed along the highway segment. We assume that of the N distributed vehicles, there are probable big vehicles that block communication links between transmitter and receiver nodes. Each smart vehicle is equipped with a global positioning system (GPS) integrated into the on-board unit (OBU) from which the state of neighboring vehicles, such as location, velocity, and lane number information, is easily obtained and also provides inter-vehicle communication through basic messages (BMS) exchange. Big vehicles do not have the smart communication capability and just obstruct communications. Moreover, overtaking tendencies of vehicles and lane changes are not permitted.
To proceed, we assume an observer position O where N vehicles with arrival rate follow a Poisson process. For each vehicle, an independent and identically distributed velocity of is given for with rates of . See details in [11]. A minimum safety distance s is maintained between vehicles at all times to prevent accidents as shown in Figure 1a, while a MAC protocol is assumed for simplicity of analysis.
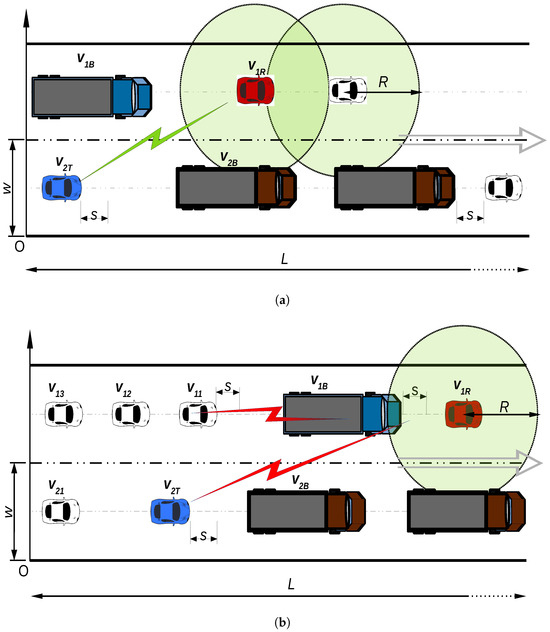
Figure 1.
System model for VANET in a two-lane one-direction road section, with safety distance s. (a) Free-flow traffic model, no big vehicle shadowing. (b) Synchronised-flow traffic model, due to big vehicle shadowing.
In Figure 1a, a free-flow traffic model is captured on the highway segment of length L where vehicle velocities V follow a Gaussian distribution [22]. A synchronized flow following GUE is considered in Figure 1b, to capture the traffic congestion effect. In the GUE case, the vehicle speeds are low, but the general flow is similar to a free-low traffic model and not in the extremely wide moving jam–where average speeds are lower than in free-flow traffic and tending towards a stop for some time. The inter-vehicle distance in this model is modeled as a Gaussian unitary ensemble of the random-matrix theory [19]. Thus, the limiting inter-vehicle distributions in a and b are the exponential and GUE as shown in Section 3.3.
Therefore, this paper seeks to use a generalized mapping distribution that captures both extremes of free-flow and synchronized traffic flow models. Typically, V2V communications are prone to a dynamic environment modeled by small-scale fading channels. With extreme specific conditions captured by the Rayleigh, Nakagami-m and Weibull distributions. The small-scale fading to no-fading conditions vary between having no line-of-sight (NLOS) to LOS components. We also include another factor of big-vehicle obstructions, which has been shown to contribute immensely to path losses of 7 dB to 20 dB on highways [13]. A signal received by from would be affected by a small-scale fading channel, H, in addition to other roadside shadowing effects, nearby vehicles, and big vehicle obstructions of .
In Figure 1a, we see that in lane 1 and in lane 2 are fully within each other’s communication range, and they can connect and establish links between them. Since we do not consider overtaking scenarios, communicating vehicle, will be slowed down by the big vehicles with speeds respectively. As is not impeded by any vehicles ahead, it drives away faster where the trailing vehicles follow. As the trailing big vehicle on the adjacent lane approaches, the effect is that the link established earlier is broken by this big vehicle. Now, a new randomized communication range can be derived by coupling both the big vehicle shadowing and the small-scale channel effects and following the limiting traffic inter-vehicle distance distributions.
3. Analytical Procedure
3.1. Static Communication Ranges
In a V2V communication between two adjacent vehicle nodes, the received power can be expressed as;
where is path-loss at unit reference distance, is inter-vehicle distance between two adjacent vehicles, is path-loss exponent.
While in a LOS (1a), for the NLOS link case, a bus shadowing effect is considered for k big vehicles (buses), each causing a path-loss as in [13] while blocking the communication link of the intended receiving vehicle (with ) in (1b). Thus if , or is determined by transmitted power, and (bus shadowing effect), then the distance between vehicle, d is considered the transmission range R, hereafter referred to as deterministic transmission range and expressed from (1) as
for (2a) without bus shadowing (WBS) and (2b) with bus shadowing effect, respectively.
3.2. Random Communications Ranges
For a general channel effect on the transmitted signal, G would be considered random due to effects of fading (fast and slow), shadowing and therefore used in deriving the random transmission ranges, R. Rayleigh, Nakagami-m fading channels and Lognormal shadowing effects coupled with bus shadowing effects are used in the derivations.
3.2.1. Rayleigh Fading Channel Effect
We assume that a slow fading channel is constant over a frame transmission period and only varies in the next data transfer period. For a received signal, the signal-to-noise ratio SNR, is Rayleigh distributed with probability density function, PDF given by [23];
where and is the noise power in the channel. Thus the average received SNR Rayleigh channel both with and without bus shadowing effect is expressed as (using range in (2))
By considering the transmission range for a received signal, the average SNR for non-bus and bus shadowing effects are respectively given as;
The received power in both cases is due transmitted through channel, and the transmission radius for each vehicle is a random variable whose distribution can be derived from the received SNR’s distribution above as follows. To successfully decode a received signal, the SNR must be greater than the receiver sensitivity (a threshold set according to coding and modulation schemes, [24]), , i.e., . Thus, the cumulative distribution function CDF, of the received SNR, is expressed as;
where average SNRs and are given above for both bus and non-bus shadowing effects, respectively. Now, if connectivity is to be established between adjacent vehicles as per the channel effects, then their geometrical spatial distance of separation must be less than the communication or transmission range of either vehicles, i.e., [25]. Thus, it can be shown that since the received SNR, is a function of transmission range R, the CDF of R can be expressed as follows
such that is a function of the transmission range, r and the PDF, is simply obtained by differentiating w.r.t. r. On substituting for the bus and non-bus shadowing related average received SNRs, and defined as before, the CDFs are given as follows respectively;
for (7a) without bus-shadowing (WBS) and (7b) with bus shadowing (BS) effect, respectively. To simplify notation hereafter, the symbols and are used to represent scaling factors of the CDFs above as follows: and . Hence, the related PDFs, are given as
For a non-negative continuous random variable, the expectation and variance of the range in this channel instance in a non-bus shadowed channel are
By replacing with whose value was defined before into and gives respectively, expectation and variance of R in a corresponding big vehicle shadowed channel scenario.
3.2.2. Nakagami-m Fading Channel Effect
For Nakagami-m fading channel with [7,26], we assume it is constant or block-fades for a period of transmission of data frames, and it varies during the next period of frame transmission. The received SNR, in this case, has a distribution with PDF given as;
where is the average received SNR, and m the fading parameter, gamma function [27]. We also follow the procedure used in the Rayleigh fading case to derive the distribution of the transmission range here. To decode the transmitted signal accurately, the received SNR, , where is dependent on receiver sensitivity. Thus;
Given is dependent of transmission range, the distribution of R can be derived as well, i.e., CDF is given by;
and after substituting in the average bus and non-bus shadowed received SNRs (2) into (11) is;
where and and . Then related PDF, . After some manipulation is given as;
for (13a) without bus and (13b) with bus shadowing effects, respectively. For the random variable range R, the expectation and variance for a non-big vehicle shadowed channel are expressed as follows using results from [23];
By replacing with into and gives the expectation and variance of R in a corresponding big vehicle shadowed channel scenario.
3.2.3. Weibull Fading Channel Effect
The range-based distribution in a Weibull fading channel follows with CDF given as;
where C is Weibull fading parameter [22] in the range , is the path-loss exponent in the range . corresponds to a Rayleigh fading channel, is path-loss constant, and is the gamma function. As before, we find the CDF as;
where , , and . Then the PDF, given by is;
(16a) for w/BS and (16b) with bus shadowing effects, respectively. The expectation and variance respectively are;
By using the corresponding big vehicle shadowed channel scenario, we swap instead of .
3.2.4. Lognormal Channel Shadowing Effect
From [22], the shadowing is given by the lognormal distribution where the signal power is in dB. Thus, the received signal SNR dependent of the transmission range is lognormal distributed. The range, R’s distribution can be derived below. If the PDF of SNR is
then the CDF of the range, R is derived as;
Suppose the mean received SNR without bus shadowing effect is . Let and . Then by change of variable and simple manipulation;
where . With a bus shadowing pathloss effect, the overall mean SNR is where k is the number of big vehicles each causing a pathloss of . Therefore, by the above procedure, the CDF of transmission range, R under big vehicle shadowing, is given by;
Shown as above, we write the CDF of R in a lognormal distributed shadowed channel as;
where and as before. The PDF of R, is derived as;
By using Leibniz integral theorem on the last term yields;
The PDF in both cases of shadowing effects (non-bus (23a) and bus (23b)), the is given by
The expectation and variance variable R, for a non-big vehicle shadowed channel using same procedure and results in [26] after some mathematical simplification yields respectively;
Indicated as before, for the corresponding big vehicle shadowed channel, substituted for instead. We give a summary for the distribution (PDFs of R) in Table 2, in the different channels and their statistics in terms of expectations and variances (where and can be used for non-bus and bus shadowing effects respectively).

Table 2.
Statistics of transmission ranges, R.
3.3. Vehicle Velocity Distribution in Traffic
Work in [28,29] indicate that the velocities of the vehicles are Gaussian distributed with PDF as;
where , are the variance and expectation respectively.
Remark 1.
It can be noted that this velocity distribution caters to traffic scenarios where overtaking is possible in the microscopic traffic model or a free-flow traffic model for which slower moving vehicles can be overtaken in a multi-lane road such as a highway or urban roads. Thus, vehicle velocities tending towards zero can be captured by this standard Gaussian distribution. On the other hand, the practicality of traffic on multi-lane urban roads or highways in a free-flow model [30], bounds vehicle velocities away from zero and cannot be negative such as in a congested traffic where vehicles can stop (due to traffic signals). Moreover, to analyse free-flow traffic with overtaking, a modified Gaussian distribution (truncated version) is considered for vehicles whose velocities are non-zero and positive. In this section, and overall in the work, we consider truncated Gaussian velocity distribution. For a modified (truncated) Gaussian velocity, the variable [20,24], where and is given by PDF;
where and whose equivalent speed is given as;
3.4. Single-Hop Inter-Vehicle Distance
3.4.1. Free-Flow Traffic
In this model, for a Poisson point process distributed N vehicles in the network with rates in a road section of length L are shown to be displaced independently given their individual velocities [30]. Moreover, the distance between any two adjacent vehicles is exponentially distributed and used typically in numerous literature on analyses of connectivity. This distance, D’s distribution PDF is: , where . To study realistic vehicle traffic, a component of safety distance s used to cater to the minimum acceptable distance of separation of vehicles and analyse connectivity of vehicles [31]. Authors in [13] use this modified version of separation distance (known as HRPPP) by incorporating s to study big vehicle shadowing effect in a multi-lane highway. The truncated exponential adjacent distance distribution PDF is;
whose exact expectation and variance are given by;
where , and is vehicles mean velocity.
3.4.2. Synchronised Transition Traffic
To consider transitions from free-flow traffic to wide moving traffic, the inter-distance of adjacent vehicles is captured using a Gaussian unitary ensemble (GUE) of a random-matrix theory. Moreover, synchronized flow can be understood as a phase from free-flow traffic to wide jam [20] whose distribution has PDF given as;
where
are the expectation and variance of adjacent inter-vehicle distances in this synchronised traffic scenario.
3.4.3. Generalised Inter-Vehicle Distribution
For a general mapped inter-vehicle distance distribution between the exponential and the General Unitary Ensemble (GUE) as discussed in [19] is given by the mapping PDF,
where . By letting gives the exponential and GUE distributions in (21) and (22) respectively.
3.5. Connection Probability Using Dynamic Communication Ranges
In this section, we analyse the connectivity probability between two adjacent vehicles communicating with each given a transmitting power, and known associated distributed communication range, R as derived in the previous section. To simplify analysis and limit space, the connectivity in the case of big-vehicle shadowing shall be included without derivation since only the constant term is replaced. For a receiving vehicle to communicate with a transmitter, their inter-vehicle distance of separation D must be less than the communication range. Then the probability of connection, given in [20,22] and with N vehicles within a network area under consideration, the overall connectivity is given by;
where is the number of communication links. Since both D and R information is known, it is simple to derive and later give the significance of the result for different road situations.
3.5.1. Case 1: Static Communication Range
The probability of connectivity for static communication ranges can be generally mapped as;
where R is range in (2), is the lower incomplete gamma function.
Proof.
Two vehicle nodes communicate when their inter-vehicle distance is less than the communication range. Thus the probability of connectivity is found as;
In above, we let and ; then using procedure in [31] in and substituting A and B gives (31). □
If we let for exponential and GUE (synchronised) inter-vehicle distance distributions respectively,
is the error function. Equation (26) can be directly evaluated for individual distributions as well.
3.5.2. Case 2: Random Distributed Communication Range
For this case, we use the random variables of range R and the separation distance D between two communicating vehicles. The connectivity probability then can be derived by conditioning on R (using the law of total probability, [26]).
Case 2.a: Nakagami-mdistributed range. For Nakagami-m fading channel, the connectivity probability was given in Section 3.2.2 and here, we provide the closed-form expression for the mapped-inter-vehicle distance distribution. Later, Rayleigh distributed probability connectivity can be derived by simple substitution of the fading factor, . For mapped inter-vehicle distance and Nakagami-m distributed range PDF in (13), connectivity probability as in (33); where is the Meijer G function [22], function, and . See Appendix A, for proof.
Then, we write generally for exponential () and GUE (synchronised) inter-vehicle distance () distributions, is as (34).
Like before, replacing with gives the connectivity probability for a bus-shadowed scenario.
Case 2.b: Weibull distributed range. The probability of connectivity of two adjacent vehicles with a generalised mapped inter-vehicle distance and Weibull distributed range is as (35); where are as defined before, and is the Meijer G function [32]. See Appendix B, for proof.
Following similar derivations as above and substituting for exponential and GUE inter-vehicle distance distributions respectively, gives (36).
Case 2.c: Rayleigh distributed range. For Rayleigh distribution, the probability of connection using the general mapped expressions and substituting either into (34) or into (36) gives (37), where is the error function.
Case 2.d: Lognormal distributed range. Using exponential inter-vehicle distance (27) and lognormal distributed range PDF in (17), connectivity probability is;
which can numerically be solved simply. For synchronised GUE distribution,
which has no closed-form solution. Swapping for gives bus-shadowed connectivity probability. We give the summary table for connectivity probability in Table 3.

Table 3.
Summary Connectivity probabilities, for fading environments.
4. Discussion
In this section, we discuss numerical results are presented for the dynamic range distribution and connectivity probability analysis. The simulation results were all obtained using MatLab 2023a [21]. General simulation parameters and their values are given in Table 4 (next page). Typical values for the mean speed and the standard deviation were adopted from [13,19]. For a road section of length L, the simulation was conducted as follows: to construct a network of N vehicles in a free-flow or synchronized traffic, a random number of vehicles was generated each separated from one another with a minimum safety distance s and velocity value selected from the truncated Gaussian distribution as in (25). Thus, with N, a total of communication links are formed. To simulate the big vehicle shadowing effect, vehicle nodes are inserted randomly between two randomly chosen vehicles in such a way that there is no link between them (rather, a path-loss value representing big vehicle obstruction effect is evaluated together with the received signal power). Due to the different fading environments, an average SNR and with or without big vehicle obstruction respectively for the two traffic scenarios above is computed for all links. With the inter-vehicle distance D and SNR threshold set, a random communication range, R is found. This procedure is repeated 10,000 times for all the fading channel environments.

Table 4.
Simulation parameters.
4.1. Distribution of Ranges
We verify the impact of big vehicle shadowing (BVS) and path-loss exponent, on the communication range distribution. The communication range distribution functions for different fading environments are plotted against a varying headway distance or inter-vehicle distance, .
4.1.1. Lognormal Distributed Ranges
Firstly, the distributions are plotted in Figure 2 with , W, for varying inter-vehicle distances. Then, the communication range is distributed below the 500 m distance mark as stipulated and recommended for short-ranges of DSRC standard. Generally, for all range distribution plots, varying impacts of the path-loss fading are seen around (Figure 2a), which is a value that differentiates typically between non-fading and fading environments. As the path-loss exponent value increases, the communication range is exponentially distributed with relative expectations ranging between 50 m and 200 m. For example, with for a fading environment on a highway, urban and suburban areas, short-range communications are expected with average ranges around 50 m with big-vehicle obstructions. Moreover, the probability of connectivity drops beyond as can be seen in Figure 2b).
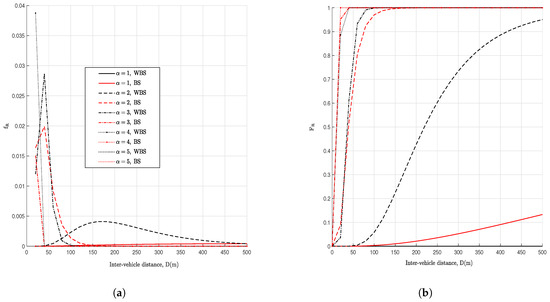
Figure 2.
Lognormal range distribution. (a) Lognormal PDF, . (b) Lognormal CDF.
4.1.2. Rayleigh Distributed Ranges
In a Rayleigh fading environment, as shown in Figure 3, shorter-communication ranges are below . We see also that these higher distributions are due to obstructions from big vehicle that contribute to overall shadowing which in turn leads to transmitter power variation. Examples of environments where such performance can be experienced are highways and urban settings.
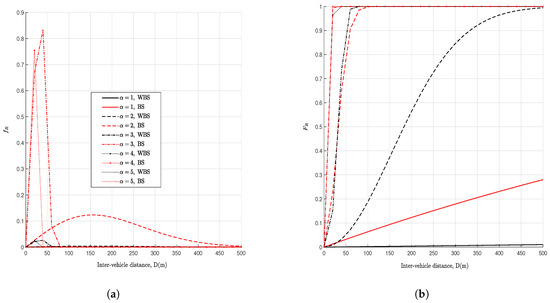
Figure 3.
Rayleigh range distribution. (a) Rayleigh PDF, . (b) Rayleigh CDF.
4.1.3. Nakagami-m Distributed Ranges
In Figure 4, Rayleigh fading distribution is plotted with a left skew around value seen. Similar to Figure 2 and Figure 3, the range distributions are heavily impacted by the path-loss coefficient, . This is in part due to the dominant NLOS signal between communicating vehicle nodes and the existing BVS nodes. As the fading worsens for inter-vehicle distances beyond 50 m or for values (i.e., for Rayleigh distribution), the communication range is Weibull-distributed with parameter C.
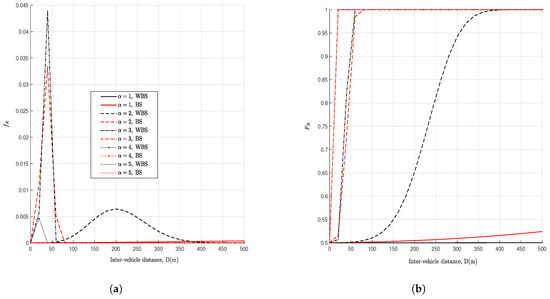
Figure 4.
Nakagami-m Range distributions for . (a) Nakagami-m PDF, . (b) Nakagami-m CDF.
4.1.4. Weibull Distributed Ranges
In Figure 5, Weibull range distribution captures a rural fading environment where, with a LOS more significant stable connectivity can be sustained for a typical VANET network. When , this represents Rayleigh fading distribution with no LOS (typical urban and suburban areas) while as the fading worsens and this is due to shadowing effects of nearby trees, neighbor vehicles among other issues such as big vehicles obstructions that add to the path-loss effects. We use provided that the vehicle arrival rates and densities are fixed and the power reception will be affected by mainly multipath fading. We see that the typical communication ranges are within an average of 50 m as in Figure 5a.
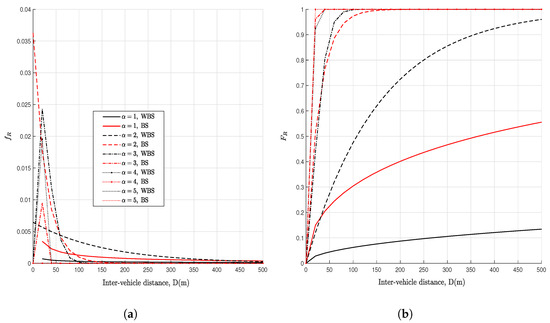
Figure 5.
Weibull Range distributions for . (a) Weibull PDF. (b) Weibull CDF.
4.2. Single-Hop Probability of Connectivity
4.2.1. Connectivity with Density
We plot the impact of vehicle density on the inter-vehicle connectivity in Figure 6 using a fixed SNR dB which signifies an ideal highway environment. A general increase can be noticed in the inter-vehicle connectivity probability with increasing vehicle densities. The static ranges due to constant transmitter power, W maintain a more fairly stable connectivity than the connectivity induced by the dynamical ranges from the different fading environments. Moreover, the synchronised traffic flow model has a better maintained connectivity than for exponential traffic due to similarity within group model scenario where the inter-vehicle distances are sustained for a longer period of time. Generally as the channel conditions improve, for the case of communication environments with and from urban environments, the connectivity probability is improved regardless of wider inter-vehicle distance (for in Figure 6b) is worse for Rayleigh dynamic ranges where the LOS path dominates. Therefore, the only significant factor affecting connectivity is the vehicle density.
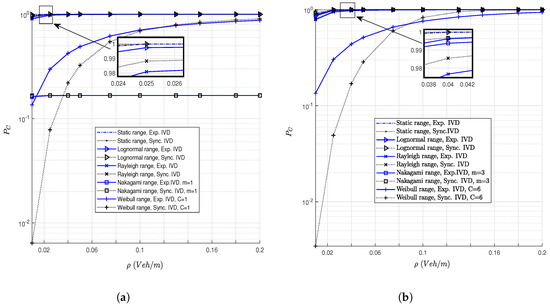
Figure 6.
Impact of vehicle density on connectivity probability analysis. (a) Connectivity probability at . (b) Connectivity probability at .
4.2.2. Connectivity with SNR
The inter-vehicle connectivity probability is plotted against SNR in Figure 7 for both (Figure 7a) and (Figure 7b). As shown in lognormal distribution plots in Figure 2 for highway environments with dominant multipaths due to shadows and obstructions, these effects are captured by Nakagami-m and Weibull fading factors, respectively. Moreover, the randomly induced communication ranges are suitable to sustain connectivity between vehicles as the SNR at the receiving vehicle increases. For vehicle density at in Figure 7b, the connectivity improves albeit lowest Weibull-induced connectivity ( due to LOS components) from communication ranges in typical urban highways characterised by many signal multipath directions and NLOS.
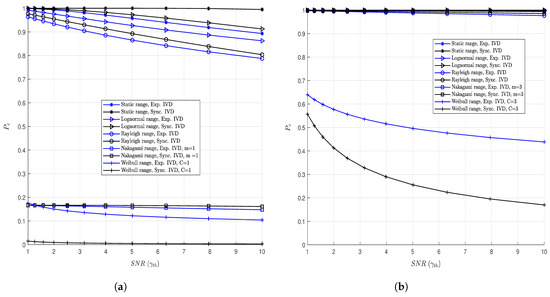
Figure 7.
Impact of SNR on connectivity probability. (a) Connectivity probability at . (b) Connectivity probability at .
4.2.3. Connectivity with Path-Loss
Figure 8 shows the connectivity probability as a function of path-loss. A significant decline in connectivity probability is observed as path-loss increases for both the exponential and synchronized traffic models. Notably, for a constant transmitter power of W and a vehicle density of , the inter-vehicle connectivity drops sharply when the path-loss exponent .
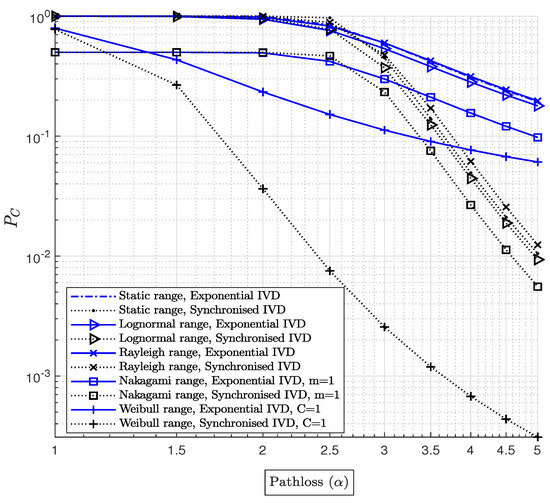
Figure 8.
Impact of pathloss on connectivity probability analysis at .
Furthermore, even with synchronized vehicle movement, connectivity is worse compared to the exponential traffic model. The Weibull distribution with exhibits the poorest connectivity, followed by the Nakagami-m distribution with , both of which reflect typical traffic conditions in urban and suburban highways. In general, the path-loss has a major impact on connectivity probability.
4.3. Big Vehicle Shadowing Effect
4.3.1. Connectivity with Big Vehicle Prob
The impact of large vehicles on network connectivity is illustrated in Figure 9. In this analysis, the network operates with a constant transmission power of W and a total of vehicle nodes. A proportion, , of these vehicles are classified as large vehicles.
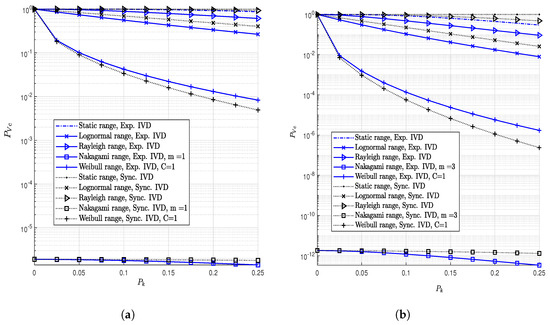
Figure 9.
Big vehicle effect on connectivity probability. (a) Connectivity probability at . (b) Connectivity probability at .
Figure 9a,b depict the connectivity probability for path-loss exponents of and , respectively. As increases, connectivity probability declines sharply in environments modeled by Weibull and Nakagami-m channel distributions. This decline is primarily due to the additional communication obstructions introduced by large vehicles, which block signal propagation between communicating nodes.
The synchronized traffic model helps maintain more stable connectivity compared to the exponential traffic model, even in the presence of large vehicle obstructions. However, as the number of communicating vehicles increases and the path-loss exponent rises, connectivity deteriorates further due to the compounded impact of signal obstructions from the large vehicle bodies.
Overall, the presence of large vehicles significantly reduces VANET connectivity, particularly in environments with higher path-loss conditions.
4.3.2. Connectivity with Number of Vehicles
In Figure 10 illustrates the effect of the number of communicating vehicles in a network, at transmitted power of and . With only a small proportion of big vehicles () and a vehicle density of , connectivity decreases depending on the traffic model used, with a more significant drop in environments with extreme fading, as represented by Nakagami-m and Weibull distributions. As discussed in the case presented in Figure 9, an increase in the number of big vehicles further degrades communication.
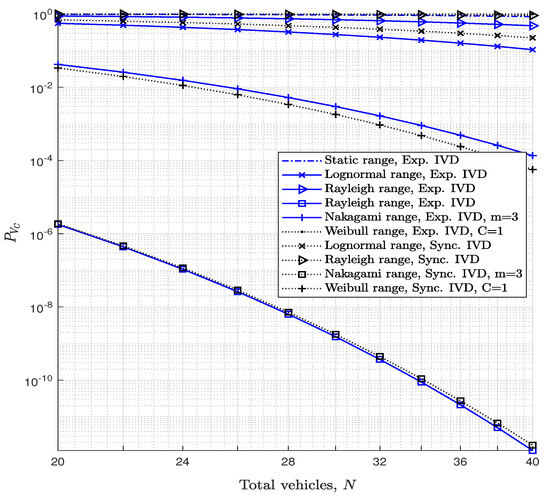
Figure 10.
Total number of vehicles effect on overall connectivity at , .
Lastly, in Figure 11 we see the combined effect of path-loss coefficient with Nakagami-m factor m and Weibull factor C on the connectivity. From the plots, it is evident that as the channel conditions worsen (increasing or m for Nakagami-m channel) in Figure 11a, the connectivity decreases; Further more, as the channel improves (increasing C) as seen in Figure 11b, the connectivity probability increases.
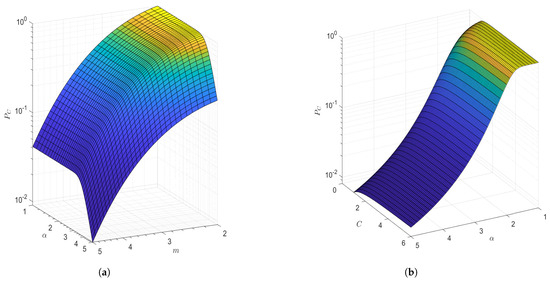
Figure 11.
Connectivity probability for distributed transmission range. (a) Connectivity with Nakagami-m range. (b) Connectivity with Weibull range.
4.4. General Observations
VANETs on highways exhibit different behaviors depending on the mobility pattern (synchronized or exponential) of vehicles and the path-loss model for signal propagation. In VANETs the interplay between vehicle density, SNR, and path-loss significantly affects network connectivity. For instance with high vehicle density, connectivity can be improved by providing more relay nodes (in the case of multi-hops) but also increases interference, leading to lower SNR due to packet collisions and co-channel interference. Conversely, low vehicle density reduces interference but increases the risk of network fragmentation and higher path loss, weakening SNR over longer distances. The path-loss factor further exacerbates connectivity issues, especially in sparse networks, as signal attenuation limits communication range. To mitigate these concerns, interference-aware MAC protocols, adaptive transmission power, multi-hop relaying, and hybrid communication strategies (e.g., DSRC and 5G) are essential. A balance may be struck between maintaining strong connectivity in dense environments while overcoming path-loss in sparse regions to ensure reliable communication in VANETs.
4.4.1. Synchronized Mobility
In this model, vehicles travel at the same speed and maintain a constant distance between each other, creating a predictable network topology. Under the synchronised mobility model with a lognormal path-loss model, signal strength decreases steadily with distance. This results in consistent network connectivity with minimal disruptions as long as vehicles remain within range. In the Rayleigh model, signal strength fluctuates rapidly due to multipath fading, leading to frequent link breakages and re-establishment even between nearby vehicles. The Nakagami-m model provides a middle ground between the lognormal and Rayleigh models, with network performance depending on the parameter m. Higher m values lead to more stable connections, while lower m values resemble Rayleigh fading. Finally, with the Weibull path-loss model, fading severity varies. At higher path-loss exponents C, the network behaves similarly to the lognormal model with smooth degradation. Lower exponents result in behavior resembling Rayleigh fading, with frequent fluctuations.
4.4.2. Exponential Mobility
In this model, vehicles follow independent random speed distributions, causing frequent changes in network topology. This creates a more dynamic and challenging environment for VANETs. With lognormal path loss, even though signal strength weakens steadily, the frequent topology changes due to varying speeds can cause link breakage, requiring more robust routing protocols. In the Rayleigh model, the already erratic signal strength is further disrupted by exponential mobility, making it difficult to maintain stable communication links. With the more general Nakagami-m model, similar to synchronised mobility, network performance depends on the m parameter. However, maintaining connections becomes more challenging due to the dynamic topology. Lastly, with Weibull path loss, network behavior is influenced by the path-loss exponent. Higher exponents provide some stability, while lower exponents exacerbate the difficulty of maintaining connections in a rapidly changing network.
In summary, synchronised mobility provides a more predictable environment for VANETs, particularly with path-loss models like lognormal, which experience a steady decrease in signal strength, similar to a static environment. In contrast, exponential mobility poses a significant challenge due to the dynamic network topology and frequent link disruptions. Path-loss models with more severe fading (such as Rayleigh, higher Nakagami-m, or lower Weibull exponents) exacerbate these challenges. Additionally, obstructions caused by big vehicles make communication in VANETs even more predictably difficult.
5. Conclusions
In this work, we have investigated the VANET connectivity probability where a generalised analysis framework has been used to capture impacts of big vehicle obstructions. The channel effects from channel models and vehicle obstructions statistics were reformulated to derive the dynamic transmission ranges for two traffic models. Parameters affecting VANET connectivity like pathloss, vehicle density, transmit power have been analysed using generalised dynamic range distribution model. The benefit of such scheme would be in designing VANET traffic models for different random environments such as urban highways with high traffic. Therefore, unlike the conventional derivation of connectivity probability from channel distributions using static communication ranges, we used statistics of dynamic communication ranges in the connectivity probability analysis of synchronised and exponential traffic models. Also, the approach we took provides a compact and simpler way of VANET traffic modeling with cases involving multiple lanes as well. Using simulations, the results agree with the theoretical model.
In future work, we will consider evaluating the framework to understand its performance in terms of PDR, and throughput. We will also consider a model to capture weather conditions (such as fogy, snowy) and how the new dynamic range models affect VANET performances.
Author Contributions
Conceptualization, K.O. and A.H.A.E.-M.; methodology, software, formal analysis, writing—original draft preparation, investigation, visualization, project administration, funding acquisition, K.O.; validation, resources, writing—review and editing, K.O., E.M. and A.H.A.E.-M.; supervision, E.M. and A.H.A.E.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
For two adjacent vehicles nodes to connect, the inter-vehicle distance must be smaller than the communication range. Thus, the probability of connectivity is;
Letting in sub-equation equal . The symbols in sub-equation , in sub-equation and in sub-equation capture the solution steps using Mellin transform pair and the procedures used in [29] and properties in [21]. Solving the integral and simplifying sub-equation where , , and gives (33).
Appendix B
For a general mapped inter-vehicle distance distribution between the exponential and the GUE in [28] given by (29), and the range-based distribution in a Weibull fading channel has CDF (14). Then the connectivity probability is;
Letting , , , , and in sub-equations above. The symbols in step , in step , and in step capture solution steps using Mellin transform pairs and procedures used in [29] and properties in [21]. Solving the integral in and simplifying gives (35) after susbtituting back in the constants.
References
- Al-Absi, M.A.; Abdulhakim, A.-A.A.; Lee, H.J. Performance Analysis for City, Highway, and Rural Area in Vehicle-to-Vehicle Network. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 17–19 October 2018; pp. 639–644. [Google Scholar]
- Dessai, S.F.; Sutar, D. Radio propagation model with obstacle effect and efficient bandwidth utilization for V2V VANET application services. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019; pp. 602–606. [Google Scholar]
- Cui, Q.; Wang, N.; Haenggi, M. Vehicle Distributions in Large and Small Cities: Spatial Models and Applications. IEEE Trans. Veh. Technol. 2018, 67, 10176–10189. [Google Scholar] [CrossRef]
- Li, F.; Chen, W.; Shui, Y. Study on Connectivity Probability of Vanets Under Adverse Weather Conditions at 5.9 GHz. IEEE Access 2020, 8, 547–555. [Google Scholar] [CrossRef]
- Li, F.; Chen, W.; Wang, J.; Shui, Y.; Yang, K.; Xu, L.; Yu, J.; Li, C. Different Traffic Density Connectivity Probability Analysis in VANETs with Measured Data at 5.9 GHz. In Proceedings of the 16th International Conference on Intelligent Transportation Systems Telecommunications (ITST), Lisboa, Portugal, 15–17 October 2018; pp. 1–7. [Google Scholar]
- Li, X.; Zhou, R.; Zhou, T.; Liu, L.; Yu, K. Connectivity Probability Analysis for Green Cooperative Cognitive Vehicular Networks. IEEE Trans. Green Commun. Netw. 2022, 6, 1553–1563. [Google Scholar] [CrossRef]
- Jameel, F.; Haider, M.A.A.; Butt, A.A. Performance analysis of VANETs under Rayleigh, Rician, Nakagami-m and Weibull fading. In Proceedings of the International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; pp. 127–132. [Google Scholar]
- Zeng, F.; Li, C.; Wang, H. Performance Evaluation of Different Fading Channels in Vehicular Ad Hoc Networks. In Proceedings of the International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 17–19 October 2018; pp. 356–361. [Google Scholar]
- Wang, Y.; Xing, X.; Fan, J. Statistical Properties Evaluation on Rayleigh VANET Fading Channels. In Proceedings of the 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010; pp. 1–6. [Google Scholar]
- Hu, M.; Zhong, Z.; Wu, H.; Ni, M. Effect of fading channel on link duration in Vehicular Ad Hoc Networks. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 1669–1673. [Google Scholar]
- Elaraby, S.; Abuelenin, S.M. Fading Improves Connectivity in Vehicular Ad-hoc Networks. arXiv 2019, arXiv:1910.05317. [Google Scholar]
- Rawat, D.B.; Shetty, S. Enhancing connectivity for spectrum-agile Vehicular Ad hoc NETworks in fading channels. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 957–962. [Google Scholar]
- Nguyen, H.; Xu, X.; Noor-A-Rahim, M.; Guan, Y.L.; Pesch, D.; Li, H.; Filippi, A. Impact of Big Vehicle Shadowing on Vehicle-to-Vehicle Communications. IEEE Trans. Veh. Technol. 2020, 69, 6902–6915. [Google Scholar] [CrossRef]
- Alwane, S.K.; Siddle, D.R.; Stocker, A.J. The effect of the vehicle size on the V2V radio channel. In Proceedings of the Antennas and Propagation Conference (APC-2019), Birmingham, UK, 11–12 November 2019; pp. 1–4. [Google Scholar]
- Zhao, Y.; Xu, X.; Gao, Y. Selective Relaying Strategy for Vehicular Communication with Big-Vehicle Shadowing. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–5. [Google Scholar]
- Chen, R.; Zhong, Z.; Leung, V.C.M.; Michelson, D.G. Performance Analysis of Connectivity for Vehicular Ad Hoc Networks with Moving Obstructions. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014; pp. 1–5. [Google Scholar]
- Vlastaras, D.; Whiton, R.; Tufvesson, F. A model for power contributions from diffraction around a truck in vehicle-to-vehicle communications. In Proceedings of the 15th International Conference on ITS Telecommunications (ITST), Warsaw, Poland, 29–31 May 2017; pp. 1–6. [Google Scholar]
- Yang, M.; Ai, B.; He, R.; Chen, L.; Li, X.; Huang, Z.; Li, J.; Huang, C. Path Loss Analysis and Modeling for Vehicle-to-Vehicle Communications with Vehicle Obstructions. In Proceedings of the 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar]
- Abuelenin, S.M.; Elaraby, S.A. Generalized Framework for Connectivity Analysis in Vehicle-to-Vehicle Communications. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5894–5898. [Google Scholar] [CrossRef]
- Babu, A.V.; Muhammed Ajeer, V.K. Analytical model for connectivity of vehicular ad hoc networks in the presence of channel randomness. Int. J. Commun. Syst. 2011, 26, 927–946. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Optimization Toolbox Version: 9.4 (R2023a). 2023. Available online: https://www.mathworks.com (accessed on 1 January 2023).
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Nagel, R. The effect of vehicular distance distributions and mobility on VANET communications. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; pp. 1190–1194. [Google Scholar]
- Cheng, J.; Tellambura, C.; Beaulieu, N.C. Performance of digital linear modulations on Weibull slow-fading channels. IEEE Trans. Commun. 2004, 52, 1265–1268. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.; Gong, Y. Study of Connectivity Probability of Vehicle-to-Vehicle and Vehicle-to-Infrastructure Communication Systems. In Proceedings of the IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–4. [Google Scholar]
- Ross, S. Introduction to Probability Models, 11th ed.; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M.; Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, And Products, 7th ed.; Elsevier: London, UK, 2007. [Google Scholar]
- Yousefi, S.; Altman, E.; El-Azouzi, R.; Fathy, M. Analytical Model for Connectivity in Vehicular Ad Hoc Networks. IEEE Trans. Veh. Technol. 2008, 57, 3341–3356. [Google Scholar] [CrossRef]
- Zhang, Z.; Mao, G.; Anderson, B.D.O. On the Information Propagation Process in Mobile Vehicular Ad Hoc Networks. IEEE Trans. Veh. Technol. 2011, 60, 2314–2325. [Google Scholar] [CrossRef]
- Chen, C.; Liu, L.; Du, X.; Wei, X.; Pei, C. Available connectivity analysis under free flow state in VANETs. J. Wirel. Commun. Netw. 2012, 2012, 270. [Google Scholar] [CrossRef]
- Li, C.; Zhen, A.; Sun, J.; Zhang, M.; Hu, X. Analysis of connectivity probability in VANETs considering minimum safety distance. In Proceedings of the 8th International Conference on Wireless Communications and Signal Processing (WCSP), Yangzhou, China, 13–15 October 2016; pp. 1–5. [Google Scholar]
- Beals, R.; Szmisgielski, J. Meijer G-functions: A Gentle Introduction. Not. Am. Math. Soc. 2013, 60, 866–872. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).