A Machine Learning-Aided Network Contention-Aware Link Lifetime- and Delay-Based Hybrid Routing Framework for Software-Defined Vehicular Networks
Abstract
1. Introduction
- We present a novel hybrid routing algorithm for SDVNs that uses collected metadata from nodes to estimate parameters at the controller to compute routes that yield the least communication cost, the highest packet delivery ratio, the least latency, and moderate channel utilization, on average, compared to routing in VANETs (AODV) and SDVNs (Dijkstra);
- This research provides insight into the employment of machine learning for accurate and computationally efficient parameter computation at the controller, such as the estimation of link delay and lifetime, satisfying the communication requirements of vehicular networks;
- This research experimentally investigates the factors under which the proposed hybrid routing framework is enhanced, so that these factors can be effectively used by future researchers to boost the performance of the proposed novel hybrid routing framework;
- The proposed routing algorithm will be very useful for more efficient dissemination of information in the data plane of future SDVNs than existing approaches.
2. Background and Literature Review
2.1. VANET
2.2. SDN
2.3. SDVN
2.4. SDVN Architectures
2.5. Routing
2.6. Routing in SDN
2.7. Routing in SDVN
2.8. Machine Learning for Routing in SDVN
3. Proposed Methodology
3.1. Overview of the Routing Framework
3.2. Estimation of Link Lifetime
Computation of the Link Lifetime Matrix
3.3. Estimation of Link Delay
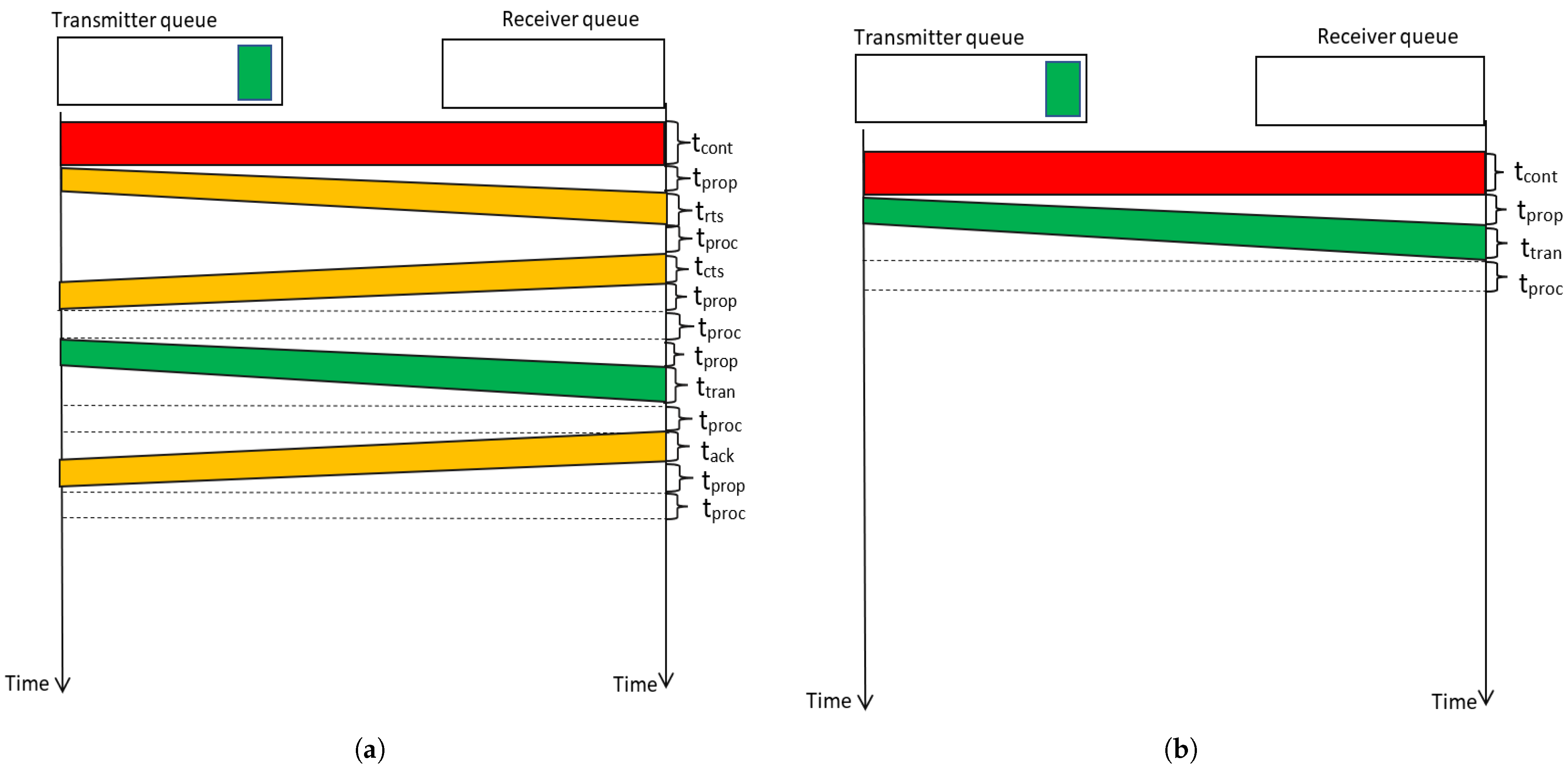
3.3.1. Investigating the Factors Affecting Collision Probability to Formulate an Average
3.3.2. Computing Average Contention Delay per Channel
3.3.3. Computing Normalized Network Contention
3.3.4. Computing Average Per-Channel Delay at Each Hop
3.3.5. Predicting Exact One-Hop Channel Delay Using Machine Learning
- Number of links in the same communication channel connected to the hop ( or );
- Average pending transmission packet distribution factor of the node and its neighbors (), which can be calculated as given in Equation (34):
- Data packet size (), packet size of RTS (), packet size of CTS (), packet size of ACK (), and data rate (DR) to compensate for transmission delay errors;
- Input Short Inter-Frame Space (SIFS) to compensate for processing delay errors;
- E, , , , 1th–6th-order terms of , and 1th–6th-order terms of .
3.3.6. Computation of the Link Delay Matrix
3.4. Hybrid Algorithm for Finding the Highest Stable Least Delay Path or Highest Stable Shortest Path
3.5. Proposed Flow Table Architecture
3.6. Flow Table Update at the Controller
3.7. Adaptive Flow Rule Computation, Update, and Installation
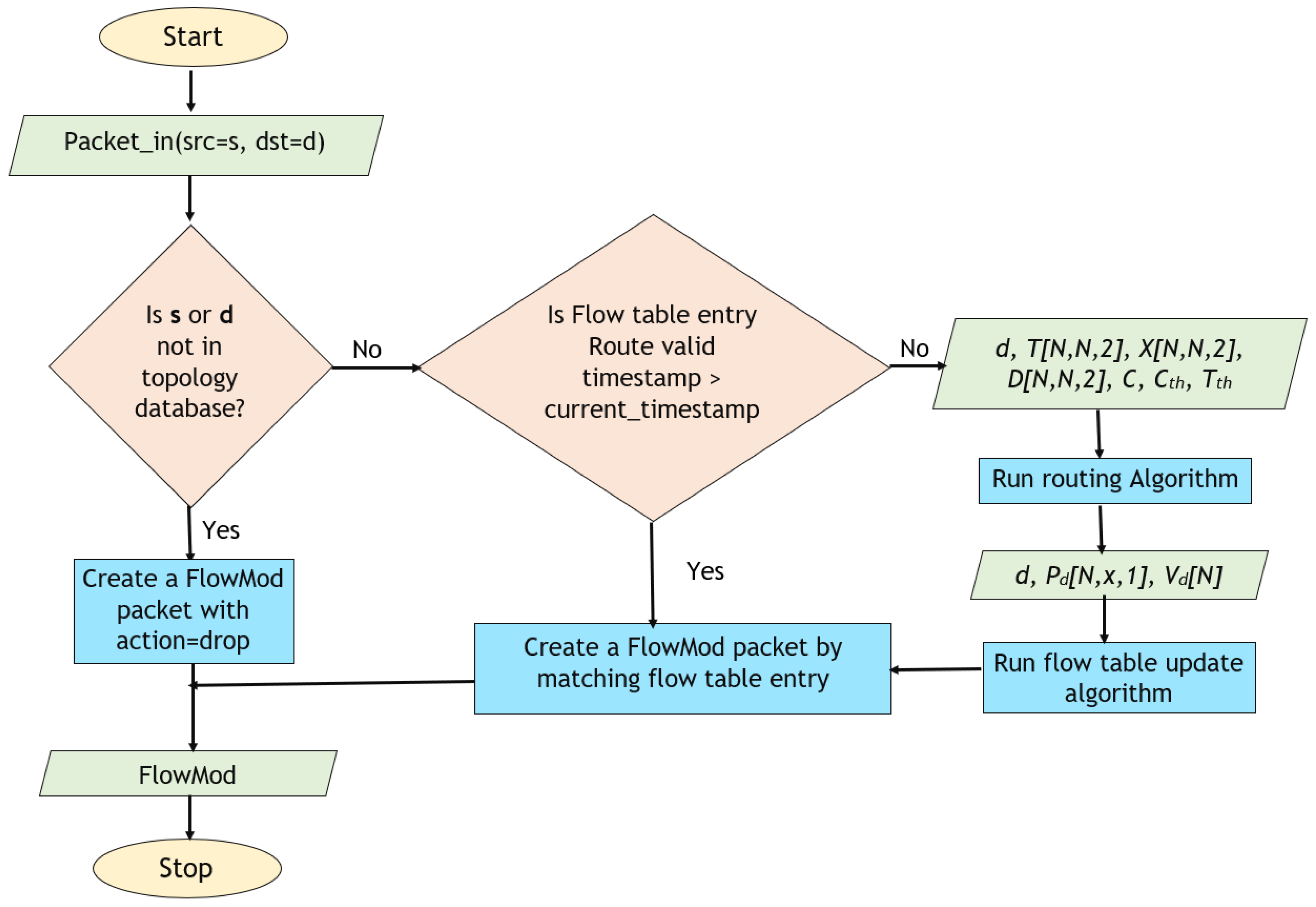
3.8. Overall Routing Process
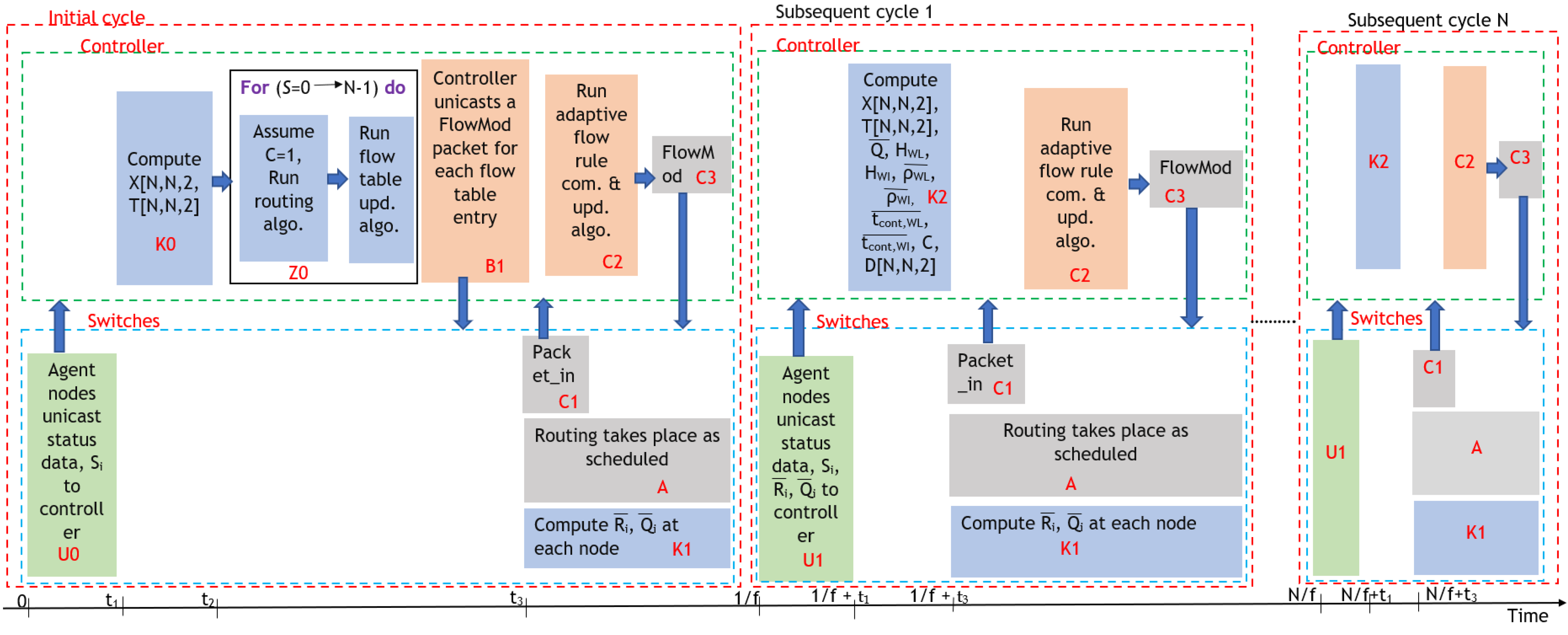
- We use the data collection optimization model proposed in our previous work [65] for metadata collection for the routing framework. Metadata refers to all data, namely, status data (node addresses, position, velocity, acceleration), node address set of all one-hop neighbors of each node (), average pending transmission packet distribution factor of each node (), and average queue size of each node (), which are required to compute the routes using the proposed hybrid routing algorithm given in Section 3.4. However, in the very first routing cycle, as routing has not taken place at least once, and cannot be collected, and only status data and are collected, as shown in block ”U0“ in Figure 13. These metadata are unicasted to the controller node from the agent nodes in the data collection optimization model. In the initial routing cycle, only and are computed at the controller node, as shown in block ”K0“ in Figure 13. (the adjacency matrix of position) is computed using the position data of all nodes, while is computed using Equation (5) with the aid of the wireless link lifetime prediction DNN by providing differential position, velocity, and acceleration to the machine learning model, as described in Section 3.2. In the very first routing cycle, cannot be computed, as data do not exist for and . Furthermore, it is not necessary to compute other parameters that are required to compute normalized network contention (), as data do not exist to compute the average pending transmission packet distribution factor of the network (). Because of this, in the very first routing cycle, the value of is assumed to be one, to utilize the highest stable least distance as the mode for the routing algorithm given in Section 3.4;
- In the initial cycle, once and are computed, routes are computed using the hybrid routing algorithm by choosing stable distance as the metric, and the output of this algorithm is fed to flow table update algorithm to update flow table entries. Routing algorithm can compute only routes from all other nodes to a given destination node, so routing algorithm and flow table update algorithm should be executed iteratively N times, where N is the total number of nodes, by varying the destination node ID, to find routes from each and every source node to each and every destination node, as shown in block “Z0” in Figure 13. Using the parent vector, path valid time vector, and destination node ID output from routing algorithm, flow table update algorithm updates flow table entries. This updating of the flow table by flow table update algorithm occurs at the end of each iteration of finding routes by routing algorithm. At the end of the functioning of block “Z0” (once the updating of the flow table is over), the controller must unicast FlowMod packets related to each flow entry of the flow table to corresponding switches, as shown in block “B1” of Figure 13;
- Routing occurs at a routing frequency (f), and, at each routing cycle, including the very first, routing occurs as packet transmissions are scheduled, as is evident from block “A” in Figure 13. Packets are forwarded through each node by inspecting the flow table of the node. Because of the implementation of route valid timestamp in the proposed flow table, when a flow table match occurs with source address not equal to destination address, action not explicitly defined to drop, and current timestamp greater than the route valid timestamp, a packet_in message will be generated and sent to the controller, as shown in block “C1” in Figure 13, as the current flow entry in the flow table at the switch has expired. Then, in response to the packet_in message, the adaptive flow rule computation, update, and installation algorithm will run as shown in block ”C2” in Figure 13 to create a FlowMod packet containing flow modification rules, which will be unicasted to the corresponding switch, as shown in block “C3” in Figure 13, to update the corresponding flow table entry in the switch with updated flow rules. Note that, if a flow table mismatch occurs due to a packet scheduled to a destination node that does not exist in the vehicular network, a packet_in message will be sent to the controller. Then, the adaptive flow rule computation and update algorithm will inspect the destination, and, as it does not exist in the topology database, a FlowMod packet to drop the packet at the switch will be sent back to the switch. During the entire routing time period (the time period during which routing occurs), each node monitors its transmission queue size at discrete time intervals and computes the parameters’ average queue size () and average pending transmission packet distribution factor (), as shown in block “K1” of Figure 13. Computed and values are kept with the nodes until they are unicasted to the controller node in the next routing cycle, along with other metadata, as shown in block “U1” of Figure 13. The routing in all routing cycles is similar (Functioning blocks “K1”, “A”, ”C1”, “C2”, and “C3” operate in each routing cycle, including the initial cycle, similarly);
- Starting from the second cycle (subsequent cycle 1) onwards, agent nodes should collect and unicast status data, a set of node addresses of one-hop neighbors of each node (), , and computed from the previous routing cycle, as evident from the “U1” block in Figure 13. Thus, at the controller node, is computed using the values received from all the nodes. and are computed at subsequent routing cycles in the same manner specified for the initial cycle. Furthermore, starting from subsequent cycle 1 onwards, normalized homogeneous link entropy with respect to wireless links (), normalized homogeneous link entropy with respect to wired links (), average collision probability for wireless links (), average collision probability for wired links (), and average contention delay for wired links () are computed, as shown in block “K2” of Figure 13. Using previously computed parameters, normalized network contention () is computed using Equation (29). Furthermore, the adjacency matrix of link delay can be found using Equation (35), with the help of the one-hop per-channel delay prediction DNN. Descriptions of the computation of the above parameters are described in Section 3.3;
- Once the link delay matrix and normalized network contention () are found, the routing algorithm will choose the mode as highest stable least distance or highest stable least delay by comparing with . However, unlike the initial cycle, routes will be computed, and flow table entries will be updated using the adaptive flow rule computation and update algorithm only upon reception of packet_in messages. As was described in the explanation of that algorithm, each packet_in message may not result in computing and updating the flow table at the controller. If the flow table entry corresponding to the packet_in message is already updated, that entry will be sent to the corresponding switch to update its flow table using a FlowMod packet.
4. Results
4.1. Performance Evaluation Metrics
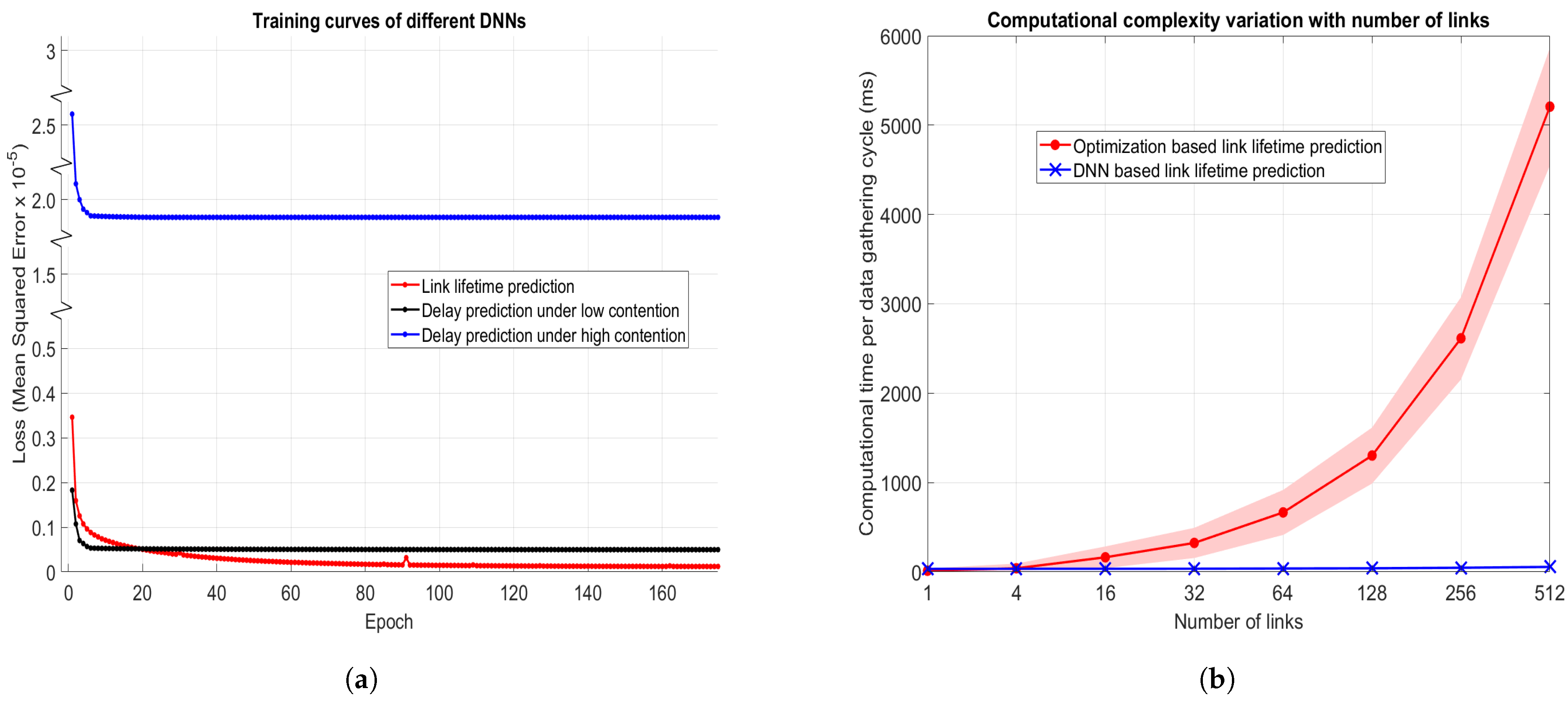
4.1.1. Root Mean Squared Error (RMSE)
4.1.2. Average Computational Time ()
4.1.3. Average Communication Cost ()
4.1.4. Average Channel Utilization ()
4.1.5. Average End to End Latency ()
4.1.6. Average Packet Delivery Ratio ()
4.2. Configuration of the Simulation Environment
4.2.1. Configuration for Routing
4.2.2. Configuration of Vehicular Mobility Scenarios
4.2.3. Configuration of DSRC
4.2.4. Configuration of LTE
4.2.5. Configuration of RSUs
4.2.6. Controller Node
4.2.7. Data Packet
4.2.8. Association of Communication Cost per Channel
4.3. Performance of Wireless Link Lifetime Prediction and One-Hop Channel Delay Prediction Using DNNs
4.4. Routing Performance Evaluation
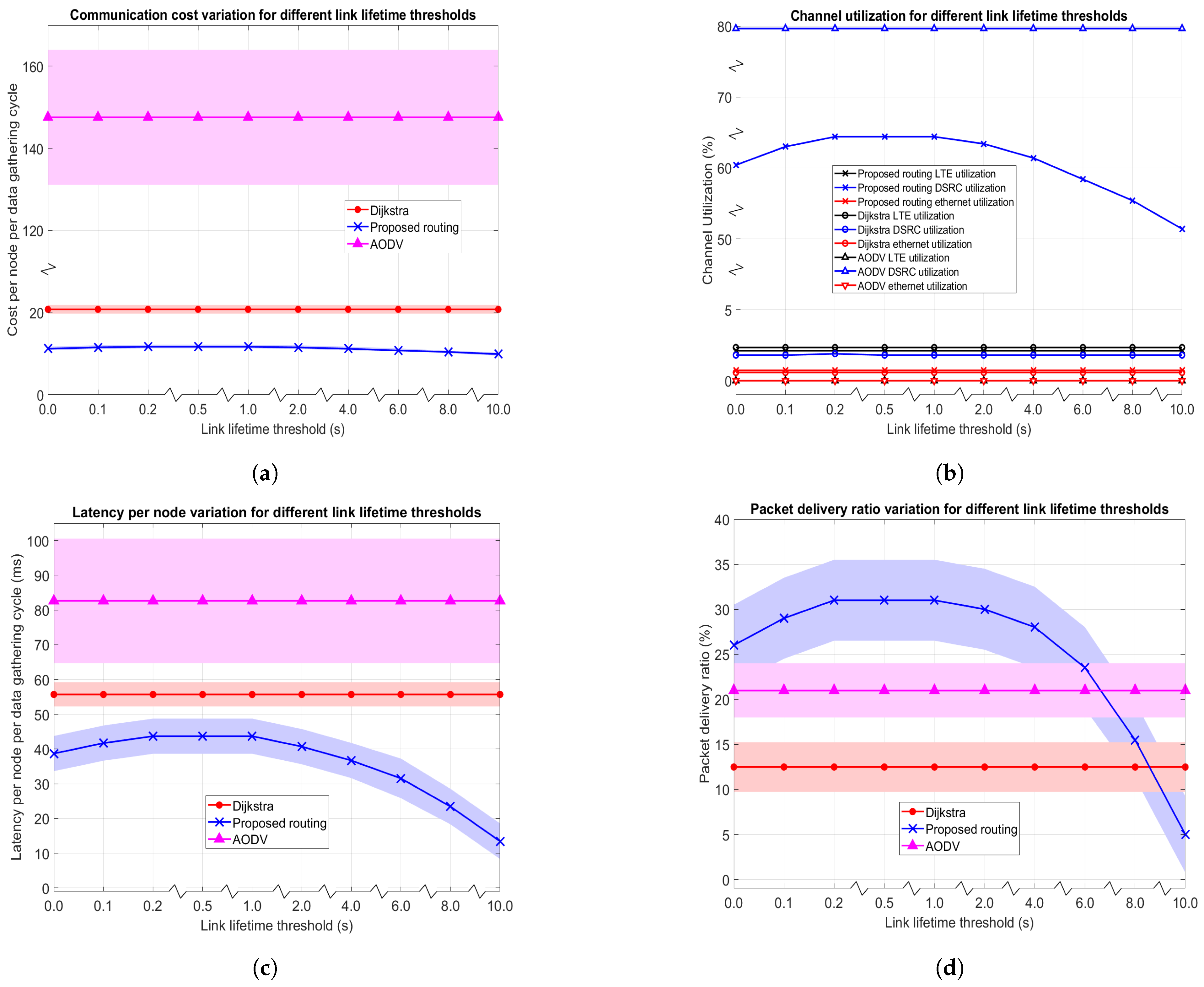
4.4.1. Impact of Link Lifetime Threshold
4.4.2. Impact of Routing Frequency
4.4.3. Impact of Network Size
4.4.4. Impact of Vehicular Mobility
5. Discussion
- H1 —The communication cost of the proposed routing is higher than AODV;
- H2—The end-to-end latency of the proposed routing is higher than Dijkstra;
- H3—The PDR of the proposed routing is lower than AODV.
6. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Metadata Collection for Routing Framework
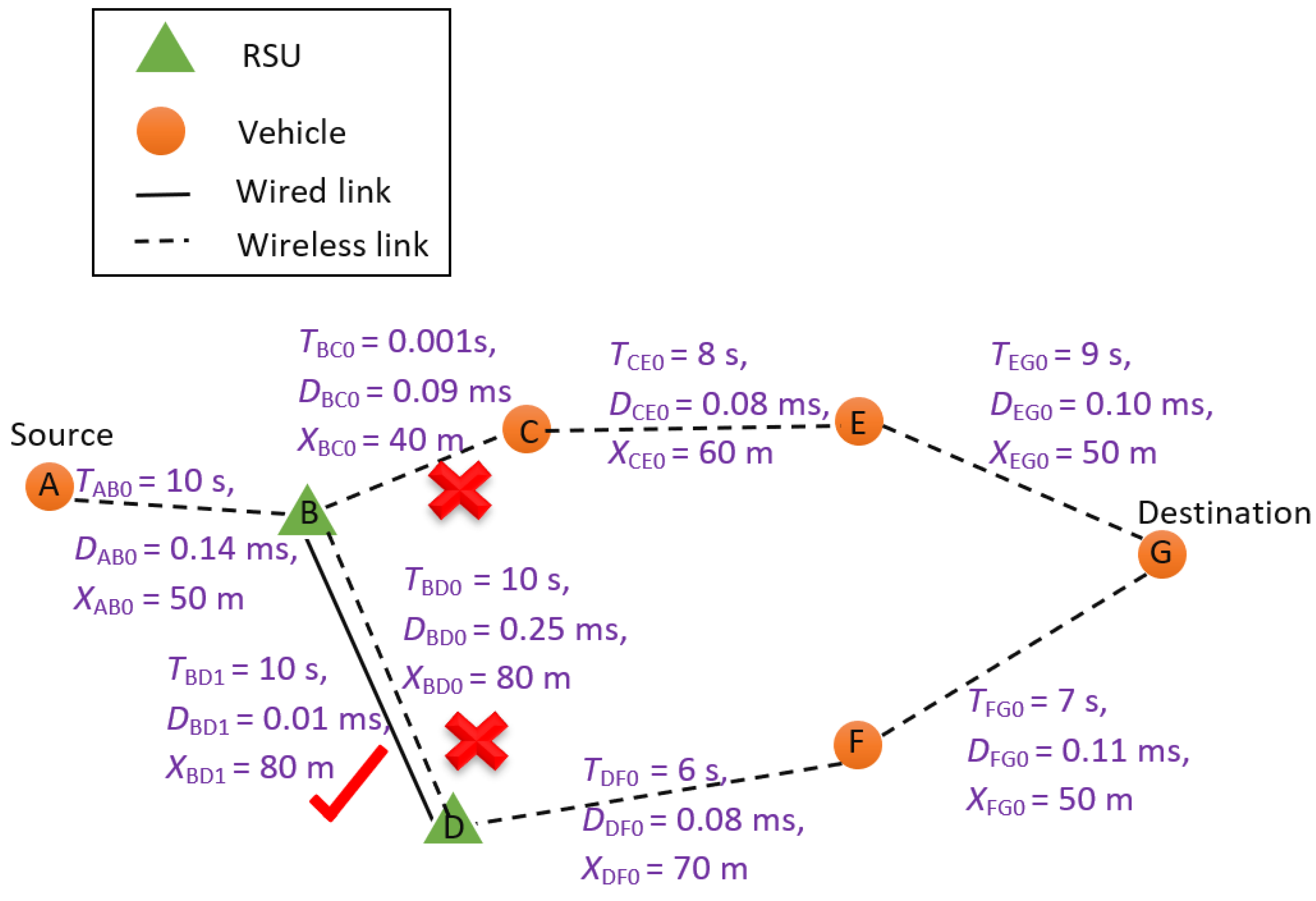
Appendix B. Sample Delay Calculations
References
- Hamdi, M.M.; Audah, L.; Rashid, S.A.; Mohammed, A.H.; Alani, S.; Mustafa, A.S. A review of applications, characteristics and challenges in vehicular ad hoc networks (VANETs). In Proceedings of the 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Copenhagen, Denmark, 26 June–1 July 2020; pp. 1–7. [Google Scholar]
- Hoebeke, J.; Moerman, I.; Dhoedt, B.; Demeester, P. An overview of mobile ad hoc networks: Applications and challenges. J.-Commun. Netw. 2004, 3, 60–66. [Google Scholar]
- Chlamtac, I.; Conti, M.; Liu, J.J.N. Mobile ad hoc networking: Imperatives and challenges. Ad Hoc Netw. 2003, 1, 13–64. [Google Scholar] [CrossRef]
- Dahiya, A.; Chauhan, R.K. A comparative study of MANET and VANET environment. J. Comput. 2010, 2, 87–92. [Google Scholar]
- Martinez, F.J.; Fogue, M.; Coll, M.; Cano, J.C.; Calafate, C.T.; Manzoni, P. Assessing the impact of a realistic radio propagation model on VANET scenarios using real maps. In Proceedings of the 2010 Ninth IEEE International Symposium on Network Computing and Applications, Cambridge, MA, USA, 15–17 July 2010; IEEE: New York, NY, USA, 2010; pp. 132–139. [Google Scholar]
- Alani, S.; Zakaria, Z.; Hamdi, M.M. A study review on mobile ad-hoc network: Characteristics, applications, challenges and routing protocols classification. Int. J. Adv. Sci. Technol. 2019, 28, 394–405. [Google Scholar]
- Sou, S.I.; Tonguz, O.K. Enhancing VANET connectivity through roadside units on highways. IEEE Trans. Veh. Technol. 2011, 60, 3586–3602. [Google Scholar] [CrossRef]
- Soni, M.; Rajput, B.S.; Patel, T.; Parmar, N. Lightweight vehicle-to-infrastructure message verification method for VANET. In Data Science and Intelligent Applications; Springer: Berlin, Germany, 2021; pp. 451–456. [Google Scholar]
- Seneviratne, C.; Wijesekara, P.A.D.S.N.; Leung, H. Performance analysis of distributed estimation for data fusion using a statistical approach in smart grid noisy wireless sensor networks. Sensors 2020, 20, 567. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Atkison, T. Vanet applications: Past, present, and future. Veh. Commun. 2021, 28, 100310. [Google Scholar] [CrossRef]
- Wijesekara, P.A.D.S.N.; Sudheera, K.L.K.; Sandamali, G.G.N.; Chong, P.H.J. Data Gathering Optimization in Hybrid Software Defined Vehicular Networks. In Proceedings of the 20th Academic Sessions, Matara, Sri Lanka, 7 June 2023; p. 59. [Google Scholar]
- Haji, S.H.; Zeebaree, S.R.; Saeed, R.H.; Ameen, S.Y.; Shukur, H.M.; Omar, N.; Sadeeq, M.A.; Ageed, Z.S.; Ibrahim, I.M.; Yasin, H.M. Comparison of software defined networking with traditional networking. Asian J. Res. Comput. Sci. 2021, 9, 1–18. [Google Scholar] [CrossRef]
- Mishra, S.; AlShehri, M.A.R. Software defined networking: Research issues, challenges and opportunities. Indian J. Sci. Technol. 2017, 10, 1–9. [Google Scholar] [CrossRef]
- Nunes, B.A.A.; Mendonca, M.; Nguyen, X.N.; Obraczka, K.; Turletti, T. A survey of software-defined networking: Past, present, and future of programmable networks. IEEE Commun. Surv. Tutor. 2014, 16, 1617–1634. [Google Scholar] [CrossRef]
- Fonseca, P.C.; Mota, E.S. A survey on fault management in software-defined networks. IEEE Commun. Surv. Tutor. 2017, 19, 2284–2321. [Google Scholar] [CrossRef]
- Nisar, K.; Jimson, E.R.; Hijazi, M.H.A.; Welch, I.; Hassan, R.; Aman, A.H.M.; Sodhro, A.H.; Pirbhulal, S.; Khan, S. A survey on the architecture, application, and security of software defined networking: Challenges and open issues. Internet Things 2020, 12, 100289. [Google Scholar] [CrossRef]
- Jagadeesan, N.A.; Krishnamachari, B. Software-defined networking paradigms in wireless networks: A survey. ACM Comput. Surv. (CSUR) 2014, 47, 1–11. [Google Scholar] [CrossRef]
- Ku, I.; Lu, Y.; Gerla, M.; Gomes, R.L.; Ongaro, F.; Cerqueira, E. Towards software-defined VANET: Architecture and services. In Proceedings of the 2014 13th Annual Mediterranean Ad Hoc Networking Workshop (MED-HOC-NET), Piran, Slovenia, 2–4 June 2014; IEEE: New York, NY, USA, 2014; pp. 103–110. [Google Scholar]
- Bhatia, J.; Modi, Y.; Tanwar, S.; Bhavsar, M. Software defined vehicular networks: A comprehensive review. Int. J. Commun. Syst. 2019, 32, e4005. [Google Scholar] [CrossRef]
- Zhu, M.; Cai, Z.P.; Xu, M.; Cao, J.N. Software-defined vehicular networks: Opportunities and challenges. In Energy Science and Applied Technology; CRC Press: Boca Raton, FL, USA, 2015; pp. 247–251. [Google Scholar]
- Wijesekara, P.A.D.S.N.; Gunawardena, S. A Review of Blockchain Technology in Knowledge-Defined Networking, Its Application, Benefits, and Challenges. Network 2023. submitted. [Google Scholar]
- Zhao, L.; Li, J.; Al-Dubai, A.; Zomaya, A.Y.; Min, G.; Hawbani, A. Routing schemes in software-defined vehicular networks: Design, open issues and challenges. IEEE Intell. Transp. Syst. Mag. 2020, 13, 217–226. [Google Scholar] [CrossRef]
- Quan, W.; Cheng, N.; Qin, M.; Zhang, H.; Chan, H.A.; Shen, X. Adaptive transmission control for software defined vehicular networks. IEEE Wirel. Commun. Lett. 2018, 8, 653–656. [Google Scholar] [CrossRef]
- Islam, M.M.; Khan, M.T.R.; Saad, M.M.; Kim, D. Software-defined vehicular network (SDVN): A survey on architecture and routing. J. Syst. Archit. 2021, 114, 101961. [Google Scholar] [CrossRef]
- Adbeb, T.; Wu, D.; Ibrar, M. Software-defined networking (SDN) based VANET architecture: Mitigation of traffic congestion. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Liu, K.; Xu, X.; Chen, M.; Liu, B.; Wu, L.; Lee, V.C. A hierarchical architecture for the future internet of vehicles. IEEE Commun. Mag. 2019, 57, 41–47. [Google Scholar] [CrossRef]
- Toufga, S.; Abdellatif, S.; Assouane, H.T.; Owezarski, P.; Villemur, T. Towards dynamic controller placement in software defined vehicular networks. Sensors 2020, 20, 1701. [Google Scholar] [CrossRef]
- Hinds, A.; Ngulube, M.; Zhu, S.; Al-Aqrabi, H. A review of routing protocols for mobile ad-hoc networks (manet). Int. J. Inf. Educ. Technol. 2013, 3, 1. [Google Scholar] [CrossRef]
- Shelly, S.; Babu, A.V. Link reliability based greedy perimeter stateless routing for vehicular ad hoc networks. Int. J. Veh. Technol. 2015, 2015, 1–16. [Google Scholar] [CrossRef]
- Pathak, C.; Shrivastava, A.; Jain, A. Ad-hoc on demand distance vector routing protocol using Dijkastra’s algorithm (AODV-D) for high throughput in VANET (Vehicular Ad-hoc Network). In Proceedings of the 2016 11th International Conference on Industrial and Information Systems (ICIIS), Roorkee, India, 3–4 December 2016; IEEE: New York, NY, USA, 2016; pp. 355–359. [Google Scholar]
- Dafalla, M.E.M.; Mokhtar, R.A.; Saeed, R.A.; Alhumyani, H.; Abdel-Khalek, S.; Khayyat, M. An optimized link state routing protocol for real-time application over Vehicular Ad-hoc Network. Alex. Eng. J. 2022, 61, 4541–4556. [Google Scholar] [CrossRef]
- Hamid, B.; El Mokhtar, E.N. Performance analysis of the Vehicular Ad hoc Networks (VANET) routing protocols AODV, DSDV and OLSR. In Proceedings of the 2015 5th International Conference on Information & Communication Technology and Accessibility (ICTA), Marrakesh, Morocco, 21–23 December 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar]
- Xie, J.; Yu, F.R.; Huang, T.; Xie, R.; Liu, J.; Wang, C.; Liu, Y. A survey of machine learning techniques applied to software defined networking (SDN): Research issues and challenges. IEEE Commun. Surv. Tutor. 2018, 21, 393–430. [Google Scholar] [CrossRef]
- Jiang, J.R.; Huang, H.W.; Liao, J.H.; Chen, S.Y. Extending Dijkstra’s shortest path algorithm for software defined networking. In Proceedings of the 16th Asia-Pacific Network Operations and Management Symposium, Hsinchu, Taiwan, 17–19 September 2014; IEEE: New York, NY, USA, 2014; pp. 1–4. [Google Scholar]
- Yanjun, L.; Xiaobo, L.; Osamu, Y. Traffic engineering framework with machine learning based meta-layer in software-defined networks. In Proceedings of the 2014 4th IEEE International Conference on Network Infrastructure and Digital Content, Beijing, China, 19–21 September 2014; IEEE: New York, NY, USA, 2014; pp. 121–125. [Google Scholar]
- Wang, J.; Miao, Y.; Zhou, P.; Hossain, M.S.; Rahman, S.M.M. A software defined network routing in wireless multihop network. J. Netw. Comput. Appl. 2017, 85, 76–83. [Google Scholar] [CrossRef]
- Azzouni, A.; Boutaba, R.; Pujolle, G. NeuRoute: Predictive dynamic routing for software-defined networks. In Proceedings of the 2017 13th International Conference on Network and Service Management (CNSM), Tokyo, Japan, 26–30 November 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Sendra, S.; Rego, A.; Lloret, J.; Jimenez, J.M.; Romero, O. Including artificial intelligence in a routing protocol using software defined networks. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; IEEE: New York, NY, USA, 2017; pp. 670–674. [Google Scholar]
- Lin, S.C.; Akyildiz, I.F.; Wang, P.; Luo, M. QoS-aware adaptive routing in multi-layer hierarchical software defined networks: A reinforcement learning approach. In Proceedings of the 2016 IEEE International Conference on Services Computing (SCC), San Francisco, CA, USA, 27 June–2 July 2016; IEEE: New York, NY, USA, 2016; pp. 25–33. [Google Scholar]
- Alvizu, R.; Troia, S.; Maier, G.; Pattavina, A. Matheuristic with machine-learning-based prediction for software-defined mobile metro-core networks. J. Opt. Commun. Netw. 2017, 9, D19–D30. [Google Scholar] [CrossRef]
- Chen-Xiao, C.; Ya-Bin, X. Research on load balance method in SDN. Int. J. Grid Distrib. Comput. 2016, 9, 25–36. [Google Scholar] [CrossRef]
- Correia, S.; Boukerche, A.; Meneguette, R.I. An architecture for hierarchical software-defined vehicular networks. IEEE Commun. Mag. 2017, 55, 80–86. [Google Scholar] [CrossRef]
- He, Z.; Zhang, D.; Liang, J. Cost-efficient sensory data transmission in heterogeneous software-defined vehicular networks. IEEE Sensors J. 2016, 16, 7342–7354. [Google Scholar] [CrossRef]
- Dong, B.; Wu, W.; Yang, Z.; Li, J. Software defined networking based on-demand routing protocol in vehicle ad hoc networks. In Proceedings of the 2016 12th International Conference on Mobile Ad-Hoc and Sensor Networks (MSN), Hefei, China, 16–18 December 2016; IEEE: New York, NY, USA, 2016; pp. 207–213. [Google Scholar]
- Zhu, M.; Cai, Z.; Cao, J.; Xu, M. Efficient multiple-copy routing in software-defined vehicular networks. In Proceedings of the 2015 International Conference on Information and Communications Technologies (ICT 2015), Xi’an, China, 24–26 April 2015. [Google Scholar]
- Zhu, M.; Cao, J.; Pang, D.; He, Z.; Xu, M. SDN-based routing for efficient message propagation in VANET. In International Conference on Wireless Algorithms, Systems, and Applications, Qufu, China, 10–12 August 2015; Springer: Cham, Switzerland, 2015; pp. 788–797. [Google Scholar]
- Sudheera, K.L.K.; Ma, M.; Chong, P.H.J. Link stability based optimized routing framework for software defined vehicular networks. IEEE Trans. Veh. Technol. 2019, 68, 2934–2945. [Google Scholar] [CrossRef]
- Sudheera, K.K.; Ma, M.; Chong, P.H.J. Cooperative data routing & scheduling in software defined vehicular networks. In Proceedings of the 2018 IEEE Vehicular Networking Conference (VNC), 2018, Taipei, Taiwan, 5–7 December 2018; IEEE: New York, NY, USA, 2018; pp. 1–8. [Google Scholar]
- Sudheera, K.L.K.; Ma, M.; Chong, P.H.J. Real-time cooperative data routing and scheduling in software defined vehicular networks. Comput. Commun. 2022, 181, 203–214. [Google Scholar] [CrossRef]
- Liyanage, K.S.K.; Ma, M.; Chong, P.H.J. Connectivity aware tribrid routing framework for a generalized software defined vehicular network. Comput. Netw. 2019, 152, 167–177. [Google Scholar] [CrossRef]
- Ghafoor, H.; Koo, I. CR-SDVN: A cognitive routing protocol for software-defined vehicular networks. IEEE Sensors J. 2017, 18, 1761–1772. [Google Scholar] [CrossRef]
- Darabkh, K.A.; Alkhader, B.Z.; Ala’F, K.; Jubair, F.; Abdel-Majeed, M. ICDRP-F-SDVN: An innovative cluster-based dual-phase routing protocol using fog computing and software-defined vehicular network. Veh. Commun. 2022, 34, 100453. [Google Scholar] [CrossRef]
- Yuan, X.S.; Caballero, J.M.; Juanatas, R. A Highway Routing Algorithm Based on SDVN. In Proceedings of the 2022 14th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 10–12 June 2022; IEEE: New York, NY, USA, 2022; pp. 1–5. [Google Scholar]
- Awad, M.K.; Ahmed, M.H.H.; Almutairi, A.F.; Ahmad, I. Machine learning-based multipath routing for software defined networks. J. Netw. Syst. Manag. 2021, 29, 1–30. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, F.R.; Yang, R. A machine learning approach for software-defined vehicular ad hoc networks with trust management. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirate, 9–13 December 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Zhao, L.; Bi, Z.; Lin, M.; Hawbani, A.; Shi, J.; Guan, Y. An intelligent fuzzy-based routing scheme for software-defined vehicular networks. Comput. Netw. 2021, 187, 107837. [Google Scholar] [CrossRef]
- Wu, J.; Fang, M.; Li, X. Reinforcement learning based mobility adaptive routing for vehicular ad-hoc networks. Wirel. Pers. Commun. 2018, 101, 2143–2171. [Google Scholar] [CrossRef]
- Li, F.; Song, X.; Chen, H.; Li, X.; Wang, Y. Hierarchical routing for vehicular ad hoc networks via reinforcement learning. IEEE Trans. Veh. Technol. 2018, 68, 1852–1865. [Google Scholar] [CrossRef]
- Wijesekara, P.A.D.S.N. Deep 3D Dynamic Object Detection towards Successful and Safe Navigation for Full Autonomous Driving. Open Transp. J. 2022, 16, e187444782208191. [Google Scholar] [CrossRef]
- Herath, H.M.D.P.M.; Weraniyagoda, W.A.S.A.; Rajapaksha, R.T.M.; Wijesekara, P.A.D.S.N.; Sudheera, K.L.K.; Chong, P.H.J. Automatic Assessment of Aphasic Speech Sensed by Audio Sensors for Classification into Aphasia Severity Levels to Recommend Speech Therapies. Sensors 2022, 22, 6966. [Google Scholar] [CrossRef] [PubMed]
- Liyanage, K.S.K.; Ma, M.; Chong, P.H.J. Controller placement optimization in hierarchical distributed software defined vehicular networks. Comput. Netw. 2018, 135, 226–239. [Google Scholar] [CrossRef]
- Small, M. Complex networks from time series: Capturing dynamics. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; IEEE: New York, NY, USA, 2013; pp. 2509–2512. [Google Scholar]
- McKeown, N.; Anderson, T.; Balakrishnan, H.; Parulkar, G.; Peterson, L.; Rexford, J.; Shenker, S.; Turner, J. OpenFlow: Enabling innovation in campus networks. ACM SIGCOMM Comput. Commun. Rev. 2008, 38, 69–74. [Google Scholar] [CrossRef]
- Fernandez, M.P. Comparing openflow controller paradigms scalability: Reactive and proactive. In Proceedings of the 2013 IEEE 27th International Conference on Advanced Information Networking and Applications (AINA), Barcelona, Spain, 25–28 March 2013; IEEE: New York, NY, USA, 2013; pp. 1009–1016. [Google Scholar]
- Wijesekara, P.A.D.S.N.; Sudheera, K.L.K.; Sandamali, G.G.N.; Chong, P.H.J. An Optimization Framework for Data Collection in Software Defined Vehicular Networks. Sensors 2023, 23, 1600. [Google Scholar] [CrossRef]
- Wijesekara, P.A.D.S.N.; Wang, Y.K. A Mathematical Epidemiological Model (SEQIJRDS) to Recommend Public Health Interventions Related to COVID-19 in Sri Lanka. COVID 2022, 2, 793–826. [Google Scholar] [CrossRef]
- Riley, G.F.; Henderson, T.R. The ns-3 network simulator. In Modeling and Tools for Network Simulation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 15–34. [Google Scholar]
- Wijesekara, P.A.D.S.N.; Sudheera, K.L.K.; Sandamali, G.G.N.; Chong, P.H.J. Machine Learning Based Link Stability Prediction for Routing in Software Defined Vehicular Networks. In Proceedings of the 20th Academic Sessions, Matara, Sri Lanka, 7 June 2023; p. 60. [Google Scholar]
- Wijesekara, P.A.D.S.N.; Gunawardena, S. A Comprehensive Survey on Knowledge-Defined Networking. Telecom 2023, submitted.
- Anand, R.; Aggarwal, D.; Kumar, V. A comparative analysis of optimization solvers. J. Stat. Manag. Syst. 2017, 20, 623–635. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, S.; Athaiya, A. Activation functions in neural networks. Towards Data Sci. 2017, 6, 310–316. [Google Scholar] [CrossRef]
- Wijesekara, P.A.D.S.N. An Accurate Mathematical Epidemiological Model (SEQIJRDS) to Recommend Public Health Interventions Related to COVID-19 in Sri Lanka. Prepr. Res. Sq. 2021. [Google Scholar] [CrossRef]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Wijesekara, P.A.D.S.N. Deep 3D Dynamic Object Detection towards Successful and Safe Navigation for Full Autonomous Driving. Prepr. TechRxiv 2022. Available online: https://www.techrxiv.org/articles/preprint/Deep_3D_Dynamic_Object_Detection_towards_Successful_and_Safe_Navigation_for_Full_Autonomous_Driving/18517925 (accessed on 28 June 2022).
- Fogue, M.; Garrido, P.; Martinez, F.J.; Cano, J.C.; Calafate, C.T.; Manzoni, P. A realistic simulation framework for vehicular networks. In Proceedings of the 5th International ICST Conference on Simulation Tools and Techniques, Sirmione, Italy, 19–23 March 2012; pp. 37–46. [Google Scholar]
- Study on Enhancement of 3GPP Support for 5G V2X Services, Document TR 22.886 V16.2.0, 3GPP. 2018. Available online: http://www.3gpp.org/ftp//Specs/archive/22_series/22.886/22886-g20.zip (accessed on 28 June 2022).
- Federal Communication Commissions (FCC). Available online: https://docs.fcc.gov/public/attachments/FCC-03-324A1.pdf (accessed on 6 September 2022).
- Silva, C.M.; Silva, L.D.; Santos, L.A.; Sarubbi, J.F.; Pitsillides, A. Broadening understanding on managing the communication infrastructure in vehicular networks: Customizing the coverage using the delta network. Future Internet 2018, 11, 1. [Google Scholar] [CrossRef]
- Chen, J.; Mao, G.; Li, C.; Zafar, A.; Zomaya, A.Y. Throughput of infrastructure-based cooperative vehicular networks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2964–2979. [Google Scholar] [CrossRef]
- Salvo, P.; Turcanu, I.; Cuomo, F.; Baiocchi, A.; Rubin, I. Heterogeneous cellular and DSRC networking for Floating Car Data collection in urban areas. Veh. Commun. 2017, 8, 21–34. [Google Scholar] [CrossRef]
- Stoffers, M.; Riley, G. Comparing the ns-3 propagation models. In Proceedings of the 2012 IEEE 20th International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunication Systems, Washington, DC, USA, 7–9 August 2012; IEEE: New York, NY, USA, 2012; pp. 61–67. [Google Scholar]
- Garg, V.K. Radio propagation and propagation path-loss models. In Wireless Communications & Networking; Springer: Berlin, Germany, 2007; pp. 47–84. [Google Scholar]
- Simonsson, A.; Furuskar, A. Uplink power control in LTE-overview and performance, subtitle: Principles and benefits of utilizing rather than compensating for SINR variations. In Proceedings of the 2008 IEEE 68th Vehicular Technology Conference, Calgary, AB, Canada, 21–24 September 2008; IEEE: New York, NY, USA, 2008; pp. 1–5. [Google Scholar]
- Haider, A.; Hwang, S.H. Maximum transmit power for UE in an LTE small cell uplink. Electronics 2019, 8, 796. [Google Scholar] [CrossRef]
- Karunathilake, T.; Förster, A. A Survey on Mobile Road Side Units in VANETs. Vehicles 2022, 4, 482–500. [Google Scholar] [CrossRef]
- Elbasher, W.S.; Mustafa, A.B.; Osman, A.A. A Comparison between Li-Fi, Wi-Fi, and Ethernet Standards. Int. J. Sci. Res. (IJSR) 2015, 4, 1–4. [Google Scholar]
- Wijesekara, P.A.D.S.N.; Sangeeth, W.M.A.K.; Perera, H.S.C.; Jayasundere, N.D. Underwater Acoustic Digital Communication Channel for an UROV. In Proceedings of the 5th Annual Research Symposium (ARS2018), Hapugala, Sri Lanka, 4 January 2018; p. E17. [Google Scholar]
- Ge, X. Ultra-reliable low-latency communications in autonomous vehicular networks. IEEE Trans. Veh. Technol. 2019, 68, 5005–5016. [Google Scholar] [CrossRef]
- Tang, J.; Chen, X.; Zhu, X.; Zhu, F. Dynamic Reallocation Model of Multiple Unmanned Aerial Vehicle Tasks in Emergent Adjustment Scenarios. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 1139–1155. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Bailly, A.; Blanc, C.; Francis, É.; Guillotin, T.; Jamal, F.; Wakim, B.; Roy, P. Effects of dataset size and interactions on the prediction performance of logistic regression and deep learning models. Comput. Methods Programs Biomed. 2022, 213, 106504. [Google Scholar] [CrossRef]
- Torres, J.F.; Galicia, A.; Troncoso, A.; Martínez-Álvarez, F. A scalable approach based on deep learning for big data time series forecasting. Integr.-Comput.-Aided Eng. 2018, 25, 335–348. [Google Scholar] [CrossRef]
- Agrawal, S.C. Deep learning based non-linear regression for Stock Prediction. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1116, p. 012189. [Google Scholar]
- Kim, H.K.; Kim, Y.; Lee, S.; Min, S.; Bae, J.Y.; Choi, J.W.; Park, J.; Jung, D.; Yoon, S.; Kim, H.H. SpCas9 activity prediction by DeepSpCas9, a deep learning–based model with high generalization performance. Sci. Adv. 2019, 5, eaax9249. [Google Scholar] [CrossRef] [PubMed]
- Wijesekara, P.A.D.S.N. A study in University of Ruhuna for investigating prevalence, risk factors and remedies for psychiatric illnesses among students. Sci. Rep. 2022, 12, 12763. [Google Scholar] [CrossRef] [PubMed]
- Wijesekara, P.A.D.S.N. Prevalence, Risk Factors and Remedies for Psychiatric Illnesses among Students in Higher Education: A Comprehensive Study in University of Ruhuna. Prepr. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Zhu, H.; Li, M.; Chlamtac, I.; Prabhakaran, B. A survey of quality of service in IEEE 802.11 networks. IEEE Wirel. Commun. 2004, 11, 6–14. [Google Scholar] [CrossRef]













| Routing Framework | Routing Technique |
|---|---|
| Hierarchical SDVN [42] | Traditional VANET routing protocols with hierarchical controllers |
| Resource scheduling scheme [43] | Greedy routing with objective of minimizing communication cost |
| On-demand routing protocol [44] | Two-level packet forwarding using Bellman Ford algorithm and improved AODV |
| Spray-and-pray multiple copy routing [45] | Graph-based least communication steps to minimize latency |
| Globally optimized routing [46] | Minimum optimistic time-based shortest path routing algorithm |
| Link stability-based routing [47] | Routing based on shortest stable path |
| Cooperative data routing and scheduling [48,49] | Routing by prioritizing traffic type to minimize service latency while maximizing packet delivery ratio |
| Tribrid routing protocol [50] | Stable shortest path routing satisfying QoS parameters |
| Cognitive routing protocol [51] | Stable path routing with spectrum sensing |
| Cluster-based routing (ICDRP-F-SDVN) [52] | Clustering algorithm with overhead reduction approach with backup VANET routing |
| Highway routing [53] | Optimal routing path selection by predicting destination vehicle location using hidden Markov model |
| Multipath routing [54] | QoS and flow rule space constrained routing using machine learning |
| Trust-based routing [55] | Selects routing paths with highest trust using Deep Q learning |
| Intelligent fuzzy-based routing [56] | Uses reinforcement learning to select most stable routing path |
| Mobility adaptive routing [57] | Routing using Q-table updated by distributed Q learning |
| Hierarchical routing [58] | Routing using optimum sequence of grids using Q learning |
| Notation | Description |
|---|---|
| , , | Wireless transmission distance, maximum wireless transmission distance, change in x direction displacement, change in y direction displacement, change in x direction velocity, change in y direction velocity, change in x direction acceleration, and change in y direction acceleration, respectively |
| Wireless link lifetime between nodes i and j | |
| , , | Total one-hop delay of node i, transmission delay of last packet of node i, queuing delay of all other packets except last packet in node i, contention delay of last packet of node i, processing delay of last packet of node i, flow control delay of last packet of node i, and propagation delay of last packet of node i, respectively |
| Average wireless one-hop link delay of node i using CSMA–CA, and average wired one-hop link delay of node i using CSMA–CD, respectively | |
| , , , , , | Transmission delay of jth packet of node i, queuing delay of jth packet in node i, contention delay of jth packet of node i, processing delay of jth packet of node i, flow control delay of jth packet of node i, and propagation delay of jth packet of node i, respectively |
| Transmission delay for transmitting RTS, CTS, and ACK packets, respectively | |
| Frame spacing in CSMA, total random backoff time of the jth packet in ith node during contention period, and total collision duration during contention for jth packet in ith node, respectively | |
| S, , , , , | Destination node, adjacency matrix of link lifetime, adjacency matrix of position, adjacency matrix of link delay, and the parent vector containing list of parent nodes and channel types (wired or wireless) in reaching destination node j from source node k, route valid time for the path from source node k to destination node j, respectively |
| Network congestion threshold, link lifetime threshold, wireless data rate, and wired data rate, respectively | |
| Normalized network per channel link entropy, homogeneous normalized entropy, normalized homogeneous link entropy with respect to wireless links, and normalized homogeneous link entropy with respect to wired links, respectively | |
| Average pending transmission packet distribution factor at node i, pending transmission factor of node i at jth time step, and average pending transmission packet distribution factor of the network, respectively | |
| Average queue size of node i, and queue size of node i at jth time step, respectively | |
| Average collision probability for wireless links, and average collision probability for wired links, respectively | |
| , , | Average contention delay for CSMA–CA, average contention delay for CSMA–CD, maximum of average contention delay for CSMA–CA, and maximum of average contention delay for CSMA–CD, respectively |
| Maximum retransmission attempts during contention, slot time, collision duration, minimum contention window, and maximum contention window, respectively | |
| Normalized network contention, normalized wireless contention, and normalized wired contention, respectively | |
| Node i’s set of one-hop neighbors’ node addresses, total one-hop neighbors of node i, total number of nodes, number of wireless links connected to node i, number of wired links connected to node i, total number of vehicle nodes, and total number of RSU nodes, respectively | |
| f, , | Data collection frequency, optimization frequency, and routing frequency, respectively |
| Parameter | Value |
|---|---|
| Network simulation | NS-3.35 |
| Optimizer | GuRoBi 10.0.0 |
| Deep Neural Network | TensorFlow 2.11.0 |
| Plotting tool | MATLAB R2021a |
| Mobility scenario generation | SUMO version and OpenStreetMap |
| Simulation time | 600 s per each run |
| Maximum vehicles | 200 |
| Maximum RSUs | 64 |
| Maximum speed of vehicles | 0–60 km/h (Urban), 0–100 km/h (Non-urban), 0–250 km/h (autobahn) |
| Transmission protocol | User Datagram Protocol (UDP) |
| Communication channels | DSRC for (I2V, V2I, V2V), point to point between RSUs, CSMA from RSU to controller node, and LTE between vehicles and controller node |
| Wifi-standard | IEEE 802.11p |
| DSRC transmission power | 33 dBm (urban), 41 dBm (non-urban), 44 dBm (highway) |
| DSRC OFDM data rate | 27 Mbps |
| DSRC propagation loss model | Cost–Hata (urban), 3-log distance (non-urban, autobahn) |
| DSRC propagation delay model | Constant speed propagation delay |
| DSRC error rate model | Nist error rate model |
| LTE pathloss model | Cost-Hata |
| LTE maximum transmit power | 23 dBm |
| LTE SRS periodicity | 2, 5, 10, 20, 40, 80, 160, 320 |
| LTE fading model | Trace fading loss model |
| LTE EPC data rate | 1000 Mbps |
| RSU backbone data rate | 1000 Mbps |
| RSU backbone delay | 10 s |
| Payload size for routing | 104 bytes |
| Broadcasting status data payload size | 104 bytes for proposed routing, 56 bytes for Dijkstra, 0 bytes for AODV |
| Unicasting uplink status & metadata payload size | bytes for proposed routing, bytes for Dijkstra, 0 bytes for AODV |
| packet_in | 24 bytes for proposed routing, 0 bytes for Dijkstra and AODV |
| FlowMod payload size | 76 bytes for proposed routing, 68 bytes for Dijkstra, 0 bytes for AODV |
| Communication cost per byte | 1—wired, 2—DSRC, 40—Cellular |
| Routing frequency | Variable () in the range [0.02, 5] |
| Number of nodes | Variable () in the range [4, 256] |
| Link lifetime threshold | Variable () in the range [0, 10] |
| Network contention threshold | 0.5 |
| Network Instance | |
|---|---|
| Link lifetime threshold of {0.0, 4.0, 6.0, 8.0, 10.0} s | {0.19, 0.07, 0.30, 0.78, 1.00} |
| Routing frequency of {0.02, 0.06, 0.10} Hz | {0.42, 0.28, 0.09} |
| Network size of {4, 8, 16, 32, 64} nodes | {0.50, 0.32, 0.29, 0.20, 0.08} |
| Urban mobility scenario at speed {0, 10, 40} km/h | {0.32, 0.19, 0.07} |
| Rural mobility scenario at speed {0, 20, 40, 60, 80, 100} km/h | {0.16, 0.33, 0.29, 0.30, 0.25, 0.21} |
| Autobahn mobility scenario at speed {0, 30, 50, 90, 130, 170, 210, 250} km/h | {0.30, 0.34, 0.39, 0.37, 0.35, 0.33, 0.32, 0.31} |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wijesekara, P.A.D.S.N.; Gunawardena, S. A Machine Learning-Aided Network Contention-Aware Link Lifetime- and Delay-Based Hybrid Routing Framework for Software-Defined Vehicular Networks. Telecom 2023, 4, 393-458. https://doi.org/10.3390/telecom4030023
Wijesekara PADSN, Gunawardena S. A Machine Learning-Aided Network Contention-Aware Link Lifetime- and Delay-Based Hybrid Routing Framework for Software-Defined Vehicular Networks. Telecom. 2023; 4(3):393-458. https://doi.org/10.3390/telecom4030023
Chicago/Turabian StyleWijesekara, Patikiri Arachchige Don Shehan Nilmantha, and Subodha Gunawardena. 2023. "A Machine Learning-Aided Network Contention-Aware Link Lifetime- and Delay-Based Hybrid Routing Framework for Software-Defined Vehicular Networks" Telecom 4, no. 3: 393-458. https://doi.org/10.3390/telecom4030023
APA StyleWijesekara, P. A. D. S. N., & Gunawardena, S. (2023). A Machine Learning-Aided Network Contention-Aware Link Lifetime- and Delay-Based Hybrid Routing Framework for Software-Defined Vehicular Networks. Telecom, 4(3), 393-458. https://doi.org/10.3390/telecom4030023







