Deep Learning Optimisation of Static Malware Detection with Grid Search and Covering Arrays
Abstract
1. Introduction
1.1. Malware and Its Detection
1.2. Brief about HPO
1.3. Generating Covering Arrays
1.4. Brief about Grid Search and Covering Arrays
1.5. Brief about Deep Learning
1.6. Hyperparameter Optimisation for Deep Learning
1.7. Paper Contribution
- 1.
- The paper presents a novel approach to improving static malware detection using deep learning models with hyperparameter optimisation through covering arrays. The study demonstrates the feasibility of using cAgen in combination with grid search to find the optimal hyperparameter values. The findings show that this approach can significantly improve the accuracy of the baseline model for both the Ember and Kaggle datasets.
- 2.
- The study provides insights into the effects of different hyperparameters and their interactions on the performance of deep learning models for static malware detection.
- 3.
- It provides a framework for researchers and practitioners to improve the performance of deep learning models for malware detection through hyperparameter optimisation using covering arrays.
- 4.
- The results of this study have implications for the wider field of cybersecurity, where accurate malware detection is critical in protecting computer systems and networks.
1.8. The Structure of the Paper
2. Related Literature
2.1. ML-Based Static Malware-Detection-Related Literature
2.2. Covering-Array-Related Literature
3. Methodology
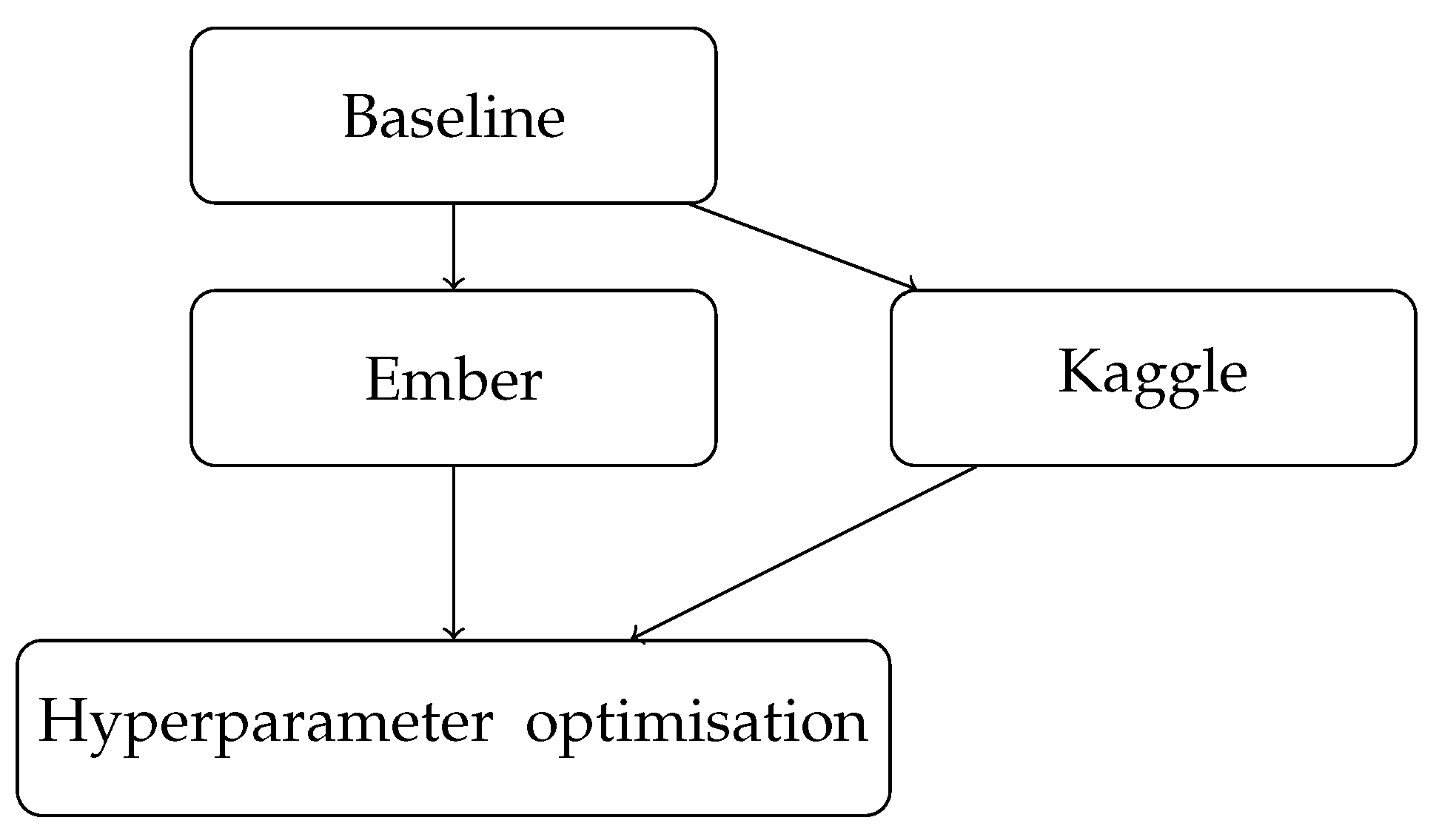
Overall Approach
4. Experiment Details and Dataset Brief
4.1. Datasets
4.2. Experiment Setup
4.3. Baseline Model
4.4. Performance Evaluation
5. Grid Search versus cAgen for NN Hyperparameter-Optimisation Tasks
5.1. Grid Search
- 1.
- Define the search space for hyperparameters and their respective values;
- 2.
- Split the data into a training set and a validation set;For each combination of hyperparameters in the search space:
- 3.
- Train a model on the training set using the current hyperparameters;
- 4.
- Evaluate the model’s performance on the validation set;
- 5.
- Select the hyperparameters that result in the best performance on the validation set.
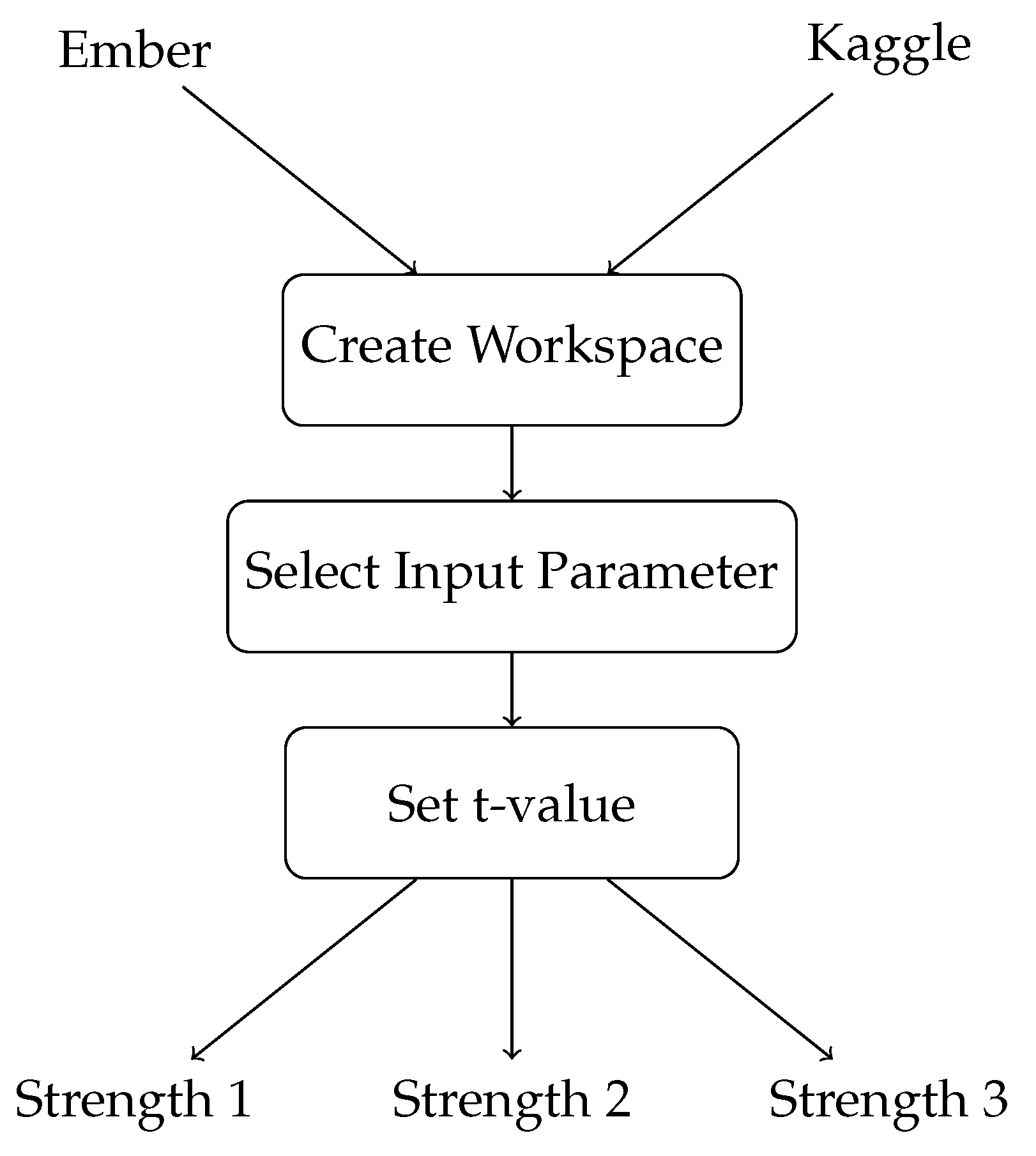
5.2. cAgen
- 1.
- Create a workspace to prepare the model;
- 2.
- Select the input parameter (IPM) to modify the model’s parameters;
- 3.
- Set the value of t, which determines the strength of the covering array;
- 4.
- Generate a covering array of hyperparameter configurations using the IPM and t-value;For each configuration in the covering array:
- 5.
- Train a model on the training set using the current hyperparameters;
- 6.
- Evaluate the model’s performance on the validation set;
- 7.
- Select the hyperparameters that result in the best performance on the validation set.
5.3. Hyperparameter Grid Search Configurations
6. Results and Discussion
6.1. cAgen Tool Hyperparameter Versus Grid Search Results
- 1.
- Both the grid search and cAgen tool were effective in finding optimal hyperparameters for the deep learning models.
- 2.
- The cAgen tool was particularly useful for finding optimal hyperparameters for the Ember dataset, which had a larger number of features and samples.
- 3.
- The optimised deep learning models achieved significantly higher accuracy than the baseline models for both datasets.
- 4.
- The optimised deep learning models achieved higher accuracy than the previous benchmark model for the Ember dataset (it was at 92%).
- 5.
- The choice of hyperparameters significantly impacted the accuracy of the models, particularly for the learning rate and number of neurons.
- 6.
- The results highlight the potential of using hyperparameter-optimisation techniques for improving the performance of deep learning models in static malware detection
6.2. Discussion
6.3. Tuning the Number of Neurons
6.4. Tuning the Number of Layers
6.5. Tuning of Activation Functions
6.6. Tuning the Dropout Relay
6.7. Choice of Optimisers
6.8. Tuning the Number of Epochs and Batch Size
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A survey of optimization methods from a machine learning perspective. IEEE Trans. Cybern. 2019, 50, 3668–3681. [Google Scholar] [CrossRef] [PubMed]
- Shafi, I.; Ahmad, J.; Shah, S.I.; Kashif, F.M. Impact of varying neurons and hidden layers in neural network architecture for a time frequency application. In Proceedings of the 2006 IEEE International Multitopic Conference, Islāmābād, Pakistan, 23–24 December 2006. [Google Scholar] [CrossRef]
- Dahl, G.E.; Sainath, T.N.; Hinton, G.E. Improving deep neural networks for LVCSR using rectified linear units and dropout. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8609–8613. [Google Scholar]
- Lei, Y.; Kacker, R.; Kuhn, D.R.; Okun, V.; Lawrence, J. IPOG: A general strategy for t-way software testing. In Proceedings of the 14th Annual IEEE International Conference and Workshops on the Engineering of Computer-Based Systems (ECBS’07), Tucson, AZ, USA, 26–29 March 2007; pp. 549–556. [Google Scholar]
- Cohen, D.M.; Dalal, S.R.; Fredman, M.L.; Patton, G.C. The AETG system: An approach to testing based on combinatorial design. IEEE Trans. Softw. Eng. 1997, 23, 437–444. [Google Scholar] [CrossRef]
- Bryce, R.C.; Colbourn, C.J. The density algorithm for pairwise interaction testing. Softw. Test. Verif. Reliab. 2007, 17, 159–182. [Google Scholar] [CrossRef]
- Bryce, R.C.; Colbourn, C.J. A density-based greedy algorithm for higher strength covering arrays. Softw. Test. Verif. Reliab. 2009, 19, 37–53. [Google Scholar] [CrossRef]
- Lei, Y.; Tai, K.C. In-parameter-order: A test generation strategy for pairwise testing. In Proceedings of the Third IEEE International High-Assurance Systems Engineering Symposium (Cat. No. 98EX231), Washington, DC, USA, 13–14 November 1998; pp. 254–261. [Google Scholar]
- Torres-Jimenez, J.; Izquierdo-Marquez, I. Survey of covering arrays. In Proceedings of the 2013 15th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, Romania, 23–26 September 2013; pp. 20–27. [Google Scholar]
- Seroussi, G.; Bshouty, N.H. Vector sets for exhaustive testing of logic circuits. IEEE Trans. Inf. Theory 1988, 34, 513–522. [Google Scholar] [CrossRef]
- Group, M.R. Covering Array Generation. 2022. Available online: https://matris.sba-research.org/tools/cagen/#/about (accessed on 21 July 2022).
- Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative study of CNN and RNN for natural language processing. arXiv 2017, arXiv:1702.01923. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Jason, B. How to Configure the Number of Layers and Nodes in a Neural Network. Available online: https://machinelearningmastery.com/how-to-configure-the-number-of-layers-and-nodes-in-a-neural-network/ (accessed on 23 April 2023).
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 1–9. [Google Scholar]
- Bengio, Y. Gradient-based optimization of hyperparameters. Neural Comput. 2000, 12, 1889–1900. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. arXiv 2012, arXiv:1206.2944. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proceedings of the International Conference on Learning and Intelligent Optimization, Rome, Italy, 17–21 January 2011; pp. 507–523. [Google Scholar]
- Karnin, Z.; Koren, T.; Somekh, O. Almost optimal exploration in multi-armed bandits. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1238–1246. [Google Scholar]
- Injadat, M.; Moubayed, A.; Nassif, A.B.; Shami, A. Systematic ensemble model selection approach for educational data mining. Knowl.-Based Syst. 2020, 200, 105992. [Google Scholar] [CrossRef]
- Claesen, M.; Simm, J.; Popovic, D.; Moreau, Y.; De Moor, B. Easy hyperparameter search using optunity. arXiv 2014, arXiv:1412.1114. [Google Scholar]
- Anderson, H.S.; Roth, P. Elastic/Ember. 2021. Available online: https://github.com/elastic/ember/blob/master/README.md (accessed on 23 April 2023).
- Mauricio. Benign Malicious. 2021. Available online: https://www.kaggle.com/amauricio/pe-files-malwares (accessed on 10 November 2021).
- Schultz, M.G.; Eskin, E.; Zadok, F.; Stolfo, S.J. Data mining methods for detection of new malicious executables. In Proceedings of the 2001 IEEE Symposium on Security and Privacy, S&P 2001, Oakland, CA, USA, 14–16 May 2001; pp. 38–49. [Google Scholar]
- Kolter, J.Z.; Maloof, M.A. Learning to detect and classify malicious executables in the wild. J. Mach. Learn. Res. 2006, 7, 2721–2744. [Google Scholar]
- Raff, E.; Barker, J.; Sylvester, J.; Brandon, R.; Catanzaro, B.; Nicholas, C.K. Malware detection by eating a whole exe. In Proceedings of the Workshops at the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Pham, H.D.; Le, T.D.; Vu, T.N. Static PE malware detection using gradient boosting decision trees algorithm. In Proceedings of the International Conference on Future Data and Security Engineering, Ho Chi Minh City, Vietnam, 28–30 November 2018; pp. 228–236. [Google Scholar]
- Fawcett, C.; Hoos, H.H. Analysing differences between algorithm configurations through ablation. J. Heuristics 2016, 22, 431–458. [Google Scholar] [CrossRef]
- Azeez, N.A.; Odufuwa, O.E.; Misra, S.; Oluranti, J.; Damaševičius, R. Windows PE Malware Detection Using Ensemble Learning. Informatics 2021, 8, 10. [Google Scholar] [CrossRef]
- ALGorain, F.T.; Clark, J.A. Covering Arrays ML HPO for Static Malware Detection. Eng 2023, 4, 543–554. [Google Scholar] [CrossRef]
- Pérez-Espinosa, H.; Avila-George, H.; Rodriguez-Jacobo, J.; Cruz-Mendoza, H.A.; Martínez-Miranda, J.; Espinosa-Curiel, I. Tuning the parameters of a convolutional artificial neural network by using covering arrays. Res. Comput. Sci. 2016, 121, 69–81. [Google Scholar] [CrossRef]
- Forbes, M.; Lawrence, J.; Lei, Y.; Kacker, R.N.; Kuhn, D.R. Refining the in-parameter-order strategy for constructing covering arrays. J. Res. Natl. Inst. Stand. Technol. 2008, 113, 287. [Google Scholar] [CrossRef]
- Lei, Y.; Kacker, R.; Kuhn, D.R.; Okun, V.; Lawrence, J. IPOG/IPOG-D: Efficient test generation for multi-way combinatorial testing. Softw. Test. Verif. Reliab. 2008, 18, 125–148. [Google Scholar] [CrossRef]
- Duan, F.; Lei, Y.; Yu, L.; Kacker, R.N.; Kuhn, D.R. Improving IPOG’s vertical growth based on a graph coloring scheme. In Proceedings of the 2015 IEEE Eighth International Conference on Software Testing, Verification and Validation Workshops (ICSTW), Graz, Austria, 13–17 April 2015; pp. 1–8. [Google Scholar]
- Anderson, H.S.; Roth, P. Ember: An open dataset for training static pe malware machine learning models. arXiv 2018, arXiv:1804.04637. [Google Scholar]
- Carrera, E. pefile. 2022. Available online: https://github.com/erocarrera/pefile (accessed on 15 January 2022).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- sklearn. sklearn-StandardScaler. 2022. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html#sklearn.preprocessing.StandardScaler (accessed on 6 July 2022).
- Saxe, J.; Berlin, K.; Vishwanathan, S. EXPOSE: A character-level convolutional neural network for predicting malware behavior. arXiv 2015, arXiv:1510.07391. [Google Scholar]
- Rajaraman, S.; Huang, Y.H.; Kim, H. Malware detection using deep neural network with multiple learning rates. In Proceedings of the 2018 IEEE International Conference on Electro Information Technology (EIT), Rochester, MI, USA, 3–5 May 2018; pp. 679–683. [Google Scholar]
- Seo, H.; Lee, J.; Lee, J. Malware detection using a hybrid convolutional neural network and long short-term memory model. Inf. Sci. 2020, 516, 423–436. [Google Scholar]
- Hayou, S.; Doucet, A.; Rousseau, J. On the impact of the activation function on deep neural networks training. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 10–15 June 2019; pp. 2672–2680. [Google Scholar]
- Huang, Y.; Xu, X.; Zhou, X.; Wu, G. Deep learning-based malware detection: A review. Comput. Secur. 2020, 92, 101716. [Google Scholar]
- Shafiq, M.; Mustafa, K.; Yaqoob, I.; Saleem, K.; Makhdoom, I.; Abbas, H. Automated malware classification using ensemble with feature selection. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; pp. 1–6. [Google Scholar]


| Reference | Methodology | Limitations | Comparison with Proposed Work |
|---|---|---|---|
| [26] | Machine learning applied to the PE format | Limited dataset size, performance varies with dataset size and complexity | Early work in the field, smaller dataset used, does not utilise covering arrays for hyperparameter optimisation. |
| [27] | Machine-learning-based classification using n-gram frequency counts | Reliance on feature engineering, performance not evaluated on large-scale dataset | Older approach, less efficient feature engineering. |
| [29] | Gradient-boosting decision tree algorithm for static detection | Limited evaluation on only one dataset | Methodology not compared with covering arrays for hyperparameter optimisation. |
| [30] | Analysis of machine learning models using a subset of the Ember dataset | Only used a subset of the Ember dataset, no comparative analysis of covering arrays | Evaluates only a subset of the Ember dataset, no comparison with covering arrays for hyperparameter optimisation. |
| [31] | Stacked ensemble of fully connected, one-dimensional CNNs | Large amount of computational resources required, the selection of hyperparameters still crucial | No comparison with covering arrays for hyperparameter optimisation. |
| [32] | Novel method for detecting malware using four machine learning techniques tuned with cAgen | Limited evaluation of only one dataset, less efficient approach for covering array generation (compatible with classical ML techniques only) | Similar approach to the proposed work, but less efficient method for covering array generation (classical ML techniques only). |
| [33] | Utilisation of mixed-level covering arrays to design and tune a CNN for audio classification | Limited to audio classification task, no comparison with grid search | Different problem domain, no comparison with grid search. |
| Dataset | Architecture | Accuracy |
|---|---|---|
| Ember | 3-layer neural network | 81.2% |
| Kaggle | 3-layer neural network | 94% |
| Hyperparameter | Grid Search Space |
|---|---|
| Number of neurons (per layer) | [1200, 1400, 1800, 2000, 2200, 2400] |
| Number of epochs | [20, 40,60, 80, 100] |
| Batch size | [16, 32, 48, 64, 80] |
| Optimiser | Adam or SGD |
| Drop-out relay | [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9] |
| Learning rate | [0.001, 0.01, 0.1, 0.11, 0.12, 0.113, 0.114, 0.2] |
| Activation function (per layer) | softmax, softplus, softsign, relu, tanh, sigmoid, hard_sigmoid, linear |
| Hyperparameter | Grid Search Space |
|---|---|
| Number of neurons (per layer) | [55, 60, 65, 70, 75, 80] |
| Batch size | [48, 64, 80, 100, 128] |
| Number of epochs | [20, 40, 60, 80, 100] |
| Optimiser | Adam or SGD |
| Drop-out relay | [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9] |
| Learning rate | [0.001, 0.01, 0.1, 0.11, 0.12, 0.113, 0.114, 0.2] |
| Activation functions (per layer) | softmax, softplus, softsign, relu, tanh, sigmoid, hard_sigmoid, linear |
| ML Algorithm | Optimal Values Found | t-Strength Values/Grid Search | Time to Complete | Number of Combinations Searched | Score (Accuracy) |
|---|---|---|---|---|---|
| DL | 75, 150, 1 SGD tanh, sigmoid 0.0 20 128 0.0112 | T2 | 7 min 36 s | 60 | 0.9814 |
| 75, 150, 1 Adam tanh, sigmoid 0.0 20 80 0.0001 | T3 | 49 m 1 s | 361 | 0.9840 | |
| 75, 80, 1 SGD tanh, relu 0.1 20 80 0.0112 | T4 | 3 h 17 min 14 s | 1452 | 0.9842 | |
| 75, 80, 80 Adam softsign, tanh 0.2 60 80 0.0112 | Full grid search | ∼4 days 3 h 6 min | all | 0.9862 |
| ML Algorithm | Optimal Values Found | t-Strength Values/Grid Search | Time to Complete | Number of Combinations Searched | Score (Accuracy) |
|---|---|---|---|---|---|
| DL | 2400, 1200, 1200 Adam softplus, relu, sigmoid 0.0 20 64 0.00001 | T1 | 15 h 31 min | 10 | 0.9562 |
| 1200, 1200, 1200 Adam sofplus, relu, sigmoid 0.5 40 128 0.0001 | T2 | 4 d 23 h 5 min 47 s | 60 | 0.9575 | |
| 2400, 1200, 1200 Adam hard_sigmoid, relu, sigmoid 0.1 40 64 0.0 | Full grid search | ∼29 days 15 h | all | 0.9542 |
| Dataset | Architecture | Accuracy |
|---|---|---|
| Ember | 6-layer neural network | 95.7% |
| Kaggle | 5-layer neural network | 98.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ALGorain, F.T.; Alnaeem, A.S. Deep Learning Optimisation of Static Malware Detection with Grid Search and Covering Arrays. Telecom 2023, 4, 249-264. https://doi.org/10.3390/telecom4020015
ALGorain FT, Alnaeem AS. Deep Learning Optimisation of Static Malware Detection with Grid Search and Covering Arrays. Telecom. 2023; 4(2):249-264. https://doi.org/10.3390/telecom4020015
Chicago/Turabian StyleALGorain, Fahad T., and Abdulrahman S. Alnaeem. 2023. "Deep Learning Optimisation of Static Malware Detection with Grid Search and Covering Arrays" Telecom 4, no. 2: 249-264. https://doi.org/10.3390/telecom4020015
APA StyleALGorain, F. T., & Alnaeem, A. S. (2023). Deep Learning Optimisation of Static Malware Detection with Grid Search and Covering Arrays. Telecom, 4(2), 249-264. https://doi.org/10.3390/telecom4020015






