Abstract
In Vehicular Ad Hoc Networks (VANETs), promoting cooperative behavior is a challenging problem for mechanism designers. Cooperative actions, such as disseminating data, can seem at odds with rationality and may benefit other vehicles at a cost to oneself. Without additional mechanisms, it is expected that cooperative behavior in the population will decrease and eventually disappear. Classical game theoretical models for cooperation, such as the public goods game, predict this outcome, but they assume fixed population sizes and overlook the ecological dynamics of the interacting vehicles. In this paper, we propose an evolutionary public goods game that incorporates VANET ecological dynamics and offers new insights for promoting cooperation. Our model considers free spaces, population density, departure rates of vehicles, and randomly composed groups for each data sender. Theoretical analysis and simulation results show that higher population densities and departure rates, due to minimum differences between pay-offs of vehicles, promote cooperative behavior. This feedback between ecological dynamics and evolutionary game dynamics leads to interesting results. Our proposed model demonstrates a new extension of evolutionary dynamics to vehicles of varying densities. We show that it is possible to promote cooperation in VANETs without the need for any supporting mechanisms. Future research can investigate the potential for using this model in practical settings.
1. Introduction
In Vehicular Ad Hoc Networks (VANETs), vehicles cooperate by sharing data and acting as routers to improve road safety, transportation security, and intelligent transportation systems. The cooperation, however, faces the tragedy of the commons challenge where vehicles may choose to free-ride [] on the contributions of other vehicles. This research is critical because finding effective solutions to incentivize cooperation among vehicles is necessary to achieve the desired network performance. To this end, the paper explores the use of game theory and incentive mechanisms to encourage cooperation in VANETs.
The paper reviews several incentive mechanisms that motivate vehicles to cooperate with one another []. These mechanisms include the Tit-for-Tat (TFT) mechanism, a multilayer credit-based incentive system, an incentive protocol that offers rewards to participating nodes, creating a honeypot that traps selfish vehicles in the network, an incentive-based protocol based on coalition game theory, and an incentive system that uses the reciprocal altruistic factor []. The paper also proposes an incentive mechanism that incorporates behavioral economics principles and combines both incentives and punishments for VANETs.
The paper also reviews game theoretical models that address the problem of free-riding in VANETs. It distinguishes between pairwise and collective games, where the former assumes that interactions are limited to two players, while the latter assumes collective interactions, where the strategy of one player can impact several other players’ strategies. The paper argues that while models with pairwise interactions are commonly used in game theory, their results cannot always be extended to games with collective interactions, leading to misleading conclusions. The cited studies used Markov decision processes, evolutionary game theory, repeated game approach, and a game-theoretic model to investigate cooperation in VANETs.
The rest of this study is organised as follows. Section 2 presents related works on the topic. In Section 3, we provide the formulation and define the game used to model cooperation in Vehicular Ad Hoc Networks. Additionally, in Section 4, we discuss the dynamical analysis and numerical simulation of the proposed model. Finally, Section 5 concludes the paper.
2. Related Work
Numerous studies have investigated methods to promote cooperation in VANETs. Among the most popular are incentive mechanisms and game theory approaches. Incentive mechanisms are designed to motivate vehicles to cooperate with one another. Shevade et al. proposed an incentive-aware routing protocol that uses a Tit-for-Tat (TFT) mechanism to maximize performance in Delay Tolerant Networks (DTNs) []. Zhu et al. developed a multilayer credit-based incentive system to encourage cooperation among DTN bundle nodes []. Lu et al. tackled the free-riding problem in DTNs by introducing an incentive protocol that offers rewards to participating nodes to promote fairness []. Patel et al. dealt with free-riding in VANETs by creating a honeypot that traps selfish vehicles in the network []. Dubey et al. developed an incentive-based protocol based on coalition game theory, in which vehicles have an incentive to forward data as members of a coalition to improve reliability and fairness in VANETs []. Liu et al. designed an incentive system that uses the reciprocal altruistic factor to reconstruct the utility function of vehicles []. They demonstrated that their system can reduce message transmission delay by up to 30% compared to other cooperative transmission mechanisms. Additionally, Liu et al. proposed an incentive mechanism from the perspective of behavioral economics that incorporates the anchoring effect and loss aversion on offloading in the Internet of Things []. They introduced the reference factor and price-break discount factor based on the anchoring effect and time pressure and regret value on loss aversion to encourage nodes to participate in data offloading. Rehman et al. developed a mechanism with both incentives and punishments for VANET []. In this mechanism, vehicles with higher weight and cooperation are elected as Heads during the election process. Vehicles that participate in the election can increase their reputation by cooperating in forwarding data, while those who exhibit repeated selfish behavior are punished.
In addition, game theory has been utilized to address the issue of free-riding in wireless network routing []. Game theory approaches can be broadly classified into two categories, pairwise and collective games. Pairwise games assume that interactions between players are limited to two players only, where the effect of a player’s strategy is only on one other player. On the other hand, collective games assume that interactions are collective, meaning that the strategy of one player can impact several other players’ strategies. The collective game category includes public goods games (PGG) and coalition games.
Previous studies have investigated the problem of cooperation in VANETs using game theory, and have utilized a model with pairwise interactions [,,,,,,]. This means that the effect of each player, or vehicle, is assumed to be limited to only one other companion player. However, this assumption may not be appropriate for the effect of forwarded messages, since each player can actually affect multiple other vehicles simultaneously. Therefore, other studies have considered the effect of each player on multiple other vehicles simultaneously, which is a more suitable assumption for the problem at hand. While models with pairwise interactions are commonly used in game theory, their results cannot always be extended to games with collective interactions, and may lead to misleading conclusions [].
The cited studies have contributed to the investigation of cooperation in VANETs through game theoretical models. Zhang et al. [] proposed a cooperative information dissemination scheme for vehicular networks using a Markov decision process. Mao et al. [,] proposed a cooperative content sharing mechanism using evolutionary game theory. Altman et al. [] considered the problem of finding stable cooperative strategies in VANETs using a repeated game approach. Naserian et al. [] proposed a game-theoretic model for cooperation in VANETs that considers the impact of obstacles on communication. Saeed et al. [] proposed a cooperative transmission mechanism that considers the impact of obstacles and interference on transmission rates.
The problem of promoting cooperation in social dilemmas involving groups of interacting individuals is traditionally investigated using the Public Goods Game (PGG), which assumes that individuals can make contributions to a public good. In VANETs, the data packet can be considered as the public good. Shivshankar and Jamalipour were the first to propose a game theoretic strategy, called Tit-for-Tat, to promote cooperation among vehicles in VANETs based on PGG. Their approach measured the cooperation level of the vehicles based on time and the number of message forwards, and they examined the effect of different parameters on the cooperation level to evaluate the performance of the proposed game [].
In a different study, Zhang et al. used PGG to investigate cooperative behavior among vehicles []. They showed that the cooperation level in VANETs is proportional to the synergy factor. Shivshankar and Jamalipour proposed a PGG framework to analyze the effects of networking properties on the dynamics of cooperation in VANETs. In another work, Ding et al. designed a PGG for VANETs with high node density. In the proposed game, vehicles could dynamically adjust their grouping strategy according to the real situation around their strategies. Additionally, they defined a hub vehicle that exchanges data packets with all neighbors to prevent isolated vehicles. The authors demonstrated that increasing the multiplication factor in the PGG would promote the cooperation level, which is an expected result for VANETs [].
In VANETs, messages sent by vehicles and road side units can impact multiple vehicles. Thus, it is more appropriate to model the effect of event messages as a multiplayer game with collective interactions rather than pairwise. However, current PGG-based models in VANETs have limitations. Researchers usually assume that each vehicle has fixed neighbors or can perfectly connect to all other players, which is not realistic in VANETs. Additionally, the topology of vehicles does not change throughout the game, which is also unrealistic. In VANETs, a vehicle benefits from diffusible messages produced by all vehicles in its group, which randomly form at each generation. Therefore, the vehicle’s payoff should be calculated by weighting the payoffs obtained in the randomly composed groups, weighted by the probability that such groups occur. Moreover, in VANETs, the PGG is played in populations of varying sizes. Small population size (or density) results in small group sizes and vice versa for a larger population size.
To address these limitations, this study models vehicles as players that form randomly composed groups at each round of the game based on the population size. This game is called ecological-aware PGG. The study investigates, for the first time to the best of our knowledge, the effect of rate of departure and density of vehicles on the cooperation dynamics in VANETs based on ecological-aware PGG.
3. The Proposed Model Based on Evolutionary Public Goods Game
The problem of cooperation in social dilemmas has been a challenging issue in evolutionary game theory for a long time. In Vehicular Ad Hoc Networks (VANETs), where effective communication and safe driving depend on vehicle cooperation, this problem becomes even more complicated due to the dynamic and uncertain nature of the network environment. To address this issue, we propose a new model for studying the ecological dynamics and evolution of cooperation in VANETs based on the evolutionary public goods game. The model takes into account the interaction between the payoff structure, spatial structure, and dynamics of network topology. Specifically, the model assumes that vehicles can interact locally and update their strategies based on the payoffs they receive from their neighbors. Furthermore, an evolutionary mechanism allows vehicles to adjust their cooperation strategies according to their own success and the success of their neighbors. The proposed model provides insights into the factors that influence the evolution of cooperation in VANETs. Overall, the proposed model offers a promising approach for understanding the evolution of cooperation in complex and dynamic social networks.
3.1. Formulation of the Model
In a typical public goods, all individuals have the opportunity to invest an amount c into a common pool. The total amount is then multiplied by a positive number r, and is distributed equally among all individuals, regardless of whether they have contributed or not. The average payoffs for cooperators and defectors among N players in an infinite population are given by
where N is group size and x is the relative frequency of the cooperation in the group. In this configuration, every individual has a temptation to defect since the cost of defection is equal to zero. Thus, each rational player avoids contributing and makes an effort to free-ride on contributions of other players. If all players follow this rationality, no one would contribute and, hence, the benefits of the public good would be equal to zero.
In a well-mixed, infinite population we assume, as is standard, that groups are formed randomly at each generation, after which fitness is calculated. The group size of public goods interactions varies in public goods game with a population of varying densities. Basically, small (large) effective group sizes are induced by small (large) population densities.
Let us call x, y, and z the frequencies of cooperators, defectors and empty spaces () in the randomly composed group of vehicles to exchange event messages. Therefore, represents the normalized density of vehicles, such that 1 corresponds to maximum density of the population and 0 shows extinction. The average payoff of cooperators, , and defectors, , are calculated by weighting the payoffs obtained in the randomly formed groups of vehicles, weighted by the probability that such group composed.
In standard PGG the probability of a group composed of X cooperators and defectors is given by
where x denotes the fraction of the cooperators. In our problem, the probability of a group composed m cooperators, defectors, and empty spaces is . Therefore, the average payoffs of the focal cooperator and defector are given by
where N is the number of vehicles within the diffusion range of the event message by a given vehicle, S is the number of individuals belonging to either type cooperator or defector, and m is the number of individuals of type cooperator. The fitness functions (4) and (5) can be reduced to:
3.2. Using the Game to Inform the Model
Now we employ replicator equations to analyze the frequency-dependent evolutionary dynamics of cooperators, defectors, and empty spaces. Let us assume , , and represent the relative frequency of cooperator, defector, and empty space, at time t, respectively. Additionally, , , and denote the changing rate of the phenotypes’ frequency. In this system we assume that new vehicles can only emerged into empty space. Hence, birth rates are proportional to empty spaces z and their payoffs. Dynamics of the individuals in this system are calculated by the following equations
where d and b indicate death and birth rates of vehicle (i.e., departure rates), , , and show rate of change of cooperator, defector, and empty space frequencies in the population, respectively. Equation (8) represents an extension on the replicator dynamics equations []. Replicator dynamics determine whether individuals in the process of evolution converges to which proportions within the population []. Equation (8) is converted to normal replicator [] if and . The equilibrium of the phenotype frequencies is calculated by setting our equation system (i.e., Equation (8)) equal to zero. As the frequencies of three phenotypes cooperator, defector, and empty space should clearly sum to one, the set of possible frequency states will be a simplex that defined by:
The replicator dynamics equations have several equilibrium (fixed) points that describe situations in which the population is no longer evolving. These equilibrium points have two types, monomorphic and polymorphic. Monomorphic point indicates a pure population state composed of one player type, where polymorphic point represents a mixed population state including more than one player type.
4. Dynamical Analysis
Equilibrium points in replicator Equation (8) are obtained by setting them to zero. In our system, this corresponds to an internal steady state between cooperators and defectors if system works infinity. In this section, we investigate the stability of the equilibrium points in parametric form and represent individuals behavior by several scenarios under different conditions. Some of these scenarios represent normal behavior and others indicate rare cases that theoretically can take place.
Scenario (i) Consider a system without any cooperators. In such situation (), according to Equation (6), the average payoff of the defector will be , hence the rate of change of defector frequencies is . This results in decreasing defector frequency in the population and, consequently, it goes extinct.
Scenario (ii) In the absence of defectors in the population (), according to Equation (6), the average payoff of cooperators is given by:
By setting in equation and based on the maximum value of the function three equilibria can be readily observed in the system. The maximum of the function is actually attained at the point and is given by:
If then population goes to extinct (i.e., , , and ), while for a bifurcation arise in the system (Figure 1) that results in one stable and one unstable interior equilibrium at higher and lower x, respectively. However, another equilibrium emerged exactly at the maximum point that represents an unstable point.
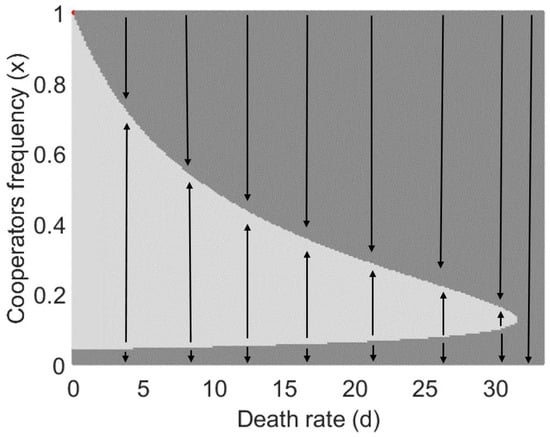
Figure 1.
Bifurcation diagram for population dynamics of the vehicles in the absence of the defectors. Darker (brighter) region indicates points that it can be moves into the basin of attraction of the unstable (stable) point (). The dynamics has been illustrated for , , and .
Figure 2 shows population dynamics in the absence of defectors for others parameters.
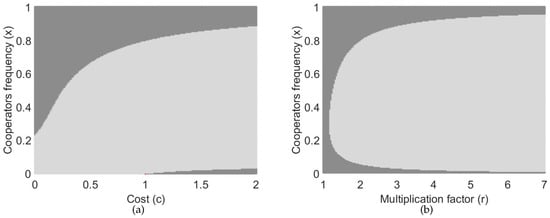
Figure 2.
Types of vehicles dynamics in the absence of the defectors with regards to the parameters c and r. Darker (brighter) region indicates points that it can be moves into the basin of attraction of the unstable (stable) point (). In panel (a) the dynamics have been illustrated for , , and , while in panel (b) the dynamics has been shown for , , and .
Scenario (iii) The system can enable cooperators to survive even when defectors free-ride on contributions of the cooperators. In order to investigate this scenario, a new variable is introduced. By using Equation (8), the changing rate of and z are given by:
and
By introducing variable the dynamic system in Equation (8) which represented by a 3-simplex reduced to a dynamics that shown in a rectangle determined by and . This sheds some new light on the vehicle dynamic from viewpoint of the evolutionary game theory. Figure 3 shows an example of vehicles dynamics for such system. As shown in this figure, natural selection favors cooperator vehicles and, eventually, all populations select this strategy. The red rectangle in this figure represents the valid region of the population dynamics induced by Equations (12) and (13). It is worth pointing out that the dynamics on the rectangle boundaries can be analyzed clearly. The boundaries and represent the scenarios i and , respectively. Definitely, on the boundary of , z will be equal to 1. However, the dynamics on the boundary has 1, 2, or 3 equilibrium states: extinction of defector (i.e., cooperator dominance), extinction of the cooperators (i.e., defector dominance), and coexistence of the cooperators and defectors.
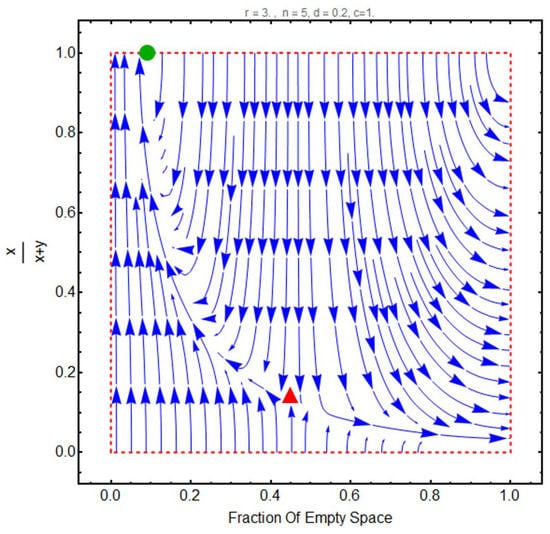
Figure 3.
An example of the population dynamics in the presence of cooperators and defectors. This game has one polymorphic stable point between and z. The red rectangle shows valid region of the dynamics. Red triangular and green solid circular represent saddle and stable points in the system, respectively.
Up to now, we have discussed about the monomorphic equilibrium points of the game which defectors or cooperators strictly dominate. Now, conditions under which a polymorphic equilibrium can arise are investigated. Since in the polymorphic equilibrium and , so in accordance with [] the equilibrium are obtained by setting and . Analyzing the parametric form of is very complicated and maybe impossible. Hence, we analyze different conditions for using numerical simulations and under various environment conditions. According to the numerical simulation we claim that for function at most has one root, and for and at most has two roots in the interval . Figure 4 shows the roots of the function for and . Consequently, there are at most two equilibrium points in the system. Figure 5 shows all dynamics of the system regards to the number of equilibria.
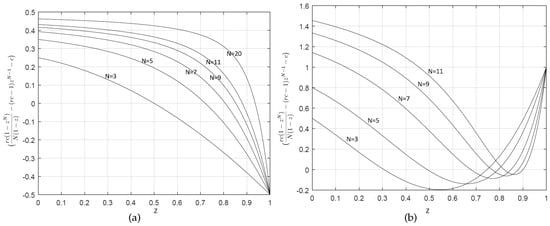
Figure 4.
Roots of function for (panel (a)) and and (panel (b)) for different values of N.
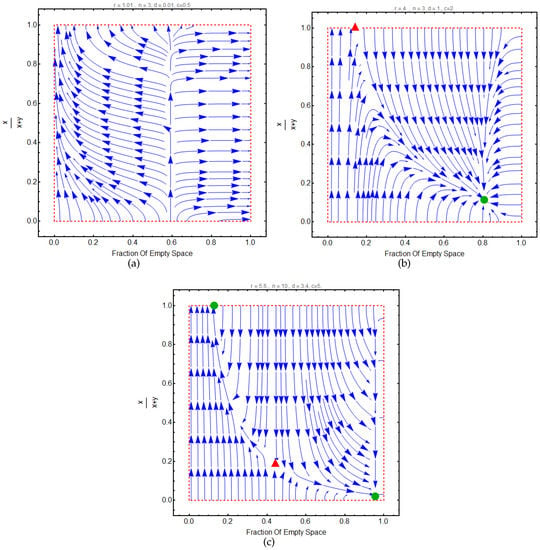
Figure 5.
Types of evolutionary dynamics with regards to the model’s parameters. The game has three types of polymorphic equilibria. 1-Panel (a): The game has no any polymorphic stable equilibrium point 2-Panel (b): The game has one polymorphic equilibrium point 3-Panel (c): The game has two polymorphic equilibria including stable and saddle points. Red triangular and green solid circular represent saddle and stable points in the system, respectively.
An equilibrium point in the system can be stable, unstable, and saddle. An equilibrium point X is stable if for every neighborhood U of X the system starts from another neighborhood of X, eventually the system goes to U. An unstable point is an equilibrium if it is not stable. A saddle point is an unstable equilibrium where it is stable at least in one direction. In general, if equilibrium points exist, their stability depend on values of the parameter. Our simulations show that the dynamical system at most can have one polymorphic stable equilibrium point (Figure 5). As can be seen in Figure 5a, the boundary is attracting for sufficiently small population densities (approximately for ). Hence, for the small population, vehicles remain unable to recover from exploitation and finally become extinct. Additionally, for large population densities, cooperation arises in the system but there is no stable point. This means that, by changing the number of defectors and cooperators, the final state maybe changed. Figure 5b shows the system has one polymorphic stable equilibrium. In this example, population goes to stable point (, ) for z more than . It is easily seen that for high population densities cooperation arises, while for medium and small densities relative defector frequency increases in the population over time and finally approaches to the stable point (, ). The important point to note here is that although in high densities cooperation arises, there is no any equilibrium in this area. Figure 5c is similar to Figure 5b except that it includes a polymorphic saddle point. For a given and low c, if population density increases, the members of the randomly composed group increase until eventually . This decreases the return from the public good (i.e., forwarded messages) and results in increasing defectors in the system. However, decreasing population density result in smaller randomly composed group until in the long run holds, and cooperator vehicles arise.
One of the advantage of the proposed model lies in the fact that cooperation level of vehicles can be determined by setting model’s parameters. Figure 6 suffice to show it. As illustrated in this figure, a high death rate, that is equal to birth rate in the proposed model, increases the chance of cooperation in large population densities while low death rate, by contrast, increases the cooperator frequency in the small population densities. This is for the simple reason that the payoff of cooperators and defectors directly influence growth by increasing d proportional to x and y (see Equation (8)), respectively.
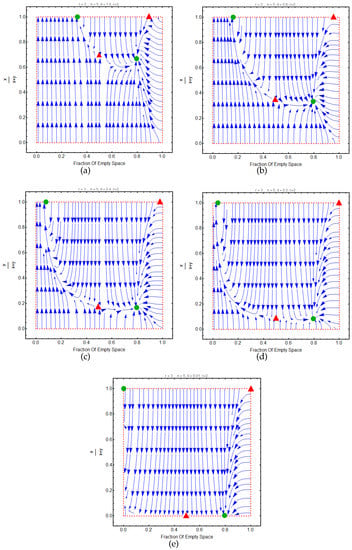
Figure 6.
Types of evolutionary dynamics with regards to d. Each graph is plotted for different values of d. 1-Panel (a): d = 1.6, 2-Panel (b): d = 0.8, 3-Panel (c): d = 0.4, 4-Panel (d): d = 0.2, 5-Panel (e): d = 0.01. Decreasing the value of d reduce the chance of cooperation between vehicles in the small population densities.
The size of randomly composed group N is another determinant element in promoting cooperation. Indeed, in our model, N determines the average number of vehicles that are able to receive the message from the focal vehicle. Generally, low (high) value of N increases (decreases) the return from the public good and leads to promote (demote) defection between the vehicles. Figure 7 shows the effect of N on the level of cooperation of vehicles.
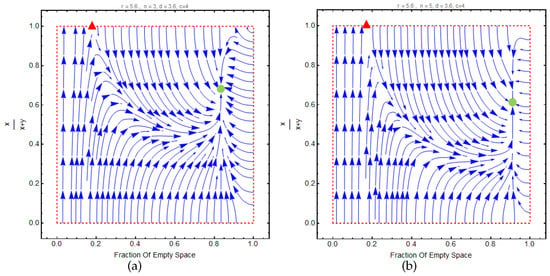
Figure 7.
Types of evolutionary dynamics with regards to n. 1-Panel (a): n = 3, 2-Panel (b): n = 5. High value of n results in decreasing the chance of cooperation between vehicles in the small population densities.
If the costs of contribution c are sufficiently small the cooperation arises between vehicles. Figure 8 represents the effect of c on the level of cooperation between the vehicles. As shown, increasing c leads to continuous loss of cooperation strength in the population insofar as (Figure 8c) results in the lowest cooperativeness.
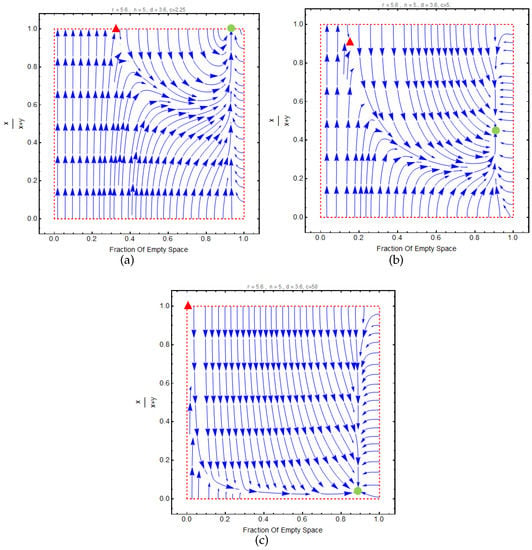
Figure 8.
Types of evolutionary dynamics with regards to c. 1-Panel (a): c = 2.25, 2-Panel (b): c = 5, 3-Panel (c): c = 50. Low value of c increases the chance of cooperation between vehicles.
5. Conclusions
This paper presents a novel approach, the ecological-aware public goods game (PGG), to investigate the evolution of cooperation between vehicles in Vehicular Ad hoc Networks (VANETs). The proposed model incorporates dynamical network topology and varying population sizes, which are two key features of VANETs. Our simulations and theoretical analyses reveal that the promotion of cooperation is influenced by various network parameters. Specifically, a higher birth rate increases the size of local communities and results in a smaller difference in payoff between cooperating and defecting vehicles, thereby reducing the probability of strategy change. On the other hand, lower densities can lead to an increase in defection due to the large difference in payoff between cooperators and defectors. The proposed model provides a useful tool for designing network properties to promote cooperation between vehicles, without the need for any additional mechanisms.
Furthermore, our results demonstrate that the topological properties of the network, such as the degree distribution and clustering coefficient, also have a significant impact on cooperation dynamics. Networks with higher degrees and clustering coefficients promote cooperation by providing more opportunities for cooperation and increasing the probability of establishing social ties between cooperators. Moreover, the departure rate of vehicles, which reflects the turnover of network participants, is found to play a crucial role in determining the stability of cooperative behavior. In general, a moderate departure rate is conducive to cooperation, as it provides a balance between introducing new cooperators and maintaining existing social ties.
To extend the findings of this study, future work could explore the effect of other network parameters, such as network size and heterogeneity, on the evolution of cooperation in VANETs. Moreover, empirical studies could be conducted to validate the effectiveness of the proposed approach in real-world scenarios. Overall, our work highlights the importance of designing appropriate network properties to promote cooperative behavior in VANETs, which can have significant implications for the development of intelligent transportation systems.
Author Contributions
Conceptualization, J.S.S.; writing—original draft preparation, J.S.S.; writing—review and editing, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data were presented in main text.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, M.; Weng, J.; Yang, A.; Liu, J.N.; Lin, X. Toward blockchain-based fair and anonymous ad dissemination in vehicular networks. IEEE Trans. Veh. Technol. 2019, 68, 11248–11259. [Google Scholar] [CrossRef]
- Hardin, G. The tragedy of the commons. Science 1968, 162, 1243–1248. [Google Scholar] [CrossRef] [PubMed]
- Ghovanlooy Ghajar, F.; Salimi Sratakhti, J.; Sikora, A. Sbtms: Scalable blockchain trust management system for vanet. Appl. Sci. 2021, 11, 11947. [Google Scholar] [CrossRef]
- Shevade, U.; Song, H.H.; Qiu, L.; Zhang, Y. Incentive-aware routing in DTNs. In Proceedings of the 2008 IEEE International Conference on Network Protocols, Orlando, FL, USA, 19–22 October 2008; pp. 238–247. [Google Scholar]
- Zhu, H.; Lin, X.; Lu, R.; Fan, Y.; Shen, X. Smart: A secure multilayer credit-based incentive scheme for delay-tolerant networks. IEEE Trans. Veh. Technol. 2009, 58, 4628–4639. [Google Scholar]
- Lu, R.; Lin, X.; Zhu, H.; Shen, X.; Preiss, B. Pi: A practical incentive protocol for delay tolerant networks. IEEE Trans. Wirel. Commun. 2010, 9, 1483–1493. [Google Scholar] [CrossRef]
- Patel, P.; Jhaveri, R. A Honeypot Scheme to Detect Selfish Vehicles in Vehicular Ad-hoc Network. In Computing and Network Sustainability; Springer: Berlin/Heidelberg, Germany, 2017; pp. 389–401. [Google Scholar]
- Dubey, B.B.; Chauhan, N.; Chand, N.; Awasthi, L.K. Incentive based scheme for improving data availability in vehicular ad-hoc networks. Wirel. Netw. 2017, 23, 1669–1687. [Google Scholar] [CrossRef]
- Liu, J.; Zhong, N.; Li, D.; Liu, H. BMCGM: A Behavior Economics-Based Message Transmission Cooperation Guarantee Mechanism in Vehicular Ad-hoc NETworks. Sensors 2018, 18, 3316. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Gao, W.; Li, D.; Huang, S.; Liu, H. An Incentive Mechanism Combined With Anchoring Effect And Loss Aversion To Stimulate Data Offloading In IoT. IEEE Internet Things J. 2018, 6, 4491–4511. [Google Scholar] [CrossRef]
- Rehman, G.U.; Ghani, A.; Zubair, M.; Naqvi, S.H.A.; Singh, D.; Muhammad, S. IPS: Incentive and Punishment Scheme for Omitting Selfishness in the Internet of Vehicles (Iov). IEEE Access 2019, 7, 109026–109037. [Google Scholar] [CrossRef]
- Charilas, D.E.; Panagopoulos, A.D. A survey on game theory applications in wireless networks. Comput. Netw. 2010, 54, 3421–3430. [Google Scholar] [CrossRef]
- Zhang, J.; Gauthier, V.; Labiod, H.; Banerjee, A.; Afifi, H. Information dissemination in vehicular networks via evolutionary game theory. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 124–129. [Google Scholar]
- Zhang, J.; Labiod, H.; Ren, M.; Tan, H.C. Cooperation behavior of vehicles in an evolutionary game for information dissemination. In Proceedings of the 2016 International Conference on Security of Smart Cities, Industrial Control System and Communications (SSIC), Paris, France, 18–19 July 2016; pp. 1–8. [Google Scholar]
- Mao, Y.; Zhu, P.; Wei, G.; Hassan, M.M.; Hossain, M.A. A game-based incentive model for service cooperation in VANETs. Concurr. Comput. Pract. Exp. 2016, 28, 674–687. [Google Scholar] [CrossRef]
- Altman, E.; Hayel, Y. A stochastic evolutionary game of energy management in a distributed aloha network. In Proceedings of the IEEE INFOCOM 2008-The 27th Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 1759–1767. [Google Scholar]
- Naserian, M.; Tepe, K. Game theoretic approach in routing protocol for wireless ad hoc networks. Ad Hoc Netw. 2009, 7, 569–578. [Google Scholar] [CrossRef]
- Mao, Y.; Zhu, P. A game theoretical model for energy-aware DTN routing in MANETs with nodes’ selfishness. Mob. Netw. Appl. 2015, 20, 593–603. [Google Scholar] [CrossRef]
- Saeed, Y.; Lodhi, S.A.; Ahmed, K. Obstacle management in vanet using game theory and fuzzy logic control. ACEEE Int. J. Commun. 2013, 4. [Google Scholar]
- Archetti, M.; Scheuring, I. Game theory of public goods in one-shot social dilemmas without assortment. J. Theor. Biol. 2012, 299, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Shivshankar, S.; Jamalipour, A. Effect of altruism and punishment on selfish behavior for cooperation in vehicular networks. In Proceedings of the 2012 1st IEEE International Conference on Communications in China (ICCC), Beijing, China, 15–17 August 2012; pp. 653–658. [Google Scholar]
- Ding, Q.; Zeng, X.; Zhang, X.; Sung, D.K. A public goods game theory-based approach to cooperation in VANETs under a high vehicle density condition. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3995–4005. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Shoham, Y.; Leyton-Brown, K. Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Taylor, P.; Jonker, L. Game dynamics and evolutionarily stable strategies. Math. Bio. Sci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Hauert, C.; De Monte, S.; Hofbauer, J.; Sigmund, K. Replicator dynamics for optional public good games. J. Theor. Biol. 2002, 218, 187–194. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).