Spatial Pattern Simulation of Antenna Base Station Positions Using Point Process Techniques
Abstract
:1. Introduction
2. Materials and Methods
Point Process Analysis
- The number of positions in a region A has a Poisson distribution with mean λN(A)
- The positions of these points are i.i.d. and uniformly distributed inside A
- The contents of two disjoint regions A and B are independent
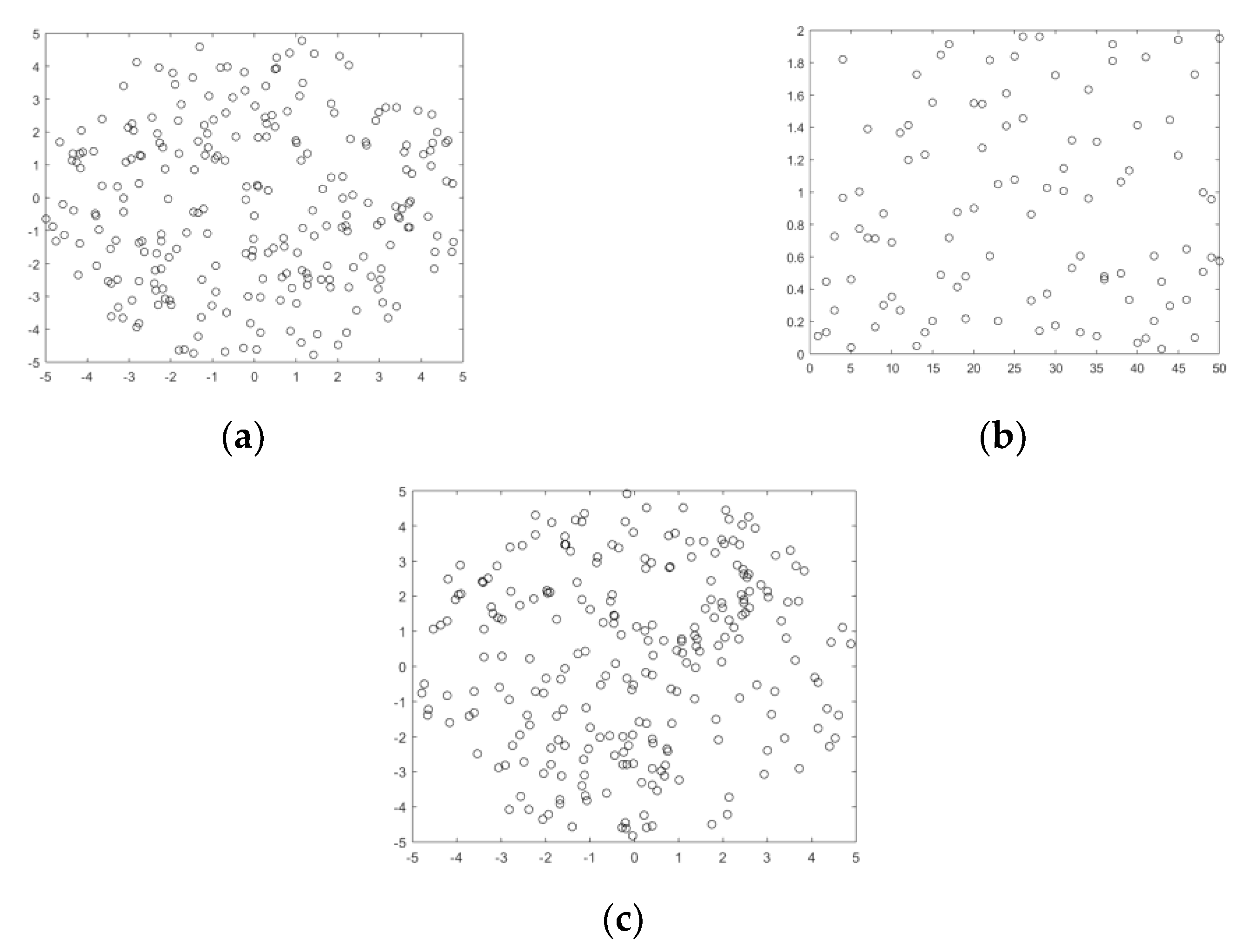
3. Results
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dale, M.R.T. Spatial Pattern Analysis in Plant Ecology; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B 1974, 3, 192–236. [Google Scholar] [CrossRef]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. Ser. B 1986, 48, 259–302. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, J.K. Spatial Processes: Models and Applications; Pion Limited: London, UK, 1981. [Google Scholar]
- Cressie, N.A. Statistics for Spatial Data (Revised Edition); John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Zimeras, S. Spatial Pattern Recognition Models with Application in Image Analysis. In Pattern Recognition Theory and Application; Zoeller, E.A., Ed.; Nova Publishers: Hauppauge, NY, USA, 2007; pp. 201–219, Chapter 7, 19. [Google Scholar]
- Diggle, P.J. Spatial Analysis of Spatial Point Patterns, 2nd ed.; Arnold Publishers: London, UK, 2003. [Google Scholar]
- Diggle, P.J. Spatial Statistics; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Ripley, B.D. Spatial Statistics; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Baddeley, A. Analysing Spatial Point Patterns in R.; CSIRO: Canberra, Australia, 2008. [Google Scholar]
- Launay, C.; Desolneux, A.; Galerne, B. Determinantal point processes for image processing. SIAM J. Imaging Sci. Soc. Ind. Appl. Math. 2020, 14, 304–348. [Google Scholar] [CrossRef]
- Agarwal, A.; Choromanska, A.; Choromanski, K. Notes on using determinantal point processes for clustering with applications to text clustering. arXiv 2014, arXiv:abs/1410.6975. [Google Scholar]
- Kulesza, A. Learning with Determinantal Point Processes. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2012. [Google Scholar]
- Vasseur, A. Analyse Asymptotique de Processus Ponctuels; Thèse de Doctorat, Informatique et Réseaux, ENST: Paris, France, 2017. [Google Scholar]
- Zimeras, S.; Matsinos, Y. Modelling Spatial Medical Data. In Effective Methods for Modern Healthcare Service Quality and Evaluation; IGI Global: Hershey, PA, USA, 2016; pp. 75–89. [Google Scholar]
- Zimeras, S.; Matsinos, Y. Modeling Uncertainty based on spatial models in spreading diseases: Spatial Uncertainty in Spreading Diseases. Int. J. Reliab. Qual. E-Healthc. (IJRQEH) 2019, 8, 55–66. [Google Scholar] [CrossRef]
- Upton, G.; Fingleton, B. Spatial Data Analysis by Example; John Wiley & Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Zimeras, S. Spreading Stochastic Models under Ising/Potts Random Fields: Spreading Diseases. In Quality of Healthcare in the Aftermath of the COVID-19 Pandemic; IGI Global: Hershey, PA, USA, 2022; pp. 65–78. [Google Scholar]
- Li, Y.; Baccelli, F.; Dhillon, H.S.; Andrews, J.G. Statistical Modeling and Probabilistic Analysis of Cellular Networks with Determinantal Point Processes. IEEE Trans. Commun. 2014, 63, 3405–3422. [Google Scholar] [CrossRef]
- Fattori, E.; Groisman, P.; Sarraute, C. Point Process Models for Distribution of Cell Phone Antennas. arXiv 2016, arXiv:1807.10975. [Google Scholar]
- Jahnel, B. Probabilistic Methods in Telecommunications; Lecture Notes; Springer: Berlin/Heidelberg, Germany, 2018; 69p. [Google Scholar]
- Guo, A.; Zhong, Y.; Haenggi, M.; Zhang, W. Success probabilities in Gauss-Poisson networks with and without cooperation. In Proceedings of the 2014 IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 30 June–5 July 2014; pp. 1752–1756. [Google Scholar]
- Deng, N.; Zhou, W.; Haenggi, M. The Ginibre point process as a model for wireless networks with repulsion. IEEE Trans. Wirel. Commun. 2015, 14, 107–121. [Google Scholar] [CrossRef]
- Diggle, P.J.; Tawn, J.A.; Moyeed, R.A. Model-based geostatistics (with discussions). Appl. Stat. 1998, 47, 299–350. [Google Scholar]
- Baddeley, A.J.; Silverman, B.W. A cautionary example of the use of second order methods for analyzing point patterns. Biometrics 1984, 40, 1089–1093. [Google Scholar] [CrossRef]
- Gatrell, A.C.; Bailey, T.C.; Diggle, P.J.; Rowlingson, B.S. Spatial point pattern analysis and its application in geographical epidemiology. Trans. Inst. Br. Geogr. 1996, 21, 256–274. [Google Scholar] [CrossRef]
- Bardenet, R.; Lavancier, F.; Mary, X.; Vasseur, A. On a few statistical applications of determinantal point processes. ESAIM Proc. Surv. 2017, 60, 180–202. [Google Scholar] [CrossRef]
- Raeisi, M.; Bonneu, F.; Gabriel, E. A spatio-temporal multi-scale model for Geyer saturation point process: Application to forest fire occurrences. Spat. Stat. 2021, 41, 100492. [Google Scholar] [CrossRef]
- Shaw, T.; Møller, J.; Waagepetersen, R.P. Globally intensity-reweighted estimators for K- and pair correlation functions. Aust. N. Z. J. Stat. 2021, 63, 93–118. [Google Scholar] [CrossRef]
- Zabarina, K. Spatial point pattern analysis and spatial interpolation. In Applied Spatial Statistics and Econometrics; Routledge: London, UK, 2020; pp. 371–432. [Google Scholar]





| References | Brief Presentation |
|---|---|
| Aurélien Vasseur (2017) [14] | Focus on Poisson point process considering probabilistic modeling using data based on antennas of the mobile network in Paris |
| Yingzhe Li, Franc¸ois Baccelli, Harpreet S. Dhillon, Jeffrey G. Andrews (2014) [19] | Poisson random point analysis using determinant point process |
| Ezequiel Fattori, Pablo Groisman, and Carlos Sarraute (2016) [20] | Modeling the spatial distribution of cell phone antennas in the city of Buenos Aires (CABA) |
| Benedikt Jahnel (2018) [21] | Probabilistic methods in Telecommunications |
| A. Guo, Y. Zhong, M. Haenggi, and W. Zhang (2014) [22] | Modeling using Gauss–Poisson point process |
| N. Deng, W. Zhou, and M. Haenggi (2015) [23] | Modeling using Ginibre point process |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimeras, S. Spatial Pattern Simulation of Antenna Base Station Positions Using Point Process Techniques. Telecom 2022, 3, 541-547. https://doi.org/10.3390/telecom3030030
Zimeras S. Spatial Pattern Simulation of Antenna Base Station Positions Using Point Process Techniques. Telecom. 2022; 3(3):541-547. https://doi.org/10.3390/telecom3030030
Chicago/Turabian StyleZimeras, Stelios. 2022. "Spatial Pattern Simulation of Antenna Base Station Positions Using Point Process Techniques" Telecom 3, no. 3: 541-547. https://doi.org/10.3390/telecom3030030
APA StyleZimeras, S. (2022). Spatial Pattern Simulation of Antenna Base Station Positions Using Point Process Techniques. Telecom, 3(3), 541-547. https://doi.org/10.3390/telecom3030030





