Abstract
Much research effort has been conducted to introduce intelligence into communication networks in order to enhance network performance. Communication networks, both wired and wireless, are ever-expanding as more devices are increasingly connected to the Internet. This survey introduces machine learning and the motivations behind it for creating cognitive networks. We then discuss machine learning and statistical techniques to predict future traffic and classify each into short-term or long-term applications. Furthermore, techniques are sub-categorized into their usability in Local or Wide Area Networks. This paper aims to consolidate and present an overview of existing techniques to stimulate further applications in real-world networks.
1. Introduction
Machine learning can be generally described as computational methods using experience to improve performance or to make accurate predictions [1]. More specifically, machine learning techniques use data-driven methods to improve the performance of a system. One major area of application for machine learning can be found in optical networks. Optical networks, based on the emergence of fiber in transport networks, provide higher capacity and reduced costs for new applications such as Video on Demand, Content Delivery Networks, Internet of Things, and Cloud Computing. They have been developed continuously to offer more flexible technology, complex algorithms, and new technologies, such as Elastic Optical Networks (EONs) [2,3] or Space Division Multiplexing (SDM) [4]. However, recent trends, such as big data, Internet of Things (IoT), and 5G networks, demand not only high-capacity optical links but effective and programmable control over the network [5].
To support efficient networking with the rapidly evolving data transfers, big data features such as Velocity, Volume, Value, Variety, and Veracity should be accommodated by networks [6]. Large-scale backbone networks require great capacity and this capacity can be increased by adding additional resources, such as adding more spectrum (either by changing the technology or simply providing more fiber links). On the other hand, such an approach is not efficient either in terms of planning or cost-efficiency. Instead, one should ask the question of how we can use data analytics to make more efficient decisions. This leads us to the concept of cognitive networks [7]. A cognitive optical network can be defined as a transport network that uses a cognitive process to perceive current network conditions. It plans, decides, and acts on these conditions, learns from the historical data, and forecasts future events. The cognitive processes, which learn or make use of history to improve performance, apply various data analytics solutions typically utilizing machine learning techniques. In particular, data analytics (DA), machine learning (ML) and deep learning (DL), or, in general, Artificial Intelligence (AI) concepts are regarded as promising methodological areas to enable cognitive network data analysis, thus enabling, e.g., automatized network self-configuration and fault management.
The Internet follows an explosive growth trend, with exponential increases in connected users, devices, and data transmission volumes. By 2023, there will be an estimated 5.3 billion Internet users, with each user connecting, on average, 3.6 devices to the network. The global average bandwidth speed is also expected to increase from 61.2 Mbps in 2020 to 110.4 Mbps in 2023 [8]. At such a large scale and growth rate, it is becoming more and more difficult to control, manage, monitor, and predict traffic patterns in optical networks using traditional manual operations. As such, machine learning can be the principal solution to automate network decisions to improve performance, mainly through traffic prediction.
Machine Learning Tasks for Optical Networks
A very popular aspect of optical network service where machine learning is applied is the network’s survivability, which describes the network’s ability to provide uninterrupted data flow [9]. Machine learning can optimize survivability rates in optical networks by recognizing issues, making self-directed decisions, and predicting traffic flows and potential failures. These different goals can be classified into standard ML tasks, which are briefly described below [1]:
- Classification: Process of assigning threat categories;
- Regression: Predicting a value for items;
- Ranking: Ordering based on some criteria.
While the majority of the work focuses on the above-mentioned aspect, another very important task is traffic prediction. Quite a few existing papers provide ML-based solutions for traffic prediction in communication networks. This survey will try to classify ML applications into their use of short-term versus long-term traffic prediction. Furthermore, short-term and long-term prediction differences will be examined in Local Area Networks (LAN) versus Wide Area Networks (WAN). In the following sections, this paper will discuss the motivations for applying ML to networks, followed by a general survey of techniques used in short-term predictions and long-term traffic predictions in Local and Wide Area Networks. The relevant papers explored in the survey will be categorized into the following techniques:
- Neural Networks;
- Support Vector Machines;
- Linear Regression;
- Principal Component Analysis;
- Statistical Models;
- Linear Time Series Models.
Figure 1 shows a high-level overview of the papers discussed in this survey, categorized into techniques that are applied to achieve the traffic prediction.
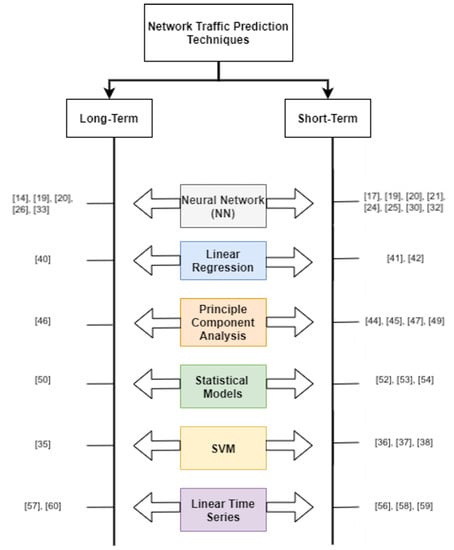
Figure 1.
Structure of the survey.
The remainder of this paper is divided as follows. Section 2 motivates our survey. We then discuss definitions of short- and long-term traffic prediction, as well as the differences between the Local Area Network and Wide Area Network, in Section 3. The following sections discuss concepts of various machine learning techniques and their application towards traffic prediction. Finally, we summarize the paper in Section 10, followed by future directions. To the best of our knowledge, this is the first survey that summarizes recent advancements related to traffic prediction based on Artificial Intelligence.
2. Motivations
The application of machine learning in optical networks can be linked to the emergence and increasing popularity of Artificial Intelligence. While AI focuses on making ‘smart’ machines, ML is a branch of AI seeking to make machines smarter through ‘learning’ [10]. In tandem with the growth and power of computing technologies, AI through ML methods has become a viable solution for optical networks because of successes in large-scale operations, faster processing speeds, and flexibility through automated decision-making. Musumeci et al. [11] classify motivations for using ML in optical networks into two broad categories: increased system complexity and increased data availability.
2.1. System Complexity
Optical networks are becoming more complex in both the physical and network layer. The physical architecture of the optical network can be reconfigured, and additional electronic components can be attached at various points to collect and monitor signal data. An example is optical-time-domain reflectometry (ODTR)-based monitoring. ODTR equipment measures traces of backscattered light by first injecting short light pulses into optical fibers. The response measured by the receiver can be used to monitor fiber performance [12]. Programmable software layered on top of physical hardware further increases system complexity. The programmability of the network provides the basis for a Software-Defined Optical Network (SDON) from which ML intelligence can be introduced to the system [13]. As systems become more complex and larger in scale, it becomes more challenging for humans to make performance-affecting decisions. This is important since optical networks often must meet a certain quality of transmission. Automatic and accurate changes and adjustments to the network would be ideal for achieving this. Thus, a well-trained machine could be supplemented with an existing human-operated network to increase its performance.
2.2. Data Availability
Alongside the data generated from physical hardware, monitoring equipment, and SDONs, there is also the ever-increasing buildup of historical data and expert knowledge. All of this information, including raw labeled or unlabeled data, can be used to better train machines in performance optimization and future predictions. For example, long-term historical data can be fed to machines as a learning mechanism to filter data noise since it can compare current changes to historical changes in signal state [14,15]. Another motivation for using ML may be to reduce the time spent in feature engineering. Determining features can be a lengthy process requiring expert knowledge from human-led feature engineering. With deep learning, it may be possible for machines to extract features by themselves, without human input. Lastly, given the amount of data available to train ML models, it becomes possible to train machines offline. Doing so would reduce the requirement for real-time online computation. This would decrease computation and resource costs while ensuring that the live network service is not compromised [13].
3. Definitions
Traffic prediction techniques can often be applied across various timescales or time-independently, so criteria are needed to classify techniques into short-term or long-term categories. For the purpose of this paper, ‘short-term’ refers to the prediction and application of techniques in the timeframe of minutes, hours, and days. ‘Long-term’ refers to the prediction and application of techniques for weeks, months, and years. A specific technique is classified as short-term or long-term depending on whether it:
- specifically discusses short-term or long-term prediction purposes;
- is applied in simulation for the short term or long term;
- predicts traffic for short-term or long-term increments of time;
- is time-dependent or -independent.
In the case where the technique is time-independent, as is often the case in predicting blocking probability, this paper will classify the technique as long-term. It is important to note that short-term predictions may become long-term predictions if deployed for a longer duration. Additionally, a technique’s purpose of prediction may be applicable for the long term, such as blocking probability estimation or power usage reduction. Henceforth, time-independent techniques are classified as long-term traffic prediction because they may be applied regardless of time duration.
Moreover, all techniques discussed in this paper apply either to Local Area Networks (LAN) or Wide Area Networks (WAN). LAN are networks where devices are connected within small geographical locations, such as a building or a group of buildings, as shown in Figure 2. Networks are considered WAN when they span larger geographical locations across large distances, such as a country-wide network or a global network, as shown in Figure 3.
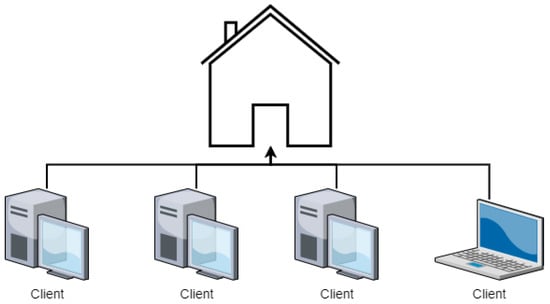
Figure 2.
Local Area Network diagram.
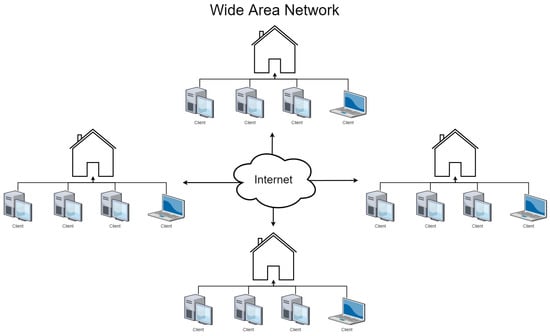
Figure 3.
Wide Area Network diagram.
4. Neural Networks
Neural Networks (NNs) are algorithms used in machine learning to solve problems via data processing. Input data move through a series of interconnected nodes, where each node is weighted initially and re-calculated as the information passes through the network. Some everyday tasks include regression and classification. A general NN consists of an input, a hidden, and an output layer. The hidden layer may have multiple layers and use different algorithms in which data are processed [16]. Figure 4 shows the general layout of a Neural Network with two hidden layers.
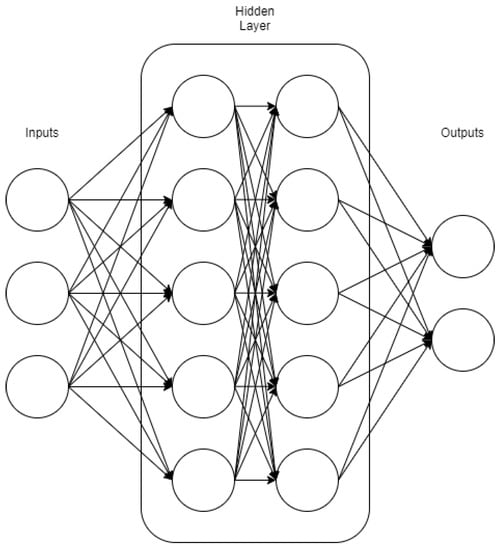
Figure 4.
General layout of a Neural Network with two hidden layers.
Neural Networks rely on training data to learn and improve their accuracy over time. However, once these learning algorithms are fine-tuned for accuracy, they are potent tools in Computer Science and Artificial Intelligence, allowing us to classify and cluster data at a high velocity. One of the possible applications of NNs in communication networks is traffic prediction. In the following subsection, we discuss the relevant papers that use NNs.
Relevant Papers
Zang et al. [17] propose a method to predict the next-hour traffic value for cell towers in a large city by feeding pre-processed time series signals into an Elman Neural Network (ENN). An ENN, a deep learning technique, differs slightly from the traditional Neural Network layout of having three main layers: input, hidden, and output. An additional context layer is attached to the hidden layer, which takes the output of the hidden layer and stores it for use in future iterations of training [18]. The city’s base stations are first split into 50 groups by K-means clustering. K-means clustering is a set of machine learning algorithms that group similar data points together, generally with each cluster having one mean center. The number of groups is fixed, and the user chooses somewhat arbitrarily based on what they know about the data and what they think is best for the work. This paper uses both unsupervised (K-clustering) and supervised (ENN) machine learning methods to achieve its goal. The base station signals are first split into low- and high-frequency components through wavelength decomposition. Each component is then fed to the ENN and eventually fused to obtain prediction results [17]. Six days of traffic data were used for training, while one day was used for the final prediction testing. The paper finds that with the pre-processing of signal data using wavelength decomposition, the next-hour traffic prediction is more accurate than simply using ENN without prior wavelength decomposition. However, one drawback of this methodology is that the prediction performance decreases as the K-value is set higher. This means that the predictive ability of this method outside of the paper’s scenario would depend on the user-selected K-value. Nevertheless, this case shows that a combination of deep learning, data clustering, and signal pre-processing could predict short-term traffic in a Wide Area Network better than traditional means.
Aibin et al. [19,20] use time series traffic data sets from a network service provider in a combined Long Short-Term Memory (LSTM) and Recurrent Neural Network (RNN) training methodology to predict network traffic at 5 min and 1 h time granularities. An RNN network contains a feedback loop in the hidden layer that ‘remembers’ the results of a previous time. The issue with RNN is that its ‘memory’ degrades over time, called vanishing gradients, and thus is not suitable to predict long-term data dependencies [21], including autocorrelation. LSTM is a variant of RNN, which reduces this issue by having each neural cell contain additional memory units, saving cell states for long periods or forgetting information deemed not applicable. In this paper, LSTM is used to predict autocorrelation better. The data are first fed through the LSTM Neural Network, and the output is then fed through a traditional DNN network (Deep Neural Network) to obtain predictive results. One downside to using the LSTM model instead of a simple one is the longer duration required for training convergence. More training iterations are required before the model can accurately predict network traffic. To overcome this issue, the authors propose to use Monte Carlo Tree Search [15]. The key novelty of their approach is the use of various selection strategies applied to the phase of building a search tree under different network scenarios, which solves the problem of long convergence time.
Peng et al. [22] use an echo state network (ESN) and autoregressive integrated moving average (ARIMA) model to forecast mobile communication traffic series. ESNs are Recurrent Neural Networks where the input is passed through a randomized but fixed-weighted ‘reservoir’ of neural nodes to produce an output. The target output is then fed back into the reservoir as input. The idea is that the reservoir, with the target input, would ‘echo’ traces of past input history [23]. On the other hand, the multiplicative seasonal autoregressive integrated moving average (MSARIMA) is a model used for forecasting time series by looking at time-lagged value errors. The smooth part of the time series is input into the ESN for forecasting, while the seasonal part is input into ARIMA for long-term predictability. The hybrid model is used for predictions 6 to 168 h into the future. This study finds that their hybrid model has a 12% improvement in prediction accuracy over other similar methods, echo state networks, SVM, and Wavelet-MSARIMA. Hybrid models, which use different ML techniques to better generate short- and long-term predictions separately before being consolidated, may be a viable solution to predicting seasonal traffic data. A potential obstacle in using hybrid models can be its requirement for data pre-processing to produce two inputs to be used in two ML networks separately. This method may require more time to prepare the data as well as to train both models before consolidating the output prediction.
Jia et al. [24] use a Backpropagation Neural Network (BPNN) to predict future links in an elastic optical network (EON) in order to achieve better performance via increasing bandwidth utilization and decreasing blocking probability. The BPNN is used to predict the arrival time and holding time of future connections. These values are called ‘future connections’ in the paper. Meanwhile, ‘assigned connections’ are connections in which the arrival time and holding time are known since spectral resources are pre-specified along a particular path. A Minimum Comprehensive Weight Algorithm (MCW) predicts future arrival and holding time values on candidate paths. On the other hand, a Minimum Network Competition Algorithm (MNC) is used to calculate the resource competition for all candidate paths to compare them. The optimal path is the path with the least competition and with the least blocking probability. The MCW and MNC are routing and spectrum assignment (RSA) algorithms with holding time awareness, proposed to achieve lower blocking probability. The study finds that the MCW performs better than other algorithms in elastic optical network performance.
Morales et al. [25] use an Artificial Neural Network model to adaptively configure virtual network topologies (VNT) to scale to increased traffic demands automatically. Their methodology, which they call the VNT reconfiguration based on traffic prediction (VENTURE), will analyze real-time-monitored traffic data to predict hour-by-hour traffic. More specifically, the model predicts the maximum bitrate for every origin–destination pair and modifies the VNT to be capable of handling this maximum bitrate. ANN fitting, in this case, is an interactive procedure to find the lowest Akaike information criterion (AIC), where a lower AIC value means higher optimization between the accuracy and number of inputs. Three separate algorithms are then used to determine the pathway for data flows in the VNT. First, flows are allocated for already existing virtual links. Secondly, new virtual links are created and fully capacitated. Lastly, any residual bitrate is served on newly created uncapacitated virtual links. These three algorithms are iterated every hour to recompute and reconfigure the VNT to account for next-hour traffic. Morales et al. find that VENTURE is able to achieve transponder savings between 8% and 42% when compared with traditional threshold-based VNT reconfiguration. By predicting the maximum bitrate hour-by-hour, VENTURE can effectively reduce energy consumption, as it automatically de-activates and re-activates transponders during low- and high-traffic hours.
Menezes Jr et al. [26] explore the use of a nonlinear autoregressive exogenous model (NARX) to predict long-term chaotic laser and variable bitrate (VBR) video traffic time series data sets. More specifically, they seek to determine the viability of using NARX for long-term data prediction. NARX differs from an RNN in that the output of the NARX is fed back into its input, while an RNN only has feedback loops within the hidden layer [27]. A NARX network has an exogenous input regressor, which, in this particular approach, contains sample values of the actual time series. Another feedback loop to the input layer is supplied with an output regressor, which contains estimated data points from the Neural Network. These combine to supply long-term information and short-term information, respectively [26], to the system in order to predict future values accurately. The authors find that NARX Neural Networks can be used for long-term prediction and improve prediction performance compared to alternative Neural Network solutions, namely Elmann and Time Delay Neural Network (TDNN) models. This is because the output regressor in NARX networks seems to have the impact of reducing the likelihood of data overfitting [26]. Overfitting is a negative effect of machine learning where accurate training results are produced with a local set of training data, but performance may be inaccurate given actual scenarios and data [28]. This means that the ML model only works well with the training data but cannot accurately reflect relationships or patterns in a production environment. The authors thus propose further studies of NARX usage for long-term prediction with other data sets such as electrical load forecasting or financial time series analysis.
Xiong et al. [29] propose a power-aware lightpath management (PALM) algorithm to reduce the power consumption of tearing down and re-establishing lightpaths. According to Bolla, R., Bruschi, R., and Lago, P., the creation of lightpaths in elastic optical networks (EONs) may account for 15% of all power consumption [30]. A traffic prediction module is attached to the EON, consisting of a Backpropagation Neural Network (BPNN) supplemented by a particle swarm optimization (PSO) algorithm to determine initial input weights. The PSO algorithm works by first initializing a random population of weights for each input. Each particle has a velocity value attached to it and remembers its previous best velocity. With each iteration, the velocity value is updated to move towards a better value given its previous best [31]. This process is iterated until the authors determine an optimal velocity value as input for the BPNN. The PALM algorithm depends on the prediction output from the PSO-BPNN to determine whether to keep a lightpath open or to re-route a traffic request to a particular idle lightpath. Simulated results show that the PSO-BPNN at an 80% utilization threshold for the lightpath has a 31–36% improvement in reduced power consumption compared to the energy-efficient manycast (EEM) algorithm over a month. PALM is successful in significantly reducing power consumption in EONs; however, it comes at the price of an approximately 5% increase in bandwidth blocking ratio [29].
Leung et al. [32] test two algorithms using the extreme machine learning (EML) framework to estimate blocking probability in optical burst switching (OBS) networks. Packet loss may occur in burst switched networks when an intermediate node drops packets because it is not reserved for a particular bandwidth. EML is a type of single-hidden-layer Neural Network where the input weights of the hidden nodes are randomized. The two algorithms are designated I-ELM and Log-I-ELM, where the Log-I-ELM algorithm is trained to map the network conditions to the blocking probability. Both algorithms train by adding new, randomly weighted, hidden nodes with each iteration. The number of hidden nodes where the mean square error is lowest is used to predict the blocking probability over different traffic loads. The results indicate that the Log-I-ELM algorithm is the most accurate in estimating blocking probability in a network.
Vinchoff et al. [33] propose a Graph Convolution Network (GCN) and Generative Adversarial Network (GAN) to predict traffic spikes for both the short term and long term. The GCN captures the topological state of the network, while the GAN is used to predict future traffic bursts. An additional Simple Feedforward Neural Network (SFNN) is used to predict the most probable future network state. One-week-long network snapshots were used in the GCN-GAN model to tackle short-term prediction, while three-month-long snapshots were used for long-term prediction. The model was validated with real traffic data from the Telus Fiber Network. The results showed that the GCN-GAN model was more effective in predicting burst traffic when compared with the LSTM model in terms of both lower mean squared error values and lower overestimation of traffic volume.
5. Support Vector Machines
A Support Vector Machine (SVM) algorithm is used to classify unlabeled data points into two labeled categories. It learns to separate a cluster of data points into distinct binary groups [34]. Figure 5 shows a cluster of data points classified into class 1 (green) and class 2 (blue). In brief, SVM performs complex data transformations depending on the selected kernel function, and, based on these transformations, it tries to maximize the separation boundaries between data points depending on the labels or classes that we have defined.
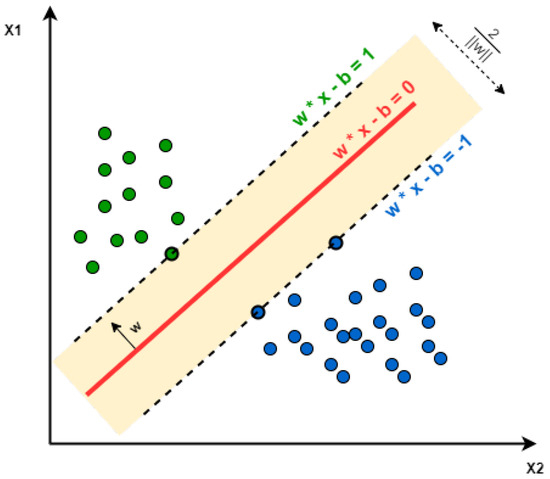
Figure 5.
Example scatterplot showing SVM classification of data points into two classes.
As we can see in Figure 5, SVM tries to find a line that maximizes the separation between a two-class data set of two-dimensional space points. To generalize, the objective is to find a hyperplane that maximizes the separation of the data points to their potential classes in an n-dimensional space. The data points with the minimum distance to the hyperplane (closest points) are called Support Vectors. The computations of data points’ separation depend on a kernel function. There are different kernel functions: Linear, Polynomial, Gaussian, Radial Basis Function (RBF), and Sigmoid.
Relevant Papers
Mata et al. [35] propose a reasoning module based on Support Vector Machines (SVMs) that have been trained with previous data in offline simulations to predict the quality of transmission (QoT) of a particular lightpath in wavelength-routed optical networks (WRONs). An SVM is an algorithm used to classify unlabeled data into labeled binary categories. Pre-existing data sets are provided to the SVM to learn a function that can accurately classify lightpaths into low- or high-quality categories based on the physical and performance attributes of the lightpath cumulated in a Q-factor variable. In doing so, the authors can quickly predict high-quality or low-quality transmission in a WRON before it is deployed. They found that the SVM approach requires the least computing time compared with alternative Q-Tool and Case-Based Reasoning (CBR) methods while maintaining the highest percentage of successful inaccurate classifications.
Stepanov et al. [36] use SVM in the edge networking paradigm, aiming to predict and optimize the network load conventionally caused by human-based traffic, which is growing each year rapidly. In their work, they propose a method to predict the LTE network edge traffic. The analysis is based on the public cellular traffic data set, and it presents a comparison of the quality metrics. In conclusion, the proposed Support Vector Machines method allows much faster training than the Bagging and Random Forest and operates well with a mixture of numerical and categorical features.
In [37], the authors use SVM to forecast traffic in Wireless LANs (WLANs). The main focus is a study of the issues of one-step-ahead prediction and multi-step-ahead prediction without any assumption on the statistical property of actual WLAN traffic. They evaluate the performance of different prediction models using four real WLAN traffic traces. The simulation results show that, among these methods, SVM outperforms other prediction models in WLAN traffic forecasting for both one-step-ahead and multi-step-ahead prediction.
Finally, Chen et al. [38] study a new hybrid network traffic prediction method (EPSVM) primarily based on Empirical Mode Decomposition (EMD), Particle Swarm Optimization (PSO), and Support Vector Machines (SVM). The EPSVM first utilizes EMD to eliminate the impact of noise signals. Then, SVM is applied to model training and fitting, and PSO optimizes the SVM parameters. The effectiveness of the presented method is examined by evaluating it with different methods, including basic SVM (BSVM), Empirical Mode Decomposition processed by SVM (ESVM), and SVM optimized by Particle Swarm Optimization (PSVM). The authors’ case studies demonstrated that the hybrid SVM performed better than the other three network traffic prediction models.
6. Linear Regression
Linear regression is a common technique used in statistical analysis to find and estimate a relationship over two or more sets of variables, regardless of how these are distributed. The variables for regression analysis have to comprise the same number of observations but can otherwise have any size or content. In other words, we are not limited to conducting regression analysis over scalars, but we can use ordinal or categorical variables as well. Figure 6 shows a scatterplot with a best fit linear trend line.
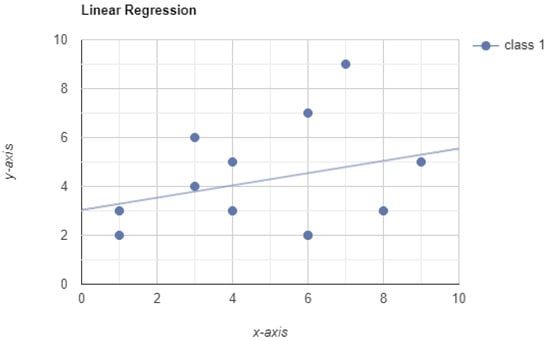
Figure 6.
Example scatterplot with a linear trendline.
Of these variables, one of them is called dependent. We imagine that all other variables take the name of ’independent variables’ and that a causal relationship exists between the independent and the dependent variables. Alternatively, at the very least, we suspect this relationship to exist, and we want to test our suspicions. Similarly, we can efficiently train linear regression models on normalized and standardized data sets. Then, we use this model to predict the outcomes for the test set and measure their performance.
Relevant Papers
While the most common case for using regression models in communication networks is failure detection or network health prediction analysis [39], a few papers discuss the application of linear regression towards traffic prediction.
Lechowicz in [40] proposed a machine learning regression model to obtain the best weights combination that minimizes the network fragmentation. He developed a fragmentation-aware algorithm showing that the proposed metric and assigned fiber weights decrease network fragmentation. Consequently, the proposed solution allows for bandwidth blocking probability reduction in the short term compared to the reference methods.
Ref. [41] describes how linear regression support can be used and shared in optical networks and the assessment of transmission quality (QoT), data traffic patterns, and crosstalk detection to help to route and distribute resources.
Finally, Huang et al. [42] propose a solution to reduce power excursions in dynamic optical networks that are equipped with an Erbium-Doped Fiber Amplifier (EDFA). An EDFA system automatically maintains power levels in network amplifiers but faces the issue of undesired power excursions. Power excursions occur when an increase in overall power results in a high-gain channel stealing power from a low-gain channel. A linear regression model is trained on 400 existing training data points until mean square error (MSE) convergence. After convergence, the model recommends channel slots to add or drop, considering their estimated standard error values. The model’s accuracy is verified with known power standard deviations measured over a week. This approach is expected to be applicable for more extended periods with different EDFA network designs.
7. Principal Component Analysis
Principal component analysis (PCA) is a data manipulation or reduction technique that reduces the dimensions of a data set while minimizing the amount of information lost, as presented in Figure 7. To do this, the initial variables are transformed into a new set of variables called principal components. PCA also works around the fact that the principal components are ordered. As a result, the beginning components keep most of the information [43].
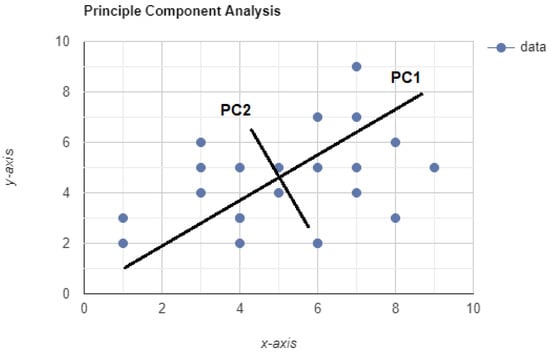
Figure 7.
Scatterplot showing an example of PCA analysis generating two principal components.
The principle of simplicity is aesthetically desirable, but it can also have advantages in data analysis. Focusing on critical parameters, such as those provided by PCA, within almost any data analysis technique will improve its efficiency and the quality of the result. Including parameters that do not contribute to the model’s behavior makes the computation less efficient, and other parameters contribute noise to the problem.
Relevant Papers
As explained by R. Filho et al. [44], PCA can be applied to the initial data to filter out outliers. This is especially useful during the pre-processing stage, before the data are passed into a machine learning algorithm. Using a network with 529 variables, the authors found that using PCA, 11 principal components were enough to be an accurate representation of the traffic data as they were able to account for 91.1% of the total variability.
Araujo et al. [45] use an Artificial Neural Network (ANN) with eight input parameters to estimate performance in wavelength-routed optical networks (WRONs). This approach differs from other Neural Network methodologies by including a physical layer input parameter in the Neural Network. The purpose of the methodology is to present a fast and easy means to estimate blocking probability in WRONs given physical impairments. Independent variables related to the physical layer and topological properties of the WRON were determined by a principal component analysis (PCA). The PCA was performed to generalize and identify variables that would make the model easier to train and use across different networks. The best set of parameters was then used to train the ANN, and the results were compared to network results simulated by a discrete event simulator called SIMPTON. SIMPTON was used to simulate networks with different traffic loads of 100 and 200 Erlangs. The results found that the ANN was an effective method to estimate blocking probability in cases where inadequate training and execution time is desired. There are two downsides to this approach. The first is that the same input criteria need to be used to estimate the blocking probability of the network accurately. Secondly, the error increases for networks with lower traffic loads.
The authors of [46] performed a comparative experimental analysis with a PCA-based method on a real-life data set and achieved better decomposition performance. In the real-life data set, results showed that, through robust PCA, most of the significant volume anomalies were short-lived and well-isolated in the residual traffic matrix while PCA failed. In traffic flow prediction experiments based on decomposition, the result based on robust PCA outperformed the PCA and simple average. This provides adequate evidence that robust PCA is more appropriate for traffic flow matrix analysis. The authors concluded that a robust PCA shows promising abilities in improving the accuracy and reliability of traffic flow analysis.
Djukic et al. [47] perform prediction of the time evolution of origin–destination (O–D) matrices using the PCA method. PCA shows that the dimensionality of the time series of O–D demand can be reduced significantly. The authors also discover that the results from the PCA method can be used to reveal the structure in the underlying temporal variability patterns in dynamic O–D matrices.
PCA has also been successfully applied to IP networks, as presented in [48]. The proposed system uses seven traffic flow attributes: bits, packets, and number of flows, to detect problems, and source and destination IP addresses and ports, to provide the network administrator with the necessary information to solve them. The authors applied a hybrid PCA method for network traffic data, and the results showed good traffic prediction and encouraging false alarm generation and detection accuracy on the detection schema using thresholds.
Finally, the authors of [49] propose a method based on principal component analysis and Support Vector Regression (PCA-SVR) for the short-term simultaneous prediction of network traffic flow that is multidimensional compared with a traditional single point. Data from a typical traffic network of Beijing City, China, are used for the analysis. Other models, such as ANN and ARIMA, are also developed as a comparison of the performance of both these techniques is carried out to show the effectiveness of the novel method.
8. Statistical Models
This section of the paper contains additional statistical means and optimization models to aid in traffic prediction.
8.1. Hidden Markov Model
The authors Chitra, K. and Senkumar M. R. [50] use a three-phased approach to improve the Quality of Service (QoS) in optical WDM networks. The proposed Load Balancing Technique to improve QoS for Lightpath Establishment (LBIQLE) evaluates a network based on throughput, blocking probability, and delay metrics. A Hidden Markov Model (HMM) was first used to predict the next future traffic load. An HMM has two layers, a hidden layer and an observable layer. To determine the most likely future state of the system, a sequence of probabilities in the hidden layer is calculated and output to the observable layer. This series of probabilities is known as the Markov chain, which assumes that the next state is only dependent on the current state of the system and not any prior past states [51]. Phase 2 of LBIQLE utilizes wavelength order to reduce crosstalk. Finally, in phase 3, a proprietary algorithm is used to modify the virtual topology to best meet the predicted traffic demand in phase 1 from the HMM. Simulated results using LBIQLE are compared with a GRASP approach and found to have higher network utilization rates. LBIQLE also reduces the blocking probability and delay while increasing the traffic throughput.
Moreover, the authors of [52] propose Monte Carlo Tree Search as a solution to the Markov Model to enable traffic prediction in inter-data center optimization problems that use Cross-Stratum Optimization architecture for provider-centric use cases.
8.2. Bayesian Estimation
In passive optical networks (PONs), an optical line terminal (OLT) sends packets of data to optical network units (ONUs) located at the user end. Dias, M., Karunaratne, B., and Wong, E. [53] use Bayesian Estimation to predict the interarrival time of packets from the OLT to the ONU. Calculations are performed at the OLT, such as the necessary sleep/doze time, and the predicted traffic accumulated during sleep is calculated. The command is then sent from the OLT to the ONU, telling it when to sleep and wake up to receive the next packet. The ONU estimates the average interarrival time of packets using Bayesian estimation and returns its estimation to the OLT for calculations. Bayesian estimation is a probability-based statistical method, used in this paper to find the most likely average number of interarrival packets. The process is iterated to update the likelihood of the average number of packets with each additional measurement. Using this method, the authors are able to achieve 63% energy savings, with a 13% reduction in the average delay that is expected from the ONU sleeping and waking.
Zhong et al. [54] propose wavelength splitting optimization algorithms to maximize traffic throughput during periods of traffic spikes in elastic optical networks. Instead of turning equipment on and off to handle high traffic volumes, traffic is split into different lightpaths when a threshold is reached. Traffic is processed through four algorithms to determine the number of splitpoints, which lightpaths to split, resource allocation after a split, and incremental traffic routing. The authors found that wavelength splitting optimization could increase the overall traffic throughput in a network, assuming that the network traffic could be split to begin with. One downside of traffic splitting is that it interrupts network traffic for a short amount of time to tear down and create new lightpaths. However, the proposed optimization technique is a viable solution for short-term traffic spikes lasting from hours to days as it only requires a few minutes of calculation and network reconfiguration.
9. Linear Time Series
The use of linear predictive models is successfully demonstrated in several papers for short-term traffic prediction. These include Auto-Regressive (AR), Moving Average (MA), Autoregressive Moving Average (ARMA), and Autoregressive Integrated Moving Average (ARIMA). Autoregressive models are created on the idea that we can try to predict future values based on past values of this same variable. Alternatively, it could be said that the current value can be described as a linear function of past values [55]. The ’auto’ portion of autoregressive indicates that we are examining the relationship of the variable against itself. For Moving Average models, past forecast errors are used for regression rather than past values. ARIMA combines these two models but includes an integrated component where differences between periods must be modeled, rather than data from the period itself [56].
Relevant Papers
Hoong et al. [57] utilized the ARMA time series model to forecast network traffic and examine the impact of data transferring in low and high forecasted traffic scenarios. The authors experimented with the ARMA model using captured network packets representing the network condition in this study. These data were transformed with log return before using the ARMA model to create a network traffic pattern for forecasting. Using both a 10 MB file and a 1 GB file, they initiate the transferring of files when the forecasted traffic is low and high to test their forecasting accuracy and observe the file transfer throughput. In their conclusions, the authors note that initiating data transfer when the next step in the traffic forecast is low would lead to more efficient throughput, and they suggest dividing larger files into smaller sizes. They suggest that using ARMA model traffic prediction could allow for more effective file transfers.
Similarly, Tan et al. [58] proposed using the ARMA model for traffic prediction in hopes of allowing application developers to find out the best periods for their users to download software patches. Given that downloading software patches can impact bandwidth during activities such as streaming videos or gaming, it would be ideal to use network traffic forecasting to avoid downloading patches or updates during these times. Using captured TCP data, the authors used the ARMA model on the log return values of the collected data and compared the forecasted pattern to the actual traffic data, varying two parameters: the sampling size of the Moving Average and the step size of the sample data. Their study finds that the ARMA model could forecast short-term traffic regardless of historical data size and suggests that this method could be suitable for forecasting software patch download periods.
Sadek et al. [59] proposed using a k-factor Gegenbauer ARMA (GARMA) model for predicting high-speed network traffic and compared it to the traditional autoregressive model. This study captured traffic data for MPEG, JPEG, video, Ethernet, and the Internet. Using the mean absolute error (MAE) and the signal to error ratio (SER), they measured the accuracy of their prediction model. The authors found that the k-factor GARMA model outperformed the autoregressive (AR) model. They suggest that this prediction model could be used to plan congestion control, such as dynamically allocating bandwidth.
Moayedi et al. [60] described the use of an ARIMA model for predicting traffic and detecting anomalies. Using a uniform random number distribution, they simulated 15 min of data from a network interface card. Using the ARIMA model to simulate traffic, anomalies were detected in the autocorrelation and partial autocorrelation plots.
10. Summary
In this section, we summarize all the discussed papers into two tables. Table 1 shows a list of the literature that has been classified for their use in short-term network traffic prediction. Table 2 shows a list of the literature that has been classified for their use in long-term network traffic prediction. Finally, each table consists of a further classification of all techniques into Local and Wide Area Network type, the metric that they use for evaluating their work, and the application (e.g., cellular networks, optical networks, and so on).

Table 1.
List of papers on short-term communication traffic prediction.

Table 2.
List of papers on long-term communication traffic prediction.
11. Conclusions and Future Opportunities
Communication networks, wired and wireless, continue to grow in size, complexity, and intelligence. Network intelligence is introduced for the network to handle high-volume situations better and to ensure the quality of service. This paper has surveyed multiple papers relevant to network traffic prediction and classified them according to their use and applicability to the short term or the long term. These methodologies have also been evaluated for their use in Local versus Wide Area Networks.
Our findings suggest that Neural Network techniques are the most common tools used in network traffic volume prediction, followed by linear time series modeling. Backpropagation Neural Networks and Recurrent Neural Networks seem to be able to more accurately predict future network states, perhaps due to their feedback mechanisms, allowing them to serve as memory. At the same time, some authors propose solutions mainly used in image processing (such as the GCN-GAN method) and adapt them to the problems related to traffic prediction. On the other hand, linear time series are mainly used in LAN for short-term traffic prediction.
Network traffic volume and blocking probability were the most desired metrics to predict in communication networks. Some papers used traffic prediction to trigger network reconfigurations adaptively. Other uses for traffic prediction include determining ideal periods for software patch downloading and file transfers.
As more research is conducted, software-defined networking is pushing high-performing, automated, and intelligent networks into the realm of reality. Machine learning and statistical modules may be loaded onto physical devices attached to the communication network for monitoring, prediction, and configuration. The increasing availability of high-quality historical data may also facilitate these models’ faster and more accurate ’learning’. What remains is to determine which methods are most viable in which network scenarios. Various factors in each technique should be considered, such as processing requirement, calculation time, power consumption, and network topology.
An attractive future opportunity is the application of epsilon greedy Q-learning in transport optical networks. The aim is to have a balance between exploration and exploitation. The optimization of Q-learning will allow us not to select local optima but instead focus on finding the global one. The strategies that can be explored are the decayed-epsilon greedy approach, since, usually, the exploration diminishes over time, and regret minimization to speed up the convergence rate of traffic prediction in large networks.
Future network solutions should manage the ever-increasing data transfer demand without adding complexity, while minimizing the network operators’ and users’ time on network operations and management. These solutions should also be easily maintainable, and their capabilities should be continuously updated by relying as little as possible on human intervention.
Author Contributions
Writing—original draft, A.C. and J.L.; Writing—review & editing, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, L.P. Mehryar Mohri, Afshin Rostamizadeh, and Ameet Talwalkar: Foundations of Machine Learning, second edition. Stat. Papers 2019, 60, 1793–1795. [Google Scholar] [CrossRef]
- Jinno, M.; Takara, H.; Kozicki, B. Concept and Enabling Technologies of Spectrum-Sliced Elastic Optical Path Network (SLICE). In Proceedings of the Asia Communications and Photonics Conference and Exhibition, Shanghai, China, 2–6 November 2009. [Google Scholar] [CrossRef]
- Gerstel, O.; Jinno, M.; Lord, A.; Yoo, S.J.B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, 12–20. [Google Scholar] [CrossRef]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Tomkos, I. Toward the 6G Network Era: Opportunities and Challenges. IT Prof. 2020, 22, 34–38. [Google Scholar] [CrossRef]
- Jain, R.; Subharthi, P. Network Virtualization and Software Defined Networking for Cloud Computing: A Survey. IEEE Commun. Mag. 2013, 51, 24–31. [Google Scholar] [CrossRef]
- Mahmoud, Q.H. Cognitive Networks: Towards Self-Aware Networks; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Cisco. Global Cloud Index: Forecast and Methodology, 2016–2021 (White Paper); Technical Report; CISCO: San Jose, CA, USA, 2018. [Google Scholar]
- Rak, J. Resilient Routing in Communication Networks; Computer Communications and Networks; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 11–43. [Google Scholar] [CrossRef]
- Woo, W.L. Future trends in IM: Human-machine co-creation in the rise of AI. IEEE Instrum. Meas. Mag. 2020, 23, 71–73. [Google Scholar] [CrossRef]
- Musumeci, F.; Rottondi, C.; Nag, A.; Macaluso, I.; Zibar, D.; Ruffini, M.; Tornatore, M. An Overview on Application of Machine Learning Techniques in Optical Networks. arXiv 2018, arXiv:1803.07976v1. [Google Scholar] [CrossRef] [Green Version]
- Rad, M.M.; Fouli, K.; Fathallah, H.A.; Rusch, L.A.; Maier, M. Passive optical network monitoring: Challenges and requirements. IEEE Commun. Mag. 2011, 49, S45–S52. [Google Scholar] [CrossRef]
- Gu, R.; Yang, Z.; Ji, Y. Machine learning for intelligent optical networks: A comprehensive survey. J. Netw. Comput. Appl. 2020, 157, 102576. [Google Scholar] [CrossRef] [Green Version]
- Aibin, M. Traffic prediction based on machine learning for elastic optical networks. Opt. Switch. Netw. 2018, 30, 33–39. [Google Scholar] [CrossRef]
- Aibin, M.; Walkowiak, K. Monte Carlo Tree Search with Last-Good-Reply Policy for Cognitive Optimization of Cloud-Ready Optical Networks. J. Netw. Syst. Manag. 2020, 28, 1722–1744. [Google Scholar] [CrossRef]
- Bengio, Y. Learning Deep Architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Zang, Y.; Ni, F.; Feng, Z.; Cui, S.; Ding, Z. Wavelet transform processing for cellular traffic prediction in machine learning networks. In Proceedings of the 2015 IEEE China Summit and International Conference on Signal and Information Processing, ChinaSIP 2015—Proceedings, Chengdu, China, 12–15 July 2015; pp. 458–462. [Google Scholar] [CrossRef]
- Ren, G.; Cao, Y.; Wen, S.; Huang, T.; Zeng, Z. A modified Elman neural network with a new learning rate scheme. Neurocomputing 2018, 286, 11–18. [Google Scholar] [CrossRef]
- Aibin, M. Deep Learning for Cloud Resources Allocation: Long-Short Term Memory in EONs. In Proceedings of the International Conference on Transparent Optical Networks, Angers, France, 9–13 July 2019; pp. 8–11. [Google Scholar]
- Aibin, M.; Chung, N.; Gordon, T.; Lyford, L.; Vinchoff, C. On Short-and Long-Term Traffic Prediction in Optical Networks Using Machine Learning. In Proceedings of the 25th International Conference on Optical Network Design and Modelling, ONDM 2021, Gothenburg, Sweden, 28 June–1 July 2021. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Peng, G. CDN: Content Distribution Network. arXiv 2004, arXiv:cs.NI/0411069. [Google Scholar]
- Jaeger, H. Echo state network. Scholarpedia 2007, 2, 2330. [Google Scholar] [CrossRef]
- Jia, W.B.; Xu, Z.Q.; Ding, Z.; Wang, K. An efficient routing and spectrum assignment algorithm using prediction for elastic optical networks. In Proceedings of the 2016 International Conference on Information System and Artificial Intelligence, ISAI 2016, Hong Kong, China, 24–26 June 2017; pp. 89–93. [Google Scholar] [CrossRef]
- Morales, F.; Ruiz, M.; Gifre, L.; Contreras, L.M.; López, V.; Velasco, L. Virtual Network Topology Adaptability Based on Data Analytics for Traffic Prediction. J. Opt. Commun. Netw. 2017, 9, A35–A45. [Google Scholar] [CrossRef]
- Menezes, J.M.P.; Barreto, G.A. Long-term time series prediction with the NARX network: An empirical evaluation. Neurocomputing 2008, 71, 3335–3343. [Google Scholar] [CrossRef]
- Sum, J.; Kan, W.K.; Young, G. A Note on the Equivalence of NARX and RNN. Neural Comput. Appl. 2014, 8, 33–39. [Google Scholar] [CrossRef]
- Schaffer, C. Overfitting Avoidance as Bias. Mach. Learn. 1993, 10, 153–178. [Google Scholar] [CrossRef] [Green Version]
- Xiong, Y.; Shi, J.; Lv, Y.; Rouskas, G.N. Power-aware lightpath management for SDN-based elastic optical networks. In Proceedings of the 2017 26th International Conference on Computer Communications and Networks, ICCCN 2017, Vancouver, BC, Canada, 31 July–3 August 2017. [Google Scholar] [CrossRef]
- Bolla, R.; Bruschi, R.; Lago, P. The hidden cost of network low power idle. In Proceedings of the IEEE International Conference on Communications, Budapest, Hungary, 9–13 June 2013; pp. 4148–4153. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Leung, H.C.; Leung, C.S.; Wong, E.W.; Li, S. Extreme learning machine for estimating blocking probability of bufferless OBS/OPS networks. J. Opt. Commun. Netw. 2017, 9, 682–692. [Google Scholar] [CrossRef]
- Vinchoff, C.; Chung, N.; Gordon, T.; Lyford, L.; Aibin, M. Traffic Prediction in Optical Networks Using Graph Convolutional Generative Adversarial Networks. In Proceedings of the International Conference on Transparent Optical Networks, Bari, Italy, 19–23 July 2020; pp. 3–6. [Google Scholar]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef]
- Mata, J.; De Miguel, I.; Durán, R.J.; Aguado, J.C.; Merayo, N.; Ruiz, L.; Fernández, P.; Lorenzo, R.M.; Abril, E.J. A SVM approach for lightpath QoT estimation in optical transport networks. In Proceedings of the 2017 IEEE International Conference on Big Data, Big Data 2017, Boston, MA, USA, 11–14 December 2017; pp. 4795–4797. [Google Scholar] [CrossRef] [Green Version]
- Stepanov, N.; Alekseeva, D.; Ometov, A.; Lohan, E.S. Applying Machine Learning to LTE Traffic Prediction: Comparison of Bagging, Random Forest, and SVM. In Proceedings of the International Congress on Ultra Modern Telecommunications and Control Systems and Workshops, Brno, Czech Republic, 5–7 October 2020; pp. 119–123. [Google Scholar] [CrossRef]
- Feng, H.; Shu, Y.; Wang, S.; Ma, M. SVM-based models for predicting WLAN traffic. In Proceedings of the IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; Volume 2, pp. 597–602. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Shang, Z.; Chen, Y.; Chaeikar, S.S. A Novel Hybrid Network Traffic Prediction Approach Based on Support Vector Machines. J. Comput. Netw. Commun. 2019, 2019, 2182803. [Google Scholar] [CrossRef]
- Mata, J.; de Miguel, I.; Durán, R.J.; Merayo, N.; Singh, S.K.; Jukan, A.; Chamania, M. Artificial intelligence (AI) methods in optical networks: A comprehensive survey. Opt. Switch. Netw. 2018, 28, 43–57. [Google Scholar] [CrossRef]
- Lechowicz, P. Regression-based fragmentation metric and fragmentation-aware algorithm in spectrally-spatially flexible optical networks. Comput. Commun. 2021, 175, 156–176. [Google Scholar] [CrossRef]
- Rai, S.; Garg, A.K. Analysis of RWA in WDM optical networks using machine learning for traffic prediction and pattern extraction. J. Opt. 2021, 1–8. [Google Scholar] [CrossRef]
- Huang, Y.; Samoud, W.; Gutterman, C.L.; Ware, C.; Lourdiane, M.; Zussman, G.; Samadi, P.; Bergman, K. A Machine Learning Approach for Dynamic Optical Channel Add/Drop Strategies that Minimize EDFA Power Excursions|VDE Conference Publication|IEEE Xplore. In Proceedings of the European Conference on Optical Communication, Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning This paper is included in the Proceedings of the TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016. [Google Scholar] [CrossRef]
- Filho, R.H.; Maia, J.E.B. Network traffic prediction using PCA and K-means. In Proceedings of the 2010 IEEE/IFIP Network Operations and Management Symposium, NOMS 2010, Osaka, Japan, 19–23 April 2010; pp. 938–941. [Google Scholar] [CrossRef]
- De Araújo, D.R.; Bastos-Filho, C.J.; Martins-Filho, J.F. Methodology to obtain a fast and accurate estimator for blocking probability of optical networks. J. Opt. Commun. Netw. 2015, 7, 380–391. [Google Scholar] [CrossRef]
- Xing, X.; Zhou, X.; Hong, H.; Huang, W.; Bian, K.; Xie, K. Traffic Flow Decomposition and Prediction Based on Robust Principal Component Analysis. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings ITSC, Gran Canaria, Spain, 15–18 September 2015; pp. 2219–2224. [Google Scholar] [CrossRef]
- Djukic, T.; Flötteröd, G.; Van Lint, H.; Hoogendoorn, S. Efficient real time OD matrix estimation based on Principal Component Analysis. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings ITSC, Anchorage, AK, USA, 16–19 September 2012; pp. 115–121. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, G.; Rodrigues, J.J.; Proença, M.L. Autonomous profile-based anomaly detection system using principal component analysis and flow analysis. Appl. Soft Comput. 2015, 34, 513–525. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, Y.; Yao, D. Simultaneously Prediction of Network Traffic Flow Based on PCA-SVR. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2007; Volume 4492, pp. 1022–1031. [Google Scholar] [CrossRef]
- Chitra, K.; Senkumar, M.R. Hidden Markov model based lightpath establishment technique for improving QoS in optical WDM networks. In Proceedings of the 2nd International Conference on Current Trends in Engineering and Technology, ICCTET 2014, Coimbatore, India, 8 July 2014; pp. 53–62. [Google Scholar] [CrossRef]
- Eddy, S.R. What is a hidden Markov model? Nat. Biotechnol. 2004, 22, 1315–1316. [Google Scholar] [CrossRef] [Green Version]
- Aibin, M.; Walkowiak, K.; Haeri, S.; Trajkovic, L. Traffic Prediction for Inter-Data Center Cross-Stratum Optimization Problems. In Proceedings of the IEEE Internation Conference on Computing, Networks and Communication, Maui, HI, USA, 5–8 March 2018. [Google Scholar]
- Dias, M.P.I.; Karunaratne, B.S.; Wong, E. Bayesian estimation and prediction-based dynamic bandwidth allocation algorithm for sleep/doze-mode passive optical networks. J. Light. Technol. 2014, 32, 2560–2568. [Google Scholar] [CrossRef]
- Zhong, Z.; Hua, N.; Tornatore, M.; Li, J.; Li, Y.; Zheng, X.; Mukherjee, B. Provisioning Short-Term Traffic Fluctuations in Elastic Optical Networks. In Proceedings of the International Conference on Transparent Optical Networks, Angers, France, 9–13 July 2019. [Google Scholar]
- Shumway, R.; Stoo, D.S. Springer Texts in Statistics Time Series Analysis and Its Applications With R Examples, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Stellwagen, E.; Tashman, L. ARIMA: The Models of Box and Jenkins. Foresight Int. J. Appl. Forecast. 2013, 30, 28–33. [Google Scholar]
- Hoong, N.K.; Hoong, P.K.; Tan, I.K.; Muthuvelu, N.; Seng, L.C. Impact of utilizing forecasted network traffic for data transfers|IEEE Conference Publication|IEEE Xplore. In Proceedings of the International Conference on Advanced Communication Technology (ICACT2011), Gangwon, Korea, 13–16 February 2011. [Google Scholar]
- Tan, I.K.; Hoong, P.K.; Keong, C.Y. Towards forecasting low network traffic for software patch downloads: An ARMA model forecast using CRONOS. In Proceedings of the 2nd International Conference on Computer and Network Technology, ICCNT 2010, Bangkok, Thailand, 23–25 April 2010; pp. 88–92. [Google Scholar] [CrossRef]
- Sadek, N.; Khotanzad, A. Multi-scale high-speed network traffic prediction using k-factor Gegenbauer ARMA model. In Proceedings of the IEEE International Conference on Communications, Paris, France, 20–24 June 2004; Volume 4, pp. 2148–2152. [Google Scholar] [CrossRef]
- Moayedi, H.Z.; Masnadi-Shirazi, M.A. Arima model for network traffic prediction and anomaly detection. In Proceedings of the International Symposium on Information Technology 2008, ITSim, Kuala Lumpur, Malaysia, 26–29 August 2008; Volume 3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).