Abstract
The further growth of the Internet faces a crucial impediment related to the ossification problem. Network virtualization is a promising and emergent solution that has been introduced as a sophisticated diversifying attribute of the future network paradigm. However, there remain many issues standing in the way of its successful realization, such as the service provisioning efficiency in the network virtualization. Many approaches and schemes have been propounded to provide efficient resource management based on game theory. This paper presents a comprehensive overview of the existing game theory solutions designed for the different network virtualization environments. We propose a taxonomy for game-theoretical approaches classification. The scope of this survey is to provide a better understanding of the game-theoretical application for resource management in network virtualization. Thus, our inclusive classification considers the various game properties and characteristics as well as the purpose of applying the game theory to the virtualization context.
1. Introduction
The internet [1] has attracted significant attention over the last few decades due to the diversity of network technologies, applications, and services. However, its rapid growth faces many problems and many issues which makes the adoption of a new architecture or the modification of an existing architecture a very challenging task. To overcome the ossification limitation, Network Virtualization (NV) has emerged as a solution to support the exponential growth of Networks [2]. It has been introduced to ensure several privileges such as providing flexibility, boosting diversity, promoting security, and enhancing network manageability [3]. The main idea of the NV is the abstracting of network resource by introducing two business entities: the Infrastructure Providers (InPs) and the Service Providers (SPs), instead of having the traditional Internet service providers. An InP manages and controls the physical infrastructure. The critical concerns of InP are service provisioning and QoS guarantee. An SP leases multiple resources (bandwidth, CPU, storage, memory, substrate links, etc.) from InPs to provide services to the end-users. One of the challenges of network virtualization is how to efficiently provide services to the users. Several approaches and techniques have been introduced for resource management to cover all the service provisioning goals such as maximizing resource allocation. Moreover, the Game Theory (GT) has drawn considerable attention by paving its way to next-generation network and gradually to modern technologies to achieve one/multiples resource management goals for the vitalization environment. In this paper, we provide a survey illustrating the game theory approaches for network virtualization. We define the game theory by presenting all the details and the concepts related to this mathematical tool. Then, we introduce a taxonomy of the game theory approaches classification for resource management in the virtualization environments. The new classification aspects are based on three axes: the game characteristics, the players during the game, and the goals for the resource management. The taxonomy should provide the reader with a better understanding of game theory solutions to the resource management problems in the NV environment. The remainder of this paper is organized as follows: We start, in Section 2, by introducing an overview of the network virtualization and explaining the main concepts and technologies. In Section 3, we will give an overview of the game theory by detailing the concept and the game characteristics, defining the components of the game analysis, and providing the different types/models of the games. In Section 4, we will present a novel sophisticated taxonomy for the classification of the game theory-based solutions in the NV that has been designed to enhance the service provisioning. We will investigate and discuss, in Section 5, the solutions by exploring the future key research. Finally, we will conclude the paper in Section 6.
2. Network Virtualization
In traditional networks, the users have requested services through a very complex and static infrastructure. All the components, such as nodes, links, and resources, were strongly dependent on the hardware layer. Moreover, the traditional architectures are mainly characterized by their high cost, non-flexibility, and non-scalability. In fact, introducing new physical equipment and/or functionality requires more time, more cost, and more resources since it is needed to respect the different protocols, standards, and technologies already installed in this complex architecture. To this end, network virtualization [4] has gained more and more attention because it makes the network not only independent from the hardware but also enables services with low cost and with more flexible resources management, setting, and control. For instance, this technology solves many networking challenges in today’s data centers, helping organizations centrally program and provision the network.
2.1. NV Typical Architecture
NV refers to the software abstraction of the traditional network resources. Moreover, NV can control multiple physical networks into virtual ones. It can also split a network into multiple VN disks. The typical architecture of the NV is depicted in Figure 1. A VN is composed of multiple virtual nodes connected through virtual links.
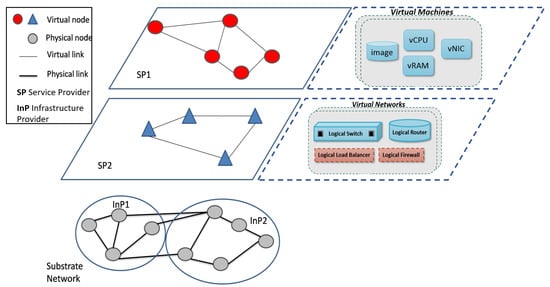
Figure 1.
Network virtualization architecture.
NV emphasises separating the roles of the traditional Internet service providers (ISPs) into two independent entities [5,6]: infrastructure providers (InPs), who are in charge of the physical infrastructure and service providers (SPs), who build VNs by combining resources from multiple InPs.
2.2. NV Enabling Technologies
The virtualization’s key enabling strategies include SDN (Software Defined Networking) and NFV (Network Functions Virtualization). NFV and SDN have similarities, but they are not identical. Both are based on network abstraction, but the way the two technologies separate functions and abstract resources make the difference.
- Software Defined Networking [7]: The traditional hardware-based networks cannot meet the computing and storage needs for the user’s service requests in an unstable and a changing environment. SDN provides a better fit in such situations by including simplified and enhanced network control, flexible and efficient network management, and improved network service performance. Moreover, the SDN separates the control plane from the data plane through a well-defined programming interface, such that the centralized controller can have a complete view of the entire network as shown in Figure 2. Thus, SDN ensures a new virtualization level through open protocols, such as OpenFlow (OF) protocols, and standardized interface between the control plane and the data plane.
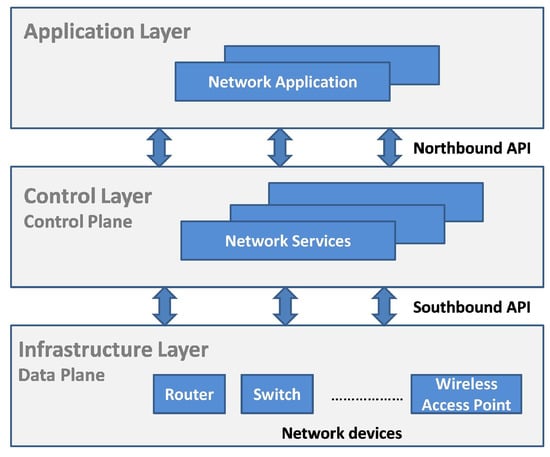 Figure 2. SDN layered architecture.
Figure 2. SDN layered architecture. - NFV: The NFV paradigm aim is to decouple network functions from dedicated physical equipment by using virtualization technology, and runs the virtual network functions (VNFs) in the general purpose physical or virtual network appliances. To conclude, the main difference between the SDN and NFV architectures is the overall focus network management responsibilities, and the standards controlling the architectural and functional deployment.
- SDN-enabled NFV architecture: Several recent approaches [8,9,10] were aimed at integrating the SDN into NFV architecture to enhance the network performance by combining the benefits of the two paradigms described by Figure 3. This revolutionary architecture concept is dedicated to adapt the increasing on-demanding services for the next-generation mobile networks such as the 5G [11] technologies and other applications, by providing more flexibility and more scalability.
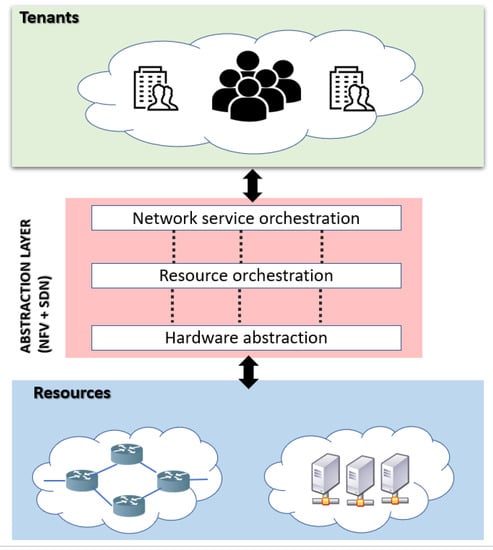 Figure 3. SDN enabled NFV: Multi-layer for unifying computer and network resources.
Figure 3. SDN enabled NFV: Multi-layer for unifying computer and network resources.
One of the most critical challenges in network virtualization is the service provisioning optimization. The efficient NFV approaches must address many objectives such as optimizing the resource utilization, ensuring load balancing, and reducing the congestion. Game theory is one of the promising solutions for the optimization problems in the network virtualization paradigms.
3. An Overview of Game Theory
In this section, we will give an understandable overview of the game theory modeling. Then, we will investigate the game theory base approaches for the NF.
3.1. Concept and Characteristics
Game theory [12,13] is a collection of mathematical models (games) and analytical tools used to study decisional and strategic interactions between decision-makers. It provides a mathematical basis for analyzing the interactive decision process among several rational actors. It also provides tools to predict what might happen when players have conflicting interests. Players or actors are the decision-making entities in the interactive decision process. In general, the games only consider the situations in which there are two or more players because the single-player game would not be an interactive process. The game is composed of a set of players who choose an action from a set of strategies denoted as the adaptations available to players. The results are determined by the actions and the particular system in which the players operate. A utility function is introduced to evaluate and develop each decision to formulate the players’ interactions in the form of a game-based model. The Game (G) is defined by the mathematical form as where N are the set of players, are the set of adapted strategies, and is the payoff function used to define the gain of the actors.
3.2. The Nash Equilibrium
Finding and reaching the Nash equilibrium [14] is challenging for any game model. It gives an optimal solution for all the players. In other words, the Nash equilibrium is a favorable situation for all agents in which no player will ever have the intention to change its strategy. It is a point resulting from the combination of multiple actions, one for each player, such that no player has benefited from unilaterally change its action. Mathematically, the game must satisfy the following condition.
Definition 1.
The Nash equilibrium is defined as a state (or set of actions) with . A combination reaches a Nash equilibrium situation if no player has interest in unilaterally deviating strategy when other players remain on the strategy profile . That is, ∀i, ∀, we obtain:
3.3. Mixed Strategies
If the game arrives at a balance situation, we speak then of a game in pure strategies. However, the Nash equilibrium concept suffers from a major limitation when the game has no Nash equilibrium or has more than a single Nash equilibrium. In a contrary case where the players will not decide on a given strategy, they will play a set of strategies with a certain probability. We then have a game in Mixed Strategies (MS) [14] explained by the following definition:
Definition 2.
Actions of the player. , denotes the probability of performing action . We have: .
3.4. Pareto Efficiency
Pareto efficiency is another important concept of game theory. A situation is said to be Pareto efficient if there is no way to rearrange things to make at least one person better off without making anyone worse off [15,16]. Mathematically, Pareto efficiency is defined as follows:
Definition 3.
Strategy profile S Pareto dominates a strategy profile if no player gets a worse payoff with S than with , i.e., for all players i and at least one player gets a better payoff with S than with , i.e., for at least one i. Strategy profile S is Pareto efficient, if there is no strategy that Pareto dominates S.
4. Taxonomy: Classification of GT Approaches in Network Virtualization
The classification of existing approaches should be very exhaustive and very efficient by covering all the game theory proprieties and all the important issues addressed by this model in the virtualization environments. Accordingly, we introduce an inclusive taxonomy, which focuses on three essential criteria: the game characteristics, the players during the game, and the goals for applying the GT into the NV environments (see Figure 4).
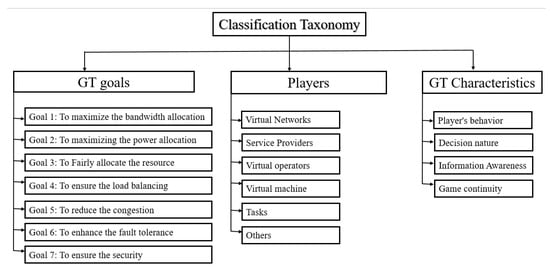
Figure 4.
Classification taxonomy for the GT solution in the NV environment.
Firstly, we will classify the approaches based on the game’s aim, where we will explain the optimization problems in the different NFV architectures treated by the proposed game-based mechanisms. Secondly, we will introduce the second classification criteria where the entities, so-called the players, are involved in the game models. Finally, we will introduce our third criteria to classify the game-theoretical approaches which is the game theory characteristic. Next, we will study separately and deeply each criterion of our classification.
4.1. Game Theory Characteristics
The game theory approaches for the NV can be classified based on player’s behavior, the nature of the player’s decisions, the information awareness, and the game’s continuity. The first criteria for our further classification of the NV solution are the GT characteristics. Figure 5 illustrates the first classification criteria defined as the GT characteristics, and Table 1 shows the classification of the game theoretical approaches for the NV in terms of GT characteristics. Each game is characterized by a specific deterministic behavior, unique decisions nature, type of shared awareness information during the game, and game’s continuity.
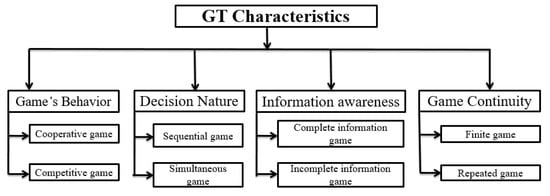
Figure 5.
GT categorization according to game characteristics.

Table 1.
GT solutions classification (II).
4.1.1. Player’s Behavior
In game theory, the players have the option to adopt the cooperative or the individual interaction with the other players. We can distinguish between two games:
- Non-cooperative games: Each player takes the best strategy to maximize their winning comparing with the strategies of other players. Each player takes their decision and reason selfishly and individually without cooperating with other agents. In [40], a non-cooperative congestion game mechanism has been proposed to solve the service chain composition problem in NFV. Thus, the service chain configuration is converted to a mathematical game model for the seeking of Nash equilibrium.
- Cooperative games: The players cooperate by exchanging information to maximize the collective gain that does not necessarily favor a player’s victory at the expense of others. We can also talk about groups of players who can form coalitions and groups and choose a panel of strategies to increase the typical gain. Jose et al. [41] investigated a new security mechanism based on a cooperative game for resilient cyber-physical systems. Several cooperative and virtualized agents decide on a set of orchestrated management decisions to enable resilient system operation in the presence of a malicious agent or severe security threat.
4.1.2. Decision Nature
During the game, the order of making-decision classifies the game models into a simultaneous and a sequential game.
- Simultaneous games: Each player chooses at the beginning of the game his strategy, once and for all, without having information about what the other players will play. Otherwise, each participant makes the decision at the same time without exchanging information with other agents. In [42], a new simultaneous game model was proposed to optimize the network slicing placement problem for many NFV network slice use cases.
- Sequential games: The game’s exact sequence is specified from the beginning of the game. Each agent considers the set of actions available when it is its turn to play. According to the strategy taken previously by the opponent, the player takes the best strategy to win the game. Typically, a simultaneous game is represented in normal form as in the previous example, while a sequential game is naturally represented in the form of a tree. Laszlo et al. [43] proposed a new sequential pricing game of NFV infrastructure providers. The interaction between the infrastructure providers and the customers was formulated as a trade-off problem to be optimized in terms of price and resource allocation.
4.1.3. Information Awareness
The game’s nature is determined by the information and the knowledge about the game (strategies, actions, etc.) offered to players to make their own decisions. According to the information awareness, the game may be complete or incomplete.
- Complete information games: In the simplest case where players have the full information about the game (such as check games and ladies game), they know the entire game until the current stage. It is a sequential game where the players have an overview of the opponent’s game and possible strategies—for example, chess games. Therefore, the player’s current action influences the next action of the other adversaries. The authors, in [44], proposed a new complete information game-theoretical model in order to ensure the relatively resources allocation among tenants in 5G systems. To this end, a bankruptcy game based on new allocation rules was formulated to meet tenants’ needs by respecting the resource’s fair distribution.
- Incomplete information games: When the player has incomplete and limited knowledge about the opponents’ game and strategies, we talk about the game with incomplete information (for example, dominoes and poker). It is a game where a part of the game is hidden, and the player has only a portion of the information about other players. Decision-making is more critical and crucial than a perfect information game. In [45], a novel incomplete information game-based model was proposed for the cloud resource allocation. An auction game model was formulated to optimize the resource allocation between multiple infrastructure providers and the service providers. A Bayesian Nash equilibrium solution is reached to improve the network performance.
4.1.4. Game Continuity
According to the continuity of the game, we can distinguish between two important GT models.
- Finite games: This game is characterized by consistent and well-known boundaries and rules. During the game, the players focus on maximizing their utility functions because the purpose of the game is winning. Shu-Ting et al. [46] introduced a new finite game-based model to provide an optimized and efficient solution to the service chain composition problem in the network function virtualization paradigm. The service chain composition is converted to the seeking of the Nash equilibrium under the formulated game model.
- Infinite games: The game is repeated where the boundaries and the rules are dynamic and infinite. Thus, the players do not have any knowledge about the beginning or end of the game. The player’s purpose is to continue playing and to sometimes bring more players into the game. However, the infinite games are the less investigated concept in the NFV paradigm compared with the finite game modeling. No research paper solved the optimization problems in the NFV through the infinite game.
4.2. Game Goals
The game theory is introduced to network virtualization to achieve a single or multiple sophisticated purposes for the resource management. In this paper, we have identified seven different goals:
- 1
- Maximize bandwidth allocation: The importance of this objective becomes apparent with data-intensive applications. Real-time video services systems are the best examples [47].
- 2
- Maximizing power allocation: Applications that consider this objective are those with very limited energy capacity. The sensor network represents a good use case [48].
- 3
- Fairly allocate the physical resource: One of the most addressed goals for cellular applications such as LTE networks [49] is to efficiently manage the physical resources by sharing them fairly among mobile devices and user applications. Network slicing is a good example.
- 4
- Ensure load balancing: Nowadays, load balancing is becoming a necessity for many emerging applications that are very resource-intensive and require a balanced allocation in cloud computing environments [50].
- 5
- Reduce congestion: the object is to ensure secure and reliable communications with the congestion problem. The need for congestion control depends on the type of applications. For example, in the vehicular ad hoc network, this issue is crucial because a congested network can have a negative impact on the reaction time of the safety equipment and thus make driving less safe [51].
- 6
- Improving Fault Tolerance: Fault tolerance is an indispensable goal for many applications such as wireless sensor networks (WSNs). WSNs are characterized by limited sensor hardware resources, resulting in power depletion, non-rechargeable batteries, and physical failures. Improving fault tolerance [52,53] by maintaining network connectivity and coverage in the presence of faulty sensors is a challenge for WSNs.
- 7
- Security: Nowadays, and with the increasing number of attackers and cybercrimes, security is increasingly becoming a key challenge for any applications or environments where new threats and vulnerabilities are raided to target network features [54].
4.2.1. Goal 1: Maximize the Bandwidth Allocation
The virtualization of the resources such as the bandwidth introduces critical challenges to be addressed and solved in the NV environment. Many solutions as static allocation are proposed to provide a sufficient bandwidth assignment by satisfying all users’ demands. The static allocation technique aims to provide fixed bandwidth to each virtual link by assigning the demanded bandwidth when VN is created. Due to the network dynamically, the static bandwidth allocation isn’t efficient anymore and suffers from many limitations and problems by leading to the degradation of the network performance. Dynamically sharing the bandwidth is a suitable solution to overcome the static allocation issues, but it remains an open problem due to its instability. According to the game theory’s dynamicity and flexibility, applying this mathematical tool for bandwidth allocation can be an up-and-coming solution. In [17], the authors applied a particular type of game theory called the Stackelberg game to allocate dynamically the bandwidths between the virtual networks competing for the physicals resources. During the Stackelberg game, the leader first selects the strategy, and then the follower chooses the appropriate action by reacting to the leader’s decision. Based on the Stackelberg game principle, the authors considered the virtual networks as a follow by playing a non-cooperative game to maximize their gain in bandwidth allocation, and the substrate network as leader by setting a price to drive virtual networks to maximize revenue. A Stackelberg equilibrium is proposed to reach the optimal solution for each player by minimizing the price of allocation. This equilibrium point offers an efficient and fair bandwidth allocation. The authors in [18] seek to treat the bandwidth allocation problem for the network virtualization. As a solution, they applied the GT to model the interaction between the InPs and the SPs deploying the customized Virtual Network (VN). Thus, they are the first contribution that presented the first paper which developed a particular case for applying the GT in the network virtualization environment. In this competitive environment, the InP aims to maximize its revenue by allocating SPs’ physical resources, seeking to allocate sufficient resources. The complex interaction between the InP and the SPs can be modeled as a non-cooperative and finite game to uniformly and efficiently allocate the physical resources among the VNs owned by the SPs. They introduced a robust payoff function based on three sub-functions: utility function, pricing function, and congestion function defined by the following formula:
The utility function is defined by which presents the gain obtained by the k-th VN from allocating the bandwidth with a predefined path rate denoted as . The pricing function computes the total cost of assigned bandwidths for the corresponding VNs. Finally, the congestion function measures the cost of congestion for the assigned bandwidths and current path rate. If the path rate of all VNs is less than the capacity of the link, the congestion cannot therefore appear. On the other hand, if the leasing of the bandwidth by the VN leads to the congestion of the link, the concerning VN must pay the cost of the occurred congestion. The next step, in the proposed scheme, is to prove the existing of the Nash equilibrium. One of the solutions is to prove the convexity of the payoff function [55]. Therefore, the authors find that the convexity is related to the congestion cost which is a convex function. Through Nash equilibrium convergence, all the players can achieve the best solution: “Maximize the utility function and optimize the cost function”. An iterative algorithm is proposed to reach the Nash equilibrium state. The convergence to Nash equilibrium is proved by a simple topology composed of two nodes and two links. Similar to the previous research, the authors in [19] proposed a game-based framework for the provisioning and the management of the bandwidth resources in the virtualized network environment. The interaction between the SPs and the InPs is modeled as a two-stage non-cooperative game. The first stage is a non-cooperative negotiation game aiming at modeling the interaction between the InP and the SP. The second stage models the resource request from multiple SPs and a single InP.
- Resource negotiation game: During the game, the SP starts by reclaiming the resource from the InP; then, it chooses to lease the resource from InP or to leave and to look for another one depending on the required QoS. Thus, the InP can admit or reject the request based on the resource sufficiency. The SP has a contract with an InP, so any direction to another InP can apply a penalty cost. When the two players are satisfied, the resource is allocated to the SP. However, if both players are dissatisfied, SP can lease the resource from another InP without any charged monetary penalty. Then, in case of only InP being satisfied, the SP must pay a penalty. The last case occurs when the SP is the only satisfied player; consequently, it is redirected to another InP without any charge. The players aim at maximizing their gains by reaching the Nash equilibrium.
- Node and link allocation games: two game models are proposed to fairly allocate the node and link resources for the SPs. The authors consider the SPs as a competitive player with selfish behaviors which aim at maximizing their utility function by consuming the maximum of the resources. The optimal solution for all players is achieved by the Nash equilibrium for each game.
Authors in [25] proposed a hierarchical Stackelberg game model to solve the bandwidths allocation competition problem between the VNs. The data center is presented as the game leader that announces bandwidths prices for the followers (VNs), attempting to maximize their profits based on willingness-to-pay strategy. They formulate the optimization problem using the following formula:
where N defines the VN number to allocate L links, is the vector of allocated bandwidths, and is the utility function for the allocation process.Finally, an optimal solution is proposed by reaching the Nash equilibrium point.
4.2.2. Goal 2: Maximize the Power Allocation
Moreover, the virtualization framework is proposed for wireless networks to support multiple heterogeneous self-interested services and improve their performance. Virtualization provides services decoupling from the wireless network infrastructure. The Wireless Virtual Network (WVN) consists of two entities: The infrastructure providers (InPs), owning all physical resources and the Virtual Network Operators (VNOs), which do not own any infrastructures or spectrum resources. The InPs share and manage their power resources with the VNOs, aiming to exploit multi-power resources from multi-owner to provide services to end-users by making their virtual networks (VN). As VNOs, the InP creates VN to serve its users called local slice and VNs generated by the VNOs’ users named foreign slice. The challenging key in the WVN environment is maximizing the resource allocation between the SPs by solving the optimization problem in terms of power allocation optimization.
The authors in [21] start with the studying of the virtualization in the wireless network to end by solving the problem of physical resources competition between the SPs. Thus, the network operators (NO) manage and control the resource allocation by pricing each bid. The interaction between the NO and the SPs can be modeled as a sequential auction game where the SPs sequentially bid on the network resources (power resources). Thus, a theoretical price is introduced as a potential congestion level that an SP expects in the future. An efficient resource allocation under the proposed framework defined as a separation between SPs and the NO is achieved through the Nash equilibrium. Motivated by the game theory concept, the authors in [23] modeled the competition between the foreign slices as a non-cooperative game. Players in this game are foreign slices and the strategy of each player is the allocated power . Each foreign slice seeks to maximize its individual revenue. A price function is introduced to the game to establish the charge to be paid by the VNOs during the power allocation game. The utility function is presented in terms of cost by the following formula:
where L bits are payloads in frames of M bits (), denotes the probability of correct reception of a frame at the receiver, r is the rate of transmission, is the allocated power, and c is a function of the total amount of the available power. The optimization power allocation problem is solved through the Nash equilibrium. No foreign slice can increase its utility function by changing individual power selection with other foreign slices’ given power. In other words, all the foreign slices can achieve the best response of the power selection.
The work in [24] is interested in proposing two auction games as a solution for the power allocation optimization problem in the virtualization of the mobile cellular as well as decoupling the services and the infrastructure network. In the first non-cooperative auction game, the authors consider the interaction between two important entities: InPs and VOs, to build an interactional game model. In the proposed auction game, the bidders are defined as VOs competing for power resources, while the auctioneer is defined as the hypervisor (InPs). During the second cooperative game, the coalition’s concept is established to maximize the payoff for all VOs. The users in a specific VO are modeled as players. Users who subscribed to the same VO can cooperate and form a coalition to maximize their gains against the other coalition. The two-stage game models tend to allocate the resource between the VOs fairly.
4.2.3. Goal 3: Fairly Allocate the Physical Resource
The fairness of the resources assignment is a very indispensable challenge faced the resource virtualization. Many solutions are proposed to satisfy all the resources claimants by achieving the allocation fairness. Authors in [26] introduced a dynamic game scheme with imperfect information to model the competitive and braining behavior among multiple cloud users. The proposed game model addresses the resource allocations problem in the competitive cloud environment. Thus, they designed a new resource pricing model based on the learning concept to predict the price of future resource allocation and satisfy the constraints related to the resource and the budget. The Nash equilibrium is investigated as a solution for the auction game to achieve the best response for all network users. This work proved that, besides the budget constraints, any bid also depends on its workload.
As well as the previous proposal, the work in [27] studied the same problem of resource allocation and pricing policies in cloud computing. Firstly, the authors formulated this problem as a non-cooperative bargaining game model. The players are the computation-intensive tasks competing for the allocation of many Virtual CPU Instances (VCI). Thus, the tasks need to satisfy certain constraints such as deadline and/or budget. To meet those requirements and to solve the previous problem, Nash Bargaining Solution (NBS) and Raiffa Kalai–Smorodinsky Bargaining Solution (RBS) are investigated where the goal is to minimize the executed time of tasks and to maximize the revenue based on the principle of pricing the mechanism.
The same tenet is adopted by the work in [22] where a cooperative game model is proposed to fairly allocate the resource between VMs. The allocation fairness concept is achieved through two fundamental objectives: to guarantee bandwidth for all the VMs according to the bandwidth requirements and to share the residual bandwidth in proportion to the weights of VMs. A bargaining game is introduced for the data-center networks to fairly allocate the bandwidths to players (VNs) by meeting the announced objectives. The VNs cooperate with each other to achieve a win-win solution, so-called, Pareto optimality where all pair-VNs involved in the game obtain the best profit. In this game, the VM-pairs are considered as players competing for limited bandwidth resources in data-centers. The authors introduce the Nash bargaining solution to solve the optimization problem.
The virtualization technologies in the cloud center lead to virtualizing the different physical resources (CPU, storage, memory, substrate links, bandwidths, and power). The sharing concept in cloud computing makes resource allocation a fundamental problem, which is treated in work [28]. A new resource allocation scheme is introduced for the cloud computing network based on the combination of the Stackelberg game and the hidden Markov model. The proposed approach aims at ensuring the resource allocation fairness between the SPs. In this competitive cloud environment, the SPs compete to rent enough resources from infrastructure suppliers (INs) to create virtual networks, and provide the services to end-users. Seeking for stable equilibrium, each SP tries to solve the optimization problem of the dynamic Stackelberg pricing game by minimizing the predicted cost of the requested resource of the CPU, bandwidth, and storage.
Moreover, the authors in [32] studied the cloud-based service as the interaction between the Software as a Service (SaaS) providers hosting their applications in the Infrastructure as a Service (IaaS) provider. They modeled the two conflicting situation based on the game theory perspective. In the first situation, each SaaS competes with the others to allocate enough resources from IaaS. In the second situation, the IaaS intends to maximize its profit defined as the revenues obtained from providing the resources to the SaaS. Then, the service-provisioning problem with the conflicting situations is modeled as a classical game. Then, Nash equilibrium is introduced as an optimal solution, where the IaaS and the SaaS adopt a strategy that cannot improve its revenue by changing its strategy unilaterally. In other words, the system reaches an optimal point for both players.
4.2.4. Goal 4: Ensure the Load Balancing
Balancing the load [56] in the network virtualization is a fundamental concept for the sharing of the workload between multidimensional resources and to distribute the local workload somewhat between nodes and links. The need for load balancing increases in a competitive environment because it leads to maximizing the user satisfaction and to enhancing the cost efficiency by adopting a robust and fair allocation scheme of all the parts of resources in the network. An appropriate load-balancing scheme can prevent the hardware failures due to the overloaded hosts by ensuring the fault tolerance and the scalability of the network. The decisions of load balancing can handle two different manners: Static and dynamic load-balancing algorithms. The major limitation of static load-balancing algorithms reside in the assumption that all the information about the resources and communication networks are initially predefined. However, in a dynamic algorithm, the load balancing decisions are made probabilistically based on the run-time state information leading to the enhancement of network performance. A hybrid solution that combines the advantages of the dynamic and the static algorithms is proposed in order to overcome the issues that the two previous designs encountered. Despite all the proposed techniques, the need for efficient and robust approaches to provide occurrence load balancing decisions remains open.
Boosted by the game theory, the authors in [30] provided a new solution for the load balancing problem as a non-cooperative game-theoretical model. In this system, the features of the schedulers are to receive the tasks from users, to decide the appropriate processor for the received task, and to send the task to the chosen processor. During this game, the schedulers tend to minimize their profits independently in terms of the task completion time average. Each player adopts a strategy where its profit is minimized. The investigated Nash equilibrium is the solution for the optimization problem in which no scheduler can increase its average task completion time by unilaterally changing its strategy. The Nash equilibrium provides the best and the efficient responses for the load balancing problems.
In [31], the authors proposed a cooperative game model as an efficient solution for the optimization and load balancing problem in the virtualized core network for all user types. They defined three user types according to the bandwidth utilization and the offered service cost: excellent, good, and fair. During the cooperative game, the players are the SP implementing their services using cloud providers’ resources. The payoff function denoted as a linear function of allocated bandwidth for the SPs is given by the following formula:
represents the allocated bandwidth to the user of type k, and represents the unit resource profit. Shapley Value is investigated to solve the optimization problem for this cooperative game.
4.2.5. Goal 5: To Reduce the Congestion
In network virtualization, sharing the physical infrastructure and the physical resource between virtual users leads to many critical obstacles being the resource congestion issue. The congestion defined by the saturation of the physical resources occurs when the amount of allocation exceeds the resource capacity. The design of a sophisticated mechanism for the network orchestration with the resource utilization adaptability is required as a solution to reduce the congestion in the NV environments. Work in [35] focuses on the optimal control and mitigation of resource congestion of a physical infrastructure based on the NFV paradigm. The authors formulated the congestion problem as an optimization game model to capture the occurrence of the congestion of physical resources. The proposed congestion prevention technique allows the dynamic control of traffic flows and system configurations to avoid the congestion of physicals resources. The Virtual Operators (VO) are the game players, which want to select the network configuration. Each VO tries to reduce the overall network congestion by solving the optimization problem based on the Nash equilibrium concept.
Moreover, many researchers become more interested in game theory tools to solve the congestion problem in the network virtualization as the authors in [57] who proposed an atomic weighted congestion game to address the problem of the Service Chain Composition (SCC) in the network function virtualization networks. The SCC problem composed of three sub-problems: the optimal number of the instances required for each VNF the efficient placement of VNF servers and their concatenation to attain the service chain for each traffic flow. In the proposed game model, the author introduced a new entity in the network the network called Service Broker (NSB). The instances for the NSBs are the players of the congestion game.
Furthermore, most of the virtualization networks’ scheduling tasks are optimization problems or so-called NP-hard problems designed to minimize a certain objective function or constraint. Many heuristic algorithms have been proposed to reach the optimal solutions for all the users. Game theory can be an appropriate tool to solve the optimization problem in which all the players can achieve the best responses. Several studies treated the NP-Hard scheduling problem using the game theory concept to model the competition between the players to use the resources and provide robust and efficient scheduling for all the users. Chuan et al. [36] proposed a matching game-based algorithm for the NFV environments to address the NP-hard VNF scheduling problem. The authors proved that the VNF scheduling problem could not be solved in polynomial time because the time to find the solution grows exponentially in terms of problem size. Hence, they formulated the optimization problem as a response to multiple constraints as follows:
where is the completion time of VNF, and is the optimization problem that assigns the processing and the link resources to the VNF at each time slot. By solving the problem, the offline scheduling algorithm based on GT provides a stable scheduling satisfying all the network constraint and requirements, and all the physical nodes and service chains are satisfied.
4.2.6. Goal 6: To Enhance the Fault Tolerance
In the virtualization environment, the physical equipment is vulnerable to several hardware and software failures that affect the virtual networks accordingly. Hence, the failure of the VNs can harm and entirely paralyze the network functionalities. Enhancing fault tolerance is one of the most indispensable challenges to be addressed in the virtualization networks. As a recovery solution, Soualah et al. [38] proposed a novel preventive reliable VN embedding algorithm based on the GT to meet three important optimization objectives: To optimize the rejection rate of the VN requests, to optimize the number of embedded VNs affected by the physical failures, and to optimize the time of failure recovery. The authors modeled two interleaved games to respond to the optimization problems. During the first game that treats the virtual routers, a second game is recalled to address the virtual links embedding. Thus, the introduced utility functions ensure the reliability of resource selection. Then, they proved that the game model reaches the Nash equilibrium, which is the state and steady-state of the system.
4.2.7. Goal 7: To Ensure Security
Authors in [39] introduced a new game model to secure the SDN environments against the Distributed Denial of Service attacks (DDOS) [58] by providing reward and punishment mechanisms to contain the effect of malicious users. The decoupling between the data and the control plane of the networking stack introduces new network security issues and reveals new challenges. The need for security increases with the network virtualization. Therefore, the authors proposed a new security scheme for the SDN based on a repeated simultaneous non-cooperate game to counter the DDOS effect. They modeled the interactions between Player 1 (P1), defined as an attacker presented by a malicious node, and Player 2 (P2) illustrated by an SDN controller which is assumed to be the game administration. The P1 can choose between two strategies (cooperate or defect): Cooperate by sending normal traffic or to defect by sending a huge amount of traffic. At the first iteration, P1 adopts the cooperative strategy by assuming that the other opponent is honest. A benign behavior is rewarded by a normal bandwidth allocation. However, every misbehavior is punished by using a rate-limiting strategy which reduces the allocation bandwidth as a punishment reaction to the malicious traffics. The proposed scheme encourages the player to maximize the gain by forcing the attackers to deviate from the malicious behaviors. Table 2 represents the payoff matrix of this game (B represents the allocated bandwidth).

Table 2.
The Payoff Matrix for P1 and the P2.
Based on the payoff matrix, the player adopted the malicious behavior obtained a less bandwidth equals to 0.75 B compared with 0.475 B when the player is malicious during two phases t 1,2. P1 must not deviate from the good behavior to obtain the best solution illustrated by the enough allocated bandwidth.
4.3. Players during the Game
The modeling process of a competitive situation in the NV environment as a game demands the decision-maker to define implicitly or explicitly the players and their adopted strategies. The player selection is the most challenging and crucial step to propose an efficient and convenient game-based approach for service provisioning. Thus, the decision-makers are our next criteria for the GT approaches’ classification. We differentiate between two types of possible players selected to model the solutions for the resource management: the real players and the virtual players.
- The real players are nominated to present physical entities such as the service provider and the cloud provider. The game schemes based on those players try fundamentally to allocate enough resources to the lessees and to maximize the revenues of the lessors.
- The virtual players are designed to model virtual entities such as the virtual network, the task, and virtual machines. Thus, the interaction between the virtual players can address the virtual resource allocation by proactively preventing the network congestion and to prevent the future allocation to support the sharing of the resources between multi-tenants.
Table 3 presents a comparison of the game-based solutions designed for the NV based on the player’s selection. According to the game-theoretical approaches for the NFV, in the literature, the critical and decisional components/tasks, which are the involved players, can be the virtual networks, virtual operators, virtual machine, services providers, or the network tasks. Thus, Table 3 illustrates the comparison of the GT solutions in terms of the goals addressing the service provisioning in the NV. The following section tries to propose a comparison of the proposed approaches according to the objectives and targets of the proposed service.

Table 3.
GT solutions classification (I).
4.3.1. Virtual Network (VN)
In the NF environment, each VN [59] is a set of virtual links and virtual nodes. The VNs are defined as the subset of the physical network resources. Many authors choose the VN to represent the players for their proposed game to address the virtual allocation by proactively preventing and avoiding the congestion problems. Authors in [20] aimed at modeling the competition between virtual networks for bandwidth allocation as a non-cooperative game to fairly and efficiently assign the resources to the different players. Firstly, they formulate the bandwidth allocation problem as an optimal problem (P1) using the same previous formula (Equation (5)). The optimal problem reveals two major constraints. In fact, for each VN, the bandwidth must be strictly positive and must be under the capacity of the link. The VNs competing for bandwidth allocation play a non-cooperative game. The optimal solution obtained at Nash equilibrium solves the optimal problem P1.
4.3.2. Service/Cloud Provider
The service/ cloud provider is the new entity derivative from the traditional Internet architecture. The SPs [60] create virtual networks and lease the physical resources from the InPs to offer end-to-end services. Two conflicting goals are addressed by the SP: to minimize the price of the resources leasing and to provide enough resources through VNs. The Cloud Providers [61] offer multiple services to their customers such as the Software as a Service (SaaS), Infrastructure as a Service (IaaS), Security as a Service (SECaaS), and Platform as a Service (PaaS). The cloud providers’ indispensable goal is to maximize their revenues based on pricing schemes, while their customer’s purpose is to reach a high level of QoS for a low price. The two previous entities are the players for many proposed GT solutions. In a cloud computing environment, the available resources can be under-utilization when the internet demand is under the capacity. Motivating by the availability of the resources, cloud providers cooperate by forming coalition to provide resource/service to public cloud users. Niyato et al. [33] highlighted the case of cooperative interactions among multiple cloud providers to maximize their revenues by adopting the service provisioning policy. The authors formulated the optimization problem of cloud providers for maximizing the revenue to provide service through the committed offer to public cloud users. Then, they investigated the efficiency coalition structure for the proposed hierarchical cooperative game model to solve the optimization problem. Moreover, during the game, the cloud providers can choose to join or to leave the coalition based on the payoff given by a formulation.
4.3.3. Virtual Operator
Virtual Operator (VNO) is a new introduced entity of the SP in the future business model which provides many features including the installation, the management, and the operation of the VN based on the SP requirements. The competitive relationships among virtual mobile operators (VMOs) are modeled as a game model in [29] to offer a dynamic and efficient wireless resource allocation in cellular network virtualization. Indeed, the fair and efficient sharing of wireless spectrum resources is the challenge addressed by this work. VMOs manage their networks by leasing the resources from the infrastructure providers (InPs). Thus, during the allocation phase, VMOs aim to maximize the resource utilization and minimize the leasing costs. When a VMO encounters intensified traffic flows, additional physical resource block (PRB) leasing is required to satisfy the new critical situation. A cost function based on the rate and type of flows is investigated to measure the PRB leasing payment for each VMO. Moreover, coalition formation between pair of players is proposed to enhance their profits by computing the Shapley value [62] denoted as the average payoff that a VMO will obtain if the player enters into the coalition in random order. The authors computed an optimization solution for each player by minimizing cost function by choosing the best coalition.
4.3.4. Virtual Machine
The migration technique is applied to ensure the load-balancing algorithm. In this context, authors in [34] proposed two non-cooperative game models to balance the load and to allocate the resource to the VMs. In the first game mode, the players are the set of agents managing a set of machines. The payoff function of the player is selected to be the maximum load on any dimension on a machine. During the game, each player tends to maximize its profit by optimizing the payoff function using the placement technique. The second game aims to migrate the virtual machine that is considered an efficient solution for the load balancing issues. Each machine is defined by a m-dimensional capacity and is controlled by the agent. The payoff function of player is defined as the portion of the machine it occupies in a given packing. An agent tries to maximize its profits by switching into different machines having enough capacities. Then, the existence of Nash equilibrium for both game models is proved.
4.3.5. Task
The task scheduling problem is considered to be an NP-hard problem. Several algorithms have been proposed to reach an optimal solution while answering the multiple constraints. An evolutional game-based algorithm is proposed in [37] to efficiently and fairly schedule the parallel tasks in the cloud computing framework in terms of time, cost, and QoS constraints. The tasks (users) are composed of parallel and dependent sub-tasks that are sharing multiple resources. They formulated that the utility function for each task was obtained from the allocation in terms of the price of the assigned resource. Then, the authors tried to find an optimal solution for the NP-hard problem by maximizing the utility function for the players while respecting the defined constraints.
5. Discussion and Future Research Directions
In this section, we will discuss the studied game theory solutions regarding the resource management in the NV environment, and we will explore the potential research directions. Figure 6 illustrates the different challenges and perspectives of the NF based on the game theory modeling.
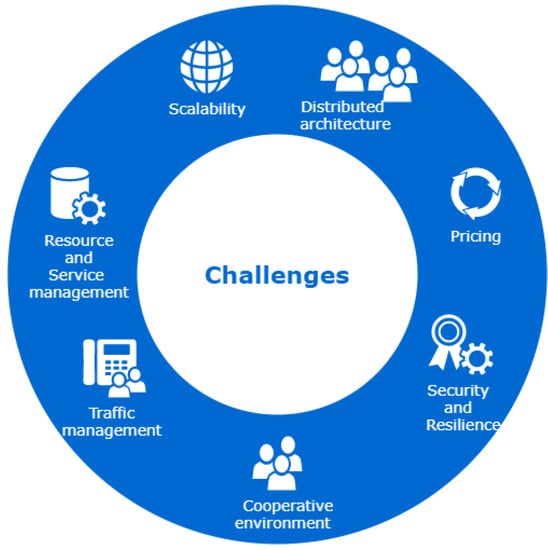
Figure 6.
Challenges and perspectives.
5.1. Cooperative Environment
The cooperative concept between the entities remains a very challenging key. In a competitive environment, each decision-maker is congenitally selfish and looks for maximizing their profit to the detriment of the others. The most proposed GT solutions for the NV are non-cooperative approaches. The major question is how to encourage the players to cooperate to enhance their utility functions and how to form the group of cooperation to share the resources and the revenues. To motivate the players to adopt the cooperative behaviors, the coalition formation must be addressed to satisfy the requirements of the group [63].
5.2. Security and Resiliency
Security is still an open research issue of any network architecture. The virtualization of the network introduces new threats and new vulnerabilities due to complex and selfish interactions between tenants and InPs. To detect the malicious behaviors and to mitigate the threats targeting the virtualization technologies, the game theory can be introduced as a promising solution to model the interactions of the players and to encourage them to behave honestly. Few game-based solutions [39,64] have been proposed to secure the SDN against the DDOS attacks and intrusion detection.
5.3. Traffic Management
Traffic management is considered a key challenge in network function virtualization [65]. All the previous game-based solutions address only the resource management in the NV. There are no approaches based on game theory for the routing protocols, forwarding mechanisms, control, and management planes. The game theory can model the interactions between the end-users and the flows, the packets to be forwarded, etc., computing to be routed first. Thus, the GT needs to meet the players’ requirements to reduce the delay, the end-to-end latency, the congestion, etc. However, the solution must consider the issues of the huge amount of data forwarded as well as the increasing numbers of services requester.
5.4. Pricing
Pricing is a crucial challenge for the service provisioning in the NV environment because it impacts the infrastructure providers’ revenues and provides many possibilities for the tenants to maximize their resources leasing by maintaining the lowest price. The majority of the proposed GT solution for the NV exploited the pricing algorithms to overcome resource leasing in multi-tenant environments.
5.5. Resource and Service Management
The first key to the efficient management of resources and services is dynamic and flexible modeling. Network services need to be efficiently modeled towards many parameters such as performance metrics, resource requirements, network configuration parameters, services management policies, etc. Flexible modeling will lead to an efficient abstraction of resources, architecture capabilities, and the providing services. In other words, it simplifies the understanding of network features by providing a generic way to represent resources and service. The second key is to optimize resource utilization while providing on-demanding services.
5.6. Scalability
Scalability refers to the capability to maintain the QoS in case of increasing network traffic. This challenge has received significant attention from researchers. SDN’s centralized controller can be affected by the congestion resulting from the growing amount of traffic [66,67]. Furthermore, this issue is addressed in NFV as it yields more entities to manage.
5.7. Decentralized Networks
This survey focused basically on the centralized networks where the controller has the full information about the network, devices, and architecture. The centralized framework maintains efficient resource management and allocation. Table 4 illustrates the benefits and the limitations of this architecture.

Table 4.
Centralized architecture: Benefits vs. limitations.
The need to apply a distributed architecture is increased due to the emergent applications such as the 5G networks and beyond. The new generations of mobile networks become more and more distributed by paving gradually its way into modern technologies since the resources can be managed and shared among individual nodes, and each player can be the consumer as well as the provider. This distributed architecture must be able to capably run applications such as device-to-device, machine-to machine, and internet of things at reduced latency. Therefore, game theory attracts a lot of attention as an efficient and suitable solution to solve the optimization problem in the decentralized architecture such as reducing latency and maximizing bandwidth between nodes. In [68,69], the authors introduced game models to the device-to-device communications to solve the interference and routing problems. Thus, using game theory for the optimization problems in the centralized and decentralized network virtualization remains a hot research topic for many researchers.
6. Conclusions
This rapid growth of Internet traffic introduces many problems and limitations related to the Internet architecture inflexibility. Network virtualization has been identified as a potential solution to overcome the ossification problem and traditional architecture limitations. Many researchers have exploited the game theory as a promising solution to address the resource management problems in the NV environments. This paper exhibited state of the art in game theory research by providing a comprehensible overview. Then, we discussed the solutions based on the GT for the resources management in the network virtualization. Moreover, we exposed an exhaustive taxonomy for the GT approaches’ classification. We also discussed and identified some of the key research directions for the potential solutions based on GT for the network virtualization environments.
Author Contributions
Conceptualization, J.B.; methodology, J.B.; validation, S.S.; investigation, S.S., H.A. and J.B; writing—original draft preparation, J.B.; review and editing, S.S. and H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Pan, J.; Paul, S.; Jain, R. A Survey of the Research on Future Internet Architectures. IEEE Commun. Mag. 2011, 49, 26–36. [Google Scholar] [CrossRef]
- Han, B.; Gopalakrishnan, V.; Ji, L.; Lee, S. Network function virtualization: Challenges and opportunities for innovations. IEEE Commun. Mag. 2015, 53, 90–97. [Google Scholar] [CrossRef]
- Jain, R.; Paul, S. Network Virtualization and Software Defined Networking for Cloud Computing: A Survey. IEEE Commun. Mag. 2010, 51, 24–31. [Google Scholar] [CrossRef]
- Chowdhury, N.M.K.; Boutaba, R. A survey of network virtualization. Comput. Netw. 2010, 54, 862–876. [Google Scholar] [CrossRef]
- Turner, J.; Taylor, D. Diversifying the Internet. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM ’05), St. Louis, MO, USA, 28 November–2 December 2005; Volume 2. [Google Scholar]
- Feamster, N.; Gao, L.; Rexford, J. How to Lease the Internet in your Spare Time? SIGCOMM Comp. Commun. Revi. 2007, 37, 61–64. [Google Scholar] [CrossRef]
- Yang, L.; Ng, B.; Seah, W.K.; Groves, L.; Singh, D. A survey on network forwarding in Software-Defined Networking. J. Netw. Comput. Appl. 2021, 176, 102947. [Google Scholar] [CrossRef]
- Tipantuña, C.; Hesselbach, X. NFV/SDN Enabled Architecture for Efficient Adaptive Management of Renewable and Non-Renewable Energy. IEEE Open J. Commun. Soc. 2020, 1, 357–380. [Google Scholar] [CrossRef]
- Saha, D.; Shojaee, M.; Baddeley, M.; Haque, I. An Energy-Aware SDN/NFV Architecture for the Internet of Things. IFIP Netw. Conf. (Netw.) 2020, 1, 604–608. [Google Scholar]
- Bonfim, M.S.; Dias, K.L.; Fernandes, S.F.L. Integrated NFV/SDN Architectures: A Systematic Literature Review. ACM Comput. Surv. 2019, 51, 1–39. [Google Scholar] [CrossRef]
- Kim, Y.H.; Gil, J.M.; Kim, D. A location-aware network virtualization and reconfiguration for 5G core network based on SDN and NFV. Int. J. Commun. Syst. 2021, 34, e4160. [Google Scholar] [CrossRef]
- Sohrabi, M.K.; Azgomi, H. A Survey on the Combined Use of Optimization Methods and Game Theory. Arch. Comput. Methods Eng. 2020, 27, 59–80. [Google Scholar] [CrossRef]
- Riahi, S.; Riahi, A. Game theory for resource sharing in large distributed systems. Int. J. Electr. Comput. Eng. (IJECE) 2019, 9, 1249–1257. [Google Scholar] [CrossRef]
- Halpern, J.Y. Computer Science and Game Theory: A Brief Survey. arXiv 2007, arXiv:cs/0703148. [Google Scholar]
- Wismans, L.J.; Brands, T.; Van Berkum, E.C.; Bliemer, M.C. Pruning and ranking the Pareto optimal set, application for the dynamic multi-objective network design problem. J. Adv. Transp. 2014, 48, 588–607. [Google Scholar] [CrossRef]
- Moeini, A.; Foumani, M.; Jenab, K. Utilisation of pruned Pareto-optimal solutions in the multi objective optimisation: An application to system redundancy allocation problems. Int. J. Appl. Decis. Sci. 2013, 6, 50–65. [Google Scholar] [CrossRef]
- Wang, C.; Yuan, Y. Game based dynamical bandwidth allocation model for virtual networks. In Proceedings of the 2009 First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009. [Google Scholar]
- Zhou, Y.; Li, Y.; Sun, G.; Jin, D.; Su, L.; Zeng, L. Game Theory Based Bandwidth Allocation Scheme for Network Virtualization. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010. [Google Scholar]
- Seddiki, M.S.; Frikha, M.; Song, Y.Q. A non-cooperative game-theoretic framework for resource allocation in network virtualization. Telecommun. Syst. 2016, 61, 209–219. [Google Scholar] [CrossRef]
- Wang, C.R.; Liu, K.; Wang, C. Game Based Virtual Bandwidth Allocation for Virtual Networks in Data Centers. Procedia Eng. 2011, 23, 780–785. [Google Scholar] [CrossRef] [Green Version]
- Fangwen, F.; Kozat, U.C. Wireless network virtualization as a sequential auction game. In Proceedings of the 2010 Proceedings IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010. [Google Scholar]
- Guo, J.; Liu, F.; Lui, J.C.; Jin, H. Fair Network Bandwidth Allocation in IaaS Datacenters via a Cooperative Game Approach. IEEE/ACM Trans. Netw. 2016, 24, 873–886. [Google Scholar] [CrossRef]
- Wei, J.; Yang, K.; Zhang, G.; Hu, Z. Pricing-based Power Allocation in Wireless Network Virtualization: A Game Approach. In Proceedings of the 2015 International Wireless Communications and Mobile Computing Conference (IWCMC), Dubrovnik, Croatia, 24–28 August 2015. [Google Scholar]
- Fan, B.; Tian, H.; Liu, B. Game Theory Based Power Allocation in LTE Air Interface Virtualization. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 9–12 March 2015. [Google Scholar]
- Yuan, Y.; Wang, C.R.; Wang, C. A Game Based Approach for Sharing the Data Center Network. Int. Symp. Neural Netw. 2012, 7367, 641–649. [Google Scholar]
- Teng, F.; Magoules, F. Resource pricing and equilibrium allocation policy in cloud computing. In Proceedings of the 2010 10th IEEE International Conference on Computer and Information Technology, Bradford, UK, 29 June–1 July 2010. [Google Scholar]
- Iyer, G.N.; Veeravalli, B. On the Resource Allocation and Pricing Strategies in Compute Clouds Using Bargaining Approaches. In Proceedings of the 2011 17th IEEE International Conference on Networks, Singapore, 14–16 December 2011. [Google Scholar]
- Wei, W.; Fan, X.; Song, H.; Fan, X.; Yang, J. Imperfect Information Dynamic Stackelberg Game Based Resource Allocation Using Hidden Markov for Cloud Computing. IEEE Trans. Serv. Comput. 2018, 11, 78–89. [Google Scholar] [CrossRef]
- Liu, B.; Tian, H. A Bankruptcy Game-Based Resource Allocation Approach among Virtual Mobile Operators. IEEE Commun. Lett. 2013, 17, 1420–1423. [Google Scholar]
- Subrata, R.; Zomaya, A.Y.; Landfeldt, B. Game-Theoretic Approach for Load Balancing in Computational Grids. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 66–76. [Google Scholar] [CrossRef]
- Khan, M.A.; Foix-Cablé, V.; Yalin, L.; Despotovic, Z. Autonomic Load Balancing In The Future Disintegrated And Virtualized Netwoks. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Istanbul, Turkey, 6–9 April 2014. [Google Scholar]
- Ardagna, D.; Panicucci, B.; Passacantando, M. A Game Theoretic Formulation of the Service Provisioning Problem in Cloud Systems. In Proceedings of the 20th International Conference on World Wide Web; ACM: New York, NY, USA, 2011. [Google Scholar]
- Niyato, D.; Vasilakos, A.V.; Kun, Z. Resource and Revenue Sharing with Coalition Formation of Cloud Providers: Game Theoretic Approach. In Proceedings of the 2011 11th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Newport Beach, CA, USA, 23–26 May 2011. [Google Scholar]
- Ye, D.; Chen, J. Non-cooperative games on multidimensional resource allocation. Future Gener. Comput. Syst. 2013, 29, 1345–1352. [Google Scholar] [CrossRef]
- Elias, J.; Martignon, F.; Paris, S.; Wang, J. Efficient Orchestration Mechanisms for Congestion Mitigation in NFV: Models and Algorithms. IEEE Trans. Serv. Comput. 2017, 10, 534–546. [Google Scholar] [CrossRef] [Green Version]
- Pham, C.; Tran, N.H.; Hong, C.S. Virtual Network Function Scheduling: A Matching Game Approach. IEEE Commun. Lett. 2017, 22, 69–72. [Google Scholar] [CrossRef]
- Wei, G.; Vasilakos, A.V.; Xiong, N. Scheduling Parallel Cloud Computing Services: An Evolutional Game. In Proceedings of the 2009 First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009. [Google Scholar]
- Soualah, O.; Fajjari, I.; Aitsaadi, N.; Mellouk, A. A Reliable Virtual Network Embedding Algorithm based on Game Theory within Cloud’s backbone. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, NSW, Australia, 10–14 June 2014. [Google Scholar]
- Chowdhary, A.; Pisharody, S.; Alshamrani, A.; Huang, D. Dynamic Game based Security framework in SDN-enabled Cloud Networking Environments. In Proceedings of the ACM International Workshop on Security in Software Defined Networks & Network Function Virtualization; ACM: New York, NY, USA, 2017; pp. 53–58. [Google Scholar]
- Le, S.; Wu, Y.; Toyoda, M. A congestion game framework for service chain composition in NFV with function benefit. Inf. Sci. 2020, 514, 512–522. [Google Scholar] [CrossRef]
- Moura, J.; Hutchison, D. Resilient Cyber-Physical Systems: Using NFV Orchestration. arXiv 2020, arXiv:2003.12401. [Google Scholar]
- Esteves, J.J.A.; Boubendir, A.; Guillemin, F.; Sens, P. Optimized Network Slicing Proof-of-Concept with Interactive Gaming Use Case. In Proceedings of the 2020 23rd Conference on Innovation in Clouds, Internet and Networks and Workshops (ICIN), Paris, France, 24–27 February 2020. [Google Scholar]
- Toka, L.; Zubor, M.; Korosi, A.; Darzanos, G.; Rottenstreich, O.; Sonkoly, B. Pricing games of NFV infrastructure providers. Telecommun. Syst. 2020, 76, 219–232. [Google Scholar] [CrossRef]
- Fossati, F.; Hoteit, S.; Moretti, S.; Secci, S. Fair Resource Allocation in Systems With Complete Information Sharing. IEEE/ACM Trans. Netw. 2018, 26, 2801–2814. [Google Scholar] [CrossRef]
- Li, Q.; Huang, C.; Bao, H.; Fu, B.; Jia, X. A Game-based Combinatorial Double Auction Model for Cloud Resource Allocation. In Proceedings of the 2019 28th International Conference on Computer Communication and Networks (ICCCN), Valencia, Spain, 29 July–1 August 2019. [Google Scholar]
- Le, S.T.; Wu, Y.; Sun, X.M. A Game Theoretic Approach for Service Chain Composition in Network Function Virtualization Network. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019. [Google Scholar]
- Wang, C.; Zhang, S.; Chen, Y.; Qian, Z.; Wu, J.; Xiao, M. Joint Configuration Adaptation and Bandwidth Allocation for Edge-based Real-time Video Analytics. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020. [Google Scholar]
- Hammood, D.A.; Alkhayyat, A.; Rahim, H.A.; Ahmad, R.B. Minimum Power Allocation Cooperative Communication based on Health-Care WBAN. Photonic Netw. Commun. 2020, 40, 194–208. [Google Scholar] [CrossRef]
- Alfoudi, A.S.D.; Newaz, S.S.; Otebolaku, A.; Lee, G.M.; Pereira, R. An Efficient Resource Management Mechanism for Network Slicing in a LTE Network. IEEE Access 2019, 7, 89441–89457. [Google Scholar] [CrossRef]
- Mishra, S.K.; Sahoo, B.; Parida, P.P. Load balancing in cloud computing: A big picture. J. King Saud Univ. Comput. Inf. Sci. 2020, 32, 149–158. [Google Scholar] [CrossRef]
- Singh, J.; Singh, K. Congestion Control in Vehicular Ad Hoc Network: A Review. Next Gener. Netw. 2017, 489–496. [Google Scholar] [CrossRef]
- Idoudi, H.; Bennaceur, J. Fault Tolerant Placement Strategy for WSN. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016. [Google Scholar]
- Shankar, A.; Sivakumar, N.R.; Sivaram, M.; Ambikapathy, A.; Nguyen, T.K.; Dhasarathan, V. Increasing fault tolerance ability and network lifetime with clustered pollination in wireless sensor networks. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2285–2298. [Google Scholar] [CrossRef]
- Berdik, D.; Otoum, S.; Schmidt, N.; Porter, D.; Jararweh, Y. A Survey on Blockchain for Information Systems Management and Security. Inf. Process. Manag. 2021, 58, 102397. [Google Scholar] [CrossRef]
- Rath, K.P. A direct proof of the existence of pure strategy equilibria in games with a continuum of players. Econ. Theory 1992, 2, 427–433. [Google Scholar] [CrossRef]
- Ghomi, E.J.; Rahmani, A.M.; Qader, N.N. Load-balancing algorithms in cloud computing: A survey. J. Netw. Comput. Appl. 2017, 88, 50–71. [Google Scholar] [CrossRef]
- D’Oro, S.; Galluccio, L.; Palazzo, S.; Schembra, G. Exploiting Congestion Games to Achieve Distributed Service Chaining in NFV Networks. IEEE J. Sel. Areas Commun. 2017, 35, 407–420. [Google Scholar] [CrossRef]
- Yan, Q.; Yu, F.R.; Gong, Q.; Li, J. Software-Defined Networking (SDN) and Distributed Denial of Service (DDoS) Attacks in Cloud Computing Environments: A Survey, Some Research Issues, and Challenges. IEEE Commun. Surv. Tutor. 2016, 18, 602–622. [Google Scholar] [CrossRef]
- Fischer, A.; Botero, J.F.; Beck, M.T.; De Meer, H.; Hesselbach, X. Virtual Network Embedding: A Survey. IEEE Trans. Netw. Serv. Manag. 2013, 15, 1888–1906. [Google Scholar] [CrossRef]
- Duan, Q.; Yan, Y.; Vasilakos, A.V. A Survey on Service-Oriented Network Virtualization Toward Convergence of Networking and Cloud Computing. IEEE Trans. Netw. Serv. Manag. 2012, 9, 373–392. [Google Scholar] [CrossRef]
- Sultan, N. Cloud computing for education: A new dawn? Int. J. Inf. Manag. 2010, 20, 109–116. [Google Scholar] [CrossRef]
- Clippel, G. Membership separability: A new axiomatization of the Shapley value. Games Econ. Behav. 2018, 108, 125–129. [Google Scholar] [CrossRef]
- Wang, T.; Liu, F.; Guo, J.; Xu, H. Dynamic SDN controller assignment in data center networks: Stable matching with transfers. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Niazi, R.A.; Faheem, Y. A Bayesian Game-Theoretic Intrusion Detection System for Hypervisor-Based Software Defined Networks in Smart Grids. IEEE Access 2019, 7, 88656–88672. [Google Scholar] [CrossRef]
- Yang, S.; Li, F.; Trajanovski, S.; Yahyapour, R.; Fu, X. Recent Advances of Resource Allocation in Network Function Virtualization. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 295–314. [Google Scholar] [CrossRef]
- Hohlfeld, O.; Kempf, J.; Reisslein, M.; Schmid, S.; Shah, N. Guest editorial scalability issues and solutions for software defined networks. IEEE J. Sel. Areas Commun. 2018, 36, 2592–2602. [Google Scholar] [CrossRef]
- Hu, T.; Guo, Z.; Yi, P.; Baker, T.; Lan, J. Multi-controller based software-defined networking: Asurvey. IEEE Access 2018, 6, 15980–15996. [Google Scholar] [CrossRef]
- Gao, J.; Tembine, H. Empathy and Berge equilibria in the Forwarding Dilemma in Relay-Enabled Networks. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications (WINCOM), Rabat, Morocco, 1–4 November 2017. [Google Scholar]
- Aslam, S.; Alam, F.; Hasan, S.F.; Rashid, M. Decentralized Interference Mitigation Technique for D2D Networks Using Game Theory Optimization. In Proceedings of the 29th International Telecommunication Networks and Applications Conference (ITNAC), Auckland, New Zealand, 27–29 November 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).