Error Performance Estimation of Modulated Retroreflective Transdermal Optical Wireless Links with Diversity under Generalized Pointing Errors
Abstract
:1. Introduction
- A novel system and channel model for MRR TOW links is developed that incorporates the basic characteristics of this type of link.
- The impact of the more realistic stochastic pointing errors with nonzero boresight is introduced and estimated in the MRR TOW area for the first time.
- A spatial-diversity technique with optimal combining is considered by employing multiple out-of-body receiver apertures, and thus, MRR TOW data transmissions of enhanced reliability are achieved.
- An outage bit error rate analysis is performed that evaluates the effectiveness of the spatial-diversity technique versus the joint impact of transdermal pathloss and generalized pointing errors with nonzero boresight.
- An average SNR estimation is performed that reveals the feasibility of the proposed MRR TOW system architecture.
- Novel analytical mathematical expressions are derived along with proper corresponding illustrated results that can be utilized in the design of MRR TOW links.
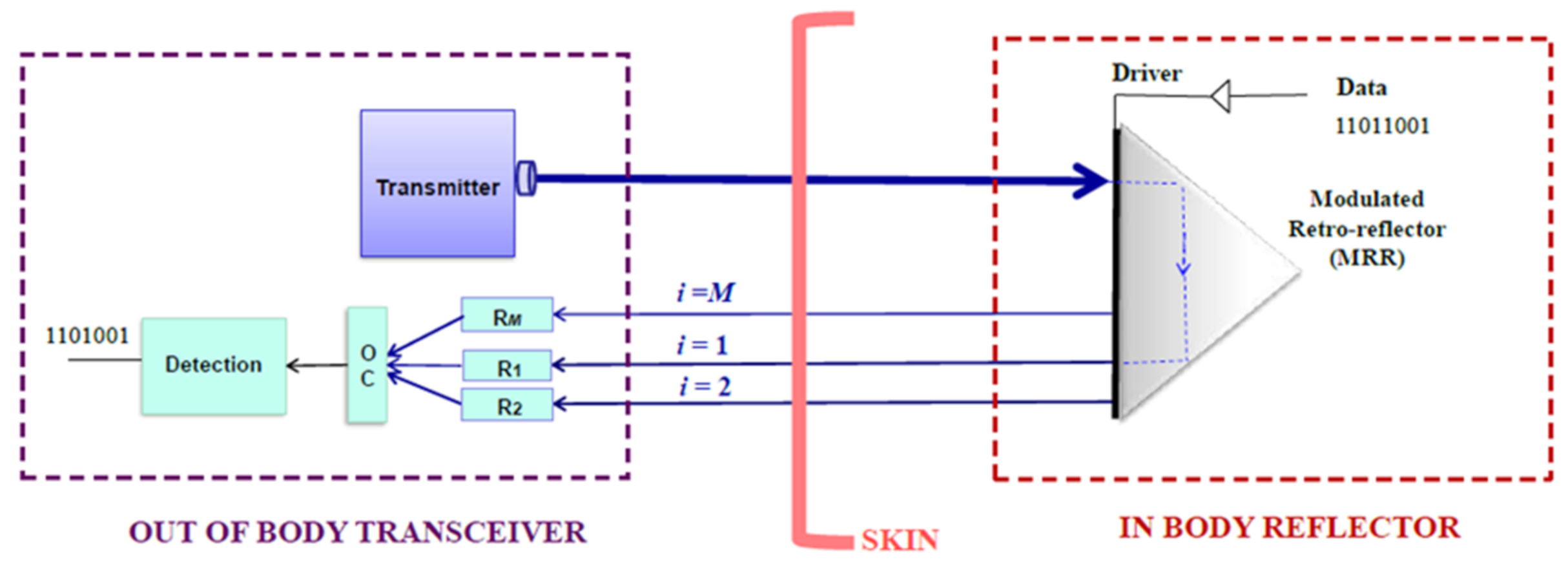
2. System and Channel Model
2.1. Signal Model
2.2. Generalized Pointing Errors with Nonzero Boresight
2.3. Joint Impact of Pathloss and Generalized Pointing Errors with Nonzero Boresight
2.4. SISO MRR TOW Links
2.5. SIMO MRR TOW Links with Spatial Diversity and OC
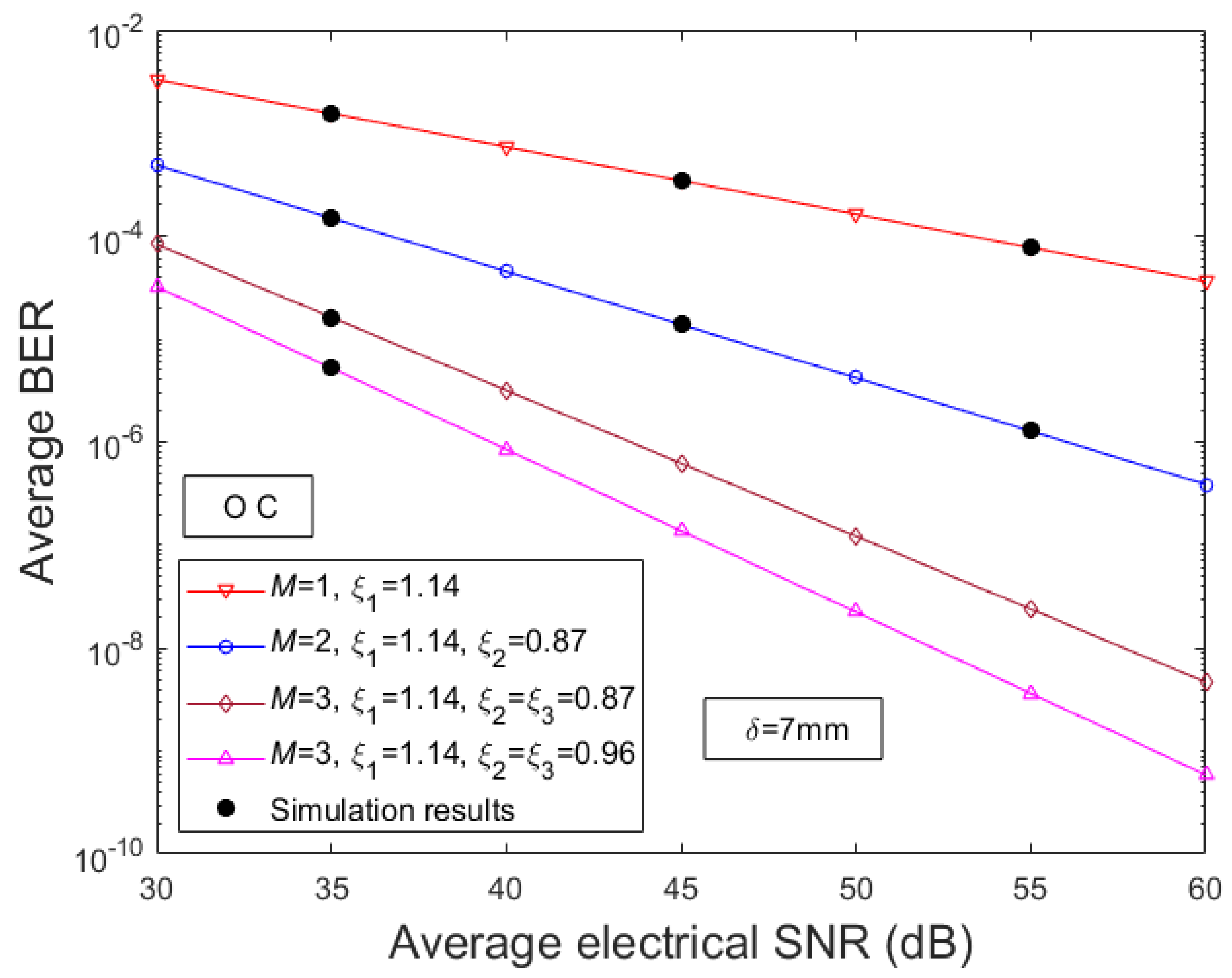
3. Analytical Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gil, Y.; Rotter, N.; Arnon, S. Feasibility of retroreflective transdermal optical wireless communication. Appl. Opt. 2012, 51, 4232–4239. [Google Scholar] [CrossRef] [PubMed]
- Guillory, K.S.; Misener, A.K.; Pungor, A. Hybrid RF/IR transcutaneous telemetry for power and high-bandwidth data. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 4338–4340. [Google Scholar]
- Abualhoul, M.Y.; Svenmarker, P.; Wang, Q.; Andersson, J.Y.; Johansson, A.J. Free space optical link for biomedical applications. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1667–1670. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Rahman, K.K.M.; Tsigopoulos, A.D.; Christofilakis, V. Average BER Estimation of Retroreflective Transdermal Optical Wireless Links with Diversity, Attenuation and Spatial Jitter. In Proceedings of the 2020 International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 7–9 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Rahman, K.K.M. Transdermal subcarrier L-PSK or DBPSK optical wireless links with time diversity, skin attenuation and spatial jitter. J. Modern Opt. 2020, 67, 14. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Rahman, K.K.M. Signal Intensity Estimation in Transdermal Optical Wireless Links with Stochastic Pointing Errors Effect. Technologies 2020, 8, 60. [Google Scholar] [CrossRef]
- Parmentier, S.; Fontaine, R.; Roy, Y. Laser diode used in 16 Mb/s, 10 mW optical transcutaneous telemetry system. In Proceedings of the Biomedical Circuits and Systems Conference, BioCAS, Baltimore, MD, USA, 20–22 November 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 377–380. [Google Scholar]
- Liu, T.; Bihr, U.; Anis, S.M.; Ortmanns, M. Optical transcutaneous link for low power, high data rate telemetry. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), San Diego, CA, USA, 28 August–1 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3535–3538. [Google Scholar]
- Liu, T.; Anders, J.; Ortmanns, M. System level model for transcutaneous optical telemetric link. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 865–868. [Google Scholar]
- Liu, T.; Bihr, U.; Becker, J.; Anders, J.; Ortmanns, M. In vivo verification of a 100 Mbps transcutaneous optical telemetric link. In Proceedings of the Biomedical Circuits and Systems Conference (BioCAS), Lausanne, Switzerland, 22–24 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 580–583. [Google Scholar]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K. Optical wireless cochlear implants. Biomed. Opt. Express 2019, 10, 707–730. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Rahman, K.K. Transdermal Optical Wireless Links with Multiple Receivers in the Presence of Skin-Induced Attenuation and Pointing Errors. Computation 2019, 7, 33. [Google Scholar] [CrossRef] [Green Version]
- Ackermann, D.M.; Smith, B.; Kilgore, K.L.; Peckham, P.H. Design of a high speed transcutaneous optical telemetry link. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 2932–2935. [Google Scholar]
- Abita, J.L.; Schneider, W. Transdermal Optical Communications; John Hopkins APL Tech: Laurel, MD, USA, 2004; Volume 25, pp. 261–268. [Google Scholar]
- Ackermann, D.M.; Smith, B.; Wang, X.F.; Kilgore, K.L.; Peckham, P.H. Designing the optical interface of a transcutaneous optical telemetry link. IEEE Trans. Biomed. Eng. 2008, 55, 1365–1373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ritter, R.; Handwerker, J.; Liu, T.; Ortmanns, M. Telemetry for implantable medical devices: Part 1-media properties and standards. IEEE Solid-State Circuits Mag. 2014, 6, 47–51. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Tombras, G.S.; Aidinis, K.; Jaber, F.; Rahman, M. On the use of diversity in transdermal optical wireless links with nonzero boresight pointing errors for outage performance estimation. In Proceedings of the 2019 International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Roumelas, G.D.; Jaber, F.; Rahman, K.K.M. Modulated Retro-Reflector Transdermal Optical Wireless Communication Systems with Wavelength Diversity over Skin-Induced Attenuation and Pointing Errors. In Proceedings of the 2020 IEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, United Arab Emirates, 10–12 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Trevlakis, S.; Boulogeorgos, A.A.; Karagiannidis, G. Signal Quality Assessment for Transdermal Optical Wireless Communications under Pointing Errors. Technologies 2018, 6, 109. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, G.K.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Tombras, G.S. SIMO Optical Wireless Links with Nonzero Boresight Pointing Errors over M modeled Turbulence Channels. Elsevier Opt. Commun. 2017, 403, 391–400. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Gappmair, W.; Sandalidis, H.G.; Tombras, G.S. SIMO subcarrier PSK FSO links with phase noise and non-zero boresight pointing errors over turbulence channels. IET Commun. 2019, 13, 831–836. [Google Scholar] [CrossRef]
- Navidpour, S.M.; Uysal, M.; Kavehrad, M. BER performanceof free-space optical transmission with spatial diversity. IEEE Trans. Wirel. Commun 2007, 6, 2813–2819. [Google Scholar]
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging optical wireless communications-advances and challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Karagiannidis, G.K. On the impact of misalignment fading in transdermal optical wireless communications. In Proceedings of the 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Karagiannidis, G.K. Outage Performance of Transdermal Optical Wireless Links in the Presence of Pointing Errors. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Li, X.; Zhao, X.; Zhang, P.; Yang, W.; Wang, T.; Jiang, H. Probability density function of turbulence fading in MRR free space optical link and its applications in MRR free space optical communications. IET Commun. 2017, 11, 2476–2481. [Google Scholar] [CrossRef]
- Farid, A.A.; Hranilovic, S. Outage capacity optimization for free space optical links with pointing errors. IEEE/OSA J. Lightwave Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Cheng, J.; Tsiftsis, T.A. Free-space optical communication with nonzero boresight pointing errors. IEEE Trans. Commun. 2014, 62, 713–725. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; Garcia-Zambrana, A.; Castillo-Vazquez, B.; Castillo-Vazquez, C. Impact of nonzeroboresight pointing error on ergodic capacity of MIMO FSO communication systems. Opt. Express 2016, 24, 3513–3534. [Google Scholar] [CrossRef] [PubMed]
- Boluda-Ruiz, R.; García-Zambrana, A.; Castillo-Vazquez, C.; Castillo-Vazquez, B. Novel approximation of misalignment fading modeled by Beckmann distribution on free-space optical links. Opt. Express 2016, 24, 22635–22649. [Google Scholar] [CrossRef] [PubMed]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 6th ed.; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House: Norwood, MA, USA, 1987. [Google Scholar]
- Helstrom, C.W. Probability and Stochastic Processes for Engineers; Macmillan Coll Division: Stuttgart, Germany, 1991. [Google Scholar]
- The Wolfarm Functions Site. 2008. Available online: https://functions.wolfram.com/ (accessed on 30 November 2020).
- Chiani, M.; Dardari, D.; Simon, M.K. New exponential bounds and approximations for the computation of error probability in fading channels. Trans. Wireless Commun. 2003, 2, 840–845. [Google Scholar] [CrossRef] [Green Version]
- Alouini, M.-S.; Simon, M.K. An MGF-based performance analysis of generalized selection combining over Rayleigh fading channels. IEEE Trans. Commun. 2000, 48, 401–415. [Google Scholar] [CrossRef]
- Maxim Integrated Products. 155 Mbps Low-Noise Transimpedance Amplifier. Available online: http://pdf.datasheetcatalog.com/datasheets2/44/444242_1.pdf (accessed on 30 November 2020).


| i | ai | bi | ci |
|---|---|---|---|
| 1 | 10 | 0.35 | 0.065 |
| 2 | 4.5 | 0.42 | 0.25 |
| 3 | 13.48 | −1.5 | 50.12 |
| 4 | 14.7 | 1442 | 49.35 |
| 5 | 7.435 | 1499 | 75.88 |
| 6 | 48 | 3322 | 1033 |
| 7 | 594.1 | −183 | 285.9 |
| 8 | 11.47 | −618.5 | 1054 |
| Parameter | Value(s) |
|---|---|
| θm | 20° |
| 1 μW/MHz–20 μW/MHz | |
| μ | 30–60 dB |
| ηm | 0.8 |
| λm | 1.1 μm |
| rm | 0.5 mm |
| δm | |
| { | |
| { | |
| { |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varotsos, G.K.; Nistazakis, H.E.; Aidinis, K.; Jaber, F.; Nasor, M.; Rahman, K.K.M. Error Performance Estimation of Modulated Retroreflective Transdermal Optical Wireless Links with Diversity under Generalized Pointing Errors. Telecom 2021, 2, 167-180. https://doi.org/10.3390/telecom2020011
Varotsos GK, Nistazakis HE, Aidinis K, Jaber F, Nasor M, Rahman KKM. Error Performance Estimation of Modulated Retroreflective Transdermal Optical Wireless Links with Diversity under Generalized Pointing Errors. Telecom. 2021; 2(2):167-180. https://doi.org/10.3390/telecom2020011
Chicago/Turabian StyleVarotsos, George K., Hector E. Nistazakis, Konstantinos Aidinis, Fadi Jaber, Mohd Nasor, and Kanhira Kadavath Mujeeb Rahman. 2021. "Error Performance Estimation of Modulated Retroreflective Transdermal Optical Wireless Links with Diversity under Generalized Pointing Errors" Telecom 2, no. 2: 167-180. https://doi.org/10.3390/telecom2020011
APA StyleVarotsos, G. K., Nistazakis, H. E., Aidinis, K., Jaber, F., Nasor, M., & Rahman, K. K. M. (2021). Error Performance Estimation of Modulated Retroreflective Transdermal Optical Wireless Links with Diversity under Generalized Pointing Errors. Telecom, 2(2), 167-180. https://doi.org/10.3390/telecom2020011







