An Improved GreenOFDM Scheme for PAPR Reduction
Abstract
1. Introduction
- (i)
- (ii)
- in order to correctly estimate the PAPR of OFDM signals in the digital domain, the computational complexity of the digital modulator is increased due to oversampling [4].
- (iii)
- the high PAPR of these signals generally increases the Power Amplifier’s (PA’s) power dissipation as its linear region has to be extended to be able to accommodate signals with wide amplitude excursions. Not doing so results in non-linear distortions and out-of-band radiations that degrade the system performances [5].
2. OFDM and PAPR
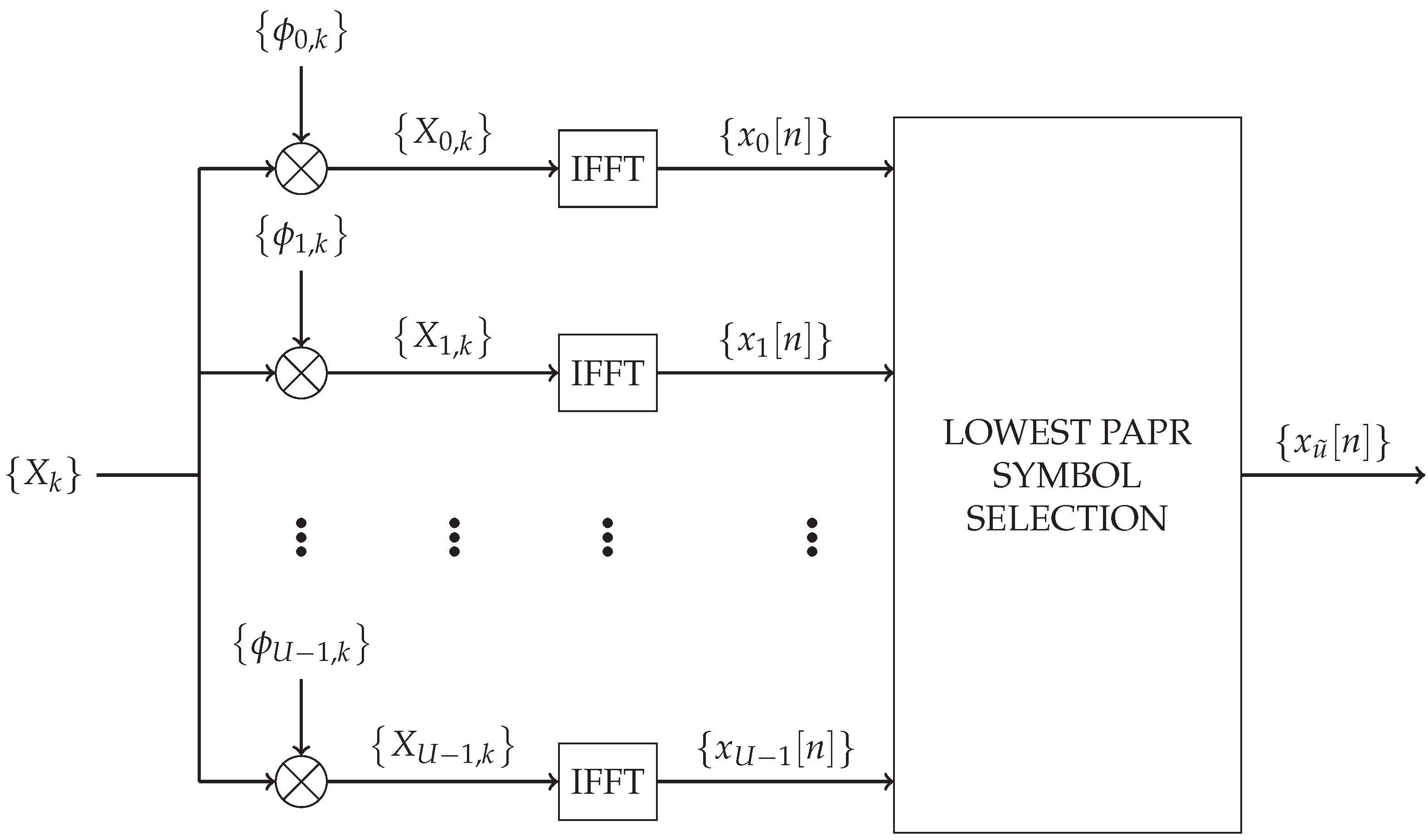
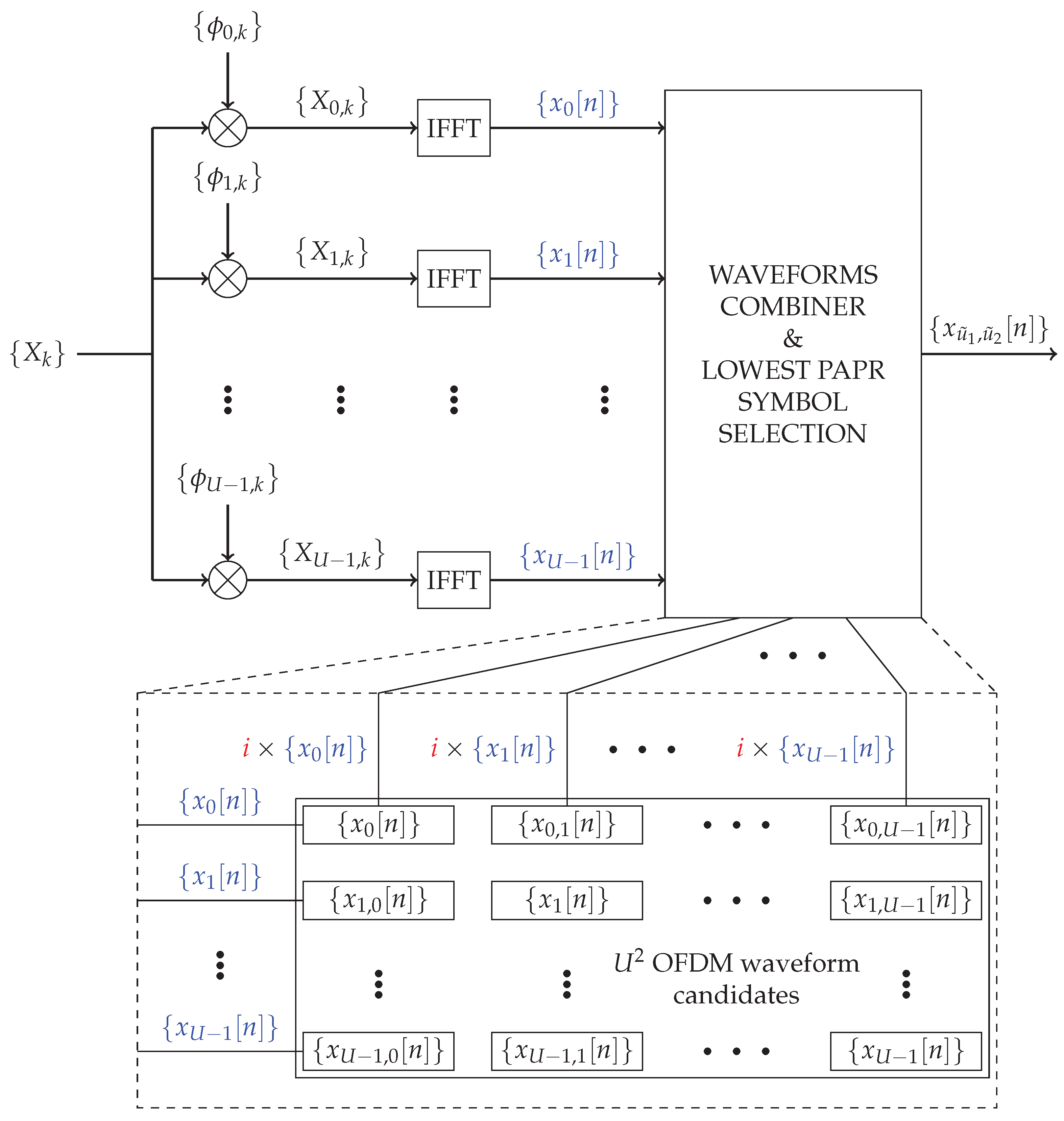
3. From SLM-OFDM to GreenOFDM
| Algorithm 1 The SeLected Mapping (SLM)-Orthogonal Frequency Division Multiplexing (OFDM) algorithm. |
| Require:, with |
| minPAPR |
| for do |
| ; |
| ; |
| if then |
| minPAPR ; |
| ; |
| end if |
| end for |
| SEND ; |
| Algorithm 2 The GreenOFDM algorithm. |
| Require: , |
| minPAPR ; |
| for do |
| for do |
| ; |
| if then |
| minPAPR ; |
| ; |
| end if |
| end for |
| end for |
| SEND ; |
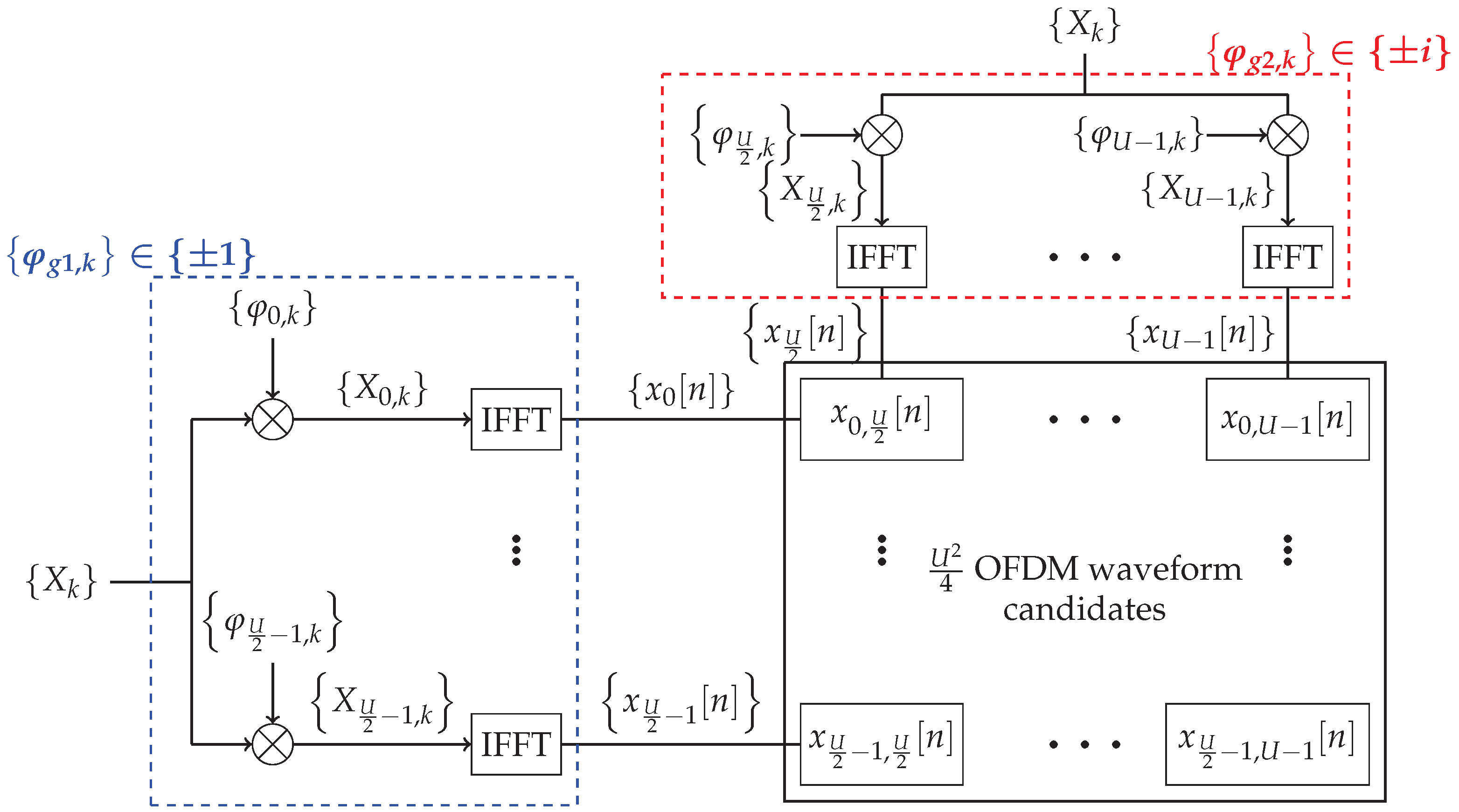
4. An Improved GreenOFDM Version
| Algorithm 3 The GreenOFDMv2 algorithm. |
| Require: |
| minPAPR ; |
| for do |
| for do |
| if then |
| ; |
| else |
| ; |
| end if |
| if then |
| minPAPR ; |
| ; |
| end if |
| end for |
| end for |
| SEND ; |
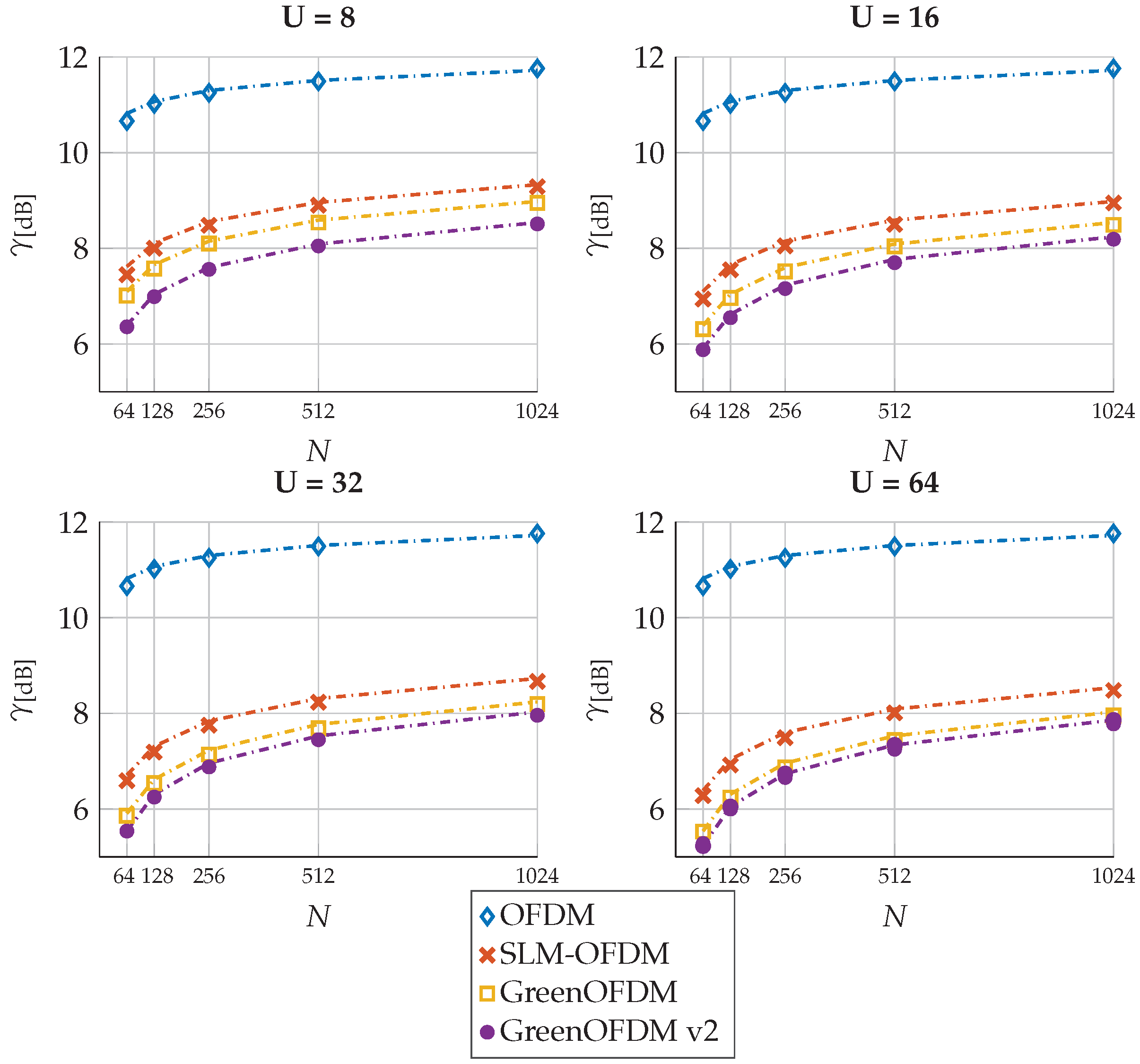
5. Simulation Results and Discussion
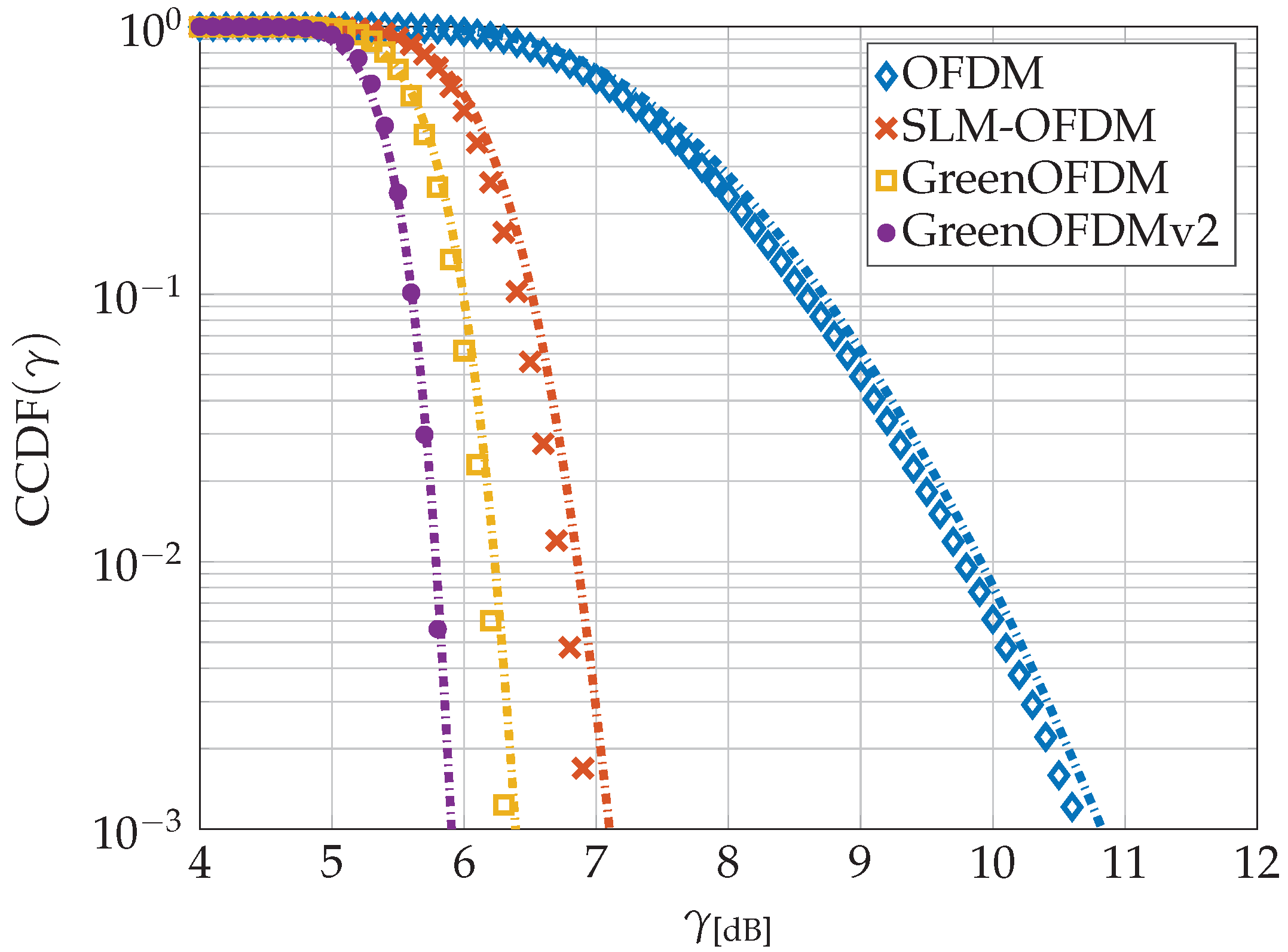
5.1. PAPR Complementary Cumulative Distribution Function (CCDF)
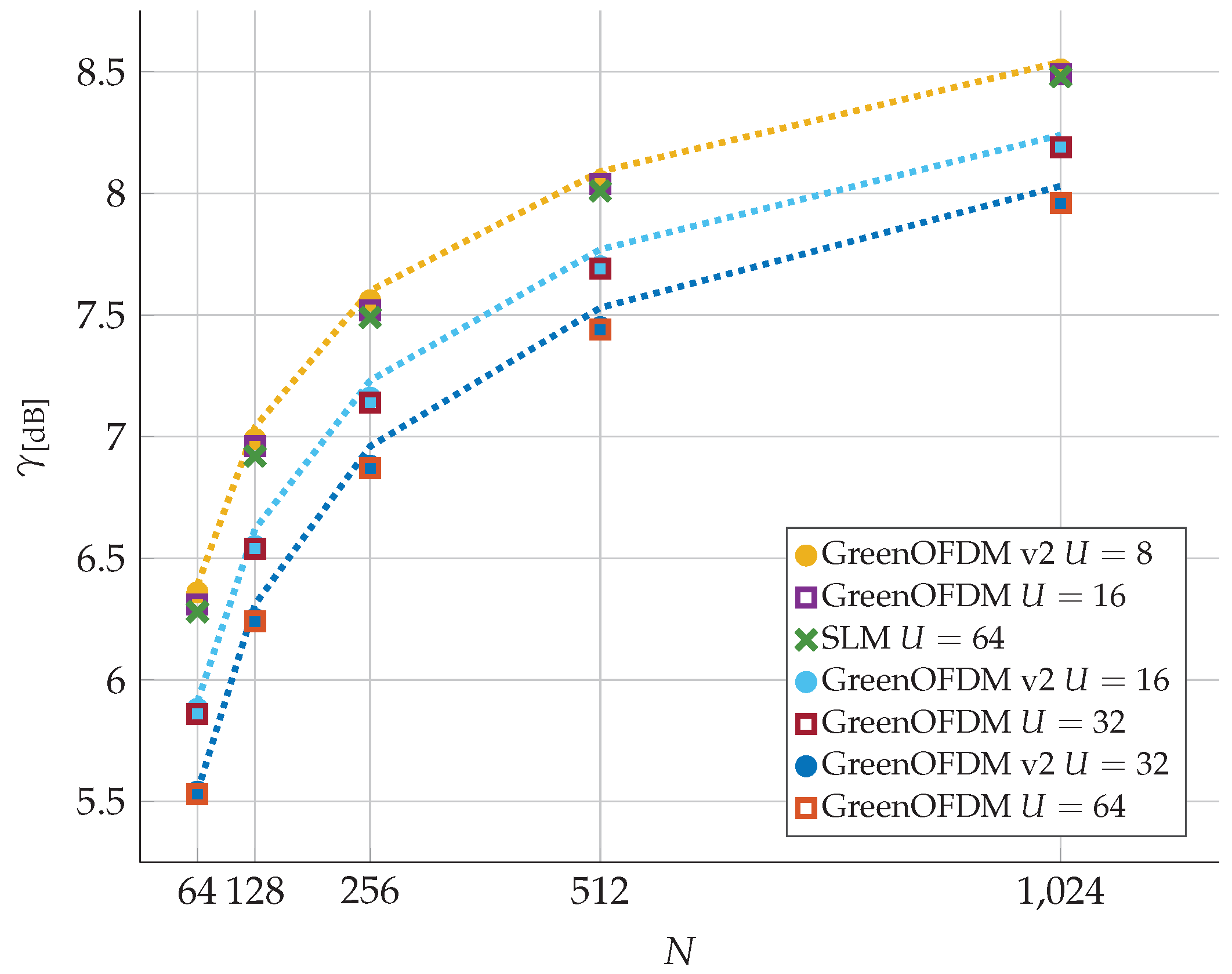
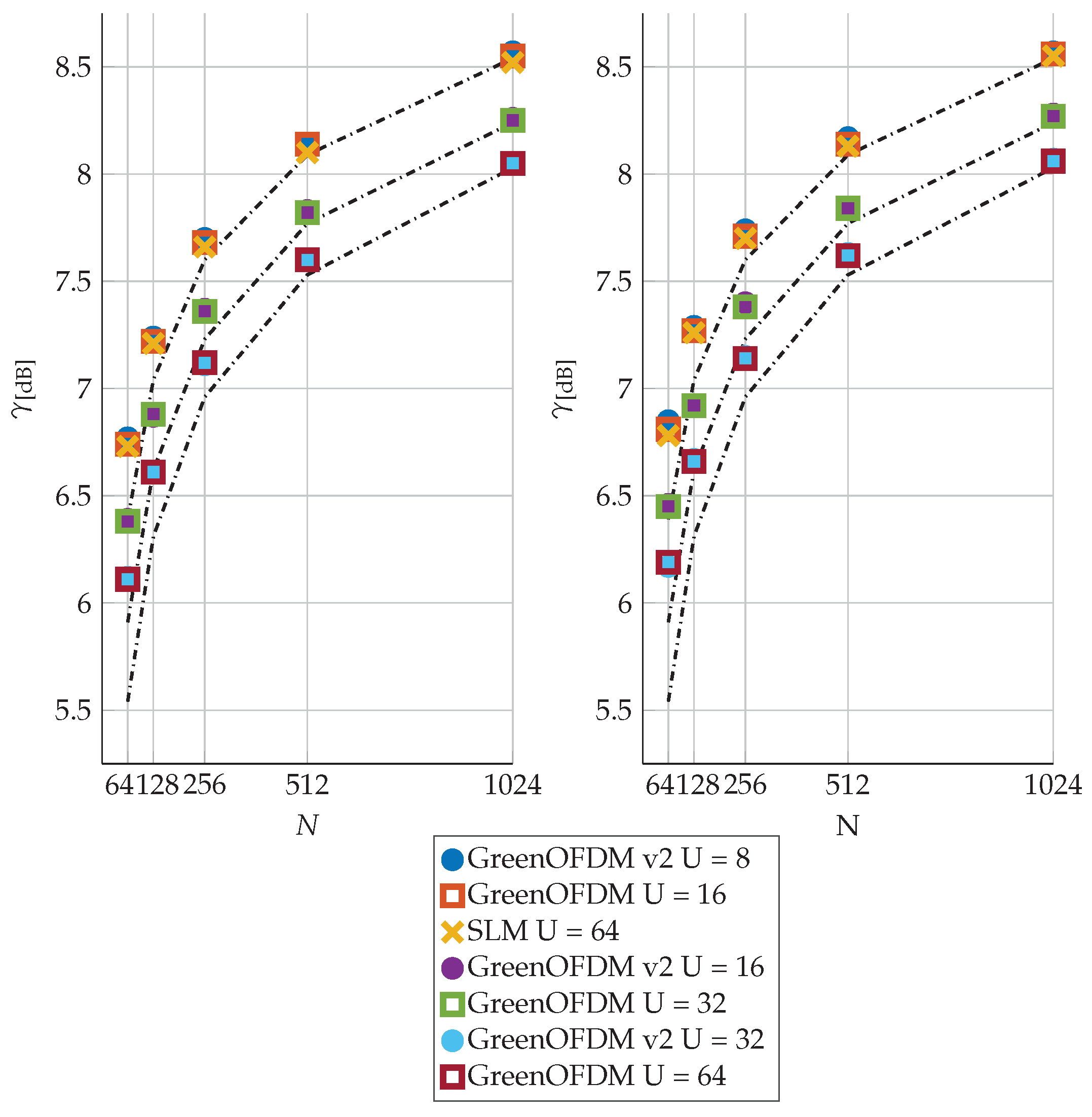
5.2. PAPR Threshold: Simulations and Approximated Formula
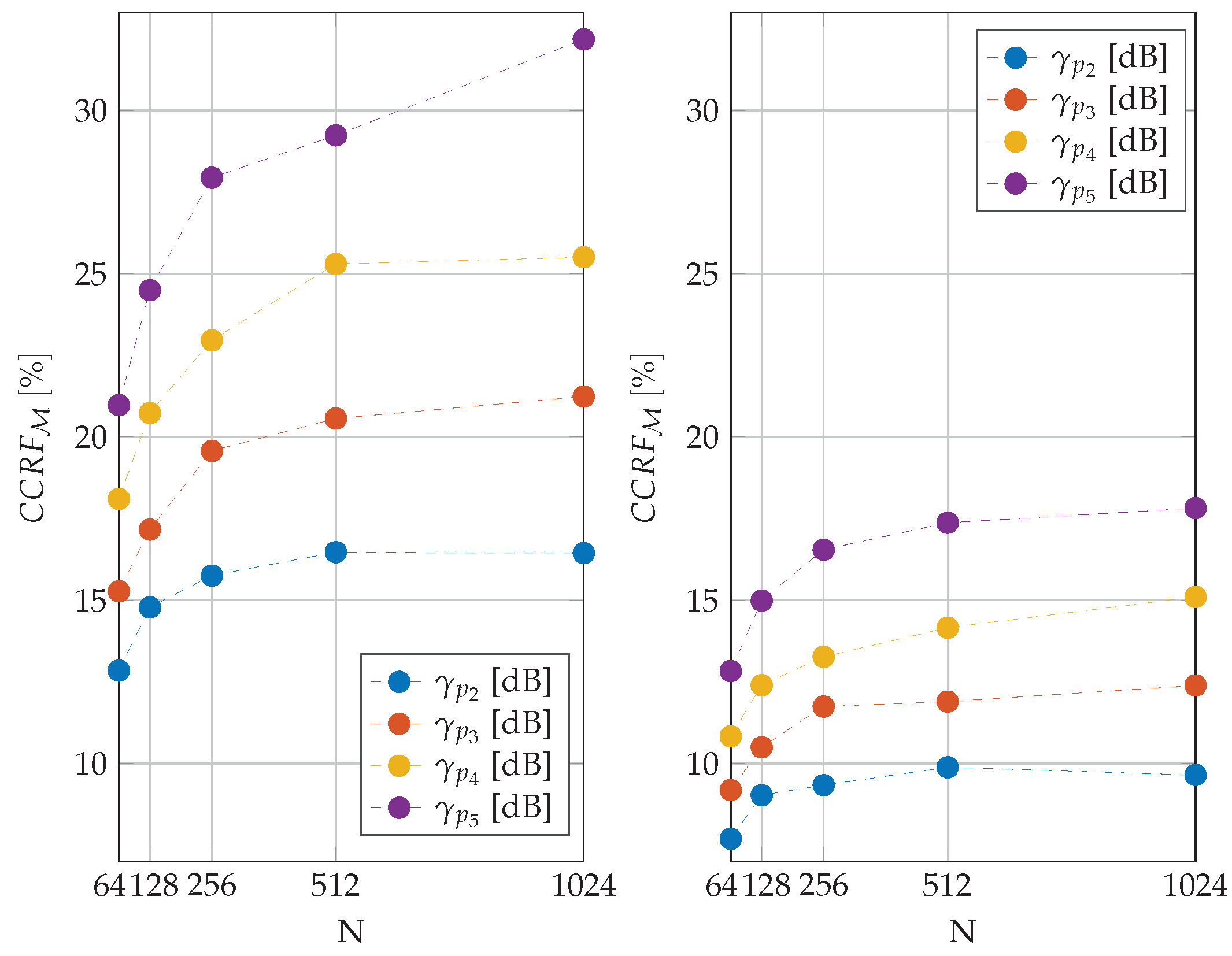
5.3. Discussion on Additional Possible Complexity Reduction
| Algorithm 4 Computational complexity reduction in the GreenOFDMv2 scheme. |
| Require: |
| ; |
| for do |
| for do |
| if then |
| ; |
| else |
| ; |
| end if |
| if then |
| ; |
| STOP(); |
| end if |
| end for |
| end for |
| SEND ; |
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CCDF | Complementary Cumulative Distribution Function |
| CCRF | Computational Complexity Reduction Factor |
| IAPR | Instantaneous-to-Average Power Ratio |
| IFFT | Inverse Fast Fourier Transform |
| OFDM | Orthogonal Frequency Division Multiplexing |
| PA | Power Amplifier |
| PAPR | Peak-to-Average Power Ratio |
| SLM | SeLected Mapping |
References
- Van Nee, R.; de Wild, A. Reducing the peak-to-average power ratio of OFDM. In Proceedings of the IEEE Vehicular Technology Conference (VTC’98), Ottawa, ON, Canada, 21 May 1998; pp. 2072–2076. [Google Scholar]
- Singh, S.; Kumar, M.S.; Mruthyunjaya, H.S. Effect of Peak-to-Average Power Ratio Reduction on the Multicarrier Communication System Performance Parameters. Int. J. Electr. Comput. Eng. 2009, 4, 779–786. [Google Scholar]
- Gustavsson, M.; Wikner, J.J.; Tan, N.N. CMOS Data Converters for Communications; Kluwer Academic Publishers: Norwell, MA, USA, 2000. [Google Scholar]
- Tellambura, C. Computation of the continuous-time PAR of an OFDM signal with BPSK subcarriers. IEEE Commun. Lett. 2001, 5, 185–187. [Google Scholar] [CrossRef]
- Mestdagh, D.J.G.; Spruyt, P.; Biran, B. Analysis of clipping effect in DMT-based ADSL systems. In Proceedings of the ICC/SUPERCOMM’94—1994 International Conference on Communications, New Orleans, LA, USA, 1–5 May 1994; Volume 1, pp. 293–300. [Google Scholar] [CrossRef]
- Jiang, T.; Wu, Y. An Overview: Peak-to-Average Power Ratio Reduction Techniques for OFDM Signals. IEEE Trans. Broadcast. 2008, 54, 257–268. [Google Scholar] [CrossRef]
- Rahmatallah, Y.; Mohan, S. Peak-To-Average Power Ratio Reduction in OFDM Systems: A Survey and Taxonomy. IEEE Commun. Surv. Tutor. 2013, 15, 1567–1592. [Google Scholar] [CrossRef]
- Sandoval, F.; Poitau, G.; Gagnon, F. Hybrid Peak-to-Average Power Ratio Reduction Techniques: Review and Performance Comparison. IEEE Access 2017, 5, 27145–27161. [Google Scholar] [CrossRef]
- Li, X.; Cimini, L.J. Effects of clipping and filtering on the performance of OFDM. In Proceedings of the IEEE 47th Vehicular Technology Conference. Technology in Motion, Phoenix, AZ, USA, 4–7 May 1997; Volume 3, pp. 1634–1638. [Google Scholar] [CrossRef]
- Armstrong, J. Peak-to-average power reduction for OFDM by repeated clipping and frequency domain filtering. Electron. Lett. 2002, 38, 246–247. [Google Scholar] [CrossRef]
- Huang, X.; Lu, J.; Zheng, J.; Letaief, K.B.; Gu, J. Companding transform for reduction in peak-to-average power ratio of OFDM signals. IEEE Trans. Wirel. Commun. 2004, 3, 2030–2039. [Google Scholar] [CrossRef]
- Mestdagh, D.J.G.; Spruyt, P.M.P. A Method to Reduce the Probability of Clipping in DMT-Based Transceivers. IEEE Trans. Commun. 1996, 44, 1234–1238. [Google Scholar] [CrossRef]
- Bauml, R.W.; Fischer, R.F.H.; Huber, J.B. Reducing the Peak-to-Average Power Ratio of Multicarrier Modulation by Selected Mapping. Electron. Lett. 1996, 32, 2056–2057. [Google Scholar] [CrossRef]
- Han, S.H.; Cioffi, J.M.; Lee, J.H. Tone injection with hexagonal constellation for peak-to-average power ratio reduction in OFDM. IEEE Commun. Lett. 2006, 10, 646–648. [Google Scholar] [CrossRef]
- Tellado, J.; Cioffi, J.M. Efficient algorithms for reducing PAR in multicarrier systems. In Proceedings of the 1998 IEEE International Symposium on Information Theory (Cat. No.98CH36252), Cambridge, MA, USA, 16–21 August 1998. [Google Scholar] [CrossRef]
- Wang, L.; Tellambura, C. Analysis of Clipping Noise and Tone-Reservation Algorithms for Peak Reduction in OFDM Systems. IEEE Trans. Veh. Technol. 2008, 57, 1675–1694. [Google Scholar] [CrossRef]
- Krongold, B.S.; Jones, D.L. PAR reduction in OFDM via active constellation extension. IEEE Trans. Broadcast. 2003, 49, 258–268. [Google Scholar] [CrossRef]
- Muller, S.H.; Huber, J.B. OFDM with reduced peak-to-average power ratio by optimum combination of partial transmit sequences. IET Electron. Lett. 1997, 33, 368–369. [Google Scholar] [CrossRef]
- Myung, H.G.; Lim, J.; Goodman, D.J. Peak-To-Average Power Ratio of Single Carrier FDMA Signals with Pulse Shaping. In Proceedings of the 2006 IEEE 17th International Symposium on Personal, Indoor and Mobile Radio Communications, Helsiniki, Finland, 11–14 September 2006; pp. 1–5. [Google Scholar]
- Wiegandt, D.A.; Nassar, C.R.; Wu, Z. Overcoming peak-to-average power ratio issues in OFDM via carrier-interferometry codes. In Proceedings of the IEEE 54th Vehicular Technology Conference, VTC Fall 2001, Proceedings (Cat. No.01CH37211), Atlantic City, NJ, USA, 7–11 October 2001; Volume 2, pp. 660–663. [Google Scholar]
- Anwar, K.; Saito, M.; Hara, T.; Okada, M.; Yamamoto, H. Simplified Realization of Pseudo-Orthogonal Carrier Interferometry OFDM by FFT Algorithm. In Multi-Carrier Spread-Spectrum; Khaled, F., Stefan, K., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 167–174. [Google Scholar]
- Mestdagh, D.J.G.; Monsalve, J.L.G.; Brossier, J.-M. GreenOFDM: A new selected mapping method for OFDM PAPR reduction. Electron. Lett. 2018, 54, 449–450. [Google Scholar] [CrossRef]
- Mestdagh, D.; Cambonie, J.; Lietar, L.; Gulfo, J. OFDM Transmission Systems with Reduced Peak-to-Average Power Ratio. Patent WO/2017/013467 (FR), 26 January 2017. [Google Scholar]
- Yu, D.; Wan, Y. A New Method for Reducing PAPR in OFDM System Based on GreenOFDM. In Proceedings of the 10th International Conference on Communications, Circuits and Systems (ICCCAS), Chengdu, China, 22–24 December 2018; pp. 227–231. [Google Scholar]
- Zhou, Z.; Wang, L.; Hu, C. Improved SLM Scheme for Reducing the PAPR of QAM OFDM Signals. In Proceedings of the 2019 IEEE 2nd International Conference on Electronics Technology (ICET), Chengdu, China, 10–13 May 2019; pp. 28–33. [Google Scholar]
- Taşpınar, N.; Şimşir, Ş. Dual symbol optimization-based partial transmit sequence technique for PAPR reduction in WOLA-OFDM waveform. Int. J. Commun. Syst. 2019, 32, e4081. [Google Scholar] [CrossRef]
- Şimşir, Ş.; Taşpınar, N. Cumulative symbol optimization–based partial transmit sequence technique for PAPR reduction in low complexity GFDM system. Trans. Emerg. Telecommun. Technol. 2020, 31, e3801. [Google Scholar] [CrossRef]
- Monsalve, J.L.G.; Mestdagh, D.J.G.; Brossier, J.-M. Computational complexity reduction of GreenOFDM. Ann. Telecommun. 2020. [Google Scholar] [CrossRef]
- Heo, S.; Noh, H.; No, J.; Shin, D. A Modified SLM Scheme With Low Complexity for PAPR Reduction of OFDM Systems. IEEE Trans. Broadcast. 2007, 53, 804–808. [Google Scholar] [CrossRef]
- Ochiai, H.; Imai, H. On the Distribution of the Peak-to-Average Power Ratio in OFDM Signals. IEEE Trans. Commun. 2001, 49, 282–289. [Google Scholar] [CrossRef]
- Monsalve, J.L.G. GreenOFDM a New Method for OFDM PAPR Reduction. Ph.D. Thesis, Communauté Université Grenoble Alpes, Grenoble, France, October 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulfo Monsalve, J.L.; Ros, L.; Brossier, J.-M.; Mestdagh, D. An Improved GreenOFDM Scheme for PAPR Reduction. Telecom 2020, 1, 196-210. https://doi.org/10.3390/telecom1030014
Gulfo Monsalve JL, Ros L, Brossier J-M, Mestdagh D. An Improved GreenOFDM Scheme for PAPR Reduction. Telecom. 2020; 1(3):196-210. https://doi.org/10.3390/telecom1030014
Chicago/Turabian StyleGulfo Monsalve, Jorge Luis, Laurent Ros, Jean-Marc Brossier, and Denis Mestdagh. 2020. "An Improved GreenOFDM Scheme for PAPR Reduction" Telecom 1, no. 3: 196-210. https://doi.org/10.3390/telecom1030014
APA StyleGulfo Monsalve, J. L., Ros, L., Brossier, J.-M., & Mestdagh, D. (2020). An Improved GreenOFDM Scheme for PAPR Reduction. Telecom, 1(3), 196-210. https://doi.org/10.3390/telecom1030014