Thermo-Kinetic Assessment of Ammonia/Syngas Combustion: Experimental and Numerical Investigation of Laminar Burning Velocity at Elevated Pressure and Temperature
Abstract
1. Introduction
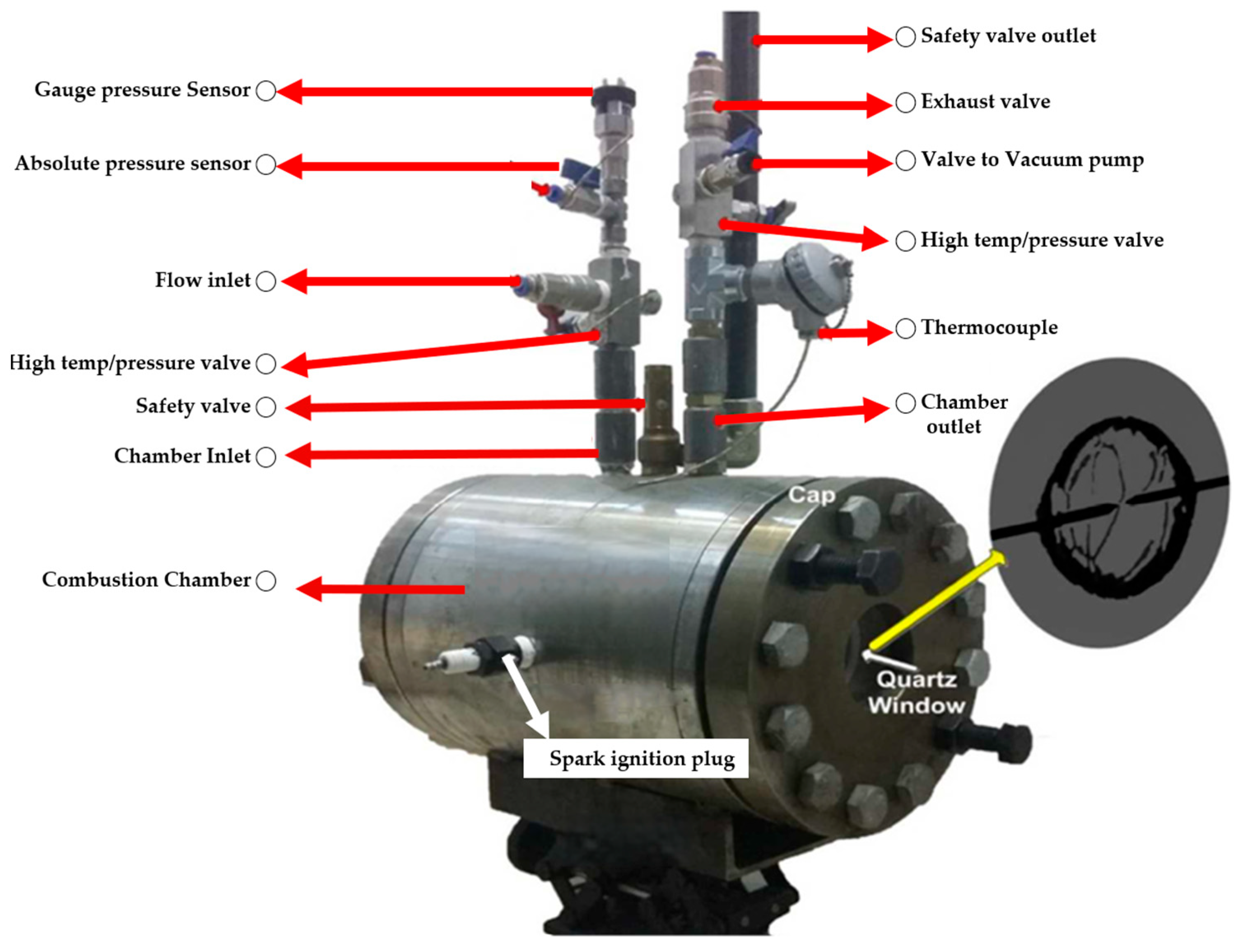
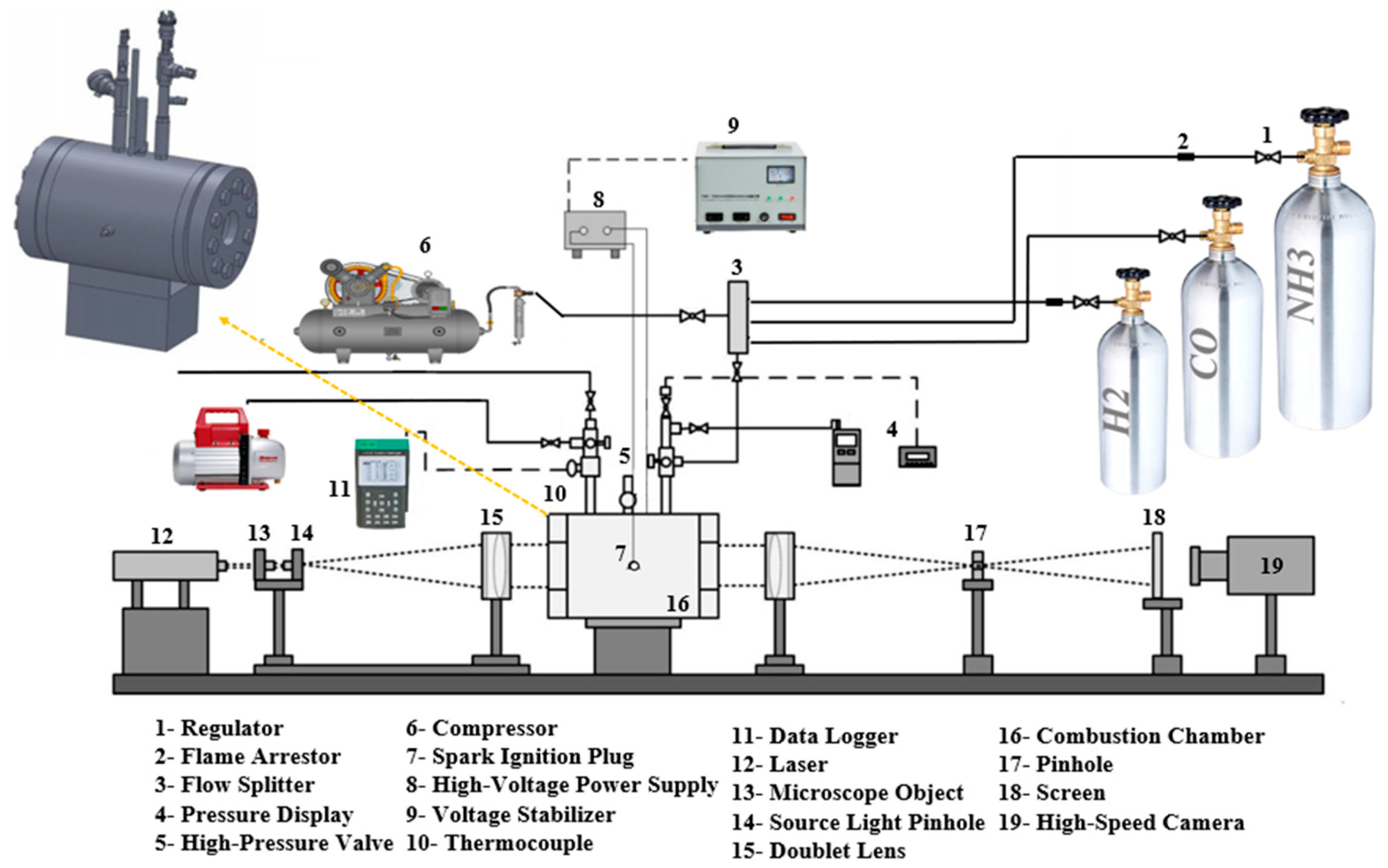
2. Experimental Setup
2.1. Experimental Facilities and Procedure
2.2. Interferometry Technique
2.2.1. The Schlieren System
2.2.2. Using the Mach–Zehnder Interferometry Technique to Measure the Flame Temperature
2.3. Determination of Laminar Burning Velocity
2.4. Uncertainty
3. Simulation
4. Results and Discussion
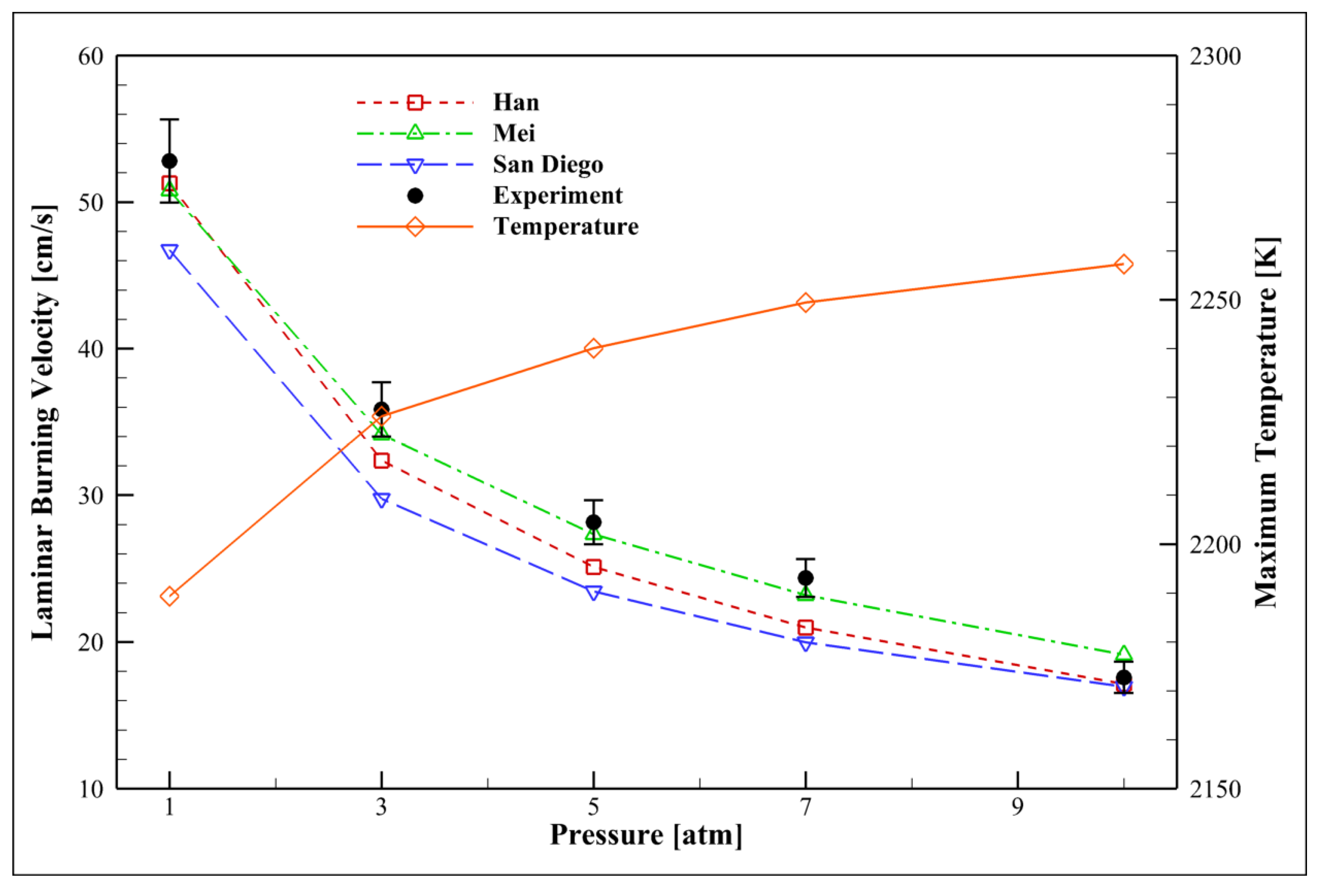
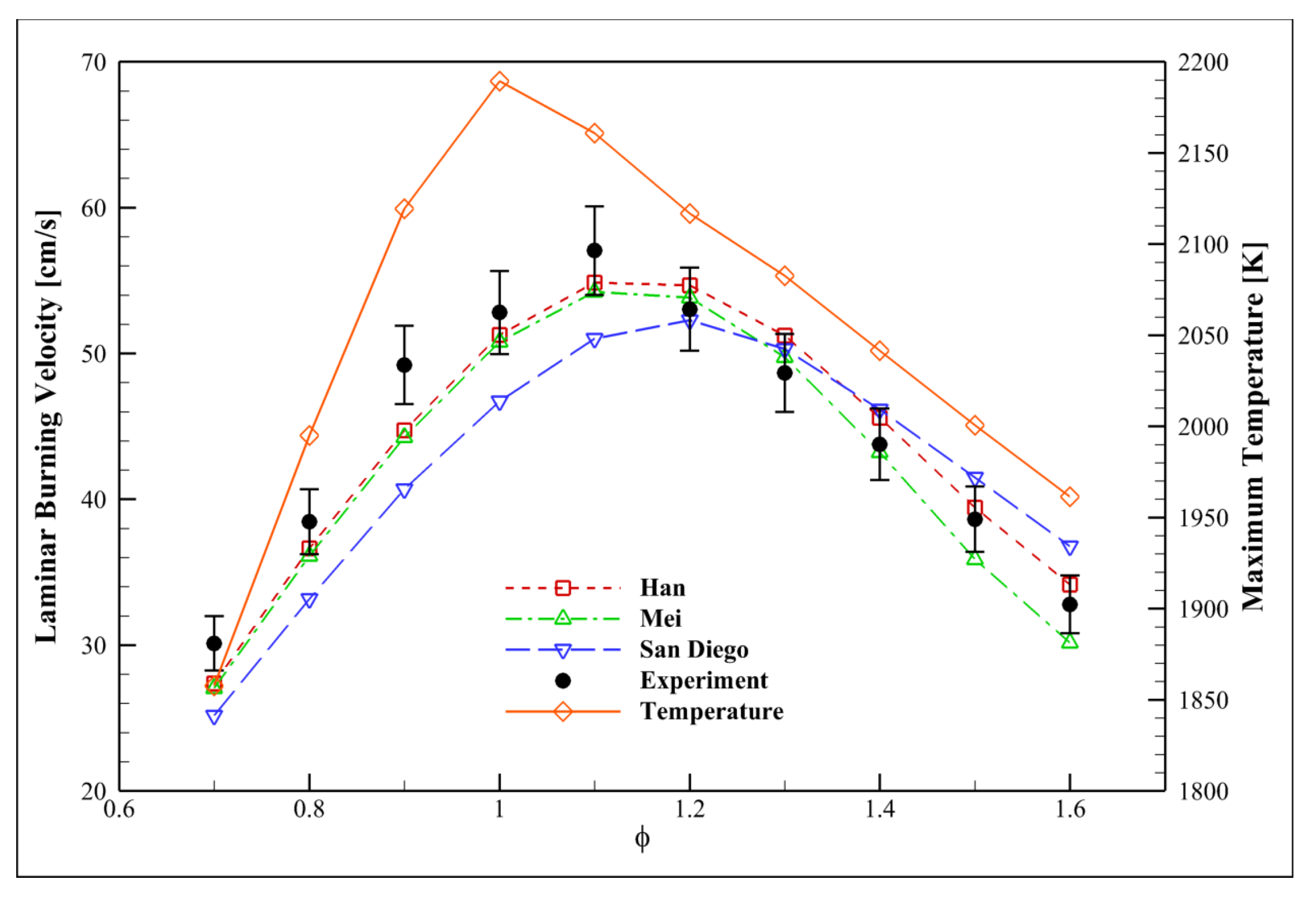
4.1. Validation
4.2. Markstein Length
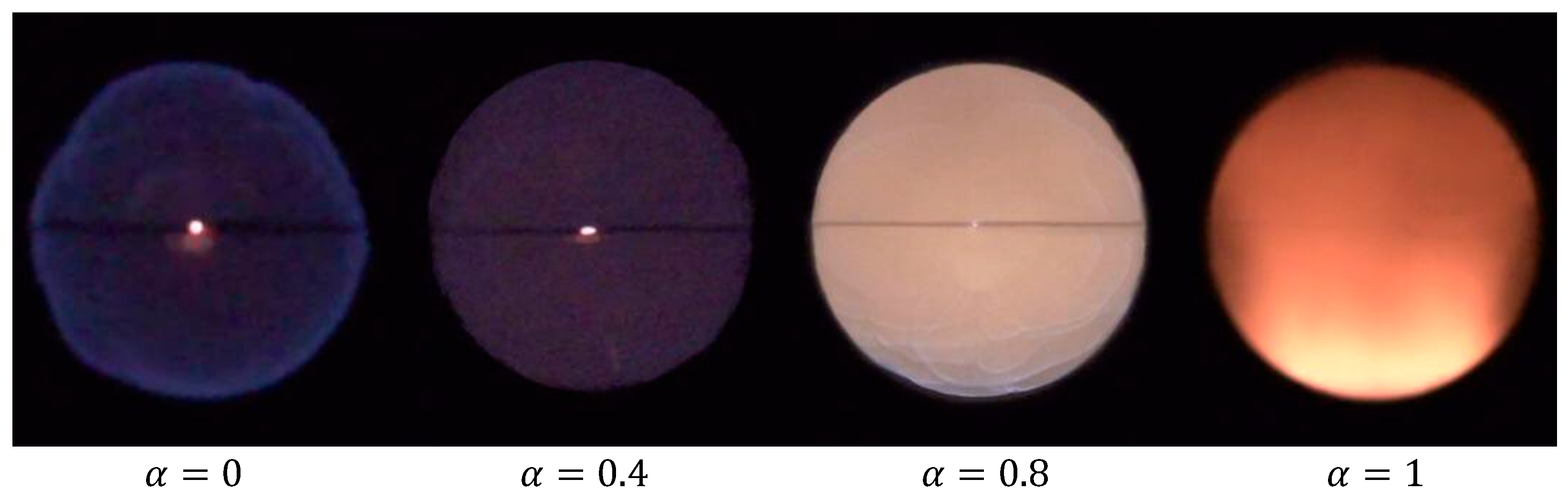
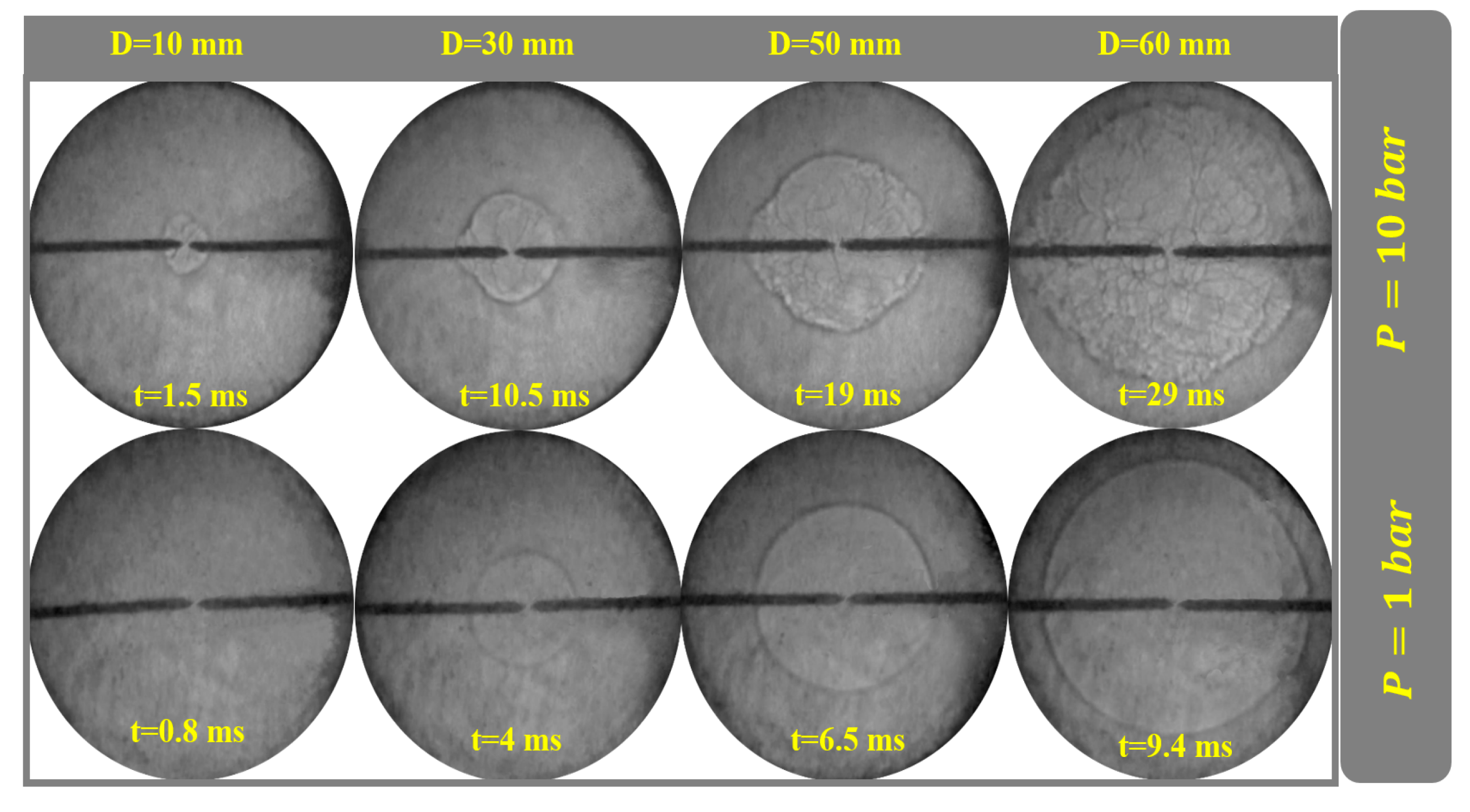
4.3. Flame Observation of Syngas/Ammonia/Air
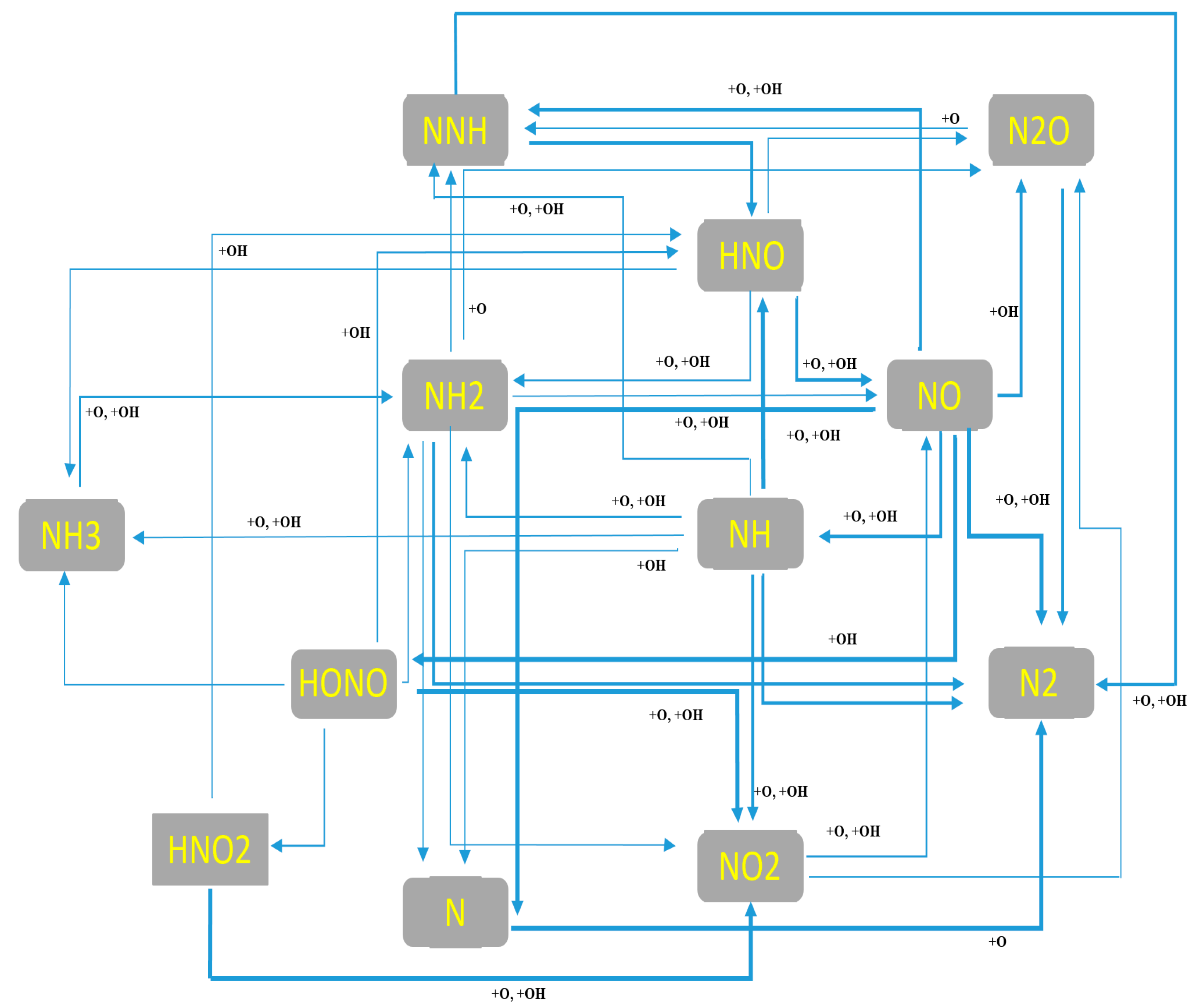
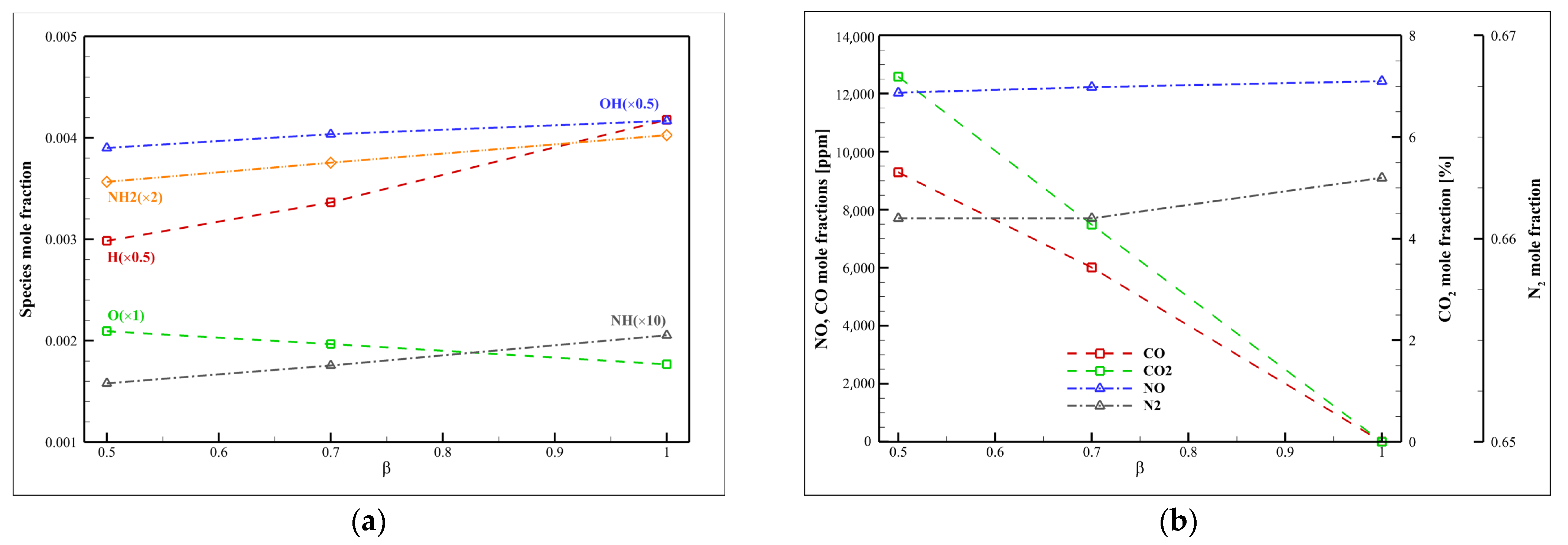
4.4. Kinetic Analysis of Syngas/Ammonia/Air
4.5. Flame Propagation at Different Conditions
4.6. Examining the Pressure Effect
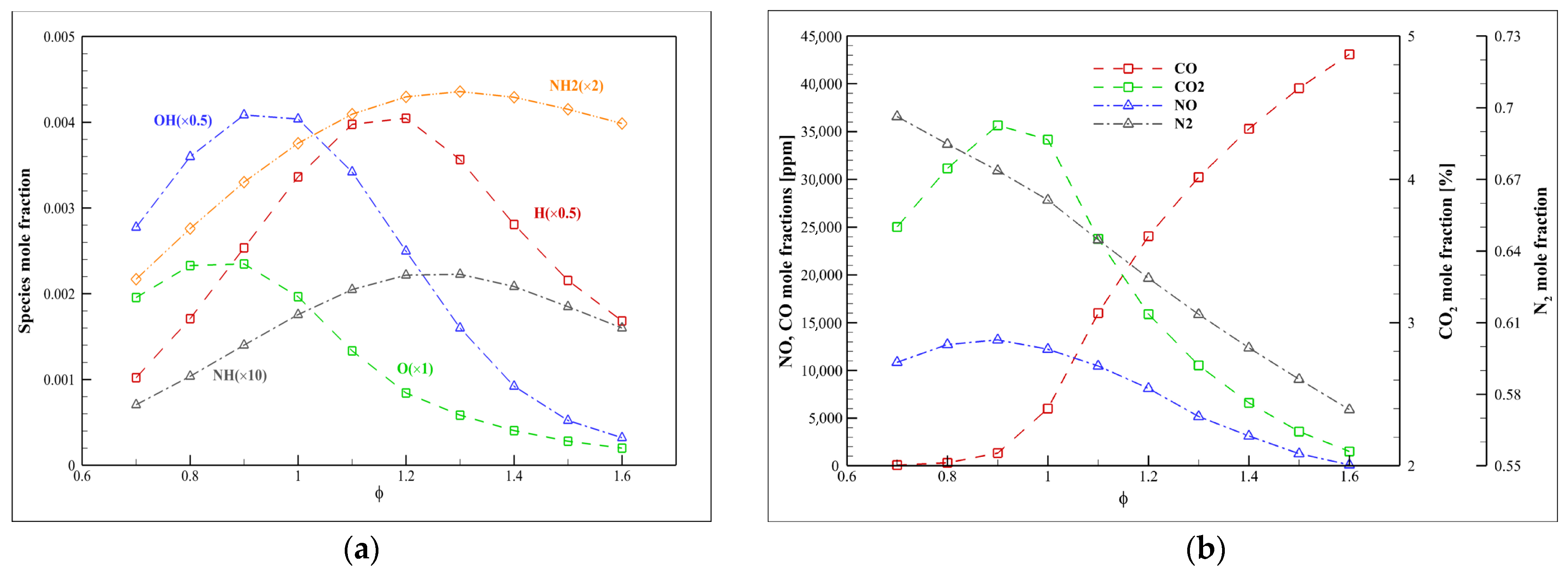
4.7. Examining the Equivalence Ratio
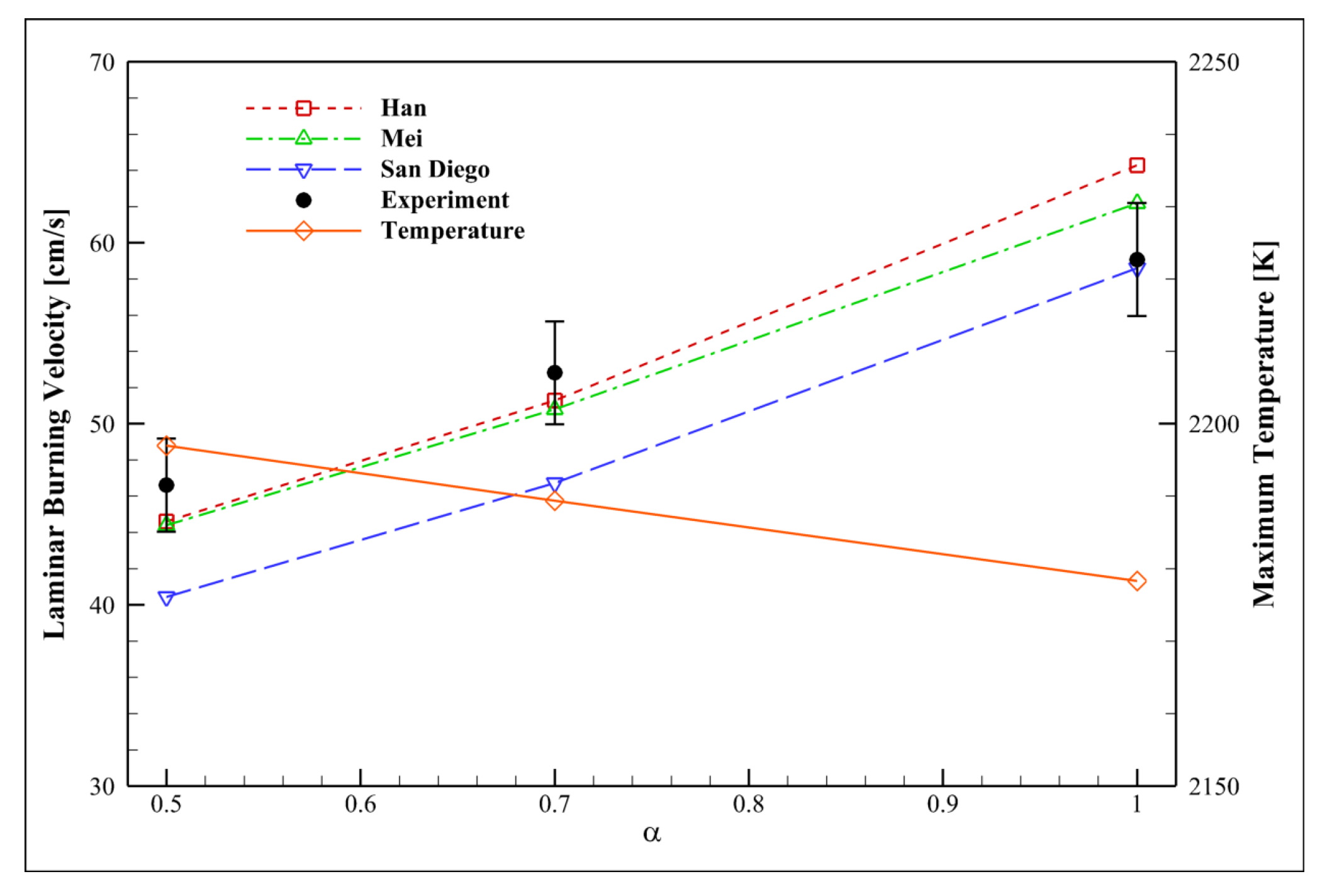
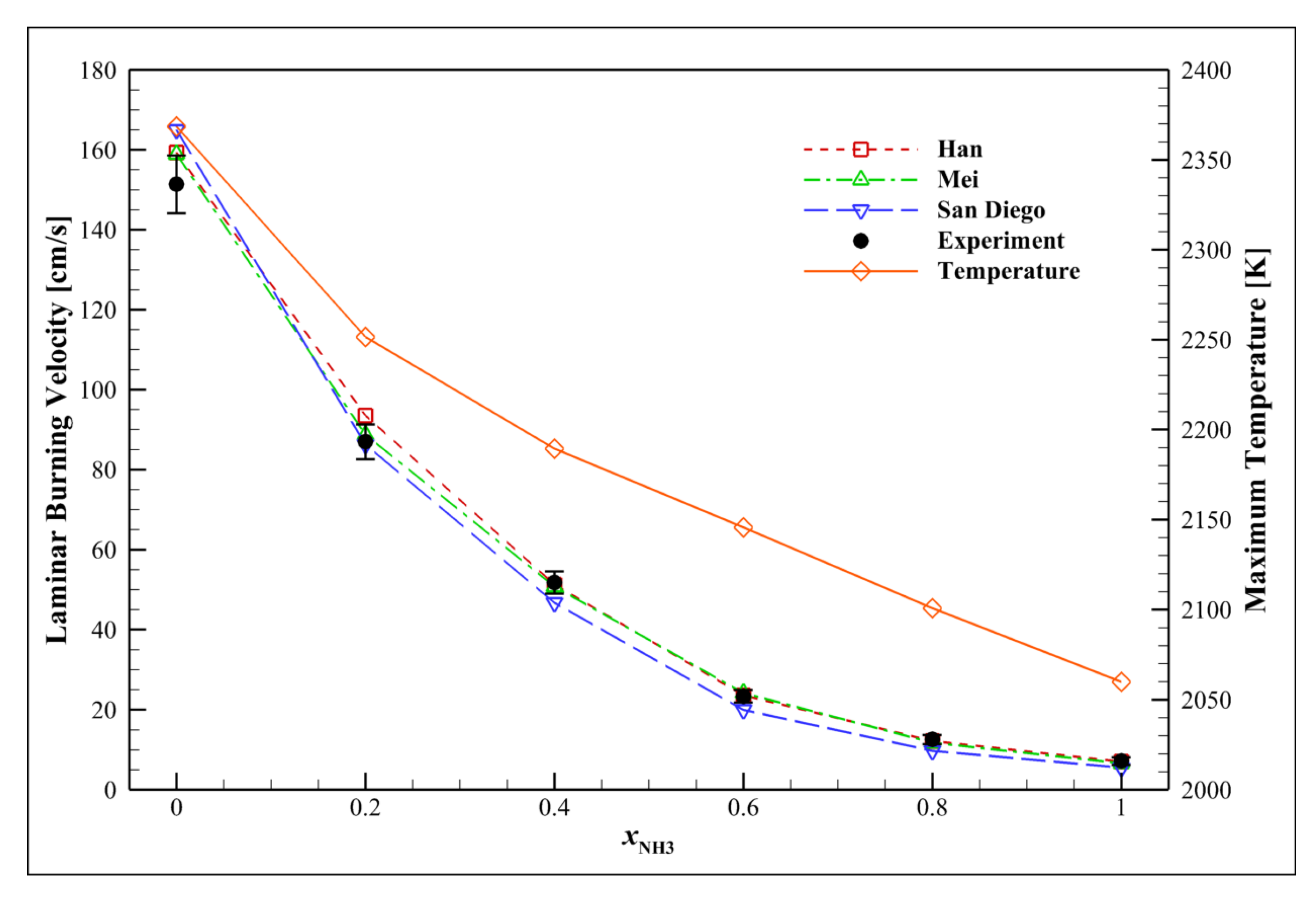
4.8. Examining the Fuel Composition Effect
4.9. Syngas
4.10. Ammonia
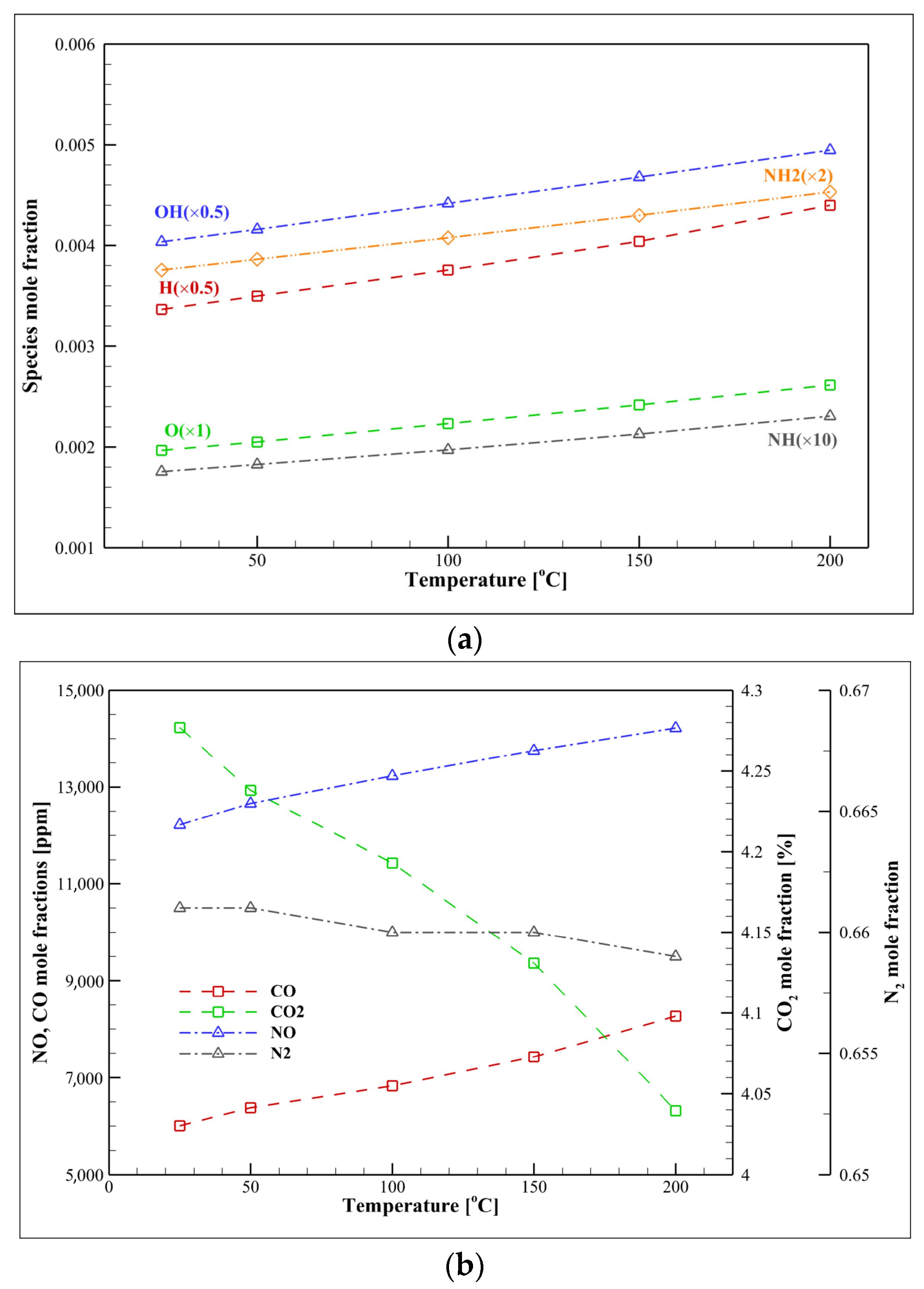
4.11. Examining the Initial Temperature Effect
5. Conclusions
- (a)
- LBV generally decreases with increasing pressure (falling below 10 cm/s at 10 atm) due to enhanced molecular interactions and reduced radical concentrations.
- (b)
- Increasing the pressure shifts the equilibrium point and consequently increases the adiabatic flame temperature (e.g., from ~1900 K at 1 atm to over 2100 K at 10 atm).
- (c)
- According to Le Chatelier’s principle, increasing pressure decreases the mole number of radicals. Thus, pressure variation has an inverse effect on NO formation.
- (d)
- LBV increases from ~65 cm/s at 300 K to ~125 cm/s at 473 K. However, higher initial temperatures () reduce the dependence of the flame on the temperature.
- (e)
- The chemical effect (especially H2) is more dominant than the thermal effect. Increasing the mole fraction of specific gases in syngas (such as H2 and CO) can reduce the thermal impact and the NH3/syngas/air flame temperature dependence.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LBV | Laminar burning velocity |
| Flame speed | |
| Tot | Total |
| Initial temperature | |
| Initial pressure | |
| Stretched flame propagation speed | |
| Flame front radius | |
| Stretched laminar flame speed | |
| t | Time |
| A | Flame front’s surface area |
| P | Pressure [bar] |
| R | radius |
| Markstein length | |
| Unstretched laminar flame speed | |
| Instrument error | |
| First-order uncertainty | |
| Total uncertainty | |
| Pressure of unburned gas | |
| Temperature of unburned gas | |
| D | Mass diffusivity |
| Thermal diffusivity | |
| Specific heat capacity | |
| k | thermal conductivity |
| Temperature coefficient reflecting the temperature dependence | |
| φ | Equivalence ratio |
| λ | Wavelength of the laser beam [m] |
| ρ | Density [kg/m3] |
| Expansion ratio of the gas | |
| Density of the unburned gas | |
| Density of the burned gas | |
| Spherical flame’s stretch rate | |
| i | Mixture component comprising syngas fuel and air |
Appendix A



References
- Al-Dawody, M.F.; Al-Obaidi, W.; Aboud, E.D.; Abdulwahid, M.A.; Al-Farhany, K.; Jamshed, W.; Eid, M.R.; Raizah, Z.; Iqbal, A. Mechanical engineering advantages of a dual fuel diesel engine powered by diesel and aqueous ammonia blends. Fuel 2023, 346, 128398. [Google Scholar] [CrossRef]
- Herbinet, O.; Bartocci, P.; Dana, A.G. On the use of ammonia as a fuel–A perspective. Fuel Commun. 2022, 11, 100064. [Google Scholar] [CrossRef]
- Alvarez, L.F.; Shaffer, J.; Dumitrescu, C.E.; Askari, O. Laminar burning velocity of Ammonia/Air mixtures at high pressures. Fuel 2024, 363, 130986. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Yu, B.; Li, X.; Zhang, L.; Zhao, Y.; Sun, S. Experimental and kinetic modeling study on laminar flame speeds and emission characteristics of oxy-ammonia premixed flames. Int. J. Hydrogen Energy 2024, 63, 857–870. [Google Scholar] [CrossRef]
- Eckart, S.; Zsély, I.G.; Krause, H.; Turányi, T. Effect of the variation of oxygen concentration on the laminar burning velocities of hydrogen-enriched methane flames. Int. J. Hydrogen Energy 2024, 49, 533–546. [Google Scholar] [CrossRef]
- Hayakawa, A.; Goto, T.; Mimoto, R.; Arakawa, Y.; Kudo, T.; Kobayashi, H. Laminar burning velocity and Markstein length of ammonia/air premixed flames at various pressures. Fuel 2015, 159, 98–106. [Google Scholar] [CrossRef]
- Mei, B.; Zhang, X.; Ma, S.; Cui, M.; Guo, H.; Cao, Z.; Li, Y. Experimental and kinetic modeling investigation on the laminar flame propagation of ammonia under oxygen enrichment and elevated pressure conditions. Combust. Flame 2019, 210, 236–246. [Google Scholar] [CrossRef]
- Han, X.; Wang, Z.; Costa, M.; Sun, Z.; He, Y.; Cen, K. Experimental and kinetic modeling study of laminar burning velocities of NH3/air, NH3/H2/air, NH3/CO/air and NH3/CH4/air premixed flames. Combust. Flame 2019, 206, 214–226. [Google Scholar] [CrossRef]
- Okafor, E.C.; Naito, Y.; Colson, S.; Ichikawa, A.; Kudo, T.; Hayakawa, A.; Kobayashi, H. Experimental and numerical study of the laminar burning velocity of CH4–NH3–air premixed flames. Combust. Flame 2018, 187, 185–198. [Google Scholar] [CrossRef]
- Okafor, E.C.; Naito, Y.; Colson, S.; Ichikawa, A.; Kudo, T.; Hayakawa, A.; Kobayashi, H. Measurement and modelling of the laminar burning velocity of methane-ammonia-air flames at high pressures using a reduced reaction mechanism. Combust. Flame 2019, 204, 162–175. [Google Scholar] [CrossRef]
- Shu, T.; Xue, Y.; Zhou, Z.; Ren, Z. An experimental study of laminar ammonia/methane/air premixed flames using expanding spherical flames. Fuel 2021, 290, 120003. [Google Scholar] [CrossRef]
- da Rocha, R.C.; Costa, M.; Bai, X.-S. Chemical kinetic modelling of ammonia/hydrogen/air ignition, premixed flame propagation and NO emission. Fuel 2019, 246, 24–33. [Google Scholar] [CrossRef]
- Kiani, M.; Houshfar, E.; Ashjaee, M. An experimental and numerical study on the combustion and flame characteristics of hydrogen in intersecting slot burners. Int. J. Hydrogen Energy 2018, 43, 3034–3049. [Google Scholar] [CrossRef]
- Kiani, M.; Houshfar, E.; Asli, A.E.N.; Ashjaee, M. Combustion of syngas in intersecting burners using the interferometry method. Energy Fuels 2017, 31, 10121–10132. [Google Scholar] [CrossRef]
- Lieuwen, T.; Yang, V.; Yetter, R. Yetter, Synthesis Gas Combustion: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Han, X.; Wang, Z.; He, Y.; Zhu, Y.; Cen, K. Experimental and kinetic modeling study of laminar burning velocities of NH3/syngas/air premixed flames. Combust. Flame 2020, 213, 1–13. [Google Scholar] [CrossRef]
- Mei, B.; Ma, S.; Zhang, Y.; Zhang, X.; Li, W.; Li, Y. Exploration on laminar flame propagation of ammonia and syngas mixtures up to 10 atm. Combust. Flame 2020, 220, 368–377. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Kobayashi, N.; He, Z.; Osaka, Y.; Zeng, T. Research on combustion and emission characteristics of ammonia under preheating conditions. J. Chem. Eng. Jpn. 2016, 49, 641–648. [Google Scholar] [CrossRef]
- Wang, N.; Li, T.; Guo, X.; Wu, Z.; Huang, S.; Zhou, X.; Li, S.; Chen, R. Laminar burning characteristics of ammonia and hydrogen blends at elevated initial pressures up to 2.5 MPa. Chem. Eng. J. 2024, 500, 157283. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Deng, L.; He, Z.; Osaka, Y.; Kobayashi, N. Effect of hydrogen addition on combustion and heat release characteristics of ammonia flame. Energy 2019, 175, 604–617. [Google Scholar] [CrossRef]
- Kumar, L.; Sleiti, A.K. Systematic review on ammonia as a sustainable fuel for combustion. Renew. Sustain. Energy Rev. 2024, 202, 114699. [Google Scholar] [CrossRef]
- Hinton, N.; Stone, R. Laminar burning velocity measurements of methane and carbon dioxide mixtures (biogas) over wide ranging temperatures and pressures. Fuel 2014, 116, 743–750. [Google Scholar] [CrossRef]
- Askari, M.H.; Ashjaee, M. Experimental measurement of laminar burning velocity and flammability limits of landfill gas at atmospheric and elevated pressures. Energy Fuels 2017, 31, 3196–3205. [Google Scholar] [CrossRef]
- Hauf, W.; Grigull, U. Optical Methods in Heat Transfer. Adv. Heat Transf. 1970, 6, 133–136. [Google Scholar] [CrossRef]
- Flack, R.D. Mach-Zehnder interferometer errors resulting from test section misalignment. Appl. Opt. 1978, 17, 985–987. [Google Scholar] [CrossRef]
- Bardolf, R.; Winter, F. Comparison of chemical kinetic mechanisms for combustion simulation of treated biogas. Holist. Approach Environ. 2014, 4, 65–69. [Google Scholar]
- Dowdy, D.R.; Smith, D.B.; Taylor, S.C.; Williams, A. The use of expanding spherical flames to determine burning velocities and stretch effects in hydrogen/air mixtures. Symp. (Int.) Combust. 1991, 23, 325–332. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. On a distorted flame front as a hydrodynamic discontinuity. Acta Astronaut. 1976, 3, 889–918. [Google Scholar] [CrossRef]
- Matalon, M.; Matkowsky, B.J. Flames as gasdynamic discontinuities. J. Fluid. Mech. 1982, 124, 239–259. [Google Scholar] [CrossRef]
- Clavin, P. Dynamic behavior of premixed flame fronts in laminar and turbulent flows. Proc. Combust. Inst. 1985, 11, 1–59. [Google Scholar] [CrossRef]
- Kelley, A.P.; Law, C.K. Nonlinear effects in the extraction of laminar flame speeds from expanding spherical flames. Combust. Flame 2009, 156, 1844–1851. [Google Scholar] [CrossRef]
- Annamalai, K.; Ryan, W. Interactive processes in gasification and combustion. Part I: Liquid drop arrays and clouds. Proc. Combust. Inst. 1992, 18, 221–295. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, W.; Tan, H.; An, Q.; Wang, J.; Dai, H.; Wang, X.; Wang, X.; Deng, S. Experimental and kinetic modeling study on NH3/syngas/air and NH3/bio-syngas/air premixed laminar flames at elevated temperature. Combust. Flame 2021, 233, 111594. [Google Scholar] [CrossRef]
- Kiani, M.; Kohansal, M.; Masoumi, S.; Ashjaee, M.; Houshfar, E. An experimental investigation on non-preheated MILD combustion of syngas/ammonia/air. J. Therm. Anal. Calorim. 2023, 148, 11783–11797. [Google Scholar] [CrossRef]
- Kiani, M.; Kohansal, M.; Masoumi, S.; Afzalnia, A.; Inanlu, M.J.; Ashjaee, M.; Houshfar, E. An experimental investigation of ammonia/landfill/air mixtures’ pollutant emissions and temperature distribution under non-preheated moderate or intense low-oxygen dilution combustion. Environ. Sci. Pollut. Res. 2023, 30, 38333–38348. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tamura, T.; Maruta, K.; Niioka, T.; Williams, F.A. Burning velocity of turbulent premixed flames in a high-pressure environment. Symp. (Int.) Combust. 1996, 26, 389–396. [Google Scholar] [CrossRef]
- Qiao, L.; Dahm, W.; Faeth, G.; Oran, E. Burning velocities and flammability limits of premixed methane/air/diluent flames in microgravity. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 959. [Google Scholar]
- Vu, T.M.; Song, W.S.; Park, J.; Bae, D.S.; You, H.S. Measurements of propagation speeds and flame instabilities in biomass derived gas–air premixed flames. Int. J. Hydrogen Energy 2011, 36, 12058–12067. [Google Scholar] [CrossRef]
- Hayakawa, A.; Goto, T.; Mimoto, R.; Kudo, T.; Kobayashi, H. NO formation/reduction mechanisms of ammonia/air premixed flames at various equivalence ratios and pressures. Mech. Eng. J. 2015, 2, 14-00402. [Google Scholar] [CrossRef]
- Pearse, R.W.B.; Gaydon, A.G. The Identification of Molecular Spectra; Chapman and Hall: London, UK, 1976. [Google Scholar]
- Mendiara, T.; Glarborg, P. Ammonia chemistry in oxy-fuel combustion of methane. Combust. Flame 2009, 156, 1937–1949. [Google Scholar] [CrossRef]
- Mikulčić, H.; Baleta, J.; Wang, X.; Wang, J.; Qi, F.; Wang, F. Numerical simulation of ammonia/methane/air combustion using reduced chemical kinetics models. Int. J. Hydrogen Energy 2021, 46, 23548–23563. [Google Scholar] [CrossRef]
- Xiao, H.; Valera-Medina, A.; Marsh, R.; Bowen, P.J. Numerical study assessing various ammonia/methane reaction models for use under gas turbine conditions. Fuel 2017, 196, 344–351. [Google Scholar] [CrossRef]
- Sabia, P.; Sorrentino, G.; Chinnici, A.; Cavaliere, A.; Ragucci, R. Dynamic behaviors in methane MILD and oxy-fuel combustion. Chemical effect of CO2. Energy Fuels 2015, 29, 1978–1986. [Google Scholar] [CrossRef]
- Yossefi, D.; Ashcroft, S.; Hacohen, J.; Belmont, M.; Thorpe, I. Combustion of methane and ethane with CO2 replacing N2 as a diluent. Modelling of combined effects of detailed chemical kinetics and thermal properties on the early stages of combustion. Fuel 1995, 74, 1061–1071. [Google Scholar] [CrossRef]
- Iliuta, I.; Tahoces, R.; Patience, G.S.; Rifflart, S.; Luck, F. Chemical-looping combustion process: Kinetics and mathematical modeling. AICHE J. 2010, 56, 1063–1079. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Goswami, M.; Derks, S.C.R.; Coumans, K.; Slikker, W.J.; de Andrade Oliveira, M.H.; Bastiaans, R.J.M.; Luijten, C.C.M.; de Goey, L.P.H.; Konnov, A.A. The effect of elevated pressures on the laminar burning velocity of methane+ air mixtures. Combust. Flame 2013, 160, 1627–1635. [Google Scholar] [CrossRef]
- Varea, E.; Modica, V.; Renou, B.; Boukhalfa, A.M. Pressure effects on laminar burning velocities and Markstein lengths for isooctane–ethanol–air mixtures. Proc. Combust. Inst. 2013, 34, 735–744. [Google Scholar] [CrossRef]
- Loo, C.E.; Tame, N.; Penny, G.C. Effect of Iron Ores and Sintering Conditions on Flame Front Properties. ISIJ Int. 2012, 52, 967–976. [Google Scholar] [CrossRef]
- Bellamy, D.J.; Clarke, P.H. Application of the Second Law of Thermodynamics and Le Chatelier’s Principle to the Developing Ecosystem. Nature 1968, 218, 1180. [Google Scholar] [CrossRef]
- Ronney, P.D.; Wachman, H.Y. Effect of gravity on laminar premixed gas combustion I: Flammability limits and burning velocities. Combust. Flame 1985, 62, 107–119. [Google Scholar] [CrossRef]
- Lhuillier, C.; Brequigny, P.; Lamoureux, N.; Contino, F.; Mounaïm-Rousselle, C. Experimental investigation on laminar burning velocities of ammonia/hydrogen/air mixtures at elevated temperatures. Fuel 2020, 263, 116653. [Google Scholar] [CrossRef]
- Skreiberg, Ø.; Kilpinen, P.; Glarborg, P. Ammonia chemistry below 1400 K under fuel-rich conditions in a flow reactor. Combust. Flame 2004, 136, 501–518. [Google Scholar] [CrossRef]
- Han, X.; Wang, Z.; He, Y.; Liu, Y.; Zhu, Y.; Konnov, A.A. The temperature dependence of the laminar burning velocity and superadiabatic flame temperature phenomenon for NH3/air flames. Combust. Flame 2020, 217, 314–320. [Google Scholar] [CrossRef]
- Tamadonfar, P.; Karimkashi, S.; Zirwes, T.; Vuorinen, V.; Kaario, O. A numerical study on premixed laminar ammonia/air flames enriched with hydrogen: An analysis on flame–wall interaction. Combust. Flame 2024, 265, 113444. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Z.; Yang, S.; Yu, F.; Belal, B.Y.; Li, G. Experimental and chemical kinetic study for the combustion of ammonia-hydrogen mixtures. Fuel 2024, 371, 131850. [Google Scholar] [CrossRef]


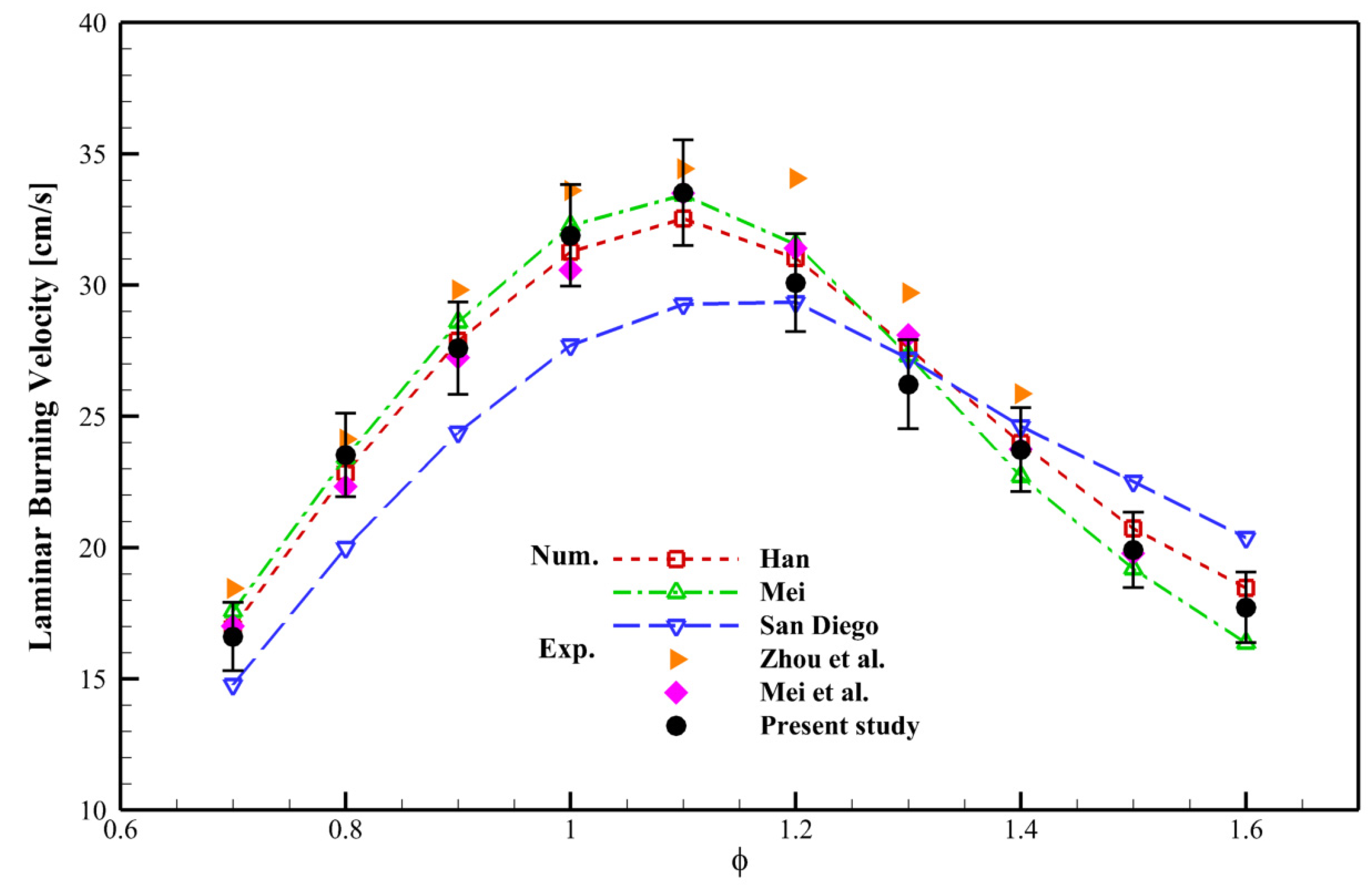



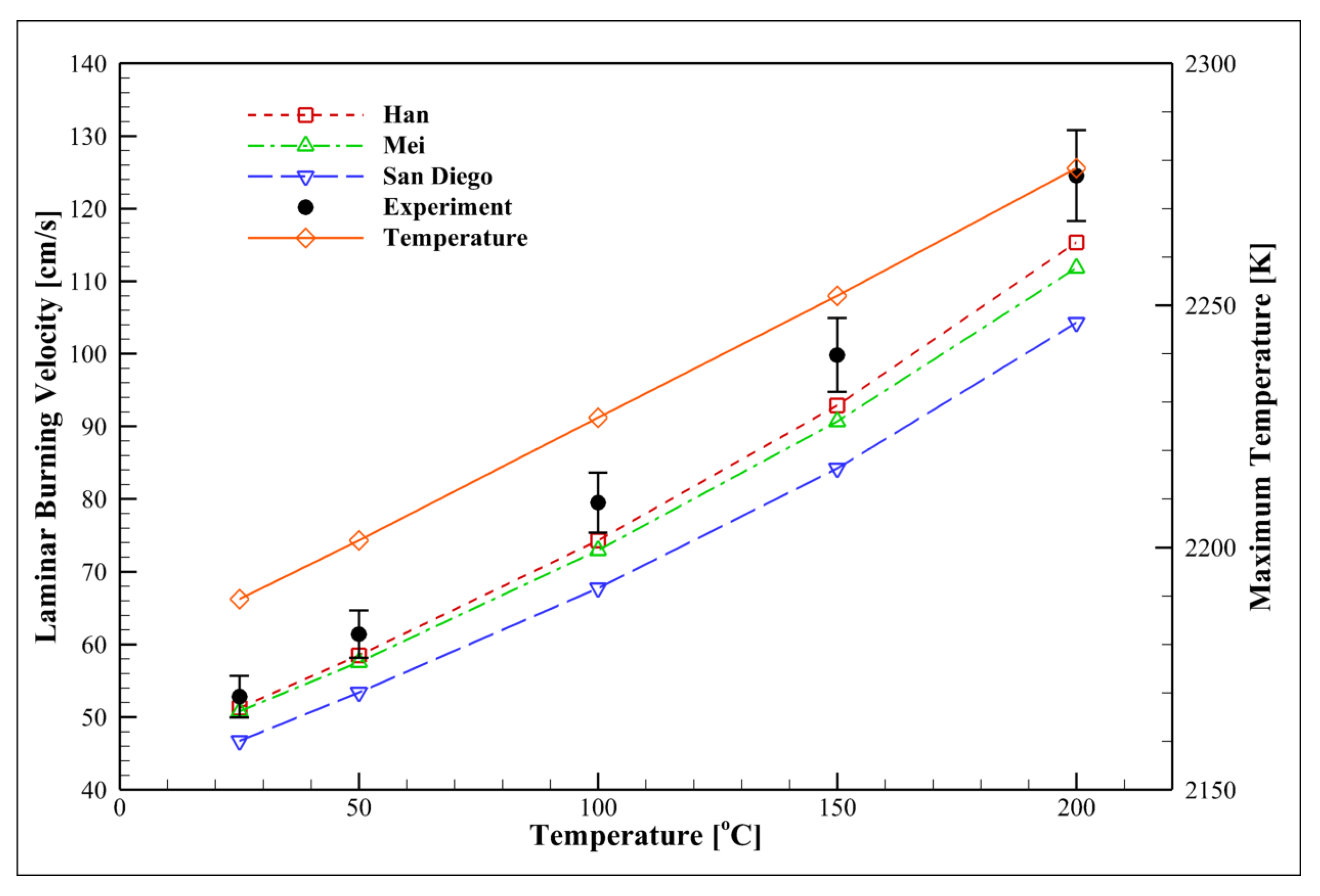
| Mechanism | Key Features | Applicability | Limitations |
|---|---|---|---|
| Mei [17] | Optimized for NH3/syngas at high pressures (up to 10 bar) | High-pressure NH3/syngas/air flames | Limited validation at T > 473 K |
| San Diego [26] | Includes detailed nitrogen chemistry | Broad range of fuels, including NH3 | Higher computational cost; less accurate for NH3/syngas LBV |
| Han [8] | Tailored for NH3/H2/CO/air mixtures | Accurate for NH3/syngas at 1–5 bar | Fewer species, potentially missing minor pathways |
| CASE | Syngas Composition | [atm] | [K] | ||
|---|---|---|---|---|---|
| 1 (base case) | 1.0 | SYN70 | 0.4 | 1 | 300 |
| 2 | 0.7:0.1:1.6 | SYN70 | 0.4 | 1 | 300 |
| 3 | 1.0 | SYN100, SYN80, SYN70, SYN50 | 0.4 | 1 | 300 |
| 4 | 1.0 | SYN70 | 0.0:0.2:1.0 | 1 | 300 |
| 5 | 1.0 | SYN70 | 0.4 | 1, 3, 5, 7, 10 | 300 |
| 6 | 1.0 | SYN70 | 0.4 | 1 | 300, 323, 373, 423, 473 |
| [K] | p [bar] | Markstein Length | |||
|---|---|---|---|---|---|
| 0.7 | 0.4 | 0.7 | 300 | 1 | −1.513 |
| 1 | 0.4 | 0.7 | 300 | 1 | −0.319 |
| 1.6 | 0.4 | 0.7 | 300 | 1 | 1.902 |
| 1 | 0.4 | 0.7 | 300 | 10 | −0.423 |
| 1 | 0.4 | 0.7 | 473 | 1 | −0.119 |
| 1 | 0 | 0.7 | 300 | 1 | 1.573 |
| 1 | 1 | 0.7 | 300 | 1 | 0.028 |
| 1 | 0.4 | 0.5 | 300 | 1 | −0.2 |
| 1 | 0.4 | 1 | 300 | 1 | −0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiani, M.; Abbasian Arani, A.A.; Houshfar, E.; Ashjaee, M.; H. Niknam, P. Thermo-Kinetic Assessment of Ammonia/Syngas Combustion: Experimental and Numerical Investigation of Laminar Burning Velocity at Elevated Pressure and Temperature. Fuels 2025, 6, 59. https://doi.org/10.3390/fuels6030059
Kiani M, Abbasian Arani AA, Houshfar E, Ashjaee M, H. Niknam P. Thermo-Kinetic Assessment of Ammonia/Syngas Combustion: Experimental and Numerical Investigation of Laminar Burning Velocity at Elevated Pressure and Temperature. Fuels. 2025; 6(3):59. https://doi.org/10.3390/fuels6030059
Chicago/Turabian StyleKiani, Mehrdad, Ali Akbar Abbasian Arani, Ehsan Houshfar, Mehdi Ashjaee, and Pouriya H. Niknam. 2025. "Thermo-Kinetic Assessment of Ammonia/Syngas Combustion: Experimental and Numerical Investigation of Laminar Burning Velocity at Elevated Pressure and Temperature" Fuels 6, no. 3: 59. https://doi.org/10.3390/fuels6030059
APA StyleKiani, M., Abbasian Arani, A. A., Houshfar, E., Ashjaee, M., & H. Niknam, P. (2025). Thermo-Kinetic Assessment of Ammonia/Syngas Combustion: Experimental and Numerical Investigation of Laminar Burning Velocity at Elevated Pressure and Temperature. Fuels, 6(3), 59. https://doi.org/10.3390/fuels6030059







