Exploration of Changes in Coal Pore Characteristics and Gas Adsorption Characteristics Based on Influence of Stress
Abstract
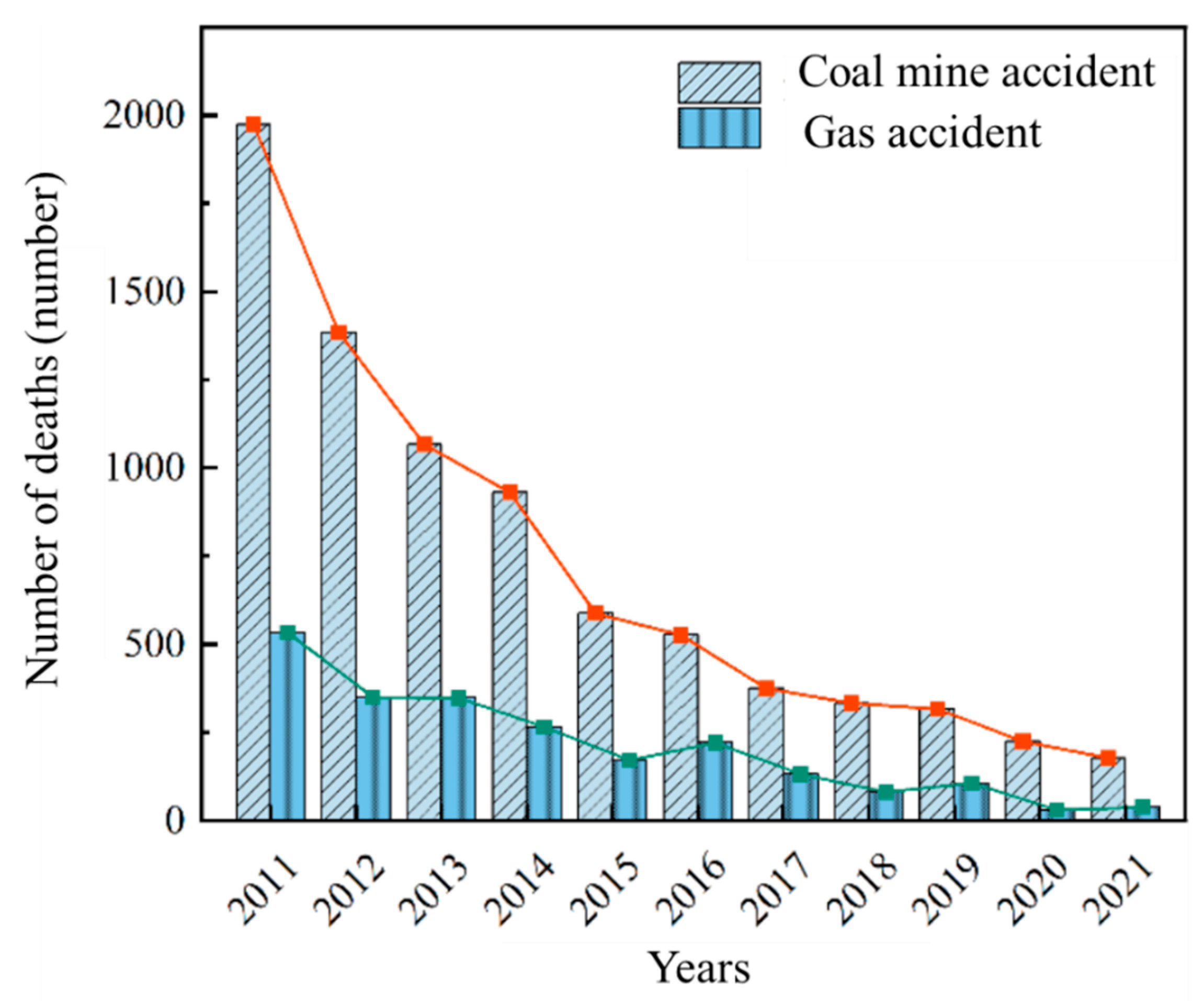
1. Introduction
2. Coal Seam Pore Analysis and Mathematical Model of Adsorption
2.1. Experimental Coal Samples
2.2. Pore Characterization Method for Coal
2.2.1. Pore Volume Measurement
2.2.2. Pore Volume Measurement
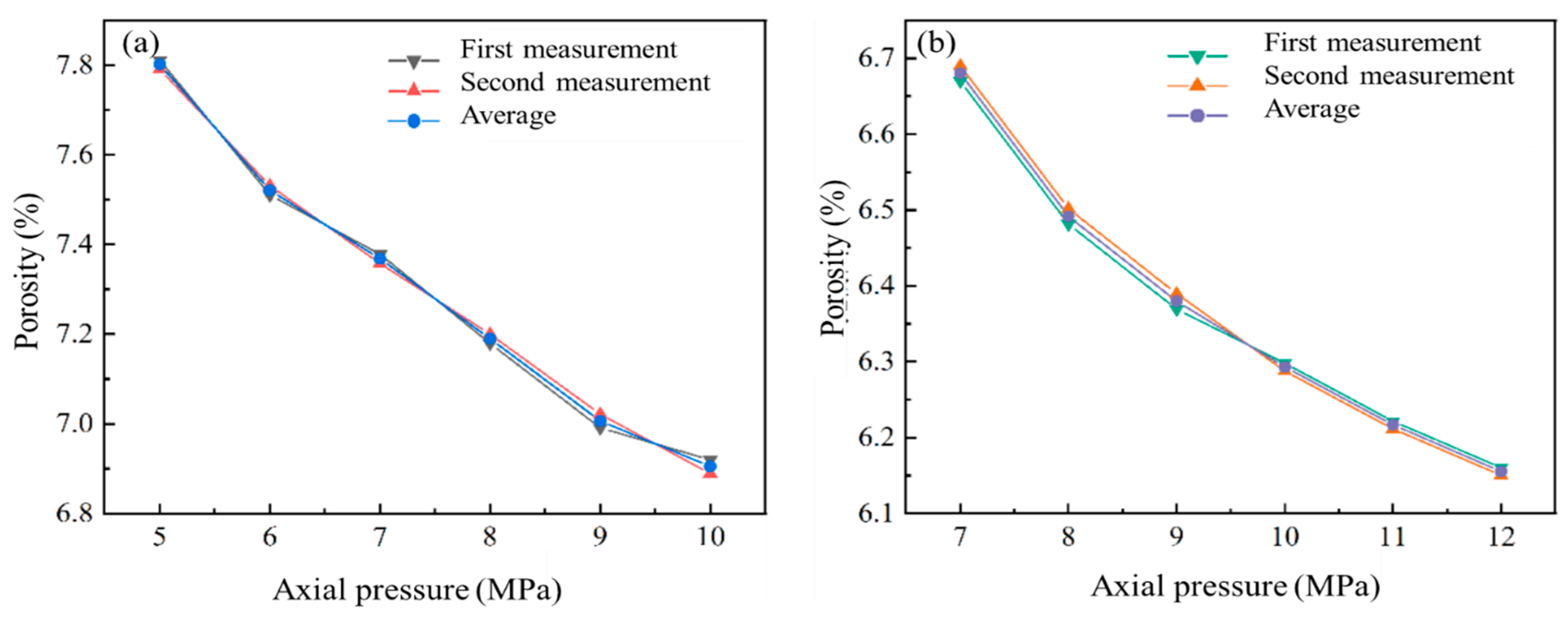
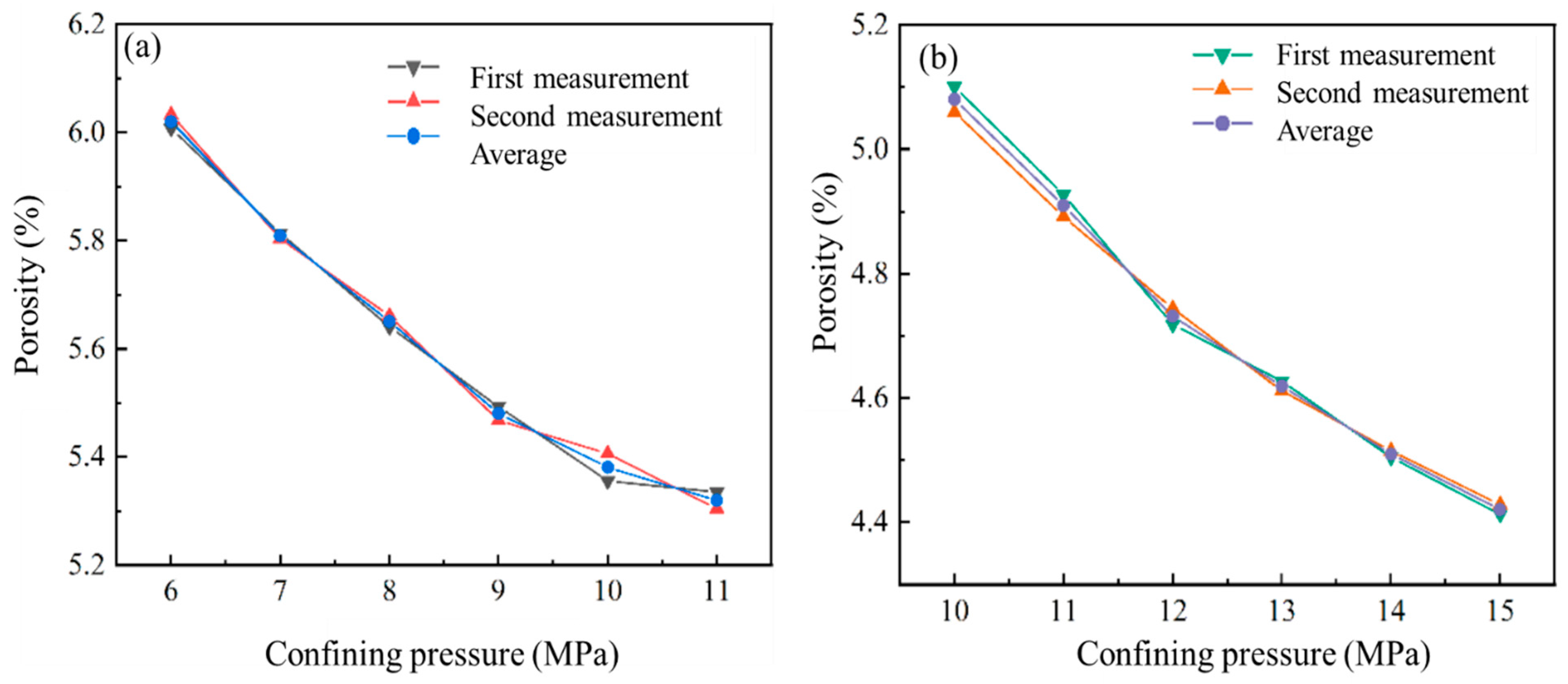
2.3. Characterization of Coal Porosity Under Stress
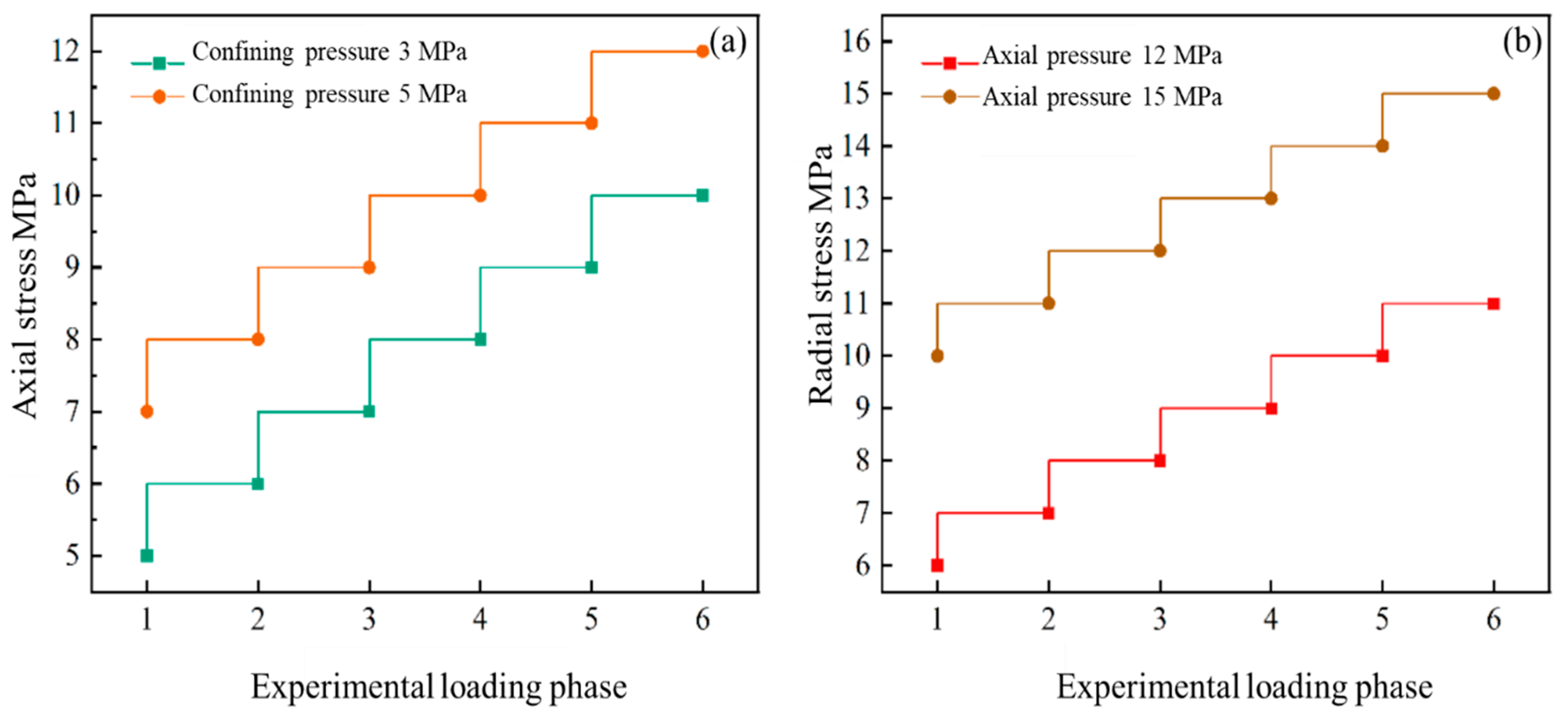
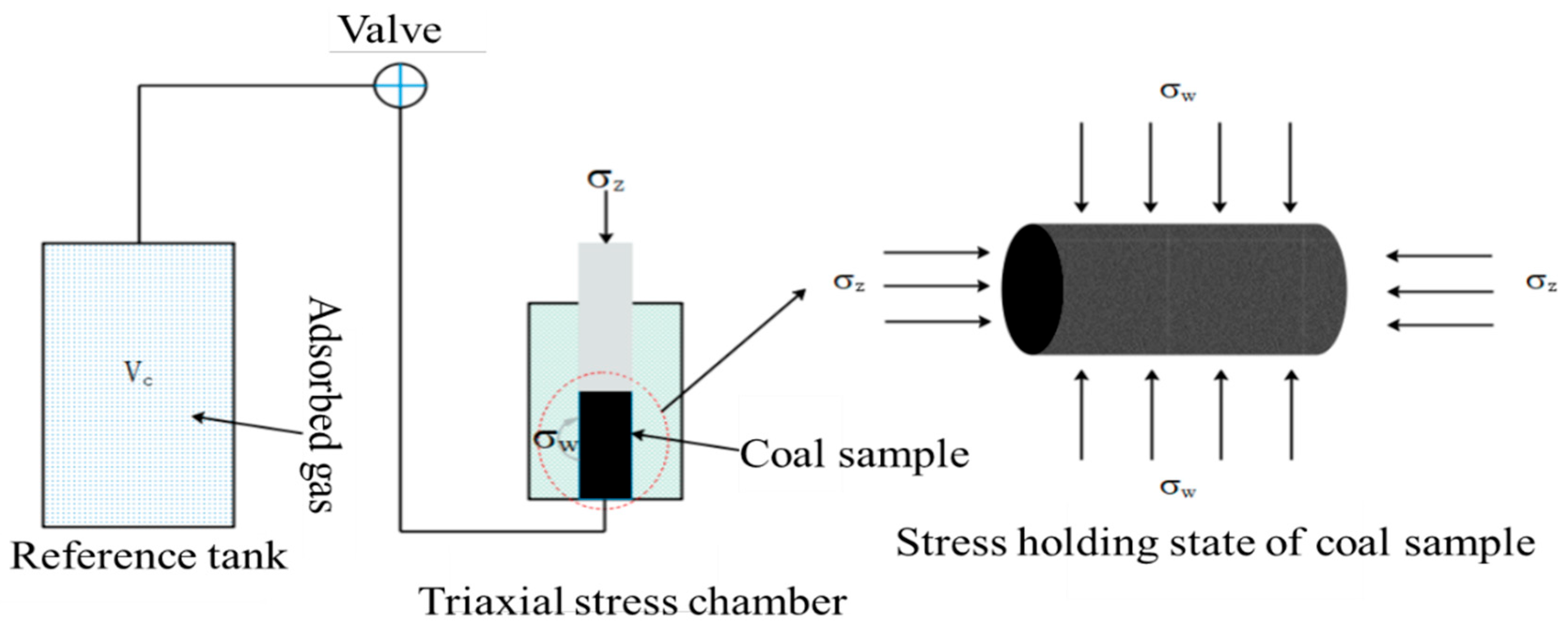
2.4. Gas Adsorption Experiment for Coal Under Stress
3. Results and Discussion
3.1. Differential Pore Volume of Coal
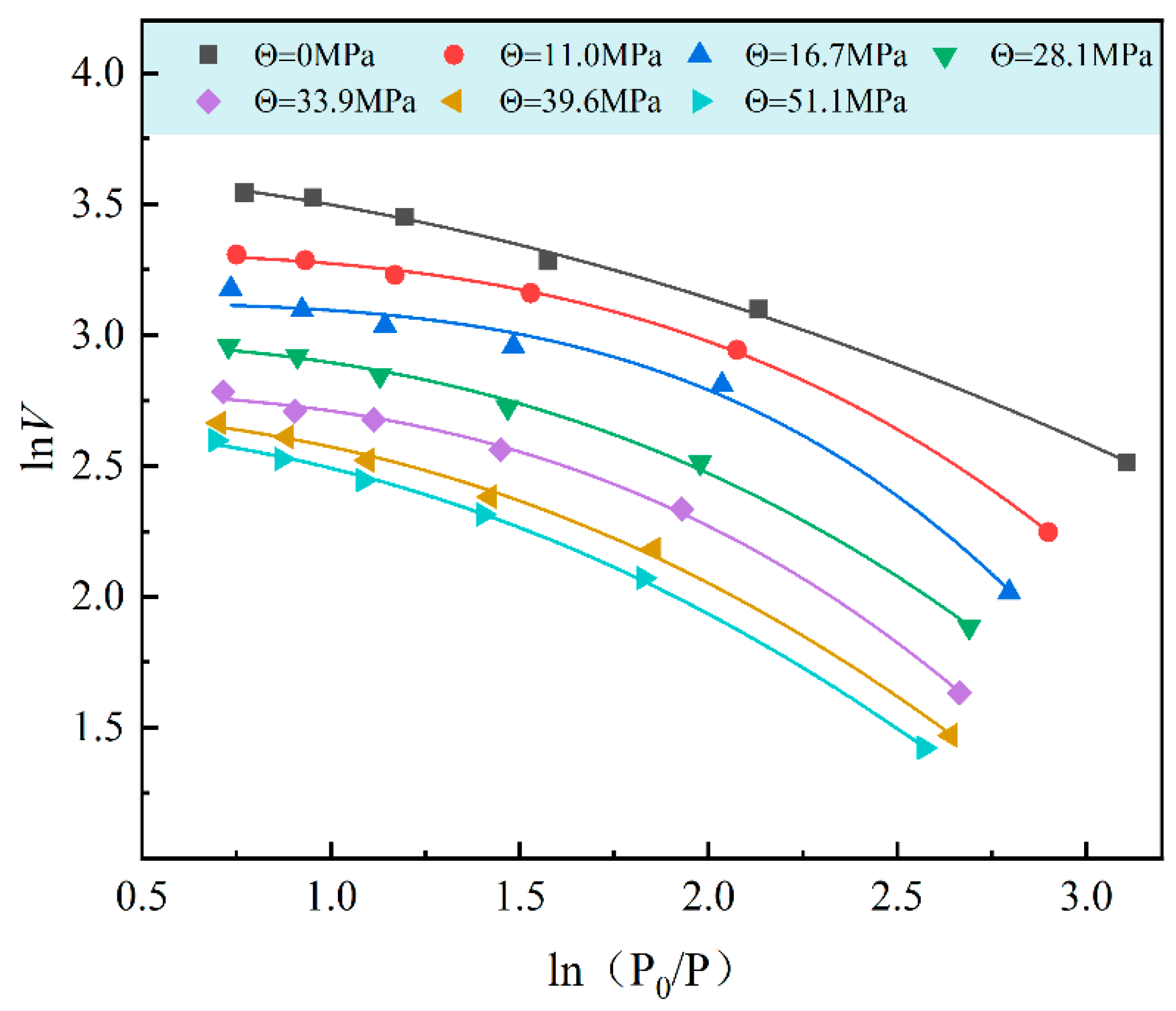
3.2. Differences in Pore Specific Surface Area of Coal
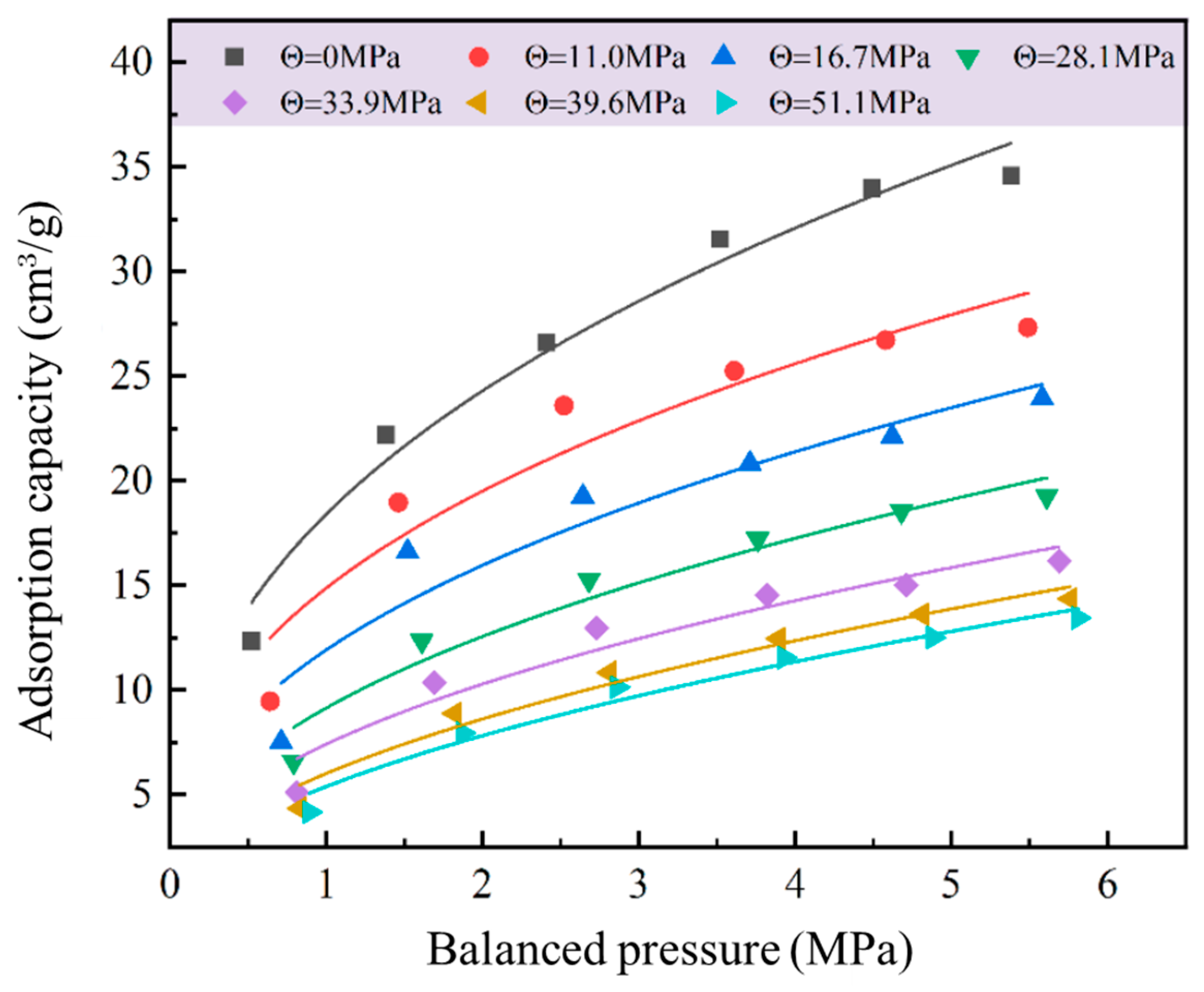
3.3. Gas Adsorption Data Fitting
3.3.1. Langmuir Equation Fitting of Adsorption Data
3.3.2. Dubinin–Astakhov Equation Fitting of Adsorption Data
3.3.3. Freundlich Equation Fitting of Adsorption Data
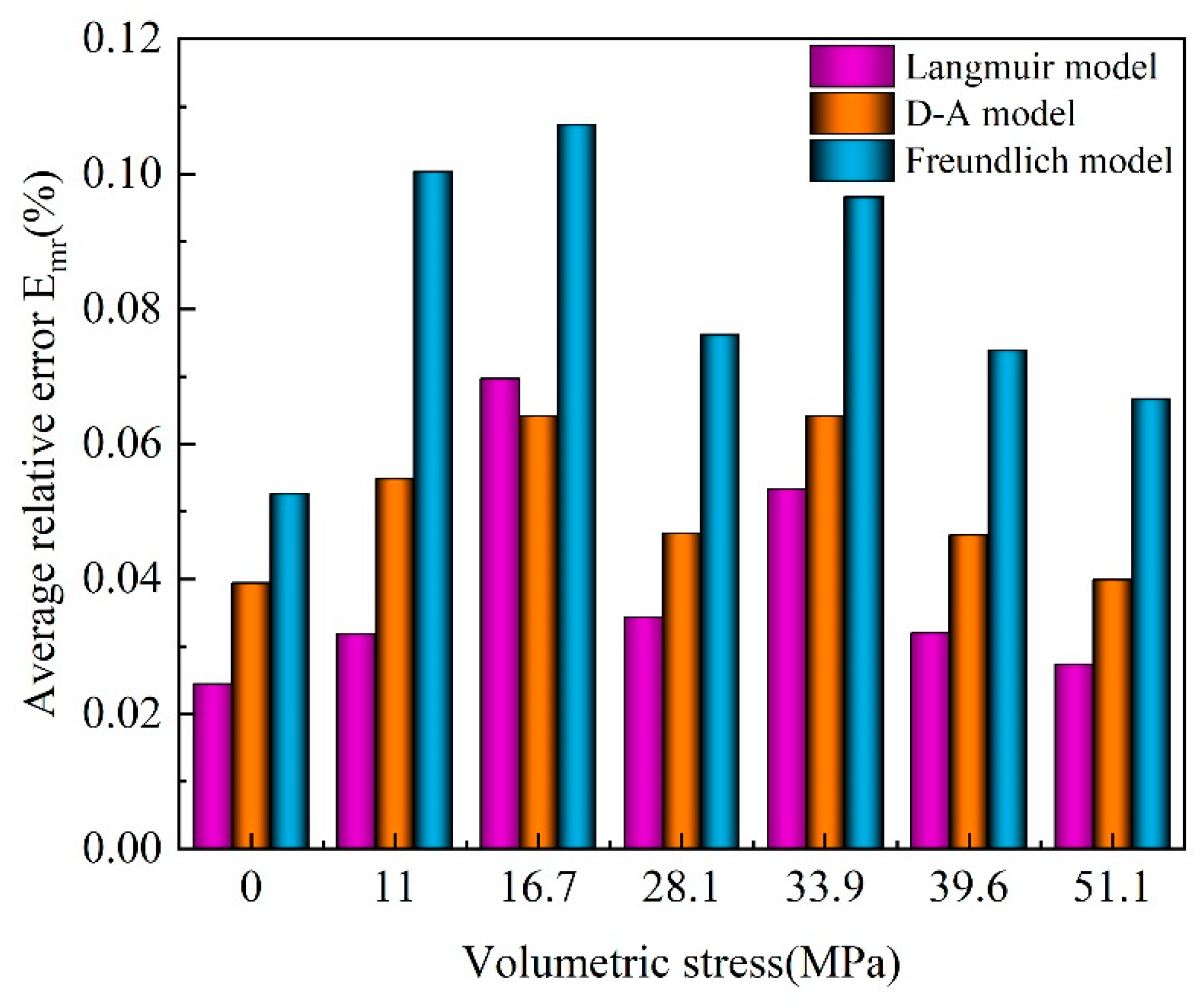
3.3.4. Comparison of Isothermal Adsorption Equations
3.4. Indirect Method for Measuring Coal Seam Gas Content
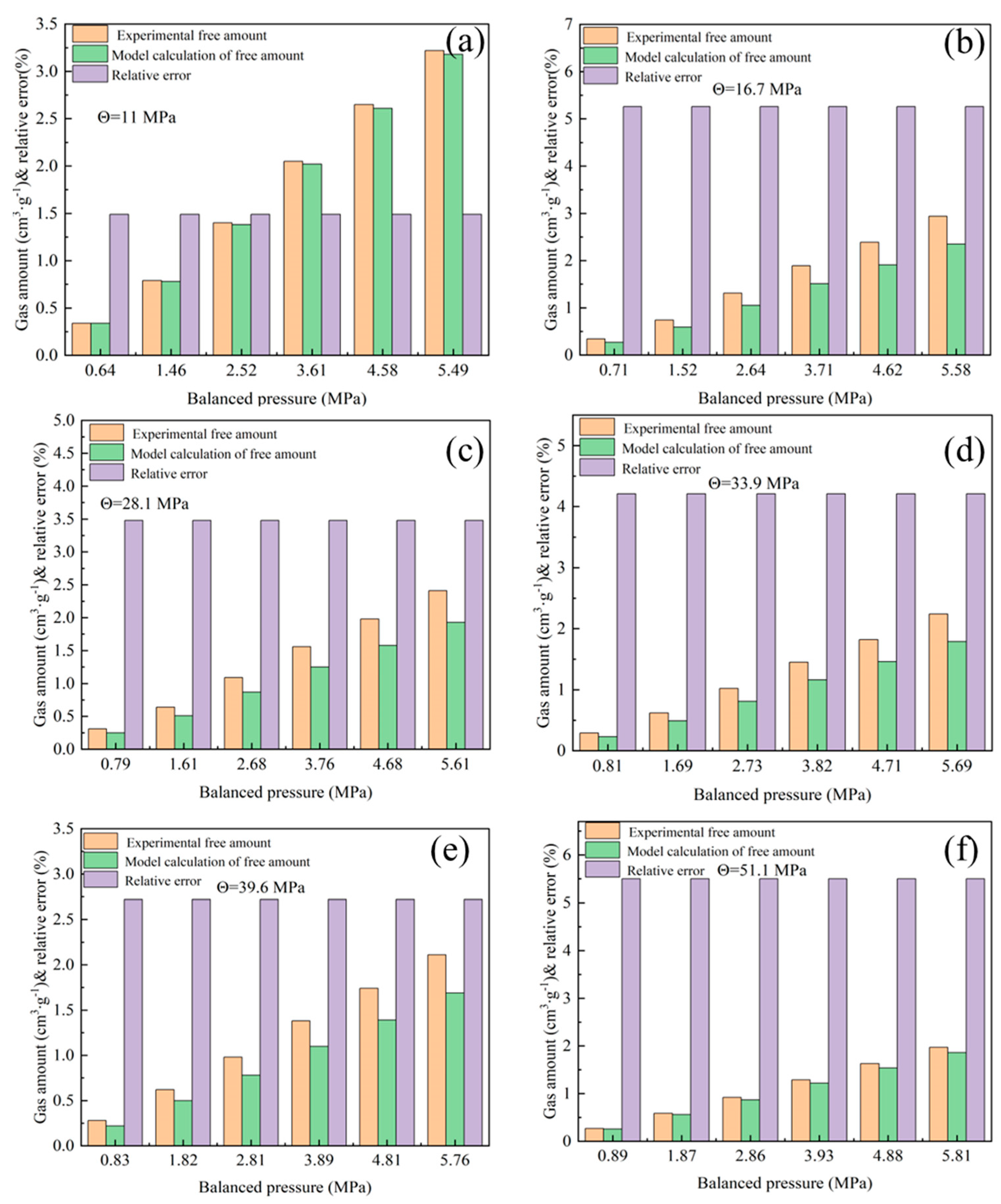
3.4.1. Calculation of Free Gas Quantity Under Stress Influence
3.4.2. Calculation of Gas Adsorption Capacity of Coal Under Stress Influence
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perera, M.S.A.; Ranjith, P.G.; Choi, S.K.; Airey, D.A. Numerical Simulation of Gas Flow Through Porous Sandstone and Its Experimental Validation. Fuel 2011, 90, 547–554. [Google Scholar] [CrossRef]
- Viete, D.R.; Ranjith, P.G. The Effect of CO2 On the Geomechanical and Permeability Behaviour of Brown Coal: Implications for Coal Seam CO2 Sequestration. Int. J. Coal Geol. 2006, 66, 204–216. [Google Scholar] [CrossRef]
- Li, Z.Q.; Liu, Y.; Xu, Y.P. Investigation of Methane Diffusion in Low-Rank Coals by a Multiporous Diffusion Model. J. Nat. Gas Sci. Eng. 2016, 33, 97–107. [Google Scholar] [CrossRef]
- Li, X.C.; Li, Z.B.; Ren, T.; Nie, B.S.; Xie, L.; Huang, T. Effects of Particle Size and Adsorption Pressure on Methane Gas Desorption and Diffusion in Coal. Arabian J. Geosci. 2019, 12, 794. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, L.B.; Cheng, Y.P.; Liu, S.M.; Guo, P.K.; Jin, K. A New Method for Accurate and Rapid Measurement of Underground Coal Seam Gas Content. J. Nat. Gas Sci. Eng. 2015, 26, 1388–1398. [Google Scholar] [CrossRef]
- Yao, Y.B.; Liu, D.M.; Yan, T.T. Geological and Hydrogeological Controls on the Accumulation of Coalbed Methane in the Weibei field, southeastern Ordos Basin. Int. J. Coal Geol. 2014, 121, 148–159. [Google Scholar] [CrossRef]
- Li, Z.Q.; Liu, Y.; Xu, Y.P. Gas Diffusion Mechanism in Multi-Scale Pores of Coal Particles and New Diffusion Model of Dynamic Diffusion Coefficient. J. China Coal Soc. 2016, 41, 633–643. [Google Scholar]
- Li, B.B.; Yang, K.; Xu, P.; Xu, J.; Yuan, M.; Zhang, M. An Experimental Study on Permeability Characteristics of Coal with Slippage and Temperature Effects. J. Petrol. Sci. Eng. 2019, 175, 294–302. [Google Scholar] [CrossRef]
- Guo, H.J.; Yuan, L.; Cheng, Y.P.; Wang, K.; Xu, C.; Zhou, A.T. Effect of Moisture on the Desorption and Unsteady-State Diffusion Properties of Gas in Low-Rank Coal. J. Nat. Gas Sci. Eng. 2018, 57, 45–51. [Google Scholar] [CrossRef]
- Hou, S.H.; Wang, X.M.; Wang, X.J.; Yuan, Y.D.; Pan, S.D.; Wang, X.M. Pore Structure Characterization of Low Volatile Bituminous Coals with Different Particle Size and Tectonic Deformation Using Low Pressure Gas Adsorption. Int. J. Coal Geol. 2017, 183, 1013. [Google Scholar] [CrossRef]
- Mastalerz, M.; Hampton, L.; Drobniak, A.; Loope, H. Significance of Analytical Particle Size in Low-Pressure N2 and CO2 Adsorption of Coal and Shale. Int. J. Coal Geol. 2017, 178, 122–131. [Google Scholar] [CrossRef]
- Wang, L.G.; Cheng, Y.P.; Li, W.; Lu, S.Q.; Xu, C. Component Fractionation of Temporal Evolution in Adsorption-Desorption for Binary Gas Mixtures on Coals from Haishiwan Coal Mine. Int. J. Min. Sci. Technol. 2013, 23, 201–205. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.B.; Zhang, Y.G.; Wang, Z.Z. The Characteristics of Methane Adsorption Capacity and Behavior of Tectonic Coal. Front. Earth Sci. 2023, 10, 1034341. [Google Scholar] [CrossRef]
- Zhou, Y.A.; Sun, W.J.; Chu, W.; Liu, X.Q.; Jing, F.L.; Xue, Y. Theoretical Insight into the Enhanced CH4 Desorption via H2O Adsorption on Different Rank Coal Surfaces. J. Energy Chem. 2016, 25, 677–682. [Google Scholar] [CrossRef]
- Chen, X.J.; Liu, J.; Wang, L.; Qi, L.-L. Influence of Pore Size Distribution of Different Metamorphic Grade of Coal on Adsorption Constant. J. China Coal Soc. 2013, 38, 285–300. [Google Scholar]
- Zheng, C.; Ma, D.; Chen, Y. Research Progress Micro Effect of Water on Coalbed Methane Adsorption/Desorption. Coal Sci. Technol. 2023, 51, 256–268. [Google Scholar]
- Chen, C.G.; Xian, X.; Xian, X.F. The Dependence of Temperature to the Adsorption of methane on anthracite coal and its char. Coal Conver. 1995, 38, 89–92. [Google Scholar]
- Gan, H.; Nandi, S.P.; Walker, P.L., Jr. Nature of the Porosity in American Coals. Fuel 1972, 51, 272–277. [Google Scholar] [CrossRef]
- Yuan, A.Y.; Yang, X.L.; Hou, J.L.; Fu, G.S. Comprehensive Characterization of Pore Structure in Coal Seams with Abnormal Gas Emission in Deep Close Range Coal Seam Clusters. Coal Sci. Tech. 2024, 1–12. [Google Scholar]
- Gensterblum, Y.; Merkel, A.; Busch, A.; Krooss, B.M. High-Pressure CH4 and CO2 Isotherms as a Function of Coal Maturity and the Influence of Moisture. Int. J. Coal Geol. 2013, 118, 45–57. [Google Scholar] [CrossRef]
- Zhong, L.W.; Zhang, H.; Yun, Z.R. Influence of Specific Pore Area and Pore Volume of Coal on Adsorption Capacity. Coal Geol. Explor. 2002, 30, 26–29. [Google Scholar]
- Wang, Q.; Wang, Z.F.; Dai, J.H.; Zhang, K.J.; Wang, L.L. Study on Methane Adsorption Characteristics of Anthracite in Deep Coal Seam. Saf. Coal Mines 2021, 52, 28–33. [Google Scholar]
- Qin, L.; Wang, P.; Lin, H.F.; Long, H. Research on Fractal Characteristics of Coal Freezing with Low Temperature Liquid Nitrogen Using Nitrogen Adsorption Method and Mercury Intrusion Method. J. Mini Saf. Eng. 2023, 40, 184–193. [Google Scholar]
- Wang, Z.; Cheng, Y.; Zhang, K. Characteristics of Microscopic Pore Structure and Fractal Dimension of Bituminous Coal by Cyclic Gas Adsorption/Desorption: An Experimental Study. Fuel 2018, 232, 495–505. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, D. Fractal Characterization of Adsorption-Pores of Coals from North China: An Investigation on CH4 Adsorption Capacity of coals. Int. J. Coal Geol. 2008, 73, 27–42. [Google Scholar] [CrossRef]
- Dubinin, M.M. The Potential Theory of Adsorption of Gases and Vapors for Adsorbents with Energetically Nonuniform Surfaces. Chem. Rev. 1960, 60, 235–241. [Google Scholar] [CrossRef]
- Song, S.B.; Liu, J.F.; Yang, D.S.; Ni, H.Y.; Huang, B.X.; Zhang, K. Pore Structure Characterization and Permeability Prediction of Coal Samples Based on SEM Images. J. Nat. Gas Sci. Eng. 2019, 67, 160–171. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Sun, Y.H.; Jiang, Y.; Chen, J.H.; Cheng, J.Y.; Wang, H.M. Effect of Structure of Carbon Adsorbent on Desorption Amount of Natural Gas. Low Car. Chem. Chem. 2003, 1, 5–7. [Google Scholar]
- Dutka, B. CO2 and CH4 Sorption Properties of Granular Coal Briquettes Under in Situ States. Fuel 2019, 247, 228–236. [Google Scholar] [CrossRef]






| Balanced Pressure/MPa | Experimental Value/cm3 g−1 | Fitting Equation Adsorption Capacity/cm3 g−1 | ||
|---|---|---|---|---|
| Langmuir Model | D-A Model | Freundlich Empirical Formula | ||
| 0.64 | 9.45 | 10.05 | 8.44 | 12.49 |
| 1.46 | 18.96 | 17.96 | 17.75 | 17.23 |
| 2.52 | 23.58 | 22.59 | 22.62 | 21.32 |
| 3.61 | 25.24 | 25.30 | 24.67 | 24.53 |
| 4.58 | 26.72 | 26.89 | 25.52 | 26.92 |
| 5.49 | 27.31 | 27.97 | 25.93 | 28.89 |
| Average relative error /% | 3.19 | 5.48 | 10.04 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.-J.; Zhu, H.-Q.; Sun, J.-F.; Ren, S.-K. Exploration of Changes in Coal Pore Characteristics and Gas Adsorption Characteristics Based on Influence of Stress. Fuels 2024, 5, 698-714. https://doi.org/10.3390/fuels5040038
Qin L-J, Zhu H-Q, Sun J-F, Ren S-K. Exploration of Changes in Coal Pore Characteristics and Gas Adsorption Characteristics Based on Influence of Stress. Fuels. 2024; 5(4):698-714. https://doi.org/10.3390/fuels5040038
Chicago/Turabian StyleQin, Le-Jing, Hong-Qing Zhu, Jian-Fei Sun, and Shao-Kui Ren. 2024. "Exploration of Changes in Coal Pore Characteristics and Gas Adsorption Characteristics Based on Influence of Stress" Fuels 5, no. 4: 698-714. https://doi.org/10.3390/fuels5040038
APA StyleQin, L.-J., Zhu, H.-Q., Sun, J.-F., & Ren, S.-K. (2024). Exploration of Changes in Coal Pore Characteristics and Gas Adsorption Characteristics Based on Influence of Stress. Fuels, 5(4), 698-714. https://doi.org/10.3390/fuels5040038






