The Role of Mobility and Sanitary Measures on the Delay of Community Transmission of COVID-19 in Costa Rica
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data. The Analysis Uses Three Different Sources of Information
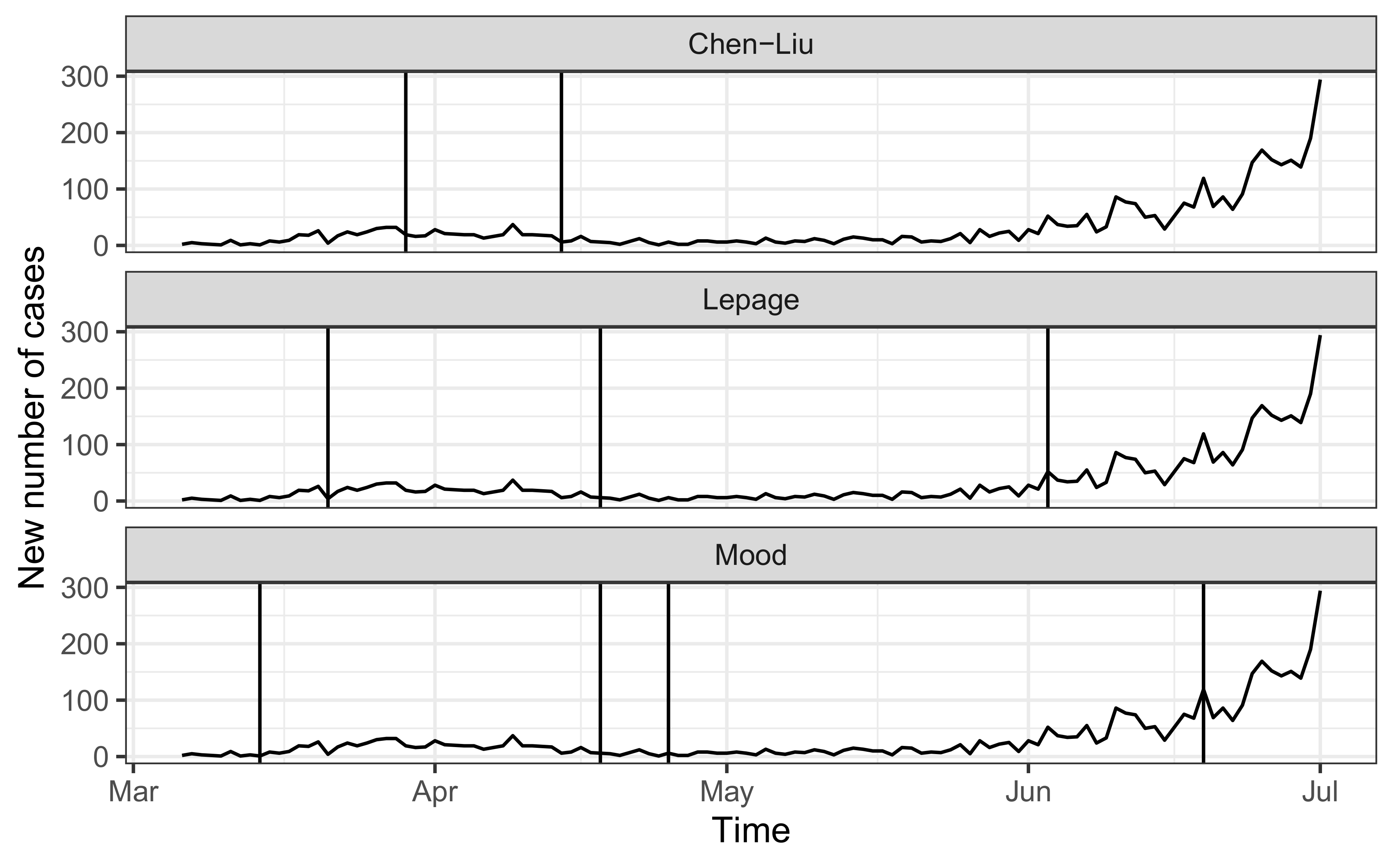
- Epidemiological data: The number of daily confirmed COVID-19 cases in Costa Rica from 6 March 2020 to 2 July 2020 was obtained from the Ministry of Health [14]. The data covers 4023 laboratory-confirmed cases from 82 municipalities across the country. On March 6, Costa Rica became the 89th country to confirm a COVID-19 patient within the national territory, a 49-year-old woman visiting from New York [14]. During the initial months of the pandemic, the growth of confirmed cases was relatively stable in Costa Rica, and the majority of patients had a known chain of transmission. Two months into the pandemic, the country was even highlighted as having the lowest COVID-19 case fatality rate in the region [15]. However, by the second week of June 2020, the daily new cases began a progressive growth. On 2 July 2020, with 4024 total confirmed cases, a 14-day case notification rate of 40.3 cases per 100,000 population and 17 deaths, the Ministry of Health declared community transmission in the Greater Metropolitan Area after being unable to establish the epidemiological nexus to 65% of all new positive cases detected over the last five days [14]. This region comprises about 50% of the national population.
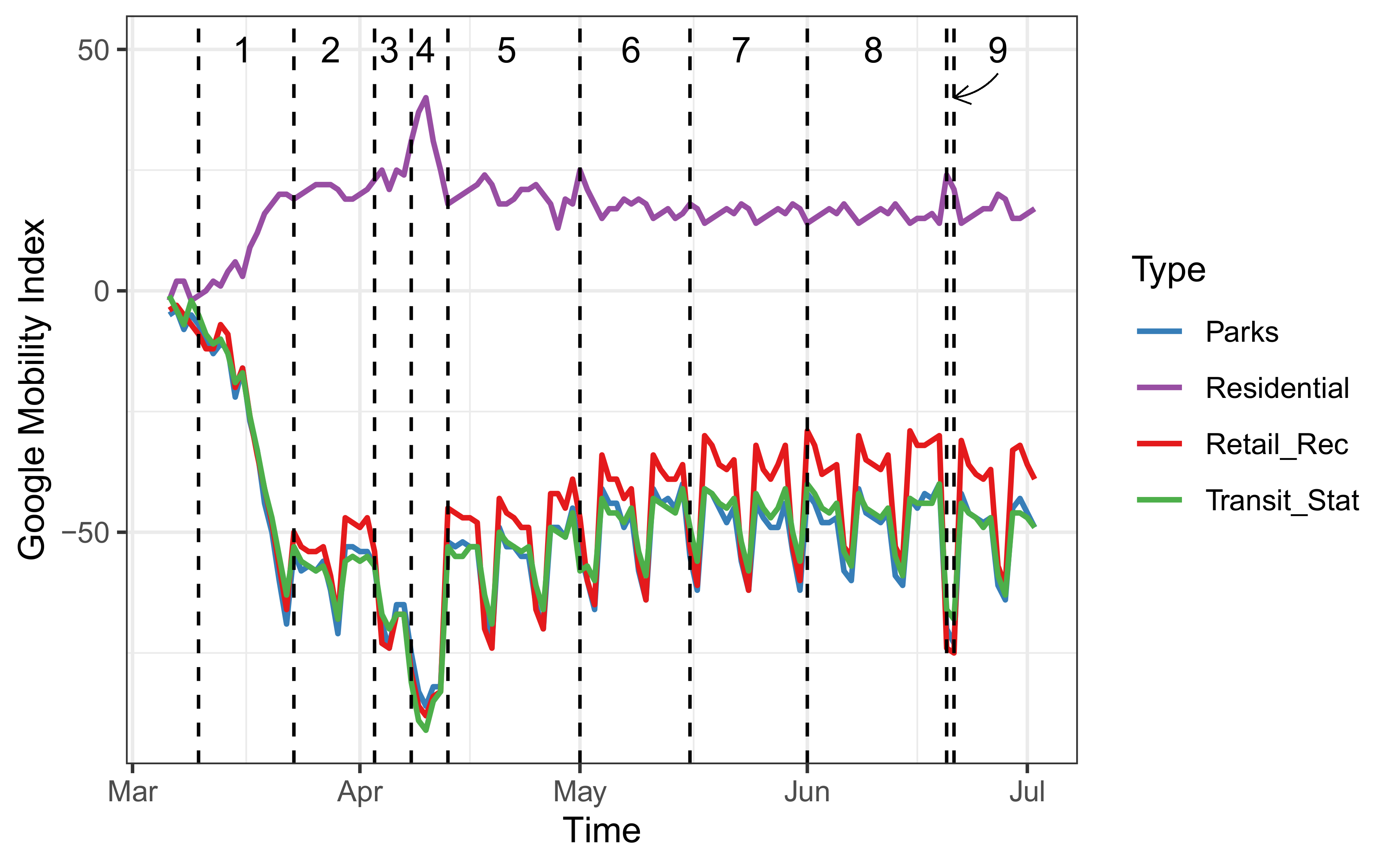
- Google’s Community Mobility Reports [16]: This data contains relative changes of mobility according to Google’s applications with respect to the data observed on a certain baseline. The baseline day is the median value using a five-week period in January and February 2020. The relative changes are computed using the following categories: Retail and Recreation, Parks, Transit stations, Residential, Grocery and Pharmacy, and Workplaces.
- Sanitary measures: Since the first reported case of COVID-19 in Costa Rica, an inter-institutional and comprehensive approach has guided the country’s response to mitigate the impact of the COVID-19 pandemic. One of the first measures aimed to promote and facilitate physical distancing took place on 10 March 2020, with the cancellation of all massive events and the instruction of working from home [14]. In the days to come, the country restricted the capacity of public meeting spaces to 50%, closed schools and universities, all air and land borders, bars, beaches, churches, gyms, theaters, and cinemas [14]. By 23 March 2020, with a total of 158 confirmed cases spread across 30 municipalities (from a total of 82), public health authorities imposed the first restriction to vehicle circulation, beginning with a nighttime restriction to circulate from 10 p.m. to 5 a.m. [14]. The opening, closure, and allowed capacity for both commercial activities and social gathering places, as well as the vehicle restrictions, have been adjusted throughout the pandemic.
2.2. Methods
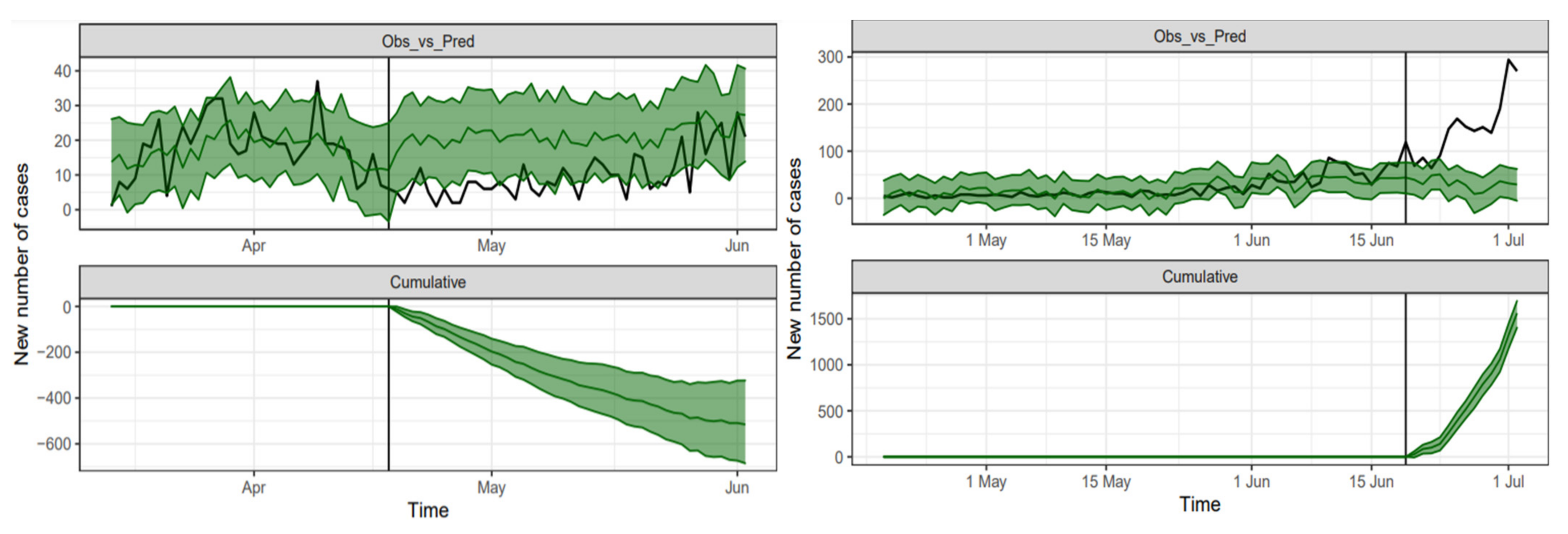
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cowling, B.J.; Aiello, A.E. Public health measures to slow community spread of coronavirus disease 2019. J. Infect. Dis. 2020, 221, 1749–1751. [Google Scholar] [CrossRef] [Green Version]
- Wilder-Smith, A.; Freedman, D.O. Isolation, quarantine, social distancing and community containment: Pivotal role for old-style public health measures in the novel coronavirus (2019-nCoV) outbreak. J. Travel Med. 2020, 27, taaa020. [Google Scholar] [CrossRef]
- Haug, N.; Geyrhofer, L.; Londei, A.; Dervic, E.; Desvars-Larrive, A.; Loreto, V.; Pinior, B.; Thurner, S.; Klimek, P. Ranking the effectiveness of worldwide Covid-19 government interventions. Nat. Hum. Behav. 2020, 4, 1303–1312. [Google Scholar] [CrossRef] [PubMed]
- Hsiang, S.; Allen, D.; Annan-Phan, S.; Bell, K.; Bolliger, I.; Chong, T.; Hannah, D.; Huang, L.Y.; Hultgren, A.; Krasovich, E.; et al. The effect of large-scale anti-contagion policies on the covid-19 pandemic. Nature 2020, 584, 262–267. [Google Scholar] [CrossRef]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.; Mellan, T.A.; Coupland, H.; Whittaker, C.; Zhu, H.; Berah, T.; Eaton, J.W.; et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 2020, 584, 257–261. [Google Scholar] [CrossRef]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Piontti, A.P.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, 395–400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kraemer, M.U.G.; Yang, C.-H.; Gutierrez, B.; Wu, C.-H.; Klein, B. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prem, K.; Liu, Y.; Russell, T.W.; Kucharski, A.J.; Eggo, R.M.; Davies, N.; Flasche, S.; Clifford, S.; Pearson, C.A.B.; Munday, J.D.; et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 2020, 5, e261–e270. [Google Scholar] [CrossRef] [Green Version]
- Cacciapaglia, G.; Sannino, F. Interplay of social distancing and border restrictions for pandemics via the epidemic renormalisation group framework. Sci. Rep. 2020, 28, 15828. [Google Scholar] [CrossRef] [PubMed]
- Badr, H.S.; Du, H.; Marshall, M.; Dong, E.; Squire, M.M.; Gardner, L.M. Association between mobility patterns and COVID-19 transmission in the USA: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 1247–1254. [Google Scholar] [CrossRef]
- Cot, C.; Cacciapaglia, G.; Sannino, F. Mining Google and Apple mobility data: Temporal anatomy for COVID-19 social distancing. Sci. Rep. 2020, 11, 1–8. [Google Scholar]
- Cazelles, B.; Comiskey, C.; Nguyen-Van-Yen, B.; Champagne, C.; Roche, B. Parallel trends in the transmission of SARS-CoV-2 and retail/recreation and public transport mobility during non-lockdown periods. Int. J. Infect. Dis. 2021, 104, 693–695. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Coronavirus Disease (COVID-19) Weekly Epidemiological Update and Weekly Operational Update. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports (accessed on 1 February 2021).
- Ministry of Health. National Situation of COVID-19. Available online: https://www.ministeriodesalud.go.cr/index.php/centro-de-prensa/noticias/741-noticias-2020/1532-lineamientos-nacionales-para-la-vigilancia-de-la-infeccion-por-coronavirus-2019ncov (accessed on 1 February 2021).
- United Nations. 5 Reasons Costa Rica is Winning Plaudits for Fighting Covid-19: A UN Resident Coordinator Blog. Available online: https://news.un.org/en/story/2020/05/1064412 (accessed on 2 February 2021).
- COVID-19 Community Mobility Reports. Available online: https://www.google.com/covid19/mobility/ (accessed on 15 January 2021).
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 2020, 369, eabb9789. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Zhao, Z.; Shao, X. Time series analysis of Covid-19 infection curve: A change-point perspective. J. Econom. 2020. [Google Scholar] [CrossRef]
- Coughlin, S.S.; Yigiter, A.; Xu, H.; Berman, A.E.; Chen, J. Early detection of change patterns in covid-19 incidence and the implementation of public health policies: A multi-national study. Public Health Pract. 2020, 2, 100064. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, D.M.; Qiu, P.H.; Kang, C.W. The Change point Model for Statistical Process Control. J. Qual. Technol. 2003, 35, 355–366. [Google Scholar] [CrossRef]
- Hawkins, D.M.; Zamba, K.D. A Change-Point Model for a Shift in Variance. J. Qual. Technol. 2005, 37, 21–31. [Google Scholar] [CrossRef]
- Ross, G.J. Parametric and nonparametric sequential change detection in R: The cpm package. J. Stat. Softw. 2015, 66, 1–20. [Google Scholar]
- Ross, G.J. Sequential change detection in the presence of unknown parameters. Stat. Comput. 2014, 24, 1017–1030. [Google Scholar] [CrossRef] [Green Version]
- Ross, G.J.; Adams, N.M.; Tasoulis, D.K.; Hand, D.J. A nonparametric change point model for streaming data. Technometrics 2011, 53, 379–389. [Google Scholar] [CrossRef]
- Buendia, C.; Batalla, R.J.; Sabater, S.; Palau, A.; Marcé, R. Runoff trends driven by climate and afforestation in a Pyrenean Basin. Land Degrad. Dev. 2016, 27, 823–838. [Google Scholar] [CrossRef] [Green Version]
- Killick, R.; Eckley, I.A.; Ewans, K.; Jonathan, P. Detection of changes in variance of oceanographic time-series using changepoint analysis. Ocean Eng. 2010, 37, 1120–1126. [Google Scholar] [CrossRef] [Green Version]
- Xue, T.; Tang, G.; Sun, L.; Wu, Y.; Liu, Y.; Dou, Y. Long-term trends in precipitation and precipitation extremes and underlying mechanisms in the US Great Basin during 1951–2013. J. Geophys. Res. Atmos. 2017, 122, 6152–6169. [Google Scholar] [CrossRef]
- Song, J.; Huang, B.; Li, R. Measuring recovery to build up metrics of flood resilience based on pollutant discharge data: A case study in East China. Water 2017, 9, 619. [Google Scholar] [CrossRef]
- Mood, A.M. On the asymptotic efficiency of certain nonparametric two-sample tests. Ann. Math. Stat. 1954, 514–522. [Google Scholar] [CrossRef]
- Lepage, Y. A combination of Wilcoxon’s and Ansari-Bradley’s statistics. Biometrika 1971, 58, 213–217. [Google Scholar] [CrossRef]
- Chen, C.; Liu, L.M. Joint estimation of model parameters and outlier effects in time series. J. Am. Stat. Assoc. 1993, 88, 284–297. [Google Scholar]
- Brodersen, K.H.; Gallusser, F.; Koehler, J.; Remy, N.; Scott, S.L. Inferring causal impact using Bayesian structural time-series models. Ann. Appl. Stat. 2015, 9, 247–274. [Google Scholar] [CrossRef]
- Palomo, J.; Dunson, D.B.; Bollen, K. Bayesian Structural Equation Modeling. In Handbook of Latent Variable and Related Models; North-Holland: Amsterdam, The Netherlands; Elsevier: Oxford, UK, 2017; pp. 163–188. [Google Scholar]
- Sánchez, B.N.; Budtz-Jørgensen, E.; Ryan, L.M.; Hu, H. Structural equation models: A review with applications to environmental epidemiology. J. Am. Stat. Assoc. 2005, 100, 1443–1455. [Google Scholar] [CrossRef] [Green Version]
- Baja, E.S.; Schwartz, J.D.; Coull, B.A.; Wellenuis, G.A.; Vokonas, P.S.; Suh, H.H. Structural equation modeling of the inflammatory response to traffic air pollution. J. Expo. Sci. Environ. Epidemiol. 2013, 23, 268–274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watad, A.; Watad, S.; Mahroum, N.; Sharif, K.; Amital, H.; Bragazzi, N.L.; Adawi, M. Forecasting the West Nile virus in the United States: An extensive novel data streams–based time series analysis and structural equation modeling of related digital searching behavior. JMIR Public Health Surveill. 2019, 5, e9176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skrondal, A.; Rabe-Hesketh, S. Some applications of generalized linear latent and mixed models in epidemiology: Repeated measures, measurement error and multilevel modeling. Nor. Epidemiol. 2003, 13, 265–278. [Google Scholar]
- World Health Organization. COVID-19 Strategy Update. Available online: https://www.who.int/publications/m/item/covid-19-strategy-update (accessed on 2 February 2021).
| Categories | Notation in (1) | Lag (Days) |
|---|---|---|
| Retail and Recreation | 7 | |
| Parks | 7 | |
| Transit stations | 7 | |
| Residential | 8 |
| Set | Date | Measures | Pillai Test |
|---|---|---|---|
| 1 | 3/10–3/22 | Cancellation of massive events and work from home instructions; closure of bars and casinos; Government declares National Emergency; Closure of all schools and borders; Closure of movies, theaters, and gymnasiums, malls at 50%. | <2.2 × 10−16 |
| 2 | 3/23–4/2 | Closure of beaches, churches, and national parks; Start of vehicle restrictions from 10 p.m. to 5 a.m.; Vehicle restriction on weekends from 8 p.m. to 5 a.m.; Closure of non-essential commercial activities starting at 8 p.m. and during the weekend. | 8.94 × 10−14 |
| 3 | 4/3–4/7 | Daytime vehicle restriction from 5 a.m. to 5 p.m., with plate distribution and nighttime vehicle restriction from 5 p.m. to 5 a.m.; Restriction of long-distance public transportation; Closure of non-essential commercial activities. | 2.38 × 10−3 |
| 4 | 4/8–4/12 | The circulation of vehicles and public transportation was suspended. | 2.71 × 10−11 |
| 5 | 4/13–4/30 | Day-time vehicle restriction from 5 a.m. to 7 p.m. with plate distribution; Total nighttime vehicle restriction from 7 p.m. to 5 a.m.; On weekends, total vehicle restriction (with exceptions to access to essential services); Commerce may function from 5 a.m. to 7 p.m., weekends delivery only. | 9.65 × 10−10 |
| 6 | 5/1–5/15 | The first phase of gradual reopening of commercial activities; Vehicle restriction from 5 a.m. to 7 p.m. with plate distribution; Total night-time restriction from 7 p.m. to 5 a.m. | 2.01 × 10−7 |
| 7 | 5/16–5/31 | The second phase of the gradual reopening of commercial activities; Vehicle restriction from 5 a.m. to 10 p.m. with plate distribution; Total nighttime restriction from 10 p.m. to 5 a.m. | 2.03 × 10−5 |
| 8 | 6/1–6/19 | The third phase of the gradual reopening of commercial activities; Vehicle restriction from 5 a.m. to 10 p.m. with plate distribution; Total nighttime restriction from 10 p.m. to 5 a.m.; Differentiated vehicle restriction in municipalities located near the northern border area of Costa Rica. | 8.84 × 10−4 |
| 9 | 6/20–6/21 | Total vehicle restriction with circulation only to essential services; Closure of non-essential commercial activities. | 8.84 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barboza, L.A.; Vásquez, P.; Mery, G.; Sanchez, F.; García, Y.E.; Calvo, J.G.; Rivas, T.; Pérez, M.D.; Salas, D. The Role of Mobility and Sanitary Measures on the Delay of Community Transmission of COVID-19 in Costa Rica. Epidemiologia 2021, 2, 294-304. https://doi.org/10.3390/epidemiologia2030022
Barboza LA, Vásquez P, Mery G, Sanchez F, García YE, Calvo JG, Rivas T, Pérez MD, Salas D. The Role of Mobility and Sanitary Measures on the Delay of Community Transmission of COVID-19 in Costa Rica. Epidemiologia. 2021; 2(3):294-304. https://doi.org/10.3390/epidemiologia2030022
Chicago/Turabian StyleBarboza, Luis A., Paola Vásquez, Gustavo Mery, Fabio Sanchez, Yury E. García, Juan G. Calvo, Tania Rivas, María Dolores Pérez, and Daniel Salas. 2021. "The Role of Mobility and Sanitary Measures on the Delay of Community Transmission of COVID-19 in Costa Rica" Epidemiologia 2, no. 3: 294-304. https://doi.org/10.3390/epidemiologia2030022
APA StyleBarboza, L. A., Vásquez, P., Mery, G., Sanchez, F., García, Y. E., Calvo, J. G., Rivas, T., Pérez, M. D., & Salas, D. (2021). The Role of Mobility and Sanitary Measures on the Delay of Community Transmission of COVID-19 in Costa Rica. Epidemiologia, 2(3), 294-304. https://doi.org/10.3390/epidemiologia2030022






