Analysis of Delayed Vaccination Regimens: A Mathematical Modeling Approach
Abstract
1. Introduction
2. Materials and Methods
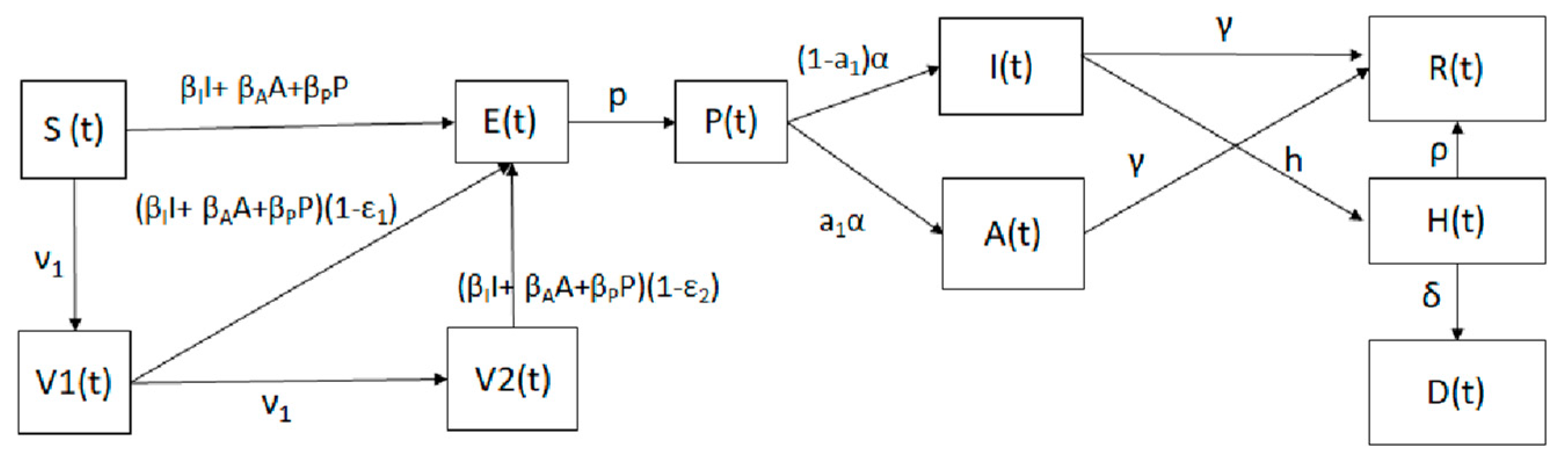
Mathematical Model
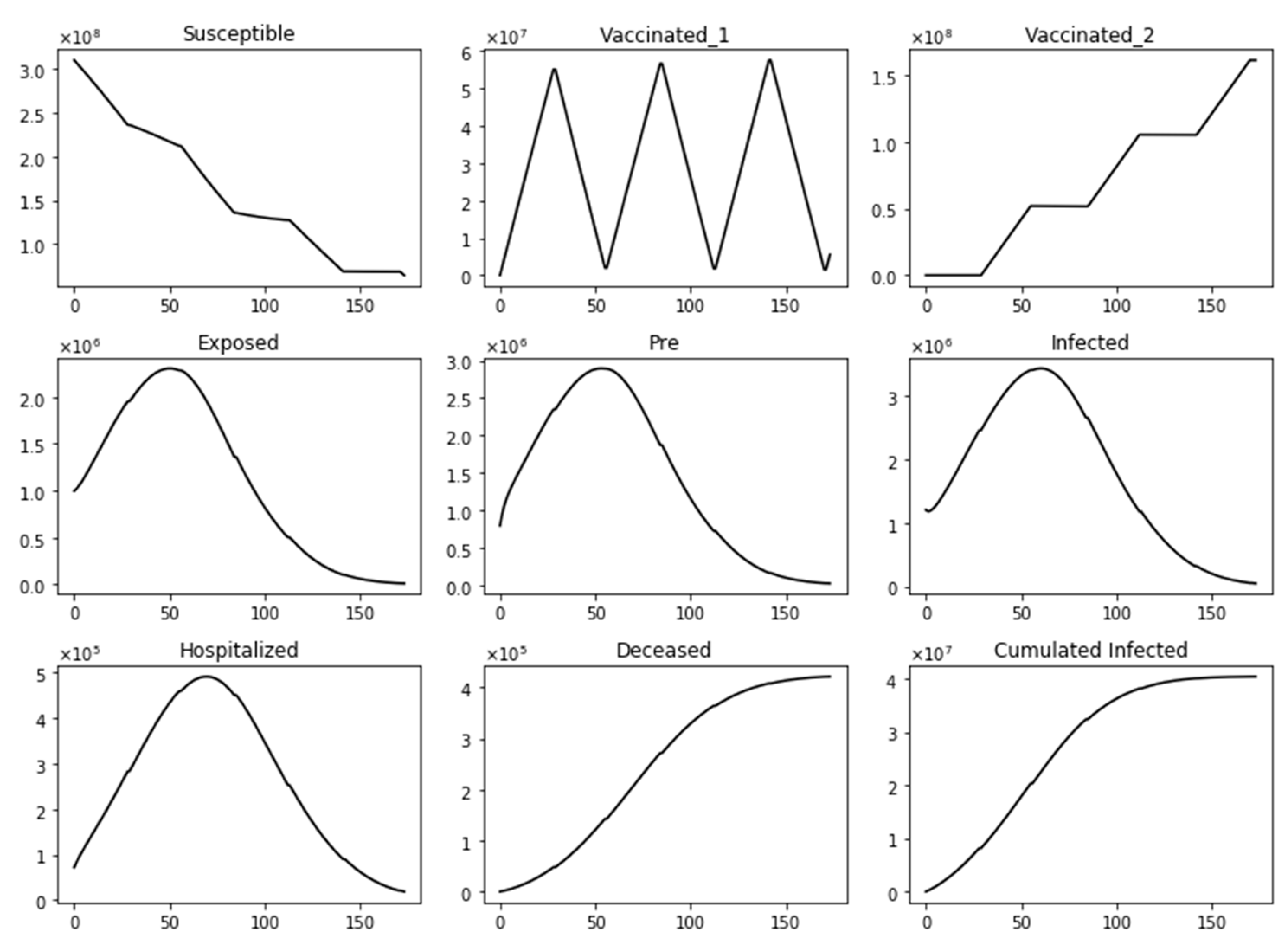
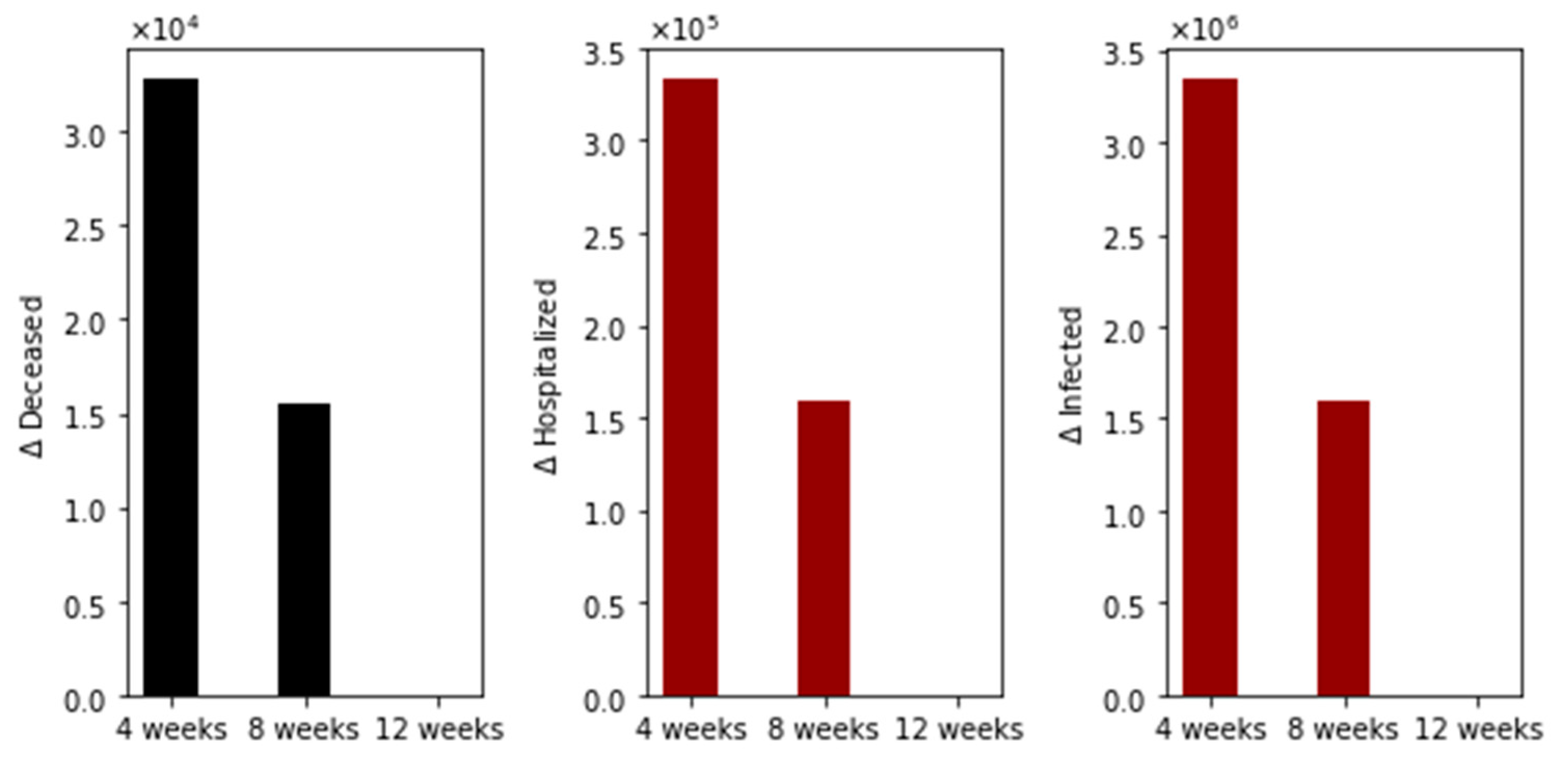
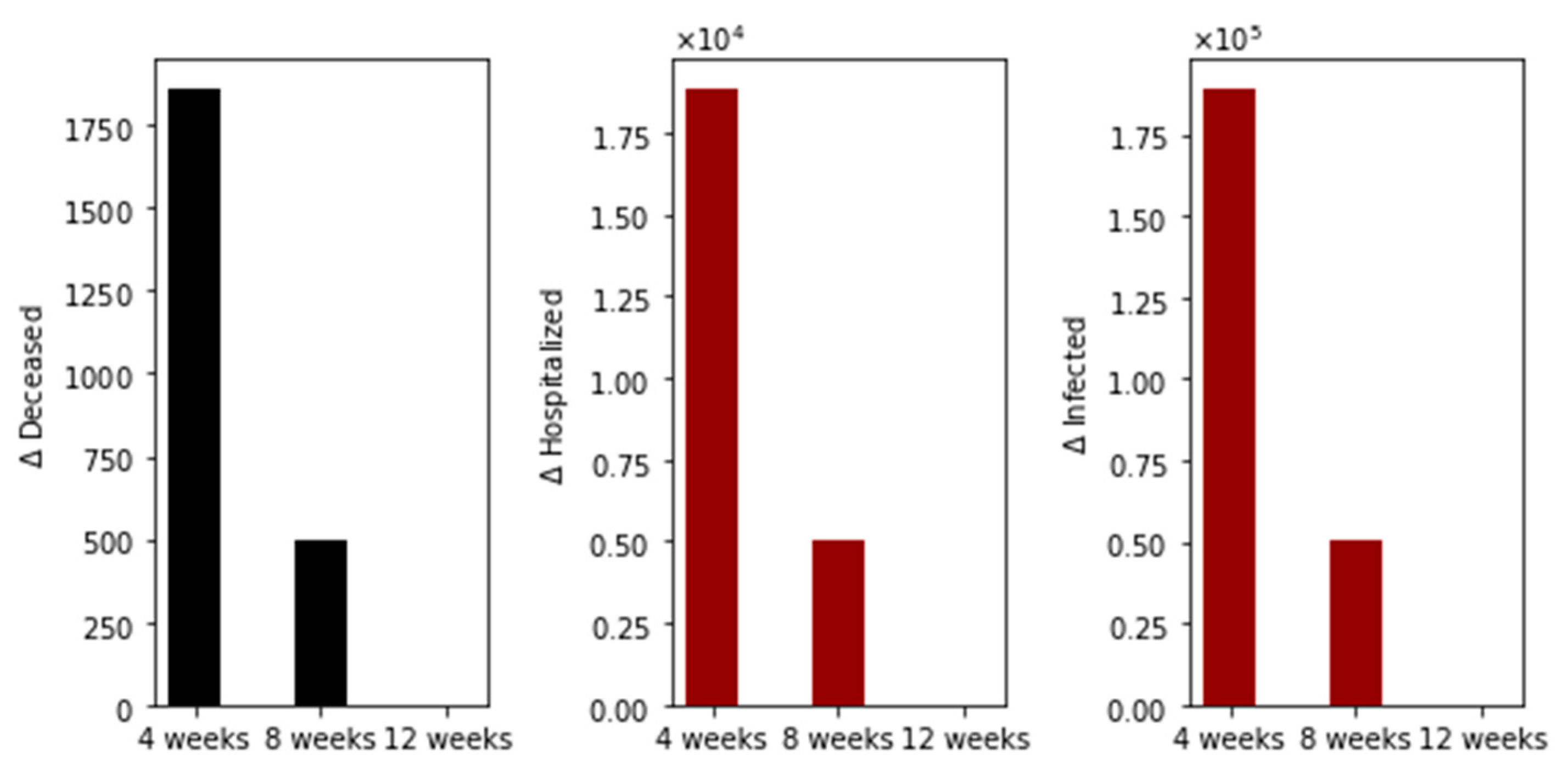
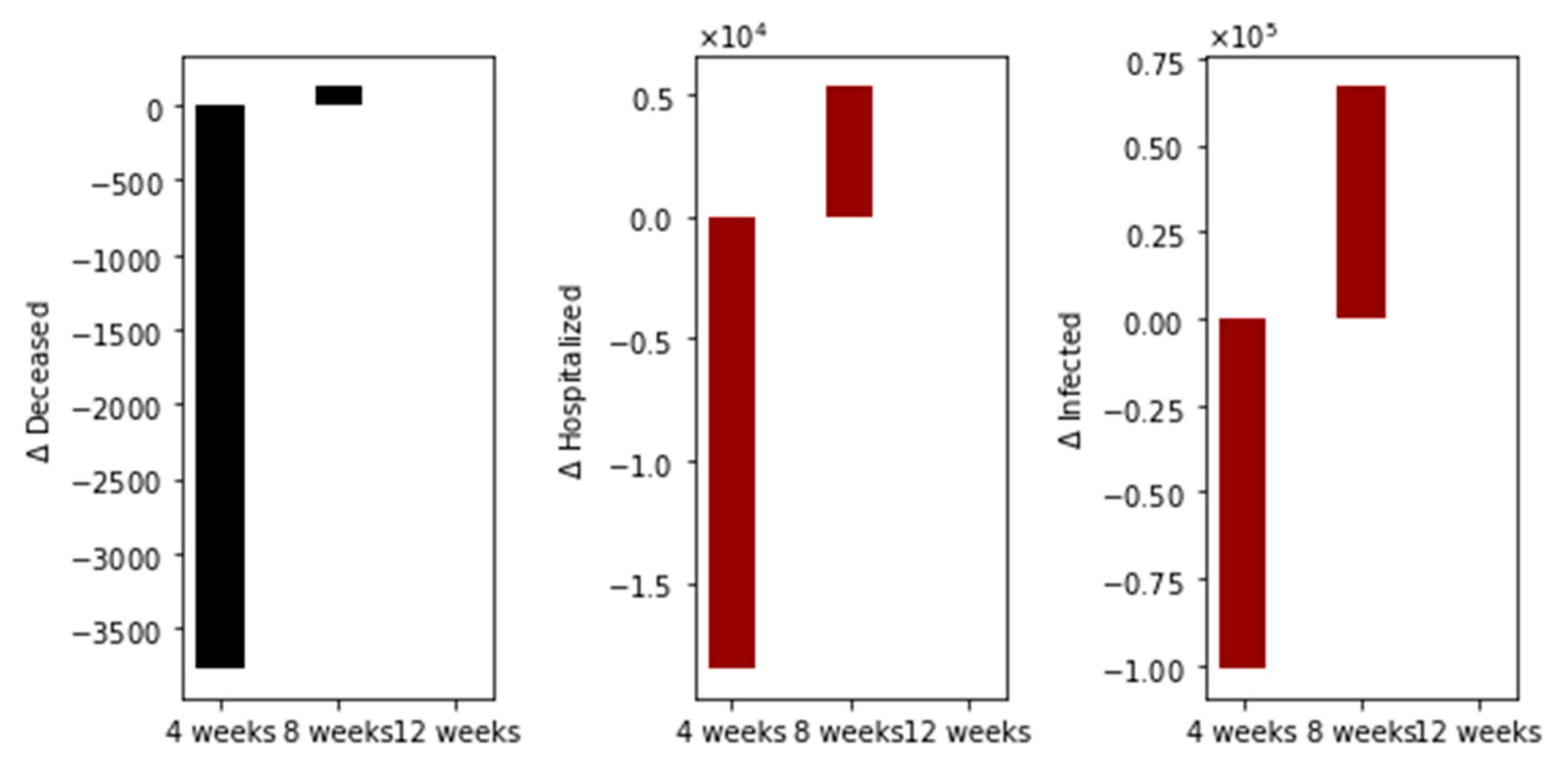
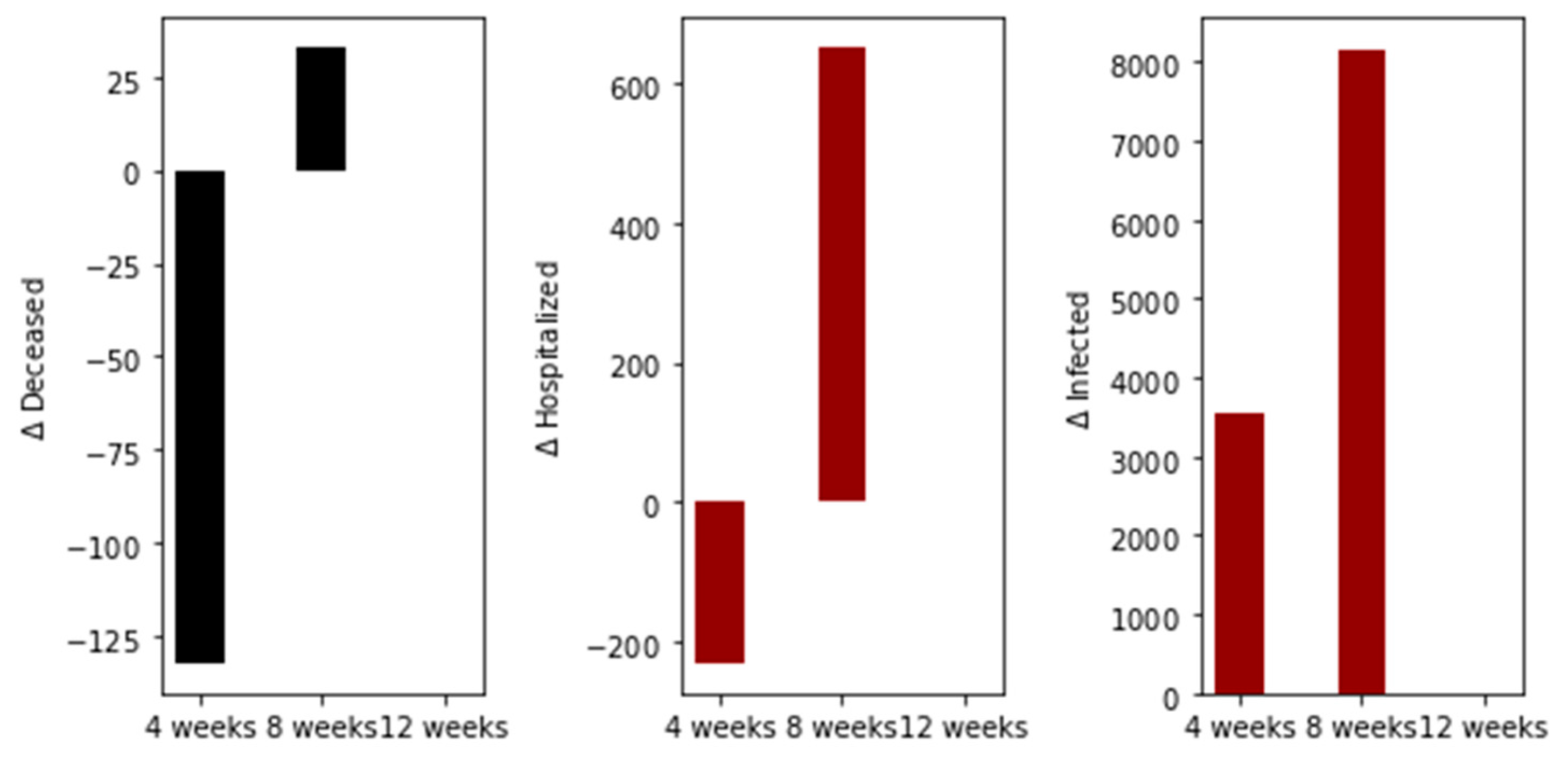
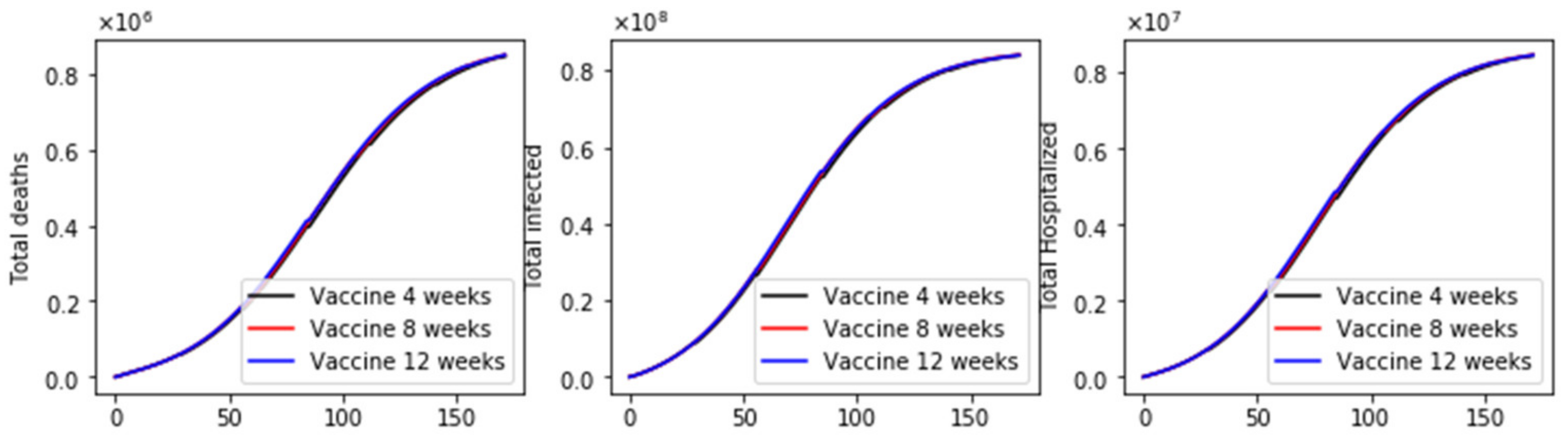
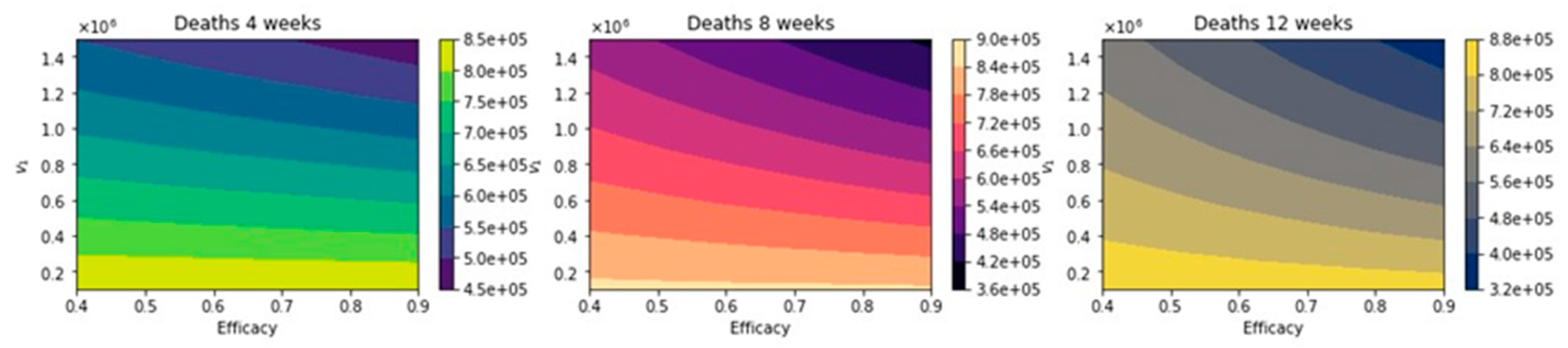
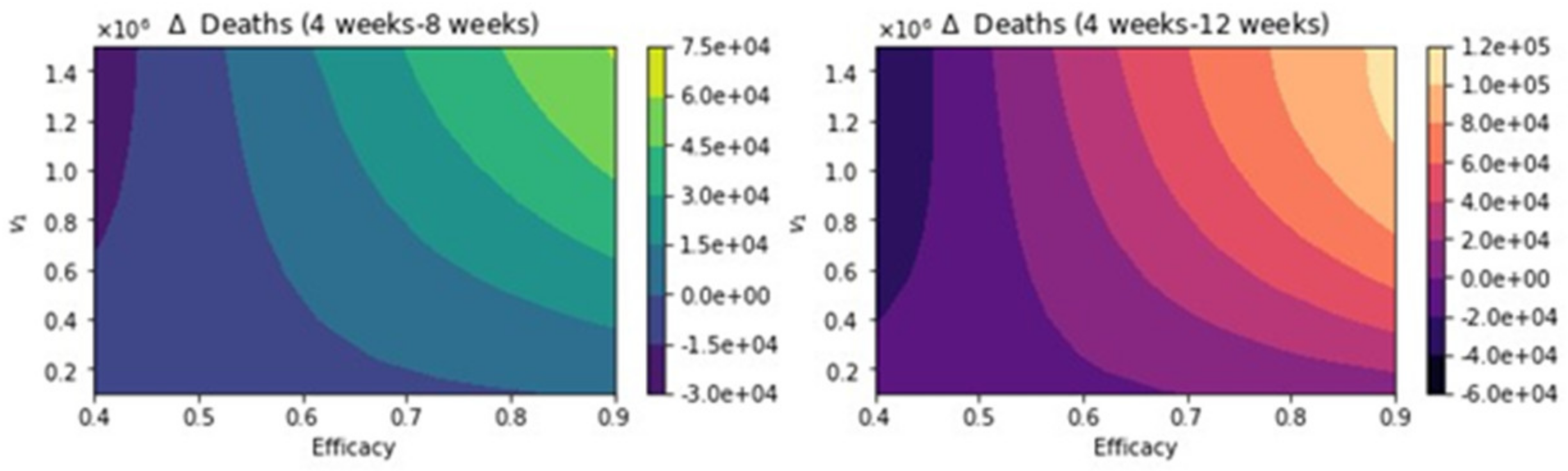
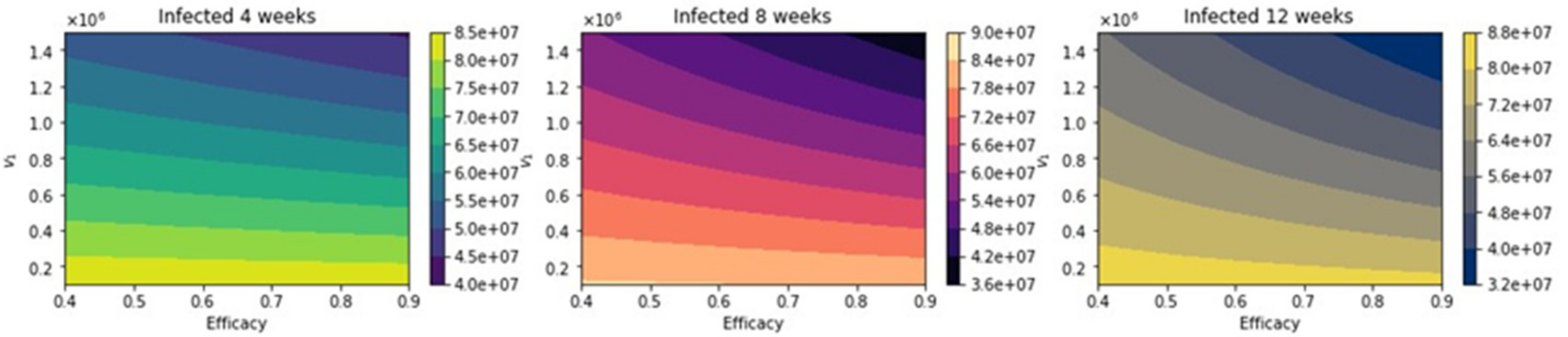
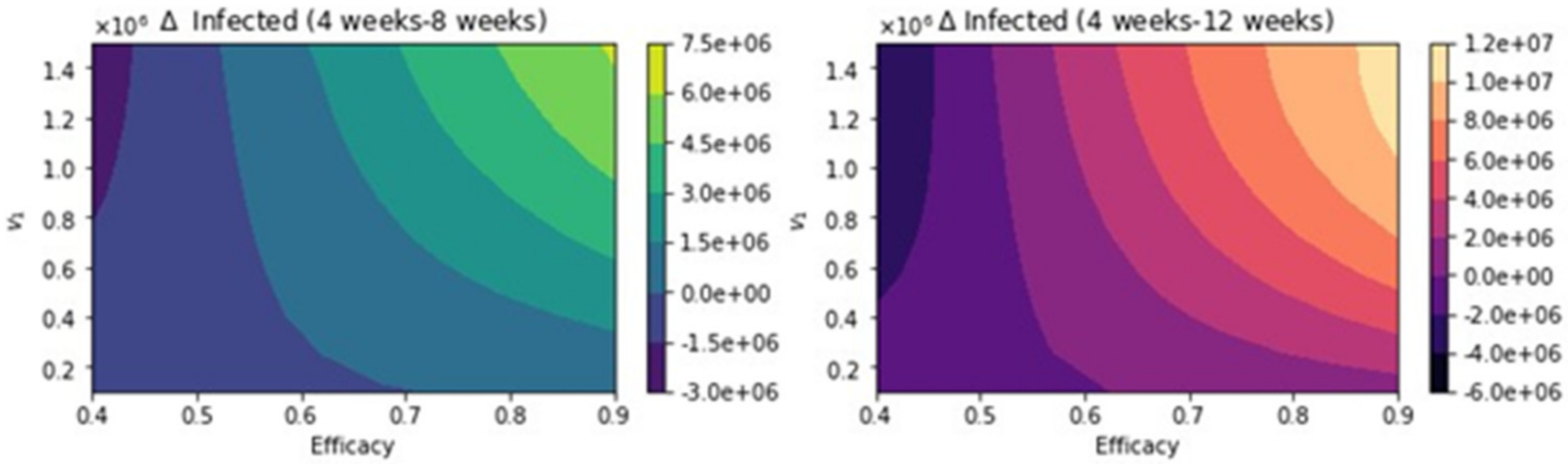
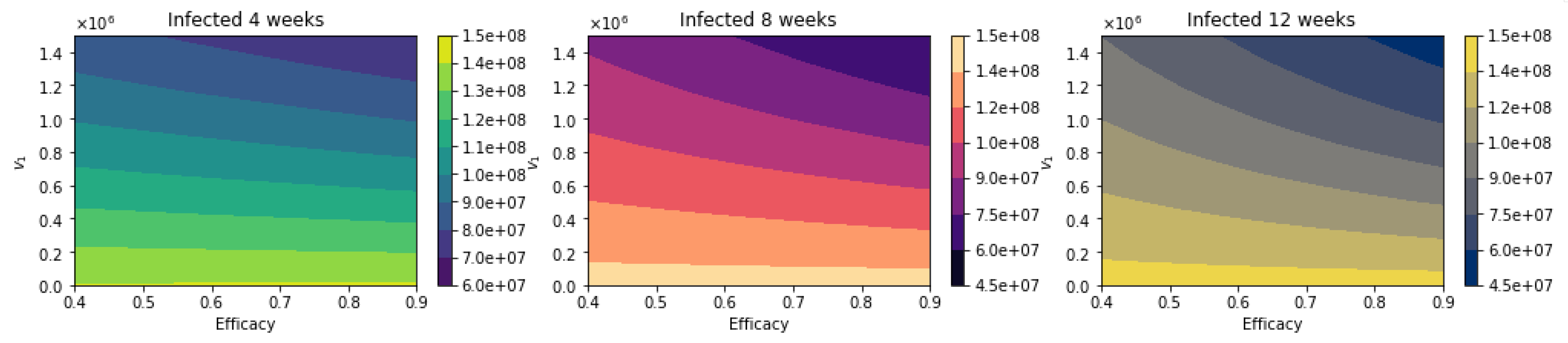
3. Results
Further Uncertainty Analysis
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Centers for Disease Control and Prevention. Available online: https://www.cdc.gov/coronavirus/2019-nCoV/index.html (accessed on 14 May 2021).
- Johns Hopkins University and Medicine. Available online: https://coronavirus.jhu.edu (accessed on 14 May 2021).
- Asamoah, J.K.K.; Owusu, M.A.; Jin, Z.; Oduro, F.; Abidemi, A.; Gyasi, E.O. Global stability and cost-effectiveness analysis of COVID-19 considering the impact of the environment: Using data from Ghana. Chaos Solitons Fractals 2020, 140, 110103. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imp. Coll. Lond. 2020, 20. [Google Scholar] [CrossRef]
- Haushofer, J.; Metcalf, C.J.E. Which interventions work best in a pandemic? Science 2020, 368, 1063–1065. [Google Scholar] [CrossRef] [PubMed]
- Moore, S.; Hill, E.M.; Tildesley, M.J.; Dyson, L.; Keeling, M.J. Vaccination and non-pharmaceutical interventions for COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2021, 21, 793–802. [Google Scholar] [CrossRef]
- Mandal, S.; Bhatnagar, T.; Arinaminpathy, N.; Agarwal, A.; Chowdhury, A.; Murhekar, M.; Gangakhedkar, R.R.; Sarkar, S. Prudent public health intervention strategies to control the coronavirus disease 2019 transmission in India: A mathematical model-based approach. Indian J. Med. Res. 2020, 151, 190. [Google Scholar] [PubMed]
- Reis, R.F.; de Melo Quintela, B.; de Oliveira Campos, J.; Gomes, J.M.; Rocha, B.M.; Lobosco, M.; dos Santos, R.W. Characterization of the COVID-19 pandemic and the impact of uncertainties, mitigation strategies, and underreporting of cases in South Korea, Italy, and Brazil. Chaos Solitons Fractals 2020, 136, 109888. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Pasco, R.F.; Du, Z.; Petty, M.; Fox, S.J.; Galvani, A.P.; Pignone, M.; Johnston, S.C.; Meyers, L.A. Impact of social distancing measures on coronavirus disease healthcare demand, central Texas, USA. Emerg. Infect. Dis. 2020, 26, 2361. [Google Scholar] [CrossRef] [PubMed]
- Pinky, L.; Dobrovolny, H.M. SARS-CoV-2 coinfections: Could influenza and the common cold be beneficial? J. Med. Virol. 2020, 92, 2623–2630. [Google Scholar] [CrossRef]
- Dobrovolny, H.M. Modeling the role of asymptomatics in infection spread with application to SARS-CoV-2. PLoS ONE 2020, 15, e0236976. [Google Scholar]
- Zhang, X.; Tan, Y.; Ling, Y.; Lu, G.; Liu, F.; Yi, Z.; Jia, X.; Wu, M.; Shi, B.; Xu, S.; et al. Viral and host factors related to the clinical outcome of COVID-19. Nature 2020, 583, 437–440. [Google Scholar] [CrossRef] [PubMed]
- Ran, L.; Chen, X.; Wang, Y.; Wu, W.; Zhang, L.; Tan, X. Risk factors of healthcare workers with corona virus disease 2019: A retrospective cohort study in a designated hospital of Wuhan in China. Clin. Infect. Dis. 2020, 71, 2218–2221. [Google Scholar] [CrossRef]
- Yang, H.; Duan, G. Analysis on the epidemic factors for the corona virus disease. Zhonghua Yu Fang Yi Xue Za Zhi Chin. J. Prev. Med. 2020, 54, E021. [Google Scholar]
- Robertson, J.F.; Sewell, H.F.; Stewart, M. Delayed second dose of the BNT162b2 vaccine: Innovation or misguided conjecture? Lancet 2021, 397, 879–880. [Google Scholar] [CrossRef]
- Acedo, L.; Diez-Domingo, J.; Morano, J.A.; Villanueva, R.J. Mathematical modelling of respiratory syncytial virus (RSV): Vaccination strategies and budget applications. Epidemiol. Infect. 2010, 138, 853–860. [Google Scholar] [CrossRef] [PubMed]
- Paltiel, A.D.; Schwartz, J.L.; Zheng, A.; Walensky, R.P. Clinical Outcomes of A COVID-19 Vaccine: Implementation Over Efficacy: Study examines how definitions and thresholds of vaccine efficacy, coupled with different levels of implementation effectiveness and background epidemic severity, translate into outcomes. Health Aff. 2020, 40, 42–52. [Google Scholar]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef]
- Kadire, S.R.; Wachter, R.M.; Lurie, N. Delayed second dose versus standard regimen for COVID-19 vaccination. N. Engl. J. Med. 2021, 384, e28. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Rodríguez, D.; Gonzalez-Parra, G.; Villanueva, R.J. Analysis of key factors of a SARS-CoV-2 vaccination program: A mathematical modeling approach. Epidemiologia 2021, 2, 12. [Google Scholar] [CrossRef]
- Tuite, A.R.; Zhu, L.; Fisman, D.N.; Salomon, J.A. Alternative dose allocation strategies to increase benefits from constrained COVID-19 vaccine supply. Ann. Intern. Med. 2021, 174, 570–572. [Google Scholar] [CrossRef] [PubMed]
- Romero-Brufau, S.; Chopra, A.; Ryu, A.J.; Gel, E.; Raskar, R.; Kremers, W.; Anderson, K.S.; Subramanian, J.; Krishnamurthy, B.; Singh, A.; et al. Public health impact of delaying second dose of BNT162b2 or mRNA-1273 COVID-19 vaccine: Simulation agent based modeling study. BMJ 2021, 373. [Google Scholar] [CrossRef]
- Moghadas, S.M.; Vilches, T.N.; Zhang, K.; Nourbakhsh, S.; Sah, P.; Fitzpatrick, M.C.; Galvani, A.P. Evaluation of COVID-19 vaccination strategies with a delayed second dose. PLoS Biol. 2021, 19, e3001211. [Google Scholar] [CrossRef]
- Block, P.; Hoffman, M.; Raabe, I.J.; Dowd, J.B.; Rahal, C.; Kashyap, R.; Mills, M.C. Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world. Nat. Hum. Behav. 2020, 4, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Eker, S. Validity and usefulness of COVID-19 models. Humanit. Soc. Sci. Commun. 2020, 7, 1–5. [Google Scholar] [CrossRef]
- Jentsch, P.C.; Anand, M.; Bauch, C.T. Prioritising COVID-19 vaccination in changing social and epidemiological landscapes: A mathematical modelling study. Lancet Infect. Dis. 2021. [Google Scholar] [CrossRef]
- Qazi, A.; Qazi, J.; Naseer, K.; Zeeshan, M.; Hardaker, G.; Maitama, J.Z.; Haruna, K. Analyzing situational awareness through public opinion to predict adoption of social distancing amid pandemic COVID-19. J. Med. Virol. 2020, 92, 849–855. [Google Scholar] [CrossRef] [PubMed]
- Altmann, D.M.; Boyton, R.J.; Beale, R. Immunity to SARS-CoV-2 variants of concern. Science 2021, 371, 1103–1104. [Google Scholar] [CrossRef] [PubMed]
- Roda, W.C.; Varughese, M.B.; Han, D.; Li, M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020, 5, 271–281. [Google Scholar] [CrossRef]
- Gonzalez-Parra, G.; Martínez-Rodríguez, D.; Villanueva-Micó, R.J. Impact of a new SARS-CoV-2 variant on the population: A mathematical modeling approach. Math. Comput. Appl. 2021, 26, 25. [Google Scholar]
- Holmdahl, I.; Buckee, C. Wrong but useful- what COVID-19 epidemiologic models can and cannot tell us. N. Engl. J. Med. 2020, 383, 303–305. [Google Scholar] [CrossRef] [PubMed]
- Jewell, N.P.; Lewnard, J.A.; Jewell, B.L. Caution Warranted: Using the Institute for Health Metrics and Evaluation Model for Predicting the Course of the COVID-19 Pandemic; American College of Physicians: Philadelphia, PA, USA, 2020. [Google Scholar]
- Kuniya, T. Prediction of the Epidemic Peak of Coronavirus Disease in Japan. J. Clin. Med. 2020, 9, 789. [Google Scholar] [CrossRef] [PubMed]
- Walensky, R.P.; Walke, H.T.; Fauci, A.S. SARS-CoV-2 variants of concern in the United States—Challenges and opportunities. JAMA 2021, 325, 1037–1038. [Google Scholar] [CrossRef] [PubMed]
- Al-Qaness, M.A.; Ewees, A.A.; Fan, H.; Abd Elaziz, M. Optimized forecasting method for weekly influenza confirmed cases. Int. J. Environ. Res. Public Health 2020, 17, 3510. [Google Scholar] [CrossRef] [PubMed]
- Aranda-Lozano, D.F.; González-Parra, G.C.; Querales, J. Modelling respiratory syncytial virus (RSV) transmission children aged less than five years-old. Rev. Salud Pública 2013, 15, 689–700. [Google Scholar] [PubMed]
- Araz, O.M.; Bentley, D.; Muelleman, R.L. Using Google Flu Trends data in forecasting influenza-like-illness related ED visits in Omaha, Nebraska. Am. J. Emerg. Med. 2014, 32, 1016–1023. [Google Scholar] [CrossRef] [PubMed]
- Chretien, J.P.; George, D.; Shaman, J.; Chitale, R.A.; McKenzie, F.E. Influenza forecasting in human populations: A scoping review. PLoS ONE 2014, 9, e94130. [Google Scholar] [CrossRef]
- Hogan, A.B.; Anderssen, R.S.; Davis, S.; Moore, H.C.; Lim, F.J.; Fathima, P.; Glass, K. Time series analysis of RSV and bronchiolitis seasonality in temperate and tropical Western Australia. Epidemics 2016, 16, 49–55. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.; Diego, F.; Aranda, L.S. Modeling the epidemic waves of AH1N1/09 influenza around the world. Spat. Spatio-Temporal Epidemiol. 2011, 2, 219–226. [Google Scholar] [CrossRef]
- González-Parra, G.; Villanueva, R.J.; Ruiz-Baragaño, J.; Moraño, J.A. Modelling influenza A (H1N1) 2009 epidemics using a random network in a distributed computing environment. Acta Trop. 2015, 143, 29–35. [Google Scholar] [CrossRef]
- Moore, H.C.; Jacoby, P.; Hogan, A.B.; Blyth, C.C.; Mercer, G.N. Modelling the seasonal epidemics of respiratory syncytial virus in young children. PLoS ONE 2014, 9, e100422. [Google Scholar]
- Osthus, D.; Hickmann, K.S.; Caragea, P.C.; Higdon, D.; del Valle, S.Y. Forecasting seasonal influenza with a state-space SIR model. Ann. Appl. Stat. 2017, 11, 202. [Google Scholar] [CrossRef] [PubMed]
- Reich, N.G.; Brooks, L.C.; Fox, S.J.; Kandula, S.; McGowan, C.J.; Moore, E.; Osthus, D.; Ray, E.L.; Tushar, A.; Yamana, T.K.; et al. A collaborative multiyear, multimodel assessment of seasonal influenza forecasting in the United States. Proc. Natl. Acad. Sci. USA 2019, 116, 3146–3154. [Google Scholar] [CrossRef] [PubMed]
- Shaman, J.; Karspeck, A. Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci. USA 2012, 109, 20425–20430. [Google Scholar] [CrossRef]
- Shaman, J.; Karspeck, A.; Yang, W.; Tamerius, J.; Lipsitch, M. Real-time influenza forecasts during the 2012–2013 season. Nat. Commun. 2013, 4, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Sloan, C.; Heaton, M.; Kang, S.; Berrett, C.; Wu, P.; Gebretsadik, T.; Sicignano, N.; Evans, A.; Lee, R.; Hartert, T. The impact of temperature and relative humidity on spatiotemporal patterns of infant bronchiolitis epidemics in the contiguous United States. Health Place 2017, 45, 46–54. [Google Scholar] [CrossRef]
- Soliman, M.; Lyubchich, V.; Gel, Y.R. Complementing the power of deep learning with statistical model fusion: Probabilistic forecasting of influenza in Dallas County, Texas, USA. Epidemics 2019, 28, 100345. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Cowling, B.J.; Lau, E.H.; Shaman, J. Forecasting influenza epidemics in Hong Kong. PLoS Comput. Biol. 2015, 11, e1004383. [Google Scholar] [CrossRef] [PubMed]
- Walton, N.A.; Poynton, M.R.; Gesteland, P.H.; Maloney, C.; Staes, C.; Facelli, J.C. Predicting the start week of respiratory syncytial virus outbreaks using real time weather variables. BMC Med. Inform. Decis. Mak. 2010, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Weber, A.; Weber, M.; Milligan, P. Modeling epidemics caused by respiratory syncytial virus (RSV). Math. Biosci. 2001, 172, 95–113. [Google Scholar] [CrossRef]
- Abila, D.B.; Dei-Tumi, S.D.; Humura, F.; Aja, G.N. We need to start thinking about promoting the demand, uptake, and equitable distribution of COVID-19 vaccines NOW! Public Health Pract. 2020, 1, 100063. [Google Scholar] [CrossRef]
- Dermody, T.S.; DiMaio, D.; Enquist, L.W. Vaccine Safety, Efficacy, and Trust Take Time. Annu. Rev. Virol. 2020, 8. [Google Scholar] [CrossRef] [PubMed]
- Lawton, G. US won’t delay second dose. New Sci. 2021, 249, 8–9. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Cham, Switzerland, 2001; Volume 40. [Google Scholar]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Chattopadhyay, I.; Kiciman, E.; Elliott, J.W.; Shaman, J.L.; Rzhetsky, A. Conjunction of factors triggering waves of seasonal influenza. eLife 2018, 7, e30756. [Google Scholar] [CrossRef]
- Hethcote, H.W. Mathematics of infectious diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef]
- Rios-Doria, D.; Chowell, G. Qualitative analysis of the level of cross-protection between epidemic waves of the 1918−1919 influenza pandemic. J. Theor. Biol. 2009, 261, 584–592. [Google Scholar] [CrossRef] [PubMed]
- Andreasen, V.; Viboud, C.; Simonsen, L. Epidemiologic Characterization of the 1918 Influenza Pandemic Summer Wave in Copenhagen:Implications for Pandemic Control Strategies. J. Infect. Dis. 2008, 197, 270–278. [Google Scholar] [CrossRef] [PubMed]
- Furati, K.; Sarumi, I.; Khaliq, A. Fractional model for the spread of COVID-19 subject to government intervention and public perception. Appl. Math. Model. 2021, 95, 89–105. [Google Scholar] [CrossRef]
- Stutt, R.O.; Retkute, R.; Bradley, M.; Gilligan, C.A.; Colvin, J. A modelling framework to assess the likely effectiveness of facemasks in combination with lock-down in managing the COVID-19 pandemic. Proc. R. Soc. A 2020, 476, 20200376. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, J.F.; Jorge, D.C.; Veiga, R.V.; Rodrigues, M.S.; Torquato, M.F.; da Silva, N.B.; Fiaccone, R.L.; Cardim, L.L.; Pereira, F.A.; de Castro, C.P.; et al. Mathematical modeling of COVID-19 in 14.8 million individuals in Bahia, Brazil. Nat. Commun. 2021, 12, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Fong, S.J.; Li, G.; Dey, N.; Crespo, R.G.; Herrera-Viedma, E. Finding an accurate early forecasting model from small dataset: A case of 2019-ncov novel coronavirus outbreak. Int. J. Interact. Multimed. Artif. Intell. 2020, 6, 132–140. [Google Scholar] [CrossRef]
- Roques, L.; Klein, E.K.; Papaix, J.; Sar, A.; Soubeyrand, S. Using early data to estimate the actual infection fatality ratio from COVID-19 in France. Biology 2020, 9, 97. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.Y.; Chen, L.; Wang, M. Presumed asymptomatic carrier transmission of COVID-19. JAMA 2020, 323, 1406–1407. [Google Scholar] [CrossRef] [PubMed]
- Buitrago-Garcia, D.; Egli-Gany, D.; Counotte, M.J.; Hossmann, S.; Imeri, H.; Ipekci, A.M.; Salanti, G.; Low, N. Occurrence and transmission potential of asymptomatic and presymptomatic SARS-CoV-2 infections: A living systematic review and meta-analysis. PLoS Med. 2020, 17, e1003346. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, X.; Zhang, X.; Wei, Z.; Zhang, L.; Xu, J.; Liang, P.; Xu, Y.; Zhang, C.; Xu, A. Rapid asymptomatic transmission of COVID-19 during the incubation period demonstrating strong infectivity in a cluster of youngsters aged 16–23 years outside Wuhan and characteristics of young patients with COVID-19: A prospective contact-tracing study. J. Infect. 2020, 80, e1–e13. [Google Scholar] [CrossRef]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef]
- Park, S.W.; Cornforth, D.M.; Dushoff, J.; Weitz, J.S. The time scale of asymptomatic transmission affects estimates of epidemic potential in the COVID-19 outbreak. Epidemics 2020, 31, 100392. [Google Scholar] [CrossRef]
- Shao, S.; Zhou, D.; He, R.; Li, J.; Zou, S.; Mallery, K.; Kumar, S.; Yang, S.; Hong, J. Risk assessment of airborne transmission of COVID-19 by asymptomatic individuals under different practical settings. J. Aerosol Sci. 2020, 151, 105661. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, M.; Yokoe, D.S.; Havlir, D.V. Asymptomatic Transmission, the Achilles’ Heel of Current Strategies to Control Covid. N. Engl. J. Med. 2020, 382, 2158–2160. [Google Scholar] [CrossRef]
- Kinoshita, R.; Anzai, A.; Jung, S.m.; Linton, N.M.; Miyama, T.; Kobayashi, T.; Hayashi, K.; Suzuki, A.; Yang, Y.; Akhmetzhanov, A.R.; et al. Containment, Contact Tracing and Asymptomatic Transmission of Novel Coronavirus Disease (COVID-19): A Modelling Study. J. Clin. Med. 2020, 9, 3125. [Google Scholar] [CrossRef]
- Han, D.; Li, R.; Han, Y.; Zhang, R.; Li, J. COVID-19: Insight into the asymptomatic SARS-COV-2 infection and transmission. Int. J. Biol. Sci. 2020, 16, 2803. [Google Scholar] [CrossRef]
- Teixeira, S.C. Mild and asymptomatic cases of COVID-19 are potential threat for faecal–oral transmission. Braz. J. Infect. Dis. 2020, 24, 368. [Google Scholar] [CrossRef]
- Pollán, M.; Pérez-Gómez, B.; Pastor-Barriuso, R.; Oteo, J.; Hernán, M.A.; Pérez-Olmeda, M.; Sanmartín, J.L.; Fernández-García, A.; Cruz, I.; de Larrea, N.F.; et al. Prevalence of SARS-CoV-2 in Spain (ENE-COVID): A nationwide, population-based seroepidemiological study. Lancet 2020, 396, 535–544. [Google Scholar] [CrossRef]
- Nikolai, L.A.; Meyer, C.G.; Kremsner, P.G.; Velavan, T.P. Asymptomatic SARS Coronavirus 2 infection: Invisible yet invincible. Int. J. Infect. Dis. 2020, 100, 112–116. [Google Scholar] [CrossRef] [PubMed]
- Kronbichler, A.; Kresse, D.; Yoon, S.; Lee, K.H.; Effenberger, M.; Shin, J.I. Asymptomatic patients as a source of COVID-19 infections: A systematic review and meta-analysis. Int. J. Infect. Dis. 2020, 98, 180–186. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Guo, Y.; Mao, R.; Zhang, J. Proportion of asymptomatic coronavirus disease 2019: A systematic review and meta-analysis. J. Med. Virol. 2021, 93, 820–830. [Google Scholar] [CrossRef]
- Johansson, M.A.; Quandelacy, T.M.; Kada, S.; Prasad, P.V.; Steele, M.; Brooks, J.T.; Slayton, R.B.; Biggerstaff, M.; Butler, J.C. SARS-CoV-2 Transmission from People Without COVID-19 Symptoms. JAMA Netw. Open 2021, 4, e2035057. [Google Scholar] [CrossRef] [PubMed]
- Lai, A.; Bergna, A.; Acciarri, C.; Galli, M.; Zehender, G. Early phylogenetic estimate of the effective reproduction number of SARS-CoV. J. Med. Virol. 2020, 92, 675–679. [Google Scholar] [CrossRef]
- Marimuthu, S.; Joy, M.; Malavika, B.; Nadaraj, A.; Asirvatham, E.S.; Jeyaseelan, L. Modelling of reproduction number for COVID-19 in India and high incidence states. Clin. Epidemiol. Glob. Health 2020, 9, 57–61. [Google Scholar] [CrossRef]
- Buckman, S.R.; Glick, R.; Lansing, K.J.; Petrosky-Nadeau, N.; Seitelman, L.M. Replicating and projecting the path of COVID-19 with a model-implied reproduction number. Infect. Dis. Model. 2020, 5, 635–651. [Google Scholar]
- Das, A. An approximation-based approach for periodic estimation of effective reproduction number: A tool for decision-making in the context of coronavirus disease 2019 (COVID-19) outbreak. Public Health 2020, 185, 199–201. [Google Scholar] [CrossRef]
- Matrajt, L.; Eaton, J.; Leung, T.; Brown, E.R. Vaccine optimization for COVID-19, who to vaccinate first? medRxiv 2020, 7, eabf1374. [Google Scholar]
- Is¸lier, Z.G.; Güllü, R.; Hörmann, W. An exact and implementable computation of the final outbreak size distribution under Erlang distributed infectious period. Math. Biosci. 2020, 325, 108363. [Google Scholar] [CrossRef]
- González-Parra, G.; Acedo, L.; Villanueva-Micó, R.J.; Arenas, A.J. Modeling the social obesity epidemic with stochastic networks. Phys. A Stat. Mech. Appl. 2010, 389, 3692–3701. [Google Scholar] [CrossRef]
- Roberts, M.; Andreasen, V.; Lloyd, A.; Pellis, L. Nine challenges for deterministic epidemic models. Epidemics 2015, 10, 49–53. [Google Scholar] [CrossRef]
- González-Parra, G.; Dobrovolny, H.M. Assessing uncertainty in A2 respiratory syncytial virus viral dynamics. Comput. Math. Methods Med. 2015, 2015. [Google Scholar] [CrossRef] [PubMed]
- Wearing, H.J.; Rohani, P.; Keeling, M.J. Appropriate models for the management of infectious diseases. PLoS Med. 2005, 2, e174. [Google Scholar] [CrossRef]
- Faes, C.; Abrams, S.; van Beckhoven, D.; Meyfroidt, G.; Vlieghe, E.; Hens, N. Time between symptom onset, hospitalisation and recovery or death: Statistical analysis of belgian COVID-19 patients. Int. J. Environ. Res. Public Health 2020, 17, 7560. [Google Scholar] [CrossRef] [PubMed]
- Faust, J.S.; del Rio, C. Assessment of Deaths From COVID-19 and From Seasonal Influenza. JAMA Intern. Med. 2020, 180, 1045–1046. [Google Scholar] [CrossRef]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Walsh, F. Loss and resilience in the time of COVID-19: Meaning making, hope, and transcendence. Fam. Process. 2020, 59, 898–911. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, B.B.; Wiegand, S.d.C.B. Losses in times of a pandemic: Bioethical perceptions about mourning caused by COVID-19 in Brazil. Voices Bioeth. 2020, 6. [Google Scholar] [CrossRef]
- Zhai, Y.; Du, X. Loss and grief amidst COVID-19: A path to adaptation and resilience. Brain Behav. Immun. 2020, 87, 80–81. [Google Scholar] [CrossRef]
- Knoll, M.D.; Wonodi, C. Oxford–AstraZeneca COVID-19 vaccine efficacy. Lancet 2020, 397, 72–74. [Google Scholar] [CrossRef]
- Krause, P.; Fleming, T.R.; Longini, I.; Henao-Restrepo, A.M.; Peto, R.; Dean, N.; Halloran, M.; Huang, Y.; Fleming, T.; Gilbert, P.; et al. COVID-19 vaccine trials should seek worthwhile efficacy. Lancet 2020, 396, 741–743. [Google Scholar] [CrossRef]
- Hodgson, S.H.; Mansatta, K.; Mallett, G.; Harris, V.; Emary, K.R.; Pollard, A.J. What defines an efficacious COVID-19 vaccine? A review of the challenges assessing the clinical efficacy of vaccines against SARS-CoV-2. Lancet Infect. Dis. 2020, 21, e26–e35. [Google Scholar] [CrossRef]
- Lipsitch, M.; Dean, N.E. Understanding COVID-19 vaccine efficacy. Science 2020, 370, 763–765. [Google Scholar] [CrossRef]
- Dubé, E.; MacDonald, N.E. How can a global pandemic affect vaccine hesitancy? Expert Rev. Vaccines 2020, 19, 899–901. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Duan, K.; Zhang, Y.; Zhao, D.; Zhang, H.; Xie, Z.; Li, X.; Peng, C.; Zhang, Y.; Zhang, W.; et al. Effect of an inactivated vaccine against SARS-CoV-2 on safety and immunogenicity outcomes: Interim analysis of 2 randomized clinical trials. JAMA 2020, 324, 951–960. [Google Scholar] [CrossRef] [PubMed]
- Dan, J.M.; Mateus, J.; Kato, Y.; Hastie, K.M.; Yu, E.D.; Faliti, C.E.; Grifoni, A.; Ramirez, S.I.; Haupt, S.; Frazier, A.; et al. Immunological memory to SARS-CoV-2 assessed for up to 8 months after infection. Science 2021, 371. [Google Scholar] [CrossRef]
- Times, N.Y. US Inoculations Are Moving More Slowly Than Expected, with 1 Million Vaccinated so Far. Available online: https://nyti.ms/37OL7ur (accessed on 25 December 2020).
- Kim, L.; Garg, S.; O’Halloran, A.; Whitaker, M.; Pham, H.; Anderson, E.J.; Armistead, I.; Bennett, N.M.; Billing, L.; Como-Sabetti, K.; et al. Risk factors for intensive care unit admission and in-hospital mortality among hospitalized adults identified through the US coronavirus disease 2019 (COVID-19)-associated hospitalization surveillance network (COVID-NET). Clin. Infect. Dis. 2020, 72, e206–e214. [Google Scholar] [CrossRef]
- Yehia, B.R.; Winegar, A.; Fogel, R.; Fakih, M.; Ottenbacher, A.; Jesser, C.; Bufalino, A.; Huang, R.H.; Cacchione, J. Association of race with mortality among patients hospitalized with coronavirus disease 2019 (COVID-19) at 92 US hospitals. JAMA Netw. Open 2020, 3, e2018039. [Google Scholar] [CrossRef]
- Mukandavire, Z.; Nyabadza, F.; Malunguza, N.J.; Cuadros, D.F.; Shiri, T.; Musuka, G. Quantifying early COVID-19 outbreak transmission in South Africa and exploring vaccine efficacy scenarios. PLoS ONE 2020, 15, e0236003. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, A.; Yi, B.; Ding, K.; Wang, H.; Wang, J.; Xu, G. The epidemiological characteristics of infection in close contacts of COVID-19 in Ningbo city. Chin. J. Epidemiol. 2020, 41, 668–672. [Google Scholar]
- Mc Evoy, D.; McAloon, C.G.; Collins, A.B.; Hunt, K.; Butler, F.; Byrne, A.W.; Casey, M.; Barber, A.; Griffin, J.M.; Lane, E.A.; et al. The relative infectiousness of asymptomatic SARS-CoV-2 infected persons compared with symptomatic individuals: A rapid scoping review. BMJ Open 2021, 11, e042354. [Google Scholar] [CrossRef]
- Orenes-Piñero, E.; Baño, F.; Navas-Carrillo, D.; Moreno-Docón, A.; Marín, J.M.; Misiego, R.; Ramírez, P. Evidences of SARS-CoV-2 virus air transmission indoors using several untouched surfaces: A pilot study. Sci. Total Environ. 2021, 751, 142317. [Google Scholar] [CrossRef] [PubMed]
- Oran, D.P.; Topol, E.J. Prevalence of Asymptomatic SARS-CoV-2 Infection: A Narrative Review. Ann. Intern. Med. 2020, 173, 362–367. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.J.; Lu, X.X.; Deng, Y.B.; Tang, Y.J.; Lu, J.C. COVID-19: Asymptomatic carrier transmission is an underestimated problem. Epidemiol. Infect. 2020, 148, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention. Available online: https://www.cdc.gov/coronavirus/2019-ncov/hcp/planning-scenarios.html (accessed on 14 May 2021).
- Santarpia, J.L.; Rivera, D.N.; Herrera, V.; Morwitzer, M.J.; Creager, H.; Santarpia, G.W.; Crown, K.K.; Brett-Major, D.; Schnaubelt, E.; Broadhurst, M.J.; et al. Aerosol and surface contamination of SARS-CoV-2 observed in quarantine and isolation care. Sci. Rep. 2020, 110, 12732. [Google Scholar] [CrossRef] [PubMed]
- Mickens, R.E. Advances in the Applications of Nonstandard Finite Difference Schemes; World Scientific: Singapore, 2005. [Google Scholar]
- Jódar, L.; Villanueva, R.J.; Arenas, A.J.; González, G.C. Nonstandard numerical methods for a mathematical model for influenza disease. Math. Comput. Simul. 2008, 79, 622–633. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.J.; Chen-Charpentier, B.M. Positive numerical solution for a nonarbitrage liquidity model using nonstandard finite difference schemes. Numer. Methods Part. Differ. Equ. 2014, 30, 210–221. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Team, I.C.F. Modeling COVID-19 scenarios for the United States. Nat. Med. 2020, 27, 94–105. [Google Scholar]
- Dehkordi, A.H.; Alizadeh, M.; Derakhshan, P.; Babazadeh, P.; Jahandideh, A. Understanding epidemic data and statistics: A case study of COVID-19. J. Med. Virol. 2020, 92, 868–882. [Google Scholar] [CrossRef]
- Quah, P.; Li, A.; Phua, J. Mortality rates of patients with COVID-19 in the intensive care unit: A systematic review of the emerging literature. Crit. Care 2020, 24, 1–4. [Google Scholar] [CrossRef]
- Thompson, M.G.; Burgess, J.L.; Naleway, A.L.; Tyner, H.L.; Yoon, S.K.; Meece, J.; Olsho, L.E.; Caban-Martinez, A.J.; Fowlkes, A.; Lutrick, K.; et al. Interim estimates of vaccine effectiveness of BNT162b2 and mRNA-1273 COVID-19 vaccines in preventing SARS-CoV-2 infection among health care personnel, first responders, and other essential and frontline workers—Eight US locations. Morb. Mortal. Wkly. Rep. 2021, 70, 495. [Google Scholar] [CrossRef] [PubMed]
- Ahn, D.-G.; Shin, H.-J.; Kim, M.-H.; Lee, S.; Kim, H.-S.; Myoung, J.; Kim, B.-T.; Kim, S.-J. Current Status of Epidemiology, Diagnosis, Therapeutics, and Vaccines for Novel Coronavirus Disease 2019 (COVID-19). J. Microbiol. Biotechnol. 2020, 30, 313–324. [Google Scholar] [CrossRef] [PubMed]
- Burki, T.K. The Russian vaccine for COVID-19. Lancet Respir. Med. 2020, 8, e85–e86. [Google Scholar] [CrossRef]
- Chagla, Z. The BNT162b2 (BioNTech/Pfizer) vaccine had 95% efficacy against COVID-19 ≥7 days after the 2nd dose. Ann. Intern. Med. 2021, 174, JC15. [Google Scholar] [CrossRef]
- Hung, I.F.N.; Poland, G.A. Single-dose Oxford-AstraZeneca COVID-19 vaccine followed by a 12-week booster. Lancet 2021, 397, 854–855. [Google Scholar] [CrossRef]
- Abu Jabal, K.; Ben-Amram, H.; Beiruti, K.; Batheesh, Y.; Sussan, C.; Zarka, S.; Edelstein, M. Impact of age, ethnicity, sex and prior infection status on immunogenicity following a single dose of the BNT162b2 mRNA COVID-19 vaccine: Real-world evidence from healthcare workers, Israel, December 2020 to January. Eurosurveillance 2021, 26, 2100096. [Google Scholar] [CrossRef]
- Yu, J.; Tostanoski, L.H.; Peter, L.; Mercado, N.B.; McMahan, K.; Mahrokhian, S.H.; Nkolola, J.P.; Liu, J.; Li, Z.; Chandrashekar, A.; et al. DNA vaccine protection against SARS-CoV-2 in rhesus macaques. Science 2020, 369, 806–811. [Google Scholar] [CrossRef]
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Perez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and Efficacy of the BNT162b2 mRNA COVID-19 Vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef]
- Tregoning, J.S.; Brown, E.S.; Cheeseman, H.M.; Flight, K.E.; Higham, S.L.; Lemm, N.M.; Pierce, B.F.; Stirling, D.C.; Wang, Z.; Pollock, K.M. Vaccines for COVID-19. Clin. Exp. Immunol. 2020, 202, 162–192. [Google Scholar] [CrossRef]
- Abu-Raddad, L.J.; Chemaitelly, H.; Butt, A.A. Effectiveness of the BNT162b2 COVID-19 Vaccine against the B.1.1.7 and B.1.351 Variants. N. Engl. J. Med. 2021, 385, 187–189. [Google Scholar] [CrossRef]
- Mahase, E. COVID-19: Moderna applies for US and EU approval as vaccine trial reports 94.1% efficacy. BMJ 2020, 371, m4709. [Google Scholar] [CrossRef] [PubMed]
- Mahase, E. COVID-19: Pfizer vaccine efficacy was 52% after first dose and 95% after second dose, paper shows. BMJ 2020, 371, m4826. [Google Scholar] [CrossRef] [PubMed]
- Shinde, V.; Bhikha, S.; Hoosain, Z.; Archary, M.; Bhorat, Q.; Fairlie, L.; Lalloo, U.; Masilela, M.S.; Moodley, D.; Hanley, S.; et al. Efficacy of NVX-CoV2373 COVID-19 vaccine against the B.1.351 variant. N. Engl. J. Med. 2021, 384, 1899–1909. [Google Scholar] [CrossRef] [PubMed]
- Nelson, R. COVID-19 disrupts vaccine delivery. Lancet Infect. Dis. 2020, 20, 546. [Google Scholar] [CrossRef]
- Weintraub, R.L.; Subramanian, L.; Karlage, A.; Ahmad, I.; Rosenberg, J. COVID-19 Vaccine to Vaccination: Why Leaders Must Invest in Delivery Strategies Now: Analysis describe lessons learned from past pandemics and vaccine campaigns about the path to successful vaccine delivery for COVID-19. Health Aff. 2020, 40, 33–41. [Google Scholar] [CrossRef]
- Bartsch, S.M.; O’Shea, K.J.; Ferguson, M.C.; Bottazzi, M.E.; Wedlock, P.T.; Strych, U.; McKinnell, J.A.; Siegmund, S.S.; Cox, S.N.; Hotez, P.J.; et al. Vaccine efficacy needed for a COVID-19 coronavirus vaccine to prevent or stop an epidemic as the sole intervention. Am. J. Prev. Med. 2020, 59, 493–503. [Google Scholar] [CrossRef] [PubMed]
- Dinleyici, E.C.; Borrow, R.; Safadi, M.A.P.; van Damme, P.; Munoz, F.M. Vaccines and routine immunization strategies during the COVID-19 pandemic. Hum. Vaccines Immunother. 2020, 17, 400–407. [Google Scholar] [CrossRef] [PubMed]
- Yamey, G.; Schäferhoff, M.; Hatchett, R.; Pate, M.; Zhao, F.; McDade, K.K. Ensuring global access to COVID-19 vaccines. Lancet 2020, 395, 1405–1406. [Google Scholar] [CrossRef]
- Mahase, E. COVID-19: Novavax vaccine efficacy is 86% against UK variant and 60% against South African variant. BMJ 2021, 372. [Google Scholar] [CrossRef]
- Iacobucci, G. COVID-19: New UK variant may be linked to increased death rate, early data indicate. BMJ 2021, 372, n230. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, F.; Abadi, A.T.B. Implications of the Emergence of a New Variant of SARS-CoV-2, VUI-202012. Arch. Med. Res. 2021. [Google Scholar] [CrossRef] [PubMed]
- Sperrin, M.; Grant, S.W.; Peek, N. Prediction models for diagnosis and prognosis in COVID-19. BMJ 2020, 369. [Google Scholar] [CrossRef] [PubMed]
- Haque, A.; Pant, A.B. Efforts at COVID-19 Vaccine Development: Challenges and Successes. Vaccines 2020, 8, 739. [Google Scholar] [CrossRef]
- Verger, P.; Dubé, E. Restoring confidence in vaccines in the COVID-19 era. Expert Rev. Vaccines 2020, 19, 991–993. [Google Scholar] [CrossRef] [PubMed]
- Ayoub, H.H.; Chemaitelly, H.; Abu-Raddad, L.J. Epidemiological Impact of Novel Preventive and Therapeutic HSV-2 Vaccination in the United States: Mathematical Modeling Analyses. Vaccines 2020, 8, 366. [Google Scholar] [CrossRef]
- Benest, J.; Rhodes, S.; Quaife, M.; Evans, T.G.; White, R.G. Optimising Vaccine Dose in Inoculation against SARS-CoV-2, a Multi-Factor Optimisation Modelling Study to Maximise Vaccine Safety and Efficacy. Vaccines 2021, 9, 78. [Google Scholar] [CrossRef]
- Chaves, L.F.; Hurtado, L.A.; Rojas, M.R.; Friberg, M.D.; Rodríguez, R.M.; Avila-Aguero, M.L. COVID-19 basic reproduction number and assessment of initial suppression policies in Costa Rica. Math. Model. Nat. Phenom. 2020, 15, 32. [Google Scholar] [CrossRef]
- Contreras, S.; Villavicencio, H.A.; Medina-Ortiz, D.; Saavedra, C.P.; Olivera-Nappa, Á. Real-time estimation of Rt for supporting public-health policies against COVID-19. Front. Public Health 2020, 8. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Parra, G.; Díaz-Rodríguez, M.; Arenas, A.J. Mathematical modeling to design public health policies for Chikungunya epidemic using optimal control. Optim. Control. Appl. Methods 2020, 41, 1584–1603. [Google Scholar] [CrossRef]
- González-Parra, G.; Díaz-Rodríguez, M.; Arenas, A.J. Optimization of the Controls against the Spread of Zika Virus in Populations. Computation 2020, 8, 76. [Google Scholar] [CrossRef]
- Nistal, R.; de la Sen, M.; Gabirondo, J.; Alonso-Quesada, S.; Garrido, A.J.; Garrido, I. A Modelization of the Propagation of COVID-19 in Regions of Spain and Italy with Evaluation of the Transmission Rates Related to the Intervention Measures. Biology 2021, 10, 121. [Google Scholar] [CrossRef]
- Shim, E. Optimal Allocation of the Limited COVID-19 Vaccine Supply in South Korea. J. Clin. Med. 2021, 10, 591. [Google Scholar] [CrossRef]
- Van Oosterhout, C.; Hall, N.; Ly, H.; Tyler, K.M. COVID-19 evolution during the pandemic–Implications of new SARS-CoV-2 variants on disease control and public health policies. Virulence 2021, 12, 507. [Google Scholar] [CrossRef]
- Zenk, L.; Steiner, G.; Pina e Cunha, M.; Laubichler, M.D.; Bertau, M.; Kainz, M.J.; Jäger, C.; Schernhammer, E.S. Fast Response to Superspreading: Uncertainty and Complexity in the Context of COVID. Int. J. Environ. Res. Public Health 2020, 17, 7884. [Google Scholar] [CrossRef]
- Gumel, A.B.; Iboi, E.A.; Ngonghala, C.N.; Elbasha, E.H. A primer on using mathematics to understand COVID-19 dynamics: Modeling, analysis and simulations. Infect. Dis. Model. 2021, 6, 148–168. [Google Scholar]
- Gupta, R.K. Will SARS-CoV-2 variants of concern affect the promise of vaccines? Nat. Rev. Immunol. 2021, 21, 340–341. [Google Scholar] [CrossRef]
- Kupferschmidt, K. Vaccinemakers ponder how to adapt to virus variants. Science 2021, 371, 448–449. [Google Scholar] [CrossRef] [PubMed]
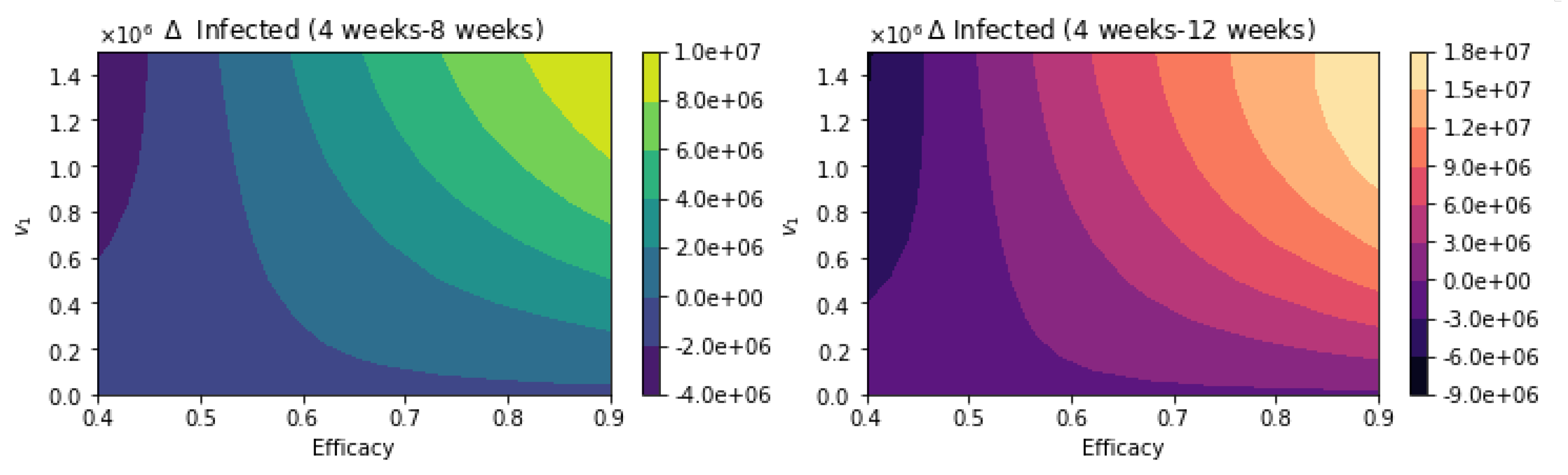
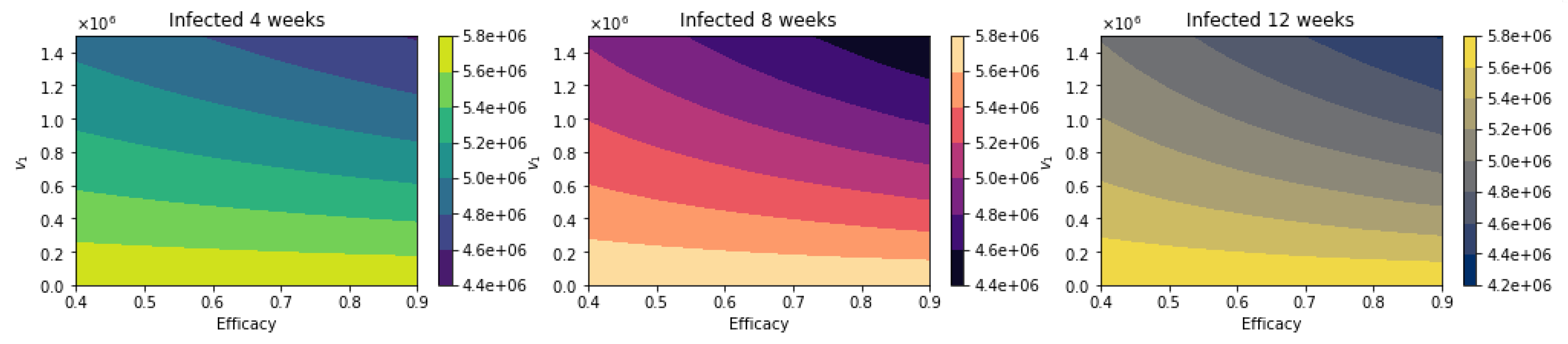

| Parameter | Symbol | Value |
|---|---|---|
| Latent | E(0) | 997,600 |
| Presymptomatic | P(0) | 791,200 |
| Infected (symptomatic) | I(0) | 1,204,000 |
| Asymptomatic | A(0) | 1,204,000 |
| Hospitalized | H(0) | 71,552 |
| Recovered | R(0) | 16,462,937 |
| Total population | N(0) | 330,705,643 |
| Parameter | Symbol | Value |
|---|---|---|
| Latent period | 1/α | 2.9 days [1,118,119] |
| Presymptomatic period | 1/p | 2.3 days [1,118,119] |
| Infectious period | 1/γ | 7 days [118] |
| Hospitalization rate | h | 0.1/7 days−1 [4,118,120] |
| Hospitalization period | ρ | 0.9/10.4 days−1 [4,118,120] |
| Death rate (hospitalized) | δ | 0.1/10.4 days−1 [17,121] |
| Probability of being asymptomatic | a | 0.5 [1,111] |
| Efficacy of the vaccines | εi | Varied |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Parra, G. Analysis of Delayed Vaccination Regimens: A Mathematical Modeling Approach. Epidemiologia 2021, 2, 271-293. https://doi.org/10.3390/epidemiologia2030021
Gonzalez-Parra G. Analysis of Delayed Vaccination Regimens: A Mathematical Modeling Approach. Epidemiologia. 2021; 2(3):271-293. https://doi.org/10.3390/epidemiologia2030021
Chicago/Turabian StyleGonzalez-Parra, Gilberto. 2021. "Analysis of Delayed Vaccination Regimens: A Mathematical Modeling Approach" Epidemiologia 2, no. 3: 271-293. https://doi.org/10.3390/epidemiologia2030021
APA StyleGonzalez-Parra, G. (2021). Analysis of Delayed Vaccination Regimens: A Mathematical Modeling Approach. Epidemiologia, 2(3), 271-293. https://doi.org/10.3390/epidemiologia2030021






