Abstract
Extracting relevant data from real-world experiments is often challenging with intrinsic materials and device property dispersion, such as in organic electronics. However, multivariate data analysis can often be a mean to circumvent this and to extract more information when larger datasets are used with learning algorithms instead of physical models. Here, we report on identifying relevant information descriptors for organic electrochemical transistors (OECTs) to classify aqueous electrolytes by ionic composition. Applying periodical gate pulses at different voltage magnitudes, we extracted a reduced number of nonredundant descriptors from the rich drain-current dynamics, which provide enough information to cluster electrochemical data by principal component analysis between Ca2+-, K+-, and Na+-rich electrolytes. With six current values obtained at the appropriate time domain of the device charge/discharge transient, one can identify the cationic identity of a locally probed transient current with only a single micrometric device. Applied to OECT-based neural sensors, this analysis demonstrates the capability for a single nonselective device to retrieve the rich ionic identity of neural activity at the scale of each neuron individually when learning algorithms are applied to the device physics.
1. Introduction
Recent machine-learning (ML) applications aim to interface sensing devices with data analysis programs and algorithms [1,2,3,4,5]. Merging both sensing hardware and ML software concepts in a sensing paradigm has often underlined the necessity to define new sensing figures of merit [6]. For as long as sensors have been developed, their well-defined standards have provided clear guidelines to engineering the subsequent sensing technologies. As examples of figures of merit, “selectivity” and “sensitivity” remain universal from one sensor technology to another [7]. As the complexity of media grows from the laboratory to practical application in the real environments, so does the dimensionality of the information space which should be characterized for optimal identification. Good examples of high-complexity environments include biological media (such as neuro-sensing via microelectrode arrays, for instance) [8,9], where the rich biochemistry easily interferes multiparametrically with any chemo-sensing technology. Selectivity can be evaluated only up to a certain extent, and sensitivity can only be assessed under “standard conditions”. Even the concept of “standard conditions” is incomplete in a framework where the environment dimensionality cannot be evaluated due to the lack of a physically nontrivial elementary vector basis characterizing the whole environment space (a relevant example of such a physically nontrivial feature space with unknown dimensionality would be olfactory spaces) [10,11,12].
Sensors are well adapted to the monovariate analysis of controlled environments. To identify multivariate information from real environments, sensing at higher orders regroups many strategies to increase the dimensionality of the output that sensing platforms can deliver [13]. These strategies can be divided into two categories: the ones increasing dimensionality by the number of sensing elements and the ones exploiting the multiparametricity of physical laws in the sensing elements’ response. Both strategies have limits: For the first strategy, hardware limits the cointegration capabilities of a large number of materials/sensing devices with an even larger number of interconnections. For the second strategy, even if the emergence of data analysis techniques has eased the processing of large-dimension vectors, one needs to identify relevant information descriptors in the sensing element response, a priori, to decrease computational costs. This is particularly essential for dynamic sensing applications.
In this framework, we propose a proof of concept for identifying the relevant descriptors for an optimal ion recognition of the dynamic analysis of electrolyte blends using organic electrochemical transistors (OECTs). OECTs are state-of-the-art technology for both neuro-sensing and neuromorphic computing [14,15,16]. The two fields attest on the challenges of complex environment interfacing and of recognizing physically nontrivial information patterns, with OECTs potentially solving high interconnection-degree issues thanks to electronic/electrolytic coupling. These ion-sensing transistors operate upon the polarization of their three electrodes (namely the source S, the drain D and the gate G electrodes as depicted in the schematic Figure 1) to promote ion accumulation in the bulk of the PEDOT:PSS doped conducting polymer channel and modulate its conductance level under a steady state regime [17]. The current response of the device is also ion sensitive under a transient regime, such that the OECT’s drain current response is dominated by ionic currents [17]. Both physical mechanisms being distinct, it has been shown by impedance spectroscopy that both uncorrelated dependencies can be probed at different frequencies to exploit the dynamic response of the OECT for biparametric sensing. As such, it allows for the extraction of a cation-specific two-dimensional footprint from the single device without chemical labelling [18]. The later modelling of the OECT impedimetric responses under different conditions has revealed that the device gathers at least eight independent ion-sensitive circuit elements, demonstrating further potential to be exploited for higher order ion sensing [19].
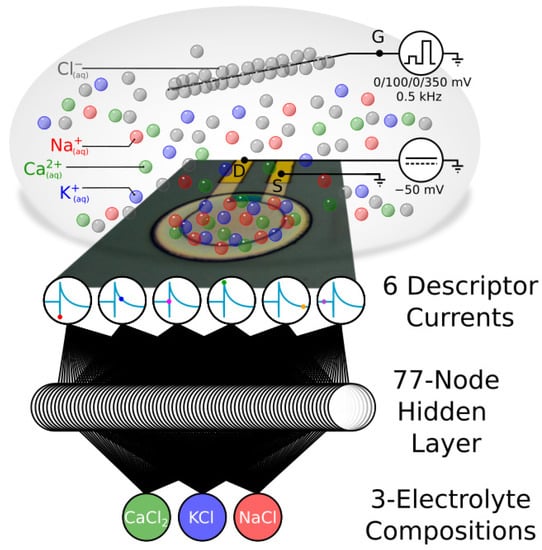
Figure 1.
Working principle: an OECT device exposed to electrolytes of different compositions records periodically transient currents, characteristics of the ions, and the applied voltages. From a restricted number of current samples extracted at specific times in the characteristic transient, one can access a specific signature of the electrolyte owing to the multiparametricity of the OECT as an ion sensor. After projection of these descriptors in an artificial neural network with a single hidden layer, it is possible to discriminate the samples according to their electrolytic composition without particular chemical probe labelling.
As confirmed in this study, the six relevant descriptors we identified in the OECT current transient allow for the classification of the ion response of different blends of salts by their ionic contents. Consequently, feeding these currents to an artificial neural network enabled the recognition of calcium, sodium and potassium ions in blends of different relative concentrations even in the case when the ion identified was a minority one at the molar level of 1/100. ANNs were previously used for recognizing the concentration measurements with some success [20,21]. While overall performance of the ANNs was good and scaled with training, the technique showed limitations in recognizing cations depending on the fact they constitute the blends in a majority or in a minority. However, the results clearly indicate that no selective materials have to be involved in recognizing cations. Here, we show that descriptors obtained by OECT enable a universal recognition of very different ionic concentration profiles without having to design the sensor to be sensitive to a particular target. We propose redefining sensors’ figures of merits (sensitivity and selectivity) for machine-learning supported multivariate analysis and revising the mastering of the device’s physico-chemical properties to promote new application-specific properties more relevant for optimal recognition.
2. Experimental Section
2.1. Device Operation
Details of the microfabrication of the PEDOT:PSS-based OECT device have been published elsewhere [22]. The micrometric device (70 μm) has a concentric electrode geometry with a central round platinum electrode as a drain, concentric to an outer annular source electrode also made of platinum. Both electrodes are electrically connected together via a thin layer (16 nm) of cation-sensitive conductive polymer, which is PEDOT:PSS.
2.2. Electrical Characterization
Transient currents were recorded using an Agilent B1500 Parameter Analyzer, and voltage inputs were addressed with Agilent B1530A waveform generators. Operated as an electrolyte-gated field-effect transistor, a macroscopic wire was used as a gate electrode, and an aqueous solution drop of metal chloride salts was used as the electrolyte (the concentration of metal ions for all experiments was fixed at 0.1 M). For each electrolyte tested, the OECT was stressed for a total duration of 200 ms with 100 periods of gate voltage (VG) stepped-frequency waveform (waveform period: 2 ms). The elementary waveform period contained two voltage-stepped levels of VG = 350 mV and 100 mV separated from the resting steps at VG = 0 V (duty cycle = 50%; see Figure 2b for the waveform). During operation, the drain electrode was steadily polarized at VD = −50 mV to promote a drain current embedding both the time dependency of the electrolytic current from the transient gate-drain polarization and the steady electronic conduction from the source-drain polarization. The source electrode was grounded. Between each of the 25 experiments with different electrolytes, the device and the gate were thoroughly rinsed with deionized water and tested in fresh deionized water with the same electrical protocol to verify the absence of ions prior to exposure of the next electrolyte.
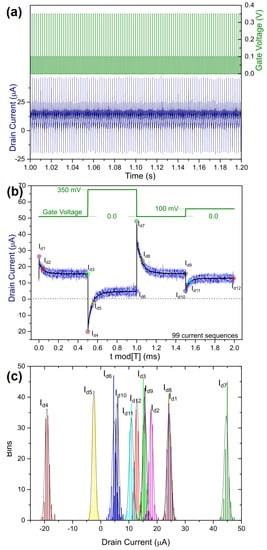
Figure 2.
(a) Drain current signal acquisition (blue) upon a squared-voltage gate stimulation (green) in 0.1 M of KCl(aq). (b) The 2 ms signal sampling which shows the stability of the drain current of a single 200 ms measurement in 0.1 M of KCl(aq) (the 99 blue-shaded curves are characteristic of the sequenced periods of drain currents, and the black curve corresponds to the averaging of the 99 drain current curves). (c) Statistic distributions of the 12 characteristic values taken from the drain current signal of a single 200 ms measurement in 0.1 M of KCl(aq).
2.3. Data Analysis
Data were analyzed as generated from the parameter analyzer without electronic or digital prefiltering. All data analyses (PCA and ANN) were performed a posteriori the acquisition. Principal component analysis (PCA) was performed using the open-access online tool ClustVis, scaled to unit variance and using the singular-value-decomposition method [23]. After this, we created an artificial neural network (ANN) in order to test the recognizability of the electrolyte composition. We analyzed a number of architectures and found that ANN that consists of 77 nodes in the hidden layer, and training with scaled conjugate gradient backpropagation provided the best results. As seen in Figure 3, the environments were reasonably well separated, and we used 99 different realizations of the same environment. During training, we chose 70% of the data as a training set, 15% as a validation set, and 15% as a testing set. We performed two different sampling methods. In the first one, we sampled training, validation, and testing sets completely randomly from all the data sets. In the second, we sampled the same ratios from each individual environment. We found that the error and error percentage were similar in both sampling methods, although the second sampling scenario was a percentage or two percentage points better. We also performed different tasks. In the first one, we considered the precise categorization of the environment with ANN; therefore, we had 25 output nodes related to each of the 25 different environments. In the second task, we evaluated whether we had categorized correctly when the data set contained more than x% of certain ionic concentration. The receiver operating characteristic (ROC) curves and confusion matrices were generated from the descriptor analysis via an artificial neural network.
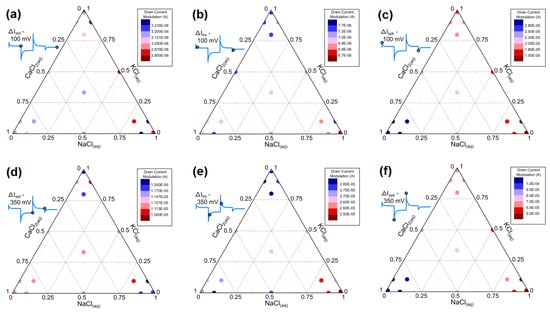
Figure 3.
Ternary diagrams representing the mean drain current modulations ΔI at the steady states (a,d), the transients (b,e), and the spikes (c,f) for the 100 mV (a–c) and the 350 mV (d–f) gate modulations for the 25 different electrolyte environments of various KCl(aq), NaCl(aq), and CaCl2(aq) compositions (details of the 25 different compositions as supporting information are provided in Table S1).
3. Results and Discussion
3.1. OECT Data Sequencing
Many concerns were taken into account to generate a sufficient amount of data from the electrolyte-dependent organic electrochemical transistor. First, we used a single device for this analysis to exclude systematic deviations in the data coming from the intrinsic device performance variabilities (for instance, from different conductivities of PEDOT:PSS formulations or inherent reproducibility dispersion associated with the device microfabrication process) [24]. Second, all data were acquired in a single time period to eliminate deviations due to device aging. While both measures were taken to reduce systematic errors for the sake of the analysis quality, the applicability of this strategy is not limited for treating data from multiple devices simultaneously nor during longer acquisition, at the condition of providing a substantially higher amount of data to the analytic system.
We dynamically analyzed the drain current of the OECT sampled as a relevant information carrier to analyze the electrolyte recognition. To embed both steady and transient information from the OECT, we applied a gate–voltage waveform, optimized for the drain current to gather a high multiparametricity of ionic information (a period higher than all the ion-specific OECT time constants) [18]. This elementary sequence used two voltage stimulations at VG = 100 mV and VG = 350 mV, which stimulated the OECT under two different regimes (as a transistor is a nonlinear element for the voltage, the two ion-specific data sets are not necessarily linearly correlated). The two voltage steps were separated by resting times (VG = 0) of equal duration to collect the ion-specific transient current of a charge and a discharge at a specific stress (as the anions and cations have different charge accumulation modes in the OECT, the asymmetry in the transient might gather a higher-order information). The duration of the voltage steps was set at 0.5 ms to collect the complete transient dynamics of the OECT charge and discharge, from which the characteristic current gathered both high-frequency and low-frequency impedance information. It has been observed that the characteristic time of the current transient could allow further downscaling of the elementary period, so such an elementary period was set below 1 ms, which was shorter than was the neural action potentials observed in neuro-sensing.
The recording of the drain current under such a gate-voltage stimulation appeared to be rather stable over time, as no current drift over time was observed for a given 100-period series (see Figure 2a). A sequence 200 ms in duration allowed us to collect 100 periods (minus the first one which was altered by the drain voltage turn-on) of an elementary stimulation (see Figure 2b). At the timescale of these elementary stimulations, it appeared that the drain current also showed very low dispersion over the whole period. Within the stimulation period, one can distinguish the dynamics of the drain current with respect to the gate-voltage transitions: the drain current exponentially increases and converges to a plateau at the beginning of a positive gate voltage polarization and decays to another plateau after the end of the positive gate-voltage polarizations (related to the behavior of a depletion mode p-type OECT characteristic from PEDOT:PSS).
For each of the four current modulations within a period, we sampled currents at three specific times delayed from the gate-voltage modulations: 1, 50, and 500 μs after each gate-voltage modulation. These were respectively characterized by four spikes, the four transients and the four steady-state plateaus of the current. Again, when focused at these 12 specific current values, we observed a very narrow relative dispersion over the 99 samples for one 200 ms sequence for each electrolyte (see Figure 2c). While some dispersions were very distinct from the others (particularly the spike currents for the highest voltage stimulation Id4 and Id7, representative of the largest current transitions in absolute value), some dispersions overlapped with one another (as current Id3 and Id9 which are both representative of the steady current at VG = 0 V characteristic of the pristine conductivity of PEDOT:PSS). Moreover, when looking at the dispersion of the 12 Id populations, one can observe their symmetry centered on a mean value, suggesting that their variance over the 99 samples was not induced by a drift of the voltage over time (one can observe in Figure 2b that the individual currents are rather noisy but centered on an average). The fact that each measurement sequence lasts for only 200 ms (which in practice is not long enough to qualify the stability of an integral OECT signal for a practical sensing application) shows that this method collects, in a rather short time, a significantly high number of drain-current samples, the analysis of which is not temporally biased.
3.2. Data Descriptor Comparison
As previous studies have compared modulations of currents [22] or impedances [18], in order to compare the effect of the electrolyte composition on the OECT electrical performances, we reduced the number of descriptors down to six current modulations using the 12 Id currents previously collected, as follows:
- -
- ΔIstd100 = Id3 − Id12 as the steady-state drain current modulation at VG = 100 mV;
- -
- ΔItrs100 = Id2 − Id11 as the 50-μs transient drain current modulation at VG = 100 mV;
- -
- ΔIspk100 = Id1 − Id10 as the 1-μs spike drain current modulation at VG = 100 mV;
- -
- ΔIstd350 = Id9 − Id6 as the steady-state drain current modulation at VG = 350 mV;
- -
- ΔItrs350 = Id8 − Id5 as the 50-μs transient drain current modulation at VG = 350 mV;
- -
- ΔIspk350 = Id7 − Id4 as the 1-μs spike drain current modulation at VG = 350 mV.
Observing previously that the 12 Id current series of 99 samples characterizing a single electrolyte measurement had the dispersion centered on a characteristic mean value, this applied also for the six ΔI descriptors. We studied the mean values of the six ΔI descriptors iteratively for the 25 different electrolytes (see Figure 3a–f). From these studies, we observed that each descriptor had an ion-specific fingerprint displaying a current-modulation map in the ternary diagrams different from one descriptor to another. For both gate voltages, we observed that the lower current modulations obtained for ΔIstd and ΔItrs generated a systematically higher variability than that for ΔIspk: for both VG = 100 mV and 350 mV, one can better see a linear gradient in the current modulations over the ternary diagram of ΔIspk than for ΔItrs and ΔIstd. These results are in line with previous impedimetric studies on pure electrolytes showing that the variability in the impedance modulation of OECTs at a low frequency is higher than that at a high frequency [18]. Practically speaking, this suggests that if such an OECT were used as monoparametric ion sensors, one would obtain fewer systemic errors by exploiting the capacitive coupling between the polymer and the gate (as done in microelectrode arrays for neural interfacing) compared to the use of ion-dependent conductance of the channel. On the ΔIspk diagrams, one can clearly notice higher modulations for the divalent cation than for the monovalent ones (which agrees with previous studies) [18]. On the other hand, data related to ΔItrs and ΔIstd appear to have a higher voltage dependency than do those related to ΔIspk [18]. Although current modulations differ with the gate voltage, their trend with the electrolyte composition of ΔIspk.at VG = 100 mV and 350 mV appears to be very similar, which might question the relevance of using both parameters as descriptors, as this may pose a risk of increasing the analysis complexity without benefits. However, in the cases of ΔItrs and ΔIstd, their voltage-dependency suggests that recording these data for different VG introduces additional ionic information which could be used for the electrolyte recognition (the voltage dependency of these modulation is associated with the gate-voltage dependency of the PEDOT:PSS dedoping) [18].
3.3. Data Separability by Electrolyte Composition
Independently of the quality of the relative concentration trends and their dependency with VG, we performed the following multivariate data analysis with all six current modulation descriptors. Principal component analysis (PCA) was performed on 25 electrolytes with a series of 99 vectors of six components (the following approach consisted of clustering the 2475 vectors of R6 by projecting the data in the relevant subspace maximizing the variance). Prior to singular value decomposition, current modulation descriptors were unit-variance scaled by default. It is worth highlighting the fact that this data preprocessing stage conditions the data to compare current modulations of OECT relative to an average at a given time and does not treat each value nominally as a value with a specific unit. Therefore, one can extrapolate that such analysis treated in parallel with many OECTs with different conductance and transconductance values might not under- or overweight the contributions of the OECTs according to their physical property dispersion. This can be compared to a microelectrode array for neuro-sensing, for which statistical thresholding for spike detection is associated to a relative value for a specific sensing electrode, which is less affected by the impedance dispersion over the population of sensing electrodes. The PCA using singular-value decomposition showed that the actual dimensionality of all data can be reduced to five since the variance of the PC6 was significantly lower than were all the others (<0.3%; see Table 1). The composition of the PC6 being almost the sum of both ΔIspk100 and ΔIspk350 confirms the irrelevance of measuring ΔIspk at the two different voltages VG = 100 mV and 350 mV (we also noticed that their contributions in all six principal components were almost identical; blue font in Table 1), although each of them had a nonnegligible and equal relevance for data separation (as the main contribution of PC1). When looking at the first two principal components, we observed that 57.9% of the total variance can be projected on the (PC1;PC2) plane. PC1 (38% of total variance) largely composed of both spike descriptors ΔIspk100 and ΔIspk350 (with a minor contribution of the other 350 mV parameters ΔItrs350 and ΔIstd350) while PC2 (19.9% of total variance) is composed of the four other parameters ΔIstd100, ΔIstd350, ΔItrs100, and ΔItrs350. This shows that all six descriptors have a contribution in the data projection on the (PC1; PC2) plane, such that a 3D projection is not required to appreciate the six-descriptor contributions on the data separability (see Figure 4a–e).

Table 1.
Factor loading matrix for the PCA exploiting the six different current descriptors.
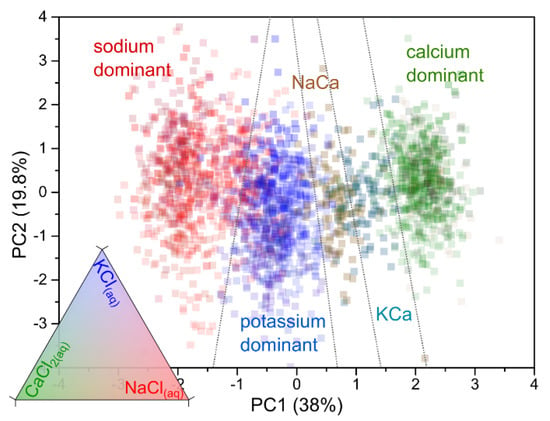
Figure 4.
Two-principal-component projections of the 99 vectors for each of the 25 electrolyte compositions. Color gradients according to the relative concentration of KCl(aq), NaCl(aq), and CaCl2(aq) in 0.1 M (the bottom-left triangle displays the 3-color shade encoding the electrolytes’ composition). The graph shows the data separability, according to the nature of the cation, into five different domains representative of the electrolyte composition.
As these projections show, the PCA successfully clusters the electrolyte data by compositions into five different sectors (see Figure 4d). The main separation in electrolyte composition occurs on the PC1 dimension, showing that the spike data have the highest importance for segregating the clusters to discriminate the electrolytes by their cation composition. Because various electrolyte compositions were used in these experiments, the five domains had strong overlaps, indicating that a linear data classifier will hardly lead to a perfect cation recognition (although we noticed that the three data series of pure salts were easily separable into ellipsoids with no overlap). In the case of these 25 mixed electrolytes, one can clearly distinguish calcium-rich, a potassium-rich, and sodium-rich domains. Considering the (PC1; PC2) projections, the potassium-rich domain being between the calcium-rich and sodium-rich domains suggests a higher difficulty in recognizing potassium compared to sodium or calcium. The relative distance of the calcium domain relative to potassium being longer than that to the sodium one suggests that Ca2+ variations might be the easiest to detect. This is of a particular relevance for Ca2+(aq) sensing in an extracellular medium composed mainly of Na+(aq) and Cl−(aq) for a total concentration in the 0.1 M range (calcium flows being particularly important in neural activity) [25,26]. Furthermore, we distinguished two other subdomains between the calcium-rich and the potassium-rich domains which correspond to the data for Na+(aq)/Ca2+(aq) (1:1) and K+(aq)/Ca2+(aq) (1:1). The separation of both domains also supports the possibility of specifically detecting Ca2+(aq) when blended with K+(aq) and Na+(aq) and vice versa, confirming its relevance when applied to the sensing of physiological fluids.
PCA performed with a reduced number of descriptors demonstrated the degree of relevance for the different descriptors in the data separation specific to the clustering by ionic composition (all detailed PCA data are available as supplementary information in Figure S1). Qualitatively, it was revealed that the transient points do not contribute significantly to the data separation. Moreover, performing the PCA without considering the 350 mV data or the steady-state data increases the separability due to systematic variations from measurement to measurement. Finally, PCA omitting the spike data seems to be very inefficient for cation recognition. In light of these different elements, it appears necessary to consider all six descriptors to identify cations.
3.4. Environment Recognition via an Artificial Neural Network
Based on the aforementioned analysis, we created artificial neural networks (ANNs) in order to test the recognizability of the electrolyte composition based on the sequential sampling of the six values of drain current modulations that were shown by PCA to embed five independent descriptors relevant for cation recognition. We analyzed a number of architectures and found that an ANN consisting of 77 nodes in the hidden single-layer, trained with scaled conjugate gradient backpropagation and sigmoid activation function provided the best results as indicated by the average positive classification rate in repeated learning scenarios [27,28]. We also used a stochastic gradient with similar performance but a longer training time and linear activation, which was less accurate in convergence and ReLU (rectified linear unit), which had very similar behavior to the sigmoid activation function. During the testing of different networks, we used 1-, 2-,and 3-layered architectures with a number of nodes ranging from 25 to 200. To test the architecture that we would adopt for the tasks, we sampled each class, trained the network, and computed the total success rate. We have then used mean success rates for each of the 25 classes to find the mean success rate over all the samples and chose the architecture that had the maximal rate. We found that a simple architecture of one layer with 77 nodes performed similarly to more complicated architectures within the margin of error and was the simplest within the architectures that had similar performance. We also employed the method described by Stathakis [29] but we found that it slowed the calculation further without improving the results within the subset of architectures we tested with this method. In supplementary information 4, we provide the standard MATLAB script used in testing the individual architectures. In essence, the ANN had a feedforward network architecture with the default tan–sigmoid transfer function in the hidden layer and a softmax transfer function in the output layer as the standards for most pattern recognition tasks. We used MATLAB R2011b with the Neural Network Toolbox.
As seen in Figure 3, environments were reasonably well separated into 25 different electrolyte compositions with various Ca2+(aq), Na+(aq), and K+(aq) contents and 99 different realizations for each electrolytic environment. To test the different ANN architectures, data were separated into three sets: The first set was used to train the ANN, which consisted of 70% of randomly picked measurements of each electrolyte environment. The second set was used as a validation, which consisted of 15% of each environment. The last set was the test set, which consisted of the last 15% of the data.
The ANN was used in two specific classifier tasks. The first task was to recognize to which of the 25 different patterns the data belonged to. The second task was set to classify the ionic concentration of the certain type of cation to be greater/less than a given threshold. The settlement of both tasks was made for clear biological relevance in the perspective of neuro-sensing applications, such that the first one could be applied for the statistical identification of unknown-cation activity in electrogenic cells while the second triggered the identification of specific ions (comparable to electrical calcium imaging) without chemically labelling the OECT materials.
The results of the first task are shown on Figure 5 in which we present the receiver operating characteristic (ROC) curves of our learning task. Curves that are well placed in the upper left corner signify excellent classification, and this is independent from the electrolyte composition. We opted for this type of graphical presentation since we have 25 different environments and more detailed presentations, such as those for confusion matrices, would be too complicated to draw. In the appendix, we have nevertheless provided the results of the confusion matrices for the whole task (see Table S2). For only two classes out of 25, we had a sensitivity below 95% of the random models. Both of these classes were mixed with classes of very similar ionic concentrations. The precision of the method was very good for all classes.
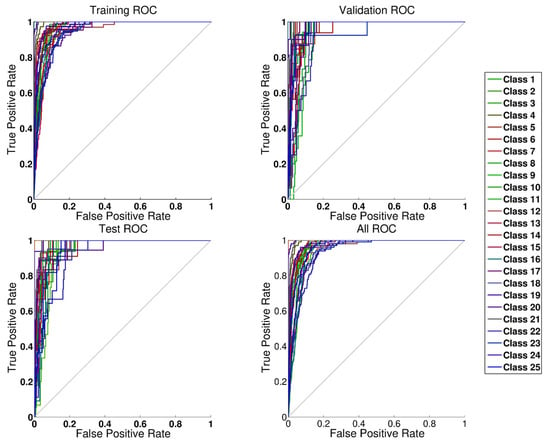
Figure 5.
ROC curve for the electrolyte classification with the ANN (details on the class definition are available as a supplementary material in Table S1).
The second task is presented in Figure 6, with confusion matrices in Figure 7 and Figure 8 (respectively for Ca2+(aq) and Na+(aq)). These confusion matrices represent the best and the worst result of the classification tasks. Figure 5 shows the correct classification total sampled over 100 different instances of learning to evaluate the variance of the expected outcome. One can immediately observe in Figure 6 that tasks involving Ca2+(aq) classification were substantially better than those involving Na+(aq) and K+(aq) for the whole range of concentration (except 0.9). This confirms the highest separability yielded from the PCA, presumably due to different ion valence, which impacts the high-frequency response [18]. We also noticed that the ANN algorithm better classified the majority ions (opened circles in Figure 6) or equimolar blends (opened squares in Figure 6) with recognition rates over 85%, while minority ion detections (opened triangles in Figure 6) were between 70% and 85% successful. Although cases of minority ion detections are more challenging to classify due to measurement perturbations which are more prevalent than for majority ions, we observed that recognition rates were higher than the those that would be expected from a purely random classification, confirming the applicability of the method for identifying Ca2+(aq) in physiological solutions. In the confusion matrices, target Class represents the true value of the sample (in Figure 7, it is 1 when the concentration of Ca2+(aq) is equal or greater than 0.33), while the Output Class represents the output value that the ANN produced. While most of the classifications correctly predicted more than 90% in the best-case scenarios, as the one presented in Figure 7, we achieved recognition of 100%. This is a success rate which suggests that even without additional fine-tuning and research, OECTs can be used in these recognition tasks. In Figure 8, we present the classification task if the data were collected from an environment which has concentration of Na+(aq) larger or equal to 0.1. The method correctly classified 74.1% of cases in the test set due to the dominance of the measurement perturbation of the majority ions. One can also notice that the error is more often assigned to concentrations of sodium smaller than 0.1 while it is in fact equal or greater. This suggests that descriptors distinguishing large concentrations of potassium and calcium ions mask the descriptors that distinguish small concentrations of sodium ions. A similar pattern can be observed in all of the tasks of distinguishing the small concentrations.
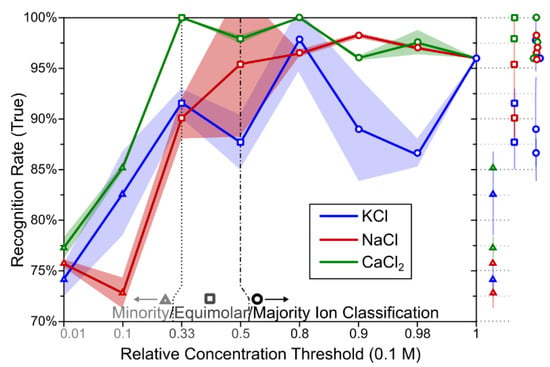
Figure 6.
True recognition rate for the thresholding task. One can observe that Ca2+(aq) is systematically better recognized than are other ions as predicted by the PCA results. Increased standard errors for the tasks Na+(aq) > 0.5 (50 mM) and K+(aq) > 0.9 (90 mM) are related to two different minima in the learning task. Excluding these minima, errors become comparable to those of the other tasks.
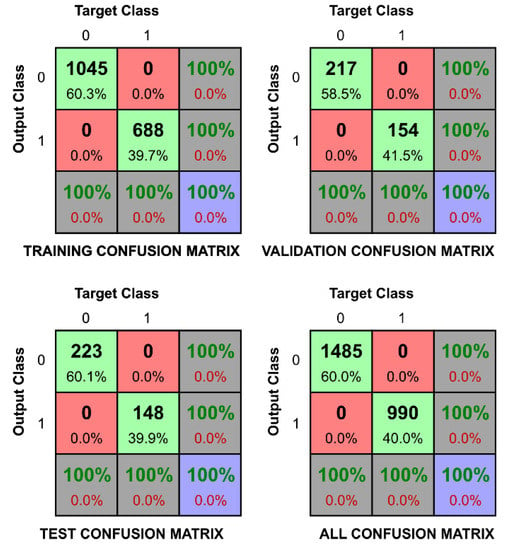
Figure 7.
Confusion matrices to verify if the level of Ca2+(aq) is larger than 0.33 (33.3 mM). In the upper left panel, the confusion matrix of the training data set is presented. In the upper right panel, the confusion matrix of the validation data set is presented. In the lower left figure, the confusion matrix of the test dataset is presented. In the lower right corner, the confusion matrix of the whole dataset is presented. 0 on the axis represents false and 1 represents true. The target class is the proper classification of the dataset, while the output class is the inferred classification of data. The variability of the confusion matrix entries is consistent across all the datasets.
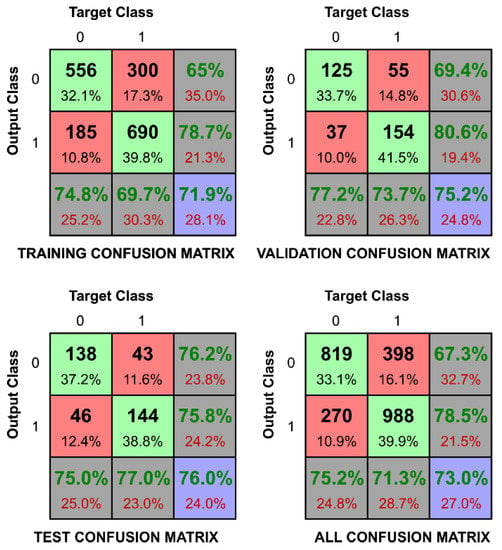
Figure 8.
Confusion matrices to verify if the level of Na+(aq) is larger than 0.1 (10.0 mM). In the upper left panel, the confusion matrix of the training data set is presented. In the upper right panel, the confusion matrix of the validation data set is presented. In the lower left figure, the confusion matrix of the test dataset is presented. In the lower right corner, the confusion matrix of the whole dataset is presented. 0 on the axis represents false and 1 represents true. The target class is the proper classification of the dataset, while the output class is the inferred classification of data. The variability of the confusion matrix entries is consistent across all the data sets.
4. Conclusions
By exploiting the ion-specific dynamics of OECTs, we successfully designed a kHz gate–voltage pulse protocol suitable for modulating its drain current response, with a regime for which the multi-parametric dynamics allows extracting sufficiently high-dimensional information to retrieve the ionic content of an electrolyte with a suitable ANN. At the rate of 12 current-data-points/2 ms, sampled at specific delays in the current transient, we identified six relevant descriptors for the ANN inputs (with 77-neuron single hidden layer architectures) to recognize Na+(aq)-, K+(aq)-, and Ca2+(aq)-rich electrolytes at the 0.1 M level. Furthermore, principal component analysis of the six current modulation descriptors showed that the total variance of the 2475 drain-current 6-dimensional vectors was gathered in the first five principal components. This not only validates the multiparametric and nonlinear physics of OECTs’ ion-dependency [19] but also demonstrates the relevance of gate-voltage multilevel-addressing for OECT arrays to recognize local ionic contents. Furthermore, the assessed capability to better recognize Ca2+(aq) in Na+(aq)- and K+(aq)-rich blends at concentrations comparable to extracellular physiology suggests considerable potential for neuro-sensing to identify the ionic identity of local transient signals for kHz-dynamic analysis.
Moreover, this study shows that by adapting experimental protocols to physical models, one can optimize the device data collection to ease/promote advanced data analysis that can provide technological added values (ion-sensing specificity for instance) without increasing the hardware complexity by adding physical functionalities in its fabrication, such as molecular functionalization to enhance sensors’ selectivity. Reciprocally, it suggests that by increasing the hardware complexity without necessarily knowing the physical model, one might succeed in efficiently classifying high-dimensional patterns with the help of an appropriate external stimulation protocol in a sufficiently rich dynamical system: such reservoir-computing machine-learning concepts applied to high-dimensional environments are a new sensing paradigm complementary to “sensors”, with the aim to provide a probabilistic answer to complex environment classification tasks as opposed to quantifying physical components obeying a model defined in idealized “standard conditions” (characterized as low-dimensional subspace groups with well-defined boundaries). With this multivariate approach, the next neuromorphic sensing challenge will be to gather all the computational resources within the reservoir to recognize physically nontrivial environment information.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/electronicmat4020007/s1. The following files are available free of charge. Supporting Information.pdf: Compositions of the 25 different electrolytes with precision/sensitivity values for the ANN recognition (Table S1), five PCA datasets with a reduced number of descriptors (Figure S1), and all the data of the 25 ROCs for each of the electrolytes (Table S2).
Author Contributions
Conceptualization, S.P and V.Z.; methodology, S.P.; software, V.Z.; validation, S.P; formal analysis, S.P and V.Z.; investigation, S.P; resources, S.P and V.Z.; data curation, S.P and V.Z.; writing—original draft preparation, S.P and V.Z.; writing—review and editing, S.P., D.V., Ž.C., I.L. and V.Z.; visualization, S.P.; supervision, S.P.; project administration, D.V. and Ž.C.; funding acquisition, D.V. and Ž.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EU: H2020 FET-OPEN project RECORD-IT (# GA 664786). Electronic Materials waived the APC.
Data Availability Statement
The data that support the findings of this study are available from the corresponding authors, upon reasonable request.
Acknowledgments
We thank the French National Nanofabrication Network RENATECH for financial support of the IEMN clean-room.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shulaker, M.M.; Hills, G.; Park, R.S.; Howe, R.T.; Saraswat, K.; Wong, H.-S.P.; Mitra, S. Three-dimensional integration of nanotechnologies for computing and data storage on a single chip. Nature 2017, 547, 74–78. [Google Scholar] [CrossRef] [PubMed]
- Mitrokhin, A.; Sutor, P.; Fermüller, C.; Aloimonos, Y. Learning sensorimotor control with neuromorphic sensors: Toward hyperdimensional active perception. Sci. Robot. 2019, 4, eaaw6736. [Google Scholar] [CrossRef] [PubMed]
- Sundaram, S.; Kellnhofer, P.; Li, Y.; Zhu, J.-Y.; Torralba, A.; Matusik, W. Learning the signatures of the human grasp using a scalable tactile glove. Nature 2019, 569, 698–702. [Google Scholar] [CrossRef]
- Lee, W.W.; Tan, Y.J.; Yao, H.; Li, S.; See, H.H.; Hon, M.; Ng, K.A.; Xiong, B.; Ho, J.S.; Tee, B.C.K. A neuro-inspired artificial peripheral nervous system for scalable electronic skins. Sci. Robot. 2019, 4, eaax2198. [Google Scholar] [CrossRef]
- de Chaumont, F.; Ey, E.; Torquet, N.; Lagache, T.; Dalongeville, S.; Imbert, A.; Legou, T.; Le Sourd, A.-M.; Faure, P.; Bourgeron, T.; et al. Real-time analysis of the behaviour of groups of mice via a depth-sensing camera and machine learning. Nat. Biomed. Eng. 2019, 3, 930–942. [Google Scholar] [CrossRef] [PubMed]
- Peveler, W.J.; Yazdani, M.; Rotello, V.M. Selectivity and Specificity: Pros and Cons in Sensing. ACS Sens. 2016, 1, 1282–1285. [Google Scholar] [CrossRef] [PubMed]
- IEEE Std 2700–2017 (Revision of IEEE Std 2700–2014); IEEE Standard for Sensor Performance Parameter Definitions. IEEE: Piscataway, NJ, USA, 2018. [CrossRef]
- Kim, G.H.; Kim, K.; Lee, E.; An, T.; Choi, W.S.; Lim, G.; Shin, J.H. Recent Progress on Microelectrodes in Neural Interfaces. Materials 2018, 11, 1995. [Google Scholar] [CrossRef]
- Seymour, J.P.; Wu, F.; Wise, K.D.; Yoo, E. State-of-the-art MEMS and microsystem tools for brain research. Microsyst. Nanoeng. 2017, 3, 16066. [Google Scholar] [CrossRef] [PubMed]
- Bushdid, C.; Magnasco, M.O.; Vosshall, L.B.; Keller, A. Humans Can Discriminate More than 1 Trillion Olfactory Stimuli. Science 2014, 343, 1370–1372. [Google Scholar] [CrossRef]
- Gerkin, R.C.; Castro, J.B. The number of olfactory stimuli that humans can discriminate is still unknown. eLife 2015, 4, e08127. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Smith, B.H.; Sharpee, T.O. Hyperbolic geometry of the olfactory space. Sci. Adv. 2018, 4, eaaq1458. [Google Scholar] [CrossRef] [PubMed]
- Hierlemann, A.; Gutierrez-Osuna, R. Higher-Order Chemical Sensing. Chem. Rev. 2008, 108, 563–613. [Google Scholar] [CrossRef] [PubMed]
- Khodagholy, D.; Doublet, T.; Quilichini, P.; Gurfinkel, M.; Leleux, P.; Ghestem, A.; Ismailova, E.; Hervé, T.; Sanaur, S.; Bernard, C.; et al. In vivo recordings of brain activity using organic transistors. Nat. Commun. 2013, 4, 1575. [Google Scholar] [CrossRef]
- Gkoupidenis, P.; Koutsouras, D.A.; Malliaras, G.G. Neuromorphic device architectures with global connectivity through electrolyte gating. Nat. Commun. 2017, 8, 15448. [Google Scholar] [CrossRef] [PubMed]
- Pecqueur, S.; Mastropasqua Talamo, M.; Guérin, D.; Blanchard, P.; Roncali, J.; Vuillaume, D.; Alibart, F. Neuromorphic Time-Dependent Pattern Classification with Organic Electrochemical Transistor Arrays. Adv. Electron. Mater. 2018, 4, 1800166. [Google Scholar] [CrossRef]
- Bernards, D.A.; Malliaras, G.G. Steady-State and Transient Behavior of Organic Electrochemical Transistors. Adv. Funct. Mater. 2007, 17, 3538–3544. [Google Scholar] [CrossRef]
- Pecqueur, S.; Guérin, D.; Vuillaume, D.; Alibart, F. Cation Discrimination in Organic Electrochemical Transistors by Dual Frequency Sensing. Org. Electron. 2018, 57, 232–238. [Google Scholar] [CrossRef]
- Pecqueur, S.; Lončarić, I.; Zlatić, V.; Vuillaume, D.; Crljen, Ž. The Non-Ideal Organic Electrochemical Transistors Impedance. Org. Electron. 2019, 71, 14–23. [Google Scholar] [CrossRef]
- Bos, M.A.; Van der Linden, W.E. Processing of signals from an ion-elective electrode array by a neural network. Anal. Chim. Acta 1990, 233, 31–39. [Google Scholar] [CrossRef]
- Abdullah, W.F.H.; Othman, M.; Ali, M.A.M.; Islam, M.S. Improving ion-sensitive field-effect transistor selectivity with backpropagation neural network. WSEAS Trans. Circuits Syst. 2010, 9, 700–712. [Google Scholar]
- Pecqueur, S.; Lenfant, S.; Guérin, D.; Alibart, F.; Vuillaume, D. Concentric-electrode organic electrochemical transistors: Case study for selective hydrazine sensing. Sensors 2017, 17, 570. [Google Scholar] [CrossRef] [PubMed]
- Metsalu, T.; Vilo, J. ClustVis: A web tool for visualizing clustering of multivariate data using Principal Component Analysis and heatmap. Nucleic Acids Res. 2015, 46, W566–W570. [Google Scholar] [CrossRef]
- Zhang, S.; Kumar, P.; Nouas, A.S.; Fontaine, L.; Tang, H.; Cicoira, F. Solvent-induced changes in PEDOT:PSS films for organic electrochemical transistors. APL Mater. 2015, 3, 014911. [Google Scholar] [CrossRef]
- Nikoletopoulou, V.; Tavernarakis, N. Calcium homeostasis in aging neurons. Front. Genet. 2012, 3, 200. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Greenberg, M.E. Calcium signaling in neurons: Molecular mechanisms and cellular consequences. Science 1995, 268, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Reed, R.; Marks, R.J., II. Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Stathakis, D. How many hidden layers and nodes? Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).