Tuning Magnetic and Transport Properties in Quasi-2D (Mn1−xNix)2P2S6 Single Crystals
Abstract
:1. Introduction
2. Experimental Methods and Crystal Growth
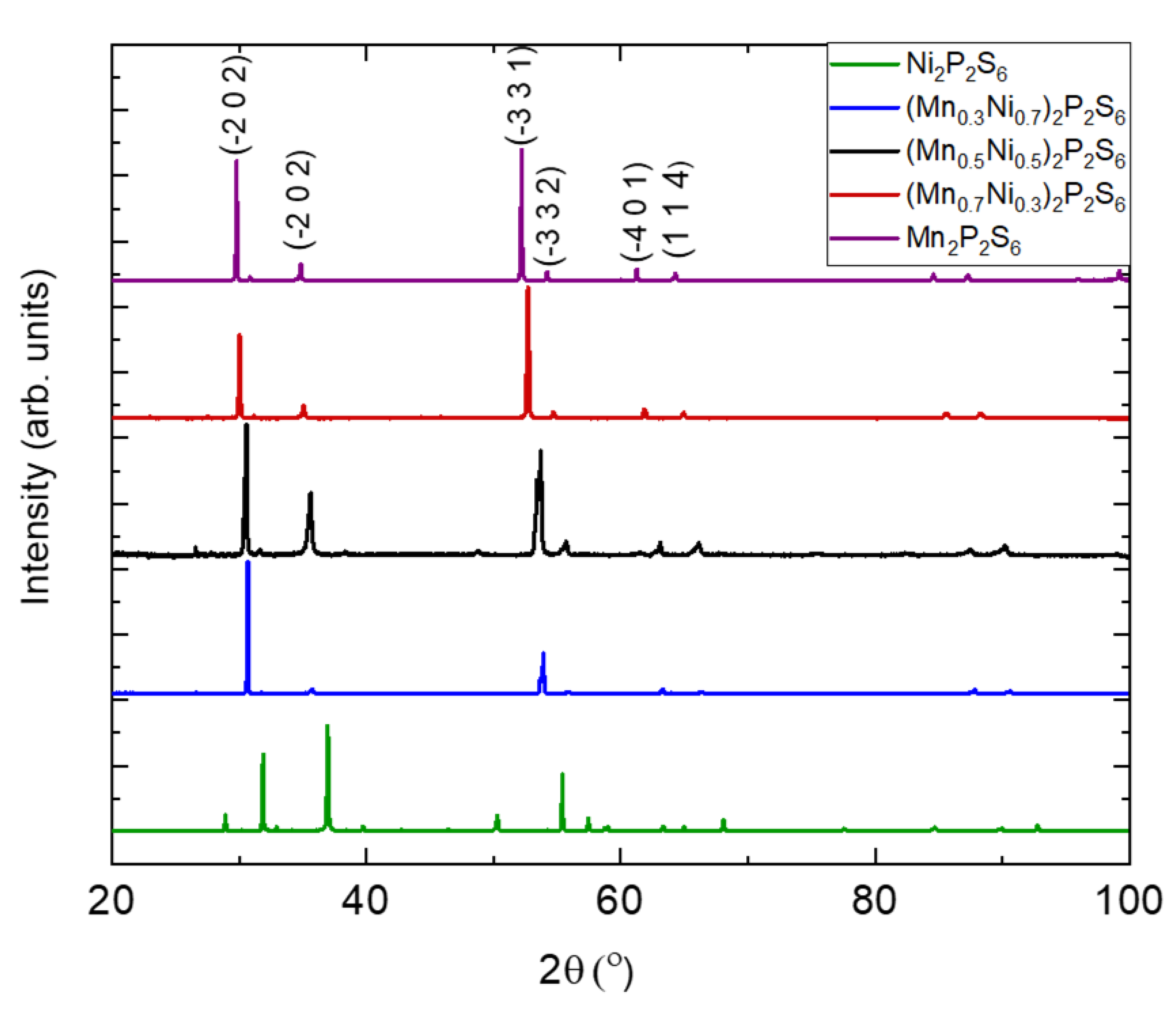
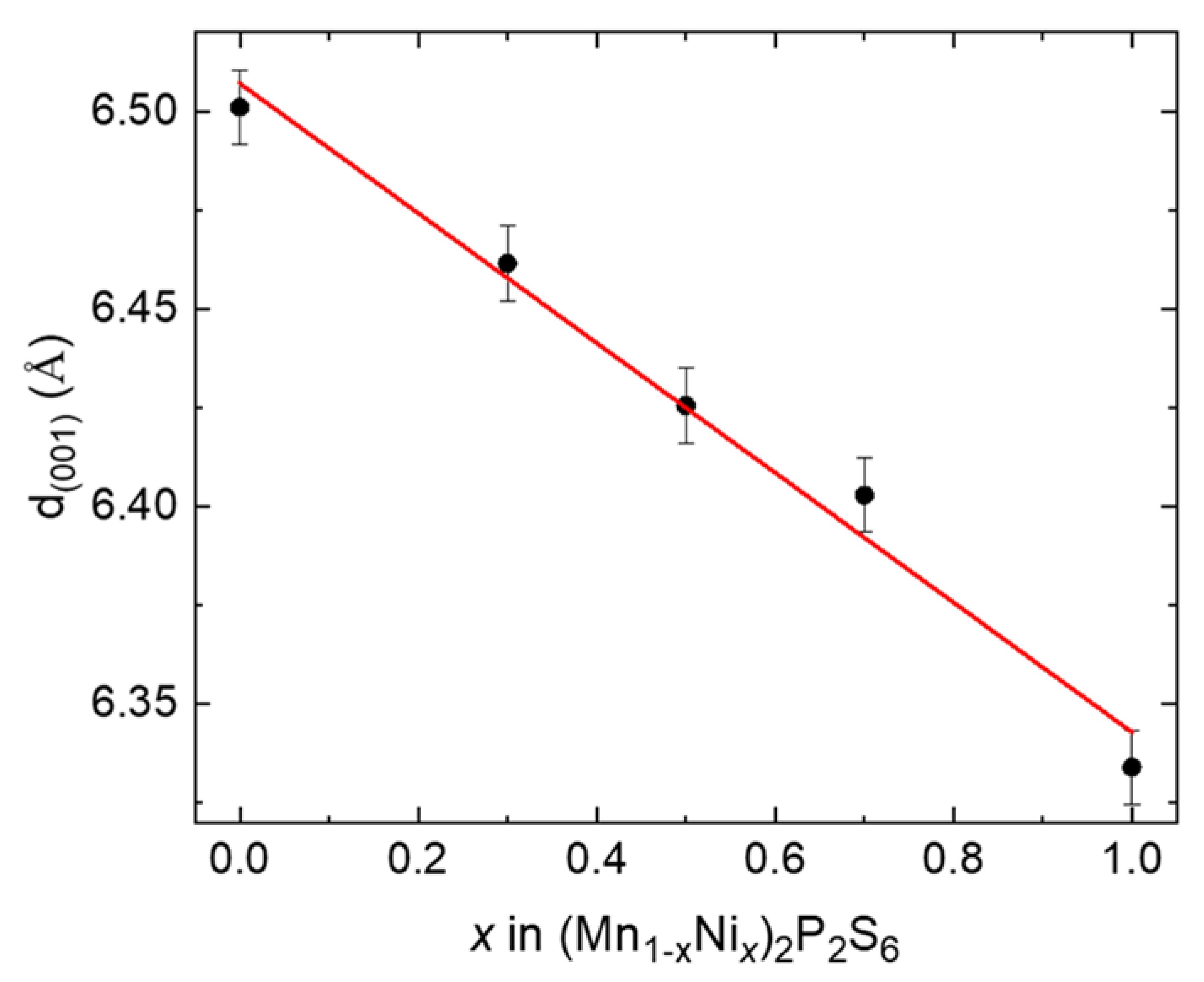
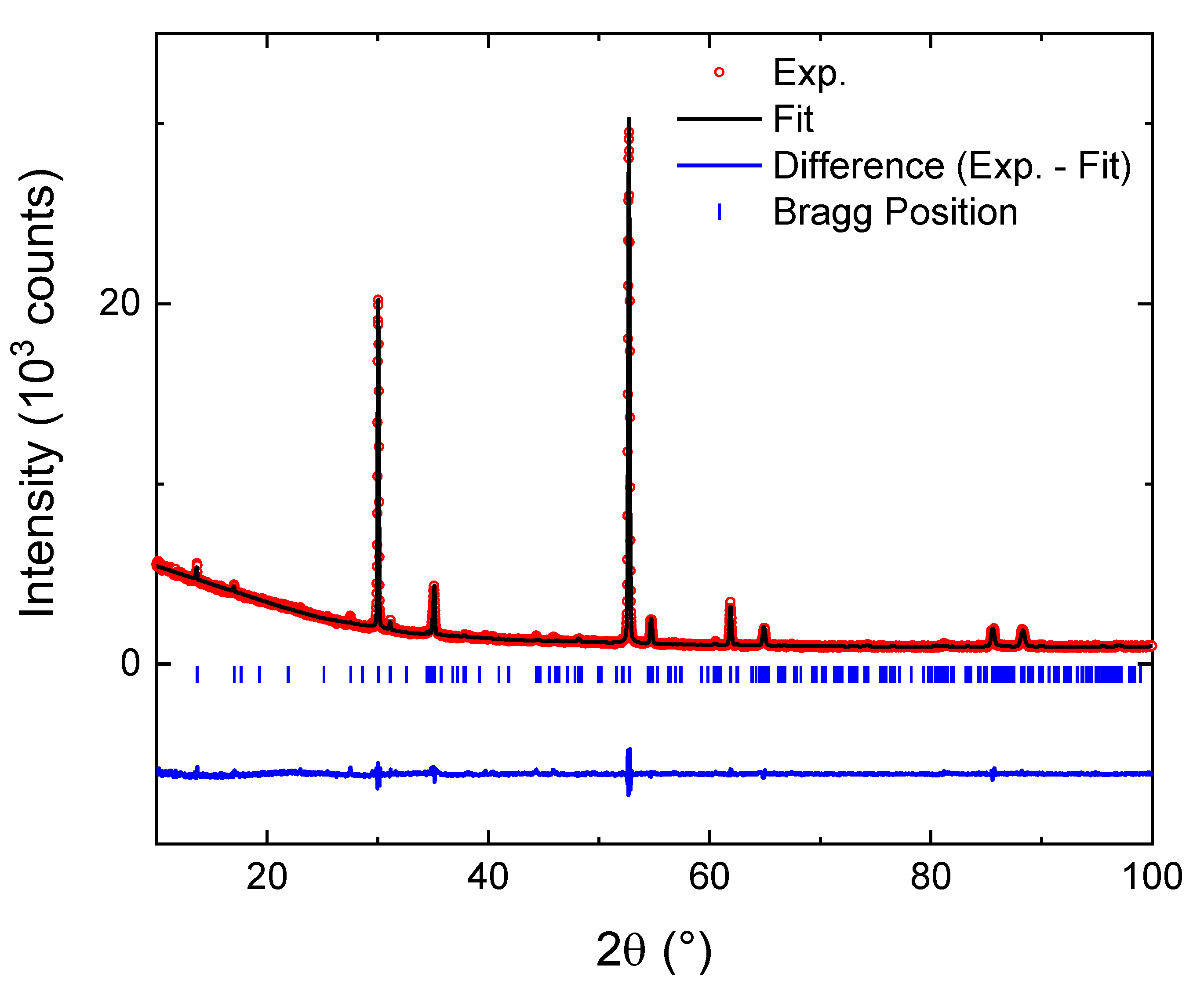
3. Characterization: Compositional and Structural Analysis
4. Magnetization and Transport
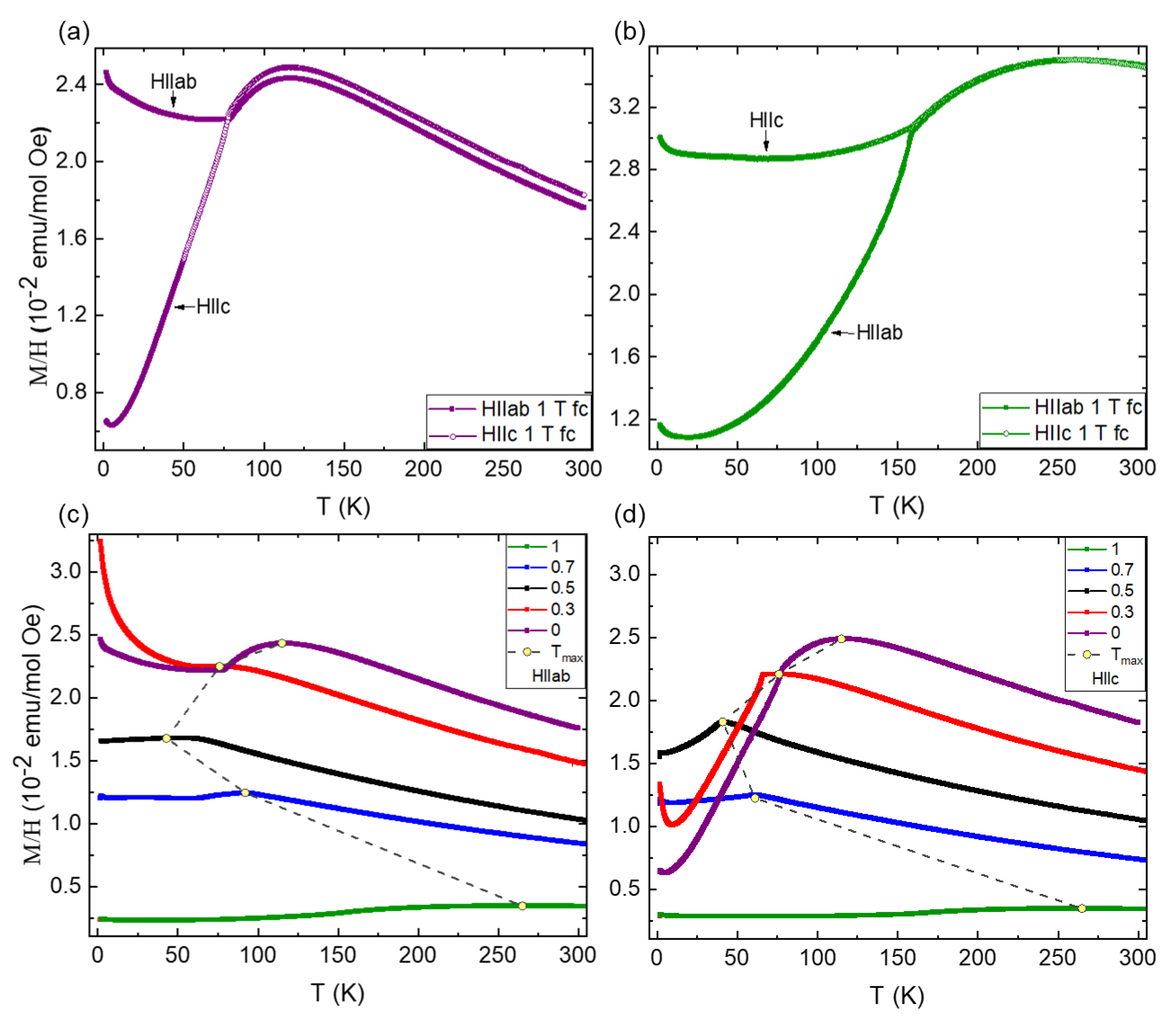
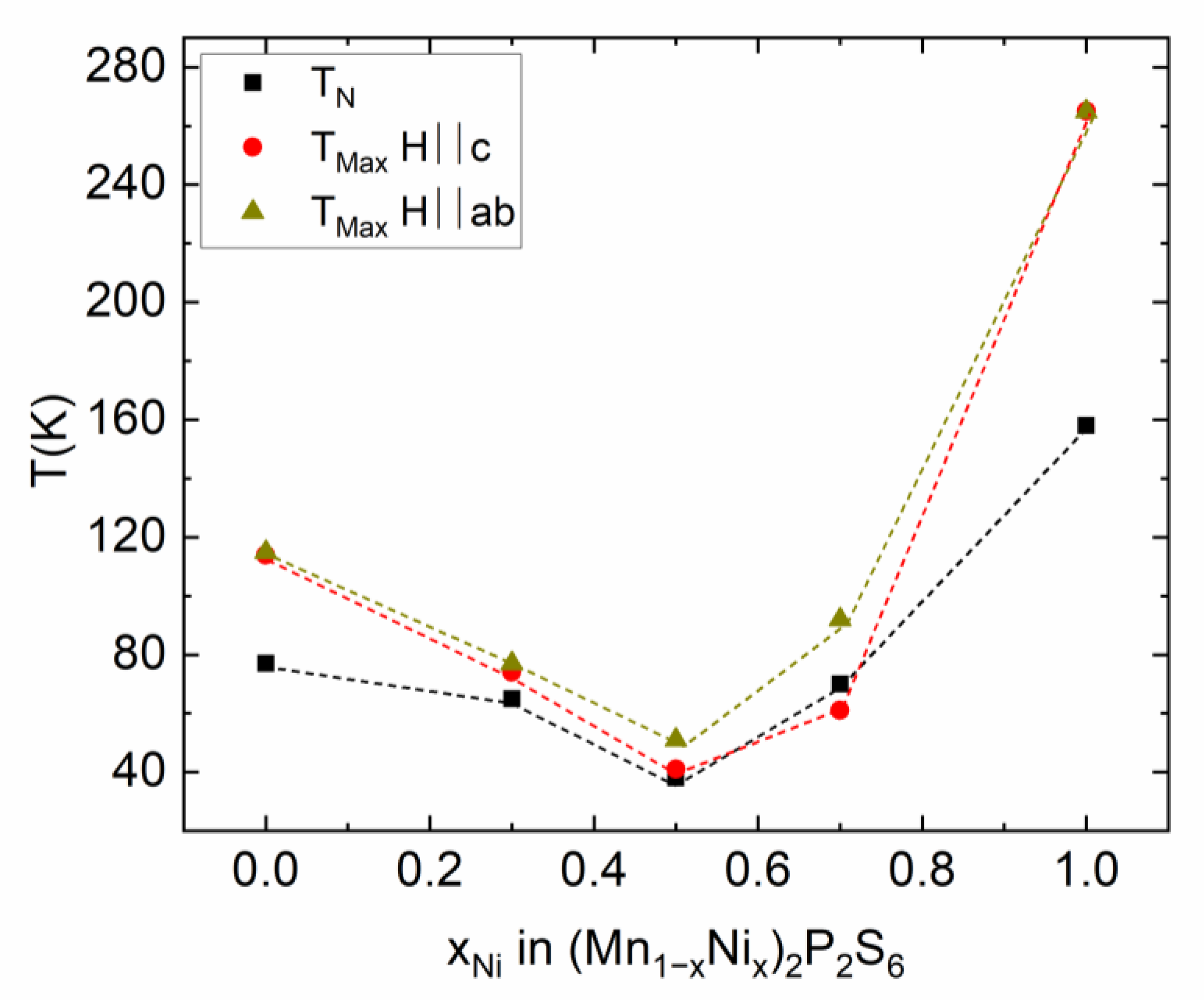
4.1. Magnetic Properties
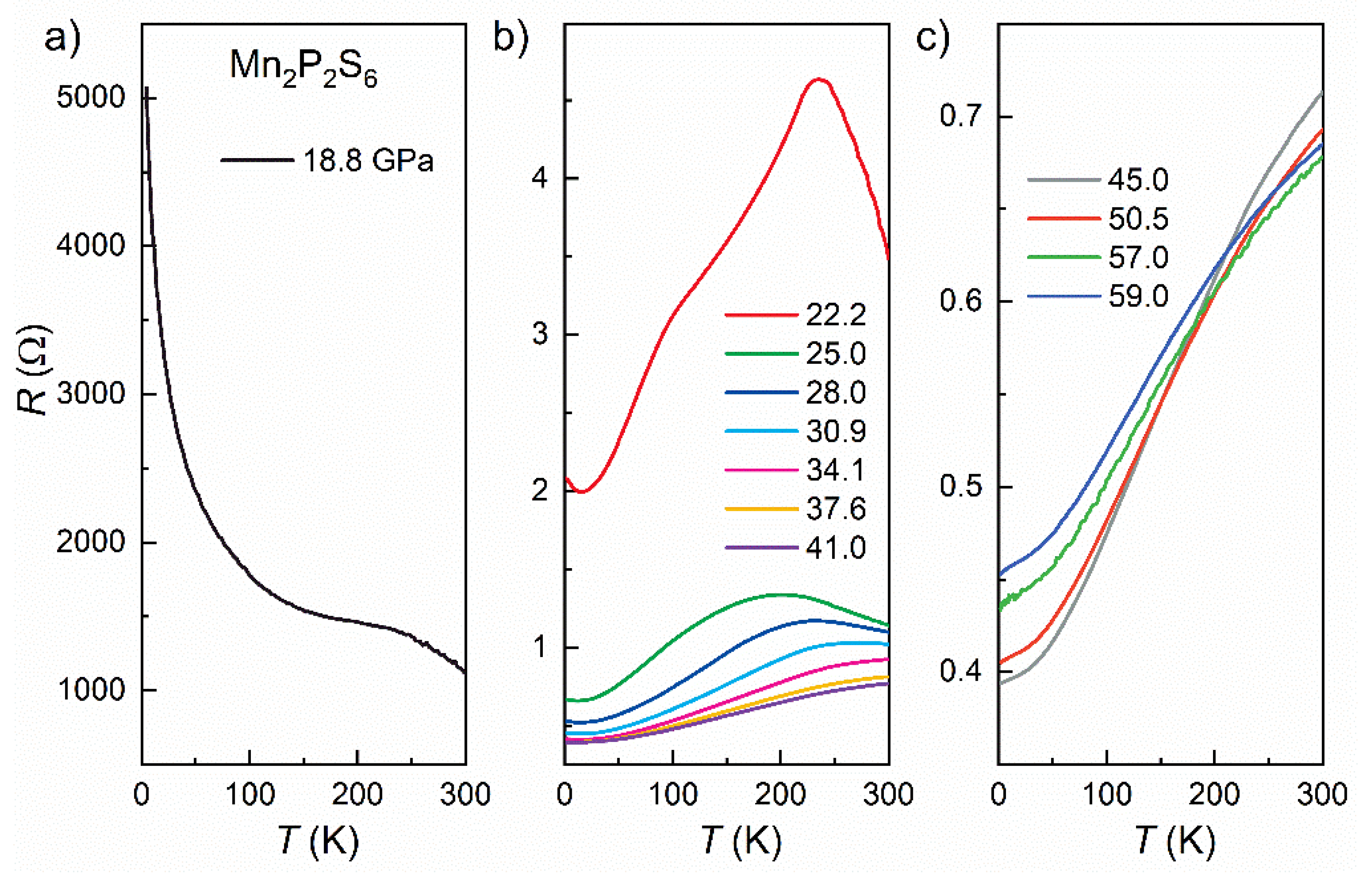
4.2. Transport Properties
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fiori, G.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerjee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768–779. [Google Scholar] [CrossRef]
- Sangwan, V.K.; Hersam, M.C. Electronic Transport in Two-Dimensional Materials. Annu. Rev. Phys. Chem. 2018, 69, 299–325. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.; Lee, D.; Kim, J.; Capasso, A.; Kang, H.S.; Park, J.-W.; Lee, C.-H.; Lee, G.-H. 2D semiconducting materials for electronic and optoelectronic applications: Potential and challenge. 2D Mater. 2019, 7, 022003. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nat. Cell Biol. 2017, 546, 265–269. [Google Scholar] [CrossRef] [Green Version]
- Selter, S.; Bastien, G.; Wolter, A.U.B.; Aswartham, S.; Büchner, B. Magnetic anisotropy and low-field magnetic phase diagram of the quasi-two-dimensional ferromagnet Cr2Ge2Te6. Phys. Rev. B 2020, 101, 014440. [Google Scholar] [CrossRef] [Green Version]
- Zeisner, J.; Alfonsov, A.; Selter, S.; Aswartham, S.; Ghimire, M.P.; Richter, M.; Brink, J.V.D.; Büchner, B.; Kataev, V. Magnetic anisotropy and spin-polarized two-dimensional electron gas in the van der Waals ferromagnet Cr2Ge2Te6. Phys. Rev. B 2019, 99, 165109. [Google Scholar] [CrossRef] [Green Version]
- Sakurai, T.; Rubrecht, B.; Corredor, L.T.; Takehara, R.; Yasutani, M.; Zeisner, J.; Alfonsov, A.; Selter, S.; Aswartham, S.; Wolter, A.U.B.; et al. Pressure control of the magnetic anisotropy of the quasi-two-dimensional van der Waals ferromagnet Cr2Ge2Te6. Phys. Rev. B 2021, 103, 024404. [Google Scholar] [CrossRef]
- McGuire, M.A.; Dixit, H.; Cooper, V.R.; Sales, B.C. Coupling of Crystal Structure and Magnetism in the Layered, Ferromagnetic Insulator CrI3. Chem. Mater. 2015, 27, 612–620. [Google Scholar] [CrossRef]
- Mak, K.F.; Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 2016, 10, 216–226. [Google Scholar] [CrossRef]
- Xia, F.; Wang, H.; Xiao, D.; Dubey, M.; Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 2014, 8, 899–907. [Google Scholar] [CrossRef]
- Dhanabalan, S.C.; Dhanabalan, B.; Ponraj, J.S.; Bao, Q.; Zhang, H. 2D-Materials-Based Quantum Dots: Gateway Towards Next-Generation Optical Devices. Adv. Opt. Mater. 2017, 5, 1700257. [Google Scholar] [CrossRef]
- Zheng, W.; Jiang, Y.; Hu, X.; Li, H.; Zeng, Z.; Wang, X.; Pan, A. Light Emission Properties of 2D Transition Metal Dichalcogenides: Fundamentals and Applications. Adv. Opt. Mater. 2018, 6, 1800420. [Google Scholar] [CrossRef]
- Wang, X.; Jones, A.M.; Seyler, K.L.; Tran, V.; Jia, Y.; Zhao, H.; Wang, H.; Yang, L.; Xu, X.; Xia, F. Highly anisotropic and robust excitons in monolayer black phosphorus. Nat. Nanotechnol. 2015, 10, 517–521. [Google Scholar] [CrossRef] [Green Version]
- McGuire, M.A.; Clark, G.; Kc, S.; Chance, W.M.; Jellison, J.G.E.; Cooper, V.R.; Xu, X.; Sales, B.C. Magnetic behavior and spin-lattice coupling in cleavable van der Waals layered CrCl3 crystals. Phys. Rev. Mater. 2017, 1, 014001. [Google Scholar] [CrossRef]
- Ovchinnikov, D.; Gargiulo, F.; Allain, A.; Pasquier, D.J.; Dumcenco, D.; Ho, C.-H.; Yazyev, F.G.D.J.P.O.V.; Kis, D.O.A.A.D.D.A. Disorder engineering and conductivity dome in ReS2 with electrolyte gating. Nat. Commun. 2016, 7, 12391. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Wang, H.; Jia, Y. Rediscovering black phosphorus as an anisotropic layered material for optoelectronics and electronics. Nat. Commun. 2014, 5, 4458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Mishchenko, A.; Carvalho, A.; Neto, A.H.C. 2D materials and van der Waals heterostructures. Science 2016, 353, aac9439. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Bampoulis, P.; Rudenko, A.N.; Yao, Q.V.; Van Houselt, A.; Poelsema, B.; Katsnelson, M.I.; Zandvliet, H.J. Structural and electronic properties of germanene on MoS 2. Phys. Rev. Lett. 2016, 116, 256804. [Google Scholar] [CrossRef] [Green Version]
- Tonkikh, A.A.; Voloshina, E.; Werner, P.; Blumtritt, H.; Senkovskiy, B.; Güntherodt, G.; Parkin, S.S.P.; Dedkov, Y.S. Structural and electronic properties of epitaxial multilayer h-BN on Ni(111) for spintronics applications. Sci. Rep. 2016, 6, 23547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.-C.; Huang, Y.; Duan, X. Van der Waals heterostructures and devices. Nat. Rev. Mater. 2016, 1, 16042. [Google Scholar] [CrossRef]
- Grasso, V.; Silipigni, L. Low-dimensional materials: The MPX3 family, physical features and potential future applications. La Riv. Del Nuovo Cim. 2002, 25, 1–102. [Google Scholar] [CrossRef]
- Ouvrard, G.; Brec, R.; Rouxel, J. Structural determination of some MPS3 layered phases (M = Mn, Fe, Co, Ni and Cd). Mater. Res. Bull. 1985, 20, 1181–1189. [Google Scholar] [CrossRef]
- Grasso, V.; Santangelo, S.; Piacentini, M. Optical absorption spectra of some transition metal thiophosphates. Solid State Ionics 1986, 20, 9–15. [Google Scholar] [CrossRef]
- Kurita, N.; Nakao, K. Band Structures and Physical Properties of Magnetic Layered Semiconductors MPS3. J. Phys. Soc. Jpn. 1989, 58, 610–621. [Google Scholar] [CrossRef]
- Zhukov, V.; Alvarez, S.; Novikov, D. Electronic band structure of the magnetic layered semiconductors MPS3 (M = Mn, Fe and Ni). J. Phys. Chem. Solids 1996, 57, 647–652. [Google Scholar] [CrossRef]
- Coak, M.J.; Son, S.; Daisenberger, D.; Hamidov, H.; Haines, C.R.S.; Alireza, P.L.; Wildes, A.R.; Liu, C.; Saxena, S.S.; Park, J.-G. Isostructural Mott transition in 2D honeycomb antiferromagnet V0.9PS3. NPJ Quantum Mater. 2019, 4, 1–6. [Google Scholar] [CrossRef]
- Monthoux, P.; Lonzarich, G.G. Magnetically mediated superconductivity: Crossover from cubic to tetragonal lattice. Phys. Rev. B 2002, 66, 224504. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Jenjeti, R.N.; Austeria, M.P.; Sampath, S. Bulk and few-layer MnPS3: A new candidate for field effect transistors and UV photodetectors. J. Mater. Chem. C 2018, 7, 324–329. [Google Scholar] [CrossRef]
- Lee, S.; Choi, K.-Y.; Lee, S.; Park, B.H.; Park, J.-G. Tunneling transport of mono- and few-layers magnetic van der Waals MnPS3. APL Mater. 2016, 4, 086108. [Google Scholar] [CrossRef] [Green Version]
- Le Flem, G.; Brec, R.; Ouvard, G.; Louisy, A.; Segransan, P. Magnetic interactions in the layer compounds MPX3 (M=Mn, Fe, Ni; X=S, Se). J. Phys. Chem. Solids 1982, 43, 455–461. [Google Scholar] [CrossRef]
- Kurosawa, K.; Saito, S.; Yamaguchi, Y. Neutron Diffraction Study on MnPS3 and FePS3. J. Phys. Soc. Jpn. 1983, 52, 3919–3926. [Google Scholar] [CrossRef]
- Brec, R. Review on Structural and Chemical Properties of Transition Metal Phosphorus Trisulfides MPS3. Intercalation Layer. Mater. 1986, 19, 93–124. [Google Scholar] [CrossRef]
- Joy, P.A.; Vasudevan, S. Magnetism in the layered transition-metal thiophosphates MPS3(M=Mn, Fe, and Ni). Phys. Rev. B 1992, 46, 5425–5433. [Google Scholar] [CrossRef] [PubMed]
- Wildes, A.R.; Simonet, V.; Ressouche, E.; Mcintyre, G.J.; Avdeev, M.; Suard, E.; Kimber, S.A.; Lançon, D.; Pepe, G.; Moubaraki, B.; et al. Magnetic structure of the quasi-two-dimensional antiferromagnet NiPS3. Phys. Rev. B 2015, 92, 224408. [Google Scholar] [CrossRef]
- Dioguardi, A.P.; Selter, S.; Peeck, U.; Aswartham, S.; Sturza, M.-I.; Murugesan, R.; Eldeeb, M.S.; Hozoi, L.; Büchner, B.; Grafe, H.-J. Quasi-two-dimensional magnetic correlations in Ni2P2S6 probed by P31 NMR. Phys. Rev. B 2020, 102, 064429. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. Space Phys. 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Selter, S.; Shemerliuk, Y.; Sturza, M.I.; Wolter, A.U.; Büchner, B.; Aswartham, S. Crystal Growth and Anisotropic Magnetic Properties of Quasi-2D (Fe1−xNix)2P2S6. arXiv 2021, arXiv:2104.00066. [Google Scholar]
- Selter, S.; Shemerliuk, Y.; Büchner, B.; Aswartham, S. Crystal Growth of the Quasi-2D Quarternary Compound AgCrP2S6 by Chemical Vapor Transport. Crystals 2021, 11, 500. [Google Scholar] [CrossRef]
- Schmidt, P.; Binnewies, M.; Glaum, R.; Schmidt, R.G.A.M. Chemical Vapor Transport Reactions—Methods, Materials, Modeling; IntechOpen: Rijeka, Croatia, 2013. [Google Scholar]
- Okuda, K.; Kurosawa, K.; Saito, S.; Honda, M.; Yu, Z.; Date, M. Magnetic Properties of Layered Compound MnPS3. J. Phys. Soc. Jpn. 1986, 55, 4456–4463. [Google Scholar] [CrossRef]
- Goldstein, J.I.; Newbury, D.E.; Echlin, P.; Joy, D.C.; Lyman, C.E.; Lifshin, E.; Sawyer, L.; Michael, J.R. Special topics in scanning electron microscopy. In Scanning Electron Microscopy and X-ray Microanalysis; Springer: Boston, MA, USA, 2003; pp. 195–270. [Google Scholar]
- Klingen, W.; Eulenberger, G.; Hahn, H. Uber die Kristallstrukturen von Fe2P2Se6 und Fe2P2S6. Z. Anorg. Allg. Chem. 1973, 401, 97–112. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Goossens, D.J.; James, D.F.V.; Dong, J.; Whitfield, R.; Norén, L.; Withers, R. Local order in layered NiPS3and Ni0.7Mg0.3PS3. J. Phys. Condens. Matter 2011, 23, 065401. [Google Scholar] [CrossRef] [PubMed]
- Lançon, D.; Ewings, R.A.; Guidi, T.; Formisano, F.; Wildes, A.R. Magnetic exchange parameters and anisotropy of the quasi-two-dimensional antiferromagnet NiPS3. Phys. Rev. B 2018, 98, 134414. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekharan, N.; Vasudevan, S. Dilution of a layered antiferromagnet: Magnetism in MnxZn1−xPS3. Phys. Rev. B 1996, 54, 14903. [Google Scholar] [CrossRef]
- Goossens, D.; Hicks, T. Investigation of the temperature/field/composition magnetic phase diagram of Mn1−xMgxPS3. J. Magn. Magn. Mater. 1998, 177–181, 721–722. [Google Scholar] [CrossRef]
- Goossens, D.; Studer, A.J.; Kennedy, S.J.; Hicks, T.J. The impact of magnetic dilution on magnetic order in MnPS3. J. Phys. Condens. Matter 2000, 12, 4233–4242. [Google Scholar] [CrossRef]
- Abramchuk, M.; Jaszewski, S.; Metz, K.R.; Osterhoudt, G.B.; Wang, Y.; Burch, K.S.; Tafti, F. Controlling magnetic and optical properties of the van der Waals crystal CrCl3−xBrx via mixed halide chemistry. Adv. Mater. 2018, 30, 1801325. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Z.; Wen, T.; Zhou, Y.; Li, N.; Han, F.; Xiao, Y.; Chow, P.; Sun, J.; Pravica, M.; et al. Pressure-Driven Cooperative Spin-Crossover, Large-Volume Collapse, and Semiconductor-to-Metal Transition in Manganese(II) Honeycomb Lattices. J. Am. Chem. Soc. 2016, 138, 15751–15757. [Google Scholar] [CrossRef]





| xnom | Expec. Comp. | Mean Comp. (EDX) | xexp |
|---|---|---|---|
| 0 | Mn2P2S6 | Mn2.02(5)P2.04(1)S5.93(5) | 0 |
| 0.3 | Mn1.4Ni0.6P2S6 | Mn1.45(1)Ni0.55(1)P2.03(6)S5.96(2) | 0.28 |
| 0.5 | MnNiP2S6 | Mn0.80(6)Ni0.91(7)P2.07(9)S6.19(8) | 0.45 |
| 0.7 | Mn0.6Ni1.4P2S6 | Mn0.62(4)Ni1.33(3)P2.04(1)S6.00(2) | 0.67 |
| 1 | Ni2P2S6 | Ni2.04(6)P2.03(2)S5.92(3) | 1 |
| pXRD | |
|---|---|
| Composition | (Mn0.7Ni0.3)2P2S6 |
| Space group | C2/m (No. 12) |
| Wavelength (Å) | 1.540560 |
| 2θ range (◦) | 10–100 |
| Step Size (◦) | 0.015 |
| Temperature (K) | 293 |
| a (Å) | 6.009 (7) |
| b (Å) | 10.405 (3) |
| c (Å) | 6.779 (3) |
| β (◦) | 107.45 (6) |
| V (Å3) | 404.40 (6) |
| Goodness-of-Fit | 2.06 |
| Bragg R-factor | 7.61 |
| RF-factor | 22.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shemerliuk, Y.; Zhou, Y.; Yang, Z.; Cao, G.; Wolter, A.U.B.; Büchner, B.; Aswartham, S. Tuning Magnetic and Transport Properties in Quasi-2D (Mn1−xNix)2P2S6 Single Crystals. Electron. Mater. 2021, 2, 284-298. https://doi.org/10.3390/electronicmat2030020
Shemerliuk Y, Zhou Y, Yang Z, Cao G, Wolter AUB, Büchner B, Aswartham S. Tuning Magnetic and Transport Properties in Quasi-2D (Mn1−xNix)2P2S6 Single Crystals. Electronic Materials. 2021; 2(3):284-298. https://doi.org/10.3390/electronicmat2030020
Chicago/Turabian StyleShemerliuk, Yuliia, Yonghui Zhou, Zhaorong Yang, Gang Cao, Anja U. B. Wolter, Bernd Büchner, and Saicharan Aswartham. 2021. "Tuning Magnetic and Transport Properties in Quasi-2D (Mn1−xNix)2P2S6 Single Crystals" Electronic Materials 2, no. 3: 284-298. https://doi.org/10.3390/electronicmat2030020
APA StyleShemerliuk, Y., Zhou, Y., Yang, Z., Cao, G., Wolter, A. U. B., Büchner, B., & Aswartham, S. (2021). Tuning Magnetic and Transport Properties in Quasi-2D (Mn1−xNix)2P2S6 Single Crystals. Electronic Materials, 2(3), 284-298. https://doi.org/10.3390/electronicmat2030020






