A Model for Bias Potential Effects on the Effective Langmuir Adsorption–Desorption Processes
Abstract
:1. Introduction
2. Bulk Response and Adsorption Dynamics
Bulk Electric Response
3. The Electric Current Density
4. Boundary Conditions
4.1. Blocking Electrodes
4.2. Adsorbing Surfaces
4.3. Adsorption in the Presence of the Bias
5. Voltammetry from a Drift–Diffusion Model
5.1. Polarized Cell
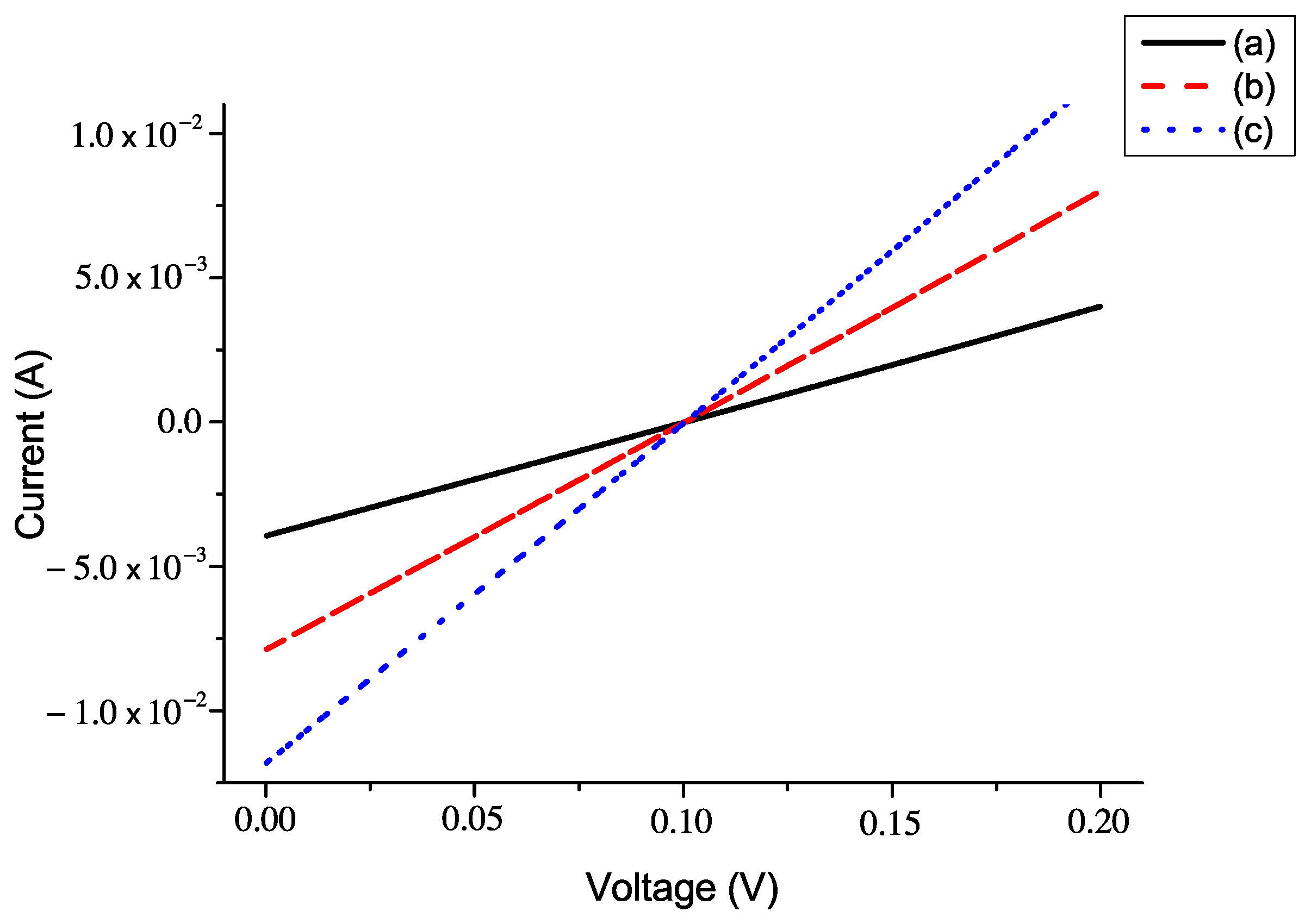
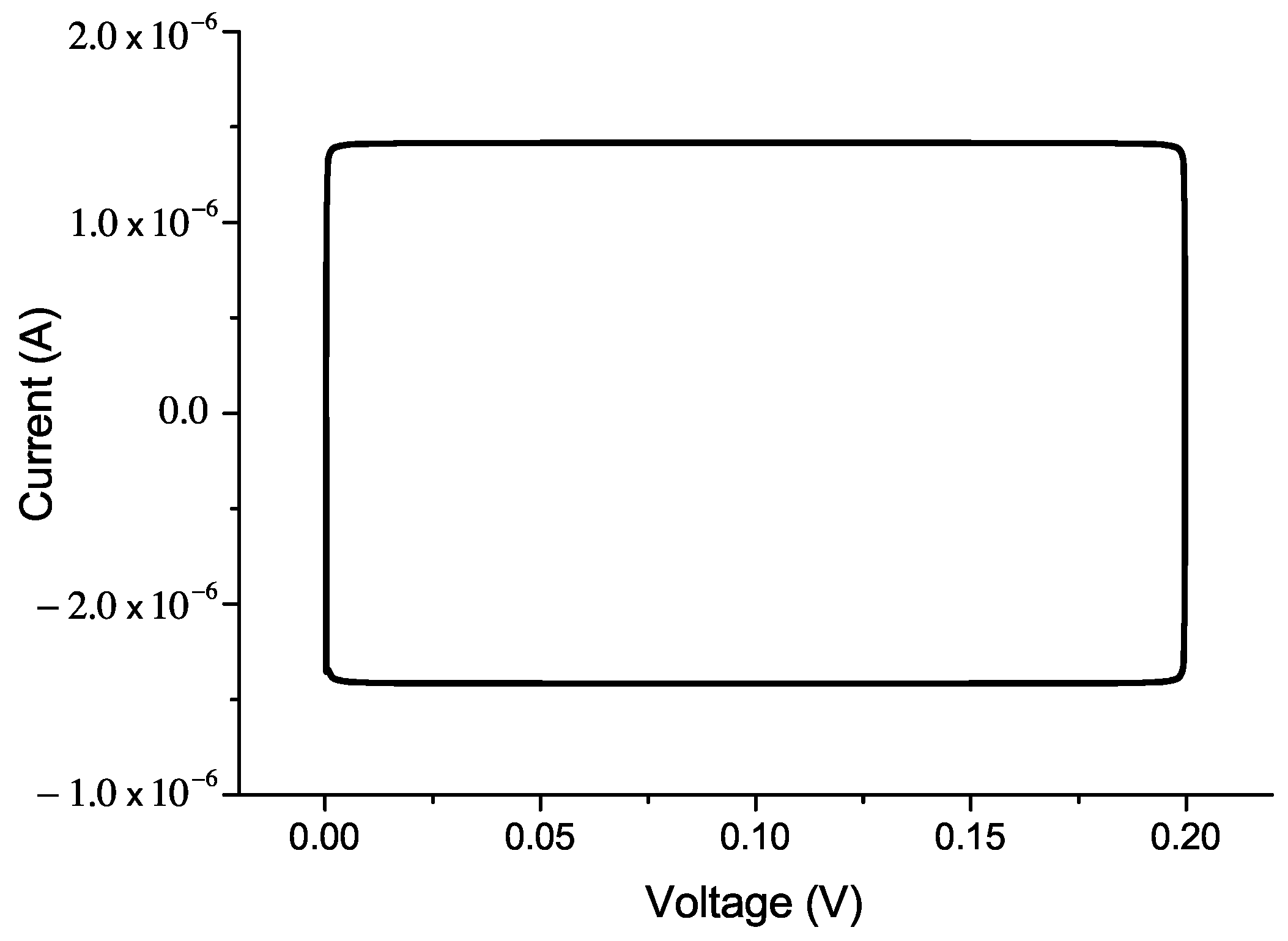
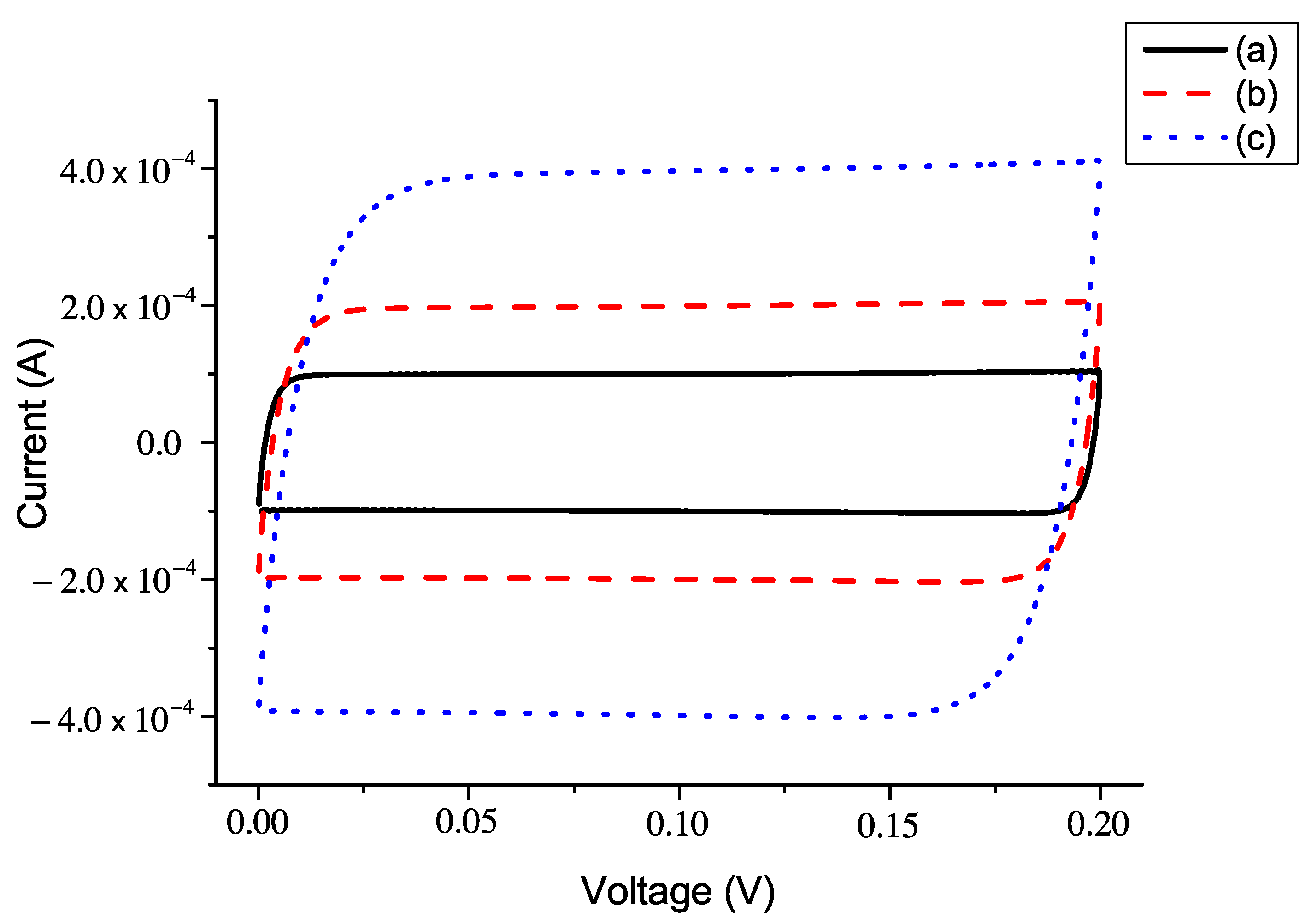
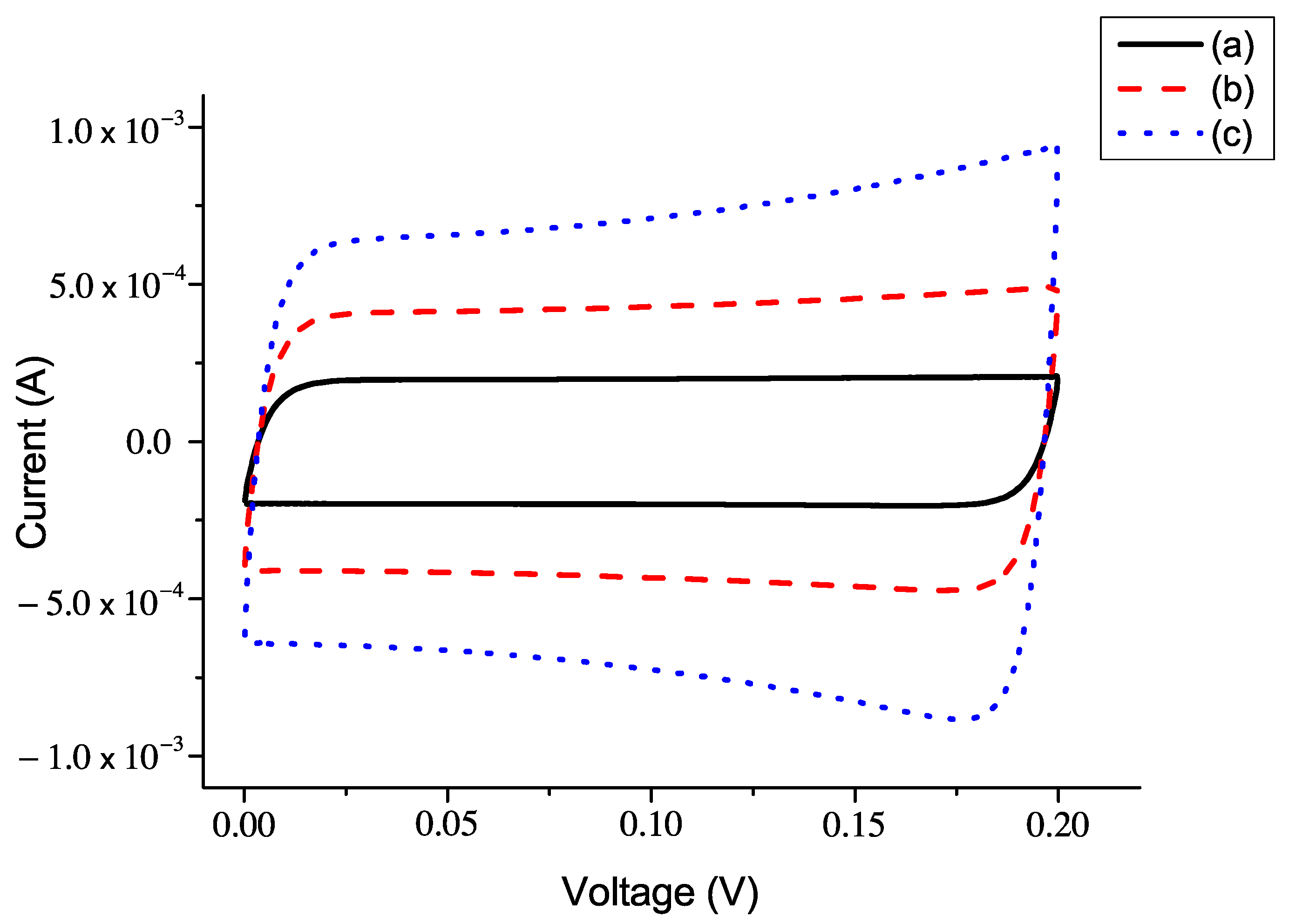
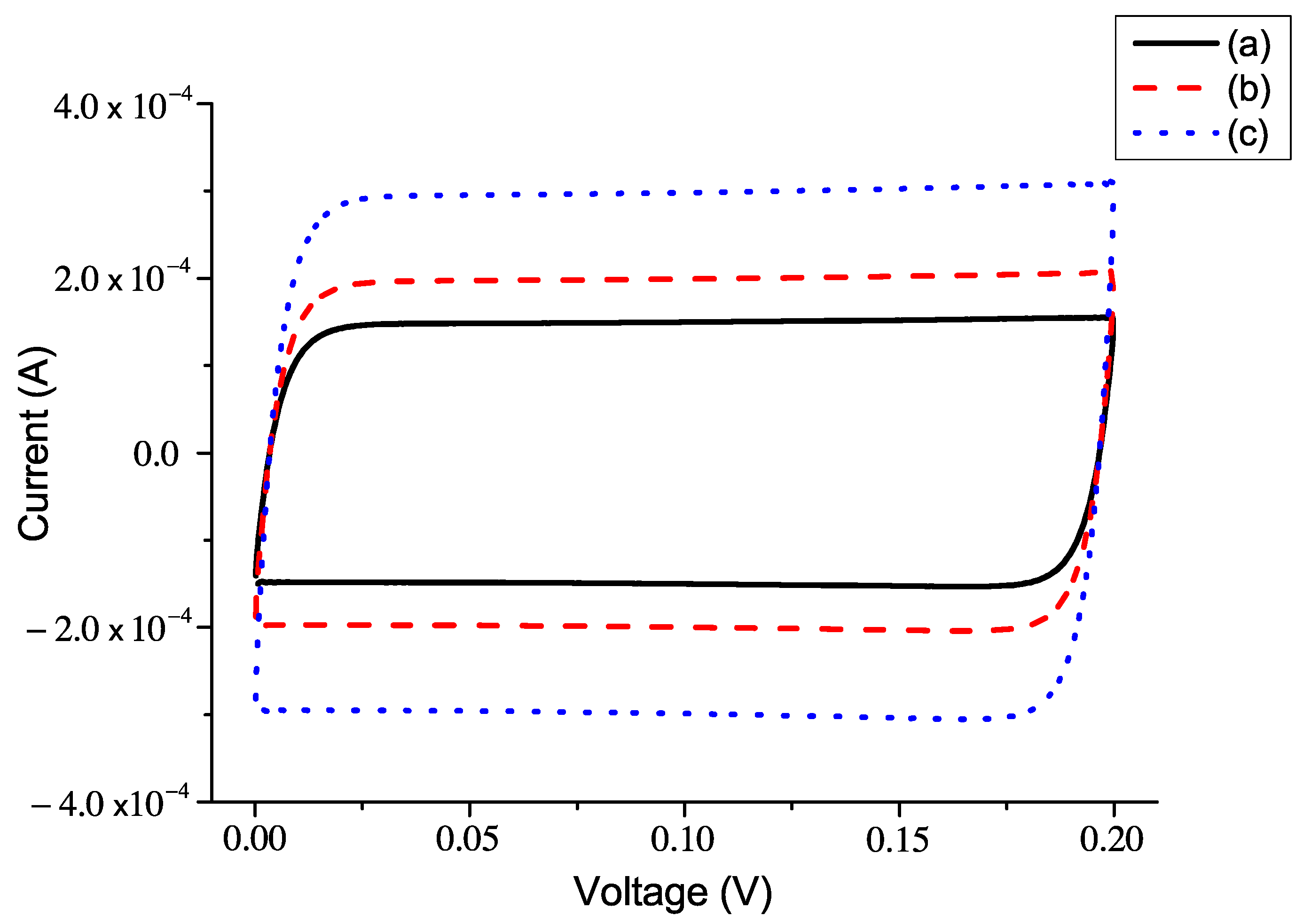
5.2. The Current–Voltage Characteristics
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Lyklema, J. Fundamentals of Interface and Colloid Science; Academic Press: London, UK, 1993. [Google Scholar]
- Crini, G.; Lichtfouse, E.; Wilson, L.D.; Crini, N.N. Adsorption-oriented process using conventional and non-conventional adsorbents for wastewater treatment. In Green Adsorbents for Pollutant Removal, Envinronmental Chemistry for a Sustainable Word 18; Crini, G., Lichtfouse, E., Eds.; Springer: New York, NY, USA, 2018; pp. 23–71. [Google Scholar]
- Li, J.R.; Kuppler, R.J.; Zhou, H.C. Selective gas adsorption and separation in metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. [Google Scholar] [CrossRef]
- Undin, T.; Lind, S.B.; Dahlin, A.P. MS for investigation of time-dependent protein adsorption on surfaces in complex biological samples. Future Sci. OA 2015, 1, FS032. [Google Scholar] [CrossRef] [Green Version]
- Brogioli, D. Extracting Renewable Energy from a Salinity Difference Using a Capacitor. Phys. Rev. Lett. 2009, 103, 058501. [Google Scholar] [CrossRef]
- Rica, R.A.; Brogioli, D.; Ziano, R.; Salerno, D.; Mantegazza, F. Ions Transport and Adsorption Mechanisms in Porous Electrodes During Capacitive–Mixing Double Layer Expansion (CDLE). J. Phys. Chem. C 2012, 116, 16934–16938. [Google Scholar] [CrossRef] [PubMed]
- Brogioli, D.; Ziano, R.; Rica, R.A.; Salerno, D.; Mantegazza, F. Capacitive mixing for the extraction of energy from salinity differences: Survey of experimental results and electrochemical models. J. Colloid Interface Sci. 2013, 407, 457–466. [Google Scholar] [CrossRef] [PubMed]
- Alexe-Ionescu, A.L.; Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Current-Voltage Characteristics and Impedance Spectroscopy: Surface Conduction and Adsorption-Desorption Effects in Electrolytic Cells. J. Phys. Chem. C 2020, 124, 3150–3158. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.R.; Olivero, D. Asymmetric ionic adsorption and cell polarization in liquid crystals. J. Appl. Phys. 2000, 87, 2646–2648. [Google Scholar] [CrossRef]
- Trefalt, G.; Beherns, S.H.; Borkovec, M. Charge Regulation in Electrical Double layer: Ion Adsorption and Surface Interactions. Langmuir 2016, 32, 380–400. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Van Limpt, B.; van der Wal, A. Dynamic Adsorption/Desorption Process Model for Capacitive Deionization. J. Phys. Chem. C 2009, 113, 5636–5640. [Google Scholar] [CrossRef]
- Carrique, F.; Arroyo, F.J.; Delgado, A.V. Electrokinetics of Concentrated Suspensions of Spherical Colloidal Particles with Surface Conductance, Arbitrary Zeta Potential, and Double-Layer Thickness in Static Electric Fields. J. Colloid Interface Sci. 2002, 252, 126–137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carrique, F.; Arroyo, F.J.; Jiménez, M.L.; Delgado, A.V. Dielectric response of concentrated colloidal suspensions. J. Chem. Phys. 2003, 118, 1945–1955. [Google Scholar] [CrossRef] [Green Version]
- Boon, N.; van Roij, R. ‘Blue energy’ from ion adsorption and electrode charging in sea and river water. Mol. Phys. 2011, 109, 1229–1241. [Google Scholar] [CrossRef] [Green Version]
- Biesheuvel, P.M.; Bazant, M.Z. Nonlinear dynamics of capacitive charging and desalination by porous electrodes. Phys. Rev. E 2010, 81, 031502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biesheuvel, P.M.; Yeqing, F.; Bazant, M.Z. Diffuse charge and Faradaic reactions in porous electrodes. Phys. Rev. E 2011, 83, 061507. [Google Scholar] [CrossRef] [Green Version]
- Alexe-Ionescu, A.L.; Barbero, G.; Evangelista, L.R.; Lamberti, A.; Pedico, A.; Pirri, C.F. Langmuir adsorption processes and ion transport under bias potential in capacitive deionisation cells. Electrochim. Acta 2020, 348, 136288. [Google Scholar] [CrossRef]
- Suss, M.E.; Porada, S.; Sun, X.; Biesheuvel, P.M.; Yoon, J.; Presser, V.V. Water desalination via capacitive deionization: What is it and what can we expect from it? Energy Environ. Sci. 2015, 8, 2296–2319. [Google Scholar] [CrossRef] [Green Version]
- Atkins, P.W. Physical Chemistry, 5th ed.; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Barbero, G.; Evangelista, L.R. Adsorption Phenomena and Anchoring Energy in Nematic Liquid Crystals; Taylor & Francis: London, UK, 2006. [Google Scholar]
- Mossad, M.; Zou, I. Evaluation of the salt removal efficiency of capacitive deionisation: Kinetics, isothems and thermodynamics. Chem. Eng. 2013, 223, 704–713. [Google Scholar] [CrossRef]
- Maximus, B.; De Ley, E.; De Meyere, A.; Pauwels, H. Ion Transport in SSFLCD’s. Ferroelectrics 1991, 121, 103–112. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Barbero, G. Statistical interpretation of the kinetic equation in the adsorption problem. Eur. Phys. J. E 2004, 15, 3–8. [Google Scholar] [CrossRef]
- Wolkenstein, T. Electronic Processes on Semiconductor Surfaces During Chemisorption; Consultants Bureau: New York, NY, USA, 1991. [Google Scholar]
- Rothschild, A.; Komen, Y.J.; Ashkenasy, N. Quantitative evaluation of chemisorption processes on semiconductors. J. Appl. Phys. 2002, 92, 7090–7097. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.R.; Lelidis, I. Effective adsorption energy and generalization of the Frumkin-Fowler-Guggenheim isotherm. J. Mol. Liq. 2021, 327, 114795. [Google Scholar] [CrossRef]
- Macdonald, J.R. Theory of ac Space-Charge Polarization Effects in Photoconductors, Semiconductors, and Electrolytes. Phys. Rev. 1953, 92, 4–17. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Chu, K.T.; Bayly, B.J. Current-Voltage relations for electrochemical thin films. SIAM J. Appl. Math. 2005, 65, 1463–1484. [Google Scholar] [CrossRef] [Green Version]
- Bisquert, J.; Bertoluzzi, L.; Mora-sero, I.; Garcia-Belmonte, G. Theory of Impedance and Capacitance Spectroscopy of Solar Cells with Dielectric Relaxation, Drift-Diffusion Transport, and Recombination. J. Phys. Chem. C 2014, 118, 18983–18991. [Google Scholar] [CrossRef]
- Sangoro, J.R.; Serghei, A.; Naumov, S.; Galvosas, P.; Kaerger, J.; Wespe, C.; Bordusa, F.; Kremer, F. Charge transport and mass transport in imidazolium-based ionic liquid. Phys. Rev. E 2008, 77, 051202. [Google Scholar] [CrossRef]
- Serghei, A.; Tress, M.; Sangoro, J.R.; Kremer, F. Electrode polarization and charge transport at solid interface. Phys. Rev. B 2009, 80, 184301. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Agapov, A.I.; Fan, F.; Hong, K.; Yu, X.; Mays, J.; Sokolov, A.P. Decoupling of ionic transport from segmental relaxation in polymer electrolytes. Phys. Rev. Lett. 2012, 108, 088303. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Sun, C.N.; Fan, F.; Sangoro, J.R.; Berman, M.B.; Greenbaum, S.G.; Zawodzinski, T.A.; Sokolov, A.P. Examination of methods to determine free-ion diffusivity and number density from analysis of electrode polarization. Phys. Rev. E 2013, 87, 042308. [Google Scholar] [CrossRef]
- Khazimullin, M.K.; Lebedev, Y.A. Influence of dielectric layer on estimates of diffusion coefficients and concentrations of ions from impedance spectroscopy. Phys. Rev. E 2019, 100, 062601. [Google Scholar] [CrossRef] [Green Version]
- Alexe-Ionescu, A.L.; Barbero, G.; Evangelista, L.R. Electric response of asymmetric electrolytic cells to small AC signals. J. Electroanal. Chem. 2020, 873, 114378. [Google Scholar] [CrossRef]
- Macdonald, J.R. One-dimensional current transport equations. J. Appl. Phys. 1975, 46, 4602. [Google Scholar] [CrossRef]
- Dubai, D.P.; Gomez-Romero, P.; Sankapal, B.R.; Holze, P. Nickel cobaltite as an emerging material for suercapacitors: An overview. Nano Energy 2015, 11, 377–399. [Google Scholar]
- Zhang, S.; Pan, N. Supercapacitors Performance Evaluations. Adv. Energy Mater. 2015, 5, 1401401. [Google Scholar] [CrossRef] [Green Version]
- Xiong, G.; Meng, C.; Reifenberger, R.G.; Irazoqui, P.P.; Fisher, T.S. A Review of Graphene-Based Electrochemical Micosupercapacitors. Electroanalysis 2014, 26, 30–51. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Chu, Q.; Wang, Z.; Wang, S. Theoretical and experimental specific capacitance of polyaniline in sulfuric acid. J. Power Sources 2009, 190, 578–586. [Google Scholar] [CrossRef]
- Song, R.Y.; Park, J.H.; Sivakkumar, S.R.; Kim, S.H.; Ko, J.M.; Park, D.Y.; Jo, S.M.; Kim, D.Y. Supercapacitive properties of polyaniline/Nafion/hydrous RuO2 composite electrodes. J. Power Sources 2007, 166, 297–301. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, J.; Chen, Y. An Overview of the Application of graphene-Based Materials in Supercapacitors. Small 2012, 8, 1805–1834. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.-M.; Ramachandran, R.; Mani, V.; Saraswathi, R. Recent Advancements in elecrode Materials for High-performance Electrochemical Supercapacitors. Int. J. Electrochem. Sci. 2014, 9, 4072–4085. [Google Scholar]
- Zaccagnini, P.; Serrapede, M.; Lamberti, A.; Bianco, S.; Rivolo, P.; Tresso, E.; Pirri, C.F.; Barbero, G.; Alexe-Ionescu, A.L. Modeling of Electrochemical Capacitors Under Dynamical Cycling. Electrochim. Acta 2018, 296, 709–718. [Google Scholar] [CrossRef]
- Barbero, G.; Alexe-Ionescu, A.L. Role of the diffuse layer of the ionic charge on the impedance spectroscopy of a cell of liquid. Liq. Cryst. 2005, 32, 943. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evangelista, L.R.; Barbero, G.; Alexe-Ionescu, A.L. A Model for Bias Potential Effects on the Effective Langmuir Adsorption–Desorption Processes. Electron. Mater. 2021, 2, 125-141. https://doi.org/10.3390/electronicmat2020011
Evangelista LR, Barbero G, Alexe-Ionescu AL. A Model for Bias Potential Effects on the Effective Langmuir Adsorption–Desorption Processes. Electronic Materials. 2021; 2(2):125-141. https://doi.org/10.3390/electronicmat2020011
Chicago/Turabian StyleEvangelista, Luiz Roberto, Giovanni Barbero, and Anca Luiza Alexe-Ionescu. 2021. "A Model for Bias Potential Effects on the Effective Langmuir Adsorption–Desorption Processes" Electronic Materials 2, no. 2: 125-141. https://doi.org/10.3390/electronicmat2020011
APA StyleEvangelista, L. R., Barbero, G., & Alexe-Ionescu, A. L. (2021). A Model for Bias Potential Effects on the Effective Langmuir Adsorption–Desorption Processes. Electronic Materials, 2(2), 125-141. https://doi.org/10.3390/electronicmat2020011






