Enhanced Thermal Performance of Variable-Density Maxwell Nanofluid Flow over a Stretching Sheet Under Viscous Dissipation: A Maritime Technology Perspective
Abstract
1. Introduction
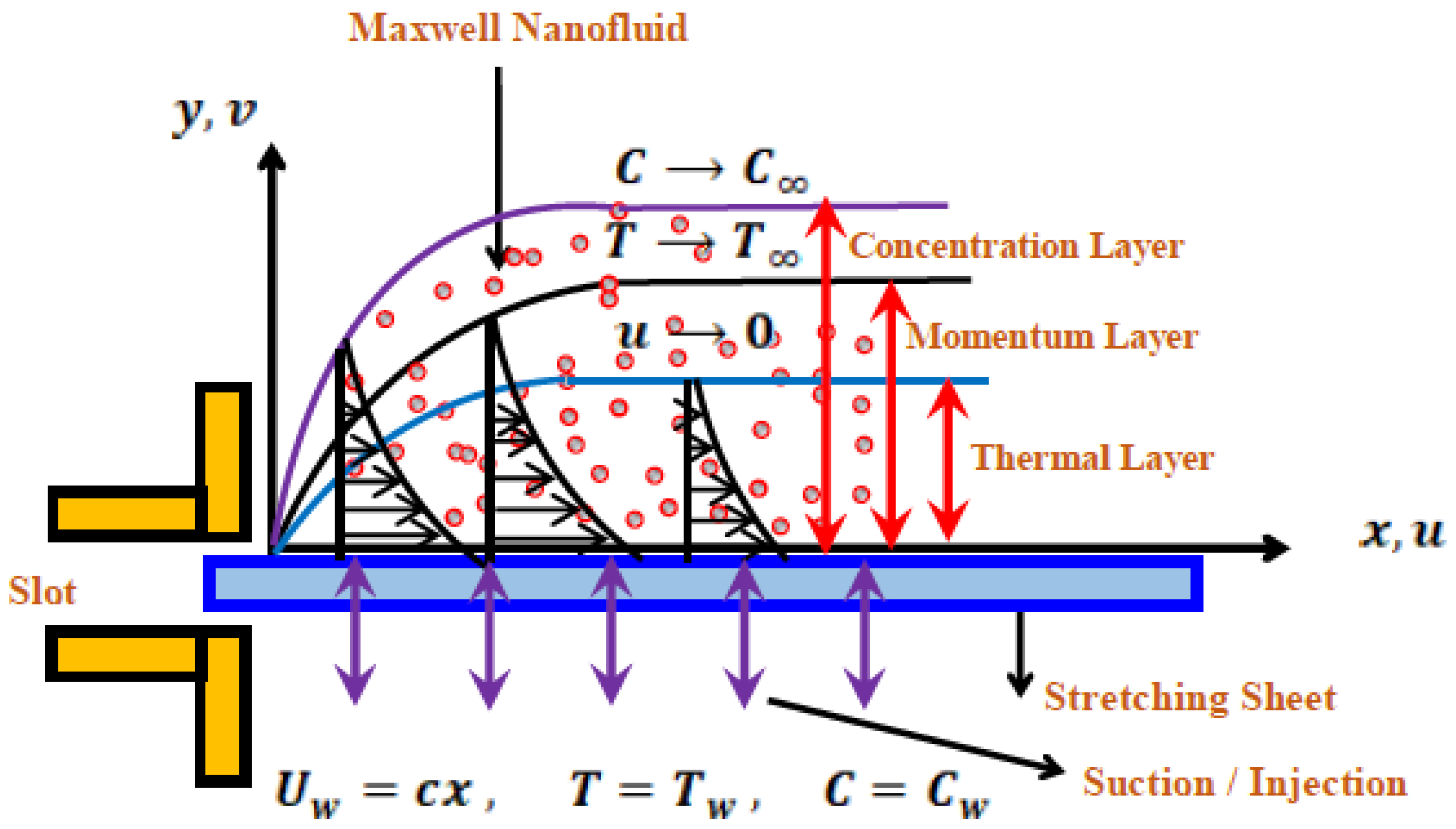
2. Mathematical Modeling
Non-Dimensionalized Governing Equations
3. Limitations and Future Work
4. Validating the Code
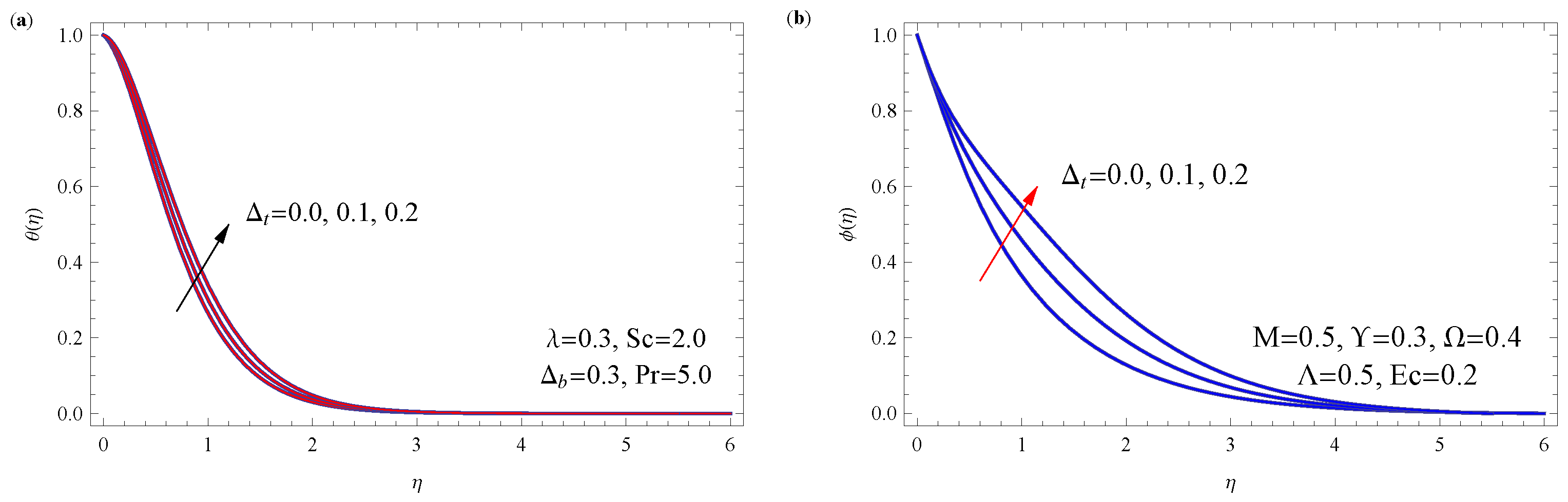
5. Interpretation of Results
6. Concluding Remarks
- Raising the Stefan blowing parameter reduces the wall shear stress and substantially reduces heat and mass transfer, highlighting its suppressive impact on momentum, thermal, and concentration exchange along the sheet.
- The porous medium and Maxwell and magnetic field parameters each boost flow resistance, which in turn increases skin friction. However, they also hinder heat and mass transfer by thickening the thermal and concentration boundary layers and through the influence of fluid elasticity and the Lorentz force.
- When Brownian motion intensifies, it leads to better heat transfer and higher surface temperatures. This also results in a lower nanoparticle concentration because of enhanced diffusion.
- A higher density parameter diminishes velocity, temperature, and concentration profiles. This occurs because increased fluid inertia weakens the transport of momentum, heat, and mass close to the stretching surface.
- A rise in the Stefan blowing parameter subtly boosts velocity but considerably increases temperature and concentration profiles. This happens because it traps heat and nanoparticles closer to the surface, making the thermal and solutal boundary layers thicker.
- Increasing the thermophoresis parameter significantly thickens the concentration boundary layer and moderately enhances the temperature profile.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| C | Concentration |
| Coefficient of Brownian motion | |
| Imposed magnetic field strength | |
| k | Porous medium permeability |
| M | Factor of magnetic field |
| c | Positive constant regarding stretching process |
| Pr | Prandtl number |
| Factor affecting nanoparticle aggregation rate on the sheet | |
| T | Nanofluid temperature |
| Reynolds number | |
| Velocity components along the x- and y-axes, respectively | |
| Schmidt number | |
| Thermal strength near the sheet | |
| Eckert number | |
| Thermal strength away the sheet | |
| f | Non-dimensional stream function |
| Heat capacity | |
| Greek symbols | |
| Viscosity of nanofluid | |
| Dimensionless similarity variable | |
| Density of nanofluid | |
| Nanofluid kinematic viscosity | |
| Dimensionless temperature | |
| Stream function | |
| Fluid relaxation time coefficient | |
| Electric conductivity | |
| Dimensionless concentration | |
| Density factor | |
| Maxwell parameter | |
| Porous factor | |
| Brownian motion factor | |
| Thermal conductivity | |
| Stefan blowing factor | |
| Thermophoresis parameter | |
| Nanoparticle-to-fluid heat capacity ratio | |
References
- Yang, J.; Yang, X.; Wang, J.; Chin, H.H.; Sundén, B. Review on thermal performance of nanofluids with and without magnetic fields in heat exchange devices. Front. Energy Res. 2022, 10, 822776. [Google Scholar] [CrossRef]
- Porgar, S.; Huminic, G.; Huminic, A.; Najibolashrafi, B.; Salehfekr, S. Application of nanofluids in heat exchangers—A state-of-the-art review. Int. J. Thermofluids 2024, 24, 100945. [Google Scholar] [CrossRef]
- Afify, A.A.; Elgazery, N.S. Effect of a chemical reaction on magnetohydrodynamic boundary layer flow of a Maxwell fluid over a stretching sheet with nanoparticles. Particuology 2016, 23, 154–161. [Google Scholar] [CrossRef]
- Kumar, M.A.; Reddy, Y.D. Computational modelling of radiative Maxwell fluid flow over a stretching sheet containing nanoparticles with chemical reaction. J. Indian Chem. Soc. 2023, 100, 100877. [Google Scholar] [CrossRef]
- Kumar, M.A.; Reddy, Y.D. Thermal radiation and chemical reaction influence on MHD boundary layer flow of a Maxwell fluid over a stretching sheet containing nanoparticles. J. Therm. Anal. Calorim. 2023, 148, 6301–6309. [Google Scholar] [CrossRef]
- Al Rashdi, S.A.S.; Ghoneim, N.I.; Amer, A.M.; Megahed, A.M. Investigation of magnetohydrodynamic slip flow for Maxwell nanofluid over a vertical surface with Cattaneo-Christov heat flux in a saturated porous medium. Results Eng. 2023, 19, 101293. [Google Scholar] [CrossRef]
- Khan, A.; Shah, I.A.; Khan, A.; Khan, I.; Khan, W.A. Numerical investigation of MHD Cattaneo-Christov thermal flux frame work for Maxwell fluid flow over a steady extending surface with thermal generation in a porous medium. Int. J. Thermofluids 2023, 20, 100418. [Google Scholar] [CrossRef]
- Khan, M.N.; Wang, Z.; Ahammad, N.A.; Rezapour, S.; Shutaywi, M.; Ali, N.B.; Elkotb, M.A. Mixed convective flow analysis of a Maxwell fluid with double diffusion theory on a vertically exponentially stretching surface. Appl. Water Sci. 2024, 14, 172. [Google Scholar] [CrossRef]
- Arif, M.S.; Abodayeh, K.; Nawaz, Y. Explicit computational analysis of unsteady maxwell nanofluid flow on moving plates with stochastic variations. Int. J. Thermofluids 2024, 23, 100755. [Google Scholar] [CrossRef]
- Manjunatha, P.T.; Chamkha, A.J.; Gowda, R.J.P.; Kumar, R.N.; Prasannakumara, B.C.; Naik, S.M. Significance of Stefan blowing and convective heat transfer in nanofluid flow over a curved stretching sheet with chemical reaction. J. Nanofluid 2021, 10, 285–291. [Google Scholar] [CrossRef]
- Haider, S.M.A.; Ali, B.; Wang, Q.; Zhao, C. Stefan blowing impacts on unsteady MHD flow of nanofluid over a stretching sheet with electric field, thermal radiation and activation energy. Coatings 2021, 11, 1048. [Google Scholar] [CrossRef]
- Jyothi, A.M.; Kumar, R.N.; Gowda, P.; Prasannakumara, B.C. Significance of Stefan blowing effect on flow and heat transfer of Casson nanofluid over a moving needle. Commun. Theor. Phys. 2021, 7319, 095005. [Google Scholar] [CrossRef]
- Saleem, M.; Hussain, M. Impression of nonlinear radiation and Stefan blowing on the magneto cross nano-Williamson fluid above exponentially stretching sheet. Results Eng. 2023, 17, 100864. [Google Scholar] [CrossRef]
- Konai, S.; Maiti, H.; Mukhopadhyay, S. Influences of Stefan blowing on unsteady flow of Casson nanofluid past a stretching surface. Forces Mech. 2023, 12, 100227. [Google Scholar] [CrossRef]
- Zhang, R.; Zaydan, M.; Wakif, A.; Alshehri, M.; Shah, N.A. Further insights into mixed convective boundary layer flows of internally heated Jeffery nanofluids: Stefan’s blowing case study with convective heating and thermal radiation impressions. Case Stud. Therm. Eng. 2024, 55, 104121. [Google Scholar] [CrossRef]
- Siddiqa, S.; Hossain, M.A.; Gorla, R.S.R. Temperature-dependent density effect on natural convection flow over a horizontal circular disk. J. Thermophys. Heat Transf. 2016, 30, 890–896. [Google Scholar] [CrossRef]
- Ullah, Z.; Hussain, A.; Aldhabani, M.S.; Altaweel, N.H.; Shahab, S. Significance of temperature-dependent density on dissipative and reactive flows of nanofluid along magnetically driven sheet and applications in machining and lubrications. Lubricants 2023, 11, 410. [Google Scholar] [CrossRef]
- Boukholda, I.; Ullah, Z.; Mahrous, Y.M.; Alamer, A.; Amara, M.B.; Alsulami, M.D.; Khedher, N.B. Analysis of thermal density and heat sink on dissipative nanofluid along magnetized sheet and applications in microelectronic cooling systems. Case Stud. Therm. Eng. 2024, 55, 104185. [Google Scholar] [CrossRef]
- Haider, I.; Younis, J.; Jabeen, N.; Hussain, A.; Shaaban, I.A.; Mohsin, M.A.; Assiri, M.A. Viscous dissipation and variable density impact on heat-mass transmission in magneto Ree-Eyring nanofluid across stretched sheet with multiple slips. Case Stud. Therm. Eng. 2025, 68, 105871. [Google Scholar] [CrossRef]
- Megahed, A.M. Improvement of heat transfer mechanism through a Maxwell fluid flow over a stretching sheet embedded in a porous medium and convectively heated. Math. Comput. Simul. 2021, 187, 97–109. [Google Scholar] [CrossRef]
- Khedher, N.B.; Ullah, Z.; Alam, M.M.; Al Arni, S.; Elbadawi, I.; Makinde, O.D.; Boujelbene, M. Significance of thermal conductivity and variable density on heat and mass transfer of MHD second-grade nanofluid along high-temperature polymer surface. Case Stud. Therm. Eng. 2025, 71, 106168. [Google Scholar] [CrossRef]
- Challa, K.K.; Rao, M.E.; Jawad, M.; Saidani, T.; Abdallah, S.A.O.; Thenmozhi, D. Enhanced heat transfer and flow dynamics of Powell-Eyring nanofluid: Unsteady stretched surface and with Stefan blowing/suction. Case Stud. Therm. Eng. 2025, 65, 105664. [Google Scholar] [CrossRef]
- Siddiqa, S.; Asghar, S.; Hossain, M.A. Radiation effects in mixed convection flow of a viscous fluid having temperature-dependent density along a permeable vertical plate. J. Eng. Phys. Thermophys. 2012, 85, 339–348. [Google Scholar] [CrossRef]
- Abel, M.S.; Tawade, J.V.; Nandeppanavar, M.M. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 2012, 47, 385–393. [Google Scholar]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 2014, 45, 121–126. [Google Scholar] [CrossRef]




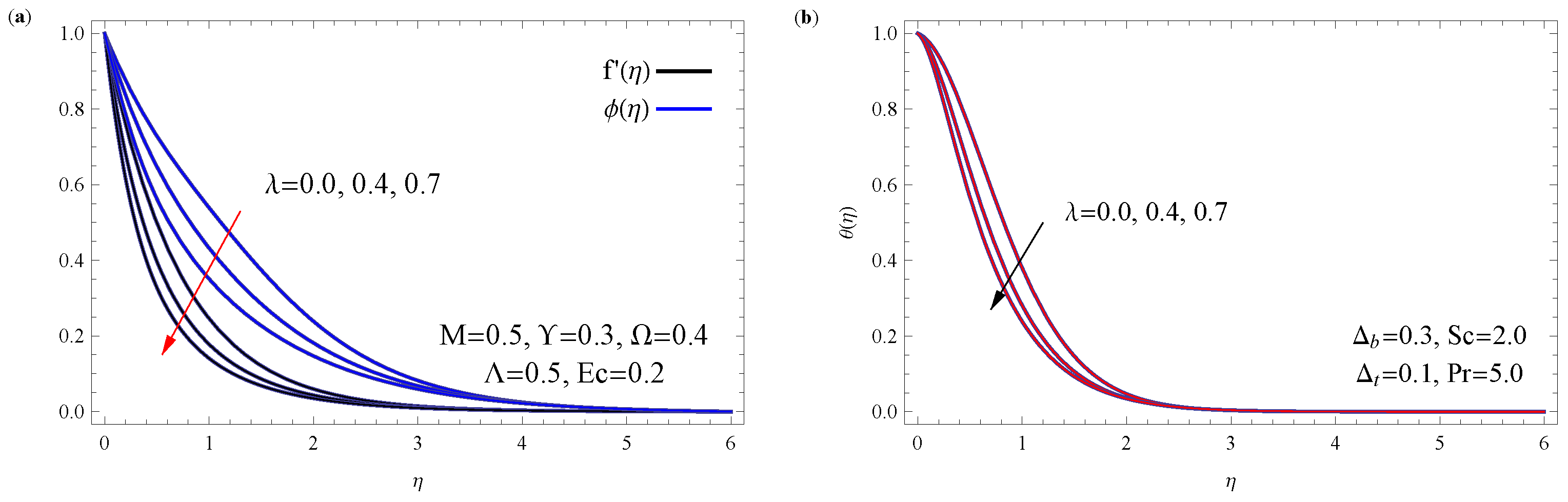

| M | Abel et al. [24] | Present Work | |
|---|---|---|---|
| 0.0 | 0.0 | 0.999962 | 0.99999988998 |
| 0.2 | 0.0 | 1.051948 | 1.05194770096 |
| 0.4 | 0.0 | 1.101850 | 1.10184899072 |
| 0.6 | 0.0 | 1.150163 | 1.15016285014 |
| 0.0 | 0.2 | 1.095445 | 1.09544488902 |
| 0.2 | 0.2 | 1.188270 | 1.18826890258 |
| 0.4 | 0.2 | 1.275878 | 1.27587777031 |
| 0.6 | 0.2 | 1.358733 | 1.35873288095 |
| Nadeem et al. [25] | Present Work | |
|---|---|---|
| 0.1 | 0.9524 | 0.952377098 |
| 0.2 | 0.6932 | 0.693189907 |
| 0.3 | 0.5201 | 0.520055911 |
| 0.4 | 0.4026 | 0.402588093 |
| 0.5 | 0.3211 | 0.321088907 |
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.85486 | 0.361815 | 0.962961 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.82521 | 0.164096 | 0.825509 |
| 0.6 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.81293 | 0.092607 | 0.770876 |
| 0.4 | 0.0 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.56683 | 0.307311 | 0.859341 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.82521 | 0.164096 | 0.825509 |
| 0.4 | 1.0 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 2.05324 | −0.02453 | 0.807554 |
| 0.4 | 0.5 | 0.0 | 0.5 | 0.3 | 0.3 | 0.1 | 1.73356 | 0.181274 | 0.834812 |
| 0.4 | 0.5 | 0.8 | 0.5 | 0.3 | 0.3 | 0.1 | 1.97355 | 0.134959 | 0.811285 |
| 0.4 | 0.5 | 1.3 | 0.5 | 0.3 | 0.3 | 0.1 | 2.11693 | 0.104591 | 0.800538 |
| 0.4 | 0.5 | 0.3 | 0.0 | 0.3 | 0.3 | 0.1 | 1.56683 | 0.307295 | 0.859341 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.82521 | 0.164096 | 0.825509 |
| 0.4 | 0.5 | 0.3 | 1.0 | 0.3 | 0.3 | 0.1 | 2.05325 | 0.024545 | 0.807498 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.0 | 0.3 | 0.1 | 1.43928 | 0.103147 | 0.675692 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.4 | 0.3 | 0.1 | 1.97875 | 0.180201 | 0.891299 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.7 | 0.3 | 0.1 | 2.53277 | 0.209633 | 1.152970 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.2 | 0.1 | 1.82901 | 0.291815 | 0.788805 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.82521 | 0.164096 | 0.825509 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.5 | 0.1 | 1.82012 | 0.004423 | 0.849231 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.0 | 1.82682 | 0.244082 | 0.816055 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.1 | 1.82521 | 0.164096 | 0.825509 |
| 0.4 | 0.5 | 0.3 | 0.5 | 0.3 | 0.3 | 0.2 | 1.82289 | 0.088690 | 0.840912 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amer, A.M.; Ghoneim, N.I.; Alghaffari, S.; Gommosani, M.E.; Megahed, A.M. Enhanced Thermal Performance of Variable-Density Maxwell Nanofluid Flow over a Stretching Sheet Under Viscous Dissipation: A Maritime Technology Perspective. Modelling 2025, 6, 134. https://doi.org/10.3390/modelling6040134
Amer AM, Ghoneim NI, Alghaffari S, Gommosani ME, Megahed AM. Enhanced Thermal Performance of Variable-Density Maxwell Nanofluid Flow over a Stretching Sheet Under Viscous Dissipation: A Maritime Technology Perspective. Modelling. 2025; 6(4):134. https://doi.org/10.3390/modelling6040134
Chicago/Turabian StyleAmer, A. M., Nourhan I. Ghoneim, Shadi Alghaffari, Mohammad E. Gommosani, and Ahmed M. Megahed. 2025. "Enhanced Thermal Performance of Variable-Density Maxwell Nanofluid Flow over a Stretching Sheet Under Viscous Dissipation: A Maritime Technology Perspective" Modelling 6, no. 4: 134. https://doi.org/10.3390/modelling6040134
APA StyleAmer, A. M., Ghoneim, N. I., Alghaffari, S., Gommosani, M. E., & Megahed, A. M. (2025). Enhanced Thermal Performance of Variable-Density Maxwell Nanofluid Flow over a Stretching Sheet Under Viscous Dissipation: A Maritime Technology Perspective. Modelling, 6(4), 134. https://doi.org/10.3390/modelling6040134






