Numerical Study on the Effects of Surface Shape and Rotation on the Flow Characteristics and Heat Transfer Behavior of Tandem Cylinders in Laminar Flow Regime
Abstract
1. Introduction
2. Numerical Model
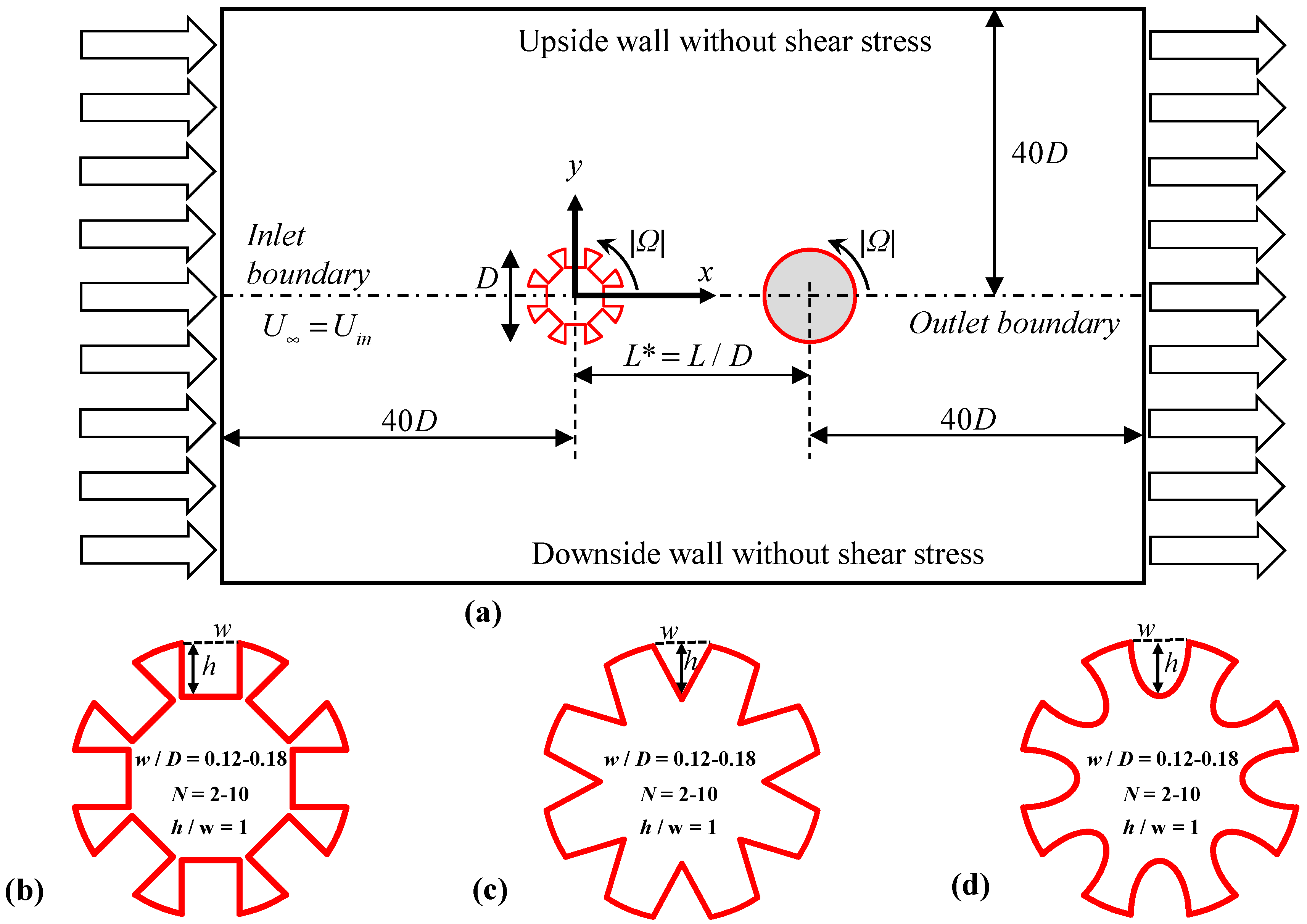
2.1. Physical Geometry
2.2. Governing Equations
2.3. Numerical Details and Boundary Conditions
3. Validation of Numerical Code
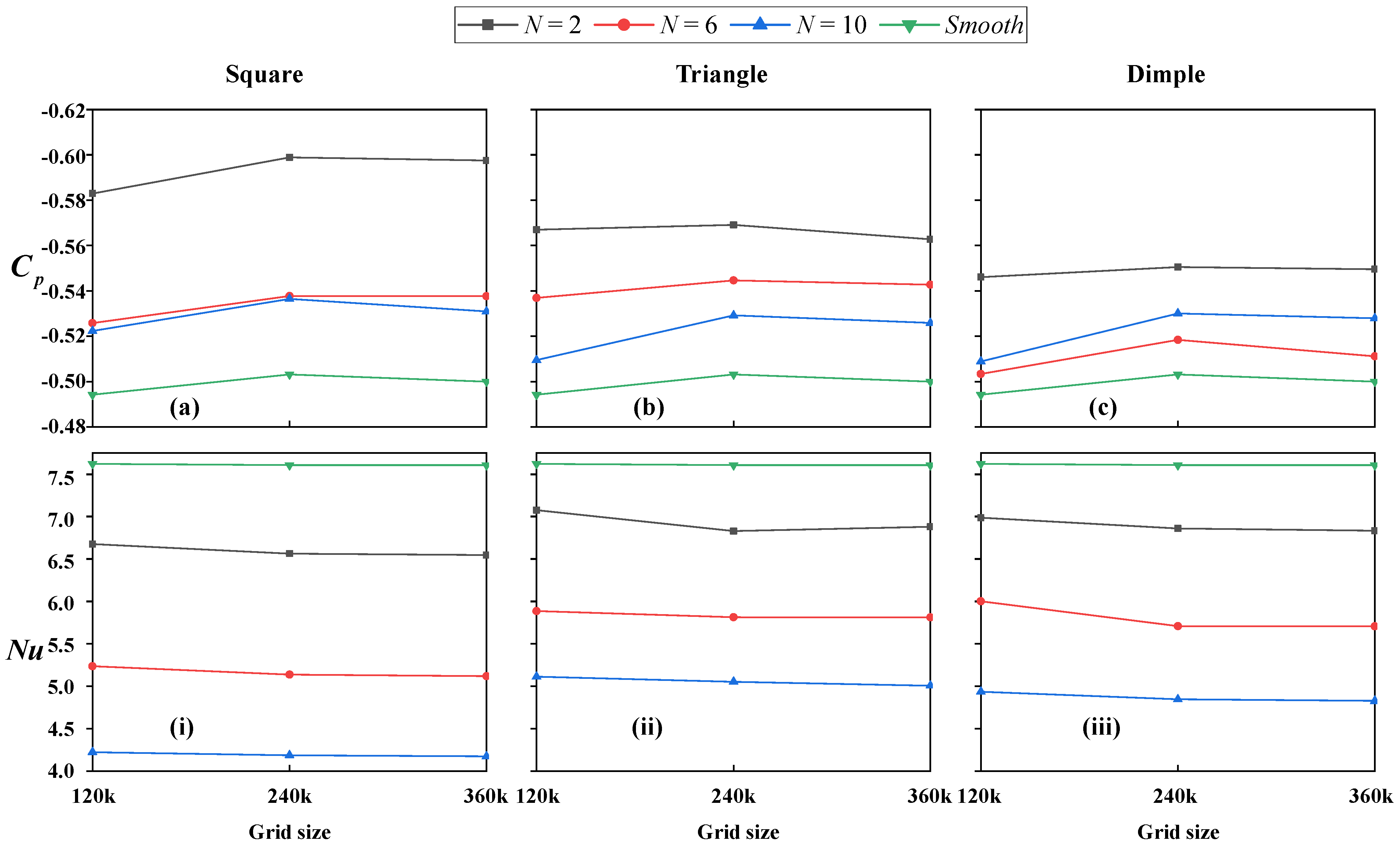
3.1. Grid Independence Study
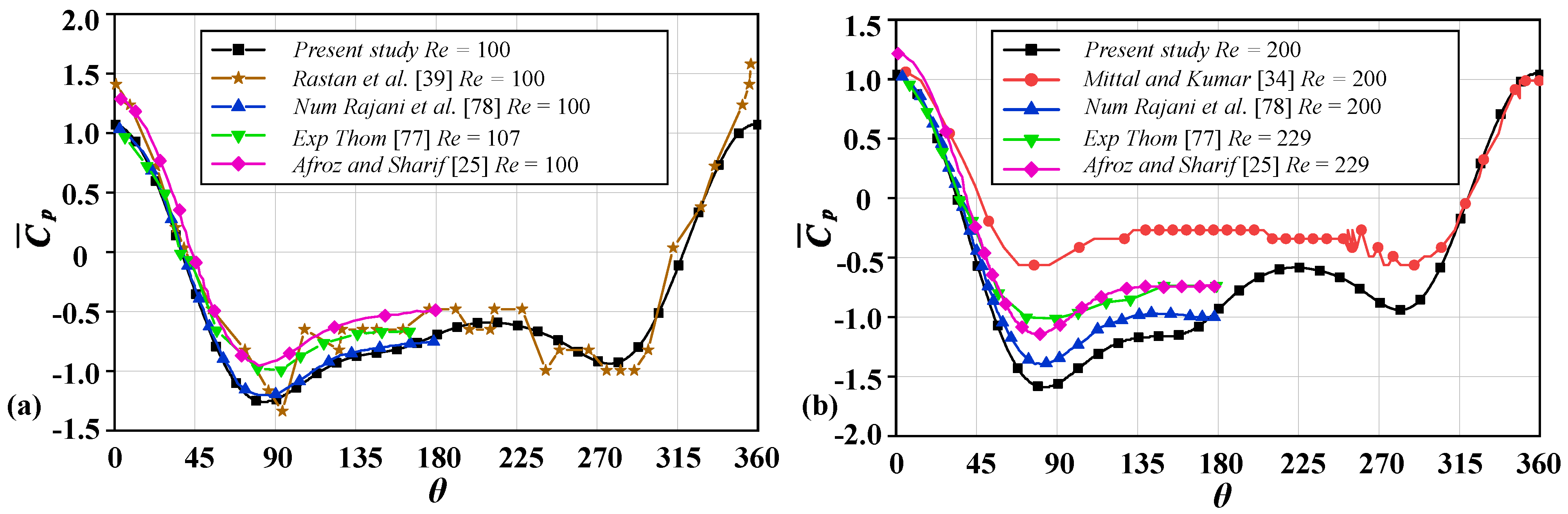
3.2. Parameter Validation
4. Results and Discussion
4.1. Flow Characteristics
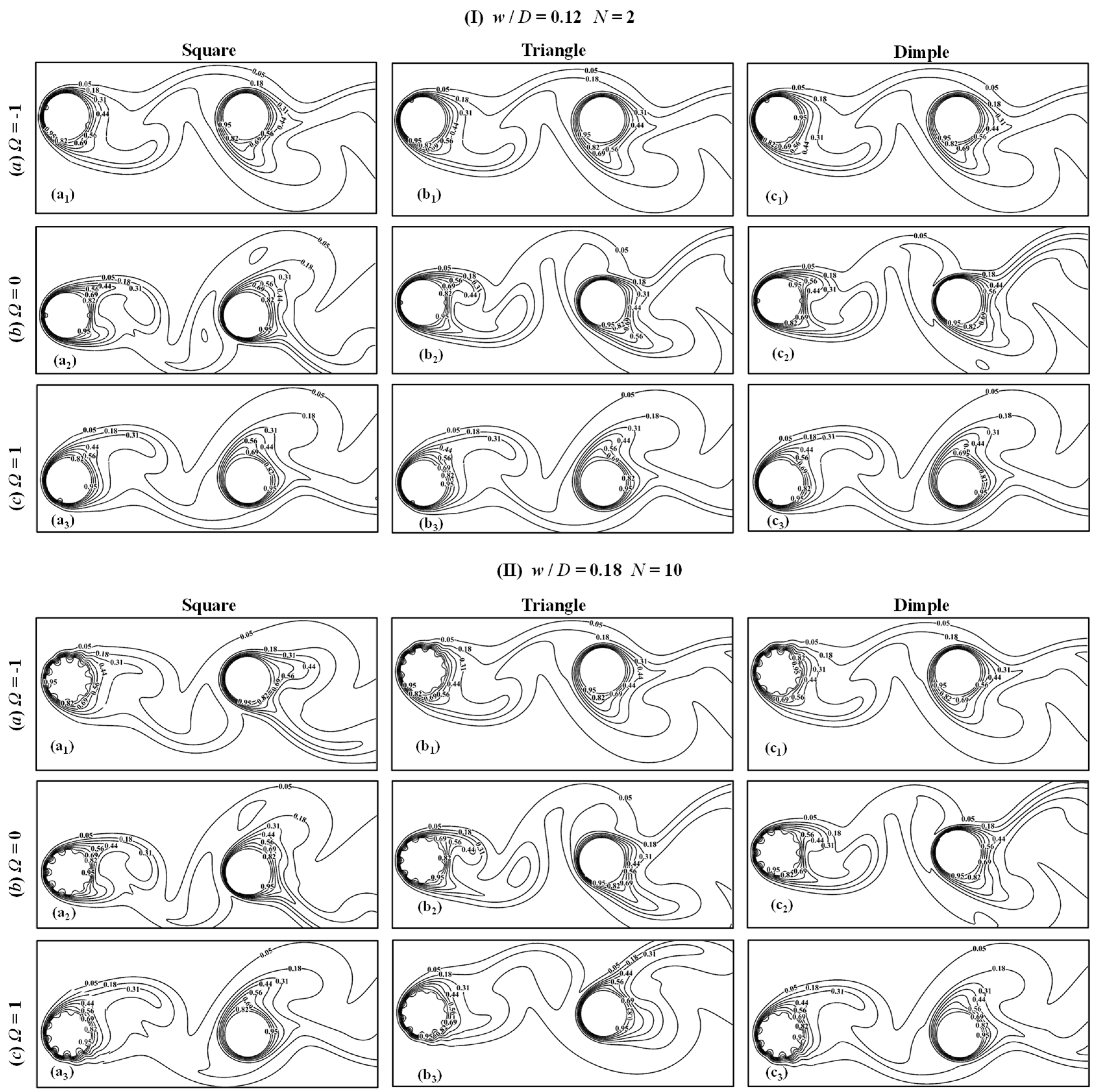
4.1.1. Streamlines
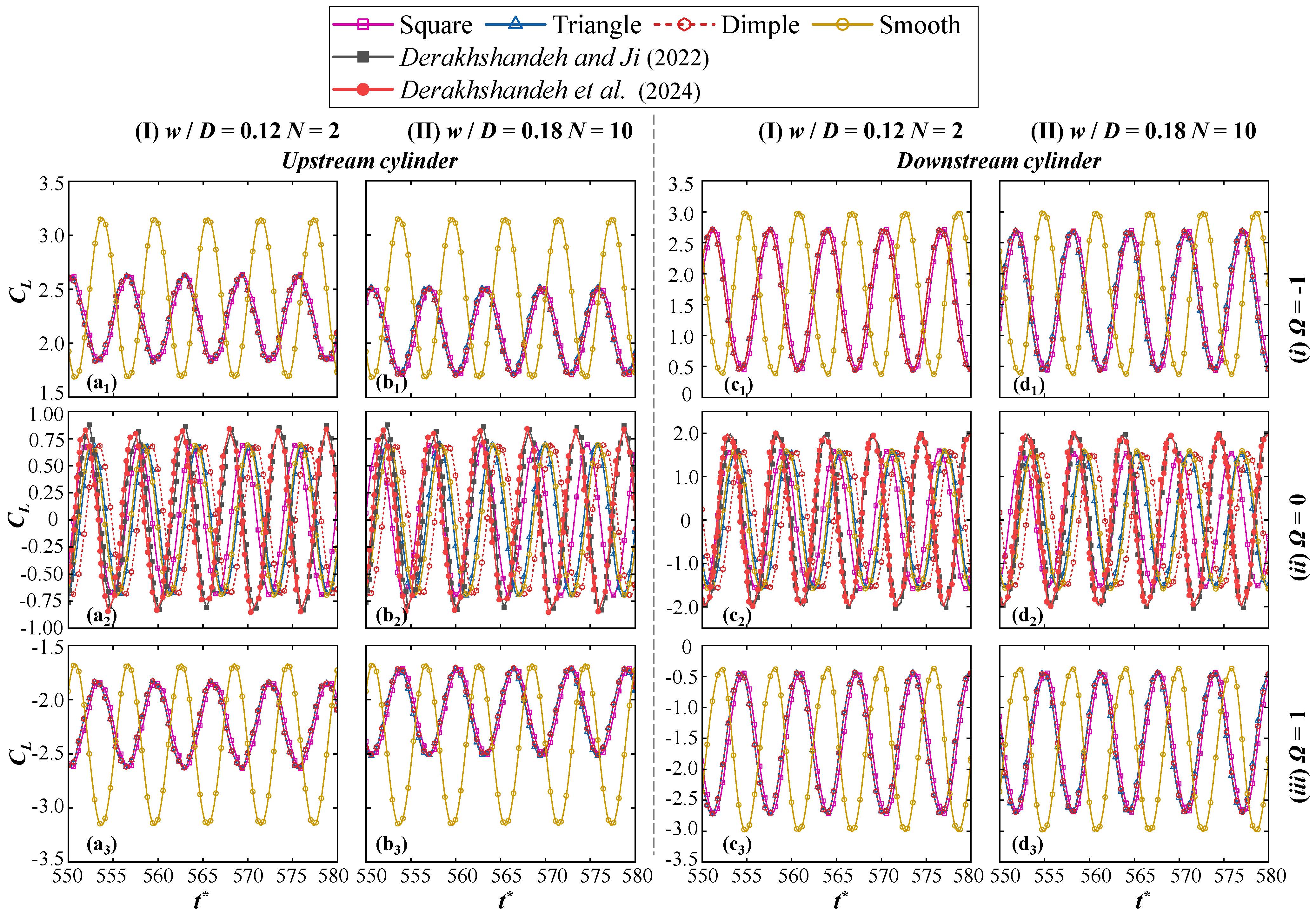
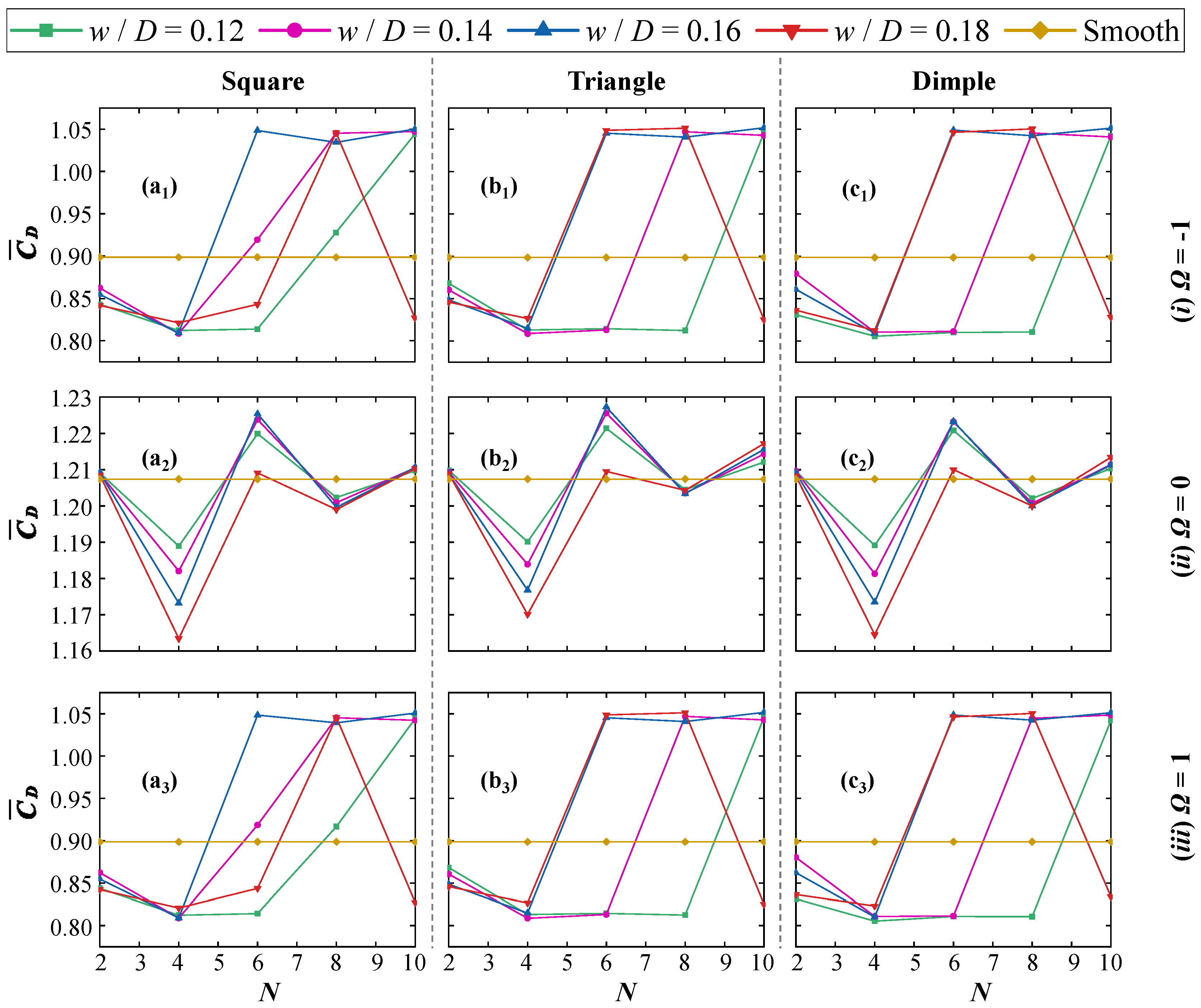
4.1.2. Drag and Lift Coefficients
4.1.3. RMS Lift Coefficient and Time-Averaged Drag Coefficient
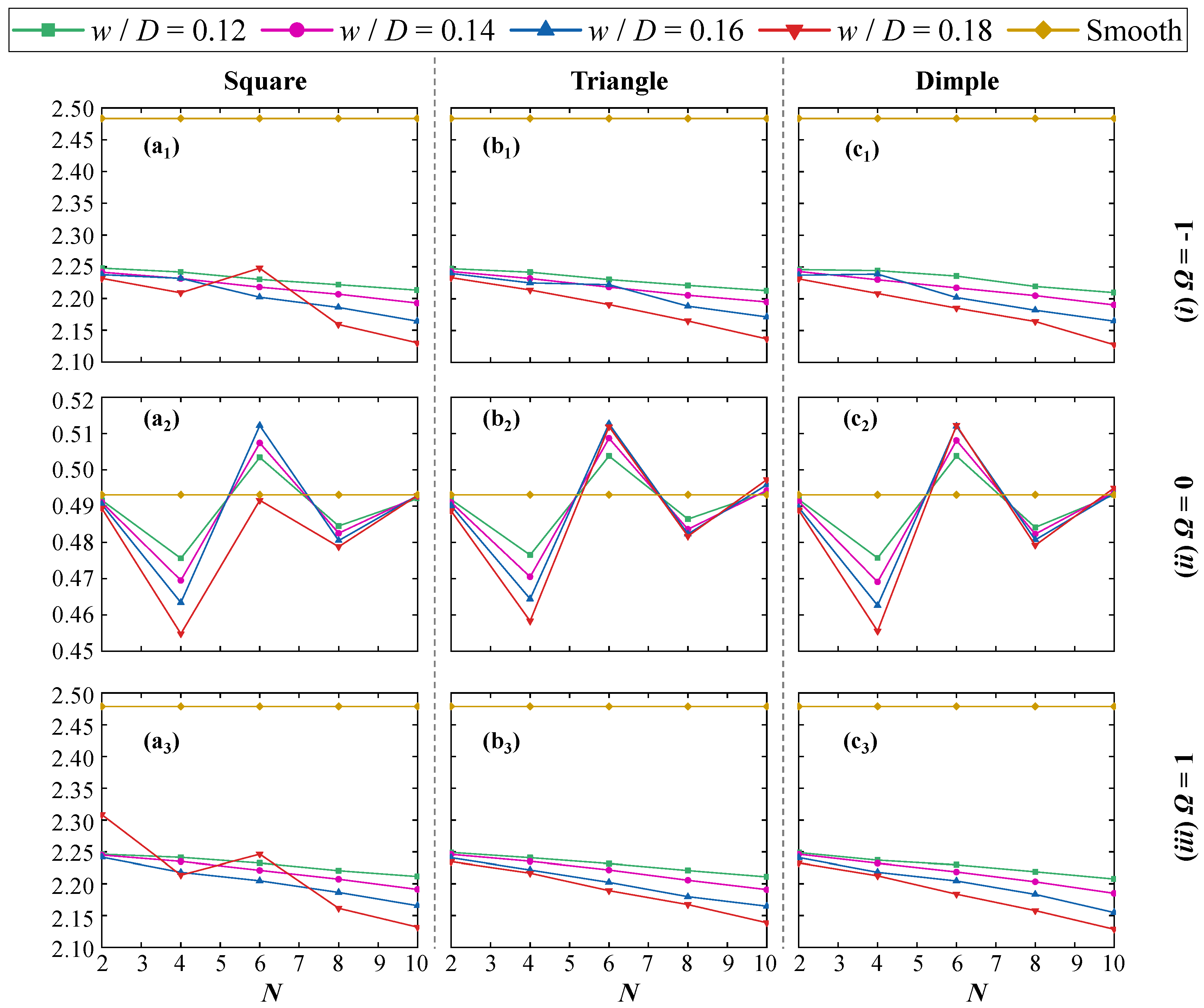
4.1.4. Strohal Number
4.1.5. Time-Averaged Pressure Coefficient
4.2. Heat Transfer
4.2.1. Isotherms
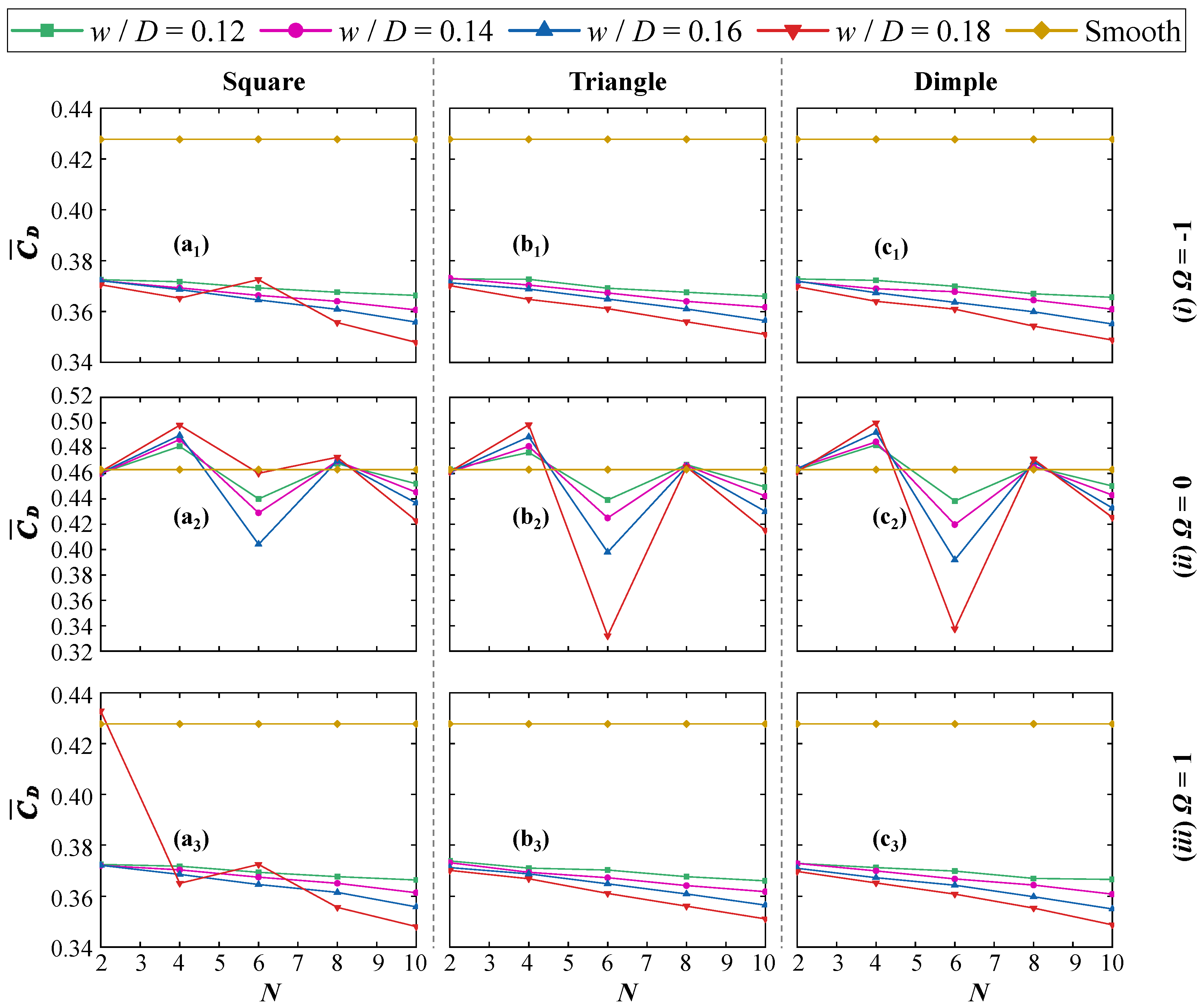
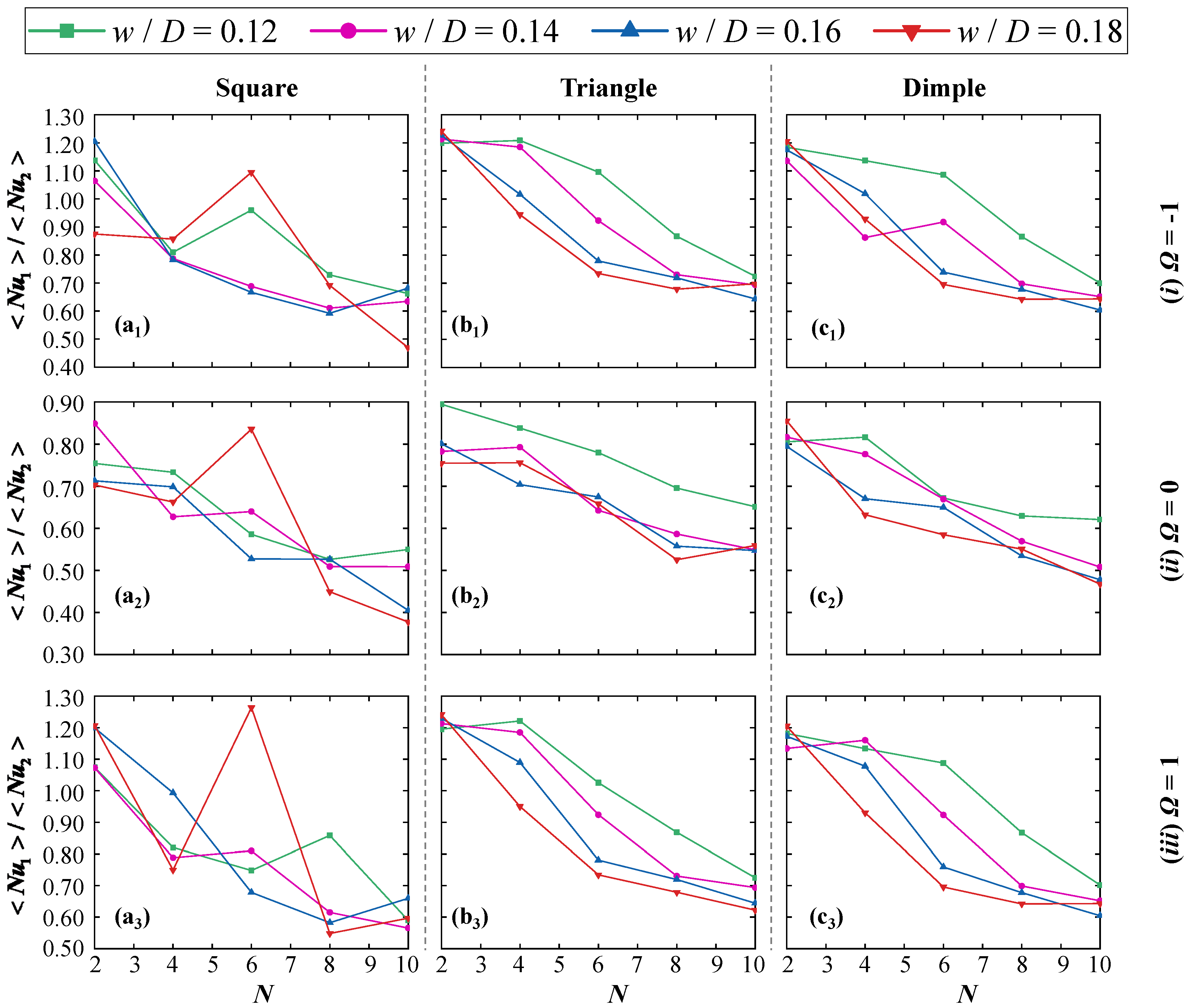
4.2.2. Comparison of Average Nusselt Number for Patterned Tandem Cylinders
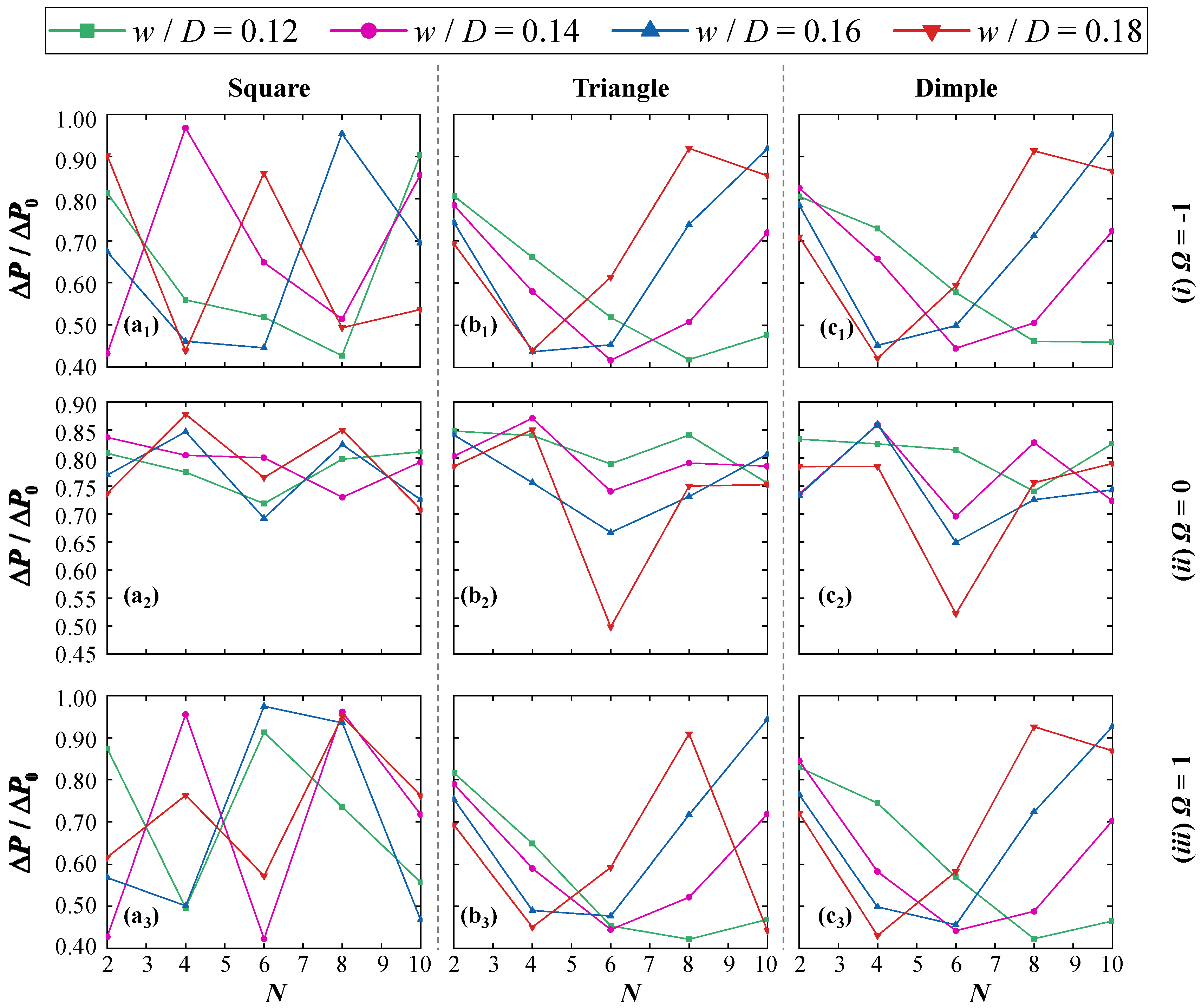
4.2.3. Thermal Performance Indicators
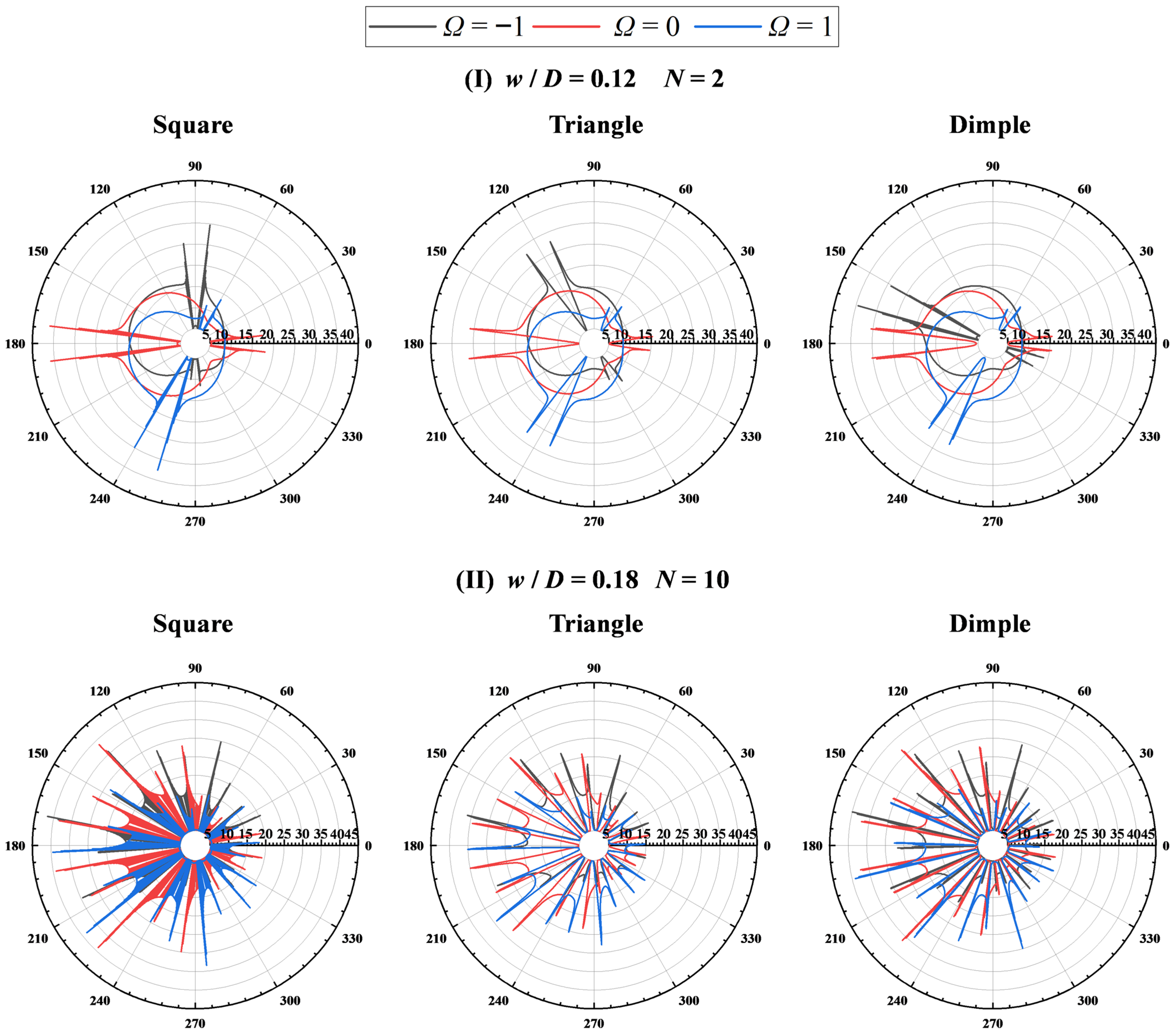
4.2.4. Analysis of Nusselt Number Distribution Characteristics on the Cylinder Surface
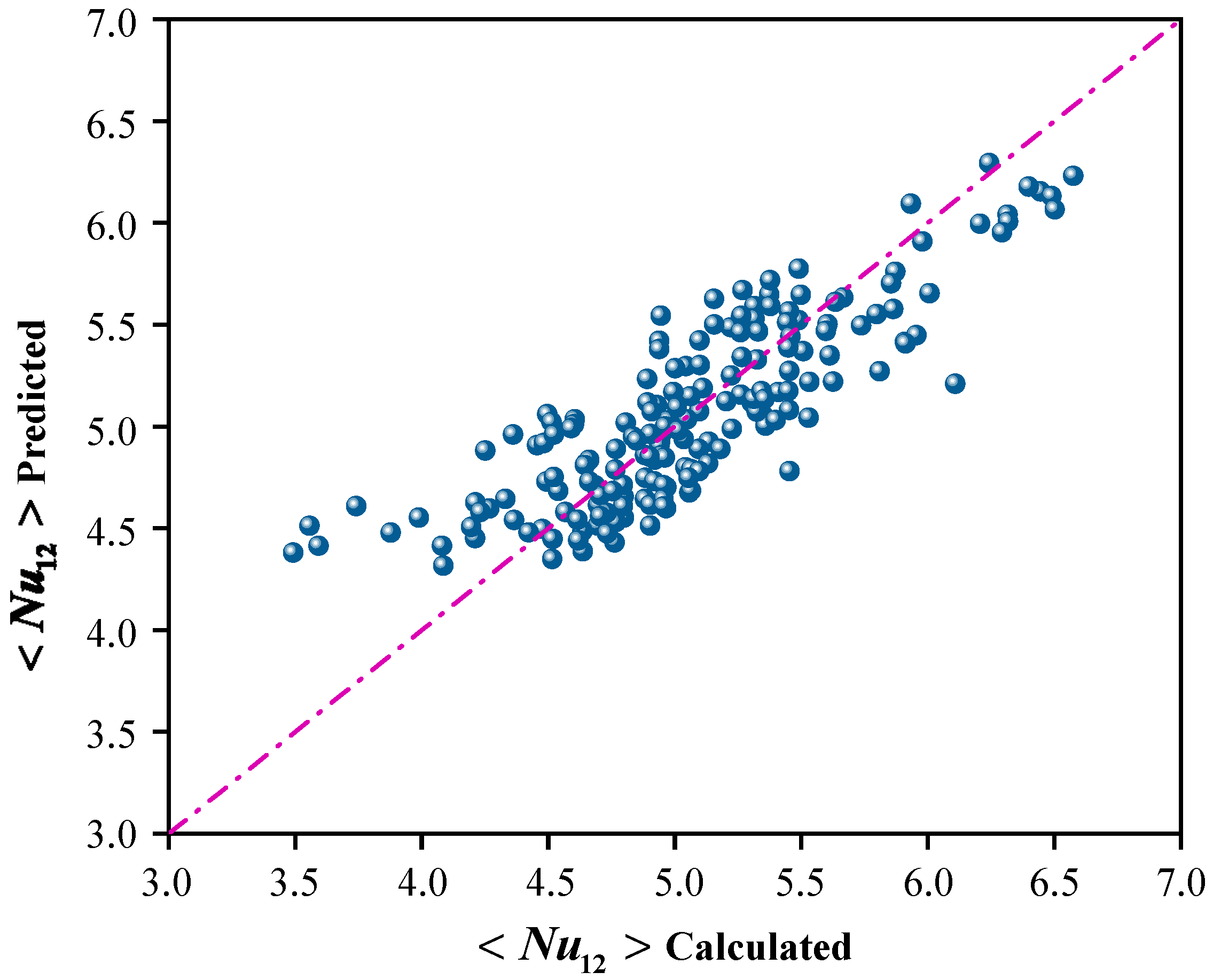
5. The Relationship Between the Average Nusselt Number, the Number of Grooves, Groove Area and Rotational Speed
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Center-to-center distance between the cylinders | α | Angular velocity | |
| Lift coefficient | Superscripts | ||
| Drag coefficient | * | Normalized | |
| Diameter of the cylinder | - | Time average | |
| Vortex shedding frequency | < > | Surface average | |
| Freestream velocity | ‘ | Root mean square | |
| Streamwise velocity | Subscripts | ||
| Cross-stream velocity | Wall | ||
| Reynolds number | Freestream | ||
| Strouhal number | 0 | Baseline | |
| Prandtl number | x,y,z | Cartesian coordinate system direction | |
| Nusselt number | 12 | Tandem cylinder | |
| Local convective heat transfer coefficient | 1 | Upstream cylinder | |
| Thermal conductivity | 2 | Downstream cylinder | |
| Temperature | max | Maximum | |
| Static pressure | min | Minimum | |
| Time | Abbreviations | ||
| Time step | CFL | Courant-Friedrichs-Lewy number | |
| Force | SIMPLE | Semi-Implicit Method for Pressure-Linked Equations | |
| Specific heat capacity | CG | Coarse Grid | |
| Vorticity | MG | Moderate Grid | |
| Pressure coefficient | FG | Fine Grid | |
| Greek alphabet | TPI | Thermal Performance Index | |
| Dynamic viscosity | SMM | Sliding Mesh Method | |
| Fluid density | |||
| Polar angle |
References
- Schmidt, H.J.; Woszidlo, R.; Nayeri, C.N.; Paschereit, C.O. Drag reduction on a rectangular bluff body with base flaps and fluidic oscillators. Exp. Fluids 2015, 56, 151. [Google Scholar] [CrossRef]
- Patel, C.G.; Sarkar, S.; Saha, S.K. Mixed convective vertically upward flow past side-by-side square cylinders at incidence. Int. J. Heat Mass Transf. 2018, 127, 927–947. [Google Scholar] [CrossRef]
- Dhiman, A.; Ghosh, R. Computer simulation of momentum and heat transfer across an expanded trapezoidal bluff body. Int. J. Heat Mass Transf. 2013, 59, 338–352. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Gharib, N. Numerical studies of laminar flow over two tandem elliptical cylinders using Ramanujan approximation. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 169. [Google Scholar] [CrossRef]
- El-Maghlany, W.M.; Alnakeeb, M.A.; Teamah, M.A.; Sorour, M.M. Experimental and numerical study of laminar mixed convection from a horizontal isothermal elliptic cylinder. Int. J. Therm. Sci. 2018, 130, 116–127. [Google Scholar] [CrossRef]
- Liao, C.C.; Lin, C.A. Influences of a confined elliptic cylinder at different aspect ratios and inclinations on the laminar natural and mixed convection flows. Int. J. Heat Mass Transf. 2012, 55, 6638–6650. [Google Scholar] [CrossRef]
- Yoon, H.S.; Nam, S.H.; Kim, M.I. Effect of the geometric features of the harbor seal vibrissa based biomimetic cylinder on the forced convection heat transfer. Int. J. Heat Mass Transf. 2020, 159, 120086. [Google Scholar] [CrossRef]
- Cattafesta, L.N.; Sheplak, M. Actuators for active flow control. Annu. Rev. Fluid Mech. 2011, 43, 247–272. [Google Scholar] [CrossRef]
- Riahi, H.; Aminossadati, S.M.; Leonardi, C. A discrete immersed boundary method for the numerical simulation of heat transfer in compressible flows. Eur. J. Mech.-B/Fluids 2025, 111, 61–71. [Google Scholar] [CrossRef]
- Wang, N.; Aminossadati, S.M.; Leonardi, C. Numerical study of vortex-induced motion and heat transfer characteristics of elliptic cylinders with different aspect ratios. Eur. J. Mech.-B/Fluids 2025, 114, 204328. [Google Scholar] [CrossRef]
- Sadeghi, S.; Aminossadati, S.M.; Leonardi, C. Numerical investigation of the role of human motion in the spread of virus-laden droplets from coughing using CFD dynamic mesh technique. Eur. J. Mech.-B/Fluids 2025, 111, 42–60. [Google Scholar] [CrossRef]
- Ji, H.; Liu, Z.; Zhao, J.; Wang, B. Enhanced cooling performance in cutting tools using TPMS-integrated toolholders: A CFD-based thermal-fluidic study. Modelling 2025, 6, 73. [Google Scholar] [CrossRef]
- Lin, P.; Yuan, X.; Liu, T. Statistical evaluation of API P–Y curve model for offshore piles in cohesionless soils. Modelling 2025, 6, 91. [Google Scholar] [CrossRef]
- Nikfarjam, F.; Sohankar, A. Power-law fluids flow and heat transfer over two tandem square cylinders: Effects of Reynolds number and power-law index. Acta Mech. 2013, 224, 1115–1132. [Google Scholar] [CrossRef]
- Nikfarjam, F.; Sohankar, A. Study of hysteresis associated with power-law fluids past square prisms arranged in tandem. Ocean Eng. 2015, 104, 698–813. [Google Scholar] [CrossRef]
- Liu, M.M.; Lu, L.; Teng, B.; Zhao, M.; Tang, G.Q. Re-examination of laminar flow over twin circular cylinders in tandem arrangement. Fluid Dyn. Res. 2014, 46, 025501. [Google Scholar] [CrossRef]
- Alam, M.M. Lift forces induced by phase lag between the vortex sheddings from two tandem bluff bodies. J. Fluids Struct. 2016, 65, 217–237. [Google Scholar] [CrossRef]
- Wang, L.J.; Alam, M.M.; Zhou, Y. Two tandem cylinders of different diameters in cross-flow: Effect of an upstream cylinder on wake dynamics. J. Fluid Mech. 2018, 836, 5–42. [Google Scholar] [CrossRef]
- Canpolat, C. Characteristics of flow past a circular cylinder with a rectangular groove. Flow Meas. Instrum. 2015, 45, 233–246. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Alam, M.M. A numerical study of heat transfer enhancement by a rectangular cylinder placed parallel to the heated wall. J. Heat Transf. 2019, 141, 091702. [Google Scholar] [CrossRef]
- El-Makdah, A.M.; Ghanem, F.O. The flow past a cactus-inspired grooved cylinder. Exp. Fluids 2013, 54, 1464. [Google Scholar] [CrossRef]
- Wang, S.F.; Liu, Y.Z.; Zhang, Q.S. Measurement of flow around a cactus-analogue grooved cylinder at ReD = 5.4 × 104: Wall-pressure fluctuations and flow pattern. J. Fluids Struct. 2014, 50, 120136. [Google Scholar] [CrossRef]
- Talley, B.S.; Mungal, G. Flow around cactus-shaped cylinders. Annu. Res. Briefs Cent. Turbul. Res. 2002, 2002, 363–376. [Google Scholar]
- Yamagishi, Y.; Oki, M. Effect of groove shape on flow characteristics around a circular cylinder with grooves. J. Visualization 2004, 7, 209. [Google Scholar] [CrossRef]
- Afroz, F.; Sharif, M.A.R. Numerical study of cross-flow around a circular cylinder with differently shaped span-wise surface grooves at low Reynolds number. Eur. J. Mech.-B/Fluids 2022, 91, 203. [Google Scholar] [CrossRef]
- Kimura, T.; Tsutahara, M. Fluid dynamic effects of grooves on circular cylinder surface. AIAA J. 1991, 29, 2062. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Gharib, N. Numerical investigations on the flow control over bumped surface circular cylinders. Ocean Eng. 2021, 240, 109943. [Google Scholar] [CrossRef]
- Li, S.; Zhou, T.; Sun, Z.; Dong, Z. External forced convection from circular cylinders with surface protrusions. Int. J. Heat Mass Transf. 2016, 99, 20. [Google Scholar] [CrossRef]
- Sharma, B.; Barman, R.N. Unsteady flow past slotted circular cylinders in laminar regime: Effect of slit shapes and Reynolds number. Phys. Fluids 2023, 35, 013602. [Google Scholar] [CrossRef]
- Priyadarsan, A.; Afzal, M.S. Numerical investigation of flow past a circular cylinder modified with a single groove at low Reynolds number. Phys. Fluids 2023, 35, 027125. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Gharib, N. Laminar flow instabilities of a grooved circular cylinder. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 580. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Tari, Z.G.; Gharib, N. Thermo-fluids effects of a grooved circular cylinder in laminar flow regimes. Int. Commun. Heat Mass Transf. 2021, 124, 105272. [Google Scholar] [CrossRef]
- Takayama, S.; Aoki, K. Flow characteristics around a rotating grooved circular cylinder with grooves of different depths. J. Vis. 2005, 8, 295. [Google Scholar] [CrossRef]
- Mittal, S.; Kumar, B. Flow past a rotating cylinder. J. Fluid Mech. 2003, 476, 303. [Google Scholar] [CrossRef]
- Paramane, S.B.; Sharma, A. Numerical investigation of heat and fluid flow across a rotating circular cylinder maintained at constant temperature in 2-D laminar flow regime. Int. J. Heat Mass Transf. 2009, 52, 3205. [Google Scholar] [CrossRef]
- Ansari, M.; Naeeni, S.T.O.; Moradi, M. Investigating the flow and heat transfer characteristics of two co/counter-rotating circular cylinders at a low Reynolds number. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 48, 193–209. [Google Scholar] [CrossRef]
- Darvishyadegari, M.; Hassanzadeh, R. Convective heat transfer and fluid flow of two counter-rotating cylinders in tandem arrangement. Acta Mech. 2018, 229, 1783–1802. [Google Scholar] [CrossRef]
- Darvishyadegari, M.; Hassanzadeh, R. Heat and fluid flow around two co-rotating cylinders in tandem arrangement. Int. J. Therm. Sci. 2019, 135, 206–220. [Google Scholar] [CrossRef]
- Rastan, M.R.; Sohankar, A.; Alam, M.M. Flow and heat transfer across two inline rotating cylinders: Effects of blockage, gap spacing, Reynolds number, and rotation direction. Int. J. Heat Mass Transf. 2021, 174, 121324. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Gharbia, Y.; Ji, C. Numerical investigations on flow over tandem grooved cylinders. Ocean Eng. 2022, 251, 111160. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Ji, C. Flow disturbances over heated indented surface cylinders arranged in a tandem. Ocean Eng. 2024, 296, 116903. [Google Scholar] [CrossRef]
- Li, Y.; Shi, F.; Xin, J.; Peng, L.; Wan, L. Numerical investigation of the heat transfer and flow pattern on tandem triangle-grooved cylinders. Case Stud. Therm. Eng. 2024, 60, 104808. [Google Scholar] [CrossRef]
- Tatsumi, K.; Kuroki, R.; Nakamura, M.; Nakabe, K. Numerical investigation on fluid flow and heat transfer characteristics in a peristaltic micropump. Prog. Comput. Fluid Dyn. Int. J. 2011, 11, 160–168. [Google Scholar] [CrossRef]
- Akbar, Y.; Abbasi, F.M.; Zahid, U.M.; Shehzad, S.A. Effectiveness of heat and mass transfer on mixed convective peristaltic motion of nanofluid with irreversibility rate. Commun. Theor. Phys. 2021, 73, 105004. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Dehkordi, R.B.; Abed, H. MHD mixed convection and entropy generation in a lid-driven cavity with rotating cylinders filled by a nanofluid using two-phase mixture model. J. Magn. Magn. Mater. 2019, 483, 224–248. [Google Scholar] [CrossRef]
- Sadr, A.N.; Shekaramiz, M.; Zarinfar, M.; Esmaily, A.; Khoshtarash, H.; Toghraie, D. Simulation of mixed convection of water and nano-encapsulated phase change material inside a square cavity with a rotating hot cylinder. J. Energy Storage 2022, 47, 103606. [Google Scholar] [CrossRef]
- Liu, X.; Toghraie, D.; Hekmatifar, M.; Akbari, O.A.; Karimipour, A.; Afrand, M. Numerical investigation of nanofluid laminar forced convection heat transfer between two horizontal concentric cylinders in the presence of porous medium. J. Therm. Anal. Calorim. 2020, 141, 2095–2108. [Google Scholar] [CrossRef]
- Al-Rashed, A.A.; Shahsavar, A.; Akbari, M.; Toghraie, D.; Akbari, M.; Afrand, M. Finite volume simulation of mixed convection in an inclined lid-driven cavity filled with nanofluids: Effects of a hot elliptical centric cylinder, cavity angle, and volume fraction of nanoparticles. Phys. A 2019, 527, 121122. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Abderrahmane, A.; Shamshuddin, M.D.; Younis, O.; Mohammed, S.; Bég, O.A.; Toghraie, D. Heat transfer and entropy generation analysis of water-Fe3O4/CNT hybrid magnetic nanofluid flow in a trapezoidal wavy enclosure containing porous media with the Galerkin finite element method. Eur. Phys. J. Plus 2021, 136, 1–23. [Google Scholar] [CrossRef]
- Mashayekhi, R.; Arasteh, H.; Toghraie, D.; Motaharpour, S.H.; Keshmiri, A.; Afrand, M. Heat transfer enhancement of water-Al2O3 nanofluid in an oval channel equipped with two rows of twisted conical strip inserts in various directions: A two-phase approach. Comput. Math. Appl. 2020, 79, 2203–2215. [Google Scholar] [CrossRef]
- Zafar, F.; Alam, M.M. Mixed convection heat transfer from a circular cylinder submerged in wake. Int. J. Mech. Sci. 2020, 183, 105733. [Google Scholar] [CrossRef]
- Bhatt, R.; Alam, M.M. Vibrations of a square cylinder submerged in a wake. J. Fluid Mech. 2018, 853, 301–332. [Google Scholar] [CrossRef]
- Zheng, Q.; Alam, M.M. Evolution of the wake of three inline square prisms. Phys. Rev. Fluids 2019, 4, 104701. [Google Scholar] [CrossRef]
- Zheng, Q.; Alam, M.M. Intrinsic features of flow past three square prisms in side-by-side arrangement. J. Fluid Mech. 2017, 826, 996–1033. [Google Scholar] [CrossRef]
- Buyruk, E. Numerical study of heat transfer characteristics on tandem cylinders, inline and staggered tube banks in cross-flow air. Int. Commun. Heat Mass Transf. 2002, 29, 353–362. [Google Scholar] [CrossRef]
- Wanderley, J.B.V.; Souza, G.H.B.; Sphaier, S.H. Vortex-induced vibration of an elastically mounted circular cylinder using an upwind TVD two-dimensional numerical scheme. Ocean Eng. 2008, 35, 1533–1544. [Google Scholar] [CrossRef]
- Sohankar, A.; Etminan, A. Forced-convection heat transfer from tandem square cylinders in cross flow at low Reynolds numbers. Int. J. Numer. Methods Fluids 2009, 60, 733–751. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Taylor & Francis: New York, NY, USA, 2018. [Google Scholar]
- Khodabandeh, E.; Rozati, S.A.; Joshaghani, M.; Akbari, O.A.; Akbari, S.; Toghraie, D. Thermal performance improvement in water nanofluid/GNP–SDBS in novel design of double-layer microchannel heat sink with sinusoidal cavities and rectangular ribs. J. Therm. Anal. Calorim. 2019, 136, 1333–1345. [Google Scholar] [CrossRef]
- Tian, S.; Arshad, N.I.; Toghraie, D.; Eftekhari, S.A.; Hekmatifar, M. Using perceptron feed-forward artificial neural network (ANN) for predicting the thermal conductivity of graphene oxide-Al2O3/water-ethylene glycol hybrid nanofluid. Case Stud. Therm. Eng. 2021, 26, 101055. [Google Scholar] [CrossRef]
- Ding, L.; Sun, Y. Heat transfer and vibration response of a stationary cylinder and an elastic cylinder under mutual interference. Int. Commun. Heat Mass Transf. 2022, 139, 106493. [Google Scholar] [CrossRef]
- Routa, C.; Balaji, P.; Sahu, A.K. Numerical investigation of effect of surface pattern and rotation on power-law fluid flow and heat transfer around a cylinder in laminar flow regime. Phys. Fluids 2023, 35, 073605. [Google Scholar] [CrossRef]
- Khan, M.N.; Karimi, M.N.; Qidwai, M.O. Effect of circular perforated pin fin on heat transfer and fluid flow characteristics of rectangular microchannel heat sink. Numer. Heat Transf. Part A 2023, 83, 594–608. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, Z.; Lan, Y.; Huang, Z.; Zhang, J. Effects of geometric parameters of circular pin-fins on fluid flow and heat transfer in an interrupted microchannel heat sink. Int. J. Therm. Sci. 2021, 165, 106956. [Google Scholar] [CrossRef]
- Li, Y.; Shi, F.; Li, J.; Xin, J. Thermal fluid dynamics interaction between dual cylinders: Numerical analysis of groove effects and rotational speed. Int. J. Heat Fluid Flow 2024, 109, 109525. [Google Scholar] [CrossRef]
- Žukauskas, A. Heat transfer from tubes in crossflow. Adv. Heat Transf. 1972, 8, 93–160. [Google Scholar]
- Knudsen, J.D.; Katz, D.L. Fluid Dynamics and Heat Transfer; McGraw Hill: New York, NY, USA, 1958. [Google Scholar]
- Churchill, S.W.; Bernstein, M. A correlating equation for forced convection from gases and liquids to a circular cylinder in crossflow. AIChE J. 1977, 23, 300–306. [Google Scholar] [CrossRef]
- Alam, M.M.; Zheng, Q.; Derakhshandeh, J.F. On forces and phase lags between vortex sheddings from three tandem cylinders. Int. J. Heat Fluid Flow 2018, 69, 117–135. [Google Scholar] [CrossRef]
- Mahir, N.; Altaç, Z. Numerical investigation of convective heat transfer in unsteady flow past two cylinders in tandem arrangements. Int. J. Heat Fluid Flow 2008, 29, 1309–1318. [Google Scholar] [CrossRef]
- Williamson, C.H.K. 2-D and 3-D aspects of the wake of a cylinder, and their relation to wake computations. Lect. Appl. Math. Am. Math. Soc. 1991, 28, 719. [Google Scholar]
- Roshko, A. On the Drag and Shedding Frequency of Two-Dimensional Bluff Bodies; NACA-TN-3169; NASA: Washington, DC, USA, 1954.
- Norberg, A. Fluctuating lift on a circular cylinder: Review and new measurements. J. Fluids Struct. 2003, 17, 57–96. [Google Scholar] [CrossRef]
- Yu, M.; Jiang, G.; Jiang, Y. Effect of acoustic waves on the flow and heat transfer around two tandem arranged cylinders. Case Stud. Therm. Eng. 2022, 40, 102573. [Google Scholar] [CrossRef]
- Kang, S.; Choi, H.; Lee, S. Laminar flow past a rotating circular cylinder. Phys. Fluids 1999, 11, 3312–3321. [Google Scholar] [CrossRef]
- Stojkovic, D.; Breuer, M.; Durst, F. Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 2002, 14, 3160–3178. [Google Scholar] [CrossRef]
- Harimi, M.; Saghafian, M. Numerical simulation of fluid flow and forced convection heat transfer from tandem circular cylinders using overset grid method. J. Fluids Struct. 2012, 28, 309–327. [Google Scholar] [CrossRef]
- Patnana, V.K.; Bharti, R.P.; Chhabra, R.P. Two-dimensional unsteady forced convection heat transfer in power-law fluids from a cylinder. Int. J. Heat Mass Transf. 2010, 53, 4152–4167. [Google Scholar] [CrossRef]
- Thom, A. The flow past circular cylinders at low speeds. Proc. R. Soc. Lond. A 1933, 141, 651–669. [Google Scholar]
- Rajani, A.; Kandasamy, A.; Majumdar, S. Numerical simulation of laminar flow past a circular cylinder. Appl. Math. Model. 2009, 33, 1228–1247. [Google Scholar] [CrossRef]
- Panda, S.K.; Chhabra, R.P. Laminar forced convection heat transfer from a rotating cylinder to power-law fluids. Numer. Heat Transf. Part A 2011, 59, 297. [Google Scholar] [CrossRef]











| Boundary | Velocity | Temperature | Pressure |
|---|---|---|---|
| Inlet (constant velocity and temperature) | u = U∞, v = 0 | T = T∞ | , |
| Outlet (zero pressure outlet) | , | p = 0 | |
| , | |||
| Cylinder (no slip wall) | u = 0, v = 0 | T = Tw | , |
| Top and bottom (slip wall) | , v = 0 | , |
| Parameters | CL,max | St | ||||||
|---|---|---|---|---|---|---|---|---|
| Sources | Re | Ω | Literature | Present | Literature | Present | Literature | Present |
| Mahir and Altaç [70] | 100/200 | 0 | 1.369 ± 0.029/1.377 ± 0.048 | 1.31/1.3 | 0.343/0.698 | 0.3/0.58 | 0.172/0.192 | |
| Williamson a [71] | 100/200 | 0 | --- | --- | 0.164/0.196 | |||
| Roshko a [72] | 100/200 | 0 | --- | --- | 0.16–0.17/0.17–0.19 | |||
| Norberg a [73] | 100/200 | 0 | --- | 0.18 ± 0.54/0.35 ± 0.70 | 0.168/0.18–0.197 | |||
| Yu et al. [74] | 100/200 | 0 | 1.385/1.353 | 0.323/0.635 | 0.167/0.198 | |||
| Li et al. [42] | 100/200 | 0 | 1.37/1.33 | 0.328/0.632 | 0.169/0.195 | |||
| Kang et al. [75] | 100 | 1 | 1.104 | 1.176 | −2.49 | −2.58 | 0.166 | 0.164 |
| Stojkovic et al. [76] | 100 | 1 | 1.108 | −2.50 | 0.166 | |||
| Paramane and Sharma [35] | 100 | 1 | 1.095 | −2.49 | 0.165 | |||
| Sources | Re = 100 | Re = 200 |
|---|---|---|
| Present | 5.23 | 7.54 |
| Harimi and Saghafian [77] | 5.0613 | 7.1079 |
| Mahir and Altaç [70] | 5.1797 ± 0.003 | 7.4747 ± 0.028 |
| Patnana et al. [78] | 5.153 | --- |
| Equation (17) | 5.10 | 7.21 |
| Equation (18) | 5.19 | 7.16 |
| Equation (19) | 5.16 | 7.19 |
| Yu et al. [74] | 5.212 | 7.354 |
| w/D | Groove | N = 2 | N = 4 | N = 6 | N = 8 | N = 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −1 | 0 | 1 | −1 | 0 | 1 | −1 | 0 | 1 | −1 | 0 | 1 | −1 | 0 | 1 | ||
| 0.12 | Square | 0.156 | 0.171 | 0.156 | 0.079 | 0.172 | 0.156 | 0.156 | 0.172 | 0.157 | 0.156 | 0.172 | 0.157 | 0.157 | 0.172 | 0.156 |
| Triangle | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | |
| Dimple | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | |
| Smooth | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | |
| 0.14 | Square | 0.156 | 0.172 | 0.156 | 0.157 | 0.173 | 0.157 | 0.158 | 0.172 | 0.156 | 0.156 | 0.173 | 0.157 | 0.157 | 0.172 | 0.158 |
| Triangle | 0.156 | 0.172 | 0.156 | 0.156 | 0.173 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.158 | 0.172 | 0.158 | |
| Dimple | 0.156 | 0.172 | 0.156 | 0.157 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.156 | 0.172 | 0.156 | 0.158 | 0.172 | 0.158 | |
| Smooth | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | |
| 0.16 | Square | 0.156 | 0.173 | 0.156 | 0.156 | 0.173 | 0.156 | 0.156 | 0.173 | 0.157 | 0.158 | 0.172 | 0.158 | 0.158 | 0.172 | 0.157 |
| Triangle | 0.156 | 0.172 | 0.156 | 0.156 | 0.173 | 0.156 | 0.156 | 0.172 | 0.156 | 0.158 | 0.172 | 0.158 | 0.158 | 0.172 | 0.158 | |
| Dimple | 0.156 | 0.172 | 0.156 | 0.156 | 0.173 | 0.156 | 0.156 | 0.172 | 0.156 | 0.158 | 0.172 | 0.158 | 0.158 | 0.172 | 0.158 | |
| Smooth | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | |
| 0.18 | Square | 0.157 | 0.172 | 0.156 | 0.156 | 0.173 | 0.158 | 0.156 | 0.172 | 0.156 | 0.157 | 0.173 | 0.158 | 0.157 | 0.173 | 0.158 |
| Triangle | 0.156 | 0.172 | 0.156 | 0.156 | 0.173 | 0.156 | 0.158 | 0.172 | 0.158 | 0.158 | 0.172 | 0.158 | 0.158 | 0.172 | 0.158 | |
| Dimple | 0.156 | 0.172 | 0.156 | 0.156 | 0.173 | 0.156 | 0.158 | 0.172 | 0.158 | 0.158 | 0.172 | 0.158 | 0.158 | 0.173 | 0.158 | |
| Smooth | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | 0.168 | 0.173 | 0.168 | |
| Parameters | Aeq | Ω | N |
|---|---|---|---|
| Ranges | 0.0072–0.050894 | −1–1 | 2–10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Shi, F.; Wang, C.; Xin, J.; Li, J. Numerical Study on the Effects of Surface Shape and Rotation on the Flow Characteristics and Heat Transfer Behavior of Tandem Cylinders in Laminar Flow Regime. Modelling 2025, 6, 132. https://doi.org/10.3390/modelling6040132
Li Y, Shi F, Wang C, Xin J, Li J. Numerical Study on the Effects of Surface Shape and Rotation on the Flow Characteristics and Heat Transfer Behavior of Tandem Cylinders in Laminar Flow Regime. Modelling. 2025; 6(4):132. https://doi.org/10.3390/modelling6040132
Chicago/Turabian StyleLi, Yafei, Fan Shi, Changfa Wang, Jianjian Xin, and Jiawang Li. 2025. "Numerical Study on the Effects of Surface Shape and Rotation on the Flow Characteristics and Heat Transfer Behavior of Tandem Cylinders in Laminar Flow Regime" Modelling 6, no. 4: 132. https://doi.org/10.3390/modelling6040132
APA StyleLi, Y., Shi, F., Wang, C., Xin, J., & Li, J. (2025). Numerical Study on the Effects of Surface Shape and Rotation on the Flow Characteristics and Heat Transfer Behavior of Tandem Cylinders in Laminar Flow Regime. Modelling, 6(4), 132. https://doi.org/10.3390/modelling6040132






