A Dual-Horizon Peridynamics–Discrete Element Method Framework for Efficient Short-Range Contact Mechanics

Abstract

Short-range forces enable peridynamics to simulate impact, yet it demands a computationally expensive contact search and includes no intrinsic damping. A significantly more efficient solution is the coupled dual-horizon peridynamics–discrete element method approach, which provides a robust framework for modeling fracture. The peridynamics component handles the nonlocal continuum mechanics capabilities to predict material damage and fracture, while the discrete element method captures discrete particle behavior. Whereas existing peridynamics–discrete element method approaches assign discrete element method particles to many or all surface peridynamics points, the proposed method integrates dual-horizon peridynamics with a single discrete element particle representing each object. Contact forces are computed once per discrete element pair and mapped to overlapping peridynamics points in proportion to shared volume, conserving linear momentum. Benchmark sphere-on-plate impact demonstrates prediction of peak contact force, rebound velocity, and plate deflection within 5% of theoretical results found in the literature, while decreasing neighbour-search cost by more than an order of magnitude. This validated force-transfer mechanism lays the groundwork for future extension to fully resolved fracture and fragmentation.

1. Introduction

The simulation of solid-particle impact presents significant computational challenges for particle-based methods. Modeling these events requires both efficient detection of contact and accurate transfer of forces between bodies. Traditional approaches are often limited by expensive pairwise distance checks and difficulties in handling localized deformation [1]. Capturing the force response during high-speed impact is particularly demanding, because deformation, momentum conservation, and damping must all be considered. These challenges are compounded in cases involving material failure or fracture, where classical continuum mechanics is not well suited [2].

Particle-level analysis is essential to accurately simulate impact dynamics and to predict damage and erosion. Analysis must encompass many parameters, such as the particle velocity, size, and impact angle, as well as the material properties of both impacted surfaces. The discrete element method (DEM) is an enabling tool for addressing these intricate challenges in simulating particle damage and erosion caused by particle impact, as introduced by Cundall and Strack [3] for simulating contact mechanics among circular particles in granular materials. The foundational principle of the DEM involves modeling discrete individual particle interactions, a key aspect for implementing damage and erosive-stress mechanics. Contact between particles is enforced through models, such as spring–dashpot models or Hertzian models for normal forces and the Coulomb law for frictional forces (refer to Horabik and Molenda [4], Berry et al. [5] for a comprehensive review of DEM contact models). DEM contact models have been extended to encompass broader interactions, such as cohesion [6], electrical charges [7], van der Waals forces [8], and liquid bridges [9]. These advancements enhance the versatility and applicability of DEM in simulating complex systems involving particle dynamics and collision, spanning fields such as manufacturing [10,11,12], mining [13], and pharmaceuticals [13].

Modeling particle breakage is another extension of the classical DEM. The three main categories of particle breakage modeling within the framework of the DEM are the bonded-particle model (BPM) [14], the particle replacement model (PRM) [15], and the finite–discrete element method [16]. These techniques typically correlate breakage energy with particle size by data fitting, rather than deriving this relationship using first-principles calculations. Although this approach does not negate the usefulness of such techniques, it highlights their limitations in the context of modeling the fundamental physics of particle breakage.

Accurate prediction and analysis of material failure, especially crack development, presents a formidable challenge due to the limitations of classical continuum mechanics. The differentiability assumption on displacement fields causes singularities in the presence of discontinuities [17], which may require complex remeshing procedures and ad hoc models to capture crack development [18]. To mitigate this issue, a nonlocal formulation of continuum mechanics, peridynamics (PD), was developed by Silling [19,20]. PD utilizes spatial integral equations that allow for natural representions of discontinuities in displacement fields, making it more suitable for solving problems involving cracks and nonlocal effects. PD has been demonstrated to accurately model composites and laminates [2,21,22,23], crack propagation and branching [24,25,26], crack nucleation [27,28], impact damage [29,30,31,32], polycrystal fracture [33,34], crystal plasticity [35], damage in concrete [36], geomaterial fragmentation [37], and dynamic blast loading [38], among other phenomena [39].

The coupling of PD with DEM provides a promising methodology to accurately capture both the impact forces (via DEM) and the damage and deformation of both the impactor and the impacted object (via PD). This coupling was introduced by Zhang et al. [40,41], who developed a novel Peridynamics–Discrete Element Method–Immersed Boundary–Cascaded Lattice Boltzmann Method (PD-DEM-IB-CLBM) framework for the prediction of the erosive impact of solid particles in viscous fluids. The influence of multiple impacts and the resulting surface damage to the fluid dynamics of the system was accurately predicted for varying impact angle variations using this method. PD-DEM coupling was also successfully demonstrated by Jha et al. [42]. The authors computed intra-particle forces using PD, whilst the forces between two impacting objects were computed using DEM contact models. Essentially, this approach replaces the short-range forces (SRFs) in PD with DEM contact models, treating every PD particle as a DEM object. The two main shortcomings of this approach are (1) the high potential for over-stiffness and/or over-damping when multiple contact points exist within a particle acting as a rigid object (as discussed in Berry et al. [5]), and (2) the high computational cost associated with treating every PD particle as a DEM object in order to determine contact forces.

Davis et al. [43] approach PD-DEM coupling from a computational point of view. Specifically, they introduce additional functionality to the ParticLS software to assist in the simulation of deformable bodies. Hartmann et al. [44] provide a generalized framework of PD-DEM coupling that considers the surface PD particles as hybrid PD-DEM particles. This approach improves the cost of the simulations by not considering every discretized point as a hybrid PD-DEM point, as is the case in Jha et al. [42] and Walayat et al. [45]. In contrast, the present work collapses the DEM side to a single surrogate particle per body and transfers contact forces to the PD discretization through volume-overlap weighting, rather than per-surface-particle assignment. While prior work has advanced PD-DEM coupled analysis as a viable alternative for simulating impact scenarios to predict material damage and erosion, a limiting drawback is the computational expense of these extensions used to capture contact.

Complementary to the present focus on reducing contact-handling cost, recent work has advanced peridynamics along three fronts: (i) dual-/multi-horizon and coupled-field formulations that improve resolution adaptivity or multiphysics fidelity (e.g., [46,47]), (ii) new PD contact formulations coupled with healing/phase-field descriptions [48], and (iii) machine learning-enabled DEM surrogates aimed at accelerating contact or parameter calibration (e.g., [49,50]).The proposed method targets interface complexity by collapsing the DEM representation to a single surrogate per body and using volume-overlap force transfer, which can coexist with (i)–(iii) without altering our core algorithm, offering advanced analysis with improved computational efficiency.

This study aims to improve both the efficiency and accuracy of contact modeling by introducing a simplified dual-horizon PD-DEM (DHPD-DEM) coupling framework. Instead of performing expensive, per-particle contact checks across all PD points, each deformable body is encapsulated by a single discrete element surrogate that handles contact detection and force evaluation. For example, for two spheres discretized by 30,000 PD points each, a brute-force SRF-PD solver must probe $9\times {10}^8$ potential contacts at every timestep. Comparatively, the proposed method requires only two checks per timestep, resulting in a reduction of 8 orders of magnitude before spatial partitioning. The computed contact forces are redistributed to the underlying PD particles based on volumetric overlap. This approach significantly reduces computational cost while also resolving key limitations of SRFs in PD, namely the lack of intrinsic damping, absence of tangential (frictional) effects, and nonphysical force spikes due to dense, point-wise interactions.

The objective of this paper is to demonstrate a validated force-transfer mechanism to build the foundation for future extension to fully resolved fracture and fragmentation prediction. Benchmark sphere-on-plate impact predictions were performed to evaluate the DHPD-DEM prediction of peak contact force, rebound velocity, and plate deflection, as well as to demonstrate computational efficiency.

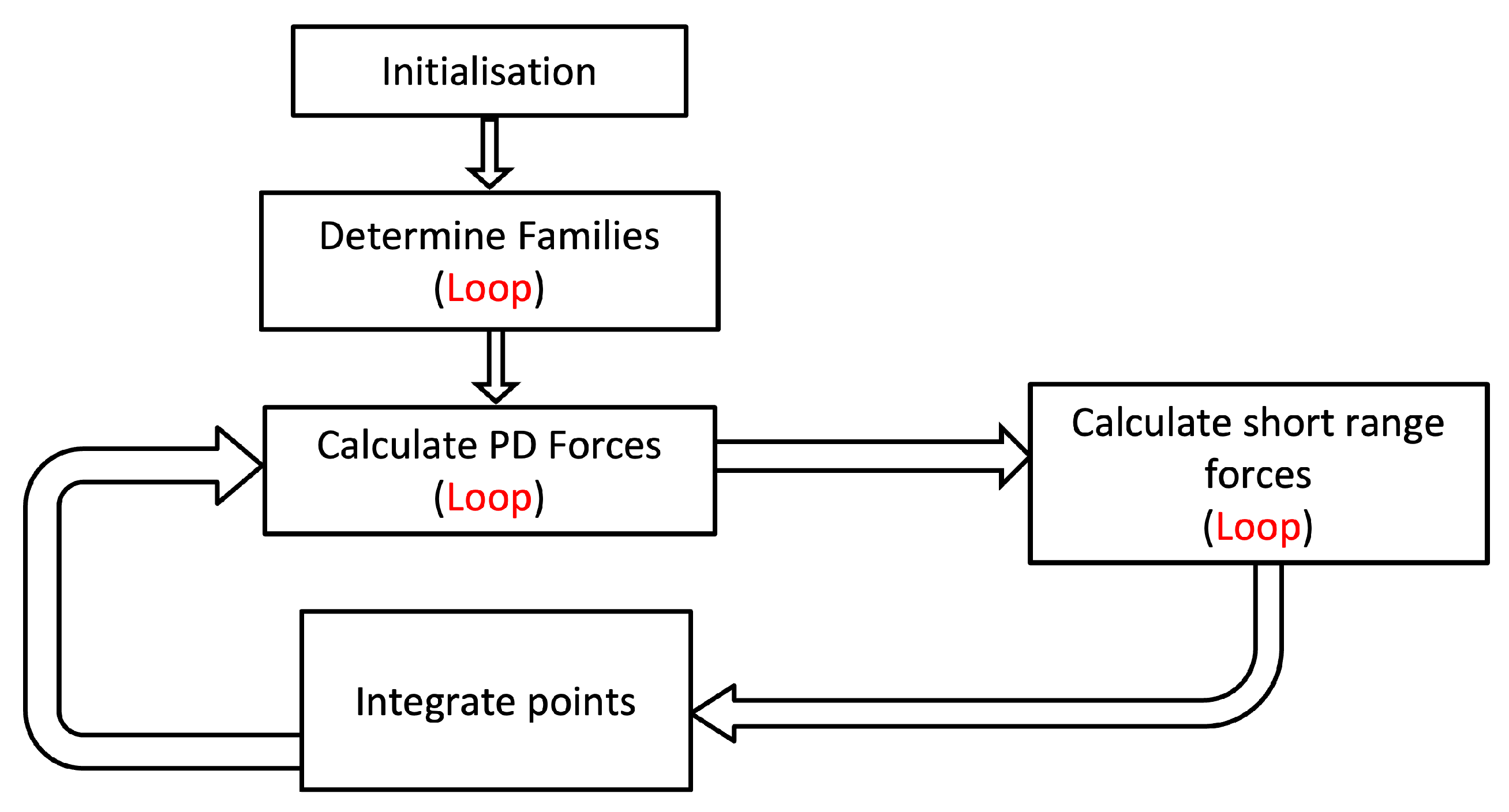
2. Materials and Methods

To simulate particle impact, two computational methods are coupled: (1) DEM to resolve the contact forces and (2) PD to resolve the damage to each object. The subsequent sections present a standard formulation and validation for the DEM and PD components, providing an overview of the methods and serving as a reference for the coupling section.

2.1. Discrete Element Method

In accordance with Newton’s second law of motion, the equation governing the translational movement of particles is given by Equation (1):

$$\overrightarrow{F_i}=m_i\overrightarrow{a_i}=m_i{\displaystyle \frac{d\overrightarrow{v_i}}{dt}}=m_i{\displaystyle \frac{d^2\overrightarrow{r_i}}{d{t}^2}},$$

(1)

where $m_i$ is the mass, $\overrightarrow{r_i}$ is the center position, $\overrightarrow{a_i}$ is the acceleration, $\overrightarrow{v_i}$ is the translational velocity, and $\overrightarrow{F_i}$ is the total force due to the particle or wall contact of particle i. The rotational motion of a spherical particle is presented in Zhao et al. [51] as Equation (2):

$$I_i{\displaystyle \frac{d}{dt}}\overrightarrow{{\omega }_i}=M_i,$$

(2)

where $I_i$ is the moment of inertia of a spherical particle, $\overrightarrow{{\omega }_i}$ is the angular velocity, and $M_i$ is the total torque [52]. These equations are used to update each individual particle’s movement over time depending on the forces exerted on the particle. The calculation methodologies employed for determining these forces serve as the distinguishing factor among various DEM approaches. This study focuses on the use of the Hertz–Mindlin [53] method for calculating contact forces; however, this choice can be readily replaced by another technique, such as the spring–dashpot model [52].

The equations of motion lead to a collection of differential equations that cannot be solved analytically. Therefore, an integration method is required in order to advance the particle movement through time. The Velocity–Verlet method [54] is commonly used in DEM approaches as it is more stable than the simple Euler method. The Velocity–Verlet scheme is given as follows:

• Update position $\overrightarrow{r}$ to $t+\Delta t$ and the velocity/angular velocity to $t+\frac{1}{2}\Delta t$ by

  $$\overrightarrow{r}(t+\Delta t)=\overrightarrow{r}(t)+\Delta t\overrightarrow{v}(t)+\frac{1}{2}\Delta t^2\overrightarrow{a}(t)$$

  $$\overrightarrow{v}(t+\frac{1}{2}\Delta t)=\overrightarrow{v}(t)+\frac{1}{2}\Delta t\overrightarrow{a}(t)$$

  $$\overrightarrow{\omega }(t+\frac{1}{2}\Delta t)=\overrightarrow{\omega }(t)+\frac{1}{2}\Delta t{\overrightarrow{a}}_{\mathrm{ang}}(t)$$
• Compute the force and acceleration at $t+\Delta t$.
• Update the velocity and angular velocity to $t+\Delta t$:

  $$\overrightarrow{v}(t+\Delta t)=\overrightarrow{v}(t+\frac{1}{2}\Delta t)+\frac{1}{2}\Delta t\overrightarrow{a}(t+\Delta t)$$

  $$\overrightarrow{\omega }(t+\Delta t)=\overrightarrow{\omega }(t+\frac{1}{2}\Delta t)+\frac{1}{2}\Delta t{\overrightarrow{a}}_{\mathrm{ang}}(t+\Delta t)$$

where ${\overrightarrow{a}}_{ang}$ is the angular acceleration vector.

The total force ${\overrightarrow{F}}_i$ and torque ${\overrightarrow{M}}_i$ acting on any individual particle is given by the sum of pairwise interaction with other particles, as described in Equations (3) and (4), respectively.

$$\overrightarrow{F_i}=m_i{\displaystyle \frac{d^2\overrightarrow{r_i}}{d{t}^2}}=\sum _{j=1,i\ne j}^{N_i}\overrightarrow{F_{ij}},$$

(3)

$$I_i{\displaystyle \frac{d}{dt}}\overrightarrow{{\omega }_i}=M_i=\sum _{j=1,i\ne j}^{N_i}\overrightarrow{M_{ij}}.$$

(4)

In the DEM, contact between two spheres i and j is defined by their overlap $\delta$. So a force is calculated between two particles only if there exists an overlap between the two, as shown in Equation (5).

$$\delta =(R_i+R_j)-\left|\right|x_i+x_j\left|\right|>0.$$

(5)

The total force $\overrightarrow{F_i}$ on particle i from particle j can be seen as the sum of both a normal and a tangential part, as shown in Equation (6):

$$\overrightarrow{F_i}=\overrightarrow{F_{ij}^n}+\overrightarrow{F_{ij}^t},$$

(6)

where $\overrightarrow{F_{ij}^n}$ and $\overrightarrow{F_{ij}^t}$ are the normal and tangential contact forces, respectively. For the Hertz–Mindlin model, the total force is calculated according to Equation (7):

$$\overrightarrow{F_i}=\overrightarrow{F_{ij}^n}+\overrightarrow{F_{ij}^t}=(k_n{\delta }_n-{\gamma }_n\overrightarrow{v_{ij}^n})\overrightarrow{n_{ij}}+(k_t{\delta }_t-{\gamma }_t\overrightarrow{v_{ij}^t})\overrightarrow{t_{ij}},$$

(7)

where $k_n$ and ${\gamma }_n$ are the normal spring and damping constants, respectively. The tangential spring and damping constants are given by $k_t$ and ${\gamma }_t$. In the Hertz model, $k_n$ behaves as a non-linear spring with units of force/area. Additional details are provided in Luding [52].

2.1.1. Contact Parameters and Calibration

The normal and tangential stiffnesses $(k_n,k_t)$ follow the Hertz–Mindlin theory based on the effective moduli and geometry. Using the effective radius $R^{*}={(R_i^{-1}+R_j^{-1})}^{-1}$, effective Young’s modulus $E^{*}$, and effective shear modulus $G^{*}$,

$$k_n={\displaystyle \frac{4}{3}}{E}^{*}\sqrt{R^{*}{\delta }_n},k_t=8G^{*}\sqrt{R^{*}{\delta }_n},$$

with the usual definitions $E^{*}={\left({\displaystyle \frac{1-{\nu }_i^2}{E_i}}+{\displaystyle \frac{1-{\nu }_j^2}{E_j}}\right)}^{-1}$ and $G^{*}={\left({\displaystyle \frac{2-{\nu }_i}{G_i}}+{\displaystyle \frac{2-{\nu }_j}{G_j}}\right)}^{-1}$ (for small oscillations, one may locally linearize around a representative overlap to obtain the constants $k_n,k_t$; in our implementation, the exact Hertz–Mindlin updates are used.).

The damping coefficients $({\gamma }_n,{\gamma }_t)$ were chosen to reproduce the analytical rebound (coefficient of restitution e) in the elastic impact benchmark. In practice, ${\gamma }_n$ governs the dissipated normal impulse, and is tuned so that the simulated rebound velocity matches the analytical value; ${\gamma }_t$ is set to achieve the target tangential damping ratio used in the Hertz–Mindlin contact law. Once ${\gamma }_n$ has been calibrated to rebound, the benchmark deviations reported in Section 4 remain within the stated bounds.

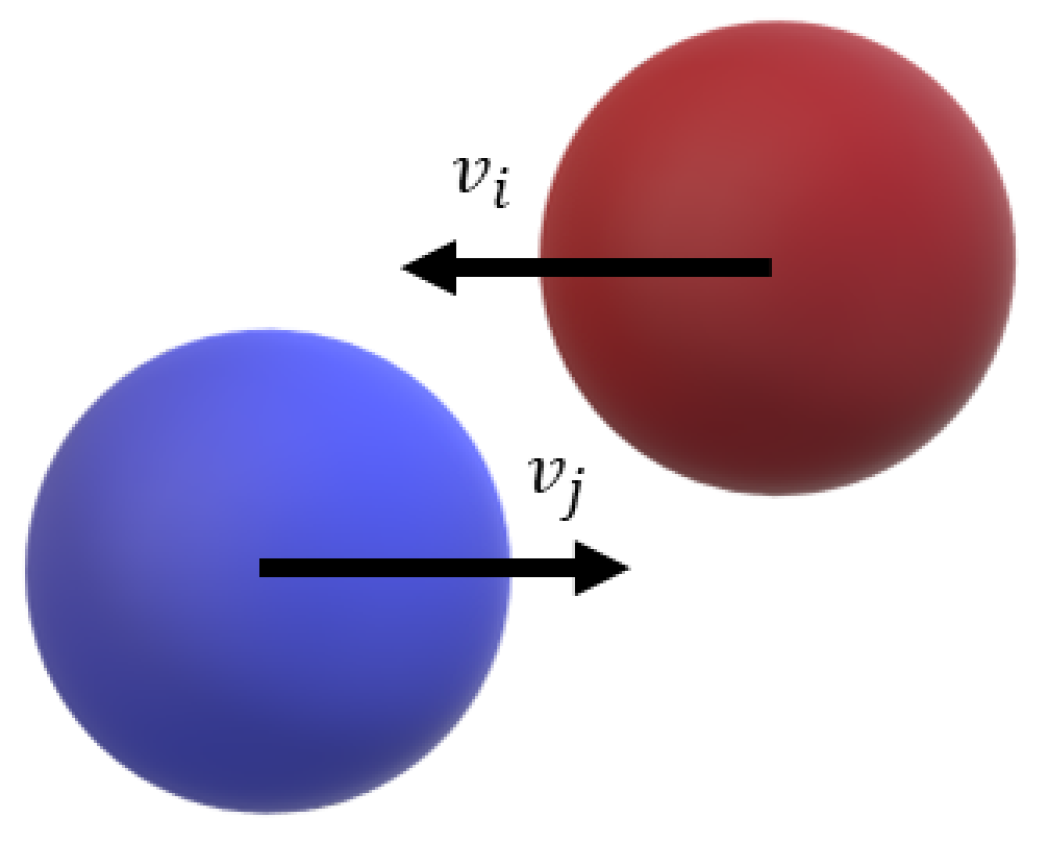
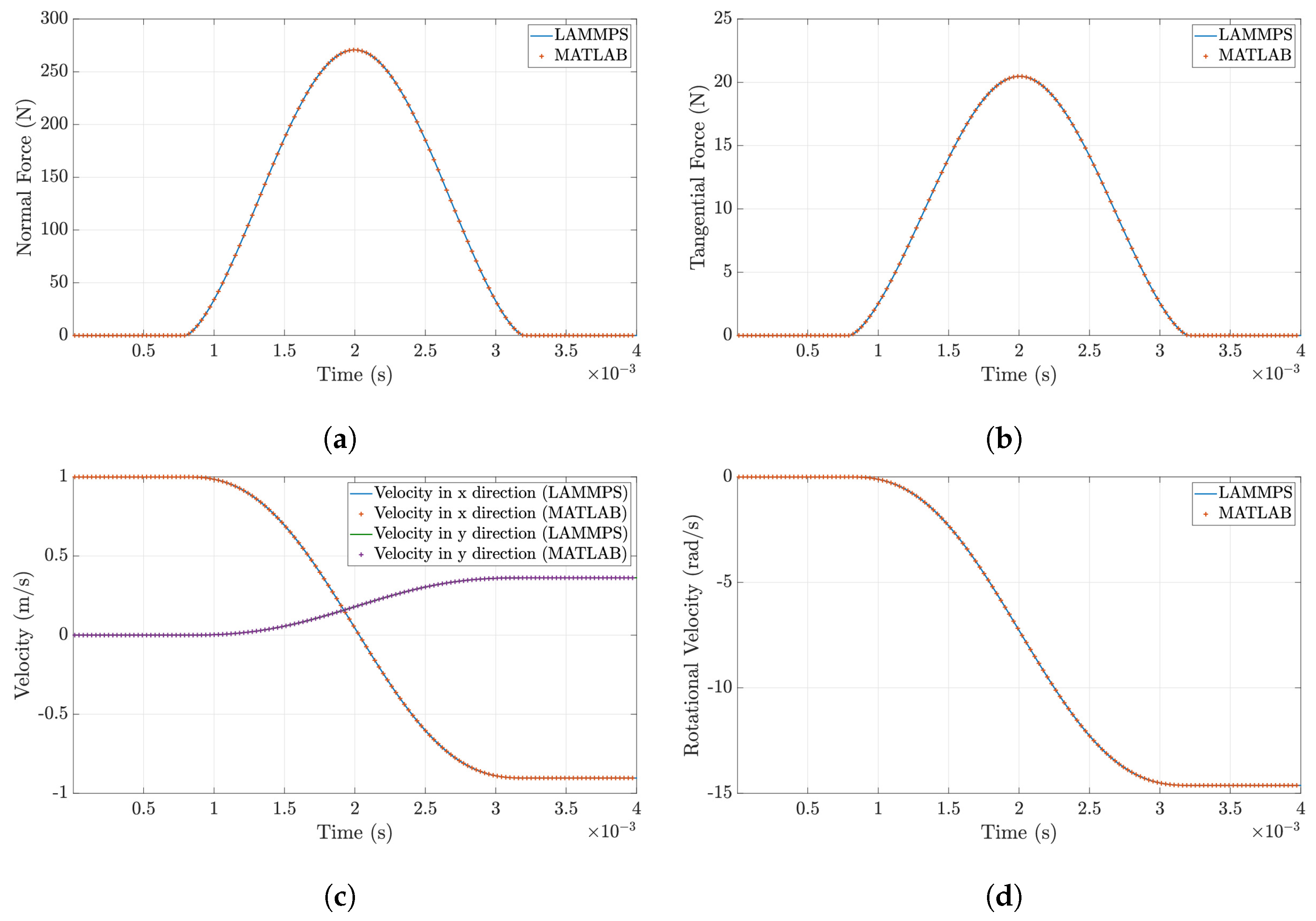
2.1.2. DEM Validation

A custom DEM code was developed in MATLAB (R2019b) and validated against the established LAMMPS (version 29 October 2020) software [55]. This bespoke development offered customization and flexibility tailored to our specific needs, while laying the foundation for the DHPD-DEM coupled code. The validation simulation consisted of two spheres colliding with an offset, as illustrated in Figure 1. The input parameters are provided in

Table 1. Material and simulation parameters.

Property	Value
Diameter	0.05 m
Young’s Modulus	$5.5\times {10}^7$ Pa
Density	2800 kg/m3
Mass	0.1833 kg
Velocity Vector	[1, 0, 0], [−1, 0, 0] m/s
Static Yield Criterion	0.5
Timestep	$5\times {10}^{-7}$ s

. The two particles were offset in the y-axis by 0.0125 m to engage the tangential forces. The DEM results were compared with those from LAMMPS and demonstrated agreement (see Figure 2).

2.2. Peridynamics

The fundamental equation for the volume of a deformable body $\mathsf{\Omega }$ in classical continuum mechanics is the balance between the rate of change in the linear momentum and the applied force (Equation (8)).

$$\rho (\overrightarrow{x})\ddot{u}(\overrightarrow{x},t)=\Delta ·\sigma +\overrightarrow{b}(x,t),\forall \overrightarrow{x}\in \mathsf{\Omega },$$

(8)

where $\overrightarrow{x}\in \mathsf{\Omega }$, $\rho$ is density, t is time, $\ddot{u}$ is acceleration, $\sigma$ is the stress tensor, and $\overrightarrow{b}$ is the body force. Equation (8) is poorly defined at cracks and discontinuities. PD aims to mitigate this issue by formulating the kinematic equation as an integral, allowing the force density equation to be formulated as shown in Equation (9).

$$\rho (\overrightarrow{x})\ddot{u}(\overrightarrow{x},t)={\int }_{H_x}\overrightarrow{f}(\overrightarrow{\eta },\overrightarrow{\xi })dV+\overrightarrow{b}(\overrightarrow{x},t),$$

(9)

where $\overrightarrow{f}$ is the pairwise force density vector function applied to particle $\overrightarrow{x}$ by another particle $\overrightarrow{x^{\prime }}$. $H_x$ is the horizon of particle $\overrightarrow{x}$, which is a spherical region of radius $\delta$. The relative position vector is given by $\overrightarrow{\xi }=\overrightarrow{x^{\prime }}-\overrightarrow{x}$, and the relative displacement vector is $\overrightarrow{\eta }=\overrightarrow{u}(\overrightarrow{x^{\prime }},t)-\overrightarrow{u}(\overrightarrow{x},t)$.

2.2.1. Bond-Based Peridynamics

The bond refers to the interaction of two peridynamic particles, x and $x^{\prime }$. In the bond-based formulation, it is assumed that the pairwise force density vector interactions are equal in magnitude and parallel to the relative position vector in the deformed state, see Figure 3.

The peridynamic formulation of Equation (9) replaces the divergence of the stress tensor in the local form with the integral of the force density of the horizon. Therefore, $\overrightarrow{f}$ contains all the material properties. For linear elastic isotropic solids, this is expressed by Equation (10):

$$\overrightarrow{f}(\overrightarrow{\eta },\overrightarrow{\xi })=C.S.\overrightarrow{n},$$

(10)

where $\overrightarrow{n}$ is calculated with Equation (11):

$$\overrightarrow{n}={\displaystyle \frac{\overrightarrow{\xi }+\overrightarrow{\eta }}{|\overrightarrow{\xi }+\overrightarrow{\eta }|}},$$

(11)

and C is the bond constant, which is a material parameter that can be expressed by considering common parameters used in both PD and classical continuum mechanics. In 3D, C is expressed according to Equation (12).

$$C={\displaystyle \frac{12E}{\pi {\delta }^4}}$$

(12)

The stretch (s) is defined in Equation (13).

$$S={\displaystyle \frac{|\overrightarrow{\xi }+\overrightarrow{\eta }|-|\overrightarrow{\xi }|}{|\overrightarrow{\xi }|}}.$$

(13)

In Equation (12), E is the modulus of elasticity as used in classical continuum mechanics. In bond-based peridynamics, the admissible Poisson’s ratio is fixed by the micro-modulus as $\nu =1/4$ for an isotropic 3D solid, and $\nu =1/3$ for 2D plane stress. For 2D plane strain, the in-plane response corresponds to the 3D constraint ($\nu =1/4$). Achieving arbitrary Poisson’s ratios requires a state-based peridynamic formulation [17,19,20].

2.2.2. Critical Stretch and Damage

The critical stretch for the micro–elastic brittle model is

$$S_0=\sqrt{{\displaystyle \frac{5G_0}{6E\delta }}},$$

(14)

as given in standard peridynamics references (e.g., [17,19,30]). In our implementation, bonds are irreversibly broken in tension when $S>S_0$; compressive bond failure is not activated unless otherwise stated. The local damage variable is

$$\varphi (\overrightarrow{x},t)=1-{\displaystyle \frac{{\int }_{H_x}\mu (\overrightarrow{x},t,\xi )\mathrm{d}V}{{\int }_{H_x}\mathrm{d}V}},$$

(15)

with the history variable

$$\mu (t,\xi )=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}S(t^{\prime },\xi )<S_0\forall t^{\prime }\in [0,t],\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(16)

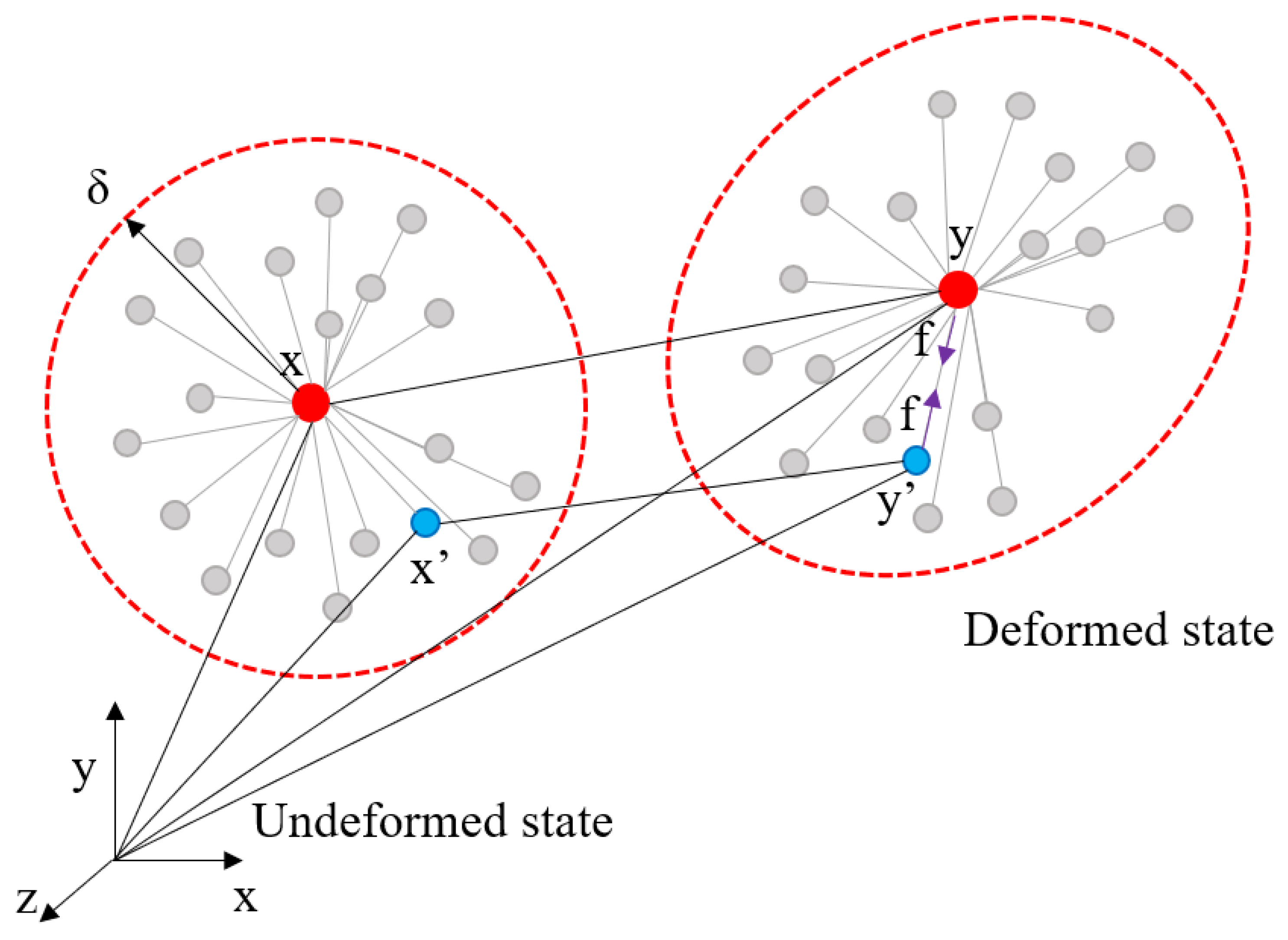
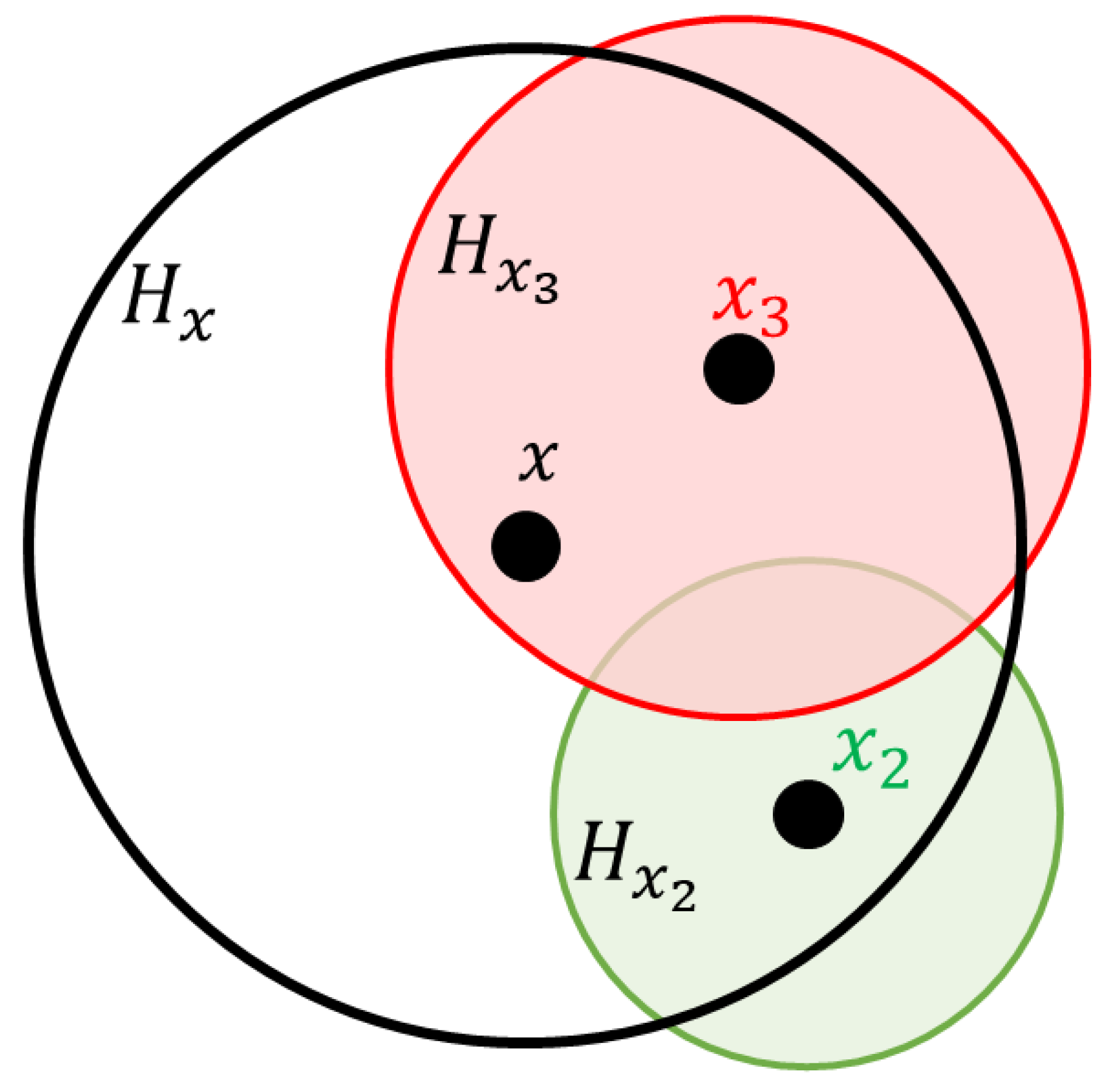
2.2.3. Dual-Horizon Peridynamics

DHPD is a formulation of PD that balances the force and reaction force on particles assigned varying horizon sizes, allowing for unequally spaced PD points [56]. This approach provides an improved definition of the contact surface and increased efficiency by densely populating areas of interest while enabling reduced PD point distribution in other areas. Additionally, the constant horizon PD requirement of equally spaced points limits the definition of a curved surface, which results in flat surfaces when trying to define spheres. This limitation alters the dispersion of forces and does not accurately represent the surface of a sphere, as illustrated in Figure 4a. Using unequal grid spacing allows for a more accurate representation of a sphere, as shown in Figure 4b.

The dual horizon of particle x includes all of the points with a horizon containing x. For example, Figure 5 shows points $x_2$ and $x_3$ in the horizon of x $(\{x_2,x_3\}\in H_x)$; however, only $x_3$ is in the dual horizon of x $(\left\{x_3\right\}\in H_x^{\prime }$ and $\left\{x_2\right\}\notin H_x^{\prime })$. To implement the dual-horizon approach, the force density equation (Equation (9)) is replaced with Equation (17), as presented in [56].

$$\rho (\overrightarrow{x})\ddot{u}(\overrightarrow{x},t)={\int }_{H_x^{\prime }}{\overrightarrow{f}}_{x{x}^{\prime }}d{V}_{x^{\prime }}-{\int }_{H_x}{\overrightarrow{f}}_{x^{\prime }x}d{V}_{x^{\prime }}+\overrightarrow{b},$$

(17)

where $H^{\prime }$ is the dual horizon. ${\overrightarrow{f}}_{x{x}^{\prime }}$ & ${\overrightarrow{f}}_{x^{\prime }x}$ are given by Equations (18) and (19):

$${\overrightarrow{f}}_{x{x}^{\prime }}=C({\delta }_{x^{\prime }}).S.\overrightarrow{n},$$

(18)

and

$${\overrightarrow{f}}_{x^{\prime }x}=C({\delta }_x).S.-\overrightarrow{n}.$$

(19)

The bond constant $C({\delta }_x)$ takes a value which is half of the constant horizon bond-based PD model, because bond energy is determined by both the horizon and the dual horizon. For 3D cases, it is calculated as follows:

$$C({\delta }_x)={\displaystyle \frac{3E}{\pi {\delta }^4(1-2v)}}.$$

(20)

This method eliminates spurious wave reflections caused by an imbalance of forces [56]. Equation (17) simplifies to constant horizon PD when $H_x^{\prime }=H_x$.

The dual horizon formulation increases the computational cost per particle, because both the dual and the normal horizon must be resolved. However, the greater flexibility in point distribution provides improved definition of curved surfaces and allows for increased point density, resulting in higher resolution in areas of interest. Decreasing the point density, if possible, in other areas potentially saves computational costs at these locations due to the reduced number of points versus a uniform distribution throughout the entire volume.

2.2.4. Volume Correction

Volume correction accounts for PD points that are partially inside the horizon. Figure 6 shows an example where the center of particle j is outside of the horizon of particle i ($H_i$). If using the normal determination of families within the horizon, the red section would not belong to the family of particle i.

To correctly determine the volume, families are defined by any overlap between the horizon and the neighbouring material points. When Equation (21) is satisfied, the 3D volume of the overlap is calculated (assuming each material point/horizon to be a sphere) according to Equation (22). This calculated area/volume of the overlap is then used in Equation (17).

$$d_{ij}<{\delta }_i+r_j,$$

(21)

where $r_j$ is the equivalent radius of point j.

$$V_{overlap}={\displaystyle \frac{\pi }{12d_{ij}}}{\left({\delta }_i+r_j-d_{ij}\right)}^2\left(d_{ij}^2+2d_{ij}\left(r_j+{\delta }_i\right)-3{\left({\delta }_i-r_j\right)}^2\right).$$

(22)

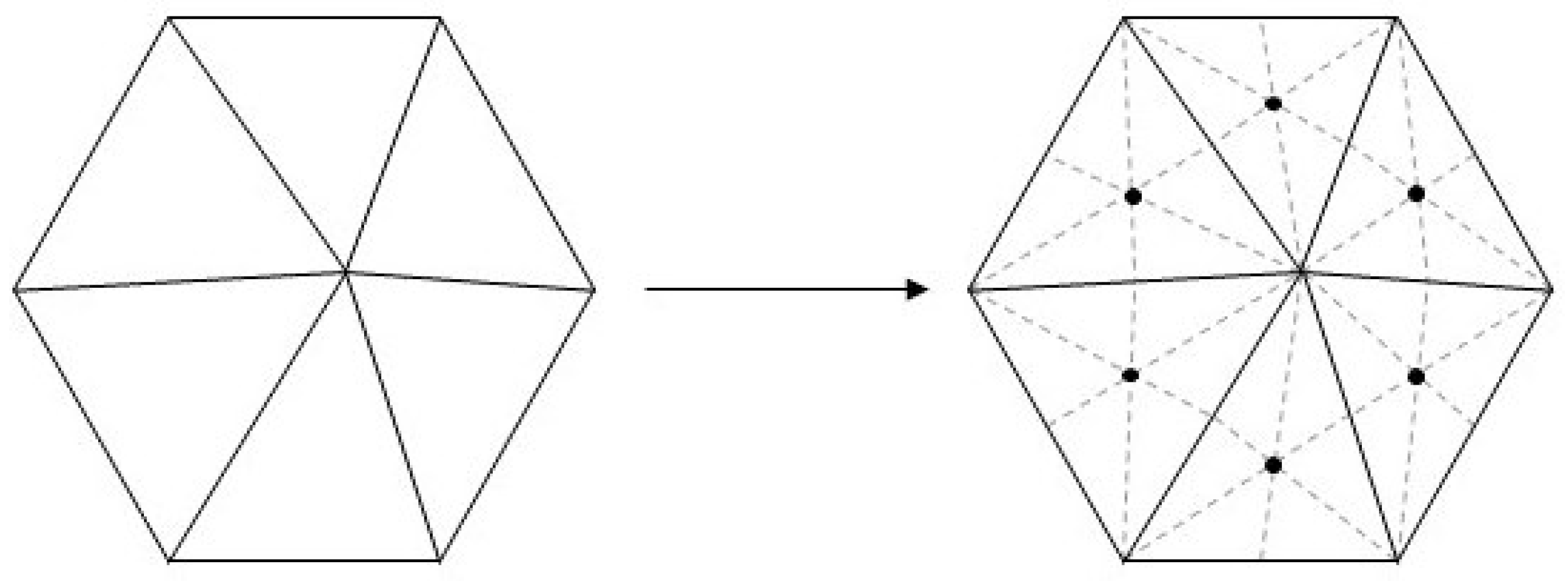
2.2.5. DHPD Discretization

The distribution of irregular PD points was achieved using Gmsh software [57]. Triangular (2D) and tetrahedral (3D) meshes were created to discretize the domain. The centroid of each element defines the PD point location, and the associated volume (or area) is that of the element. The point size $\Delta x$ is determined by assuming that each PD point is a circle (or sphere) with its equivalent diameter calculated using the volume (or area) of the element, as suggested in Jha et al. [42] and shown in Figure 7.

In the case of tetrahedral meshes, the volume associated with each PD point and the position of these points are determined based on the centroid of the tetrahedral element. The tetrahedral mesh is denoted as a set of nodes with position vectors ${\overrightarrow{p}}_1,{\overrightarrow{p}}_2,\dots ,{\overrightarrow{p}}_n$ and a set of tetrahedra, where each tetrahedron $T_j$ is defined by four nodes with indices $i_1,i_2,i_3,i_4$.

For each tetrahedron $T_j$, with vertices given by the position vectors $\overrightarrow{a}={\overrightarrow{p}}_{i_1}$, $\overrightarrow{b}={\overrightarrow{p}}_{i_2}$, $\overrightarrow{c}={\overrightarrow{p}}_{i_3}$, and $\overrightarrow{d}={\overrightarrow{p}}_{i_4}$, the volume $V_j$ is computed as follows:

$$V_j={\displaystyle \frac{1}{6}}\left|(\overrightarrow{a}-\overrightarrow{d})·((\overrightarrow{b}-\overrightarrow{d})\times (\overrightarrow{c}-\overrightarrow{d}))\right|.$$

(23)

Additionally, the centroid $C_j$ of the tetrahedron $T_j$ is computed as the arithmetic mean of the position vectors of its vertices:

$$C_j={\displaystyle \frac{1}{4}}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}).$$

(24)

Finally, the point size ($\Delta x$) is calculated as the diameter of an equivalent sphere whose volume is equal to the volume ($V_j$) of the tetrahedron, using the formula for the volume of a sphere Equation (25).

$$\Delta x=2{\left({\displaystyle \frac{3V_j}{4\pi }}\right)}^{{\displaystyle \frac{1}{3}}}.$$

(25)

2.2.6. Horizon Selection

Unless otherwise noted, the peridynamic horizon is set to

$$\delta =3.015\Delta x$$

(26)

where $\Delta x$ is the characteristic point spacing of the discretization. For non-uniform meshes (DHPD), $\delta$ is applied consistently with the local family definition and is used in computing both the micro-modulus and the critical stretch (14).

2.2.7. DHPD Validation

To evaluate the accuracy of the custom-developed DHPD implementation, we simulated the well-established Kalthoff–Winkler dynamic fracture experiment. The objective was to confirm that the implementation would reproduce expected fracture behavior that was consistent with classical peridynamic models and experimental observations.

The Kalthoff–Winkler setup (as shown in Figure 8) consists of a rectangular steel plate with two pre-cut notches, impacted by a cylindrical projectile at high velocity. Brittle fractures initiate at the notch tips and propagate diagonally through the plate. Experimental observations report crack propagation angles of approximately $68°$ relative to the horizontal [58]. The material properties for 18Ni1900 steel were adopted from Ren et al. [56], including Young’s modulus $E=190\mathrm{GPa}$, density $\rho =7800{\mathrm{kg}/\mathrm{m}}^3$, Poisson’s ratio $v=0.25$, and the critical energy release rate $G_0=6.9\times {10}^4{\mathrm{J}/\mathrm{m}}^2$. The specimen thickness was $t=0.009\mathrm{m}$ (9 mm).

The simulation used non-uniform DHPD discretization to test robustness to mesh irregularity. A total of 145,633 material points were used, with a spacing range from $\Delta x_{\min }=2.7\times {10}^{-4}\mathrm{m}$ in critical regions to $\Delta x_{\max }=1.7\times {10}^{-3}\mathrm{m}$ elsewhere. An initial velocity of $v_0=32\mathrm{m}/\mathrm{s}$ was applied to the first three layers of particles to represent the impact, while all other boundaries were traction-free.

The DHPD model successfully reproduced the expected fracture pattern, as shown in Figure 9. Cracks initiated at the notch tips and propagated at an angle of $67°$, closely matching the experimentally observed $68°$ and the simulation results reported in [17,56,58].

In summary, the DHPD implementation demonstrated strong agreement with both experimental results and established peridynamic simulations. The model reproduced the correct crack path and propagation angle, validating the accuracy and robustness of the code, even with non-uniform discretization.

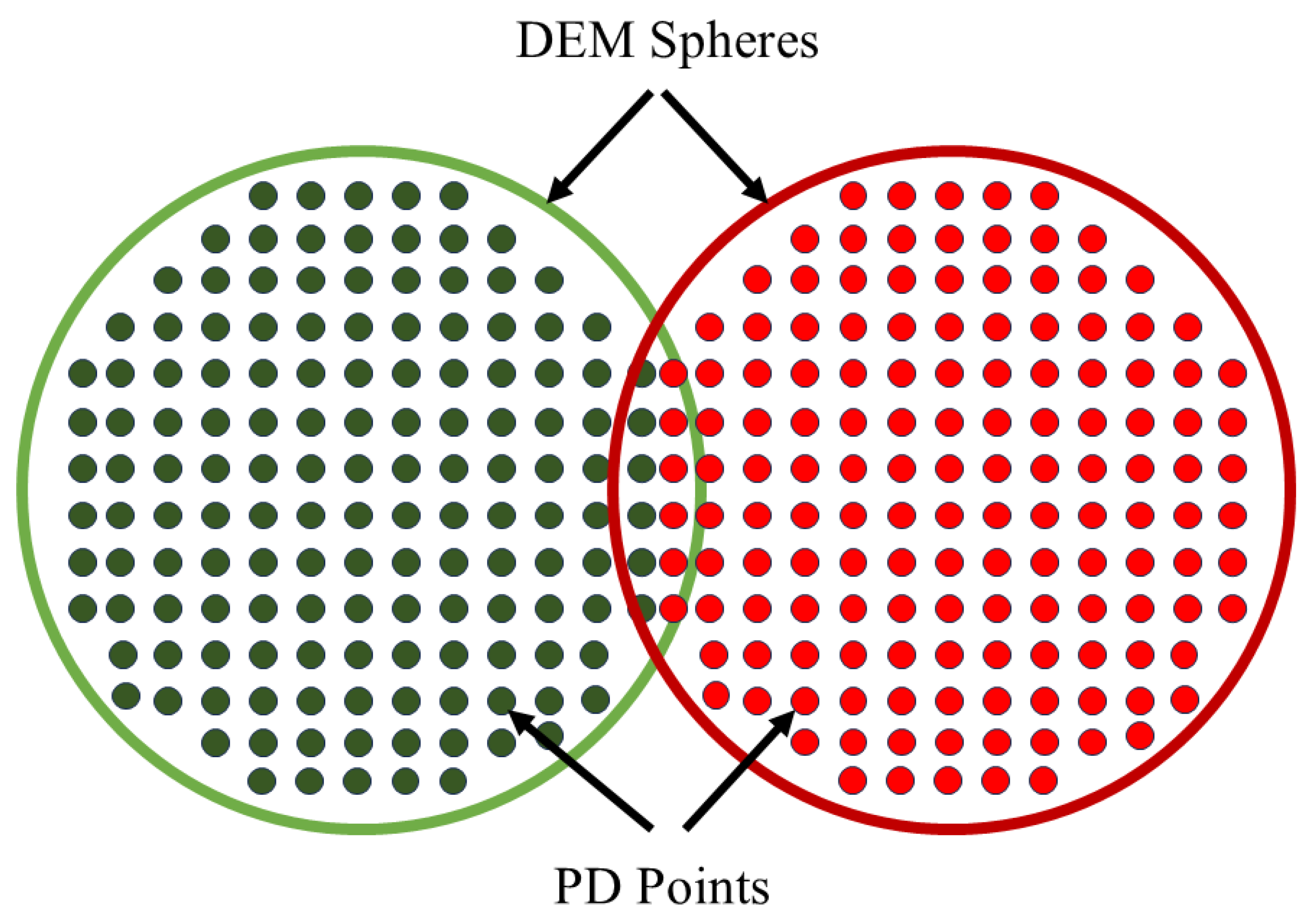
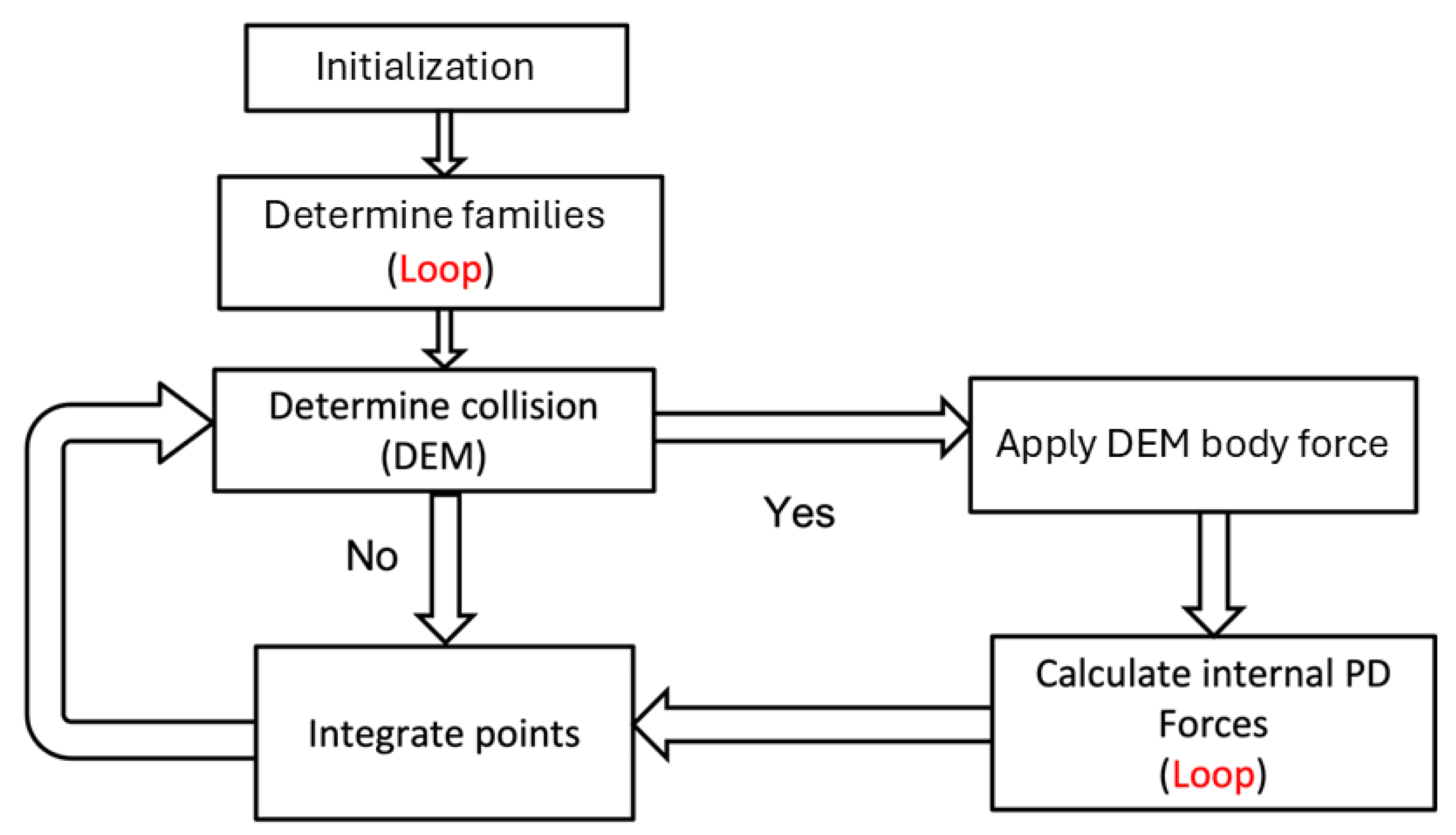
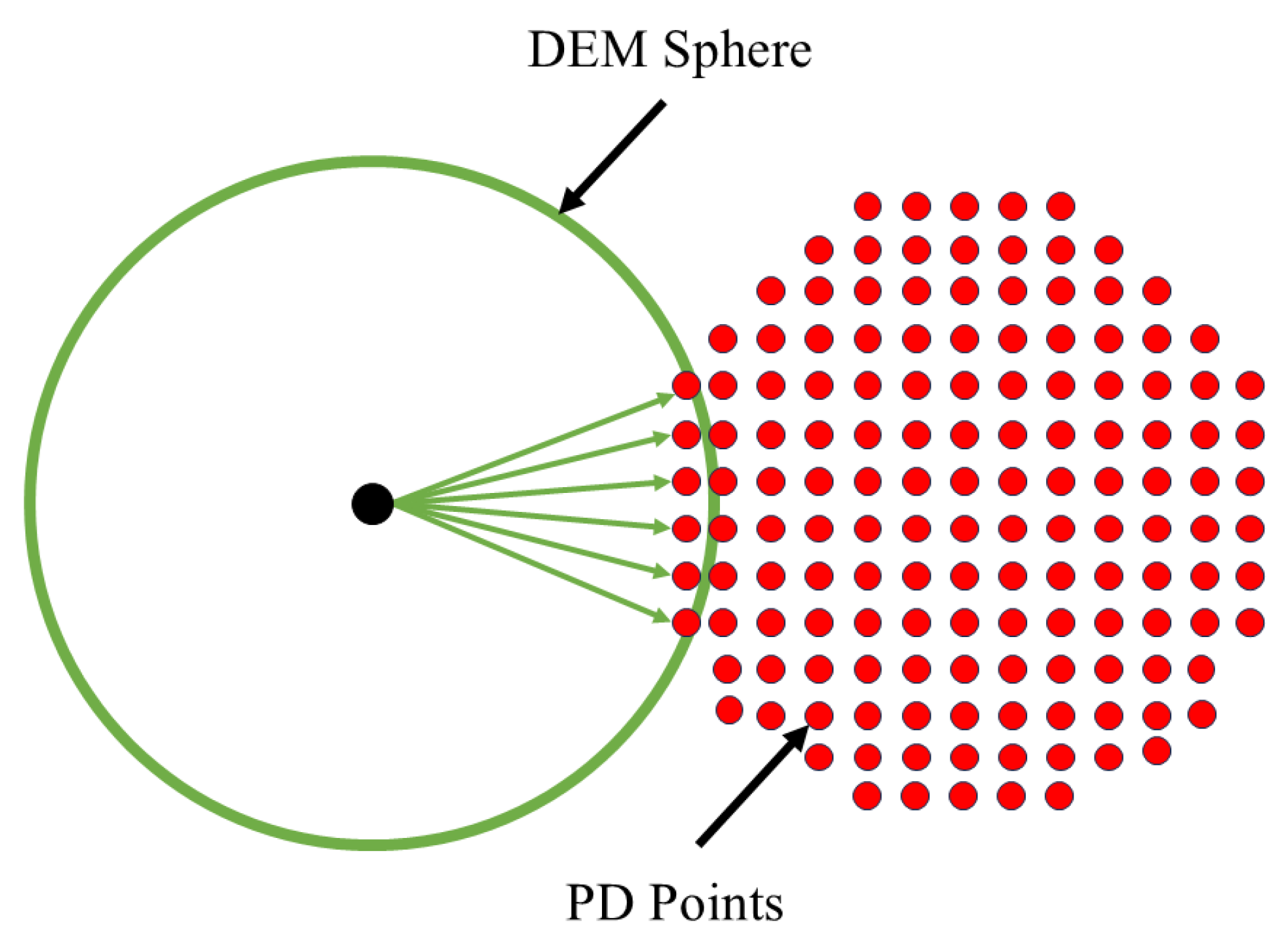
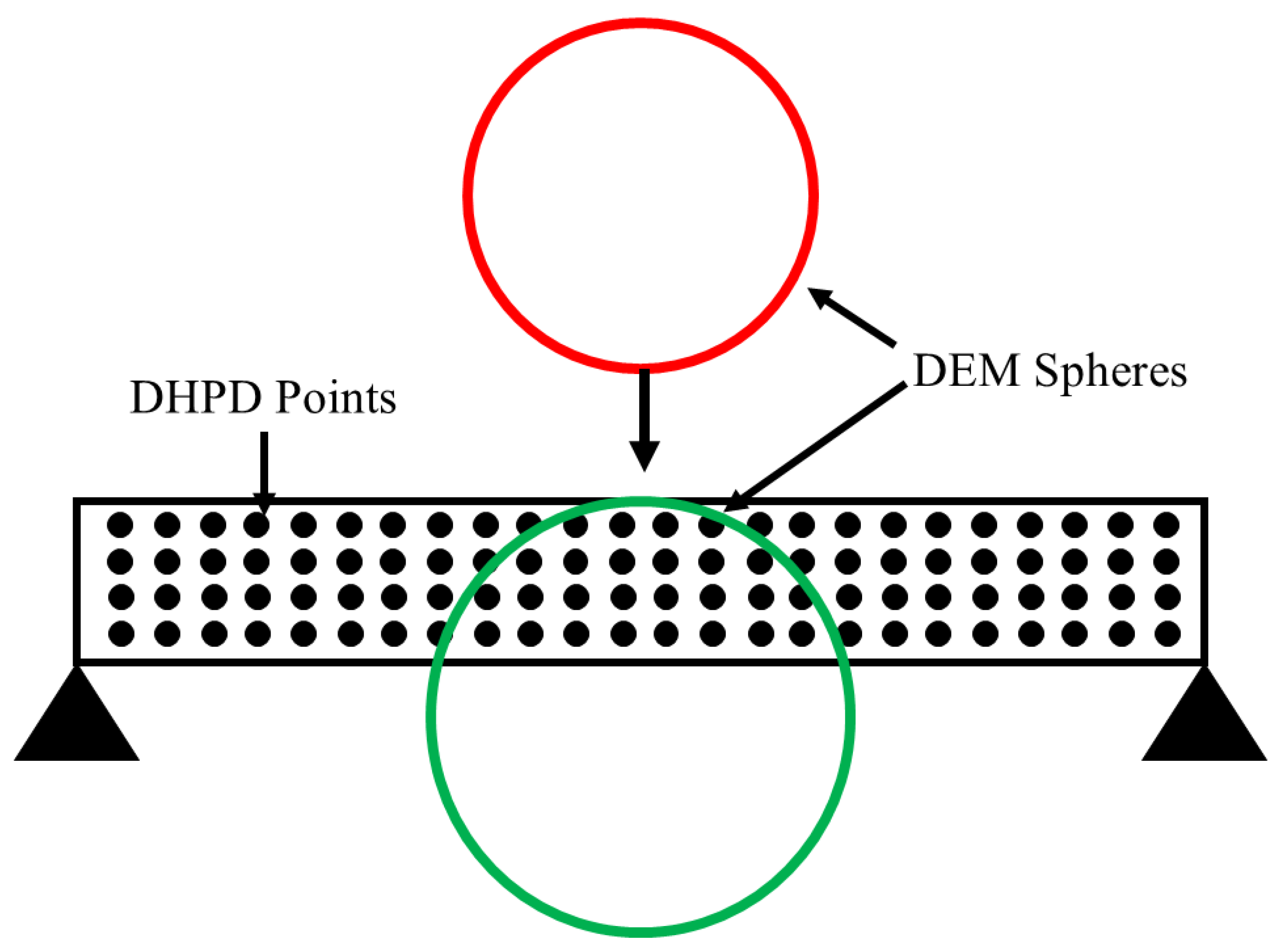
2.2.8. DHPD-DEM Coupling

A bespoke code was developed in MATLAB with FORTRAN MEX functions, based on the validated DHPD and DEM solvers. The coupling approach is generalized to reduce the computational cost of simulating interactions between discrete and deformable bodies. Each deformable body is discretized into PD points for internal mechanics, while inter-body contact is handled by a single DEM surrogate (sphere) whose contact force is redistributed to overlapping PD points via volume-overlap weighting. Contact forces are computed using the DEM (Equation (7)) and applied as external forces ($\overrightarrow{b}$ in Equation (17)) to the overlapping PD points.

In a conventional PD simulation involving the collision of two objects with SRFs, contact detection is often the most computationally expensive component. All PD points must be checked for potential short-range interactions, leading to a high number of contact checks that scale poorly (Figure 10). In the DHPD-DEM coupled formulation, contact interactions occur only between DEM spheres. Deformation and fracture within each object are resolved through internal PD interactions, with the DEM-derived contact forces acting as external loading. PD points belonging to the same object do not interact through the DEM.

This approach significantly reduces computational cost compared to existing methods [41,43,44,45]. While Hartmann et al. [44] reduced overhead by assigning DEM interactions only to surface particles, the present method advances this further by reducing each object to a single DEM entity, minimizing contact checks.

As illustrated in Figure 11, during a two-sphere collision, the PD points of each object are fully enclosed within their respective DEM spheres. Contact is handled entirely at the DEM level, while the internal peridynamic equations govern the deformation and fracture response.

By representing each object as a single DEM sphere, the proposed method drastically reduces the number of contact checks. Rather than evaluating SRFs between all PD points, contact detection is performed solely between the DEM spheres. This abstraction offers a major computational advantage, particularly in large systems or those with complex geometries (Figure 12). When there is no contact, this reduction results in significant performance gains. In contact scenarios, the primary computational cost arises from calculating internal PD forces that govern deformation and fracture within each object.

2.2.9. Distribution of Force

The one-way coupling is established by distributing the DEM force (as calculated by Equation (7)) to the PD particles. The DEM forces are distributed in proportion to the volume overlap of the PD points. For example, Figure 13 shows the force vectors of two overlapping DEM circles. The force is distributed over the PD points in the overlap region in proportion to the volume of overlap.

To calculate the force exerted on an individual PD particle due to overlap, the following method is used. First, the fraction of the volume of the overlapped region belonging to the individual PD particle relative to the total volume of overlap between the two DEM spheres is calculated by Equation (27).

$$V_{\mathrm{f}}={\displaystyle \frac{V_i}{V_{\mathrm{tot}}}},$$

(27)

where $V_{\mathrm{f}}$ is the fractional volume, $V_i$ is the volume of overlap between the PD particle i and the DEM sphere, and $V_{\mathrm{tot}}$ is the total volume of overlap between the two DEM spheres.

Next, the portion of the DEM force that belongs to the individual PD particle is computed with Equation (28).

$${\overrightarrow{F}}_{\mathrm{DEM},\mathrm{f}}={\overrightarrow{F}}_{\mathrm{DEM}}{V}_{\mathrm{f}}.$$

(28)

Next, ${\overrightarrow{F}}_{\mathrm{DEM},\mathrm{f}}$ is divded by $V_i$ in order to convert this portion of the DEM force into a force density (in units of N/m³ in 3D). This force density is applied as a body force in the PD calculations, according to Equation (29).

$${\overrightarrow{F}}_{\mathrm{PD},\mathrm{i}}={\displaystyle \frac{{\overrightarrow{F}}_{\mathrm{DEM},\mathrm{f}}}{V_i}}.$$

(29)

Because the distributed forces are normalized by the total overlap volume, their sum is exactly equal to the DEM contact force. This guarantees conservation of linear momentum regardless of mesh irregularity, and no artificial drift in momentum or energy was observed in long simulations beyond the expected physical damping and numerical integration error.

To apply this force to individual PD points, a unit vector is computed from the center of the DEM sphere to each overlapping PD point. The DEM force is then multiplied by this unit vector to assign the correct direction, as illustrated in Figure 13.

3. Case Studies

The DHPD-DEM coupling strategy is investigated through two case studies designed to evaluate its performance in distinct physical regimes. These studies serve to demonstrate both the accuracy of the coupling method (force magnitude and spatial distribution under impact) and its ability to simulate physically realistic contact responses under varying loading conditions, laying a foundation for future extensions involving fracture and fragmentation.

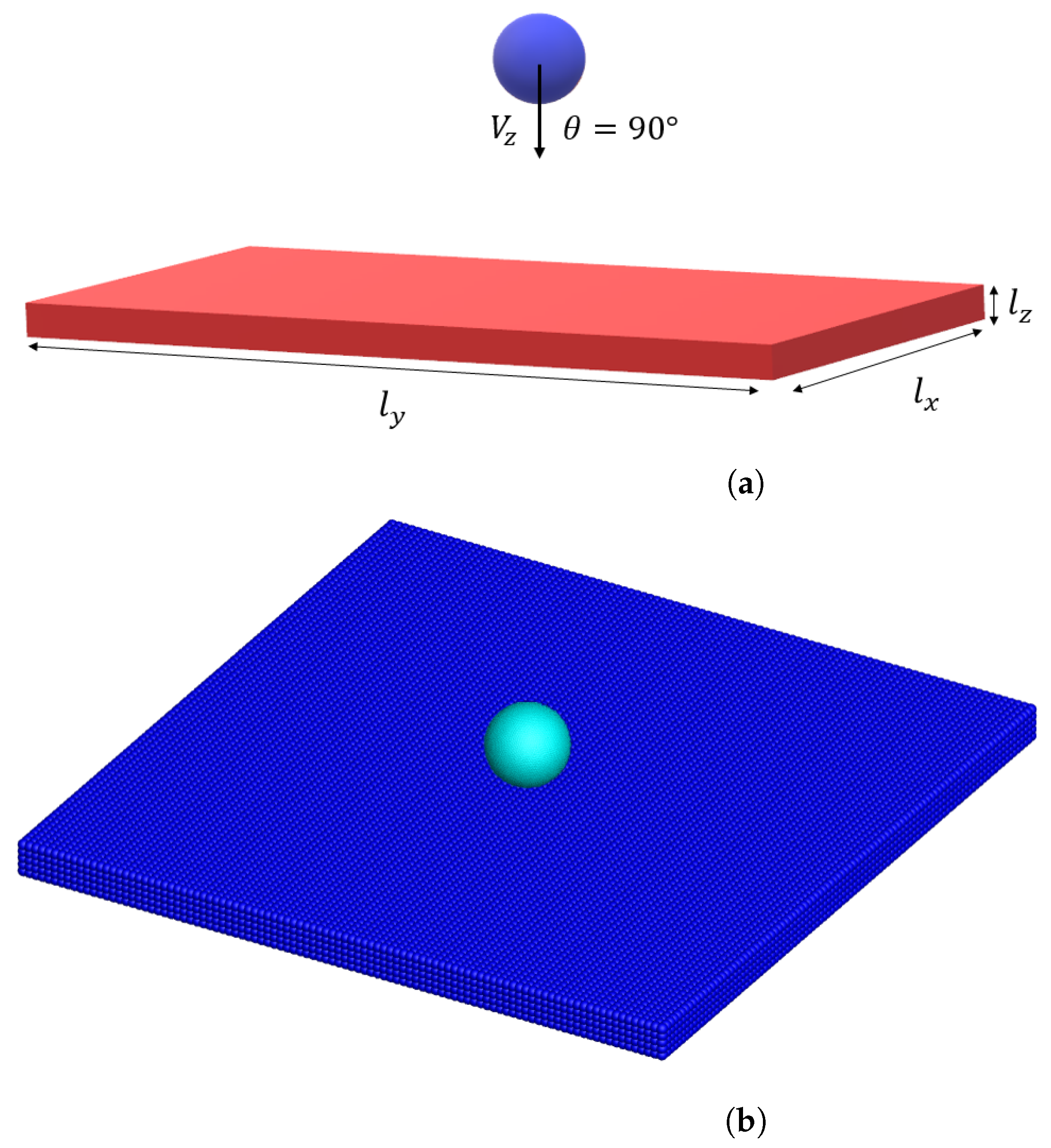
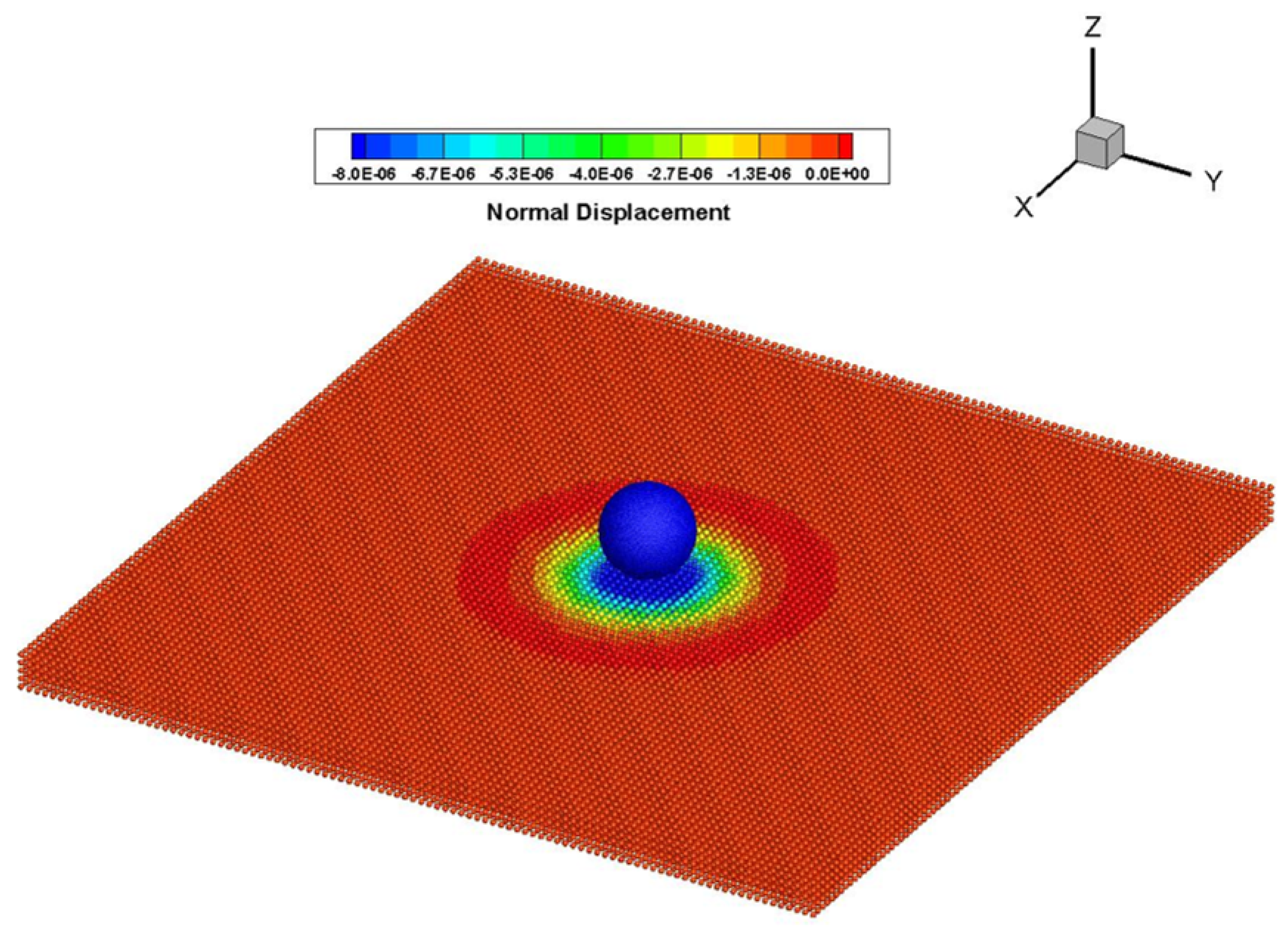
• Case Study 1 investigates the impact of a rigid sphere on a simply supported elastic plate. This case serves as a benchmark to validate the fidelity of force transfer from the DEM to DHPD, by comparing key response metrics (e.g., peak force, displacement, rebound velocity) against analytical solutions and the previous literature.
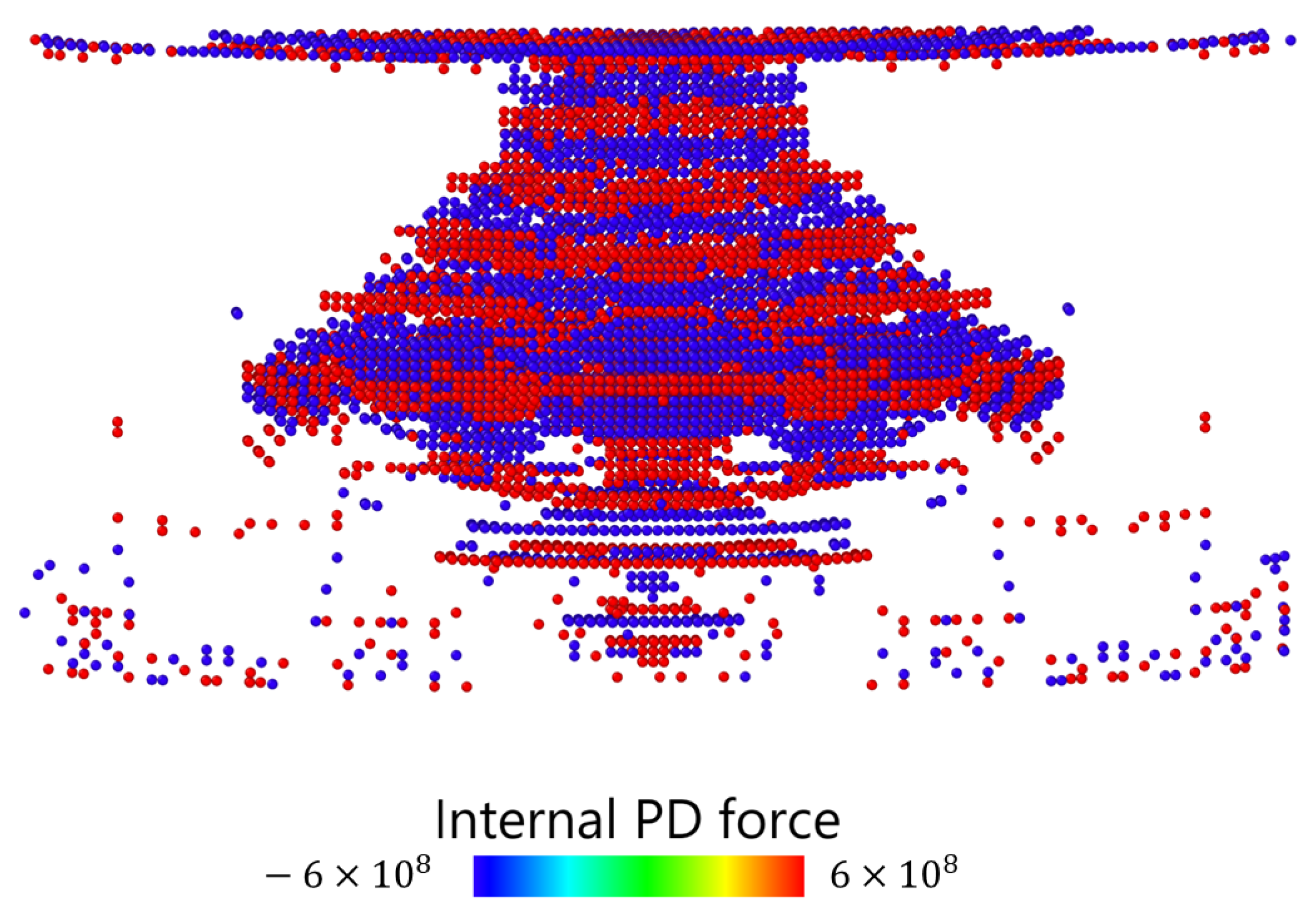
• Case Study 2 examines the high-speed impact of a steel sphere on a brittle cylindrical plate. The purpose of this case is not to capture damage or fracture (which will be added in future work), but to illustrate the directionality and localization of internal PD forces resulting from DEM contact. Qualitative alignment with observed Hertzian cone damage in experiments will be evaluated.

These two cases were selected to isolate and validate the proposed coupling itself, (1) contact detection via a single DEM surrogate per body and (2) volume-overlap force transfer to the DHPD discretization, without additional application-specific complexities. Broader application examples (e.g., layered targets or fragmentation) are left to follow-on work.

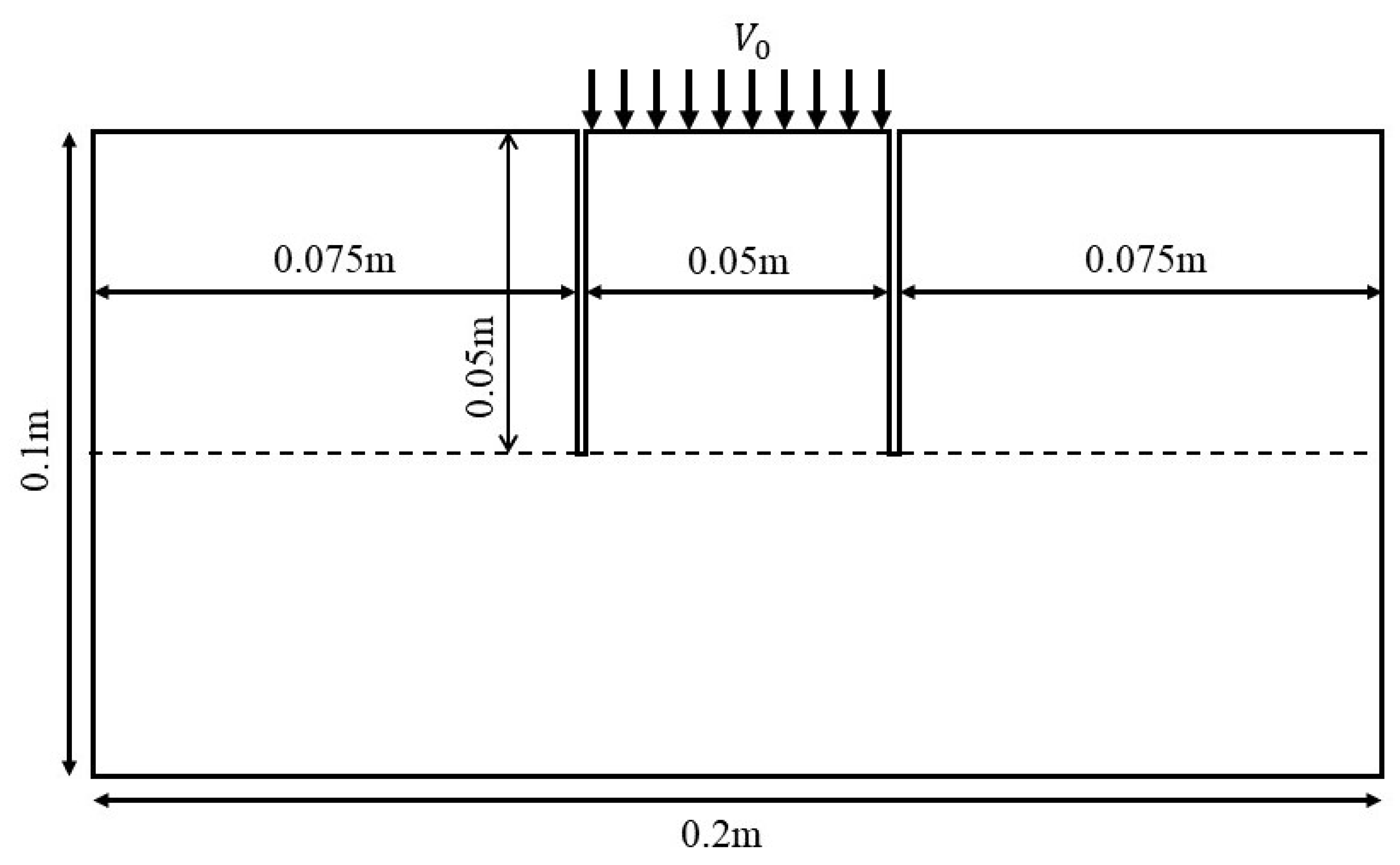
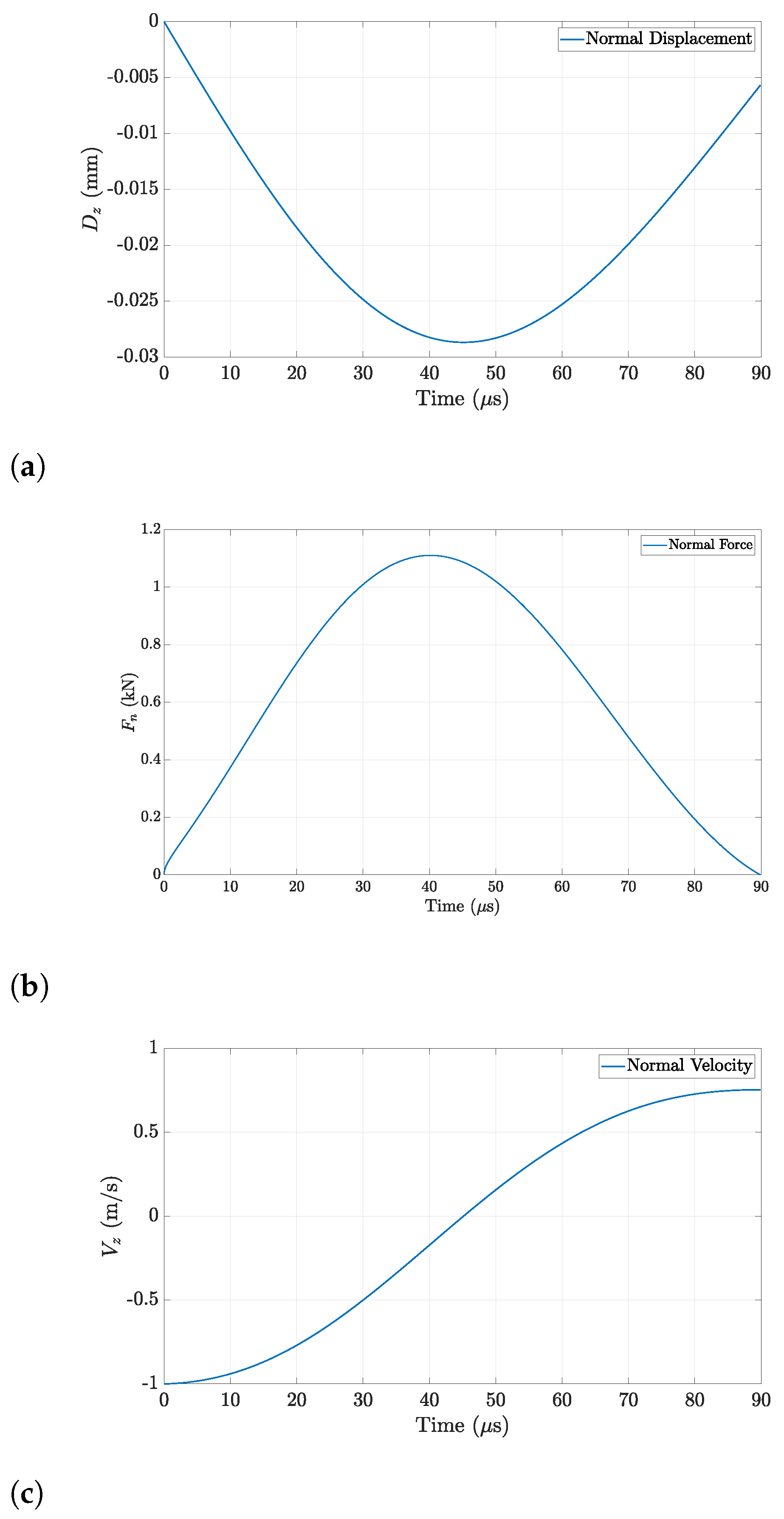
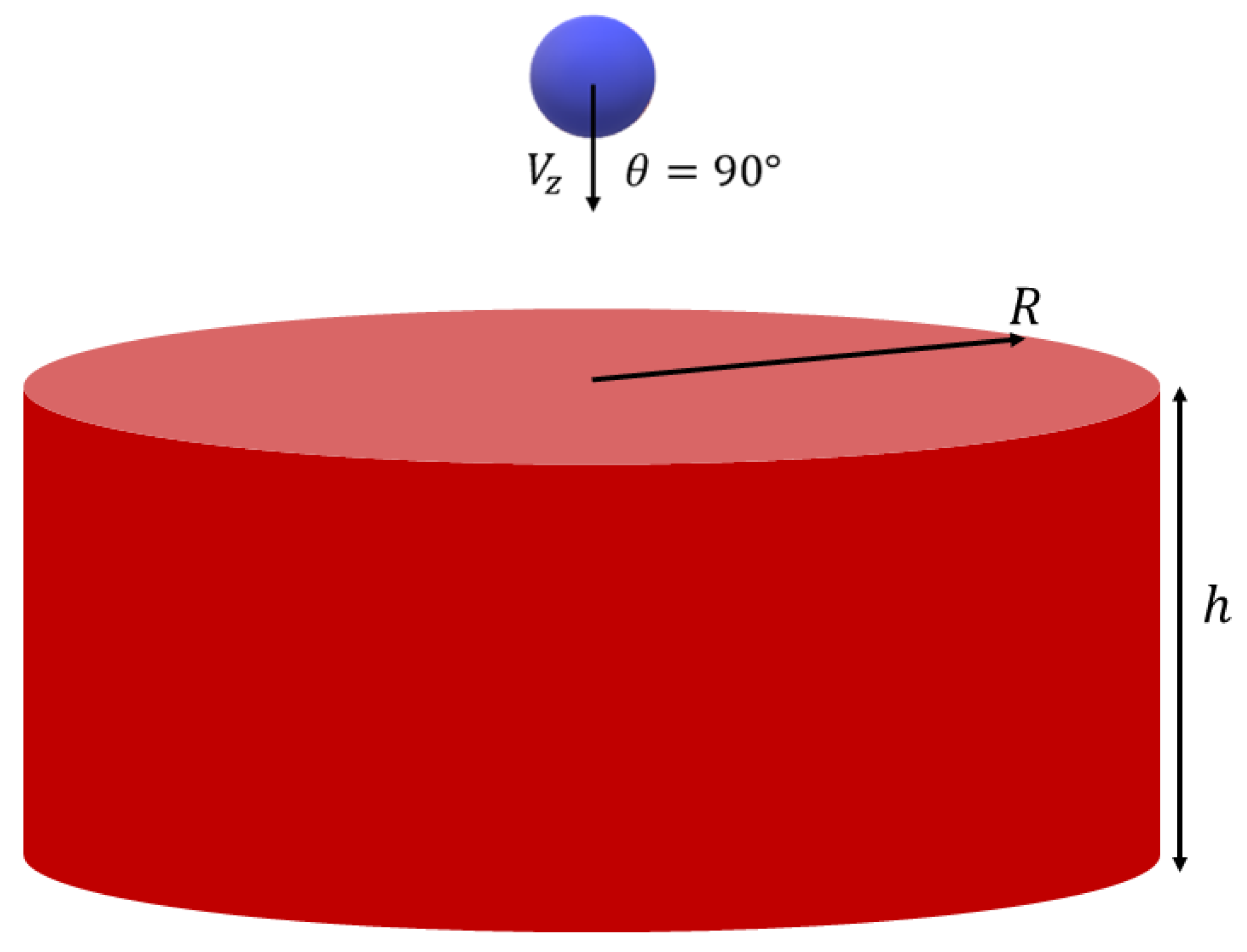
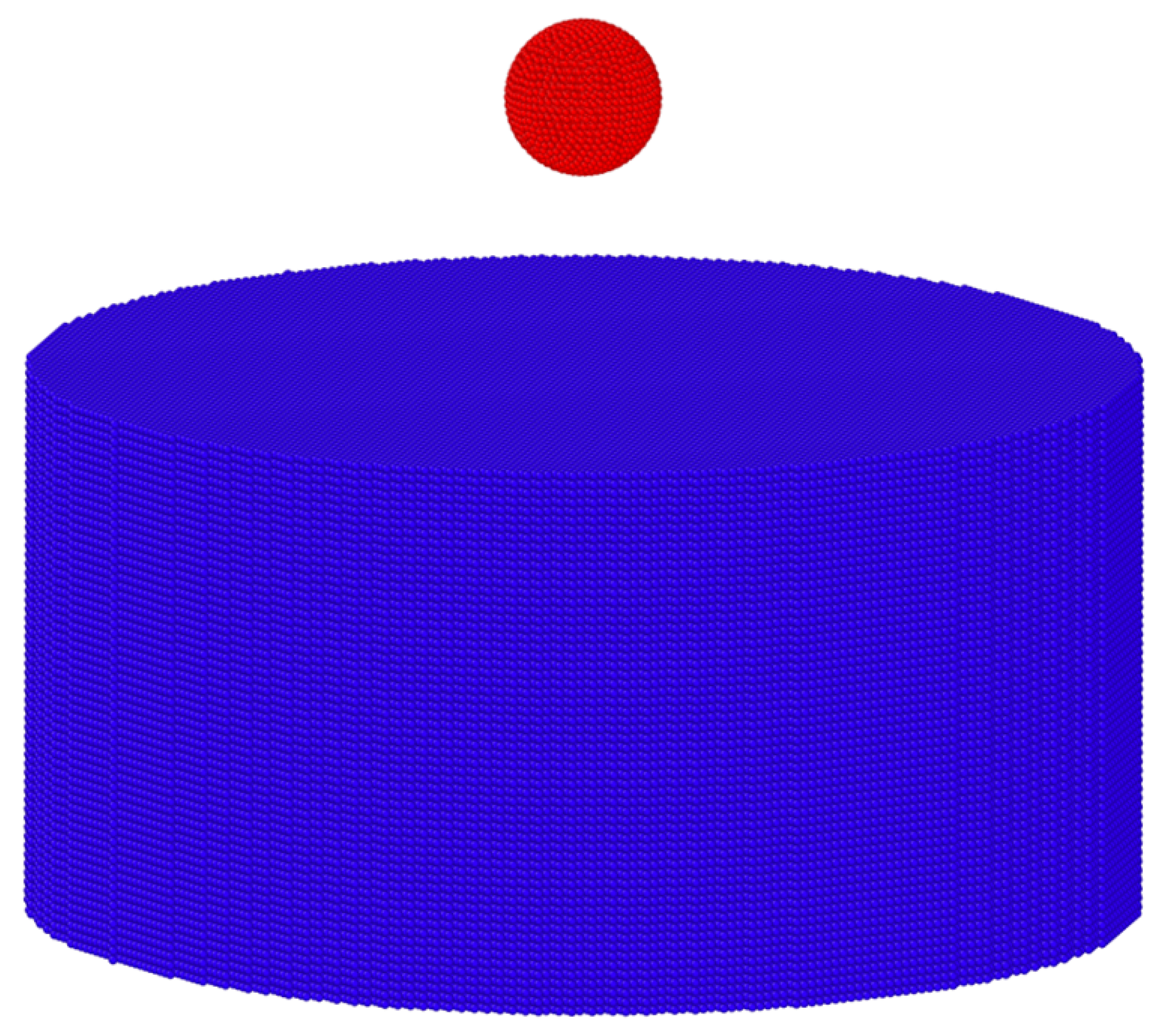
3.1. Normal Impact on a Simply Supported Plate

A rigid sphere impacting a simply supported plate is simulated to validate the force transfer from the DEM to DHPD. The impactor has a radius of 0.01 m and has a normal impact on the plate at a velocity of $V_z=1\mathrm{m}/\mathrm{s}$. The contact forces are governed by the interaction of the two DEM spheres, with the plate sphere modeled as rigid to represent a fully supported (fixed) object, as shown in Figure 14. These forces are then distributed in relation to the volume overlap between the impacting sphere and the PD points that make up the plate in order to calculate the deformation of the plate. The plate is simply supported and its dimensions are $l_x=l_y=120\mathrm{mm}$, $l_z=8\mathrm{mm}$ (Figure 15). The impactor and target are made of steel with a Young’s modulus of $206\mathrm{GPa}$, a Poisson’s ratio of $0.28$, and a density of $7833{\mathrm{kg}/\mathrm{m}}^3$. The plate is discretized into 100 × 100 × 4 points, giving a grid spacing of $2\mathrm{mm}$. The timestep size is $1.0\times {10}^{-8}$, and the total simulation time is $100\mathsf{\mu }\mathrm{s}$.

Figure 16 and Figure 17 show good agreement between the DEM impact parameters and the theoretical results as outlined in studies by Chun and Lam [59] and in Anicode et al. [60], who conducted a similar simulation using a different PD-DEM coupling method. Figure 18 reports the corresponding DEM time histories for normal displacement, normal contact force, and normal velocity. The quantitative comparison in

Table 2. Normal impact on simply supported plate: comparison of our results with results from the literature.

Object	Parameters	DHPD/DEM	Anicode and Madenci [61]	Chun and Lam [59]
Impactor	Dz,max (mm)	0.00287	0.0027	0.0025
	Vz,max	0.75	0.75	0.75
	Fn,max (kN)	1.11	1.2335	1.25
Plate	Dz,max (mm)	0.008	0.00781	0.0078

demonstrates that the plate deflection ($D_{z,max}$) and rebound velocity ($V_{z,max}$) are reproduced within 3–5% of the results from the literature. While the peak contact force ($F_{n,max}$) differs by slightly more than 5%, this parameter is directly influenced by the DEM stiffness and damping calibration, and thus is less indicative of the coupled method’s predictive accuracy. The more critical metric for validating PD–DEM force transfer, namely displacement response, is captured with high fidelity.

Table 2 shows that the displacement of PD points in the DHPD-DEM coupling method is in close agreement with other results in the literature based on the overlap of the impactor ($D_z$), rebound velocity ($V_{z,max}$), maximum force ($F_{n,max}$), and maximum deformation of the plate ($D_{z,max}$).

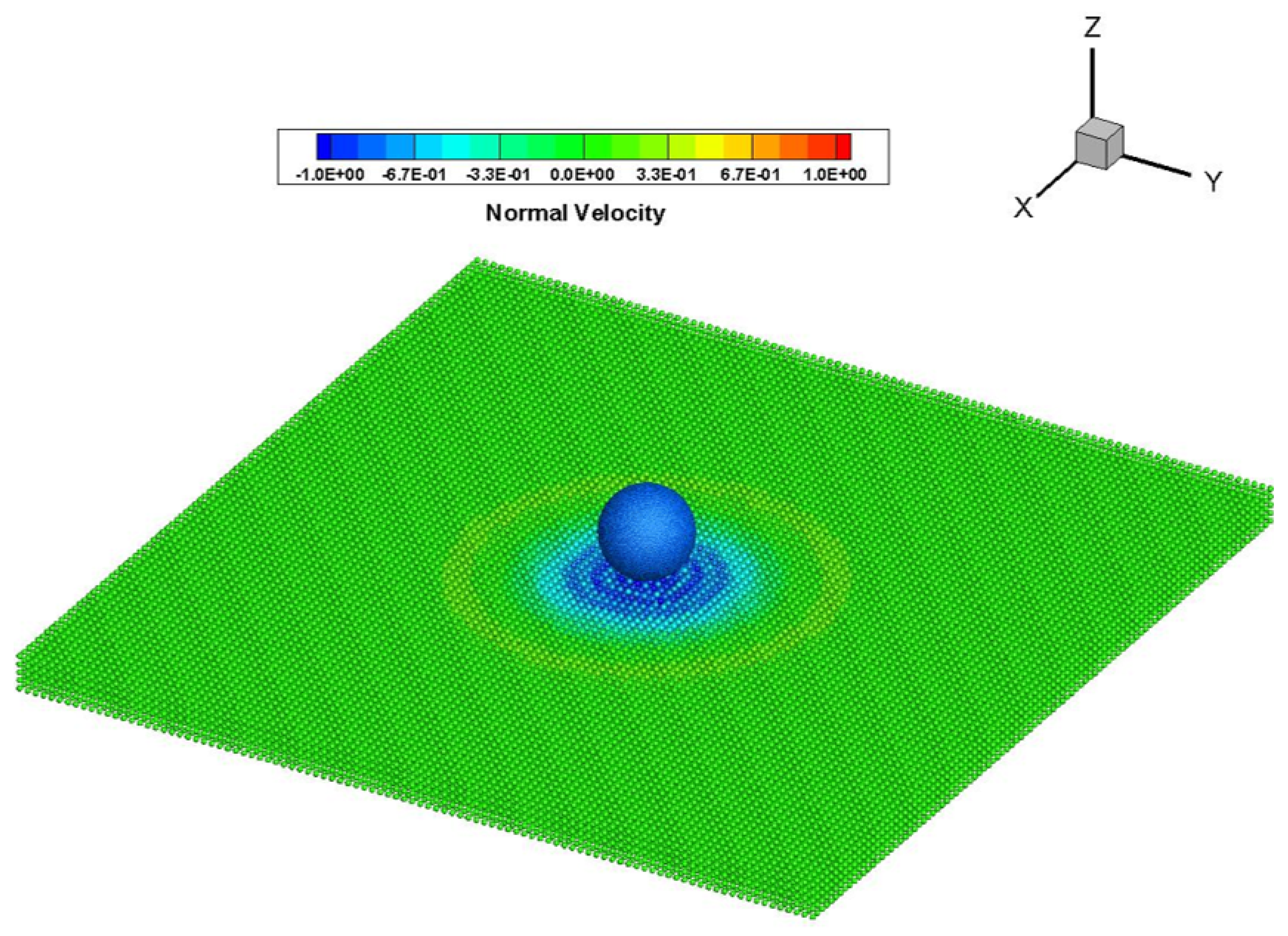
3.2. Qualitative Demonstration: High-Speed Impact of a Steel Sphere on a Brittle Cylindrical Plate

A steel sphere with a radius of $5\mathrm{mm}$ impacts a plate at a velocity of $V_z=35\mathrm{m}/\mathrm{s}$. The plate is a cylinder with radius $r=30\mathrm{mm}$ and height $h=30\mathrm{mm}$ (Figure 19). The material properties are given in

Table 3. Material parameters for normal impact of sphere on plate.

Property	Sphere	Plate
Young’s Modulus E (GPa)	205	22.35
Poisson’s Ratio v	0.25	0.25
Density $\rho$ (kg/m3)	7945	2200

. The plate is discretised with a PD point spacing of $0.5\mathrm{mm}$ with 60 points along its height, as shown in Figure 20.

The primary objective of this case is not to reproduce brittle failure or damage, but rather to demonstrate the directional fidelity of the internal force distribution resulting from the proposed DEM-to-DHPD force mapping. Specifically, this test illustrates how impact-induced forces are propagated through the PD domain in a physically consistent and spatially localized manner, aligning with expected wave fronts and stress trajectories for high-speed contact loading. The post-collision force distribution is shown in Figure 21.

It should be noted that a peridynamic damage model is not activated in this case. Thus, the simulation produces an internal force map, not a damage map. An experimental photograph illustrating the typical damage morphology under similar loading can be found in Chaudhri [62]. Figure 21 is a qualitative illustration of the mapped loading directionality and localization, not a direct validation.

3.3. Discussion

Case Study 1 provides quantitative validation (force–time, displacement–time) and demonstrates that a single-particle DEM surrogate can supply accurate, momentum-conserving contact forces to a high-resolution DHPD body at a fraction of the usual neighbor-search cost. Case Study 2 is a qualitative demonstration of the mapped loading patterns in the absence of damage.

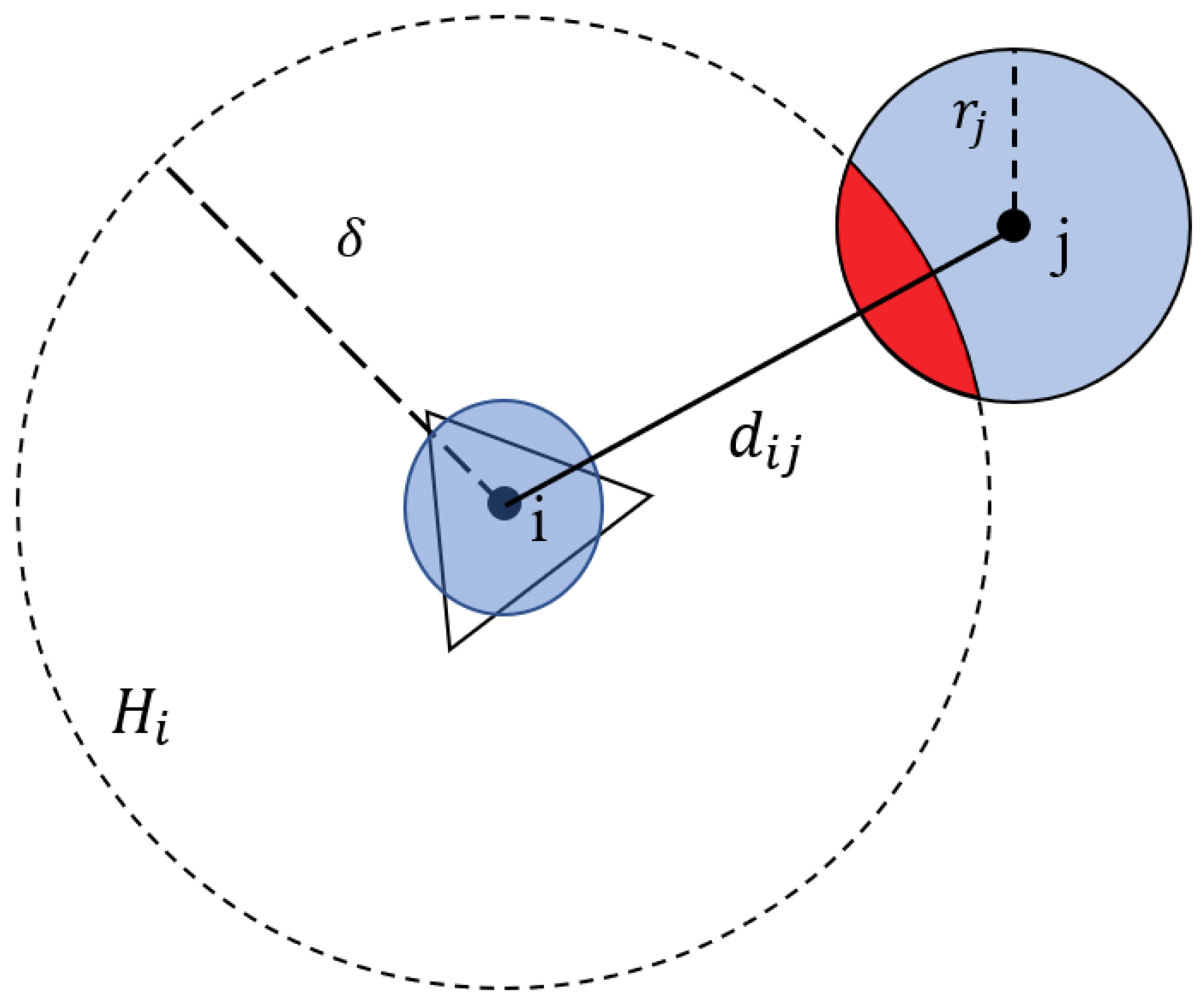
3.3.1. Contact Check Efficiency

When performing iterative calculations for multi-body systems over time, issues often arise in detecting contacts between objects. Identifying the geometric relationships between objects is crucial, as this process can consume a significant portion of the computational effort—up to 80% of the total calculation time, according to sources [63,64,65]. In the discrete element method (DEM), the contact detection algorithm generally includes a spatial sorting phase. This phase reduces the computational load by filtering out objects that are not in close proximity to the target object, thereby eliminating unnecessary comparisons. Such preprocessing significantly reduces the computation required for the subsequent contact resolution phase. Without this spatial sorting, the algorithm would necessitate a direct comparison of every possible pair of objects, escalating the time complexity to $O(N^2)$, where N represents the total number of particles used to discretize each object.

The current method would lead to a time complexity of $O(M^2)$, where M represents the number of objects in the simulation. For instance, without any time savings afforded by spatial processing, considering two spherical objects colliding, each discretized by 30,000 PD points, PD with SRFs would necessitate $9\times {10}^8$ contact checks per timestep. In contrast, the proposed method would require only two contact checks per timestep, thus substantially reducing the computational cost associated with contact checks.

3.3.2. Accuracy of Results

The results of the first case study (Table 2) show that the proposed DHPD-DEM framework accurately replicates key contact mechanics metrics, including maximum overlap, peak normal force, rebound velocity, and plate deformation, with deviations of less than 5% from both the analytical reference solution [59] and a previously validated peridynamic implementation [61]. These findings validate the effectiveness of using a single DEM surrogate for force application, confirming that the reduced-contact abstraction can maintain fidelity in contact force transmission.

Minor discrepancies are primarily attributed to the specific choice of DEM contact parameters, particularly the damping and stiffness values used in the Hertz–Mindlin model. Fine-tuning these parameters, either via parameter fitting to analytical solutions or through inverse identification using high-resolution impact data, could further reduce this deviation. Additionally, including tangential damping or rolling resistance models may improve accuracy in cases where frictional energy dissipation is more significant. Despite these small differences, the method demonstrates robust predictive performance for normal-impact scenarios.

Having validated the force transmission capability of the DHPD-DEM framework in a well-understood elastic impact scenario, a more challenging case involving brittle fracture is examined to test the model’s behavior under high-speed dynamic loading. In this second case study, the aim is to visualize the spatial and temporal evolution of the internal PD force field generated by the DEM contact load in comparison with experimentally observed fracture patterns. The internal stress distribution resulting from the impact of a steel sphere on a brittle plate reveals oscillatory force behavior, as depicted in Figure 21, where the force alternates between positive and negative values, suggesting the presence of tension/compression stress waves within the brittle glass plate. However, this is a qualitative context only, and not a one-to-one validation.

This wave propagation is typical when a dynamic impact induces rapid fluctuations in stress, reflecting the material’s response to alternating load conditions. When a sphere impacts a brittle glass plate, the initial contact generates compressive stresses at the point of impact. These stresses quickly propagate through the material as waves. Importantly, as these compressive waves travel, tension regions can also develop almost simultaneously. This complex behavior of stress distribution in brittle materials occurs because the outer regions around the impact site can experience tensile stresses as the material tries to accommodate the inward movement caused by the compression. A Hertzian cone, typically formed under such conditions, results from the radial and lateral tensile stresses exceeding the tensile strength of the glass, initiating cracks that propagate and eventually form the cone. This phenomenon is well-documented in experimental studies, such as those conducted by Chaudhri [62]. Because no damage is modeled here, we refrain from quantitative force–time or crack–metric comparisons; Figure 21 is presented strictly as a qualitative illustration of the mapped loading pattern.

The present model’s internal force patterns (Figure 21) match closely with the damage patterns found in the literature (Chaudhri [62]). Even though Figure 21 represents force distributions and the literature shows damage, the patterns are similar.

4. Conclusions

This study presents a DHPD-DEM framework in which each deformable body is represented by a single DEM particle for contact detection, with forces distributed to PD particles in a volume-consistent, momentum-conserving manner. This coupling significantly reduces the contact-search burden, shifting the computational complexity from $\mathcal{O}(N^2)$ for conventional PD to $\mathcal{O}(M^2)$.

Through two complementary case studies, the framework’s performance was compared to both classical contact benchmarks and dynamic brittle impact problems. The first case demonstrated quantitative agreement with analytical and numerical references, reproducing rebound velocity, peak normal force, and deformation metrics within 5%. The second, more challenging, case showed that the internal peridynamic force fields generated by the DEM-supplied loading closely resembled known fracture patterns in brittle materials, even without explicitly modeling damage.

Together, these results demonstrate that the proposed surrogate-based coupling achieves the following:

• It preserves essential features of contact mechanics with dramatically reduced computational effort;
• It enables realistic internal stress wave propagation in DHPD from externally applied contact forces;
• It lays the groundwork for fully resolved peridynamic fragmentation and erosion modeling using minimal contact infrastructure.

By decoupling contact detection from PD resolution, this method unlocks the scalability needed for large-system, multi-body impact simulations. It provides a robust foundation for future developments in adaptive contact modeling, damage feedback, and surrogate re-wrapping strategies. By leveraging the more mature DEM contact models, the framework provides a physically consistent and computationally scalable method for simulating impact, rebound, and early-stage erosion. This foundational effort provides a critical step towards quantitative damage analysis and implementation of advanced physics-based models and computational methods.

4.1. Future Work

While the present benchmarks omit damage modeling, crack initiation in PD would couple directly to the DEM load via the same mapping. In a bond-based formulation, bonds are irreversibly removed once the stretch or bond energy exceeds a critical threshold, after which the DEM-applied body force continues to act through the remaining intact network. Conservation is maintained without modification, though one could optionally scale the DEM load by the intact-volume fraction to avoid applying force to fully detached fragments. Exploration of this extension is left for future work.

4.2. Operator Choice for PD

The coupling is operator-agnostic: in place of the bond-based DHPD operator, a Peridynamic Differential Operator (PDDO) [66] could be used to evaluate nonlocal gradients/divergence on irregular point sets. The DEM contact traction would still enter as body-force density mapped by volume-overlap weighting; thus, the DEM contact search and the DEM → PD force transfer would remain unchanged.

4.3. Relation to Filippov Formulations

Coulomb-type contact yields a discontinuous right-hand side and can be modeled as a Filippov differential inclusion [67]. In our framework, a Filippov, event-driven contact integrator (with sliding selection and standard Runge–Kutta plus event location) could replace the DEM time-stepping to sharpen stick–slip transitions and reduce chattering, e.g., following Dieci and Lopez [68] or Algorithm 968 (DISODE45) [69]. This substitution would leave the single-surrogate representation and the volume-overlap DEM→PD force mapping unchanged.