The Mechanism of Casing Perforation Erosion Under Fracturing-Fluid Flow: An FSI and Strength Criteria Study
Abstract
1. Introduction
2. Methodology
2.1. Governing Equation of Fluid
2.2. Discrete-Phase Transport Model
2.3. Erosion Model
2.4. Governing Equation of Solid
2.5. Fluid–Structure Interaction (FSI) Coupled Governing Equations
3. Fluid–Structure Coupling Numerical Model
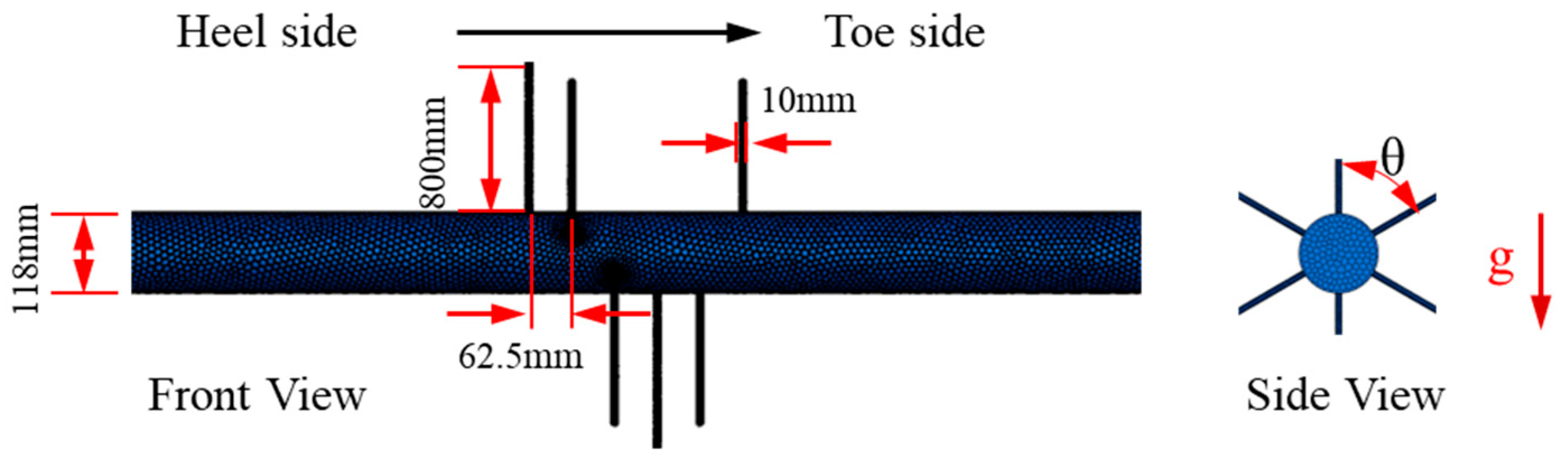
3.1. Numerical Model
3.2. Verification
4. Results
4.1. Flow Field Characteristics in the Perforated Section
4.2. Erosion of the Perforation Hole
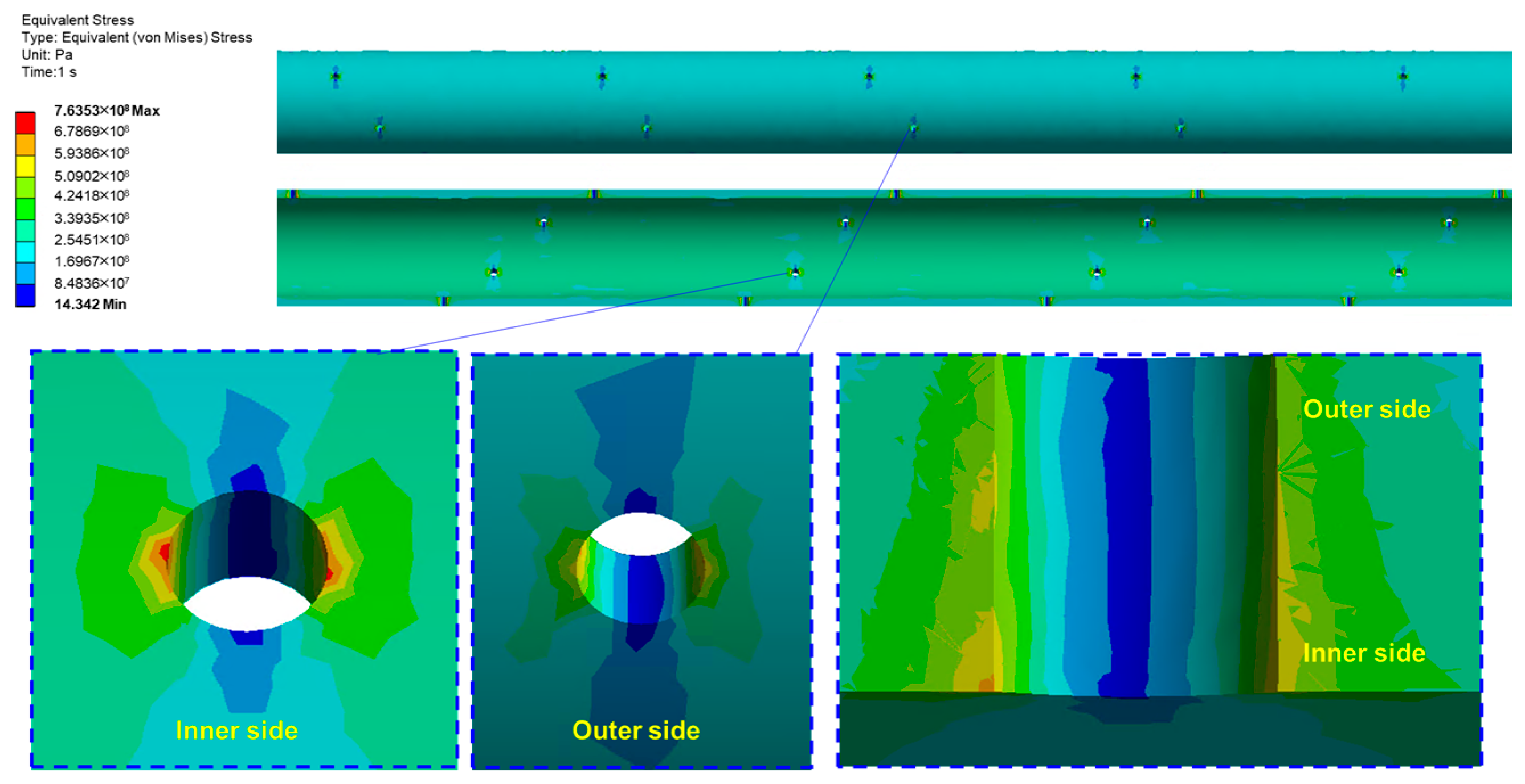
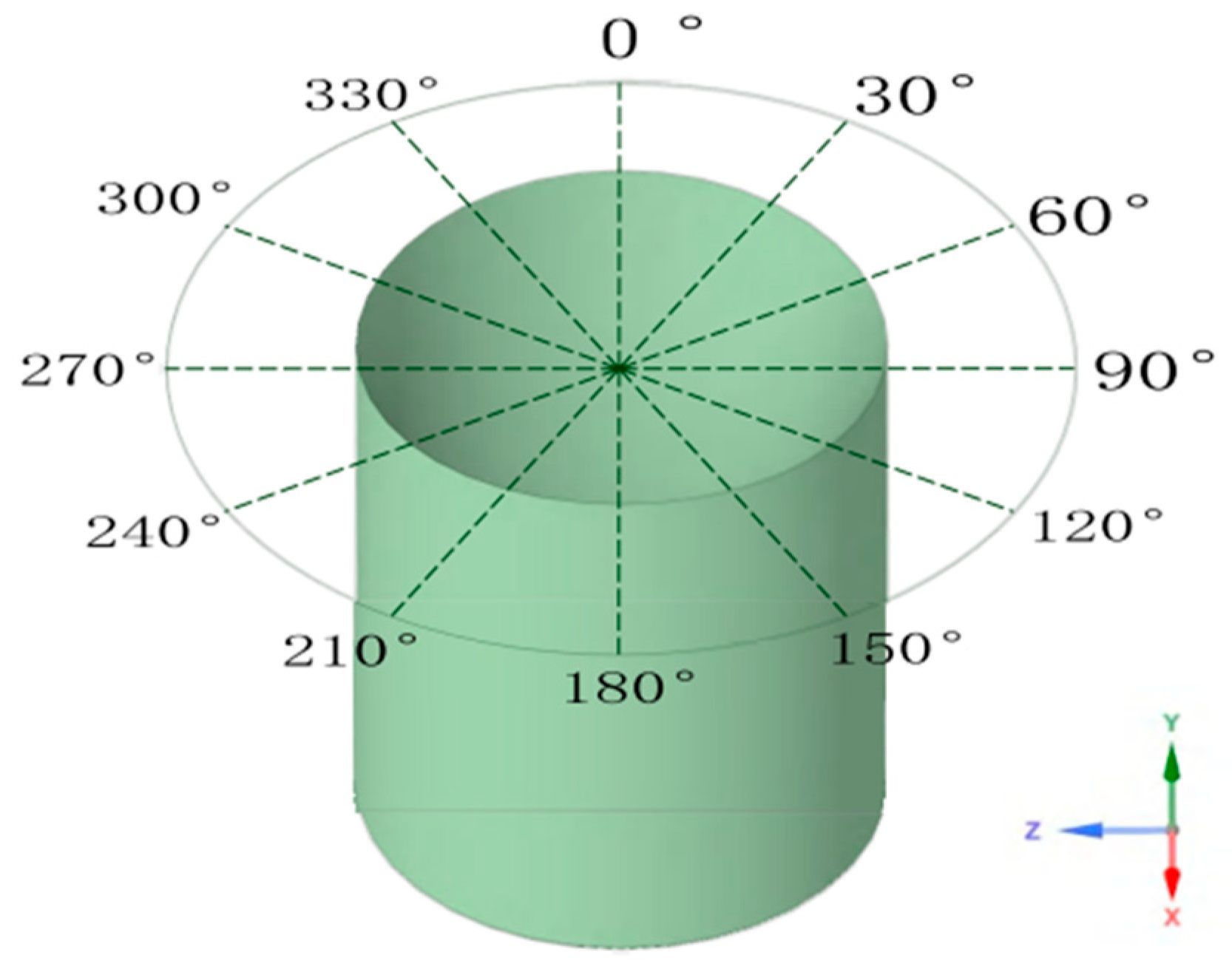
4.3. Von Mises Stress Analysis of the Casing
4.4. The Maximum Principal Stress and Shear Stress of the Casing
5. Conclusions
- (1)
- During fracturing, the flow cross-section suddenly shrinks at the entrance of the perforation hole, which contributes to an increase in the fracturing fluid’s velocity up to 323.0 m/s at the hole entrance. This acceleration causes the most severe erosion, with a maximum erosion rate of 2.26 × 10−5 kg/(m2·s). The numerical simulation results are consistent with field fracturing tests, showing wall thinning and diameter enlargement at the perforation entrance.
- (2)
- The von Mises stress around the perforation hole is symmetrically distributed along the hole axis. The maximum von Mises stress occurs at the 90° and 270° positions on the inner wall, reaching nearly 750 MPa, which remains below the material yield strength. However, the maximum shear stress reaches 325.18 MPa, exceeding the allowable shear stress of 265.74 MPa (considering a safety factor of 1.25), indicating that shear failure is the primary mechanism initiating erosion damage at the perforation.
- (3)
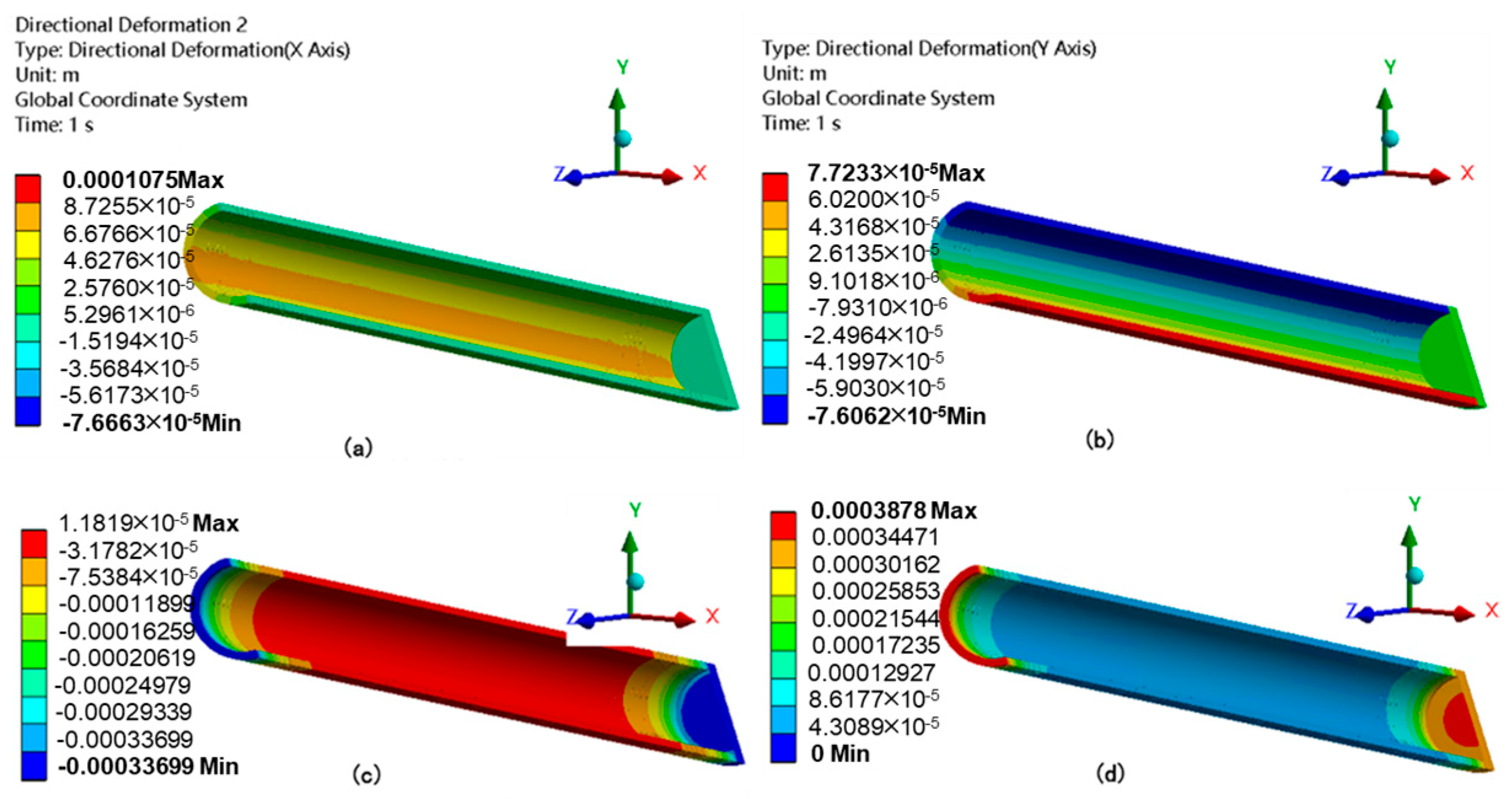
- Under the impact of fracturing fluid, the casing experiences deformations of 0.11 mm (x-direction), 0.078 mm (y-direction), and 0.38 mm (z-direction), with a total maximum deformation of 0.39 mm. The contact pressure at the first and second interfaces decreases significantly in perforated regions (e.g., from nearly 15 MPa in non-perforated areas to <5 MPa near perforations), indicating a reduction in cement bonding capacity and a potential risk to casing integrity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DPM | Discrete Phase Model |
| DDPM | Dense Discrete Phase Model |
| FSI | Fluid–Structure Interaction |
References
- Hu, Q.H.; Cheng, W.; Wang, Z.C.; Shi, Y.Z.; Jia, G.L. Transportation and sealing pattern of the temporary plugging ball at the spiral perforation in the horizontal well section. Pet. Sci. 2024, 21, 3288–3298. [Google Scholar] [CrossRef]
- Sinkov, K.; Weng, X.; Kresse, O. Modeling of Proppant Distribution During Fracturing of Multiple Perforation Clusters in Horizontal Wells. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Virtual, 4–6 May 2021. [Google Scholar] [CrossRef]
- Ibrahim, A.F.; Assem, A.; Johnston, T.; Sinky, M.; Adams, M. Comprehensive Workflow for Predicting Multistage Hydraulic Fracturing Well Performance: Analysis of Parent Well Depletion, Fracturing Stage Evaluation, and Post-Fracturing Assessment. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 17–19 June 2024. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.C.; Wang, F.L.; Ning, X.; Wang, Y.L.; Bai, B.J. Settling behavior and mechanism analysis of kaolinite as a fracture proppant of hydrocarbon reservoirs in CO2 fracturing fluid. Colloids Surf. A 2025, 724, 137463. [Google Scholar] [CrossRef]
- Li, Q. Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection. Reserv. Sci. 2025, 1, 1–2. [Google Scholar] [CrossRef]
- Kebert, B.A.; Miskimins, J.L.; Soehner, G.; Hunter, W. Computational Fluid Dynamics Modeling of Pseudotransient Perforation Erosion in a Limited-Entry Completion Cluster. SPE Prod. Oper. 2023, 38, 243–257. [Google Scholar] [CrossRef]
- Zhou, L.; Xiong, X.; Li, Y.; Liu, H.; Ding, R. Revolutionary breakthroughs and key theories and technologies in deep coalbed methane development. Nat. Gas Ind. B 2025, 45, 17–30. [Google Scholar] [CrossRef]
- He, F.; Dong, Z. Development potential of deep coalbed methane: A case study in the Daniudi gas field, Ordos Basin. Oil Gas Geol. 2022, 43, 277–285. [Google Scholar]
- Li, Y. Exploration practices of and recent production breakthroughs in deep middle-rank coalbed methane in the Daniudi gas field, Ordos Basin. Oil Gas Geol. 2024, 45, 1555–1566. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.; Gao, D.; Li, X.; Zhang, Y. Effects of Hydraulic Fracturing on Horizontal Wellbore for Shale Gas. Acta Pet. Sin. 2016, 37, 406–414. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, S.; Li, J.; Pan, Y.; Zeng, D.; Yu, H.; Zhu, H. Simulation of the erosion of casing and perforation under staged sand fracturing conditions in horizontal sections. J. Hydrodyn. 2022, 34, 725–743. [Google Scholar] [CrossRef]
- Zhang, F. Prediction of Perforation Erosion During Multi-Cluster Hydraulic Fracturing in Horizontal Wells. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2023. [Google Scholar]
- Lv, Z.; Zhang, Y.; Shi, S.; Xi, Y.; Dong, J. Downhole behavior characteristics of horizontal well volume fracturing in high-speed erosioncasing. Pet. Drill. Tech. 2024, 52, 86–96. [Google Scholar] [CrossRef]
- Cramer, D.; Friehauf, K.; Roberts, G.; Whittaker, J. Integrating Distributed Acoustic Sensing, Treatment-Pressure Analysis, and Video-Based Perforation Imaging To Evaluate Limited-Entry-Treatment Effectiveness. SPE Prod. Oper. 2020, 35, 0730–0755. [Google Scholar] [CrossRef]
- Yuan, P.; Zhang, H.; Huang, X.; Han, J.; Zhou, Q.; Alberto, M.; Bao, J. Study of proppant erosion in multistage hydraulic fracturing using computational fluid dynamics modeling. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Kingdom of Bahrain, 6–9 March 2017. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, L.; Wang, Z.; Dou, Y. Numerical Simulation of Perforation Hole Erosion during Cased Hole Fracturing. Chin. Pet. Mach. 2015, 43, 66–69. [Google Scholar]
- Shi, S.Z.; Zhang, S.S.; Cheng, N.; Tian, G.; Zeng, D.Z.; Yu, H.Y.; Wang, X.; Zhang, X. Erosion characteristics and simulation charts of sand fracturing casing perforation. Pet. Sci. 2023, 20, 3638–3653. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, G.; Weng, D.; Gao, Y.; Li, S. Dynamic Evolution of Perforation Erosion During Sand Fracturing Based on CFD-DEM Simulation. J. Eng. Thermophys. 2024, 45, 1031–1037. Available online: https://jeth.magtechjournal.com/EN/Y2024/V45/I4/1031#2 (accessed on 30 September 2025).
- Sakaida, S.; Hamanaka, Y.; Zhu, D.; Hill, A.D.; Kerr, E.; Estrada, E.; Scofield, R.; Johnson, A. Evaluation of Fluid Distribution and Perforation Erosion in Multistage Fracture Treatment. SPE J. 2024, 29, 5316–5331. [Google Scholar] [CrossRef]
- Aune, V.; Valsamos, G.; Casadei, F. Coupled Simulations of Extreme Fluid-Structure Dynamics. In Proceedings of the 10th edition of the International Conference on Computational Methods for Coupled Problems in Science and Engineering, Chania, Crete, Greece, 5–7 June 2023. [Google Scholar] [CrossRef]
- Nadda, R.; Prakash, R.; Bhusan, D.D.; Donnelly, R.F. Incorporating fluid-structure interactions for modelling of pyramidal hollow microneedles for transdermal drug delivery. J. Drug Deliv. Sci. Technol. 2025, 114, 107561. [Google Scholar] [CrossRef]
- Budiman, O.; Alajmei, S.; Bahri, A.; Aljawad, M.S.; Miskimins, J. A Review of Proppant Transport and Distribution in Slickwater Fracturing. Arab. J. Sci. Eng. 2025, 50, 5303–5322. [Google Scholar] [CrossRef]
- Segantine, E.; Souza, T.; Ribeiro, D.; Nascimento, A. Computational Fluid Dynamics modeling applied to drilling and cleaning operations: A science mapping analysis. ChemRxiv 2024. [Google Scholar] [CrossRef]
- Hojjati, S.; Pouraria, H.; Jeon, S. Numerical Modeling of Erosion in Dense Slurry Flows. In Proceedings of the 15th ISRM Congress, Salzburg, Austria, 10–13 October 2023. [Google Scholar]
- Huang, J.; Marteen, K.; Hao, Y.; Settgast, R.R.; White, J.A. A Continuum Model for Simulating Proppant Transport and Fluid Flow in Hydraulic Fractures. In Proceedings of the 55th U.S. Rock Mechanics/Geomechanics Symposium, Virtual, 18–25 June 2021. [Google Scholar]
- Chochua, G.G.; Parsi, M.; Zhang, Y.; Zhang, J.; Sedrez, T.A.; Karimi, S.; Darihaki, F.; Edwards, J.; Arabnejad, H.; Agrawal, M.; et al. A Review of Various Guidelines for Predicting Solid Particle Erosion Using Computational Fluid Dynamics Codes. In Proceedings of the CORROSION 2020, Physical Event Cancelled, 14–18 June 2020. [Google Scholar]
- Roberts, G.; Whittaker, J.; McDonald, J.; Paxson, T. Proppant Distribution Observations from 20,000+ Perforation Erosion Measurements. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020. [Google Scholar] [CrossRef]
- Qu, H.; Chen, X.; Liu, X. Particle-fluid flow and distribution in a horizontal pipe with side holes using experiment and numerical simulation. Powder Technol. 2023, 417, 118245. [Google Scholar] [CrossRef]











| Type | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) | Tensile Strength (MPa) | Shear Strength (MPa) |
|---|---|---|---|---|---|---|
| Casing | 7800 | 210 | 0.30 | 862.00 | 1050.00 | 332.17 |
| Cement | 1900 | 5.00 | 0.11 | 45.00 | 4.89 | -- |
| Formation | 1800 | 5.20 | 0.22 | -- | -- | -- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, C. The Mechanism of Casing Perforation Erosion Under Fracturing-Fluid Flow: An FSI and Strength Criteria Study. Modelling 2025, 6, 121. https://doi.org/10.3390/modelling6040121
Zhang H, Wang C. The Mechanism of Casing Perforation Erosion Under Fracturing-Fluid Flow: An FSI and Strength Criteria Study. Modelling. 2025; 6(4):121. https://doi.org/10.3390/modelling6040121
Chicago/Turabian StyleZhang, Hui, and Chengwen Wang. 2025. "The Mechanism of Casing Perforation Erosion Under Fracturing-Fluid Flow: An FSI and Strength Criteria Study" Modelling 6, no. 4: 121. https://doi.org/10.3390/modelling6040121
APA StyleZhang, H., & Wang, C. (2025). The Mechanism of Casing Perforation Erosion Under Fracturing-Fluid Flow: An FSI and Strength Criteria Study. Modelling, 6(4), 121. https://doi.org/10.3390/modelling6040121





