Investigation of Aerodynamic Pressure Characteristics Inside and Outside a Metro Train Traversing a Tunnel in High-Altitude Regions
Abstract
1. Introduction
2. Numerical Simulation
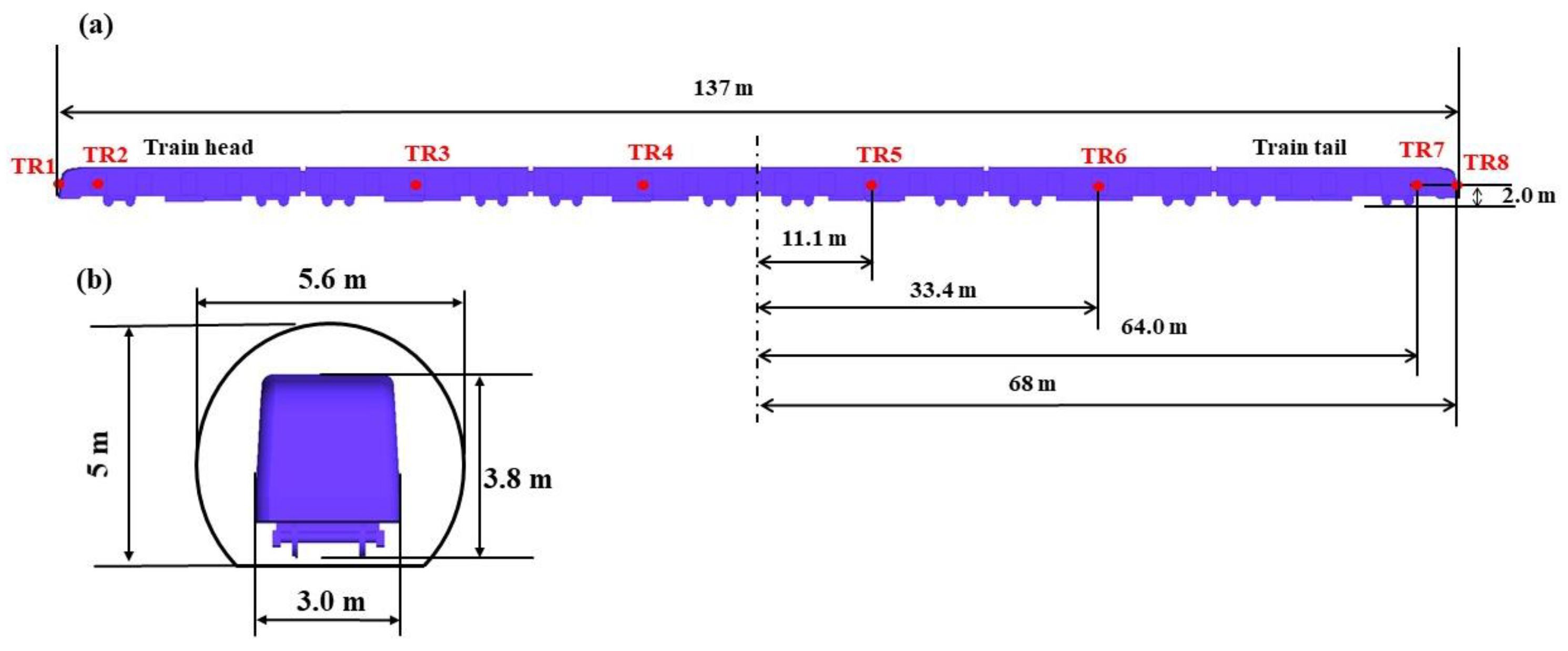
2.1. Geometry Model
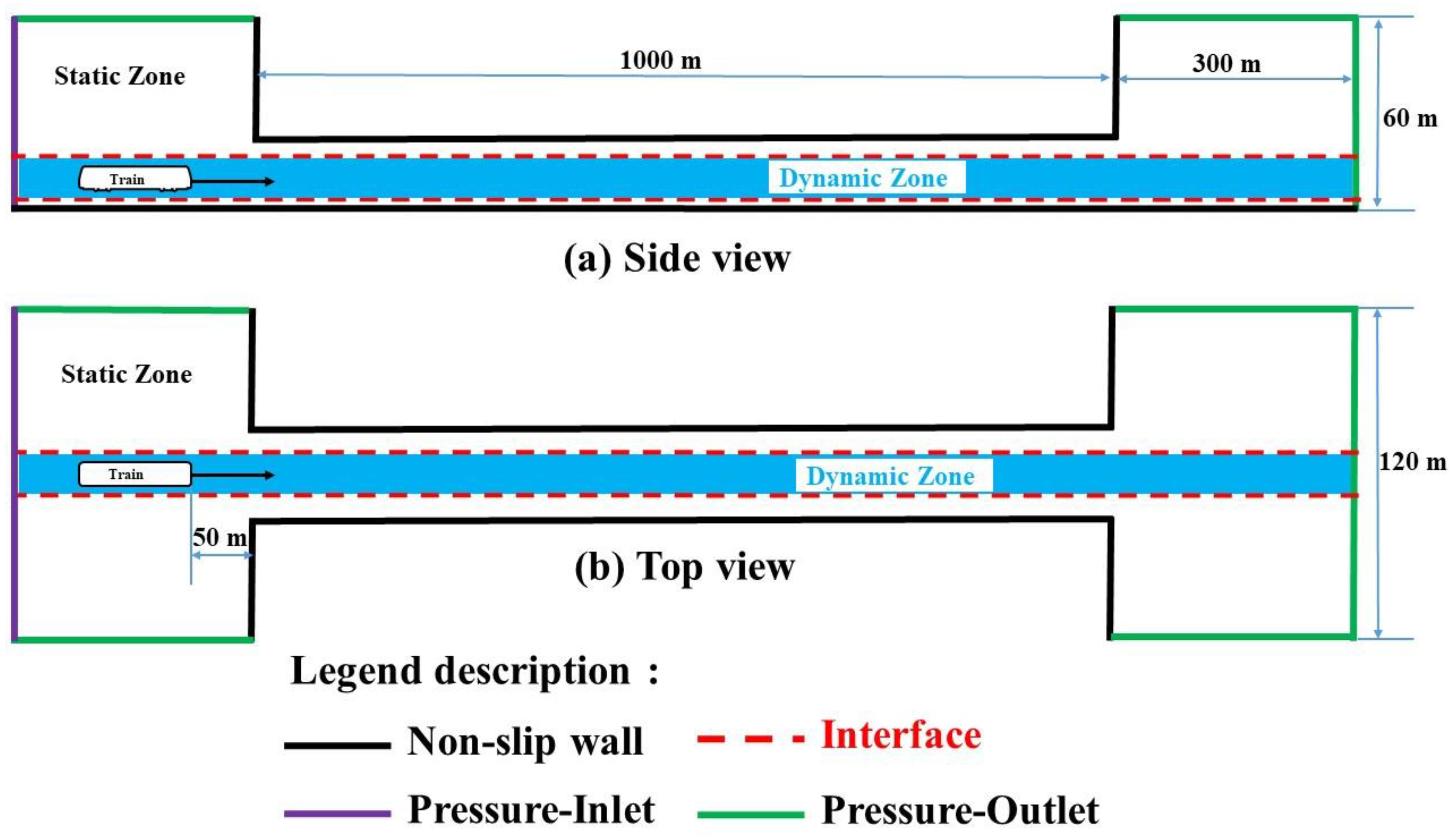
2.2. Numerical Domain and Boundary Conditions
2.3. Numerical Mesh
2.4. Solver Settings
3. Results and Discussion
3.1. Method Validation
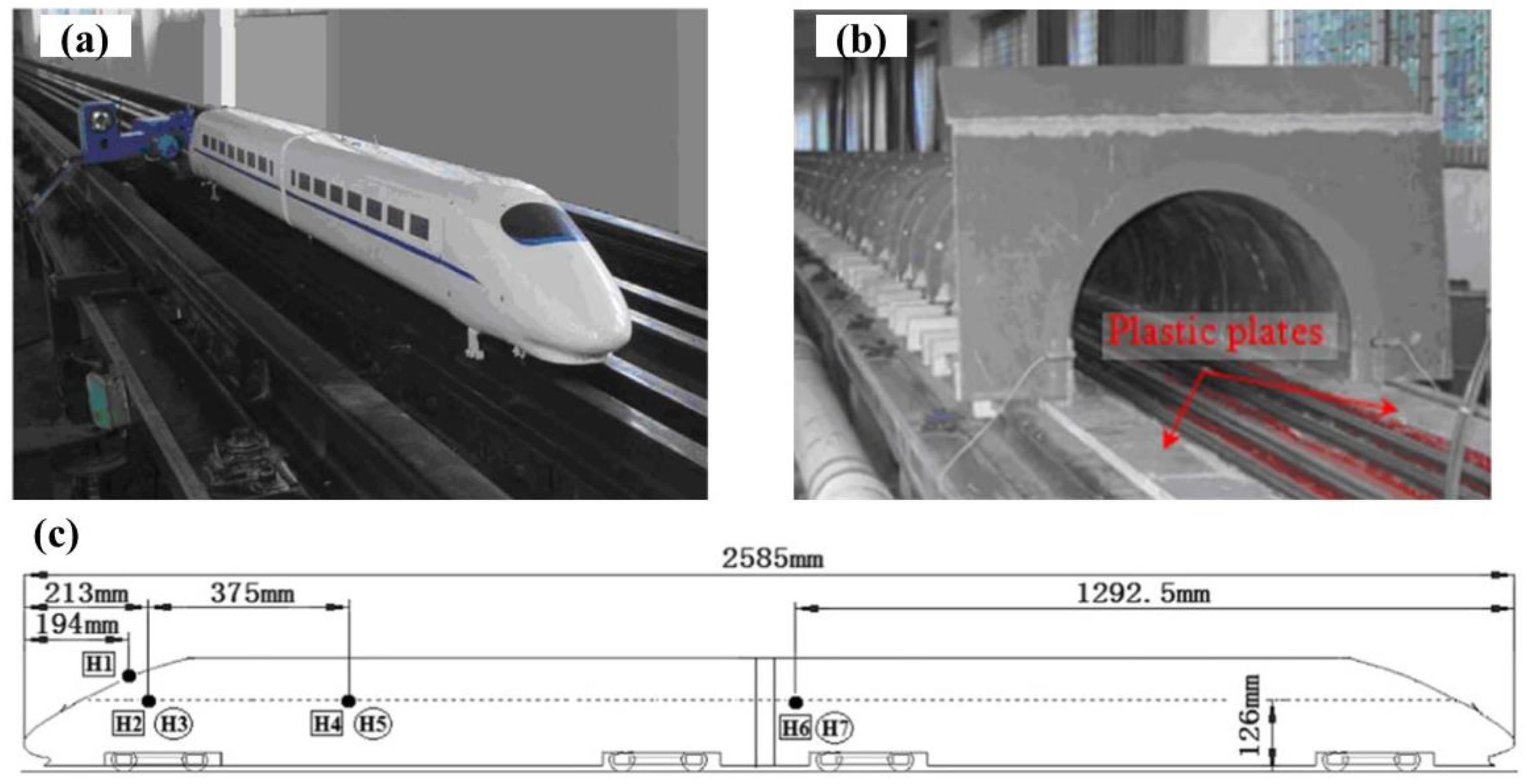
3.1.1. Overview of Experimental Studies in the Literature
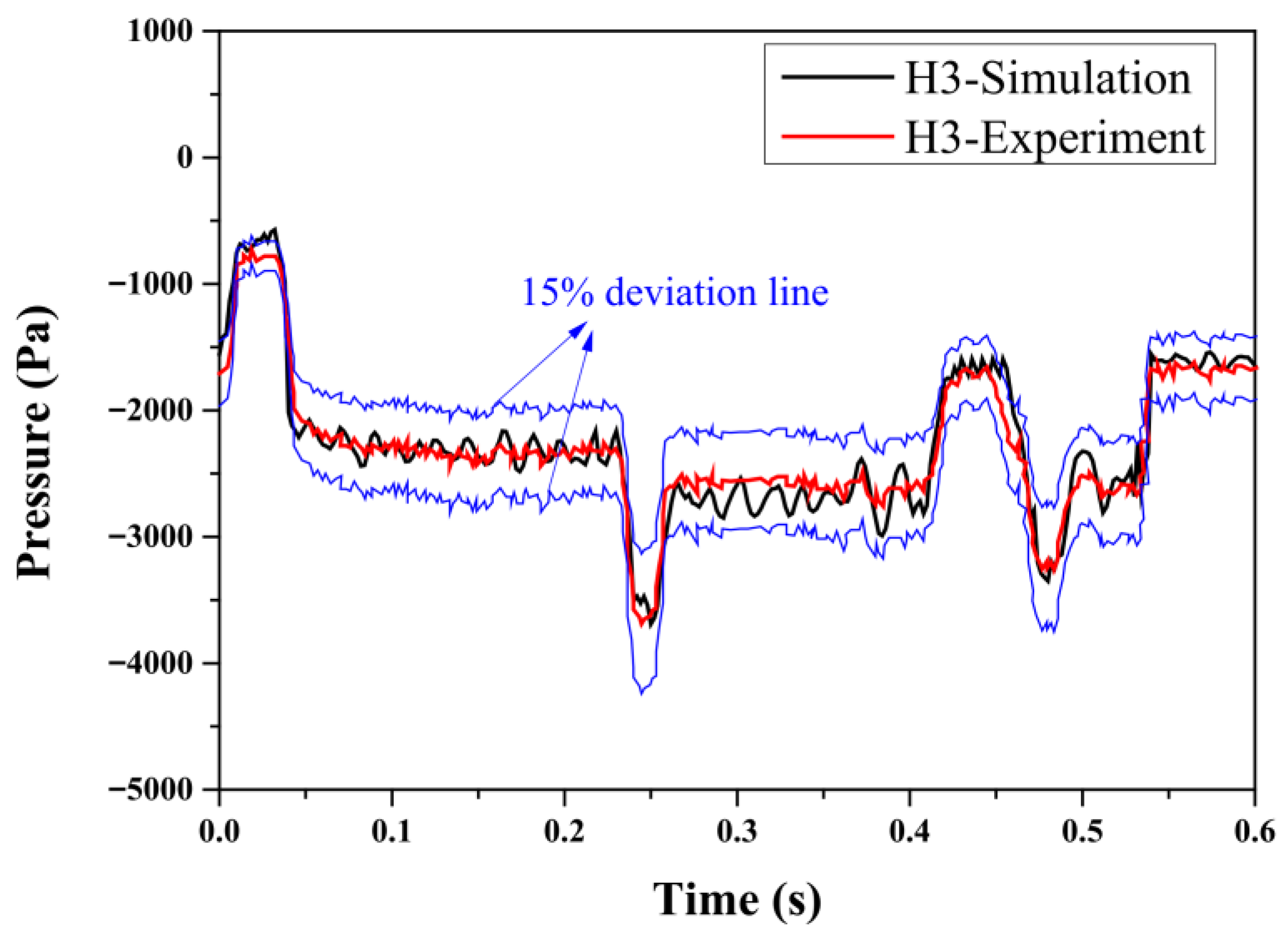
3.1.2. Numerical Simulation vs. Experimental Results
3.2. Transient Pressure Distribution
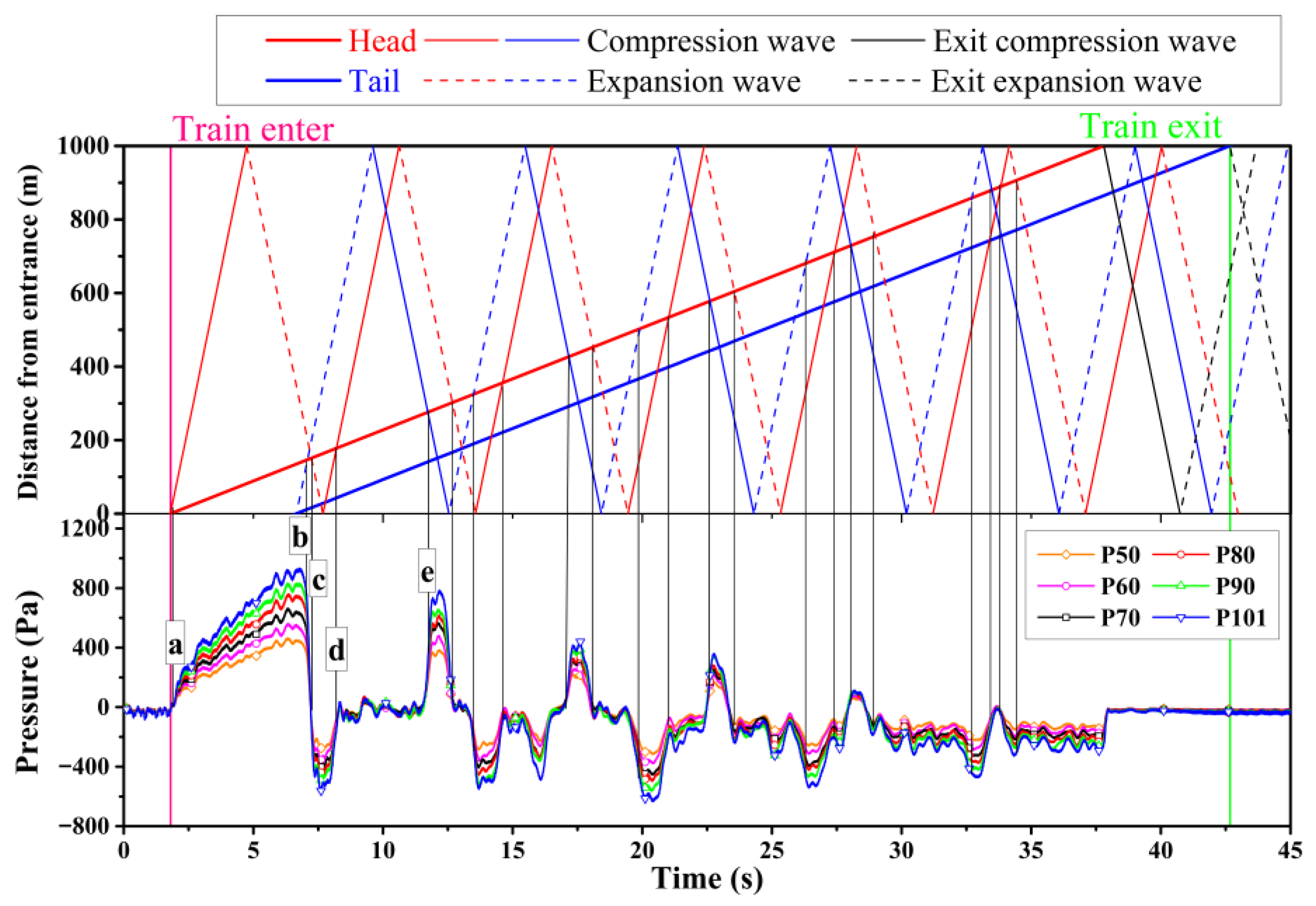
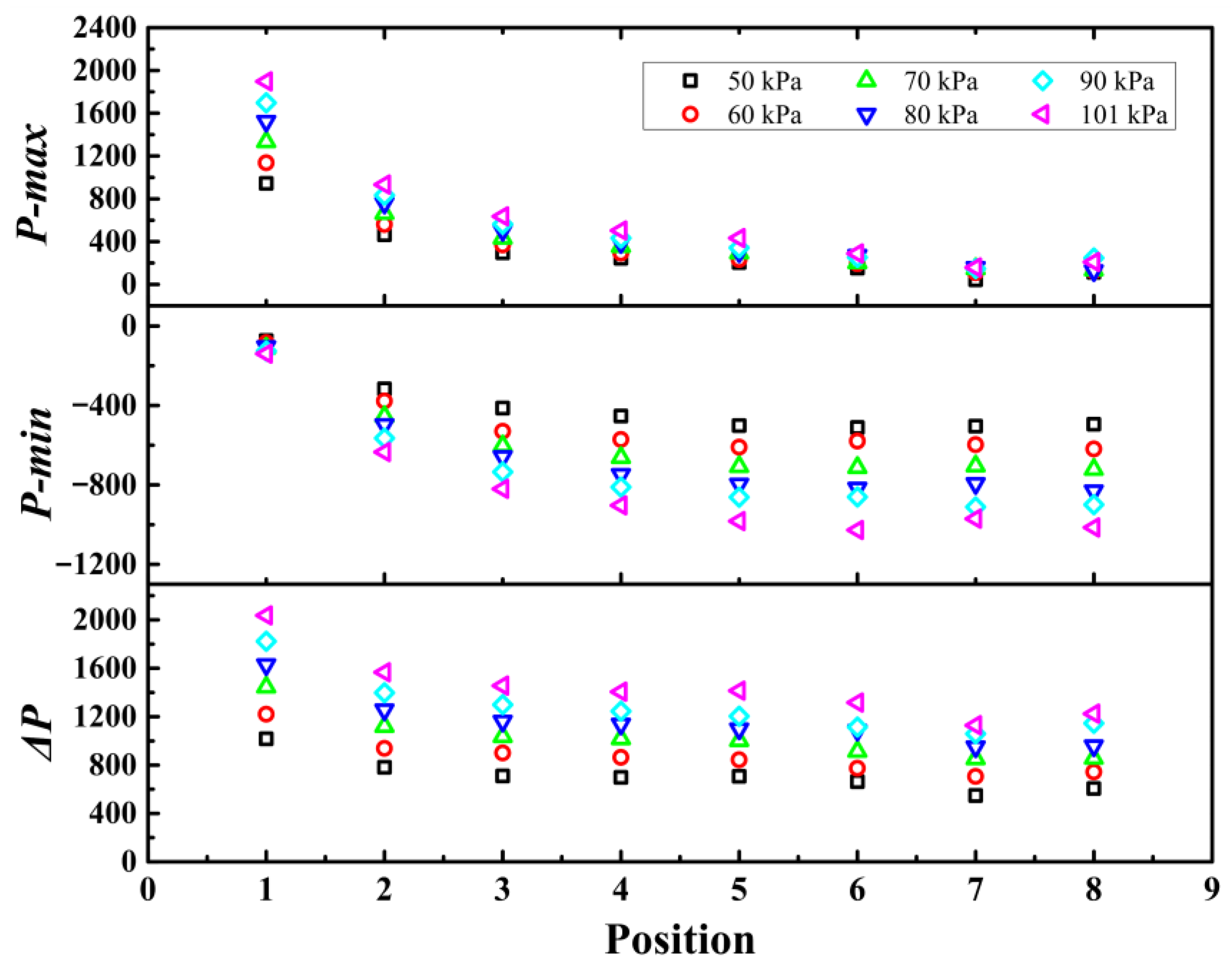
3.2.1. Exterior Pressure of the Train
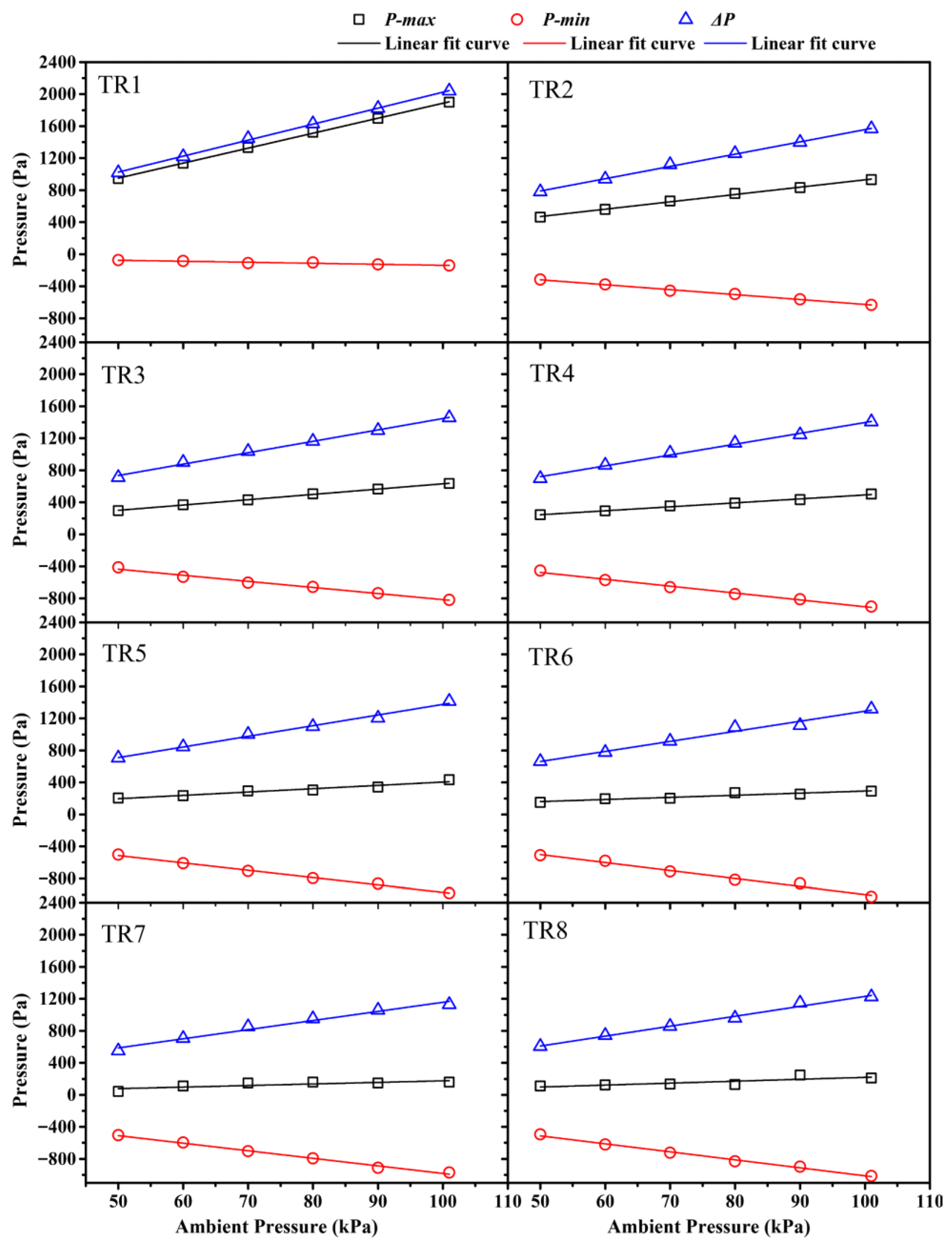
3.2.2. Interior Pressure of the Train
4. Conclusions
- (1)
- The impact of ambient pressure on train-induced transient pressure characteristics is significant, affecting both the external and internal pressure evolution of the train.
- (2)
- Ambient pressure significantly affects the transient peak value of the train’s exterior pressure. P-max and ΔP exhibit a linear increase, whereas P-min shows a linear decrease, all in response to rising ambient pressure.
- (3)
- The trend of pressure peak reduction and delay inside the metro train with a certain degree of airtightness remains well aligned for different ambient pressures. As the ambient pressure increases, the requirements for the sealing performance of the train become more stringent.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| c | The speed of sound (m/s) |
| The air’s adiabatic index | |
| The gas constant (J/(kg·K)) | |
| Temperature (K) | |
| P-max | The maximum values of the external transient pressure on the train (Pa) |
| P-min | The maximum values of the external transient pressure on the train (Pa) |
| ΔP | Peak-to-peak values of the external transient pressure on the train (Pa) |
| The sealing index (s) | |
| The pressure difference between the train’s interior and exterior (Pa) | |
| The current interior pressure (Pa) | |
| The previous step’s interior pressure (Pa) | |
| The current exterior pressure (Pa) | |
| The time interval (s) | |
| The peak pressure variations occurring within 1 s (Pa) | |
| The peak pressure variations occurring within 1 s (Pa) | |
| The peak pressure variations occurring within 3 s (Pa) |
References
- Wang, F.; Weng, M.; Han, J.; Obadi, I.; Liu, F. Effect of metro train on the critical driving force for preventing smoke back-layering in tunnel fires. Fire Mater. 2021, 46, 927–942. [Google Scholar] [CrossRef]
- Yang, X.; Shou, A.; Zhang, R.; Quan, J.; Li, X.; Niu, J. Numerical study on transient aerodynamic behaviors in a subway tunnel caused by a metro train running between adjacent platforms. Tunn. Undergr. Space Technol. 2021, 117, 104152. [Google Scholar] [CrossRef]
- GB50736-2012; Design Code for Heating Ventilation and Air Conditioning of Civil Buildings. China Architecture and Building Press: Beijing, China, 2012.
- Zhou, Y.; Wang, H.; Bi, H.; Wang, J. Experimental and numerical study of aerodynamic pressures on platform screen doors at the overtaking station of a high-speed subway. Build. Environ. 2021, 191, 107582. [Google Scholar] [CrossRef]
- Xiong, X.; Zhu, L.; Zhang, J.; Li, A.; Li, X.; Tang, M. Field measurements of the interior and exterior aerodynamic pressure induced by a metro train passing through a tunnel. Sustain. Cities Soc. 2020, 53, 101928. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Chen, Z.; Guo, Z.; Huo, X. Comparative study on the unsteady slipstream induced by a single train and two trains passing each other in a tunnel. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104095. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Martinez-Vazquez, P.; Chen, Z.; Huo, X.; Guo, Z. Influence of blockage ratio on slipstreams in a high-speed railway tunnel. Tunn. Undergr. Space Technol. 2021, 115, 104055. [Google Scholar] [CrossRef]
- Zampieri, A.; Rocchi, D.; Schito, P.; Somaschini, C. Numerical-experimental analysis of the slipstream produced by a high speed train. J. Wind. Eng. Ind. Aerodyn. 2020, 196, 104022. [Google Scholar] [CrossRef]
- Wang, F.; Liu, F.; Han, J.; Jin, H.; Weng, M.; Zeng, Z. Study on the train-induced unsteady airflow in a metro tunnel with multi-trains. Tunn. Undergr. Space Technol. 2020, 106, 103565. [Google Scholar] [CrossRef]
- Wang, F.; He, X.; Xu, L.; Zhao, S.; Weng, M. Train-Induced Unsteady Airflow in a Metro Tunnel with a Ventilation Shaft. Appl. Sci. 2024, 14, 9177. [Google Scholar] [CrossRef]
- Zarnaghsh, A.; Abouali, O.; Emdad, H.; Ahmadi, G. A numerical study of the train-induced unsteady airflow in a tunnel and its effects on the performance of jet fans. J. Wind. Eng. Ind. Aerodyn. 2019, 187, 1–14. [Google Scholar] [CrossRef]
- Li, Z.-W.; Yang, M.-Z.; Huang, S.; Liang, X. A new method to measure the aerodynamic drag of high-speed trains passing through tunnels. J. Wind. Eng. Ind. Aerodyn. 2017, 171, 110–120. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, G.; Zhou, D.; Wang, Z.; Guo, Z. Numerical investigation of the pressure and friction resistance of a high-speed subway train based on an overset mesh method. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 235, 598–615. [Google Scholar] [CrossRef]
- Izadi, T.; Abouali, O.; Mehrabian, M.A.; Salmanzadeh, M. Investigation of the effects of different parameters on the generated pressure waves inside the tunnels. SN Appl. Sci. 2020, 2, 1406. [Google Scholar] [CrossRef]
- Mei, Y. A Generalized Numerical Simulation Method for Pressure Waves Generated by High-Speed Trains Passing through Tunnels. Adv. Struct. Eng. 2013, 16, 1427–1436. [Google Scholar] [CrossRef]
- Wang, H.; Lei, B.; Bi, H.; Yu, T. Wavefront evolution of compression waves propagating in high speed railway tunnels. J. Sound Vib. 2018, 431, 105–121. [Google Scholar] [CrossRef]
- Zhang, G.; Kim, T.H.; Kim, D.H.; Kim, H.D. Prediction of micro-pressure waves generated at the exit of a model train tunnel. J. Wind. Eng. Ind. Aerodyn. 2018, 183, 127–139. [Google Scholar] [CrossRef]
- Miyachi, T.; Fukuda, T. Model experiments on area optimization of multiple openings of tunnel hoods to reduce micro-pressure waves. Tunn. Undergr. Space Technol. 2021, 115, 103996. [Google Scholar] [CrossRef]
- Raghunathan, R.S.; Kim, H.D.; Setoguchi, T. Aerodynamics of high-speed railway train. Prog. Aerosp. Sci. 2002, 38, 469–514. [Google Scholar] [CrossRef]
- Han, J.; Kwon, S.-B.; Chun, C. Indoor environment and passengers’ comfort in subway stations in Seoul. Build. Environ. 2016, 104, 221–231. [Google Scholar] [CrossRef]
- Niu, J.; Sui, Y.; Yu, Q.; Cao, X.; Yuan, Y. Aerodynamics of railway train/tunnel system: A review of recent research. Energy Built Environ. 2020, 1, 351–375. [Google Scholar] [CrossRef]
- Baker, C.J. A review of train aerodynamics Part 1—Fundamentals. Aeronaut. J. 2014, 118, 201–228. [Google Scholar] [CrossRef]
- Baker, C.J. A review of train aerodynamics Part 2—Applications. Aeronaut. J. 2014, 118, 345–382. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, T.; Yu, M.; Chen, Z.; Li, W.; Huo, X.; Liu, H. Numerical study for the aerodynamic performance of double unit train under crosswind. J. Wind. Eng. Ind. Aerodyn. 2019, 191, 203–214. [Google Scholar] [CrossRef]
- Niu, J.; Zhou, D.; Liu, F.; Yuan, Y. Effect of train length on fluctuating aerodynamic pressure wave in tunnels and method for determining the amplitude of pressure wave on trains. Tunn. Undergr. Space Technol. 2018, 80, 277–289. [Google Scholar] [CrossRef]
- Niu, J.; Wang, Y.; Zhang, L.; Yuan, Y. Numerical analysis of aerodynamic characteristics of high-speed train with different train nose lengths. Int. J. Heat Mass Transf. 2018, 127, 188–199. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, M.-Z.; Liang, X.-F.; Zhang, J. Oblique tunnel portal effects on train and tunnel aerodynamics based on moving model tests. J. Wind. Eng. Ind. Aerodyn. 2017, 167, 128–139. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, H.; Stoll, N.; Thurow, K. Influence of tunnel aerodynamic effects by slope of equal-transect ring oblique tunnel portal. J. Wind. Eng. Ind. Aerodyn. 2017, 169, 106–116. [Google Scholar] [CrossRef]
- Wang, T.; Wu, F.; Yang, M.; Ji, P.; Qian, B. Reduction of pressure transients of high-speed train passing through a tunnel by cross-section increase. J. Wind. Eng. Ind. Aerodyn. 2018, 183, 235–242. [Google Scholar] [CrossRef]
- Li, W.; Liu, T.; Huo, X.; Chen, Z.; Guo, Z.; Li, L. Influence of the enlarged portal length on pressure waves in railway tunnels with cross-section expansion. J. Wind. Eng. Ind. Aerodyn. 2019, 190, 10–22. [Google Scholar] [CrossRef]
- Yang, W.; Deng, E.; Lei, M.; Zhang, P.; Yin, R. Flow structure and aerodynamic behavior evolution during train entering tunnel with entrance in crosswind. J. Wind. Eng. Ind. Aerodyn. 2018, 175, 229–243. [Google Scholar] [CrossRef]
- Wang, L.; Luo, J.; Li, F.; Guo, D.; Gao, L.; Wang, D. Aerodynamic performance and flow evolution of a high-speed train exiting a tunnel with crosswinds. J. Wind. Eng. Ind. Aerodyn. 2021, 218, 104786. [Google Scholar] [CrossRef]
- Wang, J.; Wang, T.; Yang, M.; Qian, B.; Wang, K. Effect of localized high temperature on the aerodynamic performance of a high-speed train passing through a tunnel. J. Wind. Eng. Ind. Aerodyn. 2020, 208, 104444. [Google Scholar] [CrossRef]
- Zhou, X.-S.; Liu, T.-H.; Chen, Z.-W.; Zou, X.; Liu, D.-R. Effect of ambient wind on pressure wave generated by high-speed train entering a tunnel. J. Cent. South Univ. 2017, 24, 1465–1475. [Google Scholar] [CrossRef]
- Liu, F.; Wang, F.; Han, J.; Zhao, S.; Weng, M. Effects of ambient pressure on aerodynamic pressures induced by passing metro trains in tunnels. Tunn. Undergr. Space Technol. 2022, 126, 104540. [Google Scholar] [CrossRef]
- Wang, F.; Weng, M.; Xiong, K.; Han, J.; Obadi, I.; Liu, F. Study on aerodynamic pressures caused by double-train tracking operation in a metro tunnel. Tunn. Undergr. Space Technol. 2022, 123, 104434. [Google Scholar] [CrossRef]
- Huang, S.; Che, Z.-X.; Li, Z.-W.; Jiang, Y.-N.; Wang, Z.-G. Influence of tunnel cross-sectional shape on surface pressure change induced by passing metro trains. Tunn. Undergr. Space Technol. 2020, 106, 103611. [Google Scholar] [CrossRef]
- Zeng, L.; Wang, H.; Li, L.; Guo, W.; Yi, F. Experimental study of train-induced pressure acting on the platform screen doors in subway station. Tunn. Undergr. Space Technol. 2021, 117, 104150. [Google Scholar] [CrossRef]
- Li, C.; Liu, M.; Chang, R.; Wang, X.; Liu, W.; Zhang, H. Air pressure and comfort study of the high-speed train passing through the subway station. Sustain. Cities Soc. 2022, 81, 103881. [Google Scholar] [CrossRef]
- Xiong, K.; Weng, M.; Liu, F. Theoretical study on the most unfavorable tunnel length (MUTL) based on the interior pressure variations of high-speed subway trains. Tunn. Undergr. Space Technol. 2024, 148, 105774. [Google Scholar] [CrossRef]
- Liu, L.; Jing, L.; Li, T.; Wang, K. Effects of high geotemperature and high altitude on the pressure wave of high-speed trains running in a long tunnel. J. Zhejiang Univ.-Sci. A 2024, 25, 953–969. [Google Scholar] [CrossRef]
- Deng, E.; Yang, W.; Lei, M.; Zhu, Z.; Zhang, P. Aerodynamic loads and traffic safety of high-speed trains when passing through two windproof facilities under crosswind: A comparative study. Eng. Struct. 2019, 188, 320–339. [Google Scholar] [CrossRef]
- Deng, E.; Yang, W.; He, X.; Ye, Y.; Zhu, Z.; Wang, A. Transient aerodynamic performance of high-speed trains when passing through an infrastructure consisting of tunnel–bridge–tunnel under crosswind. Tunn. Undergr. Space Technol. 2020, 102, 103440. [Google Scholar] [CrossRef]
- Liu, T.-H.; Jiang, Z.-H.; Li, W.-H.; Guo, Z.-J.; Chen, X.-D.; Chen, Z.-W.; Krajnovic, S. Differences in aerodynamic effects when trains with different marshalling forms and lengths enter a tunnel. Tunn. Undergr. Space Technol. 2019, 84, 70–81. [Google Scholar] [CrossRef]
- Niu, J.-Q.; Zhou, D.; Liang, X.-F.; Liu, S.; Liu, T.-H. Numerical simulation of the Reynolds number effect on the aerodynamic pressure in tunnels. J. Wind. Eng. Ind. Aerodyn. 2018, 173, 187–198. [Google Scholar] [CrossRef]
- Yang, W.; Deng, E.; Lei, M.; Zhu, Z.; Zhang, P. Transient aerodynamic performance of high-speed trains when passing through two windproof facilities under crosswinds: A comparative study. Eng. Struct. 2019, 188, 729–744. [Google Scholar] [CrossRef]
- GB50157-2013; Code for Design of Metro. China Architecture and Building Press: Beijing, China, 2013.
- Ji, J.; Wang, Z.; Ding, L.; Yu, L.; Gao, Z.; Wan, H. Effects of ambient pressure on smoke movement and temperature distribution in inclined tunnel fires. Int. J. Therm. Sci. 2019, 145, 106006. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, T.; Yang, M.; Qian, B. The influence of reduced cross-section on pressure transients from high-speed trains intersecting in a tunnel. J. Wind. Eng. Ind. Aerodyn. 2020, 201, 104161. [Google Scholar] [CrossRef]
- Rabani, M.; Faghih, A.K. Numerical analysis of airflow around a passenger train entering the tunnel. Tunn. Undergr. Space Technol. 2015, 45, 203–213. [Google Scholar] [CrossRef]
- Cross, D.; Hughes, B.; Ingham, D.; Ma, L. A validated numerical investigation of the effects of high blockage ratio and train and tunnel length upon underground railway aerodynamics. J. Wind. Eng. Ind. Aerodyn. 2015, 146, 195–206. [Google Scholar] [CrossRef]
- Iida, M.; Tanaka, Y.; Kikuchi, K.; Fukuda, T. Pressure Waves Radiated Directly from Tunnel Portals at Train Entry or Exit. Q. Rep. RTRI 2001, 42, 83–88. [Google Scholar] [CrossRef][Green Version]
- The International Union of Railways (UIC). Determination of Railway Tunnel Crosssectional Areas on the Basis of Aerodynamic Considerations; Code UIC 779-11; Railway Technical Publications: Paris, France, 2005. [Google Scholar][Green Version]
- Liu, T.; Chen, M.; Chen, X.; Geng, S.; Jiang, Z.; Krajnović, S. Field test measurement of the dynamic tightness performance of high-speed trains and study on its influencing factors. Measurement 2019, 138, 602–613. [Google Scholar] [CrossRef]
- Chen, X.; Liu, T.; Xia, Y.; Li, W.; Guo, Z.; Jiang, Z.; Li, M. The evolution of airtight performance for a high-speed train during its long-term service. Measurement 2021, 177, 109319. [Google Scholar] [CrossRef]
- CJJ/T298-2019; Standard for Design of Metro Express. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.





| Parameters | Solver Setting |
|---|---|
| Algorithm | Semi-Implicit Method for Pressure-Linked Equations |
| Turbulent model | RNG k-ε model |
| Convection terms | Second-order upwind scheme |
| Diffusion terms | Second-order upwind scheme |
| Gradient | Green-Gauss cell-based |
| Time discretization | Implicit scheme |
| Model Tunnel | Model Train | |||||
|---|---|---|---|---|---|---|
| Length (m) | Distance Between Track (m) | Cross-Sectional Area (m2) | Width (m) | Height (m) | Speed (km/h) | Cross-Sectional Area (m2) |
| 50 | 0.25 | 0.2487 | 0.163 | 0.207 | 350 | 0.03108 |
| Countries | Standards | Instructions |
|---|---|---|
| Japan | Suitable for enclosed carriages can be relaxed up to 300 Pa/s | |
| America | Suitable for the subway | |
| Britain | Suitable for 225 km/h non-enclosed carriages | |
| Germany | Higher than the original standard of 200 Pa/s | |
| China | When Suitable for the subway () | |
| China | Suitable for the metro express () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Chen, H.; Liu, T.; He, X.; Cheng, C.; Xu, L.; Zhao, S. Investigation of Aerodynamic Pressure Characteristics Inside and Outside a Metro Train Traversing a Tunnel in High-Altitude Regions. Modelling 2025, 6, 113. https://doi.org/10.3390/modelling6040113
Wang F, Chen H, Liu T, He X, Cheng C, Xu L, Zhao S. Investigation of Aerodynamic Pressure Characteristics Inside and Outside a Metro Train Traversing a Tunnel in High-Altitude Regions. Modelling. 2025; 6(4):113. https://doi.org/10.3390/modelling6040113
Chicago/Turabian StyleWang, Fei, Haisheng Chen, Tianji Liu, Xingsen He, Chunjie Cheng, Lin Xu, and Shengzhong Zhao. 2025. "Investigation of Aerodynamic Pressure Characteristics Inside and Outside a Metro Train Traversing a Tunnel in High-Altitude Regions" Modelling 6, no. 4: 113. https://doi.org/10.3390/modelling6040113
APA StyleWang, F., Chen, H., Liu, T., He, X., Cheng, C., Xu, L., & Zhao, S. (2025). Investigation of Aerodynamic Pressure Characteristics Inside and Outside a Metro Train Traversing a Tunnel in High-Altitude Regions. Modelling, 6(4), 113. https://doi.org/10.3390/modelling6040113








