Dimensionless Modelling of Bond-Based Peridynamic Models and Strategies for Enhancing Numerical Accuracy
Abstract
1. Introduction
2. Dimensionless Bond-Based PD Model
2.1. Bond-Based PD Model [4]
2.2. Reference Variables
2.3. Dimensionless Model
2.4. Numerical Scheme
3. Error Sources and Numerical Strategies
3.1. Error Sources
3.2. Numerical Strategies
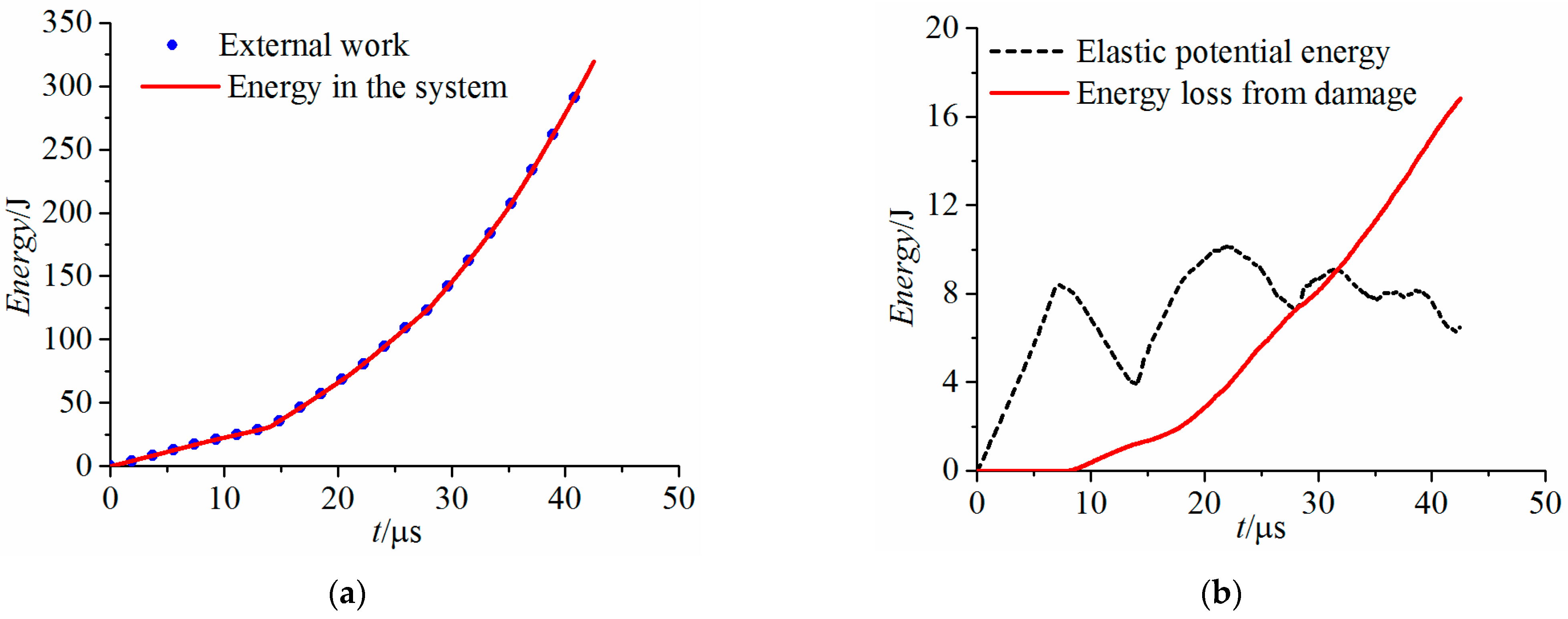
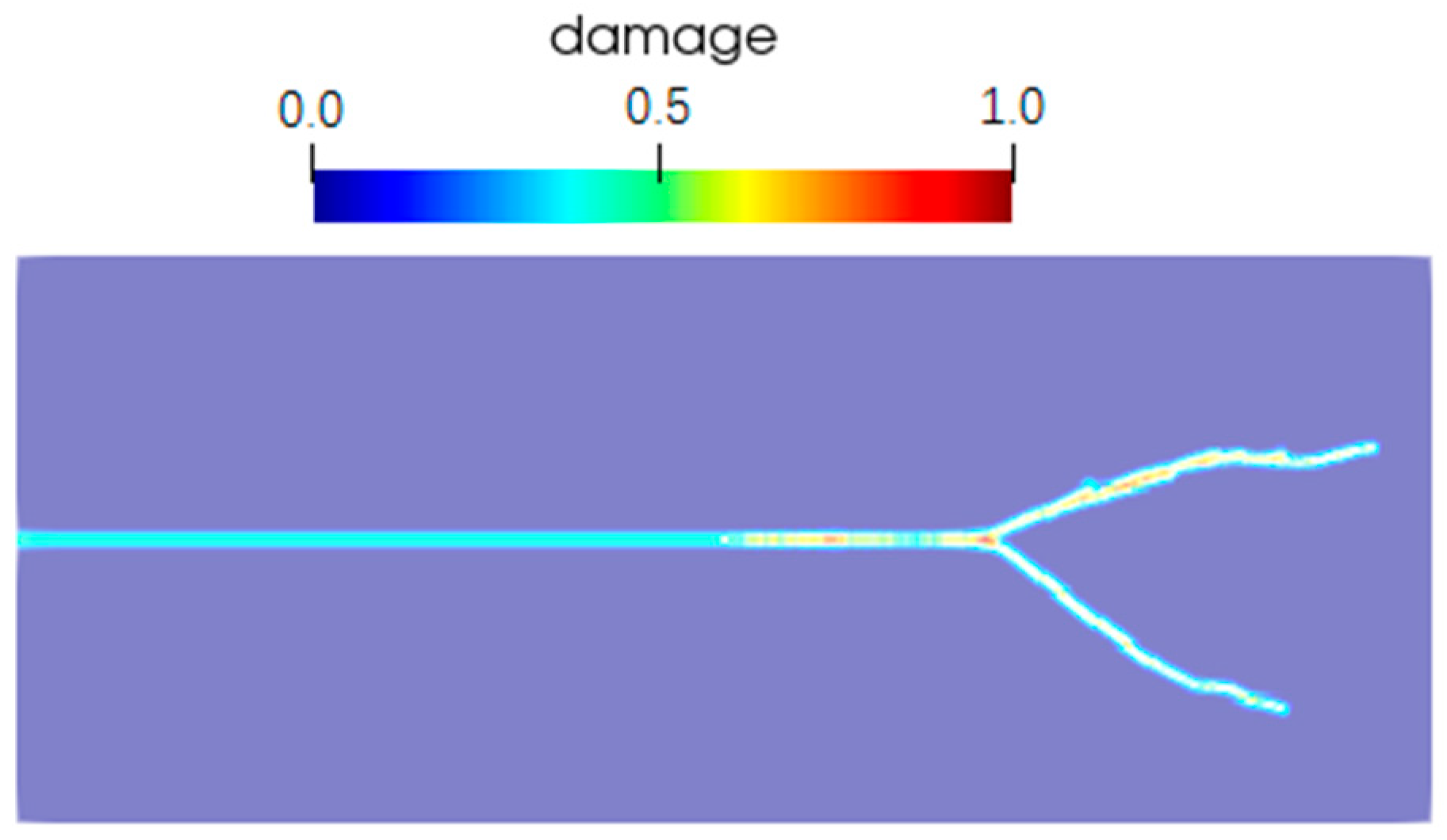
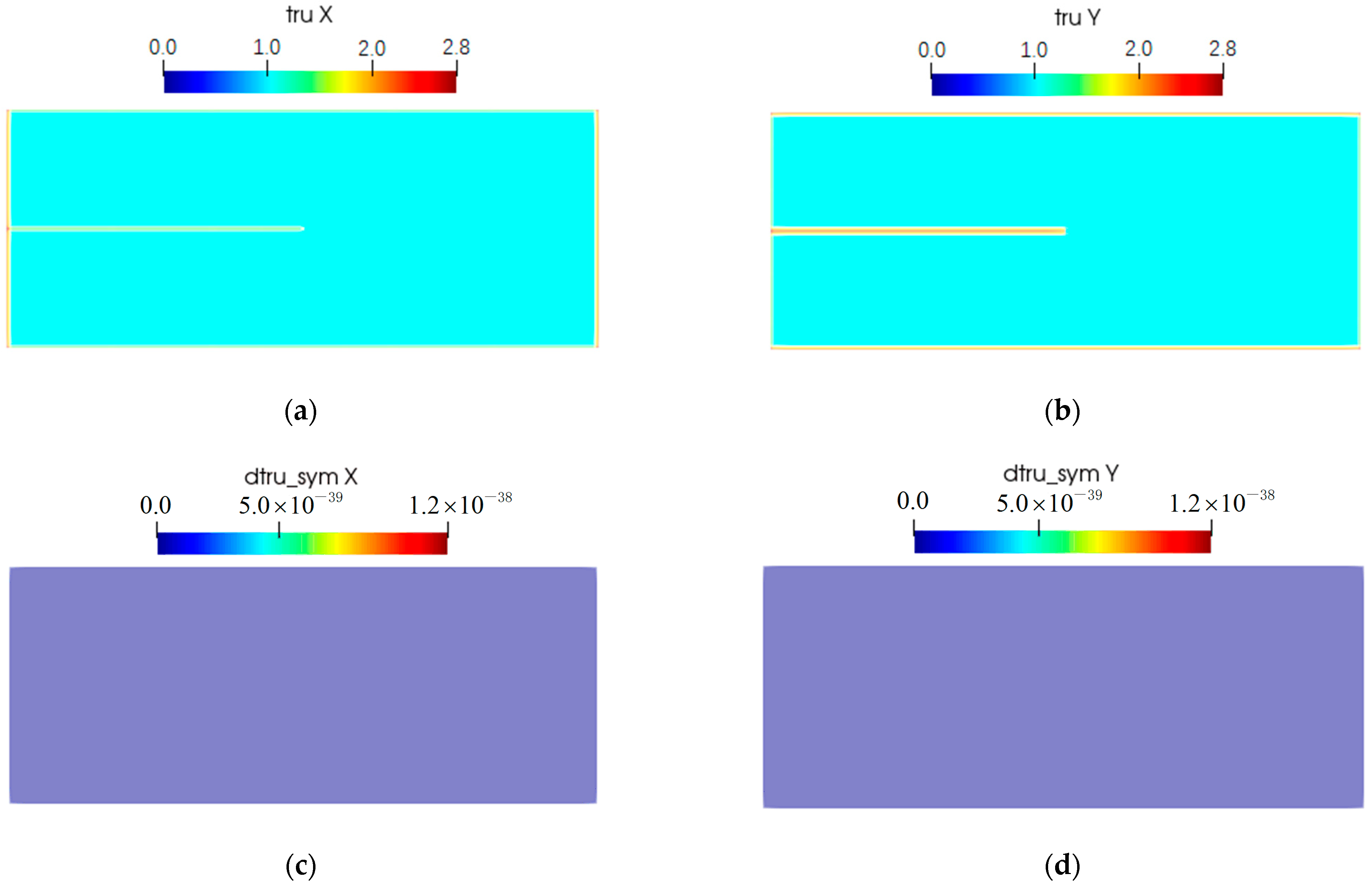
4. Results and Discussions
4.1. Results
4.2. Discussions
5. Conclusions
- (1)
- The dimensionless modelling of the bond-based PD model is correct. This modelling reduces the magnitude discrepancy between the micro-modulus and bond stretches, thereby suppressing the propagation of rounding errors in bond stretches.
- (2)
- The strategy of sorting neighborhood members by their distance to the central material point, combined with the strategy of calculating the surface-correction factors locally within the horizon, can significantly improve the accuracy of numerical results.
- (3)
- Utilizing the double-precision format for storing real variables, combined with the dimensionless bond-based PD model and the numerical processing strategies, the propagation of computational errors can be effectively suppressed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, J.-H.; Wang, H.; Belytschko, T. A Comparative Study on Finite Element Methods for Dynamic Fracture. Comput. Mech. 2008, 42, 239–250. [Google Scholar] [CrossRef]
- Xie, G.; Li, J.; Li, H.; Wang, L.; Li, X.; Geng, H. Crack Growth Evaluation Based on the Extended Finite Element and Particle Filter Combined Method. Eng. Anal. Bound. Elem. 2024, 169, 106004. [Google Scholar] [CrossRef]
- Bui, H.H.; Fukagawa, R.; Sako, K.; Ohno, S. Lagrangian Meshfree Particles Method (SPH) for Large Deformation and Failure Flows of Geomaterial Using Elastic-Plastic Soil Constitutive Model. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1537–1570. [Google Scholar] [CrossRef]
- Fan, S.; Guilin, W.; Liang, Z.; Runqiu, W.; Tianci, C.; Xiaotian, O. Material Point Method for the Propagation of Multiple Branched Cracks Based on Classical Fracture Mechanics. Comput. Methods Appl. Mech. Eng. 2021, 386, 114116. [Google Scholar] [CrossRef]
- Zhao, Y.; Xin, T.; Tang, S.; Wang, H.; Fang, X.; Hou, H. Applications of Unified Phase-Field Methods to Designing Microstructures and Mechanical Properties of Alloys. MRS Bull. 2024, 49, 613–625. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of Elasticity Theory for Discontinuities and Long-Range Forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A Meshfree Method Based on the Peridynamic Model of Solid Mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Wu, T.; Xue, T.; Wang, Y. Non-Fourier Thermoelastic Peridynamic Modelling of Cracked Thin Films Under Short-Pulse Laser Irradiation. Modelling 2025, 6, 68. [Google Scholar] [CrossRef]
- Le, Q.V.; Bobaru, F. Surface Corrections for Peridynamic Models in Elasticity and Fracture. Comput. Mech. 2018, 61, 499–518. [Google Scholar] [CrossRef]
- Jha, P.K.; Lipton, R. Numerical Convergence of Nonlinear Nonlocal Continuum Models to Local Elastodynamics. Int. J. Numer. Methods Eng. 2018, 114, 1389–1410. [Google Scholar] [CrossRef]
- Wu, X.; Chen, W. Error Estimates of the Finite Element Method for Interior Transmission Problems. J. Sci. Comput. 2013, 57, 331–348. [Google Scholar] [CrossRef]
- Lukacova-Medvid’ova, M.; Mizerova, H.; She, B.; Stebel, J. Error Analysis of Finite Element and Finite Volume Methods for Some Viscoelastic Fluids. J. Numer. Math. 2016, 24, 105–123. [Google Scholar] [CrossRef]
- Ohlberger, M.; Vovelle, J. Error Estimate for the Approximation of Nonlinear Conservation Laws on Bounded Domains by the Finite Volume Method. Math. Comput. 2006, 75, 113–150. [Google Scholar] [CrossRef]
- Palasis, A.; Liakopoulos, A.; Sofiadis, G. From Direct Numerical Simulations to Data-Driven Models: Insights into Mean Velocity Profiles and Turbulent Stresses in Channel Flows. Modelling 2025, 6, 18. [Google Scholar] [CrossRef]
- Violeau, D.; Fonty, T. Calculating the Smoothing Error in SPH. Comput. Fluids 2019, 191, 104240. [Google Scholar] [CrossRef]
- Steffen, M.; Kirby, R.M.; Berzins, M. Decoupling and Balancing of Space and Time Errors in the Material Point Method (MPM). Int. J. Numer. Methods Eng. 2010, 82, 1207–1243. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Rabczuk, T. Dual-Horizon Peridynamics: A Stable Solution to Varying Horizons. Comput. Methods Appl. Mech. Eng. 2017, 318, 762–782. [Google Scholar] [CrossRef]
- Moschou, S.P.; Hicks, E.; Parekh, R.Y.; Mathew, D.; Majumdar, S.; Vlahakis, N. Physics-Informed Neural Networks for Modelling Astrophysical Shocks. Mach. Learn. Technol. 2023, 4, 035032. [Google Scholar] [CrossRef]
- Luo, Y. Adaptive Nearest-Nodes Finite Element Method Guided by Gradient of Linear Strain Energy Density. Finite Elem. Anal. Des. 2009, 45, 925–933. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Xia, X. Voronoi-Based Peridynamics and Cracking Analysis with Adaptive Refinement. Int. J. Numer. Methods Eng. 2017, 112, 2087–2109. [Google Scholar] [CrossRef]
- Song, Y.; Yan, J.; Li, S.; Kang, Z. Peridynamic Modelling and Simulation of Ice Craters By Impact. Comput. Model. Eng. Sci. 2019, 121, 465–492. [Google Scholar] [CrossRef]
- Allahyari, M.; Yousefi, K.; Esfahanian, V.; Darzi, M. A Block-Interface Approach for High-Order Finite- Difference Simulations of Compressible Flows. J. Appl. Fluid Mech. 2021, 14, 345–359. [Google Scholar] [CrossRef]
- Daux, C.; Moës, N.; Dolbow, J.; Sukumar, N.; Belytschko, T. Arbitrary Branched and Intersecting Cracks with the Extended Finite Element Method. Int. J. Numer. Methods Eng. 2000, 48, 1741–1760. [Google Scholar] [CrossRef]
- Bautista, V.; Shahbazian, B.; Mirsayar, M. A Modified Mixed-Mode Timoshenko-Based Peridynamics Model Considering Shear Deformation. Int. J. Mech. Sci. 2025, 285, 109802. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, X. A Bond-Augmented Stabilized Method for Numerical Oscillations in Non-Ordinary State-Based Peridynamics. Eng. Fract. Mech. 2024, 307, 110276. [Google Scholar] [CrossRef]
- Wildman, R.A.; O’Grady, J.T.; Gazonas, G.A. A Hybrid Multiscale Finite Element/Peridynamics Method. Int. J. Fract. 2017, 207, 41–53. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Characteristics of Dynamic Brittle Fracture Captured with Peridynamics. Eng. Fract. Mech. 2011, 78, 1156–1168. [Google Scholar] [CrossRef]
- Liu, W.; Hong, J.-W. Discretized Peridynamics for Linear Elastic Solids. Comput. Mech. 2012, 50, 579–590. [Google Scholar] [CrossRef]
- Liu, Z.-G.; Du, S.-Y.; Yang, Y.; Ji, X.-H. A Fast Algorithm for Color Space Conversion and Rounding Error Analysis Based on Fixed-Point Digital Signal Processors. Comput. Electr. Eng. 2014, 40, 1405–1414. [Google Scholar] [CrossRef]
- Du, E.-B.; Zhou, X.-P. Non-Uniform Discretization Bond-Based Peridynamics with Constant Horizon and a Novel Volume Correction for the Cracking Behaviors. Comput. Struct. 2024, 300, 107408. [Google Scholar] [CrossRef]
- Shi, Y.; Niu, J.; Cai, M.; Xu, W. Dimensionless Study on Dynamics of Pressure Controlled Mechanical Ventilation System. J. Mech. Sci. Technol. 2015, 29, 431–439. [Google Scholar] [CrossRef]
- Huang, R.; Wu, H. A Modified Multiple-Relaxation-Time Lattice Boltzmann Model for Convection-Diffusion Equation. J. Comput. Phys. 2014, 274, 50–63. [Google Scholar] [CrossRef]
- Mandel, R.; Shooshtari, A.; Ohadi, M. A “2.5-D” Modelling Approach for Single-Phase Flow and Heat Transfer in Manifold Microchannels. Int. J. Heat Mass Transf. 2018, 126, 317–330. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, Z.-W.; Xu, X.-H.; Li, Q. A New Model of Overall Heat Transfer Coefficient of Hot Wax Oil Pipeline Based on Dimensionless Experimental Analysis. Case Stud. Therm. Eng. 2020, 20, 100647. [Google Scholar] [CrossRef]
- Laporte-Azcue, M.; Acosta-Iborra, A.; Otanicar, T.P.; Santana, D. Real-Time Estimation of the Transient Thermomechanical Behaviour of Solar Central Receivers. Therm. Sci. Eng. Prog. 2023, 41, 101834. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X. A Moving Finite Element Method for Solving Two-Dimensional Coupled Burgers’ Equations at High Reynolds Numbers. Appl. Math. Lett. 2022, 133, 108271. [Google Scholar] [CrossRef]
- Protsenko, V.S.; Danilov, F.I. Application of Dimensional Analysis and Similarity Theory for Simulation of Electrode Kinetics Described by the Marcus-Hush-Chidsey Formalism. J. Electroanal. Chem. 2012, 669, 50–54. [Google Scholar] [CrossRef]
- Zhou, H.; Han, Y.; Zhang, Y.; Luo, W.; Liu, J.; Yu, R. Numerical and Experimental Research on Similarity Law of the Dynamic Responses of the Offshore Stiffened Plate Subjected to Low Velocity Impact Loading. Metals 2022, 12, 657. [Google Scholar] [CrossRef]
- IEEE Computer Society. IEEE Standard for Floating-Point Arithmetic 2019; The Institute of Electrical and Electronics Engineers: New York, NY, USA, 2019. [Google Scholar]
- Xie, K.; Lu, Q.; Jiang, H.; Wang, H. Accurate Sum and Dot Product with New Instruction for High-Precision Computing on ARMv8 Processor. Mathematics 2025, 13, 270. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014; ISBN 9781461484653. [Google Scholar]
- Tong, Q.; Li, S. Multiscale Coupling of Molecular Dynamics and Peridynamics. J. Mech. Phys. Solids 2016, 95, 169–187. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Studies of Dynamic Crack Propagation and Crack Branching with Peridynamics. Int. J. Fract. 2010, 162, 229–244. [Google Scholar] [CrossRef]
- Bie, Y.H.; Liu, Z.M.; Yang, H.; Cui, X.Y. Abaqus Implementation of Dual Peridynamics for Brittle Fracture. Comput. Methods Appl. Mech. Eng. 2020, 372, 113398. [Google Scholar] [CrossRef]


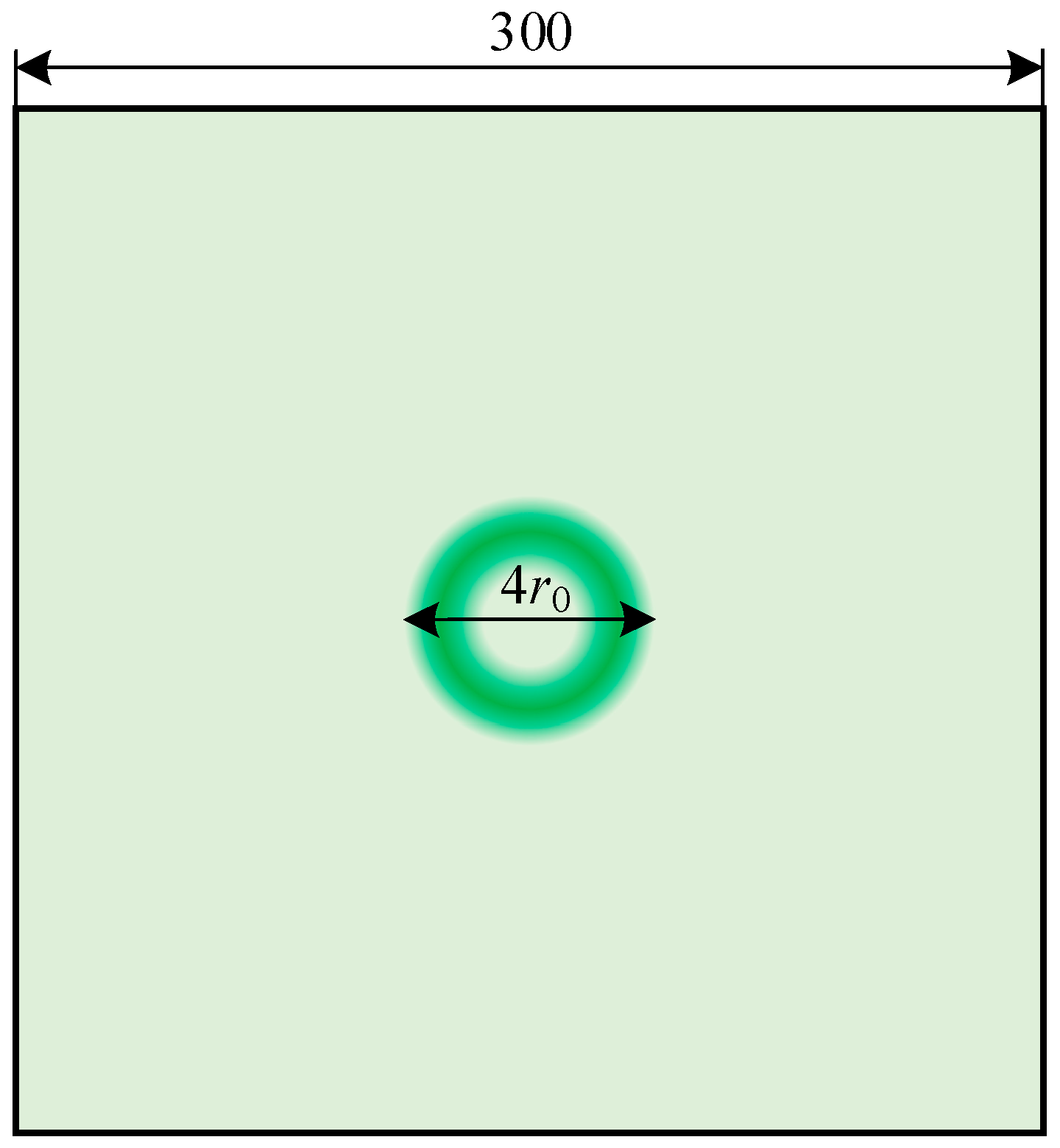
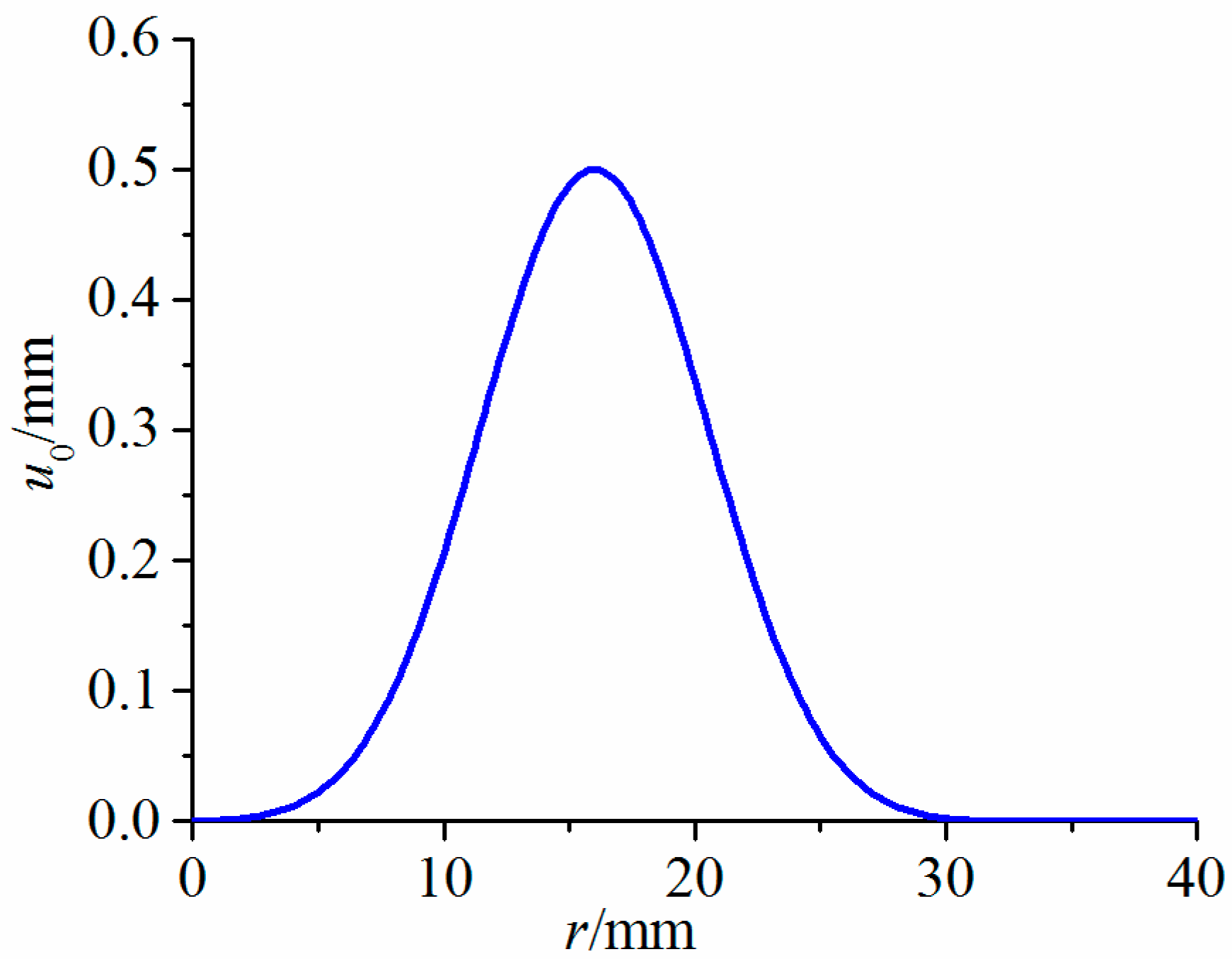

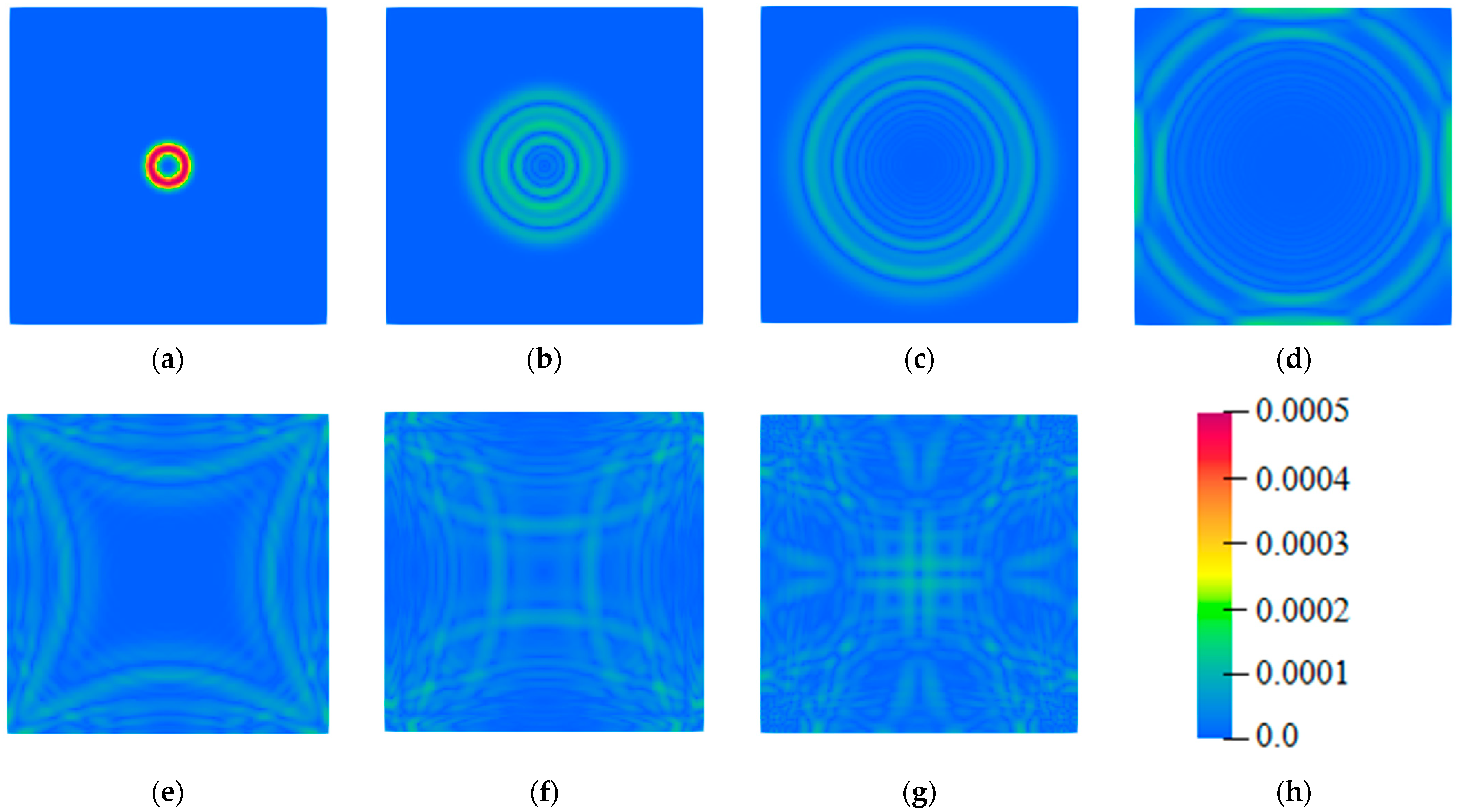


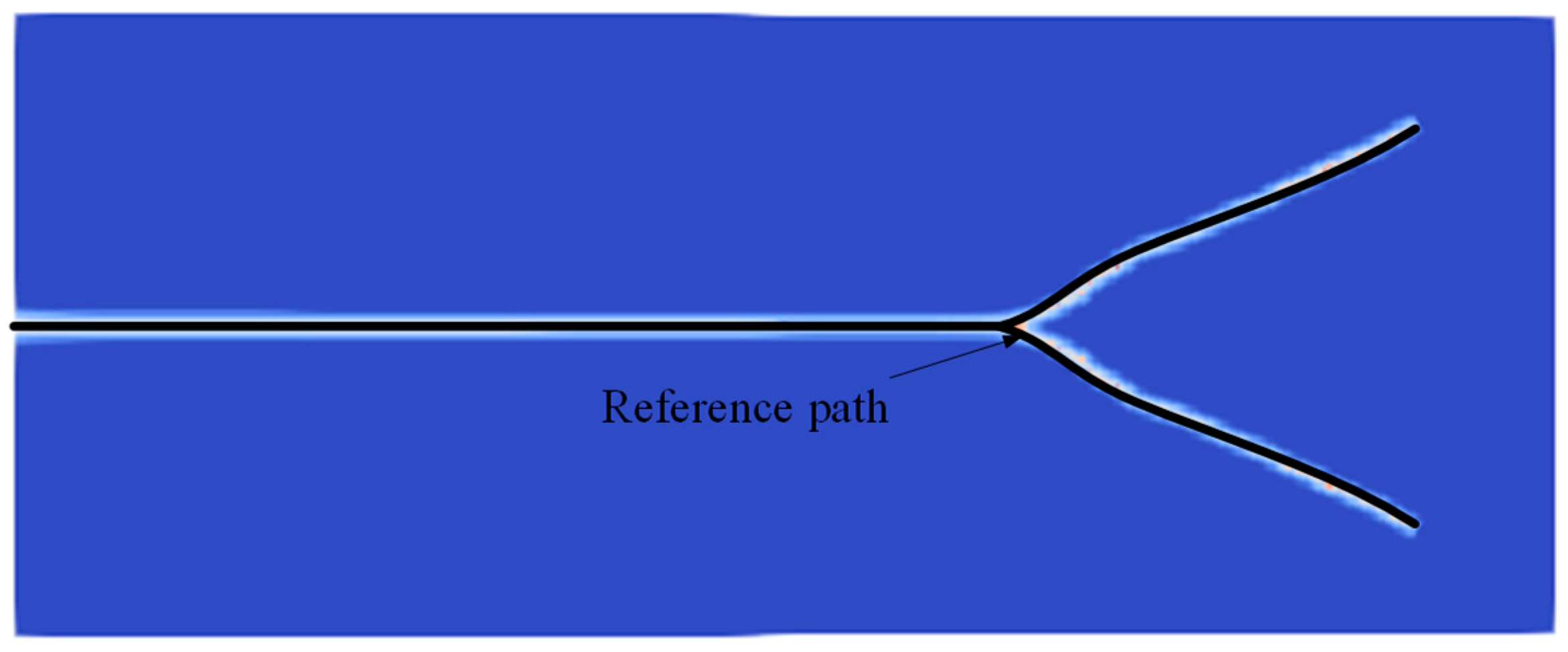



| Density/(kg/m3) | Young’s Modulus/(GPa) | Poisson’s Ratio |
|---|---|---|
| 2700.0 | 68.9 | 1/3 |
| Young’s Modulus/GPa | Density/kg∙m−3 | Poisson’s Ratio | Fracture Energy/J | Length/m | Width/m | Crack Length/m |
|---|---|---|---|---|---|---|
| 65 | 2235 | 0.2 | 204 | 0.1 | 0.04 | 0.05 |
| Case No. | Strategies | Model |
|---|---|---|
| 1 | Both S12 and S3 | Dimensionless PD |
| 2 | Both S12 and S3 | Original PD |
| 3 | Only S12 | Dimensionless PD |
| Young’s Modulus/GPa | Density/kg∙m−3 | Poisson’s Ratio | Fracture Energy/J |
|---|---|---|---|
| 72 | 2440 | 0.22 | 135 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Chen, X. Dimensionless Modelling of Bond-Based Peridynamic Models and Strategies for Enhancing Numerical Accuracy. Modelling 2025, 6, 99. https://doi.org/10.3390/modelling6030099
Hu C, Chen X. Dimensionless Modelling of Bond-Based Peridynamic Models and Strategies for Enhancing Numerical Accuracy. Modelling. 2025; 6(3):99. https://doi.org/10.3390/modelling6030099
Chicago/Turabian StyleHu, Chaobin, and Xiaomiao Chen. 2025. "Dimensionless Modelling of Bond-Based Peridynamic Models and Strategies for Enhancing Numerical Accuracy" Modelling 6, no. 3: 99. https://doi.org/10.3390/modelling6030099
APA StyleHu, C., & Chen, X. (2025). Dimensionless Modelling of Bond-Based Peridynamic Models and Strategies for Enhancing Numerical Accuracy. Modelling, 6(3), 99. https://doi.org/10.3390/modelling6030099






