Joint Estimation of SOC and SOH Based on Kalman Filter Under Multi-Time Scale
Abstract
1. Introduction
2. Methods
2.1. Lithium-Ion Battery Testing
2.1.1. Static Capacity Test
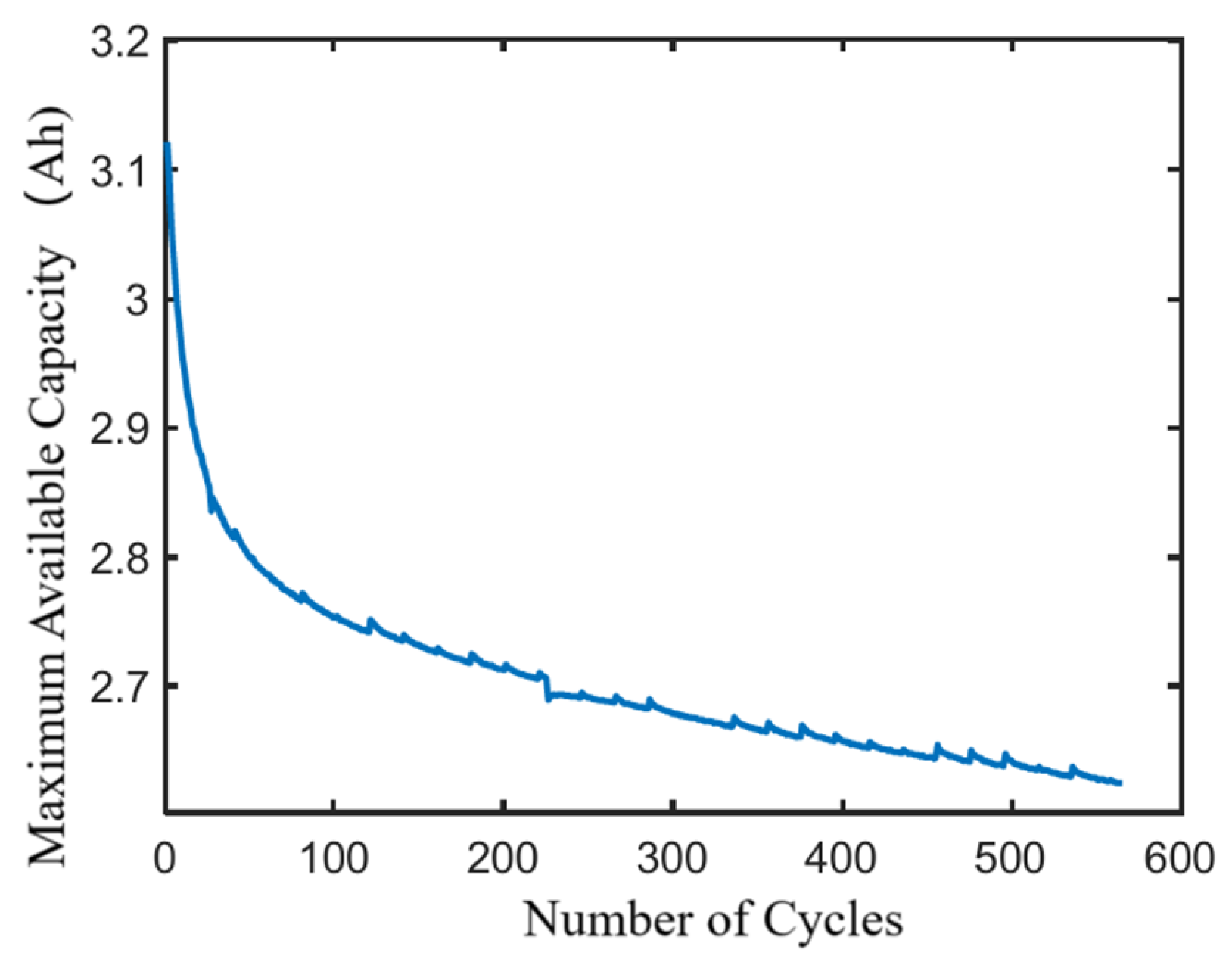
2.1.2. Battery Aging Cycle Test
2.1.3. Hybrid Pulse Power Characteristic (HPPC) Test
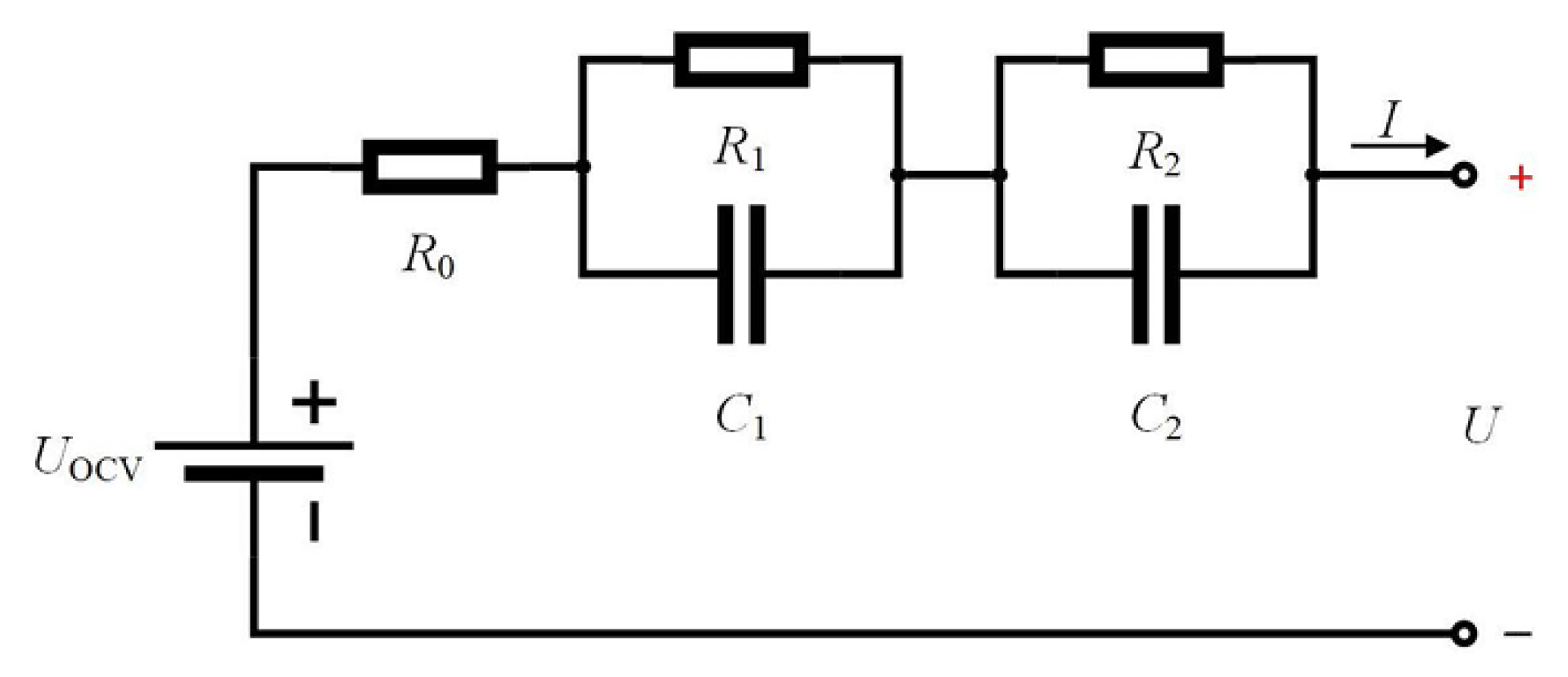
2.2. Mathematical Model of Lithium-Ion Batteries
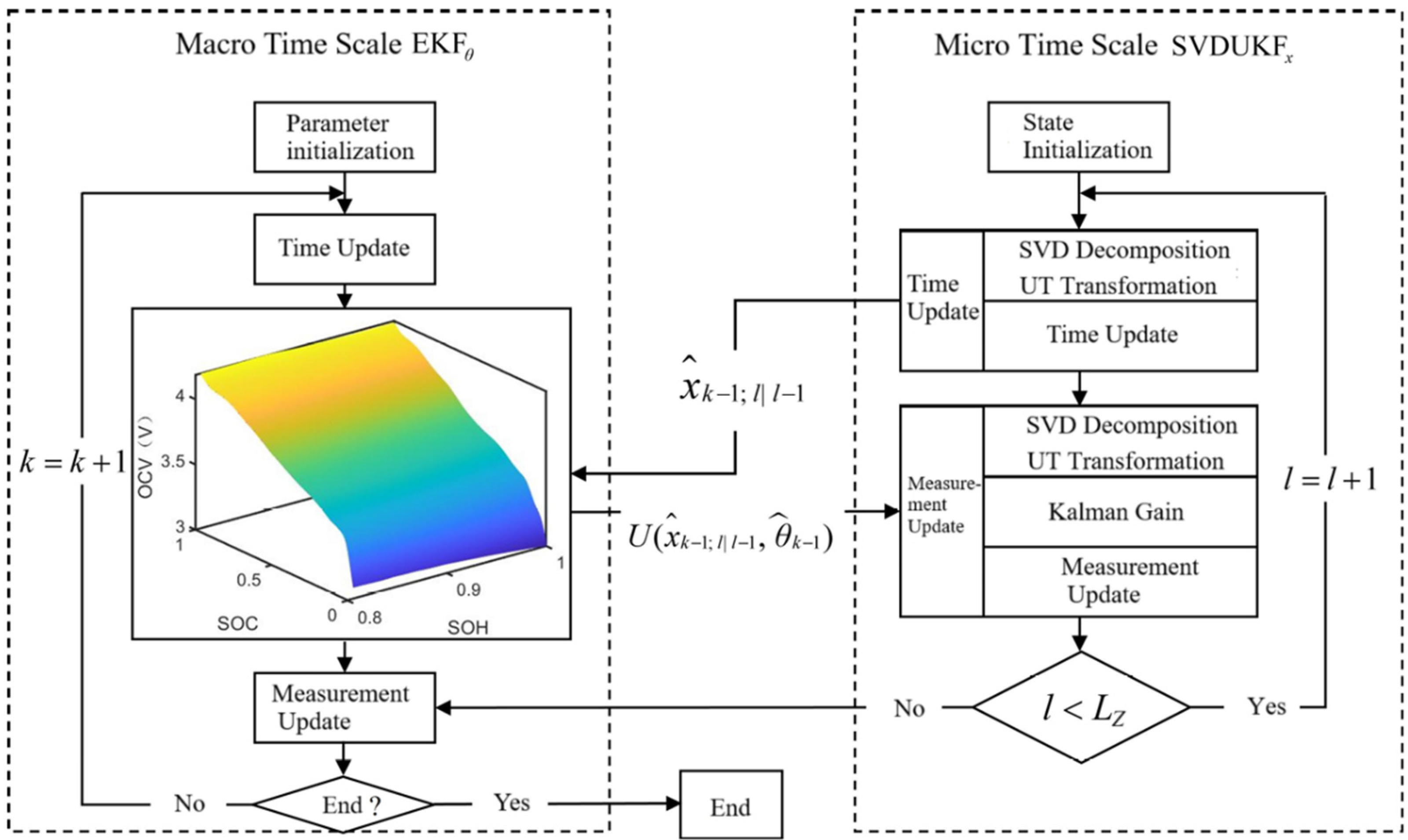
2.3. SVDUKF-EKF Joint Estimation Algorithm
- (1)
- Initialize the states, parameters, and their corresponding error covariances:
- (2)
- At the macro-time scale, perform the one-step prediction for the parameters and their error covariance matrix using the EKF algorithm:
- (3)
- At the micro-time scale, perform the one-step prediction for the state and its error covariance matrix using the SVD-UKF algorithm:
- (a)
- Perform UT transformation using SVD decomposition to construct (2n + 1) Sigma points:In the equation, n is the dimension of the state quantity, and λ is the scaling factor.
- (b)
- Calculate the mean and covariance of the one-step prediction of the state variables:
- (4)
- Measurement update of the SVD-UKF algorithm under the micro-time scale:
- (a)
- Perform UT transformation again on the predicted mean and covariance using SVD decomposition to generate new (2n + 1) Sigma points:
- (b)
- Calculate the mean of the observation variables based on the (2n + 1) Sigma points obtained in step (a), and update the variance matrix:
- (c)
- Calculate the Kalman gain, and update the system state and error covariance:
- (d)
- Repeat steps (a)–(c) in (4) until , then exit the micro-time scale state estimation and set:
- (5)
- Measurement update of the EKF algorithm parameters and their error covariances under the macro-time scale:
- (6)
- Set , then continue the iteration starting from step (2) until completion.
3. Results
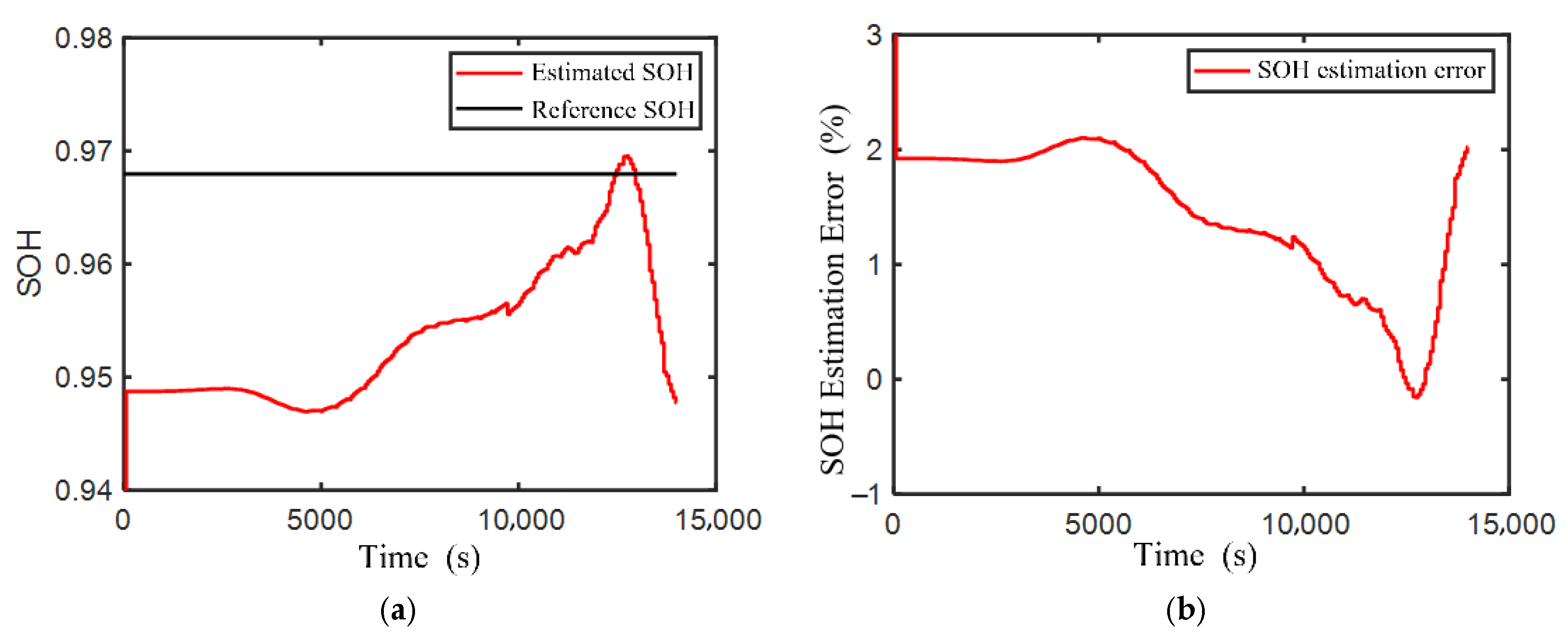
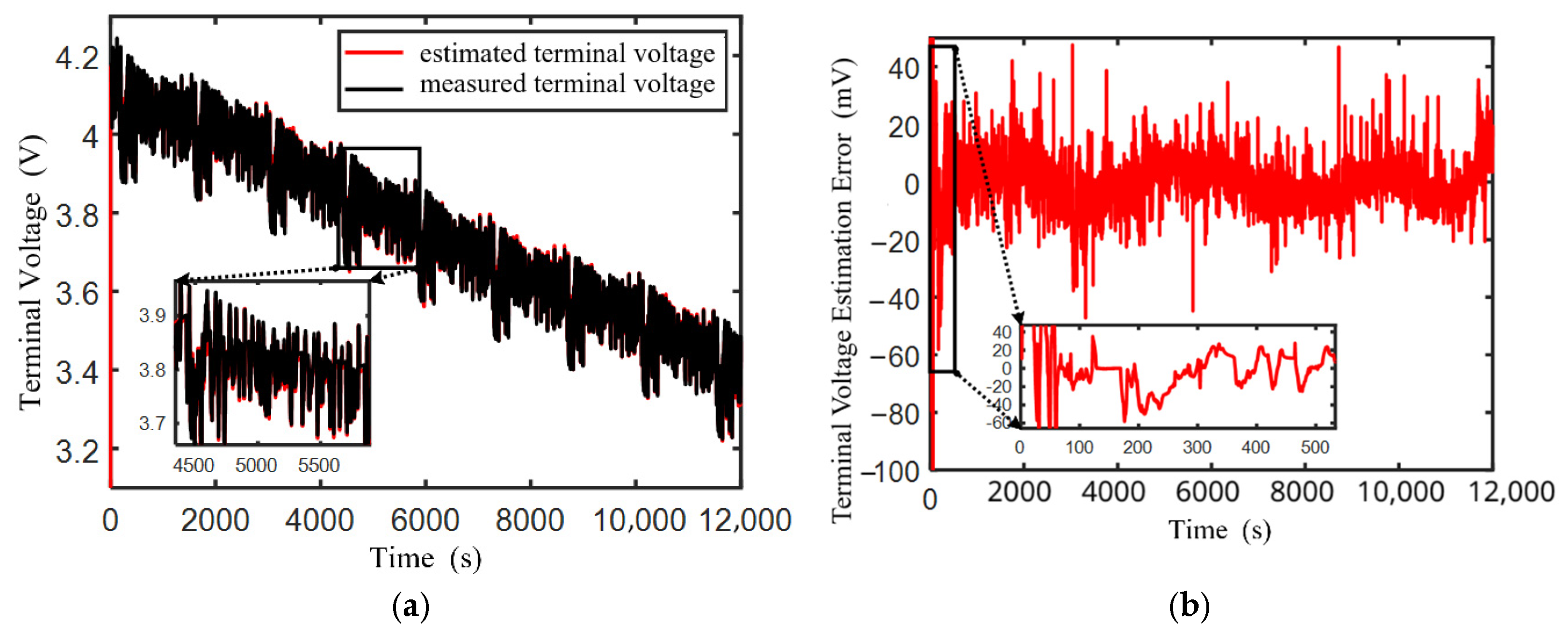
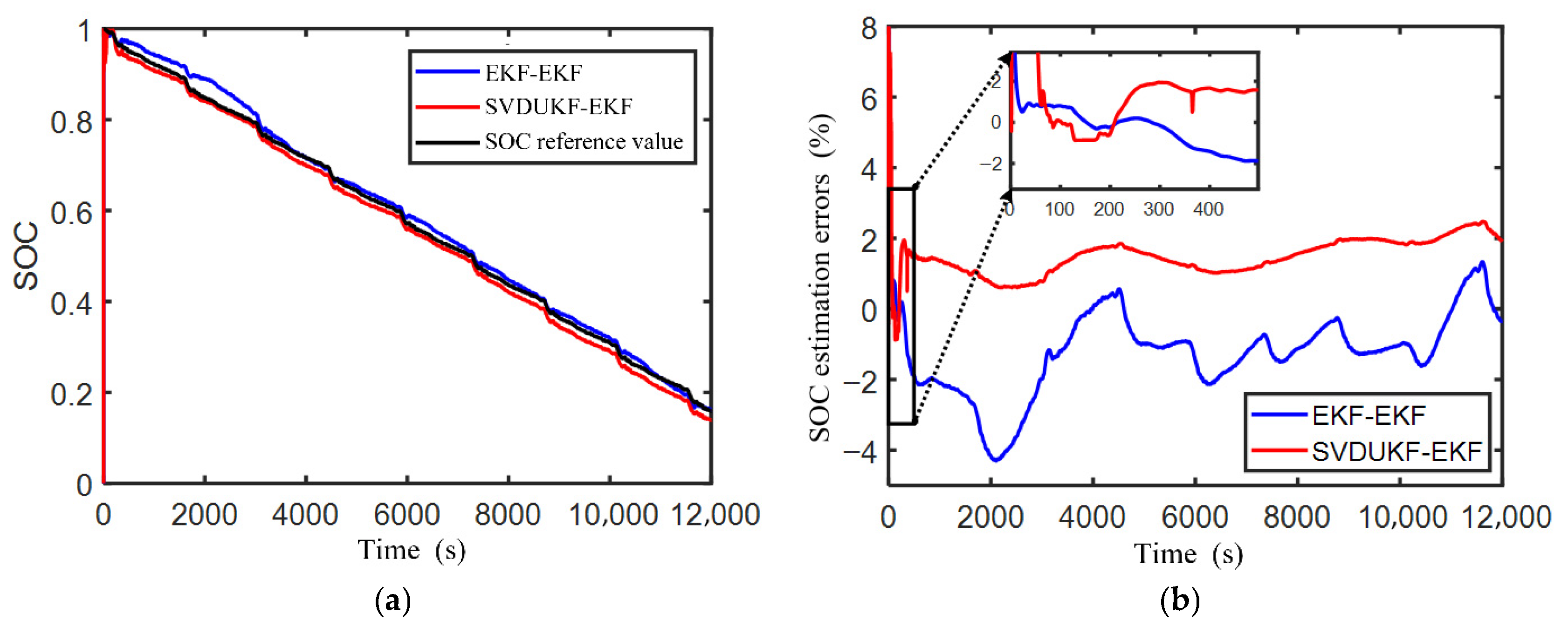
3.1. DST Operating Condition Verification
3.2. Validation Under FUDS Operating Condition
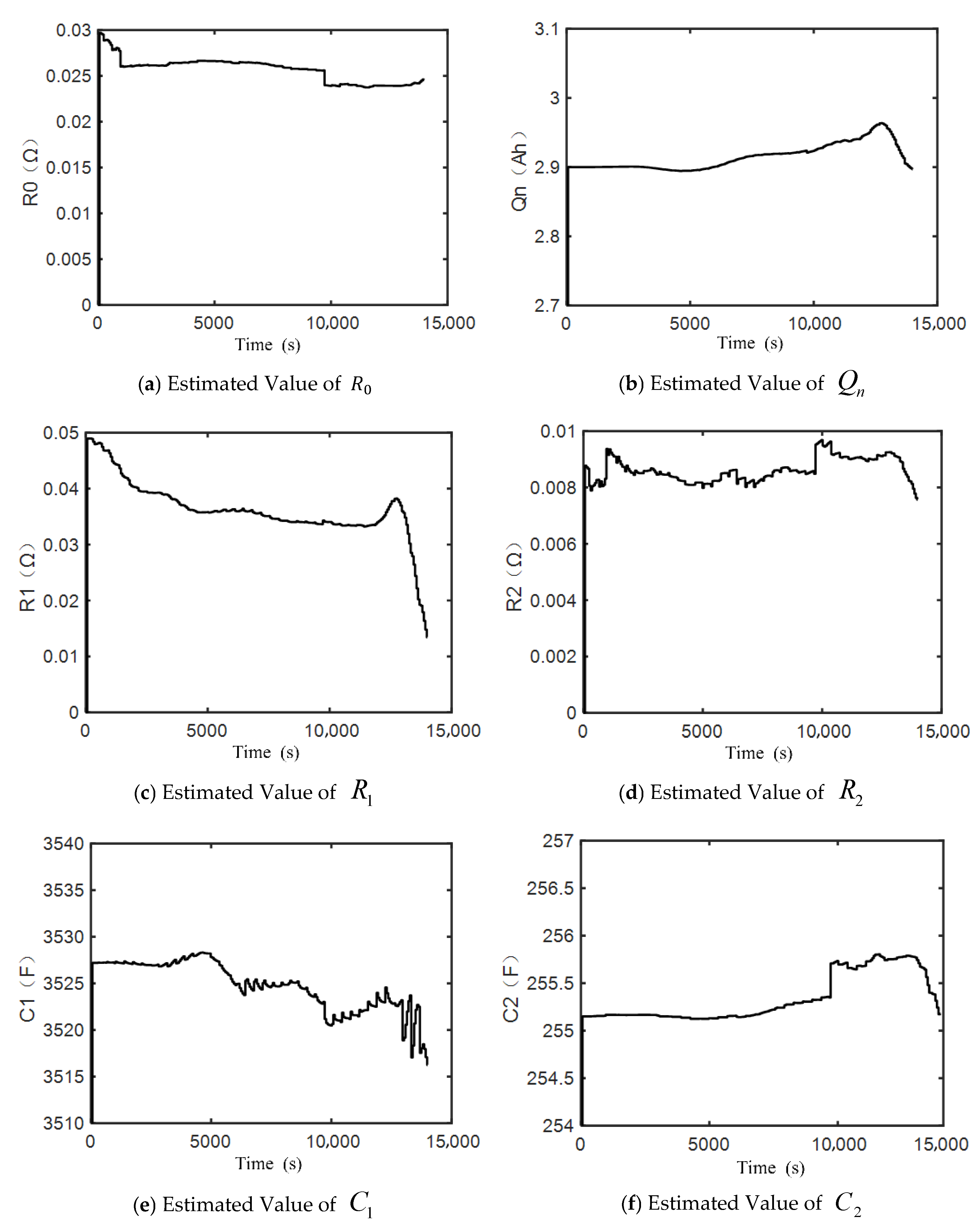
3.3. Robustness Verification
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, N.; Wu, Q.; Hu, X. Research on the Policy Evolution of China’s New Energy Vehicles Industry. Sustainability 2020, 12, 3629. [Google Scholar] [CrossRef]
- Zhao, X.; Li, M.; Yu, Q.; Ma, J.; Wang, S. State Estimation of Power Lithium Batteries for Electric Vehicles: A Review. China J. Highw. Transp. 2023, 36, 254–283. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, S. Research on aging mechanism and state of health prediction in lithium batteries. J. Energy Storage 2023, 72, 108274. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef]
- He, J.; Wan, K.; Lu, L.; Yu, M. An Online OCV Calibration-Based Adaptive SOC Estimation Approach for Lithium Battery. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P. A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Rodrigues, S.; Munichandraiah, N.; Shukla, A.K. A review of state-of-charge indication of batteries by means of a.c. impedance measurements. J. Power Sources 2000, 87, 12–20. [Google Scholar] [CrossRef]
- Chen, D.; Gao, W.; Zhang, C.; Chen, L. SOC estimation of lithium battery based on double modified ampere-hour integral method. In Proceedings of the 2022 37th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Beijing, China, 19–20 November 2022. [Google Scholar] [CrossRef]
- Gao, Y.; Plett, G.L.; Fan, G.; Zhang, X. Enhanced state-of-charge estimation of LiFePO4 batteries using an augmented physics-based model. J. Power Sources 2022, 544, 231889. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, B.; Zhang, W.; He, X.; Ma, S.; Zhang, J.; Liu, X. Error theory study on EKF-based SOC and effective error estimation strategy for Li-ion batteries. Appl. Energy 2024, 353, 121992. [Google Scholar] [CrossRef]
- Hong, S.; Qin, C.; Dai, H.; Lai, X. SOC estimation of lithium-ion batteries based on the condition of vessels. In Proceedings of the 2022 5th International Conference on Data Science and Information Technology (DSIT), Shanghai, China, 22–24 July 2022. [Google Scholar] [CrossRef]
- Yan, W.; Zhang, B.; Zhao, G.; Tang, S.; Niu, G.; Wang, X. A Battery Management System with a Lebesgue-Sampling-Based Extended Kalman Filter. IEEE Trans. Ind. Electron. 2019, 66, 3227–3236. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Ye, M.; Guo, H.; Xiong, R.; Yu, Q. A double-scale and adaptive particle filter-based online parameter and state of charge estimation method for lithium-ion batteries. Energy 2018, 144, 789–799. [Google Scholar] [CrossRef]
- Kim, T.; Wang, Y.; Sahinoglu, Z.; Wada, T.; Hara, S.; Qiao, W. State of Charge Estimation Based on a Real-time Battery Model and Iterative Smooth Variable Structure Filter. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Kuala Lumpur, Malaysia, 20–23 May 2014. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-Ion Battery Parameters and State-of-Charge Joint Estimation Based on H-Infinity and Unscented Kalman Filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Du, J.; Liu, Z.; Wang, Y.; Wen, C. An adaptive sliding mode observer for lithium-ion battery state of charge and state of health estimation in electric vehicles. Control Eng. Pract. 2016, 54, 81–90. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Ayob, A.; Saad, M.H.; Karim, T.F.; How, D.N. Data-driven state of charge estimation of lithium-ion batteries: Algorithms, implementation factors, limitations and future trends. J. Clean. Prod. 2020, 277, 124110. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, R.; Zheng, Y.; Zhang, L.; Guang, H.; Liu, X.; Gao, X.; Yang, S. Online state of health estimation for lithium-ion batteries based on gene expression programming. Energy 2024, 294, 130790. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine Learning Applied to Electrified Vehicle Battery State of Charge and State of Health Estimation: State-of-the-Art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Wittman, R.M.; Fresquez, A.; Chalamala, B.; Preger, Y. Update on Systematic Cycle and Calendar Aging of NMC and NCA 18650 Li-Ion Batteries. ECS Meet. Abstr. 2022, MA2022-02, 228. [Google Scholar] [CrossRef]
- He, J.; Meng, S.; Li, X.; Yan, F. Partial Charging-Based Health Feature Extraction and State of Health Estimation of Lithium-Ion Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 166–174. [Google Scholar] [CrossRef]
- Sun, R.; Chen, J.; Li, B.; Piao, C. State of health estimation for Lithium-ion batteries based on novel feature extraction and BiGRU-Attention model. Energy 2025, 319, 134756. [Google Scholar] [CrossRef]
- Deng, Y.; Ying, H.; E, J.; Zhu, H.; Wei, K.; Chen, J.; Zhang, F.; Liao, G. Feature parameter extraction and intelligent estimation of the State-of-Health of lithium-ion batteries. Energy 2019, 176, 91–102. [Google Scholar] [CrossRef]
- Zhang, S.; Zhai, B.; Guo, X.; Wang, K.; Peng, N.; Zhang, X. Synchronous estimation of state of health and remaining useful lifetime for lithium-ion battery using the incremental capacity and artificial neural networks. J. Energy Storage 2019, 26, 100951. [Google Scholar] [CrossRef]
- Fahmy, H.M.; Hasanien, H.M.; Alsaleh, I.; Ji, H.; Alassaf, A. State of health estimation of lithium-ion battery using dual adaptive unscented Kalman filter and Coulomb counting approach. J. Energy Storage 2024, 88, 111557. [Google Scholar] [CrossRef]
- Zheng, X.; Deng, X. State-of-Health Prediction For Lithium-Ion Batteries with Multiple Gaussian Process Regression Model. IEEE Access 2019, 7, 150383–150394. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Xia, Y.; Chen, W. A deep learning approach to estimate the state of health of lithium-ion batteries under varied and incomplete working conditions. J. Energy Storage 2023, 58, 106323. [Google Scholar] [CrossRef]
- Wang, S.; Wang, P.; Wang, L.; Li, K.; Xie, H.; Jiang, F. An enhanced deep learning framework for state of health and remaining useful life prediction of lithium-ion battery based on discharge fragments. J. Energy Storage 2025, 107, 114952. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Tian, J.; Wei, Z.; Wang, P. Health estimation of lithium-ion batteries with voltage reconstruction and fusion model. Energy 2023, 282, 128216. [Google Scholar] [CrossRef]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Li, X.; Wang, Z. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 2020, 190, 116467. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101741. [Google Scholar] [CrossRef]
- Shen, J.; Ma, W.; Shu, X.; Shen, S.; Chen, Z.; Liu, Y. Accurate state of health estimation for lithium-ion batteries under random charging scenarios. Energy 2023, 279, 128092. [Google Scholar] [CrossRef]







| EKF-EKF | SVDUKF-EKF | |
|---|---|---|
| RMSE (%) | 1.9007 | 1.0531 |
| MAE (%) | 1.7167 | 0.9710 |
| Maximum Absolute Error (%) | 2.9513 | 1.7862 |
| EKF-EKF | SVDUKF-EKF | |
|---|---|---|
| RMSE (%) | 1.6789 | 1.5611 |
| MAE (%) | 1.3723 | 1.4899 |
| Maximum Absolute Error (%) | 4.3017 | 2.4738 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Wang, S.; Li, K.; Jiang, F. Joint Estimation of SOC and SOH Based on Kalman Filter Under Multi-Time Scale. Modelling 2025, 6, 100. https://doi.org/10.3390/modelling6030100
Qin H, Wang S, Li K, Jiang F. Joint Estimation of SOC and SOH Based on Kalman Filter Under Multi-Time Scale. Modelling. 2025; 6(3):100. https://doi.org/10.3390/modelling6030100
Chicago/Turabian StyleQin, Hongyan, Shilong Wang, Ke Li, and Fachao Jiang. 2025. "Joint Estimation of SOC and SOH Based on Kalman Filter Under Multi-Time Scale" Modelling 6, no. 3: 100. https://doi.org/10.3390/modelling6030100
APA StyleQin, H., Wang, S., Li, K., & Jiang, F. (2025). Joint Estimation of SOC and SOH Based on Kalman Filter Under Multi-Time Scale. Modelling, 6(3), 100. https://doi.org/10.3390/modelling6030100





