Abstract
Active vibration control designs for journal bearings have improved rotordynamic stability and led to advancements in adjustable bearing types that enable precise control of bearing geometry. In this study, optimized machine learning (ML) algorithms were modeled and implemented to accurately predict the static performance envelope of a four-pad active journal bearing with features of controlling the radial and tilt positions of pads in real time. ML models developed for the adjustable bearing system help predict its behavior as a function of three key input parameters such as the eccentricity ratio and radial and tilt positions of pads. Four supervised regression models, such as Random Forest Regression (RFR), Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), and a feedforward Artificial Neural Network (ANN), were chosen for their demonstrated ability to capture complex nonlinear patterns and their robustness against overfitting in such tribological applications. Hyperparameter tuning for each model was performed using the Optuna framework, which applies Bayesian optimization to efficiently determine the best parameter settings. The Optuna-optimized ensemble and neural network models were used to identify the optimal combinations of input variables that maximize the static performance envelope of the active bearing system with geometric adjustments.
1. Introduction
Rotor instability remains a key challenge in high-speed machines, driving the need for stable and smart rotor systems under extreme operational conditions. In recent years, advanced active control strategies for journal bearings have emerged to enhance system stability and allow machines to operate safely across wider speed ranges. Researchers have proposed adjustable bearing mechanisms for vibration suppression, such as active oil injection, piezoactuators, and flexible sleeve designs [1,2,3]. In such flexible sleeve designs, real-time adjustment of bearing geometry to optimal conditions is crucial for enhancing performance, as it allows the bearing to adapt to varying load and speed conditions, minimizing vibration, reduce wear, and maintain stability. Studies have focused on tribotronics in fluid film bearings, using hydraulic, pneumatic, magnetic, and piezoelectric actuation with advanced lubrication to improve stiffness, damping, stability, and overall performance. Controllable fluid film bearings serve as “smart” components, enabling vibration control, enhanced dynamic performance, improved energy efficiency, and versatile applications in both rotating and reciprocating machinery [4,5]. Adjustable bearings have been integrated with active control strategies, such as Proportional-Integral (PI), Proportional-Derivative (PD), and Proportional-Integral-Derivative (PID) controllers, to dynamically modify and enhance the hydrodynamic behavior of journal bearings [6,7]. Integrating such control systems with machine learning strategies can significantly enhance model accuracy, enabling real-time adjustments with high precision to optimize bearing performance. Machine learning-based optimization strategies have seen limited application in active bearing systems, despite their potential to enhance real-time adaptability. However, research efforts have been dedicated to developing active journal bearings with adaptable or variable geometries, aiming to improve rotordynamic stability, accommodate changing operational conditions, and suppress rotor vibrations [8,9].
Focusing on improving damping and stiffness, actively lubricated journal bearings employ controlled hydrodynamic lubrication to precisely regulate lubricant supply and film pressure, thereby reducing friction while enhancing thermal performance, load capacity, and dynamic stability [5]. Santos [10] developed advanced variants of active tilting pad bearings. One design incorporated a flexible hydraulic chamber regulated by proportional and servo valves, while the other utilized an actively controlled oil film through servo valve actuation. These innovative designs demonstrated strong potential in significantly reducing rotor vibration amplitudes, particularly during critical speed transitions. Based on the concept of active adjustment of tilting pad bearings, Deckler et al. [11] designed a bearing system with feedback control mechanism to regulate the rotor orbits. Linear actuators were positioned below the pad’s pivot location to provide radial adjustments in real time and to attain precise control of shaft motion. A feedback control strategy was implemented, where the feedback gains were optimized through a performance index containing multiple scalar parameters to independently adjust the system’s dynamic coefficients. A nonlinear dynamic model of the active bearing was further developed with pad angular velocity proposed as the control input which allows active adjustment using rotary electric motors [12,13]. Varela et al. [14] introduced a modified active lubrication concept for tilting pad bearings, incorporating a leading-edge groove lubrication mechanism. By regulating the oil flow into each pad’s supply groove using servo valves, the bearing is rendered active and controllable. Model-based controllers were further designed and implemented to achieve feedback-controlled lubrication in tilting pad bearings supporting flexible rotors [15,16]. Studies have also focused on magnetorheological (MR) fluid-based actuation in hybrid journal bearings. Uretta et al. [17,18] showed that adjusting MR fluid viscosity with a magnetic field can effectively control bearing pressure and stiffness, resulting in up to a 50% increase in load and stiffness, though the approach exhibits limited responsiveness at high speeds. Bompos and Nikolakopoulos [19,20,21] demonstrated that applying a steady magnetic field to MR and nano-MR fluids increases lubricant viscosity, enabling active control of both steady-state and dynamic bearing behavior, while improving attitude angle and friction characteristics and reducing fluid flow.
Chasalevris and Dohnal [22] proposed an adjustable journal bearing with a flexible mounting which can provide an additional film thickness layer through controlled adjustments of a semi-bearing part. Such adjustments were found to reduce resonant amplitudes by up to 70% as rotors operate at critical speeds. The adjustable bearing concept was further applied to partial arc bearings to extend stable operating margins to speeds well above the first critical speed. Such a geometry aids turbine operation by introducing parametric excitation of dynamic properties at specific frequencies, generating parametric antiresonance to eliminate instability [23,24]. The modified form of adjustable bearing presented in this study is based on the bearing designs detailed in Parkins and Martin [25]. Two different designs were developed, one with adjustable segments on the shaft and the other with an adjustable mechanism on the bearing’s inner part. Experimental tests were conducted on both semi-active bearing models to investigate variations in rotor positions [26,27]. Zhang et al. [28,29] developed a variable elliptical journal bearing with varying elliptical ratio to limit the vibration magnitudes of rotor under synchronous unbalanced loads at normal operating speeds. With an increased elliptical ratio, the bearing was found to reduce the forced vibration amplitude of a rigid rotor by up to 50% under heavy static loads and up to 60% under lighter static loads. Further developments of variable geometry bearings focused on adjusting the oil film’s stiffness and damping in response to rotor vibrations, making it more adaptable than fixed-pad bearings and enhancing machine stability and reliability under changing conditions. In such bearings, reducing the radial clearance to 70% provides effective lubrication for the upper bush, and decreasing it further to 30% increases the oil film pressure more than sixfold [30,31].
Machine learning models support the development of optimization tools that connect bearing performance with design and process factors, involving careful selection of variables, precise simulation, ANN modeling, and a robust optimization approach. Bischl et al. [32] examined hyperparameter optimization (HPO) in machine learning, highlighting the limitations of manual tuning and the advantages of automated methods. They reviewed a spectrum of HPO techniques, ranging from simple search strategies to advanced approaches such as Bayesian optimization, Hyperband, and evolutionary algorithms, while providing practical guidance for their application. Their findings demonstrate that structured and automated HPO enhances efficiency and reproducibility, while also addressing emerging challenges related to scalability, interpretability, and multi-criteria optimization. Research has emphasized Automated Machine Learning (AutoML) as a way to minimize reliance on expert-driven model and hyperparameter selection, offering optimization-based methods and systems that enable more accessible, off-the-shelf ML solutions [33]. A ML based prediction model combined with numerical approach was developed by Katsaros and Nikolakopoulos [34] to predict the performance of a tilting pad thrust bearing in terms of load capacity. Numerical study results were used to train and test multiple ML models and observed that the position of the incomplete film significantly impacts the bearing’s axial load capacity, with reduced lubricant flow causing pressure drops of up to 93%. Moschopoulos et al. [35] developed an ML model using sound and vibration data to predict the performance envelope of similar bearings, highlighting the need for a broad operating range to build a more generalizable bearing model. Li et al. [36] developed an ANN model of rotor system with water-lubricated active bearings to design optimal feedback controllers for rotor positioning. From the different controllers tested, ML based Model Predictive Controller (MPC) outperformed the optimal PID and Linear Quadratic Gaussian (LQG) controllers in setpoint tracking and noise suppression. Hess and Shan [37] developed an ANN model that approximates pressure distribution in a journal bearing under static conditions by accounting for elastohydrodynamic effects and flow cavitation. A hyperparameter study led to a six-layer U-Net that accurately predicted pressure distributions and bearing loads, demonstrating its potential for integration into other fluid power models. Ravindra et al. [38] used ANN model to analyze the effect of multiple process parameters affecting lubricant film profile and frictional torque in journal bearings. Higher regression value and strong alignment between expected and predicted results confirmed the ANN’s effectiveness for optimizing journal bearing performance. Further comparative studies were performed to assess the performance of different ML-based models for designing and optimizing static loaded journal bearing. The models were found to perform well in the hydrodynamic lubrication regime, while their predictive accuracy dropped in the boundary and mixed lubrication zones [39]. The findings highlight that machine learning models can speed up performance evaluation and optimization when incorporated into rotary machine applications.
Shutin et al. [40,41] carried out multicriteria optimization of an active journal bearing using a genetic algorithm yielding a Pareto-optimal set of solutions that balance viscous friction, rotor motion stability, and the bearing’s control efficiency. The friction and control efficiency criteria were effective, but including the rotor’s oscillatory response would better capture system stability and enhance the optimization results. Researchers have explored predictive analysis techniques with ML algorithms to assess the performance state of marine journal bearings. These methods rely on datasets generated by numerically solving the Reynolds equation for static conditions, assuming isothermal and isoviscous lubricated conditions [42]. Gheller et al. [43] developed ANN models to deliver rapid predictions of tilting pad bearing behavior with accuracy comparable to more time-intensive Reynolds-based models or computational fluid dynamics (CFD) approaches. Reynolds-based thermo-hydrodynamic model generated multiple training and test datasets, and a feed-forward ANN is then trained and optimized with the best configuration to balance accuracy and dataset size for all target values. ML techniques excel in predictive tasks delivering faster and more precise results than traditional methods like finite difference method (FDM) or finite element analyses.
Multiple ANN models together with fuzzy logic were applied to FDM simulation data to predict performance parameters with minimal computational time [44,45]. The prediction accuracy of the ANN models can be further improved by using advanced optimization algorithms. Optuna optimization can be applied to fine-tune the ANN model’s hyperparameters, improving its prediction accuracy and overall reliability. Studies focused on the integration of an Optuna-optimized Deep Fuzzy neural network models designed by combining deep learning and fuzzy logic aiming to achieve highly accurate output predictions through data reduction and hyperparameter optimization [46]. This approach is well-suited for journal bearing design and analysis and has been widely used in other studies to enhance machine learning model performance in comparable engineering applications. However, such optimized ANN models for bearing performance analysis remain limited, with even fewer studies focusing on their application to adjustable bearing systems [47].
The present study focused on developing optimized ML algorithms to predict the static performance characteristics of a four-pad active bearing, using models that estimate its behavior based on journal location and pad adjustment positions. To effectively capture complex nonlinear relationships and minimize overfitting, four supervised regression models were employed: Random Forest Regression (RFR), Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), and a feedforward Artificial Neural Network (ANN). Such models are commonly applied in predictive tasks that demand capturing subtle relationships among variables, and their complementary capabilities make them ideal for comparative analysis and ensemble techniques to boost overall prediction accuracy. Hyperparameter tuning for each model was carried out with the Optuna framework, which uses Bayesian optimization to systematically identify the most effective parameter settings. The objective of this tuning process was to minimize the Root Mean Squared Error (RMSE) using five-fold cross-validation. The high-accuracy ML models were used to determine the optimal input combinations that improve the static performance of the active bearing system through appropriate pad position adjustments.
2. Analysis
2.1. Multi-Pad Adjustable Bearing Data
Adjustable fluid film bearings have the capability to actuate bearing components or sleeves by either applying forces directly to the sleeves or by controlling the pressure or flow between the sleeves and rotating shaft thereby affecting various lubrication regimes. The adjustable bearing is configured with four equally spaced pads, each subtending 48°, arranged circumferentially around the journal on a circular ring. Figure 1 illustrates this novel four-pad geometry, where each pad is designed to undergo radial and tilt motions during operation to improve system stability. Dimensional details of the pads and bearing housing are provided in Pai and Parkins [27]. These pad adjustments can be controlled manually as in the case of Pai and Parkins [27] or incorporate hydraulic or piezoelectric actuators to provide definite pad motions as per the requisite conditions. Research on adjustable journal bearings has been ongoing for the past seven years, generating substantial repository of simulation data [48,49,50]. As illustrated in Figure 1, the pad tilts about its leading edge, while both radial and tilt displacements can be applied in positive or negative directions. The radial and tilt adjustment options enable up to nine distinct configurations in the proposed pad geometry. A negative radial shift moves the pads inward, decreasing clearance, while a positive shift expands the clearance and increases lubricant film thickness. Similarly, negative tilt produces an inward corner deflection of the pad, whereas positive tilt causes the opposite effect. These adjustment modes lead to distinct, non-uniform fluid film profiles depending on the applied displacement. Such adjustments provide an effective mechanism for regulating the bearing’s radial clearance and modifying the circumferential distribution of lubricant film thickness. The design parameters of the proposed multi-pad adjustable bearing are detailed in Table 1.
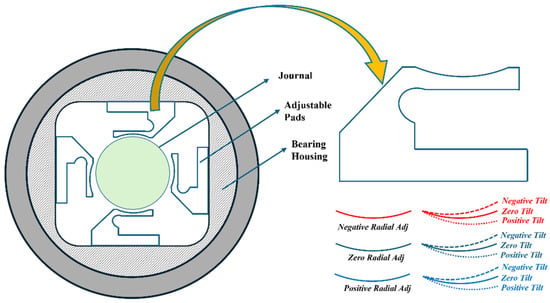
Figure 1.
Geometric Model of a Four-pad Active Journal Bearing.

Table 1.
Parameters of proposed adjustable bearing.
Currently, researchers are developing an experimental setup that incorporates multiple piezoactuators to achieve both radial and tilt actuation of the bearing pads. Achieving such multi-axis actuation demands a robust closed-loop control system, for which an intelligent machine learning model is essential. This study aims to design and implement optimized machine learning (ML) algorithms that can accurately predict and control the radial and tilt positions of the bearing pads in real time, using comprehensive lookup table data generated from previous simulations. Such adjustments can dynamically regulate lubrication conditions and adapt the bearing geometry to maintain optimal film thickness and enhance the load-carrying capacity. The dataset used in this study is derived from the static performance analysis of a multi-pad bearing conducted by Hariharan and Pai [48] and is presented in detail in Figure 2.

Figure 2.
Data distribution of static performance of multi-pad adjustable bearing [48].
The steady-state characteristics of the multi-pad adjustable bearing shown in Figure 2 are derived from the iterative solution of the Reynolds equation with simultaneous convergence of pressure and attitude angle. Using the Gauss–Seidel SOR scheme, the pressure distribution over the discretized grid is obtained, from which the film thickness for different pad adjustments is established. The resulting non-dimensional pressure field is integrated to determine the load-carrying capacity, while the corresponding frictional forces on the bearing surface are evaluated to characterize the operating performance of the adjustable bearing. Detailed methodology and governing equations related to the computation of friction forces and other steady-state characteristics have already been presented in the published work of Hariharan and Pai [48]. The total friction force is obtained by integrating the shear stress distribution over the bearing surface, accounting for contributions from both the pressure gradient and viscous shear components. For numerical convenience and generalization, the friction force is expressed in a non-dimensional form. The corresponding dimensionless friction variable is subsequently derived by normalizing the friction force with the applied load.
Figure 3 presents the correlation matrix illustrating the relationship between the steady-state characteristics of the adjustable bearing and the input parameters. The input variables considered were the eccentricity ratio (), radial adjustment (Radj), and tilt adjustment (Tilt). The output variables included maximum pressure (), dimensionless load capacity (), attitude angle (), friction force (), friction variable (), side leakage (), and the Sommerfeld number (S). From Figure 3, it can be observed that the eccentricity ratio shows a strong correlation with the side leakage, as it is directly affected by the rotor’s position. The other steady-state parameters are mainly influenced by the eccentricity ratio as well, but they exhibit lower correlation values since higher eccentricity generally reduces film pressure and load capacity. The radial and tilt pad adjustment factors exhibit moderate correlation with all output variables, as inward or outward adjustments can produce varying results and may positively or negatively influence the bearing’s performance characteristics. The generated film pressures were found to have a strong correlation with load capacity, as a thinner film typically produces higher pressures, and integrating these pressures determines the overall load-carrying capacity. The attitude angle typically exhibits a negative correlation with side leakage as higher attitude angle narrows the lubricant film clearance thereby restricting flow through the bearing.
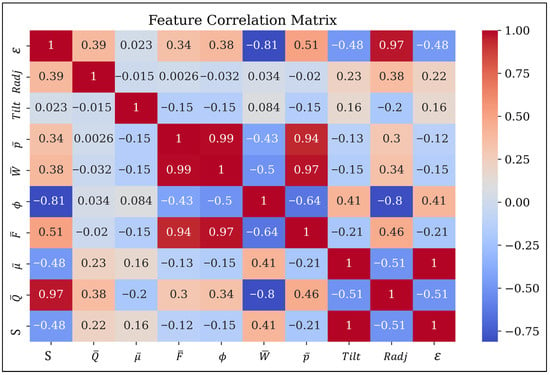
Figure 3.
Correlation matrix of steady state characteristics of adjustable bearing with input parameters.
To clarify dataset sufficiency, it is noted that the 210 data samples employed in this study were generated from high-fidelity static performance simulations of adjustable bearings reported in prior work [48,49,50]. Each data point corresponds to a unique operating configuration, where obtaining additional samples is computationally intensive due to the need for numerically resolving hydrodynamic pressure fields under different pad displacements and eccentricity ratios. Similar dataset sizes (100–1000 samples) have been adopted in tribological machine learning studies with effective predictive outcomes [37,43,44,45,51]. To further mitigate small-sample challenges, input–output normalization, five-fold cross-validation, and Optuna-based hyperparameter optimization were applied, ensuring robust generalization.
2.2. Machine Learning Models and Approach
In the present study, ML models were developed to predict the performance characteristics of an adjustable bearing system as a function of three key input parameters using a dataset comprising 210 samples: , Radj, and Tilt. The target response variables included , , , , , , S, all of which are critical in assessing bearing behavior under varying operating conditions. Prior to training, input and output features were normalized to enhance model stability and convergence during learning.
Four supervised regression models were considered in this investigation: Random Forest Regression (RFR), Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), and a feedforward Artificial Neural Network (ANN). These models were selected based on their ability to capture nonlinear relationships, robustness to overfitting, and success in similar engineering applications. The Optuna framework was employed to perform automated hyperparameter tuning for each ML model, leveraging Bayesian optimization techniques to identify the optimal model configuration. The hyperparameter tuning objective was to minimize the Root Mean Squared Error (RMSE) using five-fold cross-validation. In this approach, the dataset was split into five mutually exclusive subsets, with four used for training and one for validation in each iteration, thereby minimizing bias due to random train-test splits. The five-fold cross-validation scheme was consistently applied to all four regression models (RFR, XGBoost, LightGBM, and ANN) within the Optuna optimization framework to ensure fair and unbiased comparison of predictive performance. The objective function was defined to evaluate the average cross-validated RMSE over all target variables. For a set of actual values and predicted values , RMSE is defined as:
where is the number of samples. The optimization was performed using 50 trials for all models, for the exploration of the search space. Subsequent Section 2.2.1, Section 2.2.2, Section 2.2.3 and Section 2.2.4 describe the theoretical foundations and implementation details of each model, while Section 2.3 elaborates on the Optuna-based optimization framework utilized for model calibration.
2.2.1. Random Forest Regression (RFR)
RFR is an ensemble-based machine learning technique that constructs a multitude of decision trees during training and outputs the average prediction of the individual trees. It is particularly well-suited for capturing nonlinear relationships and mitigating overfitting by leveraging the power of bootstrap aggregation (bagging) (refer Figure 4).
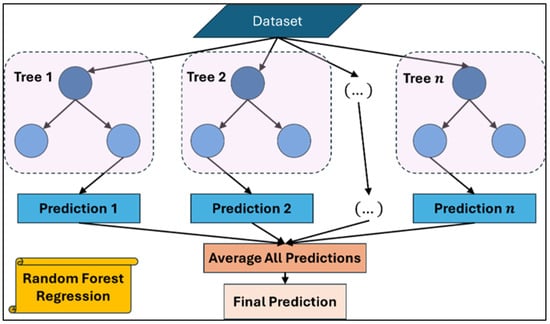
Figure 4.
Schematic representation of random forest regression.
Mathematically, each decision tree in the random forest is constructed from a bootstrap sample of the dataset, and predictions are made by averaging the outputs of all trees. For a given input vector , the RFR prediction is given by [52]
where is the number of trees in the forest, and is the prediction from the t-th decision tree. Four key hyperparameters of RFR model were tuned using the Optuna framework in the following range:
- Number of trees in the forest (n_estimators): [50, 500],
- Maximum depth of each tree (max_depth): [5, 30],
- Minimum number of samples required to split an internal node (min_samples_split): [2, 10],
- Minimum number of samples required to be at a leaf node (min_samples_leaf): [1, 5].
2.2.2. Extreme Gradient Boosting (XGBoost)
XGBoost is an advanced ensemble learning technique based on the gradient boosting framework, specifically optimized for speed and performance. It builds a series of weak learners (regression trees), where each new tree is trained to minimize the residual errors of the ensemble of previously trained trees (refer Figure 5). Owing to its regularization mechanisms and handling of missing values, XGBoost has emerged as a state-of-the-art algorithm in many regression and classification tasks.
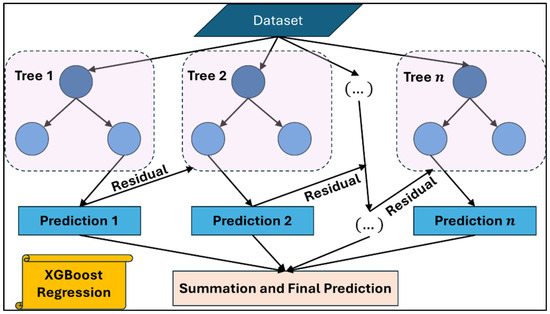
Figure 5.
Schematic representation of XGBoost regression.
XGBoost minimizes a regularized objective function that balances the model’s training loss with its complexity. The general form of the objective function is [53]
where is a differentiable loss function (e.g., squared error), represents each regression tree, and is the regularization term defined as:
Here, is the number of leaves in the tree, is the score on leaf , is the penalty for adding a leaf, and is the L2 regularization coefficient. The critical hyperparameters of XGBoost were tuned using the Optuna framework in the following range:
- Number of boosting iterations (n_estimators): [50, 500],
- Maximum tree depth for base learners (max_depth): [3, 20],
- Shrinkage factor to scale step size (learning_rate): [0.005, 0.3],
- Fraction of samples to be used per tree (subsample): [0.5, 1.0],
- Fraction of features used per tree (colsample_bytree): [0.5, 1.0],
- Minimum loss reduction to make a split (gamma): [0, 5]
- L1 regularization term on weights (reg_alpha): [0, 10].
- L2 regularization term on weights (reg_lambda): [1, 10].
2.2.3. Light Gradient Boosting Machine (LightGBM)
LightGBM is an efficient gradient boosting framework based on decision tree algorithms, specifically designed for faster training speed, lower memory usage, and improved accuracy. Unlike traditional gradient boosting methods that grow trees level-wise, LightGBM employs a leaf-wise tree growth strategy, which selects the leaf with the maximum loss reduction to grow next (refer Figure 6). This allows LightGBM to achieve deeper trees and better accuracy while maintaining computational efficiency. LightGBM introduces several enhancements over traditional boosting frameworks, such as histogram-based decision tree learning, gradient-based one-side sampling (GOSS), and exclusive feature bundling (EFB), making it particularly effective on structured datasets like the one used here. In this study, the following hyperparameters were included in the optimization search space [54].
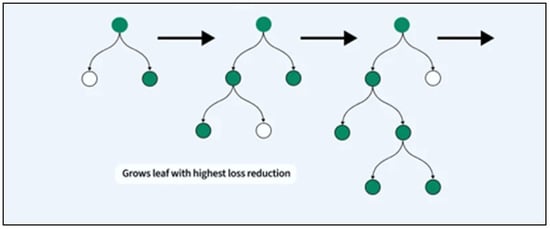
Figure 6.
Schematic representation of LightGBM regression.
- Number of boosting iterations (n_estimators): [50, 500],
- Shrinkage factor to scale step size (learning_rate): [0.005, 0.3],
- Maximum number of leaves per tree (num_leaves): [10, 100],
- Minimum number of data points in a leaf (min_child_samples): [5, 50],
- Fraction of features used per iteration (feature_fraction): [0.5, 1.0].
2.2.4. Artificial Neural Network (ANN)
Artificial Neural Networks (ANNs) are computational models inspired by the structure and function of the human brain, capable of capturing highly nonlinear and complex relationships in data. In this study, a feedforward neural network based on the Multilayer Perceptron (MLP) architecture was implemented for modeling the multi-output regression problem involving the performance characteristics of the adjustable bearing system. The network takes three input features—eccentricity ratio, radial adjustment, and tilt—and predicts seven output variables related to bearing performance (refer Figure 7).
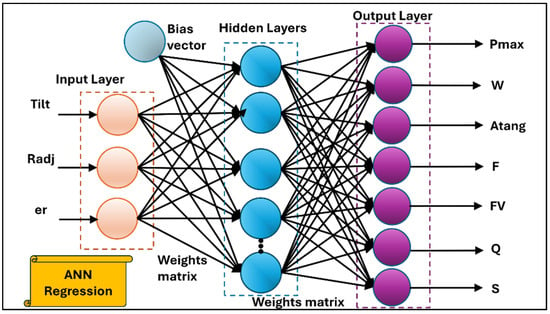
Figure 7.
Schematic representation of ANN regression.
Each MLP model consists of an input layer, one or more hidden layers with nonlinear activation functions, and an output layer. The core learning objective is to minimize the prediction error by adjusting the network’s weights through backpropagation. The mathematical formulation of a single hidden layer ANN is given by [55]
where are the input features, , are the weights for the first and second layer, respectively. , are the biases, is the activation function, is the number of hidden neurons, is the identity function in regression tasks. The hidden layers of the ANN employed the Rectified Linear Unit (ReLU) activation function, which is widely adopted in regression-oriented neural networks to promote sparse activations and efficient convergence. The output layer used a linear activation to directly predict continuous target variables.
To identify the optimal ANN configuration, Optuna was employed to tune the following hyperparameters in the optimization search space [56]:
- Number of neurons in each hidden layer (hidden_layer_size): [1, 100]
- Number of hidden layers (num_layers): [1, 2]
- Optimization algorithm for weight updates (solver): [adam, lbfgs, sgdm]
- L2 regularization parameter (alpha): [10−5, 10−1]
Model training was carried out with a maximum of 1000 iterations, and performance was evaluated using 5-fold cross-validation, where the average RMSE across all outputs served as the optimization objective. A total of 50 trials were conducted to explore the hyperparameter space.
2.3. Optuna—Automatic Hyperparameter Optimization Framework
Hyperparameter tuning is essential for achieving optimal performance of machine learning models. In this study, Optuna, a robust and flexible hyperparameter optimization framework, was utilized to automatically tune the hyperparameters of all four machine learning models. Optuna formulates hyperparameter tuning as a black-box optimization problem
where represents a vector of hyperparameters within the search space , and is the objective function, in this case, the average RMSE across 5-fold cross-validation. For each trial, Optuna samples a candidate configuration from using a Bayesian optimization strategy based on the Tree-structured Parzen Estimator [57]. The objective function is then evaluated as
where is the number of cross-validation folds, and is the RMSE on the k-th fold for the model trained with hyperparameters . This approach allows Optuna to adaptively refine its sampling strategy based on past evaluations, thereby efficiently exploring the hyperparameter space. The complete workflow is summarized in Figure 8, which shows the progression from data normalization to model finalization via Optuna optimization.
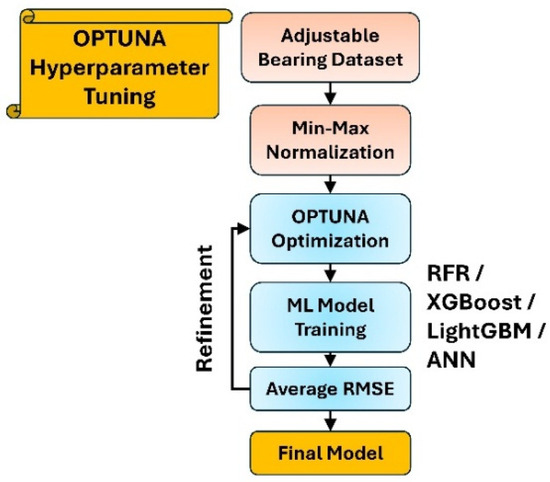
Figure 8.
Framework of Optuna—Automatic Hyperparameter Optimization.
In this study, Bayesian optimization within Optuna was implemented using the Tree-structured Parzen Estimator (TPE) sampler. The TPE algorithm models two probability density functions: , representing the distribution of hyperparameter configurations associated with low (favorable) objective values, and , representing the distribution of less favorable configurations. At each trial, Optuna evaluates the ratio and preferentially samples new hyperparameters from regions where this ratio is high, thereby biasing the search toward promising areas of the hyperparameter space.
For every candidate configuration, the model was trained and evaluated using five-fold cross-validation, and the average Root Mean Squared Error (RMSE) across all folds was returned to the optimizer as the objective value. This process was repeated for 50 trials per model, during which Optuna adaptively updated its probabilistic model based on past evaluations. In the early trials, hyperparameters were sampled broadly to explore the search space (exploration), while later trials increasingly focused on refining configurations near the most promising candidates (exploitation). Convergence was reached when improvements in RMSE became marginal across consecutive trials, as observed in the optimization history plots (Figure 9). This iterative Bayesian approach allowed efficient navigation of the hyperparameter space and ensured that the final configurations reported in Table 2 represented near-optimal trade-offs between model complexity and prediction accuracy.
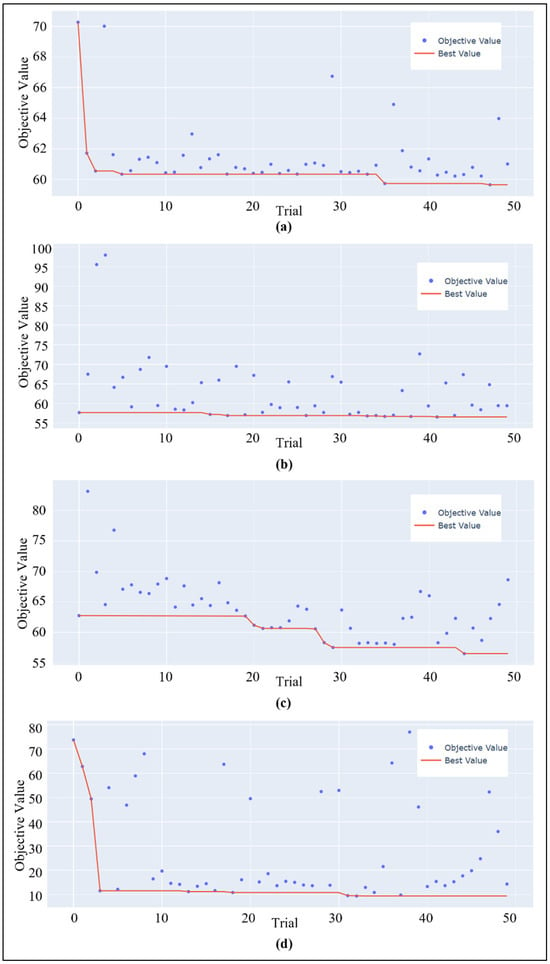
Figure 9.
Optimization history plot of (a) RFR, (b) XGBoost, (c) LigthGBM, and (d) ANN model.

Table 2.
Optimized hyperparameters of the machine learning models.
3. Results and Training Accuracy
3.1. Model Hyperparameter Optimization
Figure 9 presents the optimization history plots, showing the evolution of the objective value (RMSE) across the trials. In all models, a substantial reduction in RMSE was observed within the initial set of trials, followed by gradual refinement. Notably, RFR and ANN exhibited early convergence, while XGBoost and LightGBM showed incremental improvements over a broader range of trials. ANN showed the best convergence behavior with the minimal objective values at the end of the 50 trials. The final set of optimized hyperparameters for each model is summarized in Table 2. To further analyze the impact of each hyperparameter on model performance, Optuna’s importance evaluation tool was used.
Figure 10 highlights the relative importance scores for the key hyperparameters in each model.
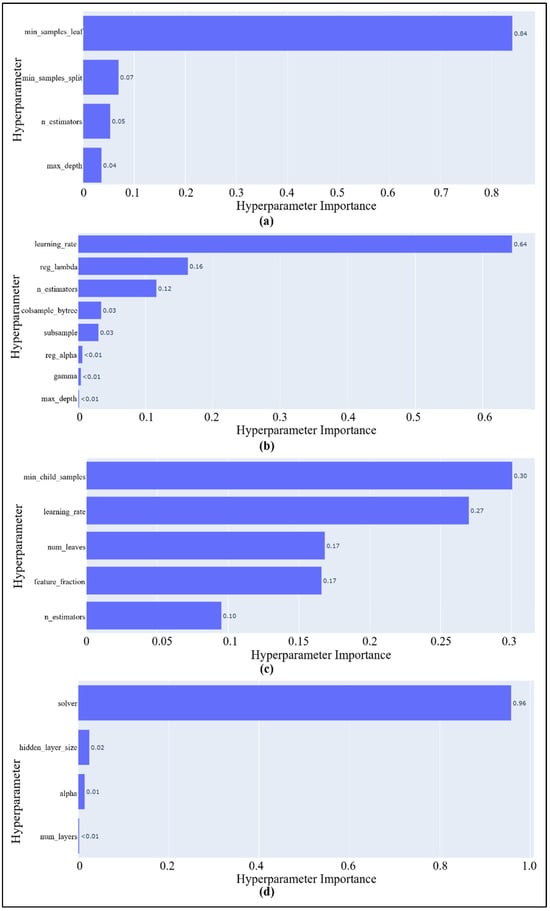
Figure 10.
Hyperparameter importance scores for (a) RFR, (b) XGBoost, (c) LigthGBM, and (d) ANN model.
- For RFR, min_samples_leaf (the minimum number of samples required to be at a leaf node) parameter overwhelmingly dominated the model’s sensitivity with an importance score of 0.84, suggesting its critical role in determining leaf node purity and thus model complexity.
- In XGBoost, the learning rate and regularization terms (reg_lambda, reg_alpha) had a notable influence, with learning rate being the most impactful (importance score of 0.64), reinforcing the sensitivity of gradient boosting models to learning rate control.
- For LightGBM, both min_child_samples (minimum number of data points in a leaf) (0.30) and learning rate (0.27) were highly influential, followed by num_leaves (maximum number of leaves per tree) and feature_fraction (fraction of features used per iteration). These findings highlight the reliance of LightGBM on leaf-wise tree growth strategy.
- The performance of ANN model was predominantly governed by the choice of solver, with a significant importance score of 0.96. Other parameters had a negligible effect in comparison.
These insights confirm the value of targeted hyperparameter optimization, especially in cases where a few key parameters dominate model performance.
3.2. Performance Evaluation of Machine Learning Models
Figure 11 presents the comparative evaluation of the machine learning models using three standard regression metrics: RMSE, MAE, and R2. The ANN model is found to significantly outperform the ensemble methods, RFR, XGBoost, and LightGBM, achieving the lowest RMSE and MAE values, and the highest R2 score close to 1.0. To visualize model agreement and standard deviation, a Taylor diagram is plotted in Figure 12. The ANN model is positioned closest to the reference point, confirming its excellent correlation and low variance compared to the other models. LightGBM and XGBoost follow with relatively strong correlation values, while RFR shows slightly reduced performance.
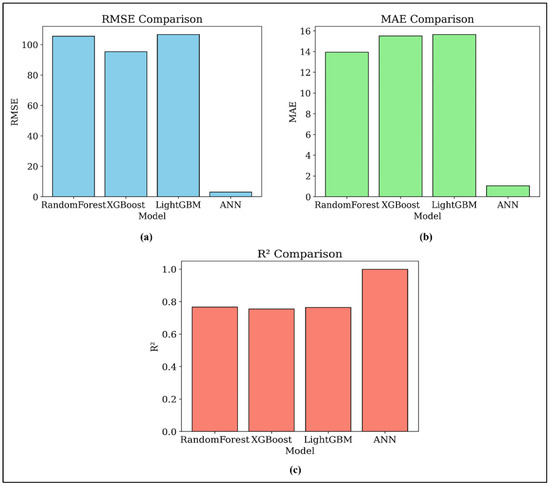
Figure 11.
Performance metrics: (a) RMSE, (b) MAE, and (c) R2 of the ML models evaluated.
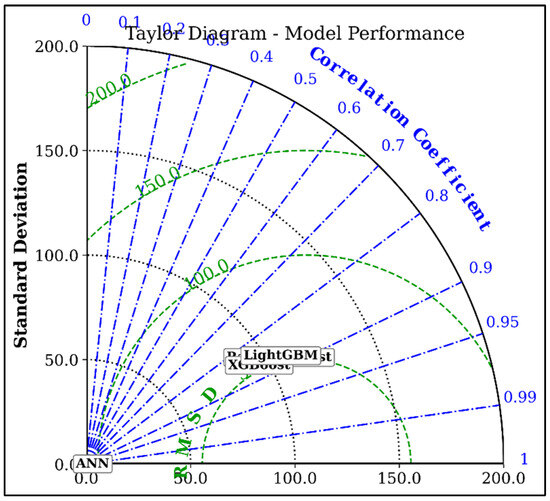
Figure 12.
Taylor diagram representing the R2 values of the ML models evaluated.
Figure 13 shows the error distribution plots for all models. The error density for ANN (Figure 13d) is highly concentrated near zero, indicating very few large errors. In contrast, the rest of the models exhibited a wider spread, with occasional extreme deviations, particularly for XGBoost and LightGBM. The predicted vs. actual plots (Figure 14) further validated the efficacy of ANN model, which demonstrated a near-perfect alignment along the diagonal line. Lastly, the violin plot in Figure 15 illustrates the distribution of MAE per sample. The ANN model showed a highly compressed distribution with minimal variability, indicating consistent performance across the dataset. Ensemble models reveal wider distributions with heavier tails, reflecting susceptibility to outlier errors.
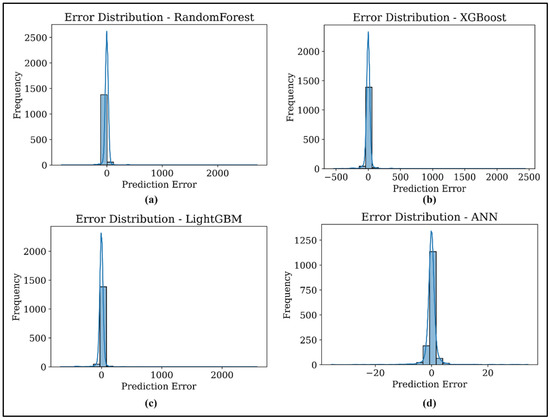
Figure 13.
Error distribution of (a) RFR, (b) XGBoost, (c) LigthGBM, and (d) ANN model.
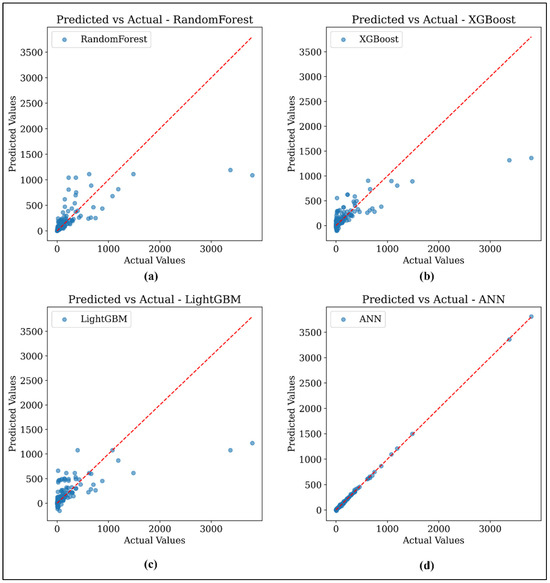
Figure 14.
Predicted vs. actual plot for (a) RFR, (b) XGBoost, (c) LigthGBM, and (d) ANN model.
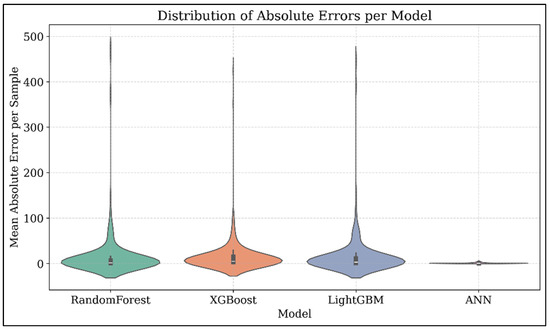
Figure 15.
Violin plot of MAE of the model models evaluated.
In addition to accuracy metrics, computational performance was assessed on a standard desktop (11th Gen Intel® i5 CPU, 8 GB RAM) in terms of inference latency and model size to verify real-time feasibility. The ANN achieved an average prediction time of 0.35 ms per sample with a compact model size of 58 kB, while LightGBM was even faster at 0.20 ms per sample with a size of 1.33 MB. By contrast, XGBoost and RFR required 1.80 ms and 1.09 ms per sample, with memory footprints of 1.57 MB and 421 kB, respectively. Although all models offer predictions several orders of magnitude faster than CFD-based simulations, ANN provided the most favorable balance between speed and compactness, making it particularly attractive for deployment in embedded real-time active bearing systems (Table 3).

Table 3.
Inference latency and model size of optimized ML models.
3.3. Interaction Effects on Static Characteristics of Adjustable Bearing Using Optimized ANN Model
Figure 16a–f details the predicted versus actual plots for the static performance parameters of multi-pad adjustable bearing under varied journal eccentricity and pad displaced conditions. From the plots, it can be observed that all the predicted and actual values closely follow a clear linear trend, indicating strong agreement between the model predictions and the numerical results. The data points remain closely clustered around the line of best fit, showing minimal scatter and confirming that the developed model reliably and accurately represents the static performance behavior of the multi-pad adjustable bearing across different journal eccentricities and pad displacement settings. The plot for frictional force (F) are not presented here, as the friction force is directly proportional to the friction variable and does not provide additional insight beyond what is already conveyed by the friction variable plot.
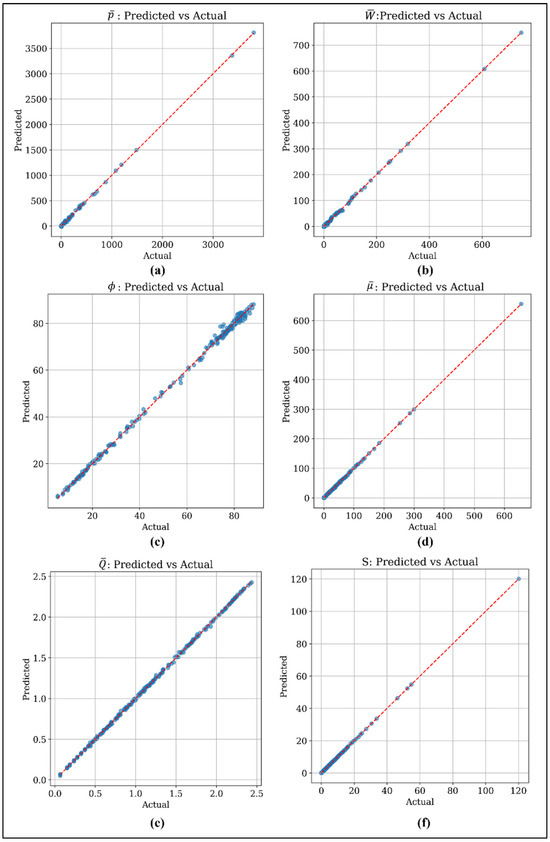
Figure 16.
Predicted vs. actual plot of (a) Maximum pressure (), (b) non-dimensional load (), (c) Attitude angle (), (d) Friction variable (), (e) side leakage (), and (f) Sommerfeld Number (S) using the optimized ANN model.
Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23 illustrates the interaction effects and 3D plots of eccentricity ratio and pad position on the different static parameters of a multi-pad adjustable bearing. The optimized ANN model developed in this study was further employed to predict variations in steady-state performance for pad adjustment values within the maximum ranges reported by Hariharan and Pai [48]. By doing so, an extended dataset can be generated within these ranges, providing valuable input for actuating the piezoactuators during the experimental phase and enhancing the control strategy for the adjustable bearing system. This approach enables the generation of an extended dataset within the specified ranges, offering valuable input for actuating the piezoactuators during experiments and improving the control strategy of the adjustable bearing system. In the proposed experimental plan for analyzing the performance of adjustable bearings, a rotating hollow shaft in an overhung configuration will be mounted on a robust test bench to suppress unwanted vibrations during high-speed operation. The bearing will be designed and fabricated with a housing and adjustable pads, which can be tuned both radially and in tilt. The system will incorporate pressure sensor and proximity probes, multiple piezoactuators, control units, and variable pad geometry to actively control the bearing during operation. The hollow shaft design facilitates the integration of a pressure sensor at the mid-plane of the bearing to directly measure film pressures. Four proximity probes will be positioned on either side of the bearing to monitor the journal position. The proximity probe signals are transmitted to a feedback controller, which processes the data using customized algorithms to generate commands for the piezoactuators. These actuators then adjust the bearing pads in both radial and tilt directions, ensuring stable operation and maintaining the desired conditions. This closed-loop arrangement provides continuous monitoring and active adjustment, ensuring stability and optimal performance. By enabling real-time autonomous control, the system achieves active vibration control (AVC), which reduces noise and enhances efficiency across applications ranging from precision engineering to heavy-duty rotating machinery.
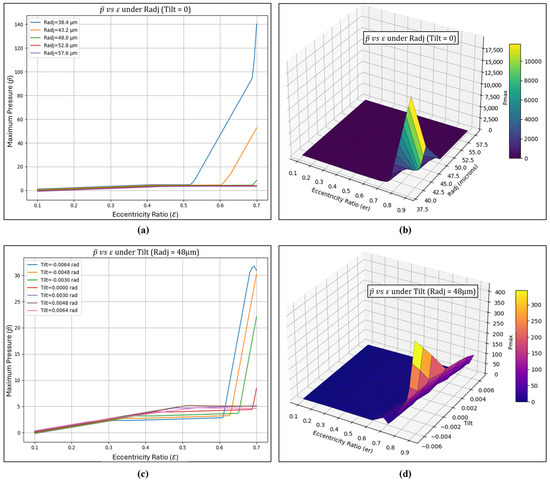
Figure 17.
Interaction effects and 3D surface plots of non-dimensional pressure () (a) Interaction effect of vs. under varied Radj and zero tilt (b) Surface plot of vs. under varied Radj and zero tilt (c) Interaction effect of vs. under constant Radj and varied tilt (d) Surface plot of vs. under constant Radj and varied tilt.
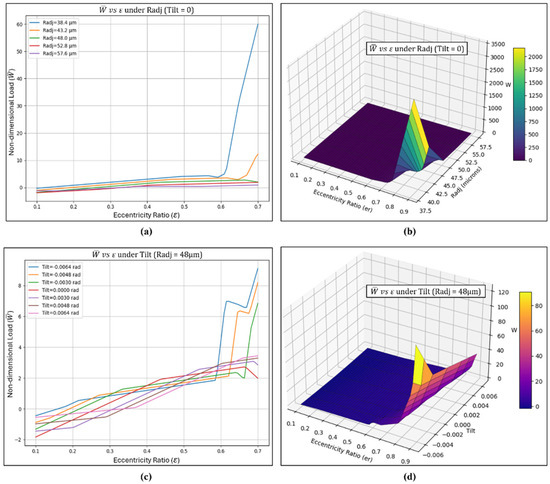
Figure 18.
Interaction effects and 3D surface plots of non-dimensional load () (a) Interaction effect of vs. under varied Radj and zero tilt (b) Surface plot of vs. under varied Radj and zero tilt (c) Interaction effect of vs. under constant Radj and varied tilt (d) Surface plot of vs. under constant Radj and varied tilt.
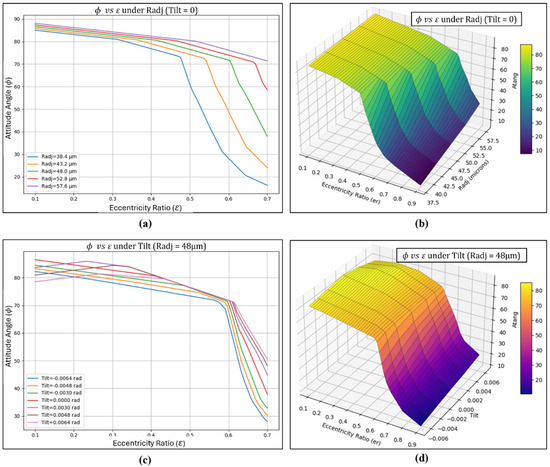
Figure 19.
Interaction effects and 3D surface plots of attitude angle () (a) Interaction effect of vs. under varied Radj and zero tilt (b) Surface plot of vs. under varied Radj and zero tilt (c) Interaction effect of vs. under constant Radj and varied tilt (d) Surface plot of vs. under constant Radj and varied tilt.
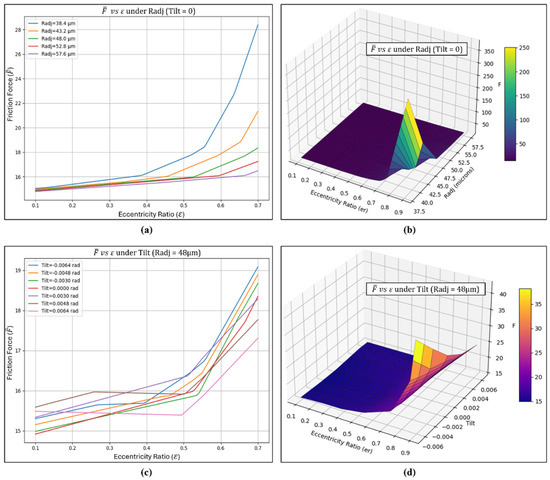
Figure 20.
Interaction effects and 3D surface plots of frictional force () (a) Interaction effect of vs. under varied Radj and zero tilt (b) Surface plot of vs. under varied Radj and zero tilt (c) Interaction effect of vs. under constant Radj and varied tilt (d) Surface plot of vs. under constant Radj and varied tilt.
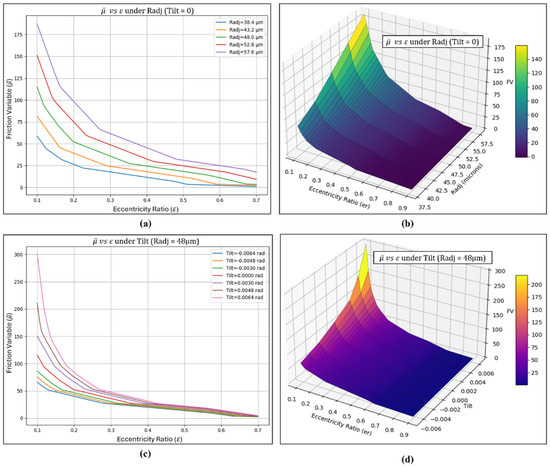
Figure 21.
Interaction effects and 3D surface plots of friction variable () (a) Interaction effect of vs. under varied Radj and zero tilt (b) Surface plot of vs. under varied Radj and zero tilt (c) Interaction effect of vs. under constant Radj and varied tilt (d) Surface plot of vs. under constant Radj and varied tilt.
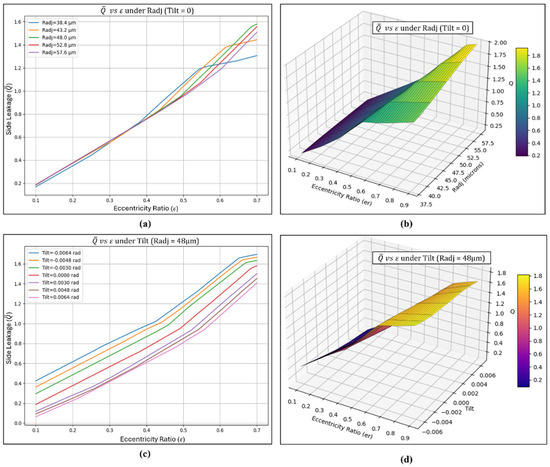
Figure 22.
Interaction effects and 3D surface plots of side leakage () (a) Interaction effect of vs. under varied Radj and zero tilt (b) Surface plot of vs. under varied Radj and zero tilt (c) Interaction effect of vs. under constant Radj and varied tilt (d) Surface plot of vs. under constant Radj and varied tilt.
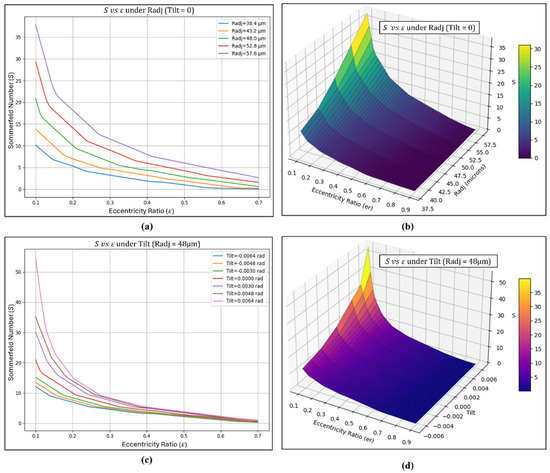
Figure 23.
Interaction effects and 3D surface plots of Sommerfeld number () (a) Interaction effect of vs. under varied Radj and zero tilt (b) Surface plot of vs. under varied Radj and zero tilt (c) Interaction effect of vs. under constant Radj and varied tilt (d) Surface plot of vs. under constant Radj and varied tilt.
In Figure 17a, increasing the eccentricity ratio leads to a notable rise in film pressure, as the reduced film thickness at higher eccentricity amplifies the wedge effect producing higher pressures in the load-carrying pad among the four pads. A radial adjustment value (Radj) of 48 µm is used as the initial reference position. A decrease in Radj indicates an inward adjustment that reduces pad clearance, while an increase signifies an outward adjustment that increases the clearance and film thickness. For varying radial pad adjustments, the film pressure exhibits minimal variation up to a certain eccentricity ratio because adequate film thickness is still maintained within this range. This means that the clearance provided by the pad settings is sufficient to sustain a stable lubricant film, preventing significant changes in pressure despite changes in eccentricity. Beyond this point, as the eccentricity continues to increase, the film thickness reduces more noticeably, making the lubricant film more sensitive to clearance changes. Consequently, the effect of pad adjustments on the pressure distribution becomes more significant as shown in the 3D plot of Figure 17b. Peak pressures have been observed under a combination of higher journal eccentricity and maximum inward radial adjustment values. The effect of pad tilt in film pressures shown in Figure 17c,d indicates that inward pad tilt position further enhances the peak hydrodynamic film pressures. Tilting the pad inward further narrows the converging fluid film wedge, which compresses the lubricant film more effectively and generates higher hydrodynamic pressures. This trend is evident in the 3D plot, where all tilt conditions generally show increased pressure values at higher eccentricities. Such intensified squeezing effect boosts the load-carrying capacity but can also increase frictional resistance and make the bearing more sensitive to variations in operating conditions. Such pad adjustments are essential for optimizing the balance between operational stability, load-carrying capacity, and frictional energy losses in fluid film bearings.
In the load capacity plot shown in Figure 18a,b, lower Radj values (i.e., inward adjustment) result in higher load capacity as the inward adjustment reduces the pad clearance, resulting in a thinner lubricant film and consequently higher-pressure buildup within this narrow film thickness. Conversely, higher Radj values (i.e., outward adjustment) increase the pad clearance, which results in a thicker lubricant film, lowering the generated pressure and thereby reducing the load capacity. The maximum load capacity was found at higher eccentricity levels, as the increased eccentricity causes a greater convergence of the lubricant film, which enhances the pressure buildup within the bearing. Such intricate variation is illustrated in detail in the 3D surface plots shown in Figure 18b. Distinct peaks can be observed for combinations of higher eccentricity and inward radial adjustment. This occurs because higher eccentricity reduces the minimum film thickness in the converging region, and inward pad adjustments further decrease this clearance, enhancing the film pressure and resulting in higher load-carrying capacity. In addition to radial adjustments, introducing pad tilt creates a non-uniform film thickness profile, which directly influences the generated hydrodynamic pressures and, consequently, the load-carrying capacity of the bearing. The outward tilt generally has a negative impact on the load-carrying capacity, as it increases the pad clearance and reduces the pressure developed in the fluid film. However, it cannot be disregarded because outward tilting can significantly affect the bearing’s dynamic characteristics, such as stiffness, damping, and stability margins under load on pad and load between pad conditions. Therefore, the influence of outward tilt should also be studied in detail, as it plays an important role in controlling clearance profiles, accommodating misalignments, and managing performance trade-offs under varying operating conditions.
For rise in eccentricity ratios in Figure 19, a significant reduction in attitude angle was observed for varying radial and tilt adjustments. For a Radj of 38.4 µm, lower attitude angle values indicate that the journal’s locus positions are aligned closer to the vertical axis. This trend suggests improved bearing stability, as the journal remains better aligned with the load line. Such alignment helps sustain a uniform lubricant film, lowers the likelihood of metal-to-metal contact, and improves the bearing’s dynamic performance across different operating conditions. In contrast, positive radial adjustments can lead to instability at higher eccentricity ratios, while showing minimal impact at lower eccentricities. However outward tilt conditions shown in Figure 19c was found to generate lower attitude angle values at smaller eccentricity ratios. This suggests that outward tilt can align the journal position more closely with the vertical load line at lower eccentricities, which may slightly improve stability under light loading conditions. Despite its negative effect on load capacity due to increased clearance, the outward tilt’s influence on attitude angle highlights its role in fine-tuning the bearing’s dynamic behavior and alignment characteristics, especially when operating near the centered position. However, a crossover trend is observed, where negative tilt produces lower attitude angle values at larger eccentricity ratios. Such behavior shows that negative tilt not only increases pressure generation by creating a narrower fluid film wedge but also helps improve directional stability as the bearing operates under higher loads. Consequently, inward tilt can be an effective adjustment for maintaining high load-carrying capacity while keeping the journal position stable in more demanding operating conditions.
The frictional force and friction variable plots in Figure 20 and Figure 21 show higher values for inward pad adjustments, as the reduced clearance leads to increased frictional forces and a corresponding rise in the friction variable. Inward pad adjustments reduce the clearance producing a thinner lubricant film that increases viscous shear stress within the fluid layer, thereby directly raising the frictional resistance between the journal and the bearing surface. As a result, the increased shear forces within the thinner fluid film led to higher frictional force and a greater friction coefficient. At larger eccentricities, the variation in frictional force becomes more pronounced across different pad adjustment settings. With the introduction of tilt adjustments, as shown in Figure 20c,d, different tilt settings resulted in varying frictional force values across the range of eccentricity ratios. Positive tilt angles with pads in the neutral position generated higher frictional forces at lower eccentricities. However, a crossover trend was observed where at higher eccentricities, negative tilt angles produced greater frictional forces than positive tilt. This suggests that inward tilting of the pads has a greater impact at higher loads, as the reduced fluid film thickness and steeper wedge shape lead to increased shear forces within the lubricant layer. As shown in the friction variable plots in Figure 21a–d, a negative radial adjustment combined with zero tilt, as well as a negative tilt with a neutral pad position, were found to produce lower friction variable values. Such variation occurs as these adjustment configurations not only generate the necessary frictional forces but also significantly enhance the load-carrying capacity of the bearing. As the friction variable is defined as a function of the ratio between the frictional force and the developed load, the higher load capacity under negative radial and negative tilt adjustments effectively reduces the resulting friction variable, indicating improved operational efficiency and better performance under these conditions.
Nominal variation in side leakage was noted for varying radial pad adjustments with cross over trend observed at higher eccentricities in Figure 22a,b. The side leakage from the pad ends tends to be higher as greater pressure gradients are generated in areas of minimal film thickness developed within the pad regions. At higher eccentricities, the inward radial adjustment (Radj = 43.2 µm) shows greater side leakage compared to the maximum inward adjustment. Such increased leakage is likely due to the converging region of the lubricant film being distributed across multiple pads promoting flow escape at the pad edges under these conditions. The surface plot clearly highlights regions of increased leakage, demonstrating that specific combinations of pad clearance and journal position promote greater flow escape, thereby providing a detailed visual insight into the leakage patterns and the hydrodynamic mechanisms governing them. For different tilt adjustments in Figure 22c,d, meaningful variation in side leakage is observed across varying eccentricities. Pads with a positive tilt were found to produce less side leakage, as the increased clearance from the positive tilt modifies the film profile, creating greater non-uniformity while reducing the likelihood of forming higher local pressure gradients. The lower pressures developed under positive tilt conditions further reduce the driving force for lubricant to escape at the pad edges, resulting in less side leakage compared to zero or negative tilt configurations. The variation in Sommerfeld number in Figure 23 was found to follow a decreasing trend with increasing journal eccentricity. At higher eccentricities, the minimum film thickness decreases while the load-carrying capacity increases, which lowers the dimensionless Sommerfeld number due to its inverse relationship with the supported load, indicating enhanced bearing performance under these conditions. The Sommerfeld number plot helps determine optimal design ranges, assess the effects of adjustments such as tilt and radial positioning, and confirm whether the bearing is operating within a stable and efficient hydrodynamic range.
Comparisons with prior Optuna-optimized models reinforce the contributions of this study. For instance, DFNN-based regression achieved R2 ≈ 0.93 with RMSE around 4–6% of the output scale [46], while Optuna-tuned gradient boosting models reported R2 ≈ 0.95 for regression tasks [47]. In contrast, the ANN developed here achieved R2 ≈ 0.99 with RMSE ≈ 3, significantly improving accuracy relative to both references. Although ensemble methods (XGBoost, LightGBM) yielded moderate performance (R2 ≈ 0.76–0.77, RMSE ≈ 106–108), they provided useful baselines that highlight the superiority of the ANN for capturing nonlinear pad displacement effects. These findings confirm that Optuna-optimized ANN models deliver enhanced predictive power for bearing-specific tasks compared with existing DFNN and gradient boosting approaches.
4. Conclusions
The present study effectively demonstrated the development and application of optimized ML algorithms for predicting the static performance characteristics of a four-pad active journal bearing system with adjustable radial and tilt pad positions. By employing advanced regression models such as RFR, XGBoost, LightGBM, and ANN, along with Optuna’s Bayesian optimization for targeted hyperparameter tuning, highly accurate predictive models were developed. To ensure stable learning and faster convergence, the input and output variables were normalized ahead of model training. The generation of predictive data for various radial and tilt pad positions, which previously demanded significant computational effort and were not readily accessible, demonstrates the practical value of the developed models. This predictive capability supports more informed design choices and operational strategies for active bearing systems. Among all the models, the ANN achieved the highest accuracy, delivering the lowest prediction errors and the strongest agreement with the actual performance data. The comparative analysis, which included error distributions, Taylor diagrams and prediction plots, confirmed the ANN model’s robustness and reliability in capturing complex nonlinear relationships. Parametric analysis further highlighted the role of eccentricity ratio, radial adjustments, and pad tilt in influencing the film pressures and load-carrying capacity. In addition to accuracy, computational performance was evaluated on a standard desktop (11th Gen Intel® i5 CPU, 8 GB RAM). The ANN achieved 0.35 ms per sample with a compact size of 58 kB, while LightGBM was faster at 0.20 ms but larger (1.33 MB). XGBoost (1.80 ms, 1.57 MB) and RFR (1.09 ms, 421 kB) were also efficient but less balanced for embedded deployment. Although all models delivered predictions orders of magnitude faster than CFD-based simulations, ANN provided the best trade-off between speed and compactness, making it the most suitable candidate for real-time active bearing systems.
Results showed that higher eccentricities combined with inward radial and tilt adjustments significantly increase film pressure, enhancing load support but also introducing higher frictional forces and side leakage. For an inward radial adjustment of 38.4 µm, lower attitude angles keep the journal closer to the vertical load line, ensuring better alignment, a stable lubricant film, and improved dynamic performance. These findings emphasize the importance of balancing operational stability, load capacity, and frictional losses when designing adjustable fluid film bearings. This work offers a valuable foundation for incorporating ML-based predictive tools into the design and control of active bearings, enabling real-time optimization while minimizing computational effort. The strong agreement between predicted and actual responses across multiple error metrics supports the adequacy of the dataset for the present application, while acknowledging that future work may explore physics-informed data augmentation strategies to expand coverage. Future research could expand this approach to include dynamic performance prediction and active control under different load and speed conditions, further enhancing the capabilities of intelligent bearing systems.
Author Contributions
Conceptualization, G.H. and S.K.B.; methodology, G.H. and S.K.B.; software, S.K.B.; validation, G.H., R.M. and S.K.B.; formal analysis, G.H. and S.K.B.; investigation, G.H. and S.K.B.; resources, R.M., N.K. and D.D.; data curation, G.M.C., D.D. and N.K.; writing—original draft preparation, G.H. and S.K.B.; writing—review and editing, G.H., N.K. and S.K.B.; visualization, G.H., R.M. and S.K.B.; supervision, D.D. and G.M.C.; project administration, D.D. and G.M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Acknowledgments
The authors would like to thank the institution for their valuable support and cooperation during this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| C | Pad clearance (m) |
| R | Journal Radius (m) |
| e | Journal eccentricity (m), |
| F | friction force (N), |
| h | Fluid film thickness (m), |
| L | Length of bearing (m) |
| N’ | Journal speed (rps) |
| p | steady state pressures (N/m2), |
| Lubricant supply pressures (N/m2) | |
| Q | flow leak (m3/s), |
| Radj | radial adjustments (m) |
| t | time (s) |
| Journal load (N), | |
| radial load component (N), | |
| Transverse load component (N), | |
| U | |
| x | |
| z | |
| Bearing pad angle (rad) | |
| tilted angle of pads (rad) | |
| lubricant viscosity (Ns/m2) | |
| Shearing force (N/m2) | |
| bearing number, | |
| coefficient of friction | |
| friction variable, | |
| attitude angle (rad) | |
| assumed attitude angle (rad) | |
| S | Sommerfeld number, |
| journal angular velocity (rad/s) |
References
- Santos, I.F.; Russo, F.H. Tilting-Pad Journal Bearings with Electronic Radial Oil Injection. J. Tribol. 1998, 120, 583–594. [Google Scholar] [CrossRef]
- Palazzolo, A.B.; Lin, R.R.; Alexander, R.M.; Kascak, A.F.; Montague, J. Piezoelectric Pushers for Active Vibration Control of Rotating Machinery. J. Vib. Acoust. 1989, 111, 298–305. [Google Scholar] [CrossRef]
- Krodkiewski, J.M.; Cen, Y.; Sun, L. Improvement of Stability of Rotor System by Introducing a Hydraulic Damper into an Active Journal Bearing. Int. J. Rotating Mach. 1997, 3, 45–52. [Google Scholar] [CrossRef]
- Santos, I.F. On the future of controllable fluid film bearings. Mech. Ind. 2011, 12, 275–281. [Google Scholar] [CrossRef]
- Santos, I. Controllable Sliding Bearings and Controllable Lubrication Principles—An Overview. Lubricants 2018, 6, 16. [Google Scholar] [CrossRef]
- Nicoletti, R.; Santos, I.F. Linear and non-linear control techniques applied to actively lubricated journal bearings. J. Sound Vib. 2003, 260, 927–947. [Google Scholar] [CrossRef]
- Breńkacz, Ł.; Witanowski, Ł.; Drosińska-Komor, M.; Szewczuk-Krypa, N. Research and applications of active bearings: A state-of-the-art review. Mech. Syst. Signal Process. 2021, 151, 107423. [Google Scholar] [CrossRef]
- Chasalevris, A.; Dohnal, F. A Journal Bearing with Variable Geometry for the Reduction of the Maximum Amplitude During Passage Through Resonance. J. Vib. Acoust. 2012, 134, 061005. [Google Scholar] [CrossRef]
- Sun, L.; Krodkiewski, J.M.; Cen, Y. Self-Tuning Adaptive Control of Forced Vibration in Rotor Systems using an Active Journal Bearing. J. Sound Vib. 1998, 213, 1–14. [Google Scholar] [CrossRef]
- Santos, I.F. On the Adjusting of the Dynamic Coefficients of Tilting-Pad Journal Bearings. Tribol. Trans. 1995, 38, 700–706. [Google Scholar] [CrossRef]
- Deckler, D.C.; Veillette, R.J.; Braun, M.J.; Choy, F.K. Simulation and Control of an Active Tilting-Pad Journal Bearing. Tribol. Trans. 2004, 47, 440–458. [Google Scholar] [CrossRef]
- Cai, Z.; de Queiroz, M.S.; Khonsari, M.M. Adaptive control of active tilting-pad bearings. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 4, pp. 2907–2912. [Google Scholar]
- Wu, A.; De Queiroz, M. A New Active Tilting-Pad Bearing: Nonlinear Modeling and Feedback Control. Tribol. Trans. 2010, 53, 755–763. [Google Scholar] [CrossRef]
- Varela, A.C.; García, A.B.; Santos, I.F. Modelling of LEG tilting pad journal bearings with active lubrication. Tribol. Int. 2017, 107, 250–263. [Google Scholar] [CrossRef]
- Salazar, J.G.; Santos, I.F. Active tilting-pad journal bearings supporting flexible rotors: Part I—The hybrid lubrication. Tribol. Int. 2017, 107, 94–105. [Google Scholar] [CrossRef]
- Salazar, J.G.; Santos, I.F. Active tilting-pad journal bearings supporting flexible rotors: Part II—The model-based feedback-controlled lubrication. Tribol. Int. 2017, 107, 106–115. [Google Scholar] [CrossRef]
- Urreta, H.; Leicht, Z.; Sanchez, A.; Agirre, A.; Kuzhir, P.; Magnac, G. Hydrodynamic Bearing Lubricated with Magnetic Fluids. J. Intell. Mater. Syst. Struct. 2010, 21, 1491–1499. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; Lopez de Lacalle, L.N. Actively lubricated hybrid journal bearings based on magnetic fluids for high-precision spindles of machine tools. J. Intell. Mater. Syst. Struct. 2019, 30, 2257–2271. [Google Scholar] [CrossRef]
- Bompos, D.A.; Nikolakopoulos, P.G. CFD simulation of magnetorheological fluid journal bearings. Simul. Model. Pract. Theory 2011, 19, 1035–1060. [Google Scholar] [CrossRef]
- Bompos, D.A.; Nikolakopoulos, P.G. Experimental and Analytical Investigations of Dynamic Characteristics of Magnetorheological and Nanomagnetorheological Fluid Film Journal Bearing. J. Vib. Acoust. 2016, 138, 031012. [Google Scholar] [CrossRef]
- Bompos, D.A.; Nikolakopoulos, P.G. Rotordynamic Analysis of a Shaft Using Magnetorheological and Nanomagnetorheological Fluid Journal Bearings. Tribol. Trans. 2016, 59, 108–118. [Google Scholar] [CrossRef]
- Chasalevris, A.; Dohnal, F. Vibration quenching in a large scale rotor-bearing system using journal bearings with variable geometry. J. Sound Vib. 2014, 333, 2087–2099. [Google Scholar] [CrossRef]
- Chasalevris, A.; Dohnal, F. Improving stability and operation of turbine rotors using adjustable journal bearings. Tribol. Int. 2016, 104, 369–382. [Google Scholar] [CrossRef]
- Chasalevris, A.; Dohnal, F. Modal interaction and vibration suppression in industrial turbines using adjustable journal bearings. J. Phys. Conf. Ser. 2016, 744, 012156. [Google Scholar] [CrossRef]
- Martin, J.K.; Parkins, D.W. Theoretical Studies of a Continuously Adjustable Hydrodynamic Fluid Film Bearing. J. Tribol. 2002, 124, 203–211. [Google Scholar] [CrossRef]
- Martin, J.K. Measuring the performance of a novel fluid film bearing supporting a rotor on a stationary shaft, by non-contacting means. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 2004, 218, 143–151. [Google Scholar] [CrossRef]
- Pai, R.; Parkins, D.W. Performance Characteristics of an Innovative Journal Bearing with Adjustable Bearing Elements. J. Tribol. 2018, 140, 041705. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, Y.; Xu, H.; Pei, S.; Zhang, L. An experimental study on vibration suppression of adjustable elliptical journal bearing-rotor system in various vibration states. Mech. Syst. Signal Process. 2020, 141, 106477. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, H.; Zhang, L.; Xing, Y.; Guo, Y. Vibration suppression mechanism research of adjustable elliptical journal bearing under synchronous unbalance load. Tribol. Int. 2019, 132, 185–198. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, H. Effect of radial clearance on the dynamic behavior of adjustable journal bearings in turbulent and laminar flow regimes. AIP Adv. 2023, 13, 025362. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, H.; Zhang, S.; Pei, S. Enhancing the stability of rotating machinery using a lower pad adjustable journal bearing. SN Appl. Sci. 2019, 1, 420. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. WIREs Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Hutter, F.; Kotthoff, L.; Vanschoren, J. (Eds.) Automated Machine Learning; The Springer Series on Challenges in Machine Learning; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-030-05317-8. [Google Scholar]
- Katsaros, K.P.; Nikolakopoulos, P.G. Performance Prediction Model for Hydrodynamically Lubricated Tilting Pad Thrust Bearings Operating under Incomplete Oil Film with the Combination of Numerical and Machine-Learning Techniques. Lubricants 2023, 11, 113. [Google Scholar] [CrossRef]
- Moschopoulos, M.; Rossopoulos, G.N.; Papadopoulos, C.I. Journal Bearing Performance Prediction Using Machine Learning and Octave-Band Signal Analysis of Sound and Vibration Measurements. Pol. Marit. Res. 2021, 28, 137–149. [Google Scholar] [CrossRef]
- Li, S.; Babin, A.; Shutin, D.; Kazakov, Y.; Liu, Y.; Chen, Z.; Savin, L. Active hybrid journal bearings with lubrication control: Towards machine learning. Tribol. Int. 2022, 175, 107805. [Google Scholar] [CrossRef]
- Hess, N.; Shang, L. Development of a Machine Learning Model for Elastohydrodynamic Pressure Prediction in Journal Bearings. J. Tribol. 2022, 144, 081603. [Google Scholar] [CrossRef]
- Ravindra, K.G.; Rudresh, B.M.; Prasanna Kumar, M.K.; Kumar, P. Optimization of design parameters to evaluate the performance of journal bearing: ANN approach. Mater. Today Proc. 2022, 54, 171–178. [Google Scholar] [CrossRef]
- Baş, H.; Karabacak, Y.E. Machine learning-based prediction of friction torque and friction coefficient in statically loaded radial journal bearings. Tribol. Int. 2023, 186, 108592. [Google Scholar] [CrossRef]
- Shutin, D.; Fetisov, A.; Savin, L. Optimization of Journal Bearings Considering Their Adjustable Design and Rotor Dynamics. In Proceedings of the International Conference on Rotor Dynamics, Beijing, China, 18–21 September 2023; pp. 364–376. [Google Scholar]
- Shutin, D.; Bondarenko, M.; Polyakov, R.; Stebakov, I.; Savin, L. Method for On-Line Remaining Useful Life and Wear Prediction for Adjustable Journal Bearings Utilizing a Combination of Physics-Based and Data-Driven Models: A Numerical Investigation. Lubricants 2023, 11, 33. [Google Scholar] [CrossRef]
- Rossopoulos, G.N.; Papadopoulos, C.I. A journal bearing performance prediction method utilizing a machine learning technique. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 1993–2003. [Google Scholar] [CrossRef]
- Gheller, E.; Chatterton, S.; Panara, D.; Turini, G.; Pennacchi, P. Artificial neural network for tilting pad journal bearing characterization. Tribol. Int. 2023, 188, 108833. [Google Scholar] [CrossRef]
- Badawi, M.B.; Awad, T.H.; El Fahham, I.M. Application of artificial intelligence for the prediction of plain journal bearings performance. Alexandria Eng. J. 2022, 61, 9011–9029. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, V.; Singh, A.K. Prediction of maximum pressure of journal bearing using ANN with multiple input parameters. Aust. J. Mech. Eng. 2022, 20, 1069–1078. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Y.; Yang, J.; Wu, M.; Yang, A.; Li, J. Optuna-DFNN: An Optuna framework driven deep fuzzy neural network for predicting sintering performance in big data. Alexandria Eng. J. 2024, 97, 100–113. [Google Scholar] [CrossRef]
- Jiang, X.; Yan, W.; Xing, H.; Feng, P.; Sun, J.; Fan, Y. A highly accurate and interpretable gradient boosting machine learning model for predicting permeability in strongly heterogeneous reservoirs using the Optuna framework. J. Geophys. Eng. 2025, 22, 810–823. [Google Scholar] [CrossRef]
- Hariharan, G.; Pai, R. Analysis on the steady state performance of a multi pad externally adjustable fluid film bearing. Ind. Lubr. Tribol. 2019, 71, 803–809. [Google Scholar] [CrossRef]
- Hariharan, G.; Pai, R. Mathematical formulation of a modified film thickness equation for multipad externally adjustable fluid film bearing. Cogent Eng. 2018, 5, 1493672. [Google Scholar] [CrossRef]
- Ganesha, A.; Pai, R.; Rao, S.; Khader, S.A. Multi-objective optimization and significant analysis of bearing element adjustments on the static performance of an innovative adjustable bearing through design of experiment. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 1820–1833. [Google Scholar] [CrossRef]
- Bian, C.; Jia, C.; Li, J.; Chen, X.; Wang, P. Rolling bearing fault diagnosis under small sample conditions based on WDCNN-BiLSTM Siamese network. Sci. Rep. 2025, 15, 29591. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, J.K.; Samikannu, R. Application of Random Forest Algorithm on Feature Subset Selection and Classification and Regression. In Proceedings of the 2017 World Congress on Computing and Communication Technologies (WCCCT), Tiruchirappalli, India, 2–4 February 2017; pp. 65–68. [Google Scholar]
- Bhat, S.K.; Ranjan, A.; Upadhyaya, Y.S.; Managuli, V. Fatigue strength prediction of Cobalt alloys using material composition and monotonic properties: ML-based approach. Mater. Res. Express 2025, 12, 046505. [Google Scholar] [CrossRef]
- Zhu, J.; Su, Y.; Liu, Z.; Liu, B.; Sun, Y.; Gao, W.; Fu, Y. Real-time biomechanical modelling of the liver using LightGBM model. Int. J. Med. Robot. Comput. Assist. Surg. 2022, 18, e2433. [Google Scholar] [CrossRef]
- Deepak, G.D.; Bhat, S.K. Predictive modeling and optimization of pin electrode based cold plasma using machine learning approach. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 2045–2064. [Google Scholar] [CrossRef]
- Doreswamy, D.; Bhat, S.K.; Hiremath, P.; Shreyas, D.S.; Bongale, A. ANN-based predictive modelling of the effect of abrasive water-jet parameters on the surface roughness of AZ31 Mg alloy. Manuf. Rev. 2024, 11, 21. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; ACM: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).