Dynamical Regimes in a Delayed Predator–Prey Model with Predator Hunting Cooperation: Bifurcations, Stability, and Complex Dynamics

Abstract

In this paper, a predator–prey model with hunting cooperation and maturation delay is studied. Through theoretical analysis, we investigate the existence of multiple stability switches of the positive equilibrium. By applying Hopf bifurcation theory, the conditions for Hopf bifurcation are derived, indicating the emergence of periodic solutions as the maturation delay passes through critical values. Utilizing center manifold theory and normal form analysis, we determine the stability and direction of the bifurcating orbits. Numerical simulations are performed to validate the theoretical results. Furthermore, the simulations vividly demonstrate the appearance of period-doubling bifurcations, which is the onset of chaotic behavior. Bifurcation diagrams and phase portraits are employed to precisely characterize the transition processes from a stable equilibrium to periodic, period-doubling solutions and chaotic states under different maturation delay values. The study reveals the significant influence of maturation delay on the stability and complex dynamics of predator–prey systems with hunting cooperation.

1. Introduction

Defined as groups of the same species co-existing within a specific geographic locale and temporal period, populations are influenced by a variety of inter-species interactions, with predation playing a pivotal role in both the persistence and decline of these groups. Predator–prey models are well recognized in both ecological and mathematical research, underscored by their significant applications in ecological forecasting and their dynamic complexity, as highlighted in [1]. The dynamic interplay between predator and prey populations has been rigorously analyzed by applying differential equations within ecological modeling [2]. Central to the study of these interactions is the functional response, which quantifies the rate at which predators consume prey relative to the prey density, thereby shaping the dynamics of these interactions. Among the diverse array of models used to describe these ecological dynamics, the Holling types of functional response [3] and their generalizations have been widely discussed in the literature [4,5,6]. These functional responses offer detailed and valuable insight into the behavior and stability of predator–prey systems, thereby enriching our understanding of the complex interactions within ecological communities.

Cooperative hunting is a captivating and widespread phenomenon in the ecological realm that can be seen in a diverse spectrum of organisms. On land, terrestrial carnivores such as lions [7], wolves [8], African wild dogs [9], and chimpanzees [10] engage in this behavior. In addition, it is also prevalent among aquatic organisms [11], as well as invertebrates like ants [12] and spiders [13], and even some bird species [14]. As a result of this cooperative hunting behavior, the predator’s attack rate is influenced by both prey and predator densities. In recent years, there has been a growing trend of studies focusing on using functional responses to describe this cooperative hunting phenomenon. For example, Cosner et al. [15] probed into predator aggregation. Subsequently, Berec [16] generalized the Holling type-II response by taking into account the attack rate and handling time. Continuing this line of exploration, Alves and Hilker [17] incorporated a cooperation term into the attack rate and presented the following hunting cooperative functional response:

$$p(u,v)=(\lambda +av)u,$$

(1)

where u represents the prey density, v represents the predator density, $\lambda >0$ denotes the attack rate per predator on the prey and $a\ge 0$ is the predator cooperation in hunting. They discovered that cooperative hunting can enhance predator persistence and is a form of foraging facilitation that may lead to strong Allee effects. In the wake of their research, an array of biological factors, such as the Allee effect, fear effect and prey refuge, along with spatial diffusion, have been incorporated into predator–prey models that incorporate cooperative hunting [18,19,20]. More recently, cooperative hunting has been analyzed under various ecological frameworks that reveal distinct dynamical consequences. Saha et al. [21] examined the dynamic characteristics of the system upon introducing a nonlocal term in cooperative contexts—wherein complex spatiotemporal patterns and pattern transitions emerge—and also addressed the existence of travelling wave solutions for predator–prey interactions involving this nonlocal cooperative hunting strategy. Ryu et al. [22] investigated a prey-taxis system with cooperative hunting and time delay, showing that predator cooperation significantly alters Hopf bifurcation thresholds and generates delay-induced oscillations. Hafdane et al. [23] focused on a reaction–diffusion system with time delay and found that cooperative hunting induces spatially heterogeneous patterns through Turing instability. Mo et al. [24] studied a stage-structured system and demonstrated that predator cooperation promotes population persistence under maturation constraints. Du et al. [25] explored how the combined effects of cooperation and the Allee phenomenon impact global stability, identifying conditions for population extinction or coexistence. Concurrently, Jang et al. [26] incorporated prey refuge into cooperative hunting models and uncovered bistable dynamics, where predator persistence depends critically on initial population sizes. These studies underscore that cooperative hunting, when combined with realistic ecological factors like time delay, spatial effects, or prey defense, can drive nontrivial bifurcations, multistability, and rich pattern formation. Such findings not only enrich the theoretical framework of ecological models and enable more accurate simulations of predator–prey interactions in the real world but also foster a deeper understanding of complex dynamics within ecosystems.

In addition, it is of great significance to incorporate time delays into systems in order to effectively reflect the dynamic behaviors of models that are influenced by past events. There are different types of delays observed in predator–prey systems, e.g., maturation delay [27,28], gestation delay [29,30], incubation delay [31], and dispersal delay [32]. Such delays make the system much more realistic in nature. The dynamics of predator–prey models with delays have different features and can exhibit more complex dynamical behaviors, such as the existence of multiple equilibria, Hopf bifurcation, Bogdanov–Takens bifurcation, homoclinic loop, and even chaos (see [33,34,35] and references therein for more related work). Here, we focus on maturation delay—the time required for juvenile individuals to reach reproductive maturity. Enatsu et al. [36] showed that the maturation delay increases the likelihood of predator species extinction and alters the bifurcation curves and bifurcation thresholds of the non-delayed system. Krishnanand [37] revealed that delay plays a stabilizing role in the prey–predator system with hunting cooperation; with discrete delay as the bifurcation parameter, the stability of coexisting equilibrium points, the existence of Hopf bifurcation, and novel dynamical behaviors (including the codimension-two Bogdanov–Takens bifurcation point) are investigated. Meanwhile, Xu et al. [38] investigated a delayed reaction–diffusion system with both group defense and cooperative hunting, identifying the occurrence of Turing–Hopf bifurcation and showing how time delay and spatial interactions jointly contribute to complex oscillatory and spatially heterogeneous population dynamics. These findings underscore the importance of maturation delay as a key factor in ecological modeling, particularly when coupled with other nonlinear mechanisms such as cooperation and spatial effects.

A typical time delay appears in the prey-specific growth term, based on the assumption that in the absence of predators, the prey satisfies Hutchinson’s equation (also called the delayed logistic equation) [39,40]:

$${\displaystyle \frac{\mathrm{d}u}{\mathrm{d}t}}=ru\left(1-{\displaystyle \frac{u(t-\tau )}{K}}\right),$$

(2)

where r is intrinsic growth rate, K is the environmental carrying capacity, and $\tau$ denotes the time delay due to the maturation of the prey. Hutchinson’s equation extends the classical logistic model by accounting for the fact that resource limitations depend on the population density at an earlier time rather than instantaneously. This delay can induce oscillations or even destabilize the equilibrium, providing a mechanistic explanation for observed fluctuations in natural populations. These intricate dynamics have important ecological and biological interpretations, affecting aspects such as species coexistence, population stability, and the overall structure of ecosystems. In ecological scenarios, this formulation illustrates the interplay between growth restrictions and developmental delays, presenting a more realistic framework for modeling predator–prey systems.

Taking into account the hunting cooperative functional response (1) and the delayed logistic Equation (2), we consider the following delayed predator–prey model:

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}u}{\mathrm{d}t}}=ru\left({\displaystyle 1-\frac{u(t-\tau )}{K}}\right)-(\lambda +av)uv,\hfill \\ {\displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}}=\mu \left(\lambda +av\right)uv-\delta v,\hfill \end{array}\right.$$

(3)

where $\mu$ is the conversion efficiency, $\delta$ is the natural death rate of predators, and the other parameters are as above. When $\tau =0$, Alves and Hilker [17] numerically investigated the positive equilibrium’s existence and stability, showing hunting cooperation benefits predators by increasing attack rate. Song et al. [41] explicitly analyzed the existence, stability, and Hopf bifurcation of the positive equilibrium for the non-diffusive system, showing that hunting cooperation affects both its existence and stability, and investigated stability and cross-diffusion-driven Turing instability for the diffusive system based on self-diffusion and cross-diffusion coefficient relationships. This research examines how cooperative hunting behaviors influence population dynamics, while simultaneously evaluating the stabilizing effects of time delay $\tau$ in system (3). Our analytical results demonstrate that the temporal delay provides a biologically meaningful mechanism for system stabilization.

The rest of this paper proceeds as follows. In Section 2, we investigate the stability and Hopf bifurcation near the positive equilibrium. In Section 3, we utilize the normal form approach and center manifold theory to analyze the direction, stability, and period of the bifurcating periodic solution at critical values of $\tau$. Section 4 presents numerical examples aimed at verifying the theoretical results and the newly discovered chaotic behavior. Finally, the paper ends with a conclusion.

2. Stability of the Positive Equilibrium and Hopf Bifurcation

For simplicity, we will analyze a nondimensionalized form of model (3). Let

$$\tilde{u}={\displaystyle \frac{\mu \lambda }{\delta }}u,\tilde{v}={\displaystyle \frac{\lambda }{\delta }}v,\tilde{t}=\delta t,$$

and rescale the parameters via

$$\tilde{\sigma }={\displaystyle \frac{r}{\delta }},\tilde{\beta }={\displaystyle \frac{\mu \lambda K}{\delta }},\tilde{\alpha }={\displaystyle \frac{a\delta }{{\lambda }^2}},\tilde{\tau }=\delta \tau .$$

After dropping the tildes, the nondimensionalized system of (3) becomes

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}u}{\mathrm{d}t}}=\sigma u\left[{\displaystyle 1-\frac{u(t-\tau )}{\beta }}\right]-(1+\alpha v)uv,\hfill \\ {\displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}}=v\left((1+\alpha v)u-1\right).\hfill \end{array}\right.$$

(4)

Let $E_{*}=(u_{*},v_{*})$ denote the positive equilibrium of system (4). Then $u_{*}=1/(1+\alpha v_{*})$, and $v_{*}$ is a positive root of the following cubic polynomial equation:

$$f\left(v\right):=\beta {\alpha }^2{v}^3+2\beta \alpha v^2+\beta (1-\alpha \sigma )v+\sigma (1-\beta )=0.$$

System (4) can have one or two positive equilibria depending on the relationship of the parameters $\sigma ,\alpha ,\beta$ (see details in [41]). In what follows, we assume that system (4) admits a positive equilibrium $E_{*}=(u_{*},v_{*})$. When $\tau =0$, the characteristic matrix at $E_{*}$ is $A={\left(a_{ij}\right)}_{2\times 2}$, where

$$a_{11}=-{\displaystyle \frac{\sigma u_{*}}{\beta }}<0,a_{12}=-(1+2\alpha v_{*})u_{*}<0,a_{21}=v_{*}+\alpha v_{*}^2>0,a_{22}=\alpha u_{*}{v}_{*}>0.$$

(5)

To investigate the effects of the delay on the stability, we make the following assumption:

$$\left(\mathrm{H}\right)T=a_{11}+a_{22}=-u_{*}\left({\displaystyle \frac{\sigma }{\beta }}-\alpha v_{*}\right)<0,D=a_{11}{a}_{22}-a_{12}{a}_{21}=(1+2\alpha v_{*})v_{*}-{\displaystyle \frac{\sigma \alpha }{\beta }}{u}_{*}^2{v}_{*}>0,$$

which implies that the positive equilibrium $E^{*}$ of system (4) (with $\tau =0$) is asymptotically stable.

From the linearized system of (4), we obtain the characteristic equation below:

$${\lambda }^2-a_{22}\lambda -a_{12}{a}_{21}+a_{11}(a_{22}-\lambda )e^{-\lambda \tau }=0.$$

(6)

Suppose that $\lambda =i\omega$ ($\omega >0$) is a root of Equation (6); we then have

$$-{\omega }^2-i{a}_{22}\omega -a_{12}{a}_{21}+a_{11}(a_{22}-i\omega )(cos\omega \tau -isin\omega \tau )=0.$$

Separating the real and imaginary parts yields

$$\left\{\begin{array}{c}{\omega }^2+a_{12}{a}_{21}=a_{11}{a}_{22}cos\omega \tau -a_{11}\omega sin\omega \tau ,\hfill \\ -a_{22}\omega =a_{11}{a}_{22}sin\omega \tau +a_{11}\omega cos\omega \tau ,\hfill \end{array}\right.$$

(7)

which leads to the following quadratic equation with respect to ${\omega }^2$:

$$g\left({\omega }^2\right)={\omega }^4+(2a_{12}{a}_{21}+a_{22}^2-a_{11}^2){\omega }^2+a_{12}^2{a}_{21}^2-a_{11}^2{a}_{22}^2=0.$$

Denote

$$\begin{array}{cc}\hfill {\Delta }_g& ={(2a_{12}{a}_{21}+a_{22}^2-a_{11}^2)}^2-4(a_{12}^2{a}_{21}^2-a_{11}^2{a}_{22}^2)\hfill \\ \hfill & ={(a_{22}^2+a_{11}^2)}^2+4a_{12}{a}_{21}(a_{22}^2-a_{11}^2).\hfill \end{array}$$

From (5) and condition (H), we have

$$a_{22}^2-a_{11}^2<0,2a_{12}{a}_{21}+a_{22}^2-a_{11}^2<0,a_{12}^2{a}_{21}^2-a_{11}^2{a}_{22}^2>0,{\Delta }_g>0,$$

which implies that $g\left({\omega }^2\right)=0$ has two positive roots, given by

$${\omega }_{\pm }^2={\displaystyle \frac{(a_{11}^2-a_{22}^2-2a_{12}{a}_{21})\pm \sqrt{{\Delta }_g}}{2}}.$$

(8)

On the other hand, from Equation (7), we obtain

$$cos\omega \tau ={\displaystyle \frac{a_{12}{a}_{21}{a}_{22}}{a_{11}(a_{22}^2+{\omega }^2)}},sin\omega \tau =-{\displaystyle \frac{{\omega }^3+(a_{22}^2+a_{12}{a}_{21})\omega }{a_{11}(a_{22}^2+{\omega }^2)}}.$$

Combining (5) and (8) leads to

$$cos\omega \tau >0,sin\omega \tau \left\{\begin{array}{c}>0,\omega ={\omega }_{+},\hfill \\ <0,\omega ={\omega }_{-};\hfill \end{array}\right.$$

(9)

then, we find the value of ${\tau }_j^{\pm }$ by solving for $\tau$ as follows:

$$\left\{\begin{array}{c}{\displaystyle {\tau }_j^{+}=\frac{1}{{\omega }_{+}}\left[arccos\frac{a_{12}{a}_{21}{a}_{22}}{a_{11}(a_{22}^2+{\omega }_{+}^2)}+2j\pi \right],j=0,1,2\cdots ,}\hfill \\ {\displaystyle {\tau }_j^{-}=\frac{1}{{\omega }_{-}}\left[2\pi -arccos\frac{a_{12}{a}_{21}{a}_{22}}{a_{11}(a_{22}^2+{\omega }_{-}^2)}+2j\pi \right],j=0,1,2\cdots .}\hfill \end{array}\right.$$

(10)

From (8) and (9), it is easy to see that ${\omega }_{+}{\tau }_0^{+}<{\omega }_{-}{\tau }_0^{-}$; so, ${\tau }_0^{-}>{\tau }_0^{+}$. Denote by

$$\lambda \left(\tau \right)=\alpha \left(\tau \right)+i\omega \left(\tau \right)$$

the root of Equation (6) satisfying

$$\alpha \left({\tau }_j^{\pm }\right)=0,\omega \left({\tau }_j^{\pm }\right)={\omega }_{\pm }.$$

We can obtain the following transversality conditions:

$${\left({\displaystyle \frac{\mathrm{d}Re\left(\lambda \right)}{\mathrm{d}\tau }}\right)}_{\lambda =i{\omega }_{+}}^{-1}={\displaystyle \frac{\sqrt{{\Delta }_g}}{a_{11}^2(a_{22}^2+{\omega }_{+}^2)}}>0,{\left({\displaystyle \frac{\mathrm{d}Re\left(\lambda \right)}{\mathrm{d}\tau }}\right)}_{\lambda =i{\omega }_{-}}^{-1}={\displaystyle \frac{-\sqrt{{\Delta }_g}}{a_{11}^2(a_{22}^2+{\omega }_{-}^2)}}<0.$$

Then, we have the following results.

Theorem 1.

Assume that condition $\left(H\right)$ holds, and let ${\tau }_j^{\pm }$ be defined by Equation (10).

(i)

If ${\tau }_0^{-}>{\tau }_1^{+}$, then the positive equilibrium $E_{*}(u_{*},v_{*})$ of system (4) has a single stability switch at $\tau ={\tau }_0^{+}$, that is, $E_{*}(u_{*},v_{*})$ is locally asymptotically stable when $0\le \tau <{\tau }_0^{+}$ and unstable when $\tau >{\tau }_0^{+}$.

(ii)

If ${\tau }_0^{-}<{\tau }_1^{+}$, then the positive equilibrium $E_{*}(u_{*},v_{*})$ of system (4) has multiple stability switches, that is, there is a positive integer N such that

$$0<{\tau }_0^{+}<{\tau }_0^{-}<{\tau }_1^{+}<{\tau }_1^{-}<\cdots <{\tau }_{N-1}^{+}<{\tau }_{N-1}^{-}<{\tau }_N^{+}<{\tau }_{N+1}^{+}<{\tau }_N^{-}<\cdots ;$$

when

$$\tau \in [0,{\tau }_0^{+})\cup ({\tau }_0^{-},{\tau }_1^{+})\cup \cdots \cup ({\tau }_{N-1}^{-},{\tau }_N^{+}),$$

$E_{*}(u_{*},v_{*})$ is locally asymptotically stable, and when

$$\tau \in ({\tau }_0^{+},{\tau }_0^{-})\cup ({\tau }_1^{+},{\tau }_1^{-})\cup \cdots \cup ({\tau }_{N-1}^{+},{\tau }_{N-1}^{-})\cup ({\tau }_N^{+},+\infty ),$$

$E_{*}(u_{*},v_{*})$ is unstable.

(iii)

System (6) undergoes a Hopf bifurcation at $E_{*}(u_{*},v_{*})$ when $\tau ={\tau }_j^{\pm },j=0,1,2\cdots$.

3. Direction and Stability of the Hopf Bifurcation

In Theorem 1, we show that system (4) undergoes a Hopf bifurcation from the positive equilibrium $\left(u_{*},v_{*}\right)$ at critical values ${\tau }_j^{\pm },j=0,1,2\cdots$. In this section, we determine the direction, stability, and period of these periodic solutions emerging from the positive equilibrium of system (4) at these critical values of $\tau$ by adopting the normal form theory and center manifold reduction developed by Hassard et al. [42].

Without loss of generality, select one critical value ${\tau }_0^{+}$ and set $\tau ={\tau }_0^{+}+\mu$. Then, $\mu$ = 0 corresponds to the Hopf bifurcation value of system (4). Let $u_1\left(t\right)=u\left(t\right)-u_{*},u_2\left(t\right)=v\left(t\right)-v_{*}$. In the fixed phase space $C=C([-\tau ,0],{\mathbb{R}}^2)$, system (4) can be rewritten as

$$\left\{\begin{array}{cc}\hfill {\displaystyle \frac{d{u}_1}{dt}}& =a_{11}{u}_1(t-\tau )+a_{12}{u}_2\left(t\right)+\sum _{\begin{array}{c}i+j+l\ge 2\end{array}}{\displaystyle \frac{f_{ijl}^{\left(1\right)}}{i!j!l!}}{u}_1^i\left(t\right)u_2^j\left(t\right)u_1^l(t-\tau ),\hfill \\ \hfill {\displaystyle \frac{d{u}_2}{dt}}& =a_{21}{u}_1\left(t\right)+a_{22}{u}_2\left(t\right)+\sum _{\begin{array}{c}i+j\ge 2\end{array}}{\displaystyle \frac{f_{ij}^{\left(2\right)}}{i!j!}}{u}_1^i\left(t\right)u_2^j\left(t\right),\hfill \end{array}\right.$$

(11)

where

$$\begin{array}{cc}\hfill f^{\left(1\right)}& =\sigma u\left({\displaystyle 1-\frac{u(t-\tau )}{\beta }}\right)-(1+\alpha v)uv,f^{\left(2\right)}=v((1+\alpha v)u-1).\hfill \\ \hfill f_{ijl}^{\left(1\right)}& ={\displaystyle \frac{{\partial }^{i+j+l}}{\partial u^i\left(t\right)\partial v^j\left(t\right)\partial u^l(t-\tau )}}{f}^{\left(1\right)}{{|}_{(u_{*},v_{*},u_{*})},f_{ij}^{\left(2\right)}={\displaystyle \frac{{\partial }^{i+j}}{\partial u^i\left(t\right)\partial v^j\left(t\right)}}{f}^{\left(2\right)}|}_{(u_{*},v_{*})},i,j,l\ge 0,\hfill \end{array}$$

with

$$\begin{array}{cccccccc}\hfill f_{110}^{\left(1\right)}& =-2\alpha v_{*}-1,\hfill & \hfill f_{020}^{\left(1\right)}& =-2\alpha u_{*},\hfill & \hfill f_{101}^{\left(1\right)}& =-{\displaystyle \frac{\sigma }{\beta }},\hfill & \hfill f_{120}^{\left(1\right)}& =-2\alpha ,\hfill \\ \hfill f_{11}^{\left(2\right)}& =2\alpha v_{*}+1,\hfill & \hfill f_{02}^{\left(2\right)}& =2\alpha u_{*},\hfill & \hfill f_{12}^{\left(2\right)}& =2\alpha .\hfill \end{array}$$

Then system (11) reduces to

$${\displaystyle \frac{du}{dt}}=L_{\mu }\left(u_t\right)+f(\mu ,u_t),$$

(12)

where $u={(u_1\left(t\right),u_2\left(t\right))}^T\in {\mathbb{R}}^2,u_t=u(t+\theta )\in C,L_{\mu }:C\to {\mathbb{R}}^2,f:\mathbb{R}\times C\to {\mathbb{R}}^2,$

$$\begin{array}{c}{L}_{\mu }\varphi =M\varphi \left(0\right)+N\varphi (-\tau ),M=\left(\begin{array}{cc}0& a_{12}\\ a_{21}& a_{22}\end{array}\right),N=\left(\begin{array}{cc}{a}_{11}& 0\\ 0& 0\end{array}\right),\hfill \end{array}$$

and

$$\begin{array}{c}\hfill f(\mu ,\varphi )=\left(\begin{array}{c}{\displaystyle \sum _{\begin{array}{c}i+j+l\ge 2\end{array}}\frac{f_{ijl}^{\left(1\right)}}{i!j!l!}{\varphi }_1^i\left(0\right){\varphi }_2^j\left(0\right){\varphi }_1^l(-\tau )}\\ {\displaystyle \sum _{\begin{array}{c}i+j\ge 2\end{array}}\frac{f_{ij}^{\left(2\right)}}{i!j!}{\varphi }_1^i\left(0\right){\varphi }_2^j\left(0\right)}\end{array}\right).\end{array}$$

(13)

According to the Riesz representation theorem, there exists a matrix function $\eta (\mu ,\theta )$ of bounded variation on $[-\tau ,0]$ such that [43]

$$\begin{array}{c}{L}_{\mu }\varphi ={\int }_{-\tau }^0{\mathrm{d}}_{\theta }\eta (\mu ,\theta )\varphi \left(\theta \right)\mathrm{for}\varphi \in C.\hfill \end{array}$$

(14)

In fact, we can choose

$$\begin{array}{c}\eta (\mu ,\theta )=M\delta \left(\theta \right)-N\delta (\theta +\tau ),\hfill \end{array}$$

(15)

where $\delta$ is the Dirac delta function.

For $\varphi \in C^1([-\tau ,0],{\mathbb{R}}^2),$ define

$$A\left(\mu \right)\varphi \left(\theta \right)=\left\{\begin{array}{cc}{\displaystyle \frac{\mathrm{d}\varphi \left(\theta \right)}{\mathrm{d}\theta },}\hfill & \theta \in [-\tau ,0),\hfill \\ {\int }_{-\tau }^0{\mathrm{d}}_s\eta (\mu ,s)\varphi \left(s\right),\hfill & \theta =0,\hfill \end{array}\right.$$

(16)

and

$$R\left(\mu \right)\varphi \left(\theta \right)=\left\{\begin{array}{cc}0,\hfill & \theta \in [-\tau ,0),\hfill \\ f(\mu ,\varphi ),\hfill & \theta =0.\hfill \end{array}\right.$$

Thus, system (11) (or (12)) is equivalent to the abstract ordinary differential equation:

$${\displaystyle \frac{d{u}_t}{dt}}=A\left(\mu \right)u_t+R\left(\mu \right)u_t$$

(17)

For $\psi \in C^1([0,\tau ],{\left({\mathbb{R}}^2\right)}^{*}),$ define

$$A^{*}\psi \left(s\right)=\left\{\begin{array}{cc}{\displaystyle -\frac{\mathrm{d}\psi \left(s\right)}{\mathrm{d}s},}\hfill & s\in (0,\tau ],\hfill \\ {\int }_{-\tau }^0{\mathrm{d}}_t{\eta }^T(0,t)\psi (-t),\hfill & s=0,\hfill \end{array}\right.$$

and a bilinear inner product

$$\begin{array}{c}\langle \psi \left(s\right),\varphi \left(\theta \right)\rangle =\overline{\psi }\left(0\right)\varphi \left(0\right)-{\int }_{-\tau }^0{\int }_{\xi =0}^{\theta }\overline{\psi }(\xi -\theta )\mathrm{d}\eta \left(\theta \right)\varphi \left(\xi \right)\mathrm{d}\xi ,\hfill \end{array}$$

where $\eta \left(\theta \right)=\eta (0,\theta )$. Then, $A\left(0\right)$ and $A^{*}$ are adjoint operators, and $\pm i{\omega }_{+}$ are the eigenvalues of $A\left(0\right)$, which are also the eigenvalues of $A^{*}$. Assume that $q\left(\theta \right)={(1,\rho )}^T{e}^{i{\omega }_{+}\theta }$ is the eigenvector of $A\left(0\right)$ associated with $i{\omega }_{+}$, and $q^{*}\left(s\right)=B(1,\gamma )e^{i{\omega }_{+}s}$ is the eigenvector of $A^{*}$ corresponding to $-i{\omega }_{+}$. From the definition of $A^{*}$ and (14) and (15), we derive

$$q\left(0\right)={(1,\rho )}^T={(1,-{\displaystyle \frac{a_{21}}{a_{22}-i{\omega }_{+}}})}^T,q^{*}\left(0\right)=B(1,\gamma )=B\left(1,-{\displaystyle \frac{a_{12}}{a_{22}+i{\omega }_{+}}}\right).$$

To satisfy the normalization condition $\langle q^{*}\left(s\right),q\left(\theta \right)\rangle =1$, we need to compute the value B. Since

$$\begin{array}{cc}\hfill \langle q^{*}\left(s\right),q\left(\theta \right)\rangle & =\overline{B}\left[(1,\overline{\gamma }){(1,\rho )}^T-{\int }_{-{\tau }_0^{+}}^0{\int }_{\xi =0}^{\theta }(1,\overline{\gamma })e^{-i(\xi -\theta ){\omega }_{+}}\mathrm{d}\eta \left(\theta \right){(1,\rho )}^T{e}^{i\xi {\omega }_{+}}\mathrm{d}\xi \right]\hfill \\ & =\overline{B}\left[1+\overline{\gamma }\rho -{\int }_{-{\tau }_0^{+}}^0(1,\overline{\gamma })\theta e^{i{\omega }_{+}\theta }\mathrm{d}\eta \left(\theta \right){(1,\rho )}^T\right]\hfill \\ & =\overline{B}\left[1+\overline{\gamma }\rho +a_{11}{\tau }_0^{+}{e}^{-i{\omega }_{+}{\tau }_0^{+}}\right],\hfill \end{array}$$

to ensure that $\langle q^{*}\left(s\right),q\left(\theta \right)\rangle =1$ and $\langle q^{*}\left(s\right),\overline{q}\left(\theta \right)\rangle =0$, we choose

$$\begin{array}{c}\hfill B={\displaystyle \frac{1}{1+\gamma \overline{\rho }+a_{11}{\tau }_0^{+}{e}^{i{\omega }_{+}{\tau }_0^{+}}}}.\end{array}$$

Following Hassard et al. [42], we begin by calculating the coordinates for the center manifold $C_0$ at $\mu =0$. Consider $u_t$ as the solution of (12) when $\mu =0$. Define

$$\begin{array}{c}\hfill z\left(t\right)=\langle q^{*},u_t\rangle ,W(t,\theta )=u_t\left(\theta \right)-2\mathrm{Re}\left\{z\left(t\right)q\left(\theta \right)\right\}.\end{array}$$

(18)

On the center mainfold $C_0$, it follows that

$$\begin{array}{c}\hfill W(t,\theta )=W(z\left(t\right),\overline{z}\left(t\right),\theta ),\end{array}$$

where

$$\begin{array}{c}\hfill W(z\left(t\right),\overline{z}\left(t\right),\theta )=W_{20}\left(\theta \right){\displaystyle \frac{z^2}{2}}+W_{11}\left(\theta \right)z\overline{z}+W_{02}\left(\theta \right){\displaystyle \frac{{\overline{z}}^2}{2}}+\cdots ,\end{array}$$

and z and $\overline{z}$ represent the local coordinates of the center manifold $C_0$ in the directions of $q^{*}$ and ${\overline{q}}^{*}$, respectively. Here, W is real valued when $u_t$ is real, and we restrict our analysis to real solutions. For any solution $u_t\in C_0$ of (11) with $\mu =0$,

$$\begin{array}{cc}\hfill {\displaystyle \frac{dz}{dt}}& =i{\omega }_{+}z+{\overline{q}}^{*}\left(\theta \right)f(0,W(z\left(t\right),\overline{z}\left(t\right),\theta )+2\mathrm{Re}\left\{zq\left(\theta \right)\right\})\hfill \\ & =i{\omega }_{+}z+{\overline{q}}^{*}\left(0\right)f(0,W(z\left(t\right),\overline{z}\left(t\right),0)+2\mathrm{Re}\left\{zq\left(0\right)\right\})\hfill \\ & :=i{\omega }_{+}z+{\overline{q}}^{*}\left(0\right)f_0(z,\overline{z}),\hfill \end{array}$$

which is rewritten as

$${\displaystyle \frac{dz}{dt}}=i{\omega }_{+}z\left(t\right)+g(z,\overline{z}),$$

where

$$\begin{array}{c}\hfill g(z,\overline{z})={\overline{q}}^{*}\left(0\right)f_0(z,\overline{z})=g_{20}{\displaystyle \frac{z^2}{2}}+g_{11}z\overline{z}+g_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+g_{21}{\displaystyle \frac{z^2\overline{z}}{2}}+\cdots .\end{array}$$

(19)

Note that $u_t\left(\theta \right)=(u_{1t}\left(\theta \right),u_{1t}\left(\theta \right))=W(t,\theta )+zq\left(\theta \right)+\overline{z}\overline{q}\left(\theta \right)$, and $q\left(\theta \right)={(1,\rho )}^T{e}^{i{\omega }_{+}\theta }$; thus, we have

$$\begin{array}{cc}\hfill u_{1t}\left(0\right)& =z+\overline{z}+W_{20}^{\left(1\right)}\left(0\right){\displaystyle \frac{z^2}{2}}+W_{11}^{\left(1\right)}\left(0\right)z\overline{z}+W_{02}^{\left(1\right)}\left(0\right){\displaystyle \frac{{\overline{z}}^2}{2}}+\cdots ,\hfill \\ \hfill u_{1t}(-{\tau }_0^{+})& =e^{-i{\omega }_{+}{\tau }_0^{+}}z+e^{i{\omega }_{+}{\tau }_0^{+}}\overline{z}+W_{20}^{\left(1\right)}(-{\tau }_0^{+}){\displaystyle \frac{z^2}{2}}+W_{11}^{\left(1\right)}(-{\tau }_0^{+})z\overline{z}+W_{02}^{\left(1\right)}(-{\tau }_0^{+}){\displaystyle \frac{{\overline{z}}^2}{2}}+\cdots ,\hfill \\ \hfill u_{2t}\left(0\right)& =\rho z+\overline{\rho }\overline{z}+W_{20}^{\left(2\right)}\left(0\right){\displaystyle \frac{z^2}{2}}+W_{11}^{\left(2\right)}\left(0\right)z\overline{z}+W_{02}^{\left(2\right)}\left(0\right){\displaystyle \frac{{\overline{z}}^2}{2}}+\cdots ,\hfill \\ \hfill u_{2t}(-{\tau }_0^{+})& =\rho e^{-i{\omega }_{+}{\tau }_0^{+}}z+\overline{\rho }{e}^{i{\omega }_{+}{\tau }_0^{+}}\overline{z}+W_{20}^{\left(2\right)}(-{\tau }_0^{+}){\displaystyle \frac{z^2}{2}}+W_{11}^{\left(2\right)}(-{\tau }_0^{+})z\overline{z}+W_{02}^{\left(2\right)}(-{\tau }_0^{+}){\displaystyle \frac{{\overline{z}}^2}{2}}+\cdots .\hfill \end{array}$$

Combining (13) and (19) leads to

$$\begin{array}{cc}\hfill g(z,\overline{z})& ={\overline{q}}^{*}\left(0\right)f_0(z,\overline{z})\hfill \\ & =\overline{B}(1,\overline{\gamma })\left(\begin{array}{c}{\displaystyle \sum _{\begin{array}{c}i+j+l\ge 2\end{array}}\frac{f_{ijl}^{\left(1\right)}}{i!j!l!}{u}_{1t}^i\left(0\right)u_{2t}^j\left(0\right)u_{1t}^l(-{\tau }_0^{+})}\\ {\displaystyle \sum _{\begin{array}{c}i+j\ge 2\end{array}}\frac{f_{ij}^{\left(2\right)}}{i!j!}{u}_{1t}^i\left(0\right)u_{2t}^j\left(0\right)}\end{array}\right)\hfill \\ & =\overline{B}\{\left({\displaystyle \frac{1}{2}}{f}_{020}^{\left(1\right)}{\rho }^2+f_{110}^{\left(1\right)}\rho +f_{101}^{\left(1\right)}{e}^{-i{\omega }_{+}{\tau }_0^{+}}\right)z^2+\overline{\gamma }\left({\displaystyle \frac{1}{2}}{f}_{02}^{\left(2\right)}{\rho }^2+f_{11}^{\left(2\right)}\rho \right)z^2\hfill \\ & +\left(f_{020}^{\left(1\right)}\rho \overline{\rho }+f_{110}^{\left(1\right)}(\rho +\overline{\rho })+f_{101}^{\left(1\right)}(e^{i{\omega }_{+}{\tau }_0^{+}}+e^{-i{\omega }_{+}{\tau }_0^{+}})\right)z\overline{z}+\overline{\gamma }\left(f_{02}^{\left(2\right)}\rho \overline{\rho }+f_{11}^{\left(2\right)}(\rho +\overline{\rho })\right)z\overline{z}\hfill \\ & +\left({\displaystyle \frac{1}{2}}{f}_{020}^{\left(1\right)}{\overline{\rho }}^2+f_{110}^{\left(1\right)}\overline{\rho }+f_{101}^{\left(1\right)}{e}^{i{\omega }_{+}{\tau }_0^{+}}\right){\overline{z}}^2+\overline{\gamma }\left({\displaystyle \frac{1}{2}}{f}_{02}^{\left(2\right)}{\overline{\rho }}^2+f_{11}^{\left(2\right)}\overline{\rho }\right){\overline{z}}^2\hfill \\ & +\overline{\gamma }[f_{11}^{\left(2\right)}\left(W_{11}^{\left(2\right)}\left(0\right)+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(2\right)}\left(0\right)+\rho W_{11}^{\left(1\right)}\left(0\right)+{\displaystyle \frac{1}{2}}\overline{\rho }{W}_{20}^{\left(1\right)}\left(0\right)\right)\hfill \\ & +{\displaystyle \frac{1}{2}}{f}_{02}^{\left(2\right)}\left(\overline{\rho }{W}_{20}^{\left(2\right)}\left(0\right)+2\rho W_{11}^{\left(2\right)}\left(0\right)\right)+{\displaystyle \frac{1}{2}}{f}_{12}^{\left(2\right)}\left({\rho }^2+2\rho \overline{\rho }\right)]z^2\overline{z}\hfill \\ & +[f_{110}^{\left(1\right)}\left(W_{11}^{\left(2\right)}\left(0\right)+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(2\right)}\left(0\right)+\rho W_{11}^{\left(1\right)}\left(0\right)+{\displaystyle \frac{1}{2}}\overline{\rho }{W}_{20}^{\left(1\right)}\left(0\right)\right)\hfill \\ & +f_{101}^{\left(1\right)}\left(W_{11}^{\left(1\right)}(-{\tau }_0^{+})+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(1\right)}(-{\tau }_0^{+})+W_{11}^{\left(1\right)}\left(0\right)e^{-i{\omega }_{+}{\tau }_0^{+}}+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(1\right)}\left(0\right)e^{i{\omega }_{+}{\tau }_0^{+}}\right)\hfill \\ & +{\displaystyle \frac{1}{2}}{f}_{020}^{\left(1\right)}\left(\overline{\rho }{W}_{20}^{\left(2\right)}\left(0\right)+2\rho W_{11}^{\left(2\right)}\left(0\right)\right)+{\displaystyle \frac{1}{2}}{f}_{120}^{\left(1\right)}({\rho }^2+2\rho \overline{\rho })]z^2\overline{z}+\cdots \}.\hfill \end{array}$$

A comparison of the coefficients in $g(z,\overline{z})$ yields

$$\begin{array}{cc}\hfill g_{20}& =2\overline{B}\left[{\displaystyle \frac{1}{2}}{f}_{020}^{\left(1\right)}{\rho }^2+f_{110}^{\left(1\right)}\rho +f_{101}^{\left(1\right)}{e}^{-i{\omega }_{+}{\tau }_0^{+}}+\overline{\gamma }\left({\displaystyle \frac{1}{2}}{f}_{02}^{\left(2\right)}{\rho }^2+f_{11}^{\left(2\right)}\rho \right)\right],\hfill \\ \hfill g_{11}& =\overline{B}\left[f_{020}^{\left(1\right)}\rho \overline{\rho }+f_{110}^{\left(1\right)}(\rho +\overline{\rho })+f_{101}^{\left(1\right)}(e^{i{\omega }_{+}{\tau }_0^{+}}+e^{-i{\omega }_{+}{\tau }_0^{+}})+\overline{\gamma }\left(f_{02}^{\left(2\right)}\rho \overline{\rho }+f_{11}^{\left(2\right)}(\rho +\overline{\rho })\right)\right],\hfill \\ \hfill g_{02}& =2\overline{B}\left[{\displaystyle \frac{1}{2}}{f}_{020}^{\left(1\right)}{\overline{\rho }}^2+f_{110}^{\left(1\right)}\overline{\rho }+f_{101}^{\left(1\right)}{e}^{i{\omega }_{+}{\tau }_0^{+}}+\overline{\gamma }\left({\displaystyle \frac{1}{2}}{f}_{02}^{\left(2\right)}{\overline{\rho }}^2+f_{11}^{\left(2\right)}\overline{\rho }\right)\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill g_{21}& =2\overline{B}[f_{110}^{\left(1\right)}\left(W_{11}^{\left(2\right)}\left(0\right)+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(2\right)}\left(0\right)+\rho W_{11}^{\left(1\right)}\left(0\right)+{\displaystyle \frac{1}{2}}\overline{\rho }{W}_{20}^{\left(1\right)}\left(0\right)\right)\hfill \\ \hfill & +f_{101}^{\left(1\right)}\left(W_{11}^{\left(1\right)}(-{\tau }_0^{+})+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(1\right)}(-{\tau }_0^{+})+W_{11}^{\left(1\right)}\left(0\right)e^{-i{\omega }_{+}{\tau }_0^{+}}+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(1\right)}\left(0\right)e^{i{\omega }_{+}{\tau }_0^{+}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{f}_{020}^{\left(1\right)}\left(\overline{\rho }{W}_{20}^{\left(2\right)}\left(0\right)+2\rho W_{11}^{\left(2\right)}\left(0\right)\right)+{\displaystyle \frac{1}{2}}{f}_{120}^{\left(1\right)}\left({\rho }^2+2\rho \overline{\rho }\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\overline{\gamma }{f}_{02}^{\left(2\right)}\left(\overline{\rho }{W}_{20}^{\left(2\right)}\left(0\right)+2\rho W_{11}^{\left(2\right)}\left(0\right)\right)+{\displaystyle \frac{1}{2}}\overline{\gamma }{f}_{12}^{\left(2\right)}\left({\rho }^2+2\overline{\rho }\rho \right)\hfill \\ \hfill & +\overline{\gamma }{f}_{11}^{\left(2\right)}\left(W_{11}^{\left(2\right)}\left(0\right)+{\displaystyle \frac{1}{2}}{W}_{20}^{\left(2\right)}\left(0\right)+\rho W_{11}^{\left(1\right)}\left(0\right)+{\displaystyle \frac{1}{2}}\overline{\rho }{W}_{20}^{\left(1\right)}\left(0\right)\right)].\hfill \end{array}$$

Next, we calculate $W_{20}\left(\theta \right)$ and $W_{11}\left(\theta \right)$ in $g_{21}$. From (17) and (18), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{dW}{dt}}& ={\displaystyle \frac{d{u}_t}{dt}}-{\displaystyle \frac{dz}{dt}}q-{\displaystyle \frac{d\overline{z}}{dt}}\overline{q}\hfill \\ \hfill & =\left\{\begin{array}{cc}AW-2Re\left\{{\overline{q}}^{*}\left(0\right)f_{0}q\left(\theta \right)\right\},\hfill & \theta \in [-{\tau }_0^{+},0),\hfill \\ AW-2Re\left\{{\overline{q}}^{*}\left(0\right)f_{0}q\left(0\right)\right\}+f_0,\hfill & \theta =0\hfill \end{array}\right.\hfill \\ \hfill & :=AW+H(z,\overline{z},\theta ),\hfill \end{array}$$

(20)

where

$$H(z,\overline{z},\theta )=H_{20}\left(\theta \right){\displaystyle \frac{z^2}{2}}+H_{11}\left(\theta \right)z\overline{z}+H_{02}\left(\theta \right){\displaystyle \frac{{\overline{z}}^2}{2}}+\cdots .$$

(21)

On the center manifold $C_0$ near the origin, we have

$${\displaystyle \frac{dW}{dt}}=W_z{\displaystyle \frac{dz}{dt}}+W_{\overline{z}}{\displaystyle \frac{d\overline{z}}{dt}}.$$

(22)

According to (20)–(22), it can be obtained that

$$(A-2i{\omega }_{+})W_{20}\left(\theta \right)=-H_{20}\left(\theta \right),A{W}_{11}\left(\theta \right)=-H_{11}\left(\theta \right).$$

(23)

For $\theta \in [-{\tau }_0^{+},0)$, we deduce from (20) that

$$H(z,\overline{z},\theta )=-{\overline{q}}^{*}\left(0\right)f_{0}q\left(\theta \right)-q^{*}\left(0\right)\overline{f_0}\overline{q}\left(\theta \right)=-g(z,\overline{z})q\left(\theta \right)-\overline{g}(z,\overline{z})\overline{q}\left(\theta \right).$$

Comparing the coefficients in (21) implies that for $\theta \in [-{\tau }_0^{+},0)$,

$$H_{20}\left(\theta \right)=-g_{20}q\left(\theta \right)-{\overline{g}}_{02}\overline{q}\left(\theta \right),H_{11}\left(\theta \right)=-g_{11}q\left(\theta \right)-{\overline{g}}_{11}\overline{q}\left(\theta \right).$$

(24)

From (16), (23), and (24), we find that

$${\displaystyle \frac{d{W}_{20}\left(\theta \right)}{d\theta }}=2i{\omega }_{+}{W}_{20}\left(\theta \right)+g_{20}q\left(\theta \right)+{\overline{g}}_{02}\overline{q}\left(\theta \right),{\displaystyle \frac{d{W}_{11}\left(\theta \right)}{d\theta }}=g_{11}q\left(\theta \right)+{\overline{g}}_{11}\overline{q}\left(\theta \right).$$

Given that $q\left(\theta \right)=q\left(0\right)e^{i{\omega }_{+}\theta }$, it is evident that

$$W_{20}\left(\theta \right)={\displaystyle \frac{i{g}_{20}}{{\omega }_{+}}}q\left(0\right)e^{i{\omega }_{+}\theta }+{\displaystyle \frac{i{\overline{g}}_{02}}{3{\omega }_{+}}}\overline{q}\left(0\right)e^{-i{\omega }_{+}\theta }+E_1{e}^{2i{\omega }_{+}\theta },$$

(25)

and

$$W_{11}\left(\theta \right)=-{\displaystyle \frac{i{g}_{11}}{{\omega }_{+}}}q\left(0\right)e^{i{\omega }_{+}\theta }+{\displaystyle \frac{i{\overline{g}}_{11}}{{\omega }_{+}}}\overline{q}\left(0\right)e^{-i{\omega }_{+}\theta }+E_2,$$

(26)

where $E_1={(E_1^{\left(1\right)},E_1^{\left(2\right)})}^T\in R^2$ and $E_2={(E_2^{\left(1\right)},E_2^{\left(2\right)})}^T\in R^2$ are constant vectors. To proceed, it is necessary to identify suitable values for $E_1$ and $E_2$. Considering (16) evaluated at $\theta =0$ along with (23) yields

$${\int }_{-{\tau }_0^{+}}^{0}d\eta \left(\theta \right)W_{20}\left(\theta \right)=2i{\omega }_{+}{W}_{20}\left(0\right)-H_{20}\left(0\right),$$

(27)

and

$${\int }_{-{\tau }_0^{+}}^{0}d\eta \left(\theta \right)W_{11}\left(\theta \right)=-H_{11}\left(0\right).$$

(28)

Let

$$\begin{array}{cccc}\hfill d_1& =f_{020}^{\left(1\right)}{\rho }^2+2f_{110}^{\left(1\right)}\rho +2f_{101}^{\left(1\right)}{e}^{-i{\omega }_{+}{\tau }_0^{+}},\hfill & \hfill d_2& =f_{02}^{\left(2\right)}{\rho }^2+2f_{11}^{\left(2\right)}\rho ,\hfill \\ \hfill d_3& =f_{020}^{\left(1\right)}\rho \overline{\rho }+f_{110}^{\left(1\right)}(\rho +\overline{\rho })+f_{101}^{\left(1\right)}(e^{i{\omega }_{+}{\tau }_0^{+}}+e^{-i{\omega }_{+}{\tau }_0^{+}}),\hfill & \hfill d_4& =f_{02}^{\left(2\right)}\rho \overline{\rho }+f_{11}^{\left(2\right)}(\rho +\overline{\rho }).\hfill \end{array}$$

From (20), we get

$$H_{20}\left(0\right)=-g_{20}q\left(0\right)-{\overline{g}}_{02}\overline{q}\left(0\right)+\left(\begin{array}{c}{d}_1\\ d_2\end{array}\right),$$

(29)

and

$$H_{11}\left(0\right)=-g_{11}q\left(0\right)-{\overline{g}}_{11}\overline{q}\left(0\right)+\left(\begin{array}{c}{d}_3\\ d_4\end{array}\right).$$

(30)

Substituting (25) and (29) into (27), we have

$$\left(2i{\omega }_{+}I-{\int }_{-{\tau }_0^{+}}^0{e}^{2i{\omega }_{+}\theta }d\eta \left(\theta \right)\right)E_1=\left(\begin{array}{c}{d}_1\\ d_2\end{array}\right),$$

that is,

$$\left(\begin{array}{cc}2i{\omega }_{+}-a_{11}{e}^{-2i{\omega }_{+}{\tau }_0^{+}}& -a_{12}\\ -a_{21}& 2i{\omega }_{+}-a_{22}\end{array}\right)E_1=\left(\begin{array}{c}{d}_1\\ d_2\end{array}\right).$$

Solving the above equations leads to

$$E_1^{\left(1\right)}={\displaystyle \frac{1}{D_1}}\left|\begin{array}{cc}{d}_1& -a_{12}\\ d_2& 2i{\omega }_{+}-a_{22}\end{array}\right|,E_1^{\left(2\right)}={\displaystyle \frac{1}{D_1}}\left|\begin{array}{cc}2i{\omega }_{+}-a_{11}{e}^{-2i{\omega }_{+}{\tau }_0^{+}}& d_1\\ -a_{21}& d_2\end{array}\right|,$$

where

$$D_1=\left|\begin{array}{cc}2i{\omega }_{+}-a_{11}{e}^{-2i{\omega }_{+}{\tau }_0^{+}}& -a_{12}\\ -a_{21}& 2i{\omega }_{+}-a_{22}\end{array}\right|.$$

Similarly, substituting (26) and (30) into (28), we obtain

$$\left(\begin{array}{cc}-a_{11}& -a_{12}\\ -a_{21}& -a_{22}\end{array}\right)E_2=\left(\begin{array}{c}{d}_3\\ d_4\end{array}\right),$$

from which we can conclude that

$$E_2^{\left(1\right)}={\displaystyle \frac{1}{D_2}}\left|\begin{array}{cc}{d}_3& -a_{12}\\ d_4& -a_{22}\end{array}\right|,E_2^{\left(2\right)}={\displaystyle \frac{1}{D_2}}\left|\begin{array}{cc}-a_{11}& d_3\\ -a_{21}& d_4\end{array}\right|,$$

with

$$D_2=\left|\begin{array}{cc}-a_{11}& -a_{12}\\ -a_{21}& -a_{22}\end{array}\right|.$$

By substituting $E_1$ and $E_2$ into (25) and (26), we can determine $W_{20}\left(\theta \right)$ and $W_{11}\left(\theta \right)$, from which we subsequently obtain $g_{21}$. Given these results, the critical parameters associated with Hopf bifurcation are calculated as follows:

$$\begin{array}{cc}\hfill & c_1\left(0\right)={\displaystyle \frac{i}{2{\omega }_{+}}}\left[g_{11}{g}_{20}-2{\left|g_{11}\right|}^2-{\displaystyle \frac{1}{3}}{\left|g_{02}\right|}^2\right]+{\displaystyle \frac{1}{2}}{g}_{21},\hfill \\ \hfill & {\mu }_2=-{\displaystyle \frac{\mathrm{Re}\left(c_1\left(0\right)\right)}{\mathrm{Re}\left({\lambda }^{\prime }\left({\tau }_0^{+}\right)\right)}},\hfill \\ \hfill & {\beta }_2=2\mathrm{Re}\left(c_1\left(0\right)\right),\hfill \\ \hfill & T_2=-{\displaystyle \frac{\mathrm{Im}\left(c_1\left(0\right)\right)+{\mu }_2\mathrm{Im}\left({\lambda }^{\prime }\left({\tau }_0^{+}\right)\right)}{{\omega }_{+}}},\hfill \end{array}$$

(31)

which determine the properties of bifurcating periodic solutions at the critical value ${\tau }_0^{+}$. The parameter ${\mu }_2$ determines the direction of Hopf bifurcation; if ${\mu }_2>0$ (${\mu }_2<0$), then Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for $\tau >{\tau }_0^{+}$ ($\tau <{\tau }_0^{+}$). The parameter ${\beta }_2$ determines the stability of the bifurcating periodic solutions; bifurcating periodic solutions are stable (unstable) if ${\beta }_2<0$ (${\beta }_2>0$). In addition, the parameter $T_2$ determines the period of the bifurcating solutions; the period increases (decreases) if $T_2>0$ ($T_2<0$).

4. Numerical Simulation

In this section, a set of numerical simulations is carried out to validate the theoretical results established in Section 2 and Section 3, while also exhibiting the chaotic behavior existing in system (4). The parameter values used in this section are chosen purely to highlight the general dynamical behavior of the system, rather than to simulate any specific ecological scenario or particular predators and prey. In the following, we select two sets of parameters to represent the two cases: $\alpha =1.97,\beta =1.96,\sigma =7.28$ for the case ${\tau }_0^{-}<{\tau }_1^{+}$, and $\alpha =2,\beta =1.2,\sigma =1$ for the case ${\tau }_0^{-}>{\tau }_1^{+}$, to reinforce the consistency between analytical results and numerical observations.

We consider system (4) with the coefficients $\alpha =1.97,\beta =1.96,\sigma =7.28$. Then, system (4) has a unique equilibrium $E_{*}=(0.2453,1.5621)$. When $\tau =0$, the positive equilibrium $E_{*}$ is asymptotically stable. Through calculation, we obtain ${\tau }_0^{+}=0.2289<{\tau }_0^{-}=1.9141<{\tau }_1^{+}=1.9616<{\tau }_2^{+}=3.6943<{\tau }_1^{-}=3.9566$ from (10). 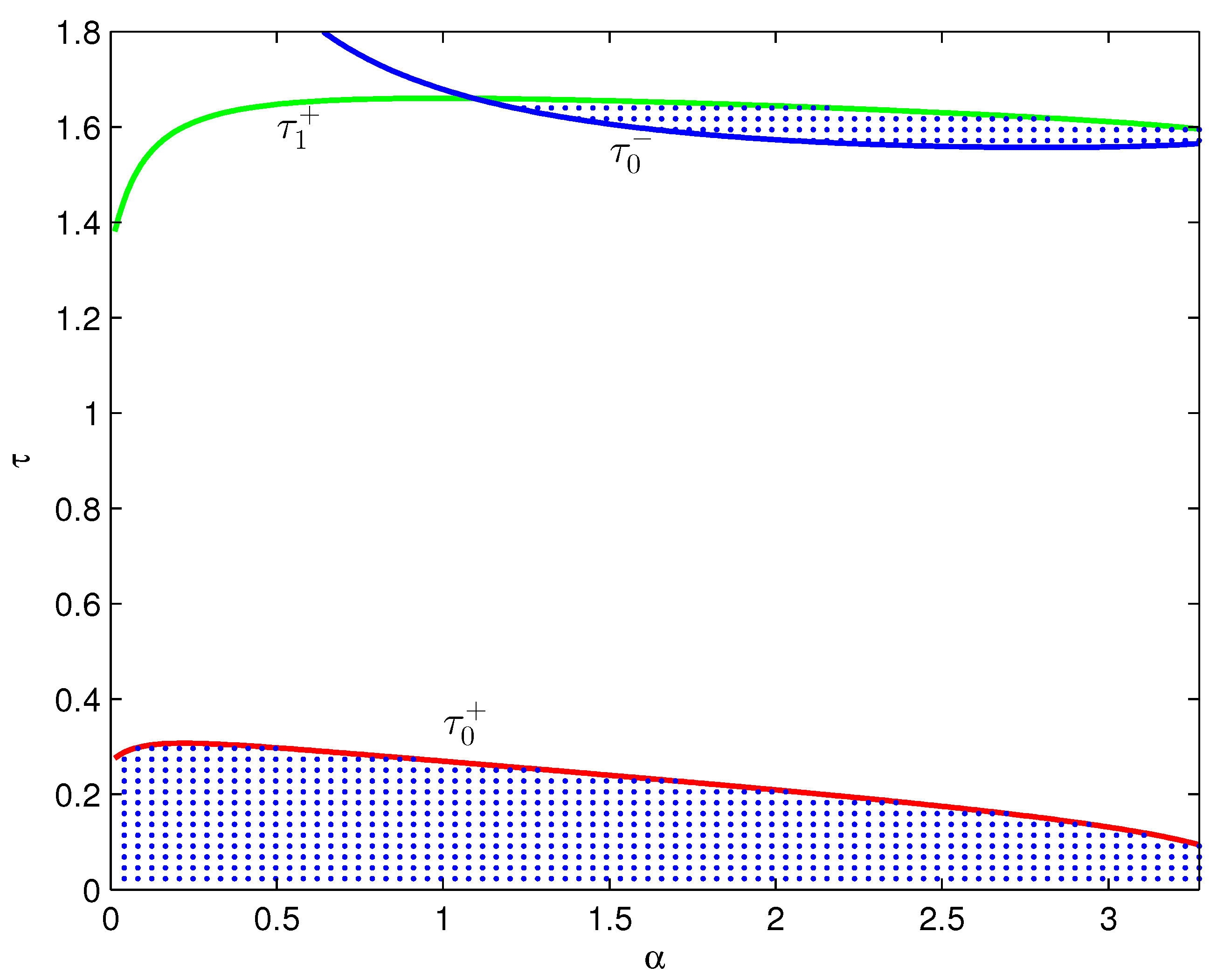$\tau$ and $\alpha$ are treated as bifurcation parameters, and the bifurcation diagram in the $\alpha -\tau$ plane, where ${\tau }_0^{+},{\tau }_0^{-}$, and ${\tau }_1^{+}$ are plotted to explore the stability regions, is presented in Figure 1. From Theorem 1 (ii), system (4) undergoes multiple stability switches: the equilibrium $E_{*}$ is asymptotically stable for $\tau \in [0,{\tau }_0^{+})\cup ({\tau }_0^{-},{\tau }_1^{+})$, but becomes unstable for $\tau \in ({\tau }_0^{+},{\tau }_0^{-})\cup ({\tau }_1^{+},\infty )$. Taking $\tau =0.1189\in (0,{\tau }_0^{+})$, $\tau =0.2389\in ({\tau }_0^{+},{\tau }_0^{-})$, and $\tau =1.948\in ({\tau }_0^{-},{\tau }_1^{+})$, respectively, we can observe two stability switches from stability to instability and then back to stability in Figure 2, Figure 3 and Figure 4. On the other hand, based on the calculations derived from (31), we obtain $c_1\left(0\right)=-4.727024-0.095516i$, ${\mu }_2=330.529142>0$, ${\beta }_2=-9.454048<0$, and $T_2=0.004984>0$. This suggests that the Hopf bifurcation of system (4) occurring at critical value ${\tau }_0^{+}$ is supercritical, and the periodic solutions bifurcating from the equilibrium point $(u_{*},v_{*})$ are stable when $\tau =0.24>{\tau }_0^{+}=0.2289$, as shown in Figure 5.

Now, to explore the chaotic behavior of system (4), we consider the parameters $\alpha =2,\beta =1.2,\sigma =1$. System (4) admits a unique equilibrium $E_{*}=(0.6254,0.2995)$. After calculation, we obtain ${\tau }_0^{-}=9.8082>{\tau }_1^{+}=7.1661$, and ${\tau }_0^{+}=1.1279$. Theorem 1 (i) shows that the positive equilibrium is stable when $\tau \in [0,{\tau }_0^{+})$, and unstable when $\tau >{\tau }_0^{+}$. The bifurcation diagram—illustrating the dynamics of the predator population v as a function of the delay parameter $\tau$—is depicted in Figure 6. As $\tau$ increases beyond critical thresholds ${\tau }_0^{+}=1.1279$, system (4) undergoes a sequence of period-doubling bifurcations: the stable equilibrium loses stability to a period-1 limit cycle, which subsequently bifurcates to period-2 and period-4 oscillations before transitioning to chaos. As shown in Figure 7, system (4) initially maintains a stable equilibrium for $\tau =1.1$, followed by a supercritical Hopf bifurcation at $\tau =1.1283$ that gives rise to a stable period-1 limit cycle. Further increases in $\tau$ lead to successive period-doubling bifurcations, with period-2 oscillations emerging at $\tau =1.47$ and period-4 oscillations at $\tau =1.62$. Finally, at $\tau =1.66$, the system transitions to a chaotic regime characterized by aperiodic dynamics and a sensitive dependence on initial conditions.

5. Conclusions

This paper systematically investigates the impact of maturation delay on the dynamics of predator–prey models incorporating hunting cooperation, with a focus on the intricate interplay between delay effects and the system’s dynamical characteristics. Through theoretical analysis and numerical simulations, it is revealed that the introduction of maturation delay induces stability switches between stable and unstable states of the positive equilibrium, as well as the emergence of chaotic behavior. These findings indicate that maturation delay modulates the system’s dynamical behavior in a nontrivial manner.

We first restrict the parameters to ensure that the system has one positive equilibrium and is stable in the absence of delay, and then study the influence of delay on the stability of this positive equilibrium. By analyzing the characteristic equation associated with the positive equilibrium, we derive the existence of Hopf bifurcation and stability-switching phenomena. System (4) displays distinct stability-switching patterns depending on parameter configurations: a single stability switch emerges when ${\tau }_0^{-}>{\tau }_1^{+}$, whereas multiple stability switches arise in scenarios where ${\tau }_0^{-}<{\tau }_1^{+}$. Then, using normal form theory and center manifold reduction, we obtain explicit formulas to determine the stability, direction, and period of bifurcating periodic solutions. Additionally, when ${\tau }_0^{-}>{\tau }_1^{+}$, the system exhibits various complex dynamical behaviors, including periodic solutions, period-doubling oscillations and chaos. Numerical simulations support these theoretical results, clearly showing that maturation delay can induce chaotic dynamics. This study advances our understanding of the complex dynamical properties of predator–prey systems with maturation delay, shedding light on the pivotal role of delay in shaping ecological interaction patterns and providing a theoretical basis for further explorations into the control and regulation of such systems in practical ecological contexts.