Numerical Analysis of Fatigue Crack Propagation of Deck-Rib Welded Joint in Orthotropic Steel Decks
Abstract
1. Introduction
2. Methods
2.1. Calculation of Stress Intensity Factor
2.2. Single Crack Propagation Model
2.3. Multi-Crack Interaction Method
2.4. Analysis Parameters
3. Results and Discussions
3.1. Single Crack Propagation
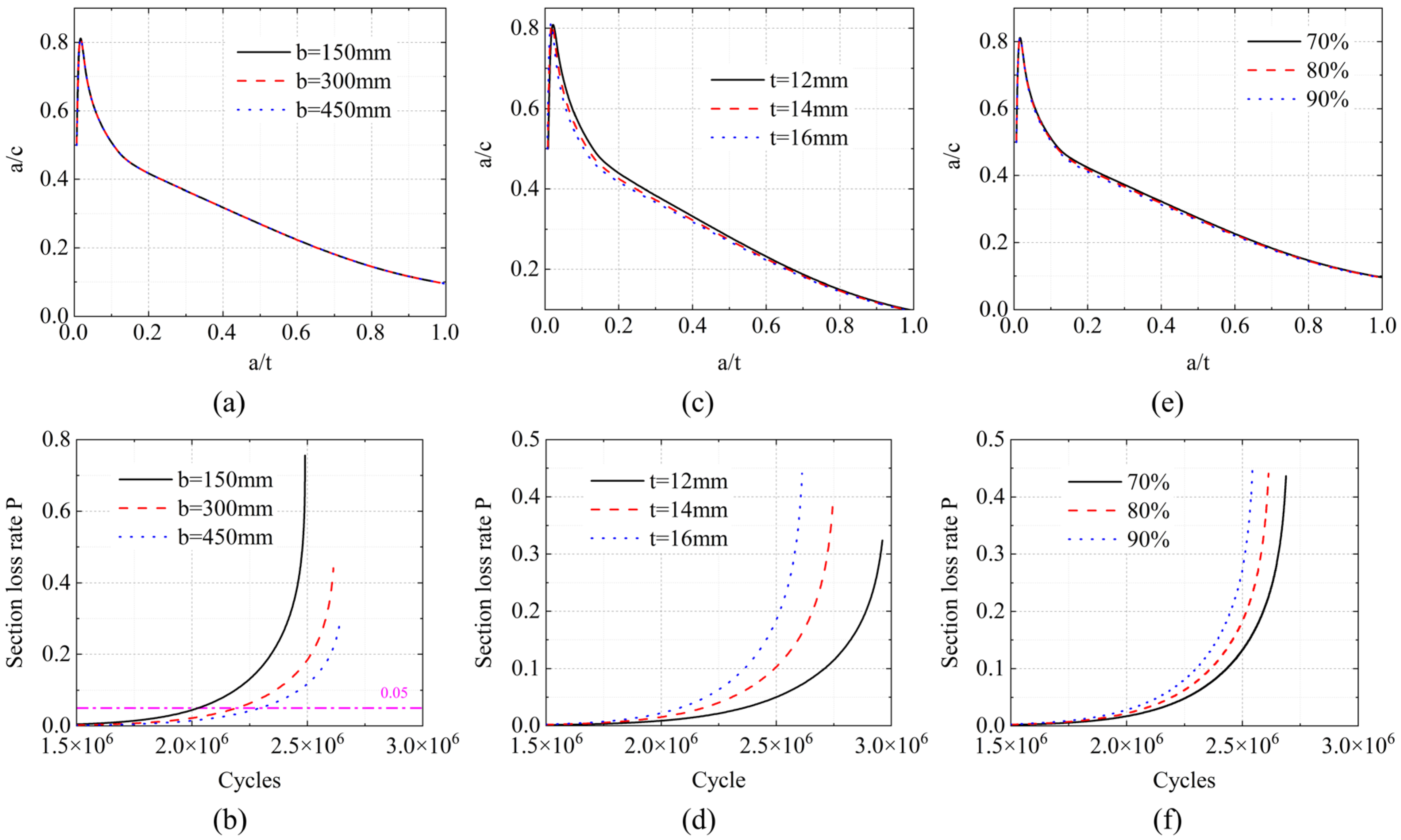
3.1.1. Effect of Geometric Dimension
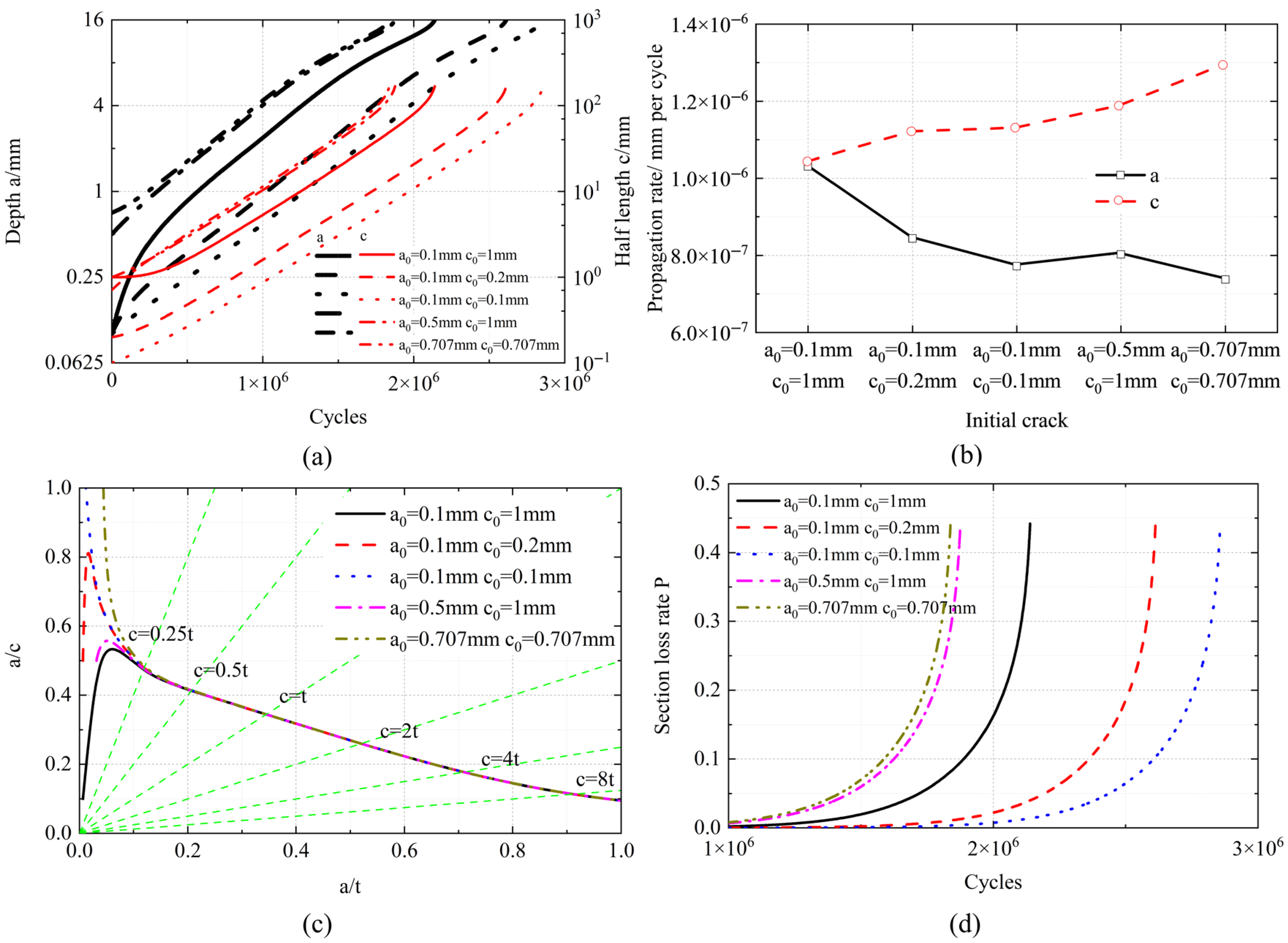
3.1.2. Effect of Initial Defect
3.2. Multi-Crack Propagation
3.2.1. Quantity of Cracks
3.2.2. Length of Cracks
3.2.3. Geometry of Cracks
4. Conclusions
- Deck widths below 300 mm produce non-representative crack growth patterns unsuitable for experimental validation. Wider decks accelerate propagation only after crack depth exceeds 50% of deck thickness. Increased deck thickness induces linearly faster propagation rates yet maintains larger residual load-bearing sections despite higher absolute section loss. Weld penetration depth linearly elevates propagation rates;
- Initial aspect ratios converge rapidly to a stable propagation trajectory, attaining early in propagation and stabilizing at at failure. Larger and shallower initial defects reduce fatigue life by ≤15% but negligibly impact final section loss;
- Defect density governs merging behavior: doubling n increases final crack count by 45%. Higher stress range and deck thickness accelerate merging rates by ≤18%, while MPa suppresses crack development. Maximum cracks strictly adhere to the single-crack propagation path. Total section loss escalates with defect density and deck thickness but remains stress range independent;
- The preferred propagation path enables crack depth estimation from crack surface length measurements during inspections. Minimizing initial defects through stringent weld quality control is paramount to delay multi-crack coalescence and to extend fatigue life.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cui, C.; Xu, Y.L.; Zhang, Q.H. Multiscale fatigue damage evolution in orthotropic steel deck of cable-stayed bridges. Eng. Struct. 2021, 237, 112144. [Google Scholar] [CrossRef]
- Deng, L.; Zou, S.; Wang, W.; Kong, X. Fatigue performance evaluation for composite OSD using UHPC under dynamic vehicle loading. Eng. Struct. 2021, 232, 111831. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Bu, Y.Z.; Li, Q. Review on fatigue problems of orthotropic steel bridge deck. China J. Highw. Transp. 2017, 30, 14–30. [Google Scholar]
- Maljaars, J.; Bonet, E.; Pijpers, R.J.M. Fatigue resistance of the deck plate in steel orthotropic deck structures. Eng. Fract. Mech. 2018, 201, 214–228. [Google Scholar] [CrossRef]
- Di, J.; Ruan, X.; Zhou, X.; Wang, J.; Peng, X. Fatigue assessment of orthotropic steel bridge decks based on strain monitoring data. Eng. Struct. 2021, 228, 111437. [Google Scholar] [CrossRef]
- Li, X.; Fu, Z.; Ji, B.; Ji, B.; Sun, G. Fatigue failure and fracture morphology of deck-rib welded joint integrating mean stress effect. J. Constr. Steel Res. 2025, 226, 109246. [Google Scholar] [CrossRef]
- Wang, D.; Xiang, C.; Ma, Y.; Chen, A.; Wang, B. Experimental study on the root-deck fatigue crack on orthotropic steel decks. Mater. Des. 2021, 203, 109601. [Google Scholar] [CrossRef]
- Zhu, A.; Ouyang, S.; Chen, Y.; Sun, Y. Fatigue test and life evaluation of rib-to-deck connections in orthotropic steel bridge decks. J. Constr. Steel Res. 2022, 197, 107442. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Zheng, Y. Analysis of fatigue crack propagation of an orthotropic bridge deck based on the extended finite element method. Adv. Civ. Eng. 2019, 2019, 6319821. [Google Scholar] [CrossRef]
- Jiang, X.; Sun, K.; Qiang, X.; Li, D.; Zhang, Q. Xfem-based fatigue crack propagation analysis on key welded connections of orthotropic steel bridge deck. Int. J. Steel Struct. 2023, 23, 404–416. [Google Scholar] [CrossRef]
- Wang, Q.; Ji, B.; Li, C.; Fu, Z. Fatigue evaluation of deck-rib welds: Crack-propagation-life predictive model and parametric analysis. J. Constr. Steel Res. 2020, 173, 106248. [Google Scholar] [CrossRef]
- Tang, K.; Cui, C.; Liu, J.W.; Ma, Y.; Zhang, Q.H.; Lao, W.L. Multiscale and multifield coupled fatigue crack initiation and propagation of orthotropic steel decks. Thin-Walled Struct. 2024, 199, 111843. [Google Scholar] [CrossRef]
- Xiao, Z.G.; Yamada, K.; Inoue, J.; Yamaguchi, K. Fatigue cracks in longitudinal ribs of steel orthotropic deck. Int. J. Fatigue 2006, 28, 409–416. [Google Scholar] [CrossRef]
- Pang, B.Z.; Cui, C.; Zheng, Q.S.; Liu, K.W.; Zhang, Q.H. Multi-crack propagation analysis of double-side welded rib-to-deck joint in orthotropic steel decks. J. Constr. Steel Res. 2024, 218, 108731. [Google Scholar] [CrossRef]
- Lu, N.; Wang, H.; Luo, Y.; Liu, X.; Liu, Y. Merging behaviour and fatigue life evaluation of multi-cracks in welds of OSDs. J. Constr. Steel Res. 2025, 225, 109189. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Ma, S.; Tu, J. Study on in-plane double-crack propagation in the rib-to-deck welded toe of steel-bridge. J. Constr. Steel Res. 2023, 203, 107838. [Google Scholar] [CrossRef]
- Jiang, X.; Cao, D.; Qiang, X.; Xu, C. Study on fatigue performance of steel bridge welded joints considering initial defects. J. Constr. Steel Res. 2024, 212, 108309. [Google Scholar] [CrossRef]
- Yamada, K.; Ya, S. Plate bending fatigue tests for root crack of trough rib of orthotropic steel deck. J. Struct. Eng. 2008, 54, 675–684. [Google Scholar]
- Cheng, B.; Ye, X.; Cao, X.; Mbako, D.D.; Cao, Y. Experimental study on fatigue failure of rib-to-deck welded connections in orthotropic steel bridge decks. Int. J. Fatigue 2017, 103, 157–167. [Google Scholar] [CrossRef]
- Fu, Z.; Ji, B.; Zhang, C.; Wang, Q. Fatigue performance of roof and U-rib weld of orthotropic steel bridge deck with different penetration rates. J. Bridge Eng. 2017, 22, 04017016. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Li, Y.S.; Zhang, D.Y. Fatigue life estimation of rib-to-deck joints in orthotropic steel decks. Adv. Mater. Res. 2010, 163, 410–416. [Google Scholar] [CrossRef]
- Hobbacher, A.F.; Baumgartner, J. Recommendations for Fatigue Design of Welded Joints and Components; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Igwemezie, V.; Mehmanparast, A.; Brennan, F. The influence of microstructure on the fatigue crack growth rate in marine steels in the Paris Region. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 2416–2440. [Google Scholar] [CrossRef]
- BS 7910:2019; Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures. British Standards Institution: London, UK, 2019.
- Zhang, H.; Liu, H.; Kuai, H. Stress intensity factor analysis for multiple cracks in orthotropic steel decks rib-to-floorbeam weld details under vehicles loading. Eng. Fail. Anal. 2024, 164, 108705. [Google Scholar] [CrossRef]
- Li, X.; Fu, Z.; Ji, B.; Sun, G. Crack Growth and Fatigue Strength of Deck-Rib Welded Joints in Orthotropic Steel Decks Integrating Mean Stress Effect. Fatigue Fract. Eng. Mater. Struct. 2025, 48, 145–157. [Google Scholar] [CrossRef]







| Geometric dimensions | 150 | 300 | 450 | |||||
| 12 | 14 | 16 | ||||||
| 70% | 80% | 90% | ||||||
| Initial defect | 0.1 | 0.1 | 0.1 | 0.5 | 0.707 | |||
| 0.1 | 0.5 | 1 | 0.5 | 1 | ||||
| 1 | 0.2 | 0.1 | 1 | 0.707 | ||||
| Parameter | Probability Distribution | Maximum Value | Minimum Value | |||
|---|---|---|---|---|---|---|
| Single sampling | Uniform distribution | 500 | - | 1000 | 0 | |
| Exponential distribution | 0.1 | - | 1 | 0.01 | ||
| Normal distribution | 0.5 | 0.16 | 1 | 0.1 | ||
| Multiple sampling | Poisson distribution | 16 24 32 | - | - | - | |
| Fixed value | 12 14 16 | - | - | - | ||
| Fixed value | 80 100 125 | - | - | - | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Fu, Z.; Guo, H.; Ji, B.; Zhang, C. Numerical Analysis of Fatigue Crack Propagation of Deck-Rib Welded Joint in Orthotropic Steel Decks. Modelling 2025, 6, 83. https://doi.org/10.3390/modelling6030083
Li X, Fu Z, Guo H, Ji B, Zhang C. Numerical Analysis of Fatigue Crack Propagation of Deck-Rib Welded Joint in Orthotropic Steel Decks. Modelling. 2025; 6(3):83. https://doi.org/10.3390/modelling6030083
Chicago/Turabian StyleLi, Xincheng, Zhongqiu Fu, Hongbin Guo, Bohai Ji, and Chengyi Zhang. 2025. "Numerical Analysis of Fatigue Crack Propagation of Deck-Rib Welded Joint in Orthotropic Steel Decks" Modelling 6, no. 3: 83. https://doi.org/10.3390/modelling6030083
APA StyleLi, X., Fu, Z., Guo, H., Ji, B., & Zhang, C. (2025). Numerical Analysis of Fatigue Crack Propagation of Deck-Rib Welded Joint in Orthotropic Steel Decks. Modelling, 6(3), 83. https://doi.org/10.3390/modelling6030083






